2 - Ortiz Calero

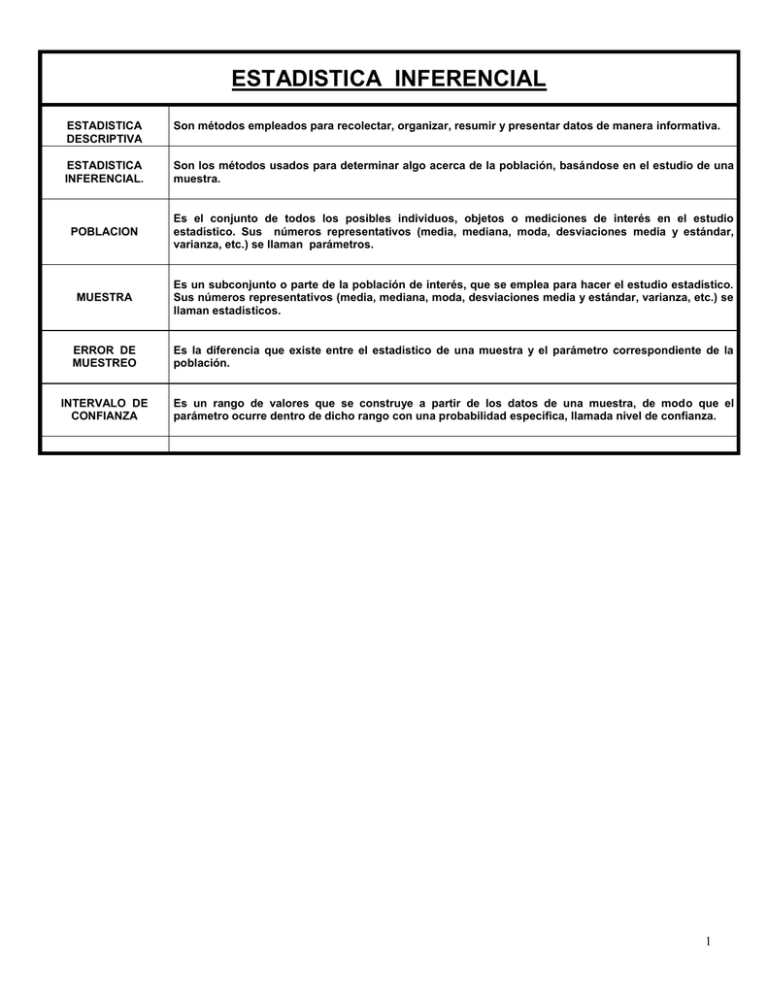
ESTADISTICA INFERENCIAL
ESTADISTICA
DESCRIPTIVA
Son métodos empleados para recolectar, organizar, resumir y presentar datos de manera informativa.
ESTADISTICA
INFERENCIAL.
Son los métodos usados para determinar algo acerca de la población, basándose en el estudio de una
muestra.
POBLACION
Es el conjunto de todos los posibles individuos, objetos o mediciones de interés en el estudio
estadístico. Sus números representativos (media, mediana, moda, desviaciones media y estándar,
varianza, etc.) se llaman parámetros.
MUESTRA
Es un subconjunto o parte de la población de interés, que se emplea para hacer el estudio estadístico.
Sus números representativos (media, mediana, moda, desviaciones media y estándar, varianza, etc.) se
llaman estadísticos.
ERROR DE
MUESTREO
Es la diferencia que existe entre el estadístico de una muestra y el parámetro correspondiente de la
población.
INTERVALO DE
CONFIANZA
Es un rango de valores que se construye a partir de los datos de una muestra, de modo que el
parámetro ocurre dentro de dicho rango con una probabilidad específica, llamada nivel de confianza.
1
INTERVALOS CONFIANZA MEDIA (MUESTRAS GRANDES)
x E
DONDE:
E  Z
2

n
1
El gerente de una tienda de autoservicio de la zona suburbana desea determinar el importe del consumo promedio de
sus clientes. Con tal objeto tomó una muestra aleatoria de 60 clientes, obteniendo en ella un promedio de $ 128.00
con una desviación estándar de $ 97.50. Halla un intervalo de confianza 0.97 para estimar el consumo promedio de los
clientes de esa tienda.
2
Una muestra aleatoria de 75 alumnos de cierta universidad dio una calificación promedio de 7.3 con una desviación
estándar de 3.45. Halla un intervalo de confianza 0.93 para estimar la calificación promedio de los alumnos de esa
universidad.
3
Una tienda de departamentos tiene 5,000 clientes con cuenta corriente. Para estimar el total adeudado por estos
clientes, se tomó una muestra aleatoria de 80 cuentas la cual dio una media de $ 1,300.00 con una desviación estándar
de $750.00. Halla un intervalo de confianza 0.94 para estimar la cantidad total adeudada por todos los clientes de esa
tienda.
4
Una encuesta que se condujo en una ciudad grande en 1986 revelo que 200 familias gastaban en promedio $218.67 por
semana en alimentos con una desviación estándar de $14.93. Ya que se desea ajustar el gasto semanal en alimentos
promedio verdadero en esa ciudad a un intervalo bastante estrecho, elabore un intervalo de confianza de 90%.
5
Una distribuidora de maquinas vendedoras de refrescos planifica usar el numero medio de refrescos vendidos durante
una semana por 60 de sus maquinas para estimar el numero promedio vendido por cualquiera de las maquinas durante
una semana. Si 60 maquinas seleccionadas al azar tuvieron una media de 255.3 refrescos con una desviación estándar
de 48.2 refrescos, construya un intervalo de confianza del 95% para el numero promedio verdadero vendido por
cualquiera de sus maquinas durante una semana.
6
Para estimar el tiempo de servicio promedio en un restaurante de hamburguesas, un consultor de la gerencia anoto los
tiempos que requirieron 35 personas que forman una muestra aleatoria para tomar una orden estándar (consistente en
dos hamburguesas, dos paquetes de papas fritas y dos bebidas). En promedio estas personas requirieron 72.2
segundos con una desviación estándar de 12.8 segundos para tomar sus ordenes. Estructure un intervalo de confianza
del 96.4% para el tiempo promedio real que una persona necesita para tomar la orden estándar.
7
Un estudio del crecimiento anual de ciertos cactus reveló que 64 de estos, seleccionados al azar en una zona
desértica, crecieron en promedio 52.8 mm. con una desviación estándar de 4.5 mm. Elabore un intervalo de confianza
del 98.6% para el crecimiento anual promedio verdadero de dicha clase de cactus.
8
125 empleados de una fabrica seleccionados al azar promedian una edad de 38 años, con una desviación estándar de 4
años. Elabore un intervalo de confianza del 97% para el promedio de edad de todos los trabajadores de esa fabrica.
9
Una tienda vende a crédito escáner de una determinada característica a un precio de $1,300.00 cada unidad.
Para estimar el total adeudado por sus 425 acreditados, se selecciona aleatoriamente una muestra de 70 de ellos, y al
hacer el análisis estadístico se obtiene un adeudo medio de $644.00 con una desviación estándar de $289.00
Determine un intervalo del 91.5% de confianza para el importe total adeudado por todos sus acreditados.
10
Escriba y describa un intervalo de confianza del 93% para el promedio de duración de una canción. Se sabe de una
muestra de 70 canciones, que en promedio duran 3.5 minutos con una desviación estándar de 0.3 minutos.
2
INTERVALOS CONFIANZA MEDIA (MUESTRAS PEQUEÑAS)
x E
DONDE:
E  t
2
s
n
1
El gerente de una tienda de autoservicio de la zona suburbana desea determinar el importe del consumo promedio de
sus clientes. Con tal objeto tomó una muestra aleatoria de 25 clientes, obteniendo un promedio de ella de $ 128.00
con una desviación estándar de $ 97.50. Halla un intervalo de confianza 0.98 para estimar el consumo promedio de los
clientes de esa tienda.
2
Una muestra aleatoria de 28 alumnos de cierta universidad dio una calificación promedio de 7.3 con una desviación
estándar de 3.45. Halla un intervalo de confianza 0.99 para estimar la calificación promedio de los alumnos.
3
Para probar la durabilidad de una pintura nueva para las líneas divisorias, un departamento de carreteras pinto franjas
de prueba en carreteras muy transitadas en ocho sitios distintos y los contadores electrónicos demostraron que se
deterioraron después de que 142600, 167800, 136500, 108300, 126400, 133700, 162000 y 149400 automóviles cruzaron
por estas. Elabore un intervalo de confianza del 95% para la cantidad promedio de transito que esta pintura puede
soportar antes de deteriorarse.
4
El propietario de una estación de servicio para camiones ha llevado registros completos de varias transacciones con
sus clientes. Si una muestra aleatoria de 18 de estos registros revela ventas promedio de 58.22 galones de diesel con
una desviación estándar de 4.80 galones, elabore un intervalo de confianza del:
a) 95%.
b) 99%.
5
En 6 ocasiones, en una muestra que se presume aleatoria, fueron necesarios 21, 26, 24, 22, 23 y 22 minutos para
limpiar la cafetería de una escuela. Elabore un intervalo de confianza del 95% para el tiempo promedio necesario.
6
En una revisión de rutina, un dentista encuentra que seis internos de una prisión, en una muestra aleatoria requieren
de 2, 3, 6, 0, 4 y 3 curaciones. Elabore un intervalo de confianza del 99% para el numero promedio de curaciones que
requieren los internos de esa prisión.
7
Registro del numero de paginas de un grupo de libros de Estadística que se recomiendan en la bibliografía de un
curso:
416
1182
584
575
821
406
556
707
624
467
762
1140
Elabore un intervalo de confianza del 95% para el numero promedio de paginas que tiene un libro de Estadística.
Antigüedad en años de un grupo de profesores de una Universidad:
8
4
17
17
3
12
20
14
17
16
13
16
17
11
13
11
22
Elabore un intervalo de confianza del 99% para el numero promedio de años de antigüedad de todos los profesores de
esa Universidad.
9
El diámetro medio de una muestra de 12 varillas incluidas en un embarque, es de 2.35 mm., con una desviación
estándar de 0.050 mm. Se supone que la distribución de los diámetros de la totalidad de las varillas incluidas en el
embarque es aproximadamente normal. Determine un intervalo de confianza del 99% para la estimación del diámetro
medio de todas las varillas incluidas en el embarque.
3
10
Una muestra aleatoria de 26 barriles de una sustancia química (tomada al azar de entre 200 barriles) tiene un peso
medio de 240.8 libras con una desviación estándar de 10.2 libras. Elabore un intervalo de confianza del 85% para
estimar el peso promedio de los 200 barriles. Se permite un error máximo de 30 libras.
11
Una tienda vende a crédito scanner al precio de $1,300.00 cada unidad.
Para estimar el total adeudado por sus 425 acreditados, se selecciona aleatoriamente una muestra de 20 de ellos, y al
hacer el análisis estadístico se obtiene un adeudo medio de $ 644. 00 con una desviación estándar de $ 289. 00
Determine un intervalo del 90% de confianza para el importe total adeudado por todos sus acreditados.
INTERVALOS DE CONFIANZA PARA PROPORCIONES
pE
DONDE:
E  Z
2
pq
n
1
Anilú, gerente general de Alfa, S.A. fabricante de blusas para mujer, desea estimar la proporción de tiendas de ropa
para mujer de la zona metropolitana que venden su marca. Con tal objeto tomó una muestra aleatoria de 42 tiendas y
encontró que en 30 de ellas se vendían las blusas de Alfa, S.A. Halla un intervalo de confianza 0.96 para estimar la
proporción de tiendas de la zona metropolitana que venden las blusas de Alfa, S.A.
2
El rector de cierta universidad desea conocer el porcentaje de alumnos que están de acuerdo con el actual sistema de
becas. Con tal objeto entrevisto aleatoriamente a 184 alumnos, de los cuales 125 aceptaron el actual sistema de becas.
Halla un intervalo de confianza 0.98 para estimar el porcentaje de alumnos de esa universidad que esta de acuerdo con
el actual sistema de becas.
3
En una muestra aleatoria, 136 de 400 personas a quienes se les administró una vacuna contra la gripe experimentaron
alguna molestia. Elabore un intervalo de confianza del 95% para la proporción real de personas que experimentarán
esta molestia como resultado de la vacuna.
4
En una muestra aleatoria de 439 personas entrevistadas en una gran ciudad, 299 decían que se oponían a la
construcción de más vías rápidas. Elabore, para la proporción de las personas de la población que se oponen a dicha
construcción:
a) un intervalo de confianza del 97%.
b) un intervalo de confianza del 93%.
5
Entre 180 pescados de un lago grande, 24 no eran comestibles como resultado de la contaminación. Elabore un
intervalo de confianza del 99% para la proporción real correspondiente.
El siguiente registro muestra el tiempo en días que tarda un medicamento en quitar la gripe a un grupo de personas
seleccionadas al azar que integran una muestra:
6
6
3
3
3
6
2
6
2
9
1
2
8
5
5
8
4
1
9
9
4
4
8
3
1
5
4
5
8
9
1
Elabore un intervalo de confianza del:
1. 96.5% para la proporción real de personas a las que quita la gripe en menos de 4 días.
2. 98.3% para la proporción real de personas a las que les quita la gripe en un máximo de 4 días.
3. 94.1% para la proporción real de personas a las que quita la gripe en 4 días.
4. 90.6% para la proporción real de personas a las que quita la gripe en mas de 4 días.
5. 92.7% para la proporción real de personas a las que quita la gripe en un mínimo de 4 días.
4
7
En una muestra aleatoria de 140 supuestos contactos con OVNIS, 119 se podrían explicar fácilmente como fenómenos
naturales. Elabore un intervalo de confianza del 97.5% para la probabilidad de que un supuesto contacto con un OVNI
no se pueda explicar fácilmente como un fenómeno natural.
8
El departamento de MKT de una refresquera desea estimar la proporción de establecimientos de una ciudad que vende
su producto. Tomo una muestra aleatoria de 58 tiendas y encontró que en 35 de ellas si se vende su refresco. Halle un
intervalo de confianza del 97% para estimar la proporción de tiendas que venden su producto.
TAMAÑO MUESTRA PARA MEDIA DE UNA POBLACION
Z
n   2 
E


1
2
El gerente de un restaurante desea determinar el importe del consumo promedio de sus clientes. De registros
anteriores obtuvo que el consumo promedio era de $ 258.00 con una desviación estándar de $ 125.00. ¿De que tamaño
deber tomar la muestra para tener una confianza de 0.96 de que el error en la estimación no excederá de $ 40.00?
2
El gerente de una empresa desea determinar el tiempo promedio que necesitan los trabajadores en hacer cierta
actividad especializada. De registros anteriores sabe que el tiempo promedio era de 28 minutos con una desviación
estándar de 20 minutos. ¿De qué tamaño se debe tomar una muestra para tener una confianza de 0.97 de que el error
máximo en la estimación no excederá de 6 minutos?
3
Se desea estimar el numero medio de horas de uso continuo hasta que cierta clase de computadora necesite
reparaciones por vez primera. Si se puede suponer que la desviación estándar es de 48 horas, ¿Qué tan grande debe
ser la muestra a estudiar, de modo que se pueda afirmar con una probabilidad de 0.99 que el error de la media de la
muestra será como máximo de 10 horas?.
4
Antes de comprar un embarque grande de carne molida, un fabricante de salchichas quiere tener una confianza del
95% de que su error no sea mayor de 2.5 gramos al estimar el contenido de grasa (por cada 100 gramos de carne). Si se
supone que la desviación estándar del contenido de grasa (por 100 gramos) de carne es de 8 gramos, ¿Qué tan grande
debe de ser la muestra en que base su estimación?
5
Suponga que queremos estimar la calificación media de ciudadanos de edad avanzada en una prueba acerca del
conocimiento sobre sucesos actuales, y que deseamos poder afirmar con una probabilidad de 0.98 que el error de
nuestra estimación de la media de una muestra aleatoria, será a lo sumo de 2.5; ¿Qué tan grande debe ser la muestra,
si sabemos que la desviación estándar de la población es de 73?.
6
Antes de concursar por un contrato, un contratista quiere tener una confianza del 95% de que su error es como máximo
de 5 minutos al usar la media de una muestra aleatoria para estimar el tiempo promedio que cierta clase de ladrillo de
adobe necesita para endurecer. ¿Cuan grande será la muestra que necesita, si puede suponer que la desviación
estándar es de 24 minutos para la población de dichos ladrillos?.
7
Una empresa necesita saber edad promedio de los consumidores de su producto, y desea afirmar con una probabilidad
del 97% que el error de su estimación será a lo sumo de 3 años. ¿Qué tan grande debe ser la muestra a estudiar, si de
estudios similares de otras empresas de la competencia sabe que la desviación estándar de la población es de 9
años?
5
8
Un analista desea estimar el salario medio por hora de los trabajadores de una determinada fabrica de componentes
de PC’s, con un margen de error no mayor a $0.25 y confianza del 90%. La desviación estándar de los índices
salariales es estimada en $1.07. ¿Cuál es el número de expedientes de personal que deberán muestrearse como
mínimo para satisfacer este objetivo de investigación?
9
Se planea una investigación para determinar la cantidad media de tiempo que los ejecutivos de una corporación ven
televisión. Una encuesta piloto indico que el tiempo medio por semana es de 13.5 horas, con una desviación estándar
de 3.4 horas. Se desea estimar el tiempo medio con un error máximo de 15 minutos.
Si se emplea un nivel de significación de 0.942, ¿A cuantos ejecutivos se debe investigar?
10
¿De que tamaño debe ser la muestra a estudiar para determinar el peso promedio de los estudiantes de una
universidad, si se desea tener una confianza del 96.3% en que el error máximo sea del 2.4 Kg., si de estudios
anteriores se sabe que la desviación estándar es de 7.7 Kg?
11
Se seleccionan aleatoriamente 18 empleados de una fábrica de insumos para el ensamble de computadoras que tiene
un gran número de trabajadores. Un análisis estadístico revela que la edad promedio es de 26 años con una
desviación estándar de 2 años. En base a dicha información:
a) Construya un intervalo de confianza del 99% para la edad media de los trabajadores
b) ¿De que tamaño deberá ser la muestra a analizar estadísticamente si se requiere un nivel de confianza del
95%, en que diferencia máxima entre los promedios de la muestra y población sea de 2.5 años?.
1.
12
2.
¿De que tamaño debe ser la muestra a estudiar de los 5000 empleados de una gran fabrica para calcular el
sueldo promedio mensual, si se desea una confiabilidad del 91% en que la media de dicha muestra y la de la
población no diferirán en más de $200?. Estudios anteriores indican que la desviación estándar es de $1,600.
Si la muestra del inciso anterior da un sueldo promedio mensual de $8640 con una desviación estándar de
$1,425, escriba un intervalo de confianza del 96.3% para la media de esa población.
TAMAÑO MUESTRA PARA PROPORCION DE POBLACION
Z
n  pq  2
E

1
2
3




2
Anilú, gerente general de Alfa, S.A. fabricante de blusas para mujer, desea estimar la proporción de tiendas de ropa
para mujer de la zona metropolitana que venden su marca. ¿De cuántas tiendas debe Anilú recabar información para
tener una seguridad del 96% de que el error en la estimación no sobrepasará del 16%?
El rector de cierta universidad desea conocer el porcentaje de alumnos que están de acuerdo con el actual sistema de
becas. ¿A cuántos alumnos debe entrevistarse para tener una confianza del 97% de que el error en la estimación no
excederá del 8%, si:
a) en una encuesta anterior el 65% de los alumnos estaban de acuerdo con el actual sistema de becas?
b) no hay ninguna información anterior?.
Suponga que un departamento de carreteras estatales quiere estimar la proporción de todos los camiones que
operan entre dos ciudades transportando carga muy pesada y desea poder afirmar con una probabilidad de por lo
menos 0.95 que su error no será mayor que 0.04. ¿Qué tan grande necesitará ser la muestra sí:
1) Sabe que la proporción real cae en algún valor del intervalo de 0.10 a 0.25?
2) No tiene idea sobre cual puede ser el valor real?.
6
4
5
6
7
8
9
10
11
Una política lleva a cabo una encuesta de la opinión privada para estimar la proporción de sus votantes que
favorecen la despenalización de ciertos delitos relacionados con narcóticos.
1) Cuán grande necesitará ser la muestra que tome la encuesta para tener una seguridad como mínimo del 95%
de que la proporción de la muestra tenga un error a lo sumo de 0.02?.
2) ¿Qué tan grande necesitara ser la muestra que tome la encuesta si sabe que la proporción real que favorece
esta despenalización es de aproximadamente 0.35?.
Un político en desgracia lleva a cabo una encuesta para estimar la proporción de electores registrados en su distrito
que planean votar por él en las próximas elecciones. Encuentre el tamaño de la muestra necesario para tener una
confianza del 94% si quiere que dicha muestra tenga una precisión de:
1) 8 puntos porcentuales.
2) 4 puntos porcentuales.
3) 2 puntos porcentuales.
4) 1 punto porcentual.
Suponga que queremos estimar la proporción de todos los conductores que exceden el limite de velocidad máxima
en un estrechamiento de la carretera entre Los Ángeles y Bakersfield. ¿Cuán grande es la muestra que necesitaremos
de modo que el error de nuestra estimación sea a lo sumo 0.04 si el nivel de confianza deseado es del:
1) 90%?.
2) 95%?
3) 99%?
Un fabricante nacional quiere determinar el porcentaje de compras de navajas para afeitar para caballero que en
realidad son hechas por mujeres. ¿Qué tan grande es la muestra de hombres que el fabricante necesita para tener
una confianza del 98% como mínimo de que el porcentaje de la muestra no tiene un error de mas de 2.5 puntos
porcentuales si:
1) No sabe nada acerca de la proporción real?.
2) Tiene buenas razones para creer que la proporción real es a lo sumo 0.30?.
En estudios previos se determino que el 30% de los turistas que van a un casino a apostar durante un fin de semana,
gastaron mas de $ 10,000. La administración del casino desea actualizar ese porcentaje, con una confianza del 90% y
dentro de 1% de tolerancia en la estimación. ¿Qué tamaño de muestra deberá usarse?.
Una compañía financiera grande quiere estimar con base en una muestra la probabilidad de que cualquiera de sus
numerosos clientes haga una compra cuantiosa de aparatos eléctricos a crédito durante el año próximo. ¿Cuán
grande es la muestra que necesitará para tener una confianza de por lo menos el 95% de que la diferencia entre la
proporción de la muestra y la probabilidad real no es mayor de 0.03 si:
1) No se sabe nada acerca de la probabilidad real?.
2) Existen buenas razones para pensar que la probabilidad real es de entre 0.15 y 0.40?.
Un congresista que quiere reelegirse desea determinar su popularidad en cierta región de un estado. Desea que la
proporción de electores que le apoyaran debe calcularse dentro de un razonable + 2% de error, y quiere tener un 94%
de confianza que el resultado tendrá dicha precisión. Determine el tamaño que deberá tener la muestra a estudiar si:
1. En la elección anterior recibió el 40% de los votos de esos votantes.
2. No tiene idea de cuales son las preferencias de los votantes.
Un canal de TV desea una estimación de la proporción de la población que apoya la política actual del gobierno con
respecto a la situación en Irak. Es conveniente para su credibilidad que la estimación este dentro del 0.04 de la
proporción verdadera. Si se desea una confianza del 92%, determine el tamaño de la muestra de publico a entrevistar
si:
1. Un analista de política del canal estima que el 60% apoya a la política actual.
2. No se tienen estimaciones previas de la proporción de la gente que apoya la política actual.
7
12
La proporción de ejecutivos júnior que salen de grandes compañías manufactureras a los tres años, se debe de
estimar con un margen de error del 3%. Para tener una confianza del 95% en la estimación:
1. ¿Cuántos funcionarios júnior deben estudiarse, si no hay información preliminar al respecto?
2. ¿Cuántos funcionarios júnior deben estudiarse, si un estudio realizado hace varios años revelo que el
porcentaje de tales ejecutivos es el 21%?
La siguiente es una serie de números de un digito generados al azar por una computadora:
13
4
7
9
4
4
5
1.
2.
4
7
7
5
4
8
8
9
7
7
5
7
1
2
1
1
2
4
5
3
4
6
4
7
1
3
4
7
8
5
6
1
6
9
8
9
7
9
3
6
7
2
Determine el tamaño de la muestra (cantidad de números aleatorios que deben generarse) que con una
confianza del 94% y un margen de error del 2%, estime la verdadera proporción de números mayores de 6
generados por estas maquinas.
Determine el tamaño de la muestra (cantidad de números aleatorios que deben generarse) que con una
confianza del 93% y un margen de error del 4%, estime la verdadera proporción de números menores de 2
generados por estas maquinas.
14
Se desea investigar la proporción de estudiantes de la universidad que tiene una impresora, empleando un nivel de
significación de 0. 07 y deseando que la proporción detectada por la muestra no difiera en mas de un 5% de la
verdadera proporción de la población. Determine el tamaño que debe tener la muestra a estudiar, si:
a) no se dispone de información preliminar.
b) de estudios anteriores, se sabe que por lo regular 65 de cada 197 alumnos tienen una impresora.
15
Una fábrica desea conocer el porcentaje de trabajadores que piden alguna incapacidad por motivos de salud
anualmente. ¿A cuantos empleados debe de investigar para tener una confianza del 93 % de que el error en la
estimación no excederá del 7 %, si:
a) no se dispone de información previa?
b) estudios anteriores indican que el 23% de los trabajadores se incapacitan al año?
16
Se observa que de una muestra de 186 hogares de una conocida colonia de la ciudad, 51 poseen una computadora.
a) Escriba un intervalo de confianza del 92.7% para la proporción de hogares de esa colonia que posee una
computadora.
b) Si no se tuviera la información previa,¿De que tamaño deberá de ser una muestra estadística a analizar para
tener una confianza del 96.7% en que la proporción que se halle no diferirá de la verdadera proporción de la
población en mas de un 4%?.
17
Se desea investigar la proporción de estudiantes de la universidad que tiene un scanner, empleando un nivel de
significación de 0. 07 y deseando que la proporción detectada por la muestra no difiera en mas de un 5% de la
verdadera proporción de la población.
Determine el tamaño que debe tener la muestra a estudiar, si:
1. no se dispone de información preliminar.
2. de estudios anteriores, se sabe que por lo regular 4 de cada 25 alumnos tienen un scanner.
8
PRUEBAS DE HIPÓTESIS ESTADISTICAS
HIPÓTESIS
NULA
HIPÓTESIS
ALTERNATIVA
Afirmación que se hace acerca de algún parámetro de la población, sin estar respaldada por un estudio
estadístico. Son valores conocidos, declaraciones verbales o escritas, etiquetas, etc.
Es la negación de una hipótesis nula. Esta siempre respaldada por el análisis estadístico de una muestra.
PRUEBAS DE
HIPÓTESIS DE
UNA Y DOS
COLAS.
FORMA DE LA
HIPÓTESIS NULA
FORMA DE LA
HIPÓTESIS ALTERNATIVA
TIPO DE PRUEBA
DE HIPOTESIS
μ=5
μ>5
ó
μ<5
UNILATERAL O
DE UNA COLA.
P = 20
P ≠ 20
BILATERAL O
DE DOS COLAS.
1.
RESULTADOS
POSIBLES DE
UNA PRUEBA
DE HIPÓTESIS
Se reserva el juicio, cuando no existen evidencias estadísticas suficientes para rechazar la hipótesis
nula. En estos casos:
Ze < Zc
2. Se rechaza la hipótesis nula, cuando existen las evidencias estadísticas suficientes para decir que
es falsa. en estos casos:
Ze > Zc
En ambos casos:
Ze = es un valor efectivo obtenido con formulas estadísticas a partir de valores provenientes de la
muestra.
Zc = es un valor crítico o limite, obtenido de la función de distribución de probabilidades que mejor
represente el caso.
Al hacer una prueba estadística de hipótesis, puede incurrirse en cualquiera de los siguientes errores:
ERRORES,
NIVELES DE
SIGNIFICACIÓN
Y DE
CONFIANZA
DECISIÓN
TOMADA
RESERVAR JUICIO
RECHAZAR LA Ho
SI LA HIPÓTESIS NULA ES:
VERDADERA
FALSA
ACIERTO
ERROR
ERROR
ACIERTO
La probabilidad de cometer uno o los dos errores señalados, recibe el nombre de nivel de significación.
Dicho nivel de significación y el nivel o grado de confianza, deben sumar 1.
9
HIPOTESIS PARA LA MEDIA DE UNA
POBLACION (MUESTRA GRANDE: n > 30).
Z
1
2
3
4
5
6
7
x

n
Distribución Normal
Atlas S. A. ha puesto en marcha una promoción comercial especial para su estufa de propano y siente que la
promoción debe provocar un cambio en el precio para el consumidor. Atlas. S. A. sabe que antes de que comenzara la
promoción, el precio promedio al menudeo de la estufa era de $4,495.00. Atlas muestreo a 40 de sus minoristas
después de iniciada la promoción y encuentra que el precio promedio de las estufas es ahora de $4,295.00 con una
desviación estándar de $575.00. A un nivel de significación de 0.02, ¿Tiene Atlas razones para creer que ha disminuido
el precio promedio al menudeo para el consumidor?
De1990 a 1996, la tasa promedio precios/utilidades (P/U) de los aproximadamente 1,800 valores inscritos en la Bolsa de
Valores de una metrópoli fue de 14.35. En una muestra de 30 valores de la Bolsa aleatoria mente escogidos, la tasa p/u
promedio en 1997 fue de 11.77 con una desviación estándar de 9.73. ¿Esta muestra presenta evidencia suficiente para
concluir que en 1997 la tasa p/u promedio para los valores de la Bolsa tuvo una disminución? Usa un nivel de
significación de 0.045.
Una distribuidora de películas sabe que cierta película de éxito se exhibió un promedio de 84 días en cada ciudad de
un estado. El administrador de la región sur del estado, interesado en comparar la popularidad de la película en su
región con los demás cines del estado, eligió aleatoria mente 75 cines de su región y encontró que proyectaron la
película un promedio de 81.5 días con una desviación estándar de l0 días. Usando un nivel de significación de 0.035,
determina cuál es la conclusión a la que llegó el administrador de la región.
La comisión promedio que cargan las compañías de corretaje de tiempo completo en una venta de valores comunes es
de $144.00. Aleida tomó una muestra aleatoria de 120 compras por parte de sus clientes y halló que habían pagado una
comisión promedio de $151.00 con una desviación estándar de $ 52.00. A un nivel de significación de 0.045, ¿Puede
Aleida concluir que las comisiones de sus clientes son mayores que el promedio de la industria?
Diariamente el Servicio de Aduanas ha interceptado a lo largo de su historia alrededor de $28 millones al día en bienes
de contrabando introducidos al país. En 60 días de 1998, elegidos al azar, el Servicio de Aduanas interceptó un
promedio de $30.3 millones con una desviación estándar de $16 millones al día en bienes de contrabando. ¿Indica esta
muestra, a un nivel de significación de 0.055; que el Comisionado de Aduanas debería preocuparse por el incremento
del contrabando por encima de su nivel histórico?
Para una muestra de 60 mujeres, tomada de una población de 5,000 inscritas en un programa de reducción de peso en
una cadena nacional de balnearios de aguas termales, la presión sanguínea diastólica media es de 90 con una
desviación estándar de 42. A un nivel de significación de 0.015, determina si las mujeres inscritas en el programa
tienen una presión sanguínea diastólica que excede el valor de 75 recomendado por diversas sociedades médicas.
El departamento de procesamiento de datos de una gran compañía de seguros de vida instaló nuevas terminales de
vídeo en color para reemplazar las unidades monocromáticas que antes usaba. Los 95 operadores capacitados para
usar las nuevas máquinas promediaron 7.2 horas antes de lograr un nivel de rendimiento satisfactorio. Su varianza fue
de 16.2 horas al cuadrado. La larga experiencia con los operadores en las viejas terminales monocromáticas indicaba
que promediaban 8.1 horas en las máquinas, antes de que su rendimiento fuera satisfactorio. A un nivel de
significación de 0.03, ¿Puede el supervisor del departamento concluir que las nuevas terminales son más fáciles de
operar?
10
8
Un documental de televisión acerca de la alimentación excesiva afirmaba que los varones tienen un sobrepeso
aproximado de 5 Kg. en promedio. Para probar esta afirmación, se examinó a 48 individuos elegidos aleatoria mente y
se encontró que su sobrepeso promedio era de 5.6 Kg. con una desviación estándar de 1.3 Kg. A un nivel de
significación de 0.015, ¿Hay alguna razón para dudar de la validez de valor dado por el documental?
9
Los estatutos ambientales federales aplicables a una cierta planta nuclear especifican que el agua Reciclada no debe,
en promedio, exceder los 28.9°C antes de que pueda ser lanzada al río que corre junto a la planta. De 70 muestras, se
encontró que el promedio de temperatura del agua reciclada era de 30.2°C con una desviación estándar de 7.5°C.
Usando un nivel de significación de 0.04, determina si la planta debería ser multada por exceder los límites.
10
11
Los inspectores del gobierno, al investigar los cargos levantados contra una embotelladora de bebidas no alcohólicas
que no llenaba adecuadamente sus productos, han muestreado 200 botellas y encontraron que el promedio de llenado
es de 935 mI con una desviación estándar de 44.36 mI. Se anuncia en la etiqueta de las botellas un contenido de 946
mI. ¿Pueden los inspectores del gobierno, al nivel de significación de 0.015, concluir que las botellas están siendo
llenadas con menor contenido?
En 1996, la tarifa aérea promedio con dos semanas de anticipación en el vuelo entre las ciudades de Veracruz y Mérida
era de $1,034.00. En una encuesta hecha en 1997 a 90 viajeros elegidos al azar entre esas dos ciudades se encontró
que habían pagado en promedio $ 965.00 con una desviación estándar de $299.00. Usando un nivel de significación de
0.035, determina si la tarifa promedio de 1997 fue diferente a la tarifa de 1996.
12
Una compañía, recientemente criticada por no pagar lo mismo a hombres que a mujeres que trabajan en los mismos
puestos, declara que el sueldo promedio pagado a todos los empleados es de $ 2,350.00. De una muestra de 39
mujeres que laboran en la compañía, se obtuvo un salario promedio de $2,300.00 con una desviación estándar de $
125.00. Usando un nivel de significación de 0.035, determina si la crítica hecha a la compañía tiene fundamento.
13
Una cadena de restaurantes afirma que el tiempo medio de espera de clientes por atender esta distribuido
normalmente con una media de 3 min. Y una desviación estándar de 1 min. Su departamento de aseguramiento de la
calidad hallo en una muestra de 50 clientes en un cierto establecimiento que el tiempo medio de espera era de 2.75
min. Al nivel de significación de 0.05 ¿Es dicho tiempo menor a 3 min?
14
Cuando fue contratada como mesera de un restaurante, Bety se dijo a si misma “Puedes obtener en promedio mas de
$200 al día en propinas”. A los primeros 35 días de su trabajo en el restaurante, el importe promedio diario de sus
propinas fue de $248.50 con una desviación estándar de $32.40; Al nivel de significación de 0.01, ¿Puede Bety concluir
que esta ganando en propinas mas de lo que se propuso al inicio?
15
16
17
Supóngase que en cierto proceso para fabricar un cable que se emplea al ensamblar PCs, la resistencia a la ruptura
que se logra es una variable aleatoria normal con una media de 90.80 Kg./mm2. Intentando reducir los costos de
producción, se prueba un nuevo proceso de fabricación. Una muestra de 47 unidades fabricadas con el nuevo proceso
tiene una media de 93.32 Kg./mm2. con una desviación estándar de 2.94 Kg./mm2. ¿Puede decirse que el nuevo
proceso tiene un efecto positivo sobre la resistencia del cable?. Use un nivel de significación de 0.10 para contestar la
pregunta.
Una empresa transnacional ha observado en una muestra de 54 empleados, que en México la edad promedio de sus
trabajadores es de 45 años con una desviación estándar de 5 años. En otros países, los empleados de esta empresa
tienen una edad media de 44 años. Al nivel de significación de 0.072 determine si existen razones en la empresa para
pensar que la edad promedio de sus trabajadores en México es diferente a la del resto del mundo.
Una encuesta nacional reciente descubrió que los estudiantes de secundaria ven un promedio de 6.8 videos por mes.
Una muestra aleatoria de 36 estudiantes de secundaria revelo que el promedio de videos que vieron en un mes fue de
6.2 con una desviación estándar de 0.5; Con un nivel de significación de 0.044, ¿es posible concluir que los
estudiantes de secundaria ven menos videos que los que dice la encuesta?.
11
18
Una operación de línea de montaje automotriz debe tener una duración media de 2.2 minutos. Para no alterar tanto a
las actividades anteriores como las posteriores del ensamble. Una muestra aleatoria de 45 operaciones de ese tipo da
como resultado una duración media de 2.39 minutos con una desviación estándar de 0.2 minutos. Emplee un nivel de
significación de 0.028 para determinar si se esta cumpliendo con la norma.
19
Los distribuidores de accesorios de computo dicen que las memorias USB de 128 mb. las venden en promedio a $475;
se selecciona una muestra al azar de 42 establecimientos que las venden, y se obtiene un precio promedio de $560 con
una desviación estándar de $30. Determine al nivel de significación de 0.04 si en la realidad ese accesorio se vende
mas caro que lo que afirman los distribuidores.
PRUEBAS DE HIPOTESIS PARA LA MEDIA DE UNA
POBLACION (MUESTRA PEQUEÑA n < 30).
t
x
s
n
Distribución “t” de Student
1
Atlas S. A. ha puesto en marcha una promoción comercial especial para su estufa de propano y siente que la
promoción debe provocar un cambio en el precio para el consumidor. Atlas. S. A sabe que antes de que comenzara la
promoción, el precio promedio al menudeo de la estufa era de $4,495.00. Atlas muestreo a 22 de sus minoristas
después de iniciada la promoción y encuentra que el precio promedio de las estufas es ahora de $4,295.00 con una
desviación estándar de $575.00. A un nivel de significación de 0.025, ¿Tiene Atlas razones para creer que ha
disminuido el precio promedio al menudeo para el consumidor?
2
Una compañía editora supone que la vida de su prensa rotativa más grande es de 14,500 horas. De una muestra de 25
prensas, la compañía encuentra una media de 13,000 horas con una desviación estándar de 2,100 horas. ¿Debe la
compañía editora suponer que la vida promedio de las prensas es menor que la hipotética de 14,500 horas? Usa un
nivel de significación de 0.025.
3
Antes del embargo petrolero de 1973 y los subsecuentes incrementos en el precio del petróleo crudo, el consumo de
gasolina en un país había aumentado a una tasa de ajuste temporal del 0.57% mensual. En quince meses elegidos
aleatoria mente entre 1975 y 1985, el consumo de gasolina aumentó en una tasa promedio de 0.33% con una desviación
estándar de 0.10% mensual. A un nivel de significación de 0.005, ¿Puede concluirse que el incremento en el uso de la
gasolina se redujo como resultado del embargo y sus consecuencias?
4
La corredora de bienes raíces Clara Céspedes tomo una muestra aleatoria de 12 casas de una prestigiada colonia de la
ciudad y encontró que el valor de mercado promedio era de $780,000.00 con una desviación estándar de $49,000.00.
En el catastro se estima que el valor promedio de las casas es de $825,000.00. Usando un nivel de significación de 0.05,
determina si las casas de la muestra tomada por Clara tienen un valor promedio menor que el señalado por el catastro.
5
Un bibliotecario universitario sospecha que el número promedio de libros sacados a préstamo por cada estudiante por
visita ha aumentado últimamente. Anteriormente se sacaba un promedio de 3,4 libros, Sin embargo, una muestra
reciente de 23 estudiantes promedió 4,3 libros por visita con una desviación estándar de 1.5 libros. Usando un nivel de
significación dé 0.025 determina la validez de la sospecha del bibliotecario.
12
6
Rentacar, renta automóviles en buenas condiciones mecánicas, pero más antiguos que aquellos que rentan las
grandes cadenas nacionales. Como resultado, anuncia que sus tarifas son considerablemente más bajas que las de
sus grandes competidores. Una encuesta de la industria estableció que el cargo total promedio por renta en una de
las mayores compañías es de $773.80. Una muestra aleatoria de 18 transacciones realizadas por Rentacar mostró un
cargo total promedio de $ 876.10 con una desviación estándar de $194.80. Al nivel de significación 0.025, determina si
el cargo total promedio de Rentacar es significativamente más alto que el de las grandes compañías.
Una muestra de alumnos de una universidad, que compraron sus PC’s con las mismas características pero en
diferentes lugares, reportan los siguientes precios (en miles de pesos) que pagaron por ellas:
7
7. 4
8. 0
8. 8
7. 2
8. 0
8. 7
7. 3
8. 8
8. 1
7. 5
7. 6
8. 4
7. 9
9. 0
8. 6
7. 6
7. 2
7. 9
8. 9
7. 3
7. 0
7. 5
7. 1
7. 7
Los maestros de Informática aseguran que en promedio ese tipo de computadora vale de $8,200.00
Pruebe al nivel de significación de 0.05 la aseveración de los maestros de Informática.
8
9
10
Un laboratorio químico afirma que su pomada para golpes leves alivia el dolor en un promedio de 20 minutos
después de aplicada. Se le aplican golpes leves a 24 sujetos e inmediatamente se les unto la pomada, y se encontró
que en promedio el dolor desapareció en 22.5 minutos con una desviación estándar de 3 minutos. Use un nivel de
significación de 0.05 para determinar si el laboratorio exagera en su afirmación.
“Encuestas Hugger” asegura que un agente realiza 53 entrevistas caseras por semana. Se ha introducido un formato
de entrevistas más moderno y rápido y Hugger desea evaluar su eficiencia. El numero de entrevistas realizadas
durante una semana según una muestra aleatoria de agentes es:
53 – 57 – 50 – 55 –58 – 54 – 60 –52 – 59 – 62 – 60 – 60 – 51 – 59 y 56.
Con un nivel de significación de 0.05 ¿es posible concluir que cambió el número promedio de entrevistas realizadas
por agentes?
Los neumáticos nuevos fabricados por una empresa deben durar (según su publicidad) en promedio 28,000 millas.
Las pruebas hechas a 20 neumáticos dan una duración promedio de 27,500 millas con una desviación estándar de
1000 millas. Use un nivel de significación de 0.056 para determinar si la duración real de los reumáticos es menor
que la anunciada.
13
PRUEBAS DE HIPOTESIS PARA LA
PROPORCION DE UNA POBLACION
Z
pM  pP
Distribución Normal
(p P )(q P )
n
1
Un laboratorio que se especializa en el uso de técnicas de reproducción de genes para lograr compuestos
farmacéuticos, desarrollo un atomizador nasal que contiene interferón con el cual se cree habrá de limitarse la
transmisión del catarro común en las familias. En general, al 15.1% de todos los individuos les dará catarro
ocasionado por un rinovirus una vez que otro miembro de la familia ha contraído catarro. El atomizador de interferón
fue probado en 180 personas, en cuyas familias uno de los miembros contrajo posteriormente un catarro ocasionado
por un rinovirus. Solo 17 de los sujetos de la prueba desarrollo catarros similares. A un nivel de significación de
0.025, ¿Puede el laboratorio concluir que el nuevo atomizador efectivamente reduce la transmisión?
2
Un fabricante de salsa de tomate esta en proceso de decidir si produce una nueva marca extra-condimentada. El
departamento de investigación de mercado de la compañía empleo una encuesta telefónica de 6,000 hogares y
encontró que la salsa de tomate extra-condimentada seria comprada por 335 de ellos. Un estudio mucho más extenso
hecho hace dos años mostraba que el 5% de los hogares de ese entonces habrían comprado el producto. A un nivel
de significación de 0.035, ¿Debe la compañía concluir que ahora existe mayor interés en el sabor extracondimentado?.
3
Celeste vende cortadoras de césped “El Rayo” en su ferretería y esta interesada en comparar la calidad de las
cortadoras que vende con otra marca de cortadoras que se venden a nivel nacional. Celeste sabe que solo el 15% de
estas requieren reparaciones durante el primer año después de la compra. Una muestra de 120 clientes de Celeste
revela que 22 de ellos requirieron reparaciones para sus cortadoras en el primer año después de su compra. Al nivel
de significación de 0.045, ¿Existe evidencia de que las cortadoras “El Rayo” difieren en calidad de las que se venden
nacionalmente?.
4
5
6
7
Dora, Gerente General de Blusas S.A., fabricante de blusas para mujer, sabe que su marca se vende en 19% de las
tiendas de ropa para mujer. Dora sospecha que la distribución de las blusas en el Sur de la República es deficiente y
con tal motivo muestreo 85 tiendas y encontró que sólo en 12 se vendían las blusas de Blusas, S.A. A un nivel de
significación de 0.04, determina si la sospecha de Dora tiene fundamento.
En un día promedio, alrededor del 5% de los valores de la Bolsa de Nueva York muestran una nueva alza para ese
año. El viernes 18 de Septiembre de 1992, el promedio industrial Dow Jones cerró en 3,882 con un fuerte volumen de
aproximadamente 136 millones de títulos negociados. Una muestra aleatoria de 120 títulos determinó qué once de
ellos habían mostrado nuevas alzas anuales ese día. Usando un nivel de significación de 0.035, ¿Podríamos afirmar
que más títulos de los habituales tuvieron alzas anuales ese día?
Eloína, corredora de bolsa, afirma que ella puede predecir, con 85% de certeza, el ascenso o caída, durante el mes
siguiente, de un valor del mercado de valores. Para probarlo, predice el resultado de 60 valores y acierta en 45, de sus
predicciones. Al nivel de significación de 0.04, determina la validez de la afirmación de Eloína.
Audio-sonido maneja una cadena de tiendas que venden sistemas y componentes estéreo de audio. Ha tenido éxito
en muchas ciudades universitarias, pero también algunos fracasos. El análisis de estas fallas la ha llevado a adoptar
la política de no abrir una tienda a menos que estén razonablemente seguros de que al menos 15% de los estudiantes
de la ciudad posean sistema estéreo con un costo de $ 2,000.00 o más. En una encuesta hecha a 300 de los 4,500
estudiantes de una ciudad, descubrió que 43 de ellos poseen un sistema estéreo con un costo de al menos $
2,000.00. Si Audio-sonido desea correr el riesgo del 5% de fracasar, ¿Debería abrir una tienda en ese lugar?
14
8
9
10
11
12
En 1997, se estimó que alrededor de 52% de los hogares de una metrópoli eran suscriptores de televisión por cable.
Los editores de una revista estaban seguros de que sus lectores tenían suscripción por cable en un promedio más
alto que la población general y querían usar este hecho para ayudar a vender más espacio de publicidad para los
canales de estreno por cable. Para comprobar esto, tomaron una muestra de 250 de los suscriptores de la revista y
encontraron que 146 de ellos tenían suscripción a la televisión por cable. A un nivel de significación de 0.015,
determina si los datos de la encuesta apoyan el parecer de los editores.
De un total de 10,200 préstamos otorgados por una unión de crédito de empleados del Estado en el último período de
cinco años, se muestrearon 350 para determinar que proporción de los préstamos se otorgaron a las mujeres. Esta
muestra indicó que 133 créditos se otorgaron a las empleadas. Un censo completo de préstamos de hace cinco años
mostraba que 41% de los prestatarios eran mujeres. A un nivel de significación de 0.02, determina si la proporción de
los préstamos otorgados a las mujeres ha disminuido últimamente.
Un innovador de la industria automotriz pensó que su nuevo automotor eléctrico captaría 48% del mercado regional
en un año, debido al bajo precio y al rendimiento superior de su producto. Existen 5,000 usuarios de automotores en
la región. Después de muestrear 10% de estos usuarios un año después de lanzar al mercado su producto, la
compañía encontró que 43% de ellos usaban los nuevos motores. Con un nivel de significación de 0.01, determine si
la compañía fracasó en alcanzar su objetivo de participación en el mercado.
Un informe asegura que el 52% de los automovilistas que usan las carreteras de cuota en México son varones. Una
muestra de 300 autos que usaron la carretera Veracruz – Xalapa en cierto día revelo que 170 eran conducidos por
hombres. Al nivel de significación de 0.01,
1. ¿Se puede concluir que una proporción mayor de varones conducen autos por la carretera Veracruz –
Xalapa, que lo que indica el citado informe?
2. ¿Se puede concluir que una proporción diferente de varones conducen autos por la carretera Veracruz –
Xalapa, que lo que indica el citado informe?
Un articulo de USA TODAY reporto que hay un empleo disponible por cada tres egresados universitarios con grado.
Las principales razones aportadas fueron que existe una sobrepoblación de graduados universitarios, y un
debilitamiento de la economía nacional. Suponga que una encuesta con 200 graduados recientes de la Universidad
ABC revela que 80 ya tienen empleo. Al nivel de significación de 0.02:
1. ¿Se puede concluir que la proporción de recién egresados de la Universidad ABC que ya tienen empleo es
mayor que la señalada nacionalmente por USA TODAY?
2. ¿Se puede concluir que la proporción de recién egresados de la Universidad ABC que ya tienen empleo es
diferente que la señalada nacionalmente por USA TODAY?
El precio que tiene cierto tipo de memoria que se emplea en el ensamble de PCs es de 30 dólares. Una muestra de
precios en negocios seleccionados al azar que venden esa memoria en una ciudad, nos da la siguiente información:
13
30
33
30
30
31
30
30
30
30
30
30
31
30
29
30
30
30
30
30
30
29
30
28
30
28
30
30
30
28
30
30
32
30
31
30
30
Pruebe al nivel de significación de 0.053 la aseveración de que 1/3 de los negocios de esa ciudad no venden a 30
dólares dicha memoria.
14
Una empresa transnacional, ha observado en una muestra de 54 empleados de su filial en México, que 24 rebasan la
edad de 45 años. La política de la empresa, es que un máximo del 33% de los empleados rebase dicha edad.
Al nivel de significación de 0.072 determine si existen razones en la empresa para pensar que la proporción de los
trabajadores en México que rebasan los 45 años es mayor que la que dictan sus políticas.
15
El gerente de una fábrica que tiene mucho personal dice que en un día normal, el 18% de sus empleados sufren de
algún atraso en su hora de entrada a laborar. En una fecha cualquiera seleccionada al azar, se toma una muestra de
76 empleados, y 17 de ellos habían sufrido de algún atraso. Determine al nivel de significación del 0.083, si en dicha
fecha la proporción de trabajadores con atraso a la entrada es diferente a la estimada por el gerente de personal.
15
PRUEBAS DE HIPOTESIS PARA LA DIFERENCIA
DE LAS MEDIAS DE DOS MUESTRAS GRANDES
Z
1
x1  x 2
 12
2
 2
n1
n2
Distribución Normal
Una fábrica de plumas ha probado dos tipos de anuncios publicitarios para su llueva pluma de tinta borrable. Un
anuncio de mostrador fue colocado en una muestra aleatoria de 40 tiendas en el mercado de prueba y un anuncio de
piso se colocó en otras 40 tiendas del área. El número medio de plumas vendidas por tienda en un mes en los lugares
donde había anuncios de mostrador fue de 42 con una desviación estándar de 8. En cuanto a los anuncios de piso, el
número medio de plumas vendidas por tienda en el mismo mes fue de 45 con una desviación estándar de 7. Al nivel de
significación de 0.015, determina si hay diferencia significativa entre las ventas de los establecimientos donde hubo
distinto tipo de publicidad.
2
En 1994, una investigación de 50 hospitales de un país revelo una tasa de ocupación media de 73.6% con una
desviación estándar de 18.2%. En otra investigación efectuada en 75 hospitales del mismo país en 1997, se obtuvo una
tasa de ocupación promedio de 68.9% con una desviación estándar de 19.7%. Al nivel de significación de 0.015,
determina si la tasa de ocupación promedio cambio durante los tres años que hay entre las dos investigaciones.
3
Se efectuó un estudio del número de comidas de negocios que los ejecutivos reclaman como gastos deducibles por
mes. Si 40 ejecutivos de la industria de los seguros promediaron 9.4 de dichas deducciones con una desviación
estándar de 3.3 en un mes determinado; mientras que 50 ejecutivos bancarios promediaron 7.9 con una desviación
estándar de 2.9. Pruebe en el nivel de significación de 0.05 si existe diferencia entre estas dos medias de muestra.
En una investigación de los tiempos de reparación de dos clases de equipo de fotocopiado, se obtuvieron estos datos:
4
Tipo de
equipo
I
II
Numero de reparaciones
60
60
Media
84.2 min.
91.6 min.
Tiempos de reparación
Desviación estándar
19.4 min.
18.8 min.
Pruebe al nivel de significación de 0.01 si existe diferencia entre estas dos medias de muestras.
5
Encuestas muestrales conducidas en un condado grande en 1960 y de nuevo en 1990, demostraron que en 1960 la
altura promedio de 400 hombres del grupo de la edad entre 18 y 24 años era de 68.4 pulgadas con una desviación
estándar de 2.6 pulgadas; mientras que en 1990 la altura promedio de 400 hombres del mismo grupo de edad era de 69.8
pulgadas con una desviación estándar de 2.5 pulgadas. Use el nivel de significación de 0.06 para probar si hubo
incremento en el promedio de las alturas en esos 30 años.
Suponga que se desea verificar si es verdad que en promedio los hombres blancos ganan más que los de color en una
fábrica. Los datos de una muestra arrojan la siguiente información:
6
Color
de piel
Blanca
Morena
Numero de
trabajadores
75
60
Media
$ 422.18
$ 381.66
Salario semanal
Desviación estándar
$ 35.20
$ 32.65
Determine al nivel de significación de 0.042 si efectivamente se paga más a los hombres de piel blanca.
16
7
8
Se realiza un estudio comparando el costo de alquilar un departamento de una recamara en Xalapa, con el
correspondiente costo en Veracruz. Una muestra de 30 departamentos en Xalapa mostró que el valor medio de las
rentas es de $3,700 con una desviación estándar de $300. Una muestra de 40 departamentos en Veracruz señaló que la
renta media en Veracruz es de $3,800 con una desviación estándar de $260. Al nivel de significación de 0.064:
1. ¿Existe diferencia en las rentas medias entre Xalapa y Veracruz?
2. ¿Es mayor la renta media en Veracruz que en Xalapa?.
Una empresa de bienes raíces esta preparando un folleto que cree puede ser de interés para compradores de casa en
dos rumbos de la ciudad. Un elemento de interés es el tiempo que el propietario que vende ha ocupado el inmueble. Una
muestra de 40 casas vendidas recientemente en la zona Norte indica que el tiempo medio de propiedad fue de 7.6 años
con una desviación estándar de 2.3 años. Una muestra de 55 casas de la zona Sur señalo que el tiempo medio era de
8.1 años con una desviación estándar de 2.9 años. Usando un nivel de significación de 0.05, ¿Se puede concluir:
1. que los residentes del Norte tienen en propiedad sus casas por tiempo mas corto?
2. que los residentes del Norte tienen en propiedad sus casas por un tiempo diferente?
Se elaboro un estudio de los ingresos anuales (en dólares) de los funcionarios en ciudades con población menor a
100,000 habitantes, y en ciudades con población mayor a 500,000 habitantes. Algunos datos estadísticos de las
muestras son los siguientes:
9
Tamaño de la muestra
Media de la muestra
Desviación estándar muestral
Población menor de 100,000
45
$ 31,290
$ 1,060
Población mayor de 500,000
60
$ 31,330
$ 1,900
Usando un nivel de significación de 0.075, ¿Puede afirmarse que:
1. ganan mas los funcionarios de ciudades con mas de 500,000 habitantes?
2. son diferentes los sueldos de los funcionarios de los dos tipos de ciudades?
La fuerza aérea de un país adiestra al personal de computación en dos bases (Cass AFB y Kingston AFB). Se aplico un
examen final común. Los resultados obtenidos en dichos exámenes se resumen en la siguiente tabla:
10
Tamaño de la muestra
Promedio de la muestra
Desviación estándar muestral
Cass AFB
40
114.6
9.1
Kingston AFB
50
117.9
10.4
Al nivel de significación de 0.9:
1. ¿Son diferentes los promedios de las muestras?
2. ¿Es mayor el promedio de los capacitados en Kingston AFB?
11
Alumnos de una Universidad seleccionaron al azar 217 autos de estudiantes y hallaron que sus edades tenían una
media de 7.89 años con una desviación estándar de 3.67 años. También escogieron al azar 152 autos de profesores y
determinaron que sus edades tenían una media de 5.99 años con una desviación estándar de 3.65 años. Use un nivel de
significación de 0.075 para probar que los autos de los estudiantes son más viejos que los de los profesores.
12
En una muestra de 45 empleados de Publicidad, se detecto que el ultimo mes recibieron un promedio de 21 correos con
una desviación estándar de 2.6; por su parte, de una muestra de 36 empleados de Ventas de la misma empresa, durante
el ultimo mes recibieron en promedio 26 correos con una desviación estándar de 3.5 ¿Es mayor el promedio de correos
recibidos por Ventas que el de Publicidad? Use un nivel de significación de 0.044
13
En una fabrica se emplean dos maquinas de distinta marca para fabricar el mismo producto. Una muestra de 18 minutos
en la maquina General Electric nos indica que es capaz de producir 28 unidades por minuto con una desviación
estándar de 4 unidades; mientras que otra muestra de 14 minutos de la maquina Panasonic (que es mas nueva) nos
indica que produce 35 unidades por minuto con una varianza de 25 unidades cuadradas. Determine al nivel de
significación de 0.05 si la nueva maquina Panasonic tiene una mayor tasa de producción que la vieja maquina General
Electric.
17
PRUEBAS DE HIPOTESIS PARA LA DIFERENCIA
DE LAS MEDIAS DE DOS MUESTRAS PEQUEÑAS
t
1
2
x1  x 2
(n 1  1)s 12  (n 2  1)s 22
(n 1  n 2  2)
Distribución “t” de Student
1
1
  
 n1 n 2 
Una organización de investigación de consumo selecciona de manera rutinaria varios modelos de automóvil cada año
y evalúa su eficiencia con respecto al combustible. En el estudio del presente año, de dos modelos compactos
fabricados por dos marcas distintas, el consumo promedio para doce automóviles de la marca Alfa fue de 13.6
kilómetros por litro (kpl), con una desviación estándar de 1.9 kpl. Los nueve automóviles de la marca Beta que fueron
probados, tuvieron un rendimiento promedio de 16.2 kpl, con una desviación estándar de 2.1 kpl. Al nivel de
significación 0.01, la organización puede concluir que los automóviles de la marca Beta tienen mayor rendimiento que
los automóviles de la marca Alfa.
Un banco quiere determinar la eficiencia de sus nuevos ejecutivos de cuenta en la obtención de clientes. Luego de
terminar su capacitación, los nuevos ejecutivos dedican varias semanas a visitar posibles clientes para que abran
cuentas en la institución. Los datos adjuntos contienen los números de cuentas nuevas abiertas en sus dos primeras
semanas por10 ejecutivas de cuenta seleccionadas al azar y por 8 ejecutivos también seleccionados al azar:
Ejecutivas
Ejecutivos
12
13
11
10
14
11
13
12
13
13
14
12
13
10
12
12
14
12
Usando un nivel de significación de 0.05, determina si las ejecutivas son más eficaces en la creación de nuevas
cuentas con respecto a los ejecutivos.
3
Para celebrar su primer aniversario, Felipe decidió comprar un par de aretes de diamante para su esposa Florencia. Le
enseñaron nueve pares de aretes con gemas que pesaban aproximadamente dos quilates por par. Debido a la
diferencia en color y calidad de las piedras, los precios variaban de una joya a la otra. El precio promedio fue de
$29,900.00, con una desviación estándar de $ 3,700.00. También le enseñaron seis pares con piedras en forma de gota,
con un peso aproximado de dos quilates por par. Estos pendientes tenían un precio promedio de $30,650.00 con una
desviación estándar de $8,050.00. Con la información anterior, ¿Puede Felipe llegar a la conclusión de que los
diamantes en forma de gota cuestan más, en promedio, que el otro tipo de diamante? Úsese un nivel de significación
de 0.05.
A nueve distribuidores de componentes para computadora que operan en el área metropolitana se les pidió los
precios de dos impresoras de matriz de puntos parecidas, con ancho estándar y fuentes de cierta calidad. Los
resultados de la investigación se consignan en pesos en la siguiente tabla:
4
Comercio
Apson
Okaydat
1
3500
3700
2
4190
4250
3
3850
3690
4
3600
3750
5
4050
3890
6
3890
3850
7
3890
3950
8
4090
4250
9
3750
4000
Usando un nivel de significación de 0.05, determina si en promedio la impresora Apson es más barata que la
impresora Okaydat.
5
A 13 vendedores se les aplica un incentivo “A”, y venden en promedio $50,000 semanales con una desviación
estándar de $12,000.
A 8 vendedores de la misma empresa se les aplica un incentivo “B” y venden en promedio $46,000 a la semana con
una desviación estándar de $ 10,000.
¿Existe diferencia entre los niveles de ventas? Use un nivel de significación de 0.05
18
6
Los módems son dispositivos que transmiten información mediante líneas telefónicas de una computadora a otra. La
velocidad de transmisión se mide en bauds, que se definen como el número de bits por segundo que pueden
transmitir. Debido a la intervención de varios factores técnicos, la rapidez de transmisión real varía de un archivo a
otro. Fernanda está en proceso de adquirir un módem nuevo de 14,400 bauds. Al probar dos de los dispositivos, con el
fin de decidir cuál comprar, transmitió siete archivos elegidos al azar utilizando ambos módems y registró las
siguientes velocidades de transmisión (en miles de bauds).
Archivo
Ultima 14.4Haynes
PerFAXtion 14.4 Extel
1
9.52
10.92
2
10.17
11.46
3
10.33
11.18
4
10.02
12.21
5
10.72
10.42
6
9.62
11.36
7
9.17
10.47
En un artículo aparecido en la revista PC Reports se afirma que en pruebas hechas por la misma revista se ha
encontrado que el módem PerFAXtion es más rápido que el Ultima Haynes. Usando un nivel de significación de 0.01,
determina si los resultados obtenidos por Fernanda confirman lo afirmado por la revista.
7
Una compañía de productos alimenticios acaba de concluir una campaña publicitaria para uno de sus productos, un
cereal natural para el desayuno que contiene nueces, cereales y fruta seca. Para probar la efectividad de la campaña,
la gerente de la marca, Helga Hernández, encuestó a once clientes antes de la campaña ya otros once después de
ésta. A continuación se da el consumo semanal (en gramos) de dicho producto por parte de los consumidores:
Antes
Después
140
230
50
140
180
130
180
290
300
330
100
110
80
20
260
250
130
210
290
260
240
340
Al nivel de significación 0.005, ¿Puede Helga concluir que la campaña ha tenido éxito?
8
Recientemente, un analgésico perdió algo de sus ventas ante un nuevo competidor. El competidor anunciaba que su
marca entra al torrente sanguíneo con más rapidez que el otro analgésico y, como resultado de ello, alivia el dolor más
pronto. Al laboratorio que fabrica el primer analgésico le gustaría probar que no existe diferencia significativa entre los
dos productos y, por consiguiente, que la afirmación de su competidor es falsa. A manera de prueba preliminar, a
nueve individuos se les suministró el analgésico del laboratorio una vez al día durante tres semanas. En las siguientes
tres semanas, a los mismos sujetos se les dio el producto de la competencia. Para cada medicamento se registró el
tiempo en minutos que le tomó aliviar el dolor:
Individuo
Analgésico
Competidor
1
16.5
12.0
2
25.5
20.5
3
23.0
25.0
4
14.5
16.5
5
28.0
24.0
6
10.0
11.5
7
21.5
17.0
8
18.5
15.0
9
15.5
13.0
Al nivel de significación 0.025, determina la conclusión a la que llegó el laboratorio que hizo la investigación.
9
Un químico que se encuentra desarrollando repelentes de insectos desea saber si una fórmula recientemente
desarrollada da mayor protección contra los piquetes de insectos que la que proporciona el producto líder del
mercado. En un experimento a 14 voluntarios se les roció uno de los brazos con el producto viejo y el otro brazo con
la nueva fórmula. Luego cada individuo metió los brazos en una cámara llena de mosquitos y otros insectos que
pican. El número de piquetes recibido en cada brazo Se registra en la tabla siguiente:
Individuo
Formula vieja
Formula nueva
1
5
3
2
2
1
3
5
5
4
4
1
5
3
1
6
6
4
7
2
4
8
4
2
9
2
5
10
6
2
11
5
3
12
7
3
13
1
1
14
3
2
Al nivel de significación 0.05, ¿Puede el químico concluir que la nueva fórmula es más efectiva?
Dos gemelos un poco flojos para estudiar, tienen los siguientes resultados de su evaluación parcial:
10
Ovonio
Inepticio
Contabilidad
5
6
Administración
8
5
Economía
5
6
Matemáticas
3
4
Derecho
6
5
Computación
4
5
Ética
6
3
¿Existe diferencia en los promedios del par de flojos?. Use un nivel de significación de 0.05
19
11
La duración en días de dos marcas distintas de discos duros de las mismas características, instalados en PC’s de un
cibercafe, se muestran en la siguiente relación:
ACME
INC
967
699
785
874
777
689
596
578
811
916
617
721
825
887
655
713
608
¿Puede afirmarse al nivel de significación de 0.05 que son diferentes las duraciones?
12
Se comparo el tiempo que pasan juntos los integrantes de parejas en las que solo trabaja uno y en las que ambos lo
hacen. De acuerdo con los registros llevados por las esposas durante el estudio, la cantidad de tiempo promedio que
pasan juntos viendo TV las parejas en que solo trabaja uno de sus integrantes fue de 61 minutos al día, con una
desviación estándar de 15.5 minutos. Para las parejas en las que ambos trabajan, el numero medio de minutos que
pasan juntos viendo la TV fue de 48.4 minutos con una desviación estándar de 18.1 minutos. En el nivel de
significancia de 0.01 ¿Es posible concluir que aquellas parejas en las que solo trabaja uno de los integrantes pasan
mas tiempo juntas viendo TV?. Se estudiaron quince parejas con un solo integrante trabajador y doce con ambos.
Una compañía del ramo de las telecomunicaciones hará próximamente una gran inversión en equipo de impresión,
razón por la cual se encuentran actualmente cotizando dos tipos de impresoras. Las siguientes tablas muestran los
precios (en miles de pesos) que tienen dichas impresoras en varias tiendas especializadas de la localidad:
13
2.6
2.9
2.0
2.1
Impresora AX – 2300
2.0
2.0
2.1
2.4
2.6
2.1
2.3
2.2
2.5
2.2
2.7
2.6
2.4
2.8
2.8
2.1
2.5
2.8
2.1
Impresora BZ – 1600
2.4
2.9
2.1
2.4
2.6
2.5
2.7
2.0
2.9
2.5
2.7
2.5
2.2
2.4
En base a dicha información, usando un nivel de significación de:
a) 0.05, determine si existe diferencia en los promedios de precios de dichas impresoras.
b) 0.067, determine si es mayor la proporción de tiendas que venden a mas de $2,600 la Impresora BZ – 1600
que la Impresora AX – 2300.
14
Un grupo de habitantes de la ciudad están preocupados por los altos cobros que realiza actualmente la CFE por el
uso de la energía eléctrica, y están haciendo un registro de los consumos bimestrales que tienen. De dicho registro
se obtuvieron las siguientes muestras aleatorias:
Muestra de la Calle Olmo
Consiste en 11 hogares, en los cuales el promedio de Kilowatts – Hora que se consumen por bimestre es de 450 con
una desviación estándar de 60. De dicha muestra, 3 hogares consumen más de 600 Kilowatts – Hora
bimestralmente.
Muestra de la Calle Pino
A continuación se citan las lecturas en Kilowatts – Hora por bimestre obtenidas en hogares de dicha calle:
380
510
432
609
421
539
671
429
648
531
462
721
422
634
542
592
680
512
En base a información brindada por las muestras:
a) Empleando un nivel de significación de 0.083, ¿Podemos afirmar que es mayor la proporción de hogares que
consumen menos de 600 Kilowatts – Hora bimestralmente en la calle Olmo que en la calle Pino?
b) Empleando un nivel de significación de 0.05, ¿Son diferentes los promedios bimestrales de consumo de energía
eléctrica en ambas calles?
Se desea comparar el índice de eficiencia en el manejo de PC en una empresa, y para ello se efectuó un examen
antes de la impartición de un curso de Microsoft Office, y otro después del mismo. Los exámenes se califican en
escala de 0 a 10, y los promedios obtenidos con sus desviaciones estándar son los siguientes:
15
Antes del curso
Después del curso
x
6
8
s
0.8
0.5
n
12
17
Determine al nivel de significación de 0.1 si puede considerarse exitoso el curso.
20
PRUEBAS DE HIPOTESIS PARA LA DIFERENCIA
DE LAS PROPORCIONES DE DOS MUESTRAS
Z
1
p1  p 2
 1
1 

p(q) 
n
n
2 
 1
Donde
p
n 1p 1  n 2 p 2
n1  n 2
Distribución Normal
Una muestra de 400 marineros se ha dividido en dos grupos iguales por selección al azar. Un grupo ha tomado la
marca A de pastillas de Un preventivo contra el mareo y el otro grupo las pastillas de la marca B. El número de cada
grupo que no se ha mareado durante una tormenta intensa ha sido de 152 y 132, respectivamente. Usando un nivel de
significación de 0.02, ¿Podríamos afirmar que las pastillas de la marca A son más eficientes que las pastillas de la
marca B?
2
Una compañía que fabrica productos medicinales está probando dos nuevos compuestos destinados a reducir la
presión sanguínea. Los compuestos son suministrados a dos diferentes conjuntos de animales de laboratorio. En el
grupo uno, 71 de 98 animales probados respondieron a la droga 1 con niveles menores de presión arterial. En el
grupo dos, 58 de 90 animales probados respondieron a la droga 2 con menores niveles de presión sanguínea. La
compañía desea probar a un nivel de significación de 0.05, si existe una diferencia entre la eficiencia de las dos
medicinas.
3
El viernes, tuvieron avance 11 acciones de una muestra aleatoria de 40 tomada de las 2,500 acciones negociadas en
la Bolsa de Valores es decir, aumentó el precio de su valor. En una muestra de 60 acciones tomada el día anterior,
jueves, 24 acciones avanzaron. Al nivel de significación 0.035, determina si un porcentaje menor de las acciones de la
Bolsa de valores avanzaron el viernes con respecto al jueves.
4
Como parte de la preparación para las negociaciones sobre la renovación del contrato colectivo de trabajo, el
Sindicato de Manufactureros hizo una investigación entre sus afiliados para saber si hay preferencia por un aumento
grande en los beneficios de retiro o un pequeño incremento al salario. En un grupo de 997 miembros masculinos que
fueron entrevistados, 743 estaban a favor de un aumento en los beneficios del retiro. De 498 miembros femeninos del
sindicato, 405 estaban a favor de un aumento en los beneficios del retiro. Al nivel de significación 0.035, determina si
el porcentaje de hombres y de mujeres que están a favor de un aumento en los beneficios de retiro es el mismo.
5
Un grupo de fisiólogos clínicos está llevando al cabo pruebas en pacientes para determinar la efectividad de una
nueva medicina contra la hipertensión. Los pacientes con alta presión sanguínea fueron seleccionados al azar y luego
fueron asignados, aleatoria mente también, a un grupo de control (donde son tratados con un medicamento contra la
hipertensión bien conocido) o al grupo de tratamiento (en el cual recibieron tratamiento con la nueva medicina). Los
médicos registraron el porcentaje de pacientes cuya presión arterial se redujo a un nivel normal después de un año de
tratamiento. Los resultaron se dan en la siguiente tabla:
Grupo
Tratamiento
Control
Porcentaje que mejoró
45
36
Número de pacientes
120
150
Al nivel de significación de 0.015, se desea determinar si la nueva medicina es significativamente más efectiva en
reducir la presión sanguínea que la medicina ya conocida.
7
Un método de estimulación de lluvias artificiales por medio de generadores de vapores químicos en tierra tuvo éxito
en 58 de 146 intentos; mientras que otro de bombardeo de nubes con avionetas tuvo éxito en 32 de 104 intentos.
Determine al nivel de significación de 0.88 si existe diferencia entre la eficiencia de ambos métodos.
21
Una empresa de encuestas efectúa interrogatorios de puerta en puerta sobre gran diversidad de asuntos. Algunas
personas cooperan con el entrevistador y llenan el cuestionario, y otras no. Se dispone de los siguientes datos:
8
Encuestados
Hombres
Mujeres
Tamaño de la muestra
200
300
Numero de personas que cooperan
110
210
¿Puede concluirse al nivel de significación de 0.07 que cooperan mas las mujeres para contestar las encuestas?
En una oficina del Gobierno Federal, no todos los empleados emplean PC en sus trabajos. La siguiente tabla muestra
el ultimo informe que presento el departamento de Informática:
9
Hombres
Mujeres
Usan PC
129
61
No usan PC
37
23
¿Es menor la proporción de hombres que usan PC que la de mujeres? Use un nivel de significación de 0.092
Una empresa de publicidad estudia la proporción de egresados de universidades públicas y privadas que encuentran
trabajo antes de que se cumpla un año de su graduación. Los datos obtenidos son los siguientes:
10
Universidad
Publica
Privada
Tamaño de la muestra
325
160
Numero de éxitos
221
119
¿Puede concluirse al nivel de significación de 0.078 que son diferentes las proporciones de éxito en los dos tipos de
universidades?
22
PRUEBA DE HIPOTESIS PARA DIFERENCIA DE LAS MEDIAS
DE MAS DE DOS MUESTRAS (ANALISIS DE VARIANZA)
Distribución F (de Fisher - Snedecor)

Hipótesis nula: Las medias de las poblaciones a que pertenecen las muestras son iguales, es
decir, todas las muestras provienen de una misma población:
H0 : µ1 = µ2 = µ3 = …….. = µk

Hipótesis alternativa: Las medias de las poblaciones a que pertenecen las muestras son
diferentes, es decir, todas las muestras provienen de diferentes poblaciones:
H0 : µ1 ≠ µ2 ≠ µ3 ≠ …….. ≠ µk
Planteo

Valor
crítico
de F.
(Fc)


Grados de libertad verticales o del numerador: glv = k - 1 donde “k” es el número
de muestras.
Grados de libertad horizontales o del denominador: gl h = k(n - 1)
donde “n” es el
número de elementos de cada muestra (todas son del mismo tamaño) y “k” es el
número de muestras.
Varianza intra-muestras:
s 12 + s 22 + .....+ s k2
VD =
k
∑(x - x ),
=
2
donde:
s
2
n -1
2
Siendo “ s ” la varianza de cada muestra, “k” el número de muestras y “n” el
número de elementos de cada muestra.
Análisis
Valor
efectivo
De F.
(Fe)

Varianza inter-muestras:
μ=
2
2
2
(x 1 - μ )
+(x 2 - μ )
+ .....+(x k - μ )
donde:
VE = n
k -1
x 1 + x 2 + ....+ x k
, siendo “xn” la media de cada muestra, y “n” el número de
k
elementos de cada muestra (todas son del mismo tamaño).
Conclusión
Fe =
VE
VD

Razón F efectiva:

Si Fe > Fc, entonces la diferencia es significativa y se rechaza la hipótesis nula.
Escribir una frase en la que se diga que se apoya con una confianza de: 1 – nivel de significación,
expresar en porcentaje:
 La hipótesis nula sí: Fe < Fc
 La hipótesis alternativa sí: Fe > Fc
23
Tabla de Distribución F (Nivel de significación de 0.05)
GRADOS DE LIBERTAD VERTICALES O DEL NUMERADOR
1
2
3
4
5
6
7
8
9
10
20
60
100
1
161.45
199.5
215.71
224.58
230.16
233.99
236.77
238.88
240.54
241.88
248.02
252.2
253.04
2
18.513
19
19.164
19.247
19.296
19.329
19.353
19.371
19.385
19.396
19.446
19.479
19.486
3
10.128
9.5521
9.2766
9.1172
9.0134
8.9407
8.8867
8.8452
8.8123
8.7855
8.6602
8.572
8.5539
4
7.7086
6.9443
6.5914
6.3882
6.2561
6.1631
6.0942
6.041
5.9988
5.9644
5.8025
5.6878
5.664
5
6.6079
5.7861
5.4094
5.1922
5.0503
4.9503
4.8759
4.8183
4.7725
4.7351
4.5581
4.4314
4.4051
6
5.9874
5.1432
4.7571
4.5337
4.3874
4.2839
4.2067
4.1468
4.099
4.06
3.8742
3.7398
3.7117
7
5.5915
4.7374
4.3468
4.1203
3.9715
3.866
3.7871
3.7257
3.6767
3.6365
3.4445
3.3043
3.2749
8
5.3176
4.459
4.0662
3.8379
3.6875
3.5806
3.5005
3.4381
3.3881
3.3472
3.1503
3.0053
2.9747
9
5.1174
4.2565
3.8625
3.6331
3.4817
3.3738
3.2927
3.2296
3.1789
3.1373
2.9365
2.7872
2.7556
10
4.9646
4.1028
3.7083
3.478
3.3258
3.2172
3.1355
3.0717
3.0204
2.9782
2.774
2.6211
2.5884
11
4.8443
3.9823
3.5874
3.3567
3.2039
3.0946
3.0123
2.948
2.8962
2.8536
2.6464
2.4901
2.4566
12
4.7472
3.8853
3.4903
3.2592
3.1059
2.9961
2.9134
2.8486
2.7964
2.7534
2.5436
2.3842
2.3498
13
4.6672
3.8056
3.4105
3.1791
3.0254
2.9153
2.8321
2.7669
2.7144
2.671
2.4589
2.2966
2.2614
14
4.6001
3.7389
3.3439
3.1122
2.9582
2.8477
2.7642
2.6987
2.6458
2.6022
2.3879
2.2229
2.187
15
4.5431
3.6823
3.2874
3.0556
2.9013
2.7905
2.7066
2.6408
2.5876
2.5437
2.3275
2.1601
2.1234
H
O
R
I
Z
O
N
T
A
L
E
S
16
4.494
3.6337
3.2389
3.0069
2.8524
2.7413
2.6572
2.5911
2.5377
2.4935
2.2756
2.1058
2.0685
17
4.4513
3.5915
3.1968
2.9647
2.81
2.6987
2.6143
2.548
2.4943
2.4499
2.2304
2.0584
2.0204
18
4.4139
3.5546
3.1599
2.9277
2.7729
2.6613
2.5767
2.5102
2.4563
2.4117
2.1906
2.0166
1.978
19
4.3808
3.5219
3.1274
2.8951
2.7401
2.6283
2.5435
2.4768
2.4227
2.3779
2.1555
1.9795
1.9403
20
4.3513
3.4928
3.0984
2.8661
2.7109
2.599
2.514
2.4471
2.3928
2.3479
2.1242
1.9464
1.9066
21
4.3248
3.4668
3.0725
2.8401
2.6848
2.5727
2.4876
2.4205
2.3661
2.321
2.096
1.9165
1.8761
22
4.3009
3.4434
3.0491
2.8167
2.6613
2.5491
2.4638
2.3965
2.3419
2.2967
2.0707
1.8894
1.8486
23
4.2793
3.4221
3.028
2.7955
2.64
2.5277
2.4422
2.3748
2.3201
2.2747
2.0476
1.8648
1.8234
0
24
4.2597
3.4028
3.0088
2.7763
2.6207
2.5082
2.4226
2.3551
2.3002
2.2547
2.0267
1.8424
1.8005
25
4.2417
3.3852
2.9912
2.7587
2.603
2.4904
2.4047
2.3371
2.2821
2.2365
2.0075
1.8217
1.7794
26
4.2252
3.369
2.9752
2.7426
2.5868
2.4741
2.3883
2.3205
2.2655
2.2197
1.9898
1.8027
1.7599
27
4.21
3.3541
2.9603
2.7278
2.5719
2.4591
2.3732
2.3053
2.2501
2.2043
1.9736
1.7851
1.7419
28
4.196
3.3404
2.9467
2.7141
2.5581
2.4453
2.3593
2.2913
2.236
2.19
1.9586
1.7689
1.7251
29
4.183
3.3277
2.934
2.7014
2.5454
2.4324
2.3463
2.2782
2.2229
2.1768
1.9446
1.7537
1.7096
30
4.1709
3.3158
2.9223
2.6896
2.5336
2.4205
2.3343
2.2662
2.2107
2.1646
1.9317
1.7396
1.695
40
4.0847
3.2317
2.8387
2.606
2.4495
2.3359
2.249
2.1802
2.124
2.0773
1.8389
1.6373
1.5892
50
4.0343
3.1826
2.79
2.5572
2.4004
2.2864
2.1992
2.1299
2.0733
2.0261
1.7841
1.5757
1.5249
60
4.0012
3.1504
2.7581
2.5252
2.3683
2.2541
2.1665
2.097
2.0401
1.9926
1.748
1.5343
1.4814
70
3.9778
3.1277
2.7355
2.5027
2.3456
2.2312
2.1435
2.0737
2.0166
1.9689
1.7223
1.5046
1.4498
80
3.9604
3.1108
2.7188
2.4859
2.3287
2.2142
2.1263
2.0564
1.9991
1.9512
1.7032
1.4821
1.4259
90
3.9469
3.0977
2.7058
2.4729
2.3157
2.2011
2.1131
2.043
1.9856
1.9376
1.6883
1.4645
1.407
100
3.9362
3.0873
2.6955
2.4626
2.3053
2.1906
2.1025
2.0323
1.9748
1.9267
1.6764
1.4504
1.3917
G
R
A
D
O
S
D
E
L
I
B
E
R
T
A
D
D
E
L
D
E
N
O
M
I
N
A
D
O
R
24
Tabla de Distribución F (Nivel de significación de 0.025)
GRADOS DE LIBERTAD VERTICALES O DEL NUMERADOR
7
8
9
10
20
937.11
948.2
956.64
963.28
968.63
993.08
1009.8 1013.2
39.331
39.356
39.373
39.387
39.398
39.448
39.481 39.488
14.885
14.735
14.624
14.54
14.473
14.419
14.167
13.992 13.956
9.6045
9.3645
9.1973
9.0741
8.9796
8.9046
8.8439
8.5599
8.3604 8.3195
7.7636
7.3879
7.1464
6.9777
6.853
6.7572
6.681
6.6192
6.3285
6.1225
7.2599
6.5988
6.2271
5.9875
5.8197
5.6955
5.5996
5.5234
5.4613
5.1684
4.9589 4.9154
6.5415
5.8898
5.5226
5.2852
5.1186
4.9949
4.8993
4.8232
4.7611
4.4668
4.2544 4.2101
7.5709
6.0595
5.416
5.0526
4.8173
4.6517
4.5285
4.4333
4.3572
4.2951
3.9994
3.7844 3.7393
9
7.2093
5.7147
5.0781
4.7181
4.4844
4.3197
4.197
4.102
4.026
3.9639
3.6669
3.4493 3.4034
10
6.9367
5.4564
4.8256
4.4683
4.2361
4.0721
3.9498
3.8549
3.779
3.7168
3.4185
3.1984 3.1517
11
6.7241
5.2559
4.63
4.2751
4.044
3.8806
3.7586
3.6638
3.5879
3.5257
3.2261
3.0035 2.9561
12
6.5538
5.0959
4.4742
4.1212
3.8911
3.7283
3.6065
3.5118
3.4358
3.3735
3.0728
2.8478 2.7996
13
6.4143
4.9653
4.3472
3.9959
3.7667
3.6043
3.4827
3.388
3.312
3.2497
2.9477
2.7204 2.6715
14
6.2979
4.8567
4.2417
3.8919
3.6634
3.5014
3.3799
3.2853
3.2093
3.1469
2.8437
2.6142 2.5646
15
6.1995
4.765
4.1528
3.8043
3.5764
3.4147
3.2934
3.1987
3.1227
3.0602
2.7559
2.5242 2.4739
16
6.1151
4.6867
4.0768
3.7294
3.5021
3.3406
3.2194
3.1248
3.0488
2.9862
2.6808
2.4471 2.3961
17
6.042
4.6189
4.0112
3.6648
3.4379
3.2767
3.1556
3.061
2.9849
2.9222
2.6158
2.3801 2.3285
18
5.9781
4.5597
3.9539
3.6083
3.382
3.2209
3.0999
3.0053
2.9291
2.8664
2.559
2.3214 2.2692
19
5.9216
4.5075
3.9034
3.5587
3.3327
3.1718
3.0509
2.9563
2.8801
2.8172
2.5089
2.2696 2.2167
20
5.8715
4.4612
3.8587
3.5147
3.2891
3.1283
3.0074
2.9128
2.8365
2.7737
2.4645
2.2234 2.1699
21
5.8266
4.4199
3.8188
3.4754
3.2501
3.0895
2.9686
2.874
2.7977
2.7348
2.4247
2.1819
22
5.7863
4.3828
3.7829
3.4401
3.2151
3.0546
2.9338
2.8392
2.7628
2.6998
2.389
2.1446 2.0901
23
5.7498
4.3492
3.7505
3.4083
3.1835
3.0232
2.9023
2.8077
2.7313
2.6682
2.3566
2.1107 2.0556
D
E
L
24
5.7166
4.3187
3.7211
3.3794
3.1548
2.9946
2.8738
2.7791
2.7027
2.6396
2.3273
2.0799 2.0243
25
5.6864
4.2909
3.6943
3.353
3.1287
2.9685
2.8478
2.7531
2.6766
2.6135
2.3005
2.0516 1.9955
D
E
N
O
M
I
N
A
D
O
R
26
5.6586
4.2655
3.6697
3.3289
3.1048
2.9447
2.824
2.7293
2.6528
2.5896
2.2759
2.0257 1.9691
27
5.6331
4.2421
3.6472
3.3067
3.0828
2.9228
2.8021
2.7074
2.6309
2.5676
2.2533
2.0018 1.9447
28
5.6096
4.2205
3.6264
3.2863
3.0626
2.9027
2.782
2.6872
2.6106
2.5473
2.2324
1.9797 1.9221
29
5.5878
4.2006
3.6072
3.2674
3.0438
2.884
2.7633
2.6686
2.5919
2.5286
2.2131
1.9591 1.9011
30
5.5675
4.1821
3.5893
3.2499
3.0265
2.8667
2.746
2.6513
2.5746
2.5112
2.1952
40
5.4239
4.051
3.4633
3.1261
2.9037
2.7444
2.6238
2.5289
2.4519
2.3882
2.0677
1.8028 1.7405
50
5.3403
3.9749
3.3902
3.0544
2.8326
2.6736
2.553
2.4579
2.3808
2.3168
1.9933
1.7211 1.6558
60
5.2856
3.9253
3.3425
3.0077
2.7863
2.6274
2.5068
2.4117
2.3344
2.2702
1.9445
1.6668
70
5.247
3.8903
3.309
2.9748
2.7537
2.5949
2.4743
2.3791
2.3017
2.2374
1.91
1.6279 1.5581
80
5.2183
3.8643
3.2841
2.9504
2.7295
2.5708
2.4502
2.3549
2.2775
2.213
1.8843
1.5987 1.5271
90
5.1962
3.8443
3.2649
2.9315
2.7109
2.5522
2.4316
2.3363
2.2588
2.1942
1.8644
1.5758 1.5028
100
5.1786
3.8284
3.2496
2.9166
2.6961
2.5374
2.4168
2.3215
2.2439
2.1793
1.8486
1.5575 1.4833
G
R
A
D
O
S
D
E
L
I
B
E
R
T
A
D
H
O
R
I
Z
O
N
T
A
L
E
S
0
1
2
3
4
5
6
1
647.79
799.48
2
38.506
39
864.15
899.6
921.83
39.166
39.248
39.298
3
17.443
16.044
15.439
15.101
4
12.218
10.649
9.9792
5
10.007
8.4336
6
8.8131
7
8.0727
8
60
1.94
100
6.08
2.128
1.8816
1.599
25
Tabla de Distribución F (Nivel de significación de 0.01)
GRADOS DE LIBERTAD VERTICALES O DEL NUMERADOR
1
2
3
4
5
6
7
8
9
10
20
60
100
1
4052.2
4999.3
5403.5
5624.3
5764
5859
5928.3
5981
6022.4
6055.9
6208.7
6313
6333.9
2
98.502
99
99.164
99.251
99.302
99.331
99.357
99.375
99.39
99.397
99.448
99.484
99.491
3
34.116
30.816
29.457
28.71
28.237
27.911
27.671
27.489
27.345
27.228
26.69
26.316
26.241
4
21.198
18
16.694
15.977
15.522
15.207
14.976
14.799
14.659
14.546
14.019
13.652
13.577
5
16.258
13.274
12.06
11.392
10.967
10.672
10.456
10.289
10.158
10.051
9.5527
9.202
9.13
6
13.745
10.925
9.7796
9.1484
8.7459
8.466
8.26
8.1017
7.976
7.8742
7.3958
7.0568
6.9867
7
12.246
9.5465
8.4513
7.8467
7.4604
7.1914
6.9929
6.8401
6.7188
6.6201
6.1555
5.8236
5.7546
8
11.259
8.6491
7.591
7.0061
6.6318
6.3707
6.1776
6.0288
5.9106
5.8143
5.3591
5.0316
4.9633
9
10.562
8.0215
6.992
6.4221
6.0569
5.8018
5.6128
5.4671
5.3511
5.2565
4.808
4.4831
4.415
10
10.044
7.5595
6.5523
5.9944
5.6364
5.3858
5.2001
5.0567
4.9424
4.8491
4.4054
4.0819
4.0137
11
9.6461
7.2057
6.2167
5.6683
5.316
5.0692
4.886
4.7445
4.6315
4.5393
4.099
3.7761
3.7077
12
9.3303
6.9266
5.9525
5.4119
5.0644
4.8205
4.6395
4.4994
4.3875
4.2961
3.8584
3.5355
3.4668
13
9.0738
6.7009
5.7394
5.2053
4.8616
4.6203
4.441
4.3021
4.1911
4.1003
3.6646
3.3413
3.2723
H
O
R
I
Z
O
N
T
A
L
E
S
14
8.8617
6.5149
5.5639
5.0354
4.695
4.4558
4.2779
4.14
4.0297
3.9394
3.5052
3.1813
3.1118
15
8.6832
6.3588
5.417
4.8932
4.5556
4.3183
4.1416
4.0044
3.8948
3.8049
3.3719
3.0471
2.9772
16
8.5309
6.2263
5.2922
4.7726
4.4374
4.2016
4.0259
3.8896
3.7804
3.6909
3.2587
2.933
2.8627
17
8.3998
6.1121
5.185
4.6689
4.336
4.1015
3.9267
3.7909
3.6823
3.5931
3.1615
2.8348
2.7639
18
8.2855
6.0129
5.0919
4.579
4.2479
4.0146
3.8406
3.7054
3.5971
3.5081
3.0771
2.7493
2.6779
19
8.185
5.9259
5.0103
4.5002
4.1708
3.9386
3.7653
3.6305
3.5225
3.4338
3.0031
2.6742
2.6023
20
8.096
5.849
4.9382
4.4307
4.1027
3.8714
3.6987
3.5644
3.4567
3.3682
2.9377
2.6077
2.5353
21
8.0166
5.7804
4.874
4.3688
4.0421
3.8117
3.6396
3.5056
3.3982
3.3098
2.8795
2.5484
2.4755
0
22
7.9453
5.719
4.8166
4.3134
3.988
3.7583
3.5866
3.453
3.3458
3.2576
2.8274
2.4951
2.4218
D
E
L
23
7.8811
5.6637
4.7648
4.2635
3.9392
3.7102
3.539
3.4057
3.2986
3.2106
2.7805
2.4471
2.3732
24
7.8229
5.6136
4.7181
4.2185
3.8951
3.6667
3.4959
3.3629
3.256
3.1681
2.738
2.4035
2.3291
25
7.7698
5.568
4.6755
4.1774
3.855
3.6272
3.4568
3.3239
3.2172
3.1294
2.6993
2.3637
2.2888
26
7.7213
5.5263
4.6365
4.14
3.8183
3.5911
3.421
3.2884
3.1818
3.0941
2.664
2.3273
2.2519
27
7.6767
5.4881
4.6009
4.1056
3.7847
3.558
3.3882
3.2558
3.1494
3.0618
2.6316
2.2938
2.218
28
7.6357
5.4529
4.5681
4.074
3.7539
3.5276
3.3581
3.2259
3.1195
3.032
2.6018
2.2629
2.1867
29
7.5977
5.4205
4.5378
4.0449
3.7254
3.4995
3.3303
3.1982
3.092
3.0045
2.5742
2.2344
2.1577
30
7.5624
5.3903
4.5097
4.0179
3.699
3.4735
3.3045
3.1726
3.0665
2.9791
2.5487
2.2079
2.1307
40
7.3142
5.1785
4.3126
3.8283
3.5138
3.291
3.1238
2.993
2.8876
2.8005
2.3689
2.0194
1.9383
50
7.1706
5.0566
4.1994
3.7195
3.4077
3.1864
3.0202
2.89
2.785
2.6981
2.2652
1.909
1.8248
60
7.0771
4.9774
4.1259
3.6491
3.3389
3.1187
2.953
2.8233
2.7185
2.6318
2.1978
1.8363
1.7493
70
7.0114
4.9218
4.0744
3.5997
3.2907
3.0712
2.906
2.7765
2.6719
2.5852
2.1504
1.7846
1.6954
80
6.9626
4.8807
4.0363
3.5631
3.2551
3.0361
2.8713
2.742
2.6374
2.5508
2.1153
1.7459
1.6548
90
6.9251
4.8491
4.0069
3.535
3.2276
3.0091
2.8445
2.7154
2.6109
2.5243
2.0882
1.7158
1.6231
100
6.8953
4.8239
3.9837
3.5127
3.2059
2.9877
2.8233
2.6943
2.5898
2.5033
2.0666
1.6918
1.5977
G
R
A
D
O
S
D
E
L
I
B
E
R
T
A
D
D
E
N
O
M
I
N
A
D
O
R
26
1
El director de capacitación de una compañía está tratando de evaluar tres métodos diferentes de entrenamiento para empleados
nuevos. El primer método consiste en asignar un empleado nuevo con un trabajador experimentado para que éste lo asista en la
fábrica. El segundo método consiste en ubicar a todos los empleados nuevos en un salón de entrenamiento separado de la fábrica, y
el tercer método consiste en utilizar películas de entrenamiento y materiales de aprendizaje programado. El director de capacitación
escoge al azar 18 nuevos empleados y aleatoria mente asigna 6 a cada uno de los métodos y registra su producción diaria ( en
unidades) después que terminaron los programas de capacitación, obteniendo los siguientes resultados:
Método 1
Método 2
Método 3
15
22
18
18
27
24
19
18
19
22
21
16
11
17
22
17
21
15
Usando un nivel de significación de 0.05, el director de capacitación desea estimar si existen diferencias en la efectividad de los tres
métodos.
Los datos de la siguiente tabla muestran el número de quejas procesadas diariamente de un grupo de cuatro empleados de
compañías de seguros observados durante seis días:
Empleado
Anabel
Aarón
Fabiola
Irán
2
15
12
11
13
17
10
14
12
14
13
13
12
Número de quejas
12
17
15
14
11
14
12
14
10
12
10
12
Al nivel de significación 0.05, determina si los promedios diarios de quejas de los empleados son iguales.
Una compañía de investigación ha diseñado tres sistemas distintos para limpiar manchas de aceite. La siguiente tabla contiene los
resultados de cada sistema, medido en qué tanta superficie (en metros cuadrados) es limpiada en una hora. Los datos se obtuvieron
probando cada método en varias sesiones:
3
Sistema
Superficie limpiada (en metros cuadrados)
A
B
C
55
57
66
60
53
52
63
64
61
56
49
57
59
62
60
La compañía necesita saber si los tres métodos tienen la misma efectividad. Usa un nivel de significación de 0.05.
Una compañía publicitaria de anuncios al aire libre desea saber si hay diferencias significativas en el tráfico automovilístico que pasa
por tres lugares distintos de una ciudad donde tiene anuncios panorámicos; debido a que la compañía cobra precios diferentes
dependiendo del número de automóviles que pasan frente al anuncio. Se mide el volumen del tráfico en los tres sitios durante
intervalos de cinco minutos elegidos aleatoria mente. La siguiente tabla muestra los datos obtenidos:
4
Lugar
A
B
30
29
45
38
C
32
44
Volumen de trafico
26
36
40
44
21
18
18
43
24
¿A qué conclusión llegaron en esa compañía? Usa un nivel de significación de 0.01.
Un ingeniero agrónomo plantó tres parcelas del mismo tamaño con cuatro variedades de trigo y obtuvo las siguientes producciones
en libras por parcela:
5
Variedad
Variedad
Variedad
Variedad
A
B
C
D
57
52
53
56
62
53
56
59
61
60
56
59
Pruebe al nivel de significación de 0.05 si las diferencias entre las medias de las cuatro medias puede atribuirse al azar.
27
Los siguientes son los rendimientos en millas que un conductor de pruebas obtuvo con cuatro galones de cinco marcas de gasolina:
Marca
Marca
Marca
Marca
Marca
6
A
B
C
D
E
30
29
32
29
32
25
26
32
34
26
27
29
35
32
31
26
28
37
33
27
Pruebe al nivel de significación de 0.01 si las diferencias entre las medias de las cinco muestras pueden atribuirse al azar.
Se hace un estudio para saber si diversas marcas de televisiones tienen la misma duración. La muestra es de 8 unidades de cada
marca, obteniéndose los siguientes datos estadísticos:
7
ABC
45 Meses
9 Meses
Duración promedio
Desviación estándar
KLM
40 Meses
11 Meses
Marcas
PQR
52 Meses
8 Meses
XYZ
48 Meses
10 Meses
Determine al nivel de significación de 0.01 si tienen igual duración las distintas marcas de televisores.
Se aplica el mismo examen de estadística a aspirantes a cursar carreras de tres áreas académicas diferentes. Los exámenes se
aplican a 10 aspirantes de cada área, obteniéndose los siguientes resultados:
8
Área técnica
6.5
2.55
Promedio
Desviación Estándar
Área Económica
5.7
2.11
Área de Sociales
4.7
2.06
Al nivel de significación de 0.01 ¿Influye el área a que pertenece el estudiante en los promedios?
Calificaciones de un examen de Microsoft Office aplicado a 8 alumnos de 5 licenciaturas:
9
Licenciatura
Administración
Contaduría
Ingeniería Industrial
Sistemas de Computo
Turismo
Promedio
8.0
7.5
8.2
8.9
7.2
Desviación estándar
1.7
1.2
1.4
1.0
1.5
Determine al nivel de significación de 0.01, si la licenciatura a que pertenecen los alumnos influye en la calificación promedio de los
mismos.
El siguiente registro muestra el numero de PCs vendidas en un negocio en sus tres sucursales durante una semana de 7 días
laborales:
10
Promedio
39
48
26
Sucursal Norte
Sucursal Centro
Sucursal Sur
Desviación Estándar
8
11
9
Determine al nivel de significación de 0.05 si influye la zona en que esta la sucursal en el promedio semanal de ventas de PCs.
Los siguientes datos se obtuvieron con muestras de ocho empleados de cada una de las cuatro empresas que se citan, con
referencia a su antigüedad en la misma:
11
Empresa
x
S2
Alfa
17
16
Beta
19
9
Delta
22
25
Gamma
17
4
Al nivel de significación de 0.05 ¿En algunas empresas la antigüedad es mayor que en otras?
28
PRUEBAS DE HIPOTESIS PARA LA DIFERENCIA DE LAS
PROPORCIONES DE MAS DE DOS MUESTRAS
Distribución Chi – cuadrada

Hipótesis nula: Las proporciones de las poblaciones a que pertenecen las muestras
son iguales, es decir, todas las muestras provienen de una misma población:
H0 : p1 = p2 = p3 = …….. = pk

Hipótesis alternativa: Las proporciones de las poblaciones a que pertenecen las
muestras son diferentes, es decir, todas las muestras provienen de diferentes
poblaciones:
H0 : p1 ≠ p2 ≠ p3 ≠ …….. ≠ pk
Planteo

Valor
crítico
de χ2


Para determinarlo, se emplea la Tabla de la Función de Distribución de
Probabilidades Chi – cuadrada (χ2 ).
Se calculan los grados de libertad: GL = (r – 1)(c – 1) donde “r” y “c” son
los números de renglones (filas) y columnas de la tabla de contingencia,
que es la que reúne la información del caso.
Se intersectan el renglón (fila) de los grados de libertad y la columna del
nivel de significación (área de extremo superior especificado de ) , para
obtener el valor crítico X 2c
Análisis
X 2e 
Valor
efectivo
de χ2


2
(ValoresObservados  ValoresEsperados )

ValoresEsperados
2
Sí X 2e es mayor que X c , las diferencias entre las proporciones son
significativas, no se deben azar, y debe rechazarse la hipótesis nula, ya
que las muestras provienen de poblaciones diferentes.
2
Sí X 2e es menor que X c , las diferencias entre las proporciones no son
significativas, se deben azar, y no debe rechazarse la hipótesis nula, es
decir, hay que reservar el juicio, ya que las muestras provienen de la
misma población.
Escribir una frase en la que se diga que se apoya con una confianza de 1 – nivel de
significación, expresada en porcentaje:
2
2
Conclusión
 La hipótesis nula sí: X e es menor que X c

2
2
La hipótesis alternativa sí: X e es mayor que X c
29
TABLA DE LA DISTRIBUCION CHI- CUADRADO
Valores críticos de la Chi-cuadrado
Para una combinación particular de grados de libertad en el numerador y en el denominador, las
entradas representan los valores críticos de la Chi-cuadrado, correspondientes a un área de extremo
superior especificado de .
Grados de
Libertad
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0.25
1.323
2.773
4.108
5.385
6.626
7.841
9.037
10.219
11.389
12.549
13.701
14.845
15.984
17.117
18.245
19.369
20.489
21.605
22.718
23.828
24.935
26.039
27.141
28.241
29.339
30.435
31.528
32.620
33.711
34.800
AREAS DE EXTREMOS SUPERIOR ()
0.10
0.05
0.025
2.706
3.841
5.024
4.605
5.991
7.378
6.251
7.815
9.348
7.779
9.488
11.143
9.236
11.071
12.833
10.645
12.592
14.449
12.017
14.067
16.013
13.362
15507
17.535
14.684
16.919
19.023
15.987
18.307
20.483
17.275
19.675
21.920
18.549
21.026
23.337
19.812
22.362
24.736
21.064
23.685
26.119
22.307
24.996
27.488
23.542
26.296
28.845
24.769
27.587
30.191
25.989
28.869
31.526
27.204
30.144
32.852
28.412
31.410
34.170
29.615
32.671
35.479
30.813
33.924
36.781
32.007
35.172
38.076
33.196
36.415
39.364
34.382
37.652
40.646
35.563
38.885
41.923
36.741
40.113
43.194
37.916
41.337
44.461
39.087
42.557
45.722
40.256
43.773
46.979
0.01
6.635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
30.578
32.000
33.409
34.805
36.191
37.566
38.832
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
0.005
7.879
10.597
12.838
14.860
16.750
18.548
20.278
21.955
23.589
25.188
26.757
28.299
29.819
31.319
32.801
34.267
35.718
37.156
38.582
39.997
41.401
42.796
44.181
45.559
46928
48.290
49.645
50.993
52.336
53.672
30
Un administrador de marca está preocupado porque su producto puede estar mal distribuido a lo largo de todo el país.
En una encuesta en que el país fue dividido en cuatro regiones geográficas, se investigó una muestra aleatoria de 100
consumidores de cada región, obteniéndose los siguientes resultados:
1
Región
Adquirieron la marca
No la adquirieron
Noreste
40
60
Noroeste
55
45
Sureste
45
55
Suroeste
50
50
Al nivel de significación 0.025, determina cuál es la conclusión a la que llegó el distribuidor de marca.
Un editor de periódicos, que trata de determinar con precisión las características de mercado de su periódico, se
pregunta si la costumbre de la gente de la comunidad de leer diarios está relacionada con el nivel educativo de los
lectores. Se aplica una encuesta a los adultos del área referente a su nivel educativo y la frecuencia con que leen
periódico. Los resultados se muestran en la tabla siguiente:
2
Frecuencia
con que lee
Nunca
Algunas veces
Mañana o tarde
Ambas ediciones
Nivel educativo
Licenciatura
Bachillerato
17
11
23
8
38
16
19
6
Postgrado
10
12
35
28
Otro
21
5
7
13
Al nivel de significación 0.025, ¿La frecuencia con que se lee el periódico depende del nivel educativo de los lectores?
En un estudio se compararon los efectos de cuatro promociones mensuales sobre las ventas de cierto producto.
Presentamos las ventas unitarias de cinco tiendas que utilizaron las cuatro promociones en meses diferentes:
3
Tipo de promoción
Muestra gratis
Regalo de un paquete
Descuento
Premio por sorteo
A
78
94
73
79
Tienda
C
81
87
69
78
B
87
91
78
83
D
89
90
83
69
E
85
88
76
81
Al nivel de significación de 0.01, determina si las promociones producen diferentes efectos sobre las ventas.
Información acerca del tipo de fabricas instaladas en un estado de la república:
4
Metalmecánica
Extractiva
Norte
7
13
Sur
4
5
Este
11
9
Oeste
7
2
Determine, al nivel de significación de 0.1, si las industrias están instaladas uniformemente.
En un estudio para determinar si existe una relación entre las costumbres de vestido de los empleados bancarios y su
progreso profesional, una muestra aleatoria dio los siguientes resultados:
5
Elegantes
Bien vestidos
Mal vestidos
Lenta
32
28
15
Velocidad de progreso
Promedio
56
69
33
Alta
32
22
13
Pruebe al nivel de significación de 0.05 si existe una relación entre las costumbres de vestido y la velocidad del
progreso personal en los empleados bancarios.
31
Datos de una encuesta diseñada para mostrar cómo se transportan los estudiantes de una universidad:
6
Ingeniería
104
22
46
28
Caminando
Automóvil
Bicicleta
Autobús
Informática
87
29
34
50
Contaduría
89
35
37
39
Derecho
72
43
32
53
Use un nivel de significación de 0.05 para probar la afirmación de que las proporciones de alumnos de las carreras
mencionadas que usan los diferentes medios de transporte son iguales.
Una fábrica de autos ha hecho una encuesta para identificar las características de seguridad más importantes
deseables por compradores de autos, por edades:
7
Jóvenes
Adultos
Frenos
de disco
29
11
Suspensión
modificada
11
9
Bolsas
de aire
48
22
Seguros
automáticos
12
38
Control de
crucero
7
23
Al nivel de significación de 0.025 ¿Son las mismas características las deseadas por jóvenes y adultos?
El administrador de una empresa estudia la relación entre el departamento a que pertenecen los empleados y su grado
de entrega al trabajo, y obtuvo la siguiente información:
8
Grado entrega / Dpto.
Excelente
bueno
regular
Administrativo
170
120
130
Mercadotecnia
124
112
90
Producción
90
100
88
¿Podemos concluir con un nivel de significancia de 0.05 que hay relación entre el departamento en que trabaja el
empleado y su nivel de entrega al mismo?
9
Se aplica el mismo examen de Estadística a aspirantes a cursar carreras de tres áreas académicas diferentes. Dichos
exámenes se aplican a 10 aspirantes de cada área, obteniéndose los siguientes resultados:
Aprobados
Reprobados
Área técnica
7
3
Área Económica
5
5
Área de Sociales
4
6
Determine al nivel de significación de 0.10 si influye el área a que pertenece el estudiante en la proporción de
aprobados.
32
PRUEBAS DE HIPOTESIS DE REGRESION LINEAL
En la práctica, es frecuente encontrar que existan relaciones entre dos o más variables, y a veces es posible expresarlas en forma matemática,
mediante una ecuación que conecte a dichas variables, de tal manera que podamos estimar (basados en los datos de una muestra) el valor de
una de las variables en función del valor de la otra. Por ejemplo, parece ser obvio que entre los siguientes pares de variables si existe alguna
relación que las conecta:
Promedio en Licenciatura...................................................................... Promedio en Maestría
Inteligencia de padres.............................................................................. Inteligencia de hijos
Nivel socio – económico......................................................................... Incidencia en delitos
Estatura …………………………………...................................................... Peso
Producto Nacional Bruto…………………………………..…………..…….. Esperanza de vida
Dosis de efedrina...................................................................................... Ritmo cardiaco
Etc.
Sin embargo, no parece tan obvio, y requeriríamos del análisis de una o varias muestras estadísticas para establecer sí existe alguna relación
de dependencia entre los siguientes pares de variables:
Tasa de crecimiento de los Ficus.................................................... Goles por temporada en la Liga Inglesa
Gastos en publicidad de una empresa........................................... Cometas avistados por año
Canales nuevos de TV por año........................................................ Numero de rinocerontes cazados ilegalmente
Edad ………………………………….................................................... Numero de pares de zapatos
Incremento de la inflación …………………………….…………..……Temperatura de una ciudad
Evolución de la resistencia de un pegamento............................... Tasa de mortandad de un país
Variables


Independiente: aquella que representa el dato conocido en un análisis de regresión.
Dependiente: es la que se trata de predecir en un análisis de regresión.

Grafica en un sistema de coordenadas, en la que en el eje horizontal (x) graduamos la variable independiente, y en
el vertical (y) la variable dependiente.
Cada dato u observación de la muestra, es un punto de coordenadas (x,y) en el sistema.
La forma en que se distribuyen los puntos en el sistema, determina el tipo de relación que existe entre las dos
variables (lineal o curvilínea).
Diagramas de
dispersión


Coeficiente de
correlación de
Pearson




Expresa cuantitativamente el grado en que dos variables están relacionadas.
Su valor varía desde -1 hasta +1.
Si es positiva, ambas variables crecen. La tendencia en el Diagrama de Dispersión es creciente hacia la derecha.
Si es negativa, una variable crece y la otra decrece. La tendencia en el Diagrama de Dispersión es decreciente hacia
la derecha.

Se calcula por medio de la siguiente fórmula:
rp 
Z
X
ZY
n
PRUEBAS DE HIPOTESIS DE REGRESIÓN LINEAL
Planteo
Hipótesis nula.- Ho: No existe relación lineal entre las variables.
Hipótesis alternativa.- H1: Si existe relación lineal entre las variables.


Análisis
re 

Conclusión
Se calcula por medio de tablas el valor crítico para el Coeficiente de Regresión Lineal de Pearson (rc)
Se calcula el valor efectivo para el Coeficiente de Regresión Lineal de Pearson por medio de la siguiente fórmula:
Z
X
ZY
n
Sí rc > re se reserva el juicio, en caso contrario se rechaza la hipótesis nula Ho.
Se hace una redacción en la que se expresa que se confía en un porcentaje de 100% menos el nivel de significación, en que si
exista o no relación lineal entre las variables (según sea el caso).
33
TABLA DE VALORES CRÍTICOS
PARA EL COEFICIENTE
DE CORRELACIÓN LINEAL DE
PEARSON (r)
ALGUNOS TIPOS
DE DIAGRAMAS
DE DISPERSIÓN
Y
Y
O
X
O
Correlación lineal positiva
Correlación lineal negativa
Y
Y
O
X
Correlación curvilínea positiva
Recta positiva con menor grado de
correlación que la de la grafica a).
O
X
Correlación curvilínea negativa
Y
O
X
Y
X
O
X
No existe correlación entre las variables
N
Nivel de
significación
de 0.05
Nivel de
significación
de 0.01
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
0.950
0.878
0.811
0.754
0.707
0.666
0.632
0.602
0.576
0.553
0.532
0.514
0.497
0.482
0.468
0.456
0.444
0.396
0.361
0.335
0.312
0.294
0.279
0.254
0.236
0.220
0.207
0.999
0.959
0.917
0.875
0.834
0.798
0.765
0.735
0.708
0.684
0.661
0.641
0.623
0.606
0.590
0.575
0.561
0.505
0.463
0.430
0.402
0.378
0.361
0.330
0.305
0.286
0.269
Para niveles de significación
comprendidos entre 0.01 y 0.05 se
pueden hacer interpolaciones.
34
El gerente de mercadotecnia de una cadena de tiendas de autoservicio desea determinar el efecto del espacio en las estanterías sobre
las ventas de alimentos para animales domésticos. Se seleccionó una muestra aleatoria de ocho tiendas cuyos resultados se presentan
en la tabla. Con un nivel de significación 0.01 determina si hay relación lineal entre las variables.
1
2
3
Tienda
Metros cuadrados de
estantería
Ventas semanales en miles
de pesos
Alameda
Buenavista
Centro
Bosque
Estancia
Américas
Garden
Poniente
1
1
2
2
3
4
5
6
16
18
30
25
50
65
75
90
Al inicio de un curso de Estadística, se somete a los estudiantes a un examen especial de Matemáticas. Se desea saber si hay o no una
relación entre la calificación de este examen especial y la calificación final en Estadística. Se selecciona una muestra aleatoria de once
estudiantes obteniéndose los siguientes resultados. Al nivel de significación 0.05 determina si hay relación lineal entre las variables.
Estudiante
Calificación examen especial
Calificación examen final
1
55
92
2
72
97
3
68
77
4
78
84
5
43
90
6
92
84
7
88
76
8
79
65
9
24
58
10
64
69
11
39
52
El administrador de una fábrica que produce cierto artículo de temporada desea estimar la función de costo total para la próxima
temporada. Con tal objeto de los archivos toma una muestra aleatoria de las últimas cinco temporadas, obteniendo la siguiente
información. Con un nivel de significación 0.02 determina si hay relación lineal entre las variables.
Temporada
Costo total anual (En miles de pesos)
Número de unidades producidas al año.
1993
1000
77
1994
2000
112
1995
3000
147
1996
2500
127
1997
2700
134
Los siguientes datos muestrales presentan la demanda de un producto (en miles de unidades) y su precio (en dólares) cobrado en seis
áreas de mercado distintas. Con un nivel de significación 0.03 determina si hay relación lineal entre las variables.
4
Precio
Demanda
18
9
10
125
14
57
11
90
16
22
13
79
Dada la información de un grupo de estudiantes, al nivel de significación 0.04 determina si hay relación lineal entre las variables.
5
6
Horas de estudio
Calificación examen
Anel
20
64
Beto
16
61
Cora
34
84
Dino
23
70
Emma
27
88
Fito
32
92
Gina
18
72
Hugo
22
77
El gerente de personal de una empresa considera que puede haber una relación entre el ausentismo al trabajo y la edad y desea usar la
edad de un empleado para predecir el número de días de ausencia durante un año. Selecciona una muestra aleatoria de diez
empleados, obteniéndose los siguientes resultados. Al nivel de significación 0.015 determina si hay relación lineal entre las variables.
Empleado
Edad en años
Días ausente al año
Anel
27
15
Beto
61
6
Claudia
37
10
Dionisio
23
18
Eufrasio
46
9
Guille
58
7
Hilario
29
14
Indalecio
36
11
Javier
64
5
Kent
40
8
El director de un programa de capacitación para supervisores en una compañía desea estudiar la relación entre la calificación de un
examen de aptitud efectuado al principio del programa y la calificación final otorgada al concluir el programa por un comité de
ejecutivos. Una muestra de ocho participantes reveló los resultados que se dan en la siguiente tabla. Con un nivel de significación
0.025 determina si hay relación lineal entre las variables.
7
8
Supervisor
A
B
C
D
E
F
G
H
Calificación examen de aptitud
63
49
72
58
78
61
59
58
Calificación en el examen final
81
65
91
78
99
74
80
77
La tabla siguiente muestra en (miles de dólares) los valores estimados y los precios de venta de ocho casas, que constituyen una
muestra aleatoria de todas las casas vendidas recientemente en un área suburbana. Con un nivel de significación 0.035 determina si
hay relación lineal entre las variables.
Valor estimado
Precio de venta
4.03
163.4
7.20
218.3
3.25
155.2
4.48
174.0
2.79
148.8
5.16
181.1
8.04
223.2
5.80
192.5
35
9
10
Los siguientes datos muestran los gastos de publicidad (expresados como un porcentaje de los gastos totales) y los beneficios
operativos netos (expresados como un porcentaje de las ventas totales) en una muestra aleatoria de 6 farmacias. Con un nivel de
significación 0.045 determina si hay relación lineal entre las variables.
Gastos en publicidad
Beneficios operativos netos
1.5
3.6
1.0
2.8
2.8
5.4
0.4
1.9
1.3
2.9
2.0
4.3
La tabla siguiente presenta el número de horas que una corredora corrió durante cada una de ocho semanas consecutivas y los
tiempos en minutos correspondientes en que corrió una milla al final de cada semana. Con un nivel de significación 0.012 determina si
hay relación lineal entre las variables.
Horas
Milla
13
5.2
15
5.1
18
4.9
20
4.6
19
4.7
17
4.8
21
4.6
16
4.9
Para los datos de la siguiente tabla de una fabrica ensambladora de automóviles, con un nivel de significación 0.022 determina si hay
relación lineal entre las variables.
11
12
13
Obrero
Meses de experiencia
Ensambles rechazados
A
7
26
B
9
20
C
6
28
D
14
16
E
8
23
F
12
18
G
10
24
H
4
26
I
2
38
J
11
22
K
1
32
L
8
25
En una universidad, se desea saber si existe alguna relación entre la calificación de los estudiantes en Matemáticas y su condición
física. Se tomo una muestra de 7 alumnos, y los datos obtenidos son los siguientes. Con un nivel de significación 0.032 determina si
hay relación lineal entre las variables.
Calificación de Matemáticas
Calificación en condición física
7. 5
6. 4
6. 7
7. 3
9. 6
8. 3
5. 6
5. 1
8. 2
9. 7
5. 2
6. 9
4.4
8.2
El coordinador de ventas de una empresa que ensambla y vende PC’s desea saber si existe alguna relación lineal entre la antigüedad
de cada vendedor y el número de PC’s que vende a la semana. El coordinador dispone de la siguiente información. Con un nivel de
significación 0.042 determina si hay relación lineal entre las variables.
Vendedor
Antigüedad en la empresa
PC’s vendidas a la semana
Ávila
4
5
Bolio
9
6
Cruz
1
2
Díaz
8
9
Elos
3
3
Fritz
6
7
Goya
6
3
Registro de la antigüedad (en años) de algunos de los trabajadores de una fabrica, y su sueldo mensual (en miles de pesos). Con un
nivel de significación 0.018 determina si hay relación lineal entre las variables.
14
15
16
Antigüedad
Sueldo
1
3
3
5
4
4
6
9
8
8
9
8
11
9
12
7
14
9
15
7
De una investigación para averiguar si existe alguna relación entre el sobrepeso en kilos de jóvenes y las horas que dedican a la
semana a ver TV y/o estar en la PC, se obtuvo la siguiente información. Con un nivel de significación 0.028 determina si hay relación
lineal entre las variables.
Nombre
Kilos sobrepeso
Horas en TV/PC
Alan
2
15
Bety
6
20
Caro
9
32
Dany
3
18
Ema
7
30
Fito
10
30
Gori
5
18
Hugo
9
24
Iris
12
31
Juan
5
22
El Depto. de Producción de NBD Electronics quiere ver la relación entre el número de empleados ensambladores y el número de
unidades ensambladas. Se seleccionaron al azar varios turnos, y se obtuvieron los siguientes resultados. Con un nivel de significación
0.038 determina si hay relación lineal entre las variables.
Empleados ensambladores en el turno
Unidades ensambladas en el turno
2
15
4
25
5
30
1
10
3
30
2
12
4
32
La tabla muestra la Temperatura en grados centígrados en una ciudad, y el número de gaseosas que se venden en un expendio cada
día. Con un nivel de significación 0.048 determina si hay relación lineal entre las variables.
17
Temperatura
Gaseosas
24°C
47
28°C
40
32°C
54
36°C
45
40°C
66
26°C
42
30°C
48
36