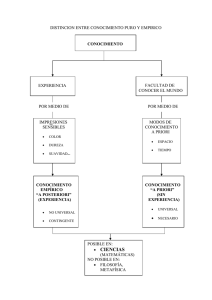
CERTEZA MATEMÁTICA Área de conocimiento: Matemáticas Millán González-Bueno Aguirre 2ºX DISTINCIÓN ANALÍTICO-SINTÉTICO • Proposición analítica: aquella que es verdad por definición. • Proposición sintética: aquella que no es analítica. EJEMPLO “Todas las casas negras son casas” “Todas las casas son negras” DISTINCIÓN A PRIORI-A POSTERIORI • Conocimiento a priori: aquel conocimiento que es independiente de la experiencia. • Conocimiento a posteriori: aquel conocimiento que no es a priori. EJEMPLO “Todos los solteros no están casados” “No todos los cisnes son blancos” TABLA DE CLASIFICACIÓN DEL CONOCIMIENTO Naturaleza de la proposición Analítica Sintética A priori 1🗸 3🗸 ¿Cómo es cognoscible? A posteriori2 ❌ 4🗸 MATEMÁTICAS COMO CONOCIMIENTO SINTÉTICO A POSTERIORI • John Stuart Mill • Generalizaciones empíricas alcanzadas por inducción. ¿Razón? • “2+2= 4” = “Todos los metales calentados se expanden” • Salto de abstracción. MATEMÁTICAS COMO CONOCIMIENTO ANALÍTICO A PRIORI • Resolver un problema sí misma . Deshacer una definición verdadera por • ¿Por qué son “complicadas” entonces las matemáticas? • Verdades triviales – no triviales. • Conjetura de Goldbach: “Todo número par mayor que dos se puede expresar como la suma de dos números primos”. • ¿Por qué encajan tan bien con la realidad? Sample Footer Text 3/11/2019 7 MATEMÁTICAS COMO CONOCIMIENTO SINTÉTICO A PRIORI • Conocimiento substancial. Verdades no triviales. • Razón como única forma de conocimiento. • Geometría euclidiana . • Modelo de pensamiento. • ¿Cómo puede la mente humana descubrir verdades en el mundo en base a la razón? CORRIENTES DE PENSAMIENTO MATEMÁTICO EMPIRISMO FORMALISMO PLATONISMO ¡MUCHAS GRACIAS POR VUESTRA ATENCIÓN! ¿Alguna pregunta?