Cuadernillo-6º-Básico-2017

COLEGIO SANTO DOMINGO
DEPARTAMENTO DE MATEMÁTICA
CUADERNILLO DE EJERCICIOS Y
PROBLEMAS DE MATEMÁTICA PARA
SEXTO BÁSICO 2017
NOMBRE:
__________________________________________________
Introducción:
Una de las formas más eficaces para estudiar matemática es repasar y aplicar
los conceptos y procedimientos analizados en clases a través de ejercicios y
problemas. Este cuadernillo pretende ser una ayuda que debes usar tanto en tu casa
como en el colegio con el fin de facilitar tu aprendizaje.
Algunos de los ejercicios
y problemas de las guías que forman parte del
cuadernillo han sido cuidadosamente seleccionados de los textos de estudio existentes
en el mercado y otros han sido creados por tus profesores.
Esperamos que este cuadernillo te sirva como apoyo para tu aprendizaje de la
asignatura de matemática en el presente año.
Muchos éxitos.
Departamento de Matemática
UNIDAD 0
Números Naturales y operaciones
Contenidos:
 Lectura y escritura de números naturales.
 Orden y composición de números naturales.
 Composición y Descomposición de números naturales.
 Adición y Sustracción de números naturales.
 Multiplicación y División de números naturales.
Objetivos:
 Leer, escribir y ordenar números de más de 6 cifras.
 Ordenar y comparar números de más de 6 cifras.
 Componer y descomponer grandes números utilizando diferentes
estrategias.
 Resolver ejercicios y problemas utilizando las cuatro operaciones.
Realiza las actividades con la información de la tabla.
Cantidad de habitantes por cada país (2013)
Estados Unidos
Australia
Brasil
318.900.000
23.130.000
200.400.000
Rusia
143.500.000
China
1.357.000.000
Canadá
35.160.000
Chile
México
Francia
17.620.000
122.300.000
66.030.000
1. Escribe con palabras la cantidad de habitantes de los países indicados.
a. Rusia 
__________________________________________________________________
b. Brasil 
__________________________________________________________________
c. Canadá 
__________________________________________________________________
2. Descompón aditivamente la superficie de los países indicados.
a. Canadá  _________________________________________________________
b. China
__________________________________________________________
c. Australia __________________________________________________________
3. Une cada descomposición de las superficies con la bandera del país que representa.
a. 1 CM+ 3 DMI+ 6 DM+5 UMI
b. 4 CM + 2 CMI
c. 1 CMI+ 5 CM+3 UMI + 4 DMI
4. Para cada par de banderas, encierra la que corresponde al país de mayor cantidad de
habitantes.
5. Responde cada pregunta utilizando la tabla inicial.
a. ¿Qué país tiene mayor cantidad de habitantes? ____________________________________
b. ¿Qué país tiene menor cantidad de habitantes? ____________________________________
c. ¿Cuántos más habitantes tiene China que Rusia? __________________________________
d. ¿Cuántos habitantes menos tiene Chile que México?
________________________________
e. ¿Cuántos habitantes reúnen Estados Unidades y Canadá? ___________________________
Resuelve:
1.-
2.-Si una persona quiere comprar los siguientes tres artículos ¿Cuánto debe pagar?
La persona debe pagar:$_________________________
Resuelve:
a)
1. 674.927
‒ 562.703
b)
223.503.482
‒ 11.672.130
c)
57.612.004
‒ 2.201.856
d) 756.250.000
‒ 12.634.561
Resuelve:
a. Se necesita repartir equitativamente 1 789 208 teléfonos celulares entre 278 tiendas.
¿Cuántos equipos llegarán a cada una?
b. Vicente quiere calcular cuántas personas podrían votar en el colegio donde estudia.
Si hay 109 mesas y en cada mesa hay 250 personas inscritas, ¿cuántas personas
podrían hacerlo?
UNIDAD I: MÚLTIPLOS Y FACTORES
Contenidos:
 Múltiplos.
 Factores.
 Números primos.
 Factorización prima.
Objetivos:




Conocer múltiplos y factores de un número.
Resolver problemas que involucren múltiplos y factores.
Reconocen los números primos menores de 30.
Calculan el Mínimo Común Múltiplo utilizando la factorización prima.
1. Aplica el método del árbol de factores para descomponer cada número en factores
primos.
48
48
282
360
360
458
100
298
2. Completa con el factor primo que falta en cada caso.
a. 120 = 2 ∙ 2 ∙ 2 ∙ ____ ∙ 3
c. 90 = 3 ∙ ____ ∙ 3 ∙ 5
b. 64 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ ___ ∙ 2
d. 150 = 5 ∙ 3 ____ ∙ 2
3. Encierra de color azul el m.c.m. y de rojo el m.c.d. entre los números dados.
a. 32 y 128
16
32
64
128
b. 24, 36 y 48
12
24
144
288
c. 40, 50 y 60
5
10
600
1 200
d. 14, 28 y 56
7
14
28
56
4. Completa con una cifra tal que el número sea divisible por el valor indicado.
Divisible por:
2
3
5
10
24___
4 5___2
2 ___25
89___
7 ___44
___5
6 47___
3 4___0
38 61___
54 78___
145 ___00
36 44___
___5 478
85___ 252
11 2___5
27 89___0
56 4___0
24 ___25
35 44___
31 42___
5. Resuelve cada problema.
a. ¿De cuántas maneras distintas se pueden repartir 64 litros de jugo en envases de
igual capacidad si estos deben tener más de 2 L y menos de 10 L?
b. Javiera, María y Constanza irán a un paseo de curso y quieren gastar la misma
cantidad de dinero cada día. ¿Cuánto dinero podrán desembolsar diariamente si el
paseo dura 3 días? ¿Y si dura 5 días? ¿Y si dura 10 días? Completa la tabla.
Nombre
Dinero ($)
Javiera
17 580
María
55 380
Constanza
35 430
3 días
5 días
10 días
6. Encierra en círculo todos los números primos que encuentres.
3
4
5
6
7
9
13
15
16
18
21
23
25
29
30
7. Anota los 8 primeros múltiplos de:
a) M 5 = {
b) M11= {
c) M 8 = {
d) M18= {
8. Encuentra el Mínimo Común Múltiplo (M.C.M) entre:
a) M.C.M 4 y 6 =
b) M.C.M 5 y 8 =
9. Escribir como producto de números primos los siguientes números
4
18
40
75
6
20
42
80
8
21
45
81
I) Encuentra el MCM ( Mínimo Común Múltiplo) de los siguientes números:
MCM (4,6)
MCM (3,4)
MCM (8,12)
MCM (5,7)
MCM (7,12)
MCM (9,15)
MCM (10,12)
MCM (25,50)
MCM (25,50)
MCM (12,24)
MCM (4,8)
MCM (3,9)
MCM (4,20)
MCM (60,90)
MCM (6,8,12)
MCM (6,8,12)
MCM (8,12,20)
MCM (10,12,15)
MCM (6,9,15)
MCM (16,20,24)
MCM (10,20,40)
II) Encontrar los conjuntos de números que cumplen con las condiciones pedidas y
anota tus respuestas en el cuaderno.
1) Múltiplos de 5 mayores que 42 y menores que 57
2) Múltiplos de 30 que sean a la vez múltiplos de 20, menores que 100
3) Múltiplos de 3 mayores que 20 y menores que 30
4) Múltiplos de 15 entre 50 y 100
5) Múltiplos de 40 que sean a la vez múltiplos de 8 entre 20 y 70
6) Múltiplos de 50 que sean menores que 200 y múltiplos de 30 a la vez
7) Números primos que sean pares
PREGUNTA 1
HABILIDAD: P. OPERACIONAL
FECHA: __________________
El resultado de la siguiente operación es
6.489
x
46
a)
b)
c)
d)
38.934
25.956
298.494
289.304
PREGUNTA 2
HABILIDAD: P. OPERACIONAL
El producto de 1.500 y 100.000 es:
a)
b)
c)
d)
150 millones
50 millones.
105 millones.
100 millones.
11
FECHA: __________________
PREGUNTA 5
HABILIDAD: P. LÓGICO
FECHA: __________________
¿Cuál es el número que sigue en la siguiente secuencia lógica 64, 49, 36, 25, ?
a)
b)
c)
d)
12
18
14
16
PREGUNTA 6
HABILIDAD: P. LÓGICO
FECHA: __________________
¿Cuál es el número que sigue en la siguiente secuencia 3, 5, 9, 11, ?
a)
b)
c)
d)
12
13
15
16
12
PREGUNTA 7
HABILIDAD: P. CRÍTICO
FECHA: __________________
Carlos ordena las fotos de sus vacaciones en un álbum; él sacó 138 fotos y cada
página del álbum tiene lugar para seis fotos ¿Cuál es la menor cantidad de
páginas que tiene ocupadas?
a)
b)
c)
d)
22
23
24
20
PREGUNTA 8
HABILIDAD: P. CRÍTICO
FECHA: __________________
Si el perímetro de un rectángulo es 44 cm, y uno de sus lados mide 13 cm.
¿cuánto mide el área?
a) 57 cm
b) 117 cm2
c)
162 cm2
d) 22 m.
13
SINTESIS UNIDAD
1. Encierra en cada fila el resultado de cada multiplicación.
a. 780 · 234

18 252
182 520
1 825 520
b. 82 678 · 45

37 205 510
370 205
3 720 510
c. 345 609 · 12

41 147 308
4 147 308
447 308
2. Encierra en cada fila el cociente de cada división.
a. 1 888 : 32

590
59
509
b. 10 230 : 3

3 410
34 410
341
c. 9 333 279 : 27

345 677
34 567
3 456
d. 2 860 560 : 36

794 609
79 640
79 460
3. Resuelve cada operación.
a. 30 · 9 + 56 : 4 =
c. (134 + 56) : 19 + 6 · (546 – 87)
b. 2 · {6 · (7 + 4) · (5 · 3 – 8)} – 4 · (45 – 8)} d. 2 800 : 2 + 904 – 228 · 3
14
4. Escribe una “V” si la afirmación es verdadera o una “F” si es falsa. Justifica las
falsas.
a. ____ 1 112 es múltiplo de 4.
_________________________________________________________
b. ____ 1 es múltiplo de todos los números naturales.
_________________________________________________________
c. ____ 2 es divisor de todos los números naturales.
_________________________________________________________
d. ____ Solo se pueden determinar los divisores de algunos números naturales.
_________________________________________________________
5. Escribe todos los divisores de cada número. Luego, identifica si el número es
primo o compuesto. Para ello, marca un  según corresponda.
Número
Divisores
Primo
Compuesto
24
17
42
23
34
45
6. Resuelve:
a. Se necesita repartir equitativamente 1 789 208 teléfonos celulares entre 278
tiendas. ¿Cuántos equipos llegarán a cada una?
b. Vicente quiere calcular cuántas personas podrían votar en el colegio donde
estudia. Si hay 109 mesas y en cada mesa hay 250 personas inscritas,
¿cuántas personas podrían hacerlo?
15
UNIDAD II: FRACCIONES
Contenidos:
 Adición y sustracción de fracciones.
 Multiplicación de fracciones.
 Fracción de una fracción.
 División de una fracción.
Objetivos:
 Resuelven adiciones y sustracciones de fracciones con distinto
denominador
 Calculan el producto entre dos o más fracciones.
 Calculan el valor de una fracción de una fracción.
 Calculan el cuociente entre dos fracciones.
1. Representa las siguientes fracciones en la recta numérica:
1 3 1 1 5
, , , ,
2 4 4 8 8
2. Expresa cada fracción impropia como número mixto.
a.
56
=
12
c.
128
=
28
e.
b.
79
=
24
d.
655
=
118
f.
765
=
60
893
=
345
3. Resuelve los siguientes problemas:
a. Manuel compró 2
3
25
kg de tomates y su vecino Javier adquirió
kg. ¿Quién
4
8
compró más tomates? ¿Por qué?
16
b. Daniela y Carla repartieron pizzas de la siguiente forma: a Jorge
1
, a Ignacio
3
1
1
y a Romina . ¿Quién comió más pizza?
8
4
4. Calcula la fracción de cada número.
a.
1
de 88 →
8
d.
5
de 36 →
6
b.
2
de 45 →
3
e.
7
de 45 →
15
c.
4
de 18 →
9
f.
9
de 52 →
13
5. Resuelve las siguientes operaciones. Recuerda simplificar cuando sea
posible.
a.
6 7
 
5 4
e.
4 2
: 
9 6
b.
4 3 2
  
5 6 4
f.
12 18
:

15 30
c.
3 4 12
 

5 8 6
g.
12 5 72
:


8 24 25
d.
6 7
: 
5 4
h.
5 16 24

:

12 25 30
17
GUÍA: FRACCIONES
I) Resolver las siguientes adiciones y sustracciones simplificando el
resultado cuando sea posible
5 2
4
2
3
7
4



1)
7)
13) 9  4
9 9
15 15 15
9
9
2)
3 5

11 11
8) 4
1
3
2
5
5
14) 7
2
4
3
5
5
3)
2 3

7 7
9) 3
3
1
5
9
9
15) 3
2
4
1
9
9
4)
5
3

10 10
10) 2
1
1
3
2
2
16) 7
5
7
6
8
8
5)
7 5

9 9
3
5
11) 1  4
6
6
17) 3
9
5
1
12
12
6)
13 5

14 14
12) 3
8
4
7
15
15
18) 7
5
2
4
6
6
II) Resolver las siguientes adiciones y sustracciones simplificando
transformando a número mixto el resultado cuando sea posible
6)
9 1

15 5
1 3

5 7
7)
5
8

12 15
2 3

3 4
8)
5 2
4) 
9 3
9)
8 3

5)
9 5
10)
1 2
1) 
7 9
2)
3)
12)
13)
3 4

8 9
2 4

3 7
3 1

16 8
14)
3 2

5 9
2 1

5 12
15)
1 8

4 6
4 1

5 6
16)
6 3

8 4
11)
3 0

4 5
18
17) 12
18)
6
3
5
3
8
6
3
1
4
7
5
19) 12
20)
y/o
5
1
3
20
2
III) Resolver los siguientes ejercicios de operatoria combinada
 5 1  1 3 
1)      1  
 6 4  2 5
2)
6)
4  1 2
  
15  5 3 
2 1 1
  
7 5 3
1 5  1
7)    
 7 14  2
 3 1 1
3)    
 4 5  10
2  3
5
 3
8)  2  4    2  3 
 5
3  4
6
4)
1  9
20 
 3
4 
9)  4  2    5
 7
2   14
21
 3 5  1 3 
5)       
 8 6   2 12 
1  1
5
 6
10)  3  4    7  3 
 8
4  2
6
IV)Resolver
las siguientes multiplicaciones de fracciones
1)
3 7

5 8
8)
5 4

9 5
15)
4 3

9 8
2)
4 5

9 11
9)
3 2

8 3
16)
7 10

15 21
3)
2 5

7 9
10)
1 2

2 5
17)
12 10

25 27
4)
3 1

4 2
11)
2 9

9 15
18)
8 15

9 16
5)
4 1

5 8
12)
5 3

6 5
19)
6 35

7 36
6)
7 3

10 7
13)
2 7

7 10
20)
4 21

7 26
7)
2 3

3 5
14)
7 2

12 7
21)
16 49

21 80
19
IV) Resolver las siguientes multiplicaciones con fracciones y números mixtos
1)
7
2
3
8
3
6)
2)
3 4
1
5 9
7)
7 4
3) 1 
8 5
8) 6
1
6
3
4
10
4)
2
1
3
3
4
9) 3
4
1
2
7
2
5)
7
1
3
8
21
10)
V) Resolver los siguientes ejercicios de operatoria combinada
5
1)  
6
1 3

2 4
 2 1 1
2)    
 3 5 6
2 4  1
3)      
 7 21  2
4)
1

4
5 4 3 
  
9  7 14 
 3 1   3 1
5)       
 4 2  5 6
20
VI) Calcular
1)
2
de 12
3
4)
4
de 28
7
7)
7
de 72
24
2)
3
de 16
4
5)
8
de 44
11
8)
8
de 39
13
3)
2
de 35
7
6)
2
de 27
3
9)
7
de 75
15
VII) Calcular
1)
3
de 18
5
4)
4
de 15
6
7)
4
de 12
7
2)
4
de 21
5
5)
9
de 28
7
8)
3
de 18
8
3)
3
de 10
7
6)
3
de 12
5
9)
5
de 23
9
VIII) Calcular
1)
5
4
de
7
9
4)
2
5
de
5
6
7)
8
5
de
9
12
2)
3
3
de
8
5
5)
1
1
de
3
4
8)
4
28
de
7
23
3)
2
3
de
3
10
6)
3
5
de
5
6
9)
17 35
de
21 51
21
IX) Resuelve las siguientes divisiones con fracciones y números mixtos
15 5
 =
16 8
12 4
 =
35 7
7 1
 =
8 2
5 7
 =
6 8
7 21
 =
8 32
7 4
 =
9 7
5 10
 =
6 21
7 5

=
12 24
5 25

=
16 32
4
1
2 4 =
7
2
X) Resuelve los siguientes ejercicios de operatoria combinada
1 1 3
  
6 2 4
3 1 3 1
    
4 2 5 6
2 1 3
  
 3 5 5
 4   5 1
  1   2  1 
 3   9 3
2 4  1 1
    
 7 21   2 4 
1
 1 5  1
2   2  2 
3
 2 6   10
5 4 3 
  
9  7 14 
 7 14   7 10 
    
 9 15   10 21 
Resolver los siguientes problemas
1) Valentina tenía 18 bolitas, perdió
1
6
de ellas en el colegio ¿Cuántas bolitas le
quedan?
22
2) La señora Álvarez utilizó todas las velas rojas de una caja y le quedaron
total de velas que traía la caja. Si
1
2
3
del
de las velas que sobraron son azules
4
¿Qué parte de la caja entera eran velas azules?
3) Paula se comió
2
3
de su chocolate en el primer recreo y le dio el resto a su
amiga Soledad; En el segundo recreo Soledad compró 3 chocolates iguales al
de Paula y se comió 2 y medio, le dio
3
4
del resto a Paula y lo que le quedó a
su hermano Jorge ¿Cuánto chocolate comió cada uno en total?
4) Álvaro compró un terreno de
3
4
de hectárea; le da a su hijo Juan Pablo
terreno. ¿De que tamaño es el terreno de Juan Pablo?
23
2
9
del
PREGUNTA 1
Los
HABILIDAD: P. OPERACIONAL
FECHA: __________________
5
4
de
son
8
7
a) 20
10
b)
14
3
c)
5
5
d)
14
PREGUNTA 2
Los
HABILIDAD: P. OPERACIONAL
2
de 45 corresponden a:
5
a)
b)
c)
d)
2
9
18
112
24
FECHA: __________________
PREGUNTA 3
HABILIDAD: COMPRENSIÓN
FECHA: __________________
La única de las siguientes multiplicaciones donde no es posible simplificar
cruzado es:
3 5

4 6
12 3

b)
25 4
5 10

c)
7 21
5 23
d)

23 24
a)
PREGUNTA 4
HABILIDAD: P. LÓGICO
FECHA: __________________
¿Cuál es el número que continua en la siguiente secuencia
48
144
120
b)
360
36
c)
96
42
d)
120
a)
25
1 2 6 24
, , , es?
3 6 18 72
PREGUNTA 5
HABILIDAD: P. LÓGICO
FECHA: __________________
¿Cuál es el número que continua en la siguiente secuencia
1 3 9 27
, , , es?
2 4 8 16
54
32
81
b)
32
36
c)
28
42
d)
36
a)
PREGUNTA 6
HABILIDAD: P. OPERACIONAL
El producto de las fracciones
2
5
y
es:
5
7
7
12
7
b)
35
2
c)
7
10
d)
12
a)
26
FECHA: __________________
PREGUNTA 7
HABILIDAD: COMPRENSIÓN
FECHA: __________________
En el dibujo se representa
a) 9
b) 15
2
c)
3
3
d)
de 15
5
PREGUNTA 8
HABILIDAD: COMPRENSIÓN
FECHA: __________________
La fracción representada con mayor grosor corresponde a:
0
2
3
2
b)
3
2
c)
5
3
d)
5
a)
27
1
PREGUNTA 9
HABILIDAD: P. LÓGICO
La fracción que sigue en la secuencia :
FECHA: __________________
1 3 5 7
, , ,
es:
3 5 9 11
3
4
8
b)
12
9
c)
13
11
d)
15
a)
PREGUNTA 10
HABILIDAD: P. LÓGICO
FECHA: __________________
La primera fracción irreductible que sigue en la secuencia
10
16
5
b)
8
13
c)
19
16
d)
22
a)
28
1 4 7
,
,
,
7 10 13
UNIDAD III: DECIMALES
Contenidos:
 Equivalencias entre fracciones y decimales
 Multiplicaciones entre decimales y naturales.
 Multiplicaciones entre decimales.
 Divisiones de decimales con cuociente decimal.
 Divisiones con dividendo decimal y divisor natural.
 Divisiones con dividendo y divisor decimal.
Objetivos:
 Representan decimales como fracción y viceversa.
 Calculan el producto entre decimales.
 Calculan el cuociente entre decimales.
1. Representa gráficamente cada número decimal.
a. 0,7
b. 0,2
c. 1,6
2. Escribe los siguientes números decimales como fracciones:
a. 2,3 =
b. 7,6535 =
c. 45,3 =
3. Resuelve las siguientes adiciones y sustracciones:
a. 0,25865 + 0,0258 =
c. 8,789 – 6,58 =
b. 822,30 – 30,29021 =
d. 16,002 + 24,25465 =
4. Completa la tabla multiplicando los números.
∙
4
16
20
28
0,25
1,87
29
70
81
100
250
5. Resuelve cada división.
a. 458,424 : 24 =
b. 856,98 : 9 =
c. 275,666 : 8 =
6. Calcula las siguientes multiplicaciones y divisiones:
a. 2,5 · 3,8
b. 1,25 · 1,7
c. 3,6 : 1,2
d. 15,4 : 5,5
NIVEL
AVANZADO
NIVEL
INTERMEDIO
NIVEL
INICIAL
7.Transforma los siguientes números decimales en fracciones.
a) 0,1 =
b) 0,001=
c) 0,00001 =
d) 0,3 =
e) 0,05 =
f) 0,009 =
g) 0,14 =
h) 0,0053=
i)
j)
k) 0,02001 =
l) 0,309 =
m) 7,2 =
n) 4,002=
o) 65,00001
q) 2,0054 =
r) 9,019 =
0,00029 =
p) 6,3 =
=
30
0,802 =
8. El siguiente cuadro muestra los precios por kilogramo de algunos productos.
Responde las preguntas considerando la información que se entrega.
Damascos
$750
Jamón
$4 120
Tomates
$620
Papas
$550
Queso
$3 980
Naranjas
$450
a. ¿Cuántos kilogramos de damascos puede comprar Camila con $1 875?
b. Luisa compró 8,6 kg de naranjas, 0,5 kg de tomates, 0,25 kg de queso y 1,5 kg
de damascos. ¿Cuánto dinero gastó?
c. Adela tenía $10 000 y compró 2,6 kg de naranjas, 1,3 kg de papas, 0,5 kg de
queso, 1,4 kg de jamón y 0,5 kg de tomates. ¿Cuánto dinero recibió de vuelto?
NIVEL
AVANZADO
NIVEL
INTERMEDIO
NIVEL
INICIAL
9. Resuelve las siguientes multiplicaciones.
a)
0,3  2 =
b)
0,7  3
c)
0,12  4 =
d)
0,25  6 =
e)
0,6  0,5 =
f)
0,8  0,1
g)
0,15  0,4 =
h)
0,32  0,7 =
i)
4,5  0,2 =
j)
5,03  1,2
k)
6,25  9,3 =
l)
1,078  6,4 =
31
GUÍA DE NÚMEROS DECIMALES
I)
Resuelve las siguientes adiciones:
1)
2,34 + 1,28
2)
0,78 + 1,45
3)
0,57 + 0,7
4)
2,67 + 0,931
5)
0,502 + 0,23
6)
0,97 + 2,451
7)
48,2 + 3,98
8)
38,04 + 7,342
9)
2,05 + 0,2
II)
Resolver las siguientes sustracciones
1)
9,04 – 6,7
2)
3,58 – 2,07
3)
2,45 – 0,8
4)
2,96 – 0,097
5)
2,4 – 1,582
6)
7,56 – 1,237
7)
8,057 – 2,75
8)
7,37 – 3,936
9)
1,04 – 0,0945
III)
Resolver las siguientes multiplicaciones
1)
2,4 · 3
2)
0,8 · 5
3)
0,56 · 4
4)
0,25 ·12
5)
2,46 · 3
6)
0,8 · 2,2
7)
1,5 ·3,8
8)
0,4 · 0,6
9)
0,56 · 3,1
IV)
Resolver las siguientes divisiones
1)
23:4
2)
45:8
3)
63: 6
4)
46,8:9
5)
6,23:7
6)
8,56 : 8
7)
2,505: 3
8)
3,45: 12
9)
0,068:4
10)
2,17: 5
V)
Resolver los siguientes ejercicios combinados:
1)
0,638 + 0,51
2)
2,19 + 6,704 + 5,8
3)
3,5 + 9,501 + 0,708
4)
12,8 + 3,26 + 6,0948 + 3
5)
( 2,4 + 3,49) - (12 - 7,92)
6)
(4,243 - 1,96) + (2,34 - 1,111)
7)
(6,78 + 2 + 3,642) - ( 13,8 - 7,94)
8)
(2 - 1,593) - (0,045 + 0,23+ 0,12)
32
GUÍA : PROBLEMAS CON DECIMALES
I) Resolver los siguientes problemas:
1) La casa de Juan queda a 1,78 km de su colegio; la de Pedro queda a 0,6
km del colegio. Un día Juan se va caminando de su casa al colegio y luego
camina del colegio a la casa de Pedro. Finalmente su papá lo va a buscar
en auto en la tarde ¿Cuánto caminó Juan ese día? ¿Si Pedro se fue
caminando de su casa al colegio ¿Cuánto caminó él ese día?
2) Gabriel pesa 14,4 kg y su hermano Simón pesa 14,64 kg; ¿Cuál es más
pesado? ¿Cuál es la diferencia de sus pesos?
3) Rodrigo debe pagar el dividendo de su casa todos los meses; el valor de
éste es de 12,9 UF siendo el valor de la UF $ 22.250,4 el día del pago
¿Cuánto pagará Rodrigo este mes por el dividendo de su casa?
4) En una carrera de 400m un corredor hace 8 metros por segundo y otro 6,75
metros por segundo ¿Cuánto antes llegará el primero?
33
PREGUNTA 1
HABILIDAD: P. OPERACIONAL
FECHA: __________________
El resultado del siguiente ejercicio 2,19 + 6,704 + 5,8 es
a)
b)
c)
d)
6,981
12,723
7,503
14,694
PREGUNTA 2
HABILIDAD: P. OPERACIONAL
El resultado del siguiente ejercicio 7 6,23 es:
a)
b)
c)
d)
0,89
89
8,9
0,089
34
FECHA: __________________
PREGUNTA 4
HABILIDAD: COMPRENSIÓN
FECHA: __________________
Cuál de los siguientes decimales es menor que 0,389
a)
b)
c)
d)
0,4
0,39
0,379
0,432
PREGUNTA 5
HABILIDAD: P. LÓGICO
En la siguiente serie 8,16 ; 8,24 ; 8,32 ; 8,4
¿Cuál es el número que continúa en la serie?
a)
b)
c)
d)
8,36
8,38
8,48
8,42
35
FECHA: __________________
PREGUNTA 6
HABILIDAD: P. LÓGICO
FECHA: __________________
Cuál de los siguientes decimales se puede intercalar para que se cumpla con el
orden establecido
0,32 <
a)
b)
c)
d)
0,47
<
<
0,62
0,398
0,439
0,690
0,58
PREGUNTA 7
HABILIDAD: P. CRÍTICO
FECHA: __________________
Un programa computacional cuesta 118 dólares. Si un dólar equivale a 471,15
pesos ¿Cuál es el valor del programa en pesos?
a)
b)
c)
d)
589,15
8.395,7
55.595,7
8.480,7
36
UNIDAD IV: RAZONES Y PORCENTAJES
Contenidos:
 Concepto de Razón
 Razones iguales
 Concepto de Porcentaje
 Porcentajes como fracciones o decimales
 Porcentaje de un número
 Cálculo del tanto por ciento
 Cálculo del 100%
Objetivos:
 Interpretar y representan razones.
 Calcular porcentajes.
GUÍA RAZONES
Escribir la razón pedida en cada uno de los siguientes casos:
1) En una fábrica trabajan 40 hombres y 25 mujeres encontrar la razón entre
 El número de hombres y el número de mujeres
 El número de hombres y el total de trabajadores
 El número de mujeres y el total de trabajadores
2) Escribir la razón que corresponde a cada una de las siguientes expresiones
 2 cucharadas por litro
 6 sobres para cada 18 personas
 10 autitos por cada 2 niños
 Dos cajas para cada 5 alumnos
 Por cada dos tazas de arroz, tres tazas de agua
3) A los alumnos de 8º básico de un colegio se les consultó acerca del lugar que
preferían para pasar sus vacaciones. Las respuestas son las siguientes:
Lugar de
vacaciones
Preferencias
Playa
Campo
14
9
Montaña Ciudad Viaje al
extranjero
6
4
12
Utilizando los resultados de esta encuesta y expresa la razón de dos formas
distintas:
a)
Entre ciudad y playa:
b)
Entre campo y montaña:
c)
Entre viaje al extranjero y playa:
d)
Entre campo y el total:
37
4. Pinta las estrellas e indica la razón del total que representan en cada conjunto
de figuras.
5. Escribe un enunciado que represente las siguientes razones:
Razón
Enunciado
5:7
3:9
6. Escribe tres razones equivalentes a la razón dada.
a.9 : 6 → _________→ _________→ _________
b.12 : 5 → _________→ _________→ _________
c.7 : 24 → _________→ _________→ _________
d.8 : 56 → _________→ _________→ _________
7. Calcular el valor de las siguientes razones
1) 24 : 8
2) 4: 8
3) 6:24
4) 21 : 7
5)
4
16
6) 8:25
38
III) Resolver los siguientes problemas
1) Una receta dice que hay que echar 5 cucharadas de azúcar por cada 2 tazas de
harina
a) Escribir la razón que se establece en la situación
b) Si en total voy a ocupar 15 tazas de harina ¿Cuánta azúcar necesito?
2) En una casa hay 2 mujeres por cada hombre. Si en la casa vive el papá, la
mamá la abuela los hijos e hijas y en total hay 9 personas ¿Cuántos hijos
hombres hay?
3) La razón entre las damas y varones en un curso es 3 : 5. En el curso hay 12
damas ¿Cuántos varones hay en el curso?
4) En un grupo scout la razón entre los niños y los adultos es 5:2 . Hay 16
adultos ¿Cuántas personas tiene el grupo scout?
39
GUÍA PORCENTAJES
1. Calcula el porcentaje utilizado por cada figura en la siguiente cuadrícula:
Figura 1:__________ Figura 2:__________ Figura 3:________
2. Crea un diseño sobre la cuadrícula, de modo que el 12 % de los cuadraditos
sea de color rojo, el 20 % de color azul, el 16 % de color amarillo, el 28 % de
color verde y el 8 % de color café. Luego, responde las preguntas.
a. ¿Qué porcentaje quedó sin colorear?
_____________________________________
b. ¿Cuántos cuadraditos no se pintaron?
____________________________________
2. Ordena de menor a mayor los siguientes valores.
20 % de 500
75 % de 300
50 % de 250
30 % de 150
_______________ < _______________ < _______________ < _______________
40
3. Completa la tabla con los valores pedidos.
Producto
Precio ($)
Descuento
(%)
Radio
13 000
18
Vestido
18 500
Bicicleta
12 000
Bolso
5 990
Valor por pagar
($)
13 875
15
1 797
Pelota
Zapatillas
Descuento
($)
8 393
8
3 597
1 952
4. Resuelve cada problema.
a. Por la compra de un computador de $199 900 se le ofrece al cliente un
descuento de 19 %. ¿A qué monto equivale el descuento?
b. Catalina quiere adquirir un pantalón que tiene 18 % de descuento y una blusa
que tiene 26 % de descuento. Si el pantalón cuesta $23 900 y la blusa $27 900,
¿cuánto deberá pagar Catalina por su compra?
c. En un curso de 45 estudiantes, 27 son mujeres. ¿Qué porcentaje de los
estudiantes del curso son hombres?
41
I) Completa la siguiente tabla:
Porcentaje
Fracción
1
2
Decimal
25%
0,45
0,75
4
5
90%
II) Transformar a fracción los siguientes tanto por ciento
1) 20%
5) 40%
9) 10%
13) 38%
17) 200%
2) 35%
6) 75%
10) 100%
14) 12%
18) 500%
3) 25%
7) 23%
11) 50%
15) 45%
19) 125%
4) 1%
8) 18%
12) 5%
16) 59%
20) 250%
III) Transformar a tanto por ciento las siguientes fracciones
1)
21
100
5)
95
100
9)
2
5
13)
1
2
17)
1
20
2)
57
100
6)
147
100
10)
23
50
14)
3
4
18)
4
50
3)
38
100
7)
350
100
11)
4
25
15)
8
25
19)
36
25
4)
79
100
8)
3
10
12)
18
40
16)
9
15
20)
27
20
42
IV) Calcular
1) El 25% de 48
6) El 8% de 25
11) El 25% de 178
2) El 5% de 60
7) El 6% de 150
12) El 75% de 345
3) El 10% de 70
8) El 4% de 75
13) El 50% de 0,6
4) El 50% de 14
9) El 70% de 120
14) El 25% de 5,2
5) El 75% de 76
10) El 85% de 220
15) El 25% de 0,28
V)Resolver
1) ¿Qué % es 30 de 40?
2) ¿Qué % es 42 de 105?
3) ¿Qué % es 15 de 60?
4) ¿Qué % es 4 de 200?
5) ¿Qué número es si el 20% es 5?
6) ¿Qué número es si el 45% es 18?
7) ¿Qué número es si el 250% es 75?
8) ¿Qué número es si el 50% es 12?
43
VI) En un supermercado se ofrece un listado de productos que tienen un 25% de
descuento. Completa la siguiente tabla de acuerdo a esa rebaja.
Precio
Rebaja
Precio final
$ 1.200
$ 5.300
$ 256
$ 10.880
VII) Resuelve los siguientes problemas:
1) Una tienda tiene todos sus artículos con un 30% de descuento, calcula el precio
de venta de los siguientes productos:
Zapatillas $ 30.000
Jeans $ 25.500
Poleras $ 9.000
Polerón $ 12.000
Cinturón $ 8.000
2) El I.V.A es un impuesto que pagan los consumidores y hoy en día equivale al
19% del precio final de un producto. Aplica el IVA a los siguientes valores y calcula
el precio final.
Producto
Automóvil
Computador
Impresora
Teléfono
Precio s/IVA
$ 5.500.000
$ 400.000
$ 36.000
$ 75.000
IVA
Precio final
3) En un curso de 40 alumnos se sabe que:
a) El 45% son mujeres
b) El 20% obtuvo nota bajo 4 en la prueba de castellano
c) El 25% obtuvo nota sobre 6 en el trabajo de ciencias
¿Cuántos hombres tiene el curso?
¿Cuántos alumnos obtuvieron en castellano una nota al menos suficiente?
¿Cuántos alumnos obtuvieron nota sobre 6 en ciencias?
44
Pregunta 1
Habilidad : Pensamiento
Fecha
Critico
Cristina ocupa 48 ovillos de hilo, para tejer 3 chalecos de igual tamaño. ¿Cuántos
ovillos necesitará para tejer 4 chalecos similares?
A)
B)
C)
D)
64
36
16
12
Pregunta 2
Habilidad : Pensamiento
Fecha
Critico
Cristián ganó $ 180.000 por 15 días de trabajo. ¿Cuánto dinero recibirá si en total
trabaja 60 días, en las mismas condiciones?
A)
B)
C)
D)
$ 12.000
$ 360.000
$ 450.000
$ 720.000
Pregunta 3
Habilidad Pensamiento
Operacional
Fecha
El valor de la razón 10 : 4 es
A)
B)
C)
D)
10,4
5,2
2,5
0,4
Pregunta 4
Habilidad Comprensión
Fecha
En un recipiente se mezclan 6 litros de pintura verde y 4 litros de pintura blanca ,
entonces la comparación por cuociente respectivamente es :
A) 4 : 6
B) 8 : 12
C) 2 : 3
D) 6 : 4
45
Pregunta 5
Habilidad Comprensión
Fecha
Dada la razón 3 : 5 entonces otra razón equivalente es :
A) 5 : 3
B) 10 : 6
C) 12 : 20
D) 21 : 5
Pregunta 6
Habilidad Pensamiento
Fecha
Crítico
Con 6 kilos de harina se fabrican 8 kilos de pan ¿Cuánta harina se necesita para
fabricar 20 kilos de pan?
A)
B)
C)
D)
80/ 3 kilos
22 kilos
20 kilos
2,4 kilos
Pregunta 7
Habilidad Pensamiento
Operacional
Fecha
La única afirmación falsa con respecto al 20% de un número es:
A)
B)
C)
D)
El 20% de un número es el doble del 10% del número
El 20% de un número es lo mismo que el número dividido en 5
El 40% de un número es el doble del 20% del mismo número
El 60% de un número es lo mismo que 4 veces el 20% del mismo número
Pregunta 8
Habilidad : Pensamiento
Operacional
El 10 % de 10 es
A)
B)
C)
D)
10
100
1
0,1
46
Fecha
Pregunta 9
Habilidad : Pensamiento
Operacional
Fecha
¿Qué porcentaje es 30 de 40?
A) 50%
B) 30%
C) 75%
D) 80%
Pregunta 10
Habilidad : Comprensión
Fecha
Si el 63% de una botella está llena. ¿Qué tanto por ciento de la botella está vacía?
A)
B)
C)
D)
73%
63%
37%
36%
Pregunta 11
Habilidad : Pensamiento
Lógico
Fecha
El 20% de las páginas de un libro corresponde a 60 páginas entonces es falso que:
A)
B)
C)
D)
El 10% de las páginas corresponde a 30 páginas
El 40% de las páginas corresponde a 120 páginas
El 50% de las páginas corresponde a 150 páginas
El 100% de las páginas corresponde a 600 páginas
Pregunta 12
Habilidad : Pensamiento Lógico
Fecha
La única asociación incorrecta es::
A) El 50% de un número equivale a su mitad
B) El 20% de un número equivale a su quinta parte
C) El 30% de un número equivale a su tercera parte
D) El 25% de un número equivale a su cuarta parte
47
UNIDAD V: INTRODUCCIÓN AL ÁLGEBRA
Contenidos:
 Lenguaje algebraico
 Secuencias
 Ecuaciones
Objetivos:
 Relacionar el lenguaje cotidiano con el lenguaje algebraico.
 Completar secuencias.
 Descubrir término general.
 Resolver ecuaciones.
I)
A partir de las siguientes situaciones contesta las siguientes preguntas
1)



El precio de un libro es X
¿Cuál es el doble de su precio?_____________
¿Cuál es la mitad de su precio?_____________
¿Cuál es su precio aumentado en $ 100?_____________
2)




La edad de Juan es Y
¿Cuál es el triple de su edad?___________
¿Cuál es su edad disminuida en 3?__________
¿Cuál será su edad en 12 años más?_________
¿Cuál era su edad hace 5 años?__________
3)






La Masa de Antonio es W
¿Cuál es el cuádruplo de su masa?_________
Si Antonio baja 6 kilos ¿Cuál es su nueva masa?________
¿Cuál es su masa aumentada en 12 kilos?__________
¿Cuál es su masa disminuida en 7 kilos?_________
¿Cuál es el triple de su masa, aumentada en 8 kilos?_________
¿Cuál es el quíntuplo de, su masa disminuido en 8?__________
4)



La temperatura interna de un refrigerador es T
Si la temperatura aumenta en 2º ¿Cuál es su nueva temperatura?________
¿Cuál es la tercera parte de, la temperatura aumentada en 5º?__________
¿Cuál es la quinta parte de la temperatura, disminuida en 3º?___________
5)



El volumen de una botella de bebida es V
Si Pedro toma 3 vasos de 200 cm3 ¿Cuánta bebida queda?__________
¿Cuánta bebida hay en 4 botellas del mismo tipo?___________
¿Cuántos vasos de 250 cm3 se pueden llenar con la botella?_________
48
II) Escribe una expresión equivalente a cada uno de los siguientes enunciados
1)
3)
5)
7)
9)
11)
13)
15)
Suma entre a y b
Diferencia entre x e y
Producto de p y q
División entre m y n
Triple de a
Mitad de u
x veces y
Doble de a
2) Restar p a q
4) Tercera parte de u
6) Aumentar p en q
8) Restar u de x
10) Cuociente entra x e y
12) El cuadrado de m
14) El cubo de x
16) La enésima potencia
de a
III) Calcular el valor numérico de las siguientes expresiones matemáticas
sabiendo que x = 3
y=2 u=5 w=7
1)
2)
3)
4)
5)
2x=
3u=
4y=
5w=
x + y=
6)
7)
8)
9)
10)
u + u=
2x + 3y=
u – x=
2w – 3y=
2u + 4y=
IV) Resolver los siguientes problemas utilizando las fórmulas de áreas
1) Calcular el área de un rectángulo cuyo largo es 36 cm si se sabe que éste
es el doble del ancho
2) El terreno donde se encuentra una cancha de fútbol mide 88 metros de
ancho y 112 de largo ¿Cuál es su área? ¿Es su superficie mayor a una
hectárea?
49
3) El perímetro de un cuadrado es 36 m .Calcular su área
4) Un sitio rectangular tiene una superficie de 320 m2. Si el frente mide 20 m
¿Cuánto metros mide el fondo?
5) ¿Cuál es el área de un cuadrado que tiene un perímetro de 48 dm?
6) La base de un triángulo mide 40 cm y su altura mide 15 cm. ¿Cuál es el área
de la región triangular?
7) Dado el triángulo ABC rectángulo en A, Calcular el área de la región
triangular.
C
3 cm
A
4,5 cm
B
50
V) Completar la tabla de acuerdo al modelo
Como suma
1) 3 +3 +3 +3 + 3
2)
3) a + a + a
4)
5) y + y + y
6) u+u +u+ u+u+u
7)
8) m +m
Como
multiplicación
53
28
3x
5p
Como suma
9)
10)
11) b+b+b+b+b+b
12)
13)
14) x+x+x+x+x+x+x+x
15) y+y+y+y+y
16)w+w+w+w+w+w
Como
multiplicación
2u
6v
5z
7q
VI) Reducir
1) 3m + 5m
2) 4x – 2x
3) 7u + 8u
4) 5w – 4w
5) 8a – 6a
6) 4p + 9p
7) 2r + 7r
8) 3h – 3h
9) 9k – 6k
10) 3y + y
VII) Completa las siguientes tablas respetando las sucesiones.
1)
2)
2
7
12
4
14
1
7
46
34
4
16
28
48
21
3)
4)
72
60
33
27
24
1
2
5
9
51
11
3
5
11
23
51
VIII)
Completa las siguientes tablas de secuencia.
1)
1
3
5
7
9
2)
2
5
8
11
14
3)
2
4
8
16
32
4)
2
5
14
41
122
5)
2
6
18
54
IX) Resuelven las siguientes ecuaciones utilizando una balanza.



En una balanza equilibrada, colocan “a” objetos iguales en el lado
izquierdo y “b” objetos iguales a los anteriores en el lado derecho.
Agregan objetos iguales en el lado de la balanza que corresponda de tal
manera que la balanza quede equilibrada.
Cuentan la cantidad de objetos que agregaron; ese corresponde al valor
de x.
1) x + 5 = 18
2) 10 = x + 7
3) 9 + x = 21
4) x + 3 = 8
5) 14 = 6 + x
6) 18 + x =18
7) x + 4 = 19
8) 12 + x = 17
X) Resuelven las siguientes ecuaciones.
1) 27 = 3 • x
2) 5 • x = 45
3) x – 12 = 5
4) x – 9 = 21
5) 3x + 10 = 25
6) 2x – 6 = 18
7) 3x + 5 = 8
8) 13 = 2x – 1
9) 2x – 17 = 9
10) 24 – 8 = 4x
11) 2x – 54 = 10
12) 3x – 81 = 54
52
UNIDAD VI: Construcciones geométricas
Contenidos:
 Ángulos
 Construcción y medición de ángulos
 Construcción de triángulos
 Traslaciones, reflexiones y rotaciones
Objetivos:
 Clasificar y construir triángulos con instrumentos geométricos
 Realizar teselados
1. Construye un ángulo según la medida dada.
28°
147°
115°
2. Construye los ángulos según la medida dada.
130º
150º
45º
53
3. Indica si las siguientes afirmaciones son verdaderas (V) o falsas (F).
a. _____ La medida de un ángulo extendido es 180º.
b. _____ Las rectas paralelas siempre se intersecan.
c. _____ El cuadrado tiene sus cuatro ángulos rectos.
d. _____ Todos los triángulos tienen sus ángulos agudos.
e. _____ El complemento de un ángulo agudo es un ángulo agudo.
f. _____ Un ángulo de medida 32º corresponde a un ángulo obtuso.
g. _____ La suma de las medidas de los ángulos interiores de un cuadrilátero es
360º.
4. Usando herramientas tecnológicas, construye y reconoce los siguientes tipos de
triángulos.
1)
Conociendo la medida de sus lados.
a)
b)
c)
d)
Medida de sus lados: 10 cm. ; 10 cm. ; 7 cm.
Medida de sus lados: 8 cm. ; 8 cm. ; 8 cm.
Medida de sus lados: 5 cm. ; 6 cm. ; 7 cm.
Medida de sus lados: 12 cm. ; 15 cm. ; 17 cm.
2) Conociendo sus ángulos interiores.
a)
b)
c)
d)
Medida de sus ángulos: 50° ; 50°. ; 80°
Medida de sus ángulos: 100°. ; 40°. ; 40°
Medida de sus ángulos: 90° ; 30° ; 60°
Medida de sus ángulos: 60° ; 60° ; 60°
3) Conociendo sus ángulos interiores y la medida de sus lados.
a)
b)
c)
d)
Medida de sus lados / ángulos: 14 cm. / 60° ; 40°
Medida de sus lados / ángulos: 8 cm. / 90° ; 30°
Medida de sus lados / ángulos: 10 cm. ; 10 cm. / 55°
Medida de sus lados / ángulos: 9 cm. ; 7 cm. / 70°
54
TESELACIONES.
Una teselación es cuando cubres una superficie con un patrón de formas
planas de manera que no se superponen ni quedan espacios en blanco
TESELACIONES REGULARES.
La teselaciones regulares son aquellas que se construyen a partir de UN
PATRÓN con una figura regular.
TESELACIONES SEMI REGULARES.
La teselaciones semiregulares son aquellas que se construyen a partir de DOS
O MÁS PATRONES de figuras regulares.
Solamente hay 8 tipos de teselaciones semiregulares:
:
55
I)
Pinta aquellas figuras regulares con las que puede construirse una teselación.
Construye una teselación con cada figura regular.
II) Reconoce que tipo de transformación se realizó al cuadrado pintado para que
comenzará a construirse la teselación. Completa la cuadrícula e indica que
otras transformaciones se pueden hacer para terminar la teselación.
56
III) Reconoce que figuras regulares conforman estas teselaciones. Pinta cada
figura de un color distinto.
1)
2)
3)
4)
57
IV) Utilizando al menos dos de las siguientes figuras, crea una teselación
semirregular.
58
GUÍA DE APRENDIZAJE UNIDAD VI.
Contenidos:
 Clasificación de ángulos.
 Medición de ángulos.
 Complemento y suplemento de un ángulo.
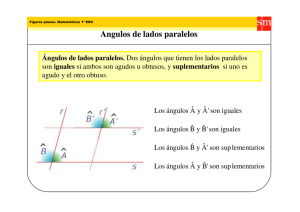
 Ángulos entre paralelas.
 Ángulos en triángulos.
 Ángulos en cuadriláteros.
Objetivos:
 Reconocen tipos de ángulos según su medida o abertura.
 Miden ángulos utilizando transportador.
 Calculan el complemento y suplemento de un ángulo cualquiera.
 Calculan la medida de parejas de ángulos entre paralelas reconociendo
si son opuestos por el vértice, suplementarios, correspondientes,
adyacentes, alternos externos alternos internos.
 Calculan la medida de ángulos interiores y/o exteriores de un triángulo.
 Calculan la medida de ángulos interiores y/o exteriores de un
cuadrilátero.
1. Mide cada ángulo con un transportador. Luego, escribe la medida en el
recuadro.
2. Clasifica cada ángulo según su medida.
59
3. Determina el valor de x en cada triángulo.
a. x =
b. x =
c. x =
4. Determina el valor de x en cada cuadrilátero.
a. x =
b. x =
5. Determina el valor de x e y según corresponda. Considera L1 // L2.
a. x =
c. x =
60
y=
b. x =
d. x =
y=
6. Construye los siguientes triángulos de acuerdo con las longitudes de sus lados.
a. 4 cm, 4 cm y 4 cm.
b. 2 cm, 3 cm y 4 cm.
7. Clasifica los siguientes triángulos de acuerdo a la longitud de sus lados.
Todos sus lados de
igual medida.
__________________
Dos de sus lados de
igual longitud y uno
diferente.
__________________
61
Todos sus lados de
distinta longitud.
__________________
8. Pinta de color amarillo los triángulos acutángulos, de color azul los triángulos
rectángulos y de color rojo los triángulos obtusángulos.
9. Construye cada triángulo con regla y transportador.
a. Un triángulo obtusángulo en el que la medida de uno de sus ángulos interiores sea
40º.
b. Un triángulo rectángulo en el que la longitud de uno de sus lados sea de 7 cm.
c. Un triángulo acutángulo en el que la medida de uno de sus ángulos interiores sea
50º.
62
Completa la siguiente tabla con el complemento y suplemento de cada ángulo.
COMPLEMENTO
ÁNGULO
a)
SUPLEMENTO
ÁNGULO
44º
c)
6º
b)
65º
d)
86º
COMPLEMENTO
SUPLEMENTO
Determina la medida del ó de los ángulos pedidos en cada caso.
b) L1 // L2
L3
a) L1 // L2
90º
x
34º
L1
L1
L2
L3
x
L2
<x=
<x=
c) M1 // M2
d) L1 // L2
M1
M3
164º
M2
x
L1
73º
x
L2
<x=
L3
<
x=
f) M1 // M2
e) L1 // L2 // L3 ; P1 // P2
M1
x
M1
108º
M2
M2
x
63º
P1
P2
M3
M3
<x=
x=
63
<
GUÍA: ÁNGULOS.
I) Clasifica los siguientes ángulos en agudos, rectos, obtusos y extendidos
II) Medir los siguientes ángulos usando transportador
III)
a)
Dibuja los siguientes ángulos
ABC= 65º
b)  DEF= 110º
c)  GHI= 45º
d)  JKL= 160º
e)  MNÑ= 80º
f)  OPQ= 140º
g)  RST= 90º
h)  XYZ = 20º
64
IV)
Copiar cada uno de los siguientes ángulos a su derecha usando compás y
verificar el que esté bien con el transportador que esté correcto.
65
VI) Calcular
a) El complemento de :
b) El suplemento de :
1) 15º
2) 36º
3) 47º
4) 68º
5) 83º
6) 71º
7) 2º
8) 11º
9) 88°
10)19°
1) 23°
2) 58°
3) 60°
4) 120°
5) 90°
6) 15°
7) 39°
8) 135°
9) 160°
10)24°
c) Si  = 15º ,  = 23º,  = 71º y  = 48º
Determinar :
1)    =
2)  +  =
3)  +  =
4)  +  =
5)  +  +  =
6)  +  +  =
7)  +  +  =
8)  +  +  =
9)  +  +  + 
10)  -  =
11)  -  =
12)  -  =
13)  -  =
14)  -  =
15)  -  =
16)  -  =
=
66
GUÍA: ÁNGULOS ENTRE RECTAS PARALELAS
I) Clasificar las siguientes parejas de ángulos.
1)
2)
3)
4)
5)
6)
7)
8)
67
9)
10)
11)
12
13)
14)
15)
16)
68
II)
Calcular el valor del ángulo x en cada uno de los siguientes ejercicios de
ángulos entre paralelas.
1)
2)
160º
x
34º
x
x=
x=
3)
4)
x
x
47º
144º
x=
5)
x=
6)
x
x
163º
123º
x=
7)
x=
8)
90º
x
x
x=
116º
x=
69
9)
10)
2x
x
x
73º
x=
11)
x=
12)
115º
103º
x
x
x=
13)
x=
14)
41º
x
61º
x
x=
15)
x=
16)
x
50º
108º
x
x=
x=
70
III)
Determinar la medida del o los ángulos pedidos en cada caso
1)
2)
.
130º
X
60º
X
X=
 X=
3) L  M, N transversal
4) L  M; P  Q
L
M
L
160º
50º
X
X
N
M
P
X =
5)
Q
X=
L // M; OP bisectriz
6) L // M ; OP bisectriz
140º
L
O
L
70º
O
M
P
X
M
X
P
X=
X=
71
7)
8)
60º
X
X
60º
X=
 X=
9) L // M; N transversal
10) L // M; P // Q
N
P
L
L
130º
M
Q
30º
X
M
X
 X=
X=
11) L // M; OP bisectriz
12)
L // M; OP bisectriz
120º
30º
X
X
 X=
 X=
13)
14)
2X
X
X
3X
2X
X=
X=
72
GUÍA: ÁNGULOS EN TRIÁNGULOS
I) Determinar el valor de los ángulos pedidos en los siguientes triángulos.
C
C
85°
1)
y
2)
40°
70°
X
A
B
A
140°
B
X
X=
X=
3)
Y=
4)
X
X
25º
130°
Y
40°
Y
10º
X=
 Y=
X=
5) AD bisectriz del EAB; y BD bisectriz
del  ABF
Y=
6) En  ABC AC  BC
C
C
x
60°
A
B
Y
80°
50°
y
E
A
B
F
X
D
X
=
Y=
X=
73
Y=
7)  MNO isósceles MD bisectriz
Del  OMN
8) En un triángulo,   = 80º,  = 3 
Luego   y   miden respectivamente:
C
O

32º
D

x
N
M

B
A
x =
=
9)
10)
80º
80º
40º
x
150º
x
x =
x =
11)
12)
40º
110º
120º
x
130º
x
x =
x =
13)
14) AD bisectriz
D
C
y
120º
x
70º
x
A
x =
x =
74
B
y=
16) En  ABC, AC  BC
15)
C
70º
60º
130º
x
x
A
x =
B
x =
17)
18)
x
110º
x
50º
55º
130º
x =
x =
20) En ABC, CD bisectriz del  ACB
19)
C
x
125º
x
60º
60º
A
x =
x =
75
D
140º
B
GUÍA: CUADRILÁTEROS
I) Clasificar los siguientes cuadriláteros en: Paralelogramo, trapecio y trapezoide.
1)
AB // CD; AD // BC
D
2)
AB // CD
C
B
A
C
D
A
_________________
B
____________________
3) No hay lados paralelos
4) AB // CD; BC // AD
D
D
C
C
A
A
B
B
___________________
5) AB // CD
___________________
6) AB // CD; AD // BC
C
D
D
A
C
B
A
________________________
B
_____________________
76
II) Considera los siguientes paralelogramos y responde las preguntas que están a
continuación
1)
2)
a
a
b
a
a
a
a
b
3)
4)
a
a
a
a
a
b
b
5)
6)
a
a
b
a
a
a
a
b
a
a) ¿Cuál es un cuadrado? ______________________
a) ¿Cuál es un rectángulo? _____________________
b) ¿Cuáles son rombos? _______________________
c) ¿Cuáles son romboides? ____________________
77
III) Determinar el o los ángulos pedidos en cada figura.
a) ABCD cuadrilátero  CDA = 80º,  X =
b) ABCD cuadrilátero DAB = 90º,
 DCB = 100º,  ABC = 35º,  X =
D
C
A
X
C
D X
B
A
X=
X=
c) DCB = 50º y DAB = 135º ; DC // AB
Calcular  X + Y =
D
B
d) ABCD cuadrilátero     X =
C
D

C

A
Y
B
X
A
X
B
X+Y=
X=
78
e) ABCD es un rombo calcular  X y Y
f) ABCD es un romboide calcular  X, Y
D
130º
C
D
C
Y
X
Y
A
B
70º
X
B
A
X=
X=
Y=
Y=
g) ABCD trapecio rectángulo
h) El trapecio PQRS es isósceles
  = 62º ,   = ?
QRS = 130º,  SPQ =?
D
C
S
R

P

A
Q
B
=
 SPQ =
79
IV) Responde las preguntas de ángulos en cuadriláteros..
1. El cuadrilátero de la figura es un paralelogramo.
D
C
A) Si AB = 6 cm, ¿cuánto mide CD?
B) Si BC = 10 cm, ¿cuánto mide AD?
C) Considerando los datos anteriores,
¿cuál es el perímetro de l paralelogramo?
D) Si  = 41º, ¿cuánto mide  ?
E) Si el perímetro del paralelogramo
es 28 cm y AB = 5 cm, ¿cuánto mide BC?




A
B
2. Los cuadriláteros de la figura son paralelogramos. Calcula la medida del
ángulo pedido en cada caso.
A)
B)

68º

103º

C)
D)


63º
56º
E)
F)


50º


109º
80

3. El cuadrilátero de la figura es un paralelogramo.
A)
B)
C)
D)
D
Si MA = 4 cm, ¿cuánto mide MC?
Si MD = 10 cm, ¿cuánto mide MB?
Si AD = 15 cm, ¿cuánto mide BC?
Si DB tiene 3 cm más que AC
y MC = 5 cm, ¿cuánto mide MB?
C
M
A
B
4. El cuadrilátero de la figura es un rombo.
D
A) ¿Cuánto mide el ángulo AMD?
B) Si AB = 12 cm, ¿cuánto mide BC?
¿Cuál es el perímetro del rombo?
C) Si AM = 9 cm, ¿cuánto mide MC?
D) Si AC = 16 cm y DB 12 cm,
¿cuál es perímetro del rombo?
(Teorema de Pitágoras)
C
M
A
B
5. Calcula la medida de los ángulos pedidos en los siguientes rombos.
A)
B)


48°
50º
C)
23º
D)
140º


81
UNIDAD VIII: MEDICIÓN.
Contenidos:
 Área y perímetro de figuras 2D.
 Área y perímetro de figuras 3D.
 Volumen de cubos y paralelepípedos.
Objetivos:
 Calculan el área y perímetro de figuras 2D.
 Calculan el área y perímetro de figuras 3D.
 Calculan el volumen de cubos y paralelepípedos.
I) Mide y calcula el área de las siguientes figuras
82
Responde:

¿Cuántas mediciones son necesarias realizar para calcular el área de un
rectángulo?

¿Cuántas mediciones son necesarias realizar para calcular el área de un
cuadrado?
II) Calcula el área de los siguientes cuadrados:
Lado : 14 cm.
Lado : 25 cm.
Lado : 81 cm.
Lado : 98 cm.
Lado : 47 cm.
A=
A=
A=
A=
A=
III) Calcula el área de los siguientes rectángulos:
5 mts
26 mts
14 mts
78 mts
96 mts
125 mts
75 mts
1589 mts
123 mts
300 mts
98 mts
458 mts
14 mts
23 mts
458 mts
1478 mts
83
IV) Calcula el área de las siguientes figuras:
a)
b)
c)
d)
e)
f)
g)
h)
un cuadrado de lados 6 mts.
un rectángulo de lados 5 y 8 mts
un cuadrado de perímetro 20 cm.
Un rectángulo de perímetro 40 cm. y lado menor 6 cm
Un rectángulo de perímetro 60 cm y lado mayor 25 cm
Un cuadrado de perímetro 56 mts
Un cuadrado de perímetro 100 km.
Un rectángulo de lados 15 y 36 metros
V) Calcula el área de las siguientes redes de cuerpos geométricos, sabiendo qué:
1) Arista mide 2 cm.
2) Arista mide 5 cm.
3) Arista mide 6 cm.
4) Arista mide 10 cm.
5) Arista mide 12 cm.
1) Arista basal 2 cm. y
altura 4 cm.
2) Arista basal 4 cm. y
altura 5 cm.
3) Arista basal 6 cm. y
altura 10 cm.
4) Arista basal 10 cm.
y altura 12 cm.
84
GUIA VOLUMEN
I) Resolver los siguientes problemas usando equivalencia de unidades de volumen:
1) Un laboratorio farmacéutico envasa el alcohol en frascos de cuatro tamaños.
Observa elvolumen en centímetros cúbicos de cada frasco y calcula la capacidad
en litros de cada frasco.
2) Un taller vende bidones de agua destilada. Observa la capacidad en litros
decada uno de los bidones y calcula el volumen en cm3de cada bidón.
3) Completa la siguiente tabla, transformando a la unidad que corresponda:
mm3
cm3
dm3 (litro)
200
500
325.000
8.375
12,5
27,54
85
m3
7
4) ¿Cuántas botellas de 750 cm3 se necesitan para envasar 12 litros de leche?
5) Una piscina tiene una capacidad máxima de 15 m3 ¿con cuántos litros se llena?
6) Luis compra 15 cajas de jugos de 200 cm3 ¿Cuántos litros de jugo compró Luis?
II) Calcula el volumen de los siguientes cuerpos de acuerdo con las medidas
dadas:
1) El prisma de la figura mide 10 cm de largo, 15 cm de ancho y 7 cm de alto
2) El prima tiene 40 cm de largo, 25 cm de ancho y 12 cm de alto; entregar el
resultado en litros
86
III) Resolver los siguientes problemas
1)
Calcular el volumen de un cubo de arista 5 cm.
2)
¿Cuál es el volumen de un prisma recto que tiene como base un cuadrado de
lado 6 cm y cuya altura es de 15 cm?
3)
Un helado viene en una caja de 30 cm de largo, 10 cm de ancho y 5 cm de alto
¿Cuántos litros de helado trae la caja?
4)
Una caja de fósforos grande mide 100 mm de largo, 50mm de ancho y 10mm
de alto. Un fósforo de la caja mide 50mm de largo, 2 mm de ancho y 2 mm de
alto. ¿Cuántos fósforos caben en la caja?
5)
Si la capacidad de un prisma recto es de 2 litros y su altura es de 40 cm, ¿cuál
es la medida de su área basal?
6)
Una piscina mide 4 m de ancho, 6 m de largo y 1,5 m de hondo:
a) ¿Cuál es la máxima cantidad de agua que puede contener?
b) La piscina se llena con una llave que entrega 6 litros por minuto ¿Cuánto
se demora en llenar la piscina?
87
UNIDAD IX: DATOS Y PROBABILIDADES
Contenidos:
 Tablas de frecuencias.
 Gráficos de barra simple, dobles y múltiples
 Gráficos circulares
 Diagrama de tallo y hoja
 Media aritmética, mediana y moda
 Experimentos aleatorios
 Espacio muestral
 Probabilidad (regla de Laplace)
Objetivos:
 Lectura, interpretación y construcción de tablas de frecuencias.
 Lectura, interpretación y construcción de gráficos de barra simple,
dobles y múltiples
 Lectura, interpretación y construcción de gráficos circulares
 Lectura, interpretación y construcción de diagrama de tallo y hoja
 Identificar experimentos aleatorios
 Definir espacio muestral
 Calcular probabilidad
1.- Los datos corresponden al total de miembros que tienen las diferentes familias
de los niños y niñas que forman un curso.
2
3
3
4
2
5
3
5
3
4
3
4
5
4
5
4
4
4
3
3
6
7
4
3
3
3
4
7
5
5
4
5
3
3
5
4
De acuerdo a estos datos, completa la siguiente tabla:
Nº de personas
2
3
4
5
6
7
8
Conteo
Frecuencia
88
2.- Observa el siguiente gráfico y responde las preguntas.
Nº Medallas de Oro obtenidas
medallas
20
15
10
5
0
colegio
10
colegio
9
colegio
8
colegio
7
colegio
6
colegio
5
colegio
4
colegio
3
colegio
2
colegio
1
coelgios
a)
b)
c)
¿Qué colegio obtuvo más medallas de oro?
¿Qué colegio obtuvo menos medallas de oro?
Haz un ranking con el lugar que obtuvo cada colegio luego de finalizar el
campeonato
3.- Un padre de familia revisa la información entregada en la boleta de pago de la
compañía de gas fijándose en el gráfico que muestra el consumo en un período de
13 meses:
mar
feb
ene
dic
nov
oct
sep
ago
jul
jun
may
abr
80
70
60
50
40
30
20
10
0
mar
metros cúbicos
Consumo últimos 13 meses

En qué meses se registró el mayor consumo de gas?

¿En qué meses se registró el menor consumo de gas?

Intenta dar una explicación a la diferencia de consumo en estos meses
89
Si se sabe que esta familia deberá pagar sólo por concepto de consumo de gas
$ 25.000 ( esto es sin contar el cargo fijo y otros cargos) en el mes de abril:

Determina el valor de 1 m3 =_______________________________________________________

Si se sabe que el valor del gas no ha variado en los últimos 12 meses,
calcula cuánto pagó esta familia sólo por concepto de consumo de gas los
siguientes meses:
Mayo:
Junio:
Septiembre:
Noviembre:
_________________ pesos
_________________ pesos
_________________ pesos
_________________ pesos
El siguiente gráfico muestra tres series de frecuencia para cada año.
1. Responde las preguntas de acuerdo al gráfico anterior.
a. ¿Cuáles son las series de frecuencia?
b. ¿Qué representan las barras rojas?
c. ¿Cuántos años se consideraron?
d. ¿Qué año la producción de tornillos fue la misma para dos fábricas?
e. ¿Qué se puede concluir con respecto a la fábrica 3? Escribe una conclusión.
90
2. Construye un gráfico de barras múltiple para los datos de la siguiente tabla.
Luego, responde las preguntas.
Cantidad de litros de bencina vendidos por tipo (miles de litros)
Tipo de
bencina
93 octanos
95 octanos
97 octanos
Mes
Enero
5
15
10
Febrero
10
25
20
Marzo
8
20
18
a. ¿Qué meses se consideraron?
b. ¿Qué tipo de bencina es el que menos se vende?
c. ¿Qué mes se vendió más bencina de 97 octanos?
d. ¿Qué se puede concluir con respecto a la bencina de 95 octanos? Escribe una
conclusión.
91
GRÁFICO CIRCULAR
1. Completa la tabla. Luego, representa la información en un gráfico circular.
Producto
Cocinas
Lavadoras
Secadoras
Refrigeradores
Total
Artículos vendidos en un mes
Cantidad
Porcentaje
15 %
Ángulo
126º
60
300
100 %
360º
2. Evalúa si las afirmaciones son verdaderas (V) o falsas (F) con respecto al
gráfico.
a. _____ El sector de mayor área representa el
porcentaje de vacas de la granja.
Distribución de animales en una
granja
b. _____ El 20 % de los animales son caballos.
c. _____ La menor cantidad de animales son
cerdos.
12%
Vacas
17%
48%
Caballos
Cerdos
d. _____ El 12 % de los animales son
corderos.
Corderos
e. _____ Si hay 300 animales en la granja, entonces 51 son cerdos.
92
DIAGRAMA DE TALLO Y HOJAS
El diagrama de tallo y hojas se utiliza para representar datos cuantitativos de una
misma variable perteneciente a uno o dos grupos diferentes.
Ejemplo:
Las edades de los jugadores de dos equipos de fútbol son las siguientes:
Equipo A: 24, 31, 25, 23, 23, 25, 27, 28, 24, 25, 26
Equipo B: 26, 27, 27, 27, 32, 24, 25, 22, 31, 24, 28
Edades
Equipo A
Equipo B
8765554433 2 244567778
1 3 12
1. Construye un diagrama de tallo y hojas y escribe dos conclusiones para la
siguiente situación:
Los meses de edad que tienen los niños que asisten a dos jardines infantiles son
los siguientes:
Jardín 1: 6, 15, 23, 12, 17, 15, 8, 8, 17, 22, 22 ,17, 11, 7, 28, 9
Jardín 2: 14, 29, 8, 9, 19, 6, 24, 14, 24, 24, 31, 25, 14, 19, 8, 7
Conclusiones:
a)_________________________________________________________________
__________________________________________________________________
b)_________________________________________________________________
__________________________________________________________________
93
II) Se realizó un certamen atlético entre 10 colegios de la comuna, a continuación
se presentan algunos de los resultados obtenidos en algunas pruebas:
1) Los resultados, en tiempo, de las carreras de 100 metros planos fueron:
Colegio 1
Colegio 2
Colegio 3
Colegio 4
Colegio 5
Tiempo: 2’: 35’’
Tiempo: 2’: 39’’
Tiempo: 2’: 25’’
Tiempo: 2’: 22’’
Tiempo: 2’: 55’’
Colegio 6
Colegio 7
Colegio 8
Colegio 9
Colegio 10
Tiempo: 2’: 11’’
Tiempo: 2’: 34’’
Tiempo: 2’: 20’’
Tiempo: 2’: 40’’
Tiempo: 2’: 53’’
a) Completa la siguiente tabla de intervalos:
Intervalos en tiempo
2’:00’’ a 2’: 14’’
2’:15’’ a 2’: 29’’
2’:30’’ a 2’: 44’’
2’:45’’ a 2’: 59’’
3’:00’’ a 3’: 14’’
Conteo
Frecuencia
b) Ubica en este podio a los tres colegios vencedores en esta prueba
1º
2º
3º
2) En el lanzamiento de la jabalina, cada participante tiene tres oportunidades de
realizar el lanzamiento, pero solo compite su mejor resultado. Aquí algunos de los
tiros:
Colegio
1
5
7
8
9
Lanzamiento 1
6,75 metros
6,81 metros
6,69 metros
6,93 metros
6,90 metros
Lanzamiento 2
6,36 metros
6,72 metros
6,52 metros
6,45 metros
6,84 metros
Lanzamiento 3
6,60 metros
6,63 metros
6,24 metros
6,33 metros
6,36 metros
a) Cuántos metros como promedio realizaron los representantes de cada colegio.
94
b) Con esta información, construye una tabla de frecuencia con intervalos cada 10
cm, partiendo en los 6 metros.
Lanzamientos en metros
–
–
–
–
–
–
–
–
–
–
Conteo
Frecuencia
3) Observa el siguiente gráfico y responde:
III) Analiza la siguiente información:
Notas prueba de Lenguaje y
Comunicación
Notas prueba de Matemática
5.1
6.7
4.8
7.0
6.0
5.4
6.0
5.8
5.8
5.9
6.0
5.8
6.0
4.3
6.0
4.0
5.2
6.6
6.4
6.3
6.0
6.0
6.0
6.5
6.4
5.3
6.2
4.3
6.4
6.0
6.0
6.0
6.6
6.0
7.0
6.0
Nota más frecuente =
Promedio del curso =
7.0
3.8
6.1
5.8
5.9
5.8
6.1
6.3
7.0
5.8
5.4
3.8
6.2
5.7
5.8
4.5
6.7
6.6
4.5
6.9
6.4
7.0
6.4
6.5
Nota más frecuente =
Promedio del curso =
a) Redacta tres preguntas a partir de la información y luego respóndelas
b) Si el promedio del curso fuera, por ejemplo, 6.4 ¿significa que todo el curso
obtuvo esa nota? ,¿por qué?
c) Las notas de Sofía en Matemática son 5.8; 6.4; 4.9; 6.3 ; ¿cuál es su
promedio?
d) Las notas de Cristián en Educación Física son 6.3; 6.8; 6.1; 7.0; 5.8 y 6.6.
Las notas de Joaquín en esta misma asignatura son 6.4; 6.0; 7.0; 6.0 y 6.5.
¿Quién tiene mejor promedio?
95
PREGUNTA 1
HABILIDAD: P. OPERACIONAL
FECHA: __________________
Calcula el promedio de las siguientes distancias
Lunes
Martes
Miércoles
Jueves
100 Km.
a)
b)
c)
d)
150 Km.
185 Km.
200 Km.
Viernes
Sábado
180 Km.
210 Km.
180 km. aproximadamente
185 km. aproximadamente
171 km. aproximadamente
200 km. aproximadamente
PREGUNTA 2
HABILIDAD: P. OPERACIONAL
FECHA: __________________
Cuál es la moda de los siguientes datos
14; 10; 8; 6; 8; 10; 8; 10; 8; 6; 10; 12; 10; 6; 6; 8; 4; 10; 6.
a)
b)
c)
d)
6
8
10
12
96
PREGUNTA 3
HABILIDAD: COMPRENSION
FECHA: __________________
A comienzos de año el entrenador de básquetbol realizó un estudio de la masa
corporal de los alumnos de la selección. Los resultados fueron los siguientes.
MASA (kg): 45, 50, 48, 51, 50, 48, 47, 50, 49
¿Cuál es la media aritmética de las masas de los alumnos?
a)
b)
c)
d)
50
49
48
51
PREGUNTA 4
HABILIDAD: COMPRENSION
Películas
15
10
Suspenso
ar
lo
C
Pe
dr
o
Pa
ul
in
a
Aventuras
0
Án
ge
l
5
s
Cantidad de
Películas
Con respecto al siguiente gráfico
Cómicas
Niños
¿Quién vio más películas de aventura?
a)
b)
c)
d)
Carlos
Ángel
Pedro
Paulina
97
FECHA: __________________
PREGUNTA 5
HABILIDAD: P. LOGICO
FECHA: __________________
El siguiente gráfico presenta el resultado de una encuesta respecto a la fruta de
preferencia en un curso. ¿Cuál es la fruta preferida del curso?
a)
b)
c)
d)
Naranja
Manzana
Uva
Pera
PREGUNTA 6
HABILIDAD: P. LOGICO
FECHA: __________________
Con respecto a la información que entrega la siguiente tabla ¿Cuál es el
promedio de los datos?
.Notas en una Prueba de Lenguaje
a)
b)
c)
d)
6,0
5,8
6,1
5,9
5,1
6,0
6,4
6,4
6,0
6,7
4,3
6,3
5,3
6,0
4,8
6,0
6,0
6,7
6,6
7,0
4,0
6,0
4,3
6,0
6,0
5,2
6,0
6,4
7,0
5,4
6,6
6,5
6,0
6,0
98
PREGUNTA 7
HABILIDAD: P. CRITICO
FECHA: __________________
Los alumnos de 6º básicos realizaron un trabajo de investigación y la cantidad
de páginas entregadas por cada uno fue la siguiente:
14; 10; 8; 6; 8; 10; 8; 10; 8; 6; 10; 12; 10; 6; 6; 8; 4; 10; 6.
Con respecto a esto se afirma:
I.- La moda de los siguientes datos es 10
II.- La mediana de los siguientes datos es 6
II.- 6 es el resultado del promedio de las hojas entregadas
IV.- La media aritmética o promedio es 8 aproximadamente
Las afirmaciones correctas son:
a)
b)
c)
d)
I y II
I, II y III
I, II y IV
I y IV
PREGUNTA 8
HABILIDAD: P. CRITICO
FECHA: __________________
Con respecto a la siguiente tabla se afirma:
I.- La reserva nacional que tiene mayor superficie es “Río Los Cipreses”
II.- La reserva nacional que tiene menor superficie es “Los Queules”
III.-La región que tiene mayor superficie es La región De Los Lagos
IV.- La región que tiene menor superficie es La región del Maule.
Es correcto:
a)
b)
c)
d)
I, II, III y IV
I, II y III
II y III
II, III y IV
Reserva Nacional
Rio Claro
Rio Los Cipreses
Bellotos El Melado
Los Queules
Llanquihue
Futaleufú
Lago General Carrera.
99
Región
Metropolitana
Libertador B. O’ Higgins.
Maule
Maule
De Los Lagos
De Los Lagos
Carlos Ibáñez del Campo
Provincia
Cordillera
Cachapoal
Linares
Cauquenes
Llanquihue
Palena
General Carrera.
Superficie
10.185
36.882
417
147
33.972
12.065
178.400
GUÍA PROBABILIDAD
I) Realizar los siguientes experimentos y contestar las preguntas
1) Lanza un moneda al aire y completa la tabla
Lanzamientos
Caras
10
20
50
100
Sellos
a) ¿En cuántos lanzamientos el resultado fue más real para ti?
b) Con relación a la pregunta anterior, ¿Qué sucedió con la mayoría del curso
2) Completen en grupo la siguiente tabla utilizando un dado y discutan acerca de
las preguntas
Lanzamientos
1
2
3
4
5
6
18
30
60
120
a) ¿Qué sucede a medida que se realizan más lanzamientos?
b) ¿Qué es más posible que salga un número par o uno impar? ¿Por qué?
c) ¿Qué es más posible que salga un múltiplo de 3 o un múltiplo de dos? ¿Por
qué?
III) Ordenar, en cada caso, de menos posible a más posible los acontecimientos
pedidos
1) Se lanza un dado
Que salga un número menor que tres
Que salga un número mayor que tres
Que salga 3
2) Se tiene un naipe inglés y se saca una carta
Que sea roja
Que sea de trébol
Que sea par
Que sea letra
100
3) En una caja hay 7 fichas rojas, 5 azules, 3 amarillas y 2 blancas; se saca sin ver
una de ellas
a) Es roja
b) Es amarilla
c) Es negra
d) El color comienza con A
e) No es blanca
4) Se tienen tres fichas; la primera es blanca por un lado y negra por el otro; la
segunda es roja por un lado y azul por el otro y la tercera es negra por un lado y
roja por el otro. Se toma una ficha sin verla y se lanza
a) Es roja
b) Es blanca
c) No es verde
d) Es negra
e) Es amarilla
5) Clasifica los experimentos en determinísticos (D) o aleatorios (A). (4 puntos)
101
6) Completa los siguientes datos con la situación que se presenta. (4 puntos)
Rafael está participando en un juego que consiste en responder en preguntas de
diversos tipos. Se debe sacar una pregunta de a caja como se muestra a
continuación:
cultura
deportes
cultura
deporte
cultura
cultura
música
música
cultura
cultura
música
música
cultura
¿Cuál es la probabilidad que Rafael saqué una pregunta de deportes?
102
DIAGRAMA DE ÁRBOL
El diagrama de árbol sirve para representar gráficamente los posibles resultados
que se pueden obtener al realizar un experimento aleatorio, es decir, el espacio
muestral.
Ejemplo: Lanzar una moneda y sacar una bolita de una urna que contiene una de
color verde, una amarilla y una roja.
Lanzamiento
moneda
Sacar una
bolita
Combinaciones
C
Verde
Amarilla
Roja
Cara, verde
Cara, amarilla
Cara, roja
S
Verde
Amarilla
Roja
Sello, verde
Sello, amarilla
Sello, roja
1. Dibuja el diagrama de árbol para el experimento “lanzar tres dados de seis caras
de forma consecutiva” y determina el espacio muestral.
2. Construye un diagrama de árbol para el siguiente menú y determina cuántos
platos tienen carne de pollo y ensalada.
Menú
Plato de fondo
Acompañamiento
Jugo
Pollo
Ensalada
Piña
Frutilla
Vacuno
Arroz
Papaya
Pescado
103
Cálculo Mental
Control nº 1.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 2.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 3.
a)
b)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
g)
Fecha:
c)
d)
e)
f)
Control nº 8.
a)
g)
Fecha:
Control nº 7.
a)
g)
Fecha:
Control nº 6.
a)
g)
Fecha:
Control nº 5.
a)
g)
Fecha:
Control nº 4.
a)
g)
g)
Fecha:
c)
d)
e)
104
f)
g)
Cálculo Mental
Control nº 9.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 10.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 11.
a)
b)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
g)
Fecha:
c)
d)
e)
f)
Control nº 16.
a)
g)
Fecha:
Control nº 15.
a)
g)
Fecha:
Control nº 14.
a)
g)
Fecha:
Control nº 13.
a)
g)
Fecha:
Control nº 12.
a)
g)
g)
Fecha:
c)
d)
e)
105
f)
g)
Cálculo Mental
Control nº 17.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 18.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 19.
a)
b)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
g)
Fecha:
c)
d)
e)
f)
Control nº 24.
a)
g)
Fecha:
Control nº 23.
a)
g)
Fecha:
Control nº 22.
a)
g)
Fecha:
Control nº 21.
a)
g)
Fecha:
Control nº 20.
a)
g)
g)
Fecha:
c)
d)
e)
106
f)
g)
Cálculo Mental
Control nº 25.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 26.
a)
b)
Fecha:
c)
d)
e)
f)
Control nº 27.
a)
b)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
c)
d)
e)
f)
b)
g)
Fecha:
c)
d)
e)
f)
Control nº 32.
a)
g)
Fecha:
Control nº 31.
a)
g)
Fecha:
Control nº 30.
a)
g)
Fecha:
Control nº 29.
a)
g)
Fecha:
Control nº 28.
a)
g)
g)
Fecha:
c)
d)
e)
107
f)
g)