FIS-110 Certamen N° 1 1er. Semestre 2001

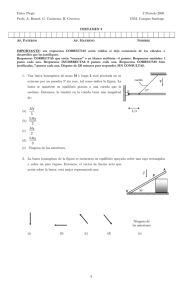
UNIVERSIDAD TÉCNICA FEDERICO S ANTA MARÍA
DEPARTAMENTO DE FÍSICA
FIS-110
AP. PATERNO
ROL USM
Certamen N° 1
AP. MATERNO
1er. Semestre 2001
NOMBRE
-
1) Un helicóptero vuela horizontalmente a 80 metros del suelo con una velocidad constante
de magnitud 6,0 [m/s]. Desde el helicóptero y en dirección opuesta a su movimiento, se
lanza horizontalmente un objeto con una rapidez inicial de 10,0 [m/s] con respecto al
helicóptero (considerar el objeto como una partícula y sin resistencia del aire). Calcular:
(a) La posición (vector) del objeto respecto del helicóptero en el instante en que el objeto
alcanza el suelo.
(b) La velocidad (vector) del objeto respecto de la tierra cuando alcanza el suelo.
(c) La velocidad (vector) del objeto respecto del helicóptero cuando alcanza el suelo.
Nota: resuelva cada parte del problema en forma simbólica y sustituya los valores
numéricos sólo al final.
AP. PATERNO
ROL USM
AP. MATERNO
NOMBRE
FIS-110 2001-1 C1
2) La barra de largo 14 [cm] está soldada a un eje vertical, que gira con ω = 60 rpm. Una
pequeña masa m se mantiene en contacto con la barra, como se indica en la figura. No
existe roce.
g
Determine el cuociente N1 / N2 entre las magnitudes de las
fuerzas de contacto (“normales”) ejercidas por la barra
sobre la masa m, en los puntos (1) y (2).
45º
(1)
Nota: resuelva el problema en forma simbólica y sustituya los valores numéricos
sólo al final. Basta que su resultado numérico sea aproximado. Use
2 ; 1,4
(2)
AP. PATERNO
ROL USM
AP. MATERNO
NOMBRE
FIS-110 2001-1 C1
3) La masa m está en equilibrio sujeta a las cuerdas ideales (1) y (2), como indica la
figura. Repentinamente se corta la cuerda (2).
Denotemos por Ta la tensión de la cuerda (1) antes de que se corte la cuerda (2), y por Td la
tensión de la cuerda (1) inmediatamente después de haberse cortado la cuerda (2).
a) Determinar la razón Ta Td . ¿Cuál de las estas
tensiones resulta mayor?
b) Determinar la rapidez angular, la aceleración
angular y la aceleración centrípeta de la masa
m inmediatamente después de haberse cortado
la cuerda (2).
g
θ
(1)
m
(2)
AP. PATERNO
ROL USM
AP. MATERNO
NOMBRE
FIS-110 2001-1 C1
Elija resolver este problema o el 4-B (en la siguiente página).
4-A) Considere una curva en una carretera totalmente plana (es decir, sin peraltes).
a) Determine el radio (de curvatura) de la curva, R, de tal manera
que ésta permita que los vehículos la puedan tomar sin resbalar
hasta con una rapidez de 120 [km/h], suponiendo un coeficiente
de roce estático µ=1,0 entre los neumáticos y el pavimento.
b) Suponga que un auto toma esta curva con una rapidez de 90 [km/h].
Determine la máxima desaceleración (tangencial) con la que podría
comenzar a frenar sin que el auto resbale.
Nota: resuelva el problema en forma simbólica y sustituya los
valores numéricos sólo al final. Basta con respuestas numéricas
aproximadas.
R
(carretera vista desde arriba)
AP. PATERNO
AP. MATERNO
NOMBRE
-
ROL USM
FIS-110 2001-1 C1
Elija resolver este problema o el 4-A (en la página anterior).
4-B) Se requiere mover una caja (masa m) sobre una superficie horizontal, tirándola con
una cuerda, como se muestra en la figura. La cuerda tira con una tensión dada T, igual a
4
m mg , donde µ es el coeficiente de roce (estático y cinético) entre la caja y la superficie.
5
a) Encuentre, en términos de µ, con qué ángulo(s) θ
es necesario tirar de la cuerda para poder mover la
caja. Basta con que Ud. presente su solución en
términos de funciones trigonométricas de θ.
b) Si µ = 1,0 , T = 80 [N] y mg = 100 [N], encuentre
la máxima aceleración con que es posible arrastrar
la caja.
T
g
θ
m
µ
Nota: resuelva el problema en forma simbólica y sustituya los valores numéricos
sólo al final. Use
2 ; 1,4