diseno-de-cimentaciones-carlos-magdaleno

Capítulo
1
INTRODUCCION
En este capítulo se presenta un panorama sobre los diversos tipos de cimentaciones para las
construcciones más comunes, así como su importancia como elemento resistente que forma parte el
sistema denominado estructura. También en forma breve, se transcribe conocimientos de la
Mecánica de Suelos necesarios para elegir y calcular las cimentaciones.
1.1
La importancia de las cimentaciones.
Los siguientes conceptos establecen la importancia que tienen las cimentaciones. El objetivo que
tienen este tipo de estructuras es transmitir las cargas de la superestructuras y el peso propio de las
mismas al terreno, pero presentan otras funciones como apoyar a la construcción, distribuir
adecuadamente las cargas considerando, un factor de seguridad adecuado entre la estructura de
cimentación y el suelo, limitar los asentamientos totales y diferenciales con la finalidad de controlar los
daños en la estructura así como en las construcciones adjuntas y mantener la posición vertical de la
estructura ante los diferentes tipos de acciones.
El Profesor Clarence W. Dunham, dice que la palabra cimentación puede tener los siguientes
significados: el terreno sobre la que se transmiten las fuerzas originadas por el peso propio de la
estructura y sobrecargas que actúan sobre la misma, y otro que es el conjunto de las partes
estructurales de la infraestructura o sea el medio que sirve para transmitir al terreno, el peso de la
superestructura, las acciones que actúan sobre ella y el peso propio de dicho medio o bien la
combinación de los dos conceptos anteriores.
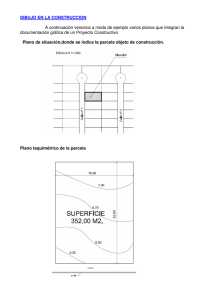
En la figura 1.1. se ilustran cimentaciones en construcciones típicas. Comúnmente se define a la
superestructura e infraestructura de la siguiente manera: la superestructura es la parte de la
construcción que se realiza con el objeto fundamental de ser utilizada por el hombre, la infraestructura
es la parte de la construcción que es necesaria para apoyar a la superestructura
2
Capítulo 1
Introducción
Figura 1.1 Cimentaciones y superestructura.
1.2
Clasificación de las cimentaciones.
En general se pueden dividir a los diversos tipos de cimentaciones en dos grandes grupos:
a) Cimentaciones superficiales.
b) Cimentaciones profundas
Capítulo 1
Introducción
3
Las cimentaciones superficiales más comunes son:
1. Zapatas aisladas.
2. Zapatas corridas o continuas.
3. Losas de cimentación.
4. Retículas de cimentación.
5. Cimentaciones a base de cascarones.
La selección del tipo de cimentación depende fundamentalmente del tipo de construcción, de las
cargas o acciones que actúan sobre de ella y del terreno donde se va a ubicar. Se dice que la elección
de una cimentación debe estar basada en los conocimientos técnicos y el buen criterio del ingeniero, lo
segundo es una cualidad que se desarrolla después de varios años de experiencia. De la referencia
18, se tomaron los siguientes criterios.
Cuando las zapatas aisladas sobre suelo compresible ocupan arriba del 30% del área de la planta del
edificio o cuando los asentamientos diferenciales permisibles no son satisfechos, resulta más
económico y conveniente usar zapatas continuas.
En el caso de tener zapatas continuas muy anchas debido a la descarga y la baja capacidad de carga
del suelo resulta conveniente usar losas con o sin contratrabes. Deberá tomarse esta decisión cuando
el área de la zapata continua ocupe arriba del 50% del área de la planta del edificio.
En las figuras 1.2 a 1.6 se muestran varios tipos de cimentaciones superficiales, se puede observar en
los esquemas que las estructuras usadas son losas y vigas estudiadas en los cursos de Análisis
Estructural y que por consiguiente se conoce el comportamiento mecánico de ellas.
Planta
Elevación
Figura 1.2 Zapatas aisladas
4
Capítulo 1
Introducción
Planta
Elevación y Planta
Elevación
Figura 1.3. Zapatas corridas o continuas
Planta
Planta
Figura 1.4. Zapatas corridas
Capítulo 1
Elevación
Planta
(a) Losa plana para cimentación
Introducción
Elevación
Planta
(b) Placa plana con bases de mayor
espesor bajo las columnas.
Elevación
Elevación
Planta
Planta
(c) Placa con vigas subterráneas
(d) Placa con pedestales en
las columnas.
Figura 1.5 Tipos de placas
5
6
Capítulo 1
Introducción
Elevación
Elevación
Planta
Planta
Figura 1.6 Losas y retículas
Es necesario enfatizar que en el análisis de cimentaciones se deben determinar los hundimientos y
presiones de contacto del suelo, así como calcular los elementos mecánicos en las piezas
estructurales de la cimentación, debidos a los movimientos diferenciales, presiones de contacto y las
cargas de la superestructura.
En el planteamiento del problema se deberá considerar la interacción suelo–estructura para suelos
compresibles interviniendo por lo tanto las propiedades del suelo. En los métodos con modelos de
mayor aproximación se trata de esta manera, En forma somera se expone este tema en el capítulo 5.
Las cimentaciones profundas se usan cuando el suelo donde se va a construir no tiene la capacidad
para resistir el peso que le va a transmitir la estructura, por lo tanto, es necesario transmitir la carga a
capas profundas que sean resistentes, por medio de otras cimentaciones, como las cimentaciones por
substitución, por flotación o a base de pilas y pilotes.
Las cimentaciones por substitución, consiste en cambiar el peso de la estructura por su equivalente en
masa de suelo, aprovechando que la capa inferior ya ha sido fatigada por el peso de la masa de suelo
que se va a substituir. Este tipo de cimentación se recomienda su uso en suelos altamente
compresibles y con poder de expansión y baja capacidad de carga.
La función de los pilotes y las pilas es la de transmitir las cargas de la estructura a las capas profundas
mas resistentes por medio de elementos verticales. Existen diferentes tipos de pilotes, una
clasificación de acuerdo a su forma de trabajo con respecto al suelo es la siguiente: pilotes de fricción
en suelos de granos gruesos muy permeables, pilotes de fricción en suelos de granos muy finos y baja
permeabilidad y pilotes resistentes de punta.
Capítulo 1
Introducción
7
Con el objeto de estudiar a las cimentaciones se ha establecido la clasificación expuesta, sin embargo
al seleccionar el tipo de cimentación pueden resultar
combinaciones de las mencionadas
anteriormente, es decir cimentaciones mixtas.
1.3
Importancia de la Mecánica de Suelos.
Seguramente se puede advertir por lo antes expuesto la necesidad de un profundo estudio del
comportamiento del suelo o sea de la Mecánica de Suelos. La actividad de la construcción se
incrementó notablemente durante las últimas décadas del siglo XX, creando obras de grandes
dimensiones y de gran peso que obligan a realizar estudios mas a conciencia de los suelos.
El diseño de una cimentación óptima para una estructura, ésta sujeta a la determinación real de las
condiciones del suelo y el comportamiento que tendrá la cimentación cuando esté afectada por la
acción de las cargas que le transmite la superestructura. La valuación de las condiciones reales del
suelo se hacen tomando muestras y realizando ensayos en el laboratorio, obteniéndose algunos
parámetros que aplicados y desarrollados proporcionan los valores de diseño.
Debido al objetivo de este trabajo no es posible profundizar en esta ciencia, además existen libros y
artículos excelentes que el estudiante puede consultar, por lo tanto solamente se resumen algunos
temas que se consideran indispensables para el diseño de cimentaciones superficiales.
1.4
Resistencia al corte.
El conocimiento de la resistencia al corte de los suelos, es requisito indispensable para cualquier
análisis que se relacione con la estabilidad de la masa de suelo. Determina factores tales como la
capacidad de carga admisible para una cimentación, la estabilidad de un talud y el empuje de un
suelo contra un muro de contención.
Coulomb postuló la ecuación de falla de la resistencia al corte, que es una expresión puramente
empírica, ésta es:
τ = c + σ tan φ
(1.1)
En donde:
Variable
Significado_______________________________________________
τ
c
σ
φ
esfuerzo cortante a la falla
cohesión del suelo
esfuerzo normal en el plano de falla
ángulo de fricción del suelo
Esta ecuación no siempre conduce a diseños satisfactorios de estructuras de suelo, lo anterior se hizo
evidente cuando el profesor Terzaghi publicó el principio de esfuerzos efectivos. Por lo que la ecuación
(1.1) en términos de esfuerzos efectivos, se expresa:
8
Capítulo 1
Introducción
τ = c’ + σ’ tan φ’
(1.2)
en la ecuación (1.2) los parámetros c’ y φ’ son propiedades de la estructura del suelo denominados
respectivamente, cohesión efectiva y ángulo de fricción efectiva. Los valores de la cohesión y ángulos
de fricción es común que se obtengan de ensayes de laboratorio realizados sobre muestras de suelo
representativos mediante el ensaye de corte directo o el ensaye de compresión triaxial.
1.5
Relación de Poisson.
El comportamiento esfuerzo-deformación de la masa del suelo rara vez es simple puede decirse que
frecuentemente es muy compleja, sin embargo dentro del contexto de la búsqueda de los esfuerzos y
deformaciones para ciertas condiciones se supone que el suelo se comporta como un material
homogéneo, isotrópico y linealmente elástico cuyas propiedades se definen con la relación de Poisson
y el módulo de elasticidad.
La relación de Poisson está definida como la relación de la deformación longitudinal a la deformación
transversal, esta es:
ε
µ= l
εt
(1.3)
En donde:
Variable
Significado_______________________________________________
µ
εl
Relación de Poisson
Deformación longitudinal
εt
Deformación transversal
Esta constante elástica es difícil de evaluar en el laboratorio pero existen otros métodos para
obtenerla.
1.6
Módulo de elasticidad.
En la práctica son de especial interés conocer las deformaciones verticales, es decir, los
asentamientos de la masa del suelo cuando se aplican las cargas. Las soluciones para conocer los
asentamientos basados en la teoría de la elasticidad utilizan el módulo de elasticidad y la relación de
Poisson, es importante hacer notar que una masa de suelo no tiene valores únicos del módulo de
elasticidad y la relación de Poisson, y es difícil obtener los valores apropiados de estos parámetros, lo
cual limita su aplicación.
Capítulo 1
Introducción
9
El módulo de elasticidad, E, se determina de la curva esfuerzo-deformación para materiales tales
como el concreto, acero y mampostería por mencionar los materiales mas comunes en las
construcciones civiles. Desafortunadamente para conocer el módulo de elasticidad del suelo existen
varios factores que complican su obtención.
La curva esfuerzo-deformación no es lineal por lo que uno se pregunta ¿que debe tomarse?, el módulo
tangente inicial, cualquier otro módulo tangente o el módulo secante, además la curva es sensible a
simples perturbaciones. Parece ser que la tendencia es usar el módulo tangente inicial, algunos
valores típicos de módulos pueden consultarse en el capítulo 2 de la referencia 7.
1.7
Módulo de cimentación.
El módulo de cimentación es usado en problemas de interacción entre el suelo y la estructura. Se
define como la relación entre la presión del suelo a la deformación de su masa.
El módulo de cimentación se tratará en el capítulo 5 cuando se estudie el problema de vigas sobre
medios elásticos, en este capítulo se menciona debido a que se considera a éste como una de las tres
propiedades elásticas del suelo junto con el módulo de elasticidad y la relación de Poisson.
1.8
Capacidad de carga.
Se le llama capacidad de carga a la máxima intensidad de presión que una estructura transmite al
suelo, que lo soporta, sin llegar a causar asentamientos que pongan en peligro la estabilidad de la
construcción o se presente falla del suelo por cortante.
El análisis de la capacidad de carga es importante en la evaluación de la estabilidad y economía de las
cimentaciones superficiales y depende de las características geométricas de la cimentación de las
propiedades mecánicas e índices del terreno, así como de la localización del nivel freático.
Se ha observado que la falla por capacidad de carga en las construcciones suceden como producto de
una rotura por corte del suelo de desplante de la cimentación. Los tres tipos de falla principales bajo
las cimentaciones son:
1. Falla por corte general
2. Falla por punzonamiento.
3. Falla por corte local.
La falla por corte general se caracteriza por la existencia, dentro del terreno, de una superficie de
deslizamiento continuo, que se inicia desde un borde de la cimentación hasta la superficie del terreno.
10
Capítulo 1
Introducción
Figuras 1.7 Tipos de falla por capacidad de carga
La falla por punzonamiento se identifica por un movimiento vertical de la cimentación, debido a la
compresión del suelo, inmediatamente debajo de dicha cimentación. El terreno que queda fuera de
área de carga presenta pequeñas alteraciones, quedando el equilibrio de la cimentación tanto vertical
como horizontal.
La falla por corte local presenta una marcada tendencia al bufamiento del suelo a los lados de la
cimentación, presentándose compresiones verticales fuertes debajo de ella, las superficies de
deslizamiento terminan en algún punto dentro de la misma masa de suelo. Este tipo de falla es una
transición entre las dos mencionadas anteriormente.
Se puede establecer, en términos generales, que el tipo de falla depende de la compresibilidad relativa
del suelo en cuanto a las condiciones geométricas y de carga actuante. Se tendrá falla por corte
general en suelos incompresibles, con una resistencia al esfuerzo cortante finita. Y falla por
punzonamiento, cuando se tenga suelos muy compresibles en relación con su resistencia. No
obstante, resulta interesante hacer notar que el tipo de suelo no determina el tipo de falla.
La determinación de la capacidad límite de falla de una cimentación es un problema de equilibrio
elastoplástico. La solución al problema presenta dificultades al encontrar las relaciones esfuerzodeformación-tiempo.
Existen varios estudios teóricos para determinar la capacidad de carga de las cimentaciones en
diferentes suelos. A continuación se presentan algunos resultados.
Karl Von Terzaghi, para determinar la capacidad de carga de una cimentación continua para falla por
Capítulo 1
Introducción
11
corte general, presentó la siguiente ecuación:
qd = c Nc + γ ZNq + 0.5 γ BNw
(1.4)
En donde:
Variable
Significado_______________________________________________
qd
c
γ
Z
B
Nc , Nq , Nw
Capacidad de carga límite en kg/m
2
Cohesión del suelo en kg/m .
3
Peso volumétrico del suelo en kg/m
Profundidad de desplante de la cimentación en metros.
Ancho de la zapata.
Factores de carga, sin dimensión, que dependen únicamente del
ángulo de fricción interna del suelo.
2
Para la capacidad de carga límite de una zapata continua para falla por corte local y punzonamiento,
presentó:
qd = c’ Nc’ + γ Z Nq’ + 0.5 γ BNw’
(1.5)
En donde:
Variable
c'= 2/3c
'
'
c,
q y
Significado_______________________________________________
Cohesión del suelo.
'
w
Factores de carga, sin dimensión.
Para zapatas cuadradas y corte general.
qd = 1.3 c Nc + γ Z Nq + 0.4 γ B Nw
(1.6)
Para zapatas cuadradas y falla por corte local o punzonamiento:
qd = 1.3 c' Nc’ + γ Z Nq’ + 0.4 γ B Nc’
(1.7)
Para zapatas circulares y falla por corte general:
qd = 1.3 c Nc + γ Z Nq + 0.6 γ R Nw
Para zapatas circulares y corte local y punzonamiento:
(1.8)
12
Capítulo 1
Introducción
qd = 1.3 c'Nc’ + γ ZNq’ + 0.6 γ RNw’
(1.9)
La capacidad de carga admisible qa, se obtiene dividiendo la capacidad de carga límite por un factor de
seguridad que Terzaghi recomienda.
qa =
qd
3
(1.10)
Skempton, para obtener la capacidad de carga en suelos cohesivos, propuso:
qd = c Nc + γ Z
(1.11)
En donde:
Variable
Significado_______________________________________________
Nc
Z
B
Varía con la relación Z/B.
Profundidad de desplante de la cimentación.
Ancho de la cimentación.
Para valores de Nc, ver por ejemplo la referencia 3.
Para obtención de la capacidad de carga de las cimentaciones sobre arenas, es conveniente hacer
uso de la presión neta, o sea, la presión en la base de la cimentación en exceso de aquella debido a la
sobrecarga del terreno que la rodea.
qd =
q d'
- γ Z 0.5 B γ Nγ + γ Z (Nq-1)
(1.12)
La capacidad de carga para cimentaciones desplantadas en terrenos inclinados puede obtenerse con
la siguiente expresión:
qd = cNcg + 0.5 B γ Nwq
(1.13)
Para zapatas cuadradas.
qd = 1.3 c Ncg + 0.4 Bγ Nwq
El factor de seguridad también se recomienda de 3.
(1.14)
Capítulo 1
1.3
Introducción
13
Asentamientos.
Los asentamientos son el resultado de varias o una de las causas siguientes: deformaciones elásticas
(asentamientos inmediatos), asentamientos catastróficos, consolidación del terreno, desplome minero
y otras causas.
Los asentamientos diferenciales son más importantes que los asentamientos totales, así por ejemplo,
cuando una columna cede 5 cm. más que las próximas a ella, producirá un efecto de mayor
trascendencia en la estructura que si toda la estructura se hundiera 15 cm uniformemente. Razón por
la cual se le da una atención mayor a los asentamientos diferenciales.
Cuando una estructura se ve sujeta a hundimientos diferenciales, se generan en ella acciones internas
o elementos mecánicos que pueden tener gran importancia. Generalmente los hundimientos
diferenciales se efectúan con relativa lentitud, de manera que para evaluar su efecto deben
considerarse módulos de elasticidad bajos, que tomen en cuenta los efectos de flujo plástico del
concreto.
Para calcular los asentamientos y comprender este interesante tema se recomienda estudiar el
capítulo X, de la referencia 1, el capítulo III de la referencia 2 y también el capítulo 21 de la referencia
13.
Capítulo
2
ZAPATAS AISLADAS
Las zapatas aisladas son estructuras constituidas principalmente por una losa que puede tener formas
diversas como cuadradas, rectangulares, circulares o cualquier otra de acuerdo a la construcción. Las
zapatas, con respecto a las acciones que actúan en ellas, puede tener cargas axiales, cargas axiales y
Pmomentos flexionantes además de las fuerzas cortantes.
Es común que este tipo de cimentaciones se use en casas habitación, edificios, naves industriales,
postes de alumbrado y puentes. Se recomienda su empleo de preferencia en suelos de baja
compresibilidad, cuando se tengan asentamientos diferenciales entre columnas que se puedan
controlar por medio de la flexibilidad de la estructura o se incluyan en el diseño nudos o rótulas que
tomen los asentamientos diferenciales y los giros sin dañar la construcción.
2.1 Hipotésis para el diseño.
Por medio de análisis teóricos elásticos y observaciones se demuestra que la distribución de esfuerzos
debajo de las zapatas cargadas simétricamente, no es uniforme. La distribución de los esfuerzos
depende del tipo de suelo debajo de la zapata y de la rigidez de la zapata misma. Para zapatas sobre
material suelto y poco cohesivo, las partículas de suelo tienden a desplazarse hacia los extremos,
quedando relativamente confinadas en el centro, como se ilustra en la figura (2.1.a). En el caso
general de zapatas rígidas sobre suelos cohesivos la figura (2.1.b), muestra la distribución teórica de
presiones. Debido a que las intensidades de la presión abajo de la zapata dependen de la rigidez de
ésta, del tipo de suelo y las condiciones del mismo, el problema es generalmente indeterminado.
16
Capítulo 2
Zapatas Aisladas
P
P
(a)
(b)
P
(c)
Figura 2.1.- Distribución de las presiones debajo de una zapata
En diseños prácticos se recomienda las siguientes hipótesis:
1.La distribución de presiones es lineal, figura 2.1.c.
2.La losa de la zapata se considera rígida.
3.No se admiten tensiones en el terreno.
2.2 Zapatas aisladas con cargas excéntricas.
Es común encontrar zapatas sujetas a carga axial y momentos flexionantes, en este caso, la resultante
de la presión del suelo no coincide con el centroide de la zapata, dos casos se muestran en la figura
2.2. La resultante de la presión coincide con la fuerza axial P, pero no con el centroide de la zapata,
resultando una distribución de esfuerzos no uniforme, es posible también que ocurra una inclinación de
la losa en su extremo. Todo esto puede ser evitado usando un factor de seguridad más grande cuando
se calcule la presión admisible del suelo. La zapata de la figura 2.2.a, tiene una excentricidad
estructural ya que la carga no es colineal con el centro del área. Debe conocerse la rigidez de la unión
zapata - columna como parte del análisis.
Capítulo 2 Zapatas Aisladas
P
P
M
C
L
R=P
17
e
e=M/P
e
L
R=P
L
e < L/6
e < L/6
e < L/6
e=L/6
qmax.
e=L/6
e < L/6
(a)
(b)
Figura 2.2.- (a) Columna colocada excéntricamente con respecto al centro de la zapata.
(b) Zapata sujeta a carga axial y momento.
La columna en la figura 2.2.b debe estar rígidamente unida a la zapata, con el objeto de transmitirle
momento. Para cualquier caso donde la columna transmita momento, la excentricidad aparante
e = M / P debida al momento, será contrarrestada por la tendencia de la zapata a rotar en la
dirección del momento.
2.3 Cálculo de las presiones de contacto
Tomando en cuenta que la losa de la zapata ha sido considerada rígida, la presión del suelo puede
ser calculada por la fórmula de la flexocompresión.
q =
P
Mc
±
A
I
I
BL2
si
=S=
;
c
6
entonces :
(2.1)
A = BL ;
M = Pe
18
q =
Capítulo 2
Zapatas Aisladas
P
6M
P
6e
±
(1 ±
)
2 =
BL
BL
BL
L
(2.2)
En donde:
Variable
Significado
P
Carga o fuerza axial
e
Excentricidad de la carga axial.
B, L
Dimensiones de la zapata.
q
Intensidad de la presión del suelo.
En la ecuación (2.2), si e es lo suficientemente grande, la presión del suelo sobre la zapata, actúa
como si ésta tratara de separarse del suelo. Los esfuerzos de tensión no son posibles, por lo que no se
consideran, dando como resultado una reducción en el área efectiva de la zapata. Resolviendo la
ecuación (2.2) para q = 0 , se obtiene e = L / 6 , que es la máxima excentricidad de la presión del
suelo, para ser soportado por toda el área de la zapata y con ningún esfuerzo de tensión debajo de
ésta.
Las presiones máximas y mínimas se calcularan con las expresiones siguientes :
q m ín =
P
6M
−
BL
B L2
y
q m ax =
P
6M
+
BL
B L2
Para excentricidades en dos direcciones, figura 2.3, las presiones de contacto se calculan con :
q =
P
M X CY
M YC
±
±
A
IX
IY
X
(2.3)
En donde:
Variable
Significado
q
Intensidad de la presión del suelo.
Mx, My
Momentos alrededor de los ejes x e y respectivamente.
Ix, Iy
Momentos de inercia con respecto a los ejes x e y.
Cx, Cy
Distancias perpendiculares de
principales a los bordes de la losa.
q m ín =
P
M X CY
M YC
−
−
A
IX
IY
q m ax =
P
M X CY
M YC
+
+
A
IX
IY
Para q mín = 0 , se tiene:
X
X
los
ejes
centroidales
Capítulo 2 Zapatas Aisladas
e
X
=
B
6
y
eY =
19
L
6
Las líneas que unen estos valores forman un área llamada núcleo central, se ilustra en la figura 2.3.
X
L.p.n
P
My
n.c.
Mx
(a)
(c)
L.p.n
B/6
B/6
(b)
Y
B
(a)
L.p.n
L
c
b
L/6 L/6
Figura 2.3.- Núcleo central y línea de presiones nulas (l.p.n.)
Considerando diferentes alternativas en la posición de una carga axial tenemos, cuando la carga esté
dentro del núcleo central, debajo de la zapata solamente se presentarán presiones de compresión
incluyendo el caso cuando actúa en el perímetro del núcleo central. En cambio, si la carga está fuera
del núcleo central, se presentarán tensiones teóricamente. En la figura 2.2 se ilustran con diferentes
tipos de líneas los diagramas de presiones de estas alternativas, tomando como referencia la
excentricidad en el sentido y.
Los puntos donde las presiones valen cero, forman una línea que denominaremos línea de presiones
nulas, como se muestra en la figura 2.3. De acuerdo a la posición de la línea de presiones nulas se
tendrán los diferentes diagramas de presiones de contacto ya mencionadas, esto es:
1. Si la línea de presiones nulas pasa por el núcleo central, el diagrama de presiones tendrá parte de
tensiones. En la figura 2.3, se marca la línea con la letra “a” y el punto donde actúa la carga axial con
la misma letra.
2. Cuando la línea de presiones nulas es tangente al perímetro de la losa de la zapata, el diagrama de
presiones es de forma triangular.
3. Y si la línea de presiones nulas está fuera de la losa, el diagrama es trapecial o sea que solamente
se tendrán esfuerzos de compresión.
Se advierte, que cuando la carga axial está en el centro del núcleo, teóricamente la línea de presiones
nulas está en el infinito, o no existe.
En la gráfica 2.1 se presentan unas gráficas para determinar las líneas de presiones, gráfica a, y
obtener las presiones máximas, gráfica b, del Prof. H. J. Plock. En el ejemplo 2.1 se ilustra su uso.
20
Capítulo 2
Zapatas Aisladas
En el diseño de zapatas sujetas a carga axial y momento, se hace la consideración, que la distribución
de presiones se mantiene lineal, y así se obtiene la expresión usada para conseguir la dimensión
reducida del cálculo de la zapata, expresión 2.4.
C
L
e
2e
B'
Figura 2.4.- Ancho reducido de zapata
B '= B − 2e
(2.4)
en donde:
Variable
Significado_______________________________________
B’
Ancho de cálculo
B
Ancho de la zapata
e
Excentricidad
Capítulo 2 Zapatas Aisladas
Gráficas2.1 a) Curvas para ubicar la línea de presiones nula en la losa de la zapata.
b) Curvas para encontrar la presión del suelo máxima.
21
22
Capítulo 2
Zapatas Aisladas
Con los valores c y d se entra a la gráfica ( a ).
c =
eX
B
;
d =
eY
L
Se intercambiarán los valores de c y d, si c > d para zapatas rectangulares
s' = B / L .
Para calcular la presión del suelo máximo se usa la expresión 2.5
pmax =
KP
BL
(2.5)
2.4 Procedimiento para el diseño de zapatas.
Para el diseño de zapatas se propone la secuela de cálculo siguiente, sin que sea rigurosa para otros
criterios de diseño :
1. Se obtienen las fuerzas axiales y momentos flexionantes últimos, mediante el uso de factores de
carga.
2. Se encuentran las dimensiones de la zapata, de tal forma que las presiones de contacto sean
menores que la admisible del suelo.
3. Obtención de las presiones de diseño.
4. Se revisa por efecto de fuerza cortante :
a) como losa.
b) como viga.
5. Se diseña por flexión, es decir, se calcula el área de acero necesario, número de varillas y su
disposición.
6. Se revisa por aplastamiento.
Para una mejor comprensión, se amplian los puntos anteriores :
1. De acuerdo con el RCDF - 93, para la obtención de las cargas y momentos flexionantes
últimos, se efectuarán las siguientes combinaciones de carga con sus respectivos factores :
PU = 1.4 (CM + CV ) o PU = 1.5 (CM + CV )
PU = 1.1 (CM + CVI + CA)
Capítulo 2 Zapatas Aisladas
23
en donde:
Variable
Significado
PU
Fuerza axial última
CM
Carga muerta
CV
Carga viva máxima
CVI
Carga viva instantanea
CA
Carga accidental
Las mismas expresiones son aplicables cuando se tienen momentos en lugar de fuerzas.
2. El dimensionamiento de la zapata se obtiene dividiendo la carga axial entre la resistencia del suelo,
lo que dará el área requerida para distribuir la carga uniformemente sin rebasar el valor de la
resistencia del terreno; de ésta manera se tiene que:
para zapatas cuadradas.
B2 =
P
qa
(2.6)
para zapatas rectangulares.
BL =
P
qa
(2.7)
Debe recorsarse que de cuando la zapata esta sujeta a caraga axial y momento, la dimensión en el
sentido en que esté aplicado el momento se reducirá debido a la excentricidad existente, obteniéndose
un nuevo valor dado por la expresión (2.4).
3. Una vez establecidas las dimensiones se obtienen las presiones de diseño que se usarán para el
cálculo de la zapata.
4. Se deberá revisar el efecto de la fuerza cortante como losa y como viga ancha, proponiendo valores
para el peralte y luego hacer las verificaciones correspondientes. Con el objeto de poder programar
una expresión por medio de la cual se obtengan, de una vez por todas, los peraltes requeridos para
satisfacer el cortante como losa y como viga ancha, se harán las consideraciones siguientes:
4a. Obtención del peralte para satisfacer el cortante como losa, llamado también por penetración.
De la figura 2.6, el perímetro crítico para la columna cuadrada mostrada es
encerrada por este perímetro es
está dada por:
qU =
PU
BL
4 ( w + d ) y el área
( w + d ) 2 . Sabiendo que la presión del suelo en la base de la zapata
(2.8)
Se puede obtener la expresión deseada, sumando las fuerzas verticales en la zona de tensión diagonal
como se muestra en la figura 2.5.
24
Capítulo 2
Zapatas Aisladas
PU − P ′ − d v c ( perímetro) = 0
(2.9)
P ′ = qU ( w + d ) 2
Substituyendo P’ en la ecuación (2.9) y reordenando términos, se obtiene :
PU = 4 v c ( w + d ) d + qU ( w + d ) 2
simplificando, se llega a la expresión deseada para columnas cuadradas :
d 2 ⋅ ( vc +
qU
q
BL − w 2
) + d ⋅ ( vc + U ) ⋅ w =
⋅ qU
4
2
4
la ecuación para columnas redondas, llamando al diámetro
d 2 ⋅ ( vc +
(2.10)
w, será :
qU
q
( BL − Ac )
) + d ⋅ ( vc + U ) ⋅ w =
⋅ qU
4
2
π
(2.11)
haciendo un planteamiento similar al anterior, se obtiene una expresión para columnas rectangulares
quedando de la siguiente forma :
d 2 ⋅ (−
qU
q
q
− 4) − d ⋅ p ⋅ ( U + 1) + U ⋅ AS = 0
vc
2vc
vc
(2.12)
En las expresiones anteriores :
Variable
Significado
d
p
AS
qU
vc
Peralte como losa
Perímetro de la columna rectangular
Area de la zapata - área de la columna
Presión última de contacto
Esfuerzo cortante que toma el concreto cuando se revisa como
losa. v c
= FR f c∗
Capítulo 2 Zapatas Aisladas
25
B
w+d
w
(2.13)
d/ 2
L
w
Sección
crítica
Pu
W
Vcr
Perimetro resistente al
cortante.
W+d
d
2
P' =qu(w+d)
Figura 2.5.- Secciones críticas al revisar el cortante como losas
4b. Peralte para satisfacer el cortante como viga ancha. En forma semejante como se hizo en la
sección anterior, es posible obtener una expresión por medio de la cual se consiga el peralte necesario
para resistir el cortante en la zapata al revisarse como viga ancha.
Del RCDF - 93, la fuerza cortante que toma el concreto para porcentajes de acero mayores de 0.01
está dada por la expresión :
vc = 0.5 ⋅ FR ⋅ b ⋅ d ⋅
f c∗
(2.14)
por lo que el esfuerzo cortante queda dado por la expresión :
vc =
Vc
Bd
en la figura 2.6 se observa que :
(2.15)
26
Capítulo 2
Vc = B ⋅ (
Zapatas Aisladas
L− A
− d ) ⋅ qU
2
(2.16)
substituyendo (2.16) en (2.15)
vc =
qU
L− A
⋅ B⋅(
− d)
Bd
2
reduciendo términos y despejando el valor de
d=
d
( L − A) ⋅ qU
2 ⋅ ( v c + qU )
(2.17)
en donde :
Variable
Significado
d
L
A
qU
vc
Peralte para resistir el cortante como viga ancha.
Largo o ancho de la zapata
Lado de la columna
Presión de diseño
Esfuerzo cortante que toma el concreto cuando se revisa como viga ancha y
vale :
v c = 0.4 ⋅ f c∗
(2.18)
d
A
B
d
L
Figura 2.6.- Sección crítica al revisar el cortante como viga ancha
Capítulo 2 Zapatas Aisladas
27
Las normas del RCDF - 93 presentan una expresión para la fuerza cortante cuando el porcentaje de
acero es menor que 0.01, por lo que es aconsejable revisar el peralte utilizando esta expresión, y en su
caso, obtener un nuevo peralte que la satisfaga. La expresión a la cual se hace mención es la
siguiente:
VC = FR ⋅ bd ⋅ ( 0.2 + 30 p) ⋅ f C∗
(2.19)
de donde :
vC = 0.8 ⋅ ( 0.2 + 30 p) ⋅ f C∗
para porcentaje de acero
≤ 0.01
Una vez obtenidos el peralte como viga ancha y el peralte como losa, se elige el mayor, como el
peralte definitivo de la zapata.
Cuando la zapata está sujeta a momento flexionante, el RCDF - 93 propone que se revise el esfuerzo
cortante de diseño, suponiendo que una fracción del momento dada por :
α = 1−
1
1 + 0.67 ⋅ ( C1 + d ) / ( C2 + d )
(2.20)
Se trasmite por excentricidad de la fuerza cortante total, con respecto al centroide de la sección crítica
mostrada en la figura 2.7. El esfuerzo cortante máximo de diseño vU , se obtendrá tomando en cuenta
el efecto de la carga axial y el momento flexionante, suponiendo que los esfuerzos cortantes varían
linealmente figura 2.7. En columnas rectangulares C1 es la dimensión paralela al momento trasmitido y
C2 es la dimensión perpendicular a C1 . En columnas circulares C1 = C2 = 0.9 ⋅ D
El esfuerzo cortante máximo de diseño no deberá exceder de :
VC = 0.8 ⋅ f C∗
(2.21)
5. El diseño por flexión estará basado en la teoría de resistencia última, para lo cual se emplea la
expresión siguiente :
a
MU = FR ⋅ AS ⋅ f Y ⋅ ( d − )
2
Se recomienda ver la figura 2.8 y relacionarla con la ecuación (2.22).
Se recordará que FR es el factor de reducción y las otras literales ya son conocidas.
(2.22)
28
Capítulo 2
Zapatas Aisladas
Para una mejor comprensión se recomienda ver la referencia 9 de la bibliografía.
V AB =
V α ⋅ M ⋅ C AB
+
AC
JC
AC = 2d ⋅ ( C1 + C2 + 2 d )
JC =
d ⋅ (C1 + d ) 3 ( C1 + d ) ⋅ d 3 d ⋅ ( C2 + d )( C1 + d ) 2
+
+
6
6
2
c1+ d
c1
V
M
c2 + d
V
AB
Sección
crítica
c
2
CAB
Figura 2.7.- Trasmisión de momento entre columna y losa
De las normas técnicas mencionadas se tiene :
a=
AS ⋅ f Y
f C'' ⋅ b
sustituyendo la ecuación (2.23) en la ecuación (2.22)
(2.23)
Capítulo 2 Zapatas Aisladas
M U = FR ⋅ AS ⋅ f Y ⋅ ( d −
29
0.5 ⋅ AS ⋅ f Y
)
f C'' ⋅ b
dividiendo ambos miembros entre f Y ⋅ FR
MU
0.5 ⋅ AS 2 ⋅ f Y
= AS ⋅ d −
f Y ⋅ FR
f C'' ⋅ b
si se hace :
F=
MU
FR ⋅ f Y
y
G=
0.5 ⋅ f Y
f C'' ⋅ b
queda la siguiente expresión :
F = AS ⋅ d − AS 2 ⋅ G
(2.24)
en las expresiones anteriores :
Variable
Significado
AS
Area de acero requerida.
MU
Momento último del cantiliver.
FR
fY
Factor de reducción por flexión.
Esfuerzo de fluencia del acero.
f C'' = 0.85 ⋅ f C∗
b
Ancho de la zapata.
La ecuación (2.24) representa una expresión fácil de programar en computadora para obtener la
cantidad de acero requerida en el diseño por flexión.
Luego se calcula el porcentaje de acero y se compara con los porcentajes de acero máximo y mínimo
permitidos por el reglamento.
Por último se propone el armado y diámetro de las varillas, las cuales deben de cumplir con los
requisitos de longitud de desarrollo y anclaje que pieden las normas técnicas del RCDF -93.
30
Capítulo 2
Zapatas Aisladas
f"c
a
C
y = d -a/2
T = As
Figura 2.8.- Obtención de las ecuaciones para el diseño de resistencia última.
6. La presión de contacto o aplastamiento ejercida por la columna sobre la zapata puede ser un factor
crítico para controlar el peralte, especialmente si el concreto de la columna tiene un esfuerzo a
'
compresión resistente f C mayor que el de la zapata, por lo tanto, las presiones de contacto no deben
ser mayores que :
f a = 0.7 ⋅ f C∗
(2.25)
y la carga máxima que soporta la zapata por aplastamiento será :
Pmáx = R ⋅ f a ⋅ AC
(2.26)
en donde :
Variable
Significado
AC
área de la columna
R=
A1
≤2
Ac
Para columnas cuadradas
A1 = ( L + 4d ) 2
(ver figura 2.9)
(2.27)
Capítulo 2 Zapatas Aisladas
31
2d
AC
A1
L
2d
2d
L
2d
Figura 2.9.- Sección crítica para revisar los esfuerzos de contacto.
Cuando la carga máxima obtenida en la ecuación (2.26) es mayor que la carga última de diseño, será
necesario proporcionar varillas de anclaje que tomen la diferencia de carga existente. Se recomienda
que el diámetro de las varillas no debe ser mayor en 4 mm. que el diámetro de las varillas de la
columna, y no poner menos de cuatro varillas.
Se anexan otras recomendaciones sobre el tema :
El espesor mínimo de la losa de zapatas de concreto reforzado será de 15 cm. y de 30 cm. si la zapata
se apoya sobre pilotes.
Para zapatas apoyadas sobre pilotes, se supondrá al calcular la fuerza cortante en una sección, que
en ella produce esfuerzos cortantes la reaccion de los pilotes cuyos centros quedan a 0.5 ⋅ dp o más
hacia fuera de dicha sección. Se supondrá que no producen cortantes las reacciones de los pilotes
cuyos centros queden a 0.5 ⋅ dp o menos, lléndose hacia dentro de la sección considerada. Para
posiciones intermedias del centro de un pliote se ineterpola linealmente.
0.5
dp
Rp
Rp
Rp
Figura 2.10.- Zapatas apoyadas en pilotes.
dp
32
Capítulo 2
Zapatas Aisladas
Respecto a la distribución de refuerzo se toman las siguientes consideraciones :
Las zapatas con refuerzo en una dirección y las zapatas cuadradas reforzadas en dos direcciones
llevarán refuerzo espaciado uniformemente.
Para zapatas rectangulares con flexión en dos direcciones, el refuerzo paralelo al lado mayor se
distribuirá uniformemente; el paralelo al lado menor se distribuirá en tres franjas en la forma siguiente:
en la franja central, de ancho a1 , una cantidad de refuerzo igual a la totalidad que debe colocarse en
esa dirección, multiplicada por (2a1 / a1 + a 2 ) , donde a1 y a 2 son respectivamente, los lados corto y
largo de la zapata. El resto del refuerzo se distribuirá uniformemente en las dos franjas extremas. Ver
ejemplos numéricos.
Se ilustran en la figura 2.11 varias secciones críticas para dimensionar por flexión.
columna
muro de piedra
o tabique
muro de
concreto
s.c.
sección
crítica
1m
s.c.
d/4
1m
1m
Figura 2.11.- Secciones críticas (S.C.) para dimensionar por flexión.
Para columnas de acero, la sección crítica será el perímetro de la columna, a menos que la rigidez y
resistencia de la placa permitan considerar una sección más alejada.
coluna de acero
soldadura
lechado de concreto
placa base
Figura 2.12 Zapatas con columna de acero
Capítulo 2 Zapatas Aisladas
2.5 Resumen de las Normas Técnicas Complementarias 96 del
RCDF-93 para el diseño de zapatas.
Factor de diseño
Artículo
Requerimientos Generales
Espaciamiento del refuerzo.
3.6.1
No menor del diámetro nominal
de varilla ni de 1.5 veces el
tamaño máximo del agregado,
ni de 2 cm.
No mayor de 50 cm., ni 1.5 h
No mayor de 2.5 d, en cargas
concentradas.
3.10
4.3.3
Empalmes
3.9
Refuerzo por temperatura
3.10
Ver en el reglamento
aS =
600 ⋅ x1
f Y ⋅ ( x1 + 100)
x1 es la dimensión mínima del
miembro medida
perpendicularmente al refuerzo
en cm.
Recubrimiento mínimo
3.4
5 cm. sin plantilla.
3 cm. con plantilla.
Diseño por flexión
2.1.2
a
M R = FR ⋅ AS ⋅ f Y ⋅ (d − )
2
A ⋅f
a = S '' Y
fC ⋅b
M R= FR ⋅ AS ⋅ fY ⋅ d ⋅ (1− 05
. q)
Refuerzo máximo.
2.1.2
Ab =
f C''
4800
⋅
⋅ bd , sin
f Y f Y + 6000
sismo
AS = 0.75 ⋅ Ab , con sismo
p=
Refuerzo mínimo
2.1.2
Módulo de Elasticidad
1.4.1
Factor de Reducción.
1.6
AS =
AS
bd
≤ pb
0.7 ⋅ f C'
⋅ bd
fY
E C = 14000 ⋅
f C'
(clase 1)
E C = 8000 ⋅
f C'
(clase 2)
0.9 para flexión.
33
34
Capítulo 2
Zapatas Aisladas
Factor de diseño
Artículo
Requerimientos Generales
0.8 para cortante y torsión.
0.7 para aplastamiento.
Combinación de Cargas.
1.4 (CM + CV) ó
CV)
1.5 (CM +
1.1 (CM + CV + CA)
Cortante viga ancha.
2.1.5
VCR = FR⋅bd⋅(02
. +30p)⋅ fc∗ si
p ≤ 001
.
VCR = 0.5 ⋅ FR ⋅ bd ⋅ f c∗ si
p > 001
.
Cortante como losa.
2.1.5
VCR = 0.5 ⋅ FR ⋅ bd ⋅ f c∗
Ver sección 2.1.5.h en el
reglamento cuando existe
momento.
Longitud de desarrollo
3.1.1.c
Ld = 0.06
aS ⋅ fY
fc'
≥ 0.006⋅ db ⋅ fY
≥ 20 cm
d b es el diámetro de la barra
en cm.
a S es el área transversal en cm2
para factor =1.0
Zapatas
4.4.1
Disposiciones generales.
Constantes de diseño
1.4.1
f c∗ = 0.8 ⋅ f c'
2.1.2
f c'' = 0.85 ⋅ f c∗
Kg/cm
si
2
fc∗ ≤250
f c∗
∗
f = (105
. −
) ⋅ f ∗ si fc > 250
1250 c
''
c
Kg/cm
Aplastamiento.
2.1.4
2
f a = 0.7 ⋅ f c∗
Capítulo 2 Zapatas Aisladas
35
Ejemplo 2.1.- Determinar la línea de presiones y la presión de contacto máxima para la siguiente
zapata.
DATOS:
Pu = 90.14 ton.
M ux = 40 ton-m
M uy = 48 ton-m
q a = 18 ton/m2
Pu
Muy
0.662
h
Y
2.50
X
2.35
2.50
L.p.n.
Figura 2.13 Ejemplo 2.1
Proponiendo :
B = 2.50 m
L = 2.50 m
Solución :
Cálculo de las excentricidades.
eX =
40
= 0.443
90.14
36
Capítulo 2
Zapatas Aisladas
eY =
48
= 0.532
90.14
Determinación de las constantes
c=
e X 0.443
=
= 0.177
B
2.50
d=
eY 0.532
=
= 0.213
L
2.50
Con los valores de
cyd
cyd
se usa las gráficas (a,), obteniendo los valores de
a y s.
a = 0.265
s
= 1.280
Obteniendo :
a ⋅ B = ( 0.265)( 2.50) = 0.6625 m.
( L − a ⋅ B) ⋅ s = (2.50 − 0.6625) ⋅ 128
. = 2.352 m.
Con los valores anteriores se localiza la línea de presiones nulas. En este caso las dimensiones de la
losa de la zapata propuesta no son adecuadas, debido a que existe una zona con reacciones
negativas (esfuerzos de tensión).
Cálculo de la presión máxima.
Con los valores de
cyd
se usa la gráficas (b), obteniendo el valor de K .
K = 4.2
pmax =
K ⋅ P (4.2)(90.14)
=
= 60.57 ton/m2
B⋅ L
(2.50) 2
La presión anterior deberá compararse con la presión admisible.
Ejemplo 2.- Diseñar una zapata de base cuadrada con los siguientes datos.
P = 50 ton. (Se incluye peso propio de la zapata).
w = 45 cm. (lado de la columna)
Capítulo 2 Zapatas Aisladas
f Y = 4200 kg/cm2
f c' = 200 kg/cm2
q a = 7 ton/m2
Constantes :
f c∗ = 0.8 f c' = 0.8 ⋅ 200 = 160 kg/cm2
f c'' = 0.85 f c∗ = 0.85 ⋅ 160 = 136 kg/cm2
Solución :
Como la zapata será cuadrada, las dimensiones de sus lados son :
B=
50
P
=
= 2.67 m.
qa
7
Se toma un valor de B = 2.8 m.
Presión de contacto :
q=
P
50
=
= 6.37 ton / m 2 ⟨ q a
Az (2.8)(2.8)
A
q
Figura 2.14 Ejemplo 2.2
37
38
Capítulo 2
Zapatas Aisladas
Presión de diseño :
Pu
70
=
= 8.93 ton/m2
Az 7.84
qu =
Cálculo del peralte para satisfacer el cortante como losa.
v c = 0.8 ⋅
vc +
f c∗ = 0.8 ⋅ 160 = 1012
. kg/cm2 = 101.2 ton/m2
qu
8.93
= 1012
. +
= 103.43
4
4
(v u +
qu
8.93
) ⋅ w = (101.2 +
) ⋅ 0.45 = 47.55
2
2
( Az − w 2 )
qu
8.93
= ( 7.84 − 0.2025) ⋅
= 17.05
4
4
Sustituyendo los valores anteriores en la ecuación (2.9)
103.43 ⋅ d 2 + 47.55 ⋅ d = 17.05
al resolver la ecuación se obtiene :
d = 0.24 m.
Cálculo del peralte para satisfacer el cortante como viga ancha.
v c = 0.4 ⋅
f c∗ = 0.4 ⋅ 160 = 5.05 kg/cm2 = 50.5 ton/m2
de la ecuación (2.16)
d=
( B − A) ⋅ q u ( 2.8 − 0.45) ⋅ 8.93
=
= 0.18 m
2 ⋅ (v c + q u )
2 ⋅ (50.5 + 8.93)
Se toma por el momento : d
= 0.24 m
Cálculo del porcentaje de acero balanceado (máximo por flexión).
Capítulo 2 Zapatas Aisladas
39
f c'' ⋅ 4800
136 ⋅ (4800 )
pb =
=
= 0.0152
f y ( f y + 6000) 4200 ⋅ (10200)
Momento último del cantiliver
L=
B − A 2.8 − 0.45
=
= 1175
.
m
2
2
q u ⋅ L2 8.93 ⋅ (1.175)2
Mu =
=
= 6.16 ton-m
2
2
Cálculo del área de acero requerida.
G=
F=
0 .5 ⋅ f y
f c''
⋅100
=
0.5 ⋅ (4200 )
= 0.154
136 ⋅ (100 )
Mu
616000
=
= 183.33
0.8 ⋅ f y 0.8 ⋅ (4200 )
Sustitutyendo valores en la ecuación (2.20)
183.33 = 24 ⋅ ( As ) − 0.15 ⋅ ( As )
2
de donde
As = 8.05 cm2/m
p=
As
8.05
=
= 0.0033
d ⋅100 24 ⋅ (100 )
p min =
0.7 ⋅
fy
f c'
=
0.7 ⋅ 200
= 0.0023
4200
Como el porcentaje de acero es menor que 0.01 se obtiene otro peralte como viga, teniendo
p = 0.0033 .
40
Capítulo 2
Zapatas Aisladas
v c = 0.8 ⋅ (0.2 + 30 p) ⋅
f c∗
v c = 0.8 ⋅ (0.2 + 30 ⋅ ( 0.0033)) ⋅ 160
v c = 3.02 kg/cm2
d=
( 2.8 − 0.45) ⋅ 8.93
= 0.268 = 0.27 m
2 ⋅ (30.2 + 8.93)
Este nuevo peralte, resulta un poco mayor que el anterior por lo que se tomará como el peralte
definitivo de la zapata.
Para el nuevo peralte la ecuación (2.20) queda :
183.33 = 27 ⋅ As − 0.154 ⋅ As 2
de donde :
As = 7.07 cm2/m
p=
7.07
= 0.0026 > pmín = 0.0023
27 ⋅ 100
AsTOT = As ⋅ B = 7.07 ⋅ 2.8 = 19.8 cm2
Usando varillas del # 4, el número de varillas es :
0V =
s=
19.8
= 16.47 ≈ 17 varillas
1.266
B ⋅100 2.80 ⋅100
=
= 16.47 ≈ 17 cm
0V
17
Ld = 0.06 ⋅
as ⋅ f y
0.06 ⋅ a s ⋅ f y
f
'
c
f c'
=
≥ 0.006 ⋅ d b ⋅ f y
0.06 ⋅ 1.266 ⋅ 4200
= 2185
. cm
200
0.006 ⋅ d b ⋅ f y = 0.006 ⋅ 1.266 ⋅ 4200 = 32.0 cm
Capítulo 2 Zapatas Aisladas
entonces :
Ld = 32.0 cm
Revisión por aplastamiento
f a = 0.7 ⋅ f c∗ = 0.7 ⋅ (160) = 112 kg/cm2
Ac = 452 = 2025 cm2
A1 = ( 45 + 4 ⋅ (27)) 2 = 23409 cm2
p máx = f a ⋅ R ⋅ Ac = 112 ⋅ (2 ) 2025 = 453600 kg
453 ton > 70 ton.
Area de acero para la barra de transmisión
As⋅mín = 0.005 ⋅ Ac = 0.005 ⋅ 2025 = 10.12 cm2
Usando varillas del # 6.
0V =
As⋅mín 1012
.
=
= 3.55 ≈ 4 varillas
As
2.85
4 Vars #6
45
17 Vars. #4@ 17(en ambas direcciones).
27
5
280
41
42
Capítulo 2
Zapatas Aisladas
17 Vars. #4@ 17(en ambas direcciones).
17 Vars. #4@ 17(en ambas direcciones).
280
Acotaciones en cm.
Figura 2.15 Ejemplo 2.2
Ejemplo 2.3. Diseñar una zapata rectangular sujeta a flexo-compresión con los datos siguientes.
A = 40 cm
(ancho de columna)
C = 60 cm
(largo de la columna)
L = 350
. m
(longitud de la zapata)
f y = 4200 kg/cm2
f c' = 200 kg/cm2
qa = 21 ton/m2
M G = 0.0 ton-m
(CM + CV)
PG = 90 ton
(CM + CV)
M A = 20 ton-m
Capítulo 2 Zapatas Aisladas
PA = 0.0 ton
Constantes :
f c∗ = 0.8 (200) = 160 kg/cm2
f c'' = 0.85 (160) = 136 kg/cm2
Solución :
Cálculo de los momentos y cargas últimas
PuG = 1.4 PG = 126 ton
M uG = 0.0 ton-m
PuA = 1.1 ( PG + PA ) = 1.1 (90) = 99 ton
M uG = 1.1 (20 ) = 22 ton-m
Se propone B = 1.70 m
Presión de contacto
q=
6 (20)
P 6M
90
± 2 =
±
A BL
1.7 (3.5) 1.7 (3.5)2
q má x = 20.88 ton/m2 < q a
qmín = 9.37 ton/m2
e=
No hay tensiones
M uA 22
=
= 0.22 m
PuA
99
L' = L − 2 e = 3.5 − 2 (0.22 ) = 3.06 m
Presión de diseño :
q uA =
q uG =
PuA
'
BL
=
99
= 19.03 ton/m2
1.7 (3.06 )
126
= 21.18 ton/m2
3.5 ⋅ (1.7 )
Obtención del peralte como losa ( carga gravitacional ).
43
44
Capítulo 2
Zapatas Aisladas
Acol = A ⋅ C = 40 ⋅ (60 ) = 2400 cm2
P = 2 ⋅ A + 2 ⋅ C = 2 ⋅ (0.4) + 2 ⋅ (0.6) = 2 m
As = Az − Acol = 5.95 − 0.24 = 5.71 m2
v c = 0.8 160 = 10.12 kg/cm2
q uG
2118
.
+4=
+ 4 = 4.21
vc
1012
.
q

 21.18

P ⋅  uG + 1 = 2 ⋅ 
+ 1 = 2.21
 2 ⋅ (101.2 ) 
 2 ⋅ vc

q uG
21.18
⋅ AsI =
⋅ (5.71) = 1.20
vc
101.2
Sustituyendo en la ecuación (2.11)
− 4.21 d 2 − 2.21 d + 1.20 = 0
de donde:
d = 0.34 m
Cálculo del peralte como viga ancha (carga gravitacional)
v c = 0.4 160 = 5.06 kg/cm2
d=
L−C
3 .5 − 0 .6
⋅ quG =
(21.18) = 0.43 m
2 (vc + quG )
2 (50.6 + 21.18)
Tomando por el momento
Lc =
d = 0.43 m
L − C 3 .5 − 0 .6
=
= 1.45 m
2
2
Mu =
quG Lc 2 21.18 (1.45)2
=
= 22.26 ton-m
2
2
Capítulo 2 Zapatas Aisladas
F=
G=
Mu
2226000
=
= 662.6
0.8 f y 0.8 (4200 )
0 .5 ⋅ f y
f c''
⋅ 100
=
0.5 (4200 )
= 0.154
136 (100 )
Sustituyendo en la ecuación (2.20)
662.5 = 43 ⋅ As − 0.154 ⋅ As 2
As = 16.37 cm2/m
p=
As
14.81
=
= 0.00381
d ⋅ 100 43 (100 )
pb = 0.0152
p máx = 0.75 (0.0152 ) = 0.0114
p mín = 0.0023
Como
p < 0.01 se calcula un nuevo peralte usando p = 0.003
vc = 0.8 [0.2 + 30 (0.003) ] 160 = 2.93 kg/cm2
d=
3 .5 − 0 .6
(21.18) = 0.60 m
2 (29.3 + 21.18)
Revisión del peralte bajo CG + CA
C1 = 60 cm
C2 = 40 cm
d = 60 cm
C1 + d = 120 cm
C2 + d = 100 cm
α = 1−
1
1 + 0.67 ⋅ (C1 + d ) / (C2 + d )
45
46
Capítulo 2
α = 1−
Zapatas Aisladas
1
= 0.423
1 + 0.67 ⋅ (120) / (100)
α ⋅ M u = 0.423 ⋅ 22 = 9.306 ton-m
Vu = 99 − (1.2 ) (1.0 ) (19.03) = 76.16
vu =
Vu α ⋅ M u ⋅ C AB
+
Ac
Jc
C AB =
C1 + d 120
=
= 60 cm
2
2
Ac = 2 (120 + 100) 60 = 26600 cm2
Jc =
60 (120) 3 120 (60) 3 60 (120) 2 (100)
+
+
6
6
2
J c = 64.8 × 106
5
76160 9.306 (10 ) 60
vu =
+
= 2.49 kg/cm2 < v c kg/cm2
6
26600
64.8 (10 )
Se observa que la carga gravitacional domina el diseño, quedando como peralte definitivo de la zapata
d = 60 cm.
Refuerzo paralelo al lado largo.
De la ecuación (2.20); pero con
d = 60 cm, se obtiene
As = 11.39 cm2/m
pero
As⋅mín = 13.8 cm2/m
As⋅TOT = As⋅mín ⋅ 1.7 = 23.46 cm2
Capítulo 2 Zapatas Aisladas
As⋅TOT 23.46
=
= 8.23 ≡ 9 varillas # 6
As
2.85
0v =
s=
1.7 (100 )
= 18.8 cm
9
Ld = 50.78 cm
Refuerzo perpendicular al lado largo.
As⋅TOT = 13.8 (3.5) = 48.3 cm2
Para la franja central la cantidad de acero requerida será:
Asc =
2 ⋅ As⋅TOT 2 (48.3)
=
= 31.59 cm2
L
3 .5
+1
+1
B
1 .7
Ase =
48.3 − 3159
.
= 8.35 cm2
2
0Vsc =
sc =
1.7 (100 )
= 15.45 cm
11
0Vse =
se =
31.59
= 11.08 ≡ 11 varillas
2.85
8.92
= 2.92 ≡ 3 varillas
2.85
0.9 (100 )
= 30 cm
3
Revisión por aplastamiento
vc = 0.7 (160 ) = 112 kg/cm2
47
48
Capítulo 2
R=
Zapatas Aisladas
510
.
= 4.6 > 2
0.24
p máx = 2 (112 ) (2400 ) = 537600 kg > 126000 kg
Area de acero para las barras de trasmisión
As⋅mín = 0.005 ⋅ Acol = 0.005 (2400 ) = 12 cm2
usando varilla del #6
0V =
12
= 4.21 ≡ 5 varillas
2.85
Ld = 48.43 cm
5 Vars. #6
40
60
11 Var. #6 @ 15
3 Vars. #6 @ 30
3 Vars. #6 @ 30
9 Vars. #6 @ 19
60
5
90
170
3 Vars. #6 @ 30
90
11 Var. #6 @ 15
170
3 Vars. #6 @ 30
9 Vars. #6 @ 19
170
350
Figura 2.16 Ejemplo 2.3
Capítulo
3
ZAPATAS CORRIDAS
Cuando las zapatas aisladas en suelos compresibles ocupan arriba del 30% del área de la
cimentación se puede usar zapatas corridas, o bien cuando se presentan cualquiera de los siguientes
casos:
a).- Cuando se tienen restricciones de lindero, si se utilizan zapatas aisladas, éstas estarían cargadas
excéntricamente, figura 3.1a y el problema que puede surgir es que la presión de contacto sea mayor
que la presión admisible del terreno, por lo que se recomienda una zapata combinada o corrida, figura
3.1 (b).
(a)
Figura 3.1
(b)
a) Zapatas aisladas b) Zapata corrida
50
Capítulo 3
Zapatas corridas
b) Cuando las columnas están muy próximas una de otras o sea que las zapatas aisladas queden muy
juntas, figura 3.2 (a) o pueden traslaparse, figura 3.2 (b)
Figura 3.2
a) Zapatas aisladas. b) Zapatas traslapadas
c) Cuando los asentamientos permisibles no sean satisfechos, en este caso los asentamientos pueden
ser reducidos por la rigidez que proporcionan las vigas (contratrabes) de la cimentación, figura 3.3.
Figura 3.3
(a) Planta (b) Isométrico de la zapata corrida
Es importante observar que para un análisis racional es conveniente estudiar este problema como
vigas sobre medios elásticos, esto es adecuado cuando el módulo de cimentación unitario es
prácticamente constante, en el capítulo 5 se trata este tema.
d) También en los casos que se presenten momentos flexionantes considerables a nivel de la
cimentación. La profundidad para desplantar la cimentación dependerá de las características del
suelo, magnitud de las cargas, cimentaciones colindantes, la presencia del N.A.F. y otros.
Capítulo 3
Zapatas corridas
51
Se propone una clasificación de éste tipo de zapatas como a continuación se indica:
a) Zapatas corridas que soportan muros de tabique o de concreto.
b) Zapatas corridas que soportan dos o más columnas sin contratrabe.
c) Zapatas corridas que soportan dos o mas columnas con contratrabes.
Se presenta un método aproximado para el análisis y diseño de zapatas corridas en el inciso 3.1,
basado en las siguientes hipótesis:
1. Se supone la losa rígida.
2. Las presiones del terreno tienen una variación lineal.
3.1
Zapatas corridas para soportar muros.
Se sugiere seguir el siguiente procedimiento:
1.Establecer las limitaciones de cálculo de acuerdo al reglamento que se use.
2. Dimensionamiento preliminar.
3. Determinar el paso de la resultante y el momento flexionante cuando exista excentricidad.
4. Revisar las presiones de contacto.
a) Se compara la presión admisible con la de contacto.
b) Se revisa que no existan esfuerzos de tensión.
5. Diseñar por flexión.
6. Revisar por cortante como viga ancha.
7. Se propone el armado.
Ejemplo 3.1. Diseñar la zapata corrida que va a soportar un muro de concreto que tiene una carga
uniforme w, tome los siguientes datos:
Figura 3.4
Zapatas corridas
52
Capítulo 3
Zapatas corridas
Datos:
w = 9 ton/m
qa = 14 ton/m2
γ = 1800 kg/m3
Df = 1.2 m
Materiales:
f ' c = 200 kg / cm 2
f y = 4200 kg / cm 2
Limitaciones:
pmin
0.7 f ' c 0.7 200
=
=
= 0.002
fy
4200
p max = 0 . 9 p b
pb =
6000 β 1 fc "
.
6000 + fy fy
f c* = 0.8 f c' = 0.8(200) = 160kg / cm 2 < 250kg / cm 2
f c' = f c* = 0.85 (160 ) = 136 kg / cm 2
f *c < 280
β1 = 0.85
5100
136
pb =
= 0.016
6000 + 4200 4200
p max = 0.9(0.016) = 0.0145
Capítulo 3
Determinación del paso de la resultante y el momento flexionante.
El peso del muro de 9 ton/m. está considerado hasta la losa.
Se supuso el espesor de la losa.
Los valores de los pesos del terreno y la losa de concreto son:
P = V γ.
P1 = 0.3 x 0.8 x 1.00 x 1.80 = 0.432 ton
P2 = 0.7 x 0.8 x 1.00 x 1.80 = 1.008 ton
P3 = 0.4 x 1.25x 1.00x 2.40 = 1.200 ton
Σp = 9 + 0.432 + 1.008 + 1.200 = 11.64 ton.
Momento respecto al punto d.
M1 = 0.432 x 1.10 = 0.475 ton - m
M2 = 1.008 x 0.35 = 0.353 ton - m
M3 =1.200 x 0.625 = 0.750 ton - m
M4 = 9.00 x 0.825 = 7.425 ton – m
ΣM = 9.003 ton - m
Por lo tanto:
El paso de la resultante se encuentra a x del punto d
x=
ΣM 9.003
=
= 0.773 m
ΣP 11.64
La excentricidad con respecto al centro de la figura en la base es:
e = 0.773 - 0.625 = 0.148 m
Zapatas corridas
53
54
Capítulo 3
Zapatas corridas
En la figura 3.5 se ilustran, la excentricidad y el efecto de flexocompresión.
(a)
Figura 3.5
(b)
a) Zapata con excentricidad. b) efecto de flexocompresión
M = ΣPe = 11.64 x 0.148 = 1.723 ton - m
Revisión de las presiones de contacto.
q =
ΣP
M
±
A
S
Donde:
A = 1.25 x 1.00 = 1.25 m2
S =
1.00 x1.252
6
= 0.26m3
Sustituyendo valores:
q =
11.64
1.723
±
1.25
0.26
qmin = 2.685 ton/m2
qmáx = 15.939 ton/m2 > 14 ton/m2
Como la presión de contacto resultó mayor que la presión admisible se procede a un segundo tanteo,
aumentando la sección ab a 40 cm. y ahora se determina el paso de la nueva resultante.
P1 = 0.4 x 0.8 x 1.00 x 1.80 = 0.576 ton
P2 = 1.008 ton
P3 = 1.35 x 0.4 x 1.00 x 2.4 = 1.296 ton
Capítulo 3
ΣP = 11.88 ton.
Momentos respecto al punto d
M1 = 0.576 x 1.15 = 0.662 ton - m
M2 = 0.353 ton - m
M3 = 1.296 x 0.675 = 0.875 ton - m
M = 7.425 ton - m
ΣM = 9.315 ton - m
x =
ΣM
9.315
=
= 0.784m
ΣP
11.88
e = 0.784 - 0.675 = 0.109 m
M = ΣP e = 11.88 x 0.109 = 1.295 ton - m
Revisión de las presiones de contacto
A = 1.35 x 1.00 = 1.35 m2
S=
1.00 x1.352
= 0.304
6
q=
11.88 1.295
±
1.35 0.304
qmin = 4.540 ton/m2
qmáx = 13.060 ton/m2 < 14 ton/m2
Zapatas corridas
55
56
Capítulo 3
Zapatas corridas
Representación esquemática de la distribución de presiones.
Figura 3.6
por triángulos semejantes
13.06 − 4.54
x
= 1
1.35
0.35
∴ x1 = 1.177
q1 = 1.177 + 4.54 = 5.717 ton/m2
13.06 − 4.54
x
= 2
1.35
0.70
∴ x 2 = 4.418
q2 = 4.418 + 4.54 = 8.958 ton/m2
Distribución lineal de presiones
Capítulo 3
Zapatas corridas
57
Diseño por flexión
Considerando el esquema de la figura 3.6 se toma la siguiente viga en cantiliver de un metro de
ancho.
Figura 3.7
Viga de ancho unitario
P = qmin (L) = 4.540 (07)=3.178 ton
P1 = (q2 - qmin )
L
= (8.958 -4.540)(0.35)
2
P1 = 1.546 ton
M r = Fr f c" bd 2q(1 − 0.5q )
pero
Mr = Mu
M u = 1. 4 ( P
L
L
+ P1 )
2
3
Mu = 1.4 (3.178 (0.35)+1.546 (0.233) ) = 2.062 ton - m
Considerando 5 cm de recubrimiento
Q =
d = 35 cm
Mu
2.062 x105
=
= 0.014
Fr f c" bd 2
0.9(136)(100)(35)2
Q = q(1 − 0.5q )
q = 1 − 1 − 2Q = 0.014
58
Capítulo 3
p=q
Zapatas corridas
f c"
136
= 0.014
= 0.0005 < pmin
fy
4200
Área de acero.
As = pbd = 0.0024 (100) (35) = 8.40 cm2
Usando varillas de 4/8”
s =
100a s
127
=
= 15.12 cm
As
8. 4
φ 4 @ 15
Acero por temperatura.
As = 0.002 (100)(35) = 7 cm2
s =
127
= 18.14 cm
7
φ 4 @ 18
Revisión por cortante.
como
p < 0.015
Vcr = Fr (0.2 + 20 p)
f c* bd
Vcr = 0.8 (0.2 + 20 (0.0024)) 160 (100) (35) = 8783.5 kg
0.35
Vu = 1.4 (4.54 +5 717)
(1.00) = 2.513 ton
2
Vcr > Vu
por lo cual el peralte propuesto se acepta.
En la figura 3.8 se representa el armado de la zapata.
Capítulo 3
Figura 3.8
Armado de la zapata
Zapatas corridas
59
60
Capítulo 3
3.2
Zapatas corridas
Zapatas corridas sin contratrabes para soportar dos o más
columnas.
Estos tipos de zapatas pueden o no tener contratrabes, como se ilustran en las figuras 3.1b y 3.3.
Cuando las fuerzas cortantes no son grandes y la losa es aproximadamente rígida, se puede proponer
una losa sin contratrabes. Para el análisis y diseño de este tipo de zapatas se recomienda la siguiente
secuela:
1. Establecer limitaciones de acuerdo al reglamento que se utilice.
2. Determinar el paso de la resultante.
3. Dimensionar preliminarmente.
4. Calcular y revisar las presiones de contacto.
5. Analizar como viga.
6. Diseñar por flexión y revisar por cortante.
7.- Armado.
Si no se tiene el dimensionamiento preliminar, se sugiere tomar de un 10% a 20% del peso de las
descargas para considerar el peso propio de la zapata.
Ejemplo 3.2. Diseñar la zapata combinada para las condiciones y datos mostrados en la siguiente
figura:
P=70 Ton
P=70 Ton
30
30
Df
h
A
60
490
60
L
Figura 3.9
Datos:
f c' = 200 kg / cm 2
f y = 4200 kg / cm 2
q a = 11000kg / m 2
℘ = 1300kg / 7 m 3
Df = 1.30m
Solución.
Zapata corrida con descarga de dos columnas
Capítulo 3
Zapatas corridas
Limitaciones.
Pmin =
0.7 f c'
fy
=
f c* = 0.8 f c' = 0.8
0.7 200
= 0.00235
4200
(200) = 160kg / cm 2
f c" = β f *C = 0.85 (160) = 136kg / cm 2
Pb =
4800 136
= 0.0152
10200 4200
∴Pmáx = 0.0152
Determinación del paso de la resultante.
Debido a la simetría la resultante pasa por el centroide del área de la zapata, x = 245 cm.
Dimensionamiento preliminar de la zapata.
Se propone:
B = 275 cm
h = 50 cm
Revisión de las presiones de contacto.
q =
PT
A
PT = ∑ Pc arg as + Ppropio + Pterreno
∑ Pc arg as = 2 (70) = 140ton
Ppropio = 6.1 (2.75) (0.5) (2,4) = 20.13 ton.
Pterreno = 6.1 (2.75) (0.8) (1.3) = 17.45 ton
61
62
Capítulo 3
Zapatas corridas
PT = 140 + 20.13 + 17.45 = 177.57 ton.
A = BL = 2.75 (6.1) = 16.77 m2
q =
177.57
= 10.59 ton / m 2 < q a = 11.00 ton / m 2
16.77
Presión de diseño.
La presión que genera momentos flexionantes y fuerzas cortantes que se consideró es la que
corresponde únicamente a las descargas, esto es sin incluir peso propio de la zapata y del relleno.
q =
140
∑P
=
= 8.35 ton/m2
A
16.77
qu = Fc q B = 1.4(8.35)(2.75) = 32.14 ton/m.l.
Esta es la carga linealmente distribuida sobre la viga simplemente apoyada, vea la figura 3.10
P
P
Figura 3.10
Actuación de la presión última
Capítulo 3
Zapatas corridas
63
Resultados del análisis de la viga Isostática.
Figura 3.11
Viga isostática
Determinación del peralte por flexión.
a)
En el sentido longitudinal de la viga, el peralte se obtendrá de acuerdo al diagrama de
momentos flexionante anterior.
d =
Mu
Kub
K u = Fr f c"q (1 − 0.5q )
Ru = Fr fy (1-0.5q)
Se propone
q=p
fy
fc"
p = 0.01
= 0.01
4200
= 0.309
136
64
Capítulo 3
Zapatas corridas
Ku = 0.9(136)(0.309)(1.0-0.5) (0.309) = 31.97
Ru 0.9(4200)(1.0-0.5) (0.309) = 3195.99
Substituyendo valores se obtiene:
d =
Mu
(90.61)105
=
= 32 cm
Kub
31.97( 275)
b)
En sentido transversal de la viga se idealiza de la siguiente forma.
Figura 3.12
Viga en voladizo
Se considera un ancho unitario para la viga.
b = 100 cm
L' =
275
− 15 = 122.5 cm
2
qu = 1.4 bq = 1.4(1.00)(8.35) = 11.69 ton/m.l.
q L
Mu = u
2
d =
2
=
11.69(1.225) 2
= 8.77 ton − m
2
(8.77) 105
= 16.5 cm
31.97(100)
por flexión rige d = 32 cm.
Determinación del peralte por cortante.
a).- Como losa.
El cortante crítico se presenta a medio peralte a partir del paño de la columna o dado.
Capítulo 3
d/2
Pu
Vcr
Figura 3.13
Vcr = Fr
Pu
p'
p'
Ilustración de la fuerza cortante crítica
f c* bo d
Donde:
Perímetro de la zona crítica.
bo = (t+d) 4
P’ = Av qu
Av = (t+d)2
qu = 1.4 (8.35) = 11.69 ton/m2
por equilibrio
Vcr + P’ – Pu = 0
Sustituyendo los valores numéricos en la ecuación anterior, se tiene:
Fr f c* bo d + A v qu – Pu = 0
0.8
Vcr
160 d(30 + d)4 + 1.169(30 +d)2 - 98000 = 0
Zapatas corridas
65
66
Capítulo 3
Zapatas corridas
Reduciendo
d2 + 0.308 d - 2328 = 0
De la solución de la ecuación cuadrática se obtiene el peralte efectivo, se considera el recubrimiento y
finalmente el peralte total.
d = 35 cm
b)
r = 5 cm
h = 40 cm.
f c*
si p < 0.01
Como viga:
Vcr = Fr (0.2+30p) bd
Vcr = 0.5 Fr bd
si p ≥ 0.01
f c*
Como no se conoce p se propone un valor y posteriormente se revisa o bien se propone como peralte
el mayor de los ya determinados, así d = 35 cm. Ahora sedeterminan las áreas de acero, y los
porcentajes de acero para cada sección de momento máximo y haciendo Vu = Vcr, en las expresiones
anteriores se determina el peralte buscado.
Para este caso se propone p = 0.01
Vcr = 0.5 Fr bd f c*
d =
Vu
0.5Fr b f c*
=
haciendo Vu = Vcr
73.9 x103
= 53cm
0.5(.8)( 275) 160
por lo que finalmente
d = 53 cm
h = 60 cm.
Diseño por flexión; sentido longitudinal
para Mu = 3.25 ton - m.
3.25x105
Q=
= 0.0034
0.9 (136)( 275)(53) 2
q = 1 - 1 − 2 ( 0.0034 ) = 0.0034
p = 0.0034
136
= 0.0001 < 0.01
4200
Zapatas corridas
Capítulo 3
As = 0.01 (275)(53) = 145 cm2
Usando varillas del No. 8; as = 5.07 cm
2
275 a s
275(5.07 )
=
= 9.6 ≈ 10cm
As
145
s=
φ 8 @ 10
Para Mu 90.61 ton - m
90.61x105
= 0.0958
0.9 (136)( 275)(53) 2
Q=
q = 1 - 1 − 2 ( 0.0958) = 0101
.
p = 0.101
136
= 0.0033 > pmin
4200
As = 0.0033(275)(53) = 47.63 cm2
275(5.07 )
= 29 cm
47.63
s=
∴ φ 8 @ 30
Armado en el sentido transversal.
Mu = 8.77 ton - m
Q=
877 x105
= 0.0255
0.9 (136)(100)(53) 2
q = 1 - 1 − 2 ( 0.0255) = 0.258
p = 0.0258
136
= 0.0008 < p min
4200
As = 0.00235(100)(53) = 12.455
usando φ 6 as = 2.85 cm.
s=
100a s
285
=
= 22.8 ≈ 23cm
As
12.455
φ 6 @ 20
En la figura 3.14 se ilustra el armado propuesto.
%o 8 @10
%o 8 @30
%o 6 @20
%o 8 @30
>t + 1.5 d
60 cm
%o 8 @10
67
68
Capítulo 3
Zapatas corridas
Figura 3.14 Armado de la zapata
3.3
Zapatas Corridas Con Contratabe.
Las contratrabes se recomiendan cuando el peralte por flexión o por cortante resulta relativamente
grande o bien como ya se mencionó, para darle mayor rigidez a la cimentación y con esto disminuir
los asentamientos diferenciales.
Procedimiento.
1. Establecer limitaciones de acuerdo al reglamento que se use.
2. Determinar la posición de la resultante del sistema de cargas.
3. Dimensionamiento preliminar.
4. Calcular y revisar las presiones de contacto.
5. Diseñar por flexión y revisar por cortante de la losa como viga ancha.
6. Analizar la contratrabe.
En este caso se sugieren dos etapas.
a).- Analizar la viga cargada con las presiones de contacto y apoyada en columnas. Cuando dicha
viga sea continua se sugiere el método de distribución de momentos para su análisis ó usar un
programa de computadora de análisis estructural de vigas.
b).- Analizar la viga sujeta a cargas Pv (cortantes desequilibrados), éstas cargas se obtienen de la
diferencia de las reacciones obtenidas en el caso (a) que llamamos Q y las descargas a la
cimentación P llevadas por las columnas (datos), para el análisis de estas vigas llamadas flotantes se
sugiere el método de N.M. Newmark.
Finalmente se superponen los diagramas de momentos y cortantes de los casos (a) y (b), obteniendo
así, los diagramas para diseño.
7.- Diseñar la Contratrabe.
8.- Armado.
Ejemplo 3.3 Un puente para un periférico va a llevar dos columnas que descargan 180 y 225 tons.
respectivamente, es necesario separarlas 6.10 m. De los estudios de mecánica de suelos se
2
determinó un esfuerzo permisible de 15 ton/m . En la siguiente figura se muestran los datos y
condiciones que deberán considerarse.
Datos:
P1 = 180 ton
P2 = 225 ton
qa = 15 ton/m2
peso específico del terrero.
γ= 1.6 ton/m3
f ’c = 200 Kg/cm2
Capítulo 3
Zapatas corridas
69
fy = 4200 Kg/cm2
Limitaciones
0.7 f c'
0.7 200
P'
=
=
= 0.00235
min
fy
4200
fc* = 0.8 fc' = 0.8 (200) = 160 kg / cm2
f c'' = 0.85 f c* = 0.85 (160) = 136 kg / cm 2
pb =
4800 13600
•
= 0.0152
10200 4200
p max = 0.0152
K u = Fr f c" q (1 − 0.5 q )
Se propone
p = 0.01 Ku = 31.97
Determinación del paso de la resultante.
Tomando momentos respecto a a
∑ M a = P2 (6.10 ) − PT x = 0
610
. P2 610
. ( 225)
=
= 3.39 m
PT
405
L
610
.
e = x − = 3.39 −
= 0.34 m
2
2
x=
Dimensionamiento preliminar.
La longitud total de la zapata L T se determina considerando que la distribución de presiones es
uniforme, para esto el paso de la resultante debe coincidir con el centro de gravedad del área de la
zapata. Aumentando 2e hacia la derecha se elimina la excentricidad, L T queda como se ilustra en la
figura 3.15.
P1
P2
PT
1.00
(a)
70
Capítulo 3
Zapatas corridas
Figura 3.15 Zapata corrida propuesta.
Se propone B = 3.25 m.
Revisión de las presiones de contacto.
Peso terrreno = 10.78 (3.25 - b) (1.0) (1.6)
Ancho propuesto para la contratrabe, b = 50 cm.
Peso terreno = 10.78 (2.75) (1.0) (1.6) = 47.43 ton
Peso propio de cimentación = 40.5 ton (10% de las descargas)
∑P = P + P
1
2
= 225 + 180 = 405ton
PT = 405 + 47.43 + 40.5 = 492.93ton
Presión de contacto
q=
PT
492.93
=
= 14.07 ton / m2 p qa
A 3.25(10.78)
Presión de diseño
qu =
1. 4 ∑ P
1.4( 405)
=
= 16.18ton / m 2
A
3.25(10.78)
Diseño por flexión de la losa.
Considerando un ancho unitario, de la losa de la zapata se obtiene una viga en cantiliver.
2
WL
2
qu = 16.18 ton/ml
1.375
Capítulo 3
Zapatas corridas
71
Figura 3.16 Viga idealizada.
Mu =
16.18(1.375)2
= 15.29 ton − m
2
d =
Mu
=
Kub
15.29 x105
= 21.8cm < 30 cm (peralte efectivo supuesto).
31.97(100)
Se puede considerar d = 22 cm, sin embargo es recomendable por hipótesis que la cimentación sea
rígida, por lo que se tomará d = 30 cm.
Cálculo del área de acero.
Q =
Mu
15.29 x 105
=
= 0.1388
Fr fc' ' bd 2 0.9 (136)(100)(30)2
q = 1−
1 − 2(0.1388 = 0.15
p = 0.15 136 = 0.00486 ⟩ p min.
4200
As = 0.00486 (100) (30) = 14.58 cm2
Seleccionando φ 6 que tiene as = 2.85 cm
s=
2
100 a s
100( 2.85)
=
= 19.5cm. φ 6 @ 20 cm.
As
14.58
El armado longitudinal de la losa se considera por temperatura.
As =.002 (100)(30) = 6 cm2.
Usando φ4”
s =
as = 1.27 cm
2
100 (1.27 )
= 21 cm
6
φ4 @ 20 cm.
Revisión por cortante.
En la figura 3.17 se muestran las dimensiones que se consideran en esta revisión.
72
Capítulo 3
Zapatas corridas
Figura 3.17 Dimensionamiento de la zapata.
Vu = Aqu = 1.00 (1.0750) (16.18) = 17.39
Como p
< 0.01
Vcr = 0.8 (0.2+30(0.00486)) (100) (30) 160 = 10498 Kg.
Vu > vcr
Por lo que se incrementa en peralte de la losa a 40 cm. y el porcentaje de refuerzo a p = 0.0065
Vu = 1.00 (0.975) (16.18) = 15.77 ton.
Vcr = 0.8 (0.2+30(0.0065)) (100) (40) 160 = 15998 Kg> Vu
Corrigiendo el armando de la losa.
As = 0.0065 (100) (40) = 26 cm2
Seleccionando varillas 6/8”
s =
as = 2.85 cm2
100 ( 2.85)
= 10.9 cm
26
Refuerzo longitudinal.
As = 0.002 (100) (40) = 8 cm2
φ6
10 cm.
Capítulo 3
Usando varillas de 4/8” as = 1.27 cm
s =
100 (1.27 )
= 15.8 cm
8
Zapatas corridas
2
φ4 @ 15 cm.
Análisis de la Viga
Pu1
Pu2
147.53
78.89
174.04
105.19
Vu
146.81
114.66
140.96
120.50
188.88
105.19
108.43
124.28
59.16
38.36
Mu
99.67
Figura 3.18
Como: Pu1 = R1 y
Pu2 = R2,
Determinación del peralte.
d =
Mu
Kub
k u = Fr f c"q(1 − 0.5q )
Viga simplemente apoyada
no hay cortantes desequilibrados.
73
74
Zapatas corridas
Capítulo 3
se propone
q = 0.01
p = 0.01
y
b = 35 cm
4200
= 0.309
136
Ku = 0.9 (136) (0.309) (1-0.5 x 0.309) = 31.97
d=
124.28 x10 5
= 105 cm
31.97(35)
Revisión de la sección por cortante.
2.5 Frb d fc* = 2.5 (0.8) (35) (105) 160 = 92971 kg
Vu = 147530 kg > 92971 kg.
la sección no se acepta por cortante
Determinación del peralte por cortante
Vu = 2.5 Frb d fc*
Se propone b = 50 cm
d =
Vu
2.5Fr b f c*
=
147.530
= 116.6
2.5(0.8)(50) 160
La sección queda b = 50
d = 120
Cálculo de áreas de acero
Para Mu = 59.16 ton – m
Q =
(59.16)105
= 0.0671
0.9(136)(50)(120)2
q = 1 − 1 − 2Q = 0.0695
h = 125 cm
Capítulo 3
p = 0.0695
Zapatas corridas
75
136
= 0.0023 < Pmin
4200
As = 0.00235 (50) (120) = 14.10 cm2 ;
3φ8
Para Mu = 99.67 ton – m
(99.67 )105
Q =
= 0.113
0.9 (136)(50)(120)2
q = 1 − 1 − 2(0.113) = 0.120
p = 0.12
136
= 0.0039 > p min
4200
A s = 0.0039 (50) (120) = 26.95 cm2
5φ8
Para Mu = 124.28 ton – m
Q=
(124.28) 105
= 0.141
0.9(136)(50)(120)2
En forma análoga se obtienen:
q = 0.1527
p = 0.0049 > pmin
As = 26.95 cm 2
6φ8
Determinación del refuerzo por cortante
Como en las tres ecuaciones de momento máximo, el porcentaje de refuerzo es menor que 0.01, el
cortante que resiste el concreto se determina con la expresión.
76
Zapatas corridas
Capítulo 3
Vcr = Fr (0.2 + 30p) bd fc*
tramo AB
Vu = 78.89 ton
p = 0.00235
Vc r = 0.8 (0.2 + 0.00235 (30)) (50) (120) 160 = 16424 kg.
Vcr < Vu
Separación de estribos
s =
Fr A v dfy
Vu − Vcr
usando estribos del No. 4
as = 1.27 cm2
Av = 2 as = 2 (1.27) = 2.54 cm2
s =
0.8 (2.54) (120) 4200
= 16.39
78890 − 16424
E φ4 @ 15 cm
pero no deberá exceder
s =
Fr A v dfy
3. 5 b
=
0.8( 2.54)( 4200)
= 68 cm
3.5(50)
1.5 Frbd fc* = 1.5(0.8)(50)(120) 160 = 91073kg
1.5 Frbd fc* > Vu
s ≤ d/2
A continuación se realiza para cada tramo el mismo procedimiento, solamente se anotarán los
resultados:
Tramo BC
Capítulo 3
Vu = 120.50 ton
Zapatas corridas
p = 0.0039
Vcr = 19247 Kg
s = 10.11 cm
E φ 4 @ 10 cm
Tramo CD
Vu = 147.53 ton
p = 0.0049
Vcr = 21068 Kg
s = 8 cm
E φ 4 @ 8 cm
Tramo DE
VU = 114.66 ton
p = 0.0049
Vcr = 21068 Kg
s = 10.9
E φ 4 @ 10 cm
Corte de varillas
Se recomienda correr un 50% de refuerzo, tanto para momento positivo como negativo.
Momento que resiste una varilla para cada sección.
Mr =
as
Mu
As
Para el momento negativo, eje B.
Mr =
5.07
(78.89) = 21.92 ton − m
18.24
Para el momento positivo
Mr =
5.07
(99.67 ) = 21.59 ton − m
23.4
77
78
Capítulo 3
Zapatas corridas
Longitud de anclaje.
La = Ld + d
Ld = 32
La = 32 + 120 = 152 cm
L.I
Ld = 45
La = 45 + 120 = 165 cm
L. S
3 %o 8
4 %o 8
5 %o 8
%o 6 @10
E %o4 @15
E %o4 @8
Figura 3.19
6 %o 8
E %o4 @10
Armado de la zapata
El armado longitudinal de la losa lleva estribos del No. 4 a cada 15 cm
Capítulo
4
RETICULAS DE CIMENTACION
Estos tipos de cimentaciones se usan en suelos compresibles, cuando el peso de la superestructura
no es conveniente soportarlo con zapatas aisladas o corridas. La primera alternativa puede ser una
placa continua o losa corrida que cubra toda la base de la construcción, como si fuera una losa de
piso, ver figura 1.5. Esta placa de cimentación puede presentar la necesidad de reforzar las franjas de
ejes de columnas, como si éstas fueran vigas conservando el peralte de la losa o pueden tener un
peralte mayor generando vigas peraltadas llamadas contratrabes, ver figura 1.6, algunos le llaman a
este tipo de cimentación placas de cimentación nervadas o reticuladas.
Los métodos de cálculo de las cimentaciones sobre terreno compresible generalmente son
discrepantes y poco racionales. Los ingenieros tienden a simplificar el problema debido a las
dificultades de análisis que se tiene entre el sistema integrado por las estructuras de sustentación y la
del suelo, así como por las incertidumbres que se presentan en la predicción del comportamiento del
suelo.
Los procedimientos prácticos para este tipo de cimentación consideran que trabajan bajo dos
condiciones, una que se presenta a corto plazo o instantáneamente y la otra a largo plazo o diferida.
Para el calculo estructural se toman las losas nervuradas como un sistema integrado por vigas o
contratrabes y un conjunto de tableros de losas. Considerando a las vigas como los elementos
primarios, se pueden definir las condiciones en la siguiente forma:
a)
A corto plazo, las vigas se suponen que se comportan como vigas continuas con apoyos fijos
en las columnas sujetas a cargas distribuidas uniformemente debido a las presiones del suelo.
b)
A largo plazo, las vigas se consideran como un sistema flotante sujeto a las descargas de la
superestructura y la reacción uniforme del terreno. La estructura experimenta asentamientos
que por lo general son máximas en el centro de cargas y mínimas en los extremos, esto indica
que el suelo reacciona en la forma no uniforme.
La primera condición conduce a elementos mecánicos relativamente pequeños en la contratrabe
porque se desprecian los efectos de asentamientos diferenciales, en la segunda condición los
elementos mecánicos son mayores pero muy conservadores, debido a que se ignora la redistribución
de presiones de contacto.
80
Capítulo 4
Retículas de cimentación
Para diseñar se puede considerar la condición más desfavorable o combinando ambas condiciones.
Los métodos tradicionales no abordan explícitamente el estudio de la interacción entre la
subestructura y el suelo, se recomienda estudiar el capítulo 5.
A continuación se presentan procedimientos aproximados que sirven para hacer estimaciones
prácticas en el diseño y no requieren el uso de computadoras. En el capítulo 5 se presenta una
introducción a los métodos que pretenden ser exactos en el análisis de la distribución de esfuerzos y
deformaciones en las cimentaciones, y se requiere el uso de computadoras.
4.1.- Losas de Cimentación.
Una placa continua de cimentación es una subestructura que transmite las cargas al suelo y que
generalmente abarca toda el área de la base de la subestructura, como si fuera una losa de piso. Una
losa de cimentación fácilmente se construye si tiene un espesor uniforme.
Se presenta un método aproximado para el análisis y diseño de placas de cimentación, suponiendo
que la placa debe ser rígida, gruesa y resistente, las columnas deberán estar apoyadas en dados o
pedestales, éstos tienen el mismo objetivo que los capiteles en una losa plana de piso, es decir,
ampliar la zona critica para absorber esfuerzos cortantes y momentos flexionantes, evitando
concentraciones de esfuerzos locales peligrosos. Se parte de considerar que la placa es rígida y la
carga constante, que el suelo plástico se comprimirá de tal manera que la carga de cada columna se
distribuirá casi uniformemente bajo la placa en las inmediaciones de dicha columna particular.
Figura 4.1 Placa de cimentación para un edificio
Capítulo 4
Retículas de cimentación
81
1.
Se colocarán dados o pedestales en cada columna con el objeto de ampliar las secciones
críticas hasta un perímetro suficiente con el fin de evitar concentraciones locales de
esfuerzos cortantes y flexionantes críticos que puedan provocar fallas en la losa; se puede
usar otras alternativas como, un armado embebido en el espesor de la losa pero
rehundido, como si fueran zapatas aisladas. Las dimensiones de la base del dado, hp
ancho del pedestal, se recomienda que este comprendido entre un quinto y un cuarto del
claro entre columnas. Con el objeto de comprender estos conceptos se recomienda
observar la figura 4.1.
2.
La obtención de las cargas o presiones de contacto sobre la losa de cimentación se
pueden obtener considerando que debido a que la placa es rígida y las cargas constantes,
el suelo plástico se comprimirá y se reajustará, de tal manera que la carga de cada
columna se repetirá casi uniformemente bajo la losa.
En la zona próxima a la columna la presión del suelo se obtiene con la expresión 4.1
q=
1 / 4(Pa + Pb + Pc + Pd ) Peso propio de la losa
+
Area a b c d
Area a b c d
abc d
(4.1)
Se puede despreciar el peso propio de la losa de acuerdo a criterio del calculista.
En los casos donde las cargas de columnas contiguas, difieran mucho, no es
recomendable usar este tipo de cimentación debido a la posibilidad de un hundimiento
local por que la placa no puede repartir cargas desiguales a distancias alejadas en suelos
compresibles.
Se recomienda que la relación entre los claros de columnas largo a corto en direcciones
ortogonales no sea mayor de 1.2. Los claros entre ejes de columnas no deben ser
mayores de 6 o hasta 7 metros, ya que de mayores dimensiones se requerirá una losa
muy gruesa.
3.
Para el análisis se considera a la losa dividida en franjas de columnas que tenga un ancho
de hp + 3d, o un valor mayor, sin rebasar la mitad de la longitud de claros de lados
contiguos, el valor d es el peralte efectivo de la losa. Como se puede observar en la figura
4.1, se obtiene una retícula de vigas o franjas de columnas, si esta retícula de vigas es el
adecuado se puede imaginar que las losas de las franjas centrales están apoyadas en las
vigas, en la figura 4.1 se ilustran las franjas de ejes y con sombra las pequeñas losas
centrales.
4.
Para canalizar las cargas o presiones del suelo, se trazan líneas a 45° a partir del centro
de columnas, resultando áreas de forma triangular o trapezoidal, vea figura 4.2. Las
presiones bajo la superficie abdc se pueden considerar que se distribuyen de la siguiente
forma, la franja de columnas soportará la carga correspondiente al área que le
corresponde a dicha franja y los pequeños triángulos sobrantes se canalizan a la losa
central ghij. En forma similar se procede a distribuir cargas correspondientes al área
aeck, y de la misma manera se realiza la distribución para toda la superficie.
5.
Ahora se procede al análisis estructural. El cálculo para las franjas de columnas o vigas
planas se puede realizar como vigas continuas, usando el método de distribución de
momentos o mas conservadoramente como vigas doblemente empotradas. En la figura
4.2 se ilustra el diagrama de momentos flexionantes, en donde debido al efecto de los
82
Capítulo 4
Retículas de cimentación
pedestales, el momento máximo en los apoyos tiende a reducirse, dicha reducción se
ilustra con líneas discontinuas en el diagrama mencionado.
Figura 4.2 Losa de cimentación y momentos flexionantes
La losa central se puede analizar como una tablero empotrado en sus cuatro bordes, por
ejemplo el tablero ghij, dichos empotres se consideran en los bordes de las vigas planas.
Otra alternativa es considerar el empotramiento a una distancia, del borde, de un 20% del
ancho de las franjas, pero sin exceder el peralte efectivo de la losa. Para analizar la losa
se puede usar cualquiera de los métodos de diseño de losas propuestos por los
reglamentos.
Capítulo 4
Retículas de cimentación
83
Una recomendación conservadora para el diseño es la siguiente, para determinar el
armado inferior se considera a la losa como si estuviera empotrada en los bordes de las
franjas y para el armado superior se considera como simplemente apoyada a lo largo de
dichos bordes.
6
Conocidos los elementos mecánicas se procede a diseñar, o sea a determinar las
cantidades de refuerzo en las vigas anchas y en las losas centrales.
Ejemplo.- Diseñar en forma practica una losa plana de cimentación con los datos que se indican a
continuación.
Datos:
La losa continua de cimentación se encuentra en suelo arcilloso plástico.
2
La resistencia del terreno es de 7 Ton/m
Materiales
2
f’c = 250 kg/cm
2
fy = 4200 kg/cm
Las cargas se ilustran en la figura 4.3
Columnas de 60x60 cm.
La estructura pertenece al grupo B
Figura 4.3 Descargas sobre la losa continua de cimentación.
84
Capítulo 4
Retículas de cimentación
Solución:
Revisión de las presiones del suelo.
Descarga total de la losa de cimentación, sumando por renglones.
∑ P = 280 + 535 + 535 + 280 = 1630
Tons.
Se supone un peralte de losa de 30 cm.
El peso de los pedestales están incluidos en las cargas
Pi
Área total de la losa
AT = (20.10)(18.60) = 373.86
Peso de la losa =
(373.86)(0.30)(2.40) = 269.18 Ton
El peso total será:
PT = 1630 + 269.18 = 1899.18 Ton
Obtención del peso de la resultante, para esto, se calcularan las excentricidades, usando el teorema
de Varignon:
X =
19.5(286) + 13.0(528) + 6.5(544)
= 9 .8 m
1630
Y=
18(280) + 12(535) + 6(535)
= 9 .0 m
1630
e X = 9.8 − 9.75 = 0.05
eY = 9.0 − 9.0 = 0
En el sentido y el diagrama de presiones es rectangular.
En el sentido x es un trapecio:
q =
1899 . 18 (1899 . 18 )( 0 . 05 )(10 . 05 )
±
= 5 . 08 ± 1 . 52
373 . 86
(( 18 . 6 )( 20 . 10 ) 2 ) / 12
q min = 3.56
No hay tensiones
q max = 6.60
< qa
Cálculo de la carga de diseño.
Capítulo 4
Retículas de cimentación
85
Para obtener la carga de diseño en forma aproximada se tomara el criterio usado anteriormente;
puede usar otro.
qu =
FC + PT
L' B
L' = L − 2e = 20.10 − 2(0.05) = 20m
qu =
(1.4)(1899.18)
= 7.15 Ton / m 2
(20)(18.6)
Revisión por penetración
Se proponen las dimensiones de la base del pedestal usando las recomendaciones anteriores.
h px =
lx
6 .5
=
= 1 .30 m
5
5
h py =
ly
5
=
6
= 1 . 20 m
5
4.2.- Retículas de Cimentación.
Las retículas de cimentación se pueden formar con zapatas corridas en ambas direcciones, figura
4.3.a. También las vigas se pueden colocar por debajo de la placa de cimentación, lo que implica que
para su construcción se tenga que realizar una retícula de cepas o zanjas primeramente y luego
colocar la losa continua de cimentación. Si se invierte la disposición de las contratrabes de tal forma
que la placa de cimentación quede en el fondo se obtiene un tipo de cimentación de uso más común
como la que se ilustra en la figura 4.3b, en este caso estos cajones no servirán de sótano y se tendrá
que poner otra losa para tapar los cajones, la infraestructura la constituye pues una losa nervada. El
método práctico que se expone en este capítulo considera a las contratrabes y los tableros de la losa
continua.
Las retículas de cimentación pueden estar sujetas a cargas verticales y/o fuerzas laterales. En este
tipo de estructuras los elementos mecánicos primarios son momentos flexionantes, fuerzas cortantes y
momentos torsionantes. Los métodos prácticos o aproximados consideran solamente momentos
flexionantes y fuerzas cortantes.
En el cálculo se consideran los siguientes puntos:
a)
b)
c)
d)
La cimentación deberá ser rígida.
La placa será una losa de gran espesor armada en una o dos direcciones.
Las losas, contratrabes y muros se deberán considerar como elementos continuos.
Se sugiere dejar juntas de construcción en la placa, así como entre la liga losa-viga. Se
recomienda que éstas juntas se coloquen en las secciones donde los esfuerzos cortantes son
pequeños.
86
Capítulo 4
Retículas de cimentación
Figura 4.3 Retículas de Cimentación.
e)
f)
g)
Las contratrabes pueden analizarse como vigas doblemente empotradas o continuas, según
sean las dimensiones de los elementos interconectados.
Al dimensionar la losa de cimentación, puede suponerse, que actúa sobre ella carga
uniformemente repartida, con las fronteras empotradas o continuas, con la advertencia del
inciso (e).
Si los muros o contratrabes llevan huecos relativamente pequeños en los centros de los
claros, dichas aberturas pueden no considerarse. En cambio si son amplios, es preferible
considerar el muro como si estuviera articulado. La parte superior e inferior de esos huecos
deberán armarse para evitar grietas.
4.3.- Procedimiento de cálculo.
A continuación se presenta el procedimiento de cálculo para el análisis aproximado y diseño de
retículas.
Hipótesis fundamentales:
Se supone el suelo como un medio elástico.
Se considera a la cimentación como un cuerpo rígido.
Se desprecian los efectos de torsión.
Descripción breve del procedimiento.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
Selección del tipo de cimentación, con los datos del terreno y la superestructura.
Determinación del centro de cargas y del centro de gravedad de áreas.
Cálculo de los esfuerzos debidos a cargas verticales.
Cálculo de los esfuerzos debidos a cargas laterales.
Resumen de todos los esfuerzos.
Revisión de las presiones de contacto.
Análisis de la retícula de contratrabes.
7.1)
Cálculo de elementos mecánicos por carga vertical.
7.2)
Cálculo de elementos mecánicos por sismo en ambas direcciones.
Combinación de efectos en las direcciones “x” y “y”.
Diseño de contratrabes.
Análisis de la losa de cimentación.
Capítulo 4
11)
Retículas de cimentación
87
Diseño de la losa de cimentación.
Ejemplo 4.1.- En la figura 4.4. se anotan las dimensiones de la base del edificio, así como las
descargas que llegan a la cimentación, las longitudes están dadas en metros y las cargas en
toneladas, considerando que la presión admisible del terreno es de 6.00 ton/m2.
Suponiendo que el peso de la cimentación tenga un valor de 8 a 10% de la descarga total, se tendrá
en forma aproximada el peso de la cimentación. En la figura 4.4. se anotan estas cargas
incrementadas por el peso de la cimentación, así por ejemplo:
Para el nodo 4-A.
Pt = 30.00 + 10%(30.00) = 33.00 ton.
O bien se puede considerar el 10% del peso total, esto es 98.8 toneladas y distribuirlas uniformemente
2
(0.343 ton/m ) en la base y luego concentrarlas bajo cada columna.
Determinación del centro de carga y del centro de gravedad.
Figura 4.4.- Descargas en la retícula.
El área de la base del edificio es:
A = 16.00 x 18.00 = 228 m2.
El centro de cargas se obtiene de la siguiente manera. Vea la figura 4.4 y tome de ahí los valores.
xc =
ΣPx
Pt
yc
ΣPy
Pt
88
Capítulo 4
Retículas de cimentación
Σ Px = 218.90(16) + 298.10(11) + 339.90(6) = 8820.9
Σ Py = 165.00(18) +341.00(13) + 380.66(6) = 9686.60
Pt = 1986.80 tons.
Sustituyendo valores, se obtiene:
Xc = 8.07 m; yc = 8.91 m.
El centro de gravedad de las áreas es:
Xg =8.00 m;
yg = 9.00 m.
Los momentos de inercia de la base con respecto a los ejes centroides son:
3
16(18)3
Ι xx = bh =
= 7776 m4
12
12
Ι yy
18(16) 3
=
= 6144 m 4
12
Cálculo de las presiones del terreno debido a cargas verticales.
a)
f1 =
b)
f2 =
Por carga axial, se tienen esfuerzos de compresión:
Pt 1086.80
=
= 3.77 ton / m 2
A
288
Por momento flexionante, se tienen esfuerzos de flexión:
Mx y
;
Ι xx
f3 =
My x
Ι yy
Las excentricidades en la base son:
Ex = 8.07 – 8.00 = 0.07 m.
Ey = 9.00 – 8.91 = 0.09 m.
Los momentos flexionantes provocados por la carga total y las excentricidades anteriores tienen los
siguientes valores.
Mx = Pt ey = 1086.80 (0.09) = 9781 ton-m.
My = Pt ex = 1086.80 (0.07) = 76.07 ton-m.
Sustituyendo valores, se obtiene:
Capítulo 4
F2 = 0.113 ton/m2 ;
Retículas de cimentación
89
f3 = 0.099 ton/m2.
Se representarán en la figura 4.5 los esfuerzos obtenidos anteriormente con el afán de ser objetivo,
marcando el centro de cargas y el centro de gravedad, así como los esfuerzos de flexocompresión.
Cálculo de esfuerzos en el terreno debido a cargas laterales.
Las cargas accidentales, fundamentalmente viento o sismo, generan efectos laterales sobre las
estructuras. Existen varias formas de análisis para obtener estas fuerzas. Así por ejemplo, para el
análisis sísmico tenemos los métodos estático y dinámico, que establece el Reglamento de
Construcciones del D. F.
Las fuerzas sísmicas que actúan en cada piso del edificio se ilustran en la figura 4.6, así como las
alturas de los diferentes niveles con respecto al nivel cero. Las fuerzas son resultado de un análisis
sísmico estático.
El momento de volteo generado por las fuerzas laterales es:
Mv = F1 h1 + F2 h2 + F3 h3 +F4 h4 + F5 h5 = 1271 ton-m.
90
Capítulo 4
Retículas de cimentación
Figura 4.5 Esfuerzos del terreno debido a cargas de gravedad.
Ahora se revisa la estabilidad del edificio.
Me = Pt (d).
D es la distancia del centro de cargas por donde pasa Pt con respecto a la orilla más próxima.
Capítulo 4
Retículas de cimentación
91
M e = 1086.8(7.93) = 8618.32 ton − m .
La condición para que no exista volteo es:
Figura 4.6 Edificio sujeto a sismo.
Me
≥ 1 .5
Mv
∴
8618.32 = 6.78 ⟩ 1.5
1271
Cálculo de los esfuerzos debido al momento de volteo Mv.
f4 =
Mx y
;
Ι xx
f5 =
Myx
Ι yy
Sustituyendo valores, se tiene:
f4 =
1271(9.00)
= 1.456 ton / m 2
7776
f5 =
1271(8.00)
= 1.640 ton / m 2
6144
En la figura 4.7 se representan gráficamente estos esfuerzos, considerando el efecto del sismo en
ambas direcciones y en ambos sentidos.
92
Capítulo 4
Retículas de cimentación
Sismo derecho-izquierdo
Sismo izquierdo-derecho (eje x-x)
Sismo inferior-superior
Sismo superior-inferior (eje y-y)
Figura 4.7 Esfuerzos del terreno debido a fuerzas sísmicas.
Resumen de los esfuerzos.
En la tabla 4.1 se muestran todos los esfuerzos anteriores, así como las combinaciones de los sismos.
Capítulo 4
Retículas de cimentación
93
Para la distribución de esfuerzos en todas las contratrabes será lineal, por lo que se puede hacer
mediante proporciones, esto es:
1
2
3
4
x
f2
f2
x1
6
3
4
5
0.113 x
=
9 .0
3
∴ x = 0.038
y x1 = 0.050
18
Revisión de las presiones de contacto.
Esta revisión se debe observar que la presión de contacto por carga estática (fe) y por la combinación
de carga estática más sismo (fE + fS) sea menor o igual que la presión admisible del terreno dada
como dato, ni tener esfuerzos de tensión (esfuerzos negativos). Favor de ver las columnas 5, 8,9, 19 y
11 de la tabla 4.1.
Análisis de la retícula de contratrabes.
a)
Cálculo de los elementos mecánicos en las contratrabes debido a las cargas verticales.
Primeramente se uniformizan las cargas (presiones del terreno) que actuarán sobre la losa de
cimentación. El esfuerzo promedio se obtiene tomando los esfuerzos en las cuatro esquinas de una
losa y dividiendo entre cuatro, esto es:
fLΙ =
f 4 A + f 4B + f 3 A + f 3B
4
Enumerando las losas con números romanos como se muestra en la figura 4.8, obteniendo los
siguientes esfuerzos o cargas uniformemente repartidas para cada una de ellas. Se toman los valores
de la columna 5 de la tabla 4.1.
FLI = 3.627 ton/m2
FLIV = 3.702
FLVII = 3.784
FLII = 3.695
FLV = 3.771
FLVIII = 3.852
FLIII = 3.756
FLVI = 3.831
FLVIX = 3.914
Ahora se canalizan las cargas de las losas a las vigas, haciendo una distribución por medio de líneas
a 45°, como se ilustra en la figura 4.8, esta es un a forma de canalizar cargas, se pueden usar otras.
Las áreas típicas de triángulos y trapecios son:
A1 =
6 +1
2.5 = 8.75m 2
2
A2 = 6.25
A3 = 9.00
A4 = 12.00
A5 = 11.25
94
Capítulo 4
TABLA 4.1
Retículas de cimentación
Capítulo 4
Retículas de cimentación
95
Figura 4.8 Canalización de cargas.
A continuación se deben analizar todas las vigas continuas, que se obtienen de aislar éstas de la
retícula de contratrabes, las cargas uniformemente distribuidas sobre las vigas se obtienen con la
siguiente expresión
W = A fL / L (ton/m)
Como ejemplo se anotan los resultados del análisis de solamente dos vigas, una en el sentido (2),
viga 1 y otra en el sentido y, viga A.
Para analizar las vigas continuas se puede usar el método de distribución de momentos en las figuras
4.9 y 4.10. Se anotan los momentos flexionantes finales, cortantes, reacciones así como se dibujan las
diagramas de momentos. Se recomienda analizar las otras seis vigas continuas.
Cálculo de los momentos flexionantes debido a los cortantes desequilibrados.
Se designarán como cortantes desequilibrados a las fuerzas que se obtienen de sumas
algebraicamente las reacciones en los nodos debidas a las presiones del terreno, determinadas al
analizar las vigas continuas anteriores (Q), más las descargas dadas como dato (Pt), por ejemplo:
Nudo 4 – A.
Pv = Q – Pt = 20.33 - 33.00 = - 12.67 ton.
96
Capítulo 4
Retículas de cimentación
VIGA DEL EJE 2.
D1
Figura 4.9 Elementos mecánicos de la viga continua (contratrabe) 2 y diagrama de
momentos flexionantes y cortantes.
Capítulo 4
Retículas de cimentación
97
VIGA DEL EJE B.
D2
Figura 4.10 Elementos mecánicos de la viga continua (contratrabe) B y diagrama de
momentos flexionantes y cortantes.
98
Capítulo 4
Retículas de cimentación
Los valores de Q están anotados en la figura 4.11.
Figura 4.11 Reacciones en los nodos debidas a la presión del suelo.
Y los valores de Pt están anotados en la figura 4.4. En la figura 4.12 están anotados los valores de los
cortantes desequilibrados.
Figura 4.12 Cortantes desequilibrados.
Se deben comprobar que la suma de los cortantes desequilibrados en la retícula es nula.
Capítulo 4
Retículas de cimentación
99
Ahora se distribuyen los cortantes desequilibrados. Para obtener el cortante que toma cada
contratrabe que llega al nodo se utilizan factores de distribución al corte. Recuerde que las rigideces al
3
corte relativas están dadas por I/L .
Se propone los siguientes momentos de inercia relativos para las contratrabes.
I = 1.5 para las contratrabes centrales.
I = 1.0 para las contratrabes perimetrales.
En la tabla 4.2 se anota en el renglón superior el nombre del nudo de la retícula, en el segundo
renglón las flechas indican la concurrencia de las contratrabes, en el tercer renglón los factores de
distribución, en el cuarto los cortantes desequilibrados y en los siguientes se anotan distribuciones y
transportes, así como los cortantes finales.
Se puede comprobar el equilibrio de cortantes en cada nudo, sumando los cortantes finales, estos
deben ser iguales al cortante desequilibrado pero con signo contrario. Por ejemplo:
En el nudo 4 – A.
Pv = 12.67 ton.
Suma de Vf
= -6.63 – 6.04 = - 12.67 ton.
Se sugiere se vea la tabla 4.2 con el auxilio de la retícula y los correspondientes nombres de los
nodos.
Análisis de las contratrabes o vigas flotantes.
En el análisis de las vigas de la retícula sujetas a los cortantes finales obtenidos de la tabla 4.2, el
objetivo es obtener momentos flexionantes y fuerzas cortantes, así como los diagramas respectivos.
En este análisis se utiliza el método numérico de Newmark. Por ejemplo vea la viga 1, en la figura
4.13.
En el nudo 1 – B se tienen dos cortantes en esa dirección cuyos valores son + 0.11 y + 3.59, la suma
es +3.70, entonces el cortante que actuará en el nudo es 3.70. Para el nudo 1 – C se procede en
forma semejante y en los nudos 1 – A y 1 – D como solo existe un cortante en esa dirección, se
pondrán esos valores.
En la tabla de la figura 4.13 para el procedimiento numérico, se anotan primeramente los claros en
metros, en el segundo renglón los cortantes (P) calculados, en el tercer renglón los cortantes
acumulados (Vi), sumándose de izquierda a derecha según indican las flechas, obteniéndose un
cortante desequilibrado de la viga (encerrado en un rectángulo). En los siguientes renglones se tienen:
100
Capítulo 4
TABLA 4.2
Retículas de cimentación
Capítulo 4
Retículas de cimentación
101
Vc es el cortante correctivo, esto se determina por medio de una corrección lineal, esto es:
− 4.16
6.00 = −1.56
16
− 4.16
=
5.00 = −1.30
16
− 4.16
=
6.00 = −1.30
16
Vc AB =
4.16
6
5
VcBC
VcCD
5
Pf representa los cortantes que mantienen en equilibrio la viga flotante, ahora se calculan nuevamente
los cortantes acumulados como se indica en la tabla.
Vd es el producto del cortante por el claro d.
M es la suma de los momentos flexionantes acumulados, que por condiciones de frontera debe ser
nulo en D, sin embargo existe un momento cuyo valor está encerrado en un rectángulo.
Mc es el momento flexionante correctivo, para que se cumpla la condición de frontera M = D. Los
valores de los momentos correctivos se obtienen de la siguiente manera:
43.30
23.62
6
5
5
62.98
62.98
6.00 = 23.62
16
62.98
McC =
11.00 = 43.30
16
McB =
Mr son los momentos flexionantes reales o finales de la viga, en la parte inferior se dibujan los
diagramas de momentos.
Con este procedimiento se analizan todas las vigas, en las figuras 4.13 y 4.14 solamente se ilustra el
cálculo de dos vigas.
102
Capítulo 4
Retículas de cimentación
VIGA DEL EJE 2.
D3
Figura 4.13 Ilustración del método de Newmark para la viga 2.
VIGA DEL EJE B.
D4
Figura 4.14 Ilustración del método de Newmark para la viga B.
Capítulo 4
Retículas de cimentación
103
Cálculo de los elementos mecánicos debidos a sismo.
Tomando los esfuerzos de la columna 7 de la tabla 4.1 estos esfuerzos son generados por el sismo en
la dirección x-x, nuevamente se ilustran en la figura 4.15a, en la figura 4.15b se presentan los
esfuerzos promedio con el objeto de concretar carga en los nodos de la retícula.
Figura 4.15 Esfuerzos debido a sismo.
En la figura 4.16 se marcan con un rayado las áreas que le corresponden a cada nudo, y estas
reacciones se obtienen en la forma siguiente:
Pv = Q − Pt
pero Pt = 0
Por ejemplo, para el nodo 4-A se tiene:
Pv = 7.50 × 1.3325 = 9.99 ton
En la figura 4.16b se anotan las reacciones sobre los nodos de la retícula.
En forma análoga se considera ahora el sismo en la dirección y-y tomando los esfuerzos de la
columna de la tabla 4.1. las figuras 4.17a y 4.17b ilustran los esfuerzos y los cortantes
desequilibrados.
Teniendo los valores de los cortantes desequilibrados debidos al sismo en la dirección x-x, se hace los
mismo que en el caso de las cargas verticales, caso 7.1, esto es, la distribución de cortantes, ver tabla
4.3 y el análisis de vigas flotantes.
104
Capítulo 4
Retículas de cimentación
Figura 4.16 Áreas y reacciones para los nodos.
Figura 4.17 Esfuerzos y cortantes desequilibrados.
Finalmente se procede en la misma forma para los efectos del sismo en la dirección y-y. Los cálculos
se tienen en la tabla 4.4 y a continuación los análisis de las vigas flotantes, solamente se anotan los
análisis de las vigas flotantes 1 y A, para ambas direcciones, ver figuras 4.18 al 4.21.
Algunos calculistas con el objeto de tener mayor aproximación incluyen las rigideces de las columnas
del primer entrepiso, usando métodos de análisis llamados exactos manuales o de computadora, sin
embargo las hipótesis de partida se siguen conservando. Este procedimiento es recomendable para
dimensionamientos preliminares de las retículas de contratrabes, falta aun el análisis de la losa de
cimentación.
Capítulo 4
TABLA 4.3
Retículas de cimentación
105
106
Capítulo 4
Retículas de cimentación
VIGA DEL EJE 2.
D5
Figura 4.18 Contratrabe con carga debido al sismo x-x.
VIGA DEL EJE B.
D6
Figura 4.19 Contratrabe debido al sismo x-x.
Capítulo 4
TABLA 4.4.
Retículas de cimentación
107
108
Capítulo 4
Retículas de cimentación
VIGA DEL EJE 2.
D7
Figura 4.20 Contratrabe con carga debido al sismo y-y.
VIGA DEL EJE B.
D8
Figura 4.21 Contratrabe con carga debido al sismo y-y.
Capítulo 4
Retículas de cimentación
109
Dimensionamiento de contratrabes.
El dimensionamiento de estos elementos se hará en base al reglamento de construcciones para el
D.F. (1993). Para poder efectuar el dimensionamiento se usan los diagramas de momentos y
cortantes últimos, los cuales se obtienen después de realizar las combinaciones de los efectos por
cargas estáticas usando los diagramas de momentos y de cortantes del tipo D1 y D2 y sísmicas, del
tipo D3 y D4. debido a que el sismo puede actuar en la direcciones x-x o y-y, las combinaciones a
realizar son las siguientes:
a)
b)
cargas estáticas mas sísmicas en dirección x-x.
Cargas estáticas mas sísmicas en dirección y-y.
De estas dos combinaciones se elegirán los casos mas desfavorables afectándolas por el factor de
carga correspondientes. La combinación seleccionada se deberá comparar con los efectos de las
cargas estáticas (C.V. + C.M.) afectadas por el factor de carga, debiendo tomar la desfavorable para el
diseño estructural.
Efectos por resistir:
a)
efectos de cargas estáticas.
C.D.=1.4(C.V.+ C.M.)
efectos de las combinaciones de cargas estáticas y sísmicas.
C.D.=1.1(C.V.+ C.M.+ C.S.)
b)
En donde:
Variable
Significado
C.D.
C.V.
C.M.
C.S.
Efectos por resistir o efectos últimos.
Efectos por cargas vivas.
Efectos por cargas muertas.
Efectos por sismo.
Diagramas de momentos flexionantes y fuerzas cortantes.
a)
Momentos flexionantes debido a cargas estáticas.
Para obtener el diagrama de momentos flexionantes, primero se hace la suma de los momentos que
genera la presión del terreno, diagramas de momentos D1 y D2, y los momentos que generan los
cortantes desequilibrados, diagramas de momentos D3 y D4. se considera que una forma practica de
trabajar es la siguiente: se cambia el signo a los diagramas de momentos D3 y D11, conservando los
signos en los primeros diagramas, ya que indican directamente la posición en que estar colocado el
acero de refuerzo, si el diagrama de momentos se encuentra por arriba de la línea de referencia el
acero de refuerzo de refuerzo se colocara en la parte superior de la contratrabe, en cambio cuando el
diagrama de momentos este por abajo de la línea de referencia el acero se colocara en la parte
inferior de la contratrabe, sin embargo se puede optar por cualquier otra forma.
Observe que se tomara en cuenta solamente el efecto que produce cada sistema de cargas. Por
ejemplo en la viga 2 el momento debido a cargas estáticas en el nodo B es igual al momento del
diagrama D1 mas el momento del diagrama D3.
M est = 36.71 + 113.94 = 150.65 ton − m
(ver diagrama D9a).
110
Capítulo 4
Retículas de cimentación
En el diagrama D9b se tiene el momento flexionante último que se determino multiplicando los
momentos del diagrama D9a por el factor de carga correspondiente. Por ejemplo en el nodo B se
tiene:
M u = 1.4 M est = 1.4 × 150.65 = 210.91 ton − m
b)
Momentos flexionantes debido a la combinación de carga estática y sismo.
En D10 se presenta el diagrama de momentos flexionantes correspondiente a la combinación
indicada, considerando el sismo en la dirección x-x y que puede actuar de derecha a izquierda o de
izquierda a derecha. El diagrama de esta combinación se obtiene sumando los efectos mencionados
anteriormente de tal manera que produzcan valores máximos. Por ejemplo, para el nodo B del
diagrama D9a se toma 150.65 ton-m y del diagrama D5, 3.90 ton-m, resultando el momento
flexionante total debido a la combinación deseada, diagrama D10a.
M est + M sis = 150.65 + 3.90 = 154.55 ton − m
y el momento flexionante último será, ver diagrama D10b.
M u = 1.1 × 154.55 = 165.92 ton − m
Para la combinación de cargas estáticas y sismo en la dirección y-y se sigue un procedimiento similar,
ver diagrama D11.
Para el dimensionamiento de las contratrabes se comparan los diagramas de momentos Mu debidos a
cargas estáticas (D9b) y los que resultaron de la combinación carga estática y sismo (D10b y D11b).
De ellos se elegirá los mas desfavorables para formar el diagrama de momentos que se deberá
emplear (D14a). El diseño de la contratrabe se hará para los momentos que se encuentran en los
paños de las columnas, se considera que las columnas son de 60x60 cm.
Diagramas de fuerzas cortantes.
Para la obtención de las fuerzas cortantes de diseño se procede en forma análoga al caso de los
momento flexionantes.
Vu = 1.4 Vest
Vu = 1.1 (Vest + Vsis )
a)
Fuerzas cortantes por cargas estáticas.
Estos diagramas se obtienen sumando los cortantes que genera la presión del terreno sobre las
contratrabes 1, 2, 3, 4, A, B, C y D y los generados por los cortantes desequilibrados de las
contratrabes de la 1 a la D. Por ejemplo para la viga del eje 2, en el nodo B, de los diagramas D1 y D3
se tiene:
Vest = 27.57 + 17.27 = 44.89 ton
en los diagramas D12a y b se presentan las fuerzas cortantes debidos a cargas estáticas y los
cortantes últimos respectivamente, estos se obtienen multiplicando los cortantes del diagrama D12a
por el factor de carga correspondiente por ejemplo, para el nodo A se tiene:
Capítulo 4
Retículas de cimentación
111
Vult = 1.4 × 44.89 = 62.85 ton
b)
Fuerza cortante debido a la combinación de carga estática y sismo.
En el diagrama D13 se tienen las fuerzas cortantes debido a la combinación indicada, considerando el
sismo en la dirección x-x. Se omite en la dirección y-y por que los valores numéricos son menores.
El diagrama D13a se obtiene sumando los cortantes estáticos, diagrama D12a, a los cortantes por
sismo en la dirección x-x, diagrama D5, de tal manera que produzcan valores máximos, por ejemplo,
para el nodo A de la viga en cuestión se tiene:
Vest + Vsis = 44.89 + 24.63 = 69.52 ton
y el cortante ultimo debido a esta combinación se obtiene multiplicando el cortante anterior por su
factor de carga correspondiente, ver diagrama D13b.
La combinación debida a cargas estática y sismo en la dirección y-y se realiza en forma similar. Estos
son menores, compruébelo.
Diseño de la contratrabe No. 2.
Datos:
f ' c = 250 kg / cm 2
f y = 4200 kg / cm 2
FR = 0.9 para flexión
FR = 0.8 para cortante
Limitaciones y constantes de cálculo.
f *c = 0.8 f ' c = 200 kg / cm 2
f ' ' c = 0.85 f *c = 0.85 × 200 = 170 kg / cm 2
Pmin =
0 .7 f ' c
fy
Pmax = 0.75 Pb
Pb =
=
cuando f *c ≤ 250 kg / cm 2
0.7 250
= 0.0026
4200
cuando se considera sismo
f ' 'c
4800
= 0.019
f y 6000 + f y
Pmax = 0.75(0.019 ) = 0.0143
L sección de la contratrabe se determina a partir de momento flexionante máximo por resistir. Del
diagrama D14a se obtienen para el nodo B, Mu = 195 ton-m.
112
Capítulo 4
Retículas de cimentación
Se propone p = 0.013, con objeto de determinar las dimensiones de la sección.
M u = FR b d 2 f ' ' c q (1 − 0.5 q )
Considerando la relación d / b = 3 y sustituyéndola en la ecuación anterior, al despejar el peralte se
obtiene
d3 =
q=
3M u
FR f ' ' c q (1 − 0.5 q )
pf y
f ' 'c
= 0.3212
Sustituyendo valores se obtiene un peralte efectivo igual
recubrimiento de r = 7 cm.
d = 112 cm y b = 37 cm, con un
Calculo del área de acero.
Q=
Mu
FR bd 2 f ' ' c
=
195 × 10 5
0.9 × 35 × 113 2 × 170
= 0.2852
Con ayudas de diseño se obtiene el porcentaje de refuerzo p = 0.0138.
As = p bd = 0.0138 × 35 × 113 = 55.16 cm 2
Para 11 varillas del # 8
As = 11 x 5.07 = 55.77 cm
2
As
55.77
=
= 0.0141
bd 35 × 113
< 0.0141 < Pmax
Preal =
Pmin
Puede calcularse el momento que resiste una varilla del # 8.
a 
 5.07 
mr =  s  M u = 
195 = 17.72 ton − m
 57.77 
 As 
Así para cubrir el momento de 152.24 ton-m, se requieren 9 varillas del # 8.
!o. de var illas =
152.24
= 8.59 ≈ 9
17.72
Y para el momento de 183 ton-m se requieren 11 varillas del # 8.
Corte de varillas.
Capítulo 4
Retículas de cimentación
113
Las longitudes constructivas de las barras y su localización se obtiene del diagrama de momentos
flexionantes, que se deberán dibujar a escala, por ejemplo, si se corren 4 varillas del # 8,
mr=4x17.72=70 ton-m, este valor se marca en la grafica para conocer donde se cortan las varillas.
Distancia a la que deben prolongarse las varillas mas allá del punto en que son necesarias.
1)
2)
Ldb = 0.06
las barras que dejan de ser necesarias por flexión se cortan o se doblan a un peralte mas
allá del punto teórico donde de acuerdo con el diagrama de momentos ya no se requieren.
A cada lado de toda sección de momento máximo la longitud de cada barra es mayor o
igual que la longitud de desarrollo.
as f y
f 'c
≥ 0.006 d b f y
En donde:
Variable
Significado
Ldb
as
db
Longitud básica.
Área transversal de la varilla.
Diámetro de la varilla.
Para el lecho inferior Ld = Ldb y para el lecho superior se tiene que aplicar un factor de corrección de
1.4; si existe cuando menos 30 cm de concreto sobre las barras que se pretende cortar.
3)
4)
( Ld
excepto en las zonas de corte próximas a los extremos libremente apoyados, las
distancias que deben prolongarse mas allá del punto en que son necesarias será: Ld + d.
La longitud que debe prolongarse, las barras mas allá del centro del apoyo en extremos
libres, será:
− 0.25 L ) ≥ 0.5 h
En donde:
Variable
Significado
Ld
L
H
Longitud de desarrollo.
Claro entre apoyos.
Peralte total.
5)
En extremos libremente apoyados se prolongará, sin doblar, hasta dentro del apoyo
cuando menos la tercera parte de refuerzo de tensión para momento positivo máximo.
Para este caso:
114
Capítulo 4
Retículas de cimentación
d = 113 cm
Ldb = 0.06
as f y
f 'c
= 0.06
5.07 × 4200
= 80 cm
250
Deberá ser mayor o igual a: Ldb = 0.006 x 2.54 x 4200 = 64 cm.
Para el lecho superior: Ld = 1.4 x 80 = 112 cm.
Rige Ld =113 cm.
De acuerdo al inciso 3:
Ld + d = 113 + 113 = 226 cm.
Del inciso 4:
≥
Ld – 0.25 L = 113 – ( 0.25 x 600 )
0.5 h = 0.5 x 120 = 60 cm.
Por el inciso 5:
2
Área de acero para momento positivo As = 55.77 cm .
Área que llega a cada extremo 4 # 8 As = 20 > 55.77 / 3.
Refuerzo por cortante.
El refuerzo debe estar formado por estribos cerrados perpendiculares u oblicuos al eje de la pieza con
un ángulo no mayor de 45°. El acero que se use para estribos no deberá tener esfuerzo de fluencia
2
mayor de 4200 kg/cm .
Cuando la fuerza cortante por resistencia Vu sea menor que la fuerza cortante que resiste la sección
Vcr se debe suministrar un refuerzo mínimo por cortante. Este refuerzo consiste en estribos verticales
no menores del # 2 a una separación de:
s = 0 .5 d ≤
FR Av f y
3 .5 b
En caso contrario, cuando Vu > Vcr, la separación se determina a partir de la siguiente expresión:
s=
FR Av f y d (senθ + cos θ )
Vu − Vcr
≤
FR Av f y
3 .5 b
En donde:
Variable
Significado
FR = 0.8
Av
Factor de reducción por cortante.
Área transversal del estribo (dos ramas).
Capítulo 4
Retículas de cimentación
θ
Ángulo que forma el estribo con el eje de la viga.
si Vu > Vcr pero Vu ≤ 1.5 FR bd
f *c
115
s max = 0.5 d
si Vu > 1.5 FR bd
f *c
s max = 0.25 d
Para que la sección pase por cortante se debe cumplir que:
Vu ≤ 2.5 FR bd
f *c
El cortante que absorbe el concreto se determina con el siguiente criterio:
si p < 0.01
Vcr = FR bd (0.2 + 30 p ) f *c
si p ≥ 0.01
Vcr = 0.5 FR bd f *c
En los tramos comprendidos a un peralte efectivo de las secciones, donde en zonas de tensión se
interrumpan, mas del 33%, la fuerza cortante máxima que puede tomar el concreto se considera de:
0.7 Vcr.
Diseño por cortante de la contratrabe 2.
Cortante que toma el concreto:
2.5 FR bd
f *c = 2.5 × 0.8 × 35 × 113 200 = 111864 kg > Vu = 76470 kg
Ver Vu del diagrama de cortantes.
Revisión para ver la necesidad de disminuir Vcr por interrupción de mas de 33% del refuerzo
longitudinal.
Corte 1 # 8 As int / As = 5.07 / 55.77 = 0.09 < 33%
Corte 2 # 8 As int / As = 10.14 / (55.77- 5.07) = 0.2 < 33%
Corte 4 # 8 As int / As = 20.28 / (50.70- 10.14) = 0.5 < 33%
Pero este corte esta en la zona de compresión, por lo tanto no es necesario reducir Vcr en ninguna
sección de la contratrabe.
Por facilidad para el calculo de Vcr se consideran 4 # 8 que se corren a lo largo de toda la viga.
4#8
As = 20.28 cm
2
116
p=
Vcr
Retículas de cimentación
Capítulo 4
20.28
= 0.0051
35 × 113
= FR bd (0.2 + 30 p ) f *c = 0.8 × 35 × 113(0.2 + 30 × 0.0051) 200 = 10795 kg
2
Separación de estribos verticales de # 4 con fy = 4200 kg/cm .
Tramo A-B
Vu = 76.47 ton.
2
Av = 2 (1.27) = 2.54 cm .
s=
FR Av f y d
Vu − Vcr
=
0.8 × 2.54 × 4200 × 113
= 15 cm
76470 − 15795
Separación máxima
s=
FR Av f y
3 .5 b
=
0.8 × 2.54 × 4200
= 69 cm
3.5 × 35
1.5 FR bd f *c = 1.5 × 0.8 × 35 × 113 × 200 = 67118 < Vu
s ≤ 0.25 d = 0.25 × 113 = 28 ≈ 25 cm
Rige s = 15 cm.
Tramo B-C
Vu = 62.79 + 10.6 = 73.39 ton
s=
964387
= 16 cm
73390 − 15795
Tramo C-D
Vu = 62.38 ton
s=
964387
= 20 cm
62380 − 15795
Capítulo 4
Retículas de cimentación
CONTRATRABE DEL EJE 2.
D9
Figura 4.22 Diagrama de momentos flexionantes debido a carga estática.
117
118
Capítulo 4
Retículas de cimentación
CONTRATRABE DEL EJE 2.
D10
Figura 4.23 Diagrama de momentos flexionantes debido a carga estática y sismo x-x.
Capítulo 4
Retículas de cimentación
CONTRATRABE DEL EJE 2.
D11
Figura 4.24 Diagrama de momentos flexionantes debido a carga estática y sismo y-y.
119
120
Capítulo 4
Retículas de cimentación
CONTRATRABE DEL EJE 2.
D12
Figura 4.25 Diagrama de fuerzas cortantes debido a cargas estática.
Capítulo 4
Retículas de cimentación
121
CONTRATRABE DEL EJE 2.
D13
Figura 4.26 Diagrama de fuerzas cortantes debido a cargas estática y sismo en la dirección x-x.
122
Capítulo 4
Retículas de cimentación
CONTRATRABE DEL EJE 2.
D14
Figura 4.27 Diagrama de momentos flexionantes y de cortantes para diseño y armado de la
contratrabe.
Capítulo 4
Retículas de cimentación
123
Diseño de la losa de cimentación.
En el diseño de losas de cimentación es importante realizar la combinación de efectos, en forma
practica se siguiere utilizar los métodos del marco equivalente y el de las normas técnicas
complementarias del reglamento de D.F.
Combinación de efectos. La combinación para el diseño de las losas se hará en forma semejante al
establecido para las contratrabes.
En la tabla 1, se tiene un resumen de esfuerzos. En la columna 5 están los esfuerzos debidos a
cargas estática y en las columna 6 y 7 están los esfuerzos debidos a sismo.
a)
Esfuerzos por resistir debidos a cargas estáticas.
FE u =1.4 FE
b)
esfuerzos por resistir debidos a la combinación de cargas estáticas y sismo.
F su = 1.1 ( f e + f s )
De las combinaciones anteriores se eligen los esfuerzos mas desfavorables para el diseño. En la tabla
4.5 se tiene un resumen de estas combinaciones, en la columna 2 se muestran los esfuerzos últimos
debidos a carga estática, para lo cual los esfuerzos de la tabla 1, columna 5, se multiplicaron por 1.4.
en la columna 3 se tiene la suma de f e + f s, recurriendo a los valores mayores de las columnas 8, 9,
10 y 11 de la mencionada tabla 4.1. en la columna 4 se tienen los esfuerzos últimos de la combinación
carga estática y sismo, tomando los valores de las columnas 3, y multiplicándolas por el factor de
carga de 1.1.
En la columna 5, se anotan los esfuerzos para el diseño de las losas que resultan de elegir los
esfuerzos desfavorables de las columnas 2 y 4.
Tabla 4.5
1
2
3
4
5
Columna
F Eu
f e+ f s
f su
Esfuerzos de
diseño
A-4
4.981
5.198
5.718
5.718
A-3
5.069
5.261
5.787
5.787
A-2
5.193
5.394
5.933
5.933
A-1
5.298
5.424
5.966
5.966
B-4
5.088
5.090
5.599
5.599
B-3
5.174
4.343
4.777
5.174
B-2
5.298
4.269
4.696
5.298
B-1
5.403
4.269
4.696
5.403
C-4
5.172
5.150
5.665
5.665
C-3
5.260
4.404
4.844
5.260
C-2
5.383
4.460
4.906
5.383
C-1
5.488
5.376
5.914
5.914
D-4
5.258
5.396
5.936
5.936
D-3
5.347
5.459
6.005
6.005
D-2
5.470
5.477
6.025
6.025
D-1
5.575
5.622
6.184
6.184
124
Capítulo 4
Retículas de cimentación
En caso de usar el método del reglamento, se enumeran las losas, y se fijan los claros corto a1 y largo
a2. Este método se usara, con ciertas reservas, pues no cumplen las losas con todas las hipótesis que
establece dicho método.
Figura 2.28 Losa de cimentación.
Cálculo de los momentos en franjas centrales. Después de haber fijado los anchos de las franjas
centrales, se obtienen los momentos para estas. Con la relación a1/a2 se toman los coeficientes “k” de
la tabla que se encuentra en las N.T.C., para tal fin y para calcular los momentos flexionantes se usa
la expresión:
Mu = k wu a1
2
En donde:
Variable
Significado
wu
a1
Carga uniformemente distribuida que actúa sobre la losa.
Claro corto de la losa
La carga uniforme se obtiene por medio del siguiente promedio de esfuerzos que actúan en cada
esquina de la losa en cuestión, por ejemplo para la losa I, se tiene:
wuI =
f 3 A + f 4 A + f 3B + f 4B
4
En el método no se consideran los efectos de sismo por lo que se sugiere tomar los valores de la
columna 2 de la tabla 4.5.
Para la determinación del peralte de la losa se usa:
d min =
Perímetro efectivo
0.034
270
4
0 .6 f y w
Capítulo 4
Retículas de cimentación
125
Revisión por cortante, se supone que la sección critica se encuentra a un peralte efectivo del paño de
la contratrabe, la fuerza cortante que actúa en un ancho unitario se calcula con la expresión:
 a1


− d  wu
a

V = 2
6
 a1 
1 +  
 a2 
Cuando se tengan bordes continuos y discontinuos, V se incrementara en 15%.
La resistencia de la losa a fuerza cortante se supone igual a:
Vcr = 0.5 FR bd f *c
Obtención del área de acero y separación de las varillas.
As = p bd
s=
a s × 100
As
s max = 2.5 d
p min = 0.002
p max = 0.75 pb
Para el armado se sugiere doblar varillas y aplicar los requisitos de anclaje, se supondrán líneas de
inflexión a un sexto del claro corto desde los bordes del tablero para momento positivos y a un quinto
del claro corto desde los bordes del tablero para momentos negativos.
b a1
+ +d
2 5
b a
= + 1 −d
2 6
Ld 1 =
Ld 2
En donde:
Variable
Significado
b
d
a1
Ancho de columna.
Peralte efectivo de la losa.
Claro corto.
Cuando se use el método del marco equivalente se recomienda incluir los efectos del sismo, siguiendo el
procedimiento que se establece en la N.T.C.. Existen otros métodos aproximados que se pueden usar para el
diseño de losas de cimentación pero se recomiendan los expuestos en el capítulo 5.
Capítulo
5
INTERACCION DEL SUELO CON LA
ESTRUCTURA.
La interacción del suelo con la estructura o suelo-estructura, es el estudio del comportamiento de la
interfase de la estructura de cimentación y la masa de suelo. Este estudio tiene como objetivo
encontrar la configuración de deformación y los elementos mecánicos de la estructura de cimentación
y el suelo, debido a las acciones o cargas gravitacionales y accidentales. La interacción sueloestructura consiste en encontrar un sistema de fuerzas que aplicadas simultáneamente a la estructura
y a la masa de suelo produzcan la misma configuración de desplazamientos diferenciales entre los dos
elementos, debiendo cumplir con las condiciones de equilibrio y continuidad, ecuaciones
fundamentales del Análisis Estructural.
Por lo tanto es necesario conocer el comportamiento de la masa del suelo y el comportamiento del
material de la estructura de cimentación, vigas, placas, pilas y pilotes entre las típicas. La primera la
estudia la Mecánica de Suelos y la segunda la Mecánica de Materiales.
Existen dos enfoques del problema de interacción suelo-estructura que se denominan: interacción
dinámica suelo-estructura e interacción estática suelo-estructura.
La interacción dinámica suelo-estructura estudia el comportamiento dinámico del sistema
cimentación-masa de suelo. El análisis del problema de interacción dinámica se inicia a fines de la
década de los años sesenta fundamentalmente por el comportamiento sísmico de plantas nucleares
desplantadas en suelos deformables, actualmente los estudios se han desarrollado para analizar los
efectos de interacción en construcciones muy esbeltas como edificios y chimeneas cimentados en
suelos compresibles.
Si tuviera que elegirse el terreno donde se ubicará la construcción se recomendaría un lugar de suelo
firme, libre de amplificaciones locales, generadas por los movimientos sísmicos, así como de
asentamientos excesivos y pérdida de capacidad de apoyo. Sin embargo si el edificio se tuviera que
cimentar en suelo blando, es conveniente usar pilas o pilotes para apoyarlo en estratos firmes. Cuando
esto no es posible se tendrán que aplicar los métodos de interacción suelo-estructura. Aunque también
se presenta la interacción entre el suelo y las pilas o pilotes.
El tema de interacción dinámica queda fuera del alcance de este libro. A continuación se tratará
brevemente la interacción estática.
128
5.1
Capítulo 5
Interacción del suelo con la estructura
INTERACCIÓN ESTATICA SUELO-ESTRUCTURA.
El objetivo de la interacción estática suelo-estructura es realizar un análisis estructural de la
subestructura y superestructura considerando el efecto de la rigidez de la masa del suelo. En las
estructuras de cimentación sobre suelos compresibles y de alta compresibilidad surge el problema de
determinar los hundimientos totales y diferenciales, éstos generan elementos mecánicos, fuerzas
axiales y cortantes y momentos flexionantes y torsionantes, en toda la construcción. Los hundimientos
dependen de la compresibilidad del suelo y de la rigidez o flexibilidad de la estructura de cimentación.
Por lo expuesto anteriormente se concluye que no en todos los casos de diseño de cimentaciones se
deberá tomar en cuenta la interacción suelo-estructura, por ejemplo en edificios pequeños cimentados
en suelos rígidos, los hundimientos diferenciales del terreno son pequeños y no tienen importancia en
el Análisis Estructural.
Debido a las características del subsuelo de la ciudad de México, varios investigadores han
desarrollado métodos que toman en cuenta las propiedades del suelo. Los estudios de Mecánica de
Suelos tienen como objetivo principal, conocer las características del subsuelo para que en función de
estas se propongan las estructuras de cimentación apropiadas.
El suelo es un medio heterogéneo, anisótropo y discontinuo estatigraficamente, generado por las
diferentes condiciones de formación y de afectación de los fenómenos naturales durante su historia
geológica. Para la evaluación de los parámetros de estudio de la interacción del suelo con la estructura
se hacen varias simplificaciones para facilitar los modelos de análisis, por ejemplo se considera al
suelo como un medio seminfinito y elástico, aun cuando se sabe que el suelo no es elástico, más bien
es elástico-plástico y viscoso.
El estudio de las propiedades elásticas del suelo se basa principalmente en la determinación de las
siguientes propiedades: módulo de elasticidad axial, módulo de elasticidad al corte y la relación de
Poisson.
Debido a que el comportamiento del suelo no es elástico lineal, para efectos prácticos, la curva
esfuerzo-deformación se linealiza, sustituyendo la curva por rectas, por esta razón el módulo de
elasticidad axial y la relación de Poisson no son constantes.
Los términos módulo tangente y módulo secante se usan de manera frecuente. El módulo tangente es
la pendiente de la curva esfuerzo-deformación en punto dado, de tal forma que el valor del módulo
tangente varia según el punto seleccionado, este módulo en el punto inicial de la curva se llama
módulo tangente inicial. El módulo secante es la pendiente de la recta que une dos puntos separados
de la curva, vea la figura 5.1.
Figura 5.1
Módulos esfuerzo-deformación.
Capítulo 5
5.2
Interacción del suelo con la estructura
129
Módulo de reacción del suelo.
El módulo de reacción del suelo o módulo de cimentación se define como la relación entre la presión
unitaria del suelo y el desplazamiento o asentamiento correspondiente, esto es:
k =
s
q
d
(5.1)
En donde:
Variable
Significado
ks
Módulo de reacción del suelo (kg / cm )
q
Presión unitaria del suelo (kg / cm )
d
Desplazamiento del suelo (cm)
3
2
El módulo de reacción se obtiene realizando una prueba de placa y graficando la curva de presiones y
desplazamientos como se ilustra en la figura 5.2.
Figura 5.2
Curvas del módulo de reacción del suelo.
La prueba de placa se realiza aplicando la carga sobre tres placas cuadradas de 75, 60 y 45 cm.,
poniendo la mayor sobre el suelo, esto se hace con el objeto de distribuir uniformemente la carga. La
gráfica se obtiene con las presiones promedio del suelo contra el promedio de los asentamientos, para
mayor información ver la referencia 2.
En la figura 5.2b se indica que la curva esta dividida en una zona lineal y una zona no lineal. Si el
desplazamiento del suelo excede el asentamiento máximo, no es aplicable la ecuación (5.1).
130
Capítulo 5
Interacción del suelo con la estructura
En algunos métodos de análisis, en lugar del módulo de reacción se puede usar
E yµ
s
sin
embargo existe una relación entre ellos. El profesor Bowles recomienda el empleo del módulo de
cimentación.
A continuación se presentan expresiones para calcular el módulo de cimentación propuesto por
algunos investigadores.
Terzaghi (1955) propuso:
Para zapatas cuadradas sobre arcilla.
k =k B
s 1
(5.2)
Para zapatas cuadradas sobre arena.
 B +1 

k = k 
s
1  2B 


2
(5.3)
Para zapatas rectangulares sobre arena de dimensiones de
B × mB
m + 0.5
k = k
s
1 1.5 m
(5.4)
En donde:
Variable
Significado
ks
Valor deseada para una zapata de tamaño real
k1
Valor de una prueba de carga correspondiente a una placa
cuadrada de 1 x 1 pulgadas.
B
Ancho de la zapata.
Vesic (1961) propuso que el módulo de cimentación se calculara usando
E B E
s
k ' = 0.65 12 s
s
E f If 1 − µ 2
(
)
E .
s
(5.5)
Capítulo 5
Interacción del suelo con la estructura
131
En donde:
Variable
Significado
Es , Ef
Módulos del suelo y de la zapata respectivamente, en las
mismas unidades.
B, If
Ancho y momento de inercia de la sección transversal de la
zapata, en las mismas unidades.
µ
Módulo de Poisson.
k'
k = s
s B
(5.6)
El producto de la ecuación (5.4) que incluye la raíz doceava por 0.65 se aproxima a la unidad, para
fines prácticos, esta ecuación se reduce a:
k =
s
E
s
(5.7)
B 1 − µ2 


Bowles (1974) presenta al módulo de reacción del suelo en función de la capacidad admisible.
F q
k = s a
s
S
(5.8)
En donde:
Variable
Significado
Fs
Factor de seguridad para asentamientos.
qa
Capacidad de carga permisible por asentamiento.
S
Asentamiento esperado.
Esta ecuación la redujo considerando un factor de seguridad de 3 y asentamientos de 1 pulgada
llegando a la expresión (5.9)
k = 120 q
s
a
(5.9)
La aproximación que se obtiene en el valor del módulo de cimentación, influye en los valores obtenidos
para los desplazamientos.
132 Capítulo 5 Interacción del suelo con la estructura
En las tablas siguientes se presentan valores del módulo de reacción del suelo, según Terzaghi y
Barkan, para diferentes tipos de suelo. Los valores dados en éstas tablas son para placas cuadradas
de 30 x 30 pulgadas y se deben modificar como se indicó anteriormente.
3
Módulo de reacción del suelo K (T / M )
Arenas
Densidad relativa
Suelta
Media
555-1940
1940- 33246
832
2494
Tipo de arena
Seca o Húmeda
Saturadas
Densa
9697 - 33246
9697
3
Tipo de arena
Rango
Valor
Recomendado
Módulo de reacción del suelo k (t/m )
Suelos cohesivos.
2
Consistencia (Resistencia no confinada qu (t/m )
Muy suave.
Rígida.
Muy rígida.
Dura.
2
2
2
2
(0-10.76 t/m )
(10.76-21.53 t/m )
(21.53-43.06 t/m )
(>43.06 t/m )
Diseñar como
Cimentaciones
1663 – 3325
3325 - 6373
>6373
Rígidas.
2355
4849
9697
Barkan también recomendó otros valores para el módulo de reacción del suelo como:
Ks
ξ qa
Ks
Módulo de reacción del suelo en Kg / cm .
qa
Capacidad permisible para cargas estáticas en Kg / cm
ξ
Factor de relación en cm
3
Categoría de suelo
I
II
III
IV
Categoría de suelo
I
II
III
IV
2
4
Descripción
Suelos débiles
Suelos de resistencia media
Suelos fuertes
Rocas.
Descripción
Suelos débiles
Suelos de resistencia media.
Suelos fuertes
Rocas
qa
1.5
1.5 - 3.5
3.5 – 5
5
2
qa (T/M )
< 15
15-35
35-50
> 50
ξ
2.00
1.43
2.00
2.00
3
Ks (T/M )
< 3000
3000 – 5000
5000 – 10000
> 10000
Capítulo 5
5.3
Interacción del suelo con la estructura
133
Teoría de vigas sobre medios elásticos.
A continuación se presenta la teoría de vigas sobre medios elásticos, determinando la ecuación
diferencial que gobierna al modelo del problema de vigas sobre el tipo de medios mencionado. Para
mayor información sobre diversos casos en cuanto a la geometría y formas de apoyo de vigas, así
como de distintas clases de cargas que actúan sobre ellas, se recomienda la referencia 5.
En la teoría de vigas sobre medios elásticos se considera que las reacciones del terreno sobre la viga
son proporcionales a los desplazamientos del punto correspondiente, a lo largo de toda la viga. Esta
suposición fue propuesta inicialmente por E. Winkler en 1867 y fue la base del trabajo de
H.Zimmerman sobre el análisis de vías de ferrocarriles, publicado en 1888.
Inicialmente estos estudios estuvieron dirigidos al suelo como un medio de apoyo de vías de
ferrocarriles, sin embargo, esta teoría puede ser aplicada a otros campos donde dicha suposición se
cumple más satisfactoriamente. Entre los campos donde se puede aplicar son: en retículas de vigas
para sistemas de pisos de barcos, en cimentaciones de edificios o puentes, en cascarones delgados
de revolución como recipientes sujetos a presión interna o contenedores, etc.
Aquí su aplicación es para vigas sobre cimentación elástica, como un método aproximado, puesto que
las propiedades del suelo son de naturaleza más complicada que lo que esta teoría propone. No
obstante bajo ciertas condiciones es innegable la condición elástica del suelo.
Presenta una debilidad esta teoría al considerar el medio en forma equivalente como una serie de
resortes independientes, omitiendo la compatibilidad de deformaciones en la masa del suelo. Algunos
investigadores al aplicarlo han corregido esta teoría en este aspecto.
No siempre resulta fácil y rápido resolver analíticamente las ecuaciones diferenciales que gobiernan el
problema, de tal manera que por este motivo se presentan los métodos numéricos de diferencias
finitas y del elemento finito.
Al recurrir al uso de estos métodos numéricos que tienen diversas aplicaciones en la Mecánica
Estructural y actualmente en diversos problemas de la Ingeniería y aun en otras áreas de la ciencia. Se
considera que el lector tiene los conocimientos fundamentales sobre los métodos citados, así como el
manejo del álgebra matricial, herramienta fundamental en dichos métodos.
En el método de las diferencias finitas es necesario expresar las derivadas de una función continua en
términos de funciones de intervalos discretos.
Planteamiento del problema.
En figura 5.3 se ilustra una viga de sección constante sobre un medio elástico, sujeta a cargas
verticales que actúan en el plano principal de la sección transversal.
Hipótesis:
a)
Al actuar las cargas sobre la viga, se produce una distribución contínua de presiones del medio
sobre la viga.
b)
De acuerdo con la suposición fundamental, la intensidad q en cualquier punto es proporcional
al desplazamiento y de la viga en esos puntos.
q=ky
Por lo anterior, el terreno o medio se supone elástico.
c)
Se supone que el medio no es capaz de soportar fuerzas o esfuerzos de tensión.
(5.10)
134
Capítulo 5
Interacción del suelo con la estructura
Figura 5.3
Viga sobre un medio elástico.
3
Llamando a ko módulo de cimentación o del medio elástico expresado en kg/cm .
y considerando un ancho b de la viga se define a:
k = bk
en kg / cm2
0
(5.11)
Por lo que se puede expresar a la ecuación 5.10 de la siguiente manera.
q = bk
0
y
(5.12)
Considerando un elemento de viga dx, como se ilustra en la figura 5.4.
Figura 5.4
En donde para la figura 5.4:
Elemento de viga de ancho diferencial
Interacción del suelo con la estructura
Variable
Capítulo 5
Significado
V
Fuerzas cortantes.
M
Momentos flexionantes.
dV
Incremento de cortante.
dM
Incremento de momento.
q dx = k y dx
Estableciendo el equilibrio de fuerzas y auxiliándose de la figura 5.4, se obtiene:
V − (V + dV ) + k y dx − w dx = 0
−dV +k y dx − w dx = 0
dV
= k y −w
dx
(5.13)
Expresando la fuerza cortante como:
V =
dM
dx
y sustituyendo esta expresión en (5.13) se llega a:
d2 M
=k y−w
dx 2
(5.14)
Usando la ecuación de la curva elástica.
EI
d2 y
= −M
2
dx
(5.15)
Sustituyendo (5.15) en (5.14) se obtiene la ecuación (5.16).
d2  d2 y 
EI
=−k y + w


dx 2 
dx 2 
(5.16)
Que es la ecuación diferencial ordinaria de la elástica de una viga sobre un medio elástico.
135
136
Capítulo 5
Interacción del suelo con la estructura
Considerando la carga distribuida
forma: EI
w = 0 y EI constante, la ecuación toma la siguiente
d4 y
= − ky
dx 4
o bien:
yIV +
k
y = 0
EI
(5.17)
Suponiendo una solución de la ecuación diferencial ordinaria de cuarto orden con coeficientes
constantes del siguiente tipo, se sugiere ver el capítulo V de la referencia 6.
y = A emx
n
(5.18)
Derivando esta expresión hasta la cuarta, se tiene:
yIV = A m4 emx
n
(5.19)
Sustituyendo las expresiones (5.18) y (5.19) en (5.17) se llega a:
A
A
n
m4 emx + A
k mx
e
= 0
n EI
k

emx  m4 +  = 0
n
EI 

(5.20)
La ecuación característica de (5.20) es:
m4 +
k
=0
EI
(5.21)
La solución de esta ecuación de cuarto grado tiene cuatro raíces de números complejos, para
obtenerlas se recurre a la expresión (5.22) tomada del capítulo 2 de la referencia 8.
1
π + 2π s
π + 2π s 

m = r n  cos
+ i sen
 ; k = 0,1,...,n − 1
n
n
n


s varia de 0, 1, 2, ..., (s-1)
Para este caso.
n=4
s = 0, 1, 2, 3
(5.22)
Capítulo 5
r =
Interacción del suelo con la estructura
k
EI
Sustituyendo estos valores en (5.22) se obtienen las raíces de la ecuación (5.21)
 k 1 
π + 2π (0)
π + 2π (0)  4 k  1
1 
m =   4  cos
+ i sen
+ i
=


1  EI 
4
4
EI  2
2


En forma similar se obtienen las otras m
k 
1
1 
m =4
−
+i


2
EI 
2
2
k 
1
1 
m =4
−
−i


3
EI 
2
2
m
k  1
1 
=4
−i


4
EI  2
2
Las raíces se pueden expresar de la siguiente forma.
m = λ (1 + i)
1
m = + λ (− 1 + i)
2
m = − λ (1 + i)
3
m
4
= − λ (− 1 + i)
En donde:
k
λ=4
4EI
Y la solución se obtiene sustituyendo estos valores en (5.18).
m
3x
m x
x
m x
m
1
2
y =A e
+A e
+ A e
+ A e 4
1
2
3
4
λ xi
λ xi
− λ xi
y = A eλx e
+ A e − λx e
+ A e − λx e
+ A eλx e − λxi
1
2
3
4
Por el teorema de Moivre. Referencia 12.
(5.23)
137
138
Interacción del suelo con la estructura
Capítulo 5
eλxi = cos λx + i sen λx
e −λxi = cos λx − i sen λx
Sustituyendo estos valores en la expresión anterior, se obtiene:
γx
y = A e (cos λ x + i sen λ x ) + A e − λx (cos λx + i sen λx ) +
1
2
A e− λx (cos λ x − i sen λ x ) + A eλx (cos λx − i sen λx )
3
4
(
)
(
)
(
)


y = A + A eλx cos λ x + i A − A eλx sen λ x + A + A  e − λx cos λ x
1 4
1
4
2
3

+ i A − A e− λx sen λx
2
3
Llamando:
(
(
)
)
A + A = C ; A − A i= C : A + A = C ; A − A i = C
1
4
1 1
4
2
2
3
3
2
3
4
Se obtiene:
(
)
y = eλx C cos λ x + C sen λ x + e− λx  C cos λx +C sen λx 
1
2
4
 3

En donde
λ
(5.24)
indica la relación de la elasticidad del medio y la rigidez flexionante de la viga, influyendo
en la forma de la elástica. Se le llama la característica del sistema y está expresado en
es una cantidad adimensional.
cm −1 .,
λx
La expresión (5.24) es la solución general de la ecuación de la elástica de una barra o viga prismática
soportada sobre un medio elástico sujeta a cargas transversales de flexión, pero sin carga w. Es
necesario un término adicional para el caso de carga distribuida.
Recordando las siguientes expresiones, conocidas en Resistencia de Materiales.
θ=
dy
dx
d2y
M = − EI
dx 2
V = − EI
d3 y
dx3
Entonces, a partir de (5.24) se pueden obtener giros, momentos flexionantes y fuerzas cortantes. Al
derivar se obtienen los siguientes resultados:
Capítulo 5
Interacción del suelo con la estructura
139
(
1
θ = eλx C (cos λx − sen λx ) +C (cos λx + sen λx ) ) −
1
2
λ
(5.25)
−
λ
x
e
( C3 (cos λx + sen λx ) − C4 (cos λx − sen λx ) )
1 d2y
= − eλx C sen λx − C cos λx + e− λx C sen λx − C cos λx
1
2
3
4
2λ2 dx 2
(
(
)
)
(5.26)
(
)
1 d3 y
= − eλx C ( cos λx + sen λx −C (cos λx − sen λx ) )+
1
2
2λ3 dx3
e− λx C (cos λx − sen λx ) + C (cos λx + senλx ) )
3
4
(
Las constantes de integración
C ,C ,C
1
2
3
y
C
4
(5.27)
dependen de las condiciones de frontera, así
como de la manera en la cual la viga está sujeta a las cargas. Por lo tanto los valores de estas
constantes pueden ser obtenidos de las condiciones existentes de la viga. De las cuatro cantidades, y,
θ , M y V, características para las condiciones de frontera, generalmente dos son conocidas en
cada extremo, las cuales son suficientes para la determinación de las constantes C.
Ejemplo 5.1.- En la figura 5.5 se muestra una viga de longitud L de sección constante sujeta a varias
cargas tales como M. P y w(x). A partir de estos datos se determinan los elementos geométricos y
mecánicos e interpretan las constantes de integración.
Figura 5.5
Viga sobre un medio elástico sujeta a varios tipos de cargas.
Solución:
Tomando en este caso x = 0, se obtienen las condiciones en el extremo izquierdo de la viga, de la
siguiente manera:
Sustituyendo
y
x =0
x = 0, se obtiene de la expresión (5.24).
(
= y = 1  C cos 0 ° + C sen 0 °  +1 C cos 0 ° + C sen 0 °
0
2
3
4
 1

)
140
Capítulo 5
y
= C + C
1
3
0
Sustituyendo
θ =λ
0
Interacción del suelo con la estructura
x = 0 en (5.25), (5.26.) y (5.27) se determina:
 C + C − C + C 
2
3
4
 1
(
M = 2 λ2 EI −C + C
0
2
4
)
(
V = 2 λ3 EI C − C − C − C
0
1
2
3
4
)
Expresando estas cuatro ecuaciones en forma matricial, esto es:
0
1
0 
 1
 λ
λ
−λ
λ 

 0
− 2λ2 EI
0
2λ2 EI 
 3

3
3
3
2λ EI − 2λ EI − 2λ EI − 2λ EI
 C1 
C 
 2 =
C 
 3
C4 
 Y0 
θ 
 0
M 
 0
 V0 
En donde las incógnitas son las constantes C y el vector de términos independientes es conocido,
puesto que son los desplazamientos o fuerzas generalizadas en las fronteras.
Resolviendo el sistema de ecuaciones anterior, se obtienen los valores de las constantes.
1
1
1
C =
y +
θ +
v
1 2 0
0
0
4λ
8 λ3 EI
1
1
1
C =
θ +
M −
v
2
0
0
0
2
3
4λ
4λ EI
8λ EI
1
1
1
C =
y −
θ0 −
v
3
0
0
2
4λ
8 λ 3 EI
C
4
=
1
1
1
θ0 +
M −
v
0
0
2
3
4λ
4λ EI
8λ EI
Sustituyendo los valores de las C en (5.24), se obtiene:
(5.28)
Capítulo 5
y =e
Interacción del suelo con la estructura

λx  1 y + 1 θ + 1 v  cos λx + ( 1 θ − 1 M − 1 v
4 λ 0 4 λ2 EI 0 8 λ3 EI 0
 2 0 4 λ 0 8 λ3 EI 0 


 1

1
1
1
1
1
e − λx  y −
θ
−
v  cos λx + (
θ
+
M −
v
4 λ 0 4 λ2 EI 0 8 λ3 EI 0
 2 0 4 λ 0 8 λ3 EI 0 


141

) sen λx  +


Agrupando:
 1
 e λx + e − λx
e λx − e − λx
1

y =
cos λx
v +
cos λx y −
θ0 +
0

3 EI 0 
2
2
2λ
4
λ


λx + e − λx
v
M
θ
e − λx + e − λx
e λx − e − λx
0 +e
0
sen λx
sen λx 0 −
sen λx
3
2
2
2
2λ
2
4 λ EI
2 λ EI
Recordando que:
Senh λx =
e λx − e − λ x
2
e λ x + e - λx
Cosh λx =
2
θ
v 
v0
y =  0 + 30  Senh λx cos λx + y 0 Cosh λx cos λx −
Cosh λx
4 λ3 EI
 2λ 4λ EI 
θ
M0
sen λx + 0 Cosh λx sen λx −
Senh λx sen λx
2λ
2λ2 EI
y = y Cosh λx cos λx + 0 (Cosh λx sen λx + Senh λx cosλx )
0
2λ
M
v
0 Senh λx sen λx −
0 (Cosh λx senλx − Senh λx cos λx )
−
2λ2EI
4λ3E
Llamando:

)sen λx 


142
Capítulo 5
Interacción del suelo con la estructura
F1 (λx) = Cosh λx cos λx
F2 (λx) = 1/2 Cosh λx sen λx + Senh λx cos λ
F3 (λx) = 1/2 Senh λx sen λ
F4 (λx) = ¼ (Cosh λx sen λx -- Senh λx cos λx)
Se obtiene la ecuación (5.29)
y = y 0 F1 (λx) +
v
θ0
M
F2 (λx) - 2 0 F3 (λx ) − 3 o F4 (λx )
λ
λ EI
λ EI
(5.29)
La expresión (5.29) es la ecuación de la curva elástica. Como ya se indicó, las constantes dependen
de los valores en la frontera, ahora las funciones hiperbólicas aparecen en lugar de las constantes en
la ecuación (5.29).
Observe que la forma desarrollada, tomando como base la expresión (5.29), es diferente a la ecuación
(5.24), este método fue desarrollado ampliamente en Rusia por Umansky.
Suponiendo que conocemos y0, θ0, M0, y V0, entonces se puede proceder del extremo izquierdo
de la viga, en la parte descargada, desde A hasta a, o sea antes de la primera carga M.
Evidentemente este momento M tiene un efecto a la derecha para
x > xa de su punto de aplicación.
Observe el momento M, es similar al M0 que aparece para el tramo A-a que revisando detalladamente
a la expresión (5.29) se observa que tiene como factor a:


1
F3 (λx)
− 2
 λ EI

Se puede concluir que si se maneja el momento M por un factor y luego se incluye
1
F3 (λ ( x − x a ))
λ EI
2
la ecuación de la elástica de la viga para el tramo a – b es:
θ
M
v
0 F (λx) − 0 F (λx) − M F (λ (x − x ) )
y = y F (λx) + 0 F (λx) −
0 1
3
4
3
a
2
2 2
λ3 EI
λ2 EI
λ EI
(5.30)
Se procederá en forma similar, para obtener la ecuación general de la elástica de este caso.
Haciendo las siguientes modificaciones.
Capítulo 5 Interacción del suelo con la estructura
Para el tramo b-c se le adiciona a la ecuación (5.29), a la expresión (5.30)
143
 1 

 F (λ ( x - x ) ) P
b
 λ3 EI  4


Se cambió de signo porque el cortante es negativo para la porción derecha del punto b.
Por último se tratará la carga distribuida w, se puede considerar a la carga como un conjunto de
cargas infinitesimales, entonces para un poco menor x > c, se le adicionará este término:
1 x
∫c F4 (λ (x − xc ) ) w dx
3
λ EI
para
x>d
el límite superior de la integral se vuelve x = d.
La expresión para este caso particular de la curva elástica es:
(
)
θ
M
v
0 F (λx) − 0 F (λx) − M F λ (x − x ) +
y = y F (λx) + 0 F (λx) −
x
0 1
3
4
3
a
2
λ 2
λ3 EI
λ2 EI
λ EI
P
1
x
F λ (x − x ) −
∫c w F4 λ (x − xc ) dx
4
b
3
3
λ EI
λ EI
(
)
(
)
(5.31)
Como se observa, en esta expresión se pueden eliminar términos si se recorre de derecha a izquierda
o sean los efectos de M, P y W.
Para obtener
θx = y 0
θx, Mx, y Vx
se deriva la expresión anterior.
d F1 (λx) θ0 d F2 (λx)
M d F3 (λx)
v d F4 (λx)
+
− 20
− 30
−
dx
dx
dx
dx
λ
λ EI
λ EI
M d F3
(λ (x − xa )) + p d F4 (λ (x − xa ) ) − 1
2
3 EI dx
3 EI
λ EI dx
∫
x
c
w
dF4 (λ ( x − x c ) )
dx
dx
Ahora derivando las funciones F.
dF
1 = (− Cosh λx sen λx + Senh λx cos λx )
dx
d F2 λ
= (Cosh λx cos λx + Senh λx sen λx − Senh λx sen λx + Cosh λx cos λx )
dx
2
144
∴
Capítulo 5
Interacción del suelo con la estructura
d F2
= λ Cosh λx cos λx
dx
dF
3 = λ ( Senh λx cos λx + Cosh λx sen λx )
dx
2
dF
4 = λ (Senh λx sen λx )
dx
2
Observe que existe una relación entre las derivadas anteriores y las funciones F.
dF
1=−4λF
4
dx
d F2
= λ F1
dx
d F3
= λ F2
dx
d F4
= λ F3
dx
Ahora se sustituyen estos valores en θx.
(
)
M
y
θ
0 λ F − 0 λ F − M F λ(x − x ) +
θ x = − y0 4λ F4 + λF1 −
2
3 λ2 EI 2
a
λ
λ2 EI
λ3 EI
(
)
(
)
P
1
x
F λ (x − x ) +
∫c w λ F3 λ (x − xc ) dx
3
b
3
3
λ EI
λ EI
Simplificando y ordenando:
1
1
θ = θ F (λx) −
M F (λ x) −
V F (λx) − 4λ y F (λx ) −
x
0 1
0 3
0 4
λ EI 0 2
λ2 EI
(5.32)
1
1
1
M F (λ (x − x a )) + 2
p F3 (λ (x − x b )) + 2
2
λ EI
λ EI
λ EI
En forma análoga:
x
∫c w F3 (λ ( x − x a )) dx
Capítulo 5
Interacción del suelo con la estructura
1
k
k
V0 F2 (λx ) + 2 y 0 F3 (λx ) + 3 θ0 F4 (λx ) +
λ EI
λ
λ
1
1 x
M F1 (λ( x − x a )) − p F2 (λ( x − xb ) − ∫c w F2 (λ( x − x a )) dx
λ
λ
145
Mx = M0 F1 (λx ) +
Vx = V0 F1 (λx ) +
(5.33)
k
k
y 0 F2 (λx ) + 2 θ0 F3 (λx ) − 4 λ M0 F4 (λx ) −
λ
λ
(5.34)
4 λ M F4 (λ( x − x a )) − p F1 (λ( x − xb )) −
x
∫c
w F1 (x − x c )) dx
Se observa que las condiciones de frontera aparecen en todas éstas ecuaciones y se presentan en
cada ecuación las cuatro condiciones de frontera. Note la forma cíclica en que se encuentran los
desplazamientos y fuerzas generalizadas, así como las funciones F.
Sustituyendo x = L en las ecuaciones anteriores, se obtiene yL, θL, ML, VL para el extremo
derecho de la viga, expresando en términos de las condiciones iniciales y cargas. Estas relaciones
pueden ser usadas para determinar las condiciones de frontera desconocidas. De las cuatro
condiciones de frontera, cuando menos dos son usualmente conocidas en cada extremo en la mayoría
de los casos.
Por ejemplo, la viga anterior tiene ambos extremos libres, por lo que se puede establecer:
Para
x=0
M0 = 0: V0 = 0:
Para
x=L
ML = 0: VL = 0
Sustituyendo estos valores en Mx y Vx, se obtienen cuatro ecuaciones, el lado izquierdo de las
ecuaciones anteriores valen cero por las condiciones de frontera y el lado derecho contendrán dos
incógnitas que son
Las dos ecuaciones simultáneas con las dos incógnitas, pueden ser determinadas sustituyendo éstas,
en turno, en las expresiones generales.
Las características de este método, es la simple interpretación física de las constantes de integración y
la forma sistemática en la cual estas constantes aparecen en las ecuaciones. Este método es práctico
siempre que no tengan cargas complicadas.
146
Capítulo 5
5.3.1
Interacción del suelo con la estructura
Clasificación de las vigas de acuerdo a su rigidez.
La cantidad
λ L es una característica de la rigidez de las vigas con respecto a la cimentación
elástica del suelo, este término define la configuración de deformación de la curva elástica y determina
el valor de la relación para la cual la carga atenúa la forma de la curva amortiguándola a lo largo de la
viga.
De acuerdo a lo anterior, λ
L origina una clasificación práctica de las vigas, que es la siguiente:
Vigas cortas
π
λL<
4
Vigas de longitud media.
π
4
< λ L <π
Vigas largas
λ L >π
En el primer grupo, para problemas prácticos de vigas sobre medios elásticos, se puede despreciar la
deformación por flexión de la viga, puesto que los desplazamientos son pequeños comparados con los
desplazamientos producidos al deformarse el suelo. En este tipo de problemas se puede suponer que
la viga tiene un comportamiento como cuerpo rígido.
En el segundo grupo, el problema es diferente y es necesario el cálculo de la deformación con
precisión de la viga. Si una fuerza actúa en un extremo de la viga el efecto se propaga hasta el otro
extremo y no se puede despreciar. Por lo tanto, en estos casos se debe aplicar la teoría expuesta.
5.4
Método de diferencias finitas.
La técnica de las diferencias finitas, consiste en expresar las derivadas de una función contínua por
expresiones en función de intervalos discretos. El medio continuo se divide en intervalos o mallas
cuyos vértices se denominan puntos pivotes, estos intervalos pueden ser iguales o diferentes.
Interacción del suelo con la estructura
Capítulo 5
147
y
y
n+1
-y
n
y
n+1
y
n
y
1
1
y
y
2
3
2
y
y
n
n+1
n
3
x=h
n+1
h
x
Figura 5.6
Función continua discretizada
La derivada de una función, se expresa como:
Lim
Lim y ( x + ∆x ) − y ( x )
dy
∆y
=
=
dx ∆x → 0 ∆ x ∆x →0
∆x
y la segunda derivada:
∆
=
dx 2 ∆x → 0 ∆ x
d2 y
Lim
Lim
 ∆y 

 =
 ∆x  ∆x →0
y ( x + ∆x ) − y ( x )
∆x
Cuando ∆ x
no tiende a cero, pero tiene un valor finito
representadas por diferencias finitas:
yn + 1 − yn yn − yn − 1
∆ y

 =
ó
h
h
 ∆ x n
−
∆x
y ( x ) − y ( x − ∆x )
∆x
h, las derivadas en un punto x = xn son
148
Interacción del suelo con la estructura
Capítulo 5
∆ y

 ∆x 2

2

=


y n +1 − y n
h
−
y n − y n −1
h
h
y n + 1 − 2 y n + y n −1
=
h2
Se puede demostrar que:
h  ∆2 y 
h 2  ∆3 y 
 dy 
 ∆y 
+L
  = y' (x n ) =   +  2  −
6  ∆ x 3 
 dx  n
 ∆x  n 2  ∆ x  n
n
O bien aproximadamente se puede expresar la derivada como:
yn + 1 − yn
 dy   ∆y 
 =
 =
h
 dx   ∆x  n
5.35
En la misma forma se expresa a la segunda derivada o derivadas superiores.
Observando el numerador de la expresión de diferencias finitas, se tienen tres posibilidades de
expresar esa diferencia, que da lugar a la siguiente clasificación:
a)
b)
c)
Diferencias finitas hacia atrás
Diferencias finitas centrales
Diferencias finitas hacia delante
Con fines ilustrativos, las diferencias finitas se expresan por medio de dibujos que se denominan
moléculas de cálculo.
DIFERENCIA FINITA HACIA ATRAS
yn − yn − 1 1
 dy 
=
{
  =
h
h
 dx  n
41
}
1
4
DIFERENCIA FINITA CENTRAL
yn + yn − 1
1
 dy 
=
{1
  =
2h
2h
 dx  n
0
1
DIFERENCIA FINITA HACIA ADELANTE
yn + 1 − yn
1
 dy 
=
{ -1
  =
h
h
 dx  n
1
}
}
Capítulo 5 Interacción del suelo con la estructura 149
De la misma manera se expresan las otras derivadas superiores, así la segunda derivada queda,
siguiendo el mismo orden que la anterior:
 d2 y 
y
− 2y n − 1 + y n − 2
1

 = n +1
= 2
2
 dx 2 
h
h

n
 d2 y 
y
− 2y n + y n − 1
1

 = n +1
= 2 { 1
2
 dx 2 
h
h

n
{
-2
1
-2
1
1
}
}
Por no ser el objetivo del tema, estudiar los métodos numéricos en forma exhaustiva, no se trata los
errores y mejoramiento en la aproximación del método.
Se tienen muchos problemas en la Ingeniería que pueden representarse por ecuaciones diferenciales
ordinarias y parciales al aplicar la técnica de diferencias finitas, éstas se reducen a un sistema de
ecuaciones algebraicas. Un problema interesante que se tiene en el método, es la aplicación de las
moléculas en la frontera.
A continuación se presenta un resumen de varias diferencias finitas en forma de moléculas de cálculo.
i, j+1
i-1, j
i+1, j
i, j
i, j-1
Molécula de cálculo del nodo N.
∂w
1
=
∂ x 2h
1
0
1
(ij)
∂2 w
∂ x2
=
1
1
-2
h2
(i,j)
1
150
∂3 w
∂x
Interacción del suelo con la estructura
Capítulo 5
3
=
1
h
3
2
-1
0
1
-2
(i,j)
∂4 w
∂ x4
=
1
1
h4
1
-4
6
-4
(i,j)
∂w
1
=
∂ y 2h
1
∂ w
0
∂Y 2
2
=
1
h2
1
∂ w
-2
∂ Y3
3
1
=
1
h3
-2
∂4 w
0
∂ Y4
1
1
=
-4
h4
6
1
1
2
4
-1
∂3 w
1
=
∂ x ∂ y 2 h3
-1
0
1
2
0
-2
1
0
-1
∂3 w
1
= 3
∂ x ∂y 2h
1
1
-2
1
0
0
0
-1
2
1
(5.26)
1
-1
∂ 2w
1
= 2
∂ x ∂ y 4h
0
1
∇
4
0
0
0
1
0
-1
w=
2
-8
2
-8
20
-8
2
-8
2
1
h4
1
1
1
5.4.1
Integración numérica de funciones continuas de carga.
Las presiones del suelo sobre la estructura de cimentación se pueden representar como funciones
lineales o no lineales. Estas presiones se pueden concentrar como cargas puntuales en puntos
discretos por medio de métodos de integración numérica.
Se presentan tres formas para concentrar las reacciones de la cimentación en los puntos pivotes,
éstos son:
a)
b)
c)
Concentración por medio de rectángulos.
Concentración lineal.
Concentración parabólica de segundo grado.
Capítulo 5 Interacción del suelo con la estructura 151
En este caso, la reacción de la cimentación se considera constante, K y, y su efecto se
trasmite en una longitud h que es simétrica al punto pivote considerado. Por lo tanto todo punto
particular n posee una reacción concentrada Rn = K yn h, como se ilustra en la figura 5.7
a)
h
0
R0 =
k y0 h
ky
1
ky
0
2
ky
1
n
ky
2
n
2
R
0
R
R
Figura 5.7
b)
R
n
2
Concentración por medio de rectángulos.
Las reacciones concentradas en los puntos pivotes, se obtienen considerando a los segmentos
de viga entre éstos puntos como vigas simplemente apoyadas, procediendo así a calcular las
reacciones en cada punto como consecuencia de las presiones trapezoidales de la
cimentación, ver figuras 5.8 y 5.9
0
ky
1
1
ky
ky
0
R
2
ky
11
n
ky
2
n
0
R
R
1
R
2
Figura 5.8
Concentración lineal
n
152
Capítulo 5
Interacción del suelo con la estructura
Ro, .....Rn, para lo
Según la figura 5.8, el problema consiste en determinar el valor correspondiente a
cual se hace la siguiente consideración, ver figura 5.9
y
p1 (0, b)
p (h, c)
a
b
c
0
1
2
2
p (-h, a)
0
h
h
R
R
x
R
ba
R
a
Figura 5.9
bc
b
R
c
Cargas trapezoidal.
De aquí se deduce que:
a = K yo ,
b = K y1 ,
c = K y2
Por otro lado,
Ra = Ra b + Rb c
Luego:
(5.36)
h (b − a) h
h
2
3
∑ M(1) = 0 = Ra h − a h 2 −
∴Ra =
Ra =
ah b − a
+
h
2
b
h
(2a + b )
6
(5.37)
Capítulo 5
Interacción del suelo con la estructura
153
Análogamente
h
(2c + b)
6
Rc =
(5.38)
Ahora:
h (b − a) 2 h
h
2
3
∑ M 0 = 0 = Rba h − ah 2 −
∴R ba =
a h (b − a )
+
h
2
3
h
R ba = (a + 2 b )
6
(5.39)
Análogamente:
Rbc =
h
(c + 2 b )
6
(5.40)
Sumando (5.39) y (5.40) se obtiene Rb
Rb =
h
(a + 4b + c )
6
O sea que para este problema, se tiene:
Para puntos extremos.
R0 =
hk
( 2 y 0 + y1 )
6
(5.41)
Para puntos centrales
R1 =
hk
( y 0 + 4 y1 + y 2 )
6
Generalizando:
Rn =
c)
(
hk
yn − 1 + 4 y n + yn + 1
6
)
(5.42)
Una parábola de segundo grado puede trazarse conociendo las ordenadas
separadas cada una por una distancia h, véase figura 5.10
0
ky
1
ky
0
R
2
ky
1
ky0, ky1 y ky2
n
ky
2
n
0
R
Parábola de 2° grado
R
1
Figura 5.10
R
2
Concentración parabólica.
n
154 Capítulo 5 Interacción del suelo con la estructura
En la figura 5.10; el problema consiste en determinar los valores correspondientes a Ro,......, Rn, para
lo cual se hace la consideración siguiente, ver figura 5.11.
Calculando los coeficientes A, B y C correspondientes a la ecuación cuadrática
empleando los puntos P1 (-h, a), P (o, b) y P2 (h, c)
2
Y = Ax + Bx + C
Se tiene:
Para el punto (-h,
a):
2
a = Ah – Bh + C
( 5.42)
Ahora para el punto (o,
b);
b=C
(5.43)
y para el punto (h, c):
2
c = Ah + BH + C
(5.44)
y
y = A x 2 + Bx + C
dA = Y dx
p1 (0, b)
p (h, c)
a
b
c
0
1
2
2
p (-h, a)
0
h
h
R
R
x
R
ba
R
a
Figura 5.11
bc
b
Carga parabólica
R
c
Capítulo 5 Interacción del suelo con la estructura 155
Sustituyendo la expresión (5.43) en las (5.42) y (5.44) y luego sumando las expresiones resultantes, se
tiene:
2
a = Ah – Bh + b
c = Ah2 + Bh + b
a + c = 2Ah2 + 2b
de donde,
a + c − 2b
2 h2
A =
Por otra parte, restando éstas mismas expresiones, resulta:
a − c = −2 Bh
Luego,
B =
c−a
2h
Efectuando M1
Rah =
∫
= 0,
−h
+ xdA =
0
∫
−h
0
x Yd x
∫
−h
x ( A x 2 + B x + C ) dx
0
−h
 A x 4 B x3
C x2 
R ah = 
+
+

3
2 0
 4
A h4 B h3
C h2
−
+
R ah =
4
3
2
Sustituyendo los valores de A, B y C, se tiene:
Rah =
a + c − 2b 4 a − c 3 b 2
h +
h + h
6h
2
8 h2
 a + c − 2b a − c b 
Ra = h 
+
+ 
8
6
2

Ra =
3a + 3c − 6b + 4a − 4c + 12 b
h
24
Luego entonces:
156
Capítulo 5
Interacción del suelo con la estructura
Ra =
h
(7a + 6 b − c )
24
y en forma semejante
Rc =
h
(7c + 6b − a)
24
Haciendo
Rb a h =
∑M
0
∫
0
=0
[h − (− x )] d A = ∫
−h
0
y (h + x ) dx =
−h
∫ (A x
0
2
−h
)
+ Bx + c (h + x ) dx
0
Rb a
 A x 4 B x 3 C x 2 A h x3

Bhx 2
+
+
+
+
+ Chx 
h=
3
2
3
2
 4
− h
 Ah4 Bh3
Ch2
Ah4
Bh3
Ch2 
= −
−
+
−
+
−

3
2
3
2
1 
 4
Ah4
Bh3
Ch2
Ah4 Bh3
Ch2
= −
+
−
+
−
+
4
3
2
3
2
1
Rb a = −
Rba =
Ah3
Bh2
Ch
a + c − 2 b h3
c − a h2 bh
+
−
= −
+
12
6
2
12
2h
6 2
2 h2
h
(3a + 10b − c )
24
R b = Rb a + Rb c =
Rb c =
h
(3 c + 10 b − a)
24
h
h
(2a + 20 b + 2c ) =
(a + 10 b + c )
24
12
O sea que para este caso se tiene:
Para puntos extremos
R0 = Ra =
hk
( 7 y 0 + 6 y1 − y 2 )
24
Para puntos centrales
(5.42)
Capítulo 5
Ri = R b =
Interacción del suelo con la estructura
hk
(2y 0 + 20 y 1 + 2y 2 )
24
157
(5.43)
Generalizando
Rm =
hk
(2 y n − 1 + 20 y n + 2 yn + 1 )
24
Ejemplo 5.2. La viga ilustrada en la figura 5.12, se encuentra sobre un suelo compresible con un
'
2
3
módulo de cimentación de 1.5 kg/cm , la viga es de concreto con un fc = 250 kg / cm
y
la
sección es de 50 x 90 cm, está cargada como se indica en la figura. Calcular los elementos
geométricos y mecánicos en cada uno de los puntos pivotes.
P =100 ton
P =75 ton
1
0
1
2
2
3
4
L
h
R
h
R
0
Figura 5.12
h
R
1
2
h
R
3
R
4
Viga sobre un medio elástico
Solución:
De acuerdo al criterio práctico expuesto para identificar el tipo de viga y cuando se debe aplicar la
teoría expuesta, se procede de la siguiente manera:
La constante elástica del suelo vale:
k = k s b = 1.5 (50) = 75 kg / cm 2
E = 14000 f 'c = 14000 250 = 221359 kg / cm 2
158
I=
Capítulo 5
Interacción del suelo con la estructura
50 x 90 3
= 3 037 500 cm 4
12
EI = 6.72379 x1011
criterio
x=4
k
75
=4
= 0.0032498
EI
6.72379 x 1011
λ L = 0.0032498 (600) = 1.95
π
⟨ λL ⟨ π
4
por lo tanto es aplicable la teoría expuesta.
Se divide la longitud de la viga en cuatro tramos iguales, como se muestra en la figura 5.12.
h = L / 4 = 1.5 m
m = 4 tramos
Se concentra la presión del suelo, en cargas puntuales usando integración parabólica, resultando:
Concentración parabólica:
R0 =
hk
( 7 y 0 + 6 y1 − y 2 )
24
R1 =
hk
(2y 0 + 20 y1 − 2y 2 )
24
R2 =
hk
(2y1 + 20 y 2 − 2y 3 )
24
R3 =
hk
(2y 2 + 20 y 3 − 2y 4 )
24
R4 =
hk
(7 y 4 + 6 y 3 − y 2 )
24
Se calculan las flechas en cada punto pivote.
(5.52)
Interacción del suelo con la estructura
Capítulo 5
159
Ecuación gobernadora:
M( x )
d2 y
=
EI
dx 2
Condiciones de frontera
M0 = M4 = 0
Molécula de cálculo de las diferencias finitas centrales.
 d2 y

1
M( x )

 =
{
}
=
y
−
2
y
+
y
n
−
1
n
n
+
1
2
 d x2

h

 EI( x )
Aplicación de la ecuación en cada punto pivote.
Punto Pivote
1
h3
y 0 − 2 y1 + y 2 = − R0
EI
Derecha
y1 − 2 y 2 + y 3 = − (2 R0 + R1 − P1 )
h3
EI
2
y1 − 2 y 2 + y 3 = − (2 R 4 + R3 − P2 )
h3
EI
3
y 2 − 2 y 3 + y 4 = − (R 4 )
2
Izquierda
(5.44)
h3
EI
∑ Fv = R0 + R1 + R 2 + R3 + R 4 − P1 − P2 = 0
Sustituyendo los valores R0, R1,
de ecuaciones (5.44), se tiene:
R2, R3, R4, en cada una de las ecuaciones que integran al sistema
y0 − 2 y1 + y2 = −
h4k
(7 y0 + 6 y1 − y2 )
24 EI
y1 − 2 y2 + y3 = −
h4k 
24 
14 y0 + 12 y1 − 2 y2 + 2 y0 + 20 y1 + 2 y2 − P1

24 EI 
k h 
160
Capítulo 5
Interacción del suelo con la estructura
y1 − 2 y 2 + y3 = −
h4k 
24 
14 y 4 + 12 y3 − 2 y 2 + 2 y 2 + 20 y3 + 2 y 4 − P2 
24 EI 
kh 
y 2 − 2 y3 + y 4 = −
h4k
(7 y 4 + 6 y 3 − y 2 )
24 EI
(9 y 0 + 28 y1 + 22 y 2 + 28 y3 + 9 y 4 )
kh
= P1 + P2
24
Cálculo de los factores:
h 4k
(150)4 (75)
=
= 0.0023528
24 EI 24 (6.72379 x 1011 )
P1
24 100 000 ( 24)
=
= 213.33
hk
(150) (75)
P2
24 75 000 ( 24)
=
= 160.00
hk
(150)(75)
(P1 + P2 )
24 175 000 ( 24)
=
= 373.33
hk
(150)(75)
Sustituyendo estos valores en las cinco ecuaciones anteriores se tiene:
y 0 − 2 y1 + y 2 = − 0.00235288 (7 y 0 + 6 y1 − y 2 )
y1 − 2 y 2 + y 3 = − 0.00235288(16 y 0 + 32 y1 − 213.33)
y1 − 2 y 2 + y 3 = − 0.00235288 (32 y 3 + 16 y 4 − 160.00)
y 2 − 2 y 3 + y 4 = − 0.00235288 (7 y 4 + 6 y 3 − y 2 )
g y 0 + 28 y1 + 22 y 2 + 28 y 3 + g y 4 = 373.33
Realizando operaciones se obtiene el siguiente sistema de ecuaciones:
432.01 y 0 − 844.02 y1 + 424.01 y 2 = 0
16 y 0 + 457.01 y1 − 850.02 y 2 + 425.01 y 3 = 213.33
425.01 y1 − 850.02 y 2 + 457.01 y 3 + 16 y 4 = 160.00
424.01 y 2 − 844.02 y 3 + 432.01 y 4 = 0
9 y 0 + 28 y1 + 22 y 2 + 28 y 3 + 9 y 4 = 373.33
Capítulo 5
0.00
0.00 
432.01 − 844.02 424.01
 16.00
457.01 − 850.02 425.01
0.00 

 0.00
425.01 − 850.02 457.01 16.00 


0.00
424.01 − 844.02 432.01
 0.00
 9.00
28.00
22.00
28.00
9.00 
Interacción del suelo con la estructura
y 0   0.00 
 y  213.333 
 1  

=
y
160
.
000
 2 

y   0.00 
 3 

y 4   373.33 
La solución del sistema es:
y0 = 4.625 cm
y1 = 4.331 cm
y2 = 3.908 cm
y3 = 3.488 cm
y4 = 2.978 cm
Cálculo de las reacciones en cada punto pivote.
Para los extremos.
Rn =
hk
(7yn + 6 yn + 1 − yn + 2 )
24
Para los puntos centrales.
Rn =
hk
(2 yn − 1 + 20 yn + 2yn + 1 )
24
Factor:
hk
150 (75)
=
= 468.75
24
24
R0 = 468.75 [7 x 4.625 + 6 x 4.331 − 3.908] = 25 524.8 kg
R1 = 468.75 [2 x 4.625 + 20 x 4.331 + 2 x 3.908] = 48 602.8 kg
R2 = 468.75 [2 x 4.331 + 20 x 3.908 + 2 x 3.488] = 43 967.8 kg
R3 = 468.75 [2 x 3.908 + 20 x 3.488 + 2 x 2.978] = 39 155.6 kg
R 4 = 468.75 [7 x 2.978 + 6 x 3.488 − 3.908] = 17 749.7 kg
Observe que la suma de las cinco reacciones es la suma de las cargas.
161
162 Capítulo 5 Interacción del suelo con la estructura
Cálculo de los momentos flexionantes.
M1 = − R0 h = − 1.5 x 25 524 = − 38 286 kg − m
M2 = − 2 R0 h − R1 h + P1 x h = 523.8 kg − m
M3 = − R 4 x h = − 26 624.5 kg − m
Cálculo de las fuerzas cortantes.
V0 = R0 = + 25.524 kg
V1 = R0 + R1 − P1 = − 25 872.4 kg
V2 = R0 + R1 + R2 − P1 = 18 095.4 kg
V3 = R0 + R1 + R2 + R3 − P1 − P2 = − 17 749 kg
Cálculo de los giros en el punto discreto.
 dy 
1

 =
{− yn − 1 + yn + 1} = θ ( x )
2h
 d x n
0
1
(− y − 1 + y1) = θ0
2h
1
1
(− y 0 + y 2 ) = θ1
2h
2
1
(− y1 + y 3 ) = θ2
2h
3
1
(− y 2 + y 4 ) = θ3
2h
4
1
(− y 3 + y5 ) = θ4
2h
Pero, por condiciones de frontera se tiene.
Capítulo 5
Interacción del suelo con la estructura
163
− y3 = y5
− y −1 = y 1
Luego entonces, el sistema de ecuaciones anterior se transforma en:
y1
= θ0
h
y2 − y0
= θ1
2h
y 3 − y1
= θ2
2h
y 4 − y 2 = θ3
− y3
= θ4
h
De donde, finalmente se obtienen los giros en los puntos pivotes.
θ0 = + 0.0288 rads
θ1 = − 0.00478 rads
θ2 = − 0.00562 rads
θ3 = − 0.00620 rads
θ4 = − 0.0232 rads
5.5 PLACAS SOBRE SUELOS ELÁSTICOS
El problema de placas sobre medios elásticos se presentan en pavimentos de concreto reforzado de
carreteras y pistas de aterrizaje de aeropuertos y en losas de cimentación de edificios.
El problema es complejo pero considerando un modelo en donde la placa se encuentre en un suelo
idealizado como un medio elástico lineal, homogéneo e isótropo, se puede usar la teoría de Winkler.
Por lo tanto la reacción de la cimentación se puede expresar como:
p 'z (x, y ) = k s w
(5.45)
164 Capítulo 5 Interacción del suelo con la estructura
La hipótesis de considerar el suelo como una masa de material elástico lineal e isótropo es solamente
una aproximación a la condición real, una mejor aproximación se obtiene considerando al suelo con un
comportamiento elástico plástico.
En este estudio de considera a la placa, también hecha de un material elástico lineal, homogéneo e
isótropo y es el caso de placas delgadas con pequeños desplazamientos, es decir que en este tipo de
placas los desplazamientos son pequeños en comparación con el espesor de la placa. En la teoría de
flexión de placas sujetas a cargas transversales, se suponen las siguientes hipótesis:
a) No existen deformaciones en la superficie media de la placa.
b) Los puntos de las placas que se encuentran inicialmente sobre un plano normal a la superficie
media, permanece en ese plano después de que se ha flexionado.
c) Los esfuerzos normales en la dirección transversal a la placa pueden ser despreciados.
5.5.1 Ecuación diferencial gobernadora de placas delgadas con pequeños desplazamientos
sobre medios elásticos.
1.
Se selecciona un sistema de coordenadas y una convención de signos, ver figura 5.13.
En la presente deducción se consideran a los elementos mecánicos, como fuerzas y
momentos por unidad de longitud, llamándolas m x , m y , m x y , qx y qz , multiplicados por
dx y dy de acuerdo a la dirección que se considere.
2.
A continuación se analiza el equilibrio del elemento diferencial de placa.
Suponiendo que la placa la sometemos exclusivamente a fuerzas transversales. Se toman de las seis
ecuaciones de equilibrio las siguientes:
∑M
x
∑M
= 0,
y
= 0
y
∑P
z
0
y
w z
dy
h
2
Qx
h
Pz
Mx
2
My +
= 0
∂ My
∂ y
M yx +
QY
M xy
M yx
dy
∂ M yx
∂ y
x
Superficie media
dy
QY +
∂ QY
∂ Y
dY
M xy +
∂ M xy
∂ x
dx
Qx +
Figura 5.13
dx
My
Mx +
∂ Qx
∂ x
∂ Mx
∂ x
dx
dx
Representación gráfica de las fuerzas externas e internas sobre el elemento de
placa.
En base a la figura 5.13, se obtiene:
∑M
y
Capítulo 5
Interacción del suelo con la estructura
165
= 0
∂qx
 dx 


 dx 
− qx dy   − mx dy −  qx +
dx  dy   +
∂x
 2 


 2 
∂ m yx




∂m x
+  m x +
dx  dy − m y x dx +  m y x +
dy  dx = 0
∂x
∂y




Haciendo las reducciones convenientes se llega a la siguiente expresión:
∂ mx
∂ m yx
+
= qx
∂x
∂y
(5.46)
Haciendo
∑ Mx = 0
∂ qy


 dy 
 dy 
− qy dx   − m y dx −  qy +
dy  dx   +
∂y
 2 
 2 


∂m




∂m
xy
+  m y +
dy  dx − m x y dy +  m x y +
dx  dy = 0


∂y
∂x




Reduciendo términos obtenemos:
∂ my
∂y
+
∂ m xy
∂x
= qy
(5.47)
Efectuando ahora la suma de fuerza vertical en la dirección z, se tiene la tercera ecuación de equilibrio.
∑ Pz = 0 − Pz' dx
∂ qy




∂ qx
dy − qx dy +  qx +
dx  dy − qy d x +  qy +
dy  dx = 0
∂x
∂y




Que al reducir se llega a la expresión siguiente:
∂ qy
∂ qx
+
= − Pz + Pz'
∂x
∂y
Sustituyendo las ecuaciones (5.46) y (5.47) en la ecuación (5.48) y considerando que
obtiene:
∂
(qx ) + ∂ qy = − Pz + Pz'
∂x
∂y
( )
(5,48)
m x y = m y x se
166
Interacción del suelo con la estructura
Capítulo 5
∂ myx 
∂ mxy 
 ∂ mx
∂  ∂m y

 +

 = − Pz (x, y ) + Pz' (x, y )
+
+
∂y  ∂ y  ∂y
∂x 
 ∂x
∂ 2 m xy
∂ 2 my
∂ 2 mx
+2
+
= − Pz (x, y ) + Pz' (x, y )
2
2
∂ x ∂y
∂x
∂y
∂
∂x
(5.49)
Los momentos flexionantes y torsionantes en la ecuación (5.49) dependen de las deformaciones,
además las deformaciones están en función directa de las componentes de desplazamiento (u,v,w).
3.
Obtención de la relación que existe entre los esfuerzos las deformaciones y los
desplazamientos.
3.a.
Primeramente se recuerda la relación que existe entre los esfuerzos y las deformaciones
longitudinales.
Para la deformación lineal en la dirección x se tiene la siguiente expresión:
εx =
σy
σx
σz
−µ
−µ
E
E
E
εx =
1
σx − µ σ y + σ
E
[
(
z
)]
Para el eje y
εy =
σy
σx
σz
−µ
−µ
E
E
E
εy =
1
σ y − µ(σ x + σ
E
[
Para el eje
z
)]
z
εz =
σz
σx
σy
−µ
−µ
E
E
E
εz =
1
σ z− µ σ x− σ
E
[
(
y
)]
Para el caso bidimensional (plano x,y ), estas relaciones se transforman en:
εx =
(
1
σ x− µ σ
E
y
)
Capítulo 5
εy =
(
1
σ y− µ σ
E
x
Interacción del suelo con la estructura
167
)
De las ecuaciones anteriores se obtiene:
σ x = Eε x + µ σ y
(5.50)
σ y = Eε y + µ σ x
(5.51)
Sustituyendo la ecuación (5.51) en (5.50) queda:
σ x = E εx + µ E εy + µ σx
(
)
σ x = E ε x + µ E ε y + µ 2σ
x
σ x − µ 2 σ x = Eε x + µ Eε y
(
σ x1− µ
σ x=
2
E
1− µ
) = E (ε
2
x+
µε
y
)
(ε x + µ ε y )
(5.52)
En forma semejante, si se sustituye la ecuación (5.50) en la ecuación (5.51) queda:
σ y=
E
1− µ
2
(ε y + µ ε x )
(5.53)
Las ecuaciones (5.52) y (5.53) dan una relación entre los esfuerzos y las deformaciones
longitudinales.
3.b.
Ahora se determina la relación que existe entre las deformaciones lineales y los
desplazamientos verticales.
Se sabe que los momentos torsionantes
m x y y m y x ocasionan esfuerzos cortantes τ
xy
y τ
yx
los cuales a la vez producen deformaciones angulares. Utilizando la Ley de Hooke se establece una
relación entre estos esfuerzos cortantes y las deformaciones que se generan, de la siguiente manera:
τ
xy=
Gγ
xy=
E
λ
2 (1 + µ )
recordando que:
E = 2 G (1 + µ )
Donde:
x y=
τ
yx
(5.54)
168
Capítulo 5
Interacción del suelo con la estructura
G = Módulo de elasticidad cortante:
Considerando la geometría deformada de la placa con el fin de expresar a los giros en función de los
desplazamientos, se hará lo siguiente, se toma una sección de la placa a una distancia “y” constante,
como se muestra en la figura 5.14.
Comparando la sección antes y después de deformarse y empleando las hipótesis que establecen:
a) Las pendientes de la superficie media deformada son pequeñas.
b) Las deformaciones son tales que las líneas rectas, inicialmente normales a la superficie media,
permanecen rectas y normales a la superficie media. Se puede expresar el ángulo de giro de las
líneas I-I y I I – I I por las relaciones:
θ = −
∂w
∂x
∂θ
dx
∂x
θ' = θ +
(5.55)
Después de deformarse el elemento, la longitud AB correspondiente a una fibra, que se localiza a una
distancia z de la superficie media, adquiere la longitud A’ B’.
ε
Considerando que la deformación lineal
provocada por un esfuerzo normal
cambio en la unidad de longitud del elemento luego entonces:
I
x
0
dx
σ , se define como un
II
x, u
h
A'
B'
I
II
Z
II
w
I
y= Constante
z
θ
z, w
Figura 5.14
ε x=
∆ dx A ' B' − AB
=
dx
AB
A'
θ
B'
θ '= θ +
∂θ
∂ x
dx
Sección antes y después de la deformación.
Capítulo 5
Interacción del suelo con la estructura
169
∂θ


dx  − dx
 dx + z
∂x 
ε x= 
dx
ε x= z
∂θ
∂x
(5.56)
Sustituyendo la primera de las ecuaciones (5.55) en (5.56), nos queda:
∂  ∂w 
∂ 2w
ε x= z −
 = −z
∂x  ∂x 
∂x 2
(5.57)
De manera semejante se deduce la deformación lineal en función de los desplazamientos verticales:
ε y = −z
3.c.
∂ 2w
∂ y2
(5.58)
Por último, se determina la relación que existe entre la distorsión angular (deformación
angular) y las componentes del desplazamiento u, v, w.
De la figura 5.14, se cumple que la componente de desplazamiento lineal en la dirección x es:
u = zθ = − z
∂w
∂x
(5.59)
En forma semejante, la componente en la dirección y es:
v = zθ = −
∂w
∂x
(5.60)
Recordando la expresión de la deformación angular y sustituyendo las expresiones (5.59) y (5.60) se
tiene:
∂ v ∂u
∂ 
∂w ∂ 
∂z
 − z
 +
 − z

+
=
∂x ∂y ∂x
∂y  ∂y
∂ x 
γ
xy =
γ
xy = − z
∂ 2w
∂ 2w
∂ 2w
−z
= −2 z
∂ x∂ y
∂ x∂ y
∂ x∂ y
(5.61)
En conclusión, la configuración deformada de la superficie media queda definida por las relaciones:
ε x= −
z ∂ 2w
∂x 2
170
Capítulo 5
ε y= −
γ
4.
Interacción del suelo con la estructura
z ∂2w
∂y 2
xy = −2
z ∂2w
∂ x∂ y
Fuerzas interiores expresadas en función de w.
Las componentes de esfuerzo σx y σy producen momentos flexionantes en un elemento de placa de
una manera semejante a la forma presentada en la teoría elemental de vigas. Por lo tanto, efectuando
la integración de las componentes de esfuerzo normal, obtenemos los momentos flexionantes que
actúan en el interior de la placa. De acuerdo con esto, se llega a:
h
2
h
2
mx = ∫σ x z d z
my = ∫σ y z d z
y
h
−
2
(5.62)
h
−
2
0
y
w
h
dy
2
z
P z dxdy
h
2
dx
σ
x
y
τ yx
τ xy
τ yz
σ
x
τ xz
Figura 5.15 Esfuerzos que actúan en un elemento diferencial de placa.
En forma semejante, los momentos torsionantes producidos por los esfuerzos cortantes
se pueden calcular por las relaciones siguientes:
τ
xy =
τ
yx
Capítulo 5
h
2
h
−
2
m xy = ∫
τ x yz d z
m xy =
y
h
2
h
−
2
∫
τ yx z d z
Interacción del suelo con la estructura
171
(5.62)
Sustituyendo las ecuaciones (5.57) y (5.58) en las ecuaciones (5.52) y (5.53). Los esfuerzos
normales σ x y σ y quedan representados en función del desplazamiento transversal de la
placa.
∂ 2w
∂2w
−
µ
z
)
∂x 2
∂ y2
σx =
E
1− µ
σ x=
− E z ∂2w
∂ 2w
(
µ
)
+
1− µ 2 ∂ x2
∂y 2
2
(−z
(5.64)
En forma semejante, se obtiene:
σy = −
Ez
∂ 2w
∂ 2w
(
+
µ
)
1− µ 2 ∂ y 2
∂x 2
(5.65)
Sustituyendo el valor de estas expresiones en la (5.62) y efectuando las integrales, se llega a:
m x= −
2E
1− µ
h
2
2 0
∫
(z
∂ 2w
∂ 2w
+
µ
z
)zdz
∂x 2
∂y 2
h
2E
m x. = −
1− µ
mx = −
2
∂ 2w z 3  2
2E
.
 −
2
3∂ x
0 1 − µ
h
2
∂ 2w µ z  2
.

3 ∂ y 2 0
Eh 3
∂ 2w
∂ 2w
(
+
µ
)
12 (1 − µ 2 ) ∂ y 2
∂y 2
Haciendo
Eh
igual a D, se puede expresar la ecuación anterior en la forma siguiente.
12 (1 − µ 2 )
m x = −D (
∂ 2w
∂ 2w
+
µ
)
∂x 2
∂y 2
(5.66)
En forma semejante:
m y = −D (
∂ 2w
∂ 2w
+
µ
)
∂y 2
∂x 2
(5.67)
172
Capítulo 5
A la relación
Interacción del suelo con la estructura
Eh 3
se le conoce como rigidez a la flexión de la placa.
12 ( 1 − µ 2 )
Los momentos torsionantes
m xy y m yx se obtienen integrando las ecuaciones (5.64), pero antes
se sustituyen los valores correspondientes a
τ xy
y
τ
yx
en dichas ecuaciones.
h
m xy = 2 ∫ 2 t xy z d z
0
h
2
0
m xy = 2 ∫
h
2
0
m xy = 2 ∫
E
2 (1 + µ )
γ xy z d z
E
∂2w
(− 2 z
)zdz
2 (1 + µ )
∂x∂y
h
2E
∂ w z 2
m xy = −
.
.
( 1 + µ ) ∂ x ∂ y 3  0
2
m xy = −
3
E h 3 (1 − µ ) ∂ 2w
.
12 ( 1 − µ 2 ) ∂ x ∂ y
Eh 3
y como
=D
12 ( 1 − µ 2 )
Entonces:
m xy = m yx = − ( 1 − µ ) D
∂ 2w
∂x∂y
(5.68)
Sustituyendo las ecuaciones (5.66 ), (5.67) y (5.68 ) en la ecuación (5.49) resulta:
∂2
∂x 2

∂ 2w
∂ 2w 
∂2
−
D
(
+
µ
)
+
2


∂x∂y
∂x 2
∂y 2 


∂ 2w 
−
(
1
−
µ
)
D


∂ x ∂ y

Interacción del suelo con la estructura
Capítulo 5
+
∂2
∂y 2
−D
173

∂ 2w
∂ 2w 
−
D
(
+
µ
) = P z ( x, y ) − Pz' ( x, y )

2
2 
∂y
∂x 

∂ 4w
∂ 4w
−
2
D
∂x 4
∂x 2 ∂y
∂ 4w
2 ∂ 4w
+
∂x 4 ∂x 2 ∂y
2
∂ 4w
∂ 4w
+
2
∂y 4
∂ x 2∂ y
+
2
2
−D
∂ 4w
= Pz ( x, y ) − Pz' ( x, y )
4
∂y
Pz ( x, y )
∂ 4w
' ( x, y )
=
−
+
P
z
D
D
∂y 4
+
[
(5.69)
]
∂ 4w 1
= Pz ( x, y ) − Pz' ( x, y )
4
D
∂y
En esta ecuación, es la ecuación gobernadora del problema de placas delgadas con pequeños
desplazamientos sobre medios elásticos.
También se puede expresar:
∇4w =
1
( Pz − kq )
D
D ∇ 4 w + kq = Pz
5.6 Método del elemento finito.
Con el surgimiento de las computadoras y la ayuda del álgebra matricial, el análisis matricial estructural
se ha desarrollado considerablemente. Por ejemplo el método del elemento finito es una técnica de
análisis matricial utilizada para resolver problemas continuos como es el caso de una cimentación.
En un modelo de elemento finito, el medio continuo es reemplazado por una malla de piezas discretas
llamadas elementos finitos.
P
P
P2
1
2
1
P3
3
P4
4
P5
5
cim e ntaciòn
K
(a)
Figura 5.16 a) Estructura continua
K
K
K
K
(b)
b) modelo a base de elementos finitos.
174 Capítulo 5 Interacción del suelo con la estructura
En la formulación matemática, la interconexión de los elementos se logra mediante un número finito de
puntos llamados nodos, como una parte de la modulación se necesita convertir las cargas aplicadas y
el peso propio en un conjunto de cargas aplicadas en los nodos denominándolas fuerzas equivalentes
nodales.
El método del elemento finito tiene ciertas ventajas con respecto a otros métodos planteados
anteriormente, como los métodos analíticos y el método de las diferencias finitas, entre otras se
mencionan las siguientes:
a)
Las condiciones de frontera se manejan en una forma mas simple.
b)
Se puede aplicar cualquier combinación de carga sin complicar el problema.
c)
Las propiedades de la cimentación pueden variar a lo largo de ésta.
d)
El módulo de cimentación puede variar a lo largo de la cimentación.
e)
Se puede escribir un programa de computadora con relativa facilidad.
5.6.1 Planteamiento general del método.
En cualquier nodo, unión de dos o mas elementos, de la estructura se puede escribir:
P i = A i Fi
esta ecuación establece que la fuerzas nodales externas P i son iguales a las fuerzas internas F i
usando la constante de proporcionalidad A. Donde P y F pueden ser fuerzas o momentos.
Considerando un conjunto de nodos e introduciendo la notación matricial, eliminando los subíndices y
omitiendo los paréntesis comúnmente usados, resulta ser:
P=AF
(5.70)
También relacionando las deformaciones internas de los miembros estructurales en el nodo con los
desplazamientos nodales externos y considerando el mismo conjunto de nodos, se tiene:
E=Bx
Donde ambos e y x pueden ser rotaciones o traslaciones. Por el principio de contra se tiene que la
t
matriz B es igual a la traspuesta de la matriz A→B = A ; así
e = At x
(5.71)
Las fuerzas internas F están relacionadas a los desplazamientos internos del miembro e como:
F=Se
(5.72)
Las ecuaciones (5.70), (5.721 y (5.72) son las ecuaciones fundamentales del elemento finito.
Sustituyendo las ecuaciones (5.71) en la (5.72), se tiene:
Interacción del suelo con la estructura
Capítulo 5
t
F=SA x
175
(5.73)
Sustituyendo las ecuaciones (5.73) en la (5.70)
t
P=ASA x
t
Si se designa k= A S A matriz de rigideces de la cimentación.
P=kx
A la expresión anterior se le llama ecuación fuerza desplazamiento.
En esta ecuación las únicas incógnitas son las x; que solucionando el sistema se tiene:
-1
X=k P
k-1 = ( A S At )-1
Conocidas las x, se pueden sustituir en la ecuación 4 para obtener las fuerzas internas F de cada
elemento, las cuales son necesarias para el diseño.
Ejemplo 5.2. Determinar la matriz de rigideces para la siguiente viga sobre un medio elástico.
1
2
h
h
3
4
h
Idealización.
K1
K2
K3
K4
P5 ,X5
P6 ,X6
P7 ,X7
P8 ,X8
P1 ,X1
P2 ,X2
F2 ,e2
F1 ,e 1
F7 ,e 7
P3 ,X3
F4 ,e 4
F3 ,e 3
F8 , e8
P4 ,X4
Cargas
externas
y
desplaza
mientos.
F6 ,e 6
Fuerzas
internasdeformaciones
.
F5 ,e5
F9 ,e 9
F10,e10
Figura 5.17 Viga sobre un medio elástico
176
Interacción del suelo con la estructura
Capítulo 5
P
P5
P
6
P1
P2
F
1
F
F3
F
3
F2
8
P3
F2
1
P
7
P4
F
F4
F1 + F
2
F+F
h
h
1
F+F
2
3
h
F
F7
4
8
F
F5
5
F4
6
F6
F+F
3
F+F
4
5
h
6
F+F
h
F
9
Figura 5.18 Diagrama de cuerpo libre para los nodos
Por equilibrio ΣFy=0.
Nodo 1
p5 −
F1 + F2
− F7 = 0
h
p5 =
F1 F2
+
+ F7
h h
Nodo 2
p6 +
F1 + F2 F3 + F4
−
− F8 = 0
h
h
p6 = −
F1 F2 F3 F4
−
+ +
+ F8
h h
h
h
Nodo 3
p7 +
F3 + F4 F5 + F6
−
− F9 = 0
h
h
p7 = −
Nodo 4
F3 F4 F5 F6
−
+
+
+ F9
h h
h
h
5
6
h
F
10
Capítulo 5
p8 +
Interacción del suelo con la estructura
F5 + F6
− F10 = 0
h
p8 = −
F5 F6
−
+ F10
h h
M=0
Nodo 5
1
− P1 + F1 = 0
∴ P1 = F1
2
− P2 + F2 + F3 = 0
∴ P2 = F2 + F3
3
− P3 + F4 + F5 = 0
∴ P3 = F4 + F5
4
− P4 + F6 = 0
∴ P4 = F6
Arreglando las ecuaciones en forma matricial.

0
0
0
0
0
1

0
1
1
0
0
0
 p1  
p  
0
0
1
1
0
 2  0
 p3  
  0
0
0
0
0
1
 p4  = 
 p5   1
1
0
0
0
0
  h
 p6   1 h 1 1
1
 p  −
0
0
−
7
h h
h
   h
1
1 1
 p8  0
0
−
−
0

h
h h

1
1
0
0
−
−
0
0
h
h

En forma reducida
P=AF
Orden de la matriz A
P →2N+2=8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1




















 F1 
F 
 2
 F3 
 
 F4 
 F5 
 
 F6 
F 
 7
 F8 
F 
 9
F10 
177
178
Capítulo 5
Interacción del suelo con la estructura
F → 3 N + 1 = 10 A 8 × 10
Matriz B
e1 = x 1 +
x5 x6
−
h
h
e2 = x 2 +
x5 x6
−
h
h
e3 = x 2 +
x6 x7
−
h
h
e4 = x3 +
x6 x7
−
h
h
e5 = x 3 +
x 7 x8
−
h
h
e6 = x 4 +
x7 x8
−
h
h
e7 = x5
e8 = x 6
e9 = x 7
e10 = x 8
En forma matricial se tiene
Capítulo 5

1

0

 e1  
 e  0
 2 
 e 3  0
  
 e4  
 e 5  0
 =
 e 6  0
e  
 7 
 e8   0
e  
 9  0
e10  
0


0
1
h
1
h
1
h
1
−
h
1
h
1
h
−
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
h
1
−
h
1
h
1
h
−



0 

0 

0 

1
−
h
1
− 
h
0 


0 

0 


1 

0
En forma reducida el sistema anterior se escribe:
e=Bx
t
Se puede observar que B es una matriz de 10x8 y B = A .
Es decir
aij = bij
Relación deformación – fuerzas internas.
Aplicando el principio de la viga conjugada se tiene:
e1 =
F1h F2h
−
3EI 6EI
e2 =
F1h F2h
−
6EI 3EI
Solucionando el sistema de ecuaciones.
Interacción del suelo con la estructura
 x1 
x 
 2
 x3 
 
x4 
 x5 
 
x6 
x 
 7
 x 8 
179
180
Capítulo 5
Interacción del suelo con la estructura
F
1
e
2
e
1
F
2
F1 h
F1 h
3EI
6EI
F2 h
F2 h
6EI
3EI
h
Figura 5.19 Elemento finito barra.
F1 =
4EI
2EI
e1 +
e2
h
h
F2 =
2EI
4EI
e1 +
e2
h
h
En forma similar para las otras barras.
F3 =
4EI
2EI
e3 +
e4
h
h
F4 =
2EI
4EI
e3 +
e4
h
h
Capítulo 5
F5 =
Interacción del suelo con la estructura
181
4E I
2E I
e5 +
e6
h
h
F
3
e
4
e
3
F
4
F
5
e
6
e
5
F
6
h
Figura 5.20 Elemento finito barra.
F6 =
2E I
4EI
e5 +
e6
h
h
Para los resortes la relación deformación – fuerza interna esta dada por:
F7 = k 1 e 7
F8 = k 2 e 8
F9 = k 3 e 9
F10 = k 4 e10
Arreglando las ecuaciones anteriores en forma matricial se obtiene la matriz superior de la página 178:
Recuérde que la ecuación carga – desplazamiento es:
P = A S At x
182
Capítulo 5
Interacción del suelo con la estructura
De manera que se puede calcular
A S A t y con esto, conocer el vector de desplazamiento x que al
sustituir en las ecuaciones (5.71) y (5.72) se obtiene
e y F respectivamente.
A S A t se determina:
Efectuando el producto
k = A S At
Esta matriz se encuentra en la parte inferior.
 4EI
 h
 2EI

 h
 F1  
F   0
 2 
 F3   0
  
 F4  
 F5   0
 =
 F6   0
F  
 7 
 F8   0
F  
 9  0
F10  
 0


 0
 4EI
 h
 2EI

 h

0

0
k = 
6EI
 2
h
− 6EI
 h2

0

0

2EI
h
4EI
h
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4EI
h
2EI
h
2EI
h
4EI
h
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2EI
h
4EI
h
0
0
4EI
h
2EI
h
0
0
0
0
0
0
0
0
k1
0
0
0
0
0
0
0
0
k2
0
0
0
0
0
0
0
0
k3
0
0
0
0
0
0
0
0
0
0
2EI
h
8EI
h
2EI
h
0
2EI
h
8EI
h
2EI
h
0
6EI
h
0
2
0
h
6EI
h
2
2
2EI
h
4EI
h
0
6EI
0
−
0
0
6EI
0
−
0
6EI
h2
h2
6EI
− 2
h
6EI
−
2
h
6EI
h

0 

0 

0 

0 

0 


0 

0 


0 

0 


k4 

 e1 
e 
 2
 e3 
 
 e4 
 e5 
 
 e6 
e 
 7
 e8 
e 
 9
e10 
6EI
h
2
−
0
2
6EI
0
12EI
3
+ k1
h
12EI
− 3
h
−
6EI
h2
6EI
0
h2
12EI
h3
24EI
3
+ k2
0
h
12EI
− 3
h
0
0
0
−




0


6EI
− 2

h

6EI

− 2

h

0



0

12EI 
− 3

h

12EI
+ k4 
3

h
0
0
h2
0
0
12EI
h3
24EI
+ k3
h3
12EI
− 3
h