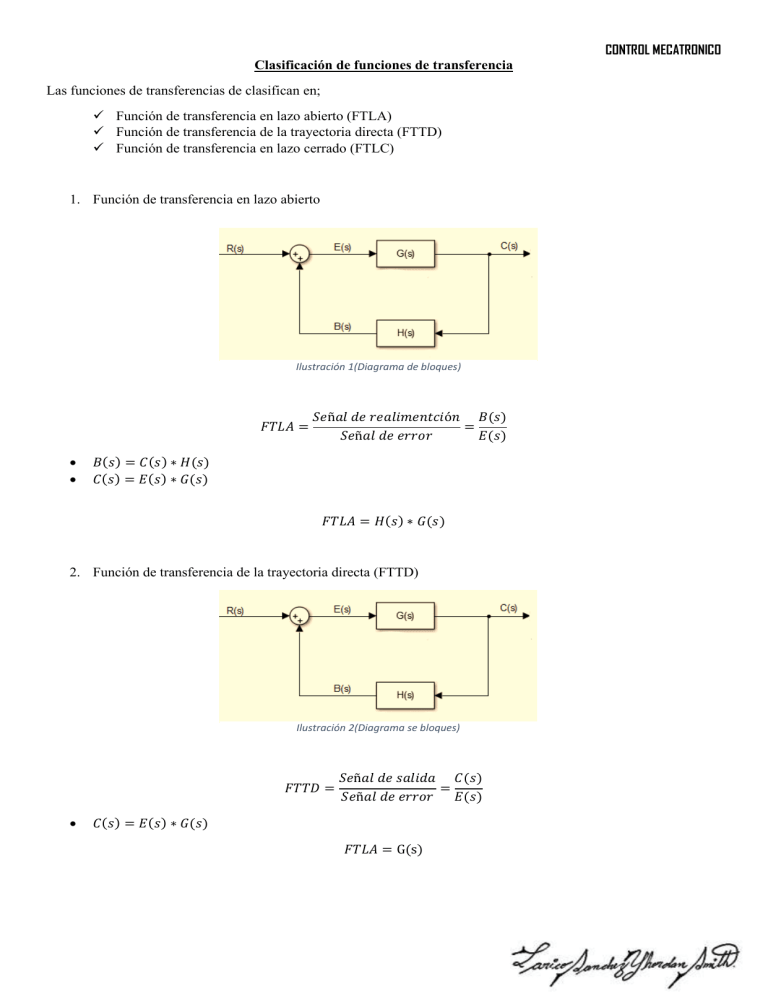
CONTROL MECATRONICO Clasificación de funciones de transferencia Las funciones de transferencias de clasifican en; Función de transferencia en lazo abierto (FTLA) Función de transferencia de la trayectoria directa (FTTD) Función de transferencia en lazo cerrado (FTLC) 1. Función de transferencia en lazo abierto Ilustración 1(Diagrama de bloques) 𝐹𝑇𝐿𝐴 = 𝑆𝑒ñ𝑎𝑙 𝑑𝑒 𝑟𝑒𝑎𝑙𝑖𝑚𝑒𝑛𝑡𝑐𝑖ó𝑛 𝐵(𝑠) = 𝑆𝑒ñ𝑎𝑙 𝑑𝑒 𝑒𝑟𝑟𝑜𝑟 𝐸(𝑠) 𝐵(𝑠) = 𝐶(𝑠) ∗ 𝐻(𝑠) 𝐶(𝑠) = 𝐸(𝑠) ∗ 𝐺(𝑠) 𝐹𝑇𝐿𝐴 = 𝐻(𝑠) ∗ 𝐺(𝑠) 2. Función de transferencia de la trayectoria directa (FTTD) Ilustración 2(Diagrama se bloques) 𝐹𝑇𝑇𝐷 = 𝑆𝑒ñ𝑎𝑙 𝑑𝑒 𝑠𝑎𝑙𝑖𝑑𝑎 𝐶(𝑠) = 𝑆𝑒ñ𝑎𝑙 𝑑𝑒 𝑒𝑟𝑟𝑜𝑟 𝐸(𝑠) 𝐶(𝑠) = 𝐸(𝑠) ∗ 𝐺(𝑠) 𝐹𝑇𝐿𝐴 = G(s) CONTROL MECATRONICO 3. Función de transferencia en lazo cerrado (FTLC) Ilustración 3(Diagrama de bloques) 𝐹𝑇𝐿𝐶 = 𝑆𝑒ñ𝑎𝑙 𝑠𝑎𝑙𝑖𝑑𝑎 𝐶(𝑠) = 𝑆𝑒ñ𝑎𝑙 𝑑𝑒 𝑒𝑚𝑡𝑟𝑎𝑑𝑎 𝑅(𝑠) 𝐶(𝑠) = 𝐸(𝑠) ∗ 𝐺(𝑠) 𝐸(𝑠) = 𝑅(𝑠) − 𝐵(𝑠) 𝐵(𝑠) = 𝐶(𝑠) ∗ 𝐻(𝑠) 𝐹𝑇𝐿𝐶 = 𝐺(𝑠) 1 + 𝐺(𝑠) ∗ 𝐻(𝑠) Análisis de respuesta a entradas de señal La señales de entrada para un diagrama de bloques de un sistema no se conoce con anticipación, y algunas señales de entrada no se pueden expresar de forma analítica, en estas situaciones el diseñador deberá de hacer pruebas con señales de prueba típicas como las siguientes funciones Señal de prueba escalón unitario Señal de prueba rampa unitaria Señal de prueba impulso unitario CONTROL MECATRONICO Señal de entrada Función Grafica de la función Escalón unitario 𝑟(𝑡) = 1 Rampa unitaria 𝑟(𝑡) = 𝑡 Impulso unitario 𝑟(𝑡) = 0 𝑠𝑖 𝑡 ≠ 0 𝑟(𝑡) = ∞ 𝑠𝑖 𝑡 = 0 Sistemas de primer orden CONTROL MECATRONICO Si tenemos el siguiente diagrama de bloque como se muestra en la ilustración, analizaremos las respuestas debidos a las entradas (escalón unitario, rampa unitaria, impulso unitario) Analizaremos los comportamientos de la señal de entrada y la señal de la salida Ilustración 4(Diagrama de bloques) Señal de entrada con escalón unitario = 𝑅(𝑠) = 𝐹𝑇𝐿𝐶 = 𝐶(𝑠) 1 = 𝑅(𝑠) 𝑇 ∗ 𝑆 1 𝑅(𝑠) 𝐶(𝑠) = = S 𝑇∗𝑆+1 𝑇∗𝑆 𝐶(𝑠) = 1 1 − 𝑆 𝑆+1 T Para graficar la entrada y la salida aplicamos la transformada inversa de Laplace Señal de entrada Señal de salida 𝑅(𝑠) = 𝐶(𝑠) = 1 𝑆 1 1 − 𝑆 𝑆+1 T 𝑅(𝑡) = 1 t 𝐶(𝑡) = 1 − e−T 1 𝑆





![[30]](http://s2.studylib.es/store/data/002283520_1-8fa2f31d0f61f2748ce92510df6c2c2b-300x300.png)


