Instituto Tecnológico de Toluca
Tarea No. 1: Los Números Reales
Ingeniería en Sistemas Computacionales
Anthony Uriostegui
Prof. Noé Roberto Vega Mejia
NUMEROS REALES
1
Los números reales
Definición:
En
matemáticas,
los números reales son aquellos que
Representación
números reales:
de
los
poseen una expresión decimal e
incluyen
tanto
a
los
números
racionales (como: 31, 37/22, 25,4)
como a los números irracionales, que
no se pueden expresar de manera
fraccionaria y tienen infinitas cifras
decimales
no
periódicas,
tales
http://asesoriamatematicaaypg.blogspot.com/201
como: √2, 𝜋.
Se define el conjunto de los números
reales como a la unión de números
racionales e irracionales. Es decir:
Clasificación:
Maneras
de
Existen Diversas
cómo
introducir
el
sistema de los números reales, pero
una de las más aceptadas inicia
considerando
sistemas
numéricos
más sencillos.
o Conjunto
Tomado de:
de
los
números
naturales: Se define el conjunto de
los números naturales como:
= {1, 2, 3, 4, 5, 6, 7, 8, 9, …}
1/05/adicion-de-numeros-con-signo-14-de.html
Propiedades de los números
reales:
Ley asociativa para la suma
(P1)a+(b+c)=(a+b)+c ∀a,b,c∈R
Existencia de una identidad para la
suma (P2)∃0∈Rtalquea+0=0+a=a
∀a∈R
Existencia de inversos para la suma
(P3) ∀ a ∈ R ∃ − a ∈ R tal que a +
(−a) = (−a) + a = 0
Ley conmutativa para la suma
o Conjunto de números enteros: Se
(P4)a+b=b+a ∀a,b∈ R
define el conjunto de los números
enteros como:
= {…, -2, -1, 0, 1, 2, …}
o Conjunto de números racionales:
Se define el conjunto de los números
Ley asociativa para la multiplicación
NUMEROS REALES 2
(P5)a·(b·c)=(a·b)·c ∀a,b,c∈ R
Existencia de una identidad para la
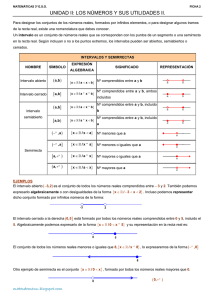
Los intervalos finitos pueden ser
multiplicación
cerrados, abiertos o semiabiertos.
(P6)∃1∈Rtalque1̸=0
Sean a y b dos números reales tales
y a·1=1·a=a∀a∈R
que a < b.
Existencia
de
inversos
para
la
Intervalo cerrado
multiplicación
Es el conjunto de números reales
(P7)∀a∈R−{0}∃a−1 ∈R tal que a·a−1
formado
=a−1 ·a=1
comprendidos entre ambos.
por
a,
b
y
todos
los
Ley conmutativa para la multiplicación
(P8)a·b=b·a
∀a,b∈
R
[a, b] = { x / a £ x £ b}
Intervalo abierto
Ley distributiva
(P9)a·(b+c)=a·b+a·c
∀a,b,c∈
R
(P10) ∀ a ∈ R se cumple una y sólo
Es el conjunto de los números reales
comprendidos entre a y b.
una de las siguientes proposiciones:
(a, b) = {x / a < x < b}
Ley de tricotomía
(ı)a=0
(ıı)a∈
P
(ııı)−a∈
P
Intervalo semiabierto a izquierda (o
semicerrado a derecha)
La suma de positivos es cerrada
Es el conjunto de números reales
(P11)a,b∈
formado por b y los números
P
⇒
a+b∈P
comprendidos entre a y b.
La multiplicación de positivos es
cerrada
(a, b] = {x / a < x £ b}
(P12)a,b∈ P ⇒ a·b∈P
Intervalos:
Un subconjunto de la
recta real se llama intervalo, y
contiene a todos los números reales
que están comprendidos entre dos
cualesquiera
de
sus
elementos.
Geométricamente
los
intervalos
Intervalo semiabierto a derecha (o
semicerrado a izquierda)
Es el conjunto de números reales
formado por a y los NUMEROS
números REALES
comprendidos entre a y b.
3
Intervalos infinitos
Referencia Apa:
Larson Hostetler Edwards. (2009).
[
a, +¥) = { x / x ³ a}
Cálculo Diferencial Matemáticas 1.
México: Mc Graw Hill.
(a, +¥) = { x / x > a}
(-¥ , b] = { x / x £ b}
(-¥ , b) = { x / x < b}
(-¥ , +¥ ) = R
Resolución de Operaciones:
o Paréntesis desde dentro hacia fuera y
desde izquierda a derecha
o Exponentes y raíces cuadradas de
izquierda a derecha (tienen la misma
prioridad)
o Multiplicaciones
y
divisiones
de
izquierda a derecha (tienen la misma
prioridad)
o Sumas y restas de izquierda a
derecha (tienen la misma prioridad)
NUMEROS REALES
4