ESTADÍSTICA
Anuncio
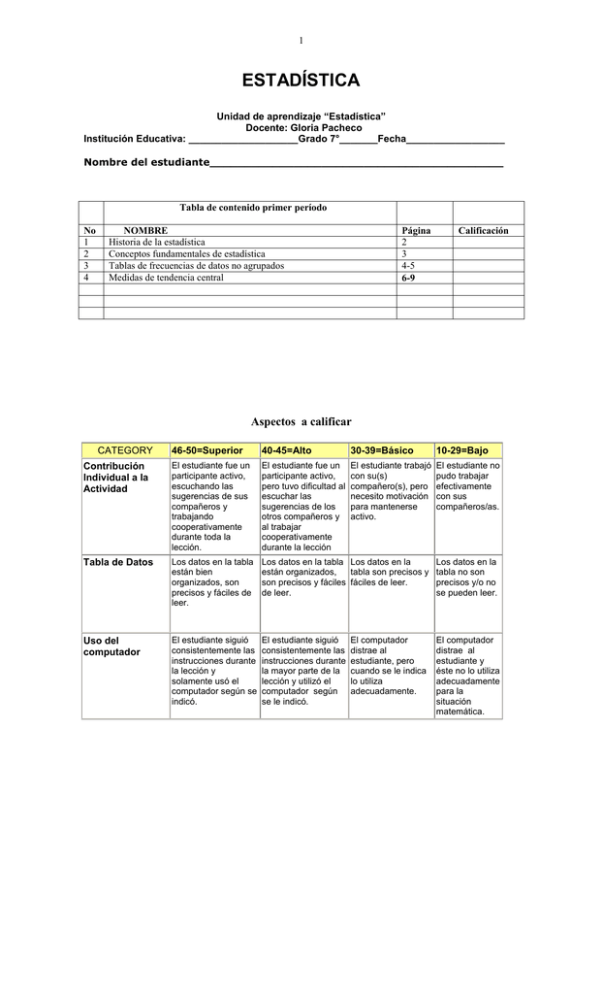
1 ESTADÍSTICA Unidad de aprendizaje “Estadística” Docente: Gloria Pacheco Institución Educativa: ____________________Grado 7°_______Fecha__________________ Nombre del estudiante__________________________________________ Tabla de contenido primer período No 1 2 3 4 NOMBRE Historia de la estadística Conceptos fundamentales de estadística Tablas de frecuencias de datos no agrupados Medidas de tendencia central Página 2 3 4-5 6-9 Calificación Aspectos a calificar 46-50=Superior 40-45=Alto 30-39=Básico 10-29=Bajo Contribución Individual a la Actividad El estudiante fue un participante activo, escuchando las sugerencias de sus compañeros y trabajando cooperativamente durante toda la lección. El estudiante fue un participante activo, pero tuvo dificultad al escuchar las sugerencias de los otros compañeros y al trabajar cooperativamente durante la lección El estudiante trabajó con su(s) compañero(s), pero necesito motivación para mantenerse activo. El estudiante no pudo trabajar efectivamente con sus compañeros/as. Tabla de Datos Los datos en la tabla están bien organizados, son precisos y fáciles de leer. Los datos en la tabla Los datos en la están organizados, tabla son precisos y son precisos y fáciles fáciles de leer. de leer. Los datos en la tabla no son precisos y/o no se pueden leer. Uso del computador El estudiante siguió consistentemente las instrucciones durante la lección y solamente usó el computador según se indicó. El estudiante siguió consistentemente las instrucciones durante la mayor parte de la lección y utilizó el computador según se le indicó. El computador distrae al estudiante y éste no lo utiliza adecuadamente para la situación matemática. CATEGORY El computador distrae al estudiante, pero cuando se le indica lo utiliza adecuadamente. 2 Historia de la Estadística Desde los comienzos de la civilización han existido formas sencillas de estadísticas, pues ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas, palos de madera y paredes de cuevas para contar el número de personas, animales o ciertas cosas. Hacia el año 3000 A.C. los babilonios usaban ya pequeñas tablillas de arcilla para recopilar datos en tablas sobre la producción agrícola y de los géneros vendidos o cambiados mediante trueque. Los egipcios analizaban los datos de la población y la renta del país mucho antes de construir las pirámides en el siglo XXXI a.C. Los libros bíblicos de Números y Crónicas incluyen, en algunas partes, trabajos de estadística. El primero contiene dos censos de la población de Israel y el segundo describe el bienestar material de las diversas tribus judías. En China existían registros numéricos similares con anterioridad al año 2000 A.C. Los griegos clásicos realizaban censos cuya información se utilizaba hacia el año 594 A.C. para cobrar impuestos. El Imperio romano fue el primer gobierno que recopiló una gran cantidad de datos sobre la población, superficie y renta de todos los territorios bajo su control. Durante la edad media sólo se realizaron algunos censos exhaustivos en Europa. Los reyes carolingios Pipino el Breve y Carlomagno ordenaron hacer estudios minuciosos de las propiedades de la Iglesia en los años 758 y 762 respectivamente. Después de la conquista normanda de Inglaterra en 1066, el rey Guillermo I de Inglaterra encargó un censo. La información obtenida con este censo, llevado a cabo en 1086, se recoge en el Domesday Book. El registro de nacimientos y defunciones comenzó en Inglaterra a principios del siglo XVI, y en 1662 apareció el primer estudio estadístico notable de población, titulado Observations on the London Bills of Mortality (Comentarios sobre las partidas de defunción en Londres). Un estudio similar sobre la tasa de mortalidad en la ciudad de Breslau, en Alemania, realizado en 1691, fue utilizado por el astrónomo inglés Edmund Halley como base para la primera tabla de mortalidad. En el siglo XIX, con la generalización del método científico para estudiar todos los fenómenos de las ciencias naturales y sociales, los investigadores aceptaron la necesidad de reducir la información a valores numéricos para evitar la ambigüedad de las descricpciones verbales. En nuestros días, la estadística se ha convertido en un método efectivo para describir con exactitud los valores de los datos económicos, políticos, sociales, psicológicos, biológicos y físicos, y sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir y tabular los datos, sino sobre todo el proceso de interpretación de esa información. El desarrollo de la teoría de la probabilidad ha aumentado el alcance de las aplicaciones de la estadística. Muchos conjuntos de datos se pueden aproximar, con gran exactitud, utilizando determinadas distribuciones probabilísticas; los resultados de éstas se pueden utilizar para analizar datos estadísticos. La probabilidad es útil para comprobar la fiabilidad de las inferencias estadísticas y para predecir el tipo y la cantidad de datos necesarios en un determinado estudio estadístico 3 Unidad de aprendizaje Estadística Institución Educativa: __________________________________ Docente: Gloria Pacheco Nombre del estudiante__________________________________ Grado 7°___Fecha_____ Reflexión: ¡Cuan preciosa, oh Dios, es tu misericordia! por eso los hijos de los hombres se amparan bajo tus alas Salmo 36:7 Tema: CONCEPTOS FUNDAMENTALES DE ESTADÍSTICA Objetivo: Reconocer algunos conceptos fundamentales de la estadística Materiales: Recortes de periódicos y revistas que muestren datos estadísticos Conceptos: CONCEPTOS FUNDAMENTALES DE ESTADÍSTICA ESTADÍSTICA. La estadística está ligada con los métodos científicos en la toma, organización, recopilación, presentación y análisis de datos, tanto para la deducción de conclusiones como para tomar decisiones razonables de acuerdo con tales análisis. Actividad 1: De un periódico recorte datos que representen estadísticas POBLACIÓN: La población, o el universo, está formado por la totalidad de los elementos que se desean estudiar, ejemplos podrían ser: La población total de Colombia, los alumnos cursantes en las universidades del país, la producción de toda una industria, a cosecha de un año dado, el rendimiento de una raza de ganado, entre otros MUESTRA:. En los estudios estadísticos, en vez de analizar la totalidad de la población o universo, se acude al recurso de considerar solamente una parte de ella, a la cual se llama muestra. Es requisito indispensable que la muestra a analizarse sea representativa realmente de la población o universo, al cual substituye en el estudio estadístico, o sea, que debe contener valores típicos del fenómeno que se desea estudiar. Actividad 2: Escriba 3 ejemplos de población y de muestras de las mismas. ESTADÍSTICA CUALITATIVA Y CUANTITATIVA ESTADÍSTICA CUALITATIVA: Cuando los datos suministrados en una encuesta son cualidades o atributos. Ejemplo: Color preferido ESTADÍSTICA CUANTITATIVA: Cuando los datos suministrados en una encuesta son numéricos. Ejemplo: Edad Actividad: Clasifica las siguientes variables en cualitativas o cuantitativas: Peso, color de los ojos, marca de automóvil, Nº de hijos, estatura, programa de Tv favorito. VARIABLES DISCRETAS Y CONTINUAS Una variable es un símbolo, tal como X, Y, H, x, B, que puede tomar un valor cualquiera de un conjunto determinado de ellos. Una variable que teóricamente puede tomar cualquier valor entre dos valores dados se llama variable CONTINUA, si solo pueden tomar valores aislados se llama DISCRETA. Ejemplo 1: En una familia el número N de hijos puede tomar cualquiera de los valores 0, 1, 2, 3, 4, 5, 6,…., pero no puede ser 2,5 o 3,842; es pues una VARIABLE DISCRETA. Ejemplo 2: La altura H de un individuo puede ser 1,6 m 1,62 metros o 1,625 metros, dependiendo de la exactitud e la medida; es una VARIABLE CONTINUA. Actividad: ¿Cuáles de las siguientes variables son discretas y cuáles son continuas?: peso, edad, tiempo de sueño, Nº de hermanos, tiempo de trabajo. Gep/11 4 Unidad de aprendizaje Estadística Institución Educativa: __________________________________ Docente: Gloria Pacheco Nombre del estudiante__________________________________ Grado 7°___Fecha_____ Reflexión: La blanda respuesta quita la ira, más la palabra áspera hace subir el furor. Proverbios 15:1 Tema: Tablas de frecuencia para datos no agrupados Objetivo: Realizar tablas de frecuencias para datos no agrupados Conceptos: TOMA DE DATOS: La toma de datos es la obtención de una colección de los mismos que no han sido ordenados numéricamente. Ejemplo: El tiempo en segundos registrado por un grupo de 40 atletas en los 100 metros planos, presenta el siguiente conjunto de datos estadísticos numéricos: 13 12 12 11 10 12 14 14 11 12 12 11 11 12 13 13 14 12 10 16 13 13 12 12 12 14 14 14 13 14 11 11 12 12 14 12 12 11 10 12 ORDENACIÓN: Una ordenación es una colección de los datos numéricos tomados, en orden creciente o decreciente de magnitud. DISTRIBUCIÒN DE FRECUENCIAS: es la representación estructurada, en forma de tabla, de toda la información que se ha recogido sobre la variable que se estudia. Xi = Tiempo Frecuencia absoluta: fa Frecuencia absoluta acumulada: Fa Frecuencia relativa fr fa N Frecuencia porcentual % fp fa .100 N Frecuencia porcentual acumulada Fp 10 11 12 13 14 15 16 Total 40 N = 40 100% 1,00 100% FRECUENCIA ABSOLUTA: La frecuencia absoluta de una variable estadística es el número de veces que aparece en la muestra dicho valor de la variable, la representaremos por fa FRECUENCIA ABSOLUTA ACUMULADA: La frecuencia absoluta acumulada de un valor de la variable, es el número de veces que ha aparecido en la muestra un valor menor o igual que el de la variable y lo representaremos por Fa. 5 FRECUENCIA RELATIVA: Es el cociente entre la frecuencia absoluta y el tamaño de la f muestra. La denotaremos por fr y su fórmula es: f r a N Donde N = Tamaño de la muestra FRECUENCIA PORCENTUAL: Esta medida resulta de multiplicar la frecuencia relativa por 100. La denotaremos por fp en donde fp = fa . 100% FRECUENCIA PORCENTUAL ACUMULADA: Viene a ser la acumulación de todas las frecuencias porcentuales hasta el mismo intervalo considerado, inclusive Ejercicios: A. a. b. c. d. e. Analizar la tabla para resolver las siguientes preguntas Establecer el número de atletas con un tiempo de 13 segundos. Establecer el porcentaje de atletas con un tiempo de 13 segundos ¿Cuántos atletas recorren los 100 metros en un tiempo inferior a 13 segundos? ¿Cuántos atletas recorren los 100 metros en un tiempo superior a 13 segundos? ¿Qué porcentaje de los atletas recorre los 100 metros en un tiempo máximo de 13 segundos? f. ¿Qué porcentaje de los atletas recorre los 100 metros en un tiempo mínimo de 13 segundos? B. Sea x la variable que representa el número de faltas de asistencia al colegio de los 50 alumnos de un curso durante un año escolar, x genera el siguiente conjunto de datos numéricos: 3,2,3,4,1,2,3,4,3,3,3,5,6,6,5,3,4,1,2,3,2,5,1,3,3,3,2,4,1,2,2,3,3,5,5,6,3,4,4,1,2,4,3,7,7, 3,7,6,5,3. Ordenar los datos, representándolos mediante una tabla de frecuencias Gep/11 6 Unidad de aprendizaje Estadística Institución Educativa: __________________________________ Docente: Gloria Pacheco Nombre del estudiante__________________________________ Grado 7°___Fecha_____ Reflexión: “Se complace Dios en los que le temen y en los que esperan en su misericordia” Salmo 147:11 Tema: ESTADÍSTICA :MEDIDAS DE TENDENCIA CENTRAL Objetivo: Reconocer la moda, la mediana y el promedio o media aritmética como medidas de tendencia central Calcular la moda y la mediana de datos no agrupados Calcular el promedio o media aritmética de datos no agrupados Conocimientos previos: Tabla de frecuencias. Conceptos: MEDIDAS DE TENDENCIA CENTRAL Permiten un mejor análisis de los datos estadísticos. Las medidas de tendencia central son: Moda, Mediana y Media. Aclaremos a través de un ejercicio cada uno de estos conceptos. Ejercicio: Sea x la variable que representa el número de faltas de asistencia al colegio de los 50 alumnos de un curso durante un año escolar, x genera el siguiente conjunto de datos numéricos: 3,2,3,4,1,2,3,4,3,3,3,5,6,6,5,3,4,1,2,3,2,5,1,3,3,3,2,4,1,2,2,3,3,5,5,6,3,4,4,1,2,4,3,7,7,3,7,6,5, 3. Ordenemos los datos, representándolos mediante una tabla de frecuencias y calculemos las medidas de tendencia central: Moda, Mediana, y Media. Llene la siguiente tabla: Xi = Nº faltas de Frecuencia Frecuencia Frecuencia absoluta: absoluta relativa acumulada: porcentual fa Fa f f p a .100 N Frecuencia Xi. fa porcentual acumulada Fp 1 2 3 4 5 6 7 Total 50 N = 50 100% 1,00 = 100% 175 7 3.1 LA MODA. La moda de una serie de datos estadísticos, ordenados en una tabla de frecuencias, es el valor de la variable que tiene la máxima frecuencia absoluta. ¿Cuál es la moda en el ejercicio realizado? __________ Actividad: a) Calcula la moda de los números: 15, 6, 3, 8, 10, 15, 8, 15 b) Calcula la moda de los números: 3, 6, 7, 10, 15, 18, 3, 11, 3, 20, 3 3.2 LA MEDIANA. La mediana de una serie de datos estadísticos numéricos, ordenados en una tabla de frecuencias, es el valor de la variable tal que entre él y sus menores cubren la mitad (50%) de la muestra. Para determinar el valor de la mediana en el ejercicio dado podemos aplicar uno de los siguientes procedimientos: c) Tomamos el valor de x que corresponde a la frecuencia acumulada inmediatamente N superior a . 2 N 50 Así: = = 25. La Ni inmediatamente superior a 25 es 30, al cual le 2 2 corresponde el valor X3 = 3. Luego, mediana = Me= 3 faltas significa que la mitad del grupo faltó tres días o más al colegio. d) En la columna de frecuencias acumuladas porcentuales, leemos aquel porcentaje que es inmediatamente superior a 50% y tomamos como mediana el valor de X que le corresponde. Así: 60% es la frecuencia acumulada porcentual inmediatamente superior al 50%; luego Me = 3 faltas. Si N 2 coincide con una frecuencia acumulada, entonces tomamos como mediana la semisuma del valor Xi correspondiente con el siguiente Xi+1 . Es decir: xi xi 1 . 2 Actividad: a) Calcula la mediana de los números: 15, 6, 3, 8, 10. b) Calcula la mediana de los números: 3, 6, 7, 10, 15, 18. 3.3 PROMEDIO O MEDIA ARITMÉTICA. La media aritmética o simplemente Media de una serie de datos estadísticos numéricos es un numero que se obtiene sumando todos los datos y dividiendo la suma por el tamaño de la muestra. Para calcular la Media cuando los datos se encuentran ordenados en una tabla de frecuencias, procedemos de la siguiente manera: Si los valores diferentes x1 , x 2 , x3 ,..., xk , se presentan con frecuencias absolutas n1 , n 2 , n3 ,...nk , entonces la media aritmética simbolizada por X es: x n x n x n ...xk nk X 1 1 2 2 N3 3 Donde N es el tamaño de la muestra. Observa la tabla y mira el encabezado de la última columna Xi.ni, cada uno de esos datos equivale a la variable multiplicada por su frecuencia absoluta, al sumar estos datos y dividirlos entre el tamaño de la muestra que en este caso es 50 obtenemos el promedio. Aplica la fórmula y obtiene el promedio de los datos. Obtendrás 3,5 faltas. 8 X= = 50 X = 3,5 faltas nos indica que en promedio los estudiantes del grupo faltan 3,5 días durante el año escolar. Actividad: a) Un urbanista tiene los siguientes lotes: l1 = 85 m2 ; l2 = 120 m2 ; l3 = 205 m2 ; l4 = 186 m2 ; l5 = 150 m2 ; l6 = 136 m2 ; l7 = 142 m2. ¿Cuál es el área promedio de los lotes? b) A una reunión asisten 6 personas con edades de15, 16, 18, 20, 12 y 14 años. ¿Cuál es la media aritmética? ¿Cuál es la mediana? ¿Cuál de estos valores es más representativo? ¿Por qué? c) Las notas obtenidas por los alumnos de 7º grado en estadística fueron: 4 alumnos obtuvieron 30; 5 alumnos obtuvieron 40; 7 alumnos obtuvieron 45; 10 alumnos obtuvieron 25; 8 obtuvieron 20; 6 obtuvieron 50, 3 obtuvieron 35; 1 obtuvo 10. Con los datos anteriores, completa la tabla. Calcula la media aritmética o nota promedio obtenida por los alumnos. Xi Fa fa c) Xi . fa Los tiempos en minutos empleados por un grupo de atletas en recorrer 15 Km. Están representados en la siguiente tabla. Calcula el tiempo promedio empleado por los atletas. Tiempo Xi Frecuencia Absoluta fa Xi . fa 120 2 130 5 135 4 180 7 200 10 215 8 230 4 N= d) Calcula la mediana y la moda en el ejercicio anterior. Gep/11 9


