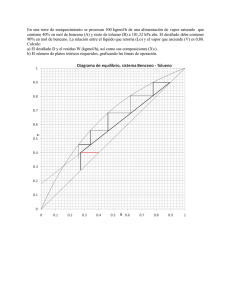
PROGRAMA UNIVERSIDAD VIRTUAL SOLUCIONARIO CAPÍTULO II LIBRO: BALANCES DE MATERIA Y ENERGÍA GIRONTZAS V. REKLAITIS POR: ING. QUÍMICO. BEN - HUR VALENCIA VALENCIA UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MANIZALES JULIO DE 2005 PRESENTACION Luego de la aparición del texto de Balances de Materia y Energía del Doctor Girontzas V. Reklaitis, en 1986, no ha habido ningún texto nuevo en el área, ni suyo ni de ningún otro autor, que trate de manera tan magistral el análisis de los Balances. El tratamiento matemático propuesto es completamente general y permite que el resolver problemas de Balance de Materia y Energía pase de arte a Ciencia, ocupando por ello – al lado de otros autores - un lugar preferencial en el desarrollo del área, vital para el estudio de la Ingeniería Química. Esta Segunda Edición del SOLUCIONARIO del Capítulo II corrige algunos errores de la Edición anterior y, lo que es más importante, muestra el uso de programas para calculadoras que permiten resolver de una manera rápida los problemas de Balances de Materia. A la forma tradicional de resolver los problemas de la anterior Edición se adiciona la solución utilizando el programa Solvesys de la calculadora Hewlett Packard 48-GX, mostrando lo valioso de esta herramienta en la solución de problemas. Este Solucionario lo complementa el trabajo sobre SOLUCION DE PROBLEMAS DE BALANCES DE MATERIA Utilizando la Hewlett Packard 48GX, 49, en el que se muestra la forma de utilizar el Programa y las recomendaciones para su aplicación en el planteamiento del Sistema de Ecuaciones de Balance, que puede consultarse en la página _______________. Como se verá en la introducción, se hace mayor énfasis en la Estrategia de Solución, en la Confirmación de los Grados de Libertad como una herramienta útil en el planteamiento de la Estrategia de Solución y la utilización de la Tabla de Balance en los problemas complejos El presente Solucionario, fruto de mi experiencia de 28 años en la cátedra de Balances de Materia y Energía, muestra una metodología de solución a partir de las ideas del profesor Reklaitis y lo presenta a sus estudiantes como un material de apoyo que les permita desarrollar y fijar los conceptos básicos en el estudio de los Balances de Materia y Energía. BEN-HUR VALENCIA V. Manizales, Julio del 2005. INTRODUCCION En la solución de los problemas se muestra la Reconfirmación de la Tabla de Grados de Libertad como una forma de poder analizar de manera cualitativa cuáles son las incógnitas y cuáles las ecuaciones para cada una de las unidades, y aún para el proceso completo. Además, la Reconfirmación se utiliza para mostrar de una manera cualitativa, también, el desarrollo de la Estrategia de solución. Lo anterior se explicará, con el problema 2.26: Su Tabla de Grados de Libertad es: Abs. NVI NBMI NFC NCC NRC R1 R2 R3 R4 G de L 12 4 0 3 (+1) Destilado Diviso Agotado Globa Mez. Proceso r r r l 9 9 7 3 26 12 3 3 3 1 14 4 0 0 0 0 0 0 2 1 2 0 6 5 – – 1 – – 1 – – – – 4 – – – 4 – – 2 2 – – – 2 – – – 2 1 1 2 1 1 1 – 1 De manera cuantitativa puede apreciarse los Grados de Libertad de cada una de las Unidades: así por ejemplo, el Destilador: 4 y el Agotador: 2. Pero como se muestra en la Reconfirmación de la Tabla de Grados de Libertad que aparece a continuación:: Absorbedor: Incógnitas = 1 2 Ecuaciones = 4 (balances) G de L 4 = 3 3 4 5 5 5 8 (N , N , N , xH2S, N , N , xCO2, xH2S) Destilador: Divisor: Agotador: Mezclador: Global: Incógnitas = 5 5 5 6 6 3 7 7 7 7 7 (N , xCO2, xH2S, N , xCO2, N , xH2S) Ecuaciones = 3 (balances) G de L = 4 Incógnitas = 8 (N , xCO2, xH2S, N , xCO2, xH2S, N , xH2S) 3 3 7 Ecuaciones = 3 (balances) + 3 (R1, R4) G de L 2 = 8 8 Incógnitas = Ecuaciones = 3 (balances) G de L = 2 Incógnitas = 3 (N , N , N ) 9 10 8 10 CO2) 5 (N , xH2S, N , N , x 4 9 11 Ecuaciones = 1 (balances) G de L = 2 Incógnitas = 7 (N , N , N , xCO2, N , x Ecuaciones = 4 (balances) + 2 (R2, R3) G de L 1 = 8 1 2 6 6 10 10 CO2, 11 N ) no solamente se conocen esos valores, sino que muestra CUÁLES son las incógnitas y CUÁLES son las ecuaciones que originan esos Grados de Libertad. Su utilización en la Estrategia de Solución es análoga. El problema tiene la siguiente estrategia: Estrategia de Solución: 1. Tomando Base de Cálculo en el Proceso Global y resolviéndolo sus balances (se 1 2 6 6 10 10 asumió que los porcentajes son molares) se conocen: N , N , N , xCO2, N , x CO2 y 11 N . Se agota el balance de Inertes. 2. Actualizando Grados de Libertad se encuentra que: 1 2 Absorbedor: G de L A = 4 – 2 (N , N ) + 1 (Balance de Inertes) = 3 6 6 Destilador: G de L A = 4 – 1 (N ) – 1 (xCO2) = 2 Agotador: Mezclador: 10 G de L A = 2 – 1 (N ) – 1 (x 11 G de L A = 2 – 1 (N ) 10 CO2) = 0 = 1 Sí en este momento consideramos la Reconfirmación de Grados de Libertad para las Unidades actualizadas, DESCONTANDO en cada una de ellas las incógnitas conocidas tendremos de nuevo una información CUALITATIVA de los Grados de Libertad con que quedan estas Unidades (se ponen en negrilla y subrayadas en la Reconfirmación inicial): Absorbedor: Destilador: Agotador: Incógnitas = 1 2 3 3 4 5 5 5 6 ( N , N , N , xH2S, N , N , xCO2, xH2S) Ecuaciones = 3 (balances) – 1 (Balance agotado) G de L = 3 Incógnitas = 5 (N , xCO2, xH2S, N , xCO2, N , xH2S) 5 5 5 6 6 Ecuaciones = 3 (balances) G de L = 2 Incógnitas = 3 (N , xH2S, N , N , x 8 8 Ecuaciones = 3 (balances) G de L 0 = 9 10 10 CO2) 7 7 Mezclador: Incógnitas = 4 9 Ecuaciones = 1 (balances) G de L 1 = 11 2 (N , N , N ) En la Estrategia se resuelve a continuación el absorbedor ya que encontramos un sistema con 8 8 9 tres ecuaciones de Balance y 3 incógnitas (N , xH2S, N ) Un análisis similar a cualquier otra Unidad nos enseña cuáles son las incógnitas, las ecuaciones y los Grados de Libertad resultantes: El análisis del Destilador muestra que tiene, en este momento: Cinco Incógnitas 5 5 7 7 xCO2, xH2S, N , xH2S) y 3 ecuaciones de Balance, siendo sus Grados de Libertad de 2. 5 (N , Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis 2.1 Ben – Hur Valencia Valencia a. El flujo de alimentación a un secador se especifica como 1000 lb/h. Calcule el flujo en kg/min b. En un proceso de amoníaco se producen 105 lbmol/día. Calcule la producción equivalente en gmol/h. SOLUCION: Los cálculos se efectúan utilizando directamente los factores de conversión, factores que siempre son iguales a la unidad. a. Flujo en kg/min. 1000 453.6 g 1 kg 1h kg lb lb = 1000 × × × = 7.56 min h h 1 lb 1000 g 60 min b. Producción equivalente en gmol/h. 10 5 2.2 453.6 gmol 1 día gmol lbmol lbmol = 10 5 × × = 1.89 × 10 7 h día día 1 lbmol 24 h Una planta produce una mezcla de 90 % en mol de etanol (C2H5OH) y el resto de agua. a. Calcule la fracción en masa de etanol. b. Si la producción de la planta es 1000 lbmol/h, calcule la producción equivalente en kg/min. c. Para la producción de (b), calcule los flujos molares de los componentes de la corriente en kgmol/h. SOLUCION: a. Fracción masa o fracción másica de etanol. Masa Molecular (MM) del etanol = 46 MM del agua = 18 1 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia Base de cálculo: 1 gmol de mezcla. Para hallar el valor pedido se calcula la masa de etanol en un gramo-mol de mezcla y la masa de un gmol de mezcla o, lo que es lo mismo, la masa molecular media. La relación entre ellas da la respuesta. Masa Molecular media = ( 0.9 gmol de etanol g de etanol × 46 + gmol de mezcla gmol de etanol 0.1 gmol de agua g de agua × 18 ) mol de mezcla gmol de agua MM media = ( 41.4 g de etanol 1.8 g de agua + ) gmol de mezcla gmol de mezcla MM media = ( 41.4 g de etanol + 1.8 g de agua ) gmol de mezcla MM media = 43.2 g de mezcla gmol de mezcla Aunque se tomó una base de cálculo de 1 gmol, recuérdese que la respuesta se cumple en otras unidades, siempre y cuando haya consistencia dimensional, pudiendo decirse que MM media = 43.2 kg de mezcla lb de mezcla Tonelada de mezcla = 43.2 = 43.2 kgmol de mezcla lbmol de mezcla Tonelada mol de mezcla = 43.2 miligramo de mezcla miligramo - mol de mezcla = 43.2 arroba de mezcla arroba − mol de mezcla Continuando con el problema: Masa de etanol = ( 0.9 = 41.4 g de etanol gmol de etanol × 46 ) gmol de etanol gmol de mezcla g de etanol gmol de mezcla 2 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Fracción másica de etanol = w C2 H5OH Ben – Hur Valencia Valencia g de etanol ⎞ ⎛ ⎟ ⎜ 41.4 gmol de mezcla ⎟ ⎜ = ⎜ g de mezcla ⎟ ⎟ ⎜ 43.2 gmol de mezcla ⎠ ⎝ w C2H5OH = 0.95833 g de etanol g de mezcla Es importante resaltar, como lo muestra el análisis dimensional, que la fracción másica - de igual manera que la fracción molar o la fracción en volumen - tiene unidades, las cuales - normalmente - no se colocan, porque puede utilizarse en cualquier tipo de unidad: w C2H5OH = 0.95833 kg de etanol lb de etanol Tonelada de etanol = 0.95833 = 0.95833 kg de mezcla lb de mezcla Tonelada de mezcla b. La producción equivalente en kg/min Utilizando los factores de conversión y la masa molecular media se encuentra, directamente, que: 1000 43.2 lb 453.6 kg 1 h kg lbmol lbmol = 1000 × × × = 326.592 h h 1 lbmol 1000 lb 60 min min c. Flujos molares para la corriente en kgmol/h. A partir del flujo, las fracciones molares y el factor de conversión puede plantearse que: N C 2 H5OH = 0.9 N H 5O = 0.1 lbmol etanol lbmol mezcla 453.6 kgmol mezcla kgmol × 1000 × = 408.24 lbmol mezcla h 1000 lbmol mezcla h lbmol mezcla 453.6 kgmol mezcla lbmol etanol kgmol × 1000 × = 45.36 h h 1000 lbmol mezcla lbmol mezcla tal como se pedía. 3 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis 2.3 Ben – Hur Valencia Valencia Una corriente que contiene: H2O 0.4 C2H5OH 0.3 CH3OH 0.1 CH3COOH 0.2 en fracciones en masa, se alimenta a una columna de destilación a razón de 1000 lb/h. Convierta estas variables de las corrientes a: a. Flujos molares por componente. b. Flujo molar total y fracciones molares. c. Fracciones molares, en base libre de agua. SOLUCION: a. Flujos molares por componente. Hallando el flujo másico de cada componente y pasándolo a moles, se plantean las siguientes expresiones (obsérvese que en este cálculo se muestran las unidades de las fracciones másicas) que dan los valores pedidos: N H 2O = 0.4 lb C 2 H 5 OH lb mezcla 1 lbmol lbmol × 1000 × = 6.5217 lb mezcla h 46 lb C 2 H 5 OH h N C2 H5OH = 0.3 N CH 3OH = 0.1 N CH 3COOH = 0.2 lb H 2 O lb mezcla 1 lbmol lbmol 1000 × = 22.2222 lb mezcla h 18 lb H 2 O h lb CH 3 OH lb mezcla 1 lbmol lbmol × 1000 × = 3.125 lb mezcla h 32 lb CH 3 OH h lb CH 3 COOH lb mezcla 1 lbmol lbmol × 1000 × = 3.333 lb mezcla h 60 lb CH 3 COOH h 4 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia b. Flujo molar total y fracciones mol. Sumando los flujos parciales de la parte (a) se encuentra el flujo molar total: Flujo molar total = (22.2222 + 6.5217 + 3.125 + 3.333) lbmol/h Flujo molar total = 35.2022 lbmol/h Las fracciones molares se encuentran dividiendo el flujo molar de cada uno de los componentes por el flujo molar total. Así, para el agua: ⎛ 22.2222 mol de agua ⎞ mol de agua ⎟⎟ = 0.63127 x H 2O = ⎜⎜ mol de mezcla ⎝ 35.2022 mol de mezcla ⎠ De nuevo puede verse que las fracciones tienen unidades. Procediendo de manera análoga, las otras fracciones molares son: x C2 H5OH = 0.18527 mol de etanol mol de mezcla x CH 3OH = 0.08877 mol de metanol mol de mezcla x CH 3COOH = 0.09469 mol de ácido acético mol de mezcla c. Fracciones mol, en base libre de agua. El cálculo puede hacerse mediante un cambio de base, utilizando los porcentajes calculados en la parte (b); o a partir del flujo total, utilizando los flujos por componente del ítem (a). Calculando la fracción molar de etanol de ambas maneras se tendrá que: Con los porcentajes de la parte (b): ⎞ 1 mol de mezcla ⎛ 0.18527 mol de etanol ⎞ ⎛⎜ ⎟ x C 2 H5OH = ⎜ ⎟×⎜ mol de mezcla ⎠ ⎝ (1 − 0.63127 ) mol de mezcla exenta de agua ⎟⎠ ⎝ 5 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis x C2 H5OH = 0.50244 Ben – Hur Valencia Valencia mol de etanol mol de mezcla exenta de agua Con los flujos por componente de la parte (a): ⎞ ⎛ 6.5217 mol de etanol ⎟⎟ x C2 H5OH = ⎜⎜ ⎝ (35.2022 − 22.222 ) mol de mezcla exenta de agua ⎠ x C 2 H5OH = 0.50244 mol de etanol mol de mezcla exenta de agua Análogamente se encuentran las otras fracciones en base seca. Con sus respectivas unidades son: xmetanol = 0.24075 xetanoico = 0.2568 2.4 mol de me tan ol mol de mezcla exenta de agua mol de etanoico mol de mezcla exenta de agua Una solución que contiene Na2S, NaOH y Na2CO3 en agua se conoce como “licor blanco” y se usa en la industria del papel para procesar pulpa de madera. Supóngase que el análisis de laboratorio indica 50 g/l de Na2S, 250 g/l de NaOH y 100 g/l de Na2CO3. Si la densidad de la solución es 1.05 g/cm3, calcule los flujos molares por componente, correspondientes a un flujo total de la corriente de 1000 kgmol/h. SOLUCION: Los resultados se muestran en la tabla siguiente. El procedimiento para construirla es: 1. Tomando como base de cálculo 1 litro de solución se calcula su masa. 2. Con los datos del problema se puede calcular la masa de cada componente y, por diferencia, la masa de agua (Columna 2). 3. Se hallan las moles de cada uno de los componentes (dividiendo por la masa molecular) (Columna 3). 6 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia 4. La suma de los valores anteriores da el número total de moles. 5. Dividiendo las moles de cada componente por el número total de moles se halla su fracción molar (Columna 4). 6. Como la fracción molar es independiente de la unidad usada para la cantidad de sustancia, se multiplica por 1000 kgmol/h cada valor hallado en el ítem 5. y se encuentra los flujos molares pedidos (Columna 5). La masa de 1 litro de solución es: Masa = 1 litro × 2.5 1000 cm 3 g x 1.05 = 1050 g 1 litro cm 3 Componente Masa g Moles gmol Fracción molar Na2S NaOH Na2CO3 H2O Totales 50 250 100 650 1050 0.641026 6.250000 0.943396 36.111111 43.945533 0.014587 0.142222 0.021467 0.821724 1.000000 Flujo molar kgmol/h 14.587 142.222 21.467 821.724 1000.000 A un proceso de producción de metano a partir de gas de síntesis y vapor de agua, se alimentan 6 kgmol/min de un gas que contiene 50 % de H2, 33 1/3 % de CO y el resto CH4 (todos en base molar), así como 72 kg/min de vapor de agua. Los productos son 3 kgmol/min de agua líquida y 95 kg/min de un gas que contiene 25 % de CH4, 25 % de CO2 y el resto H2 (todos en base molar). Vapor Gas de síntesis 50 % H2 33 1 3 CO CH4 Gas como producto CH4 25 % CO2 25 % H2 Agua 7 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia Determine, con tres cifras significativas, si: a. ¿Se conserva la masa total? b. ¿Se conservan las moles totales? c. ¿Se conservan las moles de cada tipo de átomo? d. ¿Se conserva la masa de cada tipo de sustancia química? e. ¿Qué puede concluirse que ocurre en este proceso? SOLUCION: Para la mezcla gaseosa de salida se conoce el flujo másico y su porcentaje molar, puede efectuarse un cambio de fracción molar a másica o, lo que es más sencillo, encontrar la masa molecular media de la mezcla. Procediendo de ambas maneras: Masa Molecular Media = (0.25 × 16 + 0.25 × 44 + 0.5 × 2) = 16 por tanto: ⎛ ⎜ 96 kg min Flujo molar de mezcla = ⎜ ⎜ kg ⎜ 16 ⎝ kgmol ⎞ ⎟ ⎟ = 6 kg ⎟ kgmol ⎟ ⎠ Conocida la fracción molar se toma como base un mol de mezcla y la fracción másica de cada componente se calcula dividiendo la masa de cada componente (fracción molar por masa molecular) por la masa total del mol de mezcla (o masa molecular media): w CH 4 mol de CH 4 masa de CH 4 ⎛ × 1 mol de mezcla × 16 ⎜ 0.25 mol de mezcla mol de CH 4 =⎜ ⎜ masa de mezcla 16 ⎜ mol de mezcla ⎝ ⎛ masa de CH 4 w CH 4 = 0.25 ⎜⎜ ⎝ masa total ⎞ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎟⎟ ⎠ 8 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia Para los otros componentes se procede de manera análoga (sin todas las unidades): ⎛ 0.25 × 1 × 44 ⎞⎛ masa de CO 2 w CO2 = ⎜ ⎟⎜⎜ 16 ⎝ ⎠⎝ masa total ⎛ masa de CO 2 w CO2 = 0.6875 ⎜⎜ ⎝ masa total ⎞ ⎟⎟ ⎠ ⎛ 0.5 × 1 × 2 ⎞⎛⎜ masa de H 2 w H2 = ⎜ ⎟⎜ 16 ⎝ ⎠⎝ masa total ⎛ masa de H 2 w H 2 = 0.0625 ⎜⎜ ⎝ masa total ⎞ ⎟⎟ ⎠ ⎞ ⎟⎟ ⎠ ⎞ ⎟⎟ ⎠ Para visualizar el balance de materia, se toma como base un minuto y con los flujos másicos y/o molares conocidos se construye la siguiente tabla. SALIDA ENTRADA H2 CO CH4 H2O Total kgmol kg 3 2 1 4 10 6 56 16 72 150 H2O CH4 CO2 H2 Total kgmol kg 3 1.5 1.5 3 9 54 24 66 6 150 En ella se hace inventario de las masas de los componentes y las moles totales a la entrada y a la salida: a. ¿Se conserva la masa total? Al proceso entran 150 kg y de él salen 150 kg. La masa total que entra es igual a la masa total que sale, de acuerdo con la Ley de la Conservación de la Materia. 9 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia b. ¿Se conservan las moles totales? Las moles totales no se conservan: Al proceso entran 10 kgmol y de él salen 9 kgmol. c. ¿Se conservan las moles de cada tipo de átomo? Sumando los átomos mol de cada componente a la entrada y a la salida se tiene que: ENTRADA: Los elementos que intervienen en el proceso son H, C y O. kg - átomo de H = H del H2 = 3 kgmol H2 x + H del CH4 + 2 kg − átomo H 4 kg − átomo H + 1 kgmol CH4 x + kgmol H2 kgmol CH4 4 kgmol H 2O x kg - at de C = 18 = C del CO + C del CH4 = 2 kgmol CO x kg - at de O 3 = O del CO + O del H2O = 2 kgmol CO x 2 kg − átomo H 2 kgmol H 2O 1 kg − átomo C 1 kg − átomo C + 1 kgmol CH 4 x kgmol CH 4 kgmol CO = = H del H2O 1 kg − átomo O 1 kg − átomo O + 4 kgmol H 2 O x kgmol H 2 O kgmol CO 6 10 Solucionario. Balance de Materia. Capítulo II. G. V. Reklaitis Ben – Hur Valencia Valencia SALIDA: Efectuando el mismo procedimiento para los componentes a la salida (sin colocar las unidades): kg - átomo de H kg - átomo de C kg - átomo de O = H del H2 + H del CH4 = ( 3 × 2 + 1.5 × 4 + 3 × 2) = 18 = C del CH4 + C del CO2 = ( 1.5 × 1 + 1.5 × 1) = 3 = O del H2O + = ( 3 × 1 + 1.5 × 2) = 6 + H del H2O O del CO2 Los kg – átomo que entran y salen de los elementos H, C y O son, respectivamente: 18, 3 y 6. Se conserva el número de átomos mol de cada tipo de átomo. d. ¿Se conserva la masa de cada tipo de sustancia química? Como puede verse en la tabla anterior, la masa de cada tipo de sustancia no se conserva. Esto se debe a que en el proceso ocurre una reacción química en la que, como es obvio, desaparecen unas sustancias y se forman otras. e. ¿Qué puede concluirse que ocurre en este proceso? Que hay interacción química entre los diferentes componentes. Puede plantearse que ocurre la reacción: 2 CO + H2O → 1.5 CO2 + 0.5 CH4 La cual explica que en el proceso haya desaparecido el CO, que los kg-mol de agua hayan disminuido en 1, que hayan aparecido 1.5 kg-mol de CO2 y que el número de kg-mol de CH4 haya aumentado en 0.5, tal como puede constatarse en la tabla. Para obtener las soluciones a todos los problemas vaya a la página de contenido en el curso virtual y descargue el archivo PDF. 11