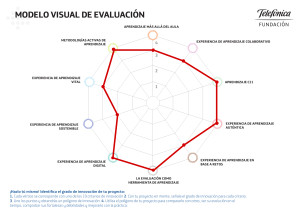
Expo ión Matesicm át y el icas ar te Te s e l a c i o n e s qui la ar n e nes lacio Tese Arte hecho con t esela cione s ☸Guía para docentes ura tect Matemáticas 2 D A D E V O N Matemáticas 2 ŗGuía para docentes Travesías es una serie diseñada por el Departamento de Proyectos Educativos de Ediciones Castillo. Autores: Elia María Covarrubias Castañeda Dirección editorial: Tania Carreño Gerente de Secundaria: Fabián Cabral Gerente de Arte y Diseño: Cynthia Valdespino Coordinación editorial: Verónica Velázquez Edición: Blanca Torres, Griselda Ortigoza Corrección de estilo: Coral Velázquez Primera edición: diciembre 2018 Matemáticas 2. Guía para docentes. Travesías Coordinación diseño: Rafael Tapia Coordinación iconográfica: María Teresa Leyva Coordinación operaciones: Gabriela Rodríguez Diseño de interiores: Gustavo Hernández y Federico Gianni Diseño de portada: Joaquín García Supervisión diseño: Mario Vázquez, Antonio Montero Diagramación: Avant Graph Iconografía: David Antonio Silva (IN Sinister) Producción: Carlos Olvera D. R. © 2018 Ediciones Castillo, S. A. de C. V. Castillo ® es una marca registrada Ediciones Castillo forma parte de Macmillan Education Insurgentes Sur 1886, Florida, Álvaro Obregón, C. P. 01030, Ciudad de México, México. Teléfono: (55) 5128-1350 Lada sin costo: 01 800 536-1777 www.edicionescastillo.com ISBN: 978-607-540-396-0 Miembro de la Cámara Nacional de la Industria Editorial Mexicana. Registro núm. 3304 Prohibida la reproducción o transmisión parcial o total de esta obra por cualquier medio o método o en cualquier forma electrónica o mecánica, incluso fotocopia o sistema para recuperar información, sin permiso escrito del editor. Impreso en México / Printed in Mexico Presentación Estimado profesor: El que todos los niños y adolescentes del país tengan la oportunidad de aprender demanda que las cuestiones sobre qué enseñar y cómo hacerlo sean el punto medular de la reflexión didáctica, ya que en la actualidad el conocimiento que adquirimos debe ampliarse y profundizarse según las rápidas transformaciones sociales. Por ello, es importante dotar a los estudiantes con herramientas para que por sí mismos adquieran conocimientos y desarrollen habilidades y actitudes que les permitan enfrentar los desafíos actuales. La serie Travesías pretende apoyarlo en la ardua labor docente promoviendo la adquisición de saberes fundamentales y el desarrollo de la capacidad de análisis, el pensamiento crítico y la participación social. Por ello, pone énfasis en: • proponer actividades diversas –realizables en el aula– que permitan desarrollar capacidades cognitivas como analizar, inferir, generalizar y abstraer; así como fortalecer el pensamiento lógico, el razonamiento inductivo, el deductivo y el analógico. • conceder al discurso visual un papel preponderante; esto es, considerar la imagen como un recurso didáctico. El libro Matemáticas 2, elaborado con base en el nuevo enfoque educativo, está dividido en tres bloques con un número variable de secuencias, dos evaluaciones (una diagnóstica y una final), y la sección Travesías sobre diversos aspectos de las matemáticas; todo ello con el propósito de facilitar su trabajo en el aula, pues los contenidos están dosificados considerando el número de horas semanales asignadas de forma oficial. Las secuencias están estructuradas con un inicio para explorar y activar conocimientos previos; un desarrollo con actividades para construir los conceptos, algoritmos y procedimientos necesarios para alcanzar los aprendizajes esperados en la secuencia; y un cierre para consolidar y aplicar el aprendizaje. La palabra travesía hace referencia a un viaje… nos hace pensar en una aventura que supone “riesgos” y sorpresas, y que sin embargo se antoja emprender. Así también es todo aprendizaje, no sólo el que se da en la escuela. Nuestro interés es ayudarlo en la formación de ciudadanos críticos, participativos y comprometidos no sólo con su comunidad; sino también con su país. Los editores 3 Índice Presentación ¿Cómo es su guía? Dosificación 3 6 8 Bloque 1 Evaluación diagnóstica 16 Secuencia 1 Multiplicación con fracciones y decimales positivos Secuencia 2 División con fracciones Secuencia 3 Multiplicación de números positivos y negativos Secuencia 4 División de números positivos y negativos Secuencia 5 Potencias con exponentes enteros Secuencia 6 Diagonales y ángulos interiores de un polígono Secuencia 7 Relaciones entre los ángulos de un polígono Secuencia 8 Múltiplos y submúltiplos del metro, litro y kilogramo Secuencia 9 El sistema inglés Secuencia 10 Histogramas y polígonos de frecuencia 18 Evaluación Travesías 4 14 24 32 40 46 54 62 70 78 84 92 94 Bloque 2 Evaluación diagnóstica 96 98 Secuencia 11 Notación científica Secuencia 12 Raíz cuadrada Secuencia 13 Problemas de proporcionalidad inversa y directa Secuencia 14 Problemas de reparto proporcional Secuencia 15 Representaciones tabular, gráfica y algebraica de la proporcionalidad inversa Secuencia 16 Otros problemas de proporcionalidad inversa Secuencia 17 Construcción de polígonos regulares y teselados Secuencia 18 Área de polígonos regulares e irregulares Secuencia 19 Área del círculo Secuencia 20 Gráficas de línea Secuencia 21 Desviación media 100 Evaluación Travesías 188 190 108 116 124 132 140 148 156 164 Bloque 3 188 Evaluación diagnóstica 190 Secuencia 22 Modelos geométricos y expresiones algebraicas Secuencia 23 Sucesiones y expresiones algebraicas equivalentes Secuencia 24 Sistemas de ecuaciones lineales con dos incógnitas Secuencia 25 Método gráfico para resolver un sistema de ecuaciones Secuencia 26 Métodos algebraicos para resolver un sistema de ecuaciones Secuencia 27 Desarrollos planos de prismas y cilindros Secuencia 28 Volumen de prismas rectos Secuencia 29 Volumen de cilindros Secuencia 30 Probabilidad teórica 196 204 212 220 228 236 244 252 260 172 180 Evaluación Travesías 268 270 5 ¿Cómo es su guía? Dosificación Bloque 1 Semana Eje Tema Aprendizaje esperado 1 1. Resuelve problemas de multiplicación y división con fracciones y decimales positivos. Dosificación En este bloque, en el eje Número, álgebra y variación, se amplían y concretan los aprendizajes relacionados con el tema de multiplicación con fracciones y decimales positivos, cuyo procedimiento se estudió en el curso anterior. Se analiza el tema de división con fracciones, la interpretación y resolución de algunos problemas. Además, se amplía el conocimiento en la operatividad de números con signo al resolver multiplicaciones y divisiones. En el eje Forma, espacio y medida, los estudiantes no sólo reconocerán las propiedades de los polígonos con relación a sus ángulos, sino también las distintas unidades de medida y equivalencias entre metro, litro y kilogramo, además de las equivalencias con el sistema inglés. En las secuencias relativas al eje Análisis de datos se estudian formas para representar información, las cuales facilitan el análisis y la toma de decisiones con respecto a ciertos fenómenos: histogramas, polígonos de frecuencias y gráficas de línea. 14 Bloque 1 Número, álgebra y variación Forma, espacio y medida Análisis de datos 1. Multiplicación con fracciones y decimales positivos 2. División con fracciones 3. Multiplicación de números positivos y negativos 4. División de números positivos y negativos 5. Potencias con exponentes enteros 6. Diagonales y ángulos interiores de un polígono 7. Relaciones entre los ángulos de un polígono 8. Múltiplos y submúltiplos del metro, litro y kilogramo 9. El sistema inglés 10. Histogramas y polígonos de frecuencia 12 3. Resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas. 6 22 a 29 Resuelve problemas de multiplicación con números enteros, fracciones y decimales positivos y negativos. 30 a 37 4. División de números positivos y negativos Resuelve problemas de división con números enteros, fracciones y decimales positivos y negativos. Eje Tema Aprendizaje esperado 7 Figuras y 9. Deduce y usa las relaciones entre cuerpos los ángulos de polígonos en la geométricos construcción de polígonos regulares. 8 Forma, espacio y medida 9 10. Resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro, kilogramo y de unidades del sistema inglés (yarda, pulgada, galón, onza y libra). Magnitudes y medidas 38 a 43 5. Potencias con exponentes enteros Resuelve problemas de potencias con exponente entero (elaboración y uso de procedimientos). Audio de comprensión oral Animaciones y tutoriales Galería de imágenes Vínculos Secuencia Contenido Págs. 6. Diagonales y ángulos interiores de un polígono Analiza las propiedades de los polígonos: número de diagonales que pueden trazar desde un vértice, número de diagonales en total y suma de sus ángulos interiores. 52 a 59 7. Relaciones entre los ángulos de un polígono Explora las relaciones entre las medidas de los ángulos interior, exterior y central de polígonos regulares. 60 a 67 8. Múltiplos y submúltiplos del metro, litro y kilogramo Resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro y kilogramo. 68 a 75 9. El sistema inglés Resuelve problemas que implican convertir unidades del Sistema Internacional y de unidades del sistema inglés (yarda, pulgada, galón, onza y libra). 76 a 81 10. Histogramas y polígonos de frecuencia Recolecta, registra y lee datos en histogramas y polígonos de frecuencia. 82 a 89 44 a 51 Análisis de datos 13. Recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea. Estadística 12 Evaluación final 90 y 91 Travesías 92 y 93 Recursos digitales* * Descargue la App Castillo para acceder a sus recursos digitales. 8 9 Ideas erróneas En ocasiones los estudiantes hacen operaciones aritméticas sin observar que hay condiciones que influyen en los procedimientos. Así, al no considerar dichas variaciones se obtienen resultados erróneos. A continuación mencionaremos algunos casos; la intención es detectarlos y dar algunas sugerencias para que no ocurran. • Es común que los estudiantes confundan los procedimientos para resolver las distintas operaciones aritméticas entre fracciones; por lo que se recomienda que las escriban a manera de resumen y las describan con sus palabras. Por ejemplo, suma y resta: son necesarias fracciones equivalentes hasta lograr que los denominadores sean iguales. Multiplicación: se multiplica numerador por numerador y denominador por denominador. División: el recíproco del divisor se multiplica por el dividendo. • Es probable que al resolver operaciones que involucran números con signo, confundan o utilicen sólo un par de reglas. Se recomienda diferenciar las reglas al resolver suma y resta de las reglas de multiplicación y división. • Dado que la operación potenciación con exponentes enteros es algo nuevo para ellos, es común que en lugar de multiplicar la base por sí misma las veces que indica la potencia, multipliquen la base por la potencia. Se recomienda repetir continuamente el significado de resolver una potencia con exponentes enteros. • Cuando se realiza la conversión de unidades, los estudiantes no saben si dividir o multiplicar. Por ello se recomienda utilizar la estructura de regla de tres. • Al estudiar el análisis de datos y construcción de histogramas y polígonos de frecuencias los estudiantes pueden cometer errores al momento de ubicar las ordenadas y las abscisas, lo cual altera la interpretación de resultados. Se recomienda aclarar la forma correcta de construir gráficas. Bloque 1 15 Evaluación diagnóstica Antes de iniciar el contenido de cada bloque encontrará una evaluación diagnóstica con el objetivo de que identifique los conocimientos, habilidades y destrezas con las que cuentan sus estudiantes los resultados le permitirán establecer medidas, emitir juicios y tomar decisiones para mejorar el aprendizaje y desempeño de los alumnos. Antecedentes 6 Resuelve problemas de división con fracciones positivas. 3. Multiplicación de números positivos y negativos Semana 11 13 • Incluye las respuestas de la evaluación del libro del alumno. • Se mencionan los antecedentes sobre lo que el alumno sabe al iniciar el bloque. • Se recomiendan algunos sitios de internet que pueden ayudar a la nivelación de los conocimientos previos. 2. División con fracciones Recursos digitales* 14 y 15 10 Bloque 1 Evaluación diagnóstica 16 a 21 En primero de secundaria, los estudiantes resolvieron problemas que involucraban las operaciones aritméticas de multiplicación y división, por lo que se espera que sean capaces de plantear y resolver problemas similares. La nueva variante consiste en la realización de operaciones con números positivos y negativos, por ello deben considerar las reglas de los signos. A su vez, en el curso anterior también se estudiaron tanto la jerarquía de las operaciones como la resolución de problemas de suma y resta con números enteros. Dicho tema es una herramienta previa para la solución de multiplicaciones y divisiones de números con signo. Mientras que, en quinto y sexto de primaria, los estudiantes resolvieron problemas que involucraban el uso de unidades de masa y longitud; ahora deberán resolver problemas de conversión de unidades. También en esos mismos grados escolares analizaron información a partir de tablas y gráficas. Finalmente, en el año escolar anterior también aprendieron a realizar gráficas circulares. Entrada de bloque Al inicio de cada bloque encontrará un resumen de los contenidos a estudiarse. Se dan algunas sugerencias para trabajar la imagen del libro del alumno y se mencionan algunas ideas y conceptos erróneos que tienen los alumnos. Sugerencias didácticas para la nivelación 6. Completa las equivalencias en las imágenes. 1. Subraya la respuesta correcta. 3 Roberto compró 5 paquetes de galletas de $12.60 cada uno y 4 kg de queso manchego que cuesta $168.75 el kilogramo. ¿Cuánto gastó en total? A) $187.10 B) $189.60 C) $197.40 D) $232.60 2. Realiza las operaciones correspondientes y contesta: un muro se adorna colocando tiras de madera alrededor de éste. Cada tira mide 0.16 m y la longitud del muro es de 8.44 m. Si las tiras de madera colocadas linealmente cubren 3.8 m, ¿cuántas tiras se deberán colocar para terminar? 100 1m= 8.44 – 3.8 = 4.64 4.64 ÷ 0.16 = 29 Para terminar se deberán colocar 29 tiras de madera. 1 kg = cm 1 000 1L= g 1 000 mL 7. Escribe la letra de la magnitud que corresponde a cada unidad de medida. Tiempo (T) Longitud (L) Masa (M) L ( 3. Subraya la opción que representa con números negativos la deuda total en un año si la deuda mensual que aparece en un recibo es de –$570. A) –$582 B) –$5 712 C) –$6 387 D) –$6 840 ( M ) libra ( T ) gramo ( L ) metro ( M ( M ( T ) segundo ( L ) pulgada ) centímetro ( L ) kilómetro ) kilogramo ) hora Recuerde que la evaluación diagnóstica tiene por objetivo tomar decisiones relacionadas con la manera de abordar los distintos temas que se estudiarán en este bloque. También le ayudará a saber si debe retomar, repetir o analizar otros temas que resultan fundamentales para mejorar el aprendizaje. Enseguida se sugieren algunas páginas de internet que pueden ser de utilidad para repasar, practicar y analizar algunos contenidos, de modo que al iniciar formalmente el bloque los estudiantes estén mejor preparados. • Suma y resta de números negativos www.edutics.mx/wYq www.edutics.mx/3jF • Producto de fracciones www.edutics.mx/wYc • Repaso de polígonos www.edutics.mx/wYp • Gráfica circular www.edutics.mx/wYG 8. Considera los datos y construye una gráfica de barras. Recuerda colocar títulos en la gráfica y en los ejes. La siguiente tabla muestra la edad de los asistentes a la presentación de una obra de teatro. 4. Traza las diagonales del hexágono irregular y marca con colores distintos los ángulos interiores del paralelogramo. Edad (años) Menores de 15 De 15 a 25 De 25 a 35 De 35 a 45 De 45 a 55 Mayores de 55 Asistentes 3 12 24 31 29 10 Asistencia por edad 35 5. Calcula la medida de los ángulos b y d. c = 152° a = 115° d b A) ∡ b = 45° y ∡ d = 180° B) ∡ b = 95° y ∡ d = 365° 16 Bloque 1 - Evaluación diagnóstica 14 C) ∡ b = 65° y ∡ d = 208° D) ∡ b = 245° y ∡ d = 28° 30 Asistentes Contenidos Págs. Resuelve problemas de multiplicación con fracciones y decimales positivos. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Nikolay Lobachevsky Secuencia © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Pida a los estudiantes que observen la imagen y respondan: • ¿Qué cuerpos geométricos identifican? Márquenlos sobre la imagen. • ¿Cómo se forman los lados de los cubos de la imagen? • ¿Cómo calcularían el volumen, en litros, de cada cuerpo? Pida a los estudiantes que imaginen la vista superior de los cuerpos de la imagen y la dibujen. Analicen las propuestas en grupo y observen las semejanzas y diferencias. Comente la importancia de aprender a visualizar figuras de tres dimensiones desde diferentes ángulos (arriba, abajo o vistas laterales). Por ejemplo, tanto la ventana de contorno rojo como la que está en uno de los costados pertenecen a planos distintos; pero si se estudia la vista frontal de la imagen, la percepción puede ser diferente. Analice con sus estudiantes la frase escrita por Nikolay Lobachevsky, y pregunte ¿Qué ramas de la matemática conocen? Si mencionan alguna rama explique en qué fenómeno del mundo real se aplica. Si los estudiantes no identifican ninguna, solicite que ennumeren fenómenos del mundo real e identifique con ellos la rama de la matemática que se aplica en tales casos. Después del análisis puede mostrar el siguiente video: www.edutics.mx/wYT 2. Resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos. Evaluación diagnóstica No hay rama de la matemática que no pueda aplicarse algún día a los fenómenos del mundo real. Sugerencias para trabajar la imagen Número, álgebra y variación 5 Presenta la propuesta para planear y organizar el trabajo en el aula para cada bloque. Los aprendizajes de cada secuencia se organizan en 36 semanas. Bloque 1 Multiplicación y división 3 4 Contenido 1. Multiplicación con fracciones y decimales positivos Evaluación diagnóstica 2 25 20 15 10 5 0 Menores de 15 De 15 a 25 De 25 a 35 De 35 a 45 Edad (años) De 45 a 55 Mayores de 55 9. Revisa los resultados con tu profesor. Juntos establezcan los temas en los que deberás poner más atención y las estrategias de estudio a implementar para que aprendas los contenidos del bloque. 15 Bloque 1 - Evaluación diagnóstica 17 Solucionario Multiplicación con fracciones y decimales positivos S1 Partimos S1 Resuelve problemas de multiplicación con fracciones y decimales positivos. Sugerencias didácticas Partimos 1. a) Glosario manzana. Espacio o bloque de casas delimitado por calles, generalmente cuatro. Nogal b) La fracción que ocupa el museo es de c) 4 860 m2 Compara tus respuestas y procedimientos con los de tus compañeros. ¿Qué operaciones utilizaron para resolver la actividad? 9 . 20 Si es necesario, guíe el análisis para resolver el inciso e) de la actividad 1 preguntando ¿Cuál es la fracción correspondiente a la longitud total del circuito? Entonces, ¿cuál es la fracción correspondiente a la mitad del circuito? ¿Cuál a la cuarta parte del circuito? Se recomienda hacer el análisis escribiendo las fracciones para tener una mejor comprensión de la situación; por ejemplo: si hay 45 entonces hay 4 pedazos de tamaño 51 , la mitad de dicha fracción es 2 pedazos de tamaño 51 , es decir, 25 . Por otro lado, y de manera más formal, puede plantear ¿Cuánto es 1 de 4 ? Una vez hecho el planteamiento, deben deducir que, para obtener la 2 5 respuesta, tendrán que multiplicar las fracciones. Explique a sus estudiantes la importancia de calcular la fracción correspondiente a un total, ya que de esta manera se obtiene el número de elementos que le corresponden a dicha fracción. 1 2 1 4 3 4 Inicio Fin 1. Lee la situación y contesta. Se construyó un museo que ocupa tres quintas partes de la cuadra sobre la calle Olivo y tres cuartas partes de la cuadra sobre la calle Nogal. Cedro a) Representa en el mapa la parte de la manzana que ocupa el museo. b) ¿Qué fracción de toda la manzana ocupa el museo? c) Si el área total de la manzana es de 10 800 m2, ¿cuántos metros cuadrados ocupa el museo? Olivo Olivo Laurel Cedro e) Expresa por medio de una multiplicación de fracciones los kilómetros que cada pareja recorrió en el tren. En primer grado aprendiste a multiplicar fracciones por fracciones y decimales por decimales. En esta secuencia aprenderás a resolver problemas que involucran multiplicaciones con fracciones y decimales, así como combinaciones que incluyen más de una operación. Las operaciones básicas, como la multiplicación, se utilizan con frecuencia en varias situaciones de la vida cotidiana por lo que es importante resolverlas satisfactoriamente con todo tipo de números. Pregunte ¿En cuántas partes se divide la manzana para saber las dimensiones del museo? Si es necesario dibuje el rectángulo en el pizarrón y pida a un alumno que haga las divisiones para calcular la fracción que se solicita. Solucionario Sugerencias didácticas Multiplicación con fracciones y decimales positivos Teresa y Claudia: Carlos y Mariela: Luis y Pedro: Solucionario Juan y Carolina: 2. Resuelvan en parejas los siguientes problemas. 1 2 a) Karla tiene 2 2 paquetes de galletas, de los cuales 3 partes son de nuez y el 2 resto de vainilla. De las galletas de nuez, 5 partes tienen chispas de chocolate, ¿qué fracción del total de galletas hay en esta combinación? Nogal Antes de resolver la actividad 1 de la sección “Recorremos”, lean la sección “Recuerda” y analicen qué operación se debe hacer para obtener la fracción de una fracción. Por ejemplo pregunte ¿Cuánto es 21 de 83 y 43 de 83 ? Haga más ejercicios como los anteriores. Sugerencias didácticas 1. a) 25 km d) Dieron 2 3 4 b) 35 km vueltas y recorrieron 11 5 c) Luis y Pedro se bajaron en el martillo, después de 1 c) 1 km km = 2.2 km. 1 4 vueltas. d) Si Juan y Carolina dieron dos vueltas completas y después se bajaron en las sillas voladoras, ¿cuántas vueltas dieron? ¿Cuántos kilómetros recorrieron a bordo del tren? 18 Bloque 1 - Secuencia 1 = 2 5 × 45 = 3 5 4 5 × 45 = 1 Juan y Carolina: 11 4 × 45 = 11 5 4 15 partes son galletas de nuez con chocolate. • 51 del total son galletas de vainilla con almendras. • Nuez con chispas de chocolate: 12 Nuez sola: 18 Vainilla con almendras: 9 Vainilla sola: 6 4 partes del total de personas eran niñas. b) • 23 × 25 = 15 • Escriban cuántas galletas hay de cada tipo considerando que en total hay 45. Nuez con chispas de chocolate: 5 4 • Nuez sola: 2 3 × 25 × 41 = 4 60 = 1 15 eran menores de 6 años. • Había 8 niñas y 2 eran menores de 6 años. Vainilla con almendras: Vainilla sola: 2 b) La familia García rentó un autobús para ir de excursión. Las 3 partes de las 2 1 personas eran mujeres, 5 partes de ellas eran niñas y 4 parte de las niñas eran menores de seis años. • ¿Qué fracción del total eran menores de seis años? • Si en total había 30 personas en el autobús, ¿cuántas niñas había y cuántas de ellas eran menores de seis años? 16 Recursos adicionales Bloque 1 - Secuencia 1 17 19 Sugerencias didácticas 3. Si las placas de los autos de carreras son como las de la imagen, ¿cuál es la cantidad máxima de autos que pueden participar en la carrera si solo se toman en cuenta los números? A) 10 autos B) 102 autos C) 103 autos D) 104 autos Analiza cada situación y subraya la opción correcta. 1. En la imagen se muestra el circuito para una competencia de carreras de autos. Analiza el letrero que se enciende en la estación 4 y responde. E4 4. Observa la pista, ¿cuántos grados debe rotarse el volante en cada vuelta? A) 360° C) 90° B) 135° D) 45° Inicio y meta • ¿A cuántos corredores se entrevistaron? A) 25 C) 100 B) 53 D) Más de 100 • Uno de los participantes terminó la carrera y otro sólo junto 85.8 puntos, ¿cuántos puntos obtuvo en total el primer participante y en qué estación quedó el segundo? A) El primero obtuvo 114.4 puntos y el segundo quedó en la estación 6. B) El primero obtuvo 100 puntos y el segundo quedó en la estación 6. C) El primero obtuvo 80.4 puntos y el segundo quedó en la estación 7. D) El primero obtuvo 57.2 puntos y el segundo quedó en la estación 5. 3 8 de la pista y 1 4 de la pista 1 B) 1 3 4 vueltas 3 5 D) 5 8 de la pista y 2 5 de la pista partes del circuito, ¿cuántas vueltas se pueden C) 2 D) 2 1 6 2 5 vueltas vueltas 2. La capacidad del tanque del auto de carreras es de 105 L de gasolina. Por cada 2 litro recorre 8 000 m y por cada estación recorrida se consumen 7 partes del tanque. ¿Cuántos galones de gasolina quedan en el tanque al terminar la tercera estación y cuántos kilómetros se habrán recorrido? A) 15 galones, 0.8 km B) 4 galones, 720 km C) 4 galones, 450 km D) 0 galones, 800 km 90 5 9 10 11 12 13 14 15 16 17 18 Edad Cabe mencionar que cada estudiante posee habilidades y capacidades variadas, por lo que se recomienda tomar en cuenta el avance propio de cada uno. La intención es medir el avance individual de los estudiantes, por lo que, debe existir una comparación con sus propios aprendizajes; esto es, analizar cómo ingresa al curso y cómo egresa de éste. La evaluación permitirá a los estudiantes poner a prueba los conocimientos y habilidades adquiridos. Es importante mencionar que la evaluación incluye algunas imágenes, las cuales aportan información a la solución del problema. Después de que los alumnos hayan resuelto la evaluación, se recomienda hacer algunos comentarios y sugerencias de análisis para la retroalimentación. Puede realizar las siguientes preguntas con base en la imagen del problema 1: ¿Cuántos lados tiene la pista? ¿Qué forma tiene la pista? ¿Cuántos ángulos internos y externos tiene? ¿Cuánto suman los ángulos externos? ¿Cómo puedes obtener el valor de un ángulo interno? Si ya se recorrió 21 de la pista, ¿cuántas estaciones de han recorrido? Si lo considera necesario, para comprobar la solución de la actividad 2, realice una tabla de valores. Pida que calculen cuánta gasolina se ha consumido en las estaciones 2, 3, 4, 5, 6, 7 y 8, pregunte ¿En qué momento debe recargar gasolina? Recuerde a sus estudiantes la importancia de generar una tabla de equivalencias entre unidades de medición. Explique que en la actividad 4 deben identificar que se requiere el valor del ángulo exterior de la pista. Dado el contexto del problema 6, recuerde a los estudiantes el procedimiento para despejar una variable. 6. Para un objeto en caída libre, la fuerza de gravedad es proporcional a la masa m, de dicho objeto, de manera que se cumple la siguiente expresión, donde g es la aceleración de la gravedad dirigida hacia abajo (– 9.8 m/s2). La fuerza se mide en newtons (N). F = mg Si sobre un cuerpo en caída libre actúa una fuerza de – 490 N, ¿cuál es la masa de dicho cuerpo? A) 50 kg B) 85 kg C) 480.2 kg D) 4 802 kg Reúnete en pareja con un compañero. Comparen sus respuestas, argumenten el porqué respondieron así. Corrijan lo que sea necesario. Coevaluación Revisa con tu profesor los resultados: ¿en qué necesitas mejorar? ¿Qué estrategias usarás? Heteroevaluación Bloque 1 - Evaluación 91 En este apartado encontrará recomendaciones bibliográficas y electrónicas extra para apoyar su clase. Evaluación 93 Contiene las respuestas a los reactivos y algunas orientaciones sobre la evaluación. Travesías Travesías Sugerencias didácticas Explique que a través de la historia el hombre ha construido objetos matemáticos que son la principal herramienta para la interpretación de fenómenos naturales y sociales. La evolución de dichas herramientas va ligada con las necesidades del hombre, el ejemplo más claro relacionado con este tema, es el tipo de registro que se menciona en “Materiales para el registro de datos estadísticos”. Aquí se habla de los materiales utilizados para el registro de información, se muestran marcas hechas en piedra o huesos. Plantee a los alumnos las siguientes preguntas para saber lo que piensan del registro de datos en la actualidad ¿Cómo se lleva a cabo el manejo de información? ¿Qué software conoces que ayuda a representar datos a través de gráficas? ¿Cuál crees que sea la principal necesidad del hombre relacionada con el manejo de información? Cuando te ofrecen nuevos productos, ¿crees que se haga un estudio para lograr más ventas? Sugerencias didácticas Los datos de ayer y hoy La recolección, registro e interpretación de datos provenientes de distintas fuentes es una práctica que se ha desarrollado desde tiempos remotos, pues en una sociedad organizada siempre surge la necesidad de poseer datos sobre su población, actividades y condiciones materiales que la rodean. Así, esta práctica ha evolucionado desde la simple recolección de datos hasta la diversa y rigurosa interpretación que en la actualidad se hace de éstos. La estadística, en general, trata de la recopilación, organización, presentación, análisis e interpretación de datos numéricos con el fi n de tomar decisiones. Los primeros registros estadísticos de los que se tiene conocimiento fueron los censos, estudios descriptivos sobre todos los integrantes de una población. En antiguas civilizaciones como la egipcia, china, griega y romana era común que se llevaran a cabo recuentos sobre características de los habitantes: nacimientos, defunciones o de aspectos económicos, impuestos, cosechas, etcétera. De acuerdo con lo que indica el historiador griego Herodoto, en Egipto algunos de los censos de riqueza y población se hacían para planificar la construcción de las pirámides. En México Los materiales empleados para el registro y comunicación de datos han evolucionado a la par de la escritura. Van desde la piedra, láminas metálicas, papiros y papel, entre otros, hasta los soportes electrónicos actuales. Travesías Se presentan sugerencias didácticas para trabajar esta sección. Hacia el año 3 000 a. n. e. los babilonios usaban pequeñas tablillas de arcilla para recopilar datos acerca de la producción agrícola y los géneros vendidos o cambiados mediante trueque. 94 Bloque 1 - Travesías 92 Recursos adicionales En el siguiente enlace podrá consultar información de los histogramas y polígonos de frecuencia: • “Histograma” y “Polígono de frecuencia”, disponible en www.edutics.mx/ wPT (consulta: 24 de agosto de 2018). Nuestro país tiene una rica tradición en materia de información estadística de la cual dan cuenta diversos códices e innumerables publicaciones, instituciones y personajes desde la época colonial hasta nuestros días. El 25 de enero de 1983 se creó, por decreto presidencial, el Instituto Nacional de Estadística, Geografía e Informática (Inegi). Con su creación, el instituto modernizó la valiosa tradición que tenía nuestro país en materia de captación, procesamiento y difusión de información acerca del territorio, la población y la economía. El 16 de abril de 2008, el Inegi cambió su personalidad jurídica, adquiriendo autonomía técnica y de gestión. A partir de entonces su nueva denominación es Instituto Nacional de Estadística y Geografía, pero aún conserva las mismas siglas. Materiales para el registro de datos estadísticos Desde la prehistoria han existido formas rudimentarias de registrar información con fines contables: montículos de piedras o señ ales en huesos, pieles, palos y paredes de cuevas. Antes de leer el subtema “En México” pregunte a los estudiantes: • ¿Qué sabes sobre la historia de México y las formas en que manejaban la información en el pasado? • ¿Qué instituciones conoces que lleven a cabo recolección de datos y manejo de información en la actualidad? • ¿Qué investigación te gustaría que se llevara a cabo? ¿Por qué? Después de responder de forma grupal las preguntas anteriores analicen dicho subtema. Enseguida aliéntelos a que visualicen la forma en que se registraba la información de los datos de tributación y cómo es que ahora se podrían registrar según los temas estudiados. Al término de la lectura y análisis del último párrafo, vuelva a preguntar: ¿qué tema te gustaría investigar? Actualmen te se dispone de medios electrónico s para resguardar información así como de las hojas de cálculo o diversos softwares que permiten introducir números y variables y, de forma casi instantánea , presentar una representac ión visual de los mismos. Plantear y resolver problemas usando herramientas matemáticas. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 5 8 15 10 0 2 5 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. B) 25 20 • Al trazar el polígono de frecuencias, ¿cuáles son los 8 puntos medios de los intervalos? A) 8, 10, 12, 14 y 16 C) 9.5, 11.5, 13.5, 15.5 y 17.5 B) 9, 11, 13, 15 y 17 D) 10.5, 12.5, 14.5, 16.5 y 18.5 • Un corredor logró avanzar hasta de la pista, y con dificultad recorrió más del resto de la pista. Inicialmente, ¿cuánto le faltaba por recorrer? y en el último tramo, ¿qué parte de la pista recorrió? 1 2 1 A) 2 de la pista y 5 de la pista C) 3 de la pista • Si en 4 de hora se recorren dar en una hora? A) Una vuelta Edad a la que los corredores de autos eligieron su profesión Cantidad de corredores 5. En el histograma se muestran los resultados de una encuesta realizada a los corredores de autos acerca de la edad en la que eligieron esa profesión. ¿Cuál fue el intervalo de edad con mayor frecuencia? A) De 16 a 18 años C) De 10 a 12 años B) De 14 a 16 años D) Más de 18 años E8 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Autoevaluación Se incluyen las respuestas a las actividades del libro del alumno. Encontrará la leyenda Respuesta libre (R. L.) o Respuesta modelo (R. M.), según se requiera. También se proporcionan recursos bibliográficos o tecnológicos complementarios. • ¿Qué fracción del total de personas eran niñas? Expliquen en grupo cuántos factores tienen las multiplicaciones con las que pueden resolverse los problemas. ¿De qué forma las resolvieron? Si hay diferencia en los resultados, revísenlos para llegar a un acuerdo. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 92 Bloque 1 - Evaluación Evaluación A lo largo del proceso de enseñanza-aprendizaje se presentan tres momentos de evaluación, cada uno de ellos tiene características que en conjunto determinan el avance de los estudiantes. El primer momento está presente al aplicar la evaluación diagnóstica, la cual marca la pauta en la toma de decisiones enfocadas en las planeaciones didácticas. Su principal objetivo es identificar las necesidades de los estudiantes para desarrollar las temáticas que se abordaran en el nuevo bloque; una vez identificadas se procede a planear los temas que se deben repasar para alcanzar los objetivos deseados. Al revisar la evaluación diagnóstica que se propone en este libro, se pueden identificar los conocimientos y habilidades que los estudiantes deben reforzar. Como segundo momento, está la evaluación formativa. Dicha evaluación está enfocada en dar un seguimiento constante al desempeño académico de los estudiantes. Su principal objetivo es determinar los aspectos en los que el estudiante debe mejorar, cuáles herramientas le han servido y en cuáles debe trabajar aún más para alcanzar los aprendizajes deseados. Puede servir como actividad de retroalimentación, en la que el estudiante reconoce sus fortalezas y deficiencias y, a partir de ellas, los aspectos que puede mejorar; es decir, se le ofrece un camino a seguir para mejorar su aprendizaje. Las técnicas más recomendadas para su realización son: observación, análisis de desempeño de los estudiantes (tanto en actitudes como en adquisición de conocimiento) y autoevaluación. En la página de internet www.edutics.mx/w2W puede consultar más información al respecto. Por último se tiene la evaluación sumativa, la cual emite un juicio final del aprovechamiento del estudiante. Este tipo de evaluación es el resultado del análisis de información que se obtiene sobre el desempeño académico del alumno a lo largo del bloque. De igual forma, ésta determina si los conocimientos planeados se alcanzaron y si las habilidades estudiadas forman parte del saber de los estudiantes. Al emitir esta evaluación se determina la acreditación del bloque. b) Carlos y Mariela bajaron en la las sillas voladoras. Solucionario Se proporcionan sugerencias didácticas para el trabajo en el aula. Evaluación 1. Analiza y contesta. Juan y sus amigos visitaron un parque de diversiones; para recorrerlo, subieron a 4 un tren cuyo circuito mide 5 km y en el cual se puede permanecer las vueltas que se deseen. Observa en la siguiente página este circuito y expresa en una fracción irreducible los kilómetros que cada una de las siguientes parejas recorrió. a) Teresa y Claudia dieron media vuelta y bajaron en la montaña rusa. Una fracción irreducible es aquella que está escrita en su forma equivalente más sencilla, con el menor numerador y el menor denominador posibles. Es decir, que no se puede simplificar más. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Recuerda Sugerencias didácticas © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Multiplicación de fracciones positivas × 3 4 2. a) • Si 5 partes de las galletas de vainilla tienen trozos de almendra, ¿qué fracción del total de galletas es de esta combinación? Multiplicación de fracciones positivas Recorremos 1 2 Carlos y Mariela: Luis y Pedro: 3 Recorremos e) Teresa y Claudia: Discute con el resto del grupo: ¿qué tipo de fracciones aparecen en los problemas? ¿Obtuvieron las mismas fracciones irreducibles? ¿Todos escribieron las mismas multiplicaciones? Verifiquen juntos si al realizar las multiplicaciones se obtiene el total de kilómetros que recorrió cada pareja. Laurel Secuencias Cada 10 años el Inegi realiza un censo de población y vivienda. El último se llevó a cabo en 2010. En 1535, por órdenes del primer virrey de la Nueva España, Antonio de Mendoza, se realiza el Códice Mendocino, que en su apartado “Matrícula de tributos” se describe la manera en que los pueblos registraba sus datos de la tributación. Î En el siglo XVII Gaspar Neumann demostró, basándose en los registros de defunciones de la época, la falsedad de la creencia popular de que en los años acabados en siete moría más gente. ¿Conoces algún otro hecho en el que la aportación estadística haya provocado un cambio de ideas? 93 Bloque 1 - Travesías 95 7 Dosificación Bloque 1 Semana Eje Tema 1 Número, álgebra y variación 5 Multiplicación y división 1. Resuelve problemas de multiplicación y división con fracciones y decimales positivos. 3 Audio de comprensión oral 2. Resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos. 3. Resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas. 6 8 Secuencia Contenido Evaluación diagnóstica 2 4 Aprendizaje esperado Animaciones y tutoriales Galería de imágenes Págs. 14 y 15 1. Multiplicación con fracciones y decimales positivos Resuelve problemas de multiplicación con fracciones y decimales positivos. 16 a 21 2. División con fracciones Resuelve problemas de división con fracciones positivas. 22 a 29 3. Multiplicación de números positivos y negativos Resuelve problemas de multiplicación con números enteros, fracciones y decimales positivos y negativos. 30 a 37 4. División de números positivos y negativos Resuelve problemas de división con números enteros, fracciones y decimales positivos y negativos. 38 a 43 5. Potencias con exponentes enteros Resuelve problemas de potencias con exponente entero (elaboración y uso de procedimientos). 44 a 51 Vínculos Recursos digitales* * Descargue la App Castillo para acceder a sus recursos digitales. Semana Eje Tema Aprendizaje esperado 7 Figuras y 9. Deduce y usa las relaciones entre cuerpos los ángulos de polígonos en la geométricos construcción de polígonos regulares. 8 Forma, espacio y medida 9 Magnitudes y medidas 10 11 12 Análisis de datos Estadística 10. Resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro, kilogramo y de unidades del sistema inglés (yarda, pulgada, galón, onza y libra). 13. Recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea. Secuencia Contenido Págs. 6. Diagonales y ángulos interiores de un polígono Analiza las propiedades de los polígonos: número de diagonales que pueden trazar desde un vértice, número de diagonales en total y suma de sus ángulos interiores. 52 a 59 7. Relaciones entre los ángulos de un polígono Explora las relaciones entre las medidas de los ángulos interior, exterior y central de polígonos regulares. 60 a 67 8. Múltiplos y submúltiplos del metro, litro y kilogramo Resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro y kilogramo. 68 a 75 9. El sistema inglés Resuelve problemas que implican convertir unidades del Sistema Internacional y de unidades del sistema inglés (yarda, pulgada, galón, onza y libra). 76 a 81 10. Histogramas y polígonos de frecuencia Recolecta, registra y lee datos en histogramas y polígonos de frecuencia. 82 a 89 Evaluación final 90 y 91 Travesías 92 y 93 Recursos digitales* 9 Dosificación Bloque 2 Semana Eje Tema 13 Aprendizaje esperado Multiplicación y división 15 3. Resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas. 16 Proporcionalidad Funciones 10 4. Resuelve problemas de proporcionalidad directa e inversa y de reparto proporcional. Número, álgebra y variación 18 19 Contenido Evaluación diagnóstica 14 17 Secuencia 6. Analiza y compara situaciones de variación lineal y proporcionalidad inversa, a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la Física y otros contextos. Págs. 96 y 97 11. Notación científica Resuelve problemas de potencias con exponente entero (notación científica). 98 a 105 12. Raíz cuadrada Aproxima raíces cuadradas. 106 a 113 13. Problemas de proporcionalidad inversa y directa Resuelve problemas de proporcionalidad inversa y compara con la proporcionalidad directa. 114 a 121 14. Problemas de reparto proporcional Resuelve problemas de reparto proporcional. 122 a 129 15. Representaciones tabular, gráfica y algebraica de la proporcionalidad inversa Analiza y compara situaciones de variación lineal y proporcionalidad inversa, a partir de sus representaciones tabular, gráfica y algebraica. 130 a 137 16. Otros problemas de proporcionalidad inversa Interpreta y resuelve problemas que se modelan con variación lineal y proporcionalidad inversa, incluyendo fenómenos de la Física y otros contextos. 138 a 145 Recursos digitales* Semana Eje 20 Tema Aprendizaje esperado Figuras y cuerpos geométricos 9. Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares. Magnitudes y medidas 11. Calcula el perímetro y área de polígonos regulares y del círculo a partir de diferentes datos. Forma, espacio y medida 21 22 13. Recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea. 23 24 25 26 Análisis de datos Estadística Secuencia Contenido Págs. 17. Construcción de polígonos regulares y teselados Resuelve problemas de construcción de polígonos regulares a partir de diferentes datos (construye teselaciones). 146 a 153 18. Área de polígonos regulares e irregulares Desarrolla y usa la fórmula para calcular el área de polígonos regulares a partir de diferentes datos. 154 a 161 19. Área del círculo Desarrolla y usa la fórmula para calcular el área del círculo a partir de diferentes datos. 162 a 169 20. Gráficas de línea Recolecta, registra y lee datos en histogramas, polígonos de frecuencia y gráficas de línea. 170 a 177 14. Usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana), el rango y la desviación media de un conjunto 21. Desviación media de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión. Usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana), el rango y la desviación media de un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión. Recursos digitales* 178 a 185 Evaluación final 186 y 187 Travesías 188 y 189 11 Dosificación Bloque 3 Semana Eje Tema 27 Patrones, figuras geométricas y expresiones equivalentes 29 31 32 12 Secuencia Contenido Evaluación diagnóstica 28 30 Aprendizaje esperado 8. Formula expresiones de primer grado para representar propiedades (perímetros y áreas) 22. Modelos de figuras geométricas y verifica equivalencia geométricos y expresiones algebraicas de expresiones, tanto algebraica como geométricamente (análisis de las figuras). 7. Verifica algebraicamente la equivalencia de expresiones de primer grado, formuladas a partir de sucesiones. Número, álgebra y variación Ecuaciones 5. Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas. Págs. 192 y 193 Formula expresiones de primer grado para representar propiedades (perímetros y áreas) de figuras geométricas y verifica equivalencia de expresiones, tanto algebraica como geométricamente (análisis de las figuras). 194 a 201 Verifica algebraicamente la equivalencia de 23. Sucesiones y expresiones algebraicas expresiones de primer grado, formuladas a partir de sucesiones. equivalentes 202 a 209 Resuelve problemas mediante la formulación y 24. Sistemas de ecuaciones lineales con solución de sistemas de dos ecuaciones lineales con dos incógnitas (procedimientos intuitivos). dos incógnitas 210 a 217 25. Método gráfico para Resuelve problemas mediante la formulación y solución gráfica de sistemas de dos ecuaciones resolver un sistema de lineales con dos incógnitas. ecuaciones 218 a 225 26. Métodos algebraicos para resolver un sistema de ecuaciones 226 a 233 Resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas. Recursos digitales* Semana Eje Tema Aprendizaje esperado 27. Desarrollos planos de prismas y cilindros 33 Forma, espacio y medida Magnitudes y medidas 12. Calcula el volumen de primas y cilindros rectos. 34 35 36 Secuencia Análisis de datos Probabilidad 15. Determina la probabilidad teórica de un evento en un experimento aleatorio. Contenido Págs. Construye desarrollos planos de prismas y cilindros. 234 a 241 28. Volumen de prismas Calcula el volumen de primas rectos (base rectos polígono regular). 242 a 249 29. Volumen de cilindros 250 a 257 Calcula el volumen de cilindros rectos. Determina la probabilidad teórica de un evento 30. Probabilidad teórica en un experimento aleatorio (comparación con la probabilidad frecuencial). Recursos digitales* 258 a 265 Evaluación final 266 y 267 Travesías 268 y 269 13 Bloque 1 Sugerencias para trabajar la imagen Pida a los estudiantes que observen la imagen y respondan: • ¿Qué cuerpos geométricos identifican? Márquenlos sobre la imagen. • ¿Cómo se forman los lados de los cubos de la imagen? • ¿Cómo calcularían el volumen, en litros, de cada cuerpo? Pida a los estudiantes que imaginen la vista superior de los cuerpos de la imagen y la dibujen. Analicen las propuestas en grupo y observen las semejanzas y diferencias. Comente la importancia de aprender a visualizar figuras de tres dimensiones desde diferentes ángulos (arriba, abajo o vistas laterales). Por ejemplo, tanto la ventana de contorno rojo como la que está en uno de los costados pertenecen a planos distintos; pero si se estudia la vista frontal de la imagen, la percepción puede ser diferente. Analice con sus estudiantes la frase escrita por Nikolay Lobachevsky, y pregunte ¿Qué ramas de la matemática conocen? Si mencionan alguna rama explique en qué fenómeno del mundo real se aplica. Si los estudiantes no identifican ninguna, solicite que ennumeren fenómenos del mundo real e identifique con ellos la rama de la matemática que se aplica en tales casos. Después del análisis puede mostrar el siguiente video: www.edutics.mx/wYT Contenidos En este bloque, en el eje Número, álgebra y variación, se amplían y concretan los aprendizajes relacionados con el tema de multiplicación con fracciones y decimales positivos, cuyo procedimiento se estudió en el curso anterior. Se analiza el tema de división con fracciones, la interpretación y resolución de algunos problemas. Además, se amplía el conocimiento en la operatividad de números con signo al resolver multiplicaciones y divisiones. En el eje Forma, espacio y medida, los estudiantes no sólo reconocerán las propiedades de los polígonos con relación a sus ángulos, sino también las distintas unidades de medida y equivalencias entre metro, litro y kilogramo, además de las equivalencias con el sistema inglés. En las secuencias relativas al eje Análisis de datos se estudian formas para representar información, las cuales facilitan el análisis y la toma de decisiones con respecto a ciertos fenómenos: histogramas, polígonos de frecuencias y gráficas de línea. 14 Bloque 1 Número, álgebra y variación Forma, espacio y medida Análisis de datos 1. Multiplicación con fracciones y decimales positivos 2. División con fracciones 3. Multiplicación de números positivos y negativos 4. División de números positivos y negativos 5. Potencias con exponentes enteros 6. Diagonales y ángulos interiores de un polígono 7. Relaciones entre los ángulos de un polígono 8. Múltiplos y submúltiplos del metro, litro y kilogramo 9. El sistema inglés 10. Histogramas y polígonos de frecuencia 12 No hay rama de la matemática que no pueda aplicarse algún día a los fenómenos del mundo real. Nikolay Lobachevsky Ideas erróneas En ocasiones los estudiantes hacen operaciones aritméticas sin observar que hay condiciones que influyen en los procedimientos. Así, al no considerar dichas variaciones se obtienen resultados erróneos. A continuación mencionaremos algunos casos; la intención es detectarlos y dar algunas sugerencias para que no ocurran. • Es común que los estudiantes confundan los procedimientos para resolver las distintas operaciones aritméticas entre fracciones; por lo que se recomienda que las escriban a manera de resumen y las describan con sus palabras. Por ejemplo, suma y resta: son necesarias fracciones equivalentes hasta lograr que los denominadores sean iguales. Multiplicación: se multiplica numerador por numerador y denominador por denominador. División: el recíproco del divisor se multiplica por el dividendo. • Es probable que al resolver operaciones que involucran números con signo, confundan o utilicen sólo un par de reglas. Se recomienda diferenciar las reglas al resolver suma y resta de las reglas de multiplicación y división. • Dado que la operación potenciación con exponentes enteros es algo nuevo para ellos, es común que en lugar de multiplicar la base por sí misma las veces que indica la potencia, multipliquen la base por la potencia. Se recomienda repetir continuamente el significado de resolver una potencia con exponentes enteros. • Cuando se realiza la conversión de unidades, los estudiantes no saben si dividir o multiplicar. Por ello se recomienda utilizar la estructura de regla de tres. • Al estudiar el análisis de datos y construcción de histogramas y polígonos de frecuencias los estudiantes pueden cometer errores al momento de ubicar las ordenadas y las abscisas, lo cual altera la interpretación de resultados. Se recomienda aclarar la forma correcta de construir gráficas. Bloque 1 13 Bloque 1 15 Antecedentes En primero de secundaria, los estudiantes resolvieron problemas que involucraban las operaciones aritméticas de multiplicación y división, por lo que se espera que sean capaces de plantear y resolver problemas similares. La nueva variante consiste en la realización de operaciones con números positivos y negativos, por ello deben considerar las reglas de los signos. A su vez, en el curso anterior también se estudiaron tanto la jerarquía de las operaciones como la resolución de problemas de suma y resta con números enteros. Dicho tema es una herramienta previa para la solución de multiplicaciones y divisiones de números con signo. Mientras que, en quinto y sexto de primaria, los estudiantes resolvieron problemas que involucraban el uso de unidades de masa y longitud; ahora deberán resolver problemas de conversión de unidades. También en esos mismos grados escolares analizaron información a partir de tablas y gráficas. Finalmente, en el año escolar anterior también aprendieron a realizar gráficas circulares. 1. Subraya la respuesta correcta. 3 Roberto compró 5 paquetes de galletas de $12.60 cada uno y 4 kg de queso manchego que cuesta $168.75 el kilogramo. ¿Cuánto gastó en total? A) $187.10 B) $189.60 C) $197.40 D) $232.60 2. Realiza las operaciones correspondientes y contesta: un muro se adorna colocando tiras de madera alrededor de éste. Cada tira mide 0.16 m y la longitud del muro es de 8.44 m. Si las tiras de madera colocadas linealmente cubren 3.8 m, ¿cuántas tiras se deberán colocar para terminar? 8.44 – 3.8 = 4.64 4.64 ÷ 0.16 = 29 Para terminar se deberán colocar 29 tiras de madera. 3. Subraya la opción que representa con números negativos la deuda total en un año si la deuda mensual que aparece en un recibo es de –$570. A) –$582 B) –$5 712 C) –$6 387 D) –$6 840 4. Traza las diagonales del hexágono irregular y marca con colores distintos los ángulos interiores del paralelogramo. 5. Calcula la medida de los ángulos b y d. c = 152° a = 115° d b A) ∡ b = 45° y ∡ d = 180° B) ∡ b = 95° y ∡ d = 365° 16 Bloque 1 - Evaluación diagnóstica 14 C) ∡ b = 65° y ∡ d = 208° D) ∡ b = 245° y ∡ d = 28° © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Antes de iniciar el contenido de cada bloque encontrará una evaluación diagnóstica con el objetivo de que identifique los conocimientos, habilidades y destrezas con las que cuentan sus estudiantes los resultados le permitirán establecer medidas, emitir juicios y tomar decisiones para mejorar el aprendizaje y desempeño de los alumnos. Evaluación diagnóstica Evaluación diagnóstica Sugerencias didácticas para la nivelación 6. Completa las equivalencias en las imágenes. 100 1m= 1 kg = cm 1 000 1L= g 1 000 mL 7. Escribe la letra de la magnitud que corresponde a cada unidad de medida. Tiempo (T) Longitud (L) Masa (M) L ( ( M ) libra ( T ) gramo ( L ) metro ( M ( M ( T ) segundo ( L ) pulgada ) centímetro ( L ) kilómetro ) kilogramo ) hora Recuerde que la evaluación diagnóstica tiene por objetivo tomar decisiones relacionadas con la manera de abordar los distintos temas que se estudiarán en este bloque. También le ayudará a saber si debe retomar, repetir o analizar otros temas que resultan fundamentales para mejorar el aprendizaje. Enseguida se sugieren algunas páginas de internet que pueden ser de utilidad para repasar, practicar y analizar algunos contenidos, de modo que al iniciar formalmente el bloque los estudiantes estén mejor preparados. • Suma y resta de números negativos www.edutics.mx/wYq www.edutics.mx/3jF • Producto de fracciones www.edutics.mx/wYc • Repaso de polígonos www.edutics.mx/wYp • Gráfica circular www.edutics.mx/wYG 8. Considera los datos y construye una gráfica de barras. Recuerda colocar títulos en la gráfica y en los ejes. La siguiente tabla muestra la edad de los asistentes a la presentación de una obra de teatro. Edad (años) Menores de 15 De 15 a 25 De 25 a 35 De 35 a 45 De 45 a 55 Mayores de 55 Asistentes 3 12 24 31 29 10 Asistencia por edad 30 Asistentes © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 35 25 20 15 10 5 0 Menores de 15 De 15 a 25 De 25 a 35 De 35 a 45 Edad (años) De 45 a 55 Mayores de 55 9. Revisa los resultados con tu profesor. Juntos establezcan los temas en los que deberás poner más atención y las estrategias de estudio a implementar para que aprendas los contenidos del bloque. 15 Bloque 1 - Evaluación diagnóstica 17 Partimos S1 Resuelve problemas de multiplicación con fracciones y decimales positivos. Sugerencias didácticas Pregunte ¿En cuántas partes se divide la manzana para saber las dimensiones del museo? Si es necesario dibuje el rectángulo en el pizarrón y pida a un alumno que haga las divisiones para calcular la fracción que se solicita. Partimos Solucionario 1. a) Glosario manzana. Espacio o bloque de casas delimitado por calles, generalmente cuatro. En primer grado aprendiste a multiplicar fracciones por fracciones y decimales por decimales. En esta secuencia aprenderás a resolver problemas que involucran multiplicaciones con fracciones y decimales, así como combinaciones que incluyen más de una operación. Las operaciones básicas, como la multiplicación, se utilizan con frecuencia en varias situaciones de la vida cotidiana por lo que es importante resolverlas satisfactoriamente con todo tipo de números. 1. Lee la situación y contesta. Se construyó un museo que ocupa tres quintas partes de la cuadra sobre la calle Olivo y tres cuartas partes de la cuadra sobre la calle Nogal. Cedro a) Representa en el mapa la parte de la manzana que ocupa el museo. b) ¿Qué fracción de toda la manzana ocupa el museo? c) Si el área total de la manzana es de 10 800 m2, ¿cuántos metros cuadrados ocupa el museo? Olivo Olivo Laurel Cedro Multiplicación con fracciones y decimales positivos Nogal b) La fracción que ocupa el museo es de c) 4 860 m2 9 . 20 Recorremos Recorremos Multiplicación de fracciones positivas Recuerda Sugerencias didácticas Antes de resolver la actividad 1 de la sección “Recorremos”, lean la sección “Recuerda” y analicen qué operación se debe hacer para obtener la fracción de una fracción. Por ejemplo pregunte ¿Cuánto es 21 de 83 y 43 de 83 ? Haga más ejercicios como los anteriores. Solucionario 1. a) 25 km d) Dieron 2 Compara tus respuestas y procedimientos con los de tus compañeros. ¿Qué operaciones utilizaron para resolver la actividad? 3 4 b) 35 km vueltas y recorrieron Una fracción irreducible es aquella que está escrita en su forma equivalente más sencilla, con el menor numerador y el menor denominador posibles. Es decir, que no se puede simplificar más. Multiplicación de fracciones positivas 1. Analiza y contesta. Juan y sus amigos visitaron un parque de diversiones; para recorrerlo, subieron a 4 un tren cuyo circuito mide 5 km y en el cual se puede permanecer las vueltas que se deseen. Observa en la siguiente página este circuito y expresa en una fracción irreducible los kilómetros que cada una de las siguientes parejas recorrió. a) Teresa y Claudia dieron media vuelta y bajaron en la montaña rusa. b) Carlos y Mariela bajaron en la las sillas voladoras. 1 11 5 c) 1 km km = 2.2 km. c) Luis y Pedro se bajaron en el martillo, después de 1 4 vueltas. d) Si Juan y Carolina dieron dos vueltas completas y después se bajaron en las sillas voladoras, ¿cuántas vueltas dieron? ¿Cuántos kilómetros recorrieron a bordo del tren? 18 Bloque 1 - Secuencia 1 Nogal 16 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Multiplicación con fracciones y decimales positivos Laurel S1 Sugerencias didácticas e) Expresa por medio de una multiplicación de fracciones los kilómetros que cada pareja recorrió en el tren. 1 2 1 4 3 4 Inicio Fin Teresa y Claudia: Carlos y Mariela: Si es necesario, guíe el análisis para resolver el inciso e) de la actividad 1 preguntando ¿Cuál es la fracción correspondiente a la longitud total del circuito? Entonces, ¿cuál es la fracción correspondiente a la mitad del circuito? ¿Cuál a la cuarta parte del circuito? Se recomienda hacer el análisis escribiendo las fracciones para tener una mejor comprensión de la situación; por ejemplo: si hay 45 entonces hay 4 pedazos de tamaño 51 , la mitad de dicha fracción es 2 pedazos de tamaño 51 , es decir, 25 . Por otro lado, y de manera más formal, puede plantear ¿Cuánto es 1 de 4 ? Una vez hecho el planteamiento, deben deducir que, para obtener la 2 5 respuesta, tendrán que multiplicar las fracciones. Explique a sus estudiantes la importancia de calcular la fracción correspondiente a un total, ya que de esta manera se obtiene el número de elementos que le corresponden a dicha fracción. Luis y Pedro: Solucionario Juan y Carolina: e) Teresa y Claudia: 1 2 × 45 = 2 5 Carlos y Mariela: 3 4 × 45 = 3 5 Discute con el resto del grupo: ¿qué tipo de fracciones aparecen en los problemas? ¿Obtuvieron las mismas fracciones irreducibles? ¿Todos escribieron las mismas multiplicaciones? Verifiquen juntos si al realizar las multiplicaciones se obtiene el total de kilómetros que recorrió cada pareja. 2. Resuelvan en parejas los siguientes problemas. 1 2 a) Karla tiene 2 2 paquetes de galletas, de los cuales 3 partes son de nuez y el 2 resto de vainilla. De las galletas de nuez, 5 partes tienen chispas de chocolate, ¿qué fracción del total de galletas hay en esta combinación? 3 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • Si 5 partes de las galletas de vainilla tienen trozos de almendra, ¿qué fracción del total de galletas es de esta combinación? • Escriban cuántas galletas hay de cada tipo considerando que en total hay 45. Nuez con chispas de chocolate: Nuez sola: Luis y Pedro: 5 4 × 45 = 1 Juan y Carolina: 2. a) 11 4 × 45 = 11 5 4 15 partes son galletas de nuez con chocolate. • 51 del total son galletas de vainilla con almendras. • Nuez con chispas de chocolate: 12 Nuez sola: 18 Vainilla con almendras: 9 Vainilla sola: 6 4 partes del total de personas eran niñas. b) • 23 × 25 = 15 • 2 3 × 25 × 41 = 4 60 = 1 15 eran menores de 6 años. • Había 8 niñas y 2 eran menores de 6 años. Vainilla con almendras: Vainilla sola: 2 b) La familia García rentó un autobús para ir de excursión. Las 3 partes de las 2 1 personas eran mujeres, 5 partes de ellas eran niñas y 4 parte de las niñas eran menores de seis años. • ¿Qué fracción del total de personas eran niñas? • ¿Qué fracción del total eran menores de seis años? • Si en total había 30 personas en el autobús, ¿cuántas niñas había y cuántas de ellas eran menores de seis años? Expliquen en grupo cuántos factores tienen las multiplicaciones con las que pueden resolverse los problemas. ¿De qué forma las resolvieron? Si hay diferencia en los resultados, revísenlos para llegar a un acuerdo. 17 Bloque 1 - Secuencia 1 19 Sugerencias didácticas Escuche las propuestas que hacen los alumnos para resolver la actividad “Integración”, escríbalas en el pizarrón y analícenlas en grupo. Después, agrupe dos factores mediante el uso de paréntesis. Se espera que de esta forma los alumnos noten que la solución va de lo particular a lo general. Por ejemplo: 2 × 3 × 1 × 7 × 3 = ( 2 × ( 3 × ( 1 × ( 7 × 3 )))). 3 4 5 3 7 3 4 5 3 7 En la actividad 3, es necesario que recabe conocimientos previos, para ello puede preguntar ¿Qué relación existe entre los números decimales y las fracciones? ¿Cuáles son las fracciones que corresponden a los números 0.5, 0.25? Si no se les ocurre algo, mencione que 0.5 es igual a cinco décimos, y que 0.25 son veinticinco centésimos. De esta forma obtendrán las respuestas casi de forma inmediata. Solucionario Integración S1 Integración • De manera grupal escriban un procedimiento para multiplicar tres o más fracciones y den un ejemplo. Procedimiento: Ejemplo: Multiplicación de fracciones por números decimales 3. En equipos analicen las imágenes y contesten. Para cada vehículo, escriban la fracción que representa el indicador de nivel de combustible y calculen la cantidad de gasolina en cada tanque a partir de su capacidad total. Multiplicación de fracciones por números decimales 3. Vehículo 1. Fracción: 43 . Combustible restante: 45.6 L Vehículo 2. Fracción: 41 . Combustible restante: 14.2 L Vehículo 3. Fracción: 35 . Combustible restante: 42.3 L Recursos adicionales En la siguiente página puede consultar más problemas de multiplicación de números decimales y fracciones: • “Multiplicar fracciones y decimales”, disponible en www.edutics.mx/wpz (consulta: 9 de agosto de 2018). Vehículo 1 Capacidad: 60.8 L Vehículo 2 Capacidad: 56.8 L Vehículo 3 Capacidad: 70.5 L Fracción: Combustible restante: Fracción: Combustible restante: Fracción: Combustible restante: Expliquen qué operaciones aritméticas utilizaron. Analicen si existe más de una forma de resolver y, de ser así, describan cada una. 4. Observen en parejas el procedimiento que emplearon cuatro alumnos para re4 solver la multiplicación 5 × 1.75 y contesten. Martín 4 175 700 7 5 × 100 = 500 = 5 Camila 4 3 4 7 7 4×7 = 5 5 ×1 4 = 5 × 4 = 5×4 20 Bloque 1 - Secuencia 1 18 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Procedimiento: Respuesta modelo (R. M.) Multiplicar todos los numeradores para obtener el numerador final y multiplicar todos los denominadores para obtener el denominador final. Después se simplifica la fracción hasta obtener una fracción irreducible. 1(2)(1) = 2 = 1 Ejemplo: 31 ( 25 )( 41 ) = 3(5)(4) 60 30 Multiplicación con fracciones y decimales positivos Sugerencias didácticas Pregunte a sus alumnos si con los cuatro procedimientos presentados en las páginas 18 y 19 se obtiene el mismo resultado. Al analizar el resultado de Julia, pida que conviertan el número 1.4 a fracción para validar los resultados. Señale las diferencias entre procedimientos; por ejemplo, la solución que propone Patricio está relacionada con la factorización de los números 175 y 100. Analicen la información de la sección “Formalización” y pregunte ¿Qué es más conveniente para resolver el problema, convertir la fracción a decimal o el decimal a fracción? Puede organizar dos equipos, pida a uno de ellos que convierta los números decimales a fracciones y al otro que convierta las fracciones a decimales. Cada equipo deberá exponer las dificultades encontradas. Por ejemplo, en el segundo caso, en el último renglón de la tabla no se puede hacer el cálculo exacto ya que el decimal asociado a la fracción es periódico. Patricio 4 175 35 7 4 × 5 × 35 5 × 100 = 5 × 25 × 4 = 25 = 5 Julia 0.8 × 1.75 = 1.4 a) ¿Cuál es la diferencia entre lo que hizo Julia y lo que hicieron los demás? b) Describan lo que hizo Camila y lo que hicieron Martín y Patricio. Solucionario c) Expliquen cómo simplificaron Camila y Patricio las fracciones. 4. a) Julia convirtió la fracción a número decimal y los demás convirtieron el número decimal a fracción. b) Camila convirtió el número decimal a fracción mixta y los demás convirtieron el número decimal a fracción decimal. c) Camila eliminó el 4 del numerador y del denominador porque 44 = 1 y no altera el resultado. Patricio utilizó el mismo recurso 4 × 55 × 4 = 1 por la misma razón. d) • No, porque el numerador y el denominador de las fracciones obtenidas no tienen divisores en común. • R. M. No hay dificultad para el procedimiento de Martín. Para el de Julia sí, porque no se puede convertir la fracción 31 a decimal finito. 5. a) 1 d) Multipliquen 3 × 1.25 utilizando los cuatro procedimientos anteriores. • Expliquen si lograron simplificar como Camila y Patricio. • ¿Encontraron alguna dificultad al utilizar el procedimiento de Martín o el de Julia? ¿Cuál? © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Comparen sus respuestas con las de otra pareja. ¿Utilizaron alguno de estos procedimientos para resolver la actividad 3? ¿Cuál les parece que se puede aplicar a cualquier multiplicación de una fracción y un número decimal? ¿Por qué? Cuando en una multiplicación los factores son números decimales y fracciones es posible realizar conversiones para utilizar un solo tipo de números. Sin embargo, dependiendo del problema y de las cantidades que intervienen es necesario decidir si es conveniente convertir a números decimales o trabajar con fracciones. 5. Resuelvan en equipos. a) En la tabla de la derecha se muestran los kilómetros que Mariana debe correr cada día que entrena durante la semana y la fracción que corrió en realidad. Complétenla. Día Distancia por recorrer (km) Fracción de distancia recorrida Lunes 0.84 Miércoles 1.75 3 4 1 1 2 Viernes 3.6 19 Día Distancia por recorrer (km) Fracción de distancia recorrida Kilómetros recorridos Lunes 0.84 3 4 0.63 Miércoles 1.75 1 21 2.625 Viernes 3.6 2 3 2.4 Kilómetros corridos 2 3 Bloque 1 - Secuencia 1 21 S1 Explique a los estudiantes que la multiplicación de fracciones implica calcular una parte de un total, es decir, 21 × 23 implica calcular un medio de un total de tres medios. Para resolver el inciso b) de la actividad 5, analicen las imágenes A, A1 y A2 por separado y utilicen diferentes procedimientos. Comente que en ocasiones las soluciones de los problemas involucran más de una operación. Plantee algunos problemas aritméticos con enteros, por ejemplo: Daniel vende tortas y tacos, los tacos cuestan $12 y las tortas $18, ¿cuánto obtuvo de ganancia si vendió 6 tacos y 9 tortas? Y pregunte ¿Qué operaciones se tienen que hacer para resolver el problema? Si lo considera necesario, haga un repaso de sumas y restas con fracciones. El objetivo es que observen las diferencias entre los procedimientos para resolver las distintas operaciones; ya que mientras la suma y la resta requieren de fracciones equivalentes, la multiplicación se resuelve casi inmediatamente multiplicando numerador por numerador y denominador por denominador. Analicen la sección “Recuerda”, pregunte ¿Por qué la segunda expresión del inciso d) de la actividad 6 no necesita paréntesis? ¿Qué indican los paréntesis de la tercera expresión? A b) Para determinar el tamaño correcto de una imagen en un cartel, primero se 3 redujo a la mitad y luego se amplio con un factor de 2 . • Si las dimensiones de la imagen A son 60 cm × 48 cm, ¿cuáles son las me1 ×2 A1 3 ×2 A2 Operaciones combinadas de suma, resta y multiplicación 6. c 1 – 1 3 a (1 – 31 ) × 63 7. a) 85 b) 1 4 5 8 d 3 3 × 31 × 63 b 1 3 × 63 c) d) $195.60 e) El libro costó $293.40 y le quedaron $293.40 • ¿Con qué factor se puede obtener la imagen A2 a partir de A? Expongan sus respuestas al grupo argumentando sus procedimientos. Operaciones combinadas de suma, resta y multiplicación 6. Lean en parejas los problemas y escriban el inciso en el círculo de la expresión numérica que los resuelve. a) Paula leyó la tercera parte de una novela de 63 páginas. ¿Cuántas páginas le quedan por leer? b) Marco y Antonio se reparten 63 libros que su abuela sacó del librero. Si Marco toma la tercera parte, ¿cuántos libros tiene? c) De los libros que se repartieron Marco y Antonio, ¿qué fracción tiene Antonio? d) De 63 alumnos que están en la biblioteca la tercera parte usa lentes, de estas personas dos terceras partes son mujeres. ¿Cuántas de ellas usan lentes? Solucionario b) • Las medidas de A1 son 30 cm × 24 cm. Las medidas de A2 son 45 cm × 36 cm. • R. M. Sí, es verdad, del cartel original se calcula la mitad de las dimensiones; es decir, 21 de cada longitud. Después, a las medidas obtenidas se les multiplica por 23 para obtener las medidas finales. • El factor es 43 o 0.75. didas de las imágenes A1 y A2? 1 3 • ¿Es verdad que al multiplicar las medidas de A por los factores 2 × 2 se obtienen las de A2? Expliquen. (1 – 31 ) Recuerda La jerarquía de operaciones establece el orden en que se realizan la suma, resta, multiplicación y división cuando aparecen al mismo tiempo en una operación. Revisa tu libro de primer grado para tomar nota del orden. 2 3 1 × 3 × 63 (1 – 31 ) × 63 1 3 × 63 7. Continúen en parejas y contesten. Esta mañana, Xóchitl gastó tres octavas partes de sus ahorros para comprar un libro de arte. En la noche, utilizó dos quintas partes de lo que le quedaba para el regalo de cumpleaños de su hermano. a) ¿Qué fracción de sus ahorros le quedaron en la tarde? b) ¿Qué fracción de sus ahorros totales utilizó en la noche? c) ¿Qué fracción de sus ahorros totales utilizó en total? d) Si tenía ahorrados $782.40, ¿cuánto dinero utilizó en el regalo de su hermano? e) ¿Cuánto costó el libro? ¿Cuánto dinero le quedó de sus ahorros? Comparen sus respuestas y procedimientos con el resto del grupo. ¿Las diferencias que encontraron son porque entendieron de manera distinta los problemas o son errores numéricos? ¿En qué problemas usaron la jerarquía de operaciones? 22 Bloque 1 - Secuencia 1 20 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Multiplicación con fracciones y decimales positivos Sugerencias didácticas Integración • En parejas planteen un problema que involucre varias operaciones y números decimales y fracciones para resolverlo. Aprendemos Reflexiona: ¿cuáles son las habilidades mentales que utilizas al plantear o inventar un problema matemático? • Intercambien problemas con otras parejas y traten de resolverlos de otras formas. 1. Analiza nuevamente el problema al inicio de la secuencia y contesta. a) En la esquina de Cedro y Laurel, sobre una superficie de 1 253.16 m2, se va 3 a construir una librería de manera que ocupe las 4 partes del área. ¿Cuál será su superficie? b) En la esquina de Laurel y Nogal se va a construir un estacionamiento para 3 el museo. El ancho, sobre la calle Nogal, será de 22.5 m y las 4 partes de él se utilizarán para la entrada. ¿Cuánto mide el ancho de la entrada del estacionamiento? Arribamos Formen dos equipos; para resolver la actividad 3 solicite que uno de ellos resuelva las operaciones utilizando fracciones y el otro utilice números decimales. Cada equipo debe explicar sus procedimientos y resultados, verifiquen que los resultados sean equivalentes. Para terminar pregunte ¿Qué significa resolver una multiplicación de fracciones? Mencionen una dificultad que puede surgir al usar decimales en lugar de fracciones. Pida a sus estudiantes que se pongan a prueba con los ejercicios sugeridos en la sección “Explora”. Aprendemos Pregunte ¿Qué es una habilidad mental? ¿Qué es lo primero que haces para resolver un problema? Una vez que has entendido el problema, ¿qué procede? La información contenida en la página de “Recursos adicionales” les permitirá responder esta sección. Si es necesario sugiera como respuesta: el análisis, percepción, atención y memoria. Solucionario 2. Resuelve los siguientes problemas. 4 2 a) Javier toma las 5 partes del jugo de piña, Mario las 3 partes del jugo de 3 durazno y Balam las 4 partes del jugo de manzana. ¿Cuántos litros tomó cada uno? Integración • Respuesta libre (R. L.) Arribamos Explora © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 0.75 L zana Man1.25 3 _ 4 0. 7 5 3 4 1.25 L L b) Al inicio de diciembre una tienda de juguetes ha vendido las tres cuartas partes del lote de juegos de mesa y a mediados del mes las dos terceras partes de los que quedaban. ¿Qué fracción del lote de juegos de mesa se vendió a mediados de diciembre? 3. Resuelve las siguientes operaciones. Cuando sea necesario, simplifica hasta que resulte una fracción irreducible y aplica la jerarquía de las operaciones. 3.6 × 2 5 5 6 × 0.8 = 3 1.2 × − 4 = 1 3 7 3.3 + 1 5 = ( ) 7 8 × 8 7 × 0.12 = ( )( ) 3 2 4 1.3 + 4 × 3 3.5 – 5 = 21 4 12.5 – 5 × 5 – 6.2 = ( ) En la siguiente página www.edutics. mx/38b podrás realizar multiplicaciones para calcular áreas de rectángulos, usando fracciones, decimales y sus combinaciones. Toma en cuenta que la coma en los números representa el punto decimal. 1. a) La superficie de la librería será de 939.87 m2. b) El ancho de la entrada del estacionamiento mide 16.875 m. 2. a) Javier tomó 0.6 L del jugo de piña. Mario tomó 0.5 L del jugo de durazno. Balam tomó 0.9375 L del jugo de manzana. b) 23 ( 41 ) = 61 , por lo tanto se vendió 61 del lote que quedaba a mediados de diciembre. 7 × 8 × 0.12 = 0.12 3. 3.6 × 25 × 0.8 = 1.152 8 7 1.2 × 65 – 43 = 41 (1.3 + 43 × 23 ) (3.5 – 45 ) = 4.86 1 (3.3 + 1 3 ) = 7 = 10.7 (12.5 – 21 ) × 45 – 6.2 = 0.44 7 5 10 5 Recursos adicionales En la siguiente página puede consultar más información relacionada con los procesos mentales: • “Procesos cognitivos”, disponible en www.edutics.mx/wQk (consulta: 9 de agosto de 2018). Compara tus procedimientos y resultados con el resto del grupo. 21 Bloque 1 - Secuencia 1 23 S2 División con fracciones Partimos Sugerencias didácticas Lea con los alumnos el título de la secuencia y pregunte ¿Qué tipo de problemas se resuelven con divisiones? Si es necesario pida que formulen problemas que involucren divisiones. Analicen el problema 1, después pregunte ¿Qué operaciones deben hacer para resolver el problema? ¿Se trata de un problema de reparto? ¿Qué se va a repartir y en cuántas partes? Pida a un alumno que pase al pizarrón a representar gráficamente la situación. S2 Resuelve problemas de división con fracciones y decimales positivos. Partimos División con fracciones Otra de las operaciones que has estudiado desde primaria es la división, la cual resolviste con números naturales y, en primer grado de secundaria, con números decimales. En esta secuencia estudiarás cómo dividir números fraccionarios. De este modo, al resolver problemas podrás combinar las cuatro operaciones básicas que conoces con las distintas expresiones numéricas positivas. 1. Observa las imágenes y responde. En una tienda de lácteos quedan las siguientes fracciones de dos tipos de queso. Solucionario 3 en cada recipiente. 1. Queso canasto: hay 16 5 en cada recipiente. Queso doble crema: hay 16 Recorremos El queso canasto se repartió equitativamente en cuatro recipientes, mientras que la fracción de doble crema, solamente en dos. a) ¿Qué fracción hay en cada recipiente para cada tipo de queso? División de fracciones entre números naturales y viceversa Discute con tus compañeros el procedimiento para hallar la respuesta. Si se divide a la mitad cada octavo del queso canasto, ¿el número de partes se puede dividir en cuatro? En el caso del queso doble crema, ¿se puede hacer lo mismo? Como es el primer acercamiento de los alumnos al tema de división con fracciones, se recomienda que resuelva gráficamente los problemas y después analice la solución. Compare las respuestas del inciso b) con las del inciso a) y plantee más ejemplos con fracciones distintas, después pida a los alumnos que formulen un procedimiento informal para resolver la división entre fracciones. Solucionario 1. a) b) c) 1 de metro 10 1 ÷5= 1 2 10 1 de metro 14 Recorremos División de fracciones entre números naturales y viceversa 1. Resuelvan en parejas. Laura cortó en cinco partes iguales una tira de medio metro de listón verde, como se muestra en la figura. 1 2 m 1m a) ¿Qué fracción de un metro representa cada parte? b) Escriban una operación que represente el corte que hizo Laura. c) Si Laura hubiera cortado el medio metro de listón en siete partes iguales, ¿cuánto mediría cada parte? 24 Bloque 1 - Secuencia 2 22 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas d) La tabla muestra los cortes hechos a otros listones. Determinen las longitudes de las partes que se obtienen en cada caso y complétenla. Color Longitud de la tira del listón (m) Número de partes Rojo 3 4 3 Azul 4 3 4 Rosa 2 5 3 Amarillo 5 6 2 Naranja 1 3 5 Longitud de cada parte (m) Expliquen a sus compañeros cómo dividieron la longitud de la tira entre el núme3 ro de partes, por ejemplo, 4 ÷ 3. Si usaron fracciones equivalentes, asegúrense de escribir los resultados con fracciones irreducibles. Discutan qué procedimiento utilizarían para comprobar sus resultados. Sugerencias didácticas Represente gráficamente las fracciones que se van a dividir en la tabla del inciso d). Permita que los alumnos trabajen solos y pregúnteles cómo encontraron los resultados que se solicitan. Analicen en grupo los números de la columna cuatro y encuentren un procedimiento general para hacer las divisiones que se piden. Haga notar que en las tres últimas filas pareciera que sólo el denominador se afecta (dado que se obtienen fracciones irreducibles), mientras que en las primeras dos no se observa lo mismo debido a que las fracciones son reducibles. Pregunte después de leer el inciso a) de la actividad 2 ¿Por qué será que la división también puede escribirse como multiplicación? ¿Cuál es la diferencia entre escribir la división y la multiplicación? ¿Qué significa 41 × 31 ? Explique que multiplicar 41 × 31 implica encontrar la cuarta parte de un tercio, es decir dividir 31 en 4 partes iguales. Solucionario d) © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 2. Continúen en parejas y contesten a partir de las imágenes. En los siguientes esquemas se representan fracciones de distintos tipos de tela divididas en partes. Escriban en la primera fila de recuadros la división que representa la zona de color más oscuro. Completen el ejemplo. 1 3 ÷4 = 1 3 ×4 = 1 Color Longitud de la tira (m) Número de trozos Longitud del trozo (m) Rojo 3 4 3 3 = 1 12 4 Azul 4 3 4 4 = 1 12 3 Rosa 2 5 3 2 15 Amarillo 5 6 2 5 12 Naranja 1 3 5 1 15 Multiplicar el número de trozos por la longitud de cada uno para obtener la longitud de la tira. a) La zona de color más oscuro también puede verse como una multiplicación que representa el área de esa parte. Escriban en el segundo renglón de recuadros las multiplicaciones correspondientes. b) ¿Qué relación hay entre los números fraccionarios utilizados en las multiplica- 2. 1 3 ÷4 = 1 12 5 6 ÷3 = 5 18 4 3 ÷2 = 4 6 1 3 × 41 = 1 12 5 6 × 5 18 4 3 × 4 6 1 3 = 1 2 = ciones y divisiones? Comparen con su grupo y analicen si con ambas operaciones obtienen el mismo resultado. Representen las divisiones de la actividad 1 como áreas de rectángulos y verifiquen si también pueden resolverlas con una multiplicación. 23 a) Las respuestas se muestran en la segunda fila. b) Uno de los factores es el inverso multiplicativo del divisor. Bloque 1 - Secuencia 2 25 S2 Pida a los alumnos que expliquen cómo se hacen las reducciones o ampliaciones de fotografías. Escuche las respuestas y resalte palabras clave como multiplicación, división y factor de escala. Continúe con la solución de la actividad 3. Para resolver el inciso a) explique que se requiere hacer una reducción, haga las siguientes preguntas ¿Cómo debe ser el factor de escala para reducir la imagen? ¿Cuál es la característica del factor que amplíe la imagen? Los alumnos deben relacionar la reducción de la imagen con una fracción propia. Pida a los estudiantes que lean la sección “Recuerda”, muestre algunos ejemplos de fórmulas que estudiaron en el curso anterior y planteen el procedimiento para dividir una fracción entre un número natural en la sección "Integración". Para resolver la actividad 4, puede convertir el total de litros de las jarras a fracciones equivalentes de 43 de litro, por ejemplo, 12 = 48 . 4 3. Completen en equipos el esquema con el factor fraccionario que reduce a la tercera parte las dimensiones de la imagen y las medidas resultantes. ÷3 1 2 m 3 4 m a) Para reducir en 3, 5 o 7 veces las dimensiones de una figura, ¿cuál es el factor por el que deben multiplicarse sus medidas, respectivamente? Comparen sus respuestas. A partir de los problemas anteriores discutan cómo se puede dividir una fracción entre un número natural utilizando una multiplicación. Convivimos Al terminar la actividad 4 analicen la sección “Convivimos”, haga una ronda de participaciones y pregunte ¿Qué beneficios trae la participación en la resolución de conflictos de una comunidad? ¿Crees que el estudio de las matemáticas te ayuda a desarrollar habilidades para mejorar la toma de decisiones? ¿Por qué? × Recuerda Las letras o literales pueden utilizarse para representar números generales con los que es posible hacer operaciones. Integración • En grupo establezcan un procedimiento para dividir una fracción División de una fracción entre un número natural a b a b ÷n = a b × n1 = a × b1 × n = ÷n = × = = 4. Analiza y resuelve. Los alumnos de una secundaria prepararon agua de distintos sabores para repartirla entre los integrantes de una brigada de reforestación. Para ello, llenaron varias bo3 tellas de 4 L. Observa a continuación los sabores y la cantidad de algunos de ellos. Integración • entre un número natural n. Represéntenlo en el siguiente esquema. Solucionario 3. Factor fraccionario: 31 Dimensiones de la imagen: 41 de base por 61 de altura. a) Los factores por los que debe multiplicarse para reducir en 3, 5 y 7 son 1 , 1 y 1 respectivamente. 3 5 7 a b a bn 4. Limón: 12 L; naranja: 6 L; sandía: 15 L; tamarindo: 7.5 L a) Hay 48 cuartos de litro en 12 litros de agua. Se llenaron 16 botellas de 3 litro de agua de limón. 4 • 12 ÷ 43 = 16 Convivimos Valora y comenta: ¿por qué es importante interesarse y participar organizadamente para resolver conflictos o afectaciones en tu comunidad? 26 Bloque 1 - Secuencia 2 Limón 12 L Naranja Sandía 15 L Tamarindo 3 a) ¿Cuántos cuartos de litro equivalen a 12 L y cuántas botellas de 4 L de agua de limón se llenaron? • Escribe la división que representa este reparto y su resultado. 24 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas División con fracciones Sugerencias didácticas Solicite a los alumnos que calculen 43 de 20, para ello plantee Si tienes 20 unidades, ¿cuál es la cuarta parte? Si 41 de 20 es 5, entonces, ¿cuánto son tres cuartos? Explique cómo el recíproco de una fracción puede ayudar para calcular la división de fracciones a partir de la multiplicación. Puede ser de utilidad que los alumnos analicen el resultado de una división de fracciones, por ejemplo, pregunte Si divides un entero entre una fracción, ¿el resultado es mayor o menor que el dividendo? Presente varios ejemplos al respecto. Complemente la actividad 5 asignando nuevas longitudes a las tiras que se muestran en la página, por ejemplo, pida que dividan una tira de 35 de metro en trozos de 23 y que dibujen la representación gráfica. Pregunte ¿En 5 , cuántos trozos de 2 caben? Resalte que inicialmente caben dos completos 3 3 y un medio más, por lo que el cociente es 2 21 . Analice con sus estudiantes el video sugerido al final de esta página. b) Si se llenaron 8 botellas de agua de naranja, ¿cuántos litros se prepararon? c) Lucía dice que sirvieron 20 botellas de agua de sandía, ¿es cierto? Escribe una división y una multiplicación que modele esta situación. d) Pedro dice que había 9 L de agua de tamarindo porque llenaron 10 botellas y no sobró agua. ¿Tiene razón? Escribe las operaciones para comprobarlo. e) ¿Cuántas botellas se llenan con 16 L de agua de jamaica? • ¿Cuánto sobra y qué fracción de la botella representa? • ¿Cuántas botellas y fracciones de botella se obtienen al dividir 16 L en botellas 3 de 4 L? Reúnete con algunos compañeros y expliquen cómo resolvieron cada inciso. ¿Todos dividieron la cantidad de agua en cuartos? Comenten de qué otra manera pueden 3 calcular cuántas porciones de 4 L hay en cierta cantidad de litros. Solucionario 5. Trabaja con un compañero. Laura necesita saber cuántas partes iguales es posible sacar de cada tira de listón si la divide en fracciones. ¿Cuál es el resultado de cada división? 3 a) Una tira de 3 m en partes iguales de 4 m. 1 1 1 3 3 3 3 3 4 4 4 4 3÷ 4 = Partes obtenidas: b) 6 litros, 43 × 8 = 6. c) Sí, es cierto, ya que 15 ÷ 43 = 20 y 20 × 43 = 15 d) No, porque 9 ÷ 43 = 12 que es distinto de 10; y 10 × 43 = 7 21 que es distinto de 9. e) Se llenan 21 botellas de agua de Jamaica y una tercera parte de otra botella. • Sobra 41 L lo que representa 31 de la botella. • 21 31 5. a) 3 ÷ 43 = 4 Partes obtenidas: 4 2 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. b) Una tira de 2 m en partes iguales de 5 m. 1 1 2 2 2 2 2 2 5 5 5 5 5 2÷ 5 = Partes obtenidas: b) 2 ÷ 2 5 =5 c) 3 ÷ 2 3 =4 Partes obtenidas: 5 1 2 Partes obtenidas: 4 1 2 Recursos adicionales c) Una tira de 3 m en partes iguales de 1 2 3 m. 1 1 2 2 2 2 3 3 3 3 2 3÷ 3 = Partes obtenidas: En la siguiente página puede encontrar una explicación para entender la división de fracciones: • “División de fracciones”, disponible en www.edutics.mx/wQL (consulta: 14 de agosto de 2018). Comparen sus respuestas y sus razonamientos con los de otra pareja. ¿Cuál fue el procedimiento que siguió Laura? Discutan cómo interpretaron el último esquema y cómo resolvieron la división. Luego, escriban una regla para dividir un número natural entre una fracción. 25 Bloque 1 - Secuencia 2 27 S2 Sugerencias didácticas Analice de forma grupal la división de un número natural entre una fracción y explique las diferencias que hay entre la multiplicación y la división de fracciones. Puede utilizar uno o varios ejemplos para ello; de preferencia que la multiplicación y la división tengan los mismos números: 5 ÷ 23 y 5 × 23 ; pregunte qué resultado es menor y por qué sucede así. Finalmente pida que expliquen de forma resumida el procedimiento para dividir un número natural entre una fracción; por ejemplo, “para obtener el resultado de la división se multiplica numerador por denominador y se divide entre el numerador de la segunda fracción”. Al terminar mencione que la división se resuelve multiplicando el número natural por el inverso multiplicativo de la fracción. Una vez realizada la actividad 6, recomiende a los estudiantes que resuelvan los ejercicios que se sugieren en la sección “Explora”. Integración 2 3 a n ÷ b = (n × b) ÷ a = Explora En la página www.edutics. mx/36N podrás resolver otros problemas de división de fracciones y números naturales. n×b a Integración • Analiza la información anterior y, a partir de las igualdades, representa la siguiente división de un número natural entre una fracción como una multiplicación. 2 × 5÷ 3 = × = = División de fracciones Solucionario • 5÷ La división de un número natural n entre una fracción se puede resolver al multiplicar el número natural por el denominador de la fracción y luego dividir el resultado entre el numerador, es decir: = 5× 3 2 = 5×3 2 = 6. Analicen y contesten en parejas. a) Para dividir tiras de madera en fracciones Mirna y sus compañeros utilizaron los siguientes esquemas aplicando la idea de cuántas veces cabe el divisor en el dividendo. Escriban la división correspondiente y su resultado. 15 2 Mirna División de fracciones 1 1 2 Joaquín: David: Elisa: 6 4 4 3 ÷ 41 = 2 3 2 ÷ 43 = 2 ÷ 49 = 3 ÷ 83 = 4 1 4 cabe dos veces en 1 2 3 4 cabe dos veces en 3 2 4 9 cabe tres veces en 4 3 3 8 cabe 4 veces en 2 1 1 4 4 1 2 1 ÷4 = Joaquín 6 4 1 1 1 2 2 2 3 3 4 4 3 ÷4 = David 1 1 1 1 3 3 3 3 4 4 4 9 9 9 4 3 ÷ = Elisa 28 Bloque 1 - Secuencia 2 1 1 1 1 1 1 4 4 4 4 4 4 3 3 3 3 8 8 8 8 26 ÷ = © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 6. a) Mirna: División con fracciones Sugerencias didácticas 3 Colabore con los alumnos para resolver el inciso b) de la actividad 6, realice el siguiente análisis: si en 43 partes de hora Jacinta recorrió 25 partes de la distancia total, ¿cuánto habrá recorrido en 41 de hora? Indique que un cuarto del tiempo es la tercera parte de lo que tardo en recorrer los 25 . Entonces 25 debe dividirse entre 3, para calcular la tercera parte. 2 b) En 4 de hora Jacinta recorrió 5 partes de la distancia total de su casa a la de sus abuelos. 1 • ¿Qué fracción del trayecto recorrió en 4 de hora? • ¿Cómo pueden calcular la fracción del trayecto que recorrió en una hora? Solucionario • Jacinta calculó la fracción del trayecto que recorrió en una hora con la siguiente cadena de operaciones. Expliquen cuál fue el razonamiento de Jacinta y resuelvan la división. 2 3 2 2 1 ÷ 4 = ( 5 ÷ 3) × 4 = ( 5 × 3 ) × 4 = 5 2 , recorrió 2 partes del trayecto en 1 de hora. b) • 25 ÷ 3 = 15 15 4 2 partes del trayecto, entonces • Dado que en 41 de hora recorrió 15 2 = 8 . en una hora recorrió cuatro veces el trayecto 4 × 15 15 • Jacinta dividió entre 3 para calcular lo que se recorre en 41 de hora y al multiplicar por 4 se calculó el trayecto de la hora completa. 7. a) ×5 Analicen sus respuestas y compárenlas con el grupo. Calculen las divisiones del inciso a) con el razonamiento de Jacinta y verifiquen que obtienen los mismos resultados. Discutan de qué otra forma pueden resolver una división de dos fracciones. Original 7. Analicen en equipos la información y resuelvan. Para revertir o deshacer la transformación que se realiza al aplicar a una cantidad un factor de proporcionalidad directa se aplica otro llamado factor inverso. a) Completen los esquemas con los factores para realizar las transformaciones que indican las flechas. × 1 5 × b) c) × 3 fraccionario que revierte dicha transformación? c) Completen el esquema con las medidas del cuadrado y los factores de cada transformación. d) Mariana afirma que como la multiplicación y la división son ope5 raciones inversas, entonces multiplicar por 3 para obtener las 3 medidas originales es equivalente a dividir entre 5 las medidas transformadas. ¿Están de acuerdo? ¿Por qué? 5 3 × 5 3 Original Transformación a 3 Original Transformación a 5 × 3 5 3 5 × 7 10 m Comparen los procedimientos de las actividades 6 y 7 y establezcan un procedimiento para calcular la división de una fracción entre otra. 27 Aumento al triple ×3 × b) Si el factor 5 puede verse como la aplicación sucesiva de los 3 1 dos factores en los esquemas ( 5 = 5 × 3), ¿cuál sería el factor 1 3 Original Aumento al triple Original × © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. × × Reducción a la quinta parte Original Reducción a la quinta parte 7 10 m 21 m 50 d) Sí, en las actividades anteriores se obtuvo la misma conclusión. Bloque 1 - Secuencia 2 29 S2 Sugerencias didácticas Plantee diferentes ejercicios para analizar la forma en que los estudiantes resuelven operaciones con fracciones. Es probable que algunos propongan soluciones variadas; si es así, pida que las escriban en el pizarrón. Haga notar que, con la variedad de soluciones, se demuestra la lógica de la matemática y la diversidad de análisis. Por ejemplo, para el problema del inciso d) de la actividad 8: • Análisis 1. Al girar 85 de vuelta en una hora y cuarto, es decir 45 de hora, significa que en un cuarto de hora giró 81 , así en 44 habrá girado 48 = 21 giro. • Análisis 2. Se divide el total del giro entre el total del tiempo: 5 ÷ 5 = 5 × 4 = 1. 8 4 8 5 2 Integración ÷ c d = a b × 2 Prenda 3 2 4 2 5 × 3 = ( 5 × 4) × 3 = ( 5 × 4) ÷ 3 4 2 4 1 2 3 Es decir, 5 ÷ 4 = 5 × 3 , donde 3 es el inverso multiplicativo de 4 . Recuerda 7y 1 son números 7 1 =1 7 5 6 y son inversos 6 5 5 6 porque × = 1 6 5 Integración • Con base en la información anterior, escribe el procedimiento general para dividir dos fracciones cualesquiera al reescribir la división como una multiplicación. a c ÷d = × b inversos porque 7 × d c 8. a) 4 recipientes • Multiplicando b) 3 y 3 20 por 4 o dividiendo 3 5 entre 4. 8. Resuelvan en equipos los siguientes problemas. 3 a) Se repartieron entre varios recipientes 5 L de acetona. Si en cada recipiente se 3 pusieron 20 L, ¿cuántos recipientes había? • ¿Cómo verificarían su resultado? Tela Largo de los Prendas que puede disponible (m) lienzos (m) hacer (piezas) Falda 1 41 1 4 5 Camisa 7 21 3 4 10 Pantalón 5 31 1 31 b) Para confeccionar diversas prendas Estela utiliza lienzos de distintos tamaños. Completen la tabla. Tela disponible (m) Prenda Falda 1 1 4 1 4 Camisa 7 1 2 3 4 Pantalón 5 1 3 4 c) Mide 87 m d) En una hora el engrane da media vuelta y tarda dos horas en dar la vuelta completa. e) Se cultivará en 4 parcelas. Largo de los lienzos (m) 1 Prendas que puede hacer (piezas) 1 3 c) ¿Cuánto mide de largo el rectángulo de la izquierda? 5 d) El engrane de una máquina da 8 de vuelta en una hora y cuarto. ¿Qué fracción de vuelta da en una hora? ¿Cuánto tiempo tardará en dar una vuelta completa? 2 3 m 7 12 m2 6 e) Las 8 partes de un terreno se dividirán en parcelas del mismo tamaño para 3 plantar árboles frutales. Si cada parcela corresponde a 16 partes del terreno, ¿en cuántas parcelas se cultivará? En grupo, expliquen cómo interpretaron y resolvieron cada problema. 30 Bloque 1 - Secuencia 2 28 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. a b ( 25 ÷ 3) × 4 = ( 25 × 31 ) × 4 = Dos números son inversos multiplicativos si su producto es 1. Por ejemplo: Solucionario • 2 Para dividir una fracción entre otra, por ejemplo 5 entre 4 , se puede primero dividir entre 3 y luego multiplicar por 4; o primero multiplicar por 4 y luego dividir entre 3. Dividir una fracción entre un número natural n es lo mismo que multi1 plicar dicha fracción por n ; por ello, las siguientes expresiones son equivalentes: División con fracciones Arribamos 1. Considera la cantidad de queso planteada al inicio de la secuencia. 1 5 Si cada pieza completa de queso pesa 4 2 kg, ¿cuántas raciones de 8 kg se pueden obtener de cada tipo de queso? Arribamos Pida a sus alumnos que respondan en el pizarrón las respuestas a ¿En qué tipo de problemas se usa la división de fracciones? ¿Cómo se resuelve la división de fracciones? ¿Cómo se relacionan la división y la multiplicación de fracciones? Aclare las dudas que surjan y continúe. Solicite que escriban diferentes formas de resolver la actividad y verifique las respuestas en grupo. Invite a los alumnos a evaluar su aprendizaje resolviendo los ejercicios interactivos de la sección “Explora”. 2. Resuelve las siguientes adivinanzas numéricas. 2 a) ¿Qué número dividido por 11 da 22? 5 3 b) ¿Qué número multiplicado por 6 da 4 ? 3 9 c) ¿2 4 entre qué número da 8 ? 13 d) ¿Qué número dividido por 5 da 2 ? 3. Resuelve los siguientes problemas. 3 a) ¿Cuántas personas hay en una fiesta si 36 mujeres son las 5 partes del total? 3 b) Elías preparó 6 4 L de jugo de naranja y lo vendió todo, ¿cuántos vasos de 3 L vendió? ¿Cuánto dinero obtuvo? 8 Solucionario 1. Queso canasto: (4 Explora Entra en la página www. edutics.mx/36x y resuelve los problemas de división de fracciones. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. c) Alondra y Guadalupe visitaron a sus abuelos recorriendo la misma distancia 2 pero a distinta velocidad. Alondra avanzó 90 km del camino en 3 de hora, 2 mientras que Guadalupe, en el mismo tiempo, recorrió 5 partes de ese mismo camino. Si Alondra llegó a casa de sus abuelos en una hora, ¿cuál es la distancia total del camino? • Como la velocidad de un móvil es la distancia recorrida entre el tiempo empleado, ¿cuál es la velocidad de Guadalupe en kilómetros por hora? 4. Explica por qué si una división de fracciones está escrita de forma vertical, como la que se encuentra al lado derecho, el resultado es una fracción cuyo numerador es el producto de los extremos y cuyo denominador es el producto de medios. 2 5 6 7 5. Resuelve las divisiones. Escribe el procedimiento. 4 2 4 5 ÷3 = 15÷6 = 7 7 8 3 7 9 4 1 ÷1 4 = = 3 1 2 8 ÷3 2 = 1 8 2 11 = Sugerencias didácticas 1 2 × 86 ) ÷ 85 = Queso doble crema: (4 2. a) 4 9 b) 10 c) 22 9 d) 65 2 1 2 27 5 = 52 5 × 85 ) ÷ 85 = 4 1 2 3. a) Había 60 personas en la fiesta. b) Vendió 18 vasos de 83 L y obtuvo $270. c) 90 ÷ 23 = 135 km • v = dt = 25 ÷ 23 × 135 = 81 km/h 4. R. M. Al escribirse la división en forma horizontal 25 ÷ 67 = 25 × 67 , se multiplica 2 por 7 y 5 por 6 que son los extremos y los medios de la división original. 5. 4 ÷ 2 = 12 = 6 7 3 14 7 1 45 ÷ 65 = 95 ÷ 65 = 54 25 7 ÷ 1 1 = 28 = 7 8 4 40 10 19 2 83 ÷ 3 21 = 38 = 28 56 3 7 4 = 3 × 47 × 9 = 21 9 4 1 8 11 = 1 × 11 × 2 = 16 8 2 11 Verifica tus respuestas con el resto del grupo. Recuerda que es importante entender a qué se refiere cada problema antes de realizar cualquier operación o cálculo. 29 Bloque 1 - Secuencia 2 31 S3 Multiplicación de números positivos y negativos Partimos Sugerencias didácticas Lea en grupo la introducción a la secuencia y si tienen dudas haga un breve recordatorio de suma y resta de números con signo. Al terminar analicen la actividad 1 y pregunte ¿Qué operación está involucrada en el cálculo del recorrido de Camila? Enseguida pida que escriban la operación y solución. Cuando analicen el recorrido de Romina, resalte el hecho de que hay un signo involucrado para que los estudiantes lo consideren en la solución. Si observa que se complica el cálculo para encontrar las respuestas analice la posición de las jóvenes después de dos horas. S3 Resuelve problemas de multiplicación con números enteros, fracciones y decimales positivos y negativos. Partimos Multiplicación de números positivos y negativos En primer grado de secundaria comenzaste el estudio de las operaciones que involucran números positivos y negativos. Aprendiste a sumar y restar números positivos y negativos y a resolver diversos problemas con ellos. Ahora, en esta secuencia, aprenderás a multiplicarlos y sabrás qué procedimiento emplear si los factores tienen un signo negativo y otro positivo o si ambos son negativos. 1. Lee la situación y contesta. Romina y Camila, como se muestra en la siguiente figura, parten de un mismo punto. Camila viaja hacia la derecha a 25 km/h y Romina hacia la izquierda a 20 km/h. Solucionario 1. a) Camila a 150 km del punto de partida y Romina a –120 km del punto de partida. − + 0 Números positivos para Camila y números negativos para Romina. a) Considera que todas las magnitudes que están a la derecha del punto de referencia son positivas y todas las que estén a la izquierda son negativas. ¿En qué posición respecto del punto de partida se encuentran Camila y Romina después de 6 horas? Recorremos Multiplicación de un número positivo y un número negativo Pida a los estudiantes que lean la sección “Recuerda” y plantee algunos ejemplos que se relacionen con una suma iterada, por ejemplo: si una paleta cuesta $8, escribe la suma que te permite encontrar el costo de 5 paletas. Después pida que hagan el cálculo con una multiplicación. Recorremos Solucionario 1. a) 2 + 2 + 2 + 2 + 2 + 2 + 2 = 7(2) = 14 • (– 3) + (– 3) + (– 3) + (– 3) Multiplicación de un número positivo y un número negativo 1. Analiza las siguientes operaciones. a) Escribe la suma iterada y la multiplicación equivalente que se representa en la recta numérica. Recuerda Una suma iterada o repetida es aquella en la que un mismo sumando se repite varias veces. 32 Bloque 1 - Secuencia 3 –16 –14 –12 –10 –8 –6 –4 –2 0 2 4 6 8 10 12 14 • De manera semejante a la anterior escribe la suma de la recta numérica de la siguiente página. 30 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Compara con tus compañeros cómo resolvieron el problema y si llegaron a las mismas respuestas. ¿Qué números emplearon para representar la ubicación de cada ciclista? Sugerencias didácticas Sugerencias didácticas –15 –12 –9 –6 –3 0 3 6 9 12 15 • Reescribe la suma con una multiplicación. • A partir de lo anterior completa el diagrama. 4×( ) = + + Se suma + veces el número . = Antes de continuar con las actividades, indique a los estudiantes que lean la sección “Notación” y que escriban un problema que involucre números negativos, revise que usen paréntesis para resolverlo y comenten las ventajas de su uso. Lean la sección “Glosario”, explique cómo se forma el conjunto de números enteros. Al terminar los problemas de esta página, explique algunas relaciones que hay en metemáticas; por ejemplo, la relación entre la suma iterada y la multiplicación, comente que por ésta razón hay diferentes formas de resolver un problema. Solucionario • 4 × (– 3) b) Considera la suma (– 4 ) + (– 4 ) + (– 4 ). • Represéntala en la siguiente recta numérica. 3 3 3 4 × (– 3) = Se suma 4 veces –3+–3+–3+–3 el número – 3. Notación –4 –3 –2 –1 0 1 2 3 4 • ¿Cuál es el número al que llegaste? • ¿Cuál es el resultado de la suma? • Escribe la suma anterior como una multiplicación y su resultado. Al realizar las operaciones el número y su signo se deben escribir entre paréntesis para no confundir con los operadores de suma y resta. = – 12 b) –4 –3 • – c) Representa la multiplicación 3 × (– 1.5) en la recta numérica que está a continuación. • – 9 4 9 4 –2 –1 0 1 2 3 4 = – 2.25 • 3 (– 43 ) = – 9 4 c) –5 –4 –3 –2 –1 0 1 2 3 4 5 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • ¿Cuál es el resultado? Compara tus respuestas con las de tus compañeros. En equipo discutan y obtengan conclusiones. ¿Cómo pueden multiplicar un número positivo por uno negativo? ¿Ocurre lo mismo si multiplican un número negativo por un decimal o fracción positiva? Utilicen la recta del inciso c) y multipliquen (2.5) × (– 1.5), ¿cómo lo hicieron? 2. Resuelvan en parejas. a) Juan organizó la rifa de un videojuego, cada boleto cuesta $20. Vendió 50 boletos, pero siete personas no le han pagado. • Escriban con una suma y una multiplicación la cantidad de dinero que le deben. Utiliza números positivos y negativos. • Indiquen la cantidad de dinero que le deben con un número entero negativo. 31 Recuerda El 0 no es un número positivo ni negativo, es un número neutro. Además, al multiplicar cualquier número por 0 se obtiene 0. Glosario números enteros. Son aquellos que comprenden el cero, los naturales 1, 2, 3, 4,… y sus negativos – 1, – 2, – 3, – 4,… –5 –4 –3 –2 –1 0 1 2 3 4 5 • – 4.5 R. M. Multiplicando los números y colocando el signo correspondiente. Se hace el mismo procedimiento si uno de los números es una fracción o un número decimal. 2. a) • (– 20) + (– 20) + (– 20) + (– 20) + (– 20) + (– 20) + (– 20) = 7 × (– 20) • – 140 pesos Recursos adicionales En la siguiente página puede consultar videos relacionados con el tema: • “Números negativos”, disponible en www.edutics.mx/wQb (consulta: 14 de agosto de 2018). Bloque 1 - Secuencia 3 33 S3 Sugerencias didácticas Sugiera a los alumnos que, antes de resolver las actividades del inciso b), lean nuevamente la sección “Recuerda” de la página anterior. Revise las respuestas y pida que comprueben sus resultados por medio de una suma iterada. De igual manera, si al terminar de completar la tabla de la actividad 3 nota que todavía se cometen errores, sugiera que utilicen la suma iterada para comprobar sus resultados. Solucionario 0 × (– 7) = 8 × (– 0.5) = 10 × (– 1.8) = 2 × (– 4 ) = 2.5 × (– 1.3) = 3 × (– 7 ) = ( 51 ) × (– 43 ) = 3 2 Reúnanse con otros equipos y corroboren sus respuestas. ¿Representaron las multiplicaciones en rectas numéricas? ¿Cómo las resolvieron? Analicen en caso de tener diferencias y corrijan si es necesario. 0 × (– 7) = 0 10 × (– 1.8) = – 18 3 × (– 27 ) = – 67 3 ( 51 ) × (– 43 ) = – 20 3. 6 × (– 1) = 3. Completa la siguiente tabla con los resultados de las multiplicaciones y responde. 9×4 a) b) c) d) e) 36 4×9 9×4 36 4×9 36 9×3 3×9 9×3 27 3×9 27 9×2 2×9 9×2 18 2×9 18 9×1 1×9 9×1 9 1×9 9 9×0 0 0×9 0 9 × (– 1) –9 (– 1) × 9 –9 9 × (– 2) – 18 (– 2) × 9 – 18 9 × (– 3) – 27 (– 3) × 9 – 27 9 × (– 4) – 36 (– 4) × 9 – 36 El número 9 De 9 en 9 Sumar – 9 o restar 9 El orden de los números que se multiplican se intercambia. No hay diferencia, son iguales. Las conclusiones anteriores aplican para todos los números, no importa si son fracciones o decimales, (– 21 ) × 8 = – 4. 9×0 27 0×9 9 × (– 1) –9 (– 1) × 9 9 × (– 2) (– 2) × 9 9 × (– 3) (– 3) × 9 9 × (– 4) (– 4) × 9 a) ¿Qué número hay que restar para pasar del resultado de 9 × 3 al resultado de 9 × 2? b) ¿De cuánto en cuánto disminuyen los valores de la segunda y cuarta columna? c) ¿Qué tienes que hacer para pasar del resultado de (– 1) × 9 al resultado de (– 2) × 9? d) ¿Cuál es la diferencia entre las expresiones de la primera columna y las de la tercera? e) ¿Cuál es la diferencia entre los números de la segunda columna con respecto a los de la cuarta? Compara tus respuestas con otro compañero. Analicen: ¿ocurre lo mismo con los signos si los números que se multiplican son fracciones o decimales? Multipliquen (– 21 ) × (8). La multiplicación de números enteros cumple la propiedad conmutativa: el orden de los factores no altera el producto. 34 Bloque 1 - Secuencia 3 32 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. b) 6 × (– 1) = – 6 8 × (– 0.5) = – 4 2 × (– 43 ) = – 23 2.5 × (– 1.3) = – 3.25 b) Realicen las siguientes multiplicaciones. Multiplicación de números positivos y negativos Sugerencias didácticas Integración Aprendemos • Completen en parejas el siguiente esquema. Producto de dos números con distinto signo Propiedad Comenta después de completar el esquema: ¿cómo te ayudan los esquemas en tu aprendizaje? Analice en grupo el esquema de la actividad “Integración”, al terminar, solicite que escriban en una ficha de trabajo la regla para multiplicar números con signos diferentes. Antes de resolver el inciso b) de la actividad 4, pida que lean la sección “Glosario”; de ser necesario muestre algunos ejemplos, pues ya que las respuestas son abiertas, pueden ser variadas. Escriba en el pizarrón algunas de ellas y analícenlas en grupo. Aprendemos Positivo por Ejemplo: Negativo por = Comente que para hacer un esquema, primero es necesario hacer un resumen y establecer la relación entre conceptos. El esquema muestra esta información de una forma más fácil de interpretar. Ejemplo: Procedimiento Solucionario Integración Resultado Producto de dos números con distinto signo Propiedad conmutativa • Analicen en grupo el texto y compárenlo con el procedimiento que escribieron en el esquema. Positivo por negativo Ejemplo: 4 × (– 9) Para resolver un producto que involucra un número positivo por un número negativo se multiplican los valores absolutos y se antepone al resultado el signo menos. Negativo por positivo Ejemplo: – 9 × 4 = © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Procedimiento Se multiplican los números y al resultado se le antepone el signo menos. 4. Analicen y contesten en equipos. a) Juan debe pagar el precio de un viaje en 16 mensualidades de $358 cada una. Indiquen, con un número negativo, la cantidad de dinero que debe. b) Escriban como producto de dos factores los siguientes números. – 11 = – 36 = – 120 = – 2.4 = 12 – 92 = – 30 = c) ¿Cuál de los números anteriores tiene sólo dos maneras de ser expresado como producto de dos factores? Expliquen su respuesta. Resultado – 36 Glosario factor. Número o expresión que puede multiplicarse para formar un producto. 12 = 3 × 2 × 2 producto factores 4. a) 16 × (– 358) = – 5 728 pesos b) – 11 = (– 1) × (11) – 36 = (– 6) × (6) – 120 = (3) × (– 40) – 2.4 = (– 2) × (1.2) 12 = ( 4 ) × (– 3 ) – 92 = (– 2) × (46) – 30 15 2 c) – 11, sólo puede escribirse como – 1 × 11 y – 11 × 1. Comparen sus respuestas con las de otro equipo. Discutan por qué en cada una de las multiplicaciones anteriores es necesario que uno de los factores sea negativo. 33 Bloque 1 - Secuencia 3 35 Sugerencias didácticas Lean en grupo las reglas del juego de la actividad 5 y, de ser posible, salgan al patio para ponerlo en práctica. Una vez concluido, pregunte ¿Qué combinación de posiciones y movimientos involucra dos signos positivos, un signo negativo y otro positivo y dos signos negativos? Se espera que después de jugarlo los alumnos deduzcan: • Dos signos positivos: mirar hacia el norte y avanzar hacia adelante. • Un signo positivo y un signo negativo: mirar hacia el norte y caminar hacia atrás, mirar hacia el sur y caminar hacia adelante. • Dos signos negativos: mirar hacia el sur y caminar hacia atrás. Otra manera de utilizar las reglas anteriores es planteando acertijos relacionados con posiciones a las que quieren que lleguen sus compañeros. Por ejemplo, puede preguntar ¿A dónde llegas si miras hacia el sur y avanzas 8 pasos hacia atrás? Al terminar el inciso d) pregunte ¿Qué nueva regla de multiplicación de signos acabas de construir a partir del juego? S3 Multiplicación de dos números negativos 5. Lean en parejas la situación y contesten. Si es posible, trabajen la actividad en el patio de su escuela. Luis y Carolina pintaron con gis una recta numérica para jugar, como se muestra en la siguiente figura. Sur Norte -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 Las reglas del juego son las siguientes: Multiplicación de dos números negativos Solucionario 5. a) – 5 b) – 3 c) Mira hacia el norte y camina 7 pasos hacia adelante. Mira hacia el sur y camina siete pasos hacia atrás. d) Inciso a): 5 × (– 1) = – 5 Inciso b): (– 3) × 1 = – 3 Inciso c): 7 × 1 = (– 7) × (– 1) = 7 • Si están mirando hacia el norte, consideren una dirección positiva y una dirección negativa si están mirando hacia el sur. • Caminar hacia adelante representa un signo positivo, pero caminar hacia atrás tiene un signo negativo. • Cada uno en su turno se coloca en el cero y, siguiendo las reglas, recibe las instrucciones de su compañero. a) Luis mira hacia el norte y camina hacia atrás 5 pasos, ¿a qué punto llegó? c) Escriban de dos formas distintas la manera en que Luis puede llegar al 7, a partir del cero, dando únicamente 7 pasos. d) Representen los movimientos de Luis y Carolina dados en los incisos anteriores utilizando una multiplicación de enteros. Expresen con 1 un paso hacia adelante y con – 1 un paso hacia atrás. Inciso a): Inciso b): Inciso c): Comparen sus resultados y sus procedimientos con los de otra pareja. ¿Cómo son los signos de los factores que representan caminar hacia atrás y mirar al sur? A partir de varios ejemplos observen cuál es el signo del resultado. 36 Bloque 1 - Secuencia 3 34 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. b) Carolina mira hacia el sur y camina hacia adelante 3 pasos, ¿a qué punto llego? Multiplicación de números positivos y negativos Sugerencias didácticas 6. Reúnanse en equipos para completar las tablas y contesten. (– 5)(3) Notación (– 7)(3) – 10 – 14 (– 5)(1) (– 7)(1) 0 0 (– 5)(– 1) (– 7)(– 1) (– 5)(– 2) (– 7)(– 2) Hay expresiones equivalentes de una multiplicación. Por ejemplo: 11 × (– 2) = (11)(– 2) 2 × (x) = (2)(x) = 2x Lea con sus alumnos la sección “Notación” y establezcan la escritura que usarán para resolver las actividades que involucren multiplicación. Antes de completar las tablas, sugiera a los estudiantes que analicen el patrón de la secuencia y apliquen la ley de signos. Solucionario 6. (– 5)(3) – 15 (– 7)(3) – 21 15 21 (– 5)(2) – 10 (– 7)(2) – 14 20 28 (– 5)(1) 35 –5 (– 7)(1) 25 –7 (– 5)(0) 0 (– 7)(0) 0 (– 5)(– 1) 5 (– 7)(– 1) 7 (– 5)(– 2) 10 (– 7)(– 2) 14 (– 5)(– 3) 15 (– 7)(– 3) 21 ¿Y del resultado de (– 7)(– 4) al resultado (– 5)(– 4) 20 (– 7)(– 4) 28 de (– 7)(– 5)? c) ¿De cuánto en cuánto aumentan o disminuyen los números de la segunda fila (– 5)(– 5) 25 (– 7)(– 5) 35 a) ¿Qué número hay que sumar o restar para pasar del resultado de (– 5)(3) al resultado de (– 5)(2)? ¿Y del resultado de (– 5)(– 2) al re- sultado de (– 5)(– 3)? b) ¿Qué número hay que sumar o restar para pasar del resultado de (– 7)(1) al resultado de (– 7)(0)? de cada una de las tablas? d) A partir de los números de las tablas, ¿cuál es el signo del resultado al multiplicar dos números negativos? © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Expliquen sus razonamientos a otros equipos y analicen otras sucesiones de multiplicaciones; observen las regularidades en los signos. 7. Continúen en equipos y realicen las siguientes multiplicaciones en la calculadora. Asegúrense de que la calculadora tenga las teclas +/– o (–) para escribir los signos negativos. -2.2 3 = 5 1.6 4.5 = -3.5 = 3 -_ 4 -17 -11 1 -_ 2 = -2.5 = 1 -_ 2 a) En ambos casos sumar 5. b) En ambos casos sumar 7. c) Aumenta de 5 en 5 para la primera tabla y de 7 en 7 para la segunda tabla. d) El signo es positivo. 7. a) Dos signos positivos o dos signos negativos. b) Un signo negativo y uno positivo. Recursos adicionales En la siguiente página puede consultar las propiedades de multiplicación de números enteros: • “Multiplicación de números enteros”, disponible en www.edutics.mx/ wQE (consulta: 14 de agosto de 2018). = a) ¿Qué signos tienen los números que al multiplicarse su resultado es positivo? b) ¿Qué signos tienen los números que al multiplicarse su resultado es negativo? Establezcan con otros compañeros cómo multiplicar dos números negativos. 35 Bloque 1 - Secuencia 3 37 S3 Sugerencias didácticas Proyecte a sus estudiantes el video sugerido en la sección “Explora” y analícenlo de forma grupal. Después completen el esquema de la actividad “Integración” y pida a los alumnos que completen la ley de los signos que complementen en la ficha de trabajo. Para resolver la actividad 8, recuerde a sus estudiantes que las operaciones inicialmente se trabajan de manera binaria; es decir, entre parejas de números, de los cuales se obtiene un resultado y se vuelve hacer binaria la operación. Dado que ya trabajan con paréntesis, pida que las agrupen con ellos. Para concluir haga el siguiente planteamiento Si una multiplicación se conforma por 100 factores, todos de signo negativo ¿qué signo tendrá el resultado? Si son 101 factores todos de signo negativo ¿qué signo tendrá el resultado? Después analicen el inciso d). Solucionario (– 3.5)(– 10)(– 10) = – 350 9. a) Positivo b) Negativo c) Cero d) Negativo, – 440 Positivo, 117 649 Negativo, – 23.38875 Neutro, 0 e) • Por – 1 • Por – 35 = – 8.75 4 • Por – 4 38 Bloque 1 - Secuencia 3 • De forma grupal completen el esquema con las reglas de los signos para la multiplicación de números enteros. • Exprésenlas en forma verbal. × + – + – (– 57 ) (– 25 ) = 1 (– 1)(– 2)(– 2 )(– 3.5) = (– 3.5)(– 10)(– 10) = × + – + + – – 9. Analicen y contesten en equipos. a) Si en una multiplicación la cantidad de factores negativos es un número par, ¿qué signo tendrá el resultado? b) Si en una multiplicación la cantidad de factores negativos es un número impar, ¿qué signo tendrá el resultado? c) Si en una multiplicación uno de los factores es 0, ¿cuál será el resultado? + d) Sin efectuar las multiplicaciones, anticipen el signo del resultado. Después corroboren sus respuestas. (– 23 )(– 4) = 8 3 5 2 10 = 2 (– 7 )(– 5 ) = 35 7 (– 1)(– 2)(– 21 )(– 3.5) = (– 2)(5)(– 11)(– 4) = (– 7)(– 7)(– 7)(– 7)(– 7)(– 7) = 3.5 (– 3.5)(1.1)(– 8.1)(– 0.75) = (– 2)(3.75)(– 4)(0)(– 2 105)( 2 ) = 1 e) Se dice que dos números son simétricos si en la recta numérica se encuentran a la misma distancia a partir del origen pero en sentidos opuestos. • ¿Por qué número debe multiplicarse 5 para obtener su simétrico? • ¿Por qué número debe multiplicarse 16 para obtener el simétrico de 140? • ¿Por qué número debe multiplicarse – 9 para obtener el simétrico de – 36? Comparen sus respuestas con el grupo. Discutan y establezcan conclusiones acerca de las propiedades del producto de números con signo. 36 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. (– 4.2)(– 1.1) = 4.62 Integración (– 4.2)(–1.1) = – 8. (– 1.7)(– 11) = 187 Explora En la página www. edutics.mx/JKu podrás observar un video con una explicación de por qué menos por menos da más. 8. Efectúa las siguientes multiplicaciones. (– 17)(– 11) = (– 23 )(– 4) = Integración • Más por más da más. Más por menos da menos. Menos por más da menos. Menos por menos da más. En un producto que involucra dos números con el mismo signo (ambos positivos o ambos negativos) el resultado es de signo positivo. Multiplicación de números positivos y negativos Arribamos 1. Considera nuevamente el problema planteado al inicio de la secuencia. a) Expresa por medio de una multiplicación la distancia, desde el punto de referencia, a la que estará Romina dentro de nueve horas. b) Expresa por medio de una multiplicación la distancia, desde el punto de referencia, a la que estaba Romina hace 10 horas. Arribamos Revise de manera grupal las respuestas a los acertijos de la actividad 2; si lo considera necesario, resuelva , con sus estudiantes, más ejercicios de éste tipo para que ellos, además de multiplicar números con signo, interpreten el problema y lo analicen. Al terminar la actividad se recomienda que hagan ejercicios adicionales que involucren sumas, restas y multiplicaciones con números enteros. Lo anterior es con la finalidad de poner en práctica el uso de las reglas de signos para las operaciones ya mencionadas, así como la jerarquía de las operaciones. Ponga a prueba las habilidades de sus estudiantes con los ejercicios de la página recomendada en la sección “Explora”. Y si le es posible revise los resultados que obtuvieron. Por último, escriba operaciones y solicite a los estudiantes que coloquen los signos para obtener los resultados señalados. Por ejemplo: coloca los signos requeridos para que la operación (5) + (3)(2) dé como resultado – 1, 1 u 11. 2. Resuelve los siguientes acertijos. Encuentra dos números que multiplicados den – 77. Encuentra dos números que multiplicados den – 132 y sumados den 16. Encuentra el número por el que hay que multiplicar al 1 276 para obtener – 1 276. Encuentra dos números que multiplicados den – 49 y sumados den – 48. 3. Efectúa las siguientes multiplicaciones. (– 5)(2)(– 34) = (– 10)(– 7)(– 4)(– 2)(– 1) = (1.5)(– 0.1)(2.3) = (– 1 – 45 )( 35 )(– 5) = Solucionario 4. Para fomentar la puntualidad del personal de una fábrica se implementaron los incentivos que se muestran en el siguiente cartel. Puntualidad: + $50.00 Retraso menor o igual a 15 minutos: – $35.00 Retraso mayor a 15 minutos: – $60.00 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas a) Calcula, utilizando números positivos y negativos, el beneficio o pérdida de cada trabajador registrado en la tabla. Alberto Beatriz Carlos Diana Días que llegó puntual 14 16 10 12 Días con retraso menor o igual a 15 minutos 3 0 3 1 Días con retraso mayor a 15 minutos 3 4 7 7 Explora Resuelve en www.edutics. mx/36u algunos ejercicios de multiplicación de enteros. 1. a) – 180 = 9 × (– 20) b) 200 = (– 10) × (– 20) 2. Encuentra dos números que multiplicados den – 77: 11(– 7) y – 7 (11). Encuentra dos números que multiplicados den – 132 y sumados den 16: 22(– 6) = – 132 y 22 + (– 6) = 16. Encuentra el número por el que hay que multiplicar al 1 276 para obtener – 1 276: Se debe multiplicar por – 1. Encuentra dos números que multiplicados den – 49 y sumados den – 48: 1 (– 49) = – 49 y 1 + (– 49) = – 48. 3. (– 5)(2)(– 34) = 340 (– 10)(– 7)(– 4)(– 2)(– 1) = – 560 (– 1 – 45 )( 35 )(– 5) = 27 (1.5)(– 0.1)(2.3) = – 0.345 5 4. a) Alberto: 14(50) + 3(– 35) + 3(– 60) = $415 Beatriz: 16(50) + 0(– 35) + 4(– 60) = $560 Carlos: 10(50) + 3(– 35) + 7(– 60) = $ – 25 Diana: 12(50) + 1(– 35) + 7(– 60) = $ 145 Compara tus respuestas con algún compañero. En caso de que sean distintas discutan si es posible tener más de una respuesta correcta. 37 Bloque 1 - Secuencia 3 39 S4 División de números positivos y negativos Partimos Sugerencias didácticas Lea con sus alumnos el párrafo introductorio y pregunte ¿Cuál es la relación que existe entre la multiplicación y la división? ¿Cómo pueden obtener una multiplicación a partir de una división? Para aclarar dudas escriba una división en el pizarrón y resuélvala, haga notar que al buscar la solución se utiliza la multiplicación. Utilice la galera y acomode los números para una mejor comprensión de la relación entre estas operaciones. Permita que los alumnos intenten resolver la actividad 1 por su cuenta y comente que es importante leer la sección “Glosario” para comprender el planteamiento del problema. Si lo considera conveniente, explique que a ÷ b = c implica que b × c = a, entonces, para resolver – 31.5 ÷ 6 = ¿? se debe encontrar un número que al multiplicarlo por 6 se obtenga – 31.5. Resalte que es importante definir el signo del número desconocido, pues un factor es positivo y el resultado es negativo. S4 Resuelve problemas de división con números enteros, fracciones y decimales positivos y negativos. Partimos Glosario División de números positivos y negativos La multiplicación y la división son operaciones que tienen una relación directa, dado que se puede obtener una a partir de la otra. En esta secuencia estudiarás la división de números positivos y negativos utilizando las propiedades de la multiplicación que trabajaste en la secuencia anterior; con ello completarás tu repertorio de operaciones básicas con todos los números que conoces hasta ahora. 1. Analiza la situación y responde. Un barco hundido se encuentra en el fondo del mar a 31.5 m de profundidad. Para conocer el pecio, uno de los buzos del equipo de investigación realizó tres descensos; por razones de seguridad, cada uno en distintas etapas como se muestra en la figura, donde cada división del segmento representa una etapa. pecio. Restos o fragmentos de un artefacto o nave que ha naufragado. 1.er descenso 2.o descenso 3.er descenso Solucionario a) ¿En cuántas etapas hizo cada descenso? b) Utiliza números negativos para denotar los metros bajo el nivel del mar a los que se encuentra el barco. c) Calcula cuántos metros bajó el buzo por etapa en cada descenso. Compara tus resultados con los de algún compañero y expliquen la interpretación que le dieron al problema. 40 Bloque 1 - Secuencia 4 38 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 1. a) Descenso 1: en 6 etapas Descenso 2: en 4 etapas Descenso 3: en 3 etapas b) – 31.5 m c) Descenso 1: – 5.25 m por etapa Descenso 2: – 7.875 m por etapa Descenso 3:– 10.5 m por etapa Recorremos El cociente de números enteros Recorremos Sugerencias didácticas Pida a los estudiantes que pasen al pizarrón a escribir las divisiones con la galera para resolver la actividad 1. Recuérdeles que dividir consiste en buscar un número que multiplicado por el divisor dé como resultado el dividendo, y que también deben identificar el signo correcto. × ¿? 12 986 1. Lee cada situación y contesta lo que se te pide. a) Luis encontró un número que multiplicado por 12 da – 96. • ¿Qué número es? • ¿Cómo determinaste el número que encontró Luis? • ¿Cuál es el resultado de dividir – 96 entre el número desconocido? = b) ¿Qué número dividido entre – 7 da como resultado – 14? El cociente de números enteros • Explica cómo obtuviste dicho número. Solucionario c) ¿Qué número multiplicado por – 23 da – 805? • ¿Cuál es el resultado de dividir – 805 entre – 23? • ¿Cuál es el signo del número que encontraste? • ¿Cómo lo determinaste? Reúnete con un compañero y expliquen con qué operaciones es posible obtener cualquiera de los elementos de la división a partir de dos conocidos; por ejemplo, calcular el dividendo a partir del cociente y el divisor. También discutan cuántas divisiones se pueden escribir a partir de una multiplicación. 2. A partir de las relaciones entre los elementos de la división, completen en parejas la siguiente tabla en la que los números de la primera fila son los dividendos y los de la primera columna los divisores. Dividendo 2 – 12 30 – 42 Dividendo 120 15 –3 4 Divisor Divisor © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. ÷ 1. a) • – 8 • R. M. Haciendo una división, 96 ÷ 12 = 8, luego, se debe elegir el signo correcto, como 12 es positivo y el resultado es negativo, entonces el número debe ser negativo: – 8. • 12 b) 98 • R. M. Multipliqué – 14 por – 7 y obtuve 98, el signo es positivo. c) 35 • 35 • El signo es positivo. • Al multiplicar el cociente por el divisor se obtiene el dividendo; el cociente debe ser positivo para que al multiplicarlo por – 23 resulte un número negativo. 2. 15 2 –5 – 24 a) Analicen los resultados de la tabla y completen. • Si el producto de dos números negativos es positivo, entonces el cociente de uno positivo entre otro negativo deber ser . • Si el producto de un número positivo y otro negativo es negativo, entonces el cociente de uno negativo entre otro negativo deber ser 39 ÷ – 12 30 – 42 120 2 –6 15 – 21 60 –3 4 – 10 14 – 40 4 –3 15 2 – 21 2 30 –5 12 5 –6 42 5 – 24 a) • Negativo • Positivo . Bloque 1 - Secuencia 4 41 S4 Sugerencias didácticas Revise las respuestas de la actividad “Integración” y pregunte ¿Cuál es la diferencia entre las leyes de signos de la multiplicación y la división? El objetivo es que los alumnos noten que no hay diferencia y que las leyes son las mismas. Después de que lleguen a dicha conclusión, analicen el recuadro de la sección “Formalización”. Analicen la sección “Recuerda” y comente que los paréntesis también indican multiplicación, por ejemplo, 5 × 3 = 5(3). Comparen sus respuestas con otra pareja. Comprueben sus divisiones multiplicando el cociente por el divisor para obtener el dividendo. Repitan las divisiones de la tabla anterior usando su calculadora y verifiquen que han obtenido los mismos resultados. Asegúrense que la calculadora que utilicen tenga las teclas +/ – o ( – ) para escribir números negativos. Integración • A partir de las actividades anteriores coloca los signos + y – según corresponda, para resumir las leyes de los signos en la división. Solucionario Integración • ÷ + = + + ÷ – = – – ÷ + = – ÷ – = + – –4 36 ×9 2 18 En matemáticas los paréntesis se utilizan para separar operaciones o agrupar términos. Por ejemplo: – 3 + (– 2) = – 3 – 2 = – 5 5 ÷ (– 3) = ÷ (– 5) – 0.7 3.5 ÷ (– – 24 ÷ (– 0.1) 1 3 ) 7 72 ÷ = ÷ = Para resolver una división de números positivos y negativos, se dividen los valores absolutos y al resultado se le aplica la regla de los signos como en el caso de la multiplicación. Así, al dividir dos números del mismo signo el resultado tiene signo positivo y el resultado es de signo negativo si se dividen dos números de signo distinto. 3. Escriban en equipos los números y los signos de multiplicación y división que faltan. 3.5 ÷ (– 9) ×9 36 ÷ 24 720 5 –3 4 × (3 – 8) = 4 × (– 5) = – 20 × (0.5) ÷ (0.1) = considerando que la regla de los signos para la multiplicación también sea válida. Recuerda ÷ (– 2) ÷ • Compara tu esquema con el de algún compañero. Si son distintos corrijan 3. ÷ (– 9) = 30 2 ÷ (– 5) 3.5 7 3.5 720 30 ÷ (– 3 ) 1 – 24 Verifiquen sus respuestas. Recuerden que una cantidad se puede expresar en fracción o decimal. 42 Bloque 1 - Secuencia 4 40 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. + ÷ División de números positivos y negativos Sugerencias didácticas Indique a los estudiantes que, para resolver la actividad 4, primero calculen cuántos grados desciende la temperatura en un minuto. 4. Resuelve los siguientes problemas. a) Los termómetros siguientes muestran cuántos grados bajó la temperatura del refrigerador de un laboratorio entre las 15:00 h y las 16:00 h. TEMP HORA 15:00 TEMP • Indica, utilizando números negativos, cuánto descendió la temperatura en una hora y qué fracción de grado descendió cada minuto. Explica tu respuesta. • Si la temperatura continúa descendiendo de forma constante, ¿a qué hora el refrigerador alcanzará – 30° C? b) En Física la fórmula que relaciona la fuerza que actúa sobre un cuerpo con la masa de éste y con la aceleración que se produce en él es F = ma. • Con base en la fórmula anterior, completa la tabla. Masa (kg) Aceleración (m/s2) – 0.8 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. – 1 2 – 18 3 4 – 4. a) • La temperatura descendió – 24 °C. Como una hora tiene 60 minutos, entonces – 24 ÷ 60 = – 25 . Por lo tanto, la temperatura desciende – 25 °C cada minuto. • A las 16:30 horas b) Masa (kg) Aceleración (m/s2) Fuerza (N) 8 – 0.1 – 0.8 12 – 1 21 – 18 3 4 – 43 9 – 16 1.25 – 100 – 125 5 8 –4 – 2.5 9 16 1.25 – 125 5 8 – 2.5 c) Encuentra dos números cuyo cociente sea – 1 y que la resta del primero menos 3 el segundo sea – 2 . Primero: Segundo: d) Encuentra dos números cuyo cociente sea 0 y que la resta del primero menos el segundo sea 1 025. Primero: Solucionario Fuerza (N) 8 –1 HORA 16:00 Segundo: Compara tus respuestas y tus procedimientos con algún compañero. Si hay diferencias utilicen la calculadora para verificar sus resultados. c) Primero: 43 ; segundo: – 43 d) Primero: 0; segundo: – 1 025 5. 136 ÷ (– 4) = – 34 – 23 ÷ 85 = – 5 12 3(– 21 ) ÷ 0.1 = – 15 2.5 ÷ (– 15 ) 2 =– 1 3 – 185 ÷ (– 10) = 18.5 – 43 ÷ (– 25 ) ÷ (– 1) = – 3 10 Recursos adicionales En el siguiente video puede consultar la explicación de cómo resolver la división de números enteros: • “Dividir números positivos y negativos”, disponible en www.edutics.mx/ wQR (consulta: 15 de agosto de 2018). 5. Resuelve las siguientes divisiones. Escribe tu procedimiento y simplifica al máximo en los casos que consideres necesario. 15 136 ÷ (– 4) = 2.5 ÷ (– 2 ) = 2 8 –3÷5 = – 185 ÷ (– 10) = 3(– 2 ) ÷ 0.1 = 1 – 4 ÷ (– 2 ) ÷ (– 1) = 3 5 41 Bloque 1 - Secuencia 4 43 S4 Sugerencias didácticas Analice en grupo la conversación de la actividad 6 y muestre mediante la solución de una división que ésta no es conmutativa. Recuerde a los estudiantes que el numerador de una fracción es el dividendo y el denominador es el divisor. Propiedades de la división Solucionario 6. a) • 6 ÷ 3 ≠ 3 ÷ 6 • 3 ÷ (– 4) = (– 3) ÷ 4 = – 43 7. a) Para el primer caso, 5 y 5 o – 5 y – 5. Para el segundo caso, 5 y – 5. • Para el primer caso, los números deben ser iguales y del mismo signo, ya sean positivos o negativos. Para el segundo caso, los números deben ser de igual magnitud pero de signo diferente. b) R. M. 0 ÷ 9 • Que siempre es cero c) R. M. 1 240 ÷ (– 10) d) R. M. 17 ÷ (– 1) y 34 ÷ (– 2) Propiedades de la división 6. Lee el siguiente diálogo y contesta. Camila: Marco, mira lo que descubrí con respecto a la división. Marco: ¿Qué?, cuéntame. Camila: Que la división no es conmutativa, pero que si los números de la división que vas a efectuar tienen signo, entonces los signos sí son conmutativos. Marco: ¿Qué?, no entendí. Camila: Mm, espera. Volvamos a leerlo con detenimiento y escribamos ejemplos. Marco: De acuerdo. A ver, mm... a) Ayuda a Marco y a Camila escribiendo un ejemplo para cada caso. • La división no es conmutativa: • Al dividir, se puede conmutar los signos: 7. Resuelvan en equipos los siguientes problemas. a) Encuentren dos números tales que al dividir uno entre otro obtengan 1 y otros dos números tales que al dividir uno entre otro obtengan – 1. Integración • R. M. • ¿Qué propiedades en común tiene cada pareja de números que encontraron? Ejemplo La división no es conmutativa. Sí importa el orden en que se realiza la división. 25 ÷ 5 ≠ 5 ÷ 25 Para que el cociente sea cero, el dividendo siempre debe ser cero. 0÷x = 0 b) Encuentren dos números tales que al dividir uno entre otro el resultado sea 0. • ¿Qué propiedad cumple el dividendo? c) Encuentren dos números enteros que al dividir uno entre otro obtengan – 124. d) Encuentra dos divisiones cuyo cociente sea – 17. Para que el cociente sea 1, tanto el numerador como el denominador deben ser iguales. 8÷8 = 1 – 9 ÷ (– 9) = 1 Para que el cociente sea – 1, la magnitud del numerador y denominador deben ser iguales pero de signos opuestos. 8 ÷ (– 8) = – 1 9 ÷ (– 9) = – 1 Comparen sus respuestas con otro equipo. ¿Encontraron los mismos números? Si fueron distintos, ¿cumplen las mismas propiedades? Integración • En grupo escriban un resumen de las propiedades de la división que analizaron en las actividades anteriores. Usen una tabla que incluya ejemplos. Propiedad Ejemplo La división no es conmutativa. Sí importa el orden en que se realiza la división. 44 Bloque 1 - Secuencia 4 42 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Propiedad División de números positivos y negativos Arribamos 1. Lee nuevamente la situación inicial. a) Expresa el problema planteado usando divisiones de números con signo. b) Considera el siguiente texto y responde. Nuestra Señora del Juncal era una embarcación que se hundió en las costas de Campeche en 1631. Desde 1995, el Instituto Nacional de Antropología e Historia implementó un proyecto de investigación que incluía su búsqueda y ubicación. Uno de los buzos profesionales, realizó tres descensos a las profundidades que se indican en la siguiente imagen. 1.er descenso 2.do descenso Arribamos Sugerencias didácticas Comente con los alumnos que, al resolver los problemas de división, es importante que identifiquen correctamente los valores del dividendo, del divisor y del cociente, ya que la operación no es conmutativa, esto facilitará la solución de la actividad 2, incisos b) y c). Al terminar las actividades de la sección “Arribamos” invite a los alumnos a resolver los ejercicios propuestos en la sección “Explora”. Convivimos 3.er descenso Al terminar la secuencia, hable con los alumnos de su trabajo en equipo y pida que escriban en el pizarrón un aspecto que puedan mejorar. También platiquen de las ventajas de compartir la información; por ejemplo, cuando los problemas pueden tener más de una respuesta. Compartir los procedimientos y resultados con otros equipos puede ser enriquecedor. -19.2 m Solucionario -23.5 m -30.8 m Explora © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • El primer descenso lo hizo en etapas de – 3.2 m, ¿en cuántas etapas terminó? • ¿En cuántas etapas de – 4.7 m hizo el segundo descenso? • Si el último descenso lo hizo en etapas de – 7.7 m, ¿en cuántas terminó? 2. Resuelve los siguientes problemas. a) Juan presentó un examen de Historia en el que otorgaban 1.4 puntos por cada respuesta correcta y – 0.5 por cada respuesta incorrecta. • Si Juan obtuvo 17.5 y contestó 15 preguntas de manera correcta, ¿en cuántas preguntas se equivocó? • Escribe una expresión matemática que modele la situación. b) Encuentra dos números cuyo cociente sea – 8 y cuyo producto sea – 32. c) Encuentra dos números cuyo cociente sea 0.75 y cuya suma sea – 7. En el siguiente enlace www.edutics.mx/3uN encontrarás ejercicios y problemas de división de enteros. Los dos puntos (:) representan el operador de división. – 3 + 8 – 25 –5 = 2 × (– 24) ÷ (– 64 + 80) – 8 = 12 × (– 8) (– 6) × 4 = (65 ÷ (– 5)) × 2 + (28 ÷ 7) = En grupo valida tus respuestas. Traten juntos de plantear problemas y acertijos que involucren divisiones de números con signo y también otras operaciones. Compartan sus planteamientos de forma ordenada y presten atención a las propuestas de sus compañeros. 43 =4 12 × (– 8) –6×4 4 5 =4 2 × (– 24) ÷ (– 64 + 80) – 8 = – 11 (65 ÷ (– 5)) × 2 + (28 ÷ 7) = – 22 3. Utiliza la jerarquía de operaciones cuando sea necesario y resuelve. 2 5 – 361 ÷ (– 19) = 3 ÷ (– 6 ) = (– 3 + 8 – 25) –5 1. a) Primer descenso: – 31.5 ÷ 6 Segundo descenso: – 31.5 ÷ 4 Tercer descenso: – 31.5 ÷ 3 b) • En 6 etapas • En 5 etapas • En 4 etapas 2. a) • Se equivocó en 7 preguntas. • 15(1.4) – 0.5x = 17.5 15(1.4) – 7(0.5) = 17.5 b) 16 y – 2 o – 16 y 2 c) – 3 y – 4 2 ÷ (– 5 ) = – 3. –361 ÷ (– 19) = 19 3 6 Convivimos Al trabajar en equipo, es importante comunicar tus ideas con respeto. Reflexiona y comparte: ¿cómo mejorarías este aspecto con tus compañeros? Recursos adicionales En la siguiente liga puede encontrar más ejercicios de multiplicación y división de números enteros: • “Multiplicación y división de números enteros”, disponible en www.edutics.mx/wEK (consulta: 15 de agosto de 2018). Bloque 1 - Secuencia 4 45 S5 Potencias con exponentes enteros Partimos Sugerencias didácticas Pida a los alumnos que lean el párrafo introductorio de la secuencia y pregunte ¿Han hecho alguna operación en la que la solución dependa de encontrar un número que multiplicado por sí mismo dé el resultado? Para resolver la actividad 1, recomiende a sus estudiantes buscar el patrón involucrado en la propagación de la noticia. Realice preguntas como ¿Qué número está involucrado? ¿De qué valor depende el siguiente número? Si a las 10:00 horas del día, ya saben la noticia 65 536 personas, ¿cómo calculan el número de personas que sabrán la noticia a las 10:15 horas? S5 Resuelve problemas de potencias con exponente entero. Partimos Potencias con exponentes enteros En esta secuencia estudiarás el caso particular de multiplicaciones en las que todos los factores son iguales, es decir, la multiplicación repetida de un número por sí mismo. Aprenderás que existe una manera especial de expresar este producto, las propiedades que cumple y las operaciones que se pueden hacer con expresiones de este tipo. 1. Lee la situación y contesta. Un viajero llega a las ocho de la mañana a un pequeño pueblo con una noticia que interesa a todos. Así, a las 8:15, el viajero ha contado la noticia a cuatro personas y continúa su viaje. En los siguientes quince minutos, cada una de ellas comparte la noticia con otras cuatro que no la conocen. Quince minutos después, cada una de estas personas la repite y continúan así, propagando la noticia, en un periodo de 15 minutos cada vez. 8:00 h Solucionario 1. a) A las 8:45 la noticia es conocida por 64 personas y a las 9:15, ya la saben 1 024 personas. b) No, porque no se puede obtener 1 000 multiplicando 4 por sí mismo varias veces. 8:15 h Recorremos 8:30 h Potencias Después de analizar el problema de la actividad 1, explique que hay varios fenómenos relacionados con el cálculo de potencias, por ejemplo, el crecimiento bacteriano, la reproducción, conteos y cálculo de probabilidades. Compara con tus compañeros tus respuestas y procedimientos. ¿Conocen alguna manera de expresar una multiplicación cuando los factores son todos iguales? Solucionario 1. a) • 2 × 2 × 2 × 2 × 2 × 2 Recorremos Potencias 1. Resuelve los siguientes problemas. a) Como has estudiado en Biología, las bacterias se reproducen asexualmente por fisión binaria (figura 5.1) y ocurre de manera muy rápida. De una célula se obtienen dos, de esas dos se obtienen cuatro células hijas, y así sucesivamente. • Escribe una operación aritmética que te permita calcular cuántas bacterias habrá después de media hora en el caso de que una bacteria se reproduzca cada cinco minutos. 46 Bloque 1 - Secuencia 5 44 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. a) ¿Cuántas personas del pueblo, sin incluir al viajero, conocen la noticia a las 8:45 h? ¿Y a las 9:15 h? b) En alguno de los periodos de quince minutos, ¿es posible que exactamente 1 000 personas conozcan la noticia? Explica tu respuesta. Sugerencias didácticas Sugerencias didácticas • ¿Cuántas bacterias habrá en ese momento? • ¿Cuántas habrá al cabo de 45 minutos? ¿Y en una hora? • Escribe las expresiones aritméticas que te permiten hacer los cálculos. Célula madre Dos células hijas Figura 5.1 En la fisión binaria la célula aumenta su tamaño y duplica su material genético y citoplasmático en dos partes idénticas para dar lugar a dos células hijas idénticas. • ¿Hay el doble de bacterias en una hora que en media hora? Explica tu respuesta. b) En un invernadero, una planta de frambuesa tiene seis ramas de las que se pueden obtener seis esquejes. Después de mes y medio, cada esqueje da a su vez una planta con seis ramas de las que nuevamente se separan seis esquejes. Si se continuara con este método de reproducción y suponiendo que ningún esqueje ni planta mueran, ¿cuántos esquejes se habrían plantado después de seis meses? • Escribe las operaciones aritméticas para calcular el resultado. Glosario esquejes. Fragmentos de plantas (tallos, brotes o trozos de raíces) que se utilizan con fines reproductivos para obtener otras plantas idénticas. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Compara tus respuestas con las de tus compañeros. ¿Cómo obtuvieron los resultados? ¿Todos utilizaron la misma operación para realizar los cálculos? Multiplicaciones con factores iguales como 2 × 2 × 2 × 2 × 2 × 2 o 10 × 10 × 10 × 10 se pueden expresar en forma abreviada como 26 o 104. A esta operación se le conoce como potenciación y a su resultado, potencia. El factor repetido se llama base y el número que indica las veces que se repite se llama exponente. Por ejemplo: Exponente 26 base Muestre un diagrama más amplio de la figura 5.1 y analice en grupo el comportamiento de la fisión binaria; esto será de utilidad para resolver la actividad del inciso a). Invite a los alumnos a leer la sección “Glosario” para resolver la actividad del inciso b), también es recomendable hacer un diagrama donde se observe el crecimiento de la planta. Al terminar, pida a los alumnos que calculen el número de esquejes que habrá después de 3 años, de manera que tengan la necesidad de escribir las operaciones de forma sintetizada en éste y otros problemas del mismo tipo. Analice con los alumnos el recuadro de “Formalización” y resalte la ventaja de utilizar potencias en lugar de escribir la multiplicación de forma desarrollada. Asegúrese de que comprendan el papel de la base y del exponente, al terminar, realicen algunas actividades de la sección “Explora”. Explora En la página www. edutics.mx/Uee podrás resolver varias actividades para familiarizarte con la operación potenciación. Se lee “dos elevado a la sexta potencia”; por lo que 64 es la sexta potencia de 2. De forma general: Exponente bn base Solucionario • 64 bacterias • Habrá 512 bacterias en 45 minutos y 4 096 en una hora. • Para 45 minutos: 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 Para 1 hora: 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 • No, ya que 4 096 no es el doble de 64. El crecimiento es exponencial, 64 veces más b) 7 776 esquejes • Multiplicando 5 veces 6: 6 × 6 × 6 × 6 × 6 = 7 776 2. 5 × 5 × 5 × 5 × 5 = 55 1 1 1 1 1 4 2 × 2 × 2 × 2 = (2) (– 2)(– 2)(– 2)(– 2)(– 2)(– 2)(– 2) = (– 2)7 1.5 × 1.5 × 1.5 × 1.5 = 1.54 15 = 151 0 × 0 × 0 = 03 m × m × m × m × m × m × m × m = m8 a × a = a2 Recursos adicionales En la siguiente página encontrará ejercicios de potencias: • “Exponentes (básico)”, disponible en www.edutics.mx/wQK (consulta: 15 de agosto de 2018). El resultado, es decir, b × ... × b (n-veces) es la enésima potencia de b. 2. Con base en la información anterior, escribe las multiplicaciones o potencias que corresponden. = 55 = (–2)7 = 151 1 2 1 1 1 ×2×2×2 = 1.5 × 1.5 × 1.5 × 1.5 = m×m×m×m×m×m×m×m = 0×0×0 = 45 a×a = Bloque 1 - Secuencia 5 47 Sugerencias didácticas S5 Deje que los alumnos resuelvan de forma independiente la actividad “Integración”, de esta manera se dará cuenta si han comprendido el concepto de potenciación de manera correcta. En el inciso a) de la actividad 3 pregunte ¿Por cuánto hay que multiplicar a un kibibyte para saber cuántos bits son? Una vez que se haya tomado la decisión de multiplicar por 8, pida que se escriba el 8 en forma de potencias. El objetivo es mostrar las operaciones resueltas con potencias. Puede desarrollar las potencias por separado y después juntarlas, como se muestra claramente en la actividad 4. Al responder el inciso b) de la actividad 4, pida que expresen en palabras cómo encontrar el exponente de una multiplicación de potencias con la misma base. Integración • Como grupo escriban los resultados de las siguientes potencias. Consideren que n es un entero positivo. • n1 = 0n = 1n = Expresen lo anterior como reglas generales para cualquier entero positivo n. 1n = n1 = 0n = Producto de potencias con la misma base 3. Analicen en parejas la información y contesten. Solucionario La capacidad de las computadoras se mide en bits y en bytes. Un bit es la unidad más pequeña y sólo puede tomar dos valores: 0 o 1. Un byte son 8 bits, que puede ser expresado como 23 bits. Debido a que la capacidad de las computadoras se ha incrementado a causa del desarrollo de sus componentes, se ha recurrido a otras unidades como kibibyte comúnmente llamado kilobyte, mebibyte (megabyte), gibibyte (gigabyte), tebibyte (terabyte), etcétera.1 Integración • 1 n = 1, n1 = n, 0n = 0 • 1 n = Uno elevado a cualquier potencia es 1. n1 = Cualquier número elevado a la potencia uno, da el mismo número. 0n = Cero elevado a cualquier potencia siempre es cero. 1 Nombres y símbolos de los prefijos utilizados en el campo de telecomunicaciones y electrónica. Sistema internacional de Unidades (SI), 8.a ed. 2006, p. 32, www.cem.es/sites/ default/files/siu8edes.pdf (consulta: 13 de mayo de 2018). Producto de potencias con la misma base 3. a) 8 × (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2) = (2 × 2 × 2) × (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2) = 23 × 210 = 213 • Con una multiplicación • 13 veces • 213 = 23 × 210 b) 220 = 210 × 210 c) 64 × (220) = 26 × 220 = 226 4. a) 35 × 32 = 37 b) La suma de 2 y 5 da como resultado 7. a) Si un kibibyte equivale a 210 bytes, ¿cuántos bits hay en un kibibyte? el número 2 como factor? • Expresen en forma de potencia la cantidad de bits hay en 1 kibibyte. b) Un mebibyte son 210 kibibytes, ¿cuál es la cantidad de bytes, escrita como potencia de 2, que hay en 1 mebibyte? c) Si a 64 personas se les envía un archivo de 1 mebibyte, ¿cuántos bytes en total se recibieron considerando a todos los destinatarios? Expresen la respuesta como potencia de 2. 4. Continúen en parejas y respondan con base en la información de la figura. a) ¿Cuál es el área del paralelogramo expresada como potencia de 3? 32 m b) ¿Cómo se relacionan los exponentes de los factores 32 y 35 con el exponte de 35 m 48 Bloque 1 - Secuencia 5 su producto? 46 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • ¿Cómo calcularon la cantidad de bits? • En la operación que utilizaron para resolver, ¿cuántas veces en total aparece Potencias con exponentes enteros Sugerencias didácticas Pida a los estudiantes que analicen la sección “Formalización” y que escriban un ejemplo en su cuaderno, anote en el pizarrón algunos de ellos. Para concretar solicite que resuelvan la actividad “Integración” y que expresen la propiedad con sus propias palabras. Antes de continuar, pregunte ¿Cómo resolverían una división de potencias? ¿Cómo calcularían una potencia de otra potencia? Esto es con el objetivo que de que se pregunten cómo pueden operar con potencias en esos casos. Enséñeles a utilizar la calculadora científica para encontrar diferentes potencias, en la actividad 6 inciso b) se menciona el uso de una tecla. Verifique que todos los alumnos la encuentren y pida que calculen (53)2 a partir de la definición, es decir, multiplicando 53 por sí mismo dos veces (53 × 53). Después solicite que desglosen cada una de las potencias. Así se obtendrá: (5 × 5 × 5) × (5 × 5 × 5) = 56. Repita el mismo procedimiento para otros ejemplos. Comparen sus respuestas y sus procedimientos con los de otra pareja. En cada caso ¿cómo se relacionan los exponentes de las potencias en los factores y su resultado? Discutan cuál podría ser una regla para multiplicar potencias que tengan la misma base y corrobórenla con la siguiente información. El producto de dos potencias con la misma base es otra potencia con la misma base y cuyo exponente es la suma de los exponentes en los factores. Integración • Con base en la información anterior, completen de forma grupal la expresión con las letras a, m y n donde corresponde. a × an = m+ 5. Coloca los exponentes necesarios para que las siguientes igualdades sean verdaderas. 5 5 10 × 106 = 107 ( 23 ) × ( 23 ) = ( 23 ) 49 × 4 = 412 (–9) × (–9) 0.52 × 0.53 × 0.56 = 0.5 a1 × a Solucionario Integración × (–9)4 = (9)7 • am × an = am + n × a3 = a6 5. 101 × 106 = 107 49 × 43 = 412 0.52 × 0.53 × 0.56 = 0.511 Potencia de potencias © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 6. Resuelvan en equipos. En cada cuadrado se indica la longitud de sus lados. Las figuras no están trazadas en la misma escala. a) Expresen el área de cada figura como la potencia de una potencia. ÁreaCuadrado A: cm2 ÁreaCuadrado B: cm2 53 cm = 125 cm Cuadrado A ÁreaCuadrado C: cm2 b) Utilicen su calculadora para encontrar el área. Si tienen una calculadora científica, pulsen la tecla ⋀ para los exponentes. ÁreaCuadrado A: cm2 ÁreaCuadrado B: cm2 ÁreaCuadrado C: cm2 c) Traten de escribir los resultados anteriores como potencias de 5, 2 y 10, respectivamente. Pueden utilizar la calculadora. ÁreaCuadrado A: cm2 ÁreaCuadrado B: cm2 28 cm = 256 cm Cuadrado B ( 23 )5 × ( 23 )5 = ( 23 )10 (– 9) × (– 9)2 × (– 9)4 = (– 9)7 a1 × a2 × a3 = a6 Potencia de potencias 6. a) ÁreaCuadrado A: (53)2 cm2 ÁreaCuadrado B: (28)2 cm2 ÁreaCuadrado C: (103)2 cm2 b) ÁreaCuadrado A: 15 625 cm2 ÁreaCuadrado B: 65 536 cm2 ÁreaCuadrado C: 1 000 000 cm2 c) ÁreaCuadrado A: 56 cm2 ÁreaCuadrado B: 216 cm2 ÁreaCuadrado C: 106 cm2 d) El producto de los exponentes en el inciso a) es igual al de los exponentes en el inciso c). 103 cm = 1 000 cm ÁreaCuadrado C: cm2 d) ¿Cómo se relacionan los exponentes de las expresiones en los incisos a) y c)? Cuadrado C 47 Bloque 1 - Secuencia 5 49 S5 Sugerencias didácticas Pida a los alumnos que escriban en una ficha de trabajo la fórmula de la sección “Formalización”, y que la expresen con sus propias palabras. Comente que la potencia de potencias es conmutativa pues amn es igual a anm. Pregunte ¿Hasta el momento cuántas reglas de potencias conoces? ¿Cuáles son? Los estudiantes deben estar conscientes de lo que han aprendido hasta el momento y el fichero es una buena herramienta para ello. Pregunte a los alumnos si en la multiplicación de potencias los exponentes se suman y en la potencia de potencias se multiplican, entonces ¿Qué ocurrirá con la división de potencias? Analice las respuestas y resuelvan en grupo el inciso c) de la actividad 8. Comparen respuestas con otros equipos. Cómo escribieron la potencia de una potencia. Con su calculadora verifiquen si sus observaciones son válidas para otros números. Alejandra (32)4 = 32 × 32 × 32 × 32 = 38 7. Nuevamente en equipos analicen lo siguiente. A tres alumnos se les pidió que escribieran un ejemplo de una potencia cuya base fuera una potencia, que la desarrollaran y escribieran el resultado como otra potencia. Julián (43)3 = 43 × 43 × 43 = 46 3 4 ( ( 21 ) ) Andrea 1 3 1 3 1 3 1 3 1 12 = (2) ×(2) ×(2) ×(2) = (2) Solucionario 7. a) Julián se equivocó, ya que (43)3 = 43 × 43 × 43 = 49. b) Los exponentes se multiplican. c) Sí, ya que la multiplicación es conmutativa. Así, (b8)2 = b8 × 2 = b2 × 8 = (b2)8 = b16. a) Revisen los resultados de cada estudiante. ¿Alguno de ellos se equivocó? Expliquen su respuesta. b) ¿Qué se hace con los exponentes en una potencia de potencias? c) Carlos afirma que el resultado de las potencias (b8)2 y (b2)8 es el mismo. División de potencias con la misma base 64 × 2 19 = 2216 2×2×2×2×2×2×2 2 ×2 26 × 210 9 10 Comparen respuestas con otros equipos. ¿Cómo hicieron para calcular las potencias de cada estudiante y verificar las que son correctas? Multiplicar una potencia por sí misma varias veces se conoce como potencia de potencias. El resultado es igual a la base elevada al producto de los exponentes. De forma general se representa: Recursos adicionales En la siguiente página puede consultar problemas y actividades variadas para sus estudiantes: • “Potencias”, disponible en www.edutics.mx/wak (consulta 9 de octubre de 2018). (am)n = amn = (an)m División de potencias con la misma base 8. Resuelvan en grupo el siguiente problema. a) ¿Cuántos archivos de 64 kibibytes pueden almacenarse en el espacio por usar en el disco de la izquierda? b) Escriban la capacidad del disco y el tamaño del archivo como potencias de 2. Espacio en el disco: bytes Tamaño de archivo: bytes c) Desarrollen las potencias en el numerador y en el denominador de la fracción que representa la división que resuelve el problema. 512 × 210 64 × 210 50 Bloque 1 - Secuencia 5 219 = 216 = 48 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 8. a) 8 archivos b) Espacio en el disco: 29 × 210 = 219 bytes Tamaño de archivo: 26 × 210 = 216 bytes 10 10 c) 512 × 210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 ×102 × 2 = Expliquen si Carlos tiene razón. Potencias con exponentes enteros Sugerencias didácticas d) Simplifiquen la expresión anterior considerando que el cociente de un número entre sí mismo es 1 y escriban el resultado en forma de potencia. 219 216 = = • ¿Fue posible simplificar? ¿Por qué? e) ¿Qué relación hay entre el exponente del resultado y los exponentes de las potencias del numerador y del denominador? Recuerde a los estudiantes que el cociente de un número entre sí mismo es igual a 1. Utilizando este resultado y desarrollando las potencias pídales que resuelvan los incisos d), e) y f) de la actividad 8. Para el caso de la actividad 9, se recomienda agrupar las divisiones y resolverlas, mencione a los alumnos que la división no es conmutativa, por lo que hay que respetar el orden en el que se restan los exponentes. Dé tiempo a los alumnos para escribir un procedimiento que les ayude a conocer el exponente del resultado en una división de potencias. Analicen en grupo algunas de las propuestas y escriba en el pizarrón las más acertadas. Solucionario d) f) Utilicen las siguientes fracciones para validar sus conclusiones. Desarrollen las potencias del numerador y del denominador, simplifiquen y escriban el resultado en forma de potencia. 47 = 44 0.26 = 0.22 (– 3)5 (– 3)4 = = f) = Escriban un procedimiento para obtener el exponente del resultado a partir de los exponentes de las potencias del numerador y del denominador. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 105 108 = 53 = 57 (– 6)2 = (– 6)7 4 d d8 = = = = = = = = = a) ¿Cuál es la diferencia entre los resultados de las divisiones anteriores y las del 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 210 2 × 2 × 2 × 2 × 2 × 2 × 210 47 44 = 4×4×4×4×4×4×4 4×4×4×4 0.26 0.22 = 0.2 × 0.2 × 0.2 × 0.2 × 0.2 × 0.2 0.2 × 0.2 (– 3)5 (– 3)4 = 23 = (– 3)(– 3)(– 3)(– 3)(– 3) (– 3)(– 3)(– 3)(– 3) = 43 = 0.24 = (– 3)1 Restar al exponente del numerador el exponente del denominador. 9. 105 108 = 10 × 10 × 10 × 10 × 10 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 1 10 × 10 × 10 53 57 = 5×5×5 5×5×5×5×5×5×5 62 67 = (– 6) × (– 6) (– 6) × (– 6) × (– 6) × (– 6) × (– 6) × (– 6) × (– 6) = 1 (– 6) × (– 6) × (– 6) × (– 6) × (– 6) = d×d×d×d d×d×d×d×d×d×d×d inciso f) de la actividad 8? b) Apliquen a los cocientes de potencias de esta actividad el procedimiento que encontraron en la actividad 8. ¿El exponente del resultado es positivo o negativo? Expliquen su respuesta. = • Sí, porque se está multiplicando y dividiendo por el mismo número. e) El exponente del resultado se obtiene de la resta del exponente del numerador y el exponente del denominador. = 9. Desarrollen en equipos las potencias del numerador y del denominador de las fracciones siguientes, simplifiquen la fracción y escriban el resultado del denominador en forma de potencia. 219 216 d4 d8 = 1 5×5×5×5 = = = = 1 103 1 54 1 (– 6)5 1 d×d×d×d = 1 d4 a) En la actividad anterior las potencias del resultado están en el numerador y en este inciso en el denominador. b) El exponente es negativo porque los exponentes se restan y el exponente del numerador es menor que el exponente del denominador. Comparen sus respuestas y procedimientos con los de otro equipo. Juntos determinen cómo pueden escribir una potencia cuyo exponente es negativo. 49 Bloque 1 - Secuencia 5 51 S5 Analice con el grupo la información de la sección “Formalización”, solicite que escriban el procedimiento en una ficha de trabajo y que agreguen esta ficha al fichero de resultados. Se sugiere que reproduzca en el pizarrón los diagramas de la actividad 10 y los estudie en grupo. Escriba los argumentos que demuestren la igualdad entre las expresiones, así los estudiantes podrán redactar las respuestas de los incisos a) y b). Aprendemos Pregunte si creen que las expresiones algebraicas generales se pueden considerar como un resumen. Mencione que para entender este tipo de “resúmenes” es necesario comprender el lenguaje algebraico. Al final, recomiende a sus alumnos estudiar mediante el uso de estas herramientas: resúmenes, mapas mentales, notas, entre otras. Al dividir dos potencias con la misma base se obtiene otra potencia con la misma base cuyo exponente es la resta del exponente del numerador menos el exponente del denominador. Aprendemos Integración • Con base en la información anterior, completa las expresiones. Al escribir las expresiones algebraicas que resumen las propiedades de la potenciación, éstas te ayudan a entender cómo hacer los cálculos. Reflexiona: ¿por qué sucede esto? Solucionario • Integración am an = am – n a– n = • 212 29 = 23 m3 m9 7– 3 74 1 an = m– 6 am – m 33 3– 3 212 29 =2 1 a–n = a Coloca los exponentes que faltan para que las igualdades sean verdaderas. – m m9 =m 33 3–3 =3 7 74 = 7–7 1 am • Expliquen por qué am es igual a a0. = 36 a0 = 1 = 7– 7 10. a) • Porque una fracción es igual a 1 si su numerador y denominador son iguales. • Porque al restar los exponentes del numerador y denominador se obtiene 0, ya que ambos exponentes son iguales. m m • Por un lado, aam = 1 y por el otro aam = a0, y como se trata de la misma expresión se concluye que a0 = 1. b) • Porque cualquier número multiplicado por uno es el mismo número. • Porque cuando se multiplican dos potencias con la misma base los exponentes se suman y la suma de n + 0 = n. • Porque ambos productos valen lo mismo, bn, entonces los factores b0 y 1 deben ser iguales. =a 10. Analicen en parejas lo siguiente. A Cuauhtémoc y a Marisol les dejaron de tarea investigar por qué cuando se eleva cualquier número a la potencia 0 se obtiene 1. a) Cuauhtémoc buscó en internet y encontró el diagrama de la izquierda en el que se indica que las cuatro expresiones son iguales. am • ¿Por qué am es igual a 1? am am • am an • ¿Cómo se llega a la conclusión de que a0 = 1? b) Marisol encontró en un libro el siguiente diagrama. • Expliquen por qué bn es igual a bn × 1. • ¿Por qué bn × b0 es igual a bn? bn × b0 bn bn × 1 • Expliquen por qué a partir de bn × b0 y bn × 1 se deduce que b0 = 1. b0 = 1 Comparen sus respuestas y razonamientos con sus compañeros. Si tienen dudas, soliciten el apoyo de su maestro. 52 Bloque 1 - Secuencia 5 50 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Potencias con exponentes enteros Arribamos 1. Lee nuevamente la situación que se plantea al inicio de la secuencia. a) Si el pueblo tiene 65 000 habitantes, ¿a qué hora todo el pueblo conocerá la noticia? b) Al empezar el último periodo de 15 minutos ¿cuántas personas conocen la noticia y a cuántas se les compartirá? c) ¿Cuántas de esas personas que ya la conocen podrán contársela a otras cuatro y cuántas no podrán hacerlo? Arribamos Permita a los estudiantes usar las fichas de trabajo al resolver operaciones con exponentes. Si es necesario ayúdelos a resolver el inciso b) de la actividad 3, recuérdeles que 1 mebibyte es equivalente a 220 bytes. Al terminar las actividades de la sección “Arribamos” pida a los alumnos que resuelvan las actividades que se sugieren en la sección “Explora”. 2. Subraya con verde las igualdades que son verdaderas y de rojo las que son falsas. a2 × a × a3 = a6 1.99 × 1.96 = 1.915 43 × 40 = 44 (m5)6 = m30 1115 114 ( ( 21 ) ) 4 0 (802)4 = 806 24 27 = 1111 b6 b8 = 23 1 = b–2 Explora A partir de 2015, los números de teléfono fijo de nuestro país tienen 10 dígitos. Para hacer una llamada de larga distancia se utiliza el Número de Identificador de Región (NIR) conocido como código de larga distancia. Por ejemplo, alguien que marca de la Ciudad de México a Guadalajara debe teclear “33” y el número de ocho dígitos, pero para marcar a una misma región bastará con que se tecleen los ocho dígitos. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Solucionario = 2 3. Resuelve los siguientes problemas. a) Lee la información y contesta. • ¿Cuántos números de teléfono fijo se pueden generar en una región del país? • Si existe la restricción de que los números de teléfono fijo no empiecen con 0, ¿cuántos números de teléfono fijo podría haber en una región del país? • Si consideras que los NIR y los números de teléfono fijo no deben empezar con 0, ¿cuántos números de teléfono fijo podría haber en todo país? b) Ana compró un disco duro como el de la imagen (1 gibibyte = 230 bytes) y un software que reduce 28 veces el tamaño de un archivo. • ¿Cuántos archivos de 2 mebibytes caben en el disco duro? • Si una carpeta ocupa 8 mebibytes y se reduce con el software, ¿cuántos bytes ocupará la carpeta? • ¿Cómo podrías expresar el resultado anterior como potencias de 2? Sugerencias didácticas En el siguiente enlace www.edutics.mx/ Uen encontrarás ejercicios y problemas que se resuelven con las propiedades de la potenciación. Los dos puntos (:) representan el operador de división. 1. a) A las 10 horas, dos horas después de que llego el viajero. En dos horas hay 8 intervalos de 15 minutos, que es lo que tarda en propagarse la noticia: 48 = 65 536. b) Después de 1 hora con 45 minutos la noticia es conocida por 47 = 16 384 personas, por lo que faltan 48 616 personas por conocerla, de las 16 384 que conocen la noticia solo 12 154 podrán compartirla a 4 personas (48 616 entre 4 = 12 154), por lo que 4 230 no podrán hacerlo. 2. 43 × 40 = 44 a2 × a × a3 = a6 1.99 × 1.96 = 1.915 (m5)6 = m30 (802)4 = 806 (( 21 )4)0 = 1115 114 24 27 b6 b8 = 1111 = 23 1 2 = b– 2 3. a) • 108, porque son 8 dígitos y cada uno tiene 10 posibilidades de ser: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. • 9 × 107 = 90 000 000 • 9 × 9 × 9 × 107 = 7 290 000 000 9 30 b) • 2 × 220 = 28 × 210 archivos 2×2 • 8 ×282 = 8 × 212 bytes • 215 bytes 4. 32 × 38 × 33 = 313 (( 21 )2)3 = ( 21 )6 20 (43 × 44)2 = 414 25 × 24 × 26 = 2– 2 29 × 28 (( 57 )3)2 (( 57 )2)3 =1 4. Resuelve las operaciones, escribe los resultados usando potencias. ( ( 57 ) ) 3 2 3 ×3 ×3 = 2 8 3 (( ) ) 1 2 2 3 = (4 × 4 ) = 3 4 2 25 × 24 × 26 29 × 28 = ( ( 57 ) ) 2 3 = Explica a tus compañeros cómo obtuviste tus resultados. Recuerden que puede haber más de una forma de resolver y llegar a la respuesta correcta. 51 Recursos adicionales En la siguiente página puede consultar más actividades relacionadas con el uso de exponentes: • “Material básico para trabajar con potencias”, disponible en www.edutics. mx/wQr (consulta: 16 de agosto de 2018). Bloque 1 - Secuencia 5 53 S6 Diagonales y ángulos interiores de un polígono Partimos Sugerencias didácticas Como introducción para la actividad pregunte ¿Qué es un polígono? ¿Qué es un polígono regular? ¿Qué es un polígono irregular? ¿Qué es una diagonal de un polígono? ¿Cómo se trazan las diagonales? Mencione que la palabra polígono se deriva de “poli” que significa “muchos” y “gono” que significa “ángulos”. Después lean la sección “Recuerda” y pida que tracen algunos polígonos con sus diagonales. Verifique sus respuestas. S6 Deduce y usa las relaciones entre los ángulos interiores y las diagonales de polígonos regulares. Partimos Diagonales y ángulos interiores de un polígono Desde primaria has estudiado los polígonos regulares e irregulares. ¿Recuerdas cuáles son las diferencias entre ellos?, ¿cómo se llaman los polígonos de tres y cuatro lados que tienen sus lados y sus ángulos iguales? En esta secuencia veremos cuántas diagonales tiene un polígono y cuál es la suma de sus ángulos interiores. 1. Utiliza tu juego de geometría para trazar lo que se solicita y contesta. Los siguientes segmentos son diagonales del polígono que se indica. Traza cada polígono y compara con un compañero tus figuras. Solucionario 1. Hexágono irregular a) R. M. El cuadrado y el hexágono regular son parecidos porque la medida de sus lados son iguales entre sí. b) R. M. Depende de la medida de sus lados y ángulos. c) Sí, el triángulo d) No existen polígonos con una diagonal, pero con dos diagonales, sí, los cuadriláteros. 54 Bloque 1 - Secuencia 6 Pentágono irregular Hexágono irregular Hexágono regular Recuerda Pentágono irregular Hexágono regular Una diagonal es un segmento de recta que une dos vértices no consecutivos de un polígono. a) ¿Qué polígonos de los trazados son iguales a los de tu compañero y cuáles diferentes? b) ¿A qué piensas que se deba que algunos de los polígonos son iguales y otros no? c) ¿Existe algún polígono que no tenga diagonales? ¿Cuál? d) ¿Hay polígonos que sólo tengan una diagonal? ¿Y dos diagonales? Compara con tus compañeros tus trazos y respuestas. Explica cómo construiste los polígonos a partir de las diagonales y señala qué otros datos requeriste para trazar las figuras y cómo los obtuviste. 52 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Cuadrado Cuadrado Recorremos Diagonales Recorremos Sugerencias didácticas Trace en el pizarrón diferentes polígonos con sus diagonales, incluya segmentos que no lo sean. Los estudiantes deben identificar cuáles segmentos no son diagonales, así como justificar su respuesta. Promueva la reflexión y el análisis, de esta forma aprenderán a argumentar y no sólo aceptar lo que alguien más dice. Para el análisis de las preguntas al final de la actividad, puede utilizar la definición de diagonal o dar contraejemplos. 1. Analiza los polígonos, realiza lo que se indica y responde. a) Considera la definición de diagonal de la sección “Recuerda” de la página 52 y marca con color verde las rectas punteadas que sean diagonales de cada polígono. Diagonales Solucionario 1. a) Polígono A © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Polígono D Polígono B Polígono E Polígono C Polígono A Polígono B Polígono C Polígono D Polígono E Polígono F Polígono F b) ¿Qué característica tienen en común las rectas de cada polígono que no coloreaste para que no sean consideradas como diagonales? c) ¿En qué polígonos coloreaste diagonales que no son segmentos inclinados? d) Un polígono se llama cóncavo si al menos alguna de sus diagonales es exterior al polígono. De los polígonos anteriores, ¿cuáles son cóncavos? A partir de tus respuestas discute en grupo lo siguiente: ¿las diagonales de un polígono siempre son segmentos inclinados? ¿El lado de un polígono puede coincidir con una diagonal del mismo? ¿Toda diagonal divide al polígono en dos partes iguales? Argumenten sus respuestas. b) No unen dos vértices del polígono. c) En los polígonos B, C, D, E y F. d) Los polígonos A y D son cóncavos. Un polígono es convexo si todas sus diagonales son interiores. Si un polígono no es convexo, se le llama cóncavo. 53 Bloque 1 - Secuencia 6 55 S6 Sugerencias didácticas Compruebe que los estudiantes distinguen los polígonos regulares de los polígonos irregulares. Y que también reconocen los polígonos cóncavos y convexos. Repase la definición de diagonal para resolver las actividades 2 y 3. Número de diagonales de un polígono Número de diagonales de un polígono 2. Lee la situación y resuelve. La imagen de la izquierda representa un terreno, el cual debe dividirse en secciones triangulares para sembrar cuatro tipos de flores distintas. a) ¿Qué forma geométrica tiene el terreno? Solucionario 2. a) Hexágono irregular b) Tres diagonales c) En cuatro triángulos 3. R. M. b) Elige otra esquina del terreno y traza todas las diagonales que partan de ese vértice. ¿Cuántas diagonales pudiste trazar? c) ¿En cuántos triángulos queda dividido el terreno al trazar esas diagonales? 3. Reúnete con un compañero y contesten. En cada uno de los siguientes polígonos elijan un vértice y, a partir de él, tracen todas las diagonales. Nombre Número de lados Número de diagonales desde un vértice Cuadrilátero 4 1 Pentágono 5 2 Hexágono 6 3 Heptágono 7 4 Octágono 8 5 Decágono 10 7 a) Completen la tabla y respondan. Nombre Número de lados Número de diagonales desde un vértice Cuadrilátero Pentágono 6 7 Octágono b) Tres, el vértice elegido y los vértices de sus dos lados consecutivos. Decágono b) ¿Cuántos y cuáles vértices no se contabilizaron para el trazo de diagonales? 56 Bloque 1 - Secuencia 6 54 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. a) Diagonales y ángulos interiores de un polígono Sugerencias didácticas Si lo considera conveniente, recomiende a sus estudiantes usar GeoGebra para trazar polígonos y analizar sus características, sobre todo para polígonos de más de 10 lados. Al terminar la actividad 4 pregunte ¿Cómo se relacionan el número de diagonales que se pueden trazar desde un vértice, el número de diagonales que se repiten y el total de diagonales de un polígono? Para mejorar el análisis tome en cuenta la respuesta del inciso d). Es probable que no se llegue a ninguna conclusión, pero los alumnos deben intentar encontrar dicha relación. Continúe con la actividad 5 y más adelante se concretará el aprendizaje. c) ¿Qué relación observan entre el número de lados de un polígono y la cantidad de diagonales que se pueden trazar desde un vértice? d) Cada uno de ustedes trace un polígono diferente de más de 10 lados y marque las diagonales desde un mismo vértice. ¿Existe la misma relación que escribieron en el inciso anterior? Expliquen. e) Si en un polígono de 20 lados trazan todas las diagonales desde un vértice, ¿cuántas son? Solucionario Reflexionen en grupo, a partir de lo anterior, cómo pueden argumentar que sus conclusiones son válidas para cualquier polígono: en un polígono con n lados, ¿cuántas diagonales se pueden trazar desde uno de sus vértices? ¿Cuántos lados tiene un polígono en el que el total de diagonales desde el vértice A es d? c) La cantidad de diagonales es el número de lados menos tres. d) Sí e) 17 diagonales 4. Resuelvan en equipos la siguiente actividad. En el polígono ABCDEF se trazaron las diagonales desde A y desde E. A F En un polígono de n lados se pueden trazar n – 3 diagonales, y un polígono que tiene un total de d diagonales tiene d + 3 lados. a) ¿Por qué la diagonal AE se coloreó dos veces? B E b) Si se trazan en color verde las diagonales desde el vértice B, expliquen por qué la diagonal BE tendría dos colores. C D c) Si trazaran en color amarillo las diagonales desde el vértice C, ¿qué diagonales tendrían dos colores? Expliquen su respuesta. d) Si trazaran con distintos colores todas las diagonales del hexágono, ¿qué diagonales tendrían dos colores. Expliquen su res- 4. a) Porque se trazó en rojo saliendo de A y en azul saliendo de B. b) La diagonal BE está en azul porque se trazó desde E y estaría en verde al trazarse desde B. c) La diagonal CE y la diagonal CA. d) Todas, porque cada una se colorea desde el vértice de donde se traza hasta el vértice que llega y viceversa. e) Un hexágono tiene en total 9 diagonales. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. puesta. e) ¿Cuántas diagonales tiene en total el hexágono? 5. Reunidos en equipos, analicen y contesten. Luis, Marco y Rosa calcularon las diagonales que tiene el heptágono de la derecha. Cada uno argumentó su respuesta. Luis: tracé una a una las diagonales y son 14. Marco Antonio: si de cada vértice se trazan 4 diagonales y la figura tiene 7 lados, entonces posee 28 diagonales. 55 Rosa: desde cada vértice se pueden trazar 4 diagonales. Como tiene 7 lados es posible dibujar 28 diagonales; pero, como cada una se cuenta dos veces, entonces sólo tenemos 14 diagonales. Bloque 1 - Secuencia 6 57 S6 Sugerencias didácticas Pida a los estudiantes que escriban la fórmula para calcular las diagonales de cualquier polígono en una ficha de trabajo. Lean el subtítulo y averigüe lo que saben acerca de los ángulos interiores de los polígonos, retome como ejemplo al triángulo y al cuadrado. a) Tracen todas las diagonales del heptágono. ¿Cuántas son? b) ¿Qué razonamiento consideran que es correcto y por qué? c) ¿Cuál de los razonamientos utilizarían para calcular el número de diagonales Solucionario de un polígono de 15 lados? Expliquen su respuesta. 5. a) Son 14 diagonales b) El de Luis y el de Rosa. Marco contó dos veces las diagonales. c) El de Rosa, porque el de Luis es largo y tedioso. • 90 diagonales, ya que desde cada vértice se trazan 15 – 3 = 12 diagonales, y si se tienen 15 lados en total son 180 diagonales, pero la mitad de ellas se repite, así son 90 diagonales en total. d) 25(22) = 275 diagonales 2 Integración Número de lados Diagonales desde un vértice Diagonales totales 4 1 2 9 6 27 11 8 44 17 14 119 • Calculen las diagonales, ¿cuántas tiene? d) Considerando el razonamiento de Rosa, escriban una operación que permita calcular el número total de diagonales de un polígono de 25 lados. En grupo comparen sus respuestas. Traten de establecer una fórmula para calcular el número de diagonales en otros polígonos y en general para cualquiera. En un polígono de n lados: • El número de diagonales que se pueden trazar desde un vértice es n – 3. • El número total de diagonales es n(n – 3) . 2 Integración • Utiliza la información anterior y completa los valores en la tabla. Número de lados Diagonales desde un vértice Diagonales totales 4 6 Suma de ángulos interiores de un polígono 11 14 Suma de ángulos interiores de un polígono 6. Realiza lo que se te pide. a) En cada uno de los siguientes polígonos, elige un vértice y traza las diagonales a partir de él. 58 Bloque 1 - Secuencia 6 56 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 6. a) Diagonales y ángulos interiores de un polígono Sugerencias didácticas b) A partir de la actividad con los polígonos anteriores completa las primeras tres columnas de la tabla. Polígono Número de lados Diagonales desde un vértice Número de triángulos en que se dividió Suma de los ángulos interiores del polígono Cuadrilátero Pentágono Hexágono Octágono Decágono c) Observa los datos en la tabla anterior y escribe una expresión algebraica que permita encontrar el número de triángulos en los que queda dividido un polígono de n lados si se trazan las diagonales desde un vértice. d) En los polígonos siguientes se trazaron las diagonales desde un vértice y se señalaron los ángulos interiores. Glosario ángulo interior de un polígono. Ángulo formado por dos lados consecutivos. Trace en el pizarrón algunos polígonos y pida a los alumnos que marquen los ángulos interiores, apóyese en la sección “Glosario” para la actividad. Pregunte también de qué manera se puede calcular la medida de la suma de los ángulos interiores de cualquier polígono. Solicite que tracen todas las diagonales desde un mismo vértice y analicen si eso les ayuda para encontrar lo que buscan. Recuérdeles el valor de la suma de los ángulos interiores de un triángulo. Explíqueles que deberán aplicar ese conocimiento en el caso del cuadrado. Pida que observen en cuántos triángulos se puede dividir y que, con esa información, encuentren la suma de sus ángulos interiores. Usen el procedimiento anterior con otros polígonos. Solucionario b) Polígono Número de lados Diagonales desde un vértice Número de triángulos en que se dividió Suma de los ángulos interiores del polígono Cuadrilátero 4 1 2 360° Pentágono 5 2 3 540° Hexágono 6 3 4 720° Octágono 8 5 6 1 080° Decágono 10 7 8 1 440° • ¿En cuántos triángulos quedó dividido cada hexágono? © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • ¿Cuál es la suma de los ángulos interiores de cada triángulo? • ¿Cuál es la suma de los ángulos de los triángulos en los que quedó dividido cada hexágono? • ¿Cuánto da la suma de los ángulos interiores de cada hexágono? e) A partir del análisis en las figuras del inciso anterior calcula el resultado de la suma total de los ángulos interiores de los polígonos en la tabla del inciso b) y completa la última columna. c) El número de triángulos en los que se divide un polígono de n lados es igual a n – 2. d) • En 4 triángulos • La suma de los ángulos interiores de cada triángulo es 180°. • La suma de los ángulos de los triángulos en los que se dividió cada hexágono es de 720°. • La suma de los ángulos interiores de un hexágono es de 720°. En algunos casos los ángulos interiores del polígono corresponden a un ángulo de algún triángulo. En otros, el ángulo del polígono queda dividido y forma parte de los ángulos de dos o más triángulos. Compara tus respuestas con las de tus compañeros. ¿Todos encontraron la misma expresión en el inciso c)? Observen los triángulos en los que se divide cada polígono, ¿sumar todos los ángulos interiores del polígono es equivalente a sumar los ángulos interiores del abanico de triángulos que lo forman? Expliquen su respuesta. 57 Bloque 1 - Secuencia 6 59 Sugerencias didácticas S6 Para responder el inciso b) de la actividad “Integración”, se recomienda usar GeoGebra para analizar la suma de los ángulos interiores de al menos dos polígonos cóncavos. Esto ayudará a que los estudiantes observen que el procedimiento funciona para cualquier polígono. Se recomienda incluir el resultado del recuadro “Formalización” en la ficha de trabajo, recuerde a sus estudiantes que la podrán usar en la sección “Arribamos”. Invite a los alumnos a realizar las actividades que se sugieren en la sección “Explora”, de ser posible, revíselos y resuelva las dudas que surjan. Finalmente analicen en grupo el último recuadro de la sección “Formalización” y pida que escriban un problema relacionado con alguno de los datos que se mencionan. Integración • Reflexiona con el resto del grupo. a) ¿Qué relación hay entre la suma de los ángulos interiores de un polígono cualquiera y el número de lados de ese polígono? b) ¿La relación anterior se cumple para polígonos cóncavos y convexos? Expliquen. La suma de los ángulos interiores de un polígono de n lados es 180°(n – 2). Solucionario 7. Resuelvan los siguientes problemas en equipo. a) ¿Cuánto suman los ángulos interiores del octágono regular de la izquierda? Integración • a) Al número de lados del polígono se le resta dos y el resultado se multiplica por 180°. b) Sí, en el caso de los polígonos cóncavos es importante trazar las diagonales apropiadas a partir de cierto vértice y así se observa el número de triángulos para determinar la suma de los ángulos internos del polígono. Siendo el mismo procedimiento que en el caso de los polígonos convexos. b) Luis quiere dibujar un polígono irregular cuya suma de ángulos interiores sea 1 440°. • Escriban una ecuación que modele la situación anterior y resuélvanla. • ¿Cuántos lados tiene el polígono? c) Consideren un polígono cuya suma de ángulos interiores sea 2 520°. • Escriban una expresión matemática que les permita encontrar el número de lados del polígono. Explora En el siguiente enlace www.edutics.mx/UnD encontrarás actividades interactivas para calcular la suma de los ángulos interiores de diversos polígonos. • ¿Cuántos lados tiene el polígono? • Si el polígono fuera regular, ¿cuánto mediría cada ángulo interior? • Si fuera irregular, ¿cuánto mediría cada ángulo interior? d) La suma de los ángulos interiores de un polígono es 2 700°. ¿Cuántas diagonales tiene? Comparen sus resultados y procedimientos con los de sus compañeros. ¿Plantearon las mismas ecuaciones? Si hay diferencias, busquen el apoyo de su maestro. A partir de la suma de los ángulos de un polígono se puede obtener mayor información del mismo: • el número de lados que tiene; • la medida de un ángulo interior del polígono si éste es regular. 60 Bloque 1 - Secuencia 6 58 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 7. a) 6 × 180° = 1 080° • El ángulo mide 135°, tiene 8 ángulos iguales entonces cada uno mide 1 080 = 135° 8 b) • 180(n – 2) = 1 440° • El polígono tiene 10 lados. c) • 180(n – 2) = 2 520 • El polígono tiene 16 lados. • Cada ángulo mediría 1 57.5° • No se puede saber porque es un polígono irregular. d) El polígono tiene 119 diagonales. • ¿Cuánto mide el ángulo marcado? Expliquen. Diagonales y ángulos interiores de un polígono Arribamos 1. Analiza la situación que se planteó al inicio de la secuencia y considera el siguiente problema. a) La figura de la derecha representa el trazo de todas las diagonales de un polígono. ¿Cuántos lados tiene? ¿De qué figura se trata? Arribamos Sugerencias didácticas Permita que los estudiantes usen la ficha de trabajo que realizaron a lo largo de la secuencia para resolver las actividades de esta sección. Al terminar los ejercicios, los estudiantes pueden verificar lo que aprendieron en la página recomendad en la sección “Explora”. 2. Encierra en un círculo rojo los polígonos en los que se trazaron rectas que no son diagonales. Convivimos Analicen la sección “Convivimos” y genere una discusión a partir de la pregunta planteada. Para complementar pregunte ¿Por qué creen que es mejor aprender en grupo? Dé oportunidad a la mayoría de participar comentando su opinión. Solucionario 3. Resuelve los siguientes problemas. a) Si un polígono tiene 21 vértices, ¿cuántas diagonales tiene en total? ¿Cuántas diagonales se pueden trazar desde uno de sus vértices? b) ¿Cuánto mide la suma de los ángulos interiores de un heptágono regular? ¿Y cada ángulo interior? c) Desde un vértice de un polígono irregular se pueden trazar 8 diagonales. ¿Cuál es la suma de sus ángulos interiores? d) Si la suma de los ángulos interiores de un polígono irregular es 720°, ¿cuánto mide uno de sus ángulos interiores? 1. a) 5, es un pentágono. 2. En estos polígonos no todas las rectas son diagonales. Explora Para practicar lo estudiado en esta secuencia, en el siguiente enlace www.edutics.mx/Unz encontrarás actividades que podrás resolver con las propiedades de los polígonos. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 4. Considera los polígonos de la imagen. 3. a) 189 diagonales, desde un vértice 18 diagonales. b) La suma de los ángulos interiores de un heptágono regular es de 900° y cada ángulo mide 128.571°. c) La suma de sus ángulos interiores es de 1 620°. d) No se puede saber porque es un polígono irregular. 4. a) Debe encerrar con azul el polígono de 9 lados, el eneágono. b) Debe encerrar con verde el polígono que tenga 10 lados, el decágono. c) Debe encerrar con rojo el polígono de 11 lados, endecágono. Recursos adicionales a) Encierra en un círculo azul el polígono cuya suma de ángulos interiores es 1 260° b) Encierra en un círculo verde el polígono cuyo ángulo interior mide 144° c) Encierra en un círculo rojo el polígono que tiene 8 diagonales desde un vértice. Compara tus respuestas con las de tus compañeros. Utilicen argumentos lógicos que les permitan comprobar las soluciones. Es importante que expliquen las dificultades a las que se enfrentaron y cómo las resolvieron. 59 Convivimos Al compartir ideas con tus compañeros, recuerda que todas las opiniones son valiosas, incluyendo la tuya. Reflexiona y conversa: ¿qué importancia le das a tus intervenciones en clase?, ¿por qué? En la siguiente página puede consultar los temas ya estudiados de manera resumida: • “Polígonos, clasificación, ángulos interiores”, disponible en www.edutics. mx/wdU (consulta: 23 de agosto de 2018). Bloque 1 - Secuencia 6 61 Relaciones entre los ángulos de un polígono Partimos Sugerencias didácticas Recuerde a los estudiantes las relaciones que ya conocen y cómo a partir de ellas pueden determinar más características de los polígonos. Por ejemplo, que expliquen cómo a partir del número de lados se puede saber el número de diagonales; o bien, cómo pueden calcular la suma de los ángulos interiores de un polígono, entre otras. Para responder el inciso a) de la actividad 1, explique qué es un ángulo exterior y trace los ángulos exteriores de un triángulo, un cuadrado, un pentágono, un hexágono, etcétera. Después pregunte ¿Cuál es la relación entre el número de lados, ángulos exteriores y ángulos interiores? Los alumnos deben observar que hay el mismo número de ángulos interiores que de exteriores. Para responder el inciso c), puede usar GeoGebra para trazar varios polígonos y determinar ángulos interiores y exteriores, de ésta forma podrán analizar las relaciones que existen entre los elementos del polígono a partir de sus ángulos exteriores. S7 Relaciones entre los ángulos de un polígono Deduce y usa las relaciones entre los ángulos interiores, exteriores y centrales de polígonos regulares. En un polígono cualquiera hay dos tipos de ángulos: los ángulos interiores, cuyas propiedades estudiaste en la secuencia anterior, y los ángulos exteriores. Además, cuando el polígono está dentro de una circunferencia, existe otro tipo de ángulo llamado ángulo central. En esta secuencia estudiarás los ángulos de un polígono regular, sus propiedades y las relaciones que existen entre ellos. Partimos 1. Analiza la situación y contesta. Al arquitecto Martínez le entregaron los viejos planos de un complejo recreativo. El papel está deteriorado y roto, por lo que ya no se aprecian todos los trazos. En el proyecto estaba contemplada la creación de un parque que tendría la forma de un polígono regular; sin embargo, lo único que se aprecia en los planos es parte de su contorno y un ángulo exterior, como se muestra en la figura. a) ¿Cuántos ángulos exteriores tiene el polígono? b) Dibuja con color rojo un ángulo interior del polígono. ¿Cuántos tendrá en total? c) ¿Cómo se puede saber el número de lados del polígono a partir de la información que da el plano? Solucionario 1. a) La misma cantidad que el número de lados. b) El número de ángulos interiores es el mismo que el de lados. c) R. M. Conociendo el valor de los ángulos exteriores se puede calcular el valor de los ángulos interiores, luego se puede calcular el número de lados. Compara tus respuestas con las de algún compañero. ¿Existen diversos procedimientos para conocer el número de lados de un polígono regular si se conoce la medida del ángulo exterior? Recorremos Ángulos interiores, exteriores y centrales F A Recomiende a los estudiantes alargar los lados del polígono. 128° Solucionario Ángulos interiores, exteriores y centrales Recorremos Sugerencias didácticas B 1. a) En cada vértice se debe dibujar el ángulo exterior correspondiente. 137° f 135° 116° 101° C 103° D 62 Bloque 1 - Secuencia 7 1. Resuelvan en parejas el siguiente problema. Se desea construir una puerta en un corral de forma irregular con seis E lados. La abertura de la puerta, ubicada en uno de ellos, debe ser tal que ésta quede alineada al lado adyacente en el que se apoya. El hexágono irregular ABCDEF muestra la representación del corral, con la medida de los ángulos interiores y la abertura de la puerta si ésta se localizara en el lado EF. a) Dibujen la abertura que tendría la puerta si se colocara en los otros lados. 60 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. S7 Sugerencias didácticas Sugiera a sus alumnos utilizar el transportador para medir los ángulos que se solicitan en la página 60 y, de ésta manera, puedan contestar el inciso b). Para responder el inciso d) utilice el resultado del valor de la suma de un ángulo interior con un ángulo exterior. Solicite que escriban éste resultado en una ficha de trabajo. Para resolver el problema 2, diga a los alumnos que lean la sección “Glosario”, explique que el prefijo “in” significa “dentro de”, así la frase “polígono inscrito en una circunferencia” significa “polígono dentro de una circunferencia”, con el mismo centro. b) Si se requiere que la puerta tenga la mayor abertura posible, ¿en qué lado conviene colocarla? c) ¿Cuánto suman la medida del ∠ AFE y la medida del ∠ f? d) Escojan cualquier ángulo interior y calculen la suma de su valor y el valor del ángulo de la abertura de la puerta correspondiente. ¿Cuánto vale dicha suma? e) ¿Cómo podrían conocer la abertura de la puerta sin utilizar transportador? Solucionario Comparen sus respuestas con sus compañeros. ¿Observaron las mismas relaciones entre los ángulos? ¿Qué contenidos de los temas estudiados en primer grado de secundaria utilizaron para resolver el problema? b) En el lado BC, vértice C. c) La suma de los ángulos AFE y f es igual a 180°. d) La suma de cualquier ángulo interior con su correspondiente ángulo exterior siempre es igual a 180°. e) Ya que ambos ángulos suman 180°, basta con restar a 180° el valor del ángulo interno. 2. R. M. El ángulo exterior de un polígono es el ángulo formado por un lado del polígono y la prolongación del lado adyacente. En cualquier polígono la suma de un ángulo interior y su exterior correspondiente es 180°. Glosario © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 2. Traza, utilizando tu juego de geometría, un polígono irregular de seis lados inscrito en la siguiente circunferencia. polígono inscrito. Un polígono está inscrito en una circunferencia si cada uno de sus vértices coincide con un punto de la circunferencia. a) R. M. Se eligen seis puntos en la circunferencia, cada uno es un vértice del polígono, y se unen con segmentos de recta para trazar los lados. b) La suma de los ángulos centrales es igual a 360°. c) R. M. No son iguales, sus medidas son diferentes. a) Explica qué procedimiento utilizaste para trazarlo. b) Traza todos los ángulos que van del centro de la circunferencia a los vértices del polígono (ángulos centrales). ¿Cuánto mide la suma de éstos? c) ¿Los ángulos centrales son iguales? Explica tu respuesta. 61 Recursos adicionales En la siguiente página puede consultar de manera más general los conceptos estudiados en esta secuencia y la anterior: • “Propiedades de los polígonos”, disponible en www.edutics.mx/wdw (consulta: 24 de agosto de 2018). Bloque 1 - Secuencia 7 63 S7 Analice en grupo la sección “Recuerda” y pregunte ¿Qué rectas son bisectrices de los ángulos DOB y GOH? ¿Qué recta es bisectriz del ángulo HOD? Como la segunda pregunta no se puede responder de acuerdo con la imagen, le servirá para verificar la comprensión del concepto de manera abstracta. Considere hacer un breve repaso de conocimientos previos y relaciónelos con los conceptos de la página, pregunte, por ejemplo ¿Qué se forma cuando trazas la bisectriz de uno de los ángulos interiores de un cuadrado? ¿Qué figuras obtienes? ¿Cuánto miden los ángulos interiores de un cuadrado? ¿Cuánto miden los ángulos que se forman cuando trazas la bisectriz? Los alumnos deben observar que la bisectriz es la diagonal. Al terminar las actividades, analicen la información de la sección “Formalización” para después preguntar ¿Cuánto mide el ángulo central de un decágono? Si un ángulo central mide 30°, ¿de qué polígono se trata? Solucionario 3. a) Un octágono • El ángulo quedó dividido en ocho partes iguales. • El ángulo DOA mide 90° y el COD mide 180°. • El ángulo DOE mide 45°, porque el segmento OE es bisectriz del ángulo DOA. • Cada uno de los ángulos centrales mide 45°. • La suma de los ángulos centrales mide 360°. • Dividiendo 360° entre 8. b) 3. Analicen en parejas las imágenes y contesten. a) Octavio trazó un polígono regular inscrito en una circunferencia, siguiendo el procedimiento que se muestra. ¿Qué polígono trazó? A A H C O D H E O C G B A Bisectriz D F B E O C G Bisectriz D F B • ¿En cuántas partes quedó dividido el ángulo completo en O? Recuerda La bisectriz de un ángulo es la recta que lo divide en dos partes iguales. • ¿Cuánto mide el DOA? ¿Y el COD? • ¿Cuánto mide el DOE? Expliquen. • ¿Cuánto mide cada uno de los ángulos centrales con vértice en O? • ¿Cuánto mide la suma de todos los ángulos con vértice en O? • ¿Cómo pueden saber cuánto mide cada uno de los ángulos con vértice en O del octágono a partir del ángulo completo en O? b) Señalen un ángulo central e indiquen su medida en cada uno de los siguientes polígonos regulares. Ángulo central: Ángulo central: Ángulo central: En grupo discutan la relación entre la medida del ángulo central de un polígono regular y el número de lados de éste. El ángulo central de un polígono está formado por dos radios que unen el centro del polígono (el cual coincide con el centro de la circunferencia que lo inscribe) y dos vértices consecutivos del mismo. • Ángulo central del hexágono: 60° • Ángulo central del pentágono: 72° • Ángulo central del heptágono: 51.428° 64 Bloque 1 - Secuencia 7 Si el polígono es regular, todos los ángulos centrales son iguales y miden donde n es el número de lados del polígono. 62 360° n , © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Relaciones entre los ángulos de un polígono Sugerencias didácticas Después de responder la actividad “Integración”, muestre la relación de los nombres de los ángulos con su ubicación así será más fácil identificarlos. Al terminar el análisis de la actividad 4, explique que las relaciones entre los conceptos y los elementos matemáticos sirven para obtener datos desconocidos a partir de los que sí se conocen; por ejemplo, la medida de un ángulo central ayuda a determinar el número de lados de un polígono. Integración • A manera de resumen, escribe el nombre de cada ángulo que se señala en el siguiente polígono. Solucionario Integración Ángulo central Suma de ángulos exteriores de un polígono convexo 4. Traza el ángulo interior correspondiente a cada ángulo exterior que se ha marcado en el cuadrilátero de la derecha. a) ¿Cuánto vale la suma de un ángulo interior con su ángulo exterior correspon- Ángulo interior Ángulo exterior diente? b) ¿Cuánto se obtiene al sumar todos los pares de ángulos interiores y exteriores marcados? c) Si a la suma de todos los ángulos marcados le restas el valor de todos los án- Suma de ángulos exteriores de un polígono convexo gulos interiores, ¿qué representa la cantidad que obtienes? 4. d) ¿Cuánto suman los ángulos interiores de un cuadrilátero? Explica tu respuesta. e) ¿Cuánto vale la suma de los ángulos exteriores de un cuadrilátero? © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Explica tu respuesta. 5. Reúnete con un compañero y realicen lo que se indica. En el siguiente pentágono regular se denotó cada ángulo interior mediante una letra minúscula y, el ángulo exterior correspondiente, con la misma letra en mayúscula. a) Escriban una expresión algebraica que represente la suma de los ángulos exteriores. b) Como los ángulos que tienen las mismas letras son suplementarios entonces: A = 180° – E A = 180° – = 180° – e a d D = 180° – = 180° – c) ¿Cuánto suman los ángulos interiores del pentágono? B b c C 63 a) La suma es igual a 180°. b) El total de la suma de todos los ángulos es igual a 720°. c) La suma de todos los ángulos exteriores. d) 360°, el número de lados menos dos por 180°, 180(4 – 2). e) 360°, 720° – 360° = 360° 5. a) A + B + C + D + E b) A = 180° – a B = 180° – b C = 180° – c D = 180° – d E = 180° – e c) 540°, utilizando la fórmula de la secuencia 6: 180(5 – 2) = 540. Bloque 1 - Secuencia 7 65 S7 Sugerencias didácticas Para comprender el proceso de solución del inciso e), escriba el desarrollo completo en el pizarrón. Explique a los estudiantes las sustituciones que se harán, y comente que se pueden hacer porque las dos expresiones son equivalentes; por ejemplo, como A + a = 180°, se puede utilizar A o 180° – a, según convenga. Al terminar la actividad 6, pida que expresen con sus palabras cuánto vale la suma de los ángulos exteriores de cualquier polígono. Por último, lean la sección “Formalización”. d) Escriban una expresión algebraica que represente la suma de los ángulos interiores del pentágono. e) Completen las igualdades. A + B + C + D + E = (180° – a) + ( +( – A + B + C + D + E = 180° + – – d) a + b + c + d + e = 540° e) A + B + C + D + E = (180° – a) + (180° – b) + (180° – c) + (180° – d) + (180° – e) A + B + C + D + E = 180° + 180° + 180° + 180° + 180° – a – b – c–d–e A + B + C + D + E = 5(180°) – (a + b + c + d + e) A + B + C + D + E = 900° – (540°) f) 360° 6. a) La suma de los ángulos interiores del octágono regular es 1 080°. b) La suma de los ángulos interiores del hexágono irregular es 720°. c) Se suma 8 veces. Equivale a 1 440°. d) Se suma 6 veces. Equivale a 1 080°. e) A: 1 440° – 1 080° = 360° B: 1 080° – 720° = 360° f) En ambos casos la suma es igual a 360°. Relaciones entre los ángulos centrales, interiores y exteriores de un polígono regular – + – ) ) + + –a–b – A+B+C+D+E = Solucionario )+( – )+( (180°) – (a + b + A+B+C+D+E = ( + + ) – (540°) f) ¿Cuánto vale la suma de los ángulos exteriores del pentágono? 6. Consideren un octágono regular A y un hexágono irregular B. a) ¿Cuánto vale la suma de los ángulos interiores de A? b) ¿Y la suma de los ángulos interiores de B? c) Si se suman todos los ángulos interiores y exteriores de A, ¿cuántas veces se suma 180°? ¿A cuántos grados equivale? d) Si se suman todos los ángulos interiores y exteriores de B, ¿cuántas veces se suma 180°? ¿A cuántos grados equivale? e) Expresa por medio de una operación cuánto vale la suma de los ángulos exteriores de A y cuánto los de B. f) ¿Cuánto vale la suma de los ángulos exteriores de A y de B? Comparen sus respuestas con las de otra pareja. Discutan si el procedimiento depende del número de lados que tiene el polígono o si depende de que el polígono sea regular o irregular. a b Relaciones entre los ángulos centrales, interiores y exteriores de un polígono regular 7. Considera el siguiente eneágono regular. Traza un ángulo interior y un ángulo central y denótalos como a y b, respectivamente. a) ¿Todos los ángulos interiores son iguales al ángulo a? Explica tu respuesta. a) Sí, porque el polígono es regular. 66 Bloque 1 - Secuencia 7 64 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. La suma de los ángulos exteriores de cualquier polígono convexo es 360°. 7. Relaciones entre los ángulos de un polígono Sugerencias didácticas Revise la respuesta del inciso d) de la actividad 8, es importante que los estudiantes aprendan a sustituir valores y a simplificar expresiones algebraicas de manera correcta. Si es necesario, intervenga en la solución de la actividad “Integración”, comente a los alumnos que observen las relaciones entre ángulos y pregunte ¿Cuál es la medida de la suma de un ángulo interior y un ángulo exterior? ¿En cuántos ángulos se divide el ángulo central de la imagen? ¿Cuánto mide la suma de los ángulos centrales? b) ¿Todos los ángulos centrales son iguales al ángulo b? Explica tu respuesta. c) ¿Cuánto mide b? Explica tu respuesta. d) ¿Cuánto mide la suma de los ángulos interiores del eneágono? Explica tu respuesta. e) ¿Cuánto mide a? Explica tu respuesta. Aprendemos f) ¿Cuánto vale la suma de un ángulo interior y un ángulo central del eneágono? Al terminar las actividades de esta página, pida que lean esta sección y escuchen de manera atenta y respetuosa los argumentos de sus compañeros. Puede poner ejemplos claros del uso de gráficos en mapas, rectas numéricas, figuras geométricas, entre otras. 8. Reúnete con un compañero. Consideren un polígono regular de n lados. a) Escriban una expresión algebraica que indique el valor de la suma de sus ángulos interiores. b) Escriban una expresión algebraica que indique el valor de un ángulo interior. Solucionario b) Sí, porque es un polígono regular. c) Dado que es un polígono regular de 9 lados entonces, un ángulo central es 360° = 40°. 9 d) 180° (n – 2) = 180° (9 – 2) = 1 260° e) Dado que es un polígono regular, tiene 9 ángulos interiores iguales, entonces, un ángulo interior es 1 260° = 140°. 9 f) La suma de un ángulo interior y uno central es igual a 180°. c) Escriban una expresión algebraica que indique el valor de un ángulo central del polígono. d) Sumen las expresiones que obtuvieron en los incisos b) y c) y simplifiquen. + = + = 8. a) 180 (n – 2) + = b) c) © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Con el resto del grupo establezcan una conclusión acerca de cuánto suman un ángulo central y un ángulo interior en un polígono regular de n lados. d) Aprendemos Integración • Contesten de forma grupal. a) ¿Cuántos grados miden los ángulos marcados en el polígono? ∡ a: c ∡ b: b ∡ c: Reflexiona: en los temas geométricos, ¿cómo te pueden ayudar los dibujos y las representaciones gráficas para resolver un problema? 180(n – 2) n 360 n 180(n – 2) n 180(n – 2) n 180(n – 2) n + + + 360 n 360 n 360 n = = 180n – 360 + 360 n 180n n = 180° Un ángulo central más un ángulo interior suman 180°. Integración ∡ a: 36° ∡ b: 144° ∡ c: 36° a 65 Bloque 1 - Secuencia 7 67 S7 Sugerencias didácticas Haga un análisis previo a la solución de la actividad 9, pregunte a los alumnos ¿Qué ángulos se deben calcular en los polígonos? ¿Cómo se calcula el ángulo central? ¿Cuál es la fórmula para calcular la suma de los ángulos interiores? ¿El ángulo z es un ángulo exterior? Para que se den cuenta de que el ángulo z no es un ángulo exterior, pida que prolonguen los lados que forman al ángulo. b) ¿Qué relación existe entre el ángulo a y el ángulo c? c) ¿La relación anterior se cumple en cualquier polígono regular? Argumenten. Solucionario d) Escriban con sus propias palabras la relación que existe entre el ángulo b) Son iguales c) Sí, porque sin importar el número de lados siempre se cumple que a + b = 180° y b + c = 180°, entonces a = c. d) R. M. En cualquier polígono regular el ángulo central es igual al ángulo exterior. central y el ángulo exterior de un polígono regular. En un polígono regular los ángulos centrales y los ángulos exteriores son iguales. 9. z y x y 9. Encuentren en equipo, en cada uno de los polígonos regulares, las medidas de los ángulos indicados. Justifiquen sus respuestas oralmente. z x x z z y y z x x x x = 144° x = 120° x = 120° y = 108° y = 60° y = 120° z = 252° z = 300° z = 240° y y z x y z x y x= x= x= y= y= y= z= z= z= z z y x x x = 90° x = 32.73° x = 102.86° y = 90° y = 147.27° y = 128.57° z = 270° z = 212.73° z = 231.43° Recursos adicionales En la siguiente página encontrará ejercicios relacionados con el tema: • “Ángulos de un polígono”, disponible en www.edutics.mx/UnD (consulta: 24 de agosto de 2018.) 68 Bloque 1 - Secuencia 7 z x y y z y x= x= x= y= y= y= z= z= z= Además de lo estudiado en la secuencia, recuerden las características de los polígonos regulares. Utilicen esa información para justificar sus argumentos sobre como obtuvieron los valores numéricos de los ángulos. 66 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. x z Relaciones entre los ángulos de un polígono Arribamos 1. Retoma el problema al inicio de la secuencia y contesta. En el plano arquitectónico también se aprecia que la fuente central del parque tendrá forma de hexágono regular, con jardineras en cada lado. ¿Cuánto miden los ángulos a y b? Arribamos Sugerencias didácticas Muestre a los estudiantes lo útil que son los esquemas o imágenes en la solución de problemas. Para ello trace en el pizarrón los dibujos A y B y pregunte ¿Cuánto miden los ángulos que se muestran en las siguientes figuras? Es importante que los estudiantes aprendan a resumir y seleccionar las herramientas que van a utilizar. A 2. Encuentra en cada polígono el valor de los ángulos señalados con letras. 72° x x 70° 90° x 148° x 155° y x= x= y= a © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. b c a= d b= c= d= 3. Escribe el nombre del polígono al que se refiere cada descripción. a) Polígono regular cuyo ángulo central mide 45°. b) Polígono regular cuyo ángulo exterior mide 72°. c) Polígono regular cuyo ángulo exterior mide el doble que su ángulo interior correspondiente. d) Polígono cuya suma de ángulos interiores es igual a la suma de sus ángulos exteriores. e) Polígono regular cuyo ángulo exterior mide 360° . n f) Polígono cuya suma de ángulos exteriores es 360°. Explora Resuelve los ejercicios en el siguiente enlace www.edutics.mx/Unj para practicar lo estudiado en esta secuencia. B Al terminar las actividades invite a los alumnos a visitar la página recomendada en la sección “Explora” y pida que resuelvan las actividades correspondientes. Solucionario 1. ∡ a = 120° y ∡ b = 60° 2. Triángulo: x = 40° Hexágono irregular: x = 135° y y = 45° Heptágono regular: a = 51.42° y b = 51.42° Dodecágono regular: c = 30° y d = 60° 3. a) Octágono b) Pentágono c) Triángulo equilátero d) Cuadrilátero e) n – ágono o polígono regular de n lados. f) Cualquier polígono. Recursos adicionales En el siguiente video puede consultar ejercicios adicionales para ayudar a los estudiantes: • “Problemas de polígonos regulares sobre ángulos y diagonales”, disponible en www.edutics.mx/wdi (consulta: 24 de agosto de 2018). Compara tus respuestas con las de tus compañeros. 67 Bloque 1 - Secuencia 7 69 Múltiplos y submúltiplos del metro, litro y kilogramo Partimos Sugerencias didácticas Solicite la participación de uno de los alumnos para leer el párrafo introductorio de la secuencia. Pregunte al grupo si conocen las unidades de medida que se mencionan, si las han utilizado y de qué manera; después pida que analicen la sección “Glosario” y pregunte ¿Qué otras magnitudes conocen?, ¿por qué son necesarias diversas escalas para la misma magnitud? Es decir, ¿por qué existe el km, m, dm, cm, mm? Permita que obtengan sus conclusiones y si es necesario intervenga ¿Qué unidad usarían para medir el grosor de un cabello? ¿Qué unidad usarían para medir la distancia del Sol a la Tierra? ¿Qué unidad utilizarían para medir la talla de un bebé? Entre otras cosas, el objetivo es que se perciba la necesidad de utilizar diferentes escalas para la misma magnitud. S8 Resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro y kilogramo. Partimos Glosario magnitud. Propiedad de los cuerpos que puede ser medida, como por ejemplo, la masa o la longitud. Múltiplos y submúltiplos del metro, litro y kilogramo En primaria aprendiste a estimar, comparar y ordenar longitudes y distancias, capacidades y masas por medio de unidades convencionales como el metro, el litro, el kilogramo (así como medios y cuartos de estas unidades), el centímetro, el milímetro, el mililitro y el gramo. En esta secuencia formularás estrategias para convertir unidades de medida para una misma magnitud. 1. Analiza la información y responde. En promedio una persona debe tomar dos litros de agua al día. En ocasiones, para señalar la cantidad de agua consumida se contabiliza en número de vasos. El equivalente a medio litro de agua en vasos se muestra en la siguiente figura. Somos 250 mL Pida a los alumnos que lean la información de esta sección y realice un pequeño análisis preguntando ¿Cuánta agua consumen al día? ¿Qué actividades físicas realizan? ¿Con qué frecuencia? Dependiendo de las respuestas sugiera actividades físicas aeróbicas para mantener ágil el cuerpo. Mencione que la OMS recomienda beber agua natural y practicar deportes para estar sanos. a) ¿A cuántos mililitros equivale un litro? b) Si una persona al cumplir 15 años, por prescripción médica, inicia el hábito de tomar dos litros de agua diariamente y vive 85 años, ¿cuántos vasos de 250 mL habrá tomado en ese tiempo? Reúnete con tus compañeros. Cada uno explique cómo entendieron y resolvieron el problema. Para calcular, ¿consideraron 85 o 70 años? ¿Por qué? Solucionario 1. a) 1 L equivale a 1 000 mL. b) 204 400 vasos Recorremos 70, ya que antes de los 15 no toma dicha cantidad de agua, así el tiempo que consumió dos litros de agua diarios es de 70 años. Unidades de longitud 1. Resuelve el siguiente problema. Gracias a una aplicación del celular de su papá, Esther sabe que para ir de la escuela a su casa la distancia es un kilómetro. Ella quiere saber cuántos pasos camina; para ello, marca en el suelo una de sus huellas y la mide con una regla de madera de un metro. Somos Valora: ¿cuál es la importancia de tener hábitos saludables como tomar agua y realizar alguna actividad física? 70 Bloque 1 - Secuencia 8 250 mL 60 cm 68 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. S8 Recorremos a) ¿Aproximadamente cuántos pasos da Esther de su casa a la escuela? Sugerencias didácticas Muestre a sus estudiantes una regla de 1 m y pregunte ¿Cuántos pasos daré en un metro? Escuche las respuestas y explique que no podrá dar dos pasos completos pero que un aproximado es 1 23 ya que es posible dar un paso y sobran 40 cm. Para resolver la actividad 1 pregunte ¿Cuántos metros hay en 1 km? ¿Qué debes hacer para calcular el total de pasos que dará en 1 km? Antes de analizar la información de la sección “Formalización”, lean la sección “Glosario” y pregunte ¿Cuál es la diferencia entre múltiplo y submúltiplo? ¿Cuál es un submúltiplo del metro y cual un múltiplo? ¿Qué medirías con cada uno? b) Esther observa en la regla de madera que en un metro hay 100 cm y encontró en internet que un kilómetro es mil veces la longitud de un metro. • ¿Cuántos metros hay en un kilómetro? • ¿Cuántos centímetros hay en un kilómetro? Describe cómo lo calculaste. 1 m = 100 cm 1 km = cm Unidades de longitud • ¿Qué fracción de un metro es un centímetro? Solucionario • ¿Qué fracción de un kilómetro es un centímetro? Explica. c) ¿Cómo utilizarías lo anterior para calcular los pasos que camina Esther? Compara tus respuestas con las de tus compañeros. ¿Cómo calcularon la cantidad de pasos? ¿La respuesta fue un número exacto? ¿Cómo lo interpretan? El metro es una unidad para medir longitudes. A partir de él se derivan otras unidades, tanto mayores (múltiplos) como menores (submúltiplos). © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Los nombres de estas unidades están formados por los prefijos griegos seguidos de la palabra metro. Los valores de algunos prefijos son los siguientes: deca: diez veces hecto: cien veces kilo: mil veces deci: una décima parte centi: una centésima parte mili: una milésima parte Glosario múltiplo. Número que contiene una cantidad exacta de veces a otro. submúltiplo. Número contenido en otro cierta cantidad de veces de manera exacta. 1. a) Esther camina 1 666.666 pasos aproximadamente. b) • 1 000 m • 100 000 cm. Ya que 1 m es igual a 100 cm y en 1 km hay 1 000 veces un metro, entonces en 1 km hay 1 000 veces 100. 1 = 0.01 • Una centésima parte, 100 • Una cien milésima parte, 1001000 . Ya que 1 km = 1 000 m = 100 000 cm, así un centímetro es la cienmilésima parte de un kilómetro. c) Dividiendo los 100 000 cm entre los 60 cm de la huella de Esther. R. M. Que dio 1 666 pasos y la fracción de un paso más. 2. Prefijo kilo hecto deca Con estos mismos prefijos es posible formar los múltiplos y submúltiplos de las unidades de medida de cualquier magnitud. unidad deci centi mili Símbolo km hm dam m dm cm mm Valor 1000 100 10 1 1 = 0.1 10 1 = 0.01 100 1 = 0.001 1 000 2. Con base en la información anterior, completen en equipos la siguiente tabla y contesten. Prefijo kilo hecto deca unidad Símbolo km hm dam Valor 1 000 deci centi mili m dm cm mm 1 1 = 0.1 10 69 Bloque 1 - Secuencia 8 71 Se recomienda establecer una relación entre los prefijos de la tabla y el valor posicional del sistema decimal. Por ejemplo, a la izquierda de la unidad están las decenas, centenas, millares, etcétera, mientras que a la derecha de la unidad están los décimos, centésimo, milésimos. Otra manera de verlo es que a la izquierda de la unidad están los múltiplos y a la derecha, los submúltiplos. Después del intercambio de problemas de la actividad “Integración”, seleccione algunos de los problemas inventados por sus estudiantes y pida que los expongan y resuelvan. Evalúe el desempeño del grupo en el desarrollo de la actividad. Lean el título del siguiente subtema y pregunte ¿Qué miden las unidades de masa? ¿Qué unidades de masa has utilizado con mayor frecuencia? ¿Qué unidad utilizan las personas para hacer sus compras en el mercado? ¿Por qué crees que son necesarios los múltiplos y submúltiplos del kilogramo? Escuche las respuestas y aclare las dudas que surjan. Al terminar la actividad 4 pregunte ¿Qué operaciones están involucradas entre el cálculo de múltiplos y submúltiplos de una unidad de medida? Los alumnos deben observar que en unas ocasiones debe utilizar multiplicaciones y en otras divisiones. Solucionario 1 = 10 10 veces, 0.1 100 veces, es un múltiplo de la unidad. 000 = 10 10 veces, 1100 El valor de la referencia contiene 10 veces al de la derecha. La referencia es contenida 10 veces con respecto al valor de la izquierda. 3. Le faltan 4 500 m = 4.5 km a) Faltan 7 500 pasos. a) b) c) d) e) Integración • R. L. S8 a) ¿Cuántas veces contiene la unidad base a la correspondiente del prefijo deci? b) ¿Cuántas veces contiene un hectómetro a un metro? ¿Es múltiplo o submúltiplo de la unidad? c) ¿Cuántas veces contiene 1 km a 1 hm? Expliquen su razonamiento. d) Tomando como referencia un múltiplo o submúltiplo, ¿cuál es la relación entre el valor de la referencia y el siguiente a la derecha? e) ¿Cuál es la relación entre el valor de la referencia y el siguiente a la izquierda? Comparen sus respuestas con otros equipos. ¿Qué relaciones encuentran entre los múltiplos y submúltiplos? Analicen: ¿es posible decir que un hectómetro es a la vez un múltiplo del metro y un submúltiplo del kilómetro? ¿Por qué? 3. Resuelvan en parejas el siguiente problema. Esther se ha entusiasmado con la idea de practicar la caminata y participa en una carrera de 5 km. Si Esther ha recorrido 500 m, ¿cuántos metros le falta por recorrer? a) ¿A cuántos pasos suyos equivale la distancia que le falta? Comparen sus respuestas y procedimientos con otras parejas. Integración • Trabaja con un compañero e inventen un problema en los que sea necesario realizar conversiones de unidades de longitud. • Intercambien con otra pareja el problema que plantearon y resuelvan el que les den. Unidades de masa Unidades de masa 4. a) Cada pieza de piloncillo tiene una masa de 220 g. 4. Lee la situación y contesta. Alan necesita 3 kg de piloncillo. En la tienda venden tanto bolsas con 5 piezas como piezas sueltas. a) ¿Cuántos gramos tiene cada pieza de piloncillo? 72 Bloque 1 - Secuencia 8 70 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Múltiplos y submúltiplos del metro, litro y kilogramo Solucionario b) b) Considera la información de la página 69 y completa la tabla. Incluye los símbolos de las unidades, múltiplos y submúltiplos. Múltiplos kilogramos hectogramos Unidad decagramos gramos Submúltiplos decigramos centigramos 3 kg Unidad kilogramos hectogramos decagramos gramos 3 kg 30 hg 300 dag 3 000 g 3 000 000 mg c) Si Alan pide 2 bolsas, ¿cuánto le falta? d) Con base en la tabla anterior, contesta. • ¿Qué operación realizaste para convertir gramos a decagramos? • ¿Qué operación realizaste para convertir gramos a decigramos? e) Para completar los 3 kg que necesita, Alan compró algunos piloncillos sueltos. Al colocarlos en la báscula pesaron 8.8 hg. ¿Cuántas piezas compró? Con tus compañeros explica las analogías entre la conversión de múltiplos y submúltiplos de las unidades de masa y longitud. Analicen las regularidades y traten de establecer una estrategia. La unidad de masa convencional no es el gramo sino el kilogramo; es la única cuyo nombre contiene un prefijo (kilo). Sin embargo, los nombres y los símbolos de los múltiplos y submúltiplos decimales de la unidad de masa se forman añadiendo los nombres de los prefijos a la palabra “gramo” y los símbolos de estos prefijos al símbolo de la unidad “g”. Por ejemplo para un decigramo el símbolo usado es dg. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Múltiplos Unidad Submúltiplos gramos decigramos centigramos miligramos 3 000 g 30 000 dg 300 000 cg 3 000 000 mg c) 800 g = 0.8 kg d) • Una división, 3 000 = 300 10 • Una multiplicación, 3 000(10) = 30 000 e) Compró 4 piezas de piloncillo. Unidades de capacidad 5. a) • 13 333.333 unidades de sangre. 60 hL = 6 000 L = 6 000 000 mL, dicha sangre se divide en unidades de 450 mL, 6 000 000 = 13 333.33 4540 • 14 700 unidades • Sí, ya que necesitaba 13 333.33 unidades como mínimo y logró recolectar 14 700 unidades. • 1 367 unidades • 615.15 L Recursos adicionales Unidades de capacidad 5. Lean y contesten en parejas. a) Los bancos de sangre colectan a través de sus donadores unidades con 450 mL de sangre cada una. Cada persona puede donar hasta una unidad de sangre cada vez. Supongan que en una campaña anual se espera juntar 60 hL de sangre y se acepta la sangre de 14 700 personas. • ¿Cuántas unidades de sangre se espera juntar? Expliquen su razonamiento. En la siguiente página puede consultar información relacionada con el tema: • “Presentación, múltiplos y submúltiplos”, disponible en www.edutics.mx/ wdS (consulta: 24 de agosto de 2018). • ¿Cuántas unidades se podrán juntar? • ¿La campaña logra colectar lo que tenían estimado? • ¿Cuál es la diferencia entre la meta y lo colectado? • ¿A cuántos litros equivale? 71 Bloque 1 - Secuencia 8 73 S8 Sugerencias didácticas Haga una lista como la siguiente, y péguela en el salón de clases. Longitud Masa Capacidad Deca 10 Decámetro Decagramo Decalitro Hecto 100 Hectómetro Hectogramo Hectolitro Kilo 1000 Kilometro Kilogramo Kilolitro Deci 0.1 Decímetro Decigramo Decilitro b) Escriban los múltiplos y submúltiplos del litro con sus equivalencias. Consideren la siguiente información. Como en el caso del metro y el kilogramo, diez unidades de medida de capacidad iguales equivalen a la unidad inmediatamente mayor. Unidad de capacidad 1L Múltiplos Centi 0.01 Centímetro Centigramo Centilitro Solucionario Nombre Símbolo decalitro daL Submúltiplos Equivalencia Nombre Símbolo Equivalencia dL hectolitro centilitro b) 1 000 L mililitro 0.001 L Unidad de capacidad Comparen sus respuestas con las de sus compañeros. Si lo consideran adecuado, hagan tablas semejantes a la anterior para los múltiplos y submúltiplos del metro y el kilogramo. 1L Submúltiplos Nombre Símbolo Equivalencia Nombre Símbolo Equivalencia daL 10 L decilitro dL 0.1 L hectolitro hL 100 L centilitro cL 0.01 L kilolitro kL 1 000 L mililitro mL 0.001 L Integración × 10 kL en otra. Escríbelas en los espacios del siguiente gráfico. kL × 10 hL ÷ 10 Integración • Determina las operaciones que es necesario realizar para convertir una unidad decalitro × 10 daL ÷ 10 × 10 L ÷ 10 × 10 dL ÷ 10 daL L dL cL mL × 10 cL ÷ 10 hL mL a) ¿Qué operación realizas para convertir una unidad en su submúltiplo siguiente? ÷ 10 b) ¿Qué operación realizas para convertir una unidad en su múltiplo siguiente? a) Multiplico por 10 la unidad de referencia. b) Divido entre 10 la unidad de referencia. Con el resto del grupo analiza si la estrategia anterior resume también cómo hacer conversiones en múltiplos y submúltiplos del metro y kilogramo. 74 Bloque 1 - Secuencia 8 72 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Múltiplos Múltiplos y submúltiplos del metro, litro y kilogramo Sugerencias didácticas Es importante que analice con los alumnos la sección “Glosario” para resolver la actividad 6. De ser posible haga una representación geométrica de la rosca, ésta puede verse como un rectángulo y los cortes longitudinales formarán 4 tiras de rosca. Para realizar correctamente las conversiones recomiende a sus estudiantes que observen si se trata de un múltiplo o submúltiplo, después deben hacer las operaciones correspondientes (división o multiplicación). Para resolver los incisos b) y c) es necesario hacer conversiones previas y después establecer la relación de proporción. Más conversiones 6. Resuelvan en equipos los siguientes problemas. a) Contesten a partir de la siguiente información. Rosca de reyes 2018 Ciudad de México La tradicional Rosca de Reyes que se partió en el zócalo de la Ciudad de México en enero de 2018 midió 1.44 km de longitud con una masa aproximada de 8 toneladas. Para su elaboración se utilizaron 5 720 kg de harina, 961 L de leche, 2 000 kg de azúcar, 3 010 kg de mantequilla, 651 L de vainilla, entre otros y se repartieron 250 000 porciones. Cabe aclarar que para este fin el pan en realidad no tiene forma de rosca sino de un gran rectángulo con un ancho de 90 cm, aproximadamente. Más conversiones Solucionario “Celebra CDMX día de reyes 2018 con mega rosca en zócalo capitalino” en Boletín CDMX, 5 de enero de 2018, www.cdmx.gob.mx/comunicacion/nota/celebra-cdmx-dia-de-reyes2018-con-mega-rosca-en-zocalo-capitalino# (consulta: 18 de mayo de 2018). Glosario • Suponiendo que se hicieron tres cortes longitudinales iguales a la rosca, es decir, a lo largo del pan rectangular como se observa en la figura; ¿cuántos metros en total medían las cuatro partes al colocarse una tras otra? Expliquen su razonamiento. • Si también se repartieron porciones iguales, ¿cuántos centímetros le tocó a cada asistente? • ¿Cuál fue la masa, en gramos, de cada porción si una tonelada equivale a longitudinal. Que sigue el sentido o dirección de la longitud de lo que se expresa. 6. a) • 5 760 m. Al hacer tres cortes longitudinales salen 4 porciones de 1 440 m cada una. • 2.304 cm, ya que 5 760 m = 5 760 000 mm al repartirla entre 760 000 = 23.04 mm = 2.304 cm. 250 000 personas, 5250 000 • 32 g, ya que 8 ton = 8 000 kg = 8 000 000 g, al dividir entre 000 000 = 32 g. 250 000 personas, 8250 000 • 143 bultos • 40 bultos de azúcar • 12 040 paquetes de mantequilla 4 500 m = 18 minutos b) 36 minutos, 45 hm = 4 500 m entonces 250 m/min c) 30 000 segundos, 8.3 h © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 1 000 kilogramos? Describan su procedimiento. • ¿Cuántos bultos de 400 hg de harina se utilizaron? • ¿Cuántos bultos de 500 hg de azúcar se utilizaron? • ¿Cuántos paquetes de 250 g de mantequilla se usaron? b) Federico se desplazará en caballo de su comunidad a la cabecera municipal, la cual se encuentra a 45 hm de distancia. La velocidad promedio de trote es de 250 m por minuto. Si consideras el tiempo total en el que va y regresa, ¿cuánto tiempo tardará? c) Una cisterna de 7 500 litros de capacidad se llena a razón de 250 mililitros por cada segundo. ¿En cuanto tiempo se llenará la cisterna en su totalidad? Expresen su respuesta en segundos y horas. Comparen sus respuestas con otros equipos. Expliquen cómo interpretaron la información para resolver cada problema. ¿Qué hicieron para expresar la respuesta del último inciso? 73 Bloque 1 - Secuencia 8 75 S8 Muestre a los estudiantes cómo se pueden hacer las conversiones utilizando regla de tres, establezca las relaciones de proporcionalidad y resuelva algunos ejemplos. Otra manera de hacer las conversiones entre múltiplos y submúltiplos es analizando la relación que hay entre las posiciones de las unidades en cuestión; por ejemplo, entre kg y mg hay seis espacios según la tabla de conversiones, es decir el valor se multiplica por 106. De mL a L, hay 3 espacios entre ellos, por lo que hay que dividir entre 103. De dam a m sólo hay una posición de diferencia, así que se multiplica por 10. Pregunte a sus estudiantes ¿Cuál es la diferencia entre convertir de dam a dm y viceversa? Finalmente analice en grupo los problemas propuestos en la página de la sección “Explora”. Solucionario 7. 4.5 kg = 4 500 mg 7 500 mL = 7.5 L 2 350 mL = 0.00235 kL 0.005 m = 5 mm 7.853 kg = 78 530 dg 1.26 cm = 0.00126 dam 8.3204 dam = 83.204 m 7500 dg = 75 0000 cg 7. Realiza las siguientes conversiones 4.5 kg = 2 350 mL = 7.853 kg = Velocidad máxima 4.1 m/s Velocidad máxima (m/s) 4.1 m/s 330 cm/s Cocodrilo Oso polar Gallina 0.00347 km/s 0.00277 km/s 566 cm/s kL dg 8.3204 dam = Explora En la siguiente página www.edutics.mx/Uhs podrás resolver problemas de conversión unidades de medida. m 7 500 mL = L 0.005 m = mm 1.26 cm = dam 7 500 dg = cg El metro, el kilogramo y el segundo son unidades básicas que pertenecen al Sistema Internacional de Unidades, el cual en realidad tiene siete magnitudes básicas con sus respectivas unidades: para la longitud, el metro (m); para la masa, el kilogramo (kg); para el tiempo, el segundo (s); para la corriente eléctrica, el amperio (A); para la temperatura, el kelvin (K); para la cantidad de sustancia, el mol (mol); y para la intensidad luminosa, la candela (cd). Las últimas cuatro magnitudes con sus unidades las estudiarás en tus cursos de Física y Química. Por cuestiones prácticas, a veces es necesario usar múltiplos o submúltiplos de unidades del Sistema Internacional (SI). Por ejemplo, para medir el líquido de una inyección se utiliza un submúltiplo del litro o para la distancia entre un continente y otro un múltiplo del metro. Los prefijos se añaden a cualquier unidad del Sistema Internacional para escribir un múltiplo o submúltiplo de ésta. 8. Resuelvan en grupo. a) Se muestra la velocidad máxima con la que se mueven algunos seres vivos. 8. Araña Cangrejo mg Velocidad máxima Araña Cangrejo Cocodrilo Oso polar Gallina 4.1 m/s 330 cm/s 0.0347 km/s 0.00277 km/s 566 cm/s Velocidad máxima (m/s) • Completen la tabla convirtiendo la velocidad de cada animal a metros por 3.3 m/s 3.47 m/s 2.77 m/s 5.66 m/s segundo. Describan su procedimiento. • ¿Cuál se desplaza con mayor rapidez? Ordenen las imágenes considerando • R. L. • La gallina es la más veloz. Quedando el orden: gallina, araña, cocodrilo, cangrejo y oso polar. la velocidad de cada uno? Comparen sus respuestas y estrategias de solución. Analicen y hagan una puesta en común sobre los procesos más sencillos y los más efectivos. 76 Bloque 1 - Secuencia 8 74 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Múltiplos y submúltiplos del metro, litro y kilogramo Arribamos 1. Considera nuevamente el problema al inicio de la secuencia. En lugar de vasos considera el siguiente recipiente y la cantidad de agua que habría tomado la misma persona en 70 años. Arribamos Sugerencias didácticas Permita a sus estudiantes usar las tablas de equivalencias para resolver las actividades de la sección. Para resolver la actividad 3, sugiera a los alumnos que realicen varias equivalencias para que puedan establecer las relaciones correspondientes. Por ejemplo: 27 kg = 27 000 g = 270hg = 2 700 dag, repitan el proceso con otras cantidades hasta que encuentren las equivalencias de la tabla. Solucionario 1. a) b) c) 2. a) 2 555 garrafones de 2 daL 20 litros 5.11 pipas • 5 mL • 7.2 L b) 180 000 kg c) 133 losetas d) 200 segundos © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. a) ¿Cuántos garrafones de 2 daL habrá bebido? b) ¿Cuál es la medida del garrafón de 2 daL en litros? c) ¿Cuántas pipas de 10 kL habrá bebido la misma persona? 2. Resuelve los problemas. a) Una gota de agua de la llave tiene el volumen aproximado que se muestra en la imagen. Supongamos que una llave con fuga deja caer 20 gotas por minuto. 1 mL 4 • ¿Cuántos mL de agua se desperdicia por minuto? • ¿Cuántos litros de agua se desperdiciarán durante un día completo? b) La pirámide de Louvre (figura 8.1) es una estructura muy famosa ubicada en el patio del museo que lleva el mismo nombre. Su altura es de 21.65 metros, la longitud del lado de la base de la pirámide es de 35 metros. La masa total de la estructura es de 180 toneladas. • ¿Cuántos kilogramos tiene la estructura completa? c) Raúl quiere poner losetas de 30 cm × 30 cm en su habitación de 3 m × 4 m. ¿Cuántas losetas necesita? d) Una oruga avanza 15 mm por segundo sobre una jardinera que mide 3 m de largo. ¿Cuánto tiempo necesita para recorrer el largo de la jardinera? 3. 27 kg 2.7 dag 2.70 g 2.7 mg 27 cg 0.27 g 27 hg 2.7 g 270 cg 0.27 kg 27 000 g 2.7 kg 270 g 0.27 cg 27 dg 2.7 dag 2.7 g 0.27 hg 2.7 mg 27 cg 0.27 g 27 hg 2.7 g 270 cg 0.27 kg 27 000 g 2.7 kg 270 g 0.27 cg 27 dg Recursos adicionales Figura 8.1 Patio principal del Museo del Louvre, París, Francia. 3. Encierra con un mismo color las cantidades equivalentes. 27 kg En la siguiente página puede consultar ejercicios relacionados con los múltiplos y submúltiplos de las unidades de masa: • “Problemas de conversión: masa”, disponible en www.edutics.mx/wdT (consulta: 24 de agosto de 2018). 0.27 hg Evalúen de manera grupal las estrategias formuladas a lo largo de la lección. Asegúrense de comprender lo que el problema solicita. 75 Bloque 1 - Secuencia 8 77 El sistema inglés S9 Partimos Sugerencias didácticas Después de leer el párrafo introductorio, pregunte a los alumnos si en las películas o en tiendas de autoservicio han visto productos con unidades de medida que sean diferentes al metro, kilogramo y litro. Si le es posible lleve a la clase empaques de algún producto que esté marcado en una medida como libras u onzas, las cuales serían las más comunes. También puede imprimir imágenes de productos que se vendan en otros países con estas unidades. Platique con sus alumnos acerca de las diferentes medidas que la gente utiliza dependiendo del lugar donde vive. Comente que en algunas comunidades se utiliza el cuartillo para medir el maíz y el frijol o que las frutas y verduras se venden a veces por bote o huacal. Pregunte si ellos conocen otras maneras de medir que sean poco comunes. Si hay tiempo solicite que pregunten a los adultos mayores que conozcan acerca del tema y pida que lo desarrollen para exponer en grupo. No tiene que ser algo elaborado, el objetivo es que se den cuenta de que no siempre se ha contado con unidades de medida universales y se han tenido que buscar equivalencias. Resuelve problemas que implican conversiones de unidades del sistema inglés (yarda, pulgada, galón, onza y libra). Partimos El sistema inglés En la secuencia anterior aprendiste a convertir múltiplos y submúltiplos de algunas unidades del Sistema Internacional. En ésta aprenderás a resolver problemas que involucran conversiones de unidades del Sistema Internacional y unidades del sistema inglés, ya que en la vida cotidiana es común utilizar estas medidas; por ejemplo, en la construcción o en los deportes. 1. Resuelve el siguiente problema. Christine es una turista extranjera que está solicitando ayuda para hacer sus compras en el mercado. Ella necesita comprar 6 libras de naranjas, 3 libras de manzanas. a) Si una libra equivale aproximadamente a medio kilo, ¿cuántos kilogramos de manzanas y de naranjas le deben despachar respectivamente? b) ¿Cuánto tiene que pagar Christine? Solucionario 1. a) Le deben dar 3 kg de naranja y 1 21 kg de manzana. b) $45 por la naranja y $60 por la manzana. Discute con tus compañeros en qué contextos conviene hacer aproximaciones al realizar cálculos. ¿Todos obtuvieron la misma respuesta? Recorremos Unidades del sistema inglés 1. Analicen en parejas la información y contesten. Tres amigos viajaron a California, EUA, para participar en una carrera de ciclismo. La dinámica consistió en recorrer la mayor distancia en un tiempo determinado. Laura: 12.5 mi, 370 yd y 58 ft Patricio: 12.3 mi, 400 yd y 175 ft Marina: 12.4 mi, 300 yd y 200 ft a) Lean la siguiente información y calculen cuántas millas recorrió cada ciclista. En los Estados Unidos de América las unidades para medir la longitud son la pulgada (in), el pie (ft), la yarda (yd) y la milla (mi). Estas unidades se relacionan entre sí de la siguiente forma: 1 ft = 12 in 1 yd = 3 ft 1 mi = 1 760 yd 78 Bloque 1 - Secuencia 9 76 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. S9 Recorremos Laura: mi Marina: mi Patricio: mi b) ¿Cuál de ellos ganó? c) La masa aproximada de un casco de ciclista es de 9 onzas y la de una bicicleta, en libras, se muestra en la imagen de la báscula. Si una libra equivale a 16 onzas, ¿cuál es la masa total de ambos? Comparen sus respuestas con sus compañeros. Expliquen cómo hicieron las conversiones de unidades mayores a menores y viceversa. Al realizar estas operaciones, ¿hay una relación de proporcionalidad entre las unidades? En el sistema inglés como en el Sistema Internacional también hay unidades específicas para la masa y la capacidad. Sugerencias didácticas Permita que los alumnos resuelvan los problemas de conversiones con sus propias herramientas. Si observa que tienen dificultades, puede replantear el problema para que utilicen sus conocimientos de proporcionalidad directa. Solicite que lean la sección “Formalización” y pregunte ¿Cuáles son las unidades de medida que se usan para la masa en el sistema internacional? ¿Qué unidades se usan para medir la capacidad de un recipiente? Explique que, a pesar de que hay diferentes sistemas de medición, siempre debe haber una equivalencia entre unidades, mencione algunos ejemplos. Unidades del sistema inglés Solucionario Masa: onza (oz) y libra (lb) Capacidad: onza fluida (fl oz) y galón (gal) Integración • En equipo respondan. Consideren también lo estudiado en la secuencia anterior. a) ¿Qué operación deben hacer para convertir una unidad menor en una mayor? b) ¿Qué operación deben hacer para convertir una unidad mayor en una menor? c) Con base en lo anterior, completen los diagramas. 15 yardas © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 15 pies 3 = 45 ft 4 400 yardas Integración a) Una división b) Una multiplicación c) millas 1 760 = 2.5 yd 4 400 Laura: 12.72 mi Patricio: 12.56 mi Marina: 12.60 mi b) Laura c) 249 oz o 15.56 lb Relaciones entre unidades de diferentes sistemas 2. Lee la situación y resuelve. Antonio trabaja en una empacadora de arándanos que exporta sus productos. Hoy deben empacar el contenido de 60 cajas, cada una de 4 kg, en paquetes de 6 onzas y con ellos llenar otras cajas de 4.5 libras cada una. a) Considerando nuevamente que una libra equivale aproximadamente a medio 15 yardas pies 15 × 3 = 45 ft 4 400 yardas millas 4 400 ÷ 1 760 = 2.5 millas Relaciones entre unidades de diferentes sistemas 2. a) Se llenarán 106.6 cajas. b) Se completarán 1 280 paquetes. kilogramo, estima cuántas cajas de 4.5 lb se llenarán. b) ¿Cuántos paquetes de 6 oz se completarán aproximadamente? Compara con un compañero tus respuestas y comenten: ¿en este contexto es suficiente hacer aproximaciones? 77 Bloque 1 - Secuencia 9 79 Sugerencias didácticas Recomiende a los estudiantes escribir en una tabla todas las equivalencias que se han estudiado en esta secuencia. Comente que es indispensable que las recuerden, si no de manera exacta, sí como una aproximación, ya que les ayudará para hacer conversiones en varias ocasiones. Después de analizar la información de la tabla de equivalencias, lean la sección “Notación” y utilicen la información dada ahí como una forma alternativa de representar las unidades que se mencionan. Revise con los alumnos los resultados de la actividad 4, asegúrese de que todos hacen las conversiones de manera correcta. Solicite que lleven a clase una calculadora de forma individual para agilizar los cálculos. Plantee más ejemplos en caso de que se requiera mayor práctica por parte de los estudiantes. Al terminar la actividad 4, analicen los ejercicios propuestos en la sección “Explora”. S9 El sistema inglés, conocido también como sistema imperial, nació en el Reino Unido y se extendió a los países anglosajones, quedando actualmente Estados Unidos de América como uno de los pocos países que lo sigue utilizando. Al utilizar medidas del sistema inglés muchas veces será necesario convertirlas al SI y para ello debes tomar en cuenta las siguientes equivalencias. Notación Medida Para representar a las pulgadas y los pies también se utilizan las comillas; dos y una, respectivamente. Por ejemplo: 2 pulgadas = 2’’ 5 pies = 5’ Unidad de medida SI Milla (mi) 1.609 km Yarda (yd) 0.9144 m Pie (ft) 30.48 cm Pulgada(in) 2.54 cm Longitud Libra (lb) 453.59 g Onza (oz) 28.35 g Galón (gal) 3.785 L Onzas fluidas (fl oz) 29.574 mL Masa Solucionario Volumen 3. a) 170.1 g b) 1 410 paquetes c) 12 paquetes, ya que una libra contiene 16 oz, así 4.5 lb son 72 oz, dividiendo 72 entre 6 oz de un paquete nos dan 12 paquetes en total. d) 117 cajas 4. a) 3.2 km b) Una libra c) 25 cm d) 28 litros e) Un cuarto de onza f) 4 onzas líquidas 3. Ya que Antonio no tiene una báscula en onzas, considera la información anterior y realiza los cálculos para obtener las cantidades reales del problema 2. a) ¿Cuál es la masa que tendrá cada paquete en gramos? b) ¿Cuántos paquetes saldrán al final del día? c) ¿Cuántos paquetes llevará cada caja de 4.5 libras? Describe tu procedimiento. d) Si únicamente se envían las cajas que cumplen con la masa requerida, ¿cuántas Compara con un compañero tus respuestas y procedimientos. ¿Qué operaciones utilizaron para hacer las conversiones? Explora En la siguiente página www.edutics.mx/Uhe encontrarás ejemplos y ejercicios de conversión entre unidades de longitud. 4. Completa las siguientes frases haciendo un cálculo mental para estimar las cantidades. Pues, si bien, no siempre recordaremos la equivalencia exacta de todas las unidades, hacer una estimación aproximada nos será útil para la vida. a) 2 millas son aproximadamente 1 b) 2 kilogramo es un poco más que c) 10 pulgadas son aproximadamente libras. centímetros. d) 7 galones son un poco menos de litros. e) 7 gramos son aproximadamente onzas. f) 120 mL son un poco menos de 80 Bloque 1 - Secuencia 9 kilómetros. 78 onzas líquidas. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. estarán listas para enviarse? El sistema inglés Sugerencias didácticas 5. Resuelvan en equipos los siguientes problemas. a) Víctor trabaja medio tiempo en el rancho de los Garza alimentando a los animales. Uno de los terneros tiene moquillo y el veterinario le recetó un medicamento; la dosis que le debe suministrar es 2.5 onzas líquidas cada 24 horas por 7 días. Víctor cuenta únicamente con jeringas de 5 mL, 10 mL y 50 mL. • ¿Cuántos mililitros debe suministrarle por día? • ¿De qué manera puede combinar las jeringas para medir el medicamento Hacemos Organízate con tu grupo para medir la masa y la estatura de algunos compañeros. Conviertan esos datos a libras y pies, consideren también pulgadas. cada día? • Si el medicamento se vende en dos presentaciones una de 600 mL y otra de 800 mL, ¿cuál le conviene comprar? Expliquen su respuesta. Hacemos Realicen de manera grupal la primera actividad propuesta en esta sección y la segunda, en equipos o de manera individual para obtener las conversiones pertinentes. Recomiende a los estudiantes organizar la información en una tabla para que, al terminar, comparen los resultados. b) La cancha de basquetbol que se muestra a continuación tiene las medidas aceptadas por la National Basketball Association (NBA). Observen detenidamente la imagen y contesten. 5.8 m Solicite a los alumnos que elaboren una cinta métrica en la que marquen centímetros y pies; para que con ella midan algunos objetos del salón de clases. Después pida que hagan la conversión a pulgadas. Al terminar, y para comprobar sus datos, proporcióneles un flexómetro para que vuelvan a medir y finalmente comparen sus resultados. También pueden convertir sus datos a millas o yardas. Utilice las envolturas, etiquetas de productos o imágenes de la sesión anterior como ejercicios de conversión a otras unidades. La intención es que practiquen este tema. 1.8 m ín ea de ntos 3 pu Área restringida 15 m 6m 1.8 m 1.2 m Línea de fondo L Línea central Solucionario Línea de tiro libre Canasta 5. a) • 73.93 mL • Una jeringa completa de 50 mL, más dos jeringas completas de 10 mL, más 4 mL de la jeringa de 5 mL. • Le conviene la presentación de 600 mL porque en total debe administrarle 517.51 mL. b) • 91.86 ft de largo y 49.21 ft de ancho. • 70.86 pulgadas • 6.34 yardas • 9.84 yardas • 322.83 pulgadas © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Tablero Recursos adicionales Línea lateral En la siguiente página encontrará ejercicios interactivos para los estudiantes: • “Ejercicios interactivos del sistema inglés”, disponible en www.edutics. mx/wd6 (consulta: 24 de agosto de 2018). 28 m • ¿Cuál es la medida de largo y ancho de la cancha expresada en pies? • ¿Cuál es la medida del largo del tablero expresada en pulgadas? • Expresen la distancia en yardas que hay desde la línea de tiro libre a la línea de fondo. • ¿Cuál es la diferencia entre la medida del ancho de la cancha y el área restringida? Expresen el resultado en yardas. • Obtengan la distancia que hay de la línea central a la línea de tiro libre expresada en pulgadas. 79 Bloque 1 - Secuencia 9 81 S9 Sugerencias didácticas Comente con los alumnos que, como bien saben, en física se estudian diferentes fenómenos y la relación entre ellos; por ejemplo, el movimiento rectilíneo uniforme, en él es importante calcular la velocidad de diferentes objetos y ésta se puede medir en m/s, km/h, mi/h, ft/s, etcétera. En algunas ocasiones se requiere realizar una conversión entre las diferentes unidades dependiendo del contexto y desarrollo del problema. Por tal motivo es importante que aprendan a hacer las conversiones de unidades de forma correcta. Para resolver la actividad “Integración”, deben utilizar el hecho de que si la unidad aparece en el numerador y en el denominador, entonces el resultado es uno (kg/kg = 1), quedando únicamente la unidad de interés. Comparen sus respuestas y procedimientos. Si hay diferencias en el procedimiento, expliquen cómo lo resolvieron y lleguen a un acuerdo. Si hay diferencias en los cálculos, verifiquen sus resultados utilizando la calculadora. Otras conversiones 6. Analicen y contesten en equipos. a) ¿Cómo convierten 250 onzas en gramos? b) ¿Existe una relación de proporcionalidad directa entre la cantidad de onzas y su equivalente en gramos? Si es así, ¿cuál es el factor o razón de proporcionalidad para convertir una unidad en otra y viceversa? Otras conversiones c) David dice que para hacer conversiones de unidades basta con multiplicar por el factor de proporcionalidad expresado como razón. Solucionario 6. a) Multiplicando 250 por 28.35 g. b) Sí, son cantidades directamente proporcionales y la razón para cong y 1 oz para convertir de gramos vertir de onzas a gramos es 28.35 1 oz 28.35 g a onzas. 28.35 g 1 oz = 250 oz × 28.35 g 1 oz = 7087.5 g 28.35 g 250 oz = 250 oz × 1 oz Integración a) R. M. Para que al eliminar las millas del numerador y del denominador queden kilómetros. b) Para que los segundos queden en el denominador al eliminar las horas del numerador y del denominador. c) Además, como el numerador y denominador de esa razón son cantidades equivalentes, la razón representa una unidad; por lo que equivale a multiplicar por 1 la cantidad que se va a convertir. Efectúen la multiplicación. 60 mi 1h = 60 mi 1h km × × 1.609 1 mi 60 mi 1h = 60 mi × 1.609 km × 1 h 1 h × 1 mi × 3600 s oz × g oz = g Comparen sus respuestas. ¿Obtuvieron los mismos resultados en los incisos a) y c)? Expliquen por qué las unidades del denominador de la fracción unitaria fueron onzas. ¿Qué harían para convertir de gramos a onzas? Integración • De forma grupal utilicen el método de David para calcular el equivalente a 1h 3600 s = 0.02 = km s Recursos adicionales En la siguiente página puede consultar algunos videos sobre conversión de unidades del sistema inglés: • “Misma longitud en distintas unidades”, disponible en www.edutics.mx/ wdu (consulta: 24 de agosto de 2018). 60 millas/hora en kilómetros/segundo. a) Expliquen por qué para convertir millas a kilómetros es necesaria la fracción unitaria 1.609 km 1 mi . b) Expliquen por qué para convertir horas a segundos es necesaria la frac1h ción unitaria 3 600 s . c) Completen la expresión y realicen los cálculos. 60 mi 60 mi km 1h = 1h × mi × 60 mi 1h = h s = 0.02 Discutan cómo es posible saber cuáles son todas las fracciones unitarias requeridas para utilizar el método de David. 82 Bloque 1 - Secuencia 9 80 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. c) 250 oz = 250 oz × 28.35g 250 oz = 250 oz × 1 oz El sistema inglés Arribamos Arribamos 1. Analiza nuevamente el problema al inicio de la secuencia. a) Si además necesita un galón de leche, ¿cuántos litros debe comprar Christine? b) ¿Cuánto gastó en total? 2. Resuelve el siguiente crucigrama. Coloca la respuesta en la sección de instrucciones hasta con dos decimales y en el crucigrama usa solamente los números enteros. Los datos que se presentan son reales. 1 2 3 4 1 7 8 9 Horizontal 4 ft largo de una cancha de fútbol americano (109.73 m) 5 6 ft altura de la torre latinoamericana (204 m) mi en total recorridas en el triatlón de los Juegos Olímpicos de Sidney 2000: natación, 1 500 m; ciclismo, 40 km; carrera, 10 km 9 mL en un café mediano de 12 fl oz Vertical © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Observe el procedimiento que utilizan los alumnos para resolver la actividad 2 si encuentra errores corríjalos y pida a los alumnos que presentan dificultades para contestar que pasen al pizarrón a resolver algunos ejemplos. Permita que utilicen la tabla de conversiones que hicieron en la ficha de trabajo y la calculadora. Finalmente pida que planteen algunos problemas de acuerdo con su experiencia y aprendizaje. Tras revisar la mayor parte posible, solicite que sean resueltos conforme los vaya revisando. Solucionario 5 6 Sugerencias didácticas 1 yd de ancho de una cancha de fútbol americano (48.77 m) 2 cm de una pantalla de televisión de 43 in 3 fl oz de sangre en el cuerpo (5 litros aproximadamente) 4 g de masa de un paquete de arroz de 14 oz 7 lb de masa de un joven adulto de 72 kg 8 gal de agua que se gastan en producir 1 kg de brócoli (37 litros) 5 1. a) 4 litros 3 b) $72.00 3 4 2. Horizontal 1 3 4 360.00 ft 5 5 669.29 ft 6 6 9 6 32.00 mi 9 6 9 354.88 mL 6 7 Vertical. 3 2 1 1 53.33 yd 9 2 109.22 cm 3 5 4 3 169.06 fl oz 4 396.9 g 8 7 158.73 lb 8 9.77 gal 3. a) 2.286 m por 3.2 m b) Sí cabe el mueble en el espacio destinado para él. 2 1 6 0 9 8 8 Recursos adicionales En la siguiente página los alumnos encontrarán ejercicios para repasar los temas de las últimas secuencias: • “Problemas verbales de conversión de unidades”, disponible en www. edutics.mx/wdE (consulta: 24 de agosto de 2018). 3. María quiere comprar un mueble nuevo para su casa. El espacio disponible para colocarlo es de 2.5 m × 3.5 m. La etiqueta de la mesa señala que mide 2.5 yd × 3.5 yd. a) ¿Cuáles son las medidas de la mesa en metros? b) ¿Cabrá el mueble en el espacio que tiene? Compara tus respuestas y explica tus procedimientos. 81 Bloque 1 - Secuencia 9 83 Partimos Sugerencias didácticas Retome los conocimientos del grado anterior y pregunte a los estudiantes ¿La información mostrada en las gráficas 1 y 2 se puede representar en gráficas circulares? ¿Qué representa cada sector circular? Si tienen dudas repase con ellos el uso y aplicaciones de las gráficas. Para responder el inciso b), puede separar la pregunta para los dos rangos de edades, de 12 a 18 años y de 18 a 24 años. Después pida a los alumnos que formulen algunas preguntas que se puedan responder con dicha información. Por último, comente a los alumnos que la información de la sección “Notación” los ayudará a comprender el significado de la marca que aparece en el eje de las abscisas en las gráficas. S10 Recolecta, registra y lee datos en histogramas y polígonos de frecuencia. Partimos Notación Cuando los datos que se quieren mostrar en una gráfica se encuentran muy alejados del cero se utiliza una línea quebrada sobre el eje para acortarlo y así no tener que mostrar toda la escala . Este trazo recibe el nombre de línea de corte. Histogramas y polígonos de frecuencia En primaria aprendiste a leer y representar en gráficas de barras la información que recolectaste después de haber realizado una investigación o experimento. En primero de secundaría, además, analizaste cómo construir gráficas circulares. En esta secuencia estudiarás nuevas formas de representar otro tipo de datos y a interpretar su significado. 1. Observa las siguientes gráficas y contesta. Gráfica 1 Población con acceso a internet en México (2016) Gráfica 2 Porcentaje de personas que tienen acceso a internet de acuerdo a su edad 60 25 50 Solucionario 20 40 Porcentaje Histogramas y polígonos de frecuencia Porcentaje S10 30 20 15 10 10 5 0 0 No usa Usa Condición respecto a uso 6 9 Fuente: ENDUTIH, Inegi, 2016 1. a) 40% (si tienen: 60%) b) El 45% de las personas entre 12 y 24 años tienen acceso a internet. 12 15 18 Edad (años) 21 24 Fuente: ENDUTIH, Inegi, 2016 a) ¿Qué porcentaje de los mexicanos no tiene acceso a internet? b) ¿Qué porcentaje de las personas entre 12 y 24 años tiene acceso a internet? Compara tus respuestas y procedimientos con los de tus compañeros. ¿Podrían decir qué porcentaje de los mexicanos mayores de 24 años tiene acceso a internet? Discutan las diferencias y similitudes entre las gráficas 1 y 2. Histogramas 1. Analiza la situación y contesta. Héctor confecciona los uniformes escolares de una comunidad y para su próxima venta quiere ofrecer paquetes de descuento para cierto número de uniformes que sean adquiridos por una misma familia. Además, quiere saber las tallas de las que debería tener mayor cantidad. Para ello, recopiló la información sobre el número de hermanos de sus vecinos y sus respectivas estaturas en centímetros, como se muestra en la siguiente tabla. Estaturas (cm) 84 Bloque 1 - Secuencia 10 Hermano 1 Hermano 2 Hermano 3 Hermano 4 Juan 114 123 156 Laura 134 Patricia 105 117 126 158 Pedro 109 132 82 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Recorremos Recorremos Hermano 2 Hermano 3 Número de hermanos Hermano 4 Perla 156 158 1 Aurora 114 128 142 150 2 Ignacio 123 129 158 3 4 Julián 108 135 150 Marcela 105 118 Alfredo 145 a) Construye una tabla de frecuencia y una gráfica de barras para mostrar el número de hermanos de los vecinos. Recuerda colocar los títulos de la gráfica y de los ejes. Frecuencia Histogramas Solucionario Número de hermanos 1. a) Número de Frecuencia hermanos Glosario intervalo. Distancia entre dos valores. Cualquier intervalo se define por dos valores llamados límites de intervalo. Uno es el límite inferior y el otro el superior. 1 2 2 3 3 3 4 2 3 Frecuencia Estaturas (cm) Hermano 1 2 1 0 1 2 3 Número 4 b) Notación b) Con la información de las estaturas, Héctor construyó una tabla en la que organizó los datos en intervalos. Completa la tabla de la derecha calculando el punto a la mitad del intervalo y la frecuencia de las estaturas. c) Completa la siguiente gráfica a partir de los datos de la tabla. Al escribir un intervalo, por ejemplo, de 100 a 110 se escribe un guión entre los límites, 100 - 110. En este caso, se consideran los datos iguales o mayores que 100 y estrictamente menores que 110. De este modo no se traslapan los intervalos. Estaturas (cm) Punto medio (cm) Frecuencia 100 - 110 105 4 110 - 120 115 4 120 - 130 125 5 130 - 140 135 3 140 - 150 145 2 150 - 160 155 7 Estatura Estaturas (cm) 8 Punto medio (cm) 100 - 110 Frecuencia c) Estatura de los hermanos 6 110 - 120 5 120 - 130 4 130 - 140 3 2 140 - 150 1 150 - 160 0 100 105 110 115 120 125 130 135 140 145 150 155 160 Estatura (cm) • ¿Cuántos intervalos hay? • ¿El tamaño de los intervalos es el mismo en cada caso? ¿Cuánto mide cada uno? 83 Frecuencia Frecuencia © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 7 8 7 6 5 4 3 2 1 0 100 105 110 115 120 125 130 135 140 145 150 155 160 Estatura (centimetros) • 6 intervalos • Sí, miden 10 cm Bloque 1 - Secuencia 10 85 S10 Analice con los alumnos las respuestas a los incisos d) y e), es importante que expliquen con sus palabras las diferencias entre las gráficas solicitadas, aclare las dudas que surjan. Concrete el aprendizaje con la información de las secciones “Formalización” y “Recuerda”. Solicite otros ejemplos de variables continuas y discretas para asegurarse de que las pueden diferenciar. Revise la tabla de valores de las estaturas y verifique que calcularon tanto el rango como los intervalos de manera correcta. Enseguida pida a los estudiantes que escriban las fórmulas necesarias en una ficha de trabajo, la cual podrán utilizar más adelante. De igual manera lea con los alumnos la información del último recuadro de la sección “Formalización” y después dibuje una gráfica siguiendo los pasos que se mencionan. Solucionario d) En la primera, las barras están separadas; en la segunda, las barras son continuas, los datos pertenecen a intervalos, representan a un conjunto y no a un solo dato. e) R. M. Porque en una gráfica los datos se agrupan en intervalos y los valores son continuos y en la otra no. d) ¿Qué diferencias hay entre la gráfica del número de hermanos y la de estaturas? e) Explica por qué en la gráfica de las estaturas, a diferencia de la gráfica de la cantidad de hermanos, no hay espacio entre las barras. Compara tus respuestas y gráficas con las de tus compañeros. Discutan sobre las semejanzas y diferencias de las tablas y las gráficas. ¿En la tabla de frecuencia de la cantidad de hermanos los datos se pueden agrupar en intervalos? ¿Por qué ? ¿Por qué las estaturas sí se pueden agrupar en intervalos? Recuerda El rango es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos. Para determinar el número de intervalos necesarios se toma en cuenta la cantidad de datos que se tienen de la muestra o experimento. Normalmente para menos de 30 datos se usan 5 intervalos. Los intervalos tienen un límite inferior y un límite superior (en el primer intervalo de la tabla de las estaturas el límite inferior es 100 y el superior, 110). Para calcular la amplitud o tamaño de cada intervalo, se calcula el rango y se divide entre el número de intervalos. El punto medio de un intervalo se obtiene al calcular el promedio entre el límite inferior y el límite superior de dicho intervalo. 2. Minutos Punto medio Frecuencia 42 - 50 46 3 50 - 58 54 6 Minutos 58 - 66 62 5 66 – 74 70 2 74 - 82 78 4 Recursos adicionales En la siguiente página puede consultar un video con un ejemplo de cómo hacer un histograma: • “Crear un histograma”, disponible en www.edutics.mx/wdZ (consulta: 22 de agosto de 2018.) Hay variables como la estatura, la masa, la distancia o la temperatura, que son de tipo continuo porque entre dos valores cualesquiera siempre hay otro. Para presentar este tipo de información, en una tabla de frecuencia y en una gráfica, se utilizan intervalos. Punto medio Frecuencia 2. Reúnete con un compañero, lean y realicen lo que se pide. En una fábrica textil cada dos horas pasan a recoger las prendas elaboradas para llevarlas al almacén. Sin embargo, con frecuencia solicitan que las recojan mucho antes de que transcurran 120 minutos, por lo que se desea saber después de cuántos minutos sería conveniente dar otra vuelta para recoger las prendas. Para ello se obtuvo el siguiente registro, en minutos, del tiempo transcurrido después de la última recolección y una nueva solicitud: 42, 56, 63, 65, 62, 46, 50, 57, 72, 82, 58, 52, 75, 65, 48, 53, 75, 66, 54 y 77. a) Completen la tabla de la izquierda agrupando los datos anteriores en cinco intervalos. Recuerden que deben ser del mismo tamaño y continuos como en la página 83. Para presentar información de variables continuas se usan los histogramas. Un histograma se construye con barras sobre dos ejes perpendiculares. En el eje horizontal (abscisas) se colocan los intervalos indicando para cada uno el límite inferior, el punto medio y el límite superior; en el eje vertical (ordenadas) se utiliza una escala adecuada que indique la frecuencia de los datos en cuestión. 86 Bloque 1 - Secuencia 10 84 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Histogramas y polígonos de frecuencia Sugerencias didácticas Cuando terminen de graficar haga las siguientes preguntas para realizar un breve análisis ¿A los cuántos minutos no conviene pasar a recoger prendas? ¿En qué intervalos hay más solicitudes para recoger las prendas? Para la segunda gráfica pregunte ¿Se puede saber cuántos goles se anotaron en los primeros cinco minutos, o tres minutos? ¿Cuántos goles se anotaron en el primer tiempo? ¿Se puede saber con la información de la gráfica por qué ocurrió así? En la página recomendada en la sección “Explora” sus estudiantes pondrán a prueba sus habilidades con una actividad dinámica. b) Construyan el histograma con la información de la tabla anterior. Solucionario b) Minutos en que se solicita una recolección de prendas • ¿Cuál es el límite inferior y superior de todos los datos? • ¿Cuál es el intervalo en el que sería conveniente recoger las prendas nueva- 7 mente? 3. Analicen en equipos cada situación y contesten. a) Fernando construyó el siguiente histograma con los datos que recopiló de todos los partidos del torneo de futbol de su escuela. Registró en qué minuto de cada partido se anotaba un gol, pues tiene la idea de que es en el segundo tiempo donde hay mayor intensidad de juego. Número de goles en cada minuto Explora En la siguiente página www.edutics.mx/U7z podrás construir un histograma para un ejemplo concreto. Frecuencia 6 Comparen su tabla y su histograma con los de otras parejas. En caso de diferencias traten de analizar a qué se deben y corrijan en caso necesario. 5 4 3 2 1 0 42 42 50 50 58 58 66 66 74 74 82 Minutos 12 Frecuencia © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. 10 8 6 4 2 0 5 10 15 20 25 30 35 40 45 50 55 Minutos del partido 60 65 70 75 80 85 90 • El límite inferior es 42 y el límite superior es 82. • De los 50 a los 58 minutos 3. a) • El intervalo en el que se anotaron más goles va del minuto 60 al 70. Se anotaron menos goles del minuto 20 al 30. • En el primer tiempo • Se anotaron 39 goles. • ¿En qué intervalo se anotaron más goles? ¿Y menos goles? • Si en un partido de futbol cada tiempo dura 45 minutos, ¿cuándo se anotaron menos goles, en los primeros tiempos o en los segundos? • ¿Cuántos goles se anotaron a partir del minuto 50? 85 Bloque 1 - Secuencia 10 87 S10 Sugerencias didácticas Al terminar el análisis de los datos de la actividad 3 inciso b), proyecte a sus estudiantes los videos sugeridos en la sección “Explora” y resuelva algunos ejemplos. Explique la importancia de comprender cada uno de los conceptos involucrados en el diseño de histogramas antes de usar algún programa, ya que se pueden cometer errores si los conceptos no se comprenden. • ¿Es posible saber en qué minuto de los partidos se anotaron la mayor cantidad de goles? b) Luisa y María fueron a pescar en un lugar donde les aseguraban que la mayoría de las truchas eran de 1 kg; por lo que registraron la masa en gramos de cada una de las truchas que pescaron: 405, 876, 567, 925, 659, 620, 750, 228, 987, 860, 634, 790, 289, 495, 550, 489, 600, 480, 375, 200, 965, 1200, 680, 705, 810, 833, 710, 1100, 745, 850. • Completen la tabla de frecuencias con cinco intervalos y construyan el histograma correspondiente. Solucionario R. M. No, porque no hay un dato sobre el número de goles que se anotan en cada minuto, se trabaja con intervalos. b) Masa (g) Punto medio Frecuencia 200 - 400 300 4 400 - 600 500 6 600 - 800 700 10 800 - 1000 900 8 1000 - 1200 1100 2 Masa (g) Punto medio (g) Frecuencia Peso en gramos de las truchas 12 • ¿Cuál fue la masa máxima y mínima de las truchas que pescaron? Explora 8 En los siguientes enlaces www.edutics.mx/U7K y www.edutics.mx/U7r podrás aprender dos formas de construir un histograma con ayuda de un software de geometría dinámica. 6 4 2 0 200 400 600 800 1000 1200 Peso en gramos • La masa mínima fue de 200 g la máxima de 1 200 g. • La masa más común estuvo en el intervalo de 600g a 800g. • No, en el histograma es la barra con menor frecuencia. Polígonos de frecuencia 4. b) Cada 10 puntos 88 Bloque 1 - Secuencia 10 • ¿Cuál fue la masa más común de las truchas pescadas? • ¿Atraparon bastantes truchas de más de 1 kg? Expliquen su respuesta. Comparen con sus compañeros. ¿Cada uno de sus intervalos tiene los mismos límites y frecuencias? Polígonos de frecuencia 4. Resuelvan en parejas. a) A partir de la tabla de frecuencias de la estatura de los hermanos (p. 83), Héctor construyó otra gráfica para representar los datos. Ubicó la frecuencia exactamente en los puntos medios de cada intervalo y luego unió los puntos mediante segmentos de recta. Ayúdenle a completar la gráfica. b) ¿Cuántos puntos hay en el eje horizontal a los que les corresponde un punto en la gráfica? 86 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Frecuencia 10 Histogramas y polígonos de frecuencia Sugerencias didácticas Explique a sus estudiantes que la gráfica recibe el nombre de polígono de frecuencias porque al unir los puntos marcados, los cuales están relacionados directamente con las frecuencias de valores, se forma algo parecido a un polígono. Se recomienda analizar de forma grupal el video sugerido en la sección “Explora”. Frecuencia Estatura de hermanos 8 7 6 5 4 3 2 1 0 Solucionario Estatura de los hermanos 95 105 115 125 135 Estatura (cm) 145 155 165 Frecuencia c) ¿Coinciden con el número de intervalos? d) ¿Qué frecuencia corresponde a los puntos medios que no aparecen en la tabla de frecuencias de la página 83? e) Expliquen cómo se obtienen los puntos medios de los extremos de la gráfica. La gráfica que acabas de construir es llamada polígono de frecuencia, la cual es otra forma de representar datos agrupados en intervalos. 95 En siguiente enlace www.edutics.mx/U7H podrás aprender cómo construir un polígono de frecuencias a partir de un histograma. 105 115 125 135 Estatura (cm) 145 155 165 c) No d) 0 e) Se toma el punto medio del intervalo anterior al primero y el punto medio del intervalo posterior al último. 5. Minutos en que se solicita una recolección de prendas 8 5. Continúen trabajando en parejas. Consideren la tabla de frecuencias de la actividad 2 de la página 84 y construyan un polígono de frecuencia para presentar los datos. 7 Frecuencia © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Un polígono de frecuencia se construye sobre dos ejes perpendiculares. En el eje horizontal (abscisas) se ubican los puntos medios de cada intervalo; en el eje vertical (ordenadas) se debe utilizar una escala adecuada para la frecuencia. Se localizan los puntos que tienen como coordenadas el punto medio de cada intervalo y su frecuencia respectiva. Además, se calcula el punto medio anterior al primer intervalo y posterior al último y se agregan al polígono de frecuencias los dos puntos asignándoles frecuencia 0. Es importante que el polígono de frecuencia inicie y termine en 0. Finalmente los puntos se unen con segmentos. Explora 8 7 6 5 4 3 2 1 0 6 5 4 3 2 1 0 38 a) Comparen su gráfica con la de otra pareja. Si hay diferencias traten de llegar a un acuerdo. 87 46 54 62 70 Minutos 78 86 Bloque 1 - Secuencia 10 89 S10 Al terminar la actividad 6 pregunte ¿Cuál es el principal beneficio al utilizar polígonos de frecuencias? ¿En los histogramas es posibles hacer una comparación de valores? ¿Por qué es importante comparar datos que representan a una misma variable? b) ¿Cuántas veces se hizo una nueva solicitud en menos de 58 minutos? c) Los empleados de la fábrica textil comentan que cuando solicitan que recojan las prendas en menos de 58 minutos es porque las máquinas de coser funcionan sin ninguna complicación. ¿Cómo describirían el funcionamiento de las Hacemos máquinas cuando se tomaron los registros? Se recomienda hacer la entrevista que se sugiere en ésta sección. Pregunte a sus estudiantes ¿Por qué es importante representar los datos que se obtengan de la entrevista? ¿Qué tipo de conclusiones se podrían generar a partir de la información obtenida? ¿Qué información va en el eje de las abscisas y cuál en las ordenadas? ¿Es posible que el número de libros forme parte de dicho estudio? Revisen sus gráficas. Analicen la información que pueden obtener de ellas de forma más sencilla que con una tabla. En una misma gráfica se pueden representar dos polígonos de frecuencia, que corresponden a dos conjuntos de datos en los que se analiza la misma variable, con la intención de comparar los conjuntos y obtener conclusiones. Solucionario b) c) 6. a) b) 9 veces R. M. Al parecer las máquinas no funcionaban bien. El metro tuvo el mayor retraso en el intervalo de 20 a 25 minutos. Le conviene el camión, no se demora tanto como el metro que ha llegado a retrasarse más de 22.5 minutos. 6. Analicen en equipos la gráfica y contesten. La siguiente gráfica muestra los minutos que José se retrasó en llegar a su trabajo considerando las veces que tomaba el metro o el camión. Registro de minutos de retraso Integración Semejanzas Diferencias El polígono de frecuencias es una línea Semejanzas: el trazada por segmentos y el histograma son eje vertical es la Histograma barras, en el polígono de frecuencia sólo misma frecuencia. y polígono aparece el punto medio en el eje horizontal de frecuencia Se usan para datos y en el histograma aparecen también los agrupados límites del intervalo Realiza una encuesta en tu comunidad tanto a jóvenes (10 a 17 años) como adultos (18 a 25 años) acerca del tiempo que dedican a leer en la semana. Entrevista a la misma cantidad de personas de cada población. Reflexiona: ¿cómo podrías utilizar las gráficas estudiadas en esta secuencia para comunicar los datos que obtengas? Frecuencia Hacemos 16 14 12 10 8 6 4 2 0 Camión Metro 2.5 7.5 12.5 17.5 Minutos 22.5 27.5 a) ¿Qué medio de transporte tuvo el mayor retraso? y ¿dentro de cuál intervalo de minutos está? b) Observando los dos polígonos de frecuencia ¿qué medio de transporte consideran que le conviene tomar a José? ¿Por qué? Integración • En grupo elaboren una tabla comparativa de las características de los histogramas y de los polígonos de frecuencia. Incluyan algunos ejemplos de uso para cada una. Semejanzas Histograma y polígono de frecuencia 90 Bloque 1 - Secuencia 10 88 Diferencias © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Sugerencias didácticas Histogramas y polígonos de frecuencia Arribamos Edad (años) Número de habitantes (millones) 6 - 12 13 12 - 18 12 18 - 24 16 2. El siguiente histograma muestra el resultado de la prueba del colesterol en miligramos por decilitro de sangre (mg/dL), realizado a 200 personas. 1. a) b) 9 1.521 12 - 18 15 2.832 18 - 24 21 3.344 2. a) b) c) d) 220 225 a) ¿Cuál es la amplitud de cada intervalo? b) Si para tener una buena salud se considera ideal tener un colesterol de entre 180 mg/dL y 200 mg/dL o menos, ¿qué porcentaje de las personas a las que se le hizo la prueba tienen un resultado considerado ideal? c) ¿Qué cantidad de colesterol tiene la mayoría de las personas? d) Explica qué observas en el histograma con relación a la salud de las personas que se realizaron la prueba del colesterol. e) Sobre el histograma anterior, construye el polígono de frecuencia correspondiente. Tiempo Niños Niñas 3. Con los datos de la tabla del tiempo que 0 10 5 2 tarda una población infantil en resolver un 10 20 40 33 problema construye en un mismo plano los polígonos de frecuencia correspondientes. 20 - 30 45 42 a) ¿Algún niño tarda más de 40 minutos en 30 - 40 10 14 resolver el problema? 40 - 50 0 9 b) ¿Cuántas niñas tardan más de 40 minutos? Explica al grupo cómo utilizaste los datos para construir las gráficas. 89 2 1 3 6 9 12 15 18 21 24 27 Edad Registro de colesterol en pruebas 80 70 60 50 40 30 20 10 0 3. 195 200 205 210 215 Colesterol (mg/dL) 220 225 Tiempo en que tardan 100 alumnos en contestar un problema matematico 50 Niñas Niños 40 Frecuencia 205 210 215 Colesterol (mg/dL) 3 5 mg/dL El 5% tiene un resultado ideal. Entre 210 y 215 mg/dL R. M. La mayoría de las personas que se realizaron la prueba tienen un colesterol más alto de lo que se considera saludable, por lo cual deben acudir con el médico. e) 200 4 0 80 70 60 50 40 30 20 10 0 195 Punto Frecuencia medio (millones) 6 - 12 Frecuencia Frecuencia Registro de colesterol en pruebas Número de personas con acceso a internet de acuerdo a su edad Solucionario Edad (años) a) En parejas, calculen el número de personas de cada intervalo de edad que representan los porcentajes en la gráfica 2. b) Elaboren la tabla de frecuencias por intervalos, ubicando el punto medio de éstos y construyan el polígono de frecuencia correspondiente. © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Arribamos Frecuencia en millones 1. Analiza nuevamente la gráfica 2 de la actividad con la que inició la secuencia. Considera la siguiente información sobre la población en México en 2016. 30 20 10 a) No b) 9 niñas 0 5 15 25 35 Minutos 45 Bloque 1 - Secuencia 10 55 91 92 Bloque 1 - Evaluación Autoevaluación Analiza cada situación y subraya la opción correcta. 1. En la imagen se muestra el circuito para una competencia de carreras de autos. Analiza el letrero que se enciende en la estación 4 y responde. E4 E8 Inicio y meta • Uno de los participantes terminó la carrera y otro sólo junto 85.8 puntos, ¿cuántos puntos obtuvo en total el primer participante y en qué estación quedó el segundo? A) El primero obtuvo 114.4 puntos y el segundo quedó en la estación 6. B) El primero obtuvo 100 puntos y el segundo quedó en la estación 6. C) El primero obtuvo 80.4 puntos y el segundo quedó en la estación 7. D) El primero obtuvo 57.2 puntos y el segundo quedó en la estación 5. 3 2 • Un corredor logró avanzar hasta 8 de la pista, y con dificultad recorrió 5 más del resto de la pista. Inicialmente, ¿cuánto le faltaba por recorrer? y en el último tramo, ¿qué parte de la pista recorrió? 1 2 1 A) 2 de la pista y 5 de la pista C) 3 de la pista 5 1 B) 8 de la pista y 4 de la pista 1 5 2 D) 8 de la pista y 5 de la pista 3 • Si en 4 de hora se recorren 5 partes del circuito, ¿cuántas vueltas se pueden dar en una hora? 1 A) Una vuelta C) 2 6 vueltas 3 2 B) 1 4 vueltas D) 2 5 vueltas 2. La capacidad del tanque del auto de carreras es de 105 L de gasolina. Por cada 2 litro recorre 8 000 m y por cada estación recorrida se consumen 7 partes del tanque. ¿Cuántos galones de gasolina quedan en el tanque al terminar la tercera estación y cuántos kilómetros se habrán recorrido? A) 15 galones, 0.8 km B) 4 galones, 720 km C) 4 galones, 450 km D) 0 galones, 800 km 90 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. A lo largo del proceso de enseñanza-aprendizaje se presentan tres momentos de evaluación, cada uno de ellos tiene características que en conjunto determinan el avance de los estudiantes. El primer momento está presente al aplicar la evaluación diagnóstica, la cual marca la pauta en la toma de decisiones enfocadas en las planeaciones didácticas. Su principal objetivo es identificar las necesidades de los estudiantes para desarrollar las temáticas que se abordaran en el nuevo bloque; una vez identificadas se procede a planear los temas que se deben repasar para alcanzar los objetivos deseados. Al revisar la evaluación diagnóstica que se propone en este libro, se pueden identificar los conocimientos y habilidades que los estudiantes deben reforzar. Como segundo momento, está la evaluación formativa. Dicha evaluación está enfocada en dar un seguimiento constante al desempeño académico de los estudiantes. Su principal objetivo es determinar los aspectos en los que el estudiante debe mejorar, cuáles herramientas le han servido y en cuáles debe trabajar aún más para alcanzar los aprendizajes deseados. Puede servir como actividad de retroalimentación, en la que el estudiante reconoce sus fortalezas y deficiencias y, a partir de ellas, los aspectos que puede mejorar; es decir, se le ofrece un camino a seguir para mejorar su aprendizaje. Las técnicas más recomendadas para su realización son: observación, análisis de desempeño de los estudiantes (tanto en actitudes como en adquisición de conocimiento) y autoevaluación. En la página de internet www.edutics.mx/w2W puede consultar más información al respecto. Por último se tiene la evaluación sumativa, la cual emite un juicio final del aprovechamiento del estudiante. Este tipo de evaluación es el resultado del análisis de información que se obtiene sobre el desempeño académico del alumno a lo largo del bloque. De igual forma, ésta determina si los conocimientos planeados se alcanzaron y si las habilidades estudiadas forman parte del saber de los estudiantes. Al emitir esta evaluación se determina la acreditación del bloque. Evaluación Evaluación Sugerencias didácticas 3. Si las placas de los autos de carreras son como las de la imagen, ¿cuál es la cantidad máxima de autos que pueden participar en la carrera si solo se toman en cuenta los números? A) 10 autos B) 102 autos C) 103 autos D) 104 autos 4. Observa la pista, ¿cuántos grados debe rotarse el volante en cada vuelta? A) 360° C) 90° B) 135° D) 45° • ¿A cuántos corredores se entrevistaron? A) 25 C) 100 B) 53 D) Más de 100 Edad a la que los corredores de autos eligieron su profesión 25 Cantidad de corredores 5. En el histograma se muestran los resultados de una encuesta realizada a los corredores de autos acerca de la edad en la que eligieron esa profesión. ¿Cuál fue el intervalo de edad con mayor frecuencia? A) De 16 a 18 años C) De 10 a 12 años B) De 14 a 16 años D) Más de 18 años 20 15 10 5 0 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. • Al trazar el polígono de frecuencias, ¿cuáles son los 8 puntos medios de los intervalos? A) 8, 10, 12, 14 y 16 C) 9.5, 11.5, 13.5, 15.5 y 17.5 B) 9, 11, 13, 15 y 17 D) 10.5, 12.5, 14.5, 16.5 y 18.5 9 10 11 12 13 14 15 16 17 18 Edad Cabe mencionar que cada estudiante posee habilidades y capacidades variadas, por lo que se recomienda tomar en cuenta el avance propio de cada uno. La intención es medir el avance individual de los estudiantes, por lo que, debe existir una comparación con sus propios aprendizajes; esto es, analizar cómo ingresa al curso y cómo egresa de éste. La evaluación permitirá a los estudiantes poner a prueba los conocimientos y habilidades adquiridos. Es importante mencionar que la evaluación incluye algunas imágenes, las cuales aportan información a la solución del problema. Después de que los alumnos hayan resuelto la evaluación, se recomienda hacer algunos comentarios y sugerencias de análisis para la retroalimentación. Puede realizar las siguientes preguntas con base en la imagen del problema 1: ¿Cuántos lados tiene la pista? ¿Qué forma tiene la pista? ¿Cuántos ángulos internos y externos tiene? ¿Cuánto suman los ángulos externos? ¿Cómo puedes obtener el valor de un ángulo interno? Si ya se recorrió 21 de la pista, ¿cuántas estaciones de han recorrido? Si lo considera necesario, para comprobar la solución de la actividad 2, realice una tabla de valores. Pida que calculen cuánta gasolina se ha consumido en las estaciones 2, 3, 4, 5, 6, 7 y 8, pregunte ¿En qué momento debe recargar gasolina? Recuerde a sus estudiantes la importancia de generar una tabla de equivalencias entre unidades de medición. Explique que en la actividad 4 deben identificar que se requiere el valor del ángulo exterior de la pista. Dado el contexto del problema 6, recuerde a los estudiantes el procedimiento para despejar una variable. 6. Para un objeto en caída libre, la fuerza de gravedad es proporcional a la masa m, de dicho objeto, de manera que se cumple la siguiente expresión, donde g es la aceleración de la gravedad dirigida hacia abajo (– 9.8 m/s2). La fuerza se mide en newtons (N). F = mg Si sobre un cuerpo en caída libre actúa una fuerza de – 490 N, ¿cuál es la masa de dicho cuerpo? A) 50 kg B) 85 kg C) 480.2 kg D) 4 802 kg Reúnete en pareja con un compañero. Comparen sus respuestas, argumenten el porqué respondieron así. Corrijan lo que sea necesario. Coevaluación Revisa con tu profesor los resultados: ¿en qué necesitas mejorar? ¿Qué estrategias usarás? Heteroevaluación 91 Bloque 1 - Evaluación 93 Travesías Travesías Sugerencias didácticas Explique que a través de la historia el hombre ha construido objetos matemáticos que son la principal herramienta para la interpretación de fenómenos naturales y sociales. La evolución de dichas herramientas va ligada con las necesidades del hombre, el ejemplo más claro relacionado con este tema, es el tipo de registro que se menciona en “Materiales para el registro de datos estadísticos”. Aquí se habla de los materiales utilizados para el registro de información, se muestran marcas hechas en piedra o huesos. Plantee a los alumnos las siguientes preguntas para saber lo que piensan del registro de datos en la actualidad ¿Cómo se lleva a cabo el manejo de información? ¿Qué software conoces que ayuda a representar datos a través de gráficas? ¿Cuál crees que sea la principal necesidad del hombre relacionada con el manejo de información? Cuando te ofrecen nuevos productos, ¿crees que se haga un estudio para lograr más ventas? Los datos de ayer y hoy Plantear y resolver problemas usando herramientas matemáticas. La recolección, registro e interpretación de datos provenientes de distintas fuentes es una práctica que se ha desarrollado desde tiempos remotos, pues en una sociedad organizada siempre surge la necesidad de poseer datos sobre su población, actividades y condiciones materiales que la rodean. Así, esta práctica ha evolucionado desde la simple recolección de datos hasta la diversa y rigurosa interpretación que en la actualidad se hace de éstos. La estadística, en general, trata de la recopilación, organización, presentación, análisis e interpretación de datos numéricos con el fi n de tomar decisiones. Los primeros registros estadísticos de los que se tiene conocimiento fueron los censos, estudios descriptivos sobre todos los integrantes de una población. En antiguas civilizaciones como la egipcia, china, griega y romana era común que se llevaran a cabo recuentos sobre características de los habitantes: nacimientos, defunciones o de aspectos económicos, impuestos, cosechas, etcétera. De acuerdo con lo que indica el historiador griego Herodoto, en Egipto algunos de los censos de riqueza y población se hacían para planificar la construcción de las pirámides. Los materiales empleados para el registro y comunicación de datos han evolucionado a la par de la escritura. Van desde la piedra, láminas metálicas, papiros y papel, entre otros, hasta los soportes electrónicos actuales. Hacia el año 3 000 a. n. e. los babilonios usaban pequeñas tablillas de arcilla para recopilar datos acerca de la producción agrícola y los géneros vendidos o cambiados mediante trueque. Desde la prehistoria han existido formas rudimentarias de registrar información con fines contables: montículos de piedras o señ ales en huesos, pieles, palos y paredes de cuevas. 94 Bloque 1 - Travesías 92 © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Materiales para el registro de datos estadísticos Sugerencias didácticas Antes de leer el subtema “En México” pregunte a los estudiantes: • ¿Qué sabes sobre la historia de México y las formas en que manejaban la información en el pasado? • ¿Qué instituciones conoces que lleven a cabo recolección de datos y manejo de información en la actualidad? • ¿Qué investigación te gustaría que se llevara a cabo? ¿Por qué? Después de responder de forma grupal las preguntas anteriores analicen dicho subtema. Enseguida aliéntelos a que visualicen la forma en que se registraba la información de los datos de tributación y cómo es que ahora se podrían registrar según los temas estudiados. Al término de la lectura y análisis del último párrafo, vuelva a preguntar: ¿qué tema te gustaría investigar? Ac tua lm ent e se dis po ne de medios electrón ico s para resguardar información así como de las hojas de cálcul o o diversos sof tw are s qu e per mi ten introducir números y variables y, de for ma casi ins tantánea, presentar un a repres ent ación visual de los mismos. En México Recursos adicionales En el siguiente enlace podrá consultar información de los histogramas y polígonos de frecuencia: • “Histograma” y “Polígono de frecuencia”, disponible en www.edutics.mx/ wPT (consulta: 24 de agosto de 2018). © Todos los derechos reservados, Ediciones Castillo, S. A. de C. V. Nuestro país tiene una rica tradición en materia de información estadística de la cual dan cuenta diversos códices e innumerables publicaciones, instituciones y personajes desde la época colonial hasta nuestros días. El 25 de enero de 1983 se creó, por decreto presidencial, el Instituto Nacional de Estadística, Geografía e Informática (Inegi). Con su creación, el instituto modernizó la valiosa tradición que tenía nuestro país en materia de captación, procesamiento y difusión de información acerca del territorio, la población y la economía. El 16 de abril de 2008, el Inegi cambió su personalidad jurídica, adquiriendo autonomía técnica y de gestión. A partir de entonces su nueva denominación es Instituto Nacional de Estadística y Geografía, pero aún conserva las mismas siglas. Cada 10 años el Inegi realiza un censo de población y vivienda. El último se llevó a cabo en 2010. En 1535, por órdenes del primer virrey de la Nueva España, Antonio de Mendoza, se realiza el Códice Mendocino, que en su apartado “Matrícula de tributos” se describe la manera en que los pueblos registraba sus datos de la tributación. Î En el siglo XVII Gaspar Neumann demostró, basándose en los registros de defunciones de la época, la falsedad de la creencia popular de que en los años acabados en siete moría más gente. ¿Conoces algún otro hecho en el que la aportación estadística haya provocado un cambio de ideas? 93 Bloque 1 - Travesías 95