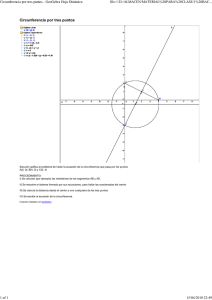
CIRCUNFERENCIA 1 Circunferencia Una circunferencia está formada por el conjunto de todos los puntos de un plano cuya distancia a un punto fijo llamado centro C es constante. La distancia se llama radio r (r>0) . C 2 Circunferencia No es lo mismo hablar de circunferencia que de círculo, la circunferencia corresponde al borde y el círculo a la región del plano limitada por la circunferencia . 3 Circunferencia con centro en el origen La circunferencia tiene centro en el origen, C (0,0) y radio r (x, y) r Aplicando la fórmula de distancia entre dos puntos se tiene: x 0 2 C y 0 r x2 y2 r 2 2 Ecuación de la circunferencia con centro C(0, 0) 4 Circunferencia con centro (h, k) y radio r Por la fórmula de distancia se tiene: x h 2 y k r 2 Luego: x h 2 y k r 2 Ecuación canónica de la circunferencia con centro en (h,k) radio r. 5 Circunferencia con centro (h, k) y radio r La ecuación general de una circunferencia esta dada en la forma: x2 y2 Ax By C 0, con A, B, C R 6 Circunferencia Ejemplo1. Determine la ecuación de la circunferencia con centro en el origen y de radio 2. (x, y) Solución. Aplicando la fórmula de la ecuación canónica se tiene. x 0 y 0 22 2 o 2 2 x 2 y2 4 7 Circunferencia Ejemplo2. Determine la ecuación de la circunferencia con centro en (1/2, -1) y de radio 1. y Solución. x Aplicando la fórmula de la ecuación canónica se tiene: ( x, y ) 1 2 1 x y ( 1 ) 2 2 (1/2, -1) 2 1 Efectuando operaciones se tiene: x2 y2 x 2 y 1 0 4 Ecuación general 8 Circunferencia Ejemplo3. Encuentre el centro y el radio de una circunferencia, que tiene como ecuación general a: 2 x 2 2 y2 7 x 4 y 6 0 Solución. Se transforma la ecuación general a ecuación canónica, con el siguiente procedimiento: Asociando los términos con x entre sí y los términos con y entre sí se obtiene: 2 x 2 7 x 2 y2 4 y 6 9 Circunferencia Continuación ejemplo3. 2 x 2 7 x 2 y2 4 y 6 completando trinomios cuadrados perfectos, se obtiene: 2 2 7 7 2 2 2 2 x x 2 y 2 y 2 2 4 = 6 49 2 8 que es equivalente a: 2 7 113 2 x y 1 4 16 y de esto se puede concluir que: C(-7/4,-1) r 113 4 10 Circunferencia La gráfica correspondiente es: C(-7/4,-1) r 113 4 11 Circunferencia Ejemplo4. Determinar la ecuación de la circunferencia si el segmento que une los puntos (4, 4) y (-2, -3) es uno de sus diámetros: Solución. Para hallar la coordenada del centro, se halla el punto medio entre (4, 4) y (-2, -3) : 4 (2) 4 (3) 1 C , 1, 2 2 2 (4, 4) r C (-2, -3) 12 Circunferencia Continuación ejemplo4. Para hallar el radio, se encuentra la distancia entre uno de los puntos y el centro : r 2 r C 85 2 Luego, la ecuación de la circunferencia con centro 85 (1,1/2) y radio es: 2 x 1 (4, 4) (-2, -3) 2 1 85 y 2 4 13 SEMICIRCUNFERENCIA Media Circunferencia 2 y r x 2 y r 2 x2 x r 2 y2 x r 2 y2 14