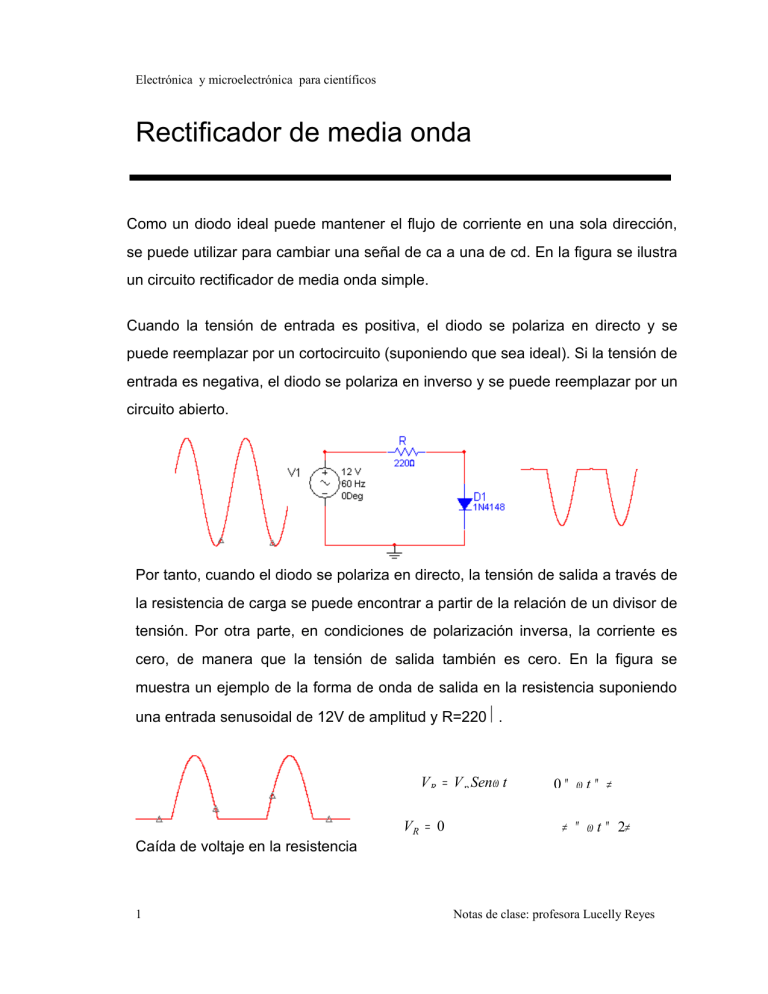
Electrónica y microelectrónica para científicos Rectificador de media onda Como un diodo ideal puede mantener el flujo de corriente en una sola dirección, se puede utilizar para cambiar una señal de ca a una de cd. En la figura se ilustra un circuito rectificador de media onda simple. Cuando la tensión de entrada es positiva, el diodo se polariza en directo y se puede reemplazar por un cortocircuito (suponiendo que sea ideal). Si la tensión de entrada es negativa, el diodo se polariza en inverso y se puede reemplazar por un circuito abierto. Por tanto, cuando el diodo se polariza en directo, la tensión de salida a través de la resistencia de carga se puede encontrar a partir de la relación de un divisor de tensión. Por otra parte, en condiciones de polarización inversa, la corriente es cero, de manera que la tensión de salida también es cero. En la figura se muestra un ejemplo de la forma de onda de salida en la resistencia suponiendo una entrada senusoidal de 12V de amplitud y R=220Ω. V R = V p Senω t VR = 0 0≤ ωt≤ π π ≤ ω t ≤ 2π Caída de voltaje en la resistencia 1 Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos Según sea la amplitud de la tensión de alimentación, tendremos un determinado nivel de tensión continua a la salida. En la figura siguiente se puede observar como el periodo de la señal de salida es el mismo que el de la señal de entrada; cada ciclo de entrada produce un ciclo de salida. Esto de debe a que la frecuencia de salida de un rectificador de media onda es igual a la frecuencia de la entrada: f salida = f entrada Esta observación es confirmada por el análisis de fourier. Donde la frecuencia dominante es igual a la frecuencia de la señal de entrada. Tensión media en la carga: Este valor nos determina la componente de c.c. de la tensión en la carga. Lo obtenemos calculando el promedio del voltaje de salida del rectificador: 2 Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos T Vdc = 1 2 1 v( t ) dt = ∫ T 0 2π π ∫0 V p Senω t dω t = Vp π = 0,318 V p así que tendremos una componente continua del orden del 30% del valor de pico. Aunque este circuito produce una tensión continua a través de la resistencia de carga, seria inaceptable como fuente de polarización en muchos dispositivos electrónicos, debido a que la tensión de salida en la carga tiene componentes alternas además de la continua. Veamos las componentes alternas, Tensión eficaz en la carga: Vrms = 1 2π ∫ 0 (V p Senω tdω t ) π 2 dω t = Vp 2 Estas señales actuarían como señales extrañas y enmascararían las señales verdaderas. Regulación: Mediante el parámetro regulación se mide la variación de la tensión continua de salida (V ) en función de la corriente continua que circula por la dc carga. Dicha variación de la tensión de salida es debida a una pequeña resistencia que presenta el devanado secundario (R ), y a la resistencia interna S del diodo cuando está conduciendo (R ).Por eso, lo más conveniente para d nuestro rectificador es que el porcentaje de regulación sea lo menor posible: r ( %) = Vdc ( envacío ) − Vdc ( aplenac arg a ) Vdc ( aplenac arg a ) × 100% Siendo el valor de tensión media en la carga: Vp − I dc ( en plena carga ) ( RS + R D ) Vdc ( enplenac arg a ) = π ( 3 ) Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos Factor de forma: FF = 0,5V p Vrms = = 1,57 Vdc 0,318V p Factor de rizado: Es una buena forma de medir el alisamiento en la salida de c.c.: FR( % ) = Vac,rms ( salida ) Vdc × 100% Sabiendo que: (Vrms ) 2 = (Vac,rms ( salida ) ) 2 + (Vdc ) 2 Valor medio de la corriente en la carga: I dc = Valor eficaz de la corriente en la carga: I rms = Ip π Ip 2 Sabiendo que: Ip = Los valores de I Vp R e I deberán tenerse en cuenta a la hora de elegir un diodo dc p semiconductor para el rectificador, siendo estos valores de intensidad los que circularán por el devanado secundario del transformador. Potencia media en la carga: Pdc = 4 (Vdc ) 2 R = ( 0,318V p ) 2 R Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos Potencia eficaz en la carga: Pac = (Vrms ) 2 R = ( 0,5V p ) 2 R Rendimiento: (Vdc ) 2 ( ) 0,318V p 2 0,101 Pdc R η = = = = = 0,404 → (40,4%) Pac (Vrms ) 2 0,25 0,5V p 2 R ( ) Ejemplo 1 Dado un rectificador monofásico de media onda con carga resistiva, cuyo esquema es el mostrado en la figura siguiente: Calcular: a) Tensión de pico en la carga. 5 Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos b) Corriente de pico en la carga. c) Tensión media en la carga. d) Corriente media en la carga. e) Corriente eficaz en la carga. f) Potencia eficaz en la carga. Solución La tensión de pico en la carga corresponderá con la tensión máxima suministrada por el secundario: V p ( c arg a ) = V p = a) 2VS = (1,414 )( 240)V = 339,4V La corriente de pico en la carga corresponde a la intensidad máxima que se obtiene de la tensión máxima: I P ( c arg a ) = I max = Vp = R 339,4 A = 16,97 A 20 b) La tensión media en la carga: Vdc = ( 0,318)V p = 108V c) La corriente media en la carga la calcularemos usando la ecuación del apartado anterior, pero sustituyendo V por I : p p I dc = 5,4 A La corriente eficaz en la carga I rms = 6 Ip 2 = 8,48 A Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos e) La potencia alterna en la carga será: Pac = ( I rms ) R = 1440W 2 Ejemplo 2 Dado el rectificador monofásico de media onda con carga puramente resistiva, del ejercicio 1. Calcular lo siguiente: a) La eficiencia de la rectificación. b) El factor de forma. c) El factor de rizado. d) El factor de utilización del transformador. e) La tensión inversa de pico en el diodo. f) El factor de cresta de la corriente de alimentación. Solución: a) Tenemos: η = b) ( 0,318V p ) 2 = 0,405 → ( 40,5% ) ( 0,5V p ) 2 Calculamos el factor de forma como: FF = c) 7 0,5V p 0,318V p = 1,57 → (157% ) Fr como:: Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos FR = 1,21 → (121% ) d) Primero necesitaremos saber el valor de la tensión eficaz y el valor eficaz de la intensidad en el secundario: VS = Vp 2 = 0,707V p IS = ( S = VS I S = 0,707V p P TUF = dc = VS I S ( 0,5V p R ) 0,5RV p Vdc I dc ( 0,318) 2 1 = = 0,286 → = 3,496 0,5V p ( 0,707 )( 0,5) TUF 0,707V p R ) e) La tensión inversa de pico en el diodo: PIV = Vmax f) El factor de cresta será: CF = I S ( pico ) IS = Vmax R 1 = = 2 0,5Vmax R 0,5 Ejemplo 3 El rectificador de media onda del ejercicio 1, es alimentado por una tensión Vs =120V, 50Hz. Expresa la tensión instantánea en la resistencia v (t), en series de i Fourier como: v (t) = V p sen wt v (t) = 0 0 < t < T /2 T /2 < t < T Solución: 8 Notas de clase: profesora Lucelly Reyes Electrónica y microelectrónica para científicos La tensión de salida en la resistencia v puede expresarse en series de Fourier i(t) como: ∞ vi ( t ) = Vdc + 1 π an = bn = 1 π 2π ∫0 2π ∫0 donde: V = V p dc π ∑ ( an senω t + bn cos ω t ) n = 1, 2,... vi (t ) sen nω t dω t = vi (t ) cos nω t dω t = 1 π π ∫0 Vp V p senω t sen nω t dω t = = 0 1 π V p senω t cos nω t dω t π ∫0 → n= 1 2 → n = 2,4,6,...... = 0 V p 1 + ( − 1) n π 1 − n2 Sustituyendo a y b la tensión instantánea en la carga será: = n vi ( t ) = Vp π Donde: 9 + Vp 2 → n = 2,4,6,..... n, senω t − V p= → n= 1 2V p 3π cos 2ω t + 2 (120 ) = 169,7 V 2V p 15π cos 4ω t − 2V p 35π cos 6ω t + ... ω = 2π ( 50 ) = 314,16 rad / seg Notas de clase: profesora Lucelly Reyes