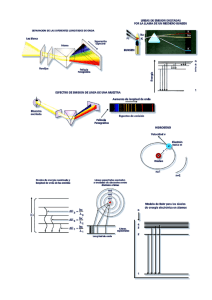
tema 42 FÍSICA Y QUÍMICA Enlace covalente: orbitales moleculares. Diagramas de energía. Geometría molecular. 25-15359-13 Estructura y propiedades de las sustancias covalentes. Temario 1993 tema 42 física y química 1. Teoría de la repulsión entre pares de electrones de la capa de valencia (RPECV) 1.1. Formas moleculares 1.2. El modelo RPEC V 2. Teoría del enlace de valencia (EV) 2.1. Introducción 2.2. Teoría EV 2.3. Polaridad del enlace 3. Hibridación de orbitales atómicos 3.1. Hibridación sp 3.2. Hibridación sp2 3.3. Hibridación sp3 3.4. Hibridación sp3d 3.5. Hibridación sp3d2 3.6. Moléculas con enlaces múltiples 3.6.1. Compuestos con dobles enlaces: eteno (C2H4) 3.6.2. Compuestos con enlaces triples: etino (C2H2) 3.7. La resonancia en la teoría EV 4. Teoría de orbitales moleculares (TOM) 4.1. Introducción 4.2. Simetría y notación de los ORBITALES MOLECULARES 4.3. Orden de energías de los orbitales moleculares 5. Estructura y propiedades de las sustancias covalentes 3 tema 42 física y química INTRODUCCIÓN El tamaño y la forma de las moléculas de una sustancia dada, junto con la fuerza y la polaridad de sus enlaces, determinan en buena medida las propiedades físicas o químicas de esa sustancia. En este tema vamos a estudiar tres modelos para analizar la geometría y los enlaces moleculares. En primer lugar, estudiaremos cómo podemos describir y predecir la forma de las moléculas utilizando un sencillo modelo basado en las estructuras de Lewis y en el concepto de repulsiones electrón-electrón, la Teoría de la repulsión entre pares de electrones de la capa de valencia (RPECV). Luego examinaremos un modelo de los enlaces moleculares, la Teoría del enlace de valencia (TEV), que nos ayuda a entender por qué se forman los enlaces en las moléculas y a qué se debe la forma de éstas. Por último, estudiaremos un modelo de enlaces químicos, la Teoría de orbitales moleculares (TOM), que permite entender mejor los aspectos energéticos de la formación de enlaces y la estructura electrónica de las moléculas. 5 tema 42 física y química 1 Teoría de la repulsión entre pares de electrones de la capa de valencia (RPECV) 1.1. Formas moleculares La forma global de una molécula está determinada por los ángulos de enlace1, es decir, los ángulos formados por las líneas que unen los núcleos de los átomos de la molécula. Estos ángulos, junto con las longitudes de enlace, definen con exactitud el tamaño y la forma de la molécula. Al estudiar la forma de las moléculas comenzaremos con las moléculas (o iones) que tienen un solo átomo central (A) unido a dos o más átomos del mismo tipo (X): XX Moléculas o iones tipo AX2 El átomo X puede ser el mismo o distinto tipo de átomo que A; tienen: Estructura lineal si el átomo central A carece de electrones no compartidos. Estructuras angulares si el átomo central tiene uno o más pares de electrones no compartidos. Así pues, puede comprobarse que CO2, N2O y N3– poseen estructuras lineales, mientras que H2O, H2S y NO2– deben ser angulares, como lo indican sus fórmulas de Lewis (Figura 1). XX Moléculas o iones de tipo AX3 El átomo X es diferente o igual a A; tienen: Estructuras planas si el átomo central A carece de electrones no compartidos. Estructuras piramidales con A en el vértice de la pirámide, si el átomo central tiene un par de electrones no compartidos. En consecuencia, CO32–, NO3– y BF3 son planas de acuerdo con sus fórmulas de Lewis, mientras que NH3, SO32– y ClO3– son piramidales, como lo indican igualmente dichas estructuras (Figura 2). XX Moléculas o iones tipo AX4 Tienen: Estructuras tetraédricas si el átomo central carece de electrones no compartidos en su capa exterior y si ésta es del tipo de la de los gases inertes. Estructuras planas si la capa exterior no es semejante a la de los gases inertes, es decir, si tiene más de cuatro pares de electrones. 1Los ángulos de enlace se estudian en el tema 41 cuando se habla de los distintos tipos de enlaces químicos. 6 tema 42 física y química No existen ejemplos bien definidos de esta regla, aunque el CH4 y NH4+ cumplen con los requisitos de la primera parte de ella, y se puede decir que los complejos coordinados de Ni(II) y Pd(II) pertenecen a la segunda parte de la misma. Figura 1. Estructuras de Lewis de moléculas o iones tipo AX2. 1.2. El modelo RPECV De las moléculas AX2 y AX3, antes mencionadas, el CO2 es lineal y el H2O es angular, mientras que el SO3 es plano trigonal y el NH3 es piramidal trigonal. ¿Por qué diferentes moléculas AXn adoptan formas distintas? Si A es un elemento representativo, podemos contestar a esta pregunta utilizando el modelo RPECV. Figura 2. Estructuras de Lewis de moléculas o iones tipo AX3. Esta teoría se conoce como teoría de la repulsión entre pares de electrones de la capa de valencia (RPECV). Como está implícito en su denominación, esta teoría explica eficazmente las formas de las moléculas que contienen pares de electrones localizados. Los pares electrónicos de la capa de valencia de un átomo tienden a orientarse por sí mismos de forma que su energía total se minimiza. Esto significa que se aproximan al núcleo lo más posible, al tiempo que permanecen lo más distanciados entre sí, minimizando así las repulsiones electrónicas. Geométricamente este máximo distanciamiento conduce a las orientaciones que se muestran en la Tabla 1. Tabla 1. Orientación molecular en función del número de pares de electrones. Nº de pares de e- Orientación Ángulos 2 Lineal 180º 3 Plana triangular 120º 4 Tetraédrica 109,5º 5 Bipiramidal 90º, 120º 6 Octaédrica 90º Cuanto más se fuercen a acercarse entre sí dos grupos de electrones, mayor será la repulsión entre ellos. La repulsión para un grupo de electrones es mucho mayor para un ángulo de 90º que para un ángulo de 120º o de 180º. Debido a que los pares solitarios están más dispersos que los pares enlazantes, el orden de intensidad de repulsión electrónica es el siguiente: PS – PS > PS – PE > PE – PE (PS = par solitario; PE = par enlazante) 7 tema 42 física y química Las interacciones para ángulos superiores a 90º (120º o 180º) suelen ser tan pequeñas que pueden despreciarse. Las interacciones PE–PE pueden despreciarse incluso a 90º. La teoría RPECV no hace distinción entre enlaces sencillos y enlaces múltiples a la hora de determinar la geometría molecular. Es decir, ésta se determina por los enlaces sencillos (llamados, enlaces σ) y los pares no enlazantes o pares solitarios. El segundo o tercer enlace (llamados enlaces π) se adicionan posteriormente. Cuando existen pares enlazantes exclusivamente, la geometría molecular coincide con la geometría de los enlaces. Cuando también existen pares solitarios no ocurre lo mismo y hay que diferenciar ambas geometrías. El tipo de geometría, molecular y de enlaces, en función del número y tipo de pares electrónicos que existen alrededor del átomo central es el indicado en la Tabla 2. Tabla 2. Clasificación de la geometría de los enlaces y molecular. Nº total de pares de e- en el átomo central 2 3 3 Geometría de los enlaces Lineal Triangular Triangular Tipos de pares de edel átomo central 2PE 3PE 2PE, 1 PS Fórmula Geometría molecular AX2 AX3 AX2 Lineal Triángulo equilátero Angular 4 Tetraédrica 4PE AX4 Tetraédrica 4 Tetraédrica 3PE, 1PS AX3 Pirámide trigonal 4 Tetraédrica 2PE, 2PS AX2 Angular 5 Bipiramidal trigonal 5PE AX5 Bipiramidal 5 Bipiramidal trigonal 4PE, 1PS AX4 Tetraedro irregular 5 Bipiramidal trigonal 3PE, 2PS AX3 Forma de T 5 Bipiramidal trigonal 2PE, 3PS AX2 Lineal 6 Octaédrica 6PE AX6 Octaédrica 6 Octaédrica 5PE, 1PS AX5 Pirámide cuadrada 6 Plano-cuadrada Octaédrica 4PE, 2PS AX4 Nota: PE = par de electrones de enlace; PS = par de electrones solitarios Ejemplo BeCl2 BCl3 SnCl2 CH4 NH3 H2 PCl5 SF4 ClF3 [ICl2]– SF6 BrF5 [ICl4]– Tomando como ejemplo la molécula de ClF3 podemos deducir su geometría usando la teoría RPECV, de la siguiente manera: Nº e– valencia de elemento representativo (Cl) = 7 Nº e– desapareados en los átomos vecinos = 3 Total = 10 electrones. Geometría orbital: bipiramidal trigonal 3 pares enlazantes y 2 solitarios Estructuras moleculares posibles (Figura 3). 8 tema 42 física y química Repulsiones a 90º en las tres posibles estructuras: PS–PS PS–PE (I) 0 6 (II) 1 3 (III) 0 4 La estructura II puede despreciarse debido a la fuerte repulsión PS–PS a 90º. De las otras dos, la III es la más favorable por su menor número de repulsiones PS–PE. Se puede predecir que la estructura molecular del ClF3 es en forma de T, con una geometría de los grupos de electrones bipiramidal trigonal. Los experimentos muestran que la molécula de ClF3 tiene realmente esta forma, pero ligeramente distorsionada debido a la diferente naturaleza de las interacciones PS–PS, PS–PE y PE–PE. La distorsión se debe en concreto a la repulsión entre los 2 pares solitarios y los pares enlazantes axiales, que hace que los ángulos F–Cl–F estén un poco «cerrados», con un valor de unos 87º. Figura 3. Estructuras posibles para el CIF3. 9 tema 42 física y química 2 Teoría del enlace de valencia (EV) 2.1. Introducción La relación del concepto de Lewis de enlace por pares de electrones junto con la idea de orbitales atómicos conducen a un modelo del enlace químico llamado teoría del enlace de valencia. En la teoría de Lewis, tiene lugar la formación de enlaces covalentes cuando los átomos comparten electrones. En la teoría del enlace de valencia, tiene lugar una acumulación de densidad electrónica entre dos núcleos cuando un orbital atómico de valencia de un átomo se fusiona con otro átomo. Se dice entonces que los orbitales comparten una región del espacio o se solapan. Este solapamiento entre dos núcleos permite a dos electrones con espín opuesto compartir el espacio común entre los núcleos y formar un enlace covalente. A partir de la teoría de Lewis, existen otras teorías que, a lo largo del tiempo, han tratado de explicar el enlace covalente mejorando aquel modelo. XX Teoría de Heitler-London Puede considerarse como una ampliación de la teoría de Lewis, pero teniendo en cuenta el concepto de «spin» electrónico, es decir, para que se apareen los electrones es necesario que éstos tengan spines antiparalelos. Es el caso de la molécula de NF3, la configuración electrónica del N nos muestra la existencia de tres electrones desapareados: N=1s2 2s2px1py1pz1 y cada uno de ellos puede ser apareado con cada uno de los del F = 1s2 2s2px2py2pz1 En definitiva, se forman tres enlaces simples N-F, en los que cada uno de los átomos contribuye con un electrón a la formación de este enlace. Con este criterio, el número de enlaces covalentes es función del número de electrones desapareados que contenga cada átomo. XX Teoría de Hund-Mulliken o de la activación electrónica Esta teoría se basa en el hecho de que se puede aumentar la posibilidad de covalencia de un átomo mediante una excitación electrónica, de forma que los electrones se promuevan a otros orbitales vacíos y estables, aumentando con ello el número de electrones desapareados en su estructura. Para que esto ocurra basta un pequeñísimo aporte de energía, ya que se trata de saltos entre orbitales equivalentes (todos los «p», los «d» o los «f») o de clases muy próximas en energía. Éste es el caso de la formación del PCl5, que no puede ser explicado por ninguna de las teorías anteriores. La configuración electrónica del P en su estado «normal» es: P = 1s2 2s2p63s22px1py1pz1 Esto significa que tiene tres electrones desapareados y, por tanto, valencia tres. 10 tema 42 física y química Sin embargo, si se aplica ahora esta teoría de la excitación, es posible el salto de uno de los electrones apareados del orbital 3s al orbital 3d, que está vacío; en estado «activado» el P tiene la siguiente configuración P* = 1s22s2p63s12px1py1pz1d1 Con ello el P adquiere valencia cinco y es posible el apareamiento de cada uno de esos cinco electrones con el desapareado de cada uno de los cinco átomos de Cl. Tipos de electrones en un átomo: a) No enlazantes: son los que están apareados y pertenecen a capas internas, razón por la cual, según esta teoría, no intervienen en el enlace. b) Enlazantes: son los que están desapareados en el estado «normal» del átomo, es decir, los tres desapareados del P y el desapareado de cada átomo de Cl. c) Antienlazantes: son aquellos que deben ser «promocionados» para que intervengan en el enlace, sucede con el 3s1 y 3d1 en el caso del P pentavalente. XX Teoría de Pauling-Slater o de los enlaces dirigidos Los orbitales atómicos, considerados como lugares geométricos de máxima probabilidad de existencia de los electrones, tienen en el espacio unas direcciones no arbitrarias, es decir, concretas; por ello los enlaces interatómicos se realizan siempre según estas direcciones. El carácter dirigido de los enlaces covalentes está por ello condicionado por las direcciones de los orbitales atómicos enlazados2. 2.2. Teoría EV En la teoría del EV se parte de considerar separados a una distancia infinita a los átomos que van a formar el enlace y se va estudiando la energía del sistema a medida que se van acercando, es decir, a medida que va disminuyendo la distancia internuclear. Para ello se elige una función adecuada y se tienen en cuenta todo tipo de interacciones (que serán fundamentalmente electrostáticas) que afecten a la energía del sistema. La condición para la formación de un enlace estable viene dada por el hecho de que, a una determinada distancia internuclear, la energía del sistema alcance un mínimo, por supuesto menor que la E energía de los átomos aislados. En la Figura 4 se muestra cómo cambia la energía potencial del sistema a medida que dos átomos de H se acercan para formar una molécula de H2. Conforme la distancia entre los átomos disminuye, el solapamiento entre sus orbitales atómicos de valencia aumenta. La distancia internuclear en el mínimo de la curva de energía potencial corresponde a la longitud de enlace observada (r0). ψ– O ψ a(1s) ro r ψ+ Figura 4. Energía de la molécula H2 en función de r. 2En el tema 34: Modelos atómicos. Evolución histórica y justificaciones de cada modificación, se analiza la representación gráfica y los tipos de los orbitales. 11 tema 42 física y química Los orbitales internos de cada átomo que interviene en el enlace no sufren ninguna perturbación, es decir, cada uno conserva su propia identidad. Cuando se forma el enlace, sólo un electrón de cada átomo que participa pierde su identidad y se desplaza en los orbitales atómicos de ambos átomos. Los e– en la molécula de H2 tienden a moverse hacia la región internuclear, por la atracción electrostática; al mismo tiempo se produce una interacción entre las funciones de onda de los e– y esa interacción depende de los espines electrónicos; se dan dos casos: Spines paralelos: la energía del sistema es muy elevada y no hay función de enlace. Spines opuestos: la energía del sistema es mínima y los dos e– podrán estar en la región internuclear unidos por una fuerza cohesiva llamada «enlace covalente». Lo importante para que haya enlace es que cada átomo tenga un e– desapareado utilizable para aparearse con el e– desapareado de otro. De esta forma se pueden formar dos tipos de enlaces: Enlace sigma (σ). Enlace pi (π). XX Enlace sigma, σ Tiene simetría axial y se forma por solapamiento de los orbitales atómicos s-s, s-px, y px-px, y en cada uno de los casos con soluciones enlazantes (refuerzan al enlace) y antienlazantes (no lo refuerzan), que simbolizan como σ y σ*. De la interacción entre orbitales «s» y orbitales «p» se obtienen también orbitales tipo σ. Se aparecen Solapan Enlazan Rebajan la energía Spines opuestos No pueden aparearse No Solapan No Enlazan Aumenta la energía Spines iguales Figura 5. Interacción entre orbitales «s». 3p (Cloro) 1s (Hidrógeno) Figura 6. Interacción entre orbitales «s» y orbitales «p». 12 6s–p (Cloruro de hidrógeno) tema 42 física y química XX Enlace pi, π Tiene carácter paraxial y se forma por solapamiento paralelo de py con py o de pz con pz. Este tipo de enlace siempre acompaña a un enlace sigma y nunca va solo, consecuencia del choque frontal de los orbitales px. Átomo Molécula Interacción destructiva Orbital molecular sigma de antienlace Interacción constructiva Orbital molecular sigma de enlace Átomo a) Interacción destructiva Átomo Molécula Orbital molecular sigma de antienlace Átomo Interacción constructiva b) Orbital molecular sigma de enlace Figura 7. Interacción entre orbitales «p». 2.3. Polaridad del enlace La forma de una molécula y la polaridad de sus enlaces determinan la distribución de cargas en la molécula. Decimos que una molécula es polar si sus centros de carga negativa y positiva no coinciden. Un extremo de una molécula polar tiene una pequeña carga positiva (δ+), y el otro, una pequeña carga negativa (δ–). Una molécula no polar carece de estas características. Un caso de molécula polar es la molécula HF, puesto que existe una gran diferencia de electronegatividad entre los átomos de H y F. Podemos indicar la polaridad de esta molécula de dos formas: į+ į- H-F HF 13 tema 42 física y química En la representación de la derecha, la flecha indica el sentido hacia donde está desplazada la carga negativa. Cuando dos cargas eléctricas de igual magnitud y de signos opuestos se encuentran separadas cierta distancia, se establece un dipolo entre ellas. Un dipolo es cualquier estructura que posee dos cargas iguales (q) y opuestas separadas por una distancia d. En un enlace químico, su momento dipolar, µ, es un vector cuyo sentido es del átomo menos electronegativo al más electronegativo. Su módulo se determina mediante la ecuación µ = q.d. La unidad de medida más usual para el momento dipolar es el Debye (D) = 10–18 uee x cm. Aunque la unidad en el sistema internacional es el C·m, siendo 1 D = 3,33·10-30 C·m. El momento dipolar total de una molécula poliatómica es la suma de sus dipolos de enlace. En esta suma se debe considerar tanto la magnitud como la dirección de los dipolos. Los dos dipolos de enlace de la molécula de CO2, aunque son de igual magnitud, son de dirección exactamente opuesta, por lo que al sumarlos se cancelan entre sí, y el momento dipolar es cero (Figura 8): No debe confundirse la polaridad de un enlace con la polaridad de una molécula. Un enlace es polar siempre que los átomos implicados en el mismo son distintos, lo que supone que tienen diferente electronegatividad. Para que una molécula sea polar es necesario, en primer lugar, que sus enlaces sean polares y, además, que la resultante de los momentos dipolares de sus enlaces sea distinta de cero. Se puede comprobar geométricamente que las siguientes estructuras moleculares poseen una resultante vectorial nula de los momentos dipolares de sus enlaces: Lineal. Triangular plana (triángulo equilátero). Tetraédrica, con el átomo central en el centro del tetraedro y los átomos periféricos en los cuatro vértices. Bipiramidal de base triángulo equilátero (bipiramidal trigonal), con el átomo central en el centro de la base o plano ecuatorial de la bipirámide y los átomos periféricos en los cinco vértices. Octaédrica, con el átomo central en el centro del octaedro y los átomos periféricos en los seis Dipolos de enlace vértices. O C Momento dipolar total = 0 Figura 8. Momento dipolar del CO2. 14 O tema 42 física y química 3 Hibridación de orbitales atómicos Si intentamos extender el método del enlace de valencia a un mayor número de moléculas, nos daremos cuenta de que en la mayoría de los casos las descripciones de la geometría molecular no están de acuerdo con los valores observados. Por ejemplo, basándonos en la configuración electrónica de la capa de valencia correspondiente al estado fundamental para el carbono: Estado fundamental: C 2s 2px 2py 2pz Utilizando sólo orbitales semillenos, prevemos la existencia de una molécula con la fórmula CH2 y un ángulo de enlace de 90º. Sin embargo, la molécula CH2 no existe de manera estable. El hidrocarburo estable más sencillo es el metano, CH4, y para explicar los ángulos de enlace experimentales de esta molécula es necesario modificar los orbitales atómicos de los átomos enlazados3. Los orbitales atómicos son expresiones matemáticas que pueden combinarse, de manera que necesitamos combinar las ecuaciones de onda del orbital 2s y los tres orbitales 2p del átomo de C para obtener un nuevo conjunto de orbitales idénticos. Estos nuevos orbitales que están dirigidos en forma tetraédrica tienen energías que son intermedias entre aquellas de los orbitales 2s y 2p. Este tratamiento de combinación de orbitales atómicos puros se denomina hibridación, y los nuevos orbitales obtenidos, orbitales híbridos. Así, el número de orbitales híbridos resultante tiene que ser igual al número de orbitales atómicos que se combinan. En este caso obtendríamos cuatro orbitales híbridos de tipo sp3, es decir, se combinan un orbital s y tres p. Así, tenemos los siguientes tipos de orbitales híbridos: Tabla 3. Orbitales híbridos. Geometría electrónica Orbitales necesarios Orbitales híbridos Ejemplos Lineal s+p sp BeCl2. CO2 Triangular plana s+p+p sp2 BF3, SnCl2, C2H4 Tetraédrica s+p+p+p sp3 CH4, NH3, H2O Bipiramidal trigonal s+p+p+p+d sp3d PCl5, SF4, ClF3, I3– Octaédrica s+p+p+p+d+d sp3d2 SF6, BrF5, XeF4 3 Voveremos a repasar estos conceptos en el tema 59 como introducción a la química orgánica. 15 tema 42 física y química 3.1. Hibridación sp El cloruro de berilio, BeCl2, es un ejemplo claro de hibridación tipo sp. Esta molécula, al igual que otras del tipo AX2, donde A,= Be, Cd y Hg y X,= Cl, Br, I, son moléculas lineales (ángulo de enlace = 180º), covalentes y apolares, aunque los enlaces individuales sean polares. Con respecto al BeCl2, conviene hacer notar que la diferencia de electronegatividad del Be y del Cl es tan elevada que cabría esperar un enlace iónico. Sin embargo, el radio del ion Be2+ es tan pequeño y su densidad de carga (cociente carga/ volumen) tan elevada, que los compuestos sencillos del berilio son covalentes en vez de iónicos. Observamos que la configuración electrónica del Be en su estado fundamental es: 1s2 2s2, lo que nos muestra que no existen electrones desapareados y, por lo tanto, imposibilitaría la formación de enlaces covalentes. El problema puede resolverse de la siguiente manera: el Be puede pasar mediante un aporte de energía pequeño al primer estado excitado, lo que supone promocionar uno de los electrones 2s a uno de los orbitales 2p; resultaría la configuración: 1s2 2s1 2p1. Ahora existen dos orbitales disponibles en el berilio que darían lugar a dos enlaces distintos, uno de ellos por solapamiento del orbital 2s de berilio y un orbital 3p de un cloro y el otro por solapamiento de un orbital 2p del berilio y uno 3p del cloro, pero siguen las discrepancias con las pruebas experimentales, que indican que los dos enlaces Be–Cl son idénticos. Esta constatación experimental, que exige que los dos orbitales del berilio sean idénticos, conduce a la obtención de dos orbitales híbridos sp; resultaría así una geometría lineal y los enlaces tendrían lugar por solapamiento de un orbital híbrido del berilio y un orbital p de cada cloro (Figura 9). La teoría de la hibridación no sólo resolvió la geometría de la molécula, sino también los problemas energéticos. El cálculo de la energía de enlace indica que con los orbitales híbridos se obtienen enlaces más fuertes que con los orbitales atómicos puros y se obtienen valores de la energía de enlace más próximos a los experimentales. En muchos casos, como en el del berilio, es necesario un estado previo excitado, para el que se requiere un aumento previo de la energía del sistema. En realidad, los orbitales híbridos representan siempre estados activados, de mayor energía. Sin embargo, esta energía queda compensada con creces debido a que los orbitales híbridos, por su mayor extensión en el espacio, pueden presentar un mayor grado de solapamiento y producir enlaces más fuertes y estables y de menor contenido energético. Cl Figura 9. Enlace en el BeCl2. 16 De acuerdo con esta teoría, la valencia de un elemento coincide con el número de electrones desapareados que posee. Un elemento podrá actuar con tantas valencias distintas como números distintos de electrones desapareados tenga en el estado fundamental X o que puedan desaparearse sin que sea necesaria para ello una energía muy alta (sin cambiar Cl Be su número cuántico principal). Así, el oxígeno puede actuar sólo con valencia 2, debido a que tema 42 física y química presenta dos electrones desapareados en el estado fundamental (1s2 2s2 2p2x 2p2y 2p1z) y no puede promocionar electrones a niveles superiores sin un gran aporte de energía, ya que en la capa 2 no hay más orbitales. En cambio, el azufre puede presentar dos electrones desapareados en el estado fundamental (1s2 2s2 2p6 3s2 3p2x 3p1y 3p1z), o bien cuatro electrones después de promocionar uno del orbital 3px a uno de los orbitales 3d o, finalmente, 6 electrones después de una nueva promoción de uno de los electrones del orbital 3s a otro de los orbitales 3d. De esta forma, puede actuar con valencias 2, 4 y 6. 3.2. Hibridación sp2 La descripción de este tipo de hibridación puede hacerse explicando la geometría de la molécula BCl3. Los datos experimentales apuntan a que los enlaces B–Cl son equivalentes y la molécula ha de ser plana con ángulos de enlace de 120º, puesto que los enlaces B–Cl son polares y, sin embargo, el momento dipolar del BCl3 es nulo. Geométricamente, para que la resultante de tres vectores iguales sea cero, aquéllos han de estar en un plano y orientados hacia los vértices de un triángulo equilátero, es decir, formando entre sí ángulos de 120º. La explicación, por un camino paralelo al visto para la molécula BeCl2 se esquematiza en la Figura 10. ↑ B [He] ↑ 2p ↑↓ 2s B [He] promoción ↑ 2s ↑ 2p B [He] hibridación ↑ ↑ ↑ 2p sp2 Figura 10. Promoción electrónica e hibridación sp2 del boro. Como dos orbitales p cualesquiera se encuentran en el mismo plano y el orbital s no es direccional, los orbitales sp2 se encuentran en el mismo plano (Figura 11). Debido a la repulsión electrónica entre centros de alta densidad electrónica, los tres orbitales híbridos sp2 están dirigidos hacia los vértices de un triángulo equilátero. El orbital p no hibridado es perpendicular al plano determinado por los híbridos. Los tres enlaces B–Cl tendrían lugar por solapamiento de cada orbital híbrido sp2 del boro con el orbital p que cada cloro tiene con un electrón desapareado. Figura 11. Orbitales híbridos sp2. 17 tema 42 física y química 3.3. Hibridación sp3 Este tipo de hibridación se da cuando alrededor del átomo central existen cuatro regiones de elevada densidad electrónica. Puede presentarse en cuatro tipos de moléculas: XX Tipo AB4 sin pares electrónicos no compartidos en A Éste es el caso del metano, CH4, y también del CF4, CCl4, SiH4 y SiF4. Al examinar experimentalmente la molécula de, por ejemplo, CH4, se observa que los cuatro enlaces C–H son equivalentes y la molécula es apolar, a pesar de que los enlaces C–H son polares. La explicación que da a estos hechos la TEV es que cada átomo del grupo 14 (carbono en este caso) debe tener cuatro orbitales equivalentes. Para ello, el carbono ha de formar cuatro orbitales híbridos sp3 promoviendo uno de sus electrones 2s al orbital 2p vacío y mezclando o combinando el orbital 2s con los tres orbitales 2p. Este proceso origina cuatro electrones desapareados, tal como se ve en la Figura 12. Los cuatro orbitales híbridos sp3 se orientan hacia los cuatro vértices de un tetraedro regular. Los enlaces tendrán lugar por solapamiento de cada uno de los híbridos sp3 del carbono y el orbital 1s que tiene cada uno de los cuatro hidrógenos con un electrón desapareado (Figura 13). Figura 13. Geometría tetraédrica de la molécula de CH4. XX Tipo AB3E con un par electrónico no compartido en A En este apartado veremos moléculas como el amoníaco, NH3, y el NF3. Ambas moléculas son polares, su forma es piramidal y tienen un par electrónico no compartido en el átomo de nitrógeno. La configuración del nitrógeno es 1s2 2s2 2p3. Aquí no es necesaria la excitación previa de ningún electrón, ya que todos los orbitales están ocupados de antemano. ↑ C [He] ↑ 2p ↑ C [He] ↑↓ 2s promoción ↑ ↑ 2p ↑ 2s ↑ C [He] hibridación ↑ ↑ sp3 ↑ Figura 12. Promoción electrónica e hibridación sp3 del carbono. ↑ N [He] ↑↓ 2s ↑ ↑ 2p N [He] hibridación Figura 14. Esquema electrónico de la hibridación sp3 del nitrógeno. 18 ↑↓ ↑ ↑ sp3 ↑ tema 42 física y química Al producirse la hibridación, uno de los cuatro orbitales híbridos sp3 resultantes ya está lleno con dos electrones. Cada uno de los otros tres orbitales sp3 solapa con el orbital 1s de un átomo de hidrógeno en el caso del NH3 y con uno de los orbitales 2p de un flúor en el caso de la molécula NF3. N H H H Figura 15. Geometría piramidal del NH3. Los ángulos de enlace son menores que en el caso del CH4, ya que el par de electrones no compartidos repele a los pares enlazantes con mayor fuerza con la que éstos se repelen entre sí. Conviene distinguir entre la geometría electrónica o geometría orbital y la geometría molecular. La primera se refiere a la ordenación geométrica de los electrones de valencia alrededor del átomo central, y la segunda a la ordenación de los átomos, o sea, de los núcleos. Así, el CH4 y el NH3 tienen geometrías electrónicas tetraédricas, ya que en los dos casos hay cuatro pares de electrones alrededor del átomo central (ambas moléculas poseen hibridación sp3). Sin embargo, las geometrías moleculares del CH4 y del NH3 no son iguales. El CH4 tiene geometría molecular tetraédrica, mientras que el NH3 la tiene piramidal, derivada de las posiciones de los núcleos atómicos, no de los pares electrónicos. Sólo hay tres átomos de hidrógeno enlazados al nitrógeno. El par solitario de electrones del nitrógeno no se tiene en cuenta al describir la geometría molecular (Figura 15). XX Tipo AB2E2 con dos pares electrónicos no compartidos en A Los ejemplos más comunes de este tipo son H2O, H2S, N2O y OCl2. Todas estas moléculas son polares y angulares. En concreto veremos la molécula de agua, cuyo ángulo de enlace es de 104,5º y es muy polar. Las pruebas experimentales apuntan a la existencia de cuatro orbitales híbridos sp3; dos intervienen en el enlace y los otros dos sirven para acomodar los dos pares solitarios. Configuración del oxígeno en el estado fundamental: 1s2 2s2 2p2x 2p1y 2p1z Configuración del oxígeno con hibridación sp3: 1s2 2(sp3)2 2(sp3)2 2(sp3)1 2(sp3)1 La geometría electrónica es tetraédrica, pero los dos pares no compartidos se repelen entre sí y repelen a los dos pares enlazantes muy fuertemente. Estas fuerzas obligan a los pares enlazantes H a acercarse, haciendo que el ángulo de sp 3 enlace pase de 109,5º O (tetraedro) a los 104,5º O de la práctica. H H H 2O H Figura 16. Molécula de agua según la teoría de la hibridación. 19 tema 42 física y química Algunas veces, como ocurre con el H2S, aunque la geometría de la molécula puede explicarse mediante el mecanismo de la hibridación, puede prescindirse de ella. En efecto, en esta molécula los ángulos de enlace son de 92º y no es preciso postular orbitales híbridos. Los dos enlaces son casi perpendiculares entre sí, con ángulos cercanos a los 90º, que corresponden a los orbitales 3p del azufre. XX Tipo ABE3 con tres pares electrónicos no compartidos en A Éste es el caso del HF, HCl, HBr y HI. Todas ellas son muy polares y aunque su geometría molecular es obviamente lineal, su geometría electrónica es tetraédrica. Tomemos, por ejemplo, el HF. Al producirse la hibridación, tres de los cuatro orbitales híbridos sp3 se rellenan con pares no enlazantes y el otro es el que sirve para enlazar con el hidrógeno: La molécula de HF es muy polar, como cabe esperar de la gran diferencia de electronegatividades entre el flúor y el hidrógeno. Los tres pares solitarios de los orbitales híbridos sp3 contribuyen también a dicha polaridad. El enlace en el HF podría también intentar explicarse por el solapamiento del orbital 2p semiocupado del flúor y el orbital 1s del hidrógeno, sin recurrir al mecanismo de la hibridación. Sin embargo, de esta manera uno de los pares no compartidos quedaría en el orbital 2s de simetría esférica, lo que haría decrecer la polaridad de la molécula. Además, este modelo no satisfaría la TRPECV, que dice que los cuatro centros de alta densidad electrónica que hay alrededor del flúor se disponen con la máxima separación posible entre ellos. 3.4. Hibridación sp3d Este tipo de hibridación se da cuando alrededor del átomo central existen cinco regiones de alta densidad electrónica; puede presentarse en cuatro tipos de moléculas. XX Tipo AB5 sin pares electrónicos no compartidos en A A este caso pertenecen moléculas del tipo AB5, donde el elemento A es un elemento del grupo 15 excepto el nitrógeno, es decir, puede ser P; un ejemplo es el PF5, cuya molécula tiene forma de bipirámide trigonal. sp 3 F H HF Figura 17. Dos esquemas distintos de la hibridación y enlace en la molécula HF. 20 tema 42 física y química XX Tipo AB4E con un par electrónico no compartido en A Éste es el caso de moléculas como la del TeCl4. La geometría molecular es la de un tetraedro distorsionado, en concordancia con la TRPECV. XX Tipo AB3E2 con dos pares electrónicos no compartidos en A Un ejemplo de este tipo de moléculas es el ClF3. En este caso, como se comprueba también por la TRPECV, la molécula tiene forma de T. XX Tipo AB2E3 con tres pares electrónicos no compartidos en A Éste es el caso de la especie iónica I3–. Estas moléculas son lineales. 3.5. Hibridación sp3d2 Este tipo de hibridación tiene lugar cuando alrededor del átomo central existen seis regiones de elevada densidad electrónica. De las cinco posibilidades diferentes sólo se conocen los tres tipos siguientes: XX Tipo AB6 sin pares electrónicos no compartidos en A Un ejemplo lo constituye el hexafluoruro de azufre (SF6). Esta molécula es apolar y su forma es octaédrica. XX Tipo AB5E con un par electrónico no compartido en A Éste es el caso del IF5. Aquí el par no enlazante se sitúa en uno cualquiera de los vértices del octaedro. La geometría de la molécula es la de una pirámide, con el yodo en el centro de la base. XX Tipo AB4E2 con dos pares electrónicos no compartidos en A Un ejemplo de estas moléculas es el ICl4–. En ella, los dos pares no enlazantes se sitúan en esquinas opuestas del octaedro, haciendo que la forma de la molécula sea plano-cuadrada. 3.6. Moléculas con enlaces múltiples 3.6.1. Compuestos con dobles enlaces: eteno (C2H4) En este apartado utilizaremos como ejemplo específico el enlace doble carbonocarbono en el eteno o etileno, C2H4. Las pruebas experimentales indican que la molécula es plana, con ángulos de enlace de 120º. Cada carbono se encuentra en el centro de un plano triangular. Según su estructura de Lewis, tendríamos la molécula con la siguiente fórmula molecular: H H H—C=C—H 21 tema 42 física y química La teoría RPECV trata cada átomo de C como si estuviera rodeado por tres grupos de electrones en una ordenación trigonal plana. Esta teoría no indica que los dos grupos –CH2 sean coplanares, pero, como veremos, la teoría de enlace de valencia sí lo hace. La hibridación que se produce en ellos es del tipo sp2 entre los orbitales 2s, 2px y 2py, quedando otro electrón en el orbital 2pz, perpendicular al plano de los tres híbridos sp2. De los tres orbitales híbridos que se producen, dos enlazan con sendos átomos de hidrógeno, y el otro con el otro carbono. Tomando la terminología de la teoría de los orbitales moleculares, este enlace entre los orbitales híbridos de los dos carbonos se llama enlace sigma (σ) y se produce por solapamiento de los orbitales atómicos a lo largo de la línea internuclear, como se muestra en la Figura 18. El enlace entre los otros dos híbridos y los orbitales 1s de cada hidrógeno también es de tipo σ. El enlace entre los orbitales 2pz de los carbonos tiene lugar de forma lateral por encima y por debajo de la línea internuclear y da lugar a lo que se llama un enlace pi (π). Ambos enlaces, σ y π, forman un enlace doble. Una característica interesante del doble enlace es su rigidez torsional, no presenta rotación libre debido al solapamiento de los dos orbitales p. Si se efectúa trabajo para distorsionar la configuración plana, el enlace se debilita. Esto se consigue con poca energía, lo cual explica la reactividad del doble enlace. Se produce una sustitución de un enlace por otro, con lo Enlaces σ Enlaces π que la energía del sistema disminuye. 3.6.2. Compuestos con enlaces triples: etino (C2H2) Un ejemplo de molécula con este tipo de enlace lo constituye el etino, de fórmula C2H2. En esta molécula hay un enlace triple entre los dos carbonos. H 120º Orbital 2p La molécula es lineal (ángulos de enlace de 180º), lo que se corresponde con una hibridación del tipo sp; quedan semiocupados los orbitales 2py y 2pz, que son perpendiculares entre sí y perpendiculares a su vez a los dos orbitales híbridos sp. Cada uno de los orbitales híbridos de cada carbono origina dos enlaces, uno con otro de los híbridos del otro carbono y el segundo con el orbital 1s de uno de los hidrógenos. Además, se forman dos enlaces entre los orbitales 2py y 2pz de los dos carbonos, como se muestra en la Figura 19. 22 H H Orbital sp2 Figura 18. Formación del enlace doble en la molécula de eteno. Enlaces π 180º Enlaces π Enlaces σ Figura 19. Formación del enlace triple en la molécula de etino. tema 42 física y química 3.7. La resonancia en la teoría EV La teoría de enlace de valencia contempla una distinción entre los electrones de valencia que siguen perteneciendo exclusivamente a cada átomo y los que participan en el enlace. Estos últimos contribuyen a la existencia de una alta densidad de carga negativa en el espacio comprendido entre dos átomos. Precisamente a esa acumulación de carga entre dos átomos se atribuye el enlace. Esa carga acumulada puede responder a un par de electrones (enlace simple), a dos pares (enlace doble) o a tres pares (enlace triple). La intensidad y longitud del enlace dependen del número de electrones que participen en él. Al aumentar el número de electrones, la distancia del enlace se hace más corta y su energía aumenta. En todo caso, los electrones se encuentran localizados, bien en los átomos, o bien en el espacio comprendido entre ellos. Sin embargo, surgieron problemas al tratar de aplicar estas teorías a un número relativamente grande de moléculas, porque era posible asignarles más de una estructura. La solución a estos problemas se resolvió introduciendo el concepto de resonancia. La aplicación de dicho concepto establece que la estructura de la molécula en el estado fundamental no está representada por ninguna de esas estructuras, compatibles todas ellas con la teoría del enlace, sino por otra que consiste en un estado intermedio o de resonancia entre todas ellas. La molécula, por tanto, vibra entre todas esas formas concretas, denominadas formas canónicas. Desde el punto de vista matemático, una estructura resonante entre varias se describe como una combinación lineal de ellas. La selección de las estructuras hipotéticas a partir de las cuales, mediante una combinación lineal, se obtiene la verdadera estructura, no se hace de una forma arbitraria. Las estructuras que contribuyen de una manera efectiva son aquellas que: Tienen energías semejantes. Sus núcleos ocupan las mismas posiciones relativas. Tienen el mismo número de electrones desapareados. 23 tema 42 física y química 4 Teoría de orbitales moleculares (TOM) 4.1. Introducción Las estructuras de Lewis, la teoría RPECV y el método de enlace de valencia forman una poderosa combinación para describir el enlace covalente y las estructuras moleculares. Los resultados son buenos para la mayor parte de los casos, pero a veces es necesaria una mayor comprensión de las estructuras y las propiedades de lo que estos métodos proporcionan. Por ejemplo, ninguno de estos métodos proporciona una explicación de los espectros electrónicos de las moléculas, de porqué el oxígeno es paramagnético o por qué el H2+ es una especie estable. Para responder a estas cuestiones necesitamos describir el enlace químico mediante un método diferente. Hund y Mulliken propusieron una teoría diferente para el enlace covalente conocida como teoría de los orbitales moleculares (TOM). Esta teoría comienza considerando ya a los núcleos en su distancia internuclear de equilibrio, es decir, considera a la molécula ya formada. Este sistema que llamamos molécula posee electrones que ocuparán unos determinados niveles energéticos cuantizados. Éstos son niveles moleculares, no atómicos, ya que estos últimos han perdido su identidad como tales. Los niveles energéticos moleculares u orbitales moleculares (OM) son orbitales multicéntricos que se extienden sobre dos o más núcleos. El método de los orbitales moleculares considera a la molécula como un todo, como un «átomo polinuclear» y le aplica los métodos mecanocuánticos conocidos. Por tanto, no es más que una repetición, en una escala más complicada, del procedimiento usado en la construcción de la estructura electrónica de los átomos, que se apoya en tres supuestos fundamentales: 24 Cada uno de los electrones de una molécula puede describirse mediante una función de onda ψ. A cada orbital molecular le corresponde una energía. Es posible, al igual que ocurría en los orbitales atómicos, que existan varios orbitales moleculares degenerados, es decir, a los que les corresponde la misma energía. Para determinar la estructura electrónica de una molécula se calculan en primer lugar las energías de los diferentes orbitales moleculares y a continuación se sigue el principio del Aufbau introduciendo electrones en esos orbitales moleculares sin violar el principio de exclusión de Pauli y teniendo en cuenta la regla de máximo desapareamiento de Hund en el estado fundamental. tema 42 física y química 4.2. Simetría y notación de los ORBITALES MOLECULARES Los orbitales moleculares se obtienen mediante combinación lineal de los orbitales atómicos (CLOA). Sin embargo, no siempre es posible la combinación lineal de orbitales atómicos para obtener OM. Aquéllos han de cumplir una serie de requisitos para poder combinarse. En general, las condiciones que deben cumplir los orbitales atómicos para que puedan dar lugar a orbitales moleculares son: 1. Deben solapar lo más posible. 2. Deben tener la simetría apropiada. Debido a este condicionamiento es posible la combinación de un orbital s y un orbital px (eligiendo como eje internuclear el eje X), pero no es posible la CLOA entre un orbital s y un orbital py o pz. En este caso la integral de solapamiento vale cero. 3. Deben tener energías del mismo orden. En el caso de moléculas homonucleares, los orbitales iguales de ambos átomos tienen la misma energía. En el caso de moléculas heteronucleares, hay que conocer la energía de los distintos orbitales de ambos átomos antes de aventurarse a combinarlos. El caso más sencillo es la molécula de H2, donde la combinación de dos orbitales atómicos 1s da lugar a dos orbitales moleculares en una molécula H2. Uno de los orbitales moleculares, denominado σ1s, tiene una energía menor que los orbitales atómicos 1s. A este OM se le denomina orbital molecular enlazante, porque describe una densidad de carga electrónica alta entre los dos núcleos. Una densidad de carga electrónica alta entre los núcleos reduce las repulsiones entre los núcleos cargados positivamente y provoca la formación de un enlace más fuerte. El otro orbital molecular, denominado σ∗1s, tiene una energía mayor que los orbitales atómicos 1s, y se denomina orbital molecular antienlazante. Cuando la densidad electrónica está distribuida a lo largo de la línea internuclear, como en este caso, a los orbitales moleculares se les denomina tipo σ, y como provienen de dos orbitales 1s se les denomina orbitales moleculares σ1s. En el enlazante la máxima densidad electrónica se localiza entre los dos núcleos; por lo tanto, los electrones que se encuentren en él tienden a mantener unidos a los núcleos y contribuyen a la estabilidad de la molécula. En el antienlazante, que se simboliza con un asterisco como superíndice (σ*), la máxima densidad electrónica está fuera de la región siψ = (1s ) + (1s ) tuada entre los núcleos. En conse+ + cuencia, los electrones colocados • • dentro de este orbital molecular 1s 1s producen inestabilidad en la molé+ + • • cula. Como es de esperar, también + es posible dibujar orbitales de este + – tipo para la combinación de cual• • quier par de orbitales atómicos ns. a a b σ 1s enlazante • • b ψ = (1sa) + (1s b) = (1s a) + (–asb) • • σ*1s antienlazante Figura 20. Representación de la geometría de los orbitales σ1s y σ*1s. 25 tema 42 física y química 2p x 2p x Los orbitales p también pueden combinarse para dar lugar a los correspondientes orbitales moleculares. Se ha escogido arbitrariamente hacer corresponder al eje internuclear con el eje x del sistema de coordenadas. Con este convenio, puede observarse que la combinación de los orbitales px da lugar a dos orbitales σ, enlazante y antienlazante. En cambio, la combinación σ de py con py (Figura 21) o pz con pz da lugar a sendas parejas de orbitales moleculares que σ surgen como consecuencia de un solapamiento lateral. En ellos la densidad electrónica no se localiza a lo largo de la línea internuclear, sino en dos regiones por encima π y por debajo de la misma: en el enlazante, en la zona comprendida entre los núcleos, y en el antienlazante, fuera de la región comprendida entre ellos. A los orbitales moleculares que tienen esta simetría se les denomina π tipo π. * 2p x 2p x 2p y 2p y * 2p y 2p y Figura 21. Formación de orbitales moleculares a partir de los orbitales atómicos p. El solapamiento (matemáticamente la combinación lineal) de orbitales d da lugar, igualmente, a orbitales moleculares con ambos tipos de simetría. 4.3. Orden de energías de los orbitales moleculares Con el fin de poder aplicar el principio del Aufbau molecular para establecer las configuraciones electrónicas moleculares, es necesario conocer el orden de energía de los diferentes orbitales moleculares. Para ello se resuelve de forma aproximada la ecuación de onda de Schrödinger que lleva de forma natural a la definición de unos parámetros n, l, y λ semejantes a los números cuánticos atómicos y que definen los correspondientes estados energéticos. En la determinación del orden de energía creciente de los orbitales moleculares existen tres reglas generales útiles: 1. La energía de los orbitales moleculares está fuertemente influenciada por la energía de los orbitales atómicos con los que están relacionados. 2. Si dos orbitales atómicos están confinados en su mayor parte a regiones cercanas a sus respectivos núcleos atómicos y, por tanto, no se solapan extensamente, los orbitales moleculares que se forman a partir de ellos no serán ni fuertemente enlazantes ni fuertemente antienlazantes. 3. Si los orbitales atómicos se solapan extensamente, el orbital molecular enlazante tendrá una energía bastante menor que la de los orbitales atómicos y su compañero antienlazante tendrá correspondientemente una energía bastante más alta que la de ellos. La descripción cuantitativa de las energías de los orbitales moleculares puede lograrse únicamente de forma experimental o, en casos favorables, por extensos cálculos mecanocuánticos. Cada molécula y cada ión tienen su patrón de niveles 26 tema 42 física y química de energía que les es propio y único. Sin embargo, se pueden hacer ciertas generalizaciones útiles y para moléculas diatómicas homonucleares con número total de electrones inferior o igual al N2 se obtiene (Figura 22 b): σ1s < σ*1s < σ2s < σ*2s < π2py = π2pz < σ2px < π*2py = π*2pz < σ*2px Para moléculas con mayor número de electrones el esquema varía ligeramente, invirtiéndose el orden de energías de los orbitales moleculares σ2px y π2py , π2pz (Figura 22 a) manteniéndose intacto el resto de la representación: σ1s < σ*1s < σ2s < σ*2s < σ2px < π2py = π2pz < π*2py = π*2pz < σ*2px La teoría de orbitales moleculares se puede usar también para predecir el orden aproximado de las energías de enlace (o energía de disociación en el caso de moléculas diatómicas) a través del orden de enlace (o. e.), que se define mediante la ecuación: Orden de enlace nº e- en OM enlazantes nº e- en OM antienlazantes 2 Sin embargo, la energía de enlace depende de otros factores, además del orden de enlace. Entre estos factores, se encuentran la carga nuclear efectiva de los núcleos, el carácter más o menos difuso de los orbitales y la presencia de mayor o menor número de electrones antienlazantes, que desestabilizan la molécula. De este modo, no es de extrañar que moléculas con el mismo orden de enlace presenten diferentes energías de enlace. Los órdenes de enlace iguales a 1, 2 y 3 equivalen, de forma aproximada, al enlace sencillo, doble y triple de la teoría de EV. Sin embargo, la teoría de orbitales moleculares contempla enlaces intermedios entre ellos, cosa que no ocurría en las anteriores teorías. A mayor orden de enlace, mayor energía E σ* σ* de enlace y mayor estabilidad de la molécula. π* π* π* π* 2p y 2p z 2p y 2p z 2p 2p σ 2p πy πz πy πz σ 2p σ*2s 2s σ*2s 2s 2s 2s σ 2s σ 2s (a) (b) Figura 22. Diagramas de energía de los orbitales moleculares para las moléculas con orbitales 2s de baja energía (a) y para el nitrógeno y moléculas diatómicas más ligeras (b). 27 tema 42 física y química 5 Estructura y propiedades de las sustancias covalentes Dentro de las sustancias covalentes es necesario distinguir entre aquellas en las que los enlaces covalentes se extienden a toda la masa de la sustancia, de manera que se origina una macromolécula, y aquellas otras en las cuales los enlaces covalentes se dan entre un determinado número de átomos vecinos, formando moléculas discretas que se repiten para formar la masa total del compuesto. Tanto las propiedades de unas como de otras se estudian mejor partiendo del estado sólido. En los sólidos covalentes, llamados también sólidos atómicos, las unidades que ocupan los puntos de la red cristalina son átomos unidos mediante enlaces covalentes que se extienden, en general, en las tres direcciones del espacio. Hay que tener cuidado en no confundirlos con los cristales moleculares de sólidos moleculares, cuyas «moléculas» son en realidad átomos o moléculas «monoatómicas», como los gases inertes. Uno de los casos más conocidos de cristal atómico es el cristal de diamante (Figura 23), en donde cada átomo de carbono está ligado covalentemente a otros cuatro átomos. Cada carbono presenta hibridación sp3 y ocupa el centro de un tetraedro, en cuyos vértices se encuentran otros cuatro átomos de C con los que se encuentra unido. El resultado es una malla rígida tridimensional, que une a cada uno de los átomos con todos los otros. En efecto, la totalidad del cristal es una sola molécula. Debido a que todos los enlaces C-C son muy fuertes, el diamante se caracteriza por su gran dureza (dureza 10 en la escala de Mohs), su elevadísimo punto de fusión y su insolubilidad en cualquier disolvente. Es muy mal conductor de la electricidad, ya que los electrones se encuentran localizados entre cada par de átomos vecinos, formando enlaces covalentes. Un ejemplo semejante lo constituye el cuarzo (SiO2). Cada átomo de silicio presenta hibridación sp3, ocupa el centro de un tetraedro y se une covalentemente a los cuatro átomos de oxígeno que ocupan los vértices. Cada átomo de oxígeno se encuentra unido a dos átomos de silicio, es decir, forma parte de dos tetraedros. Esta disposición se extiende hasta el infinito en las tres direcciones, de manera que no existen moléculas discretas de fórmula SiO2, como pudiera pensarse a la vista de la formulación del compuesto. La fórmula SiO2 corresponde a la composición neta de la celda elemental, el tetraedro: Si + 4(½O). Figura 23. Estructura del diamante. 28 tema 42 física y química En algunos cristales los enlaces covalentes sólo se extienden en dos direcciones, constituyendo redes covalentes bidimensionales infinitas. El ejemplo más conocido es el de la estructura del grafito, mostrada en la Figura 24. Cada átomo de carbono presenta hibridación sp2 y está ligado covalentemente a otros tres, de tal manera que todos los átomos que hay en un solo plano se enlazan formando una estructura laminar. En el cristal de grafito, estas láminas infinitas de átomos están reunidas, formando una estructura en donde las fuerzas de atracción entre las diferentes capas son del tipo de Van der Waals. La longitud del enlace C-C de las láminas es del mismo orden que en el benceno (0,142 nm). En cambio, la distancia entre capa y capa es mucho mayor (~0,35 nm). Las propiedades derivadas son fáciles de entender: el grafito es perfectamente exfoliable, ya que es fácil separar una capa de otra. Es untuoso al tacto y buen conductor de electricidad. Su densidad es menor que la del diamante y su dureza mucho menor (1-2 en la escala de Mohs). Se utiliza como lubricante en seco, para fabricar minas de lápices y como moderador de neutrones en algunos reactores nucleares. Finalmente, es posible que los enlaces covalentes entre átomos se orienten en una determinada dirección del espacio, dando lugar a largas cadenas lineales. Un ejemplo característico lo constituye una de las formas alotrópicas del azufre, denominado azufre plástico, y compuestos como el disulfuro de silicio, SiS2. Estos materiales, al igual que las sustancias iónicas, poseen puntos de fusión muy altos, pues cualquier cambio físico en un sólido covalente implica la rotura de enlaces covalentes, lo cual requiere cantidades considerables de energía. Además, los sólidos covalentes tridimensionales son los más duros e incompresibles de todos los materiales. Con respecto a la volatilidad y a las propiedades mecánicas, los cristales covalentes son similares a los sólidos iónicos. Los enlaces son tan fuertes y direccionales que es necesaria mucha energía para romperlos o despedazarlos. Finalmente, en este tipo de estructura no hay iones móviles o electrones, de modo que estos sólidos son no conductores eléctricos típicos. En realidad, la conductividad de un sólido covalente es nula a 0 K. A temperaturas mayores de 0 K, si bien es observable, en general es muy pequeña; aunque puede aumentar a medida que la temperatura se eleva, no sube en forma brusca cuando funde la sustancia. Existen excepciones, como el grafito. Este sólido es conductor en la dirección de la estructura laminar debido a la deslocalización de los electrones de los orbitales π no hibridados. Figura 24. Estructura atómica del grafito. 29 tema 42 física y química CONCLUSIÓN El enlace iónico es fuerte y direccional, y tiende a formar estructuras cristalinas infinitas con el empaquetamiento máximo que permita la relación de radios, el tamaño de los iones y el cumplimiento de ciertas reglas de geometría de modo que las fuerzas atractivas sean máximas y las repulsivas mínimas. La fuerza de estas estructuras cristalinas la determina la energía reticular (U) de la red, que puede determinarse experimentalmente de forma indirecta siguiendo el ciclo de Born-Haber. Los sólidos iónicos tienen propiedades particulares; las más importantes son los altos puntos de fusión y ebullición, que son duros y quebradizos y que son conductores cuando están disueltos o fundidos. Los sólidos iónicos en disolución pueden ser identificados siguiendo procesos analíticos complejos de identificación de aniones y cationes y su uso es muy diverso dependiendo de la naturaleza del compuesto. 30 tema 42 física y química BIBLIOGRAFÍA BIBLIOGRAFÍA COMENTADA BROWN, T. L.; LEMAY, H. E. y BURSTEN, B. E. (1998): Química. La ciencia central. México: Prentice Hall. Libro que proporciona una introducción sencilla de los conceptos de la química. CHANG, R. (2003): Química general. México: McGraw-Hill. Texto de química general que expone de forma clara las diferentes teorías del enlace químico. PETRUCCI, R. H. y HARWOOD, W. S. (1998): Química General. Principios y aplicaciones modernas. México: Prentice Hall. Esta obra contiene numerosos ejemplos que proporcionan a los estudiantes una aplicación inmediata de los principios ilustrados en el texto. WEBGRAFÍA http://www.wikipedia.org http://es.wikipedia.org/wiki/Imagen:Diamonds_glitter.png http://es.wikipedia.org/wiki/Grafito 31 tema 42 física y química RESUMEN Enlace covalente: orbitales moleculares. Diagramas de energía. Geometría molecular. Estructura y propiedades de las sustancias covalentes. 1. Teoría de la repulsión entre pares de electrones de la capa de valencia (RPECV) 1.1. Formas moleculares La forma global de una molécula está determinada por los ángulos de enlace. Tipos: AX2, AX3, AX4. 1.2. El modelo RPECV Esta teoría explica eficazmente las formas de las moléculas que contienen pares de electrones localizados. Cuando existen pares enlazantes exclusivamente, la geometría molecular coincide con la geometría de los enlaces. Cuando también existen pares solitarios no ocurre lo mismo y hay que diferenciar ambas geometrías. 3. Hibridación de orbitales atómicos 3.1. Orbitales híbridos sp Un orbital atómico s + un orbital atómico p. Geometría lineal: BeCl2 3.2. Orbitales híbridos sp2 Un orbital atómico s + dos orbitales atómicos p. Geometría angular: BCl3 3.3. Orbitales híbridos sp3 Un orbital atómico s + tres orbitales atómicos p. Geometría tetraédrica: CH4 3.4. Orbitales híbridos sp3d 2. Teoría del enlace de valencia (TEV) 2.1. Introducción 2.2. Teoría EV La condición para la formación de un enlace estable viene dada por el hecho de que, a una determinada distancia internuclear, la energía del sistema alcance un mínimo, por supuesto menor que la energía de los átomos aislados. 2.3. Polaridad del enlace Decimos que una molécula es polar si sus centros de carga negativa y positiva no coinciden. Un orbital atómico s + tres orbitales atómicos p + un orbital atómico d Casos: AB5, AB4E, AB3E2, AB2E3 3.5. Orbitales híbridos sp3d2 Un orbital atómico s + tres orbitales atómicos p + dos orbitales atómicos d Casos: AB6, AB5E, AB4E2 3.6. Moléculas con enlaces múltiples 3.6.1. Compuestos con dobles enlaces: eteno (C2H4) La hibridación que se produce en ellos es del tipo sp2 entre los orbitales 2s, 2px y 2py, quedando otro electrón en el orbital 2pz, perpendicular al plano de los tres híbridos sp2. 33 tema 42 física y química 3.6.2. Compuestos con enlaces triples: etino (C2H2) La molécula es lineal (ángulos de enlace de 180º), lo que se corresponde con una hibridación del tipo sp; quedando semiocupados los orbitales 2py y 2pz, que son perpendiculares entre sí y perpendiculares a su vez a los dos orbitales híbridos sp. 3.7. La resonancia en la teoría EV La estructura de la molécula en el estado fundamental no está representada por ninguna estructura en concreto, sino por otra que consiste en un estado intermedio o de resonancia entre todas las posibles estructuras. 4. Teoría de orbitales moleculares (TOM) 4.1. Introducción 4.2. Simetría y notación de los OM El caso más sencillo es la molécula de H2, donde la combinación de dos orbitales atómicos 1s da lugar a dos orbitales moleculares en una molécula H2. Uno de los orbitales moleculares, denominado σ1s, tiene una energía menor que los orbitales atómicos 1s, y se denomina orbital molecular enlazante, y otro denominado σ∗1s, que tiene una energía mayor que los orbitales atómicos 1s, y se denomina orbital molecular antienlazante. 34 4.3. Orden de energías de los OM Cada molécula y cada ión tienen su patrón de niveles de energía que les es propio y único. Sin embargo, se pueden hacer ciertas generalizaciones útiles y para moléculas diatómicas homonucleares. La teoría de OM se puede usar también para predecir el orden aproximado de las energías de enlace (o energía de disociación en el caso de moléculas diatómicas) a través del orden de enlace. 5. Estructura y propiedades de las sustancias covalentes En los sólidos covalentes las unidades que ocupan los puntos de la red cristalina son átomos unidos mediante enlaces covalentes que se extienden, en general, en las tres direcciones del espacio. Ejemplos: diamante, grafito, cuarzo. tema 42 física y química AUTOEVALUACIÓN 1. Los resultados inmediatos de la resolución de la ecuación de onda de Schrödinger para átomos y moléculas, a partir de los cuales se obtienen otras propiedades, son: a) Momentos dipolares. b) Diagramas de densidad electrónica. c) Órdenes de enlace. d) Energía y función de onda del sistema. 2. En los iones moleculares BC+, C2+ y CN+, los orbitales moleculares π2p tienen menor energía que los σ2p. ¿Qué cabe esperar para estos iones?. a) Que todos tengan el mismo orden de enlace. b) Que todos sean diamagnéticos. c) Que todos sean paramagnéticos. d) Que sólo sean paramagnéticos BC+ y C2+. 3. Basándonos en la teoría de orbitales moleculares se puede afirmar que: a) La energía de enlace de la molécula FN es mayor que la de FN+. b) La distancia de enlace de FN es mayor que la de FN–. c) La energía de enlace de FN– es menor que la de FN. d) En FN hay un enlace σ y dos enlaces π. 4. De las moléculas CN, N2, NO y O22+ se podría predecir, según el modelo de orbitales moleculares, que la de menor energía de ionización es: a) CN b) NO c) N2 d) O22+ 5. En el CH4, las cuatro longitudes de enlace C-H son iguales. Entonces cabe esperar que: a) La molécula sea cuadrada, con el C en el centro. b) La molécula sea tetraédrica, con el C en el centro. c) La molécula sea piramidal cuadrangular. d) El C presente hibridación sp2. 35 tema 42 física y química 6. En la molécula de formaldehído, H2C=O, la forma geométrica de la molécula, donde el C utiliza orbitales híbridos sp2, debe ser: a) Plana, con el C en el centro de un triángulo equilátero cuyos vértices son los otros átomos. b) Plana, con el C en el centro de un triángulo isósceles cuyos vértices son los otros átomos. c) Tetragonal irregular, con cada átomo en un vértice del polígono. d) El C ocupa el centro de un sistema cartesiano ortogonal cuyos ejes son dos enlaces C-H y uno C-O. 7. En la molécula HgCl2, la hibridación del átomo central y la geometría de la molécula, son, respectivamente: a) sp2, angular. b) sp3, angular. c) sp, lineal. d) sp3d, lineal. 8. De la molécula XCl3 se tienen los siguientes datos: 1) es polar y 2) tiene un ángulo de enlace Cl-X-Cl de 180º y dos ángulos de enlace Cl-X-Cl de 90º. Por tanto, se puede afirmar que: a) X no tiene pares electrónicos solitarios. b) X tiene un par electrónico solitario. c) X tiene dos pares electrónicos solitarios. d) X tiene tres pares electrónicos solitarios. 9. La molécula de CO2 tiene orbitales π deslocalizados. ¿Cuál de los siguientes hechos, todos ciertos, no implica deslocalización de electrones?: a) La molécula es lineal. b) La energía de enlace es igual a 383 Kcal/mol CO2. c) La longitud de enlace es igual a 1,16 Å. d) La energía de resonancia es 33 Kcal/mol CO2. 10. ¿En cual de las siguientes moléculas no podríamos explicar sos constantes físicas sin considerar las estructuras resonantes?: a) H2C=CH2 (distancia C-C 1,34 Å). b) H2N=NH2 (distancia N-N 1,47 Å). c) CO (distancia C-O 1,13 Å). d) O3 (distancia O-O 1,28 Å). 36