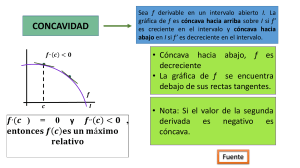
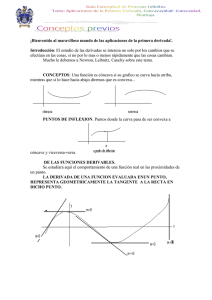
En algunos sitios me he encontrado que una función es cóncava en un punto cuando f''(x)>0 mientras que en otros, al revés. ¿Podrías aclararme cuando es cóncava y convexa una función, y hacia donde está la curvatura en cada caso? FUNCIÓN CÓNCAVA Una función y=f(x) es cóncava en el intervalo (a,b) si los puntos de la misma están por arriba de los puntos de la tangente a curva en un punto interior de dicho intervalo. La función y = f(x) es cóncava si f ’’(x) > 0. FUNCIÓN CONVEXA Una función y=f(x) es convexa en el intervalo (a,b) si los puntos de la misma están por debajo de los puntos de la tangente a la curva en un punto cualquiera de dicho intervalo. La función y = f(x) es convexa si f ’’(x) < 0.
