[1] [2] [3] [4] [5]PLL – lazo de fijación de fase
Un lazo de fijación de fase (PLL, siglas en inglés de phase locked loop), inventado por el ingeniero
francés Henri de Bellescize en 1932; es un circuito que permite que una señal de referencia
externa controle la frecuencia y la fase de un oscilador, contando para ello con una
realimentación que compara la fase de las dos señales y actúa modificando la frecuencia de la
señal oscilante generada por el oscilador.
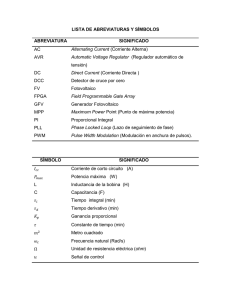
Diagrama esquemático de un lazo de fijación de fase
Como parte del circuito PLL, se utiliza un oscilador controlado por tensión (VCO, siglas en inglés),
que es un oscilador que varía su frecuencia (no su fase) en función de la tensión aplicada a su
entrada.
El comparador de fase produce una señal KD⋅Δϕ proporcional a la diferencia de fase entre la
señal de entrada v1 y la señal v2 generada por VCO que, amplificada por el amplificador, se
aplica a la entrada vc del VCO. Esto produce una frecuencia f2 que varía linealmente con vc. Las
señales se sintonizan cuando la señal KD⋅Δϕ amplificada, al ser aplicada al VCO, hace que éste
oscile exactamente a la misma frecuencia que la entrada. En efecto, si fuera, por ejemplo, f1 >
f2, la diferencia de fase iría en aumento, lo cual haría que f2 aumentara, tendiendo a acercarse
a f1; y a la inversa si f1 < f2.
Análisis de PLL
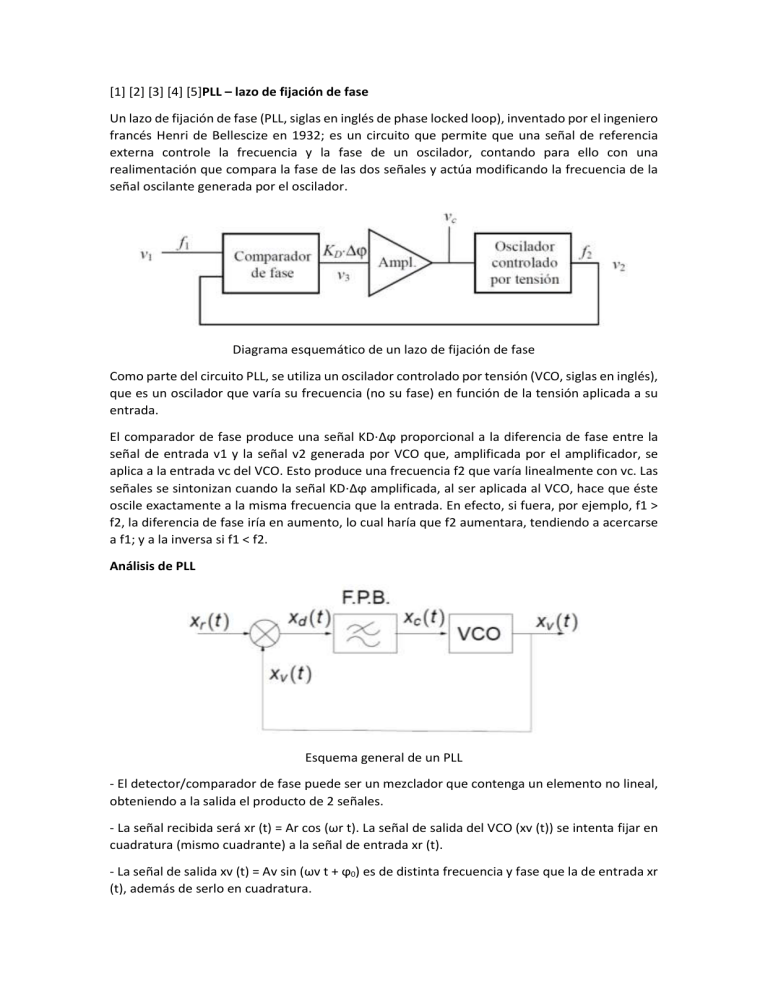
Esquema general de un PLL
- El detector/comparador de fase puede ser un mezclador que contenga un elemento no lineal,
obteniendo a la salida el producto de 2 señales.
- La señal recibida será xr (t) = Ar cos (ωr t). La señal de salida del VCO (xv (t)) se intenta fijar en
cuadratura (mismo cuadrante) a la señal de entrada xr (t).
- La señal de salida xv (t) = Av sin (ωv t + ϕ0) es de distinta frecuencia y fase que la de entrada xr
(t), además de serlo en cuadratura.
El término ϕ0 es el error de fase o diferencia de fase respecto a la cuadratura de la señal de
entrada.
A la salida del detector de fase se tiene:
𝑥𝑑 (𝑡) = 𝑥𝑟 (𝑡) ∗ 𝑥𝑣 (𝑡)
𝑥𝑑 (𝑡) = Ar cos(ωrt) ∗ 𝐴𝑣 𝑠𝑒𝑛(𝜔𝑣𝑡 + φ0)
𝑥𝑑(𝑡) =
𝐴𝑟 ∗ 𝐴𝑣
{𝑠𝑒𝑛((𝜔𝑣 − ωr)𝑡 + φ0) + 𝑠𝑒𝑛((𝜔𝑣 + ωr)𝑡 + φ0)}
2
Habrá enganche en frecuencia entre el VCO y la señal recibida cuando: (𝜔𝑣 = ωr)
𝑥𝑑(𝑡) =
𝐴𝑟 ∗ 𝐴𝑣
{𝑠𝑒𝑛(φ0) + 𝑠𝑒𝑛((2ωr)𝑡 + φ0)}
2
Al pasar el filtro pasa bajo de lazo se elimina el término de frecuencia doble 2ωr
xd(t) =
𝐴𝑣 ∗ 𝐴𝑟
sen(φ0)
2
Si el error de fase es pequeño entonces sen(ϕ0) → ϕ0
xd(t) =
𝐴𝑣 ∗ 𝐴𝑟
φ0
2
La señal a la salida del detector de fase es proporcional a la diferencia de fase entre las dos
señales. El proceso continúa hasta que las fases de las dos señales se igualan, momento en el
que el circuito está enganchado en fase.
Estados de funcionamiento
Estado de corrida libre
Esta condición ocurre cuando no hay señal de entrada o hay una señal de entrada a la cual el
lazo no tiene posibilidades de enganchar. En esta condición, generalmente el voltaje de entrada
al VCO es igual a 0 Vc= VDD/2, cuando el chip es alimentado con una fuente de tensión VDD no
partida.
Estado fijo
Es el que corresponde cuando el lazo está enganchado en fase, frecuencia de señal de referencia
fs=f0 frecuencia de señal del oscilador, salvo una diferencia finita de fase θd(diferencia entre
fases θs-θ0).
Rangos de funcionamiento
Vd=voltaje de entrada de VCO
ff=frecuencia de corrida libre, determinada por la red RC o LC.
2fc=rango de captura
2fp=rango de tracción
2fL=rango de seguimiento o enganche
Siempre se cumple que 2fc < 2fp < 2fL
El rango de seguimiento 2fL no depende de las características del filtro. Los límites superior y/o
inferior quedan definidos por el dispositivo que primero se sature, puede ser el comparador de
fase, el VCO o algún otro dispositivo activo del lazo.
Dentro del rango de captura sólo es posible un estado de equilibrio, correspondiente al PLL
enganchado. Fuera del rango de captura, pero dentro del rango de enganche, son posibles dos
situaciones: enganchado u oscilando a la frecuencia libre, dependiendo si se entra en esa región
estando el PLL enganchado o no. Finalmente, fuera del rango de enganche, sólo funcionará
desenganchado.
Rechazo a ruido
El PLL puede se utiliza como herramienta para recuperar o demodular señales o portadoras
inmersas en ruido. Esto causa en el PLL la aparición de fluctuaciones de fase aleatorias
denominadas jitter. Éste también se traduce en variaciones de frecuencia. Si las fluctuaciones
de fase son suficientes para sacar al detector de fase de su zona operativa (entre 0 y π) se
produce el desenganche, perdiéndose el sincronismo entre la entrada y la salida del VCO. Para
garantizar que el enganche se produzca y mantenga, será necesario que la relación señal a ruido
sea mayor que 6 dB.
Función de transferencia del PLL
En los PLL, algunos valores de reposo no están vinculados en forma lineal. Por lo que se buscará
un modelo equivalente lineal válido únicamente en un restringido rango de operación.
Función de transferencia del detector
𝑉𝑒(𝑡) = 𝑘𝑑 𝜃𝑑 (𝑡), 𝑉𝑒(𝑠) = 𝑘𝑑 𝜃𝑑 (𝑠) ∴
𝑉𝑒(𝑠)
= 𝑘𝑑
𝜃𝑑 (𝑠)
Función de transferencia del VCO
𝜔0 (𝑡) = 𝑘𝑑 𝑉𝑑 (𝑡)
𝜔0 =
𝑑𝜃0 (𝑡)
∴ 𝜃0 (𝑡) = ∫ 𝜔0 (𝑡) 𝑑𝑡
𝑑𝑡
𝜃0 (𝑡) = 𝑘𝑜 ∫ 𝑉𝑑 (𝑡) 𝑑𝑡
𝜃0 (𝑠) =
𝑘𝑜
𝑉 (𝑠)
𝑠 𝑑
El VCO, actúa para la fase como un integrador, por lo tanto, ningún error estático (Ve y θd)
puede mantenerse en el tiempo debido a este efecto.
Función de transferencia total
Combinando todos los bloques constitutivos se obtiene la función de transferencia:
𝜃𝑜
𝐴(𝑠)
=
𝜃𝑠 1 + 𝐴(𝑠)𝛽(𝑠)
𝜃𝑜
=
𝜃𝑠
𝑘𝑑 𝑘𝑜 𝐹(𝑠)
𝑘𝑑 𝑘𝑜 𝐹(𝑠)
𝑠
=
𝑘 𝑘𝑜 𝐹(𝑠)
𝑘 𝑘 𝐹(𝑠)
1 + 𝑑 𝑠𝑁
𝑠 + 𝑑 𝑜𝑁
Filtro pasabajos (FPB)
Los filtros pasabajos más comunes usados en PLL son los siguientes:
Función de transferencia del PLL con FPB FB(s)
𝜃𝑜
𝑘𝑑 𝑘𝑜
=
𝜃𝑠 𝑇1 + 𝑇2
𝑇2𝑠 + 1
1 + 𝑘𝑑 𝑘𝑜 𝑇2⁄𝑁
𝑘𝑑 𝑘𝑜
𝑠2 + 𝑠
+
𝑇1 + 𝑇2
𝑁(𝑇1 + 𝑇2)
𝜃𝑜
𝑘𝑑 𝑘𝑜
𝑇2𝑠 + 1
=
𝜃𝑠 𝑇1 + 𝑇2 𝑠 2 + 2𝜁𝜔𝑛 𝑠 + 𝜔𝑛 2
Donde
𝑘𝑑 𝑘𝑜
𝜔𝑛 = √
𝑁(𝑇1 + 𝑇2)
𝜁=
𝜔𝑛
𝑁
(𝑇2 +
)
2
𝑘𝑑 𝑘𝑜
Despejando
𝑇2 =
2𝜁
𝑁
−
𝜔𝑛 𝑘𝑑 𝑘𝑜 𝑑
Diseño de PLL
Función de transferencia lineal en dominio Z de PLL tipo 2 Digital
El modelo PLL analizado es un tipo 2, con un lazo de filtro compuesto por un PI. Los PLLs
digitales se analizan en términos de su modelo analógico equivalente y sus parámetros de
amortiguamiento ζ y su frecuencia natural ωn
Modelo en dominio Z de un PLL tipo 2 Digital
La función de transferencia en dominio Z de un PLL está dado por
𝐻(𝑍) =
̂ (𝑧)
Θ
Θ(𝑧)
La función de transferencia de filtro de lazo está dada por:
𝐹(𝑧) = 𝐾1 + 𝐾2 ∗
1
1 − 𝑧 −1
Función de transferencia del NCO (Numerically Controlled Oscillator), oscilador controlado
numéricamente.
𝑉(𝑧) = 𝐾𝑜 ∗
𝑧 −1
1 − 𝑧 −1
̂ (𝑧) se puede expresar como:
Θ
̂ = 𝐾𝑝[Θ(𝑧) − Θ
̂ (𝑧)] [𝐾1 + 𝐾2 ∗
Θ
1
𝑧 −1
[𝐾
∗
]
]
𝑜
1 − 𝑧 −1
1 − 𝑧 −1
Es posible derivar una expresión para H(z) en términos de los coeficientes del lazo K0, K1,K2 y Kp
̂ = [Θ(𝑧) − Θ
̂ (𝑧)] [𝐾1 𝐾𝑝 𝐾𝑜
Θ
𝑧 −1
𝑧 −1
1
+
𝐾
𝐾
𝐾
]
2
𝑝
𝑜
−1
−1
1−𝑧
1 − 𝑧 1 − 𝑧 −1
Haciendo una sustitución
α = [𝐾1 𝐾𝑝 𝐾𝑜
𝑧 −1
𝑧 −1
1
+
𝐾
𝐾
𝐾
]
2 𝑝 𝑜
−1
−1
1−𝑧
1 − 𝑧 1 − 𝑧 −1
La expresión de la función de transferencia en términos de α será:
̂ (𝑧)(1 + 𝛼) = 𝛼Θ(𝑧)
Θ
H(z) =
̂ (𝑧)
Θ
𝛼
=
Θ(𝑧) 1 + 𝛼
Sustituyendo α y realizando las respectivas simplificaciones se obtiene la función de
transferencia del PLL
H(z) =
𝐾𝑝 𝐾𝑜 (𝐾1 + 𝐾2 )𝑧 −1 − 𝐾1 𝐾𝑝 𝐾𝑜 𝑧 −2
1
1 − 2 (1 − 2 𝐾𝑝 𝐾𝑜 (𝐾1 + 𝐾2 )) 𝑧 −1 + (1 − 𝐾1 𝐾𝑝 𝐾𝑜 )𝑧 −2
Kp= ganancia del detector de fase.
Ko=ganancia del oscilador.
El equivalente de la función de transferencia del PLL en su versión análoga será:
H(s) =
̂ (𝑠)
Θ
2𝜁𝜔𝑛 𝑠 + 𝜔𝑛2
= 2
Θ(𝑠) 𝑠 + 2𝜁𝜔𝑛 𝑠 + 𝜔𝑛2
Para obtener los coeficientes del modelo digital del PLL, igualamos las dos ecuaciones, digital y
análoga, esto se logra aplicando la transformada bilineal a la función de transferencia del
modelo análogo.
Así, se obtiene los coeficientes del modelo digital:
𝐾1 𝐾𝑝 𝐾𝑜 =
4𝜁𝜃𝑛
1 + 2𝜁𝜃𝑛 + 𝜃𝑛2
𝐾2 𝐾𝑝 𝐾𝑜 =
4𝜃𝑛 2
1 + 2𝜁𝜃𝑛 + 𝜃𝑛2
Donde
𝜃𝑛 =
𝐵𝑛 𝑇𝑠
1
𝑅(𝜁 + 4𝜁 )
Y
𝑅=
𝑇𝑠
𝑇
Ts es el periodo del símbolo y R representa el radio de sobremuestreo.
Bn= ancho de banda
T=tiempo de muestreo
ζ= factor de amortiguamiento
Aplicaciones del PLL
Los PLL se usan básicamente para:
-Generadores de portadoras para emisión con modulación de ángulo o no.
-Generación de osciladores locales en recepción.
-Sintetizadores de frecuencia.
-Demoduladores de señales moduladas en ángulo.
-Recuperación de impulsos de reloj en transmisiones digitales.
-Circuitos de sincronismo para barrido horizontal y vertical en receptores de televisión.
-Recepción de señales satelitales de satélites no geoestacionarios.
Filtros
El PLL permite la realización de filtros de fase para recuperar o reconstruir una señal de
entrada corrupta por ruido de fase, causadas por la intermodulación con ruido en algún punto
de su recorrido o bien por “jitter”. El efecto del jitter, si no es corregido, incrementa el ruido
equivalente de la señal.
Demoduladores
Los demoduladores pueden ser de tipo analógico o digital. Los demoduladores analógicos
requieren que el VCO sea muy lineal. Los demoduladores digitales se utilizan para demodular
señales FSK (frequency shift keying). En este caso, normalmente la señal contiene saltos de
frecuencia entre un valor mínimo y uno máximo. La precaución por tomar es que la respuesta
transitoria no produzca sobrepicos que pudieran alterar la señal decodificada.
Receptor Homodino o Sincrodino
Se refiere a la recepción sincrónica de señales de radio moduladas en AM. Para demodular
sincrónicamente una señal de AM hay que mezclarla con una portadora con la misma
frecuencia y fase. Las señales de radio frecuentemente se desvanecen o son acompañadas por
ruido. El PLL puede recuperar la portadora aún con altos niveles de ruido.
Barrido horizontal de televisión
Fue la primera aplicación comercial generalizada. La forma antigua de sincronizar el barrido
horizontal (y vertical también) de televisión se hacía mediante el uso de un oscilador astable.
Este oscilador cuando oscila libremente tiene un período ligeramente mayor al período del
barrido horizontal.
El uso de un PLL ajusta la frecuencia y fase de los circuitos de barrido en base al promedio de
cientos de pulsos de sincronismo.
Conclusiones
Se ha demostrado que el uso de circuitos PLL en el área de comunicaciones digitales es muy
útil al momento de reconstruir o demodular señales que han sido afectadas por el ruido en
algún punto de la transmisión. Con el uso de filtros pasa-bajo y amplificadores dentro de su
circuito, se busca que la señal de salida del PLL contenga la mayor parte de características e
información de la señal original transmitida, para esto, el PLL considera también que la
relación señal/ruido de la señal entrante sea óptima.
El uso más común de los circuitos PLL es en sintonizadores. Por sus características de acoplar la
fase de la señal de análisis con una señal de referencia, se ha usado en sistemas comunes
como televisores, para la corrección de sincronía de imágenes; también su uso se aplica para la
recepción de señales satelitales, ayudando a mejorar la relación señal/ruido de la señal
transmitida por los satélites, que poseen transmisores de baja potencia.
[1] Q. Chaudhari, «Phase Locked Loop,» de Wireless Communications from the Ground Up: An
SDR Perspective, CreateSpace Independent Publishing Platform, 2018, pp. 237-268.
[2] «Principal PLL,» de Software Defined Radio Using MATLAB & Simulink and the RTL-SDR, pp.
593-606.
[3] F. Miyara, «Lazos de Fijación de Fase,» Universidad Nacional de Rosario, RosarioArgentina, 2005.
[4] D. Rabinovich y O. Santa Cruz, «PLL - PHASE LOCKED LOOP - Lazos Enganchados de Fase,»
de Electrónica Aplicada III, 2010, pp. 1-34.
[5] F. D. Quesada Pereira, «Lazo enganchado en fase,» Universidad Politécnica de Cartagena,
Cartagena, 2010.