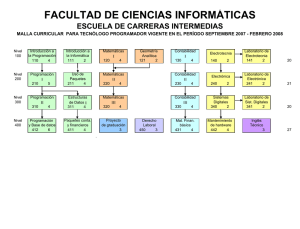
ELECTROTECNIA III-1 UNIDAD 1. FASORES Y NOMENCLATURA. 1. INTRODUCCIÓN. Los fasores son importantes para analizar, documentar y entender la operación de los circuitos y sistemas eléctricos. Por consiguiente, un conocimiento sólido teórico y práctico de estos es un medio fundamental y valioso. 2. FASORES. El Diccionario de la IEEE ( IEEE 100 - 1996 ) define un fasor como “ (1) (medición). Un número complejo, asociado con cantidades eléctricas que varían senoidalmente, tal que el valor absoluto (módulo) del número complejo corresponde al valor máximo o el valor medio cuadrático (valor eficaz) que valoran la cantidad, y la fase (argumento) al ángulo de fase en el momento cero. Por extensión el término fasor también se puede aplicar a la impedancia y a las cantidades complejas relacionadas que no dependen del tiempo. (2) Un número complejo que expresa la magnitud y fase de una cantidad que varía con el tiempo. A menos que otra cosa se especifique, sólo se usa dentro del contexto de los sistemas lineales en el estado permanente. En coordenadas polares, se puede escribir como Ae jφ donde A es la amplitud o magnitud (normalmente el valor eficaz, pero a veces se indica como el valor máximo) y es el ángulo de fase. El ángulo de fase no se debe confundir con el ángulo en el espacio de un vector. (3). El equivalente complejo de una cantidad de onda senoidal simple tal que el módulo del complejo es la amplitud de la onda senoidal y el ángulo del complejo (en la forma polar) es el ángulo de fase de la onda senoidal.” En este curso, el término fasor se usará para designar las tensiones, corrientes, flujos, impedancias y potencia compleja en corriente alterna. Por muchos años, los fasores fueron designados como “ vectores “, pero este uso se ha desaprobado para evitar confusiones con los vectores en el espacio. Sin embargo, el uso anterior ocasionalmente subsiste. 3. REPRESENTACIÓN DEL FASOR. La forma gráfica común para representar cantidades fasoriales eléctricas y magnéticas es usando las coordenadas cartesianas con x ( la abcisa ) como el eje de las cantidades reales y y ( la ordenada ) como el eje de las cantidades imaginarias. Esto se ilustra en la figura número 1. Así el punto c sobre el plano complejo x - y se puede representar como se muestra en esta figura, y documentarlos matemáticamente por medio de algunas formas alternativas dadas en las ecuaciones número 1. FASOR c FORMA RECTANGULAR x+jy FORMA FORMA COMPLEJA EXPONENCIAL c (cos + j sen ) c ej FORMA POLAR (1) c + 1 ELECTROTECNIA III-2 Algunas veces es útil la forma conjugada: * c = x - j y = c ( cos - j sen ) = c e-j = c - (2) donde: c = Fasor. * c = su conjugado. x = valor real ( alternativa; Re c o c ' ) '' y = valor imaginario ( alternativa: Im c o c ) c = módulo ( magnitud o valor absoluto ) = ángulo de fase ( argumento ), ( alternativa: arg c ) ordenada y c c y (a) abcisa x x +X +Q (b) +R -R -X -P +P -Q FIGURA NÚMERO 1. EJES DE REFERENCIA PARA CANTIDADES FASORIALES: (a) COORDENADAS CARTESIANAS x - y ; (b) EJES PARA FASORES DE IMPEDANCIA; (c) EJES PARA FASORES DE POTENCI A. 2 ELECTROTECNIA III-3 El módulo ( magnitud o valor absoluto ) del fasor es, c x2 y 2 3 De las ecuaciones ( 1) y (3) tenemos, * 1 c c 2 * 1 y cc 2 x 4 5 4. DIAGRAMAS FASORIALES PARA CANTIDADES SENOIDALES. Para aplicar la notación anterior a las tensiones, corrientes y flujos senoidales ( C. A. ), los ejes se consideran fijos, con las cantidades fasoriales girando con una velocidad angular constante. La norma internacional es que los fasores siempre giran en sentido contrario a las manecillas del reloj. Sin embargo, por conveniencia, los diagramas fasoriales siempre se muestran “fijos” para la condición dada. La magnitud del fasor ( c ) puede ser ya sea el valor pico o el valor eficaz de la correspondiente cantidad senoidal, en este curso siempre consideraremos que se tratan de valores eficaces, a menos que se establezca específicamente otra cosa. Así un diagrama fasorial muestra respectivamente tensiones, corrientes, flujos, etcétera, que existen en un circuito eléctrico. Solamente se deben indicar las magnitudes y las relaciones relativas de ángulo de fase entre esas diferentes cantidades. Así todos los diagramas fasoriales requieren una escala o indicaciones completas de las magnitudes físicas de las cantidades mostradas, así que el cero o ángulo de referencia se puede variar por conveniencia. Como un ejemplo, en el cálculo de las características de las cargas es preferible usar la tensión ( V ) a 00 a lo largo del eje x así que el ángulo de la corriente ( I ) representa su valor real de atraso o adelanto. Otros ejes de referencia de uso común se muestran en las figuras números 1b y 1c. Para trazar la impedancia, resistencia y reactancia se usan los ejes R - X de la figura número 1b. La (c) reactancia inductiva es + X y la reactancia capacitiva es - X. Para trazar los fasores de potencia, se usa la figura número 1c. P es la potencia activa ( W, kW, MW ) y Q es la potencia reactiva ( var, kvar, Mvar ). A pesar de que se representan como fasores, los “fasores” de impedancia y potencia no giran con la frecuencia del sistema. 5. COMBINACIÓN DE FASORES. A continuación se presentan las diferentes leyes para combinar los fasores como una referencia general. 3 ELECTROTECNIA III-4 Multiplicación. Las magnitudes se multiplican y los ángulos se suman. V I V I φV φ I V I V I φV φ I 7 * 2 * I I I I2 6 8 División. Las magnitudes se dividen y los ángulos se restan. V V φV φ I I I 9 Potencias. I I e n jφ n n n I e jφn I n I e jφ / n 10 11 6. LOS DIAGRAMAS FASORIALES REQUIEREN UN DIAGRAMA DE CIRCUITO. Los diagramas fasoriales definidos anteriormente tienen un significado indeterminado o vago a menos que se les acompañe de un diagrama del circuito. El diagrama del circuito identifica el circuito especifico involucrado con la localización y la dirección considerada para las corrientes y las tensiones indicadas en el diagrama fasorial. Las direcciones no son críticas, ya que el diagrama fasorial confirmará si las consideraciones fueron correctas y suministrará las relaciones de las magnitudes y ángulos de fase correctas. Estos dos diagramas son complementarios ( fasorial y del circuito ) y de preferencia se mantienen separados para evitar confusiones y errores en su interpretación. 4 ELECTROTECNIA III-5 7. NOMENCLATURA PARA TENSIÓN Y CORRIENTE. Puesto que no hay una nomenclatura normalizada1 para la representación de las funciones o constantes que se utilizan en el campo eléctrico, como son la tensión y la corriente, puede existir confusión entre varios autores y publicaciones. La nomenclatura que se utilizará a través de este curso se ha manejado durante muchos años y se ha encontrado que es práctica y flexible y que es compatible con los circuitos eléctricos y sistemas de potencia prácticos. Para representar las funciones del tiempo se usarán las letras minúsculas y para las constantes las letras mayúsculas. En los diagramas eléctricos de los circuitos se indicará la corriente compleja ya sea designándola con una letra como I con una flecha de referencia para considerar su dirección; o por medio de una letra con doble subíndice, donde el orden de los subíndices indica la dirección de ella. La dirección que se considera es la correspondiente al medio ciclo positivo de la onda senoidal. La convención anterior se ilustra en la figura número 2. a + E da + V ad I ab + I b c V ab + VR I s I bc V bc + I cd + VXC V cd V XL d FIGURA NÚMERO 2. DIAGRAMA DEL CIRCUITO MOSTRANDO LA LOCALIZACIÓN Y DIRECCIONES CONSIDERADAS DE CORRIENTE, CAÍDAS DE TENSIÓN Y FUERZA ELECTROMOTRIZ. Así se considera que en el medio ciclo positivo la corriente está fluyendo de arriba hacia abajo, como se indica por la dirección de la flecha usada como I s o designándola por las letras con doble subíndice I ab , I bc e I cd , no se requieren las flechas con I ab , I bc e I cd pero con frecuencia se usan para dar claridad. Cuando la flecha se refiere a una malla atribuirá sentido a una línea curva determinando la malla. Es muy importante tener en cuenta en esas asignaciones en el circuito que las flechas no indican fasores, sino que ellas solo asumen la dirección y localización de las indicaciones. 1 La CEI ( Comisión Electrotécnica Internacional, también IEC, International Electrotechnical Commission) elabora solo recomendaciones, sin carácter obligatorio, salvo que los reglamentos oficiales las incluyan total o parcialmente. 5 ELECTROTECNIA III-6 Las tensiones pueden ser elevaciones ( fuentes ) o caídas. Las letras “e” o “E” se utilizan para fuerzas electromotrices de un elemento activo ( fuentes ), las letras “v”, “V” o “U” se establecen para las caídas de tensión a través de los elementos pasivos ( resistencias, inductancias o capacitancias ) En la figura número 2 la expresión E da indica una fuerza electromotriz o una elevación de tensión desde el punto “d” al punto “a”; la indicación V ad significa una caída de tensión desde el punto “a” al punto “d”. En la figura número 2 la elevación de tensión E da es igual a la caída de tensión V ad . Puede resultar mucha confusión por no mencionar claramente cual es la convención que se está aplicando o por mezclar las dos prácticas en los diagramas de los circuitos. Esta se puede evitar estandarizando una y solo una de las prácticas. Como las caídas de tensión son las que con más frecuencia se manejan en los circuitos eléctricos y los sistemas de potencia, todas las tensiones que se muestren siempre se considerarán como caídas de tensión. La adopción consistente de únicamente caídas no causa dificultades. Un generador o una fuente viene a ser una caída negativa puesto que la corriente fluye del punto de tensión más baja al punto de tensión más alta. Las tensiones ( siempre caídas ) se indican ya sea ( 1 ) con una letra con doble subíndice, o ( 2 ) con un pequeño signo más que muestra el punto que se considera con el potencial relativamente más alto. Así durante el medio ciclo positivo de la onda senoidal, la caída de tensión se indica por el orden de los dos subíndices cuando se utiliza este método, o por el signo ( + ) marcado en el extremo de más alta tensión. Esto se ilustra en la figura número 2, donde se muestran ambos métodos. Es preferible mostrar flechas en ambos extremos de las designaciones de la caída de tensión para evitar posibles confusiones. Puede ser útil considerar la corriente como una cantidad “ de un lado a otro “ y la tensión como una cantidad “ a través de “. En este sentido en la representación de la figura número 2, la misma corriente fluye de un lado a otro, en todos los elementos en serie, así que I ab I bc I ca I s . En contraste, la caída de tensión V ab se aplica solamente a través de los nodos “a” y “b” , la caída de tensión V bc a través de los nodos “b” y “c”, y la caída de tensión V cd a través de los nodos “c” y “d”. 8. EL DIAGRAMA FASORIAL. Con la identificación apropiada y las direcciones consideradas establecidas en el circuito, se puede dibujar el diagrama fasorial correspondiente de los datos calculados o de prueba. Para el diagrama del circuito de la figura número 2, se muestran dos tipos de diagramas fasoriales en la figura número 3. El diagrama de la figura número 3a se refiere como un diagrama “de tipo abierto“, donde todos los fasores se desarrollan desde un origen común. El diagrama de la figura número 3b se refiere como un diagrama “de tipo cerrado“, donde los fasores de tensión se suman en conjunto de izquierda a derecha del mismo circuito. Ambos tipos son útiles y se utilizan dependiendo del análisis del circuito que esta bajo estudio. 6 ELECTROTECNIA III-7 V bc a V bc V ab V cd I ab I bc I cd I s b V ab V ac V cd V ad I ab I bc I cd I s FIGURA NÚMERO 3. DIAGRAMAS FASORIALES a). TIPO ABIERTO. b). TIPO CERRADO. 7 ELECTROTECNIA III-8 UNIDAD 2. SISTEMA MONOFÁSICO DE TRES HILOS O CONDUCTORES. 1. INTRODUCCIÓN Cuando se tiene que distribuir energía eléctrica en baja tensión, se puede perder una proporción considerable de la potencia debido al calentamiento de los conductores a menos que estos sean desmesuradamente gruesos. El reconocimiento de este hecho por las compañías suministradoras de energía llevo al diseño de sistemas de distribución de tres hilos. Una fuente monofásica de tres hilos se define como una fuente que tiene tres terminales de salida, como a, n y b; en la figura número 1 los fasores de tensión son V an y V nb y son iguales. Esta fuente se puede representar por la combinación de dos fuentes de tensión idénticas, como en la figura número 1c, V an V nb V . Es evidente que V ab 2V an 2V nb , por lo tanto, se tiene una fuente a la que se pueden conectar cargas que operen con cualquiera de las dos tensiones. Transformador de distribución a Fuente monofásica de tres hilos n AT b (a) (b) a a n BT n b b (c) FIGURA NÚMERO 1. FUENTE MONOFÁSICA DE TRES HILOS En nuestro país la norma mexicana NMX-J-098-ANCE-1999. SISTEMAS ELÉCTRICOS DE POTENCIA - SUMINISTRO – TENSIONES ELÉCTRICAS NORMALIZADAS, para este tipo de suministro indican las tensiones siguientes: tensión eléctrica nominal del sistema 120/240 V, tensión eléctrica de servicio máxima 126/252 V y mínima 108/216 V, y tensión eléctrica nominal de utilización 115/230 V. Los aparatos de mayor tensión generalmente son aquellos que absorben mayores cantidades de potencia, por lo que las intensidades de corrientes que originan son sólo la mitad de la intensidad de corriente que se necesitaría al operar con la misma potencia y la mitad de la tensión. Esto significa que el diámetro de los alambres en el aparato, en la instalación eléctrica del usuario y del suministrador puede ser menor. El nombre de monofásico surge por que, al ser iguales las tensiones V an y V nb deben tener el mismo ángulo de fase. En la figura número 2 se muestra como, mediante el uso de una fuente de tensión monofásica de tres hilos, se puede suministrar energía a las cargas con mayor eficiencia con una línea de distribución de tres hilos, cada uno de los cuales tiene una resistencia R, que si la carga total fuera alimentada por una línea de dos hilos, cada uno de los cuales tuviera una resistencia R como en la figura número 2a. 8 ELECTROTECNIA III-9 f I a I /2 R R Fuente V an V Fuente P P/2 N V nb V P/2 R Fuente b (a) V R n R n A I /2 B (b) FIGURA NÚMERO 2. CIRCUITOS MONOFÁSICOS DE 2 Y 3 HILOS En la figura número 2a la carga de potencia P toma una corriente I con una tensión V habiendo una pérdida en la línea igual a 2 I2 R. En el sistema de tres hilos, figura número 2b, la carga se divide en dos partes iguales, cada una igual a P/2, con una tensión cada una de V . Un conductor llamado neutro conecta el punto medio de la fuente de tensión a la conexión común de las dos mitades de la carga. En estas condiciones se dice que la carga está balanceada, y no pasa corriente por el conductor del neutro. Si se usan conductores, de la misma resistencia que los de la figura número 2a, la corriente es I / 2 , y las pérdidas correspondientes en la línea son (I/2)2(2R), o sea I2R/2. Luego las pérdidas de la línea quedan reducidas a una cuarta parte del valor correspondiente al sistema de dos conductores sin ninguna reducción en la cantidad de energía suministrada a la carga. Interpretando el resultado de otra manera, el circuito equilibrado de tres hilos puede operar con la misma eficiencia de distribución que el sistema de dos hilos si se diseña de manera que cada conductor del circuito de tres hilos tenga cuatro veces la resistencia, o sea una sección transversal igual a la cuarta parte, de un conductor del sistema de tres hilos. Luego el sistema de tres hilos equilibrado necesita sólo tres octavos de la cantidad de cobre que requiere un sistema de dos hilos para transmitir la misma cantidad de energía con igual rendimiento. Como el conductor del neutro es indispensable en cualquier caso en que se pueda presentar un desequilibrio, el sistema de tres conductores requiere tres hilos, cada uno de los cuales tiene la cuarta parte de cobre que los dos conductores del sistema de dos hilos, el neutro no lleva fusible ni ningún otro dispositivo protector de manera que proporciona a la corriente camino de retorno a la fuente. Así se mantienen las tensiones de las cargas aproximadamente constantes en cada caso de que las cargas no estén equilibradas. El neutro se conecta usualmente a tierra, limitándose de esta manera la diferencia de potencial del circuito con respecto a tierra. En la práctica, las relaciones teóricas exactas deducidas en el párrafo anterior no pueden conseguirse usualmente debido a la necesidad de usar los calibres normalizados de los conductores, a las regulaciones de seguridad y a que la carga raramente está balanceada. La figura número 3 ilustra un sistema de distribución monofásico de tres hilos de un transformador de la compañía suministradora de energía eléctrica a un servicio que tiene un circuito trifilar, habiéndose omitido por simplicidad los interruptores, fusibles y derivaciones usuales. La fuente de alimentación proviene ordinariamente de un sistema de distribución de tensión media (tal como 34,5 kV) al primario del transformador. 9 ELECTROTECNIA III-10 Lámparas y aparatos eléctricos de poco consumo Sistema de alimentación de la compañia suministradora Alambrado del usuario a A n N b B Aparatos eléctricos de mayor consumo, hornos eléctricos, calentadores de agua, etc. FIGURA NÚMERO 3. CIRCUITO SECUNDARIO DE TRES HILOS DE LA COMPAÑIA SUMINISTRADORA A LA CARGA DEL USUARIO. Los secundarios están conectados con sus polaridades en el mismo sentido, como se muestra en la figura número 3. De esta manera se tiene una tensión aproximada de 230 V entre los conductores de línea entre A y B, y se tiene disponible la mitad de esta tensión entre un hilo de la línea y el neutro, el sistema es monofásico teniendo una relación fasorial como la que se muestra en la figura número 4. V ab V an V nb FIGURA NÚMERO 4. DIAGRAMA VECTORIAL DE LAS TENSIONES DEL TRANSFORMADOR DE LA FIGURA NÚMERO 3. Una ventaja del sistema de tres hilos es que se pueden operar en el mismo circuito cargas que requieren dos tensiones diferentes, tales como lámparas de 115 V y calentadores de 230 V. 2. ANÁLISIS CON DIFERENTES TIPOS DE CARGAS Y CONDICIONES. 2.1. Cargas balanceadas Carga entre conductores de línea y el conductor del neutro, con la alimentación aplicada directamente en sus terminales. 10 ELECTROTECNIA III-11 I aA a A I nN n Z N I Bb Z b B FIGURA NÚMERO 5. En la figura número 5, el circuito contiene cargas idénticas Z entre cada hilo exterior y el neutro. Como, V an V nb V Las corrientes son, I aA V Z ; I Bb V Z Y la corriente en el conductor del neutro es, I nN I Bb I aA 0 No hay corriente en el conductor del neutro. Ejemplo 2-1. El sistema monofásico de tres hilos balanceado de la figura número 5, tiene una tensión eléctrica de 115,0/230 V, las impedancias conectadas entre las líneas A y N, y N, y B son iguales y tienen un valor de Z = 2,27 /31,00 . Encuentre las corrientes que toman las impedancias y la corriente en el conductor del neutro. SOLUCIÓN. Las tensiones son, V AN V NB V 115, 0 0, 00 V Las corrientes en las impedancias son, I AN I NB V 115, 0 0, 0 50, 7 31, 00 A Z 2, 27 31, 0 En virtud de que la carga es balanceada, la corriente en el conductor del neutro es igual a cero. I nN 0 11 ELECTROTECNIA III-12 Carga entre conductores de línea y el conductor del neutro, con la alimentación suministrada a través de líneas de alimentación. En la figura número 6, el circuito contiene cargas idénticas Z entre cada hilo exterior y el neutro que están alimentadas a través de líneas de impedancia ZL. ZL a I aA A I AN ZN Z I nN N n I NB ZL Z I Bb b B FIGURA NÚMERO 6. Las tensiones son, V an V nb V Puesto que el circuito está balanceado, la corriente en el conductor del neutro es igual con cero, esto es, I nN 0 De donde el circuito se puede simplificar quedando como se muestra en el diagrama siguiente: ZL a I aA A I AN Z N n I NB ZL b Z I Bb B 12 ELECTROTECNIA III-13 La corriente I aA es, I aA V ab 2V an V an 2Z L Z 2Z L Z Z L Z Y la corriente I bB es, I bB I aA Ejemplo 2-2. El sistema monofásico de tres hilos de la figura 6, alimenta con tensiones de 120,0/240 V, las cargas conectadas entre líneas y el conductor del neutro, con valores iguales a Z = 20,0 /36,90 . Las impedancias de las líneas de alimentación son de ZL = 0,500 /22,00 , cada una. a). Encuentre las corrientes del sistema; b). Las caídas de tensión en las cargas y c). Las caídas de tensión en las líneas. SOLUCIÓN. La tensiones de alimentación son, V an V nb 120,0 / 0,00 V Puesto que el circuito está balanceado, la corriente en el conductor del neutro es igual con cero, I nN 0 a). De donde las corrientes en el sistema son, I aA 120, 0 / 0, 0 V an 5,86 / 36,50 A Z L Z 0,500 / 22, 0 20, 0 / 36,9 I bB I aA 5,86 / 36,50 A = 5,86 /143,50 A b). Las caídas de tensión en las cargas son, V AN V NB Z I aA 20, 0 / 36,9 5,86 / 36,5 117, 2 / 0, 40 V c). Las caídas de tensión en las líneas son, V aA Z L I aA 0,500 / 22, 0 5,86 / 36,5 2,93/ 14,50 V 13 ELECTROTECNIA III-14 V bB Z L I bB 0,500 / 22, 0 5,86 / 36,5 2,93/165,50 V Carga entre conductores de línea y el conductor del neutro, más carga entre líneas, con la alimentación aplicada directamente en sus terminales. En la figura número 7, se muestran las condiciones anteriores, las corrientes tomadas por las cargas son, I AN V AN V V NB V ; I NB Z Z Z Z I aA ; I AN I NB ; I AB A a I AN Z I nN n N I NB I AB ZAB Z I Bb b V AB 2V Z AB Z AB B FIGURA NÚMERO 7. Analizando el nodo A, tenemos I aA I AN I AB Analizando el nodo B, tenemos I Bb I NB I AB De donde, I aA I Bb Analizando el nodo N, tenemos I nN I AN I NB ; I nN I NB I AN 0 No hay corriente en el conductor del neutro. Ejemplo 2-3. El sistema monofásico de tres hilos de 115,0/230 V, de 60 Hz, que se muestra en la figura número 7, suministra energía eléctrica a tres cargas, las cargas entre A y N y entre N y B, tienen impedancias iguales de un valor de Z = 10,00 ; la carga que se conecta entre A y B tiene una impedancia igual a ZAB = 16,00 + j 12,00 . Determine las corrientes que toman las cargas y la corriente en el conductor del neutro. SOLUCIÓN. 14 ELECTROTECNIA III-15 Las tensiones son, V AN V NB V 115, 0 0, 00 V ; V AB V AN V NB 2V 230 0, 00 V Las corrientes en las cargas son, I AN V AN V 115, 0 0, 0 11,50 0, 00 A Z Z 10, 00 0, 0 I NB V NB V 115, 0 0, 0 11,50 0, 00 A Z Z 10, 00 0, 0 I AB V AB 2V 2 115, 0 0, 0 11,50 36,90 A Z AB Z AB 16, 00 j12,00 Puesto que se tiene un circuito con cargas balanceadas, no hay corriente en el conductor del neutro, esto es I nN 0 Carga entre conductores de línea y el neutro, más carga entre líneas, con la alimentación suministrada a través de líneas de alimentación. El análisis del circuito se puede efectuar mediante el método de mallas. Las tensiones de la fuente son, V an V nb V ZL a I1 ZN I aA A I AN Z I nN N I3 n I2 ZL b I NB I AB ZAB Z I Bb B FIGURA NÚMERO 8. La ecuación de la malla 1 es, 15 ELECTROTECNIA III-16 V Z L Z Z N I1 Z N I 2 Z I 3 La ecuación para la malla 2 es, V Z N I1 Z N Z Z L I 2 Z I 3 Igualando las ecuaciones anteriores, tenemos Z L Z Z N I1 Z N I 2 Z I 3 Z N I1 Z N Z Z L I 2 Z I 3 Z L Z Z N Z N I1 Z N Z Z L Z N I 2 De donde I1 I 2 La corriente en el conductor del neutro I nN es, I nN I 2 I 1 0 No hay corriente en el conductor del neutro. En virtud de que no hay corriente en el conductor del neutro podemos eliminarlo y redibujar el circuito para determinar las corrientes en las líneas y cargas. ZL I aA I AN a A I AB Z n I1 b ZL I2 N I Bb ZAB Z I NB B FIGURA NÚMERO 9. Las corrientes de malla son iguales a, 16 ELECTROTECNIA III-17 I 1 2 Z L 2 Z I 2 2 Z 1 V AB 2 Z Z AB 0 2Z De donde las corrientes en las líneas y las cargas son, I aA I Bb I 1 I AN I NB I 1 I 2 I AB I 2 Ejemplo 2-4. El sistema monofásico de tres hilos de 120,0/240 V, de 60 Hz, que se muestra en la figura número 9, alimenta tres cargas, las cargas entre las líneas y el conductor del neutro son iguales y tienen una impedancia de Z = 2,88 /0,00 , la impedancia entre las líneas A y B tiene un valor igual a ZAB = 5,76 /36,90 . Estas cargas se alimentan a través de líneas que tienen una impedancia de 0,250 /0,00 . Calcule las corrientes en las líneas de alimentación y las caídas de tensión en las cargas. SOLUCIÓN. Puesto que el circuito está balanceado, no hay corriente en el conductor del neutro, esto es I nN 0 Utilizando el método de mallas tenemos las corrientes de mallas, I 1 2 Z L 2 Z I 2 2 Z I 1 2 0, 250 0, 0 2 2, 88 0, 0 2 2, 88 0, 0 I 2 1 V AB 2 Z Z AB 0 2Z 1 240 0, 0 2 2, 88 0, 0 5, 76 36, 9 0 2 2, 88 0, 0 I 1 6, 26 0, 0 5, 76 0, 0 1 240 0, 0 68, 3 15, 9 36, 0 34, 4 0 I 2 5, 76 0, 0 10, 93 18, 5 De donde las corrientes de línea son, I aA I Bb I 1 68, 3 15,90 A Las corrientes en las cargas son, I AN I NB I 1 I 2 68, 3 15,9 36,0 34,4 36,0 2,60 A 17 ELECTROTECNIA III-18 I AB I 2 36, 0 34, 40 A Las caídas de tensión en las cargas son, V AN V NB Z I AN Z I NB 2, 88 0.0 36, 0 2, 6 103, 7 2, 60 V V AB Z AB I AB 5,76 36,9 36,0 34,4 207 2,50 V 2.2. Cargas desbalanceadas Carga entre conductores de línea y el conductor del neutro, con la alimentación aplicada directamente en sus terminales. En la figura número 10, el circuito contiene cargas diferentes Z1 y Z2, entre cada hilo exterior y el neutro. Las tensiones son, V an V nb V I aA a n A I nN Z1 N I Bb b Z2 B FIGURA NÚMERO 10. Las corrientes son, I aA V an V V nb V ; I Bb Z1 Z1 Z2 Z2 I nN I aA I Bb ; I nN I Bb I aA Hay corriente en el conductor del neutro. 18 ELECTROTECNIA III-19 Ejemplo 2-5. El sistema monofásico de tres hilos de la figura número 10, tiene una tensión de 115,0/230 V, de una frecuencia de 60 Hz, la impedancia Z1 tiene un valor de 13,23 /0,00 y la impedancia Z2 tiene un valor de 15,60/36,90 . ¿Cuál es el valor de las corrientes en las líneas y en el conductor del neutro? SOLUCIÓN. Las tensión son, V AN V NB V 115, 0 0, 00 V V AB V AN V NB 2V 230 0, 00 V Las corrientes en las líneas son, I aA I Bb V AN 115, 0 0, 0 8, 69 0, 0 A Z 1 13, 23 0, 0 V NB 115, 0 0, 0 7, 37 36, 90 A Z 2 15, 60 36, 9 La corriente en el conductor del neutro es, I nN I Bb I aA 7, 37 36,9 8,69 0,0 5, 23 122, 30 A Carga entre conductores de línea y el conductor del neutro, con la alimentación suministrada a través de líneas de alimentación. ZL a I aA A I AN I1 ZN Z1 I nN N n I NB I2 ZL b Z2 I Bb B FIGURA NÚMERO 11. El análisis del circuito se puede efectuar mediante el método de mallas. Las tensiones en la fuente son, 19 ELECTROTECNIA III-20 V an V nb V Las ecuaciones de mallas son, V Z L Z1 Z N I 1 Z N I 2 V Z N I1 Z N Z 2 Z L I 2 La solución matemática de las ecuaciones se puede realizar por diferentes métodos. Aquí utilizaremos la solución de ellas por medio del cálculo matricial. La ecuación correspondientes es, V Z L Z 1 Z N ZN V I1 Z N Z 2 Z L I 2 ZN La ecuación para obtener las corrientes de malla es, I 1 Z L Z 1 Z N ZN I 2 ZN Z N Z 2 Z L 1 V V Las corrientes del sistema son, I aA I AN I 1 I Bb I NB I 2 I nN I 2 I 1 Ejemplo 2-6. El sistema monofásico de tres hilos que se muestra en la figura número 11, tiene tensiones en la fuente de 120,0/240 V, y alimenta las cargas Z1 = 25,0 /32,00 y Z2 = 38,0 /26,50 a través de líneas de alimentación con impedancias de 0,800 /12,00 , cada una, el conductor del neutro tiene una impedancia igual a las de las líneas. a). Determine las corrientes del sistema; b). las caídas de tensión en las cargas y c). Las caídas de tensión en las líneas y el conductor del neutro. SOLUCIÓN. Las tensiones en la fuente son, 20 ELECTROTECNIA III-21 V an V nb V 120,0 / 0,00 V Las corrientes de malla son, I 1 2 0,800 /12, 0 25, 0 / 32, 0 0,800 /12, 0 I 2 1 120, 0 / 0, 0 2 0,800 /12, 0 38, 0 / 26,5 120, 0 / 0, 0 0,800 /12, 0 I 1 4, 63 / 31,1 I 2 3,35 / 26,5 a). Las corrientes del sistema son, I aA I AN I 1 4, 63/ 31,10 A I Bb I NB I 2 3,35 / 26,50 A I nN I 2 I 1 3,35 / 26,5 4,63/ 31,11,318 /137,10 A b). Las caídas de tensión en las cargas son, V AN Z 1 I AN 25, 0 / 32, 0 4, 63/ 31,10 115,8 / 0,90 V V NB Z 2 I NB 38, 0 / 26,5 3,35 / 26,5 127,3/ 0, 00 V c). Las caídas de tensión en las líneas y el conductor del neutro son, V aA Z L I aA 0,800 /12, 0 4, 63/ 31,1 3, 70 / 19,10 V V Bb Z L I Bb 0,800 /12, 0 3,35 / 26,5 2, 68 / 14,50 V V nN Z N I nN 0,800 /12,0 1,318/137,1 1,054 /149,10 V Carga entre conductores de línea y el conductor del neutro, más carga entre líneas, con la alimentación aplicada directamente en sus terminales. En la figura número 12, se muestran las condiciones anteriores. 21 ELECTROTECNIA III-22 I aA a n I AN I AB A Z1 I nN I NB Z2 I Bb b Z3 N B FIGURA NÚMERO 12 Las tensiones son, V an V nb V ; V ab 2V Las corrientes son, I AN V an V V nb V V ab 2V ; I NB ; I AB Z1 Z1 Z2 Z2 Z3 Z3 I aA I AN I AB ; I Bb I NB I AB I nN I AN I NB ; I nN I NB I AN V V Z 2 Z1 Hay corriente en el conductor del neutro. Ejemplo 2-7. En un sistema monofásico de tres hilos con tensiones de 115,0/230 V, se conectan cargas, como se muestra en la figura número 12, donde Z1 es igual a 50,0 /0.00 , Z2 es igual a 100,0 /0,00 y Z3 es igual a 20,0 + j 10,00 . Se quiere analizar el sistema para determinar la potencia disipada en cada una de las tres cargas, así como la potencia total disipada por el sistema. SOLUCIÓN. Las tensiones son, V AN V NB V 115, 0 0, 00 V V AB V AN V NB 2V 230 0, 00 V Las corrientes en las cargas son, 22 ELECTROTECNIA III-23 I AN I NB I AB V AN 115, 0 0, 0 2, 30 0, 00 A Z1 50, 0 0, 0 V NB 115,0 0,0 1,150 0,00 A Z 2 100,0 0,0 V AB 230 0, 0 10, 29 26, 60 A Z 3 20, 0 j10,00 La corriente en el conductor del neutro es, I nN I NB I AN 1,150 0, 0 2, 30 0, 0 1,150 180, 00 A a).Las potencias disipadas por las cargas son, 2 PAN R1 I AN 50,0 2, 302 265 W 2 PNB R2 I NB 100,01,1502 132, 3 W 2 PAB R3 I AB 20,0 10, 292 2,12 103 W b). La potencia total disipada por el sistema es, P PAN PNB PAB 265 132, 3 2,12 103 2,52 103 W Carga entre conductores de línea y el conductor del neutro, más carga entre líneas, con la alimentación suministrada a través de líneas de alimentación. En la figura número 13, se muestran las condiciones anteriores. El análisis del circuito se puede efectuar mediante el método de mallas. Las tensiones en la fuente son, V an V nb V ; V ab 2V 23 ELECTROTECNIA III-24 ZL a I aA I1 ZN n I2 I AN Z1 I nN I NB ZL I AB A I3 N Z3 Z2 I Bb b B FIGURA NÚMERO 13 Las ecuaciones de las mallas son, V an I 1 Z L Z 1 Z N I 2 Z N I 3 Z 1 V nb I 1 Z N I 2 Z N Z 2 Z L I 3 Z 2 0 I1 Z1 I 2 Z 2 I 3 Z1 Z 2 Z 3 La solución matemática de las ecuaciones se puede realizar por diferentes métodos. Aquí utilizaremos la solución de ellas por medio del cálculo matricial. La ecuación para obtener las tensiones son, V an Z 11 V nb Z 21 0 Z 31 Z 12 Z 22 Z 32 Z 13 I 1 Z L Z 1 Z N Z 23 I 2 ZN Z 33 I 3 Z1 ZN ZN Z2 ZL Z2 I1 Z2 I 2 Z 1 Z 2 Z 3 I 3 Z1 La ecuación para obtener las corrientes de malla son, I 1 Z Z Z 1 N L ZN I2 Z1 I 3 ZN ZN Z2 ZL Z2 Z2 Z 1 Z 2 Z 3 Z1 1 V an V nb 0 Corriente en el conductor del neutro, 24 ELECTROTECNIA III-25 I nN I 2 I 1 Hay corriente en el conductor del neutro. Las corrientes en las líneas son, I aA I 1 ; I Bb I 2 Las corrientes en las cargas son, I AN I 1 I 3 ; I NB I 2 I 3 ; I AB I 3 Ejemplo 2-8. Se desea analizar el circuito mostrado en la figura número 13, para determinar la potencia activa disipada por cada una de las tres cargas y la potencia activa disipada en las líneas y el conductor del neutro. Las tensiones en la fuente son de 120,0/240 V; las impedancias de la carga son Z1 = 50,0/0,00 , Z2 =100,0 /0,00 y Z3 =22,4 /26,60 ; las impedancias de las líneas son de ZL =1,000 /0,00 y la del conductor del neutro es de 3,00 /0,00 . SOLUCIÓN, Las corrientes de malla son, I 1 1, 000 / 0, 0 50, 0 / 0, 0 3, 00 / 0, 0 3, 00 / 0, 0 I 2 50, 0 / 0, 0 I 3 3, 00 / 0, 0 3, 00 / 0, 0 100, 0 / 0, 0 1, 000 / 0, 0 100, 0 / 0, 0 100, 0 / 0, 0 50, 0 / 0, 0 100, 0 / 0, 0 22, 4 / 26, 6 50, 0 / 0, 0 1 120, 0 / 0, 0 120, 0 / 0, 0 0 I 1 11, 71/ 20, 0 I 2 10,80 / 22, 0 I 3 9, 78 / 24, 7 Las corrientes en las líneas son, I aA I 1 11, 71/ 20, 00 A I Bb I 2 10,80 / 22, 00 A La corriente en el conductor del neutro es, I nN I 2 I 1 10,80 / 22, 0 11, 71/ 20, 0 0,991/177, 60 A Las corrientes en las cargas son, I AN I 1 I 3 11,71/ 20,0 9,78 / 24,7 2,12 / 2, 20 A 25 ELECTROTECNIA III-26 I NB I 2 I 3 10,80 / 22,0 9,78/ 24,7 1,129 / 2,10 A I AB I 3 9, 78 / 24, 70 A a). Las potencias activas disipadas en cada una de las cargas son, 2 P1 R1 I AN 50,0 2,122 225 W 2 P2 R2 I NB 100,0 1,1292 127,5 W 2 P3 R3 I AB 22, 4 cos 26, 6 9, 782 1916 W b). Las potencias activas disipadas en las líneas y el conductor del neutro son, 2 PaA RL I aA 1, 000 11, 712 137,1 W 2 PBb RL I Bb 1, 000 10,802 116, 6 W 2 PnN RN I nN 3, 00 0,9912 2,95 W 3. MEDICIÓN DE LA POTENCIA ACTIVA. EL TEOREMA DE BLONDEL. El conocimiento de los principios de la medición de la potencia eléctrica es de gran importancia. El teorema de Blondel relaciona el tipo de sistema con el número de elementos necesarios para medir su potencia activa, dicho teorema se enuncia en la forma siguiente: En una red eléctrica alimentada con n hilos o conductores, la potencia activa total de la red esta dada por la suma algebraica de las indicaciones de n wáttmetros monofásicos, conectados en tal forma que cada uno de los hilos contenga una bobina de corriente de un wáttmetro, con sus correspondientes circuitos de tensión conectados entre los hilos de sus bobinas de corriente y un punto común a todos los circuitos de tensión. Si el punto común queda localizado en uno de los hilos, entonces la potencia activa total de la red estará dada por la indicación de n-1 wáttmetros o elementos. Para demostrar el teorema, vamos a considerar un circuito de n hilos como el mostrado en la figura número 14. Designemos los hilos con los número 1, 2, ..., n; con v1, v2, ..., vn, las tensiones instantáneas de cada uno de los hilos y con i1, i2, ..., in, las corrientes instantáneas en cada uno de ellos. La suma de las indicaciones de los n wáttmetros es igual a, 1 1 WM T i v v dt T i v T 0 T 1 1 0 0 2 2 v0 dt ... 1 T i v T 0 n n v0 dt por otro lado tenemos que, 26 ELECTROTECNIA III-27 i1 i2 ... in 0 y como consecuencia, n i1 v0 i2 v0 ... in v0 v0 ik 0 1 Sustituyendo esta condición en la suma de las indicaciones tendremos, 1 WM T T 0 i1 v1 dt 1 T T 0 i2 v2 dt ... 1 T T 0 in vn dt Suma que es igual a la ecuación de la potencia media o activa total de la red, anteriormente determinada, con lo cual queda demostrado en su primera parte el teorema de Blondel. i1 BC1 v1 1 i2 BP1 RP1 BP2 RP2 BC2 v 2 2 FUENTE i3 BC3 CARGA v3 3 v0 ik BP3 RP3 BPk RPk BPn RPn BCk v k k in BCn vn n FIGURA NÚMERO 14. RED DE n HILOS CON n WÁTTMETROS Se puede observar que si el punto común se hace coincidir con uno de los n hilos, el circuito de tensión del wáttmetro correspondiente tendrá aplicada una tensión igual a cero, de aquí que la potencia activa total de la red, en este caso, esté dada solamente por las indicaciones de n-1 27 ELECTROTECNIA III-28 wáttmetros, y podemos retirar el wáttmetro que no está dando indicación. Con este razonamiento sencillo queda probada la segunda parte del teorema de Blondel. La demostración anterior es completamente general y por consiguiente se aplica a todos los casos que se presentan en la medición de la potencia activa eléctrica. De acuerdo con el teorema de Blondel, la potencia activa de un circuito monofásico de tres hilos se puede medir con 3 o 2 wáttmetros, siendo el más usual el que consta de dos wáttmetros, como se muestra en la figura número 15. FUENTE a I aA * * BC1 BP1 RP1 WM1 n I nN CARGA WM2 * BP2 RP2 I bB b * BC2 FIGURA NÚMERO 15 La indicación de cada uno de los wáttmetros es igual a, WM1 V AN I aA VAN I aA cos VI aAAN V WM2 V BN I bB VBN I bB cos VIbBBN V * * AN I aA BN I bB La suma de las indicaciones de los wáttmetros, de acuerdo con el teorema de Blondel, nos dará la potencia activa total del circuito. P WM1+ WM2 Ejemplo 2-9. Una fuente monofásica de tres hilos de 240/120 V alimenta dos cargas de 120,0 V de tensión nominal y una carga de 240 V nominales. Las cargas son entre A y N un conjunto de 10 lámparas incandescentes de 75 W nominales cada una, entre N y B se tiene un conjunto de 6 lámparas incandescentes de 60 W cada una y 3 lámparas incandescentes de 150 W cada una, y entre A y B se tiene un motor de inducción monofásico de 4 kW con factor de potencia 0,800 atrasado. La resistencia de las líneas de alimentación es de 0,01000 . Determinar: a). Las corrientes en las líneas y el conductor del neutro; b). Las potencias compleja, aparente, activa y reactiva tomadas por la carga; c). Las potencias compleja, aparente, activa y reactiva suministradas por la fuente. d).Si se quiere medir la 28 ELECTROTECNIA III-29 potencia activa con wáttmetros monofásicos, muestre el diagrama eléctrico que se utilizaría para realizar la medición, utilizando la cantidad mínima de wáttmetros y calcule la indicación de cada uno de ellos. RL a A RL N n RL b B SOLUCIÓN. Las resistencias e impedancias del circuito son, RAN 2 VAN 120, 02 19, 20 PAN 10, 00 75, 0 Z AN 19, 20 / 0, 00 2 VNB 120, 02 RNB 17, 78 PNB 6 60 3 150 Z NB 17, 78 / 0, 00 PAB 4, 00 103 S AB 5, 00 103 VA FPAB 0, 800 S AB S AB / cos1 FPAB 5,00 103 / 36,90 VA 2 VAB 2402 Z AB 11, 52 S AB 5, 00 103 Z AB 11, 52 / 36, 90 Redibujando el circuito tenemos, 29 ELECTROTECNIA III-30 0,01 I A A a V an I 1 0,01 I N n N I3 V nb I 2 0,01 I B b B Utilizando el método de mallas tenemos, que las impedancias propias y mutuas de las mallas son, Z 11 0, 01 / 0, 0 19, 20 / 0, 0 0, 01 / 0, 0 19, 22 / 0, 00 Z 12 Z 21 0, 01 / 0, 00 Z 13 Z 31 19, 20 / 0, 00 Z 22 0, 01 / 0, 0 17, 78 / 0, 0 0, 01 / 0, 0 17, 80 / 0, 00 Z 23 Z 32 17, 78 / 0, 00 Z 33 19, 20 / 0, 0 11, 52 / 36, 9 17, 78 / 0, 0 46, 7 / 8, 50 La ecuación matricial del circuito es, 1 I 1 19, 22 0, 0 0, 01 0, 0 19, 20 0, 0 120, 0 0, 0 I 2 0, 01 0, 0 17, 80 0, 0 17, 78 0, 0 120, 0 0, 0 19, 20 0, 0 17, 78 0, 0 46, 7 8, 5 0 I 3 Resolviendo la ecuación tenemos, I1 26,1 / 28, 5 I 2 26, 5 / 28, 0 20, 8 / 36, 8 I 3 a) Las corrientes en las líneas y en el conductor del neutro son, I A I 1 26,1/ 28,50 A I B I 2 26,5 / 152,00 A 30 ELECTROTECNIA III-31 I N I 2 I 1 26,5 / 28,0 26,1/ 28,5 0,461/ 1,60 A b) Las corrientes en las cargas son, I AN I 1 I 3 26,1/ 28,5 20,8 / 36,8 6, 28 / 0,10 A I NB I 2 I 3 26,5 / 28,0 20,8 / 36,8 6,74 / 0, 20 A I AB I 3 20,8 / 36,80 A Las potencias complejas tomadas por las cargas son, 2 S AN Z AN I AN 19, 20 / 0, 0 6, 28 2 757 / 0, 0 0 VA 757 j0 VA 2 S NB Z NB I NB 17, 78 / 0, 0 6, 742 808 / 0, 00 VA 808 j0 VA 2 S AB Z AB I AB 11, 52 / 36, 9 20, 82 4, 98 103 / 36, 9 VA 3,98 10 3 j2,99 10 3 VA Las potencias aparentes tomadas por las cargas son, S AN 757 VA S NB 808 VA S AB 4, 98kVA Las potencias activas tomadas por las cargas son, PAN 757 W PNB 808 W PAB 3, 98kW Las potencias reactivas tomadas por las cargas son, QAN 0 QNB 0 QAB 2, 99kvar IND c) La potencia compleja suministrada por la fuente es, 31 ELECTROTECNIA III-32 * * S F V an I A V bn I B 120, 0 / 0, 0 26,1 / 28, 5 120, 0 / 180, 0 26, 5 / 152, 0 6, 31 103 / 28, 50 VA 5,56 103 j2,98 103 VA La potencia aparente suministrada por la fuente es, S F 6, 31kVA La potencia activa suministrada por la fuente es, PF 5, 56kW La potencia reactiva suministrada por la fuente es, QF 2, 98kvar IND d). Puesto que se tiene un circuito de tres hilos, el número mínimo de wáttmetros que se pueden utilizar para realizar la medición solicitada es de 2. Conectados como se muestra en la figura siguiente. WM1 RL a * BC1 BP1 V an A * RL n N V nb BP2 RL b * * BC2 B WM2 Las lecturas de los wáttmetros son, WM1=V AN I A VAN I A cos VAN IA WM2 =V BN I B VBN I B cos VBN IB Donde las tensiones aplicadas a los wáttmetros son, V AN Z AN I AN 19, 20 0,0 6, 28 0,1 120,6 0,10 V 32 ELECTROTECNIA III-33 V BN Z NB I BN 17,78 0,0 6,74 179,8 119,8 179,80 V Los ángulos de las corrientes son, 152,00 V AN IB 28,60 28,20 IA V BN -179,80 Sustituyendo valores en las ecuaciones de las indicaciones de los wáttmetros tenemos, WM1=120,6 26,1 cos 28,6 2, 76 10 3 W = 2,76kW WM2 =119,8 26,5cos 28, 2 2, 80 103 W = 2,80kW Utilizando otra alternativa de cálculo tenemos, WM1= WM2 = V * V AN I A 2, 76 10 * BN IB 2, 80 10 3 3 120, 6 0,1 26,1 28, 5 3,15 103 28, 6 j1, 507 103 2, 76 103 W = 2,76kW 119, 8 179, 8 26, 5 152, 0 3,17 103 28, 2 j1, 500 103 2, 80 10 3 W = 2,80kW 4. EJERCICIOS. Ejercicio 2-1. El sistema monofásico de tres hilos balanceado de la figura, tiene una tensión V AN de 220 V de una frecuencia de 60 Hz, las impedancias ZAN y ZNB son de un valor de 5,00 + j 2,00 . a) ¿Cuál debe ser el valor de la capacitancia C para proporcionar un factor de potencia unitario a la carga? b) ¿ De cuantos kvar debe ser el capacitor? 33 ELECTROTECNIA III-34 A a IA Z AN N n C IN Z NB IB b B SOLUCIÓN. Tomando como referencia a la tensión V AN , la corriente I AN es igual a, I AN V AN 220 0,0 220 0,0 40,8 21,80 A Z AN 5,00 j 2,00 5,39 21,8 La potencia compleja, en la misma carga es, * S AN V AN I AN 220 0, 0 40,8 21,8 8,98 103 21,80 VA 8,98 21,80 kVA Puesto que la carga entre N y B es igual a la carga entre A y B, entonces la potencia compleja para estas dos cargas es, S 2 8,98 21,8 17,96 21,8 0 kVA 16,68 j 6,67 kVA De donde podemos deducir que la potencia reactiva tomada por las cargas ZAN y ZNB es, Q 6,67 kvar IND Para llevar el circuito a tener un factor de potencia unitario es necesario contrarrestar ésta potencia reactiva inductiva con una potencia reactiva capacitiva del mismo valor, lo cual se logra con la adición de un capacitor al circuito. La corriente que debe tomar éste capacitor es, IC 6,67 10 3 Q 15,16 A V AB 440 La reactancia capacitiva del capacitor es, 34 ELECTROTECNIA III-35 XC V AB 440 29,0 I C 15,16 Considerando que la fuente tiene una frecuencia de 60 Hz, la capacitancia debe ser de 1 1 91,5 10 6 F 91,5 F 2 f X C 2 60 29,0 C De los cálculos anteriores tenemos que, a) El valor de la capacitancia del capacitor para proporcionar un factor de potencia unitario al circuito es, C 91,5 F b) La potencia reactiva que debe suministrar el capacitor es, QC 6,67 kvar CAP Ejercicio 2-2. Un sistema monofásico de tres hilos balanceado, de una frecuencia de 60 Hz, tiene cargas ZAN = ZNB formadas por una resistencia de 5,00 en serie con una inductancia de 5,31 mH, y una carga ZAB formada por una resistencia de 12,00 y una inductancia de 31,8 mH. Suponga que en las tres líneas no existe resistencia. Sea V an V nb 115, 0 0, 00 V. a) Encuentre las corrientes en las cargas. b) El sistema se desbalancea al conectar otra resistencia de 10,00 en paralelo con ZAN. Encuentre las corrientes en las líneas y en el conductor del neutro. I aA a A ZAN I nN n N ZAB ZNB I bB b B SOLUCIÓN. a). Las tensiones son, V AN V NB V 115, 0 0, 00 V 35 ELECTROTECNIA III-36 V AB V AN V NB 2V 230 0, 00 V Las impedancias de las cargas son, Z AN Z NB R j2 f L 5,00 j2 60 5, 31103 5, 39 21,80 Z AB RAB j2 f LAB 12,0 j2 60 31,8103 20,0 36,80 Las corrientes en las cargas son, I AN V an 115, 0 0, 0 21, 4 21, 80 A Z AN 5, 39 21, 8 I NB V nb 115, 0 0, 0 21, 4 21, 80 A Z NB 5, 39 21, 8 I AB V ab 230 0, 0 11, 50 36, 80 A Z AB 20, 0 36, 8 De donde las corrientes en las líneas son, I aA I AN I AB 21, 4 21, 80 11, 50 36, 8 32, 6 27, 00 A I bB I NB I AB 21, 4 21, 8 11, 50 36, 8 32, 6 153, 00 A Por estar la carga balanceada la corriente en el conductor del neutro vale cero. I nN 0 b) A a I aA Z AN Z N n Z AB I nN Z NB I bB b B 36 ELECTROTECNIA III-37 La impedancia entre A y N es, Z1 Z AN Z 5, 39 21, 8 10, 00 0, 0 3, 57 14, 20 Z AN Z 5, 39 21, 8 10, 00 0, 0 Las corrientes en la carga son, I AN V an 115, 0 0, 0 32, 2 14, 20 A Z1 3, 57 14, 2 I NB 21, 4 21, 80 A I AB 11, 50 36, 80 A Las corrientes en las líneas son, I aA I AN I AB 32, 2 14, 2 11, 50 36, 8 43, 0 20,10 A I bB I NB I AB 21, 4 21, 8 11, 50 36, 8 32, 6 153, 00 A La corriente en el conductor del neutro es I nN I NB I AN 21, 4 21, 8 32, 2 14, 2 11, 35 179, 80 A Ejercicio 2-3. El circuito mostrado en la figura representa un sistema monofásico de tres hilos, de 60 Hz. La carga son 20 casas, cada una requiere en promedio de 12,00 kW con factor de potencia 0,950 atrasado. La impedancia de la línea es de 2,70 + j 4,00 . Considere un transformador ideal con tensión primaria de 8,00 kV y tensiones secundarias de 120,0/240 V. a) ¿Cuál debe ser la magnitud de la corriente en el primario del transformador? b) ¿Cuáles son las pérdidas de potencia en la línea? c) ¿Cuál es el valor del capacitor a través del primario del transformador que hace mínimas las pérdidas de la línea?, considere que la tensión en la carga es constante. d) ¿Cuáles son las pérdidas de potencia en la línea con el factor de potencia corregido? ZL A N CARGA B 37 ELECTROTECNIA III-38 SOLUCIÓN. Las potencias activa y compleja entre la línea y el neutro son, PAN PNB 10 12,00 10 3 120,010 3 W 120,0 kW S AN S BN PAN 120,0 10 3 cos1 0,950 18,2 126,3 10 3 18,2 0 VA 126,3 18,20 kVA FP 0,950 Las corrientes de línea en el secundario son, * I AN S AN 126,3 103 18, 2 1 053 18, 20 A 120, 0 0, 0 V AN I AN I NB 1 053 18, 20 A La relación del transformador es, n a) V P 8,00 10 3 33,3 V AB 240 De donde la corriente en el primario es, ' IA IP I AN 1 053 18, 2 31, 6 18, 20 A n 33,3 b) Las pérdidas de potencia en la línea son, PL R L I P2 2,70 31,6 2 2,70 10 3 W 2,70 kW c) La potencia compleja total de la carga es, S S AN S NB 2 126,3 10 3 18,2 253 10 3 18,2 0 VA 253 18,20 kVA 240 j 78,9 kVA De donde la potencia reactiva total de la carga es, Q 78 ,9 kvar IND Para contrarrestar esta potencia reactiva inductiva se necesita un capacitor que tome la misma magnitud pero de potencia capacitiva, esto es, QCAP 78 ,9 kvar CAP La corriente que toma el capacitor es, I CAP QCAP 78,9 10 3 9,86 A VP 8,00 10 3 38 ELECTROTECNIA III-39 La reactancia del capacitor es, XC VP 8,00 10 3 811 I CAP 9,86 Y su capacitancia es, C 1 1 3,27 10 6 F 3,27 F 2 f X C 2 60,0 811 d) La corriente que ahora toma la línea es, I LC I P I CAP 31, 6 18, 2 9,86 90, 0 30, 0 0, 00 A Las pérdidas en la línea con el factor de potencia corregido son, 2 PLC R L I LC 2,70 30,0 2 2,43 10 3 W 2,43 kW Ejercicio 2-4. En una ciudad se distribuye la energía eléctrica con un sistema trifásico de 12,5 kV entre fases. Cada grupo de casas se alimenta con una fase y tierra, a través de un transformador monofásico de tres hilos con tensiones secundarias de 240/120 V, como se muestra en la figura. a 12,5/ 3 kV n A 120 V N 120 V B 240 V A tierra A tierra a) ¿Cuál es la relación de espiras (primarias/secundarias) con respecto a la tensión de 240 V? b) ¿Cuando se conecta una secadora de pelo, de 1 500 W, cuanto aumenta la corriente en la fase de alta tensión?. Considere que el factor de potencia es unitario y que el transformador es 100 % eficiente. SOLUCIÓN. a) La tensión de fase a tierra en el primario es, Vn Vl 12,50 10 3 7,22 10 3 V 3 3 39 ELECTROTECNIA III-40 La relación de espiras del devanado primario al devanado secundario del transformador es, n Van 7,22 10 3 30,1 V AB 240 ; n 30,1:1 b) La relación de espiras del devanado primario a la parte del secundario que está conectado a tierra es, nn Van 7,22 10 3 60,2 V AN 120 ; nn 60,2 :1 La corriente en el secundario debida a la conexión de la secadora es, IS P 1500 12,50 A V AN 120 La cual referida al lado de alta tensión es, IP I S 12,50 0,208 A nn 60,2 Ejemplo 2-5. El circuito secundario de un transformador monofásico de tres hilos, de 120,0/240 V, suministra energía a un grupo de residencias que tienen alumbrado de dos hilos, como se muestra en la figura. Cada rectángulo representa una residencia cuya carga es de 1 200 W, a 125 V nominales y tiene un factor de potencia unitario. Las impedancias de las líneas de alimentación son cada una de 0,1000 + j 0,0400 . Determinar: a) las corrientes en las líneas y en el conductor del neutro, b) las potencias compleja, aparente, activa y reactiva tomadas por la carga, y c) las potencias compleja, aparente, activa y reactiva suministradas por la fuente. Z a V an Z n A N V nb Z b B SOLUCIÓN. La carga nominal entre A y N es, PAN 125 5 1200 6, 00 103 W La cual representa una resistencia equivalente de, 40 ELECTROTECNIA III-41 RAN 2 V125 125, 02 2, 60 PAN 125 6, 00 103 La carga nominal entre N y B es, PNB125 4 1200 4,80 103 W La cual representa una resistencia equivalente de, RNB 2 V125 125, 02 3, 26 PNB125 4, 80 103 El circuito eléctrico queda como, Z = 0,1000 + j 0,0400 A a I1 V an 120, 0 0, 0 0 V n Z V nb 120, 0 0, 0 0 V V nb RAN 2, 60 0, 0 0 N I2 RNB 3, 26 0, 0 0 Z b B Analizando el circuito por el método de mallas y escribiendo la matriz correspondiente tenemos, - 2, 80 0,1000 j 0,0400 - j 0,0400 0,1000 3,46 j 0,0400 I 1 120, 0 / 0, 0 j 0,0800 I 2 120, 0 / 0, 0 Resolviendo la ecuación matricial, las corrientes de malla son, I 1 44,1/ 1,00 A I 2 36,0 / 0,50 A a) Las corrientes en las líneas son, I aA I AN I 1 44,1/ 1,00 A I bB I NB I 2 36,0 / 179,50 A 41 ELECTROTECNIA III-42 La corriente en el conductor del neutro es, I Nn I 1 I 2 44,1/ 1,0 36,0 / 0,5 8,11/ 3, 20 A b) Las potencias complejas tomadas por las cargas son, * 2 S AN Z AN I AN I AN Z AN I AN 2,60 / 0,0 44,12 5,06 103 / 0,0 VA 0 2 S NB Z NB I NB 3, 26 / 0, 0 36, 02 4, 22 10 3 / 0, 00 VA Las potencias aparentes tomadas por las cargas son, S AN 5,06 103 VA 5,06kVA SNB 4, 22 103 VA 4,22kVA Las potencias activas tomadas por las cargas son, PAN 5, 06kW PNB 4, 22kW Las potencias reactivas tomadas por las cargas son, QAN QNB 0 c) La potencia compleja suministrada por la fuente es, * * S F V an I AN V bn I BN 120, 0 / 0, 0 44,1 / 1, 0 120, 0 / 180, 0 36, 0 / 179, 9 9, 61 103 / 0, 80 VA 9, 61 / 0, 80 kVA 9,61 j0,1300kVA La potencia aparente suministrada por la fuente es, S F 9, 61kVA La potencia activa suministrada por la fuente es, PF 9, 61kW La potencia reactiva suministrada por la fuente es, QF 130, 0 var IND 42 ELECTROTECNIA III-43 Ejercicio 2-6. Un circuito monofásico de tres hilos de 60 Hz se utiliza para alimentar un servicio comercial de trabajo ligero que consiste de cargas de iluminación, calefacción y motores pequeños, como se muestra en la figura a). Las cargas de iluminación y calefacción son esencialmente resistencias y, por ello, con un factor de potencia unitario, mientras que las cargas de motores tienen un factor de potencia atrasado. Suponga que la resistencia de los conductores de fase y del neutro son cada una de 0,050 . Se desea diseñar una configuración balanceada para la red y determinar su viabilidad económica. a). Calcular las corrientes de fase y del neutro, la potencia compleja y el factor de potencia de cada fuente; b) Enseguida desplace la carga de calentamiento (tablero H) al punto b, como se muestra en la figura b. Esto se llama “balancear” la carga, repetir el análisis de a). c) Evalúe las pérdidas de las líneas del sistema para a) y b). d). Se quiere medir la potencia activa utilizando wáttmetros monofásicos, dibuje el circuito eléctrico correspondiente y calcule las indicaciones de ellos. 0,050 IA a IL Tablero L 5,00 kW a 120,0 V 0 120,0 /0,0 V 0,050 IH IM Tablero H 5,00 kW a 120,0 V IN Tablero M 10,00 kVA FP = 0,800 AT a 240 V n 0 120,0 /0,0 V 0,050 IB b (a) 43 ELECTROTECNIA III-44 IA 0,050 a IL IM Tablero L 5,00 kW a 120,0 V 0 120,0 /0,0 V IN 0,050 n IH Tablero M 10,00 kVA FP = 0,800 AT a 240 V Tablero H 5,00 kW a 120,0 V 0 120,0 /0,0 V IB 0,050 b (b) SOLUCIÓN. a) La impedancia de los tableros L y H son, 2 V L (120, 0 0, 0)2 ZL ZH 2, 88 0, 00 3 S L 5, 00 10 0, 0 La impedancia del tablero M es, 2 VM (240 0, 0)2 ZM 5, 76 36, 90 3 S M 10, 00 10 ARCcos 0,800 El paralelo de las impedancias ZL y ZH es, Z LH ZL ZH 2, 88 0, 0 2, 88 0, 0 1, 440 0, 00 Z L Z H 2, 88 0, 0 2, 88 0, 0 El circuito de la figura a) queda como, 44 ELECTROTECNIA III-45 0 I A 0,050 /0,0 I1 IN n 120,0 /0,00 V 0,050 /0,00 I2 5,76 /36,90 1,440 /0,00 120,0 /0,00 V a IB b 0,050 /0,00 El análisis del circuito se puede efectuar utilizando el método de mallas y escribiendo la matriz correspondiente. Las impedancias son, 0 Z 11 0, 050 0, 0 1, 440 0, 0 0, 050 0, 0 1, 540 0, 0 Z 12 Z 21 1,440 0,0 0,050 0,0 1,490 0,00 Z 22 0,050 0,0 1,440 0,0 5,76 36,9 0,050 0,0 7,05 29,40 La ecuación matricial para obtener las corrientes de malla es, I 1 1, 540 0, 0 1, 490 0, 0 1 120, 0 0, 0 111, 9 12, 0 I 2 1, 490 0, 0 7, 05 29, 4 120, 0 0, 0 40, 4 36, 4 Las corrientes de malla son, I 1 111, 9 12, 00 A I 2 40,4 36,40 A Las corrientes en el circuito son, I A I 1 111,9 12,00 A I N I 1 I 2 111, 9 12, 0 40, 4 36, 4 76, 9 0, 50 A I B I 2 40, 4 36, 40 A 45 ELECTROTECNIA III-46 IL IH I N 76, 9 0, 5 38, 5 0, 50 A 2 2 I M I 2 40, 4 36, 40 A La potencia compleja y el factor de potencia para cada fuente son, * S a V an I A 120, 0 0, 0 111, 9 12, 0 13, 43 103 12, 00 VA 13,43 12,0 0 kVA 13,14 j2,79kVA FPa cos(12,0) 0,978 AT y de manera similar, * S b V nb I B 120, 0 0, 0 40, 4 36, 4 4, 85 10 3 36, 4 0 VA 4,85 36,4 0 kVA 3,90 j2,88kVA FPb cos(36,4) 0,805 AT b) Bajo la condición balanceada el circuito queda como, IN N n 120,0 /0,00 V 0,050 /0,00 I3 IB b 2,88 /0,00 I1 0,050 /0,00 2,88 /0,00 120,0 /0,00 V a A IL I2 IH IM 5,76 /36,90 0 I A 0,050 /0,0 B Las impedancias de malla son, Z 11 0,050 0,0 2,88 0,0 0,050 0,0 2,98 0,00 Z 12 Z 21 2,88 0,00 Z 13 Z 31 0,050 0,00 46 ELECTROTECNIA III-47 Z 22 2,88 0,0 5,76 36,9 2,88 0,0 10,93 18,50 Z 23 Z 32 2,88 0,00 Z 33 0,050 0,0 2,88 0,0 0,050 0,0 2,98 0,00 Analizando el circuito por el método de mallas y escribiendo la ecuación matricial correspondiente tenemos, 1 I 1 2, 98 0, 0 2, 88 0, 0 0, 050 0, 0 120, 0 0, 0 76, 6 17, 9 40, 4 36, 4 0 I 2 2, 88 0, 0 10, 93 18, 5 2, 88 0, 0 0, 050 0, 0 2, 88 0, 0 2, 98 0, 0 120, 0 0, 0 76, 6 17, 9 I 3 Las corrientes de malla son, I 1 76, 6 17, 90 A I 2 40,4 36,40 A I 3 76, 6 17, 90 A Las corrientes en el circuito son, I A I 1 76, 6 17, 90 A I N I 1 I 3 76,6 17,9 76,6 17,9 0 I B I 3 76, 6 17, 90 A I L I 1 I 2 76,6 17,9 40,4 36,4 40,4 0,60 A I H I 3 I 2 76,6 17,9 40,4 36,4 40,4 0,60 A I M I 2 40, 4 36, 40 A La potencia compleja y el factor de potencia para cada fuente son, * S a V an I A 120, 0 0, 0 76, 6 17, 9 9,19 103 17, 90 VA 9,19 17,90 kVA 8,75 j2,82kVA FPa cos(17,9) 0,952 AT 47 ELECTROTECNIA III-48 * S b V nb I B 120, 0 0, 0 76, 6 17, 9 9,19 103 17, 9 VA 9,19 17,9kVA 8,75 j2,82kVA FPb cos(17,9) 0,952 AT c) La potencia activa pérdida en las líneas en kW, en el caso desbalanceado es, Pd R I A2 I B2 I N2 0, 050 111, 92 76, 92 40, 42 1003 W 1,003kW La potencia activa pérdida en las líneas en kW, en el caso balanceado es, PB 0, 050 76, 62 0 76, 62 586 W 0,586kW Del análisis anterior se puede observar que el caso balanceado produce menos pérdidas de distribución por lo que se considera el caso más económico. d). En virtud de que tenemos un circuito de tres hilos, utilizaremos dos wáttmetros para realizar la medición solicitada, conectados como se muestra en la figura siguiente. WM1 RL a * BC1 BP1 V an A * RL n N V nb BP2 RL * b * BC2 B WM2 Las lecturas de los wáttmetros son, WM1=V AN I A VAN I A cos WM2 =V BN I B VBN I B cos VAN IA VBN IB Donde las tensiones aplicadas a los wáttmetros son, V AN Z L I AN 2, 88 0, 0 40, 4 0, 6 116, 4 0, 60 V 48 ELECTROTECNIA III-49 V BN Z H I H 2, 88 0, 0 40, 4 179, 4 116, 4 179, 40 V Sustituyendo valores en las ecuaciones de las indicaciones de los wáttmetros tenemos, WM1=116,4 76,6 cos 0,6 +17,9 8, 46 10 3 W = 8,46kW WM2 =116,4 76, 6cos 179, 4 197, 9 8, 46 10 3 W = 8,46kW Utilizando otra alternativa de cálculo tenemos, WM1= WM2 = V * AN IA 8, 46 10 3 * V BN I B 8, 46 10 3 116, 4 0, 6 76, 6 17, 9 8, 92 103 18, 5 j2, 83 103 8, 46 103 W = 8,46kW 116, 4 179, 4 76, 6 197, 9 8, 92 103 18, 5 j2, 83 103 8, 46 103 W = 8,46kW 49 ELECTROTECNIA III-50 UNIDAD 3. GENERACIÓN DE TENSIONES POLIFÁSICAS 1. INTRODUCCIÓN. Un sistema polifásico consiste de dos o más tensiones desfasadas entre ellas, las cuales alimentan cargas conectadas entre ellas. Las tensiones polifásicas se generan en la misma forma que las tensiones monofásicas. Un sistema polifásico, simplemente es un conjunto de sistemas monofásicos desfasados uno con respecto a los demás un determinado ángulo que depende del arreglo geométrico de los devanados dispuestos en la máquina rotatoria. El sistema más común es el trifásico, que es la interconexión de tres sistemas monofásicos, cuyas tensiones, aunque semejantes en amplitud y frecuencia, están desplazadas en 120 grados eléctricos entre sí. Los equipos utilizados en los sistemas polifásicos presentan muchas ventajas sobre los monofásicos. Los generadores son más económicos por kilowatt, y funcionan con mayores eficiencias; esto significa que las grandes plantas generadoras polifásicas (trifásicas en su mayoría) pueden construirse de modo que suministren servicios en gran escala a un costo bajo. Las líneas de transmisión y distribución de energía son comparativamente menos costosas, por que por ejemplo para líneas trifásicas, el peso de cobre o aluminio es igual a tres cuartas partes del necesario para en una línea monofásica equivalente. Los motores polifásicos y equipos asociados (conmutadores, transformadores y elementos de control) pueden ser también de capacidades mayores cuando funcionan en servicios polifásicos. Estas consideraciones revisten gran importancia en el funcionamiento de los equipos industriales. Un serio inconveniente para el uso de potencia monofásica es su naturaleza pulsante; ello es particularmente notable en los motores, donde no solamente se anula la potencia cuatro veces en cada ciclo, sino también se hace negativa durante dos intervalos de tiempo en cada ciclo. De esto resulta un par motor no uniforme aplicado a la carga, y la velocidad es variable de instante en instante. En cambio los motores polifásicos funcionan con esfuerzo uniforma y consumen potencia a un ritmo constante, sin inversiones; son también más económicos y eficientes, y menos sujetos a interrupciones de servicio que los motores monofásicos. 2. GENERACIÓN DE TENSIONES TRIFÁSICAS. En la figura número 1 se muestra una bobina AA' sobre la armadura de una máquina de dos polos. Cuando los polos están en la posición mostrada, la tensión en el conductor A, de la bobina AA', es máxima. Si tenemos otro conductor B, de una bobina BB', desplazado 120 grados de la posición del conductor A, este alcanzará su tensión máxima 120 grados después que el conductor A, de la misma forma, si tenemos un conductor C, de una bobina CC', desplazado 240 grados de la posición del conductor A, éste alcanzará su tensión máxima 240 grados después que el conductor A. Así, las bobinas AA', BB' y CC' tienen sus tensiones desfasadas 120 grados en tiempo, como se muestra en la figura número 2. A este sistema se le denomina trifásico, puesto que hay tres ondas desfasadas en tiempo. En general, el desplazamiento entre fases para un sistema simétrico de n fases es de 360/n grados eléctricos. 50 ELECTROTECNIA III-51 A B’ 120,00 N C C’ S B A’ 120,00 FIGURA NÚMERO 1. GENERADOR TRIFÁSICO ELEMENTAL Si las tres bobinas son iguales, el proceso de inducción de las fuerzas electromotrices será idéntico, incluso en lo cuantitativo. La diferencia está en que, siendo T el periodo de giro, en la bobina BB’ todo el proceso se realiza con un retraso de T/3, esto es 120,0 grados eléctricos, y en la bobina CC’ con un retraso de 2T/3, esto es 240,0 grados eléctricos. 1,2 eBB’ eAA’ 1,0 eCC’ 0,8 0,6 Tensión 0,4 0,2 0,0 -0,2 -0,4 -0,6 -0,8 -1,0 -1,2 00 30º 60º 90º 120º 150º 180º 210º 240º 270º 300º 330º 360º Grados FIGURA NÚMERO 2. GRÁFICA DE LAS TENSIONES GENERADAS Las tensiones se pueden expresar matemáticamente en el dominio del tiempo como, e AA' E AA' sen t E sen t eBB ' E BB ' sen t 120, 00 E sen t 120, 0 0 51 ELECTROTECNIA III-52 eCC ' E CC ' sen t 240, 00 E sen t 240, 00 y se muestran gráficamente en el plano cartesiano como se indica en la figura número 2. En la figura número 3 se muestra las tensiones en el dominio de la frecuencia, como un diagrama fasorial, esto es E C 'C abc C 120,00 C’ 120,00 B’ E A' A A’ A 120,00 B E B' B FIGURA NÚMERO 3.DIAGRAMA FASORIAL DE LAS FUERZAS ELECTROMOTRICES En la generación de tensiones del sistema trifásico, de la figura número 1, se consideró una rotación del campo en sentido de las manecillas del reloj, lo que corresponde a una rotación de las tensiones en sentido contrario a las manecillas del reloj, esta consideración hace que la tensión de la bobina B esté atrasada 120 grados con respecto a la tensión de la bobina A y que la tensión de la bobina C esté atrasada 120 grados con respecto a la tensión de la bobina B o 240 grados con respecto a la tensión de la bobina A. En otras palabras, el orden en el cual las tensiones de las bobinas, o fases, A, B y C obtienen sus valores máximos es ABC, a esto se le denomina secuencia de fases. Si la rotación se invierte, la secuencia de fases será ACB, esto significa que la tensión de la fase C estará atrasada 120 grados con respecto a la tensión de la fase A, en lugar de 240 grados como en el primer caso. En general, la secuencia de fases de las tensiones aplicadas a una carga se fija por el orden en el cual la línea trifásica se conecta, intercambiando cualquier par de líneas se invierte la secuencia. En un motor de inducción trifásico el efecto de invertir la secuencia da como resultado una inversión en su rotación. Lo que se acaba de explicar no constituye un alternador trifásico, sino un alternador utilizado para generar tres tensiones monofásicas desfasadas sin conexión. Generador conectado en estrella. Si se unen los extremos A', B' y C', o los A, B y C, de las bobinas del generador de la figura número 1, formando un neutro, se obtiene lo que se denomina una conexión en estrella del generador, y si además del punto neutro sacamos una línea para conectarla a la carga se obtiene lo que se denomina un sistema de generación de tres fases, cuatro hilos, conexión estrella, el cual se muestra en la figura número 4. Como mencionamos en la parte de la nomenclatura convencional que utilizaremos, con el fin de evitar confusiones, al emplear fuerzas electromotrices y caídas de tensión en un mismo circuito, utilizaremos sólo la nomenclatura de caídas de tensión, recordando que una fuerza electromotriz es una caída de tensión con sentido contrario. Además consideraremos que las tensiones generadas son simétricas. 52 ELECTROTECNIA III-53 a V an n c V ab V ca V bn b V cn V bc FIGURA NÚMERO 4. TENSIONES DE UN GENERADOR CONECTADO EN ESTRELLA El sistema de tensiones generadas se define como tensiones de línea a neutro (o tensiones al neutro o tensiones de fase), por ejemplo V an , o como tensiones de línea a línea (o tensiones de línea), por ejemplo V ab . Cuando una u otra definición se da la otra se puede determinar, teniendo en cuenta la secuencia de fases, como se muestra en la figura número 5. De la figura número 5 se tiene que las tensiones de línea a neutro (tensiones al neutro) son las mismas que las tensiones de fase (o de bobina). Así para una secuencia de fases abc tenemos, V an V 0, 00 V V bn V 120, 00 V V cn V 240, 00 V = V 120, 00 V 53 ELECTROTECNIA III-54 V ca abc V cn V an 120,00 V ab abc V cn V bn 150,00 30,00 120,00 V an V bn 120,00 V an V bn 120,00 V cn V bc FIGURA NÚMERO 5. DIAGRAMAS FASORIALES DE LAS TENSIONES AL NEUTRO Y DE LÍNEA DE UN GENERADOR CONECTADO EN ESTRELLA, CON SECUENCIA DE FASES abc. Las tensiones de línea a línea (tensiones de línea) son, V ab V an V bn V 0, 0 V 120, 0 3 V 30, 00 V En la ecuación anterior se puede observar que la tensión de línea es neutro (o fase) y que está adelantada 30,0 grados con respecto a ella. 3 veces mayor que la tensión al En forma similar para las otras tensiones de línea tenemos, V bc V bn V cn V 120, 0 V 240, 0 3 V 90, 00 V V ca V cn V an V 240, 0 V 0, 0 3 V 210, 00 V Ejemplo 3-1. La tensión de fase o al neutro de una fuente conectada en estrella simétrica, con secuencia de fases abc es V an = 127,0 /90,00 V. Determine las tensiones de línea de esta fuente. SOLUCIÓN. La magnitud de la tensión de línea está dada por la ecuación, VL 3 V fn 3 127,0 220 V Puesto que la tensión de línea está 30 grados adelante de la tensión de fase, cuando se tiene una secuencia de fases abc, entonces, V ab VL 90,0 30,0 220 120,00 V Como las tensiones son simétricas, entonces, 54 ELECTROTECNIA III-55 V bc 220 0, 00 V V ca 220 120, 00 V V ab abc V an V bc V cn V bn V ca De manera análoga para una secuencia de fases acb o negativa, de la figura número 6 tenemos que las tensiones de fase o al neutro son, V an V 0, 00 V V bn V 240, 00 V =V 120, 00 V V cn V 120, 00 V 55 ELECTROTECNIA III-56 V bc V cn acb acb V bn V bn 0 120,0 120,00 V an 120,00 V an 30,00 120,00 150,00 V ca V cn V bn V cn V an V ab FIGURA NÚMERO 6. DIAGRAMAS FASORIALES DE LAS TENSIONES AL NEUTRO Y DE LÍNEA DE UN GENERADOR CONECTADO EN ESTRELLA, CON SECUENCIA DE FASES acb. Las tensiones de línea son, V ab V an V bn V 0, 0 V 240, 0 3 V 30, 00 V V bc V bn V cn V 240, 0 V 120, 0 3 V 270, 00 V = 3 V 90, 00 V V ca V cn V an V 120,0 V 0,0 V 3 V 150,00 V Aquí también las tensiones de línea son atrasadas 30,0 grados con respecto a ellas. 3 veces mayores que las tensiones de fase o al neutro, pero están Ejemplo 3-2. Una fuente de tensión trifásica con secuencia de fases acb conectada en una estrella simétrica, tiene una tensión de línea de V ab = 208 /0,00 V. Determine las tensiones de fase o al neutro de la fuente. SOLUCIÓN. La magnitud de la tensión de fase o al neutro esta dada por la ecuación, Vn VL 3 208 120,0 V 3 En virtud de que cuando se tiene una secuencia de fases acb la tensión de fase o al neutro está 30 grados adelante de la tensión de línea, tenemos, V an 120,0 / 30,00 V V bn 120, 0 / 210, 00 V 56 ELECTROTECNIA III-57 V cn 120, 0 / 90, 00 V V bc acb V an V bn 30.0° V ab V bn V cn V ca Generador conectado en delta. Si en el generador de la figura número 1, se unen los extremos de las bobinas A’ con el B, y los extremos B’ con el C y finalmente los extremos C’ con el A, como se muestra en la figura número 7, se obtiene lo que se denomina como una conexión en delta ( o triángulo), por supuesto que se puede obtener otra conexión en delta uniendo los extremos A’ con C, C’ con B y B’ con A, únicamente que esta conexión estaría a 180,0 grados de la anterior. Como se puede observar en la figura número 7, las tensiones de línea a línea son las mismas que las que les corresponden a las bobinas (o fase). Así para una secuencia de fases abc tenemos, V ab V AA' V 0, 00 V V bc V BB ' V 120,0 V V ca V CC ' V 240, 00 V V 120, 00 V C B’ C V ca B B V bc C’ A’ AA V ab FIGURA NÚMERO 7. TENSIONES DE UN GENERADOR CONECTADO EN DELTA. Como se muestra en la figura número 8. 57 ELECTROTECNIA III-58 V ca abc V ab V bc FIGURA NÚMERO 8. DIAGRAMA FASORIAL DE LAS TENSIONES DE FASE O LÍNEA DE UN GENERADOR CONECTADO EN DELTA, CON SECUENCIA DE FASES abc: De manera similar para una secuencia de fases acb o negativa tenemos, V ab V AA' V 0, 00 V V bc V BB ' V 240,00 V = V 120,00 V V ca V CC ' V 120, 00 V Como se muestra en la figura número 9. V bc acb V ab V ca FIGURA NÚMERO 9. DIAGRAMA FASORIAL DE LAS TENSIONES DE FASE O LÍNEA DE UN GENERADOR CONECTADO EN DELTA, CON SECUENCIA DE FASES acb: 3. GENERACIÓN DE TENSIONES POLIFÁSICAS. Por ser más empleados se han estudiado los circuitos trifásicos. En general, un generador polifásico genera, simultáneamente, n tensiones, siendo n un número entero que da el número de fases del sistema de generación. 58 ELECTROTECNIA III-59 En la práctica las tensiones generadas tienen módulos idénticos y están cíclicamente dispuestas según ángulos de fase que difieren 360/n grados eléctricos (2/n radianes). En la figura número 10, se representa el diagrama fasorial de una generación exafásica. FIGURA NÚMERO 10 Si las tensiones no tuvieran el mismo módulo, o los ángulos de diferencia de fase no fueran, en este caso, regularmente 600, el sistema de generación sería asimétrico. Realmente en la generación se usan sistemas simétricos, salvo para sistemas bifásicos. Entre los infinitos sistemas polifásicos posibles, aparte de los conocidos monofásicos y trifásicos, únicamente se usan los exafásicos y dodecafásicos. Los sistemas exafásicos y dodecafásicos se utilizan prácticamente en todos los rectificadores de arco de mercurio, para fines de potencia, con la finalidad de lograr tensiones unidireccionales más alisadas, o sea tensiones continuas con menor contenido de armónicas. Además la mayor parte de los convertidores rotatorios son de seis fases. Aunque de uso restringido ha de mencionar el sistema bifásico, especialmente para evitar una posible confusión. Este sistema genera las dos tensiones indicadas, a trazo continuo, en la figura número 11. Como se ve, realmente se trata de la mitad de un sistema tetrafásico . El sistema bifásico debería ser el representado en b), aun cuando prácticamente se confunde con un sistema monofásico con una derivación central, divisora de tensión. 59 ELECTROTECNIA III-60 (a) (b) FIGURA NÚMERO 11 Los sistemas polifásicos se pueden conectar en estrella o en malla (polígono), sus diagramas se ven en la figura número 12. El primer sistema dispone de neutro. Obsérvese que, además de las tensiones simples, existen varias tensiones compuestas llamadas poligonales, algunas de ellas son adyacentes y otras son alternadas. FIGURA NÚMERO 12. Generador conectado en estrella. En las figuras 13 y 14 se muestran, respectivamente, el circuito y el diagrama fasorial de dos fases adyacentes de un sistema en estrella de n fases. n a b FIGURA NÚMERO 13 V an 3600/n V bn FIGURA NÚMERO 14 La tensión de línea V ab es V an V bn . Recordando que el ángulo de diferencia de fase entre tensiones adyacentes es 3600/n, y llamando VF a la magnitud de la tensión de fase, el cálculo general de la tensión de línea puede ser comprendido observando las relaciones fasoriales mostradas en la figura número 15. 60 ELECTROTECNIA III-61 3600/n VF V an 1800/n VL/2 = VF sen (1800/n) 1800/n V ab V an V bn VL/2 = VF sen (1800/n) VL V ab V bn FIGURA NÚMERO 15. COMBINACIÓN DE DOS TENSIONES DE FASE A NEUTRO PARA DAR TENSIONES DE LÍNEA, EN UNA ESTRELLA DE n FASES De aquí que las tensiones de línea sean, 1800 VL 2VF sen n Según el circuito de la figura número 10, es evidente que las corrientes de línea y de fase sean idénticas. De donde, IL IF Ejemplo 3-3. Encuentre la tensión entre líneas adyacentes de un sistema conectado en estrella, de doce fases simétricas, si las tensiones de fase tienen una magnitud de 50,0 V. Ilustre la solución por medio de un diagrama fasorial. SOLUCIÓN. De la expresión general tenemos, VL 2 VF sen 180 180, 0 2 50, 0 sen 25,9 V n 12 VF 360/12 = 30,00 VL VF Generador conectado en malla. Para un circuito en malla o polígono, aplicando los principios previamente establecidos y los diagramas fasoriales mostrados en la figura número 16, tenemos, 61 ELECTROTECNIA III-62 I bb´ I ab I bc IL IF a I bb´ I L I bc b’ IL b I ab I bc IF c IL 3600/n V ab I ab 1800/n 3600/n I L / 2 I F sen 180 0 / n 0 180 /n V bc I bc FIGURA NÚMERO 16. DIAGRAMA DE UN CIRCUITO DE FASES ADYACENTES Y DIAGRAMAS FASORIALES CORRESPONDIENTES, PARA UNA MALLA DE n FASES. VL VF I L 2 I F sen 1800 n Ejemplo 3-4. Se tiene un generador conectado en malla, de ocho fases simétricas. Determine la magnitud de las corrientes de línea que parten del generador , así como el ángulo que forman las corriente de línea y las corrientes de fase. Si la corriente de fase tiene una magnitud de 60,0 A. SOLUCIÓN. IL IF IF IL IF 67,50 45,00 IF Empleando la ecuación general, tenemos que la magnitud de las corrientes de línea es, I L 2 I F sen 180 180 2 60, 0 sen 45,9 A n 8 Por otro lado tenemos que 62 ELECTROTECNIA III-63 I L I F / 0,0 I F / 45,0 60,0 / 0,0 60,0 / 45,0 45,9 / 67,50 A De donde el ángulo entre la corriente de línea y la corriente de fase es de 67,5 0. 4. EJERCICIOS. Ejercicio 3-1. Escribir expresiones complejas para el conjunto simétrico de tensiones de (a) secuencia de fases positiva y (b) secuencia de fases negativa de los diagramas (a) y (b), respectivamente, de la figura. La magnitud de las tensiones de fase es de 277 V. abc acb V ca C V an V cn B A 30,00 V bc V ab V bn V bn 30,00 V cn V bc V an C B V ab A V ca (a) (b) SOLUCIÓN. Para el conjunto de secuencia de fases positiva de las tensiones simétricas que aparece en la figura “a”, las tensiones de fase son, V an V fn 30,00 277 30,00 240 j138,5 V V bn V fn 90,00 277 90,00 0 j277 V V cn V fn 150,00 277 1500 240 j138,5V y como la tensión de línea es 3 V fn 3 277 480V , las tensiones de línea son, V ab Vl 60, 00 480 60, 00 240 j416 V V bc Vl 60, 00 480 60, 00 240 j416 V 63 ELECTROTECNIA III-64 V ca Vl 180, 00 480 180, 00 480 j0 V Para el sistema de secuencia de fases negativa de la figura “b”, las tensiones de fase son, V an 277 30, 00 240 j138,5 V V bn 277 90,00 0 j277 V V cn 277 150, 00 240 j138, 5 V y las tensiones de línea son, V ab 480 60, 00 240 j416 V V bc 480 60, 00 240 j416 V V ca 480 180, 00 480 j0 V Ejercicio 3-2. Tres fuentes monofásicas se conectan en estrella como una fuente trifásica, para obtener tensiones de línea trifásicas de 208 V. a)¿Cuál será la tensión entre fases si el generador se conecta en delta? b) ¿Qué sucede si una de las tres fases en la delta se invierte, pero el anillo no se cierra? c) ¿Cuáles serán las tensiones entre el juego de cuatro terminales. SOLUCIÓN. La tensión de fase o al neutro del sistema conectado en estrella es, VN VL 3 208 120,0 V 3 64 ELECTROTECNIA III-65 c V ca c' a' n a b´ b V cn V an V an V bn V bc Así, la conexión en delta da una tensión trifásica de 120,0 V. b' c c V bc c' b a' b b' c' a' a V ca V ab a ¿Qué sucede si una de las tres fases de la delta se invierte, pero el anillo no se cierra? ¿Cuáles serán las tensiones entre el juego de cuatro terminales? El diagrama fasorial de tensiones del sistema es, c V bc V ca b V ab a V dc 240 V d El juego de tensiones es, Vab 120,0 V Vbc 120,0 V Vca 120,0 V Vdc 240V Ejercicio 3-3. Encuentre la tensión entre líneas alternas de un sistema en estrella de seis fases simétricas, si las tensiones de fase tienen una magnitud de 132,8 V. 65 ELECTROTECNIA III-66 SOLUCIÓN. El ángulo de desfasamiento entre tensiones de fase es, 360 360 60, 00 n 6 El ángulo entre líneas alternadas es, 2 60,0 120,00 De donde, V L VF / 0,0 VF / 120,0 132,8/ 0,0 132,8/ 120,0 230 / 30,00 V VL 230 V VF 60,00 VL 60,00 VF VF Ejercicio 3-4. Encuentre las magnitudes de las corrientes de línea que parten de un generador conectado en malla, de seis fases simétricas, si se sabe que las corrientes de fase tienen una magnitud de 100,0 A. SOLUCIÓN. Empleando la relación general tenemos, I L 2 I F sen 180 180, 0 2 100, 0sen 100, 0 A n 6 Por otro lado tenemos, I L I F / 0, 0 I F / 60, 0 I F / 60, 00 I L 100, 0 / 0, 0 100, 0 / 60, 0 100, 0 / 60, 00 A 66 ELECTROTECNIA III-67 IL IF IL = IF IF IF 0 60 IF Ejercicio 3-5. Se dan seis bobinas cada una de las cuales tiene una tensión inducida de 63,5 V. Las tensiones adyacentes de las bobinas están 600 desfasadas. ¿De cuántos modos se pueden conectar estas bobinas, para formar un sistema balanceado de tensiones trifásicas conectadas en estrella, si para cada sistema se deben usar todas las bobinas y si debe ser diferente la magnitud de las tensiones de línea de cada sistema? ¿Cuáles son las tensiones al neutro para cada sistema? f g f' d g' d' c' f b' c d a' g d' c' a f' g' b' c b a' a b SOLUCIÓN. Se pueden obtener tres modos de conectar las bobinas para formar sistemas balanceados conectados en estrella, con tensiones de línea diferentes, siendo estos los siguientes: Modo 1. f VN f' g c' d d' g' a' a b' b c VN VN Modo 2. 67 ELECTROTECNIA III-68 VN f f' b' b d' a' gd a VN g' c' c VN Modo 3. d d' VN f f' VN a' b' a c' g b g' c VN Los valores de los fasores de las bobinas son, V aa ' 63,5 / 0, 00 V ; V bb ' 63,5 / 60, 00 V ; V cc ' 63,5 / 120, 0 0 V V dd ' 63,5 /180, 00 V ; V ff ' 63,5 / 240, 00 V ; V gg ' 63,5 / 60, 0 0 V Las tensiones al neutro para el modo 1 son, V AN V aa ' V bb ' 63,5 / 0, 0 63,5 / 60, 0 110, 0 / 30, 00 V V BN V cc ' V dd ' 63,5 / 120, 0 63,5 /180, 0 110, 0 / 150, 00 V V CN V ff ' V gg ' 63,5 / 240, 0 63,5 / 60, 0 110, 0 / 90, 00 V VN 110, 0 V Las tensiones al neutro para el modo 2 son, 68 ELECTROTECNIA III-69 V AN V aa ' V dd ' 63,5 / 0, 0 63,5 /180, 0 127, 0 / 0, 00 V V BN V cc ' V gg ' 63,5 / 120, 0 63,5 / 60, 0 127, 0 / 120, 00 V V CN V ff ' V bb ' 63,5 / 240, 0 63,5 / 60, 0 127, 0 / 120, 00 V VN 127, 0 V Las tensiones al neutro para el modo 3 son, V AN V aa ' V cc ' 63,5 / 0, 0 63,5 / 120, 0 63,5 / 60, 00 V V BN V bb ' V gg ' 63,5 / 60, 0 63,5 / 60, 0 63,5 /180, 00 V V CN V ff ' V dd ' 63,5 / 240, 0 63,5 / 180, 0 63,5 / 60, 00 V VN 63,5 V Ejercicio 3-6. Un generador tiene seis bobinas, estando desplazadas 30,0 grados eléctricos las bobinas adyacentes. Si la tensión de cada bobina es de 114,0 V, muéstrese cómo conectarlas y calcúlese la tensión de línea o terminal para una estrella de tres fases. Repítase para la malla trifásica. SOLUCIÓN. a b c a' b' c' d' g' f' d f g V aa ' 114,0 / 90,00 V V bb ' 114,0 / 60,00 V V cc ' 114,0 / 30,00 V V dd ' 114,0 / 0,00 V V ff ' 114, 0 / 30, 00 V V gg ' 114, 0 / 60, 00 V a) 69 ELECTROTECNIA III-70 b A V AN b’ a C a’ N f' c V CN f g’ d c’ d’ V BN B g V AN V aa ' V bb ' 114,0 / 90,0 114,0 / 60,0 220 / 75,00 V V BN V ff ' V gg ' 114, 0 / 30, 0 114, 0 / 60, 0 220 / 45, 00 V V CN V cc ' V dd ' 114, 0 / 30, 0 114, 0 / 0, 0 220 / 165, 00 V b) a b f’ V ab f g’ b’ a g V bc a’ V ca d’ b c d c’ c V ab V ff ' V gg ' 114,0 / 30,0 114,0 / 60,0 220 /135,00 V 70 ELECTROTECNIA III-71 V bc V cc ' V dd ' 114,0 / 30,0 114,0 / 0,0 220 /15,00 V V ca V aa ' V bb ' 114, 0 / 90, 0 114, 0 / 60, 0 220 / 105, 00 V 71 ELECTROTECNIA III-72 UNIDAD 4. CIRCUITOS TRIFÁSICOS CON CARGAS CONECTADAS EN ESTRELLA, ALIMENTADAS CON TENSIONES SIMÉTRICAS. 1. CARGAS BALANCEADAS. 1.1 Cargas de cuatro hilos. Cuando se conectan tres impedancias idénticas, como se muestra en la figura número 1, estas constituyen una carga balanceada conectada en estrella, y si el punto común de las tres cargas es accesible, se tiene una estrella de cuatro hilos. IA A V CN ABC V BN Z IN IB V AB ,V L N Z Z B V AN , V N C V BN IC FIGURA NÚMERO 1. Alimentadas directamente en sus terminales. Si dicha carga se alimenta directamente en sus terminales, con un sistema trifásico simétrico, con secuencia de fases ABC, considerando como referencia a la tensión V AN las corrientes de fase o línea son, IA IB V AN V / 0, 0 V / 0 Z IF / Z Z Z / Z Z V BN V / 120, 0 V / 120 Z I F / 120, 0 Z Z Z / Z Z IC V CN V / 240, 0 V / 240 Z I F / 240 Z Z Z / Z Z 72 ELECTROTECNIA III-73 De donde se puede concluir que las magnitudes de las intensidades de corriente en las impedancias son iguales, pero están desfasadas 120,00 entre si. Aplicando la ley de corrientes de Kirchhoff al nodo N tenemos, I N I A IB IC IN V AN V BN V CN 1 V AN V BN V CN Z Z Z Z Puesto que la suma fasorial de las tres tensiones simétricas es igual con cero, entonces IN 0 Lo que indica que en un circuito con tensiones simétricas, que alimenta una carga balanceada, conectada en estrella de cuatro hilos, la intensidad de corriente en el conductor del neutro es igual con cero. Es importante observar que aunque tenemos un circuito trifásico, compuesto por tres tensiones y tres cargas, podemos analizar sólo una fase y usar la secuencia de fases para obtener las corrientes y tensiones de las otras fases. Esto es, por supuesto, un resultado directo de la condición de tener una fuente simétrica y carga balanceada. IF IL F Z VF N FIGURA NÚMERO 2 En virtud de los argumentos anteriores, se puede obtener el circuito monofásico equivalente de la figura número 2, el cual presenta una fase del sistema original con la tensión de fase a al neutro, considerándola convencionalmente como referencia. Esto hace que I F I L I L / Z donde Z es el ángulo de la impedancia. Si se desean las corrientes reales de las líneas I A , I B e I C se pueden encontrar sus ángulos de fase añadiendo -Z a los ángulos de fase de las tensiones V AN ,V BN y V CN . Se puede observar que el ángulo de I L da el factor de potencia para cada fase y del sistema, FP cos . Ejemplo 4-1. Una fuente trifásica simétrica, conectada en estrella, con secuencia de fases positiva (ABC), con una tensión de fase o al neutro de 120,0 V, suministra potencia a una carga balanceada conectada en estrella de cuatro hilos. La impedancia de la carga por fase es de 40,0 + j 10,00 . Si V AN 120, 0 0, 0 V, determine las tensiones de fase y de línea del circuito y las corrientes de línea. Trace el diagrama fasorial del circuito. 0 73 ELECTROTECNIA III-74 A Z N Z B Z C SOLUCIÓN. El diagrama del circuito monofásico equivalente se muestra en la figura número 2. La corriente en la carga es, 120, 0 / 0, 00 VF IL 2, 91 / 14, 00 A Z 40, 0 j 10,00 Las tensiones de fase o al neutro son, V AN 120,0 / 0,00 V ; V BN 120,0 / 120,00 V ; V CN 120,0 / 240,00 V Las tensiones de línea son, V AB 3 120, 0 / 30, 0 0 V = 208 / 30, 0 0 V V BC 208 / 30, 0 120, 0 208 / 90, 0 0 V V CA 208 / 30, 0 240, 0 208 / 210, 0 0 V Las corrientes en las fases son, I A I L / 0 14, 0 2, 91 / 14, 0 0 A I B 2, 91 / 120, 0 14, 0 2, 91 / 134, 0 0 A I C 2, 91 / 240, 0 14, 0 2, 91 / 254, 0 0 A El diagrama fasorial es, 74 ELECTROTECNIA III-75 V CN V CA IC abc V AB 0 30,0 V AN -14,00 I A B I V BN V BC Ejemplo 4-2. Una carga balanceada conectada en estrella, con impedancias de 65,0 /-20,00 , está conectada a un sistema trifásico con tensiones simétricas de cuatro hilos, con secuencia de fases CBA, en el cual la tensión V AB 460 / 120,00 V . Obtenga las tres corrientes de línea, las tensiones de fase, las tensiones entre líneas y trace el diagrama fasorial correspondiente. SOLUCIÓN. Puesto que las tensiones son simétricas y la carga está balanceada, utilizaremos el método del circuito monofásico equivalente para la solución, cuyo circuito se muestra en la figura número 2. La tensión de fase o al neutro es, VF VN VL 3 460 3 266 V La corriente de línea es, IL Considerando el fasor V AB 266 / 0, 0 VF 4, 09 / 20, 00 A Z 65, 0 / 20, 0 como referencia y la secuencia de fases CBA, las tensiones de línea son, V AB 460 / 120, 00 V V BC 460 / 120, 0 240, 0 460 / 0, 0 0 V V CA 460 / 120, 0 120, 0 460 / 240, 0 0 V Las tensiones de fase o al neutro son, 75 ELECTROTECNIA III-76 V AN 266 / 120, 0 30, 0 266 / 90, 0 0 V V BN 266 / 0, 0 30, 0 266 / 30, 0 0 V V CN 266 / 240, 0 30, 0 266 / 210, 0 0 V Las corrientes de línea son, I A I L / 90, 0 20, 0 4, 09 / 70, 0 0 A I B I L / 30, 0 20, 0 4, 09 / 50, 0 0 A I C I L / 210, 0 20, 0 4, 09 / 190, 0 0 A El diagrama fasorial del circuito es, V CA ACB IB 20,00 V CN V BN 30,00 IC V BC IA V AN 120,00 V AB Ejemplo 4-3. Supóngase que se tiene una carga balanceada conectada en estrella de cuatro hilos, formada por una impedancia de Z = 59,9 /- 36,90 en paralelo con una carga de alumbrado de 200 W por fase, que se alimenta con tensiones simétricas de 300 V de línea, con una secuencia de fases ABC. Determine las corrientes de línea. SOLUCIÓN. Puesto que tenemos un circuito con tensiones simétricas y carga balanceada, podemos utilizar el método del circuito monofásico equivalente, esto es, 76 ELECTROTECNIA III-77 IL I1 I2 V N 200 W Z 59,9 / 36,9 0 La magnitud de la tensión de fase o al neutro es, VF VN VL 3 300 3 173, 2 V La magnitud de la corriente que toma la carga de alumbrado es, I1 Pa 1 200 1,155 A VN cos a 1 173, 2 1, 000 Tomando como referencia a la tensión V N , la corriente I1 como favor es, I 1 1,155 / 0,00 A La corriente de la carga con impedancia Z es, I2 V N 173, 2 / 0, 0 2, 89 / 36, 90 A Z 59, 9 / 36, 9 y la corriente de línea es, I L I 1 I 2 1,155 / 0,0 2,89 / 36,9 3,88 / 26,60 A Considerando como referencia a la tensión V AN , y puesto que tenemos secuencia de fases ABC, las corrientes en las fases o líneas son, I A 3,88 / 26,60 A I B 3,88 / 120,0 26,6 3,88 / 93,40 A I C 3,88 / 240,0 26,6 3,88 / 213,40 A Ejemplo 4-4. A una fuente simétrica conectada en estrella con tensiones de 220/127Y V, se le conectan en paralelo dos cargas. Una de ellas es un calentador resistivo trifásico de 77 ELECTROTECNIA III-78 2 kW por fase, conectado en estrella, y la otra es un motor de inducción que entrega 15 CP, conectado en estrella, cuando se encuentra operando con 80 % de eficiencia, con un factor de potencia de 0,90 atrasado. Determine la corriente total en la línea. A B C N CALENTADOR TRIFÁSICO MOTOR SOLUCIÓN. En virtud de que tenemos tensiones simétricas y cargas balanceadas el circuito se puede resolver utilizando el método del circuito monofásico equivalente, quedando como se muestra en la figura siguiente: F IL VF 2 kW FP=1 PM/3 N La potencia activa por fase de entrada del motor es, Pm PM CP 746 15, 00 746 4, 66 103 W 3 3 3 0, 800 Por otro lado tenemos que la potencia activa por fase del motor se puede expresar como, Pm VFN I M cosθM De donde la corriente que toma el motor es, Pm 4, 66 103 IM 40, 8 A VF cos M 127, 0 0, 900 En forma alternativa, la corriente que toma el motor se puede obtener de la ecuación siguiente: 78 ELECTROTECNIA III-79 CP 746 IM 3 VL FP 15, 00 746 3 220 0, 800 0, 900 40, 8 A Esta corriente como fasor, teniendo en cuenta el factor de potencia del motor, es, I M I M / cos1 0,90 40,8 / 25,80 A La corriente tomada por el calentador es, IR PR 2, 00 103 15, 75 A VF cos R 127, 0 1, 000 Y como fasor es, I R 15, 75 0, 00 A De donde la corriente de línea es, I L I M I R 40,8 / 28,5 15,75 / 0,0 55,4 / 18,70 A Otro procedimiento de solución es trabajando con las potencias complejas de las cargas. La potencia compleja del motor es, SM CP 746 15, 00 746 / cos 1 FP / cos 1 0, 90 15, 54 103 / 25, 80 VA FP 0, 800 0, 900 La potencia compleja del calentador, considerando que es una carga resistiva, es, S R 3 Pr / 0, 0 3 2, 00 103 / 0.0 6, 00 103 / 0, 00 VA La potencia compleja total es, S S M S R 15, 54 103 / 25, 8 6, 00 103 / 0, 0 21,1 103 / 18, 7 0 VA También tenemos que, * S 3V FN I L De donde, * IL S 3V FN 21,1 103 / 18, 7 3 127, 0 / 0, 0 55, 4 / 18, 70 A Y la corriente de línea es, I L 55,4 / 18,70 A 79 ELECTROTECNIA III-80 Con impedancias mutuas iguales, alimentadas directamente en sus terminales. IA A Z ZM IB B N Z IC ZM ZM Z C FIGURA NÚMERO 3 Aplicando la ley de tensiones al circuito de la figura número 3 tenemos, V AN Z I A Z M I B Z M I C Z I A Z M I B I C Z I A Z M I A I A Z Z M V BN Z M I A Z I B Z M I C I B Z Z M V CN Z M I A Z M I B Z I C I C Z Z M Despejando a las corrientes tenemos, IA V / AN V AN I F / AN e Z Z M Z e / e IB V / BN V BN I F / BN e Z Z M Z e / e IC V / CN V CN I F / CN e Z Z M Z e / e De las ecuaciones anteriores se puede deducir que las magnitudes de las intensidades de corriente en las líneas son iguales, pero están desfasadas 120,00 entre ellas. De donde en éste circuito se puede utilizar el método del circuito equivalente monofásico para obtener las corrientes de línea por medio de la ecuación siguiente: IF IL V I L / V Ze Ze Ejemplo 4-5. Obtenga las corrientes de fase y la potencia compleja del sistema de una carga balanceada con Z = 8,00 + j 6,00 y ZM = - j 2,00 , cuando se alimenta de una fuente con tensiones simétricas de 120,0 V por fase, con secuencia de fases abc. 80 ELECTROTECNIA III-81 SOLUCIÓN. El circuito se muestra en la figura número 3. Aplicando el método del circuito equivalente monofásico tenemos, IF IL F Ze Z ZM VF N Z e Z Z M 8, 00 j6, 00 j2, 00 11, 31 / 45, 00 Considerando a la tensión V AN como referencia y secuencia de fases ABC, las corrientes de línea son, IF IL V F 120, 0 / 0, 0 10, 61/ 45, 00 A Z e 11, 31/ 45 I A 10,61/ 0,0 45,00 10,61/ 0,00 A I B 10,61/ 120,0 45,0 10,61/ 165,00 A I C 10,61/ 240,0 45,0 10,61/ 75,00 A La potencia compleja es, * S 3V F I F S 3 120, 0 / 0, 0 10, 61 / 45, 00 3, 82 10 3 / 45, 0 0 VA S 2,70103 j2,70103 VA Las potencias activa, reactiva y aparente del sistema son, PT 2, 70kW QT 2, 70kvar IND ST 3, 82kVA 81 ELECTROTECNIA III-82 Alimentadas a través de líneas. I aA a abc A Z V an I Nn n V bn V cn ZL ZN N Z I bB ZL I cC ZL Z B C b c FIGURA NÚMERO 4. DIAGRAMA DEL CIRCUITO Aplicando la ley de corrientes de Kirchhoff al nodo N tenemos, I Nn I aA I bB I cC (1) Aplicando la ley de tensiones de Kirchhoff a los diferentes circuitos cerrados tenemos, Circuito naANn:V an I aA Z L Z I Nn Z N Circuito nbBNn:V bn I bB Z L Z I Nn Z N Circuito ncCNn:V cn I cC Z L Z I Nn Z N Sumando las tres ecuaciones de tensión obtenemos, V an V bn V cn I aA Z L Z I bB Z L Z I cC Z L Z 3 I Nn Z N I aA I bB I cC Z L Z 3 I Nn Z N Sustituyendo la ecuación (1) de corrientes en la ecuación anterior tenemos, V an V bn V cn I Nn Z L Z 3 Z N Puesto que la suma de tres tensiones simétricas es igual con cero, 0 I Nn Z L Z 3 Z N Dividiendo ambos miembros de la ecuación anterior entre la suma de las impedancias tenemos, 0 I Nn 82 ELECTROTECNIA III-83 Lo que demuestra que en un circuito con fuentes simétricas conectadas en estrella que alimenta una carga balanceada conectada en estrella de cuatro hilos, la intensidad de corriente en el conductor del neutro es igual con cero. I Nn I aA I bB I cC 0 De aquí que en este sistema simétrico con carga balanceada y tensiones y corrientes senoidales, el punto neutro de la carga esta al mismo potencial que el punto neutro de la fuente. Por consiguiente, el conductor del neutro no lleva corriente y se puede omitir bajo condiciones especiales. Ahora se pueden determinar fácilmente las corrientes de cada línea, por medio de las ecuaciones sencillas siguientes: I aA V an ZL Z I bB V bn ZL Z I cC V cn ZL Z V cn V CN I cC abc V an I bB I aA V AN V BN V bn FIGURA NÚMERO 5. DIAGRAMA FASORIAL. CIRCUITO MONOFÁSICO EQUIVALENTE. Es importante observar que aunque tenemos un circuito trifásico compuesto de tres fuentes y tres cargas, podemos analizar sólo una fase y usar la secuencia de fases para obtener las tensiones y corrientes de las otras fases. Esto es, por supuesto, un resultado directo de la condición de tener una fuente simétrica y cargas balanceadas. Podemos tener, incluso, impedancias presentes en las líneas; sin embargo, mientras el sistema permanezca balanceado, sólo necesitamos analizar una fase. Si las impedancias en las líneas A, B y C son iguales el sistema está balanceado. Es conveniente recordar que el balance del sistema no se ve afectado por el valor de la impedancia del conductor del neutro, y como la impedancia de este conductor puede ser cualquiera, podemos suponer que es cero (es decir, un corto circuito). 83 ELECTROTECNIA III-84 En virtud de los argumentos anteriores, se puede obtener el circuito monofásico equivalente de la figura número 6, el cual presenta una fase del sistema original con la tensión de fase o al neutro, considerándola convencionalmente como referencia. Esto hace I L = IL -e, donde e es el ángulo de la impedancia equivalente. Si se desean las corrientes reales de las líneas I aA , I bB e I cC se pueden encontrar sus ángulos de fase añadiendo - e a los ángulos de fase de las tensiones V an , V bn y V cn . Se puede observar que el ángulo de I L da el factor de potencia para cada fase. FP = cos . IL f V ZL F Z f n N FIGURA NÚMERO 6. DIAGRAMA DEL CIRCUITO MONOFÁSICO EQUIVALENTE Ejemplo 4-6. En la figura el generador trifásico tiene una tensión simétrica entre líneas de 220 V, con una secuencia de fases abc. Las impedancias de las líneas y de la carga son respectivamente de, 2,00 + j 4,00 y 15,00 + j 10,00 en cada fase. Determinar las corrientes de línea y las tensiones en la carga. a n c IA ZL IN ZN IB ZL A Z N b B IC Z Z C ZL SOLUCIÓN. En virtud de que el circuito tiene tensiones simétricas y carga balanceada, este se puede resolver usando la técnica del circuito monofásico equivalente, quedando como se muestra en la figura número 6. La tensión al neutro es, Vf Vl 3 220 3 127, 0 V 84 ELECTROTECNIA III-85 De donde, considerando a la tensión V an como referencia y teniendo en cuenta que tenemos una secuencia de fases positiva, las tensiones de fase o al neutro son, V an 127,0 / 0,00 V V bn 127,0 / 120,00 V V cn 127,0 / 240,00 V La corriente de fase o línea es, IL 127, 0 / 0, 0 Vf 5, 77 / 39, 50 A ZL Z 2, 00 j4,00 15, 00 j10,00 Las corrientes de línea o fase son, I A 5,77 / 39,50 A I B 5,77 / 39,5 120,0 5,77 / 159,50 A I C 5,77 / 39,5 240,0 5,77 / 279,50 A La caída de tensión en la carga es, V F Z I L 15,00 j10,00 5,77 / 39,5 104,0 / 5,80 V Las caídas de tensión en la carga son, V AN 104,0 / 5,80 V V BN 104,0 / 5,8 120,0 104,0 / 125,80 V V CN 104,0 / 5,8 240,0 104,0 / 245,80 V El diagrama fasorial del circuito es, 85 ELECTROTECNIA III-86 V ca V cn V CN IC abc V ab 5,80 V an 33,7 0 IB V AN 39,5 0 V BN IA V bn V bc Ejemplo 4-7. Considere la red de la figura, alimentada con tensiones simétricas de 220/127,0 V, con una secuencia de fases abc; la fase “a” suministra servicio monofásico a los usuarios del circuito 1, la fase “b” suministra servicio monofásico a los usuarios del circuito 2, la fase “c” suministra servicio monofásico a los usuarios del circuito 3, las cargas concentradas de cada uno de los circuitos es de 25,0 kW, con factor de potencia unitario y de una tensión nominal de 120,0 V. Además se alimenta una carga trifásica balanceada, conectada en estrella, de una industria pequeña que toma 60,0 kW con factor de potencia 0,85 atrasado y de una tensión de línea nominal de 230 V. La resistencia de cada una de las líneas de alimentación es de 0,1200 . Determine las corrientes y potencias suministradas por la fuente, así como las caídas de tensión en las cargas. a ZL B b ZL C c ZN N n CIRCUITO 1 CIRCUITO 2 CIRCUITO 3 CIRCUITO TRIFÁSICO INDUSTRIAL SOLUCIÓN. Observando el circuito y los datos del ejemplo, se llega a la conclusión que se tiene un sistema con cargas balanceadas, por lo que para su solución se puede utilizar el método del circuito monofásico equivalente. El cual se muestra, para este caso, en la figura siguiente: 86 ELECTROTECNIA III-87 f IL ZL F Z Vn n f ZL Vn VN ZIF IL n N F Ze VN N Las impedancias de las cargas son: Z VN2 1 120, 02 / cos 1 FP1 / cos 1 1, 00 0, 576 / 0, 00 S 25, 0 103 Z IF VNI2 / cos 1 FPI SI / 3 Donde VNI SI VLNI 3 230 3 132, 8 V PI 60, 0 103 / cos 1 FPI / cos 1 0, 85 70, 6 103 / 31, 80 VA FPI 0, 85 3 S I 70, 6 10 / 31, 8 23, 5 10 3 / 31, 80 VA 3 3 Sustituyendo valores, Z IF 132, 82 / cos 1 0, 85 0, 750 / 31, 80 23, 5 103 La impedancia equivalente es, 0,576 / 0,0 0,750 / 31,8 Z Z IF 0, 339 / 13,80 Z Z IF 0,576 / 0,0 0,750 / 31,8 Tomando como referencia a la tensión al neutro en la fuente, la corriente de línea o fase Ze es, IL IF 127, 0 / 0, 0 Vn 278 / 10, 20 A Z L Z e 0,1200 / 0, 0 0, 339 / 13, 8 Tomando como referencia a la tensión V an , las corrientes en las líneas o fases son, 87 ELECTROTECNIA III-88 I A I L / 0 L 278 / 0 10, 2 278 / 10, 20 A I B I L / 120, 0 L 278 / 120, 0 10, 2 278 / 130, 2 0 A I C I L / 240, 0 L 278 / 240, 0 10, 2 278 / 250, 20 A La potencia compleja suministrada por la fuente es, * S f 3V n I L 3 127, 0 / 0, 0 278 / 10, 2 105, 9 10 3 / 10, 20 VA =104, 2 103 j18,76 103 VA Las potencias activa, reactiva y aparente suministradas por la fuente son, Pf 104, 2 103 W =104,2kW Q f 18, 76 103 var ind =18,76kvar ind S f 105, 9 103 VA =105,9kVA La caída de tensión en la carga es, V N Z e I L 0, 339 / 13,8 278 / 10, 2 94, 2 / 3,60 V Las caídas de tensión en las cargas son, V AN 94, 2 / 3,60 V V BN 94, 2 / 116,40 V V CN 94, 2 / 236,40 V 1.2. Cargas de tres hilos. La solución de este tipo de circuitos es igual a la que se utiliza para las cargas de cuatro hilos , ya que se menciono anteriormente que un circuito de cuatro hilo cuando las cargas están balanceadas, no importa el valor de la impedancia del conductor del neutro, por lo que esta puede tomar valores desde cero (corto circuito) hasta infinito (circuito abierto), esto último equivale a que no se tenga conductor entre los neutros, que es lo mismo a que se tenga una carga conectada en estrella con tres hilos, como se muestra en la figura número 7. 88 ELECTROTECNIA III-89 A Z V CA FIGURA NÚMERO 7 V AB N Z Z B C V BC Alimentada directamente en sus terminales. Aplicando el método del circuito monofásico equivalente, y puesto que tenemos tensiones simétricas la tensión al neutro es igual a, VN VL 3 Ejemplo 4-8. En el circuito mostrado en la figura, la carga está balanceada y tiene una impedancia por fase de Z = 6,00 + j 2,50 , está se alimenta con una fuente simétrica con una tensión de línea de VL = 460 V. Determinar: a) las caídas de tensión en la carga, b) las corrientes de línea o fase, c) la potencia aparente, d) el factor de potencia y e) la potencia activa tomada por la carga A Z N Z Z B C SOLUCIÓN. Aplicando el método del circuito monofásico equivalente tenemos, a) La caída de tensión en la carga es, VN VL 3 460 3 266 V b) La corriente de fase o línea es, 89 ELECTROTECNIA III-90 IL IF VN Z La impedancia de la carga es, Z 6, 00 j2, 50 6, 50 / 22, 60 Sustituyendo valores, IF IL 266 40, 9 A 6, 50 La potencia aparente es, S 3VN I F 3 266 40,9 32,6 103 VA = 32,6kVA d) El factor de potencia es, FP cos / Z cos 22, 6 0, 923 AT e) La potencia activa es, P S cos FP 32,6 103 0,923 30,1 103 W= 30,1kW Ejemplo 4-9. Una carga balanceada conectada en estrella se conecta a una fuente trifásica simétrica de 60 Hz, con una secuencia de fases ABC, con una tensión de línea V AB = 440 /0,00 V. Cada fase toma una potencia activa de 9,00 kW, con un factor de potencia de 0,500 atrasado. (a) Calcule la corriente de línea y encuentre I A , I B e I C , así como la impedancia por fase Z. (b) ¿Qué valor de capacitancia C se debe poner en paralelo con cada elemento de carga para hacer mínima la corriente que toma la fuente?, y (c) ¿cuál es la corriente de línea resultante en estas condiciones? A Z C V AB C C Z B Z C SOLUCIÓN. 90 ELECTROTECNIA III-91 Resolviendo el problema por medio del circuito equivalente monofásico, ya que tenemos tensiones simétricas y cargas balanceadas, tenemos, F C VN Z N La tensión de fase al neutro es, VN VL 3 440 3 254 V Puesto que el circuito tiene secuencia ABC, las tensiones de fase están 30 grados atrasadas con respecto a las tensiones de línea, considerando a esta última como la referencia tenemos, V AN 254 / 30,00 V V BN 254 / 150,00 V V CN 254 / 270,00 V a) La corriente de línea es, PF 9, 00 103 IL 70, 9 A VN cos 254 0, 500 Tomando en cuenta que la carga tiene un factor de potencia de 0,500 atrasado, la corriente de fase debe estar atrasada con respecto a su tensión de fase o al neutro un ángulo de 60 0, de donde, I A 70,9 / 30,0 60,0 70,9 / 90,00 A I B 70,9 / 210,00 A I C 70,9 / 3300 A La magnitud de la impedancia por fase es, Z VN 254 3, 58 I L 70, 9 91 ELECTROTECNIA III-92 En virtud de que el circuito tiene un factor de potencia 0,500 atrasado, entonces la impedancia en forma de complejo es, Z 3, 58 / 60, 00 b) La potencia reactiva inductiva que toma la carga por fase es, QF VN I L sen 254 70,9 sen600 15,60 103 var ind 15,60kvar ind Para que la corriente sea mínima se debe tener un factor de potencia unitario, por lo que se debe contrarrestar la potencia reactiva con un juego de capacitores que suministren el mismo valor de potencia reactiva pero de característica capacitiva. La reactancia del capacitor por fase es, XC VN2 2542 4,14 QC 15, 60 103 De donde los capacitores que se conectan por fase, cada uno debe tener una capacitancia de, C 1 1 641 10 6 F 641 F 2 f X C 2 60, 0 4,14 c) Puesto que en las condiciones en que están conectados los capacitores se tiene como resultado que el circuito tiene factor de potencia unitario, entonces la corriente de línea es, PF 9, 00 103 I L1 35, 4 A VN cos 1 254 1, 000 Alimentadas a través de líneas. El método de solución de estos circuitos es el mismo que el que se utiliza para las cargas conectadas en estrella de cuatro hilos. Ejemplo 4-10. En la figura se muestra un sistema trifásico balanceado de tres hilos con una secuencia de fases positiva. Sea V BC = 460 /60,00 V y RL = 0,600 . Si la carga total (incluso la resistencia del hilo) absorbe 20,0 kVA a un FP = 0,800 atrasado, encuentre a) la potencia total que se pierde en la resistencia de las líneas y b) la tensión V an en la fuente. 92 ELECTROTECNIA III-93 RL a A V an Z n V cn c Z V bn b RL N Z B C RL SOLUCIÓN. Puesto que tenemos tensiones simétricas y carga balanceada, utilizaremos el método del circuito monofásico equivalente. RL f F Z Vn n N Teniendo en cuenta la tensión V BC y la secuencia de fases positiva, las tensiones de línea en la carga son, V AB 460 / 60,0 120,0 460 / 180,00 V V CA 460 / 60,0 120,0 460 / 60,00 V De donde la tensión V AN VAB 3 / AB 30, 0 460 3 / 180, 0 30, 0 266 / 210, 0 0 V V BN 266 / 330,00 V = 266 /30,00 V V CN 266 / 90,00 V La corriente tomada por la carga es, IL S F 20, 0 103 25,1 A 3Vn 3 266 Las corrientes en cada fase son, 93 ELECTROTECNIA III-94 I A I L / AN cos 1 0, 800 25,1/ 210, 0 36, 9 25,1/ 246, 90 A I B 25,1/ 6,90 A I C 25,1/ 126,90 A a) La potencia activa total que se pierde en las líneas es, PL 3 RL I L2 3 0,600 25,12 1134 W b) La caída de tensión en las líneas de alimentación es, VLL RL I L 0, 600 25,1 15, 06 V La caída de tensión en la fase “a” como fasor es, V aA 15,06 / 246,90 V De donde la tensión en la fase “a” en la fuente es, V an V AN V aA 266 / 210,0 15,06 / 246,9 278 / 148,10 V Ejemplo 4-11. Una carga trifásica conectada en estrella balanceada es abastecida por una fuente trifásica, conectada en estrella simétrica con secuencia de fases abc, con una tensión de línea de 480 V. Si la impedancia de la línea y la impedancia de la carga por fase son de 1,000 + j 1,000 y 20,0 + j10,00 , respectivamente, determinar el valor de la corriente de línea y las caídas de tensión en la carga. SOLUCIÓN. Puesto que el circuito tiene tensiones simétricas y carga balanceada este se puede resolver utilizando la técnica del circuito monofásico equivalente, quedando como se muestra en la figura. 94 ELECTROTECNIA III-95 ZL f F Z Vn n VN N La tensión de fase o al neutro es, Vn Vl 3 480 3 277 V Tomando como referencia a la tensión V n , la corriente de línea es, IL 277 / 0,0 Vn 11,68 / 27, 60 A Z Z L 1,000 j1,000 20,0 j10,00 La caída de tensión en la carga es, V N Z I L 20,0 j10,00 11,68 / 27,6 261/ 1,00 V Tomando como referencia a la tensión V an y con secuencia de fases abc, las caídas de tensión en las fases son, V AN 261/ 1,00 V , V BN 261/ 121,00 V , V CN 261/ 241,00 V Ejemplo 4-12. La tensión de fase o al neutro en las terminales de una carga trifásica balanceada conectada en estrella, es de 2,40 kV. La carga tiene una impedancia de 16,00 + j 12,00 por fase, y se alimenta a través de unas líneas con una impedancia de 0,1000 + j 0,800 cada una. La fuente está conectada en estrella en el extremo emisor de la línea, tiene una secuencia de fases acb y una impedancia interna de 0,0200 + j 0,1600 por fase. Use la tensión al neutro de la fase A de la carga como referencia, y calcule a) las corrientes de línea, b) las tensiones de línea de la fuente y c) las tensiones internas de fase de la fuente. 95 ELECTROTECNIA III-96 ZL a A ZF a' Z b' c' c b C B SOLUCIÓN. Puesto que el circuito tiene tensiones simétricas y cargas balanceadas, usaremos la técnica del circuito monofásico equivalente para resolver el problema. ZL a ZF A a' Z ' an N a) Tomando como referencia a la tensión V AN , la corriente I aA es, V n I aA 3 3 V AN 2, 40 10 / 0, 0 2, 40 10 / 0, 0 120, 0 / 36, 90 A Z 16, 00 j12,00 20, 0 / 36, 9 Considerando secuencia acb, las otras corrientes de línea son, I bB 120,0 / 83,10 A I cC 120,0 / 156,90 A b) Las tensiones al neutro en las terminales de la fuente son, V an V aA V AN I aA Z L V AN 120, 0 / 36, 9 0,1000 j0,800 2, 40 103 / 0, 0 2, 47 10 3 / 1, 60 V V bn 2,47 103 / 121,60 V ; V cn 2,47 103 / 118,40 V Las tensiones de línea en las terminales de la fuente son, 96 ELECTROTECNIA III-97 V ab 3 2,47 103 / 1,6 30,0 4, 28 103 / 28,40 V V bc 4, 28 103 / 91,60 V V ca 4, 28 103 / 148,40 V c) Las tensiones internas de fase o al neutro de la fuente son, ' V an V an V aa ' V an I aA Z F 2, 47 103 / 1, 6 120, 0 / 36, 9 0, 0200 j0,1600 2, 48 103 / 1, 90 V ' ' V bn 2,48 103 / 121,90 V ; V cn 2,48 103 / 118,10 V 2. CARGAS DESBALANCEADAS. 2.1 Cargas de cuatro hilos. Si las impedancias mostradas en la figura número 8 no son idénticas constituyen lo que se denomina como carga desbalanceada conectada en estrella. IA A ZA IN IB B IC N ZB ZC C FIGURA NÚMERO 8. Alimentadas directamente en sus terminales. Si dicha carga se alimenta directamente en sus terminales, con una fuente trifásica simétrica, las corrientes de fase o línea se pueden calcular con las ecuaciones siguientes: IA V AN ZA IB V BN ZB 97 ELECTROTECNIA III-98 IC V CN ZC En virtud de que las cargas toman corrientes diferentes, entonces para que en el punto neutro se tenga un equilibrio de las corrientes, de acuerdo con la ley de corrientes de Kirchhoff, debe existir una corriente en el conductor del neutro, esto es, I A I B IC I N 0 De donde, I N I A IB IC Ejemplo 4-13. El sistema de la figura número 8 se alimenta con tensiones simétricas, con una secuencia de fases ABC, y de un valor Vn = 120 V; donde las impedancias tienen los valores siguientes: ZA = 4,00+ j 4,00 , ZB = 12,00 + j 20,0 y ZC = 8,00 + j 2,00 . Determine: a) la corriente a través de cada fase de la carga, b) la corriente en el conductor del neutro, c) las potencias totales activa, reactiva y aparente, y d) el factor de potencia vectorial del sistema. SOLUCIÓN. a) Tomando como referencia a la tensión V AN , las corrientes en las fases o líneas son, IA V AN 120, 0 / 0, 0 21, 2 / 45, 00 A Z A 4, 00 j4, 00 IB V BN 120,0 / 120,0 5,14 / 179,00 A Z B 12,00 j20,0 IC V CN 120, 0 / 240, 0 14, 55 / 106, 00 A ZC 8, 00 j2, 00 b) La corriente en el conductor del neutro es, I N I A I B I C 21, 2 / 45,0 5,14 / 179,0 14,55 / 106,0 5,94 / 10,60 A c) La potencia compleja es, * * * S V AN I A V BN I B V CN I C 120, 0 / 0, 0 21, 2 / 45, 0 120, 0 / 120, 0 5,14 / 179, 0 120, 0 / 240, 0 14, 55 / 106, 0 4, 70 103 / 35, 80 VA = 3,81 103 j2, 75 103 VA De donde las potencias son, P 3,81kW 98 ELECTROTECNIA III-99 Q 2,75kvar ind S 4,70kVA d) El factor de potencia vectorial del sistema es, FP cos 35,8 0,811at Ejemplo 4-14. Un sistema trifásico de cuatro hilos, con tensiones simétricas, con secuencia de fases cba, con tensiones de línea de 208 V, tiene impedancias conectadas en estrella, con los valores siguientes: ZA = 3,00 /0,00 ; ZB = 3,61 /56,30 y ZC = 2,24 /-26,60. Considere como referencia la tensión V BC . Determine las corrientes de línea, así como la corriente en el conductor del neutro. IA A ZA IN IB B IC N ZB ZC C SOLUCIÓN. La magnitud de la tensión de fase o al neutro, siendo el sistema simétrico es, VN VL 3 208 3 120,1V Puesto que se tiene secuencia de fases cba, las tensiones de fase o al neutro están 30 grados adelante de las tensiones de línea, por lo que considerando como referencia a la tensión V BC tenemos, V BN 120,1/ 30,00 V V AN 120,1/ 90,00 V V CN 120,1/ 210,00 V Las corrientes de línea son, IA V AN 120,1 / 90, 0 40, 0 / 90, 00 A ZA 3, 00 / 0, 0 99 ELECTROTECNIA III-100 IB IC V BN 120,1 / 30, 0 33, 3 / 26, 30 A ZB 3, 61 / 56, 3 V CN 120,1 / 210, 0 53, 6 / 183, 40 A ZC 2, 24 / 26, 6 La corriente en el conductor del neutro es, I N I A I B I C 40,0 / 90,0 33, 3 / 26, 3 53,6 / 183,4 56,7 / 114,60 A Ejemplo 4-15. Considere la red de 60 Hz, con secuencia de fases abc, de la figura, con tensiones simétricas de línea de 460 V, la fase “A” suministra servicio monofásico a los usuarios de la calle A, la fase “B” abastece a los usuarios de la calle B y la fase “C” alimenta a los usuarios del mismo tipo de la calle C. Además alimenta la carga trifásica balanceada conectada en estrella de una industria pequeña. a).Determine la corriente en el conductor del neutro. b). Si se quiere medir la potencia activa, suministrada por la fuente, con wáttmetros monofásicos, muestre el diagrama eléctrico que se usaría para realizar la medición, utilizando la cantidad mínima de wáttmetros y calcule la indicación de cada uno de ellos. IA IB IC A B C I A2 I B2 IC2 A B C Calle A 48,0 kW I A1 IN N Calle B 30,0 kW I B1 Carga trifásica de 36,0 kW FP = 0,500 AT Calle C 60,0 kW I C1 N SOLUCIÓN. a) La tensión de fase a neutro es, VFN VL 3 460 3 266 V Considerando a la tensión V AN como referencia, las corrientes en las cargas monofásicas son, * I A1 * I B1 S AN V AN S BN V BN 48, 0 103 / 0, 0 266 / 0, 0 30, 0 103 / 0, 0 266 / 120, 0 180, 5 / 0, 00 A , I A1 180, 5 / 0, 00 A 112, 8 / 120, 00 A , I B1 112, 8 / 120, 00 A 100 ELECTROTECNIA III-101 I * C1 S CN V CN 60, 0 103 / 0, 0 266 / 240, 0 226 / 240, 00 A , I C 1 226 / 240, 0 0 A La corriente de línea en la carga trifásica es, P IL 3 VL cos 36, 0 103 3 460 0, 500 90, 4 A De donde las corrientes de línea tomadas por la carga trifásica son, I A2 90,4 / 60,00 A , I B 2 90,4 / 180,00 A , I C 2 90,4 / 300,00 A Las corrientes totales de línea son, I A I A1 I A2 180,5 / 0,0 90,4 / 60,0 239 / 19,10 A I B I B1 I B 2 112,8 / 120,0 90,4 / 180,0 176, 3 / 146,40 A I C I C 1 I C 2 226 / 240,0 90,4 / 300,0 282 / 103,90 A De donde la corriente en el conductor del neutro es, I N I A I B I C 239 / 19,1 176, 3 / 146,4 282 / 103,9 98,6 / 83,40 A b) El diagrama eléctrico para la medición de la potencia activa total es, A B C IA IB IC WM1 * * * WM3 * * * WM2 I A2 I B2 IC2 A B Carga trifásica de 36,0 kW FP = 0,500 AT C Calle A 48,0 kW I A1 IN N Calle B 30,0 kW I B1 Calle C 60,0 kW I C1 N Las indicaciones de los wáttmetros son, WM1= V * AN IA 60,1 10 3 266 / 0, 0 239 / 19,1 63, 6 10 3 / 19,1 j20,8 10 3 60,1 10 3 W = 60,1kW 101 ELECTROTECNIA III-102 WM2 = WM3 = V * BN IB 42, 0 10 V * CN 3 266 / 120, 0 176, 3 / 146, 4 46, 9 10 j20,9 10 42, 0 10 W = 42,0kW 3 3 / 26, 4 3 / 16,1 3 266 / 240, 0 282 / 103, 9 75, 0 10 j20,8 10 72,1 10 W = 72,1kW IC 72,1 10 3 3 3 Realizando los cálculos de las indicaciones, utilizando otra alternativa, tenemos WM1=VAN I A cos VAN IA VBN IB WM2=VBN I B cos WM3 =VCN IC cos 266 239cos19,1 60,1103 W=60,1kW 266 176, 3cos 26,4 42,0 103 W=42,0kW VCN IC 266 282cos16,1 72,1103 W = 72,1kW Carga con impedancias mutuas. IA A ZA IN ZAB ZB IB B IC N ZCA ZC C ZBC FIGURA NÚMERO 9 Las caídas de tensión en las fases son, V AN Z A I A Z AB I B Z AC I C V BN Z BA I A Z B I B Z BC I C V CN Z CA I A Z CB I B Z C I C Resolviendo las ecuaciones anteriores por medio de matrices y considerando las corrientes como las incógnitas tenemos, 102 ELECTROTECNIA III-103 I A Z A I B Z BA Z I C CA Z AC Z BC Z C Z AB ZB Z CB 1 V AN V BN V CN Ejemplo 4-16. Sea una carga desbalanceada de ZA = 10,00 /60,00 , ZB = 10,00 /- 60,00 , ZC = 5,00 /0,0 y ZAB = ZBC = ZCA = - j 2,00 , conectada a una fuente con tensiones simétricas de 120,0 V por fase, con secuencia de fases ABC. Obtenga las corrientes de fase y del conductor del neutro, así como la potencia compleja del sistema. 0 SOLUCIÓN. IA A ZA ZAB IN IB B ZB IC ZCA N ZBC ZC C Resolviendo por matrices tenemos, I A Z A I B Z BA Z I C CA Z AB ZB Z CB Z AC Z BC Z C 1 V AN V BN V CN I A 10, 00 / 60, 0 2, 00 / 90, 0 2, 00 / 90, 0 1 120, 0 / 0, 0 I B 2, 00 / 90, 0 10, 00 / 60, 0 2, 00 / 90, 0 120, 0 / 120, 0 2, 00 / 90, 0 2, 00 / 90, 0 5, 00 / 0, 0 120, 0 / 240, 0 I C 9, 72 / 59, 2 13, 66 / 72, 4 24, 7 / 98, 0 Las corrientes de línea son, I A 9,72 / 59, 20 A 103 ELECTROTECNIA III-104 I B 13,66 / 72,40 A I C 24,7 / 98,00 A La corriente en el conductor del neutro es, I N I A I B I C 9,72 / 59, 2 13,66 / 72,4 24,7 / 98,0 6,46 / 28,60 A La potencia compleja del sistema es, * * * S T S A S B S C V AN I A V BN I B V CN I C 120, 0 / 0, 0 9, 72 / 59, 2 120, 0 / 120, 0 13, 66 / 72, 4 120, 0 / 240, 0 24, 7 / 98, 0 1,166 103 / 59, 2 1, 639 103 / 47, 6 2, 96 10 3 / 22, 0 4, 54 103 / 11, 40 VA 4,45 103 j900 VA Las potencias activa, reactiva y aparente del sistema son, PT 4,45103 W QT 900 var IND ST 4,54 103 VA Alimentadas a través de líneas. En la figura número 10 se muestra una carga desbalanceada de tres fases, cuatro hilos conectada en estrella de cuatro hilos, alimentada a través de líneas. 104 ELECTROTECNIA III-105 I aA a n V bn IA A I1 abc V an V cn Z aA I Nn I bB ZN I2 Z bB b I cC Z cC V AN ZA N IB I 3 IC ZB B ZC V BN V CN C c FIGURA NÚMERO 10. Resolviendo el circuito por medio del método de mallas tenemos. Las impedancias propias y mutuas de las tres mallas son, Z 11 Z aA Z A Z N Z 12 Z N Z 13 Z N Z 21 Z N Z 22 Z bB Z B Z N Z 23 Z N Z 31 Z N Z 32 Z N Z 33 Z cC Z C Z N Las impedancias equivalentes de las fuentes se desprecian, o bien se pueden considerar que están incluidas en las impedancias de las líneas. Las ecuaciones de mallas son, 105 ELECTROTECNIA III-106 V an Z 11 I 1 Z 12 I 2 Z 13 I 3 V bn Z 21 I 1 Z 22 I 2 Z 23 I 3 V cn Z 31 I 1 Z 32 I 2 Z 33 I 3 Resolviendo el juego de tres ecuaciones por medio del cálculo matricial tenemos, V an Z 11 V bn Z 21 V cn Z 31 Z 13 I 1 Z 23 I 2 Z 33 I 3 Z 12 Z 22 Z 32 Considerando a las corrientes como incógnitas, tenemos, I1 Z 11 I 2 Z 21 Z I 3 31 Z 12 Z 22 Z 32 Z 13 Z 23 Z 33 1 V an V bn V cn Las corrientes de línea son, I A I1 ; I B I 2 ; IC I 3 La corriente en el conductor del neutro es, I N I A IB IC Ejemplo 4-17. Una fuente trifásica simétrica, conectada en estrella de cuatro hilos, con una frecuencia de 60,0 Hz, con una secuencia de fases abc, con tensiones de 220/127 V, alimenta una carga como se muestra en la figura número 10, donde la rama A está formada por una resistencia de 4,00 en serie con una inductancia de 20,0 mH, la rama B formada por una resistencia de 10,00 en serie con una inductancia de 40,0 mH, la rama C formada por una resistencia de 8,00 en serie con una inductancia de 30,0 mH. La impedancia de las líneas está formada por una resistencia de 1,000 en serie con una reactancia inductiva de 0,500 , la impedancia del conductor del neutro es igual a la de las líneas. Determinar: a) Las corrientes de línea y en el conductor del neutro, b) las caídas de tensión de las fases de la carga, y c) las tensiones de línea en la carga. SOLUCIÓN. Las impedancias de las cargas y de las líneas son, 106 ELECTROTECNIA III-107 X A 2 f LA 2 60,0 20,0 103 7,54 Z A 4, 00 j7,54 8,54 / 62,10 X B 2 f LB 2 60,0 40,0 103 15,08 Z B 10, 00 j15,08 18,09 / 56,50 X C 2 f LC 2 60,0 30,0 103 11, 31 Z CN 8, 00 j11,31 13,85 / 54,7 0 Z L Z N 1, 000 j0,500 1,118 / 26,60 El problema se resolverá por el método de mallas. Las impedancias de las mallas y las impedancias comunes a las mallas son, Z 11 Z L Z A Z N 1,118 / 26, 6 8, 54 / 62,1 1,118 / 26, 6 10, 44 / 55, 00 Z 12 Z 21 Z N 1,118 / 26, 60 Z 13 Z 31 Z N 1,118 / 26, 60 Z 22 Z L Z B Z N 1,118 / 26, 6 18, 09 / 56, 5 1,118 / 26, 6 20,1 / 53, 3 0 Z 23 Z 32 Z N 1,118 / 26, 60 Z 33 Z L Z C Z N 1,118 / 26, 6 13, 85 / 54, 7 1,118 / 26, 6 15, 86 / 50, 90 La ecuación matricial que nos determina las corrientes de malla es, I 1 10, 44 / 55, 0 1,118 / 26, 6 1,118 / 26, 6 1 127, 0 / 0, 0 12, 89 / 57, 6 I 2 1,118 / 26, 6 20,1 / 53, 3 1,118 / 26, 6 127, 0 / 120, 0 6, 72 / 177, 0 1,118 / 26, 6 1,118 / 26, 6 15, 86 / 50, 9 127, 0 / 240, 0 8, 80 / 68, 9 I 3 a ) Las corrientes de línea y del conductor del neutro son, I A I 1 12,89 / 57,60 A I B I 2 6,72 / 177,00 A 107 ELECTROTECNIA III-108 I C I 3 8,80 / 68,90 A I N I A I B I C 12,89 / 57,6 6,72 / 177,0 8,80 / 68,9 4,52 / 42,00 A b) Las caídas de tensión de las fases de las cargas son, V AN Z A I A 8,54 / 62,112,89 / 57,6 110,1/ 4,50 V V BN Z B I B 18,09 / 56,5 6,72 / 177,0 121,6 / 120,50 V V CN Z C I C 13,85 / 54,7 8,80 / 68,9 121,9 / 123,60 V c) Las tensiones de línea en la carga son, V AB V AN V BN 110,1/ 4,5 121,6 / 120,5 206 / 33,50 V V BC V BN V CN 121,6 / 120,5 121,9 / 123,6 206 / 88,40 V V CA V CN V AN 121,9 / 123,6 110,1/ 4,5 200 / 152, 30 V Ejemplo 4-18. Un sistema trifásico de cuatro hilos conectado en estrella, como el mostrado en la figura número 10, tiene líneas con una impedancia de 0,400 /0,00 y un conductor del neutro con una impedancia igual a las de las líneas, y con cargas de impedancia iguales a ZA = 7,80 /75,10 , ZB = 40,0 /0,00 y ZC = 11,35 /84,90 , las cuales se alimentan de un sistema con tensiones simétricas con una secuencia de fases abc, con una tensión de 480/277 V. Determine: a) Las corrientes de fase y en el conductor del neutro, b) las potencias suministradas por la fuente, c) las potencias consumidas por la carga, y d) la potencia perdida en las líneas y el conductor del neutro. SOLUCIÓN. Considerando como referencia a la tensión V an , las tensiones en la fuente son, V an 277 / 0,00 V ; V bn 277 / 120,00 V ; V cn 277 / 240,00 V El problema se resolverá por el método de mallas. Las impedancias de las mallas y las impedancias comunes a las mallas son, Z 11 Z L Z A Z N 0, 400 / 0, 0 7, 80 / 75,1 0, 400 / 0, 0 8, 04 / 69, 6 0 Z 12 Z 21 Z N 0, 400 / 0, 00 Z 13 Z 31 Z N 0, 400 / 0, 00 Z 22 Z L Z B Z N 0, 400 / 0, 0 40, 0 / 0, 0 0, 400 / 0, 0 40, 8 / 0, 0 0 108 ELECTROTECNIA III-109 Z 23 Z 32 Z N 0, 400 / 0, 00 Z 33 Z L Z C Z N 0, 400 / 0, 0 11, 35 / 84, 9 0, 400 / 0, 0 11, 45 / 80, 90 La ecuación matricial que nos determina las corrientes de malla es, I 1 8, 04 / 69, 6 0, 400 / 0, 0 0, 400 / 0, 0 1 277 / 0, 0 33, 6 / 70, 4 I 2 0, 400 / 0, 0 40, 8 / 0, 0 0, 400 / 0, 0 277 / 120, 0 6, 82 / 122, 9 0, 400 / 0, 0 0, 400 / 0, 0 11, 45 / 80, 9 277 / 240, 0 25, 5 / 38,1 I 3 a ) Las corrientes de línea y del conductor del neutro son, I A I 1 33,6 / 70,40 A I B I 2 6,82 / 122,90 A I C I 3 25,5 / 38,10 A I N I A I B I C 33,6 / 70,4 6,82 / 122,9 25,5 / 38,1 35,1/ 38,10 A b) La potencia compleja suministrada por la fuente es, * * * S f S a S b S c V an I A V bn I B V cn I C 277 / 0, 0 33, 6 / 70, 4 277 / 120, 0 6, 82 / 122, 9 277 / 240, 0 25, 5 / 38,1 16, 96 103 / 69, 30 VA = 6,00 103 j15, 86 103 VA De donde las potencias suministradas por la fuente son, Pf 6, 00kW ; Q f 15, 86kvar ind ; S f 16, 96kVA c) La potencia compleja consumidas por la carga es, S CAR S A S B S C Z A I A2 Z B I B2 Z C I C2 7, 80 / 75,1 33, 6 2 40, 0 / 0, 0 6, 82 2 11, 35 / 84, 9 25, 5 2 16, 57 10 3 / 73, 20 VA = 4, 78 10 3 j15, 86 10 3 VA De donde las potencias consumidas por la carga son, PCAR 4,78kW ; QCAR 15,86kvar ind ; SCAR 16,57kVA d) La potencia compleja perdida en las líneas y el conductor del neutro es, 109 ELECTROTECNIA III-110 S LL S LA S LB S LC S N Z L I A2 Z L I B2 Z L I C2 Z N I N2 Z L I A2 I B2 I C2 I N2 0, 400 / 0, 0 33, 62 6, 822 25, 5 2 35,12 1223 / 0, 00 VA =1223 + j0,0 VA De donde la potencia perdida en las líneas y el conductor del neutro es, PLL 1223 W =1,223kW S LL S LA S LB S LC S N Z L I A2 Z L I B2 Z L I C2 Z N I N2 Z L I A2 I B2 I C2 I N2 0, 400 / 0, 0 33, 62 6, 822 25, 5 2 35,12 1223 / 0, 00 VA =1223 + j0,0 VA De donde la potencia perdida en las líneas y el conductor del neutro es, PLL 1223 W =1,223kW Resolviendo el circuito de la figura número 11 por el método del desplazamiento del neutro tenemos. I aA a V an V cn Z aA IA A abc n V bn V AN ZA I Nn ZN N I bB Z bB IB I cC Z cC IC ZB B b ZC V BN V CN C c FIGURA NÚMERO 11. Haciendo, Z A1 Z aA Z A ; Y A1 1 Z A1 110 ELECTROTECNIA III-111 Z B 1 Z bB Z B ; Y B 1 1 Z B1 Z C 1 Z cC Z C 1 Z C1 ; Y C1 Tenemos el circuito equivalente siguiente: IA Tensión de desplazamiento del neutro A a abc IN V Nn I N Z N ZN N n V bn V cn V AN 1 Z A1 V an IB b Z C1 Z B1 B V BN 1 V CN 1 C IC c FIGURA NÚMERO 12. Considerando que la fuente suministra tensiones simétricas y que su secuencia de fases es abc (+), podemos trazar los diagramas fasoriales de tensión en la fuente y en la carga. 111 ELECTROTECNIA III-112 CARGA DESBALANCEADA Caídas de tensión en la carga equivalente C FUENTE SIMÉTRICA secuncia abc c abc V ca V cn n V an a V bc V bn V ab V CA1 V CN 1 V BC 1 V BN 1 b V AN 1 N A V AB 1 B FIGURA NÚMERO 13. Haciendo un solo diagrama fasorial tenemos. V Nn c C V ca V CN 1 V bc Tensión de desplazamiento del neutro V cn V bn V an n N V ab bB a A V AN 1 V BN 1 FIGURA NÚMERO 14. De acuerdo con la ley de tensiones de Kirchhoff tenemos, V an V AN 1 V Nn 0 V bn V BN 1 V Nn 0 V cn V CN 1 V Nn 0 Las caídas de tensión en la carga equivalente son, 112 ELECTROTECNIA III-113 V AN 1 I A Z A1 V BN 1 I B Z B1 V CN 1 I C Z C 1 Sustituyendo en las ecuaciones de la ley de tensiones las ecuaciones de las caídas de tensión en la carga equivalente, tenemos, V an I A Z A1 V Nn 0 V bn I B Z B1 V Nn 0 V cn I C Z C 1 V Nn 0 Despejando a las corrientes, IA V an V Nn Y A1 V an V Nn Y A1 V an Y A1 V Nn Z A1 IB V bn V Nn Y B1 V bn V Nn Y B1 V bn Y B1 V Nn Z B1 IC V cn V Nn Y C 1 V cn V Nn Y C 1 V cn Y C 1 V Nn Z C1 Sumando las corrientes tenemos, I A I B I C Y A1 V an Y B1 V bn Y C 1 V cn V Nn Y A1 Y B1 Y C 1 De la ley de corrientes de Kirchhoff tenemos, I A IB IC I N Además de que, IN V Nn V Nn Y N ZN Sustituyendo tenemos, V Nn Y N Y A1 V an Y B1 V bn Y C 1 V cn V Nn Y A1 Y B1 Y C 1 V Nn Y A1| Y B1 Y C 1 Y N Y A1 V an Y B1 V bn Y C 1 V cn 113 ELECTROTECNIA III-114 Despejando la caída de tensión del desplazamiento del neutro obtenemos, V Nn Y A1 V an Y B1 V bn Y C 1 V cn Y A1 Y B1 Y C 1 Y N Las corrientes de línea y del conductor del neutro son, I A Y A1 V an V Nn ; I B Y B1 V bn V Nn ; I C Y C 1 V cn V Nn I N I A IB IC Ejemplo 4-19. Resolviendo el problema 4-17 por medio del método del desplazamiento del neutro tenemos. Una fuente trifásica simétrica, conectada en estrella de cuatro hilos, con una frecuencia de 60,0 Hz, con una secuencia de fases abc, con tensiones de 220/127 V, alimenta una carga como se muestra en la figura número 10, donde la rama A tiene una impedancia ZA = 8,54 /62,10 , la rama B tiene una impedancia ZB = 18,09 /56,50, la rama C tiene una impedancia ZC = 13,85 /54,70 . La impedancia de las líneas tiene una impedancia ZL = 1,118 /26,60 , la impedancia del conductor del neutro es igual a la de las líneas. Determinar: a) Las corrientes de línea y en el conductor del neutro, b) las caídas de tensión de las fases de la carga, y c) las tensiones de línea en la carga. SOLUCIÓN. Las impedancias y admitancias de las fases y del conductor del neutro son, Z A1 Z L Z A 1,118 / 26, 6 8, 54 / 62,1 9, 47 / 58, 2 0 Y A1 1 1 105, 6 103 / 58, 20 S Z A1 9, 47 / 58, 2 Z B1 Z L Z B 1,118 / 26, 6 18, 09 / 56, 5 19, 07 / 54, 80 Y B1 1 1 52, 4 103 / 54, 80 S Z B1 19, 07 / 54, 8 Z C 1 Z L Z C 1,118 / 26, 6 13, 85 / 54, 7 14, 85 / 52, 7 0 Y C1 1 1 67, 4 103 / 52, 70 S Z C 1 14, 85 / 52, 7 YN 1 1 894 103 / 26, 60 S Z N 1,118 / 26, 6 114 ELECTROTECNIA III-115 a) La caída de tensión del desplazamiento del neutro es, V Nn V Nn Y A1 V an Y B1 V bn Y C 1 V cn Y A1 Y B1 Y C 1 Y N 105,6 103 / 58, 2 127,0 / 0,0 52,4 10 3 / 54,8 127,0 / 120,0 67,4 103 / 52,7 127,0 / 240,0 105,6 103 / 58, 2 52,4 10 3 / 54,8 67,4 10 3 / 52,7 894 10 3 / 26,6 V Nn 5,07 / 15, 30 V Las corrientes de línea y del conductor del neutro son, I A Y A1 V an V Nn 105, 6 103 / 58, 2 127, 0 / 0, 0 5, 07 / 15, 3 12, 90 / 57, 60 A I B Y B1 V bn V Nn 52, 4 103 / 54, 8 127, 0 / 120, 0 5, 07 / 15, 3 6, 73 / 177, 00 A I C Y C 1 V cn V Nn 67, 4 103 / 52, 7 127, 0 / 240, 0 5, 07 / 15, 3 8, 81/ 68, 9 0 A I Nn I A I B I C 12, 90 / 57,6 6, 73 / 177,0 8, 81/ 68, 9 4, 52 / 42, 00 A b) Las caídas de tensión de las fases de las cargas son, V AN Z A I A 8,54 / 62,1 12,90 / 57,6 110, 2 / 4,50 V V BN Z B I B 18,09 / 56,5 6,73 / 177,0 121,8 / 120,50 V V CN Z C I C 13,85 / 54,7 8,81/ 68,9 122,0 / 123,60 V c) Las tensiones de línea en la carga son, V AB V AN V BN 110, 2 / 4,5 121,8 / 120,5 206 / 33,50 V V BC V BN V CN 121,8 / 120,5 122,0 / 123,6 207 / 88,40 V 115 ELECTROTECNIA III-116 V CA V CN V AN 122,0 / 123,6 110, 2 / 4,5 200 / 152, 30 V Con impedancias mutuas. En la figura número 15 se muestra un circuito trifásico conectado en estrella de cuatro hilos, con tensiones simétricas, con cargas desbalanceadas e impedancias mutuas entre líneas. IA Za A a Z an V an n V bn V cn b I Nn Z ac Zn N Z bn Z ab Zb IB Z cn Zc c ZA Z cb ZC ZB B C IC FIGURA NÚMERO 15. En el circuito trifásico de cuatro hilos de la figura se tiene que, V an V aA Z A I A V Nn V bn V bB Z B I B V Nn (1) V cn V cC Z C I C V Nn I A I B IC I N Las caídas de tensión en los conductores de las fases y el conductor del neutro son, V aA Z a I A Z ab I B Z ac I C Z an I N V bB Z ba I A Z b I B Z bc I C Z bn I N V cC Z ca I A Z cb I B Z C I C Z cn I N (2) 116 ELECTROTECNIA III-117 V Nn Z na I A Z nb I B Z nc I C Z n I N Sustituyendo el grupo de ecuaciones (2) en el grupo de ecuaciones (1), obtenemos el juego de ecuaciones (3). V an Z a I A Z ab I B Z ac I C Z an I N Z A I A Z na I A Z nb I B Z nc I C Z n I N Z a I A Z ab I B Z ac I C Z an I A Z an I B Z an I C Z A I A Z na I A Z nb I B Z nc I C Z n I A Z n I B Z n I C I A Z a Z an Z A Z na Z n I B Z ab Z an Z nb Z n I C Z ac Z an Z nc Z n I A Z A Z a 2 Z an Z n I B Z ab Z an Z bn Z n I C Z ac Z an Z nc Z n V bn Z ba I A Z b I B Z bc I C Z bn I N Z B I B Z na I A Z nb I B Z nc I C Z n I N Z ba I A Z b I B Z bc I C Z bn I A Z bn I B Z bn I C Z B I B Z na I A Z nb I B Z nc I C Z n I A Z n I B Z n I C I A Z ba Z bn Z na Z n I B Z b Z bn Z B Z nb Z n I C Z bc Z bn Z nc Z n I A Z ba Z bn Z an Z n I B Z B Z b 2 Z bn Z n I C Z bc Z bn Z nc Z n V cn Z ca I A Z cb I B Z c I C Z cn I N Z C I C Z na I A Z nb I B Z nc I C Z n I N Z ca I A Z cb I B Z c I C Z cn I A Z cn I B Z cn I C Z C I C Z na I A Z nb I B Z nc I C Z n I A Z n I B Z n I C I A Z ca Z cn Z na Z n I B Z cb Z cn Z nb Z n I C Z c Z cn Z C Z nc Z n I A Z ca Z nc Z an Z n I B Z cb Z cn Z bn Z n I C Z C Z c 2 Z nc Z n Llamando a, Z a n Z a 2 Z an Z n Z ab n Z ab Z an Z bn Z n Z ac n Z ac Z an Z cn Z n (4) Z b n Z b 2 Z bn Z n Z bc n Z bc Z bn Z cn Z n Z c n Z c 2 Z cn Z n Sustituyendo el grupo de ecuaciones (4) en el grupo de ecuaciones (3), tenemos V an I A Z A Z a n I B Z abn I C Z ac n V bn I A Z abn I B Z B Z bn I C Z bc n V cn I A Z ac n I B Z bc n I C Z C Z c n 117 ELECTROTECNIA III-118 Las ecuaciones anteriores se pueden representar mediante un circuito equivalente, donde el neutro está desprovisto de impedancia. IA Z an A a V an n V bn V cn ZA Z ac n I Nn N Z ab n Z bn IB ZB ZC B C b Z cb n Z cn c IC FIGURA NÚMERO 16. La matriz de las ecuaciones anteriores es, V an Z Z a n A V bn Z ab n V cn Z ac n I A Z Z a n A I B Z ab n Z ac n I C Z ab n Z B Z bn Z bc n Z ab n Z B Z bn Z bc n I A Z bc n I B Z C Z c n I C Z ac n Z bc n Z C Z c n Z ac n 1 V an V bn V cn Ejemplo 4-20. Sea una carga desbalanceada con impedancias iguales a ZA = 24,5 /0,00 , ZB = 9,18 /75,60 y ZC = 10,82 /68,80 , alimentada a través de líneas con una impedancia de 0,500 /0,00 , con un conductor del neutro con una impedancia igual a la de las líneas, las cuales tiernen impedancias mutuas iguales a Zab = Zbc = Zca = 0,850 /-90,00 y Zan = Zbn = Zcn = 1,200 /-90,00 . La fuente es simétrica conectada en estrella, con tensiones de 13,80/7,97 kV, con una secuencia de fases abc. En la figura número 15 se muestra el circuito. Obtenga las corrientes de fase y del conductor del neutro. SOLUCIÓN. El problema se resolverá utilizando el diagrama del circuito equivalente mostrado en la figura número 16, donde las impedancias equivalentes son iguales a, 118 ELECTROTECNIA III-119 Z a n Z a 2 Z an Z n Z L 2 Z an Z n 0, 500 / 0, 0 2 1, 200 / 90, 0 0, 500 / 0, 0 2, 60 / 67, 40 Z ab n Z ab Z an Z bn Z n 0, 850 / 90, 0 1, 200 / 90, 0 1, 200 / 90, 0 0, 500 / 0, 0 3, 29 / 81, 30 Z ac n Z ac Z an Z cn Z n 0, 850 / 90, 0 1, 200 / 90, 0 1, 200 / 90, 0 0, 500 / 0, 0 3, 29 / 81, 30 Z b n Z b 2 Z bn Z n Z L 2 Z bn Z n 0, 500 / 0, 0 2 1, 200 / 90, 0 0, 500 / 0, 0 2, 60 / 67, 40 Z bc n Z bc Z bn Z cn Z n 0, 850 / 90, 0 1, 200 / 90, 0 1, 200 / 90, 0 0, 500 / 0, 0 3, 29 / 81, 30 Z c n Z c 2 Z cn Z n Z L 2 Z cn Z n 0, 500 / 0, 0 2 1, 200 / 90, 0 0, 500 / 0, 0 2, 60 / 67, 40 Z A Z a n 24, 5 / 0, 0 2, 60 / 67, 4 25, 6 / 5, 4 Z B Z b n 9,18 / 75,6 2,60 / 67,4 7, 27 / 63, 2 Z C Z c n 10,82 / 68,8 2,60 / 67,4 9,12 / 57,4 La ecuación matricial que resuelve para las corrientes de fase es, I A Z Z a n A I B Z ab n Z ac n I C Z ab n Z B Z bn Z bc n Z bc n Z C Z c n Z ac n 1 V an V bn V cn Sustituyendo valores tenemos, I A 25, 6 / 5, 4 3, 29 / 81, 3 3, 29 / 81, 3 1 7, 97 10 3 / 0, 0 254 / 29, 2 3 I B 3, 29 / 81, 3 7, 27 / 63, 2 3, 29 / 81, 3 7, 97 10 / 120, 0 1151 / 163, 2 3, 29 / 81, 3 3, 29 / 81, 3 9,12 / 57, 4 7, 97 10 3 / 240, 0 633 / 79, 7 I C 119 ELECTROTECNIA III-120 De donde las corrientes de fase son: I A 254 / 29, 20 A ; I B 1151/ 163, 20 A ; I C 633 / 79,7 0 A Y la corriente en el conductor del neutro es, I N I A I B I C 254 / 29, 2 1151/ 163, 2 633 / 79,7 1131/ 132,70 A Solución de un circuito conectado en estrella, con cargas desbalanceadas, utilizando el método de componentes de fase. Un modelo general para un circuito trifásico con impedancias desbalanceadas se muestra en la figura número 17. a IA b IB c IC V ab V ca V bc ZA a' Z ab ZB Z ca b' Z bc ZC c' FIGURA NÚMERO 17. Si las terminales a’b’c’ se conectan juntas y se aterrizan , y si todas las impedancias son diferentes una de otra , tenemos un circuito trifásico con cargas desbalanceadas para el cual, V an Z A V bn Z ba Z V cn ca Z ab ZB Z cb Z ac I A Z bc I B Z C I C (1) Si las terminales a’b’c’ no están en corto circuito, y si, nuevamente todas las impedancias son diferentes una de otra, tenemos una línea trifásica desbalanceada para la cual, V 'an Za V 'bn Z ba ' V cn Z ca Z ab Zb Z cb Z ac I A Z bc I B Z c I C (2) Escribimos una ecuación matricial para representar las ecuaciones (1) y (2) en conjunto, esto es, 120 ELECTROTECNIA III-121 V F ZF IF (3) donde V F es el vector columna de las componentes de fase de tensión, Z F es la matriz de las componentes de fase de las impedancias, e I F es el vector columna de las componentes de fase de las corrientes. Entonces cuando V F es dada o conocida, se puede obtener el vector de corrientes como, 1 I F Z F V F Y F V F (4) 1 donde Y F Z F es la matriz de las componentes de fase de la admitancia. Podemos tratar estas cantidades como vectores matrices, en cálculos subsecuentes, como si ellas fueran elementos simples. Por ejemplo, la potencia compleja del sistema se calcula con la ecuación siguiente: t * S V F I F (5) o por consiguiente de las ecuaciones (3) y (4), t * S IF ZF IF t t S V F Y F V F * (6) (7) Note que, ZF ZF t , Y F Y F t puesto que ellas son matrices simétricas. En el caso particular de, Z ab Z bc Z ca 0 La matriz de impedancias de las componentes de fase es, Z A Z F 0 0 0 ZB 0 0 0 Z A Z B Z C Z C Ejemplo 4-21. Se tiene una carga desbalanceada con ZA = 36,2 /37,20 , ZB = 28,5 /34,60 y ZC = 42,3 /26,8 , alimentada por medio de líneas con una impedancia ZL = 0,620 /0,00 , con un conductor del neutro con impedancia despreciable, las líneas tienen impedancias mutuas iguales de ZM = 2,00 /-90,00 . La fuente es simétrica, conectada en estrella, con tensiones de fase de 120,0 V, con una secuencia de fases abc. 0 Obtenga: a) las corrientes de fase, b) la corriente en el conductor del neutro y c) la potencia compleja. SOLUCIÓN. El circuito se puede dibujar como se muestra en la figura número 17. Las impedancias de fase son, 121 ELECTROTECNIA III-122 Z L Z A 0, 620 / 0, 0 36, 2 / 37, 2 36, 7 / 36, 6 0 Z L Z B 0, 620 / 0, 0 28, 5 / 34, 6 29, 0 / 33, 90 Z L Z C 0, 620 / 0, 0 42, 3 / 26, 8 42, 9 / 26, 40 La ecuación matricial que resuelve las corrientes de fase es, I A Z Z A L I B Z ba Z ca I C Z ab ZL ZB Z cb Z bc Z Z L C Z ac 1 V an V bn V cn Sustituyendo valores tenemos, I A 36, 7 / 36, 6 2, 00 / 90, 0 2, 00 / 90, 0 1 120, 0 / 0, 0 3, 22 / 40, 2 I B 2, 00 / 90, 0 29, 0 / 33, 9 2, 00 / 90, 0 120, 0 / 120, 0 4, 02 / 155, 6 2, 00 / 90, 0 2, 00 / 90, 0 42, 9 / 26, 4 120, 0 / 240, 0 2, 66 / 91, 0 I C a) De donde las corrientes de fase son, I A 3, 22 / 40, 20 A ; I B 4,02 / 155,60 A ; I C 2,66 / 91,00 A b) La corriente en el conductor del neutro es, I N I A I B I C 3, 22 / 40, 2 4,02 / 155,6 2,66 / 91,0 1,650 / 139,10 A c) La potencia compleja es, 3, 22 / 40, 2 S V I 120, 0 / 0, 0 120, 0 / 120, 0 120, 0 / 240, 0 4, 02 / 155, 6 2, 66 / 91, 0 0 1185 / 35, 2 VA t F * F Ejemplo 4-22. Resolviendo el problema 4-17 por medio del método de componentes de fase tenemos. Una fuente trifásica simétrica, conectada en estrella de cuatro hilos, con una frecuencia de 60,0 Hz, con una secuencia de fases abc, con tensiones de 220/127 V, alimenta una carga como se muestra en la figura número 10, donde la rama A tiene una impedancia ZA = 8,54 /62,10 , la rama B tiene una impedancia ZB = 18,09 /56,50, la rama C tiene una impedancia ZC = 13,85 /54,70 . La impedancia de las líneas tiene una impedancia ZL = 1,118 /26,60 , la impedancia del conductor del neutro es igual a la de las líneas. Determinar: a) Las corrientes de línea y en el 122 ELECTROTECNIA III-123 conductor del neutro, b) las caídas de tensión de las fases de la carga, y c) las tensiones de línea en la carga. SOLUCIÓN. El problema se resolverá por el método de componentes de fase. El circuito equivalente con el conductor del neutro desprovisto de impedancia se muestra en la figura siguiente: Za-n IA A a V an n V bn V cn ZA I Nn N Zb-n ZB IB ZC B C b Zc-n c IC Las impedancias del circuito equivalente son, Z a n Z L 2 Z an Z N 1,118 26,6 0 1,118 26,6 2, 24 26,60 Z abn Z ab Z an Z bn Z N 0 0 0 1,118 26,6 1,118 26,60 Z ac n Z ac Z an Z cn Z N 0 0 0 1,118 26,6 1,118 26,60 Z bn Z L 2 Z bn Z N 1,118 26,6 0 1,118 26,6 2, 24 26,60 Z bc n Z bc Z bn Z cn Z N 0 0 0 1,118 26,6 1,118 26,60 Z c n Z L 2 Z cn Z N 1,118 26,6 0 1,118 26,6 2, 24 26,60 La matriz de las ecuaciones anteriores es, I A Z Z a n A I B Z ba n Z ca n I C Z ab n Z B Z bn Z cb n Z bc n Z C Z c n Z ac n 1 V an V bn V cn 123 ELECTROTECNIA III-124 I A 8,54 / 62,1 2, 24 / 26,6 1,118 / 26,6 I B 1,118 / 26,6 I C 1,118 / 26,6 18,09 / 56,5 2, 24 / 26,6 1,118 / 26,6 1,118 / 26,6 13,85 / 54,7 2, 24 / 26,6 1,118 / 26, 2 1 127,0 / 0,0 127,0 / 120,0 127,0 / 240,0 I A 10, 45 / 54, 9 1,118 / 26, 6 1,118 / 26, 6 1 127, 0 / 0, 0 12, 89 / 57, 6 I B 1,118 / 26, 6 20,1 / 53, 3 1,118 / 26, 6 127, 0 / 120, 0 6, 72 / 177, 0 1,118 / 26, 6 1,118 / 26, 6 15, 86 / 50, 9 127, 0 / 240, 0 8, 80 / 68, 9 I C a) Las corrientes de línea y del conductor del neutro son, I A 12,89 / 57,60 A I B 6,72 / 177,00 A I C 8,80 / 68,90 A I N I A I B I C 12,89 / 57,6 6,72 / 177,0 8,80 / 68,9 4,52 / 42,00 A b) Las caídas de tensión en las fases de la carga son, V AN Z A I A 8,54 / 62,1 12,89 / 57,6 110,1/ 4,50 V V BN Z B I B 18,09 / 56,5 6,72 / 177,0 121,6 / 120,50 V V CN Z C I C 13,85 / 54,7 8,80 / 68,9 121,9 / 123,60 V c) Las tensiones de línea en la carga son, V AB V AN V BN 110,1/ 4,5 121,6 / 120,5 206 / 33,50 V V BC V BN V CN 121,6 / 120,5 121,9 / 123,6 206 / 88,40 V V CA V CN V AN 121,9 / 123,6 110,1/ 4,5 200 / 152, 30 V 2.2. Cargas de tres hilos. Alimentadas directamente en sus terminales. En la figura número 18 se muestra un circuito conectado en estrella de tres hilos, algunas veces denominado como de neutro flotante. 124 ELECTROTECNIA III-125 IA A a ZA I1 N b c IB B ZB IC I2 C ZC FIGURA NÚMERO 18. Solución por el método de mallas. Escribiendo las ecuaciones de malla de la figura número 18, tenemos, I 1 Z A Z B I 2 Z B 1 V ab Z B Z C V bc ZB De donde las corrientes de línea o fase son, I A I1 ; I B I 2 I1 ; IC I 2 Las caídas de tensión en las cargas son, V AN Z A I A ; V BN Z B I B ; V CN Z C I C Ejemplo 4-23. Utilizando el método mallas determine las corrientes de línea y las caídas de tensión de la carga mostrada en la figura. Considerando que la carga se alimenta de una fuente trifásica simétrica, con secuencia de fases ACB y de una tensión entre líneas de 208 V. Considere la tensión V bc como referencia. A V ca acb ZA = 6,00 /0,0 0 ZB = 6,00 /30,00 N V bc 208 / 0, 0 0 V ZC = 5,00 /45,00 B V ab C SOLUCIÓN. Las tensiones de línea son, 125 ELECTROTECNIA III-126 V ab 208 / 120,00 V V bc 208 / 0,00 V V ca 208 / 240,00 V A ZA = 6,00 /0,00 I1 N ZB = 6,00 /30,00 ZC = 5,00 /45,00 B I2 C Escribiendo las ecuaciones de mallas en forma de matrices, tenemos I 1 Z A Z B I 2 Z B 1 V ab Z B Z C V bc ZB 6, 00 / 0, 0 6, 00 / 30, 0 6, 00 / 30, 0 1 208 / 240, 0 23, 3 / 98, 9 6, 00 / 30, 0 5, 00 / 45, 0 208 / 0, 0 26, 5 / 63, 6 6, 00 / 30, 0 Las corrientes de línea son, I A I 1 23, 3 / 98,90 A I B I 2 I 1 26,5 / 63,6 23, 3 / 98,9 15,43 / 2,80 A I C I 2 26,5 / 63,6 26,5 / 116,40 A Las caídas de tensión en la carga son, V AN Z A I A 6,00 / 0,0 23, 3 / 98,9 139,8 / 98,90 V V BN Z B I B 6,00 / 30,0 15,43 / 2,8 92,6 / 27, 20 V V CN Z C I C 5,00 / 45,0 26,5 / 116,4 132,5 / 161,40 V Solución por el método del desplazamiento del neutro. 126 ELECTROTECNIA III-127 En este caso tenemos que el conductor del neutro es un aislador ideal, o no existe o bien está abierto como se muestra en la figura número 19. A A Z N Z N ZA Y N 0 ZA Y N 0 ZN N N ZC ZB B ZC ZB C B C FIGURA NÚMERO 19. Recordando la ecuación general de este método tenemos, V Nn Y A V an Y B V bn Y C V cn Y A Y B Y C Y N En virtud de que en este caso ZN = y por consiguiente YN = 0, tenemos por sustitución en la ecuación anterior, el resultado siguiente: V Nn Y A V an Y B V bn Y C V cn Y A Y B Y C Ejemplo 4-24. En el sistema trifásico de la figura, suponga una fuente simétrica con una secuencia de fases positiva. Determine las tensiones V AN , V BN y V CN , utilizando el método del desplazamiento del neutro. A a abc V an 120, 0 / 0, 0 0 V 60 Hz n c V cn 15,00 mH 10,00 V bn b B N 0,250 mF C SOLUCIÓN. Las tensiones al neutro en la fuente son, V an 120,0 / 0,00 V ; V bn 120,0 / 120,00 V ; V cn 120,0 / 240,00 V Las impedancias y admitancias de la carga son, 127 ELECTROTECNIA III-128 Z A 2 π f L 2 π 60,0 15,00 10-3 5,65 1 1 Z A 5, 65 / 90, 00 ; Y A 0,1768 / 90, 00 S Z A 5, 65 / 90, 0 1 1 Z B 10, 00 / 0, 0 0 ; Y B 0,1000 / 0, 0 0 S Z B 10, 00 / 0.0 1 1 ZC 10, 61 2 π f C 2 π 60,0 0,250 10-3 1 1 Z C 10, 61 / 90, 00 ; Y C 94, 2 10 3 / 90, 0 0 S Z C 10, 61 / 90, 0 ZN ; Y N 0 Sustituyendo valores en la ecuación de la tensión del desplazamiento del neutro, tenemos, V Nn V Nn Y A V an Y B V bn Y C V cn Y A Y B Y C 0,1768 / 90, 0 120, 0 / 0, 0 0,1000 / 0, 0 120, 0 / 120, 0 94, 2 103 / 90, 0 120, 0 / 240, 0 0,1768 / 90, 0 0,1000 / 0, 0 94, 2 103 / 90, 0 312 / 73, 40 V Las caídas de tensión en la carga son, V AN V an V Nn 120,0 / 0,0 312 / 73,4 301/ 84,10 V V BN V bn V Nn 120,0 / 120,0 312 / 73,4 246 / 127,40 V V CN V cn V Nn 120,0 / 240,0 312 / 73,4 430 / 110, 30 V 128 ELECTROTECNIA III-129 c, C Vcn VCN Van n a, A VAN Vbn VNn b, B VBN N Alimentadas a través de líneas. En la figura número 20 se muestra un circuito conectado en estrella de tres hilos, alimentado a través de líneas. Za IA A a ZA I1 N Zb b Zc c IB B ZB IC I2 ZC C FIGURA NÚMERO 20. Solución por el método de mallas. Escribiendo las ecuaciones de mallas de la figura número 20, en forma de matriz, para determinar las corrientes de las mallas tenemos, 129 ELECTROTECNIA III-130 I 1 Z a Z A Z B Z b Zb ZB I 2 Zb ZB 1 V ab Z b Z B Z C Z c V bc De donde las corrientes de línea o fase son, I A I1 ; I B I 2 I1 ; IC I 2 Las caídas de tensión en la carga son, V AN Z A I A ; V BN Z B I B ; V CN Z C I C Ejemplo 4-25. Una fuente de tensiones simétricas, con una secuencia de fases abc, y tensiones de línea de 440 V, alimenta un conjunto de cargas no balanceadas, conectadas en estrella de tres hilos, con impedancias de valores ZA = 10,00 /45,00 , ZB = 8,00/-30,00 y ZC = 5,00 /0,00 . La impedancia de las líneas de alimentación es de 0,215 /0,20 . El diagrama del circuito se muestra en la figura número 20. a) Calcule el valor de las corrientes en cada línea o fase, b) las caídas de tensión en las fases de la carga, c) las caídas de tensión de línea en la carga. Tome como referencia la tensión V ab . SOLUCIÓN. La ecuación matricial para obtener las corrientes de las mallas es, I 1 Z L Z A Z B Z L ZL ZB I 2 ZL ZB Z L Z B Z C Z L 1 V ab V bc Donde, Z L Z A Z B Z L 0, 215 / 0, 2 10, 00 / 45, 0 8, 00 / 30, 0 0, 215 / 0, 2 14, 75 / 12, 00 Z L Z B 0, 215 / 0, 2 8, 00 / 30, 0 8,19 / 29, 20 Z L Z B Z C Z L 0, 215 / 0, 2 8, 00 / 30, 0 5, 00 / 0, 0 0, 215 / 0, 2 12, 99 / 17, 90 Sustituyendo valores en la ecuación matricial tenemos, 1 I 1 14, 75 / 12, 0 8,19 / 29, 2 440 / 0, 0 26, 9 / 70, 5 I 2 8,19 / 29, 2 12, 99 / 17, 9 440 / 120, 0 50,1 / 95, 4 a) De donde las corrientes de línea o fase son, I A I 1 26,9 / 70,50 A I B I 2 I 1 50,1/ 95,4 26,9 / 70,5 28,1/ 119, 20 A 130 ELECTROTECNIA III-131 I C I 2 50,1/ 95,4 50,1/ 84,60 A b) Las caídas de tensión en las fases de la carga son, V AN Z A I A 10,00 / 45,0 26,9 / 70,5 269 / 25,50 V V BN Z B I B 8,00 / 30,0 28,1/ 119, 2 225 / 149, 20 V V CN Z C I C 5,00 / 0,0 50,1/ 84,6 251/ 84,60 V c) Las tensiones de línea en la carga son, V AB V AN V BN 269 / 25,5 225 / 149, 2 436 / 0,10 V V BC V BN V CN 225 / 149, 2 251/ 84,6 425 / 120,70 V V CA V CN V AN 251/ 84,6 269 / 25,5 426 / 120,90 V Solución por el método del desplazamiento del neutro. En este caso tenemos el circuito que se muestra en la figura número 21. Za a IA A ZA N Zb b Zc c IB B IC ZB ZC C FIGURA NÚMERO 21. La ecuación general de este método es, V Nn Y A1 V an Y B1 V bn Y C 1 V cn Y A1 Y B1 Y C 1 Y N En virtud de que en este caso ZN = y por consiguiente YN = 0, tenemos por sustitución en la ecuación anterior, el resultado siguiente: V Nn Y A1 V an Y B1 V bn Y C 1 V cn Y A1 Y B1 Y C 1 131 ELECTROTECNIA III-132 Ejemplo 26. Resolviendo el ejemplo 25 por medio del método del desplazamiento del neutro tenemos, Una fuente de tensiones simétricas, con una secuencia de fases abc, y tensiones de línea de 440 V, alimenta un conjunto de cargas no balanceadas, conectadas en estrella de tres hilos, con impedancias de valores ZA = 10,00 /45,00 , ZB = 8,00/-30,00 y ZC = 5,00 /0,00 . La impedancia de las líneas de alimentación es de 0,215 /0,20 . El diagrama del circuito se muestra en la figura número 21. a) Calcule el valor de las corrientes en cada línea o fase, b) las caídas de tensión en las fases de la carga, c) las caídas de tensión de línea en la carga. Tome como referencia la tensión V ab . SOLUCIÓN. Las impedancias y admitancias equivalentes son, Z A1 Z L Z A 0, 215 / 0, 2 10, 00 / 45, 0 10,15 / 44,10 Y A1 1 1 0, 0985 / 44,10 S Z A1 10,15 / 44,1 Z B1 Z L Z B 0, 215 / 0, 2 8, 00 / 30, 0 8,19 / 29, 2 0 Y B1 1 1 0,1222 / 29, 20 S Z B1 8,19 / 29, 2 Z C 1 Z L Z C 0, 215 / 0, 2 5, 00 / 0, 0 5, 21 / 0, 0 0 Y C1 1 1 0,1918 / 0, 00 S Z C 1 5, 21 / 0, 0 Las tensiones al neutro en la fuente son, V an Vab 3 / ab 30, 0 440 3 / 0, 0 30, 0 254 / 30, 00 V V bn 254 / 150,00 V ; V cn 254 / 270,00 V Sustituyendo valores, la tensión del desplazamiento del neutro es, V Nn Y A1 V an Y B1 V bn Y C 1 V cn Y A1 Y B1 Y C 1 132 ELECTROTECNIA III-133 V Nn 0, 0985 / 44,1 254 / 30, 0 0,1222 / 29, 2 254 / 150 0,1918 / 0, 0 254 / 270, 0 0, 0985 / 44,1 0,1222 / 29, 2 0,1918 / 0, 0 25,1 / 166,10 V Las tensiones al neutro son, V AN 1 V an V Nn 254 / 30,00 25,1/ 166,1 273 / 26, 30 V V BN 1 V bn V Nn 254 / 150,00 25,1/ 166,1 230 / 148, 30 V V CN 1 V cn V Nn 254 / 270,00 25,1/ 166,1 261/ 84,60 V a) Las corrientes de fase o línea son, IA IB V AN 1 273 / 26, 3 26, 9 / 70, 40 A Z A1 10,15 / 44,1 V BN 1 230 / 148, 3 28,1 / 119,10 A Z B1 8,19 / 29, 2 IC V CN 1 261 / 84, 6 50,1 / 84, 60 A Z C 1 5, 21 / 0, 0 b) las caídas de tensión en las fases de la carga son, V AN Z A I A 10,00 / 45,0 26,9 / 70,4 269 / 25,40 V V BN Z B I B 8,00 / 30,0 28,1/ 119,1 225 / 149,10 V V CN Z C I C 5,00 / 0,0 50,1/ 84,6 251/ 84,60 V c) Las caídas de tensión de línea en la carga son, V AB V AN V BN 269 / 25,4 225 / 149,1 436 / 0,00 V V BC V BN V CN 225 / 149,1 251/ 84,6 424 / 120,80 V V CA V CN V AN 251/ 84,6 269 / 25,4 426 / 121,00 V 133 ELECTROTECNIA III-134 3. MEDICIÓN DE LA POTENCIA ACTIVA. 3.1 Carga de cuatro hilos. Tomando en cuenta el teorema de Blondel, para una carga de cuatro hilos, la potencia activa del circuito se puede medir con cuatro o tres wáttmetros, siendo el arreglo más común el que utiliza el mínimo de wáttmetros, esto es tres, como se muestra en la figura número 22. IA BC1 A WM1 IB BC2 BP1 RP1 B WM2 FUENTE CARGA IC BC3 BP2 RP2 C WM3 IN BP3 RP3 N FIGURA NÚMERO 22. Donde las indicaciones de los wáttmetros son, WM1=V AN I A VAN I A cos VAN IA V WM2 =V BN I B VBN I B cos VBN IB V WM3 =V CN I C VCN IC cos VCN IC V AN I A* BN I B* CN IC* Por lo que la potencia activa total de la carga es, P WM1+ WM2+ WM3 Ejemplo 27. Una fuente trifásica simétrica, con secuencia de fases ABC, conectada en estrella, con tensiones de fase a neutro de 120,0 V, alimenta una carga trifásica conectada en estrella de cuatro hilos. Tomando como referencia la tensión V AN , las corrientes tomadas la carga son: Ay I A 9,82 / 44,10 A, I B 13,82 / 129,80 I C 17,56 / 84,10 A. Con los wáttmetros conectados como se muestra en la figura número 22, a) determine las indicaciones de cada uno de los wáttmetros y b) la potencia activa total. SOLUCIÓN. 134 ELECTROTECNIA III-135 a) Las indicaciones de los wáttmetros son, WM1=V AN I A =VAN I A cos VAN IA WM2 =V BN I B =VBN I B cos VBN IB WM3 = V CN I C = VCN I C cos VCN IC Puesto que, V AN 120,0 / 0,00 V Entonces, V BN 120,0 / 120,0 V ; V CN 120,0 / 240,0 V Los ángulos involucrados en las indicaciones de los wáttmetros son, 0 VAN IA VAN IA 0, 0 44,1 44,1 0 VBN IB VBN IB 120, 0 129, 8 9, 8 0 0 VCN IC VCN IC 240, 0 84,1 324,1 35, 9 a) Sustituyendo valores en las ecuaciones de las lecturas de los wáttmetros sus indicaciones son, WM1=120, 0 9, 82cos 44,1 846 W WM2 =120, 0 13, 82cos 9, 8 1634 W WM3 =120, 0 17, 56cos 35, 9 1707 W b) La potencia activa total consumida es, P WM1+ WM2 WM3 846 1634 1707 4,19 103 W=4,19 kW Alternativa para el cálculo de las indicaciones de los wáttmetros. WM1 V * AN IA 120, 0 / 0, 0 9, 82 / 44,1 1,178 10 3 / 44,1 846 j820 846 W WM2 V * BN IB 120, 0 / 120, 0 13, 82 / 129, 8 1, 658 10 3 / 9, 8 1634 j282 1634 W 135 ELECTROTECNIA III-136 WM3 V * CN IC 120, 0 / 240, 0 17, 56 / 84,1 2,1110 3 / 35, 9 1707 j1236 1707 W 3.2. Carga de tres hilos. Considerando el teorema de Blondel, para un circuito de tres hilos, podemos utilizar tres o dos wáttmetros, siendo el arreglo más común el que utiliza un número mínimo de wáttmetros, esto es dos. Como se muestra en la figura número 23. IA * A BC1 * BP1 RP1 FUENTE CARGA WM1 IB B * C WM2 BP2 RP2 IC * BC2 FIGURA NÚMERO 23. Donde las indicaciones de los wáttmetros son, WM1=V AB I A VAB I A cos VAB IA V WM2 =V CB I C VCB IC cos VCB IC V AB I A* CB IC* La potencia activa total es, P WM1+ WM2 Ejemplo 28. La potencia activa se mide con dos wáttmetros conectados como se indica en la figura. Si, V AB 460 / 0,00 V ; I A 20,0 / 30,00 A ; I C 46, 2 / 132,50 A calcular el valor de I B y determinar la lectura de cada uno de los wáttmetros. La fuente es simétrica y la secuencia de fases es ABC. 136 ELECTROTECNIA III-137 WM1 IA * A * IC C WM2 IB * B CARGA TRIFÁSICA DE TRES HILOS * SOLUCIÓN. a) Como I A I B IC 0 entonces I B I A I C 20, 0 / 30, 0 46, 2 / 132, 5 27, 8 / 60, 00 A b) Con los wáttmetros conectados como se muestra en la figura, WM1=V AC I A VAC I A cos VI AAC y WM2=V BC I B VBC I B cos VIBBC Puesto que V AB 460 / 0,00 V Entonces V BC 460 / 120,00 V , V CA 460 / 120,00 V ; V AC 460 / 60,00 V Los ángulos involucrados en las indicaciones de los wáttmetros son, VI AAC 60, 0 30, 0 30, 00 ; VI BBC 120, 0 60, 0 60, 00 Sustituyendo valores en las ecuaciones de las lecturas de los wáttmetros tenemos, WM1=460 20,0 cos 30=7,97 103 W 7,97kW WM2=460 27,8 cos 60=6,39 103 W 6, 39kW y la potencia activa total consumida es, P WM1+ WM2=7,97 103 6, 39 103 14, 36103 W=14,36kW 137 ELECTROTECNIA III-138 Alternativa para el cálculo de las lecturas de los wáttmetros, WM1= 7, 97 10 V WM2 = * V AC I A * BC 3 3 / 30, 0 j4, 60 103 7, 97 103 W = 7,97 kW 460 / 120, 0 27, 8 / 60, 0 12, 79 10 IB 6, 39 10 3 460 / 60, 0 20, 0 / 30, 0 9, 20 10 3 / 60, 0 j11, 07 103 6, 39 103 W = 6,39kW 4. EJERCICIOS. Ejercicio 4.1. Una carga balanceada conectada en estrella se conecta a una fuente trifásica simétrica de 60 Hz, con una secuencia de fases abc, con una tensión de línea V AB = 208 /0,00 V. Cada fase toma una potencia activa de 6,00 kW, con un factor de potencia de 0,500 atrasado. (a) Calcule la corriente de línea y encuentre las corrientes de línea I A , I B e I C , así como la impedancia por fase ZY. (b) ¿Qué valor de capacitancia C se debe poner en paralelo con cada elemento de carga para hacer mínima la corriente que toma la fuente?, y (c) ¿cuál es la corriente de línea resultante en estas condiciones? A ZY C N C ZY C ZY B C SOLUCIÓN. Resolviendo el problema por medio del circuito monofásico equivalente, ya que tenemos tensiones simétricas y cargas balanceadas, tenemos, F VF C ZF 208 120,1V N La tensión de fase al neutro es, VF VL 3 3 138 ELECTROTECNIA III-139 Puesto que el circuito tiene secuencia abc, las tensiones de fase están 30 grados atrasadas con respecto a las tensiones de línea, considerando a esta última como la referencia tenemos, V AN 120,1/ 30,00 V ; V BN 120,1/ 150,00 V ; V CN 120,1/ 270,00 V a) La corriente de línea es, PF 6, 00 103 IL 99, 9 A VF cos 120,1 0, 500 Tomando en cuenta que la carga tiene un factor de potencia de 0,500 atrasado, la corriente de fase debe estar atrasada con respecto a su tensión de fase o al neutro un ángulo de 60 0, de donde, I A 99,9 / 30,0 60,0 99,9 / 90,00 A I B 99,9 / 210,00 A ; I C 99,9 / 330,00 A = 99,9 / 30,00 A La magnitud de la impedancia por fase es, ZY VF 120,1 1, 202 I L 99, 9 En virtud de que el circuito tiene un factor de potencia 0,500 atrasado, entonces la impedancia en forma de complejo es, Z Y 1, 202 / 60, 00 b) La potencia reactiva inductiva que toma la carga por fase es, QF VF I L sen 120,1 99,9 0,866 10, 39103 var ind 10,39kvar ind Para que la corriente sea mínima se debe tener un factor de potencia unitario, por lo que se debe contrarrestar la potencia reactiva con un juego de capacitores que suministren el mismo valor de potencia reactiva pero de característica capacitiva. La reactancia del capacitor por fase es, VF2 120,12 XC 1, 388 QC 10, 39 103 De donde los capacitores que se conectan por fase, cada uno debe tener una capacitancia de, C 1 1 1911 10 6 F 1911 F 2 f X C 2 60, 0 1, 388 139 ELECTROTECNIA III-140 c) Puesto que en las condiciones en que están conectados los capacitores se tiene como resultado que el circuito tiene factor de potencia unitario, entonces la corriente de línea es ' IL PF 6, 00 103 50, 0 A VF cos ' 120,1 1, 000 Ejercicio 4.2. Determinar: a) las corrientes de fase, b) las potencias activa, reactiva y aparente totales, y c) el factor de potencia del sistema que se muestra en la figura, que tiene cargas balanceadas con Z = 4,00+ j 7,52 , con impedancias mutuas iguales con valor de ZM = 2,31 /-90,00 , cuando se alimenta de una fuente de tensiones simétricas, con una tensión de fase de 266 V, con una secuencia de fases ABC. A R X VL N ZM ZM X X R R ZM B C SOLUCIÓN. Aplicando el método del circuito monofásico equivalente tenemos, IF IL F Ze Z ZM VF N La impedancia propia de la carga, en forma polar es, Z 4, 00 j7, 52 8, 52 / 62, 00 La impedancia equivalente es, Z e Z Z M 8, 52 / 62, 0 2, 31 / 90, 0 10, 62 / 67, 9 0 140 ELECTROTECNIA III-141 Considerando a la tensión V F como referencia, las corrientes de línea tienen un valor de, IF IL 266 / 0, 0 VF 25, 0 / 67, 90 A Z e 10, 62 / 67, 9 a) Tomando como referencia a la tensión V AN las corrientes en las fases son, I A I F / AN e 10, 62 / 0, 0 67, 9 10, 62 / 67, 90 A I B 10,62 / 187,9 A ; I C 10,62 / 307,9 A =10,62 /52,10 A b) La potencia compleja es, * S 3V F I F S 3 266 / 0, 0 25, 0 / 67, 9 19, 95 10 3 / 67, 9 0 VA = 7,51 103 j18, 48 103 VA De donde las potencias activa, reactiva y aparente totales son, P 7,51kW ; Q 18,48k var ind ; S 19,95kVA El factor de potencia del sistema es, FP cos 67,9 0, 376 AT Ejercicio 4-3. Tres cargas balanceadas conectadas en estrella se instalan sobre un sistema trifásico balanceado de cuatro hilos. La carga 1 toma una potencia total de 6,00 kW con factor de potencia unitario, la carga 2 requiere 10,00 kVA con un factor de potencia de 0,960 atrasado, y la carga 3 necesita 7,00 kW con factor de potencia 0,850 atrasado. La tensión de fase en las cargas es de 135,0 V, la resistencia en cada línea de alimentación es de 0,1000 y la resistencia del conductor del neutro es de 1,000 , encuentre: a) la potencia activa total que toman las cargas; b) el factor de potencia combinado de las cargas; c) la potencia activa total pérdida en las tres líneas de alimentación; d) la tensión de fase en la fuente; e) el factor de potencia al cual está operando la fuente. SOLUCIÓN. Puesto que el circuito tiene tensiones simétricas y carga balanceada este se puede resolver usando la técnica del circuito monofásico equivalente, quedando como se muestra en la figura siguiente: 141 ELECTROTECNIA III-142 RL f F IL Z1 Vn n Z2 Z3 N a) La potencia activa total que toman las cargas, PCAR PZ 1 PZ 2 PZ 3 6,00 10,00 0,960 7,00 22,6kW b) La potencia compleja de la carga es, S CAR 6, 00 j0 9,60 j2,80 7,00 j4,34 22,6 j7,14 23,7 /17,50 kVA De donde el factor de potencia combinado de la carga es, FP cos 17, 5 0, 954 AT c) La potencia compleja tomada por las cargas también se puede expresar como, * S CAR 3V N I L Tomando como referencia la tensión V N * IL S CAR 3V N 23, 7 103 / 17, 5 3 135, 0 / 0, 0 58, 5 / 17, 50 A I L 58,5 / 17,50 A Y la potencia activa total pérdida en las tres líneas es, PL 3 RL I L2 3 0,1000 58,52 1027 W d) La caída de tensión en la línea es, V LL RL I L 0,1000 58,5 / 17,5 5,85 / 17,50 V La tensión de fase o al neutro en la fuente es, V n V N V LL 135,0 / 0,0 5,85 / 17,5 140,6 / 0,70 V 142 ELECTROTECNIA III-143 e) El factor de potencia al que está operando la fuente es, FPf cos 17, 5 0, 7 0, 957 AT Donde (17,5 –0,7) es el ángulo que forman la tensión V n y la corriente I L . Ejercicio 4-4. 143 ELECTROTECNIA III-144 UNIDAD 5. CIRCUITOS TRIFÁSICOS CON CARGAS ALIMENTADAS CON TENSIONES SIMÉTRICAS. CONECTADAS EN DELTA, 1. CARGAS BALANCEADAS. Alimentadas directamente en sus terminales. Cuando se conectan tres impedancias idénticas, como se muestra en la figura, estas constituyen una carga balanceada conectada en delta. IA A Z I AB IB B IC I CA I CA ABC Z I AB , I F Z C I BC I BC I CA I A, IL FIGURA NÚMERO 1. Si dicha carga se alimenta con un sistema trifásico simétrico, se puede concluir que las magnitudes de las intensidades de corriente en las impedancias deben ser iguales, esto es, I AB I BC ICA I F y la corriente de línea de la fase A es, I A I AB I CA I F / 0,0 I F / 240,0 3 I F / 30,00 Puesto que las corrientes están desfasadas entre si 120 grados, podemos observar que la magnitud de la corriente I A es 3 veces mayor que la magnitud de la corriente I AB o I CA y que está atrasada 30 grados con respecto a la corriente I AB , cuando tenemos secuencia de fases abc. Ya que el sistema está balanceado, podemos concluir que lo mismo sucede con las otras dos fases, por lo que la magnitud de las corrientes de línea serán 3 veces mayores que las corrientes de fase, esto es, IL 3 IF 144 ELECTROTECNIA III-145 En el caso de tener una alimentación con secuencia de fases acb, las corrientes de línea se adelantan 30 grados con relación a sus respectivas tensiones de fase. Ejemplo 5-1. La impedancia de la carga conectada en delta que se muestra en la figura está formada por un resistor de 2,50 y un inductor de 9,28 mH por fase, dicha carga tiene una caída de tensión de línea de 460 V, de una frecuencia de 60 Hz, con una secuencia de fases ABC. Tomando como referencia a la caída de tensión V determine: a) las corrientes de fase, b) las corrientes de línea. AB , A Z Z B Z C SOLUCIÓN. La reactancia inductiva por fase es, X L 2 f L 2 60,0 9, 28 103 3,50 La impedancia por fase es, Z 2, 50 j3,50 4,30 /54,50 Las tensiones de línea son, V AB 460 / 0,00 V V BC 460 / 120,00 V V CA 460 / 240,00 V a) Las corrientes de fase son, IF 460 / 0, 0 VF 107, 0 / 54, 50 A Z 4, 30 / 54, 5 145 ELECTROTECNIA III-146 I AB 107,0 / 54,50 A ; I BC 107,0 / 174,50 A ; I CA 107,0 / 294,50 A b) las corrientes de línea son, I L 3 I F / IF 30, 0 3 107, 0 / 54, 5 30, 0 185, 3 / 84, 50 A I A 185, 3 / 84,50 A ; I B 185, 3 / 204,50 A ; I C 185, 3 / 324,50 A V CA I CA IC IB V AB I BC - 54,50 I AB 0 - 30,0 I CA V BC IA Ejemplo 5-2. Cada fase de una carga trifásica balanceada conectada en delta () consiste de un inductor de 0,200 H en serie con la combinación en paralelo de un capacitor de 5,00 F y una resistencia de 200 . Suponga una tensión de línea de 200 V, con una frecuencia angular = 400 rad/s. Encuentre: a) la corriente de fase, b) la corriente de línea y c) la potencia activa total absorbida por la carga. 146 ELECTROTECNIA III-147 IL 0,200 H 200 5,00 F IF SOLUCIÓN. La impedancia del inductor es, Z L j L j400 0,200 80,0 /90,00 La impedancia del capacitor es, ZC j 1 1 / 90, 0 500 / 90, 00 C 400 5, 00 106 La impedancia del resistor es, Z R 200 / 0, 00 La impedancia de fase es, ZF ZL a) 500 / 90,0 200 / 0,0 ZC Z R 80,0 / 90,0 172,8 / 3,7 0 ZC Z R 500 / 90,0 200 / 0,0 La corriente de fase es, IF 200 / 0, 0 VL 1,157 / 3, 7 0 A Z F 172, 8 / 3, 7 b) La corriente de línea es, I L 3 I F 3 1,157 2, 00 A c) La potencia activa es, P 3VL I F cos 3 200 1,157 cos 3, 7 693 W Ejemplo 5-3. Dos motores eléctricos trifásicos están conectados a una red trifásica cuya tensión de línea VL es de 460 V, ver la figura. Los datos de los motores eléctricos son: P1 (en la flecha) = 10,00 kW, cos 1 = 0,900 y 1 = 85 %; P2 (en la flecha) = 8,00 kW, cos 2 = 0,800, 2 = 90 %. Determine: a) la corriente de línea del conjunto, b) el factor de potencia en la instalación del conjunto, y c) la potencia eléctrica consumida por los motores. 147 ELECTROTECNIA III-148 A B C M1 M2 SOLUCIÓN. La corriente tomada por el motor 1 es, I1 P1 3 VL cos 1 1 10, 00 103 3 460 0, 900 0, 850 16, 41A Tomando en cuenta el ángulo del factor de potencia del motor 1, tenemos I 1 16,41/ cos 1 0,900 16,41/ 25,80 A La corriente tomada por el motor 2 es, I2 P2 3 VL cos 2 2 8, 00 103 3 460 0, 800 0, 900 13, 95 A Tomando en cuenta el ángulo del factor de potencia del motor 2, tenemos I 2 13,95 / cos1 0,800 13,95 / 36,90 A a) La corriente tomada por el conjunto de motores es, I I 1 I 2 16,41/ 25,8 13,95 / 36,9 30, 2 / 30,90 A b) El factor de potencia del conjunto es, FP cos(30,9) 0,858 AT c) La potencia eléctrica consumida por los motores es, P 3 VL I cos 3 460 30, 2 0,858 20,6 103 W 20,6kW Alimentadas a través de líneas. 148 ELECTROTECNIA III-149 ZL I cC c IC C I BC V bc Z V ca ZL I aA b I A I CA a V ab Z B A ZL I bB I AB Z IB FIGURA NÚMERO 2. Puesto que la alimentación es simétrica las caídas de tensión también son simétricas, de aquí que Vab Vbc Vca Vl Cuando las cargas conectadas en delta están balanceadas y las impedancias de las líneas son iguales entonces, Z AB Z BC Z CA Z Z aA Z bB Z cC Z L Para determinar la relación de las corrientes en la carga con las tensiones en la fuente, se aplica la ley de tensiones de Kirchhoff a los circuitos cerrados. Para el circuito aABba. V ab I A Z L I AB Z I B Z L Z L I A I B I AB Z Sustituyendo las expresiones de las corrientes de línea por las de sus componentes de fase, tenemos V ab Z L I AB I CA I BC I AB Z I AB Z L 2 I AB I CA I BC Z I AB Por otro lado tenemos que, I AB I BC I CA 0 Despejando a I AB , I AB I BC I CA Sustituyendo en la ecuación de V ab tenemos, 149 ELECTROTECNIA III-150 V ab 3 Z L I AB Z I AB I AB 3 Z L Z Despejando a I AB tenemos, I AB V ab 3ZL Z En forma similar se pueden obtener las otras corrientes, por medio de las fórmulas siguientes: I BC V bc 3ZL Z I CA V ca 3ZL Z Ejemplo 5-4. Se da el circuito de la figura donde, la tensión de línea en la fuente es igual a 240 V, las impedancias de fase son Z = 10,00 /0,00 y la impedancia de las líneas es ZL = 0,500 /0,00 . Determinar: a) las corrientes de línea y de fase del sistema, b) las tensiones en la carga, c) la caída de tensión en la línea, d) la potencia activa consumida por la carga, e) la potencia pérdida en las líneas y f) construir el diagrama fasorial de tensiones y corrientes. Considere la tensión V ab como referencia y una secuencia de fases abc. A a ZL Z Z B b ZL C Z c ZL SOLUCIÓN. Las tensiones de línea son, V ab 240 / 0,00 V ; V ab 240 / 120,00 V ; V ab 240 / 240,00 V 150 ELECTROTECNIA III-151 a) Las corrientes de fase son, 240 / 0, 0 V ab 20, 9 / 0, 00 A 3 Z L Z 3 0, 500 / 0, 0 10, 00 / 0, 0 I AB I BC 20,9 / 120,00 A ; I CA 20,9 / 240,00 A Las corrientes de línea son 3 veces mayores que las corrientes de fase y están 30,00 atrasadas con respecto a ellas, de donde I A 3 I AB / AB 30, 0 3 20, 9 / 0, 0 30, 0 36, 2 / 30, 0 0 A I B 36, 2 / 150,00 A ; I C 36, 2 / 270,00 A b) Las caídas de tensión en la carga son, V AB Z I AB 10,00 / 0,0 20,9 / 0,0 209 / 0,00 V V BC 209 / 120,00 V ; V CA 209 / 240,00 V c) Las caídas de tensión en las líneas son, V aA Z L I A 0,500 / 0,0 36, 2 / 30,0 18,10 / 30,00 V V bB 18,10 / 150,00 V ; V cC 18,10 / 270,00 V d) La potencia activa consumida por la carga es, P 3VL I F cos F 3 209 20,9 cos(0,0) 13,10103 W 13,10kW e) La potencia activa pérdida en las líneas es, PL 3VlL I L cos lL 3 18,10 36, 2 1 1, 966 103 W 1,966kW f) Diagrama fasorial. 151 ELECTROTECNIA III-152 IC V ca abc I CA I AB V ab 30,00 I BC IB IA V bc Ejemplo 5-5. El sistema de la figura muestra una fuente y su carga conectada en delta balanceada, determine: a) las corrientes de fase en la carga, b) las corrientes de línea, c) las caídas de tensión en la carga, d) las potencias activa, reactiva y aparente, y e) los factores de potencia de la carga y del sistema. abc 1,000 c IC C 1,330 mH V bc V ca Z ZL 60 Hz b 10,60 mH IA a V ab 120, 0 / 0, 0 0 V A ZL Z 3,00 B IB SOLUCIÓN. Las impedancias de la línea y la carga son, X L 2 f LL 2 601, 330103 0,501 Z L 1, 000 j0,501 1,118 /26,60 X 2 f L 2 60 10,60 103 4,00 Z 3, 00 j4,00 5,00 /53,10 Las tensiones de línea son, 152 ELECTROTECNIA III-153 V ab 120,0 / 0,00 V ; a) V bc 120,0 / 120,00 V ; V ca 120,0 / 240,00 V Las corrientes de fase en la carga son, I AB 120, 0 / 0, 0 V ab 14, 74 / 42, 50 A 3 Z L Z 3 1,118 / 26, 6 5, 00 / 53,1 I BC 14,74 / 162,50 A ; I CA 14,74 / 282,50 A b) Las corrientes de línea son 3 veces mayores que las corrientes de fase y están 30,0 0 atrasadas con respecto a ellas, de donde I A 3 I AB / AB 30, 0 3 14, 74 / 42, 5 30, 0 25, 5 / 72, 50 A I B 25,5 / 192,50 A ; I C 25,5 / 312,50 A b) Las caídas de tensión en la carga son, V AB Z I AB 5,00 / 53,1 14,74 / 42,5 73,7 / 10,60 V V BC 73,7 / 109,40 V ; V CA 73,7 / 229,40 V c) La potencia compleja tomada por la carga es, S 3 Z I F2 3 5, 00 / 53,1 14, 742 3, 26 10 3 / 53,10 VA 3,26 /53,10 kVA 1,957 103 j2,61 10-3 VA 1,957 j2,61kVA De donde las potencias activa, reactiva y aparente tomadas por la carga son, P 1,957kW ; Q 2,61 k var IND ; S 3, 26kVA La potencia compleja tomada por las líneas es, S L 3 Z L I L2 3 1,118 / 26, 6 25, 5 2 2,18 10 3 / 26, 6 0 VA =1,950 10 3 j977 VA De donde las potencias activa, reactiva y aparente tomadas por las líneas son, PL 1,950kW ; QL 977 k var IND ; S L 2,18kVA La potencia compleja suministrada por la fuente es, 153 ELECTROTECNIA III-154 S f S L S 2,18 103 / 26, 6 3, 26 103 / 53,1 5, 30 10 3 / 42, 5 0 VA = 3,91 103 j3,57 103 VA De donde las potencias activa, reactiva y aparente suministradas por la fuente son, Pf 3,91kW ; Q f 3, 57k var IND ; S f 5, 30kVA d) El factor de potencia de la carga es, FP cos cos 53,10 0,600 AT El factor de potencia del sistema es, FPf cos f cos 42, 50 0, 737 AT Ejemplo 5-6. Una fuente trifásica simétrica, con tensiones de línea de 480 V, alimenta a través de líneas, con impedancia de ZL = 0,0800 /0,00 , dos cargas balanceadas conectadas en delta, cuyas características son: Carga 1 de 80,0 kVA, con factor de potencia 0,800 adelantado, con una tensión nominal de 440 V; Carga 2 de 75,0 kW, con un factor de potencia 0,800 atrasado, con una tensión nominal de 440 V. Determinar: a) las corrientes de línea totales que toman las cargas, b) las caídas de tensión en la carga, c) las potencias activa, reactiva y aparente que suministra la fuente, y d) el factor de potencia del sistema. ZL A a ZL B b ZL C c CARGA 1 CARGA 2 SOLUCIÓN. La potencia compleja se puede expresar como, S V2 Z * De donde las impedancias de las cargas son, 154 ELECTROTECNIA III-155 2 VFN 4402 Z 7, 26 / 36, 90 3 1 S 1F 80, 0 10 / cos 0, 800 / 3 * 1 Z 1 7, 26 / 36, 90 Z2 * 2 VFN S 2F 2 VFN P2 / cos 1 FP2 3 cos 2 4402 75, 0 103 / cos 1 0, 800 3 0, 800 6, 20 / 36, 90 Z 2 6, 20 / 36, 90 La impedancia equivalente es, Z Z 1 Z 2 7, 26 / 36, 9 6, 20 / 36, 9 4,17 / 3, 40 Z 1 Z 2 7, 26 / 36, 9 6, 20 / 36, 9 Tomando como referencia la tensión V ab , con secuencia de fases abc, las corrietes de fase totales son, I AB 480 / 0, 0 V ab 108, 9 / 3, 20 A 3 Z L Z 3 0, 0800 / 0, 0 4,17 / 3, 4 I BC 108,9 / 123, 20 A ; I CA 108,9 / 243, 20 A a) Las corrientes de línea son, I A 3 I AB / AB 30, 0 3 108, 9 / 3, 2 30, 0 188, 6 / 33, 20 A I B 188,6 / 153, 20 A ; I C 188,6 / 273, 20 A b) Las caídas de tensión en la carga son, V AB Z I AB 4,17 / 3,4 108,9 / 3, 2 454 / 0, 20 V V BC 454 / 119,80 V ; V CA 454 / 239,80 V c) La potencia compleja tomada por las cargas es, * S car 3V L I F 3 454 / 0, 2 108, 9 / 3, 2 148, 3 10 3 / 3, 4 0 VA La potencia compleja tomada por las líneas es, 155 ELECTROTECNIA III-156 S L 3 Z L I L2 3 0, 0800 / 0, 0 188, 62 8, 54 10 3 / 0, 00 VA De donde la potencia compleja suministrada por la fuente es, S f S car S L 148, 3 103 / 3, 4 8, 54 103 / 0, 0 156, 8 10 3 / 3, 20 VA =156,6 103 j8,80 103 VA Las potencias activa, reactiva y aparente suministradas por la fuente son, Pf 156, 6kW ; Q f 8, 89kvar IND ; S f =156,8kVA d) El factor de potencia del sistema es, FPf cos f cos 3, 2 0, 998 AT Circuito equivalente monofásico de una carga conectada en delta balanceada. Las ecuaciones de las corrientes de fase para cargas balanceadas conectadas en delta (), muestran que al igual que un circuito con cargas balanceadas en estrella (Y), se pueden resolver utilizando la técnica del circuito equivalente monofásico. Con frecuencia los circuitos conectados en delta se pueden resolver en términos de una estrella equivalente. En este circuito equivalente en estrella, las corrientes de línea y las tensiones de línea son las mismas que en un circuito delta. El generador conectado en delta se reemplaza por uno conectado en estrella. Similarmente, el juego de cargas conectadas en delta se reemplaza por un juego de cargas conectadas en estrella, el cual visto desde sus terminales es indistinguible del juego de cargas conectadas en delta. La relación entre las impedancias equivalentes que se usan para convertir una carga balanceada conectada en delta a una carga conectada en estrella y para invertir la operación se determinan rápidamente. En la figura las impedancias de fase conectadas en delta se denominan cada una como Z y las impedancias de fase conectadas en estrella como ZY. A A Z ZY Z ZY ZY B B Z C C IMPEDANCIAS BALANCEADAS EQUIVALENTES FIGURA NÚMERO 3. Se puede demostrar que, 156 ELECTROTECNIA III-157 Z 3ZY ; ZY Z 3 Las impedancias en estrella por fase, equivalentes de la impedancia en delta son, ZY Z 3 La tensión al neutro equivalente en la fuente es, Vn VL 3 / L 30, 0 El circuito equivalente monofásico es, f F IL ZL ZY Vn n VN N FIGURA NÚMERO 4. La caída de tensión al neutro en la carga, aplicando la regla de la división de tensión es, V N V n ZY ZL Z Y La caída de tensión de línea en la carga es, V L 3 VN / N 30, 0 La corriente de línea es, IL VN ZY La corriente de fase en la carga conectada en delta es, IF IL 3 / L 30, 0 Ejemplo 5-7. La carga balanceada conectada en delta () de la figura, con impedancias por fase de Z = 60,6 /53,10 , se alimenta con una fuente simétrica conectada en delta, con tensiones de línea de 220 V, y tiene una secuencia de fases abc, las impedancias de las líneas, cada una, son de ZL = 0,1118 /26,60 . Encuentre: a). Las corrientes en la carga, b). Las caídas de tensión en la carga, c). Las potencias tomadas por la carga y d). Las potencias suministradas por la fuente. Tome como referencia la tensión V ab . 157 ELECTROTECNIA III-158 I cC c ZL IC C I BC V bc Z V ca I aA b ZL I A I CA a V ab Z B A I bB ZL Z I AB IB SOLUCIÓN. Utilizando la técnica del circuito equivalente monofásico tenemos el circuito siguiente: f F IL ZL ZY Vn n VN N La tensión equivalente al neutro en la fuente, tomando como referencia a la tensión V ab , es Vn 220 3 / 30, 0 127, 0 / 30, 00 V Convirtiendo las impedancias en delta a impedancias en estrella tenemos, ZY Z 60, 6 / 53,1 20, 2 / 53,10 12,13 j16,15 3 3 a). La corriente de línea es, IL 127, 0 / 30, 0 Vn 6, 26 / 83, 00 A Z L Z Y 0,1118 / 26, 6 20, 2 / 53,1 Las corrientes en las líneas son, I A 6, 26 / 83,00 A ; I B 6, 26 / 203,00 A ; I C 6, 26 / 323,00 A Las corrientes de fase, en la carga son, IF IL 3 / θ L 30, 0 6, 26 3 / 83, 0 30, 0 3, 61 / 53, 00 A Las corrientes en las cargas son, 158 ELECTROTECNIA III-159 I AB 3,61/ 53,00 A ; I BC 3,61/ 173,00 A ; I CA 3,61/ 293,00 A b). Las caídas de tensión en la carga son, V L Z I F 60,6 / 53,10 3,61/ 53,0 219 / 0,10 V Las caídas en las cargas son, V AB 219 / 0,10 V ; V BC 219 / 119,90 V : V CA 219 / 239,90 V c). La potencia compleja tomada por la carga es, * S C 3V L I F 3 219 / 0,1 3, 61 / 53, 0 2, 37 103 / 53,10 VA 1,423 103 j1,895 103 VA De donde las potencias activa, reactiva y aparente tomadas por la carga son, PC 1,423kW ; QC 1,895kvar IND ; SC 2, 37kVA d) La potencia compleja suministrada por la fuente es, * S f 3V n I L 3 127, 0 / 30, 0 6, 26 / 83, 0 2, 39 10 3 / 53, 0 VA 1,438 103 j1,909 10 3 VA De donde las potencias suministradas por la fuente son, Pf 1, 438kW ; Q f 1, 909kvar IND ; S f 2, 39kVA Ejemplo 5-8. El motor M de la figura tiene aplicadas en sus terminales tensiones simétricas de 2,30 kV y toma 120,0 kVA con un factor de potencia de 0,600 adelantado. Calcule: a) las tensiones de línea en la fuente, b) la potencia suministrada por la fuente y c) el factor de potencia en la fuente. (2) 0,500 + j 2,00 a - j 1 000 - j 1000 - j 1 000 - j 250 0,500 + j 2,00 - j 250 0,500 + j 2,00 b - j 1 000 0,500 + j 2,00 - j 250 0,500 + j 2,00 (3) - j 1 000 - j 1 000 0,500 + j 2,00 - j 1 000 (1) MY c SOLUCIÓN. 159 ELECTROTECNIA III-160 Puesto que se trata de cargas balanceadas, la solución del problema se puede obtener utilizando la técnica del circuito equivalente monofásico. Representando el circuito como su equivalente monofásico tenemos, IL f ZL (1) ZL I 12 (2) I1 I2 Z1 Z2 I 23 (3) I M I3 Z3 Z MY n La impedancia de la línea en forma polar es, Z L 0, 500 j2,00 2,06 /76,00 La impedancia del motor por fase es, 2 VL 2 2 2, 30 10 3 3 VL Z MY 44,1 S S 120, 0 10 3 3 Z MY ZMY / cos1 FPMY 44,1/ cos1 0,600 44,1/ 53,10 Las impedancias equivalentes de los grupos de capacitores son, Z1 Z 1 1000 / 90, 0 333 / 90, 00 3 3 Z2 Z 2 250 / 90, 0 83, 3 / 90, 00 3 3 Z3 Z 3 1000 / 90, 0 333 / 90, 00 3 3 Las tensiones y corrientes en el circuito, considerando la tensión al neutro en la carga como referencia son, V 3N VL 3 / 0, 0 2, 30 103 3 / 0, 0 1, 328 103 / 0, 00 V 160 ELECTROTECNIA III-161 3 V 3 N 1, 328 10 / 0, 0 IM 30,1 / 53,1 A Z MY 44,1 / 53,1 I3 3 V 3 N 1, 328 10 / 0, 0 3, 99 / 90, 00 A Z3 333 / 90, 0 I 23 I M I 3 30,1/ 53,1 3,99 / 90,0 33,4 / 57, 20 A V 23 I 23 Z L 33,4 / 57, 2 2,06 / 76,0 68,8 / 133, 20 V V 2 N V 23 V 3 N 68,8 / 133, 2 1, 328 103 / 0,0 1, 282 103 / 2, 20 V I2 3 V 2 N 1, 282 10 / 2, 2 15, 39 / 92, 20 A Z2 83, 3 / 90, 0 I 12 I 23 I 2 33,4 / 57, 2 15, 39 / 92, 2 46,8 / 68,10 A V 12 I 12 Z L 46,8 / 68,1 2,06 / 76,0 96,4 / 144,10 V V 1n V 12 V 2 N 96,4 / 144,1 1, 282 103 / 2, 2 1, 208 / 5,00 V I1 3 V 1n 1, 208 10 / 5, 0 3, 63 / 95, 00 A Z1 333 / 90, 0 I L I 1 I 12 3,63 / 95,0 46,8 / 68,1 50,1/ 70,00 A a) Las tensiones de línea en la fuente son, VL 3 V1 N 3 1, 208 103 2, 09 103 V La potencia compleja es, * S 3V 1n I L 3 1, 208 103 / 5, 0 50,1 / 70, 0 181, 6 10 3 / 65, 0 0 VA 181,6 /-65,00 kVA 76, 7 j164,6kVA b) De donde las potencias activa, reactiva y aparente suministradas por la fuente son, P = 76,7 kW ; Q = 164,6 kvar CAP ; S = 181,6 kVA El factor de potencia en la fuente es, FP = cos-1 (65,00) = 0,423 AD 161 ELECTROTECNIA III-162 Ejemplo 5-9. La carga 1 de la figura tiene una configuración en estrella balanceada, mientras que la carga 2 tiene una configuración en delta balanceada. Encontrar. a) el valor absoluto de la corriente I A , b) el valor absoluto de la tensión en la carga V AB , c) la potencia activa total tomada por cada carga y d) el factor de potencia visto por el generador cuando: Vab 658V ; Z L 6,00 j0 ; Z Y1 20,0 j0 ; Z 2 36,0 j72,0 ZL a Generador b trifásico c IA A Carga 1 ZL IB ZL IC B Carga 2 C SOLUCIÓN. Puesto que se tienen cargas balanceadas, se puede utilizar el método del circuito equivalente monofásico. El circuito equivalente es, f IL ZL Z Y1 Vn f IL F Z Y2 Vn n N n ZL F Z YP N Donde la tensión al neutro es, Vn Vl 3 658 3 380 V Convirtiendo las cargas en delta a una configuración en estrella tenemos que su impedancia equivalente por fases es, Z Y2 Z 2 36, 0 j72,0 12, 00 j24,0 26,8 /63,40 3 3 La impedancia en paralelo de la carga es, Z YP Z Y1 Z Y2 20, 0 j0 12, 00 j24,0 12, 00 j6,00 13,42 /26,60 ZY1 Z Y2 20,0 j0 12,00 j24,0 Y la corriente de línea es, 162 ELECTROTECNIA III-163 IL 380 / 0, 0 Vn 20, 0 / 18, 40 A Z L Z YP 6, 00 / 0, 0 13, 42 / 26, 6 a) De donde el valor absoluto de la corriente de línea I A es, I A 20, 0 A b) La caída de tensión al neutro en la carga es, V N Z YP I L 13,42 / 26,6 20,0 / 18,4 268 / 8, 20 V El valor absoluto de la tensión en la carga es, VAB 3 VN 3 268 464 V c) La corriente en la carga 1 es, I1 I L 26,8 / 63,4 Z Y2 20,0 / 18,4 13,41/ 8, 20 A Z Y1 ZY2 20,0 / 0,0 26,8 / 63,4 La corriente en la carga 2 es, I2 IL 20, 0 / 0, 0 Z Y1 20, 0 / 18, 4 10, 01/ 55, 20 A Z Y1 ZY2 20, 0 / 0, 0 26, 8 / 63, 4 Las potencias activas totales tomadas por las cargas son, P1 3 I12 RY1 313,412 20,0 10,79 103 W 10,79kW P2 3 I 22 RY2 310,012 12,00 3,61103 W 3,61kW d) El factor de potencia visto por la fuente es igual al coseno del ángulo de la corriente suministrada por la fuente, esto es, FPf cos 18, 4 0, 949 AT Ejemplo 5-10. Calcule las potencias totales, aparente, activa y reactiva, y el factor de potencia del sistema de la figura. 163 ELECTROTECNIA III-164 ABC A 15, 00 20, 0 9 125, 0 / 0, 00 V 12 20, 0 12 12 9 9 B 15, 00 15, 00 20, 0 C SOLUCIÓN. Las impedancias son, Z 15, 00 j20,0 25,0 /53,10 Z Y 9, 00 j12,00 15,00 /-53,10 Transformando las cargas conectadas en estrella a cargas conectadas en delta tenemos, Z 3 Z Y 3 15,00 / 53,1 45,0 / 53,10 ' La impedancia equivalente de las ramas en paralelo es, ' Z P Z Z Z Z ' 25, 0 / 53,1 45, 0 / 53,1 25, 0 / 53,1 45, 0 / 53,1 25, 0 / 20, 80 La corriente de fase es, IF V L 125, 0 / 0, 0 5, 00 / 20, 80 A Z P 25, 0 / 20, 8 La corriente de línea es, I L 3 I F / θ F 30, 0 3 5, 00 / 20, 8 30, 0 8, 66 / 50, 8 0 A La potencia compleja es, * S 3V F I F 3 125,0 / 0,0 5,00 / 20,8 1875 / 20,8 0 VA 1753 j666 VA De donde, 164 ELECTROTECNIA III-165 S 1875 VA ; P 1753 W ; Q 666 var IND El factor de potencia del sistema es, FP cos 20,8 0,935 AT 2. CARGAS DESBALANCEADAS. Alimentadas directamente en sus terminales. IA A I CA Z AB I AB IB B IC Z CA Z BC C I BC FIGURA NÚMERO 5. Si las impedancias de la carga mostrada en la figura no son idénticas, constituyen lo que se denomina una carga desbalanceada conectada en delta. Si una fuente trifásica se conecta a esta carga, las caídas de tensión en las impedancias se conocen y las corrientes en las líneas se pueden establecer sumando fasorialmente las dos corrientes de las fases involucradas en la línea en cuestión. Las corrientes en las cargas son, I AB V AB Z AB I BC V BC Z BC I CA V CA Z CA Y las corrientes de línea son, I A I AB I CA 165 ELECTROTECNIA III-166 I B I BC I AB I C I CA I BC Ejemplo 5-11. Una fuente trifásica simétrica de tres hilos y 240 V, cuya secuencia de fases es ABC, está conectada a una carga desbalanceada conectada en delta con las impedancias siguientes: Z AB 10, 00 / 20, 00 Z BC 5, 00 / 90, 00 ; IA A Z AB I AB IB B IC ; Z CA 8, 00 / 20, 00 I CA Z CA Z BC C I BC Determinar la corriente que hay en cada fase de la carga y en cada línea. Tome como referencia la tensión de línea V AB 240 / 30,00 V V. Dibujar el diagrama fasorial para la carga. SOLUCIÓN Las corrientes de fase son I AB I BC I CA 240 / 30, 0 V AB 24, 0 / 10, 00 A Z AB 10, 00 / 20, 0 V BC 240 / 90, 0 48, 0 / 180, 00 A Z BC 5, 00 / 90, 0 V CA 240 / 210, 0 30, 0 / 190, 00 A Z CA 8, 00 / 20, 0 Las corrientes de línea son, I A I AB I CA 24,0 / 10,0 30,0 / 190,0 53, 2 / 1,10 A I B I BC I AB 48,0 / 180,0 24,0 / 10,0 71,8 / 176,70 A I C I CA I BC 30,0 / 190,0 48,0 / 180,0 19,18 / 15,80 A 166 ELECTROTECNIA III-167 V AB V CA IB I BC I CA IC I AB IA V BC Ejemplo 5-12. Una fuente trifásica, conectada en delta (), con tensiones de línea de 220 V, con secuencia de fases ABC, tiene conectada una carga desbalanceada conectada en delta, como se muestra en la figura, con los valores de ZAB = 10,00 /0,00 , ZBC = 25,0 /0,00 y ZCA = 20,0 /30,00 . Obtenga: a) las corrientes de línea, b) las potencias totales, c) trace el diagrama fasorial y d) dibuje, el triángulo de potencias de la carga. IA A I CA Z AB I AB IB B IC Z CA Z BC C I BC SOLUCIÓN. Las tensiones de línea, considerando a la caída de tensión V AB como referencia, son V AB 220 / 0,00 V ; V BC 220 / 120,00 V ; V CA 220 / 240,00 V Las corrientes de fase son, I AB 220 / 0, 0 V AB 22, 0 / 30, 00 A Z AB 10, 00 / 30, 0 167 ELECTROTECNIA III-168 I BC I CA V BC 220 / 120, 0 8, 80 / 120, 00 A Z BC 25, 0 / 0, 0 V CA 220 / 240, 0 11, 00 / 210, 00 A Z CA 20, 0 / 30, 0 a) Las corrientes de línea son, I A I AB I CA 22,0 / 30,0 11,00 / 210,0 33,0 / 30,00 A I B I BC I AB 8,80 / 120,0 22,0 / 30,0 23,7 / 171,80 A I C I CA I BC 11,00 / 210,0 8,80 / 120,0 14,09 / 111, 30 A b) Las potencias complejas por fase son, * S AB V AB I AB 220 / 0, 0 22, 0 / 30, 0 4, 84 103 / 30, 0 VA 4,84 / 30,00 kVA 0 * S BC V BC I BC 220 / 120,0 8,80 / 120,0 1,936 103 / 0,00 VA 1,936 / 0,00 kVA * S CA V CA I CA 220 / 240, 00 11, 00 / 210, 0 2, 42 103 / 30, 00 VA 2,42 / - 30,00 kVA La potencia compleja total es, S S AB S BC S CA 4, 84 10 3 / 30, 0 1, 936 10 3 / 0, 0 2, 42 10 3 / 30, 0 8, 31 10 3 / 8, 40 VA 8,22 10 3 j1,210 10 3 VA 8,31 / 8,4 0 kVA De donde las potencias totales son, S 8, 31kVA ; P 8, 22kW ; Q 1, 210kvar IND c) El diagrama fasorial es, 168 ELECTROTECNIA III-169 V CA IC I CA IB I BC I AB V AB IA V BC d) El triángulo de potencias es, S = 8,31 kVA Q = 1,210 kvar IND P = 8,22 kW Ejemplo 5-13. La fuente de la figura es simétrica y tiene una secuencia de fases positiva. Encuentre: a) I aA , b) I bB , c) I cC , d) la potencia compleja total proporcionada por la fuente. b B 10,00 n a A j5,00 120,0 /0,00 V -j10,00 c C SOLUCIÓN. Puesto que tenemos tensiones simétricas y secuencia de fases positiva, la tensión V AB tendrá una magnitud 3 veces mayor que la tensión V an y estará 30,00 adelante de ella, esto es V AB 3 120, 0 / 0, 0 30, 0 208 / 30, 00 V 169 ELECTROTECNIA III-170 Y las otras tensiones de fase son, V BC 208 / 90, 00 V , V CA 208 / 210, 00 V Las corrientes de fase son, I AB I BC I CA V AB 208 / 30.0 20,8 / 30,00 A Z AB 10,00 j0,0 V BC 208 / 90, 0 41, 6 / 180, 00 A Z BC 0, 0 j5, 00 V CA 208 / 210, 0 20,8 / 120, 00 A Z CA 0, 0 j10,00 Las corrientes de línea son, a) I aA I AB I CA 20,8/ 30,0 20,8/ 120,0 40, 2 / 45,00 A b) I bB I BC I AB 41, 6 / 180, 0 20,8 / 30, 0 60,5 / 170,10 A c) I cC I CA I BC 20,8 / 120, 0 41, 6 / 180, 0 36, 0 / 30, 00 A d) La potencia compleja total es, * * * S S AB S BC S CA V AB I AB V BC I BC V CA I CA 208 / 30, 0 20,8 / 30, 0 208 / 90, 0 41, 6 / 180, 0 208 / 210, 0 20,8 /120, 0 6,12 103 / 45, 00 VA = 6,12 /45,00 kVA Alimentadas a través de líneas. 170 ELECTROTECNIA III-171 Za a V ca V ab b V bc A I1 Zb c IA Z AB I AB IB B I2 Zc I CA Z CA I3 C I BC Z BC IC FIGURA NÚMERO 6. Utilizando el método de mallas tenemos que las ecuaciones de las corrientes de malla son, V ab Z a Z AB Zb I 1 Z b I 2 Z AB I 3 V bc Z b I 1 Z b Z BC Z c I 2 Z BC I 3 0 Z AB I 1 Z BC I 2 Z AB Z BC Z CA I 3 Utilizando el álgebra matricial para la solución de las ecuaciones tenemos, V ab Z Z Z AB b a Zb V bc 0 Z AB Zb Z b Z BC ZC Z BC I1 Z BC I 2 Z AB Z BC Z CA I 3 Z AB Si las corrientes son las incógnitas, I 1 Z Z Z AB b a Zb I2 Z AB I 3 Zb Z b Z BC Z C Z BC Z BC Z AB Z BC Z CA Z AB 1 V ab V bc 0 Las corrientes de fase son, I A I1 I B I 2 I1 IC I2 171 ELECTROTECNIA III-172 Ejemplo 5-14. La carga conectada en delta de la figura es desbalanceada, con impedancias por fase de ZAB = 54,7 /37,60 , ZBC = 88,1 /79,50 y ZCA = 88,1 /79,50 , esta se alimenta con una fuente simétrica conectada en delta, con secuencia de fases positiva, con tensiones de 127,0 V. Considere que las resistencias de los alimentadores son cada una de 0,500 . Encuentre: a) las corrientes de línea, b) las corrientes de fase y c) las caídas de tensión en la carga. Za a V ca V ab I1 Zb c V bc b IA Z AB I AB IB B I2 Zc A I3 Z BC I CA Z CA C I BC IC SOLUCIÓN. Empleando el método de corrientes de malla, tenemos Las tensiones en la fuente son, considerando la tensión V ab como referencia, V ab 127,0 / 0,00 V ; V bc 127,0 / 120,00 V ; V ca 127,0 / 240,00 V Las impedancias de las mallas son, Z 11 Z L Z AB Z L 0, 500 / 0, 0 54, 7 / 37, 6 0, 500 / 0, 0 55, 5 / 37, 0 0 Z 12 Z 21 Z L 0, 500 / 0, 00 Z 13 Z 31 Z AB 54, 7 / 37, 60 Z 22 Z L Z BC Z L 0, 500 / 0, 0 88,1 / 79, 5 0, 500 / 0, 0 88, 3 / 78, 90 Z 23 Z 32 Z BC 88,1 / 79, 50 Z 33 Z AB Z BC Z CA 54, 7 / 37, 6 88,1 / 79, 5 88,1 / 79, 5 220 / 69, 90 Utilizando el álgebra matricial tenemos, 172 ELECTROTECNIA III-173 I 1 55, 5 / 37, 0 0, 500 / 0, 0 54, 7 / 37, 6 1 127, 0 / 0, 0 2, 43 / 71, 9 I 2 0, 500 / 0, 0 88, 3 / 78, 9 88,1 / 79, 5 127, 0 / 120, 0 2, 49 / 168, 6 54, 7 / 37, 6 88,1 / 79, 5 1, 432 / 138, 8 220 / 69, 9 0 I 3 a) Las corrientes de línea son, I A I 1 2,43 / 71,90 A I B I 2 I 1 2,49 / 168,6 2,43 / 71,9 3,68 / 150,40 A I C I 2 2,49 / 11,40 A b) Las corrientes en las fases son, I CA I 3 1,432 / 41, 20 A I AB I A I CA 2,43 / 71,9 1,432 / 41, 2 2, 29 / 36,70 A I BC I CA I C 1,432 / 41, 2 2,49 / 11,4 1,436 / 161,70 A c) Las caídas de tensión en la carga son, V AB Z AB I AB 54,7 / 37,6 2, 29 / 36,7 125, 3 / 0,90 V V BC Z BC I BC 88,1/ 79,5 1,436 / 161,7 126,5 / 118,80 V V CA Z CA I CA 88,1/ 79,5 1,432 / 41, 2 126, 2 / 120,70 V Ejemplo 5-15. La fuente de la figura es simétrica y exhibe una secuencia de fases (+). La resistencia de las líneas es de 1,000 , las impedancias de la carga son Z AB 10, 00 / 0, 00 , Z BC 5, 00 / 90, 00 y Z CA 10, 00 / 90, 00 . Encuentre: a) las corrientes de línea y b) la potencia compleja total proporcionada por la fuente. Considere como referencia a la tensión V ab 208 / 0,00 V . 173 ELECTROTECNIA III-174 Za a V ca V ab I1 Zb c V bc b IA Z AB I AB IB B I2 Zc A I3 Z BC I CA Z CA C I BC IC SOLUCIÓN. Las tensiones en la fuente son, V ab 208 / 0,00 V ; V bc 208 / 120,00 V ; V ca 208 / 240,00 V Las impedancias de las mallas son, Z 11 Z L Z AB Z L 1, 000 / 0, 0 10, 00 / 0, 0 1, 000 / 0, 0 12, 00 / 0, 0 0 Z 12 Z 21 Z L 1, 000 / 0, 00 Z 13 Z 31 Z AB 10, 00 / 0, 00 Z 22 Z L Z BC Z L 1, 000 / 0, 0 5, 00 / 90, 0 1, 000 / 0, 0 5, 39 / 68, 2 0 Z 23 Z 32 Z BC 5, 00 / 90, 00 Z 33 Z AB Z BC Z CA 10, 00 / 0, 0 5, 00 / 90, 0 10, 00 / 90, 0 11,18 / 26, 60 Utilizando el álgebra matricial tenemos, I 1 12, 00 / 0, 0 1, 000 / 0, 0 10, 00 / 0, 0 1 208 / 0, 0 33, 9 / 15, 2 I 2 1, 000 / 0, 0 5, 39 / 68, 2 5, 00 / 90, 0 208 / 120, 0 25, 2 / 142, 4 10, 00 / 0, 0 5, 00 / 90, 0 11,18 / 26, 6 22, 4 / 24,1 0 I 3 174 ELECTROTECNIA III-175 a) Las corrientes de línea son, I A I 1 33,9 / 15, 20 A I B I 2 I 1 25, 2 / 142,4 33,9 / 15, 2 53,1/ 173,00 A I C I 2 25, 2 / 142,4 25, 2 / 37,60 A b) Las corrientes de fase son, I AB I A I CA 33,9 / 15, 2 22,4 / 155,9 12, 27 / 1, 20 A I BC I CA I C 22,4 / 155,9 25, 2 / 37,6 40,9 / 171, 20 A I CA I 3 22,4 / 24,10 22,4 / 155,90 A c) La potencia compleja tomada por la carga es, 2 2 2 S CAR Z AB I AB Z BC I BC Z CA I CA 10,00 / 0,0 12,27 2 5,00 / 90,0 40,9 2 10,00 / 90,0 22, 42 3,67 103 / 65,80 VA La potencia compleja tomada por las líneas es, S LIN Z L I A2 Z L I B2 Z L I C2 1, 000 / 0, 0 33, 92 1, 000 / 0, 0 53,12 1, 000 / 0, 0 25, 2 2 4, 60 103 / 0, 00 VA La potencia compleja total suministrada por la fuente es, S f S CAR S LIN 3, 67 103 / 65, 8 4, 60 103 / 0, 0 6, 96 103 / 28, 7 0 VA 6,10 103 j3,35 103 VA Solución del circuito utilizando el método de conversión delta a estrella. Un método alternativo de solución es convertir las cargas conectadas en delta a su equivalente conectado en estrella. La relación entre las impedancias en delta y sus impedancias equivalentes en estrella se muestra en la figura siguiente. 175 ELECTROTECNIA III-176 A A ZA Z AB Z CA ZB B B C Z BC C ZC FIGURA NÚMERO 7. Las ecuaciones para las equivalencias son, De delta () a estrella (Y). ZA Z AB Z CA Z AB Z BC Z CA ZC ; ZB Z AB Z BC Z AB Z BC Z CA ; Z BC Z CA Z AB Z BC Z CA La transformación de una conexión en delta a una conexión en estrella reemplaza las cargas conectadas en delta por las cargas en estrella, como se muestra en la figura.número 8. a ZL IA A ZA I1 N b c ZL IB ZL IC ZB ZC B C I2 FIGURA NÚMERO 8. Aplicando el método de mallas y utilizando el algebra matricial tenemos que las corrientes de mallas son, I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 2 Z L Z B Z C 1 V ab V bc De donde las corrientes de línea son, 176 ELECTROTECNIA III-177 I A I1 ; I B I 2 I1 ; IC I 2 Las caídas de tensión en la carga equivalente en estrella son, V AN Z A I A ; V BN Z B I B ; V CN Z C I C Lasa caídas de tensión en la carga conectada en delta son, V AB V AN V BN ; V BC V BN V CN ; V CA V CN V AN Las corrientes de fase en la carga son, I AB V AB Z AB ; I BC V BC Z BC ; I CA V CA Z CA Ejemplo 5-16. La carga conectada en delta de la figura es desbalanceada, con impedancias por fase de ZAB = 54,7 /37,60 , ZBC = 88,1 /79,50 y ZCA = 88,1 /79,50 , esta se alimenta con una fuente simétrica conectada en delta, con secuencia positiva, con tensiones de 127,0 V. Considere que las resistencias de los alimentadores son cada una de 0,500 . Encuentre: a) las corrientes de línea, b) las caídas de tensión en la carga c) las corrientes de fase en la carga, d) la potencia compleja tomada por la carga y e) la potencia compleja subintrada por la fuente. ZL a V ca V ab V bc A I CA Z AB ZL c IA b ZL IB IC Z CA I AB B Z BC I BC C SOLUCIÓN. Las tensiones en la fuente son, considerando la tensión V ab como referencia, V ab 127,0 / 0,00 V ; V bc 127,0 / 120,00 V ; V ca 127,0 / 240,00 V Las impedancias equivalentes de delta a estrella son, 177 ELECTROTECNIA III-178 ZA 54, 7 / 37, 6 88,1/ 79, 5 Z AB Z CA 21, 9 / 47, 20 Z AB Z BC Z CA 54, 7 / 37, 6 88,1/ 79, 5 88,1/ 79, 5 ZB 54, 7 / 37, 6 88,1/ 79, 5 Z AB Z BC 21, 9 / 47, 20 Z AB Z BC Z CA 54, 7 / 37, 6 88,1/ 79, 5 88,1/ 79, 5 ZC 88,1/ 79, 5 88,1/ 79, 5 Z BC Z CA 35, 3 / 89,10 Z AB Z BC Z CA 54, 7 / 37, 6 88,1/ 79, 5 88,1/ 79, 5 a) Las corrientes de malla, utilizando el circuito equivalente en estrella de la figura número 8 son I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 2 Z L Z B Z C 1 V ab V bc Los términos de la matriz de mallas son, 2 Z L Z A Z B 2 0, 500 / 0, 0 21, 9 / 47, 2 21, 9 / 47, 2 44, 5 / 46, 3 0 Z L Z B 0, 500 / 0, 0 21, 9 / 47, 2 22, 2 / 133, 7 0 2 Z L Z B Z C 2 0, 500 / 0, 0 21, 9 / 47, 2 35, 3 / 89,1 53, 9 / 72, 3 Sustituyendo valores en la ecuación de las corrientes de malla tenemos, I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 1 V ab 2 Z L Z B Z C V bc 1 I 1 44, 5 / 46, 3 22, 2 / 133, 7 127, 0 / 0, 0 2, 43 / 71, 9 I 2 22, 2 / 133, 7 53, 9 / 72, 3 127, 0 / 120, 0 2, 49 / 168, 7 De donde las corrientes de línea son, I A I 1 2,43 / 71,90 A I B I 2 I 1 2,49 / 168,7 2,43 / 71,9 3,68 / 150, 30 A I C I 2 2,49 / 168,7 2,49 / 11, 30 A b) Las caídas de tensión en la carga equivalente conectada en estrella son, 178 ELECTROTECNIA III-179 V AN Z A I A 21,9 / 47, 2 2,43 / 71,9 53, 2 / 24,70 V V BN Z B I B 21,9 / 47, 2 3,68 / 150, 3 80,6 / 162,50 V V CN Z C I C 35, 3 / 89,1 2,49 / 11.3 87,9 / 100,40 V Y las caídas de tensión en la carga son, V AB V AN V BN 53, 2 / 24,7 80,6 / 162,5 125, 2 / 0,90 V V BC V BN V CN 80,6 / 162,5 87,9 / 100,4 126,4 / 118,90 V V CA V CN V AN 87,9 / 100,4 53, 2 / 24,7 126, 2 / 120,60 V d) Las corrientes de fase en la carga son, I AB I BC V AB 125, 2 / 0, 9 2, 29 / 36, 70 A Z AB 54, 7 / 37, 6 V BC 126, 4 / 118, 9 1, 437 / 161, 60 A Z BC 88,1 / 79, 5 I CA V CA 126, 2 / 120, 6 1, 432 / 41,10 A Z CA 88,1 / 79, 5 d) La potencia compleja tomada por la carga es, 2 2 2 S CAR Z AB I AB Z BC I BC Z CA I CA 54, 7 / 37, 6 2, 29 2 88,1 / 79, 5 1, 437 2 88,1 / 79, 5 1, 4322 607 / 61,10 VA e) La potencia compleja tomada por las líneas es, S L Z L I A2 Z L I B2 Z L I C2 Z L I A2 I B2 I C2 0, 500 / 0, 0 2, 432 3, 682 2, 492 12, 87 / 0, 00 VA Y la potencia compleja suministrada por la fuente es, 179 ELECTROTECNIA III-180 S f S CAR S L 607 / 61,1 12, 87 / 0, 0 613 / 60, 00 VA Ejemplo 5-17. La fuente de la figura es simétrica y exhibe una secuencia de fases (+). La resistencia de las líneas es de 1,000 , las impedancias de las cargas son Z AB 10,00/ 0,00 , Z BC 5,00/ 90,00 y Z CA 10,00/ 90,00 . Encuentre: a) las corrientes de línea y b) la potencia compleja total proporcionada por la fuente. Considere como referencia a la tensión V ab 208 / 0,00 V . ZL a V ca IA V ab Z AB ZL c V bc A I CA b ZL IB IC Z CA I AB B Z BC I BC C SOLUCIÓN. Las tensiones en la fuente son, V ab 208 / 0,00 V ; V bc 208 / 120,00 V ; V ca 208 / 240,00 V Las impedancias equivalentes de delta a estrella son, ZA 10,00 / 0,0 10,00 / 90,0 Z AB Z CA 8,94 / 63,40 Z AB Z BC Z CA 10,00 / 0,0 5,00 / 90,0 10,00 / 90,0 ZB 10,00 / 0,0 5,00 / 90,0 Z AB Z BC 4,47 / 116,6 0 Z AB Z BC Z CA 10,00 / 0,0 5,00 / 90,0 10,00 / 90,0 ZC 5,00 / 90,0 10,00 / 90,0 Z BC Z CA 4,47 / 26,60 Z AB Z BC Z CA 10,00 / 0,0 5,00 / 90,0 10,00 / 90,0 a) Las corrientes de malla, utilizando el circuito equivalente en estrella de la figura número 8 son 180 ELECTROTECNIA III-181 I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 1 V ab 2 Z L Z B Z C V bc Los términos de la matriz de mallas son, 2 Z L Z A Z B 2 1, 000 / 0, 0 8, 94 / 63, 4 4, 47 / 116, 6 5, 66 / 45, 0 0 Z L Z B 1, 000 / 0, 0 4, 47 / 116, 6 4,12 / 75, 90 2 Z L Z B Z C 2 1,000 / 0,0 4,47 / 116,6 4,47 / 26,6 7, 21/ 56, 3 Sustituyendo valores en la ecuación de las corrientes de malla tenemos, I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 2 Z L Z B Z C 1 V ab V bc 1 I 1 5, 66 / 45, 0 4,12 / 75, 9 208 / 0, 0 33, 9 / 15, 2 I 2 4,12 / 75, 9 7, 21 / 56, 3 208 / 120, 0 25, 2 / 142, 4 De donde las corrientes de línea son, I A I 1 33,9 / 15, 20 A I B I 2 I 1 25, 2 / 142,4 33,9 / 15, 2 53,1/ 173,00 A I C I 2 25, 2 / 142,4 25, 2 / 37,60 A b) Las tensiones equivalentes al neutro en la fuente son, V an Vab 3 / ab 30, 0 208 3 V bn 120,0 / 150,00 V ; /0 - 30,0 =120,0 /-30,00 V V cn 120,0 / 270,00 V La potencia compleja total suministrada por la fuente es, * * * S V an I A V bn I B V cn I C 120,0 / 30,0 33,9 / 15, 2 120,0 / 150,0 53,1/ 173,0 120,0 / 270,0 25, 2 / 37,6 6,97 103 / 28,7 0 VA 181 ELECTROTECNIA III-182 3. EFECTO DE LA IMPEDANCIA DE UNA FUENTE CONECTADA EN DELTA. En todos los ejemplos anteriores , se ha considerado que son conocidas las tensiones en las terminales del generador, y que son independientes de las corrientes suministradas por el generador. Esta consideración con frecuencia es bastante práctica; no obstante, en muchos casos también se deben tomar en cuenta las impedancias de la fuente. En este caso la solución de los problemas se complica bastante, debido a la reacción de las corrientes de las diferentes fases dentro de la máquina, la cual requiere del uso de las reactancias propias y mutuas de los devanados como se estudia en los cursos de máquinas rotatorias. Si la fuente trifásica consiste de tres transformadores monofásicos, o uno trifásico, cuyas impedancias internas se conocen, el circuito bajo estudio se puede resolver rápidamente por cualquiera de los deferentes métodos ya expuestos, aplicando el que presente mayores ventajas. Las impedancias serie localizadas en las fases de una conexión en estrella no presentan problema especial para el análisis del circuito. Para impedancias en serie en las fases de una fuente conectada en delta, se pueden obtener tres ecuaciones para las caídas de tensión alrededor de las mallas. Para este propósito, es conveniente convertir el circuito del diagrama de la figura 9A al diagrama de la figura 9B el cuál es eléctricamente idéntico al anterior, cuya simetría geométrica facilita el establecimiento de las ecuaciones. Se considera que la carga está conectada en estrella. Si la carga está conectada en delta, es conveniente transformar la carga a una estrella antes de que se realice la solución. Za a Z ca A ZA V ab V ca N Z ab ZB b c Zb B ZC C Z bc V bc Zc FIGURA NÚMERO 9A. Las impedancias del circuito de la nueva estrella son, Z aN Z a Z A ; Z bN Z b Z B ; Z cN Z c Z C 182 ELECTROTECNIA III-183 a Z ca V ab I3 Z cNN V ca Z aN I1 Z Z ab bN I2 c b Z bc V bc FIGURA NÚMERO 9B. Resolviendo el circuito de la figura número 9B, por el método de mallas tenemos que las impedancias propias y comunes de las mallas son, Z 11 Z aN Z bN Z ab Z 12 Z 21 Z bN Z 13 Z 31 Z aN Z 22 Z bN Z cN Z bc Z 23 Z 32 Z cN Z 33 Z aN Z cN Z ca Escribiendo la solución de las corrientes de malla en forma matricial tenemos, I1 Z 11 I 2 Z 21 Z 31 I 3 Z 12 Z 22 Z 32 Z 13 Z 23 Z 33 1 V ab V bc V ca Y las corrientes de línea son, I aN I A I 1 I 3 ; I bN I B I 2 I 1 ; I cN I C I 3 I 2 Ejemplo 5-18. La carga conectada en delta de la figura es desbalanceada, y está formada por las impedancias siguientes: entre las fases A y B tiene un resistor de 30,0 en serie con un inductor de 80,0 mH, entre las fases B y C tiene un resistor de 20,0 y entre las fases C y A tiene un resistor de 10,00 en serie con un capacitor de 265 F. La carga se alimenta con una fuente simétrica conectada en delta, con una tensión de 125,0 V por fase, con una frecuencia de 60,0 Hz, con una secuencia de fases abc, que tiene una impedancia interna de 0,1000 por fase. La fuente se une a la carga por medio de líneas que tienen una 183 ELECTROTECNIA III-184 impedancia de 0,1000 . Determinar: a). Las corrientes de línea, b). Las caídas de tensión en la carga, y c). Las corrientes de fase en la carga. ZL a V ca ' Zf V ab ' a' b' A ZAB ZCA Zf c b Z f c' V bc ' ZL C B ZBC ZL SOLUCIÓN. Las impedancias de la carga son, Z AB 30, 0 j2 60,0 80,0 10-3 42, 6 / 45, 20 Z BC 20, 0 / 0, 00 Z CA 10, 00 j 1 14,15 / 45, 00 -6 2 60,0 265 10 Los fasores de tensión de la fuente, considerando a V ab ' como referencia son, V ab' 125,0 / 0,00 V ; V bc ' 125,0 / 120,00 V ; V ca ' 125,0 / 240,00 V Convirtiendo la carga en delta a una carga en estrella tenemos, ZA 42,6 / 45, 2 14,15 / 45,0 Z AB Z CA 9,52 / 18,40 Z AB Z BC Z CA 42,6 / 45, 2 20,0 / 0,0 14,15 / 45,0 ZB 42, 6 / 45, 2 20, 0 / 0, 0 Z AB Z BC 13, 45 / 26, 60 Z AB Z BC Z CA 42, 6 / 45, 2 20, 0 / 0, 0 14,15 / 45, 0 ZC 20,0 / 0,0 14,15 / 45,0 Z BC Z CA 4,47 / 63,60 Z AB Z BC Z CA 42,6 / 45, 2 20,0 / 0,0 14,15 / 45,0 184 ELECTROTECNIA III-185 A ZA ZAB ZCA N ZB B ZC C ZBC Adicionando a la estrella las impedancias de las líneas tenemos, a ZL A ZA ZB B ZL b N ZC C ZL c Z aN Z A Z L 9, 52 / 18, 4 0,1000 / 0, 0 9, 61 / 18, 20 Z bN Z B Z L 13, 45 / 26, 6 0,1000 / 0, 0 13, 54 / 26, 4 0 Z cN Z C Z L 4, 47 / 63, 6 0,1000 / 0, 0 4, 52 / 62, 50 Redibujando el circuito tenemos, 185 ELECTROTECNIA III-186 a ZL Zf a' V ca ' I3 ZA I1 b' Zf N C ZC ZL c V ab ' A Zf I2 ZB c' B ZL b V bc ' Resolviendo el circuito por el método de mallas tenemos, Las impedancias propias y mutuas de las mallas son, Z 11 Z aN Z bN Z f 9, 61 / 18, 2 13, 54 / 26, 4 0,1000 / 0, 0 21, 6 / 8, 0 0 Z 12 Z 21 Z bN 13, 54 / 26, 40 Z 13 Z 31 Z aN 9, 61 / 18, 20 Z 22 Z bN Z cN Z f 13, 54 / 26, 4 4, 52 / 62, 5 0,1000 / 0, 0 14, 46 / 8, 00 Z 23 Z 32 Z cN 4, 52 / 62, 50 Z 33 Z aN Z cN Z f 9, 61 / 18, 2 4, 52 / 62, 5 0,1000 / 0, 0 13, 31 / 31, 80 Escribiendo las ecuaciones en forma matricial tenemos, 1 I 1 21, 6 / 8, 0 13, 54 / 26, 4 9, 61 / 18, 2 125, 0 / 0, 0 14, 46 / 8, 0 4, 52 / 62, 5 125, 0 / 120, 0 I 2 13, 54 / 26, 4 9, 61 / 18, 2 4, 52 / 62, 5 13, 31 / 31, 8 125, 0 / 240, 0 I 3 De donde, I 1 4,56 / 1, 20 A ; I 2 3,44 / 100,00 A ; I 3 7, 22 / 143,80 A Las corrientes de línea son, 186 ELECTROTECNIA III-187 I A I aN I 1 I 3 4,56 / 1, 2 7, 22 / 143,8 11, 26 / 22,80 A I B I bN I 2 I 1 3,44 / 100,0 4,56 / 1, 2 6,12 / 147,40 A I C I cN I 3 I 2 7, 22 / 143,8 3,44 / 100,0 9, 27 / 124, 30 A b). Las caídas de tensión en la carga son, V AB V AN V BN I A Z A I B Z B 11, 26 / 22, 8 9, 52 / 18, 4 6,12 / 147, 4 13, 45 / 26, 6 122, 8 / 0,10 V V BC V BN V CN I B Z B I C Z C 6,12 / 147, 4 13, 45 / 26, 6 9, 27 / 124, 3 4, 47 / 63, 6 123, 7 / 120, 30 V V CA V CN V AN I C Z C I A Z A 9, 27 / 124, 3 4, 47 / 63, 6 11, 26 / 22, 8 9, 52 / 18, 4 122, 6 / 119, 50 V c). Las corrientes de fase en la carga son, I AB I BC V AB 122, 8 / 0,1 2, 88 / 45,10 A Z AB 42, 6 / 45, 2 V BC 123, 7 / 120, 3 6,19 / 120, 30 A Z BC 20, 0 / 0, 0 I CA V CA 122, 6 / 119, 5 8, 66 / 164, 50 A Z CA 14,15 / 45, 0 Método alternativo de solución utilizando la conversión de la fuente de tensión conectada en delta a fuente de tensión conectada en estrella. Un método alternativo es convertir la fuente de tensión conectada en delta a una fuente equivalente conectada en estrella, y entonces resolver el circuito del problema como un circuito, conectado en estrella desbalanceado, utilizando los métodos ya descritos. Cuando las impedancias de la fuente todas son iguales, este puede ser un método más rápido. Las relaciones necesarias para la conversión de la fuente conectada en delta a la fuente conectada en estrella se dan en las ecuaciones siguientes. V a 'n V ab Z ca V ca Z ab Z ab Z ca Z ab Z bc Z ca Z ab Z bc Z ca V ab V ca Z Z ca ab 187 ELECTROTECNIA III-188 V b'n V bc Z ab V ab Z bc Z bc Z ab Z ab Z bc Z ca Z ab Z bc Z ca V bc V ab Z bc Z ab V c'n V ca Z bc V bc Z ca Z ca Z cb Z ab Z bc Z ca Z ab Z bc Z ca V ca V bc Z ca Z bc a a Z ca V ca Z ca V ab V ca Z ab c b V ab Z ab Z ca Z ab Z bc c Z bc V bc b V bc Z bc A: Generador conectado en delta desbalanceada con impedancia interna B: Fuentes de corriente conectadas en delta desbalanceada, equivalentes a las fuentes de tensión de la figura A. FIGURA NÚMERO 10. Las ecuaciones anteriores se pueden obtener de la manera siguiente. La figura número 10A representa la fuente desbalanceada conectada en delta, cuyas tensiones son V ab ,V bc y V ca , que corresponden a las tensiones inducidas en los devanados de las fases componentes de la fuente; ellas no son las tensiones en los bornes terminales. Cada fuente de tensión con su impedancia asociada en serie, se convierte a una fuente equivalente de corriente como se muestra en la figura número 10B. Enseguida las impedancias conectadas en delta, de la figura número 10B, se convierten a impedancias equivalentes conectadas en estrella, como se muestra en la figura número 11. Al mismo tiempo cada fuente de corriente se divide en dos como se muestra, así que de las mismas fuentes de corriente salen y accesan las terminales a, b y c como antes, mientras que las corrientes en la unión de la estrella suman cero. 188 ELECTROTECNIA III-189 a a V ca Z ca V ca Z ca Z1 V bc Z bc Z3 c V ab V ca Z Z ca ab V ab Z ab Z3 Z2 Z2 c b V bc V ab Z bc Z ab V bc V ab Z Z ab bc Z1 V ca V bc Z ca Z bc b FIGURA NÚMERO |2 Combinación de las fuentes de corriente en paralelo conectadas en estrella de la figura número 11. FIGURA NÚMERO 11 Transformación de fuentes de corriente conectadas en delta a fuentes de corriente conectadas en estrella. A continuación las fuentes de corriente resultantes a través de cada impedancia de la estrella se combinan en una fuente de corriente, como se muestra en la figura número 12. Ahora el circuito de la figura número 12 se puede convertir a fuentes de tensión equivalentes con impedancia en serie, dando la configuración de la figura número 13, la cual es la fuente de tensión deseada en estrella desbalanceada equivalente. Las nuevas tensiones V a ' n ,V b ' n y V c ' n son las tensiones individuales que se tienen en cada fase de la fuente conectada en estrella, sin embargo ellas no son las tensiones que realmente se tienen disponibles en las terminales del generador, excepto en circuito abierto. a Z1 a' V a´ n V c´ n Z3 c' n V b´ n b' Z2 b c Circuito equivalente de fuentes conectadas en estrella de las fuentes de tensión conectadas en delta FIGURA NÚMERO 13. En la mayoría de los casos prácticos, las tensiones de la fuente en delta y sus impedancias son simétricas y balanceadas, bajo tales condiciones y considerando la tensión V ab como referencia y con secuencia de fases abc tenemos, Z ab Z bc Z ca Z f Vab Vbc Vca Vl 189 ELECTROTECNIA III-190 V ab Vl / 0,0 0 ; V bc Vl / 120,0 0 ; V ca Vl / 240,0 0 Sustituyendo las ecuaciones anteriores tenemos, 2 V a 'n ZF 3Z f Vl / 0, 0 Vl / 240, 0 1 Vl / 30, 0 Vl / 0, 0 Vl / 240, 0 Zf 3 Zf 3 V b'n Vl / 150, 0 ; V c ' n Vl ZY Z1 Z 2 Z 3 Zf 3 3 / 270, 0 Y las impedancias de las ramas son, 3 Ejemplo número 5-19. Resolver el ejemplo número 5-18, utilizando la conversión de la fuente conectada en delta a fuente conectada en estrella. Solución. Los fasores de tensión de la fuente conectada en delta, considerando a V ab ' como referencia son, V ab' 125,0 / 0,00 V ; V bc ' 125,0 / 120,00 V ; V ca ' 125,0 / 240,00 V Los fasores de tensión de la fuente en estrella equivalente son, V a 'n Vab ' 3 / 0, 0 30, 0 125, 0 3 / 30, 0 72, 2 / 30, 00 V V b' n 72, 2 / 150,00 V ; V c 'n 72, 2 / 270,00 V Las impedancias en estrella de la fuente equivalente de la fuente conectada en delta son, ZY Z 0,1000 / 0, 0 33, 3 103 / 0, 00 3 3 Las impedancias de la carga son, Z AB 30, 0 j2 60,0 80,0 10-3 42, 6 / 45, 20 Z BC 20, 0 / 0, 00 Z CA 10, 00 j 1 14,15 / 45, 00 -6 2 60,0 265 10 190 ELECTROTECNIA III-191 Convirtiendo la carga en delta a una carga en estrella tenemos, ZA 42,6 / 45, 2 14,15 / 45,0 Z AB Z CA 9,52 / 18,40 Z AB Z BC Z CA 42,6 / 45, 2 20,0 / 0,0 14,15 / 45,0 ZB 42, 6 / 45, 2 20, 0 / 0, 0 Z AB Z BC 13, 45 / 26, 60 Z AB Z BC Z CA 42, 6 / 45, 2 20, 0 / 0, 0 14,15 / 45, 0 ZC 20,0 / 0,0 14,15 / 45,0 Z BC Z CA 4,47 / 63,60 Z AB Z BC Z CA 42,6 / 45, 2 20,0 / 0,0 14,15 / 45,0 El circuito equivalente es, ZL a ZY a' A I1 ZA n c ZY c' N b' Z Y b ZL ZL B ZB ZC C I2 Resolviendo el circuito por el método de mallas tenemos, Las impedancias propias y comunes de las mallas son, Z 11 Z Y Z L Z A Z B Z L Z Y 2 Z Y 2 Z L Z A Z B 2 33, 3 103 / 0, 0 2 0,1000 / 0, 0 9, 52 / 18, 4 13, 45 / 26, 6 21, 5 / 8,10 Z 12 Z 21 Z Y Z L Z B 33, 3 103 / 0, 0 0,1000 / 0, 0 13, 45 / 26, 6 13, 57 / 26, 3 0 Z 22 2 Z Y 2 Z L Z B Z C 2 33, 3 103 / 0, 0 0,1000 / 0, 0 13, 45 / 26, 6 4, 47 / 63, 6 14, 42 / 8, 00 Las tensiones son, V a 'b' 125,0 / 0,00 V ; V b'c ' 125,0 / 120,00 V 191 ELECTROTECNIA III-192 Escribiendo la solución de las corrientes de malla en forma matricial tenemos, 1 I 1 21, 5 / 8,1 13, 57 / 26, 3 125, 0 / 0, 0 11, 30 / 22, 8 125, 0 / 120, 0 9, 29 / 55, 5 13, 57 / 26, 3 14, 42 / 8, 0 I 2 De donde, las corrientes de línea son, I A I 1 11, 30 / 22,80 A I B I 2 I 1 9, 29 / 55,5 11, 30 / 22,8 6,11/ 147,60 A I C I 2 9, 29 / 124,50 A Los parámetros restantes se calculan en la misma forma que con la alternativa anterior. Ejemplo 5-20. Una fuente simétrica conectada en delta, con secuencia de fases positiva, tiene una impedancia interna de 0,01800 + j 0,1620 por fase. Cuando no hay carga las tensiones en las terminales de la fuente son de 600 V. La fuente se conecta a una carga balanceada conectada en estrella que tiene una impedancia de 7,92 – j 6,35 por fase, a través de una línea de distribución con una impedancia de 0,0740 + j 0,296 por fase. Determinar a) las corrientes de línea, b) las corrientes de fase en la fuente, y c) las tensiones en las terminales en la fuente con carga. ZL a Zf A V abv V cav Z Zf Z N Z ZL c Zf V bcv b B C ZL SOLUCIÓN. Transformando las fuentes de tensión en delta a fuentes de tensión en estrella tenemos, que puesto que se tienen tensiones simétricas, las tensiones al neutro de la estrella equivalente, considerando la tensión V abv en vacío como la referencia, son 192 ELECTROTECNIA III-193 V a´ n Vabv 3 / abv 30, 0 600 3 / 0, 0 30, 0 346 / 30, 00 V V b´ n 346 / 150,00 V ; V c´ n 346 / 270,00 V En virtud de que la fuente tiene impedancias iguales conectadas en delta, la estrella equivalente tiene una impedancia por fase de, Z Yf Zf 3 0, 01800 j0,1620 0, 0543 / 83, 7 0 3 ZL a A ZY a' Z n ZY N b' c' c ZY ZL b B Z Z C ZL Ya que el circuito equivalente tiene tensiones simétricas y cargas balanceadas, se puede utilizar el circuito equivalente monofásico para resolver el problema. El diagrama equivalente del circuito monofásico es, Z Yf a' a ZL V an' n A Z N a) A partir del circuito equivalente. Las corrientes de línea son, IA 346 / 30,0 0,0543 / 83,7 0,0740 j0, 296 7, 92 j6,35 34,6 / 6,90 A I B 34,6 / 113,10 A ; I C 34,6 / 233,10 A b) Las corrientes en la fuente son, 193 ELECTROTECNIA III-194 I ba IA 3 / A 30, 0 34, 6 3 I cb 19,98 / 83,10 A ; / 6, 9 30, 0 19, 98 / 36, 90 A I ac 19,98 / 203,10 A c) Las tensiones al neutro equivalentes son, V a ' n V a 'a V aN V aN V an V a ' n V a ' a V a ' n 0, 0543 / 83, 7 I A 346 / 30, 0 0, 0543 / 83, 7 34, 6 / 6, 9 347 / 30, 30 V Las tensiones de línea en las terminales de la fuente son, V ab 3 V an / an 30, 0 3 347 / 30, 0 30, 0 601/ 0, 3 0 V V bc 601/ 120, 3 V ; V ca 601/ 240, 3 V 0 4. MEDICIÓN DE LA POTENCIA ACTIVA. Recordando el teorema de Blondel, para una carga de tres hilos conectada en delta, la potencia activa del circuito se puede medir con tres o dos wáttmetros, siendo el arreglo más común el que utiliza el mínimo de wáttmetros, esto es dos. Como se muestra en la figura número 14. 194 ELECTROTECNIA III-195 WM1 BC1 1 A * a * BP1 Z AB Z CA B C RP1 b RP2 Z BC * BP2 c * BC2 WM2 FIGURA NÚMERO 14. Donde las indicaciones de los wáttmetros son, WM1= V ab I A Vab I A cos Vab IA V I WM2 = V cb I C Vcb I C cos Vcb IC V I ab cb * A * C Y la potencia activa total de la carga es, P WM1+ WM2 Ejemplo 21. Una fuente trifásica simétrica de 440 V, con una secuencia de fases abc, alimenta una carga conectada en delta, con las impedancias de fase siguientes: Z AB 10, 00 / 90, 00 ; Z BC 20, 0 / 90, 00 ; Z CA 10, 00 / 0, 0 0 Calcular la corriente que hay en cada línea. La potencia de la carga se mide mediante dos wáttmetros; uno tiene la bobina de corriente en la línea A y el otro en la línea C, como se muestra en la figura número 14. Determinar la lectura de cada instrumento y la potencia total consumida por el circuito. SOLUCIÓN. Tomando la tensión V AB 440 / 30,00 V. Las corrientes de fase son I AB 440 / 30, 0 V AB 44, 0 / 60, 00 A Z AB 10, 00 / 90, 0 195 ELECTROTECNIA III-196 I BC I CA V BC 440 / 90, 0 22, 0 / 0, 00 A Z BC 20, 0 / 90, 0 V CA 440 / 210, 0 44, 0 / 210, 00 A Z CA 10, 00 / 0, 0 Las corrientes de línea son I A I AB I CA 44,0 / 60,0 44,0 / 210,0 85,0 / 45,00 A I B I BC I AB 22,0 / 0,0 44,0 / 60,0 38,1/ 90,00 A I C I CA I BC 44, 0 / 210, 0 22, 0 / 0 64, 0 / 159, 9, 00 A Las lecturas de cada wáttmetro son WM1= Re V AB I A Re 440 /30,0 85, 0 / 45, 0 Re 37,4 10 3 / 75, 0 9, 68 103 W * WM2 = Re V CB I C Re 440 /90,0 64, 0 / 159, 9 Re 28,2 103 / 69, 9 9, 68 103 W * La potencia total es P WM1+ WM2=9,68103 9,68103 19, 36 103 W 19, 36kW Ejemplo 22. En la figura V ab ,V bc y V ca , representan un sistema trifásico simétrico de caídas de tensión , siendo la magnitud de cada una de 200 V. La secuencia de fases de la tensión es abc. Dos cargas trifásicas balanceadas, indicadas por los círculos, están conectadas a las terminales A, B y C, como se muestra en la figura. Además de las dos cargas balanceadas, a través de las terminales B y C, como se indica, ha sido colocada una carga monofásica de factor de potencia unitario y de 4,00 kW. a). Encuentre las lecturas de los wáttmetros y b) encuentre el factor de potencia vectorial combinado de la carga compuesta. a WM1 * A * B b c 3,00 kW FP = 0,500 atrasado (1) * * 4,00 kW FP = 1 (3) C 4,00 kVA FP = 0,800 adelantado (2) WM2 SOLUCIÓN. 196 ELECTROTECNIA III-197 Las tensiones, tomando como referencia a la tensión V AB son, V AB 200 / 0,00 V ; V BC 200 / 120,00 V ; V CA 200 / 240,00 V La potencia activa en la carga 1 se expresa como, P1 3 VL I1 cos θ1 De donde, I1 P1 3 VL cos 1 3, 00 103 3 200 0, 500 17, 32 A Considerando el factor de potencia de la carga y su característica inductiva, la corriente I 1 como fasor es, I 1 I1 / cos 1 1 30, 0 17, 32 / cos 1 0, 500 30, 0 17, 32 / 90, 00 A Tomando como referencia a la tensión V ab , las corrientes se pueden expresar como, I A1 17, 32 / 90,00 A ; I B1 17, 32 / 210,00 A ; I C 1 17, 32 / 330,00 A La potencia aparente de la carga 2 se expresa como, S2 3 VL I 2 De donde la corriente tomada por la carga 2 es, I2 S2 3 VL 4,00 103 3 200 11,55 A Considerando el factor de potencia de la carga 2 y su característica capacitiva, la corriente I 2 como fasor es, I 2 I 2 / cos 1 2 30, 0 11, 55 / cos1 0, 800 30, 0 11, 55 / 6, 90 A Las corrientes se pueden expresar como, I A2 11,55 / 6,90 A ; I B 2 11,55 / 113,10 A ; I C 2 11,55 / 233,10 A La corriente que toma la carga 3 es, P3 4, 00 103 IB3 20, 0 A VL cos 3 200 1 Considerando el factor de potencia de la carga 3, la corriente I B 3 como fasor es, 197 ELECTROTECNIA III-198 I B 3 20,0 / 120,0 A Las corrientes de línea son, I A I A1 I A2 17, 32 / 90,0 11,55 / 6,9 19,63 / 54, 30 A I B I B1 I B 2 I B 3 17, 32 / 210,0 11,55 / 113,1 20,0 / 120,0 35, 3 / 146,90 A I C I C 1 I C 2 I B 3 17, 32 / 330,0 11,55 / 233,1 20,0 / 120,0 39,6 / 62, 80 A Las indicaciones de los wáttmetros son, 3 WM1 VAB I A cos VAB IA 200 19, 63cos 0, 0 54, 3 2, 29 10 W 3 WM2 VCB I C cos VCB IC 200 39, 6 cos 60, 0 62, 8 7, 91 10 W b). La potencia compleja es, S S1 S 2 S 3 3, 00 103 / 60, 0 4, 00 103 / 36, 9 4, 00 103 / 0, 0 10, 57 / 15, 30 A 0, 500 De donde el factor de potencia vectorial combinado de la carga es, FP cos 15, 3 0, 965 AT 5. DELTA DE CUATRO HILOS. En algunos circuitos de distribución de energía eléctrica, cuando la carga es mediana se utilizan los sistemas monofásicos de tres hilos, cuando la carga crece en este tipo de circuitos, es conveniente, en este caso, alimentar la carga en forma trifásica, lo que normalmente se hace adicionando dos transformadores más de las mismas características pero sin derivación central, lo que da lugar a que se forme una fuente con una conexión en delta de cuatro hilos como se muestra en la figura número 15. ALTA TENSIÓN BAJA TENSIÓN a T2 T3 T3 T1 T1 n T2 b c FIGURA NÚMERO 15. 198 ELECTROTECNIA III-199 La solución de este tipo de circuitos se realiza utilizando los mismos principios que se han mencionado para la solución de los circuitos conectados en delta. Ejemplo 5-23. Los secundarios de un banco de transformadores de distribución, conectados en delta de cuatro hilos, con tensión de línea de 240 V y de 120 V en el secundario con derivación central, alimentan un grupo de residencias con cargas formadas por lámparas incandescentes y motores trifásicos pequeños, dichas cargas en forma concentrada se pueden representar como se muestra en la figura siguiente: a A 1 500 W c n N 10 CF M C 1 500 W b B Las características nominales de las cargas concentradas son, lámparas de 125,0 V y 1 500 W; motor trifásico de 220 V, potencia 10,00 CF; eficiencia 90,0% y factor de potencia 85,0 % atrasado. Determinar: a) las corrientes tomadas por cada grupo de cargas y b) las corrientes suministradas por el secundario del banco de transformadores. SOLUCIÓN. La impedancia de cada grupo de lámparas es, ZL Vn2 125, 02 10, 42 PL 1500 Z L 10, 42 / 0, 00 La impedancia por fase del motor, considerándolo como conectado en delta es, S CF 746 10, 00 746 9, 75 103 VA FP 0, 900 0, 850 ZM VL2 3VL2 3 2202 14, 89 S S 9, 75 103 3 199 ELECTROTECNIA III-200 Z M Z M / cos 1 0, 850 14, 89 / 31, 80 Redibujando el circuito tenemos, a IA I AN c ZL IN n I BN IB b I A1 A IC N ZL B ZM I AB I CA C ZM ZM I B1 I C1 I BC Tomando como referencia a la tensión V ab , las tensiones son, V ab 240 / 0,00 V : V bc 240 / 120,00 V ; V ca 240 / 240,00 V V AN 120,0 / 0,00 V ; V NB 120,0 / 0,00 V a) Las corrientes tomadas por las cargas son, I AN 0 V AN 120, 0 / 0, 0 11, 52 / 0, 00 A Z L 10, 42 / 0, 0 I NB I AB V NB 120, 0 / 0, 0 11, 52 / 0, 00 A Z L 10, 42 / 0, 0 240 / 0, 0 V ab 16,12 / 31, 80 A Z M 14, 89 / 31, 8 I BC 16,12 / 151,80 A I CA 16,12 / 271,80 A I L 3 I F / F 30, 0 3 16,12 / 31, 8 30, 0 27, 9 / 61, 8 0 A I A1 27,9 / 61,80 A ; I B1 27,9 / 181,80 A ; I C 1 27,9 / 301,80 A b) Las corrientes suministradas por los secundarios de los transformadores son, 200 ELECTROTECNIA III-201 I A I A1 I AN 27,9 / 61,8 11,52 / 0,0 34,9 / 44,90 A I B I B1 I NB 27,9 / 181,8 11,52 / 0,0 39,4 / 178,7 0 A I C I C 1 27,9 / 301,80 A I N I NB I AN 11,52 / 0,0 11,52 / 0,0 0 6. EJERCICIOS. Ejercicio 5-1. Si tres impedancias de 10,00 /30,00 conectadas en delta, se alimentan de una fuente trifásica simétrica, de tres hilos, con una secuencia de fases ABC, de 440 V, calcular las corrientes de fase y de línea que hay en el sistema y dibujar el diagrama fasorial para la carga. Considere la tensión V AB 440 / 30,00 V . SOLUCIÓN. IC C I CA Z A Z I AB I BC IB Z B IA El diagrama del circuito aparece en la figura y las tensiones de línea son, V AB 440 / 30,00 V ; V BC 440 / 90,00 V ; V CA 440 / 150,00 V Y las corrientes de fase son, I AB 440 / 30, 0 V AB 44, 0 / 0, 00 A Z 10, 00 / 30, 0 I BC 44,0 / 120,00 A ; I CA 44,0 / 240,00 A Y las corrientes de línea correspondientes son, I A 3 I AB / AB 30, 0 3 44, 0 / 0, 0 30, 0 76, 2 / 30, 00 A I B 76, 2 / 150,00 A ; I C 76, 2 / 270,00 A El diagrama fasorial se muestra en la figura siguiente: 201 ELECTROTECNIA III-202 IC V CA I CA I BC 30,00 I AB 30,00 I AB 30,00 IB V AB I BC I CA IA V BC Ejercicio 5-2. A una línea trifásica con tensiones simétricas de línea de 380 V, de una frecuencia de 60 Hz, están conectadas tres cargas, representadas por trazo continuo en la figura, en la que se ven las características de los consumos. La tercera carga está formada por tres elementos iguales de Z3 = 3,00 + j 3,00 cada uno, reunidos en una conexión en delta. Determinar: a) Las corrientes que toman cada una de las cargas, y la corriente de línea total, b) Las potencias aparente, activa y reactiva proporcionadas a través de las líneas. c) Se desea mejorar el factor de potencia del conjunto, a base de un grupo de capacitores (en trazos discontinuos en la figura), calcular el grupo de capacitores para mejorar el factor de potencia hasta la unidad. IL A B C I1 I2 100,0 kVA cos = 0,800 capacitivo I3 IC 100,0 kW cos = 0,800 inductivo C Z3 SOLUCIÓN. a) La potencia aparente en la carga 1 se expresa como, S1 3 VL I1 De donde 202 ELECTROTECNIA III-203 I1 S1 3 VL Se toma como referencia la tensión V corrientes de línea. AB 100, 0 103 3 380 151, 9 A y la secuencia de fases abc, para determinar los ángulos de las Considerando el factor de potencia de la carga 1 y su característica capacitiva, la corriente I 1 como fasor es, I 1 I1 / cos1 1 151, 9 / cos 1 0, 800 30, 0 151, 9 / 6, 9 0 A La potencia activa de la carga 2 se puede expresar como, P2 3 VL I 2 cos θ2 De donde, I2 P2 3 VL cos 2 100,0 103 3 380 0,800 189,9 A Considerando el factor de potencia de la carga 2 y su característica inductiva, la corriente I 2 como fasor es, I 2 I 2 / cos 1 2 30, 0 189, 9 / 66, 90 A Para la carga 3 tenemos que su impedancia por fase es, Z 3 3,00 j3,00 4,24 45,00 La corriente de línea que toma la carga es, I3 3 IF 3 3 VL 380 3 155,1 A Z3 4, 24 Considerando el ángulo de la impedancia, la corriente I 3 como fasor es, I 3 I 3 / 3 30, 0 155,1/ 45, 0 30, 0 155,1/ 75, 00 A La corriente total suministrada por la línea es, I L I 1 I 2 I 3 151,9 / 6,9 189,9 / 66,9 155,1/ 75,0 405 / 49,10 A b) Las potencias tomadas por cada carga son, Para la carga 1. S1 100, 0kVA 203 ELECTROTECNIA III-204 P1 S1 cos 1 100, 0 0, 800 80, 0kW Q1 S12 P12 100, 02 80, 02 60, 0kvar CAP Para la carga 2. P2 100, 0kW P2 100, 0 S2 125, 0kVA cos 2 0, 800 Q2 S22 P22 125, 02 100, 02 75, 0kvar IND Para la carga 3. S3 3 VL I 3 3 380 155,1 102,1 103 VA 102,1kVA P3 S3 cos 3 102,1 0,707 72, 2kW Q3 S 32 P32 102,12 72, 22 72, 2kvar IND De donde las potencias suministradas por la línea son, P P1 P2 P3 80,0 100,0 72, 2 252kW Q Q1 Q2 Q3 60,0 75,0 72, 2 87, 2kvar IND S P 2 Q 2 2522 87, 22 267kVA c) Para mejorar el factor de potencia hasta la unidad, es necesario adicionar un grupo de capacitores que tome una potencia reactiva igual a la del conjunto de cargas sin capacitores, esto es, QC 87, 2kvar CAP La potencia reactiva capacitiva por fase que hay que adicionar es, QC 87, 2 29,1kvar CAP 3 3 Considerando los capacitores conectados en estrella, como se muestra en la figura, la reactancia capacitiva por fase es, QFC 204 ELECTROTECNIA III-205 2 XC VY QFC 380 3 1, 654 29,1 10 3 Y la capacitancia por fase es, C 1 1 1, 604 10 3 F =1604 F 2 f X C 2 60 1, 654 Ejercicio 5.3. En un sistema trifásico balanceado la carga consiste de una estrella balanceada en paralelo con una delta balanceada. La impedancia por fase para la estrella es 8,00+ j 4,00 y para la delta es 18,00 + j 6,00 . La fuente es una estrella simétrica con una secuencia de fases abc y tiene una tensión V an 120,0 / 60,00 V . Si la impedancia de la línea de alimentación es de 1,000 + j 1,000 . Determine las corrientes de fase en cada una de las cargas. ZL a V an ZY Z n c b SOLUCIÓN. En virtud de que se tienen cargas balanceadas y tensiones simétricas, para la solución del ejercicio utilizaremos el método del circuito monofásico equivalente. La carga conectada en delta se puede convertir en una carga equivalente conectada en estrella , esto es, Z YE Z 18, 00 j6, 00 6, 00 j2, 00 3 3 El circuito equivalente monofásico queda como, 205 ELECTROTECNIA III-206 f IL ZL F ZY Z YE N n La corriente de línea es, IL Vn Z Z Z L Y YE Z Y Z YE Considerando como referencia la tensión V an , y sustituyendo los valores de las impedancias, la corriente de línea de la fase A es, IA 120, 0 / 60, 0 V an 23, 8 / 31, 90 A Z Z 8, 00 j4, 00 6, 00 j2, 00 Z L Y YE 1, 000 j1, 000 Z Y Z YE 8, 00 j4, 00 6, 00 j2, 00 Aplicando la regla de la división de corriente tenemos que las corrientes en la carga en estrella y en la carga en estrella equivalente son, I AY I A I AYE I A 6, 00 j2, 00 Z YE 23, 8 / 31, 9 9, 88 / 27,10 A Z Y Z YE 8,00 + j4,00 6, 00 j2, 00 8, 00 j4, 00 ZY 23, 8 / 31, 9 13, 98 / 35, 30 A Z Y Z YE 8,00 + j4,00 6, 00 j2, 00 Y la corriente de fase en la carga conectada en delta es, I AB IA 3 / θ A 30 13, 98 3 / 35, 3 30 8, 07 / 65, 30 A Las corrientes de fase en las cargas conectadas en estrella y en delta son, Para la carga conectada en estrella, I Y 9, 88 A Para la carga conectada en delta, I 8, 07 A 206 ELECTROTECNIA III-207 Ejercicio.5-4. La carga balanceada conectada en delta () de la figura, requiere 15 kVA con factor de potencia 0,800 atrasado. Suponga una secuencia de fases positiva, con V BC = 180,0 /30,00 V. Si RL = 0,750 , encuentre a). la tensión V bc en la fuente; b). La potencia compleja total suministrada por la fuente. RL IA RL IB RL IC a b c A B C SOLUCIÓN. La potencia compleja total tomada por la carga se puede expresar como, * * S 3V L I F 3V BC I BC Despejando al conjugado de la corriente tenemos, I * BC S 3V BC 15, 00 103 / 36, 9 3 180, 0 / 30, 0 27, 8 / 6, 90 A De donde, I BC 27,8 / 6,90 A La impedancia por fase es, Z V BC I BC 180, 0 / 30, 0 27, 8 / 6, 9 6, 47 / 36, 90 Puesto que tenemos cargas balanceadas, I BC V bc 3ZL Z a). Despejando a la tensión, tenemos 207 ELECTROTECNIA III-208 V bc I BC 3 Z L Z 27, 8 / 6, 9 3 0, 750 / 0, 0 6, 47 / 36, 9 233 / 20, 7 0 V b). La magnitud de la corriente de línea es, I L 3 I F 3 27, 8 48, 2 A La potencia compleja tomada por las tres líneas de alimentación es, S L 3 Z L I L2 3 0, 750 / 0, 0 48, 2 2 5, 23 10 3 / 0, 0 0 VA La potencia compleja total suministrada por la fuente es, S f S S L 15, 00 103 / 36, 9 5, 23 103 / 0, 0 19, 44 103 / 27, 60 VA Ejercicio 5-5. Una carga desbalanceada conectada en delta, como la mostrada en la figura, se alimenta con un sistema trifásico simétrico, con tensiones de línea de 660 V, con una secuencia de fases positiva. Determinar: a) las corrientes de línea, b) las potencias totales activa, reactiva y aparente tomadas por la carga. Tome como referencia la tensión V BC . A 50,0 /0,00 40,0 /-20,00 B C 20,0 /30,00 SOLUCIÓN. Las tensiones son, V BC 660 / 0,00 V ; V AB 660 / 240,00 V ; V CA 660 / 120,00 V Las corrientes de fase son, I AB V AB 660 / 240, 0 13, 20 / 240, 00 A Z AB 50, 0 / 0, 0 I BC 660 / 0, 0 V BC 33, 0 / 30, 00 A Z BC 20, 0 / 30, 0 208 ELECTROTECNIA III-209 I CA a) V CA 660 / 120, 0 16, 50 / 100, 00 A Z CA 40, 0 / 20, 0 Las corrientes de línea son, I A I AB I CA 13, 20 / 240,0 16,50 / 100,0 27,9 / 97,70 A I B I BC I AB 33,0 / 30,0 13, 20 / 240,0 44,9 / 38,40 A I C I CA I BC 16,50 / 100,0 33,0 / 30,0 31,4 / 179,50 A Las potencias complejas tomadas por las fases son, * S AB V AB I AB 660 / 240,0 13, 20 / 240,0 8,71 10 3 / 0,00 VA * S BC V BC I BC 660 / 0, 0 33, 0 / 30, 0 21, 8 103 / 30, 00 VA * S CA V CA I CA 660 / 120,0 16,50 / 100,0 10,89 103 / 20,00 VA La potencia compleja total es, S S AB S BC S CA 8, 71 103 / 0, 0 21, 8 103 / 30, 0 10, 89 10 3 / 20, 0 38, 5 10 3 / 10, 70 VA 37,8 103 j7,18 103 VA Las potencias tomadas por la carga son, P 37,8kW Q 7,18kvar IND. S 38,5kVA Ejercicio 5.6. En la figura, M1 representa un motor de inducción monofásico de 5,00 CF que opera a plena carga con un factor de potencia de 85,0 % atrasado y con una eficiencia de 83,0 %, la carga M 2 representa un motor de inducción trifásico de 10,00 CF, operando a plena carga con un factor de potencia de 80,0 % atrasado y con una eficiencia de 90,0 %. Estos se alimentan con una fuente con tensiones simétricas de tres hilos, con una tensión de 220 V, de 60 Hz y con secuencia abc. 209 ELECTROTECNIA III-210 A IA IB B C IC I1 I A2 I B2 I C 2 M1 M2 Se desea conocer: a). Las corrientes de línea que toman cada uno de los motores y la corriente total en la línea. b). Las potencias aparente, activa y reactiva proporcionadas a través de las líneas. c) Se desea mejorar el factor de potencia del conjunto a base de un banco de capacitores, conectado en estrella. Calcule el banco de capacitores para mejorar el factor de potencia hasta 95,0 %. d). Encontrar la potencia activa total del conjunto, sin banco de capacitores, realizando mediciones con wáttmetros monofásicos. Determine el circuito a utilizar y las indicaciones de los instrumentos. SOLUCIÓN. a). La corriente tomada por el motor M1 es, I1 CF1 746 5, 00 746 24, 0 A VL 1 FP1 220 0, 830 0, 850 El ángulo del factor de potencia del motor es, 1 cos1 FP1 cos1 0,850 31,80 Tomando como referencia a la tensión V AB , y teniendo en cuenta la secuencia de fases, tenemos, V BC 220 / 120,00 V De donde el fasor corriente que toma el motor es, I 1 I1 / 120, 0 1 24, 0 / 120, 0 31, 8 24, 0 / 151, 80 A 210 ELECTROTECNIA III-211 V CA V AB I1 31,8 0 120,0 0 V BC La corriente de línea tomada por el motor M2 es, I L2 CF2 746 3 VL 2 FP2 10, 00 746 3 220 0, 900 0, 800 27, 2 A El ángulo del factor de potencia del motor 2 es, 2 cos1 0,800 36,90 De donde el fasor corriente que toma el motor es, I L2 I L2 / 30,0 36,9 27, 2 / 66,90 Las corrientes tomadas por el motor son, I A2 27, 2 / 66,90 A ; I B 2 27, 2 / 186,90 A ; I C 2 27, 2 / 306,90 A Las corrientes totales de línea son, I A I A2 27, 2 / 66,90 A I B I 1 I B 2 24,0 / 151,8 27, 2 / 186,9 48,8 / 170,50 A I C I C 2 I 1 27, 2 / 306,9 24,0 / 151,8 50,0 / 41,4 A 0 b). Las potencias tomadas por el motor 1 son, P1 CF1 746 5, 00 746 4, 49 10 3 W 1 0, 830 P1 4, 49 103 S1 5, 28 103 VA cos 1 0, 850 Q1 S12 P12 5, 28 10 4, 49 10 3 2 3 2 2, 78 103 var IND 211 ELECTROTECNIA III-212 Las potencias tomadas por el motor M2 son, P2 CF2 746 10, 00 746 8, 29 10 3 W 2 0, 900 P2 8, 29 103 S2 10, 36 103 VA cos 2 0, 800 Q2 S22 P22 10, 36 10 8, 29 10 3 2 3 2 6, 21 10 3 var IND Las potencias proporcionadas a través de las líneas son, P P1 P2 4,49103 8, 29103 12,78 103 W Q Q1 Q2 2,78103 6, 21103 8,99103 var IND S P 2 Q2 12, 78 10 8, 99 10 3 2 3 2 15, 63 103 VA c). La potencia reactiva que se tiene con un factor de potencia de 95,0 % atrasado y seguir suministrando la misma potencia activa es, Q95 P tancos 1 0, 950 12, 78 103 tan18, 2 4, 20 103 var IND Por lo que para llegar a este valor es necesario compensar la potencia reactiva con un banco de capacitores de una potencia reactiva de, QC Q Q95 8,99 103 4, 20 103 4,79 103 var CAP S QC Q Q 95 P Si el banco de capacitores está conectado en estrella, la reactancia capacitiva por fase es, 2 VL 2 220 2 3 VL XC 10,10 QC QC 4, 79 10 3 3 La capacitancia por fase es, 212 ELECTROTECNIA III-213 C 1 1 263 10 6 F = 263 F 2 f X C 2 60, 0 10,10 d). Utilizando el método de los dos wáttmetros y considerando que estos se intercalan en las fases A y C tenemos, WM1 BC1 IA A * * BP1 RP1 IB CARGA B * BP2 RP2 IC C * BC2 WM2 Las indicaciones de los wáttmetros son, WM1 I A V AB I A VAB cos VAB IA WM2 I C V CB I C VCB cos VCB IC El diagrama fasorial de la medición es, 213 ELECTROTECNIA III-214 V CA V CB IC WM2 0 60,0 18,6 0 41,4 0 V AB WM1 IB 66,9 0 IA V BC Del diagrama fasorial de la medición tenemos, 0 0 VAB ; VCB IA 66, 9 IC 60, 0 41, 4 18, 6 WM1 27,2 220 cos66,9 2,35103 W WM2 50,0 220 cos18,6 10,43 103 W De donde la potencia activa total es, P WM1 WM2 2,35103 10,43 103 12,78 103 W Cantidad que corresponde al valor calculado anteriormente. Ejercicio 5-7. La carga conectada en delta de la figura es desbalanceada, con impedancias por fase de ZAB = 50,0 /36,90 , ZBC = 65,0 /60,00 y ZCA = 100,0 /25,80 , esta se alimenta con una fuente simétrica conectada en delta, con secuencia de fases positiva, con tensiones de 220 V. Considere que las impedancias de los alimentadores son cada una de 0,509 /11,30 . Encuentre: a) las corrientes de línea, b) las caídas de tensión en la carga y c) las corrientes de fase. 214 ELECTROTECNIA III-215 Zc c IC C I BC V bc V ca Za b I A I CA a V ab Z BC Z CA B A Zb Z AB I AB IB SOLUCIÓN. Las tensiones en la fuente son, considerando la tensión V ab como referencia, V ab 220 / 0,00 V ; V bc 220 / 120,00 V ; V ca 220 / 240,00 V Las impedancias equivalentes de delta a estrella son, ZA 50,0 / 36,9 100,0 / 25,8 Z AB Z CA 24,0 / 24,10 Z AB Z BC Z CA 50,0 / 36,9 65,0 / 60,0 100,0 / 25,8 ZB 50,0 / 36,9 65,0 / 60,0 Z AB Z BC 15,62 / 58, 30 Z AB Z BC Z CA 50,0 / 36,9 65,0 / 60,0 100,0 / 25,8 ZC 65, 0 / 60, 0 100, 0 / 25, 8 Z BC Z CA 31, 2 / 47, 20 Z AB Z BC Z CA 50, 0 / 36, 9 65, 0 / 60, 0 100, 0 / 25, 8 a) Las corrientes de malla, utilizando el circuito equivalente en estrella de la figura número 8 son I 1 2 Z L Z A Z B I 2 Z L Z B ZL ZB 2 Z L Z B Z C 1 V ab V bc Los términos de la matriz de mallas son, 2 Z L Z A Z B 2 0, 509 / 11, 3 24, 0 / 24,1 15, 62 / 58, 3 38, 9 / 36, 8 0 Z L Z B 0, 509 / 11, 3 15, 62 / 58, 3 15, 97 / 123, 0 0 2 Z L Z B Z C 2 0,509 / 11, 3 15,62 / 58, 3 31, 2 / 47, 2 47,4 / 50,1 215 ELECTROTECNIA III-216 Sustituyendo valores en la ecuación de las corrientes de malla tenemos, 1 I 1 38, 9 / 36, 8 15, 97 / 123, 0 220 / 0, 0 5, 93 / 52, 3 47, 4 / 50,1 220 / 120, 0 3, 87 / 145, 0 I 2 15, 97 / 123, 0 De donde las corrientes de línea son, I A I 1 5,93 / 52, 30 A I B I 2 I 1 3,87 / 145,0 5,93 / 52, 3 7, 23 / 160,00 A I C I 2 3,87 / 145,0 3,87 / 35,00 A b) Las caídas de tensión en la carga equivalente conectada en estrella son, V AN Z A I A 24,0 / 24,1 5,93 / 52, 3 142, 3 / 28, 20 V V BN Z B I B 15,62 / 58, 3 7, 23 / 160,0 112,9 / 141,70 V V CN Z C I C 31, 2 / 47, 2 3,87 / 35,0 120,7 / 82, 20 V Y las caídas de tensión en la carga son, V AB V AN V BN 142, 3 / 28, 2 112,9 / 141,7 214 / 0,7 0 V V BC V BN V CN 112,9 / 141,7 120,7 / 82, 2 217 / 119,00 V V CA V CN V AN 120,7 / 82, 2 142, 3 / 28, 2 216 / 120, 30 V c) Las corrientes de fase en la carga son, I AB I BC 214 / 0, 7 V AB 4, 28 / 36, 20 A Z AB 50, 0 / 36, 9 V BC 217 / 119, 0 3, 34 / 179, 00 A Z BC 65, 0 / 60, 0 I CA V CA 216 / 120, 3 2,16 / 94, 50 A Z CA 100, 0 / 25, 8 216 ELECTROTECNIA III-217 Ejercicio 5-8. Una fuente con tensiones simétricas, con secuencia de fases positiva, conectada en delta, tiene una impedancia interna de 0.0900 + j 0,810 por fase. La fuente alimenta una carga balanceada a través de líneas de igual impedancia. La corriente de línea en la fase b, I B , es de 6,00 / -120,00 A, y la tensión de línea V ab en los bornes de la fuente es de 480 /60,00 V. Determine las tensiones internas de la fuente. SOLUCIÓN. Transformando la fuente de tensión en delta a una fuente de tensión en estrella, tenemos a a IA + Z IA ZY a’’ + n + c + c’ + b IB + b’ c b IC IB IC Las tensiones en los bornes de la fuente son, V ab 480 / 60,00 V ; V bc 480 / 60,00 V , V ca 480 / 180,00 V Las corrientes de línea son, I B 6,00 / 120,00 A ;I A 6,00 / 0,00 A ; I C 6,00 / 240,00 A Las impedancias de la estrella equivalente son, ZY Z 0, 0900 j0,810 0, 272 / 83, 7 0 3 3 Las tensiones de fase equivalentes de la fuente en estrella son, V an Vab 3 / ab 30, 0 480 3 / 60, 0 30, 0 277 / 30, 00 V V bn 277 / 90,00 V ; V cn 277 / 210,00 V Las tensiones de fase internas de la fuente equivalente son, V a ' n V an V aa ' V an Z Y I A 277 / 30, 0 0, 272 / 83, 7 6, 00 / 0, 0 278 / 30, 30 V V b' n 278 / 89,70 V ; V c ' n 278 / 209,70 V 217 ELECTROTECNIA III-218 De donde las tensiones internas de la fuente de línea a línea son, V a ' b ' 3 Va ' n / a´ n 30, 0 3 278 / 30, 3 30, 0 482 / 60, 30 V V b'c ' 482 / 59,70 V ; V c 'a ' 482 / 179,70 V Ejercicio 5-9. Un sistema trifásico simétrico de tres hilos, con secuencia de fases ABC y tensión de línea de 440 V tiene las corrientes de línea siguientes: I A 30,0 / 90,00 A I B 10,00 / 100,00 A ; I C 39,9 / 87,50 A ; Determinar la lectura de cada uno de los wáttmetros conectados para medir la potencia activa total, si sus bobinas de corriente están en las líneas (a) A y B, (b) B y C, (c) A y C. La tensión V AN se toma como referencia. SOLUCIÓN. (a). Wáttmetros con las bobinas de corriente en las líneas A y B. Las lecturas de los wáttmetros son y WM2 = V AC 440 / 30,00 V y V BC 440 / 90,00 V WM1= V * AC IA V * BC IB donde De donde WM1= 440 /-30,0 30, 0 / 90, 0 13,20 10 WM2 = 440 /-90,0 10, 00 / 100, 0 4,40 10 3 / 60, 0 6, 60 10 3 W 3 / 10, 0 4, 33 103 W y la potencia activa total consumida es P WM1+ WM2=6,60103 4, 33 103 10,93 103 W=10,93kW (b). Wáttmetros con las bobinas de corriente en las líneas B y C. Las lecturas de los wáttmetros son WM1= V * BA IB y WM2 = V * CA IC donde V BA 440 / 150,00 V y V CA 440 / 150,00 V 218 ELECTROTECNIA III-219 De donde WM1= 440 /-150,0 10, 0 / 100, 0 4, 40 10 WM2 = 440 /150,0 39, 9 / 87, 5 17,56 10 / 50, 0 2, 83 103 W 3 3 / 62, 5 8,11 103 W y la potencia activa total consumida es P WM1+ WM2= 2,83 103 8,11103 10,94 103 W=10,94kW (c). Wáttmetros con las bobinas de corriente en las líneas A y C. Las lecturas de los wáttmetros son y WM2 = V CB 440 / 90,00 V y V AB 440 / 30,00 V WM1= V * CB IC V * AB IA donde De donde WM1= 440 /90,0 39, 9 / 87, 5 17, 56 10 WM2 = 440 /30,0 30, 0 / 90, 0 13,20 10 3 3 / 2, 5 17, 54 10 3 W / 120, 0 6, 60 10 3 W y la potencia activa total consumida es P WM1+ WM2=17,54 103 6,60 103 10,94 103 W=10,94kW Ejercicio 5-10. Se da el circuito de la figura donde, RA = 2,00 , RB = 4,00 , RC = 8,00 , RAB = 7,00 , RBC = 28,0 y RCA = 14,00 . Las tensiones de línea del generador son, Vab = 250 V, Vbc = 300 V y VCA = 200 V. Determinar: a) Las corrientes de línea y fase, b) las tensiones en la carga, c) las caídas de tensión en las líneas, d) la potencia consumida por la carga, e) la potencia pérdida en las líneas f) las indicaciones de los wáttmetros y g) construir el diagrama fasorial de tensiones y corrientes. Si el conductor de la línea a se interrumpe (RA = ), determinar: h) las corrientes de línea y fase y i) la potencia consumida en la carga, según las indicaciones de los wáttmetros. 219 ELECTROTECNIA III-220 WM1 BC1 1 RA * a A RAB * BP1 RP1 RB RCA B C b * RBC RP2 BP2 RC c * BC2 WM2 SOLUCIÓN. Las tensiones en la fuente se pueden dibujar como un triángulo, como se muestra en la figura siguiente y posteriormente calcular sus ángulos utilizando la ley de los cosenos de la trigonometría. V ca V bc cos V ab Vab2 Vca2 Vbc2 2502 2002 3002 0,1250 ; 82, 80 2Vab Vca 2 250 200 cos cos Vab2 Vbc2 Vca2 2502 3002 2002 0, 750 ; 41, 40 2Vab Vbc 2 250 300 Vbc2 Vca2 Vab2 3002 2002 2502 0, 0, 563 ; 55, 80 2Vbc Vca 2 300 200 De la figura tenemos que, V ab 250 / 0,00 V 220 ELECTROTECNIA III-221 V bc 300 / β -180,0 300 / 41,4 180,0 300 / 138,60 V V ca 200 / 180,0 α 200 / 180,0 82,8 200 / 97, 20 V Resolviendo el circuito por el método de corrientes de mallas tenemos, RA IA a A I AB I1 I CA RAB RCA I2 RB IB b B C RBC I BC I3 RC c IC Las ecuaciones de mallas son, V ab RA RAB RB I 1 RAB I 2 RB I 3 250 / 0, 0 2, 00 7, 00 4, 00 I 1 7, 00 I 2 4, 00 I 3 13, 00 I 1 7, 00 I 2 4, 00 I 3 0 RAB I 1 RAB RBC RCA I 2 RBC I 3 0 7, 00 I 1 7, 00 28, 0 14, 00 I 2 28, 0 I 3 7, 00 I 1 49, 0 I 2 28, 0 I 3 V bc RB I 1 RBC I 2 RB RBC RC I 3 300 / 138, 6 14, 00 I 1 28, 0 I 2 4, 00 28, 0 8, 00 I 3 14, 00 I 1 28, 0 I 2 40, 0 I 3 Las corrientes de las mallas son, I 1 13, 00 j0 I 2 7, 00 j0 - 4,00 j0 I 3 - 7,00 j0 - 4,00 j0 49,0 j0 - 28,0 j0 - 28,0 j0 40,0 j0 1 250 / 0, 0 20, 0 / 20, 7 0 7,14 / 82, 8 300 / 138, 6 11, 08 / 106, 4 a) Las corrientes de línea y de fase son, I A I 1 20,0 / 20,70 A 221 ELECTROTECNIA III-222 I B I 3 I 1 11,08 / 106,4 20,0 / 20,7 22,1/ 170,60 A I C I 3 11,08 / 106,4 11,08 / 73,60 A I AB I 1 I 2 20,0 / 20,7 7,14 / 82,8 17,81/ 0,00 A I BC I 3 I 2 11,08 / 106,4 7,14 / 82,8 5, 36 / 138,60 A I CA I 2 7,14 / 82,8 7,14 / 97, 20 A b) Las caídas de tensión en la carga son, V AB I AB Z AB 17,81/ 0,0 7,00 / 0,0 24,7 / 0,00 V V BC I BC Z BC 5, 36 / 138,6 28,0 / 0,0 150,1/ 138,60 V V CA I CA Z CA 7,14 / 97, 2 14,00 / 0,0 100,0 / 97, 20 A c) Las caídas de tensión en las líneas son, V aA I A Z A 20,0 / 20,7 2,00 / 0,0 40,0 / 20,70 V V bB I B Z B 22,1/ 170,6 4,00 / 0,0 88,4 / 170,60 V V cC I C Z C 11,08 / 73,6 8,00 / 0,0 88,6 / 73,60 A d) La potencia consumida por la carga es, VBC VCA PC VAB I AB cos VAB IAB VBC I BC cos IBC VCA I CA cos ICA 124, 7 17, 81cos 0 150,1 5, 36cos 0 100, 0 7,14cos 0 3, 74 103 W 3,74kW e) La potencia consumida por las líneas es, VbB VcC PL VaA I A cos VaA IA VbB I B cos IB VcC I C cos IC 40, 0 20, 0cos 0 88, 4 22,1cos 0 88, 6 11, 08cos 0 3, 74 103 W 3,74kW f) Las indicaciones de los wáttmetros son, 3 WM1 Vab I A cos Vab IA 250 20, 0cos 20, 7 4, 68 10 W 3 WM2 Vcb I C cos Vcb IC 300 11, 08cos 73, 6 41, 4 2, 81 10 W 222 ELECTROTECNIA III-223 g) El diagrama fasorial de tensiones y corrientes es, V ca V CA I C I CA V AB I AB IB I BC V ab IA V BC V bc h) Con el conductor de la línea a interrumpido, las resistencias RAB y RCA quedan en serie, y este conjunto a su vez queda en paralelo con la resistencia RBC, de aquí que ahora la resistencia equivalente entre los puntos B y C es, RBAC RBC RAB RCA 28, 0 7, 00 14, 00 12, 00 RAB RBC RCA 7, 00 28, 0 14, 00 WM1 BC1 RA * a * RAB BP1 RP1 A RB RCA B C b * RBC RP2 BP2 RC c * BC2 WM2 Las corrientes de línea son, I A 0 IB 300 / 138,6 V bc 12,50 / 138,60 A RB RBAC RCA 4,00 12,00 8,00 I C I B 12,50 / 138,6 12,50 / 41,40 A 223 ELECTROTECNIA III-224 Las corrientes de fase son, I AB I CA I B I BC I B RBC 28, 0 12, 50 / 138, 6 7,14 / 41, 40 A RBC RAB RCA 28, 0 7, 00 14, 00 RAB RCA 7, 00 14, 00 12, 50 / 138, 6 5, 36 / 138, 60 A RBC RAB RCA 28, 0 7, 00 14, 00 i) La potencia consumida en la carga, según las indicaciones de los wáttmetros es, WM1= 0; No circula corriente por su bobina de corriente. 3 WM2 Vcb I C cos Vcb IC 300 12, 50cos 41, 4 41, 4 3, 75 10 W V cb IC 41,40 WM2 V ab V bc 224 ELECTROTECNIA III-225 UNIDAD 6. COMPONENTES SIMÉTRICAS. 1. INTRODUCCIÓN. Las componentes simétricas suministran un instrumento de gran potencia para determinar analíticamente el comportamiento de cierto tipo de circuitos eléctricos no balanceados que contienen máquinas eléctricas rotatorias. Este instrumento es particularmente útil en el análisis del rendimiento de máquinas eléctricas polifásicas cuando se hacen funcionar desde sistemas de tensión asimétricos. Así para redes desbalanceadas que contienen máquinas rotatorias el método de componentes simétricas, suministra el único procedimiento práctico para calcular los efectos no balanceados de estas máquinas. Este método también es útil para entender y analizar la operación de los sistemas eléctricos de potencia durante condiciones de desbalanceo. El desbalanceo de los sistemas eléctricos trifásicos se puede deber a una o más de las condiciones siguientes: a). Fuentes asimétricas. b). Líneas de transmisión desbalanceadas. c). Fallas en los sistemas de transmisión. d). Cargas desbalanceadas. La primera condición ocurre muy raramente, puesto que todas las máquinas sincronas se diseñan para generar tensiones simétricas de secuencia positiva. De donde cualquier asimetría de tensiones se debe al efecto de otras componentes, tales como las líneas de transmisión de alta o muy alta tensión desbalanceadas debido especialmente a la falta de transposición de los conductores, así como a sistemas de transmisión con fallas que da como resultado el desbalanceo, a menos que ocurra una falla trifásica simétrica. El método de componentes simétricas fue finalmente desarrollado en 1913 por Charles L. Fortescue , cuando investigaba matemáticamente la operación de motores de inducción bajo condiciones de desbalanceo, él presentó una ponencia titulada “método de coordenadas simétricas aplicado a la solución de redes polifásicas”, la cuál fue publicada en la memoria de la AIEE de junio de 1918. La aplicación del método al estudio de disturbios y corto circuitos en los sistemas eléctricos fue realizado por C. F. Wagner y R. D. Evans. Ellos publicaron sus trabajos en una serie de artículos en la revista “The Electrical Journal” de la Westinghouse en 10 números de 1928 a 1931. Esta serie de artículos fue publicada en un libro clásico pero muy útil denominado “Symmetrical Components” publicado por “McGraw-Hill Book Company, New York, 1933. El método de componente simétricas, en su forma más utilizada, se funda en el teorema de C. L. Fortescue (L. G. Stokvis), relativo a la solución en componentes simétricas de sistemas asimétricos o desbalanceados. Aunque las presentes notas se limitarán a los sistemas trifásicos, cualquier sistema polifásico de fasores se puede resolver por medio de un sistema balanceado de fasores, llamado componentes simétricas. El teorema de Fortesue, aplicado a un sistema trifásico general de fasores establece que, 225 ELECTROTECNIA III-226 Cualquier sistema trifásico, asimétrico o desbalanceado, se puede descomponer en tres sistemas simétricos o balanceados: uno de secuencia positiva (o de orden directo), otro de secuencia negativa (o de secuencia inversa) y el tercero de secuencia cero (u homopolar). 2. SISTEMA DE COMPONENTES SIMÉTRICAS. El sistema original de fasores asimétricos o desbalanceados. Cualquier número de fasores, hasta tres inclusive, se puede considerar como asimétrico o desbalanceado de fasores trifásicos. Los fasores que forman el sistema asimétrico o desbalanceado pueden tener cualquier magnitud dada y cualquier posición de fase dadas, uno con respecto al otro. En la figura número 1 se muestra un grupo de tres fasores asimétrico o desbalanceado, que posteriormente se descompondrán en sus componentes simétricas. Si los fasores que forman el grupo original asimétrico o desbalanceado se dan como tres fasores determinados, se les puede asignar arbitrariamente los subíndices a, b y c, en el orden mostrado en la figura 1. Así a los fasores originales V a ,V b y V c se les asigna arbitrariamente la secuencia de fases abc. Aunque los fasores mostrados en la figura están marcados como tensiones, la solución propuesta se aplica igualmente bien a un sistema de fasores de corriente. Vc Va Eje de referencia Vb FIGURA NÚMERO 1. Debido al hecho de que las componentes simétricas tendrán que llevar un subíndice adicional, para designar el sistema a que pertenecen, la notación con un sólo subíndice se empleará con respecto a los fasores originales, siempre que esto se pueda hacer sin mengua de la claridad. Para obtener una determinación completa, los sentidos positivos del circuito de las tensiones o corrientes originales trifásicos se debe indicar en un diagrama separado del circuito. La importancia de una determinación completa se hará evidente cuando se estudien los problemas numéricos. El sistema de secuencia de fases positiva. Como se expuso anteriormente, el sistema original asimétrico o desbalanceado de fasores se debe descomponer en dos sistemas trifásicos balanceados y un sistema monofásico. Se demostrará a continuación que los sistemas trifásicos simétricos o balanceados deben ser de secuencia de fases opuesta. Por tanto, un sistema simétrico o balanceado tiene la misma secuencia de fases que el sistema trifásico original y el otro tiene una secuencia de fases opuesta a la del sistema original. El sistema simétrico o balanceado de fasores trifásico que tiene la misma secuencia de fases que el sistema original se llama el sistema de secuencia positiva. Si se da a los fasores originales la secuencia de fases abc, entonces 226 ELECTROTECNIA III-227 la secuencia de fases de los fasores de secuencia positiva es abc, como se muestra en la figura número 2. Los fasores de secuencia positiva quedan completamente determinados cuando se conoce la magnitud y posición de fase de cualquiera de ellos. Los fasores de secuencia positiva se designan como V a 1 ,V b1 y V c 1 El subíndice 1 indica que el fasor así marcado pertenece al sistema de secuencia positiva. Las letras se refieren al fasor original de que es parte componente el fasor de secuencia positiva. V a1 V c1 Eje de referencia V b1 FIGURA NÚMERO 2. Este juego de componentes simétricas consiste de tres fasores que son de igual magnitud y con un desplazamiento angular de 120,00 entre ellos. Estos fasores giran en sentido contrario a las manecillas del reloj. Los fasores anteriores se pueden relacionar uno con otro mediante un operador fasorial unitario, al cuál denominaremos como “a”, y que tiene un desplazamiento angular de 120,00. Algunas de las propiedades de este fasor son, a =1 / 120,00 ; a 2 1 / 240, 00 ; a 3 1 / 0, 00 a4 1 / 120, 00 ; 1 a + a 2 0 ; 1 a = - a 2 1 / 60, 0 0 1 a2 a =1/ -60,00 ; a +a2 1/ 0,0 1/ 180,00 ; 1 a = 3 / 30,00 1 a2 3 / 30,00 ; a-a2 3 / 90,00 El operador a, aplicado a un fasor cualquiera, hace girar a ese fasor 120,00, en sentido positivo o sea contra las manecillas del reloj. El operador a2 hace girar a ese fasor 240,00 en sentido positivo, que es, por supuesto, equivalente a una rotación de 120,00 en sentido negativo. Así el juego de secuencia positiva se puede designar como, V a1 V a1 227 ELECTROTECNIA III-228 V b1 a2 V a1 V a1 / 120,00 (1) V c1 aV a1 V a1 / 240,00 Es importante enfatizar que el juego de fasores de secuencia siempre existe por definición como V a 1 ,V b1 y V c1 , nunca pueden existir solas o en pares, siempre deben existir las tres. Así solamente es necesario definir uno de los fasores, a partir del cuál se pueden determinar los otros dos. El sistema de secuencia de fases negativa. El sistema simétrico de fasores trifásico opuesto en secuencia de fases al de los fasores originales, se denomina como sistema de secuencia de fases negativa. Si los fasores originales tienen una secuencia de fases abc, los fasores de secuencia negativa tienen una secuencia de fases acb, como se muestra en la figura número 3. Puesto que el sistema de secuencia negativa es simétrico, queda completamente determinado cuando se conoce uno de los fasores. Los fasores del sistema de secuencia negativa se designan como, V a 2 ; V b2 ; V c2 V c2 V a2 Eje de referencia V b2 FIGURA NÚMERO 3. El subíndice 2 indica que los fasores pertenecen al sistema de secuencia negativa. Los subíndices a, b y c indican las componentes de V a ,V b y V c , respectivamente. Si V a 2 es conocido , el sistema de secuencia negativa se puede escribir en la forma siguiente: V a 2 V a 2 V b 2 aV a 2 V a 2 / 120,0 V a 2 / 240,00 (2) V c 2 a2 V a 2 V a 2 / 240,00 V a 2 / 120,00 El sistema de secuencia de fases cero. Este sistema restante consta de tres fasores idénticos en magnitud y ángulo de fase, como se muestra en la figura número 4. Estos fasores forman lo que se conoce como el sistema de secuencia cero y tienen una importancia especial en ciertos problemas físicos. Por el momento 228 ELECTROTECNIA III-229 bastará con considerar a los tres fasores de secuencia cero como componentes de los fasores originales, V a ,V b y V c . Los fasores de secuencia cero se designan como, V a 0 ; V b0 ; V c 0 Eje de referencia V a 0 V b 0 V c0 FIGURA NÚMERO 4 Puesto que los fasores anteriores son iguales tenemos, V a 0 V a 0 V b 0 V a 0 (3) V c 0 V a 0 Composición de los fasores de secuencia para obtener los fasores originales. Es evidente que V a1 V a 2 V a 0 V b1 V b 2 V b 0 (4) y V c1 V c 2 V c 0 forman un sistema trifásico de fasores asimétrico que, en general no es simétrico. Las composiciones indicadas se efectúan gráficamente en la figura número 5 empleando los fasores particulares contenidos en las figuras números 2, 3 y 4. 229 ELECTROTECNIA III-230 V c V c1 V c 2 V c 0 V c0 V a2 V a0 V c2 V a1 V a V a1 V a 2 V a 0 V c1 Eje de referencia V b1 V b2 V b V b1 V b 2 V b 0 V b0 FIGURA NÚMERO 5. El sistema resultante mostrado en la figura número 5 es idéntico al sistema asimétrico que se muestra en la figura número 1. Ecuaciones generales. En cualquier sistema de fasores asimétrico o desbalanceado se pueden determinar sus secuencias componentes. Para el caso particular considerado está claro que, V a V a1 V a 2 V a 0 V b V b1 V b 2 V b 0 (5) V c V c1 V c 2 V c 0 En función del operador a, las ecuaciones anteriores se pueden expresar como, V a V a1 V a 2 V a 0 V b a2 V a1 aV a 2 V a 0 (6) V c aV a 1 a 2 V a 2 V a 0 El juego de ecuaciones (6) se pude escribir en forma matricial quedando como, 230 ELECTROTECNIA III-231 V a 1 2 V b a a V c 1 V a 1 1 V a 2 1 V a 0 1 a a 2 (7) Denominando a, 1 A = a 2 a 1 a a2 1 1 (8) 1 De donde, V a V a 1 V b A V a 2 (9) V c V a 0 Resolviendo para las componentes de las secuencias tenemos, V a 1 V a -1 V a 2 A V b (10) V a 0 V c Con el objeto de tener un juego de ecuaciones similares a las del grupo (6), resolveremos la ecuación matricial (10). La matriz inversa de A es igual a la matriz adjunta de A dividida por el determinante de A, esto es, A -1 Matriz adjunta de A Determinante de A Resolviendo el determinante de A por menores tenemos, a 1 a 2 1 a 2 A =1 2 1 1 a 1 a 1 a a a2 a a2 a2 a a4 - a 2 a - a 2 a - a 2 a - a 2 3 a - a 2 La matriz transpuesta de A es, 231 ELECTROTECNIA III-232 1 a 2 A t 1 a 1 1 a a2 1 Puesto que la matriz adjunta de A es igual a la matriz de los cofactores de la matriz transpuesta de A, tenemos a 1 2 a Adj A = - 1 2 a a a2 1 a 1 1 1 a a2 1 1 a - a2 a - a2 a a2 1 a 1 1 a - a2 a 1 a 2 2 - a a 1 1 1 4 2 a a a 1 a 2 a 2 1 a 1 a 2 - 1 1 - 1- a 2 1- a 1 a2 2 a - a 1- a - a a 2 a 1 1 a 1- a a 1 a - a a - a 2 2 2 2 Sustituyendo en la ecuación de la matriz inversa de A tenemos, A -1 1 3 a-a 2 a - a2 a - a2 a - a2 a 1 1 a 1- a a 1 a - a a - a 2 2 2 2 Además tenemos que, 2 a 2 1 a a 2 1 a 3 a a a -1 a a - a2 a a - a2 a2 a3 a 2 -1 2 1-a a2 1-a a 2 -a 3 a 1-a a2 a -a2 a2 a -a 2 a 3 -a4 1-a Sustituyendo en la ecuación de la matriz inversa se obtiene 1 a 1 -1 A 1 a 2 3 1 1 a2 a 1 Sustituyendo en la ecuación (10) obtenemos, 232 ELECTROTECNIA III-233 V a 1 1 a 1 2 V a 2 1 a 3 1 1 V a 0 a 2 V a a V b (11) 1 V c De donde se obtiene el juego de ecuaciones para determinar las componentes simétricas, siguiente: V a1 V a2 1 V a aV b a 2 V c 3 1 V a a2 V b aV c 3 V a0 1 V a V b V c 3 (12) Ejemplo 6-1. Obtener las componentes simétricas de los fasores siguientes: V a 10,00 / 30,00 ; V b 30,0 / 60,00 ; V c 15,00 / 145,00 SOLUCIÓN. La ecuación matricial para determinar los fasores de las componentes simétricas de los fasores es, V a 1 V a 1 2 -1 V a 2 A V b a a V a 0 V c 1 a a2 1 1 1 1 10, 00 / 30, 0 17, 58 / 45,1 30, 0 / 60, 0 8, 24 / 156, 3 15, 00 / 145, 0 5, 60 / 47, 4 De donde las componentes simétricas de los fasores son, Componentes de secuencia positiva, V a1 17,58 / 45,10 , V b1 17,58 / 74,90 ; V c1 17,58 / 194,90 Componentes de secuencia negativa, V a 2 8, 24 / 156, 30 V b 2 8, 24 / 36, 30 ; V c 2 8, 24 / 83,70 Componentes de secuencia cero, V a 0 5,60 / 47,40 ; V b 0 5,60 / 47,40 ; V c 0 5,60 / 47,40 Ejemplo 6-2. Si las componentes simétricas de la fase a de un sistema de fasores son, 233 ELECTROTECNIA III-234 Secuencia positiva, V a1 17,58 / 45,10 unidades Secuencia negativa, V a 2 8, 25 / 156, 30 unidades Secuencia cero, V a 0 5,60 / 47,40 unidades Determine los fasores originales. SOLUCIÓN. La ecuación matricial para determinar los fasores originales es, V a V a 1 1 2 V b A V a 2 a V c V a 0 a 1 a a2 1 17, 58 / 45,1 9, 99 / 30,1 1 8, 25 / 156, 3 30, 0 / 60, 0 1 5, 60 / 47, 4 15, 00 / 145, 0 Los fasores originales son, V a 9,99 / 30,10 u ; V b 30,0 / 60,00 u ; V c 15,00 / 145,00 u Vc Va Eje de referencia Vb Ejemplo 6-3. Calcule las componentes simétricas de las corrientes siguientes de un sistema trifásico desequilibrado: I A 5,00 / 0,00 A , I B 5,00 / 233,10 A e I C 1,414 / 45,00 A SOLUCIÓN. La ecuación matricial para resolver el problema es, I a1 Ia 1 2 -1 I a 2 A I b a a I a 0 I c 1 a a2 1 1 1 1 5, 00 / 0, 0 2, 88 / 6, 4 5, 00 / 233,1 2, 29 / 60, 3 1, 414 / 45, 0 1, 943 / 59, 0 De donde las componentes simétricas del sistema de fasores son, 234 ELECTROTECNIA III-235 I a1 2,88 / 6,40 A , I b1 2,88 / 126,40 A e I c1 2,88 / 246,40 A I a 2 2, 29 / 60, 30 A , I b 2 2, 29 / 179,70 A e I c 2 2, 29 / 59,70 A I a 0 I b 0 I c 0 1,943 / 59,00 A Ejemplo 6-4. En un sistema trifásico asimétrico son conocidas las componentes simétricas de las corrientes de línea: I b 1 = 10,00 A, componente de secuencia positiva de la corriente de la fase B; I c 2 =5,00 A, componente de secuencia negativa de la corriente de la fase C; el ángulo entre ellas es de 30,0 0; como se muestra en la figura. Considere la componente de secuencia cero igual a 0. Determinar las corrientes de línea del sistema. I b1 I c2 30,00 SOLUCIÓN. Los diagramas fasoriales de las componentes simétricas de las corrientes, tomando a I b 1 como referencia son, I a1 abc acb I b1 I c1 I c2 I a2 30,00 I b2 De donde, I a1 10,00 / 120,00 A , I a 2 5,00 / 150,00 A I a 0 0 235 ELECTROTECNIA III-236 Las corrientes de línea son, I A I a1 1 2 I B A I a 2 a a I C I a 0 1 a a2 1 10, 00 / 120, 0 14, 55 / 129, 9 1 5, 00 / 150, 0 11,18 / 26, 6 6, 20 / 96, 2 1 0 De donde las corrientes de línea son, I A 14,55 / 129,90 A , I B 11,18 / 26,60 A e I C 6, 20 / 96, 20 A Ejercicio 6-5. En la figura se muestra un sistema asimétrico de fasores de tensión. A 90,00 N V AN VCN 100, 0 V B VBN 173, 0 V 90,00 C Descomponer este sistema asimétrico de fasores de tensión en componentes simétricas. Tome como referencia la tensión V AN . SOLUCIÓN. Tomando como referencia a la tensión V AN tenemos, V AN 100,0 / 0,00 V , V BN 173,0 / 90,00 V y V CN 100,0 / 180,0 0 V Utilizando el álgebra matricial tenemos, V a 1 V AN 1 2 -1 V a 2 A V BN a a V a 0 V CN 1 a a2 1 1 1 1 100, 0 / 0, 0 115, 4 / 30, 0 0 173, 0 / 90, 0 100, 0 / 180, 0 57, 7 / 90, 0 Las componentes de secuencia positiva son, V a1 115, 4 30, 00 V , V b1 115, 4 90, 00 V y V c1 115, 4 210, 00 V Las componentes de secuencia negativa son, 236 ELECTROTECNIA III-237 V a 2 V b 2 V c 2 0 Las componentes simétricas de secuencia cero son, V a 0 V bo V c 0 57,7 / 90,00 V V c1 V a1 V a 2 ,V b 2 ,V c 2 V a 0 ,V b0 ,V c 0 V b1 3. POTENCIA EN TÉRMINOS DE COMPONENTES SIMÉTRICAS. Si se conocen las componentes simétricas de corriente y tensión, se puede calcular directamente la potencia compleja de un circuito trifásico a partir de las componentes simétricas. La demostración de esta afirmación constituye un buen ejemplo del manejo de las componentes simétricas por medio del cálculo matricial. La potencia compleja total suministrada a un circuito trifásico a través de las tres líneas A, B y C es * * * S 3φ P jQ =V A I A V B I B V C I C donde V A , V B y V C son las tensiones en las terminales respecto al neutro, e I A , I B e I C son las corrientes que fluyen dentro del circuito en las tres líneas. La conexión al neutro puede o no estar presente. Si hay una impedancia en la conexión del neutro a tierra, entonces las tensiones V A , V B y V C se deben interpretar como las tensiones desde línea a tierra, en lugar de al neutro. En notación matricial, * T * I A V A I A S 3φ V A V B V C I B V B I B I C V C I C donde se entiende que la conjugada de una matriz está compuesta por los elementos que son los conjugados de los respectivos elementos de la matriz original. Para tomar en cuenta las componentes simétricas de las tensiones y corrientes recordemos que, 237 ELECTROTECNIA III-238 V A V a1 1 2 V B A V a2 a V C V a0 a 1 V a1 1 V a2 1 V a0 1 a a2 de donde se obtiene en notación matricial abreviada, T S 3φ A V 120 A I 120 * Siendo V a1 V 120 V a2 V a0 I a1 I 120 I a2 I a0 e La regla de la inversión del álgebra matricial establece que la transpuesta del producto de dos matrices es igual al producto de las transpuestas separadas de las matrices en orden inverso. De acuerdo con esta regla T A V 120 V 120 AT T y así S 3φ V 120 AT A T * I 120 V 120 AT A* I 120 T * La matriz transpuesta es, 1 a 2 AT 1 a 1 1 a a2 1 Puesto que a y a2 son conjugados, la matriz conjugada es 1 A a a 2 * 1 a 2 a 1 1 1 Y el producto de AT y A* es 1 a 2 AT A* 1 a 1 1 a 1 a 2 a 1 a 2 1 a 2 a 1 3 0 0 1 0 0 1 0 3 0 3 0 1 0 3 U 0 0 1 1 0 0 3 Al sustituir en la ecuación de la potencia compleja total, se tiene 238 ELECTROTECNIA III-239 * V a1 V a2 V a0 I a1 * * * S 3φ 3 0 0 0 I a2 3V a1 I a1 3V a2 I a2 3V a0 I a0 0 0 0 I a0 que muestra como se puede calcular la potencia compleja (en voltampere) a partir de las componentes simétricas de las tensiones de referencia (en volt) y de las corrientes de línea (en ampere) de un circuito trifásico desbalanceado. Es importante observar que la transformación de las tensiones y corrientes A-B-C en componentes simétricas se da sin variación en la potencia, solamente si cada producto de la tensión de secuencia (en volt) por el complejo conjugado de la correspondiente corriente de secuencia (en ampere) se multiplica por 3, como se muestra en la ecuación anterior. Sin embargo, cuando la potencia compleja S3 se expresa en por unidad de una base trifásica de voltampere, desaparece el multiplicador 3. Ejemplo 6-6. Un conjunto trifásico de tensiones asimétricas suministra las corrientes siguientes: I A 20,0 / 0,00 A ; I B 20,0 / 143,10 A ; I C 20,0 / 126,90 A Si las tensiones de suministro son, V AN 100,0 / 0,00 V ; V BN 100,0 / 90,00 V ; V CN 100,0 / 90,00 V calcular las componentes simétricas de las tensiones y las corrientes, y determinar la potencia compleja suministrada por la fuente para cada conjunto de componentes simétricas. ¿Cuál es la potencia total suministrada? SOLUCIÓN. Las componentes simétricas de las corrientes son, I a1 I A 1 2 -1 I a 2 A I B a a I a 0 I C 1 a a2 1 1 1 1 20, 0 / 0, 0 19, 50 / 5, 3 20, 0 / 143,1 3, 29 / 8, 5 20, 0 / 126, 9 2, 98 / 153, 5 De donde las componentes simétricas de las corrientes, Secuencia positiva: I a1 19,50 / 5, 30 A Secuencia negativa: I a 2 3, 29 / 8,50 A Secuencia cero: I a 0 2,98 / 153,50 A Las componentes simétricas de las tensiones son, 239 ELECTROTECNIA III-240 V a 1 V AN 1 2 -1 V a 2 A V BN a V a 0 V CN a 1 1 1 1 a a2 1 100, 0 / 0, 0 91,1 / 0, 0 100, 0 / 90, 0 24, 4 / 180, 0 100, 0 / 90, 0 33, 3 / 0, 0 De donde las componentes simétricas de las tensiones son, Secuencia positiva: V a1 91,1/ 0,00 V Secuencia negativa: V a 2 24,4 / 180,00 V Secuencia cero: V a 0 33, 3 / 0,00 V La figura siguiente muestra los diagramas fasoriales correspondientes. V c2 V CN I c2 I c1 IC V c1 V a1 V a0 IA I a1 V AN V a2 TENSIONES I a2 I a0 CORRIENTES IB I b1 V b1 I a1 I b2 V BN V b2 La potencia compleja suministrada por las componentes de secuencia positiva es, * S 1 3V a1 I a1 3 91,1/ 0, 0 19, 50 / 5, 3 5, 33 103 / 5, 30 VA La potencia compleja suministrada por las componentes de secuencia negativa es, * S 2 3V a 2 I a 2 3 24, 4 / 180, 0 3, 29 / 8, 5 241/ 171, 50 VA La potencia compleja suministrada por las componentes de secuencia cero es, * S 0 3V a 0 I a 0 3 33, 3 / 0, 0 2, 98 / 153, 5 298 / 153, 50 VA La potencia compleja total suministrada por la fuente es, 240 ELECTROTECNIA III-241 * V a 1 V a 2 V a 0 I a 1 91,1 / 0, 0 24, 4 / 180, 0 33, 3 / 0, 0 19, 50 / 5, 3 3, 29 / 8, 5 S 3 3 0 0 0 I a 2 3 0 0 0 0 I 0 0 0 0 0 2, 98 / 153, 5 a 0 4, 82 103 / 4, 7 0 0 De donde la potencia compleja total es igual a, S 3 4, 82 103 / 4, 7 0 VA = 4,80 103 j395 VA Y las potencias aparente, activa y reactiva son, S 3 4, 82 103 VA P3 4, 80 103 W Q3 395 var IND Ejemplo 6-7. Una fuente trifásica simétrica de cuatro hilos, con una tensión de fase de 289 V, cuya secuencia de fases es ABC, alimenta una carga conectada en estrella, que toma corrientes cuyas componentes simétricas son I a1 37,0 / 6, 30 A ; I a 2 19, 26 / 4, 30 A I a 0 27,7 / 168,50 A ; Tomando como referencia a la tensión V AN , calcular la potencia compleja suministrada por cada una de las componentes simétricas y determinar la potencia compleja total consumida. SOLUCIÓN. Puesto que se tiene una fuente simétrica, la tensión solo tiene componentes de secuencia positiva, de donde V a1 289 / 0,00 V ; V a2 0 ; V a0 0 La potencia suministrada por cada una de las componentes simétricas es Componente de secuencia positiva, * S a1 3V a1 I a1 3 289 / 0, 0 37, 0 / 6, 3 32,1 103 / 6, 30 VA Componente de secuencia negativa, * S a 2 3V a 2 I a 2 0 241 ELECTROTECNIA III-242 Componente de secuencia cero, * S A 0 3V a 0 I a 0 0 Y la potencia compleja total es S 3 S a 1 S a 2 S a 0 32,1 103 0 0 32,1 103 VA 4. REDES DE SECUENCIA DE LAS IMPEDANCIAS DE LAS CARGAS. La figura número 6 muestra una carga conectada en estrella con impedancias balanceadas. La impedancia de cada fase está designada como ZY , la impedancia del neutro como ZN y está conectada entre el neutro de la carga y tierra. IA A ZY IN N IB ZY ZY B ZN C IC n FIGURA NÚMERO 6. En la figura número 6, la tensión de línea a tierra es V an y es igual a, V an Z Y I A Z N I N Z Y I A Z N I A I B I C ZY Z N I A Z N I B Z N I C 13 Se pueden escribir ecuaciones similares para V bn y V cn , esto es. 242 ELECTROTECNIA III-243 V bn Z N I A Z Y Z N I B Z N I C 14 V cn Z N I A Z N I B Z Y Z N I C 15 Las ecuaciones (13), (14) y (15) se pueden escribir en forma de matriz como, V an Z Z N Y V Z bn N ZN V cn ZN ZY Z N ZN I A ZN I B Z Y Z N I C ZN 16 Esta ecuación se puede escribir en forma compacta utilizando la simbología del álgebra matricial como, 17 V f ZF IF Donde V f es el vector de tensiones de línea a tierra ( o tensiones de fase), I F es el vector de las corrientes de línea ( o fase) y Z F es la matriz 3 x 3 de las impedancias de fase. Ahora se pueden sustituir las ecuaciones de las componentes simétricas de las tensiones y las corrientes en la ecuación número (17), para determinar la relación entre las tensiones de secuencia y las corrientes de secuencia. AV S Z F A I S (18) Premultiplicando ambos lados de la ecuación número (18) por A-1, tenemos, V S A-1 Z F A I S (19) o V S ZS IS (20) donde Z S A-1 Z F A (21) La matriz de impedancias definida en la ecuación número (21) es la llamada matriz de impedancias de secuencia Z S para la carga balanceada conectada en estrella. Esta también se puede escribir como. 1 a 1 Z S 1 a 2 3 1 1 a 2 Z Y Z N a ZN 1 ZN ZN ZY Z N ZN 1 2 ZN a Z Y Z N a ZN 1 a a2 1 1 (22) 1 Realizando las multiplicaciones indicadas en la ecuación número (22) y usando la identidad ( 1 + a + a 2) = 0, obtenemos 243 ELECTROTECNIA III-244 ZY ZS 0 0 0 ZY 0 0 (23) Z Y 3 Z N 0 Como se muestra en la ecuación número (23), la matriz de impedancias de secuencia Z S , para la carga balanceada conectada en estrella, de la figura número 6 es una matriz diagonal, de donde la ecuación número (20) se puede representar como tres ecuaciones desacopladas. V a 1 Z Y V a 2 0 0 V ao 0 ZY 0 I a1 0 I a 2 (24) Z Y 3 Z N I a 0 0 Escribiendo la ecuación número (24) como tres ecuaciones separadas tenemos, V a1 Z Y I a1 (25) V a2 ZY I a2 (26) V a0 ZY 3 Z N I a0 (27) Como se muestra en la ecuación número 25, la tensión de secuencia positiva V a 1 solamente depende de la corriente de secuencia positiva I a 1 y de la impedancia Z 1 Z Y llamada impedancia a la secuencia positiva. Similarmente, V a 2 depende solamente de I a 2 y la impedancia a la secuencia negativa Z 2 Z Y . También como se muestra en la ecuación número 27, la tensión de secuencia cero V a 0 depende solamente de la corriente de secuencia cero I a 0 y la impedancia Z Y 3 Z N , esta impedancia es llamada la impedancia a la secuencia cero y se denomina como Z 0 . Las ecuaciones números 25, 26 y 27 se pueden representar por tres redes como se muestra en la figura número 7. Estas redes se denominan como las redes de secuencia positiva, negativa y cero. I a1 I a2 + I a0 + V a1 Z1 ZY Red de secuencia positiva + V a2 Z 2 ZY Red de secuencia negativa V a0 Z0 Z y 3Z N Red de secuencia cero FIGURA NÚMERO 7. 244 ELECTROTECNIA III-245 Como se muestra en la figura número 7, cada red de secuencia está separada, esto es están desacopladas. La separación de estas redes de secuencia es una consecuencia del hecho de que Z S es una matriz diagonal para una carga balanceada conectada en estrella. Esta separación resalta la ventaja de las componentes simétricas. Se puede observar que la impedancia del neutro no aparece en las redes de secuencia positiva y negativa de la figura número 7. Esto ilustra el hecho de que las corrientes de secuencia positiva y negativa no circulan por la impedancia del neutro. Sin embargo, la impedancia del neutro está multiplicada por 3 y colocada en la red de secuencia cero. La tensión 3 Z N I a 0 a través de la impedancia 3 Z N es la caída de tensión Z N I N a través de la impedancia del neutro en la carga de la figura número 6, de donde I N 3 I a0 (28) Cuando el neutro de la carga en estrella en la figura número 6 no tiene trayectoria de retorno, entonces la impedancia del neutro Z N es infinita y el término 3 Z N en la red de secuencia cero de la figura número 7 viene a ser un circuito abierto. Bajo esta condición de un neutro abierto no existe corriente de secuencia cero. Sin embargo, cuando el neutro de la carga en estrella está sólidamente a tierra con un conductor con cero ohms, y la impedancia del neutro es cero y el término 3 Z N en la red de secuencia cero viene a ser un circuito corto. Bajo esta condición de un neutro sólidamente a tierra la corriente de secuencia cero I a 0 puede existir cuando hay una tensión de secuencia cero debido a una asimetría de las tensiones aplicadas a la carga. Ejemplo 6-8. Una carga balanceada conectada en estrella tiene una impedancia por fase de ZY = 3,00 + j 4,00 y su neutro está conectado a tierra a través de una reactancia inductiva de XN = 2,00 , esta se alimenta con tensiones asimétricas de valores V an 100,0 / 0,00 V , V bn 200 / 90,00 V y V cn 100,0 / 135,0 0 V . a)Dibuje las redes de secuencia para esta carga. b) Calcule las impedancias de secuencia de la carga y c) las corrientes de línea y del conductor del neutro. SOLUCIÓN. a) Las redes de secuencia son, I a1 I a2 + I a0 + V a1 Z1 ZY + V a2 Red de secuencia positiva Z 2 ZY Red de secuencia negativa V a0 ZY 3 Z N Red de secuencia cero b) Las impedancias de secuencia son, Z 1 Z 2 3, 00 j4, 00 5, 00 / 53,10 245 ELECTROTECNIA III-246 Z 0 Z Y 3 Z N 3, 00 j4, 00 3 j2, 00 10, 44 / 73, 3 0 c) Las componentes simétricas de las tensiones son, V a 1 V an 100, 0 / 0, 0 130, 2 / 18, 8 1 1 V a 2 A V bn A 200 / 90, 0 33, 0 / 178, 0 100, 0 / 135, 0 44, 2 / 77, 2 V a 0 V cn Las componentes simétricas de las corrientes son, I a1 V a1 130, 2 / 18, 8 26, 0 / 34, 30 A Z 1 5, 00 / 53,1 I a2 V a 2 33, 0 / 178, 0 6, 60 / 124, 90 A Z2 5, 00 / 53,1 I a0 V a 0 44, 2 / 77, 2 4, 23 / 150, 50 A Z 0 10, 44 / 73, 3 De donde las corrientes de línea son, I A I a1 26, 0 / 34, 3 18, 02 / 38, 9 I B A I a 2 A 6, 60 / 124, 9 35, 6 / 147,1 4, 23 / 150, 5 24, 9 / 78, 8 I C I a 0 I A 18,02 / 38,90 A ; I B 35,6 / 147,10 A ; I C 24,9 / 78,80 A La corriente en el conductor del neutro es, I N 3 I a 0 3 4, 23 / 150,5 12,69 / 150,50 A Ejemplo 6-9. Las tensiones V an 280 / 0,00 V , V bn 290 / 130,50 V y V cn 260 /110,0 0 V se aplican a una carga balanceada conectada en estrella, con impedancias por fase de 6,00 + j 8,00 . La carga tiene su neutro conectado sólidamente a tierra. a) Dibuje las redes de secuencia para esta carga. b) Calcule las componentes de secuencia de las corrientes de línea y c) las corrientes de línea y del conductor del neutro. SOLUCIÓN. a) Las redes de secuencia para esta carga son, 246 ELECTROTECNIA III-247 I a1 I a2 + I a0 + V a1 + V a2 Z1 ZY Red de secuencia positiva Z 2 ZY V a0 Red de secuencia negativa Z 0 ZY Red de secuencia cero Donde, Z Y 6, 00 j8, 00 10, 00 / 53,10 b) Las componentes simétricas de las tensiones son, V a 1 V an 280 / 0, 0 276 / 6, 6 1 1 V a 2 A V bn A 290 / 130, 0 24, 9 / 79, 4 260 / 110, 0 7, 55 / 78,1 V a 0 V cn De donde las componentes simétricas de las corrientes son, I a1 V a 1 276 / 6, 6 27, 6 / 59, 70 A Z 1 10, 00 / 53,1 I a2 V a 2 24, 9 / 79, 4 2, 49 / 26, 30 A Z 2 10, 00 / 53,1 I a0 V a 0 7, 55 / 78,1 0, 755 / 25, 00 A Z 0 10, 00 / 53,1 c) Las corrientes de línea y del neutro son, I A I a1 27, 6 / 59, 7 28, 0 / 53,1 I B A I a 2 A 2, 49 / 26, 3 29, 0 / 176, 9 0, 755 / 25, 0 26, 0 / 56, 9 I C I a 0 I A 28,0 / 53,10 A ; I B 29,0 / 176,90 A ; I C 26,0 / 56,90 A I N 3 I a 0 3 0,755 / 25,0 2, 27 / 25,00 A 247 ELECTROTECNIA III-248 Ejemplo 6-10. Una carga balanceada conectada en estrella de tres hilos, tiene una impedancia por fase Z Y 25, 4 / 30, 20 . Esta se alimenta con una fuente asimétrica con tensiones de línea de V AB 250 / 0,00 V , V BC 300 / 138,60 V y V CA 200 / 97,2 0 V . a) Dibuje las redes de secuencia para esta carga, b) calcule las corrientes de línea. SOLUCIÓN. a) Las redes de secuencia para la carga son, I a1 I a2 + I a0 0 + V a1 + V a2 Z1 ZY Z 2 ZY V a0 ZY Z0 Red de secuencia positiva Red de secuencia negativa Red de secuencia cero b) Las componentes simétricas de las tensiones de línea son, V ab1 V AB 250 / 0, 0 246 / 13, 5 1 1 V ab 2 A V BC A 300 / 138, 6 58, 7 / 79, 7 200 / 97, 2 0 V ab 0 V CA Las componentes simétricas de secuencia positiva y negativa de las tensiones al neutro son, V a1 Vab1 V a2 3 / ab1 30, 0 Vab 2 3 246 / ab 2 30, 0 3 / 13, 5 30, 0 142, 0 / 43, 50 V 58, 7 3 / 79, 7 30, 0 33, 9 / 109, 7 0 V Las componentes simétricas de las corrientes son, I a1 V a 1 142, 0 / 43, 5 5, 59 / 73, 50 A Z1 25, 4 / 30, 2 248 ELECTROTECNIA III-249 I a2 V a 2 33, 9 / 109, 7 1, 335 / 79, 50 A Z 2 25, 4 / 30, 2 I a0 0 Las corrientes de línea son, I A I a1 5, 59 / 73, 5 4, 44 / 65, 7 I B A I a 2 A 1, 335 / 79, 5 6, 75 / 172, 7 5, 81 / 33, 2 0 I C I a 0 I A 4,44 / 65,70 A ; I B 6,75 / 172,50 A ; I C 5,81/ 33, 20 A La figura número 8 muestra una carga balanceada conectada en delta y su carga equivalente conectada en estrella balanceada. A A Z B C ZY Z Z ZY N Z 3 ZY B C FIGURA NÚMERO 8. Puesto que la carga conectada en delta no tiene conexión al neutro, la carga equivalente conectada en estrella tiene su neutro abierto. Las redes de secuencia de la carga equivalente conectada en estrella corresponden a las de la carga balanceada conectada en delta y se muestran en la figura número 9. 249 ELECTROTECNIA III-250 I a1 I a2 + I a0 0 + V a1 Z1 + V a2 Z 3 Z2 Z 3 V a0 Z 3 Z0 Red de secuencia positiva Red de secuencia negativa Red de secuencia cero FIGURA NÚMERO 9. Como se muestra en la figura número 9 la impedancia equivalente conectada en estrella Z Y Z / 3 aparece en cada una de las redes de secuencia. También, la red de secuencia cero tiene un circuito abierto, puesto que Z 0 , lo que corresponde a un neutro abierto. No hay corriente de secuencia cero en la carga equivalente conectada en estrella. Las redes de secuencia de la figura número 9 representan la carga balanceada conectada en delta vista desde sus terminales, pero ellas no representan las características internas de la carga. Las corrientes I a 1 , I a 2 e I a 0 en la figura número 9 son las componentes de secuencia de las corrientes de línea que alimentan a la delta, no las corrientes dentro de la delta. Las corrientes de secuencia dentro de la delta están relacionadas con las corrientes de secuencia de línea por medio de las ecuaciones siguientes: I ab1 I a1 I ab 2 Ia 2 3 3 / a 1 30, 0 (29) / a 2 30, 0 (30) I ab 0 0 Ejemplo 6-11. Las tensiones de línea V ab 517 / 25,00 V , V bc 477 / 101, 80 V y V ca 443 /146,5 0 V se aplican a una carga balanceada conectada en delta de 12,00 + j 16,00 por fase. a) Dibuje las redes de secuencia. b) Calcule las corrientes de línea y c) las corrientes de fase dentro de la delta. SOLUCIÓN. a)La impedancia equivalente en estrella tiene una impedancia por fase de, ZY Z 12, 00 j16, 00 6, 67 / 53,10 3 3 Las redes de secuencia son, 250 ELECTROTECNIA III-251 I a1 I a2 + I a0 0 + V a1 + V a2 Z1 ZY Z 2 ZY V a0 ZY Z0 Red de secuencia positiva Red de secuencia negativa Red de secuencia cero b) Las componentes simétricas de las tensiones de línea son, V ab1 V ab 517 / 25, 0 478 / 23, 2 1 1 V ab 2 A V bc A 477 / 101, 8 42, 5 / 47, 6 443 / 146, 5 0 V ab 0 Vca Las componentes simétricas de secuencia positiva y negativa de las tensiones de línea a neutro son, V a1 V a2 Vab1 3 Vab 2 3 / ab1 30, 0 478 / ab 2 30, 0 42, 5 3 3 / 23, 2 30, 0 276 / 6, 80 V / 47, 6 30, 0 24, 5 / 77, 6 0 V Las corrientes de secuencia son, I a1 V a1 276 / 6, 8 41, 4 / 59, 90 A Z 1 6, 67 / 53,1 I a2 V a 2 24, 5 / 77, 6 3, 67 / 24, 50 A Z 2 6, 67 / 53,1 I a0 0 De donde las corrientes de línea son, I A I a1 41, 4 / 59, 9 41, 9 / 54, 9 I B A I a 2 A 3, 67 / 24, 5 44, 4 / 177, 3 38,1 / 57, 8 0 I C I a 0 251 ELECTROTECNIA III-252 I A 41,9 / 54,90 A ; I B 44,4 / 177, 30 A ; I C 38,1/ 57,80 A c) Las corrientes de secuencia dentro de la delta son, I ab1 I a1 I ab 2 3 / a 1 30, 0 Ia 2 3 41, 4 / a 2 30, 0 3 / 59, 9 30, 0 23, 9 / 29, 90 A 3, 67 3 / 24, 5 30, 0 2,12 / 5, 5 0 A I ab 0 Las corrientes de fase dentro de la delta son, I AB I a1 23, 9 / 29, 9 25, 8 / 28, 0 I BC A I a 2 A 2,12 / 5, 5 23, 8 / 155, 0 22, 2 / 93, 3 0 I CA I a 0 I AB 25,8 / 28,00 A ; I BC 23,8 / 155,00 A ; I CA 22, 2 / 93, 30 A 5. APLICACIÓN DE LAS COMPONENTES SIMÉTRICAS A CARGAS DESBALANCEADAS. La figura número 10 representa un circuito trifásico general con una carga con impedancias lineales. La carga puede representar una carga balanceada ya sea conectada en estrella o conectada en delta, o una carga conectada en estrella con impedancias desbalanceadas. a b c n Impedancia de una carga trifásica FIGURA NÚMERO 10. Las relaciones generales de las tensiones de línea a tierra y las corrientes de línea para esta carga se pueden escribir como, V an Z A I A Z N I N Z A I A Z N I A I B I C Z A Z N I A Z N IB Z N IC (31) 252 ELECTROTECNIA III-253 V bn Z B I B Z N I N Z B I B Z N I A I B I C Z N I A ZB Z N IB Z N IC (32) V cn Z C I C Z N I N Z C I C Z N I A I B I C Z N I A Z N I B ZC Z N IC (33) Expresando las ecuaciones 31,32 y 33 en forma de matrices tenemos, V an Z Z N A V Z bn N ZN V cn ZN ZB ZN ZN I A ZN I B Z C Z N I C ZN (34) y utilizando la notación matricial tenemos, V f ZF IF (35) donde V f es el vector de tensiones de línea a tierra , I F es el vector de corrientes de línea y Z F es la matriz 3 X 3 de las impedancias de fase. Sustituyendo la tensión y la corriente por las ecuaciones de sus componentes simétricas y puesto que V f AV S ; I F A I S AV S Z F A I S Premultiplicando ambos miembros de la ecuación por A-1 tenemos, A-1 AV S A 1 Z F A I S Puesto que A-1 A es igual a la unidad, V S A1 Z F A I S A la expresión A-1 ZF A se le denomina como la matriz de las impedancias de secuencia y se representa por ZS. La matriz de las impedancias de secuencia de fase está dada por una matriz 3 X 3 con las impedancias de, 253 ELECTROTECNIA III-254 Z1 Z S Z 21 Z 01 Z 12 Z2 Z 02 Z 10 Z 20 Z 0 (36) Las impedancias de la diagonal de la matriz Z1, Z2 y Z0 son las autoimpedancias de las redes de secuencia positiva, negativa y cero. Las impedancias fuera de la diagonal son las impedancias mutuas entre las redes de secuencia. Usando las definiciones de A-1, A, ZF y ZS tenemos, Z1 Z S Z 21 Z 01 Z 12 Z2 Z 02 a 2 Z A Z N a ZN 1 ZN 1 a Z 10 1 Z 20 1 a 2 3 1 1 Z 0 ZN (37) Z C Z N ZN ZN ZB ZN ZN Realizando las multiplicaciones indicadas y usando la identidad (1 + a + a2) = 0, se pueden obtener los términos de la matriz de impedancias de secuencia. Z A ZB ZC 1 Z S Z A a Z B a2 Z C 3 Z A a2 Z B a Z C Z A Z a Z a Z Z Z a Z a Z a Z Z Z Z 9 Z a2 Z B a Z C Z Z Z a Z A A 2 A B C 2 B C A B C (38) 2 B C A B C N De donde Z1 Z 2 1 Z A ZB ZC 3 Z 12 Z 20 Z 01 1 Z A a2 Z B a Z C 3 Z 10 Z 21 Z 02 1 Z A a Z B a2 Z C 3 Z0 1 Z A ZB ZC 9 Z N 3 En el caso de tener una estrella sin impedancias en el neutro entonces, 254 ELECTROTECNIA III-255 Z A ZB ZC 1 ZS Z A a Z B a2 Z C 3 Z A a2 Z B a Z C Z A Z a Z a Z Z Z a Z a Z a Z Z Z Z a2 Z B a Z C Z Z Z a Z A A 2 A B C 2 B B C A B C 2 C A B C Ejemplo 6-12. En el sistema que se muestra en la figura se tiene una carga desbalanceada conectada en estrella, donde Z A 10, 00 j5, 00 , Z B 8, 00 j5, 00 y Z C 12,00 j0 ; esta carga se alimenta con tensiones simétricas donde V an 100,0 / 0,00 V y tiene una secuencia de fases positiva, a través de líneas con una impedancia de Z L 2, 00 / 0, 00 , el conductor del neutro tiene una impedancia igual a la de las líneas. Determine las corrientes de línea y del conductor del neutro. ZL B b Z ZN B n c a ZL ZL ZC C N ZA A SOLUCIÓN. Las componentes simétricas de las tensiones son, V a1 V an 100,0 / 0,00 V ; V a 2 0 ; V a 0 0 La matriz de impedancias de secuencia es, Z L Z A Z N ZS A ZN ZN 1 ZN ZL ZB ZN ZN ZN A Z L Z C Z N ZN En donde Z L Z A Z N 2, 00 / 0, 0 10, 00 j5, 00 2, 00 / 0, 0 14, 87 / 19, 7 0 A Z L Z B Z N 2, 00 / 0, 0 8, 00 j5, 00 2, 00 / 0, 0 13, 00 / 22, 6 0 A 255 ELECTROTECNIA III-256 Z L Z C Z N 2, 00 / 0, 0 12, 00 j0 2, 00 / 0, 0 16, 00 / 0, 0 0 A Sustituyendo valores en la ecuación de Z S , 14, 87 / 19, 7 2, 00 / 0, 0 2, 00 / 0, 0 Z S A 2, 00 / 0, 0 13, 00 / 22, 6 2, 00 / 0, 0 A 2, 00 / 0, 0 2, 00 / 0, 0 16, 00 / 0, 0 1 12, 00 / 0, 0 1, 975 / 43,1 3, 93 / 111, 5 3, 93 / 111, 5 12, 00 / 0, 0 1, 975 / 43,1 1, 975 / 43,1 3, 93 / 111, 5 18, 00 / 0, 0 Las componentes simétricas de las corrientes son, 1 IS ZS V S 12, 00 / 0, 0 1, 975 / 43,1 3, 93 / 111, 5 I S 3, 93 / 111, 5 12, 00 / 0, 0 1, 975 / 43,1 1, 975 / 43,1 3, 93 / 111, 5 18, 00 / 0, 0 1 100, 0 / 0, 0 0 0 I a 1 7, 58 / 2, 3 I S I a 2 2, 29 / 64, 0 1, 331 / 133, 8 I a 0 Las corrientes de línea son, I A I a1 7, 58 / 2, 3 8,12 / 19, 5 I B A I a 2 A 2, 29 / 64, 0 9,17 / 142, 3 1, 331 / 133, 8 6, 58 / 118, 7 I C I a 0 I A 8,12 / 19,50 A ; I B 9,17 / 142, 30 A ; I C 6,58 / 118,70 A La corriente en el conductor del neutro es, I N 3 I a 0 3 1, 331/ 133,8 3,99 / 133,80 A 256 ELECTROTECNIA III-257 Ejemplo 6-13. Sea una carga desbalanceada Z A 10, 00 / 60, 00 , de Z B 10, 00 / 60, 00 y Z C 5,00 / 0,0 0 , con una impedancia en el conductor del neutro de Z N 0, 0800 / 0, 00 ; conectada a una fuente asimétrica de V an 100,0 / 30,00 V , V bn 50,0 / 90,00 V y V cn 86,6/180,0 0V . a) Calcule las corrientes de línea y b) la potencia compleja. SOLUCIÓN. a) El vector de las tensiones de las componentes simétricas es, V an 100, 0 / 30, 0 76, 4 / 40, 9 V S A 1 V bn A 1 50, 0 / 90, 0 28, 9 / 0, 0 86, 6 / 180, 0 0 V cn La matriz de las impedancias de secuencia es, Z A Z N ZS A ZN ZN 1 ZN ZB ZN ZN ZN A Z C Z N ZN Donde, Z A Z N 10, 00 / 60, 0 0, 0800 / 0, 0 10, 04 / 59, 60 Z B Z N 10, 00 / 60, 0 0, 0800 / 0, 0 10, 04 / 59, 6 0 Z C Z N 5, 00 / 0, 0 0, 0800 / 0, 0 5, 08 / 0, 0 0 Sustituyendo valores en la ecuación matricial tenemos, 10, 04 / 59, 6 0, 0800 / 0, 0 0, 0800 / 0, 0 Z S A 1 0, 0800 / 0, 0 10, 04 / 59, 6 0, 0800 / 0, 0 A 0, 0800 / 0, 0 0, 0800 / 0, 0 5, 08 / 0, 0 5,00 /0,0 5,00 /120,0 5,00 /60,0 = 5,00 /60,0 5,00 /0,0 5,00 /120,0 5,00 /120,0 5,00 /60,0 5,24 /0,0 257 ELECTROTECNIA III-258 Las componentes simétricas de las corrientes son, 1 IS ZS V S I a 1 5,00 /0,0 5,00 /120,0 5,00 /60,0 1 76, 4 / 40, 9 I S I a 2 5,00 /60,0 5,00 /0,0 5,00 /120,0 28, 9 / 0, 0 5,00 /120,0 5,00 /60,0 5,24 /0,0 0 I a 0 7, 63 / 40, 4 8, 66 / 60, 0 2, 82 / 120, 0 Las corrientes de línea son, I A I a1 7, 63 / 40, 4 10, 06 / 29, 8 I B A I a 2 A 8, 66 / 60, 0 4, 95 / 29, 7 2, 82 / 120, 0 17, 26 / 179, 6 I C I a 0 I A 10,06 / 29,80 A ; I B 4,95 / 29,70 A ; I C 17, 26 / 179,60 A La corriente en el conductor del neutro es, I N 3 I a 0 3 2,82 / 120,0 8,46 / 120,00 A b) La potencia compleja es, * * * S 3V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 76, 4 / 40, 9 7, 63 / 40, 4 3 28, 9 / 0, 0 8, 66 / 60, 0 0 2, 23 103 / 17, 40 VA 2, 23 / 17, 4 0 kVA Ejemplo 6-14. Una carga desbalanceada conectada en estrella con su neutro sólidamente a tierra, con impedancias de Z A 28, 3 / 45, 00 , Z B 31, 6 / 18, 40 y Z C 22,4 / 63,4 0 , se conecta a una fuente asimétrica con tensiones de V AN 707 / 8,10 V , V BN 537 / 136,50 V y V CN 587 / 135,7 0V . a) Obtenga las corrientes de línea y del conductor del neutro, y b) la potencia compleja. 258 ELECTROTECNIA III-259 SOLUCIÓN. a) El vector de tensiones de las componentes simétricas es, V AN 707 / 8,1 144, 3 / 7, 0 1 1 V S A V BN A 537 / 136, 5 594 / 3, 4 587 / 135, 7 59, 3 / 128,1 V CN La matriz de las impedancias de secuencia es, Z A Z S A 0 0 1 0 ZB 0 28, 3 / 45, 0 0 0 0 1 0 AA 0 31, 6 / 18, 4 0 A Z C 0 0 22, 4 / 63, 4 20, 3 / 9, 4 9, 04 / 16, 6 16, 55 / 121, 5 16, 55 / 121, 5 20, 3 / 9, 4 9, 04 / 16, 6 9, 04 / 16, 6 16, 55 / 121, 5 20, 3 / 9, 4 Las componentes simétricas de las corrientes son, 1 IS ZS V S 20, 3 / 9, 4 9, 04 / 16, 6 16, 55 / 121, 5 I S 16, 55 / 121, 5 20, 3 / 9, 4 9, 04 / 16, 6 9, 04 / 16, 6 16, 55 / 121, 5 20, 3 / 9, 4 1 144, 3 / 7, 0 11, 59 / 124, 2 594 / 3, 4 16, 54 / 1, 3 59, 3 / 128,1 11,15 / 63, 5 Las corrientes de línea son, I A I a1 11, 59 / 124, 2 24, 9 / 53,1 I B A I a 2 A 16, 54 / 1, 3 16, 97 / 118, 2 11,15 / 63, 5 26, 2 / 72, 4 I C I a 0 I A 24,9 / 53,10 A ; I B 16,97 / 118, 20 A ; I C 26, 2 / 72,40 A La corriente del conductor del neutro es, 259 ELECTROTECNIA III-260 I N 3 I a 0 3 11,15 / 63,5 33,5 / 63,50 A b) La potencia compleja es, * * * S 3 V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 144, 3 / 7, 0 11, 59 / 124, 2 3 594 / 3, 4 16, 54 / 1, 3 3 59, 3 / 128,1 11,15 / 63, 5 28,1 103 / 3, 20 VA 28,1 / 3, 2 0 kVA Aplicación de las componentes simétricas a las cargas desbalanceadas de tres hilos. Componentes de secuencia positiva, negativa y cero de la impedancia. Para los fines de algunos análisis, tres auto impedancias se pueden dividir o resolver en sus componentes simétricas, exactamente como tres tensiones o corrientes. Si las tensiones o corrientes que se han de asociar con estas impedancias se deben descomponer en el orden ABC, entonces las impedancias se deben descomponer en el mismo orden. El término auto impedancia implica que no existe acoplamiento mutuo entre las impedancias individuales. A fin de distinguir las componentes de auto impedancia de las componentes de impedancia mutua que se tratarán posteriormente, se usan subíndices dobles, del tipo que se da a continuación. Las componentes simétricas de las tres auto impedancias ZA, ZB y ZC son, Z aa 1 Z A 1 Z A -1 Z a 2 aa 2 B Z aa 0 Z C a 1 a a2 1 1 1 1 1 Z A a Z B a2 Z C 3 1 Z aa2 Z A a 2 Z B a Z C 3 1 Z aa0 Z A Z B Z C 3 Z aa1 Z A Z B Z C Como se definieron anteriormente, Zaa1, Zaa2 y Zaa0 se llaman respectivamente, impedancia de secuencia positiva, impedancia de secuencia negativa e impedancia de secuencia cero. Estas impedancias componentes tienen escaso significado físico, pero son útiles en la formulación matemática general de la teoría de las componentes simétricas. Al llegar aquí se debe hacer notar que las partes resistivas de las impedancias componentes pueden tener signos negativos, aún cuando las partes reales de ZA, ZB y ZC sean todas positivas. Las componentes simétricas anteriores de un grupo de impedancias no balanceado, no se deben confundir con las impedancias a las corrientes de secuencia positiva, negativa y cero que se definen como sigue: Impedancia a la corriente de secuencia positiva, Z a1 V a1 Impedancia a la corriente de secuencia negativa, Z a 2 I a1 V a2 I a2 260 ELECTROTECNIA III-261 Impedancia a la corriente de secuencia cero, Z a 0 V a0 I a0 Estas impedancias opuestas a las corrientes de secuencia generalmente se aplican a sistemas en que las impedancias de todas las fases son iguales o están balanceadas. A fin de evitar la confusión se usará un subíndice formado por dos letras en las componentes de secuencia positiva, negativa y cero de la impedancia. En ambos casos los subíndices numéricos 1, 2 y 0 indicarán respectivamente, secuencia positiva, negativa y cero. Ejemplo 6- 15. Supóngase que las impedancias conectadas en estrella de la figura son, Z A 6, 00 / 0, 00 , Z B 6, 00 / 30, 00 y Z C 12,00 / 90,0 0 . Encuentre las componentes simétricas de las impedancias. A ZA ZB N ZC B C SOLUCIÓN. La matriz de las componentes simétricas de las impedancias es, 6, 00 / 0, 0 5, 46 / 0, 0 Z aa 1 Z A 1 1 Z SS Z aa 2 A Z B A 6, 00 / 30, 0 4, 38 / 136, 8 12, 00 / 90, 0 4, 79 / 38, 8 Z aa 0 Z C De donde, Z aa 1 5, 46 / 0, 00 ; Z aa 2 4, 38 / 136, 8 0 ; Z aa 0 4, 79 / 38, 8 0 Regla de la secuencia aplicada a las caídas de tensión componentes. Si se formula la caída de tensión a través de una fase, digamos la fase A, en función de las componentes simétricas de la corriente y la impedancia, aparecen nueve tensiones componentes, esto es, V A I A Z A I a1 I a 2 I a 0 Z aa 1 Z aa 2 Z aa 0 I a1 Z aa 1 I a1 Z aa 2 I a1 Z aa 0 I a 2 Z aa 1 I a 2 Z aa 2 I a 2 Z aa 0 I a 0 Z aa 1 I a 0 Z aa 2 I a 0 Z aa 0 261 ELECTROTECNIA III-262 Estas nueve tensiones componentes se pueden agrupar de manera que formen las componentes de secuencia positiva, negativa y cero de V A y este agrupamiento se puede hacer de acuerdo con una regla muy fácil de recordar. REGLA DE LA SECUENCIA. “El orden del sistema de tensiones a que pertenece una caída I Z es igual a la suma de los órdenes de los sistemas a que pertenecen I y Z individualmente.” En la aplicación de la regla de la secuencia los términos de secuencia positiva son de primer orden, los términos de secuencia negativa son de segundo orden y los términos de secuencia cero son de orden cero o tercer orden. Al sumar los órdenes (1 + 0), como (2 + 2) se consideran como de primer orden, pues el orden 4 se considera como orden 1, ya que sólo hay tres ordenes, En este caso particular, el cero existente en (1 + 0) se puede contar como cero o como tres. (1 + 2) es de orden tres, o un término de secuencia cero. Aplicada la regla de la secuencia a las tensiones componentes se establece: V a1 I a1 Z aa 0 I a 2 Z aa 2 I a 0 Z aa1 (39) V a 2 I a1 Z aa1 I a 2 Z aa 0 I a 0 Z aa 2 (40) V a 0 I a1 Z aa 2 I a 2 Z aa1 I a 0 Z aa 0 (41) Obviamente, la base real que ha servido para la formulación de las ecuaciones anteriores es que, tal como están formuladas satisfacen las definiciones que fueron originalmente dadas para V a 1 , V a 2 y V a 0 . Para satisfacer estas definiciones, V a 1 debe ser la componente de secuencia positiva del vector básico V A , V a 2 debe ser la componente de secuencia negativa del vector básico V A y V a 0 debe ser la componente de secuencia cero del vector básico V A . La prueba de que V a1 , tal como está formulada la ecuación (39), satisface la definición de una tensión de secuencia positiva se describe a continuación. Aplicando la ecuación (39) a la fase B y haciendo las sustituciones procedentes tenemos V a1 I a1 Z aa 0 I a 2 Z aa 2 I a 0 Z aa1 orden 1 V b1 I b1 Z bb 0 I b 2 Z bb 2 I b 0 Z bb1 a 2 I a 1 Z aa 0 a I a 2 a Z aa 2 I a 0 a 2 Z aa1 a 2 I a 1 Z aa 0 a 2 I a 2 Z aa 2 a 2 I a 0 Z aa1 orden 1 (42) La comparación de las ecuaciones (42) y (39) muestra que V b1 es igual en magnitud a V a 1 y está 120 grados detrás de V a 1 , como, por supuesto debe ser, si V a 1 , V b1 y V c 1 han de formar un sistema de tensiones de secuencia positiva. Aplicando la ecuación (39) a la fase C y haciendo las sustituciones que proceden, tenemos 262 ELECTROTECNIA III-263 V c1 I c1 Z cc 0 I c 2 Z cc 2 I c 0 Z cc 1 a I a 1 Z aa 0 a 2 I a 2 a 2 Z aa 2 I a 0 a Z aa1 a I a 1 Z aa 0 a I a 2 Z aa 2 a I a 0 Z aa1 orden 1 (43) La comparación de las ecuaciones (43) y (39) muestra que V c 1 es igual en magnitud a V a 1 y está 120 grados adelante de V a 1 , requisito necesario para que V a 1 , V b1 y V c 1 formen un sistema de tensiones de secuencia positiva. De manera semejante a la delineada anteriormente, se puede demostrar que V a 2 en la ecuación (40) es miembro de un sistema balanceado de tensiones de secuencia negativa, V a2 , V b2 y V c2 . V a 2 I a1 Z aa1 I a 2 Z aa 0 I a 0 Z aa 2 orden 2 V b 2 I b1 Z bb1 I b 2 Z bb 0 I b 0 Z bb 2 a 2 I a 1 a 2 Z aa 1 a I a 2 Z aa 0 I a 0 a Z aa 2 orden 2 a I a 1 Z aa 1 a I a 2 Z aa 0 a I a 0 Z aa 2 V c 2 I c1 Z cc1 I c 2 Z cc 0 I c 0 Z cc 2 a I a 1 a Z aa 1 a 2 I a 2 Z aa 0 I a 0 a 2 Z aa 2 orden 2 a 2 I a 1 Z aa 1 a 2 I a 2 Z aa 0 a 2 I a 0 Z aa 2 En la misma forma anterior, se puede demostrar que V a 0 de la ecuación (41), forma parte de un sistema de tensiones de secuencia cero. V a 0 I a1 Z aa 2 I a 2 Z aa1 I a 0 Z aa 0 orden 0 V b 0 I b1 Z bb 2 I b 2 Z bb1 I b 0 Z bb 0 a 2 I a 1 a Z aa 2 a I a 2 a 2 Z aa 1 I a 0 Z aa 0 I a 1 Z aa 2 I a 2 Z aa 1 I a 0 Z aa 0 V a 0 (orden 0) V c 0 I c 1 Z cc 2 I c 2 Z cc 1 I c 0 Z cc 0 a I a 1 a 2 Z aa 2 a 2 I a 2 a Z aa 1 I a 0 Z aa 0 I a 1 Z aa 2 I a 2 Z aa 1 I a 0 Z aa 0 V a0 (orden 0) En forma matricial las ecuaciones (39), (40) y (41), se pueden escribir como, V a 1 Z aa 0 V a 2 Z aa 1 V a 0 Z aa 2 Z aa 2 Z aa 0 Z aa 1 Z aa 1 I a 1 Z aa 2 I a 2 Z aa 0 I a 0 263 ELECTROTECNIA III-264 Despejando de la ecuación anterior a las corrientes tenemos, I a1 Z aa 0 I a 2 Z aa 1 Z I a 0 aa 2 Z aa 2 Z aa 0 Z aa 1 Z aa 1 Z aa 2 Z aa 0 1 V a 1 V a 2 V a 0 Si se expresan las corrientes de línea desbalanceadas en términos de sus componentes simétricas, tenemos que la corriente en el conductor del neutro es, I I I I N I a 1 I a 2 I a 0 I b1 I b 2 I b 0 I c 1 I c 2 I c 0 a1 I b1 I c 1 a2 I b2 I c2 a0 I b0 I c 0 3 I a0 Ya que la suma de los términos de secuencia positiva y de secuencia negativa son iguales a cero. Puesto que para un circuito trifilar no se puede obtener la componente de secuencia cero de la tensión el neutro, por medio de las componentes simétricas de las tensiones de línea, ya que V ab 0 0 , entonces haciendo uso de las ecuaciones (39) y (40), y considerando que en este tipo de circuitos no se tiene corriente de secuencia cero, esto es I a 0 0 , tenemos V a1 I a1 Z aa 0 I a 2 Z aa 2 V a 2 I a1 Z aa1 I a 2 Z aa 0 Resolviendo, en forma matricial, las ecuaciones anteriores tenemos, I a 1 Z aa 0 I a 2 Z aa 1 1 Z aa 2 V a 1 Z aa 0 V a 2 Utilizando la ecuación (41) y considerando que I a 0 0 , tenemos V a 0 I a1 Z aa 2 I a 2 Z aa1 De donde las tensiones al neutro en función de las componentes simétricas son, V AN V a 1 V BN A V a 2 V CN V a 0 264 ELECTROTECNIA III-265 Y las corrientes de línea son, I A I a1 I B A I a2 I C I a 0 Ejemplo 6-16. Obtenga: a) las tensiones de fase y b) las corrientes de una carga desbalanceada conectada en Z A 10, 00 / 30, 00 , Z B 10, 00 / 30, 00 y estrella de tres hilos, con impedancias iguales a, Z C 8,00 / 0,0 0 , alimentada de una fuente asimétrica, con secuencia de fases ABC, con tensiones de línea de V AB 120,0 / 0,00 V , V BC 80,0 / 90,00 V y V CA 144,2 / 146,3 0 V . SOLUCIÓN. Las componentes simétricas de las tensiones de línea son, V ab1 V AB 120, 0 / 0, 0 111, 7 / 18,1 -1 1 V ab 2 A V BC A 80, 0 / 90, 0 37, 3 / 68, 3 144, 2 / 146, 3 0 V ab 0 V CA V ab1 111,7 / 18,10 V , V ab 2 37, 3 / 68, 30 V y V ab0 0 Las componentes simétricas de secuencia positiva y negativa de las tensiones de fase son, V a1 V a2 Vab1 3 Vab 2 3 / ab1 30, 0 111, 7 / ab 2 30, 0 37, 3 3 3 / 18,1 30, 0 64, 5 / 11, 9 0 V / 68, 3 30, 0 21, 5 / 38, 3 0 V Las componentes simétricas de las impedancias son, 10, 00 / 30, 0 3,11 / 60, 0 Z aa 1 Z A Z A -1 Z A 1 10, 00 / 30, 0 2, 67 / 120, 0 aa 2 B 8, 00 / 0, 0 8, 44 / 0, 0 Z aa 0 Z C Las corrientes de secuencia positiva , negativa y cero son, I a 1 Z aa 0 I a 2 Z aa1 1 1 Z aa 2 V a 1 8,44 / 0,0 2,67 / 120,0 64,5 / 11,9 6,93 / 17,9 Z aa 0 V a 2 3,11/ 60,0 8,44 / 0,0 21,5 / 38, 3 3, 29 / 88, 2 265 ELECTROTECNIA III-266 I a1 6,93 / 17,90 A , I a 2 3, 29 / 88, 20 A e I a 0 0 La componente de secuencia cero de las tensiones de fase se obtiene de la ecuación, V a 0 I a1 Z aa 2 I a 2 Z aa1 6, 93 / 17, 9 2, 67 / 120, 0 3, 29 / 88, 2 3,11/ 60, 0 14, 22 / 68, 80 V a) Las tensiones de fase son, V AN V a 1 64, 5 / 11, 9 86, 2 / 8, 9 V BN A V a 2 A 21, 5 / 38, 3 37, 3 / 158, 8 14, 22 / 68, 8 75, 2 / 117, 6 V CN V a 0 V AN 86, 2 / 8,90 V , V BN 37, 3 / 158,80 V y V CN 75, 2 / 117,60 V b) Las corrientes son, I A I a1 6, 93 / 17, 9 8, 62 / 39, 0 I B A I a 2 A 3, 29 / 88, 2 3, 74 / 128, 8 9, 40 / 117, 6 0 I C I a 0 I A 8,62 / 39,00 A , I B 3,74 / 128,80 A e I C 9,40 / 117,60 A 6. APLICACIÓN DE LAS COMPONENTES SIMÉTRICAS A LAS CARGAS CON ACOPLAMIENTO MAGNÉTICO ENTRE FASES. Si las tres fases (incluyendo los conductores de la línea) tienen un acoplamiento magnético de la clase mostrada en la figura 266 ELECTROTECNIA III-267 IA a Z AA Z AB Z CA IB b IC Z BB Z BC ZC C c FIGURA NÚMERO 11. La caída de tensión en la fase A debida al acoplamiento magnético con las fases B y C es V Am I B Z AB I C Z CA (44) donde el subíndice m designa el hecho de que esta caída de tensión no incluye la caída de tensión de la auto impedancia a saber, I A Z AA . Si está involucrado un acoplamiento magnético simple Z AB j X AB j M AB (45) Z BC j X BC j M BC (46) Z CA j X CA j M CA (47) Los signos de las reactancias mutuas se definen por los sentidos fijados al flujo de la corriente y los modos de embobinar las bobinas acopladas mutuamente. La caída de tensión en la impedancia de la fase A, debida a la auto impedancia de esta fase, será llamada V AA y la caída de tensión total en la fase A, entonces es V an V AA V Am I A Z AA I B Z AB I C Z CA (48) En forma similar las caídas de tensión en las fases B y C son, V bn I B Z BB I A Z AB I C Z BC I A Z AB I B Z BB I C Z BC (49) V cn I C Z CC I A Z CA I B Z BC I A Z CA I B Z BC I C Z CC (50) De donde la matriz de impedancias de secuencias es, 267 ELECTROTECNIA III-268 Z AA Z S A 1 Z F A A 1 Z BA Z CA Z AB Z BB Z CB Z AC Z BC A Z CC (51) El vector de tensiones de componentes simétricas es, V a 1 V an V S V a 2 A 1 V bn V a 0 V cn Y el vector de corrientes de componentes simétricas es, I a1 1 I S I a2 Z S V S I a 0 Las corrientes de línea son, I A I a1 I L I B A I S A I a2 I C I a 0 La corriente en el conductor del neutro es, I N 3 I a0 La potencia compleja del sistema es, * * * S 3V a 1 I a 1 3 V a 2 I a 2 3 V a 0 I a 0 Ejemplo 6-17. Obtenga: a) las corrientes de fase y b) la potencia compleja de una carga balanceada con Z A Z B Z C 10, 00 / 36, 90 y Z AB Z BC Z CA 2,00 / 90,0 0 , cuando se alimenta con una fuente simétrica de 120,0 V por fase. SOLUCIÓN. La matriz de impedancias de secuencia es, 268 ELECTROTECNIA III-269 Z AA Z S A Z BA Z CA -1 10, 00 / 36, 9 2, 00 / 90, 0 2, 00 / 90, 0 Z AC 1 Z BC A = A 2, 00 / 90, 0 10, 00 / 36, 9 2, 00 / 90, 0 A 2, 00 / 90, 0 2, 00 / 90, 0 10, 00 / 36, 9 Z CC Z AB Z BB Z CB 11, 31 / 45, 0 0 0 = 0 11, 31 / 45, 0 0 0 0 8, 24 / 14,1 El vector de tensiones de componentes simétricas es, V a 1 V an 120, 0 / 0, 0 120, 0 / 0, 0 -1 -1 1 V S V a 2 A V N A V bn A 120, 0 / 120, 0 0 120, 0 / 240, 0 0 V V a 0 cn El vector de corrientes de componentes simétricas es, 1 I a1 11, 31 / 45, 0 120, 0 / 0, 0 0 0 1 I S I a2 Z S V S 0 11, 31 / 45, 0 0 0 0 0 8, 24 / 14,1 0 I a 0 10, 61 / 45, 0 0 0 El vector de las corrientes de línea es, I A I a1 10, 61 / 45, 0 10, 61 / 45, 0 10, 61 / 165, 0 I L I B A I S A I a 2 A 0 0 10, 61 / 285, 0 I C I a 0 De donde las corrientes de línea son, I A 10,61/ 45,00 A ; I B 10,61/ 165,00 A ; I C 10,61/ 285,00 A La potencia compleja es, * * * S 3 V a 1 I a 1 3 V a 2 I a 2 3V a 0 I a 0 3 120, 0 / 0, 0 10, 61/ 45, 0 0 0 3, 82 103 / 45, 00 VA 269 ELECTROTECNIA III-270 Ejemplo 6-18. Sea una carga Z A 10,00 60,00 , Z CA 2,00 / 90,0 0 , conectada a una desbalanceada Z B 10,00 60,00 , Z C 5,00 0,00 y Z AB Z BC con fuente simétrica de 120,0 V por fase. Obtenga: a) las corrientes de línea y del conductor del neutro, así como b) la potencia compleja. SOLUCIÓN. La matriz de las impedancias de secuencia es, Z AA Z S A Z BA Z CA -1 Z AB Z BB Z CB 10, 00 / 60, 0 2, 00 / 90, 0 2, 00 / 90, 0 Z AC 1 Z BC A = A 2, 00 / 90, 0 10, 00 / 60, 0 2, 00 / 90, 0 A 2, 00 / 90, 0 2, 00 / 90, 0 Z CC 5, 00 / 0, 0 5, 39 / 21, 8 5, 00 / 120, 0 5, 00 / 60, 0 5, 00 / 60, 0 5, 39 / 21, 8 5, 00 / 120, 0 5, 00 / 120, 0 5, 00 / 60, 0 6, 40 / 38, 7 El vector de tensiones de componentes simétricas es, V a 1 120, 0 / 0, 0 120, 0 / 0, 0 V S V a 2 A -1 V N A 1 120, 0 / 120, 0 0 0 120, 0 / 240, 0 V a 0 El vector de corrientes de componentes simétricas es, I a1 1 I S I a2 Z S V S I a 0 5, 39 / 21, 8 5, 00 / 120, 0 5, 00 / 60, 0 5, 00 / 60, 0 5, 39 / 21, 8 5, 00 / 120, 0 5, 00 / 120, 0 5, 00 / 60, 0 6, 40 / 38, 7 1 120, 0 / 0, 0 0 0 12, 60 / 11, 4 11, 52 / 143, 4 2,14 / 28, 2 a) El vector de las corrientes de línea es, I A 12, 60 / 11, 4 9, 72 / 59,1 I L I B A I S A 11, 52 / 143, 4 13, 65 / 72, 4 2,14 / 28, 2 24, 6 / 98,1 I C De donde las corrientes de línea son, 270 ELECTROTECNIA III-271 I A 9,72 / 59,10 A ; I B 13,65 / 72,40 A ; I C 24,6 / 98,10 A Y la corriente en el conductor del neutro es, I N 3 I a 0 3 2,14 / 28, 2 6,42 / 28, 20 A b) La potencia compleja es, * * * S 3 V a 1 I a 1 3 V a 2 I a 2 3V a 0 I a 0 3 120, 0 / 0, 0 12, 60 / 11, 4 0 0 4, 54 103 / 11, 40 VA Ejemplo 6-19. Se tiene una carga balanceada conectada en estrella con ZA = ZB = ZC = 10,00 /36,90 , con impedancias mutuas iguales a ZAB = ZBC = ZCA = 2,00 /-90,00 , alimentada con una fuente asimétrica con tensiones de V an 100,0 / 30,00 V, V bn 50,0 / 90,00 V y V cn 86,6 / 180,0 0 V . Obtenga: a) las corrientes de línea y del conductor del neutro; b) la potencia compleja del sistema. SOLUCIÓN. La matriz de las impedancias de secuencia es, Z AA Z S A -1 Z F A = A -1 Z BA Z CA Z AB Z BB Z CB 10, 00 / 36, 9 2, 00 / 90, 0 2, 00 / 90, 0 Z AC Z BC A = A 1 2, 00 / 90, 0 10, 00 / 36, 9 2, 00 / 90, 0 A 2, 00 / 90, 0 2, 00 / 90, 0 10, 00 / 36, 9 Z CC 11, 31 / 45, 0 0 0 0 11, 31 / 45, 0 0 0 0 8, 24 / 14,1 El vector de las componentes simétricas de las tensiones es, V a 1 V an 100, 0 / 30, 0 76, 4 / 40, 9 -1 -1 V S V a 2 A V bn A 50, 0 / 90, 0 28, 9 / 0, 0 86, 6 / 180, 0 0 V a 0 V cn El vector de corrientes de las componentes simétricas es, 1 I a1 11, 31 / 45, 0 76, 4 / 40, 9 6, 76 / 4,1 0 0 1 I S I a2 Z S V S 0 11, 31 / 45, 0 0 28, 9 / 0, 0 2, 56 / 45, 0 0 0 8, 24 / 14,1 0 0 I a 0 a) Las corrientes de línea son, 271 ELECTROTECNIA III-272 I A I a1 6,76 /-4,1 8, 86 / 15, 0 I L I B A I S A I a 2 A 2,56 /-45,0 4, 42 / 135, 0 7, 67 / 135, 0 0 I C I a 0 I A 8,86 / 15,00 A ; I B 4,42 / 135,00 A ; I C 7,67 / 135,00 A La corriente en el conductor del neutro es, I N 3 I a0 0 b) La potencia compleja es, * * * S 3 V a 1 I a 1 3 V a 2 I a 2 3V a 0 I a 0 3 76, 4 / 40, 9 6, 76 / 4,1 3 28, 9 / 0, 0 2, 56 / 45, 0 0 1, 771 103 / 45, 00 VA Ejemplo 6-20. Obtenga: a) las corrientes de línea y del conductor del neutro, y b) la potencia compleja del sistema, de una carga desbalanceada conectada en estrella de valores ZA = 9,52 /-62,80 , ZB = 8,16 /56,40 , ZC = 6,22 /0,00 , con impedancias mutuas de ZAB = ZBC = ZCA = 2,24 /-90,00 , alimentada de una fuente con tensiones asimétricas iguales a V an 263 / 10,50 V , V bn 386 / 142,50 V y V cn 200 /118,4 0 V . SOLUCIÓN. La matriz de las impedancias de secuencia es, Z AA Z S A -1 Z F A = A -1 Z BA Z CA Z AB Z BB Z CB 9, 52 / 62, 8 2, 24 / 90, 0 2, 24 / 90, 0 Z AC Z BC A = A 1 2, 24 / 90, 0 8,16 / 56, 4 2, 24 / 90, 0 A 2, 24 / 90, 0 2, 24 / 90, 0 Z CC 6, 22 / 0, 0 5, 30 / 18, 5 3, 82 / 64, 9 5, 01 / 117, 4 5, 01 / 117, 4 5, 30 / 18, 5 3, 82 / 64, 9 3, 82 / 64, 9 5, 01 / 117, 4 7,12 / 45, 0 El vector de las componentes simétricas de las tensiones es, V a 1 V an 263 / 10, 5 280 / 13, 9 1 -1 V S V a 2 A V bn A 386 / 142, 5 64, 7 / 57, 8 200 / 118, 4 59, 5 / 143, 2 V a 0 V cn El vector de corrientes de las componentes simétricas es, 272 ELECTROTECNIA III-273 1 I a1 5, 30 / 18, 5 3, 82 / 64, 9 5, 01 / 117, 4 280 / 13, 9 1 I S I a 2 Z S V S 5, 01 / 117, 4 5, 30 / 18, 5 3, 82 / 64, 9 64, 7 / 57, 8 3, 82 / 64, 9 5, 01 / 117, 4 7,12 / 45, 0 59, 5 / 143, 2 I a 0 24, 4 / 29, 7 21, 7 / 3, 4 22, 0 / 133, 5 a) Las corrientes de línea son, I A I a1 24,4 /-29,7 28, 2 / 10, 5 I L I B A I S A I a 2 A 21,7 /3,4 52, 8 / 155, 7 22,0 /133,5 32, 6 / 140, 0 I C I a 0 I A 28, 2 / 10,50 A ; I B 52,8 / 155,70 A ; I C 32,6 / 140,00 A La corriente en el conductor del neutro es, I N 3 I a 0 3 22,0 / 133,5 66,0 / 133,50 A b) La potencia compleja es, * * * S 3 V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 280 / 13, 9 24, 4 / 29, 7 3 64, 7 / 57, 8 21, 7 / 3, 4 3 59, 5 / 143, 2 22, 0 / 133, 5 26,1 103 / 29, 7 0 VA Aplicación a cargas trifilares con cargas desbalanceadas. En el caso de tener cargas trifilares desbalanceadas con impedancias mutuas es necesario recurrir al procedimiento en el que interviene la regla de la secuencia. En las ecuaciones números (39), (40) y (41) se tienen las ecuaciones para las caídas de tensión debidas a las auto impedancias, quedando el problema de hacer intervenir las caídas por inductancias mutuas, para adicionarlas a las ecuaciones mencionadas. Ahora se dará la solución del problema de expresar las caídas de tensión en las impedancias de la ecuación (48), en función de componentes simétricas. Es obvio que I A , I B e I C se pueden expresar en función de las componentes simétricas de cualquiera de estas corrientes, y que ZAA se puede descomponer en componentes simétricas, si son conocidas las otras auto impedancias, ZBB y ZCC. En este aspecto 273 ELECTROTECNIA III-274 Z aa 1 Z AA Z A -1 Z aa 2 BB Z aa 0 Z CC La caída de tensión de la auto impedancia de la fase A se puede formular en función de las componentes simétricas con la regla de la secuencia. V AA V aa1 V aa 2 V aa 0 (52) donde V aa 1 I a 1 Z aa 0 I a 2 Z aa 2 I a 0 Z aa 1 (53) V aa 2 I a 1 Z aa 1 I a 2 Z aa 0 I a 0 Z aa 2 (54) V aa 0 I a 1 Z aa 2 I a 2 Z aa 1 I a 0 Z aa 0 (55) Descomponiendo las impedancias mutuas Z AB , Z BC y Z CA en componentes simétricas que se puedan asociar ventajosamente con las corrientes I a 1 , I a 2 e I a 0 , para justificar la presencia de I B Z AB e I C Z CA en la ecuación (48). En esta etapa del desarrollo es un tanto difícil decir cuál de las tres impedancias mutuas se debe considerar como la base de las impedancias mutuas. Resulta que las componentes simétricas de ZBC se prestan a ser asociadas del modo más conveniente con I a 1 , I a 2 e I a 0 . Descomponiendo las impedancias mutuas en componentes simétricas, con ZBC como base, se obtiene Z bc 1 Z BC Z A -1 Z bc 2 CA Z bc 0 Z AB (56) En términos de componentes simétricas las caídas por impedancias mutuas son, V Am I B Z AB I C Z CA a 2 I a1 a I a 2 I a 0 a Z bc 1 a 2 Z bc 2 Z bc 0 a I a1 a 2 I a 2 I a 0 a 2 Z bc 1 a Z bc 2 Z bc 0 (57) Si se efectúan las multiplicaciones indicadas en la ecuación (57) aparecen dieciocho tensiones componentes. Estas componentes se pueden agrupar en términos de secuencia positiva, negativa y cero, de acuerdo con la regla de la secuencia. Por ejemplo, las tensiones componentes de primer orden son: V am1 I a1 a2 Z bc 0 I a 2 Z bc 2 I a 0 a Zbc1 I a1 a Zbc 0 I a 2 Z bc 2 I a 0 a2 Z bc1 (58) Si en la ecuación anterior se hace una reagrupación de los términos semejantes, se obtiene V am 1 I a 1 Z bc 0 a 2 a I a 2 Z bc 2 1 1 I a 0 Z bc1 a + a 2 I a 1 Z bc 0 2 I a 2 Z bc 2 I a 0 Z bc1 (59) 274 ELECTROTECNIA III-275 Las tensiones componentes de segundo orden o de secuencia negativa son, V am 2 a 2 I a 1 a Z bc 1 a I a 2 Z bc 0 I a 0 a 2 Z bc 2 a I a 1 a 2 Z bc 1 a 2 I a 2 Z bc 0 I a 0 a Z bc 2 I a 1 Z bc 1 a 3 a 3 I a 2 Z bc 0 a + a 2 I a 0 Z bc 2 a 2 a 2 I a 1 Z bc 1 I a 2 Z bc 0 I a 0 Z bc 2 (60) Las tensiones componentes de orden cero o secuencia cero son, V am 0 a 2 I a 1 a 2 Z bc 2 a I a 2 a Z bc 1 I a 0 Z bc 0 a I a 1 a Z bc 2 a 2 I a 2 a 2 Z bc 1 I a 0 Z bc 0 I a 1 Z bc 2 a 4 a 2 I a 2 Z bc 1 a 2 + a 4 2 I a 0 Z bc 0 I a 1 Z bc 2 I a 2 Z bc 1 2 I a 0 Z bc 0 (61) Las ecuaciones (59), (60) y (61) contienen todas las dieciocho tensiones componentes representadas en la ecuación (57) y estas ecuaciones se pueden combinar sistemáticamente con las ecuaciones (53), (54) y (55) para dar las componentes de secuencia positiva, negativa y cero de la tensión completa de fase a saber, V AN V AA V Am . Sumando miembro a miembro las ecuaciones (48) y (59), las ecuaciones (49) y (60), y las ecuaciones (50) y (61), resulta V a 1 V aa 1 V am 1 I a1 Z aa 0 I a 2 Z aa 2 I a 0 Z aa 1 I a1 Z bc 0 2 I a 2 Z bc 2 I a 0 Z bc 1 I a1 Z aa 0 Z bc 0 I a 2 Z aa 2 2 Z bc 2 I a 0 Z aa 1 Z bc1 (62) V a 2 V aa 2 V am 2 I a1 Z aa 1 I a 2 Z aa 0 I a 0 Z aa 2 2 I a1 Z bc1 I a 2 Z bc 0 I a 0 Z bc 2 I a1 Z aa 1 2 Z bc1 I a 2 Z aa 0 Z bc 0 I a 0 Z aa 2 Z bc 2 (63) V a 0 V aa 0 V am 0 I a 1 Z aa 2 I a 2 Z aa1 I a 0 Z aa 0 I a 1 Z bc 2 I a 2 Z bc1 I a 0 Z bc 0 I a1 Z aa 2 Z bc 2 I a 2 Z aa1 Z bc1 I a 0 Z aa 0 2 Z bc 0 (64) El grupo anterior de ecuaciones representa un instrumento muy potente en el análisis de circuitos, por que con la ayuda del mismo se puede manejar cualquier grado de desbalance y cualquier grado de acoplamiento capacitivo o magnético, a base de componentes simétricas. Las ecuaciones (62), (63) y (64) son particularmente útiles para incluir en los cálculos las caídas de tensión reactivas de las líneas de transmisión, porque estas caídas de tensión reactivas resultan del acoplamiento mutuo entre los conductores de las líneas. Estas ecuaciones también son útiles para el cálculo de la impedancia mutua del cuarto hilo de un sistema trifásico de cuatro hilos. Las ecuaciones (62), (63) y (64) se pueden expresar en forma matricial como, V a 1 Z Z aa 0 bc 0 V a 2 Z aa 1 2 Z bc 1 V a 0 Z aa 2 Z bc 2 Z aa 2 2 Z bc 2 Z aa1 Z bc1 I a1 Z aa 0 Z bc 0 Z aa 2 Z bc 2 I a 2 Z aa1 Z bc1 Z aa 0 2 Z bc 0 I a 0 (65) 275 ELECTROTECNIA III-276 Si las corrientes son los valores desconocidos, entonces estas se pueden determinar con la ecuación matricial siguiente: I a1 Z Z aa 0 bc 0 I a 2 Z aa 1 2 Z bc 1 Z Z aa 2 bc 2 I a 0 Z aa 2 2 Z bc 2 Z aa1 Z bc1 Z aa 0 Z bc 0 Z aa 2 Z bc 2 Z aa1 Z bc1 Z aa 0 2 Z bc 0 1 V a 1 V a 2 (66) V a 0 Recordando que en un circuito trifilar no se puede obtener la componente de secuencia cero de la tensión al neutro, por medio de las componentes simétricas de las tensiones de línea ya que V ab 0 y puesto que no se tiene corriente de secuencia cero, esto es I a 0 0 , entonces las componentes de secuencia positiva y negativa de la tensión al neutro son, V a1 I a1 Z aa 0 Z bc 0 I a 2 Z aa 2 2 Z bc 2 V a 2 I a1 Z aa1 2 Z bc1 I a 2 Z aa 0 Z bc 0 Resolviendo en forma matricial las ecuaciones anteriores, considerando a las corrientes como incógnitas tenemos, I a 1 Z aa Z bc 0 I a 2 Z aa 1 2 Z bc1 Z aa 2 2 Z bc 2 Z aa 0 Z bc 0 1 V a1 (67) V a 2 La componente de secuencia cero de las tensiones al neutro es, V a 0 I a1 Z aa 2 Z bc 2 I a 2 Z aa1 Z bc1 (68) De donde las tensiones al neutro en función de las componentes simétricas son, V AN V a 1 V BN A V a 2 V CN V a 0 y las corrientes de línea son, I A I a1 I B A I a2 I C I a 0 276 ELECTROTECNIA III-277 Ejemplo 6-21. Se tiene una carga desbalanceada con ZA = 10,00 /45,00 , Z B 8, 00 / 30, 0 y 0 Z C 5,00 / 0,0 0 , e impedancias mutuas de ZAB = ZBC = ZCA = 2,00 asimétrica con tensiones de línea de /-90,00 , alimentada con una fuente V ab 382 / 23,80 V , V bc 412 / 161, 20 V y V ca 290/ 82,0 0 V . Obtenga: a) las corrientes de línea y b) las tensiones de fase o al neutro y c) la potencia compleja del sistema. SOLUCIÓN. El vector matriz de las componentes simétricas de las tensiones de línea es, V ab1 V ab 382 / 23, 8 358 / 34, 2 1 -1 V SL V ab 2 A V bc A 412 / 161, 2 71, 3 / 41, 3 290 / 82, 0 0 V ab 0 V ca Las componentes simétricas de secuencia positiva y negativa de las tensiones de fase son, V a1 Vab1 V a2 3 / ab1 30, 0 Vab 2 3 358 / ab 2 30, 0 3 / 34, 2 30, 0 207 / 64, 20 V 71, 3 3 / 41, 3 30, 0 41, 2 / 71, 30 V Las componentes simétricas de las impedancias de fase son, 10, 00 / 45, 0 3, 89 / 66, 9 Z aa 1 Z A Z A -1 Z A -1 8, 00 / 30, 0 2, 59 / 107, 7 aa 2 B 5, 00 / 0, 0 6, 42 / 9, 2 Z aa 0 Z C Las componentes simétricas de las impedancias mutuas son, 2, 00 / 90, 0 0 Z bc 1 Z BC Z A -1 Z A -1 2, 00 / 90, 0 0 bc 2 CA 2, 00 / 90, 0 2, 00 / 90, 0 Z bc 0 Z AB Las corrientes de secuencia positiva, negativa y cero son, I a 1 Z aa 0 Z bc 0 I a 2 Z aa1 2 Z bc1 Z aa 2 2 Z bc 2 Z aa 0 Z bc 0 1 V a 1 V a 2 Donde, Z aa 0 Z bc 0 6, 42 / 9, 2 2, 00 / 90, 0 7, 02 / 25, 50 277 ELECTROTECNIA III-278 Z aa 2 2 Z bc 2 2, 59 / 107, 7 0 2, 59 / 107, 7 0 Z aa 1 2 Z bc1 3, 89 / 66, 9 0 3, 89 / 66, 90 Sustituyendo en la ecuación de las corrientes de secuencia positiva y negativa tenemos, 1 I a1 7, 02 / 25, 5 2, 59 / 107, 7 207 / 64, 2 27, 7 / 78, 6 I a 2 3, 89 / 66, 9 7, 02 / 25, 5 41, 2 / 71, 3 15, 76 / 121,1 I a0 0 La componente de secuencia cero de las tensiones de fase es, V a 0 I a 1 Z aa 2 Z bc 2 I a 2 Z aa 1 Z bc1 27, 7 / 78, 6 2, 59 / 107, 7 0 15, 76 / 121,1 3, 89 / 66, 9 0 26, 4 / 85, 7 0 V a) Las corrientes de línea son, I A I a1 27,7 /-78,6 13, 92 / 101, 0 I B A I a 2 A 15,76 /121,1 34, 2 / 171, 7 41, 0 / 27, 0 0 I C I a 0 I A 13,92 / 101,00 A ; I B 34, 2 / 171,70 A ; I C 41,0 / 27,00 A b) Las tensiones de fase o al neutro son, V AN V a 1 207 /-64,2 160, 4 / 49, 0 V BN A V a 2 A 41,2 /71,3 247 / 172, 2 26,4 /85,7 221 / 48, 9 V CN V a 0 V AN 160,4 / 49,00 V ; V BN 247 / 172, 20 V ; V CN 221/ 48,90 V c) La potencia compleja del sistema es, * * * S 3 V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 207 / 64, 2 27, 7 / 78, 6 3 41, 2 / 71, 3 15, 76 / 121,1 0 18,13 10 3 / 8, 90 VA 278 ELECTROTECNIA III-279 7. EJERCICIOS. Ejercicio 6-1. En la figura se representa el esquema de los devanados de un generador. El devanado B del mismo se encuentra defectuoso a tal grado que no suministra tensión; la tensión de fase VF es igual a 127,0 V. A 60,00 B N 60,00 C Determinar el coeficiente de asimetría. Se llama coeficiente de asimetría a la relación de las componentes de tensión de secuencia negativa, a las componentes de secuencia positiva. SOLUCIÓN. Tomando como referencia a la tensión V AN , las tensiones del generador son, V AN 127,0 / 90,00 V ; V BN 0 y V CN 127,0 / 30,00 V Las componentes simétricas de secuencia negativa y positiva de las tensiones son, V a 1 V AN 127, 0 / 90, 0 42, 3 / 150, 0 V S V a 2 A 1 V BN A 1 0 84, 7 / 90, 0 127, 0 / 30, 0 42, 3 / 30, 0 V a 0 V CN V a1 42, 3 / 150,00 V ; V a 2 84,7 / 90,00 V ; V a 0 42, 3 / 30,00 V De donde el coeficiente de asimetría es, k Va 2 84, 7 2, 00 Va 1 42, 3 Ejercicio 6-2. En un sistema trifásico asimétrico son conocidas las componentes simétricas de las corrientes de línea: I b1 =10,00 A , componente de secuencia positiva de la corriente de la fase B, I c 2 = 5,00 A , componente de secuencia negativa de la corriente de la fase C; el ángulo entre ellas es de 30,0 0; como se muestra en la figura. Considere la componente de secuencia cero igual a 0. Determinar las corrientes de línea del sistema. 279 ELECTROTECNIA III-280 I b1 I c2 30,00 SOLUCIÓN. Los diagramas fasoriales de las componentes simétricas de las corrientes, tomando a I b 1 como referencia son, I a1 acb abc I a2 I c2 30,00 I b1 I b2 I c1 De donde, I a1 10,00 / 120,00 A ; I a 2 5,00 / 150,00 A Las corrientes de línea son, I A I a1 10, 00 / 120, 0 14, 55 / 129, 9 I L I B A I S A I a 2 A 5, 00 / 150, 0 11,18 / 26, 6 6, 20 / 96, 2 0 I C I a 0 De donde las corrientes de línea son, I A 14,55 / 129,90 A ; I B 11,18 / 26,60 A e I C 6, 20 / 96, 20 A Ejemplo 6-3. En el banco de transformadores estrella/delta (Y/) mostrado en la figura, el funcionamiento de los tres transformadores y las polaridades de los devanados son tales que, 280 ELECTROTECNIA III-281 V A' B ' nV AN (transformador A) V B 'C ' nV BN V C ' A' nV CN (transformador B) (transformador C ) en donde n es la relación de transformación de tensión de los transformadores. Las tensiones de línea no son simétricas, al extremo que V ab1 4,00 103 / 60,00 V y V ab 2 1,000 103 / 90,00 V . ( V ab1 y V ab 2 están, por supuesto, formuladas con respecto a un eje común de referencia). Se supone que la secuencia de fases de las tensiones de línea es abc y V an 0 se toma como cero. a) Encuentre la magnitud y la posición fasorial de V AB ,V BC y V CA . b) Si la relación de transformación de los transformadores es 10, encuentre la magnitud y posición fasorial de V A ' B ' ,V B ' C ' y V C ' A ' . a (TC) Fuente (TA) (TC) Secundario (TA) c’ n (TB) c a’ (TB) b’ b SOLUCIÓN. a) Las magnitudes y las posiciones fasoriales de las tensiones de línea son, V AB V ab1 4, 00 103 / 60, 0 4, 89 103 / 65, 9 V L V BC A V SL A V ab 2 A 1, 000 10 3 / 90, 0 3,17 10 3 / 170, 9 4,12 103 / 74, 0 0 V CA V ab 0 De donde, V AB 4,89 103 / 65,90 V , V BC 3,17 103 / 170,90 V y V CA 4,12 103 / 74,00 V b) Las componentes simétricas de las tensiones al neutro, en el primario son, V an1 V ab1 3 / 30, 0 4, 00 103 / 60, 0 3 / 30, 0 2, 31 10 3 / 90, 0 0 V 281 ELECTROTECNIA III-282 V an 2 V ab 2 3 / 30, 0 1, 000 103 / 90, 0 3 / 30, 0 577 / 60, 00 V V an 0 0 Las tensiones al neutro en el primario son, V AN V an1 2, 31 103 / 90, 0 2, 82 103 / 84,1 V N V BN A V S A V an 2 A 577 / 60, 0 2, 38 10 3 / 136, 0 1, 833 103 / 39,1 0 V CN V an 0 V AN 2,82 103 / 84,10 V ; V BN 2, 38 103 / 136,00 V y V CN 1,833 10 3 / 39,10 V Las tensiones de línea en el secundario son, V A' B ' nV AN 10 2,82 103 / 84,1 28, 2 103 / 84,10 V V B 'C ' nV BN 10 2, 38 103 / 136,0 23,8 103 / 136,00 V V C ' A' nV CN 10 1,833 103 / 39,1 18, 33 103 / 39,10 V Ejercicio 6-4. Una fuente trifásica simétrica de cuatro hilos, con una tensión de fase de 289 V, cuya secuencia de fases es ABC, alimenta una carga conectada en estrella, que toma corrientes cuyas componentes simétricas son, I a1 37,0 / 6, 30 A ; I a 2 19, 26 / 4, 30 A I a 0 27,7 / 168,50 A ; Tomando como referencia a la tensión V AN , calcular la potencia compleja suministrada por cada una de las componentes simétricas y determinar la potencia compleja total consumida. SOLUCIÓN. Puesto que se tiene una fuente simétrica, la tensión solo tiene componentes de secuencia positiva, de donde V a1 289 / 0,00 V ; V a2 0 V a0 0 ; La potencia compleja suministrada por cada una de las componentes simétricas es * S a1 3V a1 I a1 3 289 / 0, 0 37, 0 / 6, 3 32,1 103 / 6, 30 VA * * S a 2 3V a 2 I a 2 0 ; S a 0 3V a 0 I a 0 0 Y la potencia total es 282 ELECTROTECNIA III-283 S S a 1 S a 2 S a 0 32,1 103 / 6, 3 0 0 32,1 103 / 6, 30 VA Ejercicio 6-5. Una carga desbalanceada de tres hilos, conectada en estrella, alimentada de una fuente cuya secuencia de fases es ABC, tiene las tensiones de fase y las corrientes de fase siguientes: V AN 100, 2 / 32,80 V ; I A 9,82 / 44,10 A ; V BN 69,1/ 140, 20 V ; V CN 150,0 / 63,50 V I B 13,82 / 129,80 A ; I C 17,56 / 84,10 A Determinar la potencia compleja suministrada por cada una de las componentes simétricas y la potencia compleja total consumida por la carga. SOLUCIÓN. Las componentes simétricas de las tensiones son, V a 1 V AN 100, 2 / 32, 8 97, 4 / 57, 9 V S V a 2 A 1 V N A 1 V BN A 1 69,1 / 140, 2 13,19 / 90, 9 150, 0 / 63, 5 52, 7 / 51, 7 V a 0 V CN V a1 97,4 / 57,90 V ; V a 2 13,19 / 90,90 V ; V a 0 52,7 / 51,70 V Las componentes simétricas de las corrientes son, I a1 I A 9, 82 / 44,1 13, 32 / 29, 2 1 1 1 I S I a 2 A I L A I B A 13, 82 / 129, 8 4, 60 / 175, 7 17, 56 / 84,1 0 I a 0 I C I a1 13, 32 / 29, 20 A ; I a 2 4,60 / 175,70 A ; I a0 0 Las potencias complejas suministradas por las componentes simétricas son * S a1 3V a1 I a1 3 97,4 / 57,9 13, 32 / 29, 2 3,89 103 / 28,7 0 VA * S a 2 3 V a 2 I a 2 3 13,19 / 90, 9 4, 60 / 175, 7 182, 0 / 84, 80 VA * S a 0 3 V a 0 I a 0 0 La potencia total es S S a 1 S a 2 S a 0 3, 89 103 / 28, 7 182, 0 / 84, 8 0 3, 82 10 3 / 26, 2 VA 283 ELECTROTECNIA III-284 Ejercicio 6-6. Tres impedancias iguales de 21,0 /90,00 se conectan en delta como se muestra en la figura. a) Dibujar las redes de secuencia para esta carga y b) calcule las impedancias de secuencia de la carga. 21, 0 / 90, 0 0 La impedancia equivalente en estrella tiene una impedancia de, ZY Z 21, 0 / 90, 0 7, 00 / 90, 00 3 3 a) Las redes de secuencia son, I a1 I a2 + I a0 0 + V a1 Z1 ZY + V a2 Z 2 ZY V a0 ZY Z0 Red de secuencia positiva Red de secuencia negativa Red de secuencia cero b) Las impedancias de secuencia de la carga son, La impedancia de secuencia positiva es, Z 1 Z Y 7, 00 / 0, 00 La impedancia de secuencia negativa es, Z 2 Z Y 7, 00 / 0, 00 La impedancia de secuencia negativa es, Z0 Ejercicio 6-7. Una carga balanceada conectada en estrella se conecta en paralelo con un banco de capacitores balanceado conectado en delta. La carga conectada en estrella tiene una impedancia 284 ELECTROTECNIA III-285 Z Y 3, 00 j4, 00 por fase, y su neutro esta a tierra a través de una reactancia inductiva de X N 2, 00 . El banco de capacitores tiene una reactancia de X C 30,0 por fase. a) Dibuje las redes de secuencia para esta carga y b) calcule las impedancias de secuencia de la carga. SOLUCIÓN. En la figura se muestran las redes de secuencia. En los circuitos de secuencia positiva y negativa, la impedancia de la carga en delta se divide por tres y se coloca en paralelo con la impedancia de la carga conectada en estrella. En la red de secuencia cero la impedancia de la carga conectada en estrella está en serie con tres veces la impedancia del neutro; y la rama correspondiente a la carga en delta está abierta, por lo que por esta no fluye corriente de secuencia cero. I a1 I a2 + I a0 + + j 4,00 V a2 j 4,00 V a0 j 4,00 - j 30,0/3 V a1 3,00 - j 30,0/3 3,00 - j 30,0/3 3,00 3 (j 2,00) Red de secuencia positiva Red de secuencia negativa Red de secuencia cero b) Las impedancias equivalentes de secuencia son, Impedancia equivalente de secuencia positiva, Z j30, 0 3, 00 j4, 00 3 3 Z1 7, 45 / 26, 60 Z j30, 0 ZY 3, 00 j4, 00 3 3 ZY Impedancia equivalente de secuencia negativa, Z 2 Z 1 7, 45 / 26, 60 Impedancia de secuencia cero, Z 0 Z Y 3 Z N 3, 00 j4, 00 3 j2, 00 10, 44 / 73, 3 0 Ejercicio 6-8. Una fuente asimétrica conectada en estrella, con secuencia de fases abc, con tensiones de V an 277 / 0,00 V , V bn 260 / 120,00 V y V cn 295 /115,0 0 V , se aplica a una carga conectada en 285 ELECTROTECNIA III-286 delta balanceada con impedancias por fase de Z 30, 0 / 40, 0 . Las impedancias de las líneas entre la fuente 0 y la carga son de Z L 1, 000 / 85, 0 , cada una. Calcule las corrientes de línea. 0 SOLUCIÓN. La impedancia equivalente conectada en estrella, correspondiente a la conexión delta es, ZY Z 30, 0 / 40, 0 10, 00 / 40, 00 3 3 Las componentes simétricas de las tensiones son, V a 1 V an 277 / 0, 0 277 / 1, 8 1 1 1 V S V a 2 A V n A V bn A 260 / 120, 0 9, 22 / 143, 4 295 / 115, 0 15, 91 / 62,1 V a 0 V cn Estas tensiones se aplican a las redes de secuencia, que contienen las impedancias de la línea y la carga, como se muestra en la figura, I a1 ZL I a2 + V a1 ZL I a0 0 + Z 3 V a2 ZL + Z 3 Red de secuencia positiva Red de secuencia negativa V a0 Z 3 Red de secuencia cero Las corrientes de secuencia son, I a1 277 / 1, 8 V a1 25, 8 / 45, 60 A Z L Z Y 1, 000 / 85, 0 10, 0 / 40, 0 I a2 9, 22 / 143, 4 V a2 0, 859 / 172, 80 A Z L Z Y 1, 000 / 85, 0 10, 0 / 40, 0 I a0 0 De donde las corrientes de línea son, 286 ELECTROTECNIA III-287 I A I a1 25, 8 / 45, 6 25,1 / 46, 8 I L I B A I S A I a 2 A 0, 859 / 172, 8 25, 7 / 163, 7 26, 6 / 73, 7 0 I C I a 0 I A 25,1/ 46,80 A ; I B 25,7 / 163,70 A ; I C 26,6 / 73,70 A Ejercicio 6-9. Una fuente trifásica simétrica, conectada en estrella de cuatro hilos, con una frecuencia de 60,0 Hz, con una secuencia de fases abc, con tensiones de 220/127 V, alimenta una carga como se muestra en la figura, donde la rama A tiene una impedancia de Z A 8, 54 / 62,10 , la rama B tiene una impedancia de Z B 18, 09 / 56, 50 , la rama C tiene una impedancia de Z C 13, 85 / 54, 7 0 . La impedancia de las líneas es de Z L 1,118 / 26, 60 , la impedancia del conductor del neutro es igual a la de las líneas. Determinar: a) Las corrientes de línea y en el conductor del neutro. b) la potencia compleja suministrada por la fuente. Z aA a IA A V an I Nn n c V AN ZA V cn V bn b ZN N Z bB IB Z cC IC ZB B ZC V BN V CN C SOLUCIÓN. Las impedancias de las fases son, Z aa Z aA Z A Z N 1,118 / 26, 6 8, 54 / 62,1 1,118 / 26, 6 10, 44 / 55, 0 0 Z bb Z bB Z B Z N 1,118 / 26, 6 18, 09 / 56, 5 1,118 / 26, 6 20,1 / 53, 3 0 Z cc Z cC Z C Z N 1,118 / 26, 6 13, 85 / 54, 7 1,118 / 26, 6 15, 86 / 50, 9 Z ab Z bc Z ca Z N 1,118 / 26, 60 La matriz de las impedancias de componentes simétricas es, 287 ELECTROTECNIA III-288 Z aa Z S A 1 Z F A A 1 Z ba Z ca Z ab Z bb Z cb Z ac Z bc A Z cc 10, 44 / 55, 0 1,118 / 26, 6 1,118 / 26, 6 Z S A 1 1,118 / 26, 6 20,1 / 53, 3 1,118 / 26, 6 A 1,118 / 26, 6 1,118 / 26, 6 15, 86 / 50, 9 14, 47 / 54, 8 2, 53 / 103,1 3, 06 / 154, 8 3, 06 / 154, 8 14, 47 / 54, 8 2, 53 / 103,1 2, 53 / 103,1 3, 06 / 154, 8 17, 49 / 4 9, 6 El vector de tensiones de componentes simétricas es, V a 1 127, 0 / 0, 0 127, 0 / 0, 0 V S V a 2 A 1 V n A 1 127, 0 / 120, 0 0 127, 0 / 240, 0 0 V a 0 El vector de las corrientes de componentes simétricas es, 1 I a1 14, 47 / 54, 8 2, 53 / 103,1 3, 06 / 154, 8 127, 0 / 0, 0 1 I S I a 2 Z S V S 3, 06 / 154, 8 14, 47 / 54, 8 2, 53 / 103,1 0 2, 53 / 103,1 3, 06 / 154, 8 17, 49 / 49, 6 0 I a 0 9, 46 / 55, 4 2,13 / 78, 6 1, 511 / 41, 9 a) Las corrientes de línea son, I A 9, 46 / 55, 4 12, 90 / 57, 6 I L I B A I S A 2,13 / 78, 6 6, 72 / 176, 9 1, 511 / 41, 9 8, 80 / 68, 9 I C I A 12,90 / 57,60 A ; I B 6,72 / 176,90 A ; I C 8,80 / 68,90 A La corriente en el conductor del neutro es, I N 3 I a 0 3 1,511/ 41,9 4,53 / 41,90 A 288 ELECTROTECNIA III-289 b) La potencia compleja del sistema es, * * * S 3V a1 I a1 3V a 2 I a 2 3V a 0 I a 0 3 127,0 / 0, 0 9, 46 / 55, 4 0 0 3, 60 10 3 / 55, 4 0 VA Ejercicio 6-10. Se tiene una carga desbalanceada conectada en estrella con impedancias de Z A 12, 36 / 62, 50 , Z B 9, 65 / 56, 50 y Z C 6,80 / 12,0 0 , alimentada de una fuente asimétrica con tensiones de V AN 116, 2 / 30, 20 V , V BN 86,4 / 87,80 V y V CN 94,2/179,6 0 V . Calcule: a) las corrientes de línea y del conductor del neutro, b) la potencia compleja del sistema. SOLUCIÓN. El vector matriz de las componentes simétricas de las tensiones es, V a 1 V AN 116, 2 / 30, 2 96, 3 / 40, 0 V S V a 2 A 1 V N A 1 V BN A 1 86, 4 / 87, 8 24, 2 / 13, 4 94, 2 / 179, 6 9, 62 / 70, 7 V a 0 V CN La matriz de impedancias de secuencia es, Z AA Z S A Z F A A Z BA Z CA 1 1 Z AB Z BB Z CB 12, 36 / 62, 5 Z AC 0 0 1 Z BC A A 0 9, 65 / 56, 5 0 A Z CC 0 0 6, 80 / 12, 0 5,92 /4,9 5,96 /109,7 5,18 /69,4 = 5,18 /69,4 5,92 /4,9 5,96 /109,7 5,96 /109,7 5,18 /69,4 5,92 /4,9 Las componentes simétricas de las corrientes son, 1 I a1 5,92 /4,9 5,96 /109,7 5,18 /69,4 96, 3 / 40, 0 1 I S I a 2 Z S V S 5,18 /69,4 5,92 /4,9 5,96 /109,7 24, 2 / 13, 4 5,96 /109,7 5,18 /69,4 5,92 /4,9 9, 62 / 70, 7 I a 0 7, 06 / 53, 7 7, 26 / 64, 8 4, 21 / 80, 8 a) Las corrientes de línea son, I A 7, 06 / 53, 7 9, 41 / 32, 4 I L I B A I S A 7, 26 / 64, 8 8, 96 / 31, 3 4, 21 / 80, 8 13, 86 / 168, 5 I C 289 ELECTROTECNIA III-290 I A 9,41/ 32,40 A ; I B 8,96 / 31, 30 A ; I C 13,86 / 168,50 A La corriente en el conductor del neutro es, I N 3 I a 0 3 4, 21/ 80,80 12,63 / 80,80 A b) La potencia compleja del sistema es, * * * S 3V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 96, 3 / 40, 0 7, 06 / 53, 7 3 24, 2 / 13, 4 7, 26 / 64, 8 3 9, 62 / 70, 7 4, 21 / 80, 8 2, 21 103 / 1, 40 VA Ejercicio 6-11. Se tiene una carga desbalanceada conectada en estrella de tres hilos, con impedancias de Z A 10, 00 / 45, 00 , Z B 8, 00 / 30, 00 y Z C 5,00 / 0,0 0 , alimentada con una fuente asimétrica, con secuencia de fases abc, con tensiones de línea de V AB 382 / 23,80 V , V BC 412 / 161, 20 V y V CA 290 / 82,0 0 V . Obtenga: a) las tensiones de fase y b) las corrientes de línea. SOLUCIÓN. Las componentes simétricas de las tensiones de línea son, V ab1 V AB 382 / 23, 8 358 / 34, 2 1 1 1 V SL V ab 2 A V L A V BC A 412 / 161, 2 71, 3 / 41, 3 290 / 82, 0 0 V ab 0 V CA V ab1 358 / 34, 20 V ; V ab 2 71, 3 / 41, 30 V ; V ab 0 0 Las componentes simétricas de secuencia positiva y negativa de las tensiones de fase son, V a1 Vab1 V a2 3 / ab1 30, 0 Vab 2 3 358 / ab 2 30, 0 3 / 34, 2 30, 0 207 / 64, 20 V 71, 3 3 / 41, 3 30, 0 41, 2 / 71, 30 V V a1 207 / 64, 20 V ; V a 2 41, 2 / 71, 30 V Las componentes simétricas de las impedancias son, 10, 00 / 45, 0 3, 89 / 66, 9 Z aa 1 Z A Z A 1 Z A 1 8, 00 / 30, 0 2, 59 / 107, 7 aa 2 B Z aa 0 Z C 5, 00 / 0, 0 6, 42 / 9, 2 290 ELECTROTECNIA III-291 Las corrientes de secuencia positiva, negativa y cero son, I a1 Z aa 0 I a 2 Z aa1 Z aa 2 Z aa 0 1 1 V a1 6, 42 / 9, 2 2, 59 / 107, 7 207 / 64, 2 27, 6 / 65, 2 V a 2 3, 89 / 66, 9 6, 42 / 9, 2 41, 2 / 71, 3 15, 67 / 149, 9 I a1 27,6 / 65, 20 A ; I a 2 15,67 / 149,90 A ; I a 0 0 La componente de secuencia cero de las tensiones de fase se obtiene de la ecuación, V a 0 I a1 Z aa 2 I a 2 Z aa1 27, 6 / 65, 2 2, 59 / 107, 7 15, 67 / 149, 9 3, 89 / 66, 9 12, 41/ 71, 70 V Las tensiones de fase son, V AN V a 1 207 / 64, 2 172, 8 / 51, 7 V BN A V a 2 A 41, 2 / 71, 3 244 / 175, 6 12, 41 / 71, 7 212 / 45, 9 V CN V a 0 V AN 172,8 / 51,70 V ; V BN 244 / 175,60 V ; V CN 212 / 45,90 V b) Las corrientes de línea son, I A I a1 27, 6 / 65, 2 17, 31 / 96, 6 I B A I a 2 A 15, 67 / 149, 9 30, 5 / 154, 4 42, 3 / 45, 8 0 I C I a 0 I A 17, 31/ 96,60 A ; I B 30,5 / 154,40 A ; I C 42, 3 / 45,80 A Ejercicio 6-12. Se tiene una carga desbalanceada conectada en estrella con valores de ZA = 12,42 /-24,50 , ZB = 8,54 /43,80 y ZC = 10,56 /12,50 con impedancias mutuas de ZAB = ZBC = ZCA = 3,12 /-90,00 , alimentada de una fuente con tensiones asimétricas iguales a V AN 322 / 5,40 V , V BN 216 / 158, 60 V y V CN 254 / 122,2 0 V . Obtenga: a) las corrientes de línea y del conductor del neutro y b) la potencia compleja del sistema. SOLUCIÓN. El vector matriz de las componentes simétricas de las tensiones es, 291 ELECTROTECNIA III-292 V a 1 V AN 322 / 5, 4 253 / 11, 8 1 1 -1 V S V a 2 A V N A V BN A 216 / 158, 6 79, 3 / 10, 0 254 / 122, 2 35, 7 / 98, 5 V a 0 V CN La matriz de las impedancias de secuencia es, Z AA Z S A Z F A = A Z BA Z CA -1 -1 Z AB Z BB Z CB 12, 42 / 24, 5 3,12 / 90, 0 3,12 / 90, 0 Z AC 1 Z BC A = A 3,12 / 90, 0 8, 54 / 43, 8 3,12 / 90, 0 A 3,12 / 90, 0 3,12 / 90, 0 10, 56 / 12, 5 Z CC 10,14 / 24,1 2, 80 / 42, 4 4, 28 / 90, 3 4, 28 / 90, 3 10, 14 / 24,1 2, 80 / 42, 4 2, 80 / 42, 4 4, 28 / 90, 3 10, 63 / 29, 4 El vector de corrientes de las componentes simétricas es, I a1 1 I S I a2 Z S V S I a 0 10,14 / 24,1 2, 80 / 42, 4 4, 28 / 90, 3 4, 28 / 90, 3 10,14 / 24,1 2, 80 / 42, 4 2, 80 / 42, 4 4, 28 / 90, 3 10, 63 / 29, 4 1 253 / 11, 8 79, 3 / 10, 0 35, 7 / 98, 5 18, 66 / 38, 9 11, 90 / 17, 7 12, 74 / 118, 3 a) Las corrientes de línea son, I A I a1 18,66 /-38,9 20, 2 / 11, 7 I L I B A I S A I a 2 A 11,90 /-17,7 30, 6 / 148, 2 12,74 /118,3 24, 7 / 118, 9 I C I a 0 I A 20, 2 / 11,70 A ; I B 30,6 / 148, 20 A ; I C 24,7 / 118,90 A La corriente en el conductor del neutro es, I N 3 I a 0 3 12,74 / 118, 3 38, 2 / 118, 30 A b) La potencia compleja del sistema es, 292 ELECTROTECNIA III-293 * * * S 3V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 253 / 11, 8 18, 66 / 38, 9 3 79, 3 / 10, 0 11, 90 / 17, 7 3 35, 7 / 98, 5 12, 74 / 118, 3 17, 87 103 / 20, 90 VA Ejercicio 6-13. Una fuente asimétrica con tensiones de línea de V ab 216 / 28, 20 V , V bc 276 / 86,50 V y V ca 270 / 140,1 0 V , se aplica a una carga desbalanceada de tres hilos conectada en estrella, con impedancias de Z A 12, 36 / 42, 4 , Z B 10, 32 / 29, 8 y Z C 9,16 / 5,6 e 0 0 0 impedancias mutuas de Z AB Z BC Z CA 2,18 / 90, 0 . Determinar: a) las corrientes de línea, b) las 0 caídas de tensión en las fases y c) la potencia compleja total. SOLUCIÓN. El vector matriz de las componentes simétricas de las tensiones de línea es, V ab1 V ab 216 / 28, 2 253 / 27, 3 1 -1 V SL V ab 2 A V bc A 276 / 86, 5 36, 9 / 158, 4 270 / 140,1 0 V ab 0 V ca Las componentes simétricas de secuencia positiva y negativa de las tensiones de fase son, V a1 V a2 Vab1 3 Vab 2 3 / ab1 30, 0 / ab 2 30, 0 253 3 36, 9 3 / 27, 3 30, 0 146,1 / 2, 7 0 V / 158, 4 30, 0 21, 3 / 128, 40 V Las componentes simétricas de las impedancias de fase son, 12, 36 / 42, 4 3, 87 / 62, 8 Z aa 1 Z A Z A -1 Z A -1 10, 32 / 29, 8 3, 92 / 115, 8 aa 2 B 9,16 / 5, 6 9,17 / 8, 6 Z aa 0 Z C Las componentes simétricas de las impedancias mutuas son, 2,18 / 90, 0 0 Z bc 1 Z BC Z A -1 Z A -1 2,18 / 90, 0 0 bc 2 CA 2,18 / 90, 0 2,18 / 90, 0 Z bc 0 Z AB Las corrientes de secuencia positiva, negativa y cero son, I a 1 Z aa 0 Z bc 0 I a 2 Z aa1 2 Z bc1 Z aa 2 2 Z bc 2 Z aa 0 Z bc 0 1 V a 1 V a 2 293 ELECTROTECNIA III-294 Donde, Z aa 0 Z bc 0 9,17 / 8, 6 2,18 / 90, 0 9, 74 / 21, 4 0 Z aa 2 2 Z bc 2 3, 92 / 115, 8 0 3, 92 / 115, 80 Z aa 1 2 Z bc1 3, 87 / 62, 8 0 3, 87 / 62, 80 Sustituyendo en la ecuación de las corrientes de secuencia positiva y negativa tenemos, 1 I a 1 9,17 / 8, 6 3, 92 / 115, 8 146,1 / 2, 7 12, 79 / 7, 3 I a 2 3, 87 / 62, 8 9,17 / 8, 6 21, 3 / 128, 4 7, 72 / 134, 3 I a0 0 La componente de secuencia cero de las tensiones de fase es, V a 0 I a 1 Z aa 2 Z bc 2 I a 2 Z aa 1 Z bc1 12, 79 / 7, 3 3, 92 / 115, 8 0 7, 72 / 134, 3 3, 87 / 62, 8 0 20, 3 / 108, 50 V a) Las corrientes de línea son, I A I a1 12,79 /-7,3 10, 21 / 44, 4 I B A I a 2 A 7,72 /-134,3 12, 08 / 91, 3 20, 5 / 110,1 0 I C I a 0 I A 10, 21/ 44,40 A ; I B 12,08 / 91, 30 A ; I C 20,5 / 110,10 A b) Las caídas de tensión en las fases son, V AN V a 1 146,1 /-2,7 126, 3 / 2, 0 V BN A V a 2 A 21,3 /-128,4 124, 7 / 121, 0 20,3 /108,5 187, 4 / 115, 7 V CN V a 0 V AN 126, 3 / 2,00 V ; V BN 124,7 / 121,00 V ; V CN 187,4 / 115,70 V c) La potencia compleja del sistema es, 294 ELECTROTECNIA III-295 * * * S 3 V a 1 I a 1 3V a 2 I a 2 3V a 0 I a 0 3 146,1 / 2, 7 12, 79 / 7, 3 3 21, 3 / 128, 4 7, 72 / 134, 3 0 6,10 103 / 4, 7 0 VA 295 ELECTROTECNIA III-296 UNIDAD 7. REPRESENTACIÓN DE LOS SISTEMAS DE POTENCIA Y CANTIDADES POR UNIDAD. 1. INTRODUCCIÓN. El diagrama completo para un sistema trifásico rara vez es necesario para llevar la información más detallada y uniforme de un sistema eléctrico. De hecho, el diagrama completo frecuentemente oculta, en vez de aclarar, la información que buscamos desde el punto de vista del sistema. En esta parte veremos lo que significa un diagrama unifilar y cómo éste describe el sistema. De gran importancia es la introducción de cantidades por unidad, que se usan en muchos cálculos en lugar de volt, ampere y otras unidades semejantes. Aunque el concepto de por unidad es muy simple su aplicación a circuitos trifásicos requiere de algunas aclaraciones. 2. DIAGRAMA UNIFILAR. Un sistema trifásico simétrico y balanceado se resuelve siempre como un circuito monofásico, formado por una de las tres líneas y un conductor del neutro; por esta razón, muy rara vez, es necesario representar en el diagrama eléctrico del circuito, más de una fase y el neutro. Con frecuencia se hace todavía otra simplificación mayor, suprimiendo el cierre del circuito por el neutro e indicando sus partes componentes por medio de símbolos normalizados, mejor que por sus circuitos equivalentes. Los parámetros del circuito no se indican, y la línea de transmisión se representa por una sola línea entre los dos extremos. Al diagrama resultante de esta simplificación de un sistema eléctrico se le llama el diagrama unifilar. Representa por medio de una línea simple y de símbolos normalizados, a las líneas de transmisión y aparatos asociados con un sistema eléctrico. El objeto de un diagrama unifilar es de suministrar de manera concisa los datos más significativos e importantes de un sistema. La importancia de las diferentes características de un sistema varía según el problema que se considere y la cantidad de información que se incluya en el diagrama depende del fin para el que se desea. Por ejemplo, la colocación de los interruptores y los relevadores no tiene importancia en un estudio de cargas; por lo tanto, éstos no se pondrán si el fin primario del diagrama es realizar tal estudio. Por otra parte, la determinación de la estabilidad de un sistema en condiciones de régimen transitorio, resultante de fallas, depende de la velocidad con que los relevadores e interruptores del circuito aislen la parte del sistema con falla. Por tanto, la información sobre los interruptores puede ser de importancia trascendental. Algunas veces, los diagramas unifilares incluyen información sobre los transformadores de corriente y potencial que unen los relevadores de protección al sistema o que están instalados para medición. La información contenida, pues, en un diagrama unifilar, varía según el problema que se estudia y según la práctica de la compañía en particular que lo prepare. La “American National Institute” (ANSI) y el “Institute of Electrical and Electronic Engineers” (IEEE) han publicado un conjunto de símbolos normalizados para los diagramas eléctricos. La figura número 1 muestra algunos de los símbolos comúnmente usados. El símbolo básico para una máquina o inducido giratorio es un circulo, pero hay relacionadas tantas adaptaciones al símbolo básico, que pueden ser representadas todas las partes de la máquina eléctrica giratoria de uso común. Para el que no trabaje constantemente con los diagramas unifilares es más claro indicar una máquina determinada por medio de símbolo básico seguido de la información sobre su tipo y régimen. 296 ELECTROTECNIA III-297 Máquina o inducido giratorio V Vóltmetro Transformador de potencia o de distribución de dos devanados A Ampérmetro Transformador de potencia de tres devanados Seccionador en aire, operación sin carga Fusible Seccionador en aire, operación con carga Transformador de corriente Interruptor termomagnético Transformador de potencial o tensión Interruptor de transferencia Interruptor de circuitos de potencia en aceite u otro líquido Apartarayos Interruptor de circuito en aire Y Y M Conexión trifásica en estrella sin puesta a tierra del neutro Equipo de medición Conexión trifásica en estrella con neutro a tierra Tablero de alumbrado Tablero de distribución Conexión trifásica en delta Conexión a tierra FIGURA NÚMERO 1. Es importante conocer la situación de los puntos en los que un sistema está unido a tierra, con objeto de calcular la corriente que circula cuando se produce una falla asimétrica que incluye la tierra. El símbolo normalizado para designar una estrella trifásica con el neutro a tierra, se ha representado en la figura número 1. Si se intercala un resistor o un reactor entre el neutro de la estrella y tierra para limitar la corriente durante la falla, se pueden añadir los símbolos adecuados al símbolo normalizado de la estrella a tierra. La figura número 2 es el diagrama unifilar de un sistema de potencia sencillo. Dos generadores, uno puesto a tierra a través de una reactancia y el otro a través de una resistencia, están conectados a una barra colectora y, a través 297 ELECTROTECNIA III-298 de un transformador elevador, a una línea de transmisión. Un tercer generador, puesto a tierra por una reactancia, está conectado a una barra colectora y, por un transformador, al otro extremo de la línea de transmisión. A cada barra está unida una carga. En el diagrama se incluyen datos sobre las cargas, el régimen de los generadores y transformadores y las reactancias de las diversas partes del circuito. Las resistencias se desprecian muchas veces al efectuar los cálculos de fallas y se omite la información que acompaña a la figura número 2. Para los estudios de cargas hay que incluir las resistencias. Y G1 T1 Y G2 Y Y T2 G3 Y Carga B Y Carga A G1. Generador de 20 MVA; 6,6 kV; X’’ = 0,655 . G2. Generador de 10 MVA; 6,6 kV; X’’ = 1,130 . G3. Generador de 30 MVA; 3,81 kV; X’’ = 0,1452 . T1 y T2. Transformadores en banco trifásico, cada uno de ellos de 10 MVA 3,81:38,1 kV; X = 14,52 referidos al lado de alta tensión. Reactancia de la línea de transmisión = 17,40 . Carga A = 15 MVA; 6,6 kV; FP = 0,9 atrasado. Carga B = 30 MVA; 3,81 kV; FP = 0,9 atrasado. FIGURA NÚMERO 2. Las reactancias especificadas para los generadores en la figura número 2 se conocen como reactancias subtransitorias. El estudio de las máquinas de corriente alterna, demuestra que la corriente que circula inmediatamente después de producirse una falla, depende de un valor de la reactancia en el generador o el motor, que es diferente del valor que la que se determina en régimen permanente. En la figura número 3, se muestra el diagrama unifilar de una industria pequeña. 298 ELECTROTECNIA III-299 Compañía suministradora 13,2 kV, 3F, 3H PCC = 250 MVA 1 13,2 kV 100 A 1000 kVA 13,2 kV: 440/254 V Z=5% Y 1600 AD 2 440 V 15 AD 400 AD 400 AD 200 AD 200 AD 70 AD Y 5 HP 200 HP 200 HP X = 25 % X = 25 % X = 25 % 100 HP 100 HP 150 AD X = 25 % X = 25 % 3 45 kVA 440:220/127 V Z=3% 220 V FIGURA NÚMERO 3. Diagramas de impedancias y reactancias. Para estudiar el comportamiento de un sistema en condiciones de carga o al presentarse un cortocircuito, el diagrama unifilar tiene que transformarse en un diagrama de impedancias que muestre el circuito equivalente de cada componente del sistema, referido al mismo lado de uno de los lados de los transformadores. La figura número 4 representa el diagrama detallado de impedancias correspondiente a la figura número 2. El circuito equivalente de la línea de transmisión se representa, con la exactitud suficiente, por medio de una nominal que tenga la resistencia total y la reactancia inductiva de la línea en su brazo serie y la capacitancia total al neutro, dividida entre sus brazos en paralelo. En cada transformador se muestra la resistencia, la reactancia de dispersión y el paso para la corriente de magnetización. Cada generador está representado por la tensión generada en serie con valores adecuados de resistencia y reactancia. Si hay que hacer un estudio de cargas, las cargas atrasadas A y B están representadas por una resistencia y una reactancia inductiva en serie. El diagrama de impedancias no incluye las impedancias limitadoras de corriente, representadas en el diagrama unifilar entre los neutros de los generadores y tierra. Porque en condiciones de simetría y balanceo, no circulan corrientes por la tierra y los neutros de los generadores están al mismo potencial que el neutro del sistema. Puesto que la corriente de magnetización de un transformador es, generalmente, insignificante comparada con la corriente de plena carga, la admitancia en paralelo se suprime normalmente en el circuito equivalente del transformador. 299 ELECTROTECNIA III-300 + E1 - + + E2 E3 - Generadores 1y2 - Carga A Transformador 1 Línea de transmisión Transformador 2 Carga B Generador 3 FIGURA NÚMERO 4. Como se ha mencionado antes, la resistencia se omite algunas veces aún en programas de computadora digital. Por supuesto, esta eliminación de la resistencia introduce errores, pero los resultados pueden ser satisfactorios ya que la reactancia inductiva de un sistema es mucho mayor que su resistencia. La resistencia y la reactancia inductiva no se suman directamente y la impedancia no es muy diferente a la reactancia inductiva si es pequeña la resistencia. Las cargas que no incluyen maquinas rotatorias, tienen poco efecto sobre la corriente total de la línea durante una falla, por lo que, frecuentemente se omiten. Por el contrario, las cargas con motores síncronos se incluyen siempre al hacer cálculos de fallas, por que sus fuerzas electromotrices generadas contribuyen a la corriente de cortocircuito. Si el diagrama se ha de utilizar para determinar la corriente, inmediatamente después de que se produce una falla, se deben tener en cuenta los motores de inducción, con una fuerza electromotriz generada en serie con una reactancia inductiva. Los motores de inducción se ignoran en el cálculo de la corriente, unos pocos ciclos después de que se produce una falla, por que la corriente con que un motor de inducción contribuye, desaparece muy rápidamente al quedar el motor en cortocircuito. Si queremos simplificar nuestros cálculos de la corriente de falla, suprimiendo todas las resistencias, la corriente de magnetización de cada transformador y la capacitancia de las líneas de transmisión, el diagrama de impedancias se reduce al diagrama de reactancias de la figura número 5. Estas simplificaciones se aplican únicamente al cálculo de fallas y no al estudio de flujos de carga. Los diagramas de impedancias y reactancias que aquí se presentan, se llaman algunas veces diagramas de secuencia positiva, puesto que representan las impedancias para las corrientes equilibradas de un sistema trifásico simétrico y balanceado. 300 ELECTROTECNIA III-301 j 65,5 (j 0,45) + E1 G1 - T1 Línea T2 j 14,52 (j 0,10) j 17,40 (j 0,12) j 14,52 (j 0,10) j 131,0 (j 0,90) + E2 G2 - j 43,6 (j 0,30) Conductor del neutro + E3 G3 - Figura número 5. Diagrama de reactancias adaptado de la figura número 4, suprimiendo todas las cargas, resistencias y admitancias en paralelo. Las reactancias están en ohm referidas a los lados de alta tensión de los transformadores. Los valores entre paréntesis son reactancias en por unidad, con base de 30 MVA y 66 kV. Cuando se representa un transformador por un circuito equivalente, no hay transformación correspondiente a la transformación de tensión entre los lados de alta y baja tensión del transformador real. La corriente en ambos extremos del circuito equivalente es idéntica si se deprecia la corriente de magnetización. En un transformador real, la corriente en los devanados de alta y baja tensión sería idéntica únicamente para igual número de vueltas en el primario que en el secundario, despreciando la corriente de magnetización. En un circuito en el que los transformadores están representados por sus circuitos equivalentes, las impedancias adecuadas son las del circuito real, referidas al lado del transformador para el que se construye el circuito equivalente. Las reactancias del diagrama de la figura número 5 están en ohm, respecto al circuito de alta tensión. Como la línea de transmisión que se considera es la parte de alta tensión del circuito, no es necesario hacer modificaciones en el valor de la reactancia colocada en el circuito equivalente para representar la línea de transmisión. La información contenida en el diagrama unifilar, especifica la reactancia de dispersión de los transformadores del lado de alta tensión, no siendo necesario hacer modificacioness en los valores de la reactancia de pérdidas en el circuito equivalente. La teoría de los transformadores demuestra que la impedancia del devanado secundario de un transformador se puede referir a la del primario, multiplicando dicha impedancia por el cuadrado de la relación de espiras del devanado primario a las del devanado secundario. Los generadores de la figura número 2 están en los lados de baja tensión de los transformadores, y sus reactancias se deben referir al circuito de alta tensión para el que se ha dibujado la figura número 5. Los generadores 1 y 2 están conectados al circuito de alta tensión a través de transformadores; comúnmente podríamos esperar un transformador simple trifásico conectado internamente en estrella/estrella (Y/Y). Aquí se describen tres transformadores monofásicos para resaltar el hecho de que cada fase se considera separadamente como parte de un sistema trifásico. La teoría es la misma para un transformador trifásico que para un banco de transformadores monofásicos conectados para formar un circuito trifásico. La figura número 6 se aplica en cualquier caso para una conexión Y/Y. Los devanados del transformador están representados esquemáticamente, y las fases de los devanados primario y secundario están dibujados en direcciones paralelas sobre el mismo transformador monofásico o para la unidad trifásica sobre la misma sección del núcleo magnético y enlazados por flujos idénticos excepto por las pérdidas. 301 ELECTROTECNIA III-302 GENERADOR TRANSFORMADOR LÍNEA 6,6 kV 66 kV 3,81 kV 0,655 38,1 kV FIGURA NÚMERO 6. Parte del circuito trifásico de la figura número 2 que muestra el generador 1 y el transformador T1. La reactancia de 0,655 en fase del generador 1 está (en serie con la tensión interna) a través del devanado de 3,81 kV del transformador sin importar si hay o no conexión entre el neutro del generador y la carga, puesto que el sistema es simétrico y balanceado, La reactancia del generador 1 referida al lado de alta tensión del transformador es, 2 X ´´ G1_ 66 X ´´ G1_ 6,6 kVT 38,1 0, 655 65, 5 3, 81 kVG1 2 (1) En la misma forma, la reactancia del generador 2 referida al lado de alta tensión del transformador es, 2 X ´´ G2_66 X ´´ G2_6,6 kVT 38,1 1, 310 131, 0 3, 81 kVG2 2 (2) El procedimiento en el caso del generador 3, que está conectado a la línea a través de un transformador conectado en delta/estrella (/Y), no es tan obvia. La conexión del transformador se muestra en la figura número 7a. El generador, conectado en estrella (Y), está sobre el lado de la delta () del transformador. La tensión de la línea es de 66 kV sobre el lado de la estrella (Y) y se reduce a 3,81 en el lado de baja tensión. En cuanto se refiere a la tensión en el lado de baja tensión, el transformador estrella/delta (Y/) se puede reemplazar por un banco de transformadores estrella/estrella (Y/Y) que tiene una relación de espiras para cada transformador individual (o para cada par de devanados por fase del transformador trifásico) de 38,1/2,2 kV, como se muestra en la figura número 7b. 302 ELECTROTECNIA III-303 LÍNEA TRANSFORMADOR 2 GENERADOR 3 3,81 kV 66 kV 3,81 kV 38,1 kV 0,1452 (a) EQUIVALENTE DEL TRANSFORMADOR 2 LÍNEA 66 kV 3, 81 38,1 kV 3 GENERADOR 3 3,81 kV 2, 2 kV 0,1452 b FIGURA NÚMERO 7. Parte del circuito trifásico de la figura número 2, mostrando el generador 3 con (a) el transformador 2 y (b) el equivalente en estrella del transformador 2. La reactancia del generador 3 referida al lado de alta tensión del transformador es, 2 2 X ´´ G3 _ 66 X ´´ G _ 3,81 38,1 kVT 43, 6 0,1452 kVG3 3, 81/ 3 (3) La figura número 7b nos muestra que, vista desde el lado de alta tensión del transformador 2, la reactancia del generador 3 es (38,1/2,2)2 X 0,1452 = 43,6 . Este factor de multiplicación es 2 3 10 , que equivale al cuadrado de la relación de espiras de los devanados individuales del transformador estrella/delta (Y/). Este estudio nos lleva a la conclusión de que para referir el valor óhmico de la impedancia desde el nivel de tensión sobre un lado del transformador trifásico hasta el nivel en el otro lado, el factor de multiplicación es el cuadrado de la relación de las tensiones de línea sin que importe si la conexión es estrella/estrella (Y/Y) o delta/estrella (/Y). Esto es, 2 X ´´ G 1_ 66 X ´´ G 1_ 6,6 kVTL 66 0, 655 65, 5 6, 6 kVG1L 2 303 ELECTROTECNIA III-304 2 X ´´ G 2 _ 66 X ´´ G 2 _ 6,6 kVTL 66 1, 310 131, 0 6, 6 kVG2L 2 2 X ´´ G 3 _ 66 X ´´ G 3 _ 6,6 kVTL 66 0,1452 43, 6 3, 81 kVG3L 2 En general varias ramas de un sistema eléctrico de potencia o de distribución funcionan a diferentes tensiones. Al representar el sistema mediante un sistema de impedancias, es conveniente utilizar un esquema que permita la combinación de las diferentes impedancias de manera que la red pueda ser representada por una sola impedancia entre la fuente y el punto bajo estudio. Esto plantea la exigencia de que se determine una impedancia Z2, que se puede usar con una tensión V 2 , arbitrariamente seleccionada, denominada como tensión base, de tal manera que tome los mismos kVA que cuando se usa la impedancia real Z1, en conjunto con la tensión real V 1 . Expresando el enunciado anterior algebraicamente tenemos, V 2 I 2 V 1 I 1 (4) Como, V 1 Z1 I1 y V 2 Z 2 I 2 Entonces, I1 V1 Z1 e I2 V2 Z2 Sustituyendo en la ecuación número (4), V2 V2 V1 V 1 Z2 Z1 2 2 V2 V1 Z 2 Z1 Despejando a Z2 tenemos, 2 V 2 Z 2 Z 1 (5) V1 La ecuación número 5 muestra que la impedancia original se debe multiplicar por el cuadrado de la relación de la tensión base a la tensión nominal de funcionamiento de la impedancia. La corriente en función de la tensión nominal se determina multiplicando el resultado en función de la tensión base, por la relación de las tensiones, esto es, I1 I 2 V2 V1 (6) 304 ELECTROTECNIA III-305 3. CANTIDADES POR UNIDAD. Para estudiar el comportamiento de los sistemas eléctricos, con frecuencia, las tensiones, corrientes, impedancias, así como de las potencias, se expresan sus valores en por unidad o por ciento de un valor base o de referencia. Por ejemplo, si se elige una tensión base de 120 kV, las tensiones, cuyos valores sean 108, 120 y 126 kV, se transforman en 0,90, 1,00 y 1,05 por unidad, o 90, 100 y 105 %, respectivamente. El valor por unidad de una magnitud cualquiera se define como la relación de su valor al valor base, expresado como un decimal. El valor en por ciento es igual a 100 veces el valor por unidad. Los métodos de cálculo que utilizan los valores por unidad o por ciento son mucho más sencillos que usando los valores nominales en volt, ampere y ohm. El método por unidad tiene una ventaja sobre el método en por ciento y es que el producto de dos magnitudes expresadas en por unidad, viene a su vez, expresado en por unidad, en tanto que el producto de dos magnitudes en por ciento, tiene que dividirse por 100 para obtener el resultado en por ciento. Las tensiones, corrientes, impedancias y potencias, están relacionadas entre sí, de tal forma que la elección de valores base para dos cualesquiera determinan los valores base de las otras dos. Si se especifican los valores base de la tensión y la corriente, se pueden determinar la impedancia base y la potencia base. La impedancia base es aquella que da lugar a una caída de tensión igual a la tensión base, cuando la corriente que circula por dicha impedancia sea igual al valor base de la corriente. Las potencias base, en sistemas monofásicos, son el producto de la tensión base en kV por la corriente base en ampere. Normalmente, las magnitudes elegidas para seleccionar las bases son la potencia en kVA y la tensión en kV. En sistemas monofásicos o trifásicos en los que el término “corriente” se refiere a la corriente de línea, el término tensión se refiere a la tensión al neutro y la potencia son kVA por fase, relacionándose las diversas magnitudes por medio de las fórmulas siguientes: Sistemas monofásicos. Si designamos la cantidad base con el subíndice B tendremos, Potencia base = Tensión base = S 1 B VNB La corriente base y la impedancia base se calculan como, Corriente base en A, I B Potencia base monofásica S1B kVA1B Tensión al neutro base VNB kVNB 2 Tensión base VNB VNB Impedancia base , Z B Corriente base I B S1B Tensión base en kVNB 2 1000 kVA1B Tensión base en kVNB 2 MVA1B En las ecuaciones anteriores los subíndices 1 y N indican “por fase” y “al neutro” respectivamente, donde las ecuaciones se apliquen a circuitos trifásicos. Si las ecuaciones se emplean para circuitos monofásicos, kV N significa la tensión a través de la línea monofásica o de línea a tierra, si un lado de la línea está a tierra. Teniendo definidas las cantidades base, podemos normalizar cualquier cantidad del sistema dividiéndola por la cantidad de base de la misma magnitud. Así, la impedancia por unidad Zp.u., queda definida como, Impedancia por unidad de un elemento de circuito = Impedancia nominal en Impedancia base en 305 ELECTROTECNIA III-306 Z p .u Zn , p.u ZB , (7) En esta ecuación las dimensiones se cancelan y el resultado es una cantidad adimensional cuyas unidades se especifican en por unidad, o p.u. Si escribimos Z = R + j X en , podemos dividir ambos lados de esta ecuación por ZB y obtenemos, Z R j X (en ) Z p .u p.u (8) ZB Z B (en ) R p .u R p.u ZB (9) X p .u X p.u ZB (10) De la misma manera podemos escribir S = P + j Q en VA y dividiendola por la potencia base S1B , obtenemos S P jQ p.u SB S1B S p .u De donde, Pp . u P en watt y Q p .u S1B Q en var S1B (11) p.u (12) p.u (13) Circuitos trifásicos. Como los circuitos trifásicos se resuelven como una línea simple con retorno al neutro, las bases para las magnitudes del diagrama de impedancias son kVA por fase y kV de línea a neutro. Los datos se dan normalmente como kVA totales trifásicos o MVA y kV de línea. A causa de esta costumbre de especificar las tensiones de línea y los kVA o MVA totales, se puede originar una confusión sobre la relación existente entre el valor por unidad de la tensión de línea y el valor de la tensión de fase. Aunque se puede especificar como base una tensión de línea, la tensión en el circuito monofásico, necesaria para la solución, es la tensión al neutro. La tensión base, respecto al neutro, es la tensión báse de línea dividida por 3 . 306 ELECTROTECNIA III-307 VN VL V 3 Dado que éste es también el valor de la relación entre las tensiones de línea y la tensión al neutro en un sistema trifásico simétrico, el valor por unidad de una tensión de línea el mismo punto, con tensión base de línea, si el sistema es simétrico. De igual forma, los kVA trifásicos son tres veces los kVA por fase y los kVA en base trifásica son tres veces los kVA base por fase. S1B S3 B 3 Por lo tanto, el valor por unidad de los kVA trifásicos base, es idéntico al valor por unidad de los kVA por fase con kVA por fase de base. Un ejemplo numérico puede servir para entender las relaciones discutidas. Por ejemplo si kVA3B base S3B 30000kVA y kVL base =VLB 120kV donde los subíndices 3 y L significan “trifásico” y “de línea” respectivamente, S1B kVA1 base = S 3B 3 30 000 10 000kVA 3 y VNB kVN base = VLB 3 120 3 69, 2kV Para una red con una tensión de línea de 108 kV, la tensión al neutro es de 108 / 3 62, 3kV , y Tensión por unidad = V p . u VL 108 VLB 120 VN 62, 3 0, 90p.u VNB 69, 2 Para la potencia trifásica total de 18 000 kW, la potencia por fase es 6 000 kW, y 307 ELECTROTECNIA III-308 Potencia por unidad. = S p . u S3 18 000 S3 B 30 000 S1 S1B 6 000 0, 60 10 000 Desde luego, en todo lo antedicho, se pueden sustituir kW y kVA por MW y MVA. A menos que se especifique de otra manera, el valor dado para la tensión base de un sistema trifásico es la tensión de línea y el valor dado para los kVA base o MVA base es la potencia total trifásica. La corriente base y la impedancia base se pueden calcular directamente a partir de los valores trifásicos base en kV y kVA. Si interpretamos que los kVA base, son los totales de las tres fases y la tensión base en kV es la tensión base de línea, tenemos, Corrientebase, A = I B S3B 3 VLB Potencia base kVA (14) 3 tensión base en kVL Y de la ecuación de la impedancia, Impedancia base = Z B V LB / 3 S 3 B / 3 2 V LB 2 / 3 1000 Potencia base kVA 3 / 3 Tensión base en kVL 1000 V2 Impedancia base = Z B LB S3B Potencia base kVA 3 (15) 2 Impedancia base = Z B Tensión base en kVL (16) 2 Potencia base en MVA 3 (17) Así tenemos que, Z p.u S Z Z 2 Z 32B Z B VLB VLB S3 B (18) Escribiendo la ecuación de la impedancia por unidad Zp.u con la tensión en kV y la potencia en MVA tenemos, 308 ELECTROTECNIA III-309 Z p .u Z MVA 3B 2 kVLB (19) Si queremos convertir los valores en de las reactancias del diagrama de la figura número 5 a valores por unidad, podemos elegir como base 30 MVA (S3B) y 66 kV (VLB), con lo que determinamos la impedancia base, en la forma siguiente: Impedancia base = Z B Tensión base en kVL 2 MVA 3B 662 145, 2 30 Dividiendo cada uno de los valores de la reactancia óhmica del diagrama por la impedancia base de 145,2 , se obtendrán los valores por unidad de tales reactancias. X G1_p.u X G1 j65,5 j0,45p.u ZB 145,2 X G2_p.u X G2 j131,0 j0,90p.u ZB 145,2 X G3_p.u X G3 j43, 6 j0,30p.u ZB 145,2 X T1_p.u X T1 j14,52 j0,10p.u ZB 145,2 X T2_p.u X T2 j14,52 j0,10p.u ZB 145,2 X L_p.u X L j17,40 j0,12p.u ZB 145,2 Cada una de las reactancias , por unidad, se han puesto en la figura número 5 dentro de un paréntesis debajo del valor óhmico correspondiente. En el estudio de los sistemas, la pregunta que a veces se hace es ¿Dada una impedancia en por unidad referida a una base, cuál será su valor por unidad referido a una nueva base? Cambio de base para los valores por unidad. Algunas veces la impedancia por unidad de un componente de un sistema se expresa sobre una base distinta que la seleccionada como base para la parte del sistema en la cual está situado dicho componente. Dado que todas las impedancias de cualquier parte del sistema tienen que ser 309 ELECTROTECNIA III-310 expresadas respecto a la misma impedancia base, al hacer los cálculos, es preciso tener un medio para pasar las impedancias por unidad de una a otra base. Sustituyendo en la expresión de la impedancia base tenemos, impedancia base por unidad de un elemento de circuito, Z p.u kVA1B S1B Z Z Z Z 2 2 2 Z B kVNB 1000 kVNB 1000 kVNB 1000 kVA1B Z p.u kVA 3 B S3 B Z Z Z Z 2 2 Z B kVLB 2 1000 kVLB 1000 kVLB 1000 kVA 3 B Zp.u Impedancia base en kVA base Tensión base en kV 2 Z SB VB2 Las ecuaciones anteriores demuestran que la impedancia por unidad es directamente proporcional a los kVA base e inversamente proporcional al cuadrado de la tensión base. Dos impedancias en por unidad referidas a sus respectivas cantidades base se pueden escribir ahora usando los subíndices “d” para el valor dado y “n” para el valor nuevo. Zd Z SBd S p.u ; Z n Z Bn p.u 2 2 VBd VBn Puesto que Z es igual para cualquier base, entonces 2 Z d VBd Z V2 n Bn SBd SBn De donde, 2 V S Znp.u Zdp.u Bd Bn VBn SBd Por lo tanto, para cambiar la impedancia por unidad respecto a una base nueva, se aplicará la ecuación siguiente: 2 kV base dados kVA base nuevos Znuevap.u Zdada p.u kV base nuevos kVA base dados 310 ELECTROTECNIA III-311 Esta ecuación no tiene ninguna relación con la transferencia del valor óhmico de la impedancia de un lado del transformador a otro. El gran valor de la ecuación está en el cambio de la impedancia por unidad que se da de una base particular a otra base, sin tener conocimiento del valor óhmico de Z. Conversión de valores en por unidad a valores reales. Una vez que los cálculos en por unidad en algún sistema se han terminado y se requiere convertir alguna o todas estas cantidades a valores reales, el procedimiento se realiza en forma inversa, esto es I Ip.u I B en A V Vp.u VB en V P Pp.u SB en W Q Qp.u SB en var En general no es necesario convertir una impedancia en por unidad en una impedancia en ohm, pero el procedimiento es exactamente el mismo. Z Zp.u Z B en Ejemplo 7-1. La reactancia subtransitoria X’’ de un generador es de 0,20 por unidad basada en la placa del generador de 13,2 kV, 30,0 MVA. La base para los cálculos es de 13,8 kV y 50,0 MVA. Encuentre la reactancia subtransitoria en esta nueva base. SOLUCIÓN. 2 V S X Bd Bn VBn S Bd '' n '' Xd 2 13, 20 50, 0 0, 20 0, 30por unidad 13, 80 30, 0 Selección de la base para los valores por unidad. La selección de los valores base en kV y kVA se hace con el objeto de reducir al mínimo, en la medida de lo posible, el trabajo exigido por el cálculo. Primero se selecciona una base para una parte del circuito. Después debe determinarse, de acuerdo con los principios que se desarrollarán en esta sección, la base en otras partes del circuito, separadas de la primera parte por los transformadores. La base elegida debe ser tal que lleve a valores por unidad de la tensión y la 311 ELECTROTECNIA III-312 corriente del sistema, aproximadamente iguales a la unidad, de forma que se simplifique el cálculo. Se ahorrará mucho tiempo si la base se selecciona de forma que pocas magnitudes, por unidad, ya conocidas, tengan que convertirse a una nueva base. Cuando un fabricante da la resistencia y la reactancia de un aparato en por ciento o por unidad, se sobreentiende que las bases son los kV y kVA nominales del aparato. Hay tablas disponibles que dan los valores aproximados de las impedancias por unidad de generadores, transformadores, motores síncronos y motores de inducción. Los valores obtenidos de las tablas están basados en valores medios para aparatos de tipo y tamaño similar. Los valores de la resistencia óhmica y la reactancia de pérdidas de un transformador dependen de que se midan en el lado de alta o baja tensión del transformador. Si se expresan por unidad, los kVA base se sobreentiende que son los nominales del transformador. La tensión base se sobreentiende que es la tensión nominal en el devanado de baja tensión del transformador y la tensión nominal en el devanado de alta tensión, si están referidos al lado de alta tensión del transformador. La impedancia por unidad de un transformador es la misma, no importa si se determina desde los valores óhmicos referidos a los lados de alta o baja tensión de los transformadores. Ejemplo 7-2. Un transformador monofásico se especifica como 110:440 V, 2,50 kVA. La reactancia de pérdidas medida desde el lado de baja tensión es 0,0600 . Determine la reactancia de pérdidas por unidad. SOLUCIÓN. Impedancia base de baja tensión Z B , BT Tensión en baja tensión en kV 2 1000 kVA 0,110 1000 4, 84 2, 50 2 En por unidad, X pu X d , Z B , BT 0,0600 0,0124pu 4,84 Si la reactancia de pérdidas se ha medido en el lado de alta tensión el valor es, X d , AT V X d , BT n X d , BT AT VBT 2 2 2 440 0, 0600 0, 960 110 312 ELECTROTECNIA III-313 Impedancia base de alta tensión Z B , AT Tensión en alta tensión en kV 2 1000 kVA 0, 440 1000 77, 5 2, 50 2 En por unidad, X pu X d , Z B , AT 0, 960 0, 0124pu 77, 5 Se consigue una gran ventaja en el cálculo por unidad, por selección adecuada de bases diferentes para circuitos interconectados por un transformador. Para conseguir esta ventaja en un sistema monofásico, las tensiones base para circuitos conectados por un transformador deben estar en la misma relación que el número de vueltas de los devanados del transformador. Con esta elección de tensiones base y los mismos kVA base, el valor por unidad de una impedancia será el mismo si se expresa respecto a la base elegida para su propio lado del transformador que si refiere al otro lado del transformador y se expresa respecto a la base de este lado. Ejemplo 7-3. Las tres partes de un sistema eléctrico monofásico, designadas por A, B y C, están interconectadas por medio de transformadores en la forma representada en la figura. Los transformadores tienen las características siguientes: A-B 10 000 kVA; 13,8 : 138 kV; reactancia de dispersión, 10 %. B-C 10 000 kVA; 69 : 138 kV; reactancia de dispersión, 8 %. Si en el circuito B se toma como base 10 000 kVA (kVA1B,B) y 138 kV (kV1B,B) determinar la impedancia por unidad de una carga óhmica pura de 300 en el circuito C, referida a los circuitos C, B y A. Dibujar el diagrama de impedancias despreciando la corriente de magnetización, las resistencias de los transformadores y las impedancias de las líneas. Determinar la regulación de tensión si la tensión en la carga es de 66 kV, con la hipótesis de que la tensión de entrada del circuito A permanece constante. 13,8 kV 1:10 138 kV A 2:1 B 69 kV C B-C A-B SOLUCIÓN. Las relaciones de los transformadores son, n1 138 138 10 ; n 2 2 13, 8 69 313 ELECTROTECNIA III-314 La tensión base para el circuito A es, kV1B,A 1 1 kV1B,B 138 13, 8kV n1 10 La tensión base para el circuito C es, kV1B,C 1 1 kV1B,B 138 69kV n2 2 La impedancia base del circuito C es, Z B ,C kV12B,C 1000 692 1000 476 kVA1B 10 000 La impedancia de la carga, por unidad, en el circuito C es, ZC , pu R 300 0, 63pu Z B ,C 476 Como la selección de la base en las diversas partes del circuito se determinó por la relación de espiras de los transformadores, la impedancia por unidad de la carga referida a cualquier parte del sistema, será la misma. Esto se comprueba como sigue: La impedancia base del circuito B es, kV12B,B 1000 1382 1000 Z B,B 1904 kVA1B 10 000 La impedancia de la carga referida al circuito B es, ZB R n22 300 22 1200 La impedancia de la carga, por unidad, referida a B es, Z B,pu Z B 1200 0, 63pu Z B , B 1904 La impedancia base del circuito A es, kV12B,A 1000 13, 82 1000 Z B ,A 19, 0 kVA1B 10 000 La impedancia de la carga referida al circuito A es, 314 ELECTROTECNIA III-315 2 1 1 Z A R 2 n 22 300 22 12, 0 n1 10 La impedancia de la carga, por unidad, referida a A es, Z A,pu Z A 12, 0 0, 63pu Z B ,A 19, 0 El diagrama de impedancias, por unidad es, j 0,1 j 0,08 0,63 + j 0 El cálculo del factor de regulación se lleva a cabo en la forma siguiente: Tensión en la carga, por unidad V LN C ,pu V LNC 66 0, 957 j0pu VLNB ,C 69 Corriente, por unidad I pu V LNC ,pu 0, 957 j0 1, 52 j0pu Z C ,pu 0,63 j0 Tensión de entrada, por unidad V LNA,pu I pu Z AB , pu Z BC , pu VLNC ,pu 1,52 j0 j0,10 j0,08 0,957 j0 0,995 / 16,0 0 pu Por lo tanto la regulación es, Regulación VLNA,pu VLNC ,pu VLNC ,pu 100 0, 995 0, 957 100 3, 97% 0, 957 La ventaja antes señalada es la causa de que el principio seguido en el ejemplo anterior (Ejemplo 7-3) de selección de base para las diversas partes del sistema, se siga al efectuar cálculos por unidad o por ciento. La base en kVA debe ser la misma en todas las partes del sistema y la elección de los kV base en una parte de él determinan los kV base que se deben asignar a las otras partes del sistema. Siguiendo este principio de asignar kV base, es posible combinar en un diagrama de impedancias las impedancias por unidad determinadas en las diferentes partes del sistema. Por ejemplo, una potencia base de 30 000 kVA y una tensión base 315 ELECTROTECNIA III-316 de 66 kV en la línea de la figura número 2 exigira una potencia base de 30 000 kVA y una tensión base de 3,81 kV para el circuito que contiene el generador 3 y una tensión base de 6,6 kV para el circuito de los generadores 1 y 2. Las reactancias para los elementos del circuito de la figura número 2 son, X ´´ G1_p.u X ´´ G1_ kVA B kV 2 kV 2 30000 j0, 90p.u 6, 62 1000 0,1452 30000 j0, 30p.u 3, 812 1000 1000 kVA B kV 2 B_G3 X T1_p.u X T1_ 1, 310 kVA B B_G2 X ´´G3_p.u X ´´G3_ 30000 j0, 45p.u 6, 62 1000 1000 B_G1 X ´´ G2_p.u X ´´ G2_ 0, 655 kV 1000 kVA B BL_T1 2 1000 14, 52 30000 j0,10p.u 662 1000 X T2_p.u X T1_p.u j0,10p.u X L_p.u X L_ kV kVA B BL_L 2 1000 17, 40 30000 j0,12p.u 662 1000 A fin de preparar un diagrama de impedancias con impedancias por unidad, empezamos con el diagrama unifilar y la información nominal impresa en generadores, transformadores y motores y sus valores óhmicos o impedancias en por unidad o por ciento, más los datos acerca de las líneas de transmisión. Los puntos siguientes se deben tener en cuenta. 1. Se selecciona una base en kVA y kV en una parte del sistema. Los valores base para un sistema trifásico se entiende que son los kVA o MVA trifásicos y los kV de línea. 2. Para otras partes del sistema, esto es, en otros lados de los transformadores, los kV base para cada parte se determinan de acuerdo con la relación de las tensiones de línea de los transformadores. Los kVA base serán los mismos en todas las partes del sistema. Será de gran ayuda marcar los kV base de cada parte del sistema sobre el diagrama unifilar. 3. La información de la impedancia disponible para transformadores trifásicos, generalmente se da en términos de unidades o por ciento y es la base determinada por las especificaciones. 316 ELECTROTECNIA III-317 4. Para tres transformadores monofásicos conectados como una unidad trifásica se extraen de las especificaciones monofásicas de cada transformador individual. La impedancia en por ciento para la unidad trifásica es la misma que para cada transformador individual. 5. La impedancia por unidad dada sobre una base diferente a la determinada para la parte del sistema en el cual está localizado el elemento se cambia a la base adecuada. Ejemplo 7-4. Un generador trifásico de 30 000 kVA y 13,8 kV tiene una reactancia subtransitoria del 15 % y está conectado en estrella con su neutro a tierra a través de una inductancia. El generador alimenta a dos motores a través de una línea de transmisión, con transformadores en ambos extremos, tal como se representa en el diagrama unifilar de la figura. Los motores tienen capacidades nominales de 20 000 y 10 000 kVA, ambos a 12,5 kV, con reactancia subtransitoria de 20 %. El transformador trifásico T1 tiene como valores nominales 35 000 kVA, 13,2 : 115 Y kV, con reactancia de dispersión de del 10 %. El transformador T2 está compuesto de tres transformadores monofásicos, cada uno especificado como de 10 000 kVA, 12,5 : 67 kV, con reactancia de dispersión del 10 %. La reactancia en serie de la línea de transmisión es de 80 . Dibuje el diagrama de reactancias con todas las reactancias indicadas por unidad. Elija la especificación del generador como base. Si los motores tienen capacidades de 16 000 y 8 000 kW respectivamente, a 12,5 kV y ambos con un factor de potencia unitario, encuentre la tensión en las terminales del generador. SOLUCIÓN. 13,8 kV Y T1 120 kV T2 12,9 kV M1 Y G M2 Y Y Y 1. Cantidades base. 13,8 kV y 30 000 kVA 2. Las tensiones base en otras partes del circuito son. Tensión base para la línea. kVBL kVB kVAT.T1 115 13, 8 120kV kVBT.T1 13, 2 Tensión base del circuito de la barra de los motores, 317 ELECTROTECNIA III-318 kVBM kVBL kVBT.T2 12, 5 120 12, 9kV kVAT.T2 3 67 3. Reactancias por unidad. La reactancia, por unidad, del generador es, X G" X G % 15 0,15pu 100 100 La reactancia, por unidad, del transformador T1 es, 2 kV kVABn 10 13, 2 30 000 X T 1n X T 1d Bd 0, 0784pu kVBn kVABn 100 13, 8 35 000 2 La reactancia por unidad de la línea es, X L X L kVA B 30 000 80 0,1667 pu 2 kVBL 1000 120 2 1000 La reactancia por unidad del transformador 2 es, 2 kV kVABn 10 12, 5 30000 X T 2 n X T 2d Bd 0, 0939pu kVBn kVABd 100 12, 9 3 10000 2 La reactancia del motor 1, es 2 X " m 1, n X " m 1, d kVBd kVABn 12, 5 30 000 0, 20 0, 282pu 12, 9 20 000 kVBn kVABd 2 La reactancia del motor 2 es, 2 X " m 2, n X " m 2, d kVBd kVABn 12, 5 30 000 0, 20 0, 563pu 12, 9 10 000 kVBn kVABd 2 318 ELECTROTECNIA III-319 T1 j0,0784 T2 j0,0940 LIN j0,1670 G j0,1500 M1 j0,282 + M2 j0,563 + + Eg Em1 E m2 - - - Diagrama de reactancias, por unidad La potencia tomada por ambos motores es de 24 000 kW, esta potencia por unidad es Spu P1 P2 16 000 8 000 0, 8pu SB 30 000 La tensión, por unidad, en las terminales de los motores es, Vm ,pu kVBd / 0, 0 12, 5 / 0, 0 0, 969 / 0, 00 pu kVBn 12, 9 La corriente por unidad es, I pu Spu V m,pu 0,8 0,826 / 0,00 pu 0,969 / 0,0 La tensión, por unidad, en las terminales del generador es, V G ,pu V m ,pu I pu X T 1,pu X L,pu X T 2,pu 0, 969 / 0, 0 0, 826 / 0, 0 j0,0784 j0,1670 j0,0940 1, 009 / 16,10 pu La tensión, en kV, en las terminales del generador es, VG VG ,pu kVB 1,009 13,8 13,92kV Impedancia por unidad de transformadores de tres devanados. Los devanados primario y secundario de un transformador de dos devanados tienen los mismos kVA nominales, pero los tres devanados de un transformador de tres devanados puede tener distintos kVA nominales. La impedancia de cada devanado de un transformador de tres devanados puede venir dada en por ciento o por unidad sobre base del valor nominal de su propio devanado, o pueden realizarse pruebas para determinar las impedancias. En cualquier caso, todas 319 ELECTROTECNIA III-320 las impedancias por unidad en el diagrama de impedancias se deben expresar respecto a los mismos kVA base. Se pueden medir tres impedancias por medio de una prueba normal de corto circuito, como sigue: MEDICIÓN Z PS MEDICIÓN Z ST P S T P S T MEDICIÓN Z PT P S T CIRCUITOS PARA LA MEDICIÓN DE LAS IMPEDANCIAS DE UN TRANSFORMADOR DE TRES DEVANADOS. Donde, Z PS Impedancia de dispersión, medida en el primario con el secundario en corto circuito y el terciario abierto. Z ST Impedancia de dispersión, medida en el secundario con el terciario en corto circuito y el primario abierto. Z PT Impedancia de dispersión, medida en el primario con el terciario en corto circuito y el secundario abierto. Si las tres impedancias medidas en ohms, se refieren a la tensión de uno de los devanados, la teoría de los transformadores demuestra que las impedancias de cada devanado por separado, referidas al mismo devanado, están relacionadas con las medidas en la forma siguiente: Z PS Z P Z S Z PT Z P Z T Z ST Z S Z T en las que Z P , Z S y Z T son las impedancias de los devanados primario, secundario y terciario, referidas al circuito primario si Z PS , Z PT y Z ST son las impedancias medidas referidas al circuito primario. Resolviendo las ecuaciones anteriores, se obtiene 320 ELECTROTECNIA III-321 Z PS 1 1 0 Z P Z 1 0 1 Z PT S Z ST 0 1 1 Z T 1 0, 5 0, 5 Z PS Z P 1 1 0 Z PS 0, 5 Z 1 0 1 Z 0, 5 0, 5 0, 5 Z S PT PT Z T 0 1 1 Z ST 0, 5 0, 5 0, 5 Z ST 1 2 Z PS Z PT Z ST 0, 5 Z PS 0, 5 Z PT 0, 5 Z ST 1 0, 5 Z PS 0, 5 Z PT 0, 5 Z ST Z PS Z ST Z PT 2 0, 5 Z PS 0, 5 Z PT 0, 5 Z ST 1 Z PT Z ST Z PS 2 De donde, ZP 1 Z PS Z PT Z ST 2 ZS 1 Z PS Z ST Z PT 2 1 Z PT Z ST Z PS 2 Las impedancias de los tres devanados están conectadas en estrella para representar el circuito equivalente monofásico del transformador de tres devanados, despreciando la corriente de magnetización, como se muestra en la figura siguiente: ZT ZS S ZP P P S T T A). Símbolo para el diagrama unifilar ZT B). Circuito equivalente El punto común es ficticio y no tiene relación con el neutro del sistema. Los puntos P, S y T están conectados a las partes del sistema unidas a los devanados primario, secundario y terciario del transformador. Como los valores óhmicos de las impedancias deben estar referidos a 321 ELECTROTECNIA III-322 la misma tensión, se sigue que la conversión a impedancias por unidad requiere los mismos kVA base para los tres circuitos y tensiones base, en los circuitos, que estén en la misma relación que las tensiones de línea nominales de los tres circuitos del transformador. Ejemplo 7-5. Los valores nominales trifásicos de un transformador de tres devanados son, Primario: conectado en estrella, 66 kV, 15 MVA. Secundario: conectado en estrella, 13,2 kV, 10 MVA. Terciario: Conectado en delta, 2,3 kV, 5 MVA. Despreciando la resistencia, las impedancias de pérdidas valen: Zps = 7 %, sobre la base de 15 MVA, 66 kV. Zpt = 9 %, sobre la base de 15 MVA, 66 kV. Zst = 8 %, sobre la base de 10 MVA, 13,2 kV. Determinar las impedancias por unidad del circuito equivalente, conectado en estrella, para una base de 15 MVA y 66 kV en el circuito primario. Si una fuente de tensión constante (barra infinita) alimenta a una carga óhmica pura de 5 MVA y 2,3 kV y a un motor síncrono de 7,5 MVA y 13,2 kV, con una reactancia subtransitoria de X” = 20 %. La fuente se conecta al primario del transformador, descrito anteriormente. El motor y la carga óhmica están conectados al secundario y el terciario del transformador. Dibujar el diagrama de impedancias por unidad, para una base de 66 kV y 15 MVA en el primario. SOLUCIÓN. Con una base en el circuito primario de 15 MVA y 66 kV, las bases adecuadas para las impedancias por unidad del circuito equivalente son 15 MVA, 66 kV para las magnitudes del circuito primario, 15 MVA y 13,2 kV para las del circuito secundario y 15 MVA, 2,3 kV para las del terciario. El diagrama unifilar del circuito se muestra en la figura siguiente: 2,3 kV 5 MVA 66 kV 15 MVA 13,2 kV 10 MVA FUENTE 2,3 kV 5 MVA 13,2 kV 7,5 MVA 322 ELECTROTECNIA III-323 Zps y Zpt se han medido en el circuito primario y están ya, por consiguiente, expresadas en la base adecuada para el circuito equivalente. No es necesario cambio de tensión para Zst. El cambio de kVA base se hace en la forma siguiente: Z st ,n % Z st ,d % MVA n 15 8 12% MVA d 10 Las impedancias del circuito equivalente, en por unidad, respecto a la base especificada, son, Z P 1 1 0 Z 1 0 1 S Z T 0 1 1 Z P j0, 02p.u 1 1 Z PS 1 1 0 Z 1 0 1 PT Z ST 0 1 1 ; Z S j0, 05p.u ; j0, 07 j0, 02 j0, 09 j0, 05 j0,12 j0, 07 Z T j0, 07 p.u La fuente de tensión constante se puede representar por un generador sin impedancia interna. La resistencia de la carga es de 1,0 por unidad, sobre las bases de 2,3 kV y 5 MVA, valores que son sus datos nominales en el terciario. Expresada sobre la base de 2,3 kV y 15 MVA, la resistencia de carga es, Rn ,pu Rd ,pu MVA Bn 15 1, 0 3, 0p.u MVA Bd 5 Cambiando la reactancia del motor a una base de 13,2 kV y 15 MVA, se obtiene " X pu X % MVA Bn 20 15 0, 40p.u 100 MVA Bd 100 7, 5 El diagrama de impedancias, por unidad, para una base de 66 kV y 15 MVA se muestra en la figura siguiente: 323 ELECTROTECNIA III-324 j 0,05 j 0,02 j 0,40 + j 0,07 - + 3,0 Em - Ventajas de los cálculos por unidad. Efectuar los cálculos de sistemas eléctricos en función de los valores por unidad representa una enorme simplificación del trabajo. La verdadera apreciación del valor del método por unidad la da la experiencia; sin embargo resumiremos brevemente algunas de sus ventajas. 1. Los fabricantes indican normalmente la impedancia de un elemento de un aparato en por ciento o por unidad de los valores nominales que figuran en la placa de características. 2. Las impedancias por unidad de máquinas del mismo tipo, con valores nominales dentro de un amplio margen, tienen valores dentro de un margen muy estrecho, aunque los valores óhmicos difieran materialmente para máquinas de distintos valores nominales. Por esta razón, si no se conoce la impedancia, generalmente es posible seleccionarla a partir de datos medios tabulados, que proporcionan un valor razonablemente correcto. La experiencia en el trabajo por unidad familiariza con los valores adecuados de las impedancias por unidad para diferente tipo de aparatos. 3. Si se especifica la impedancia en ohms en un circuito equivalente, cada impedancia se debe referir al mismo circuito multiplicando por el cuadrado de la relación de las tensiones nominales de los dos lados del transformador que conecta el circuito de referencia y el circuito que contiene la impedancia. La impedancia por unidad, una vez expresada en la base adecuada, es la misma referida a los dos lados del transformador. 4. La forma en que los transformadores se conectan en los sistemas trifásicos no afectan a las impedancias por unidad del circuito equivalente, aunque la conexión determina la relación entre las tensiones base de los dos lados del transformador. 4. EJERCICIOS. Ejercicio 7-1. Un transformador de 50 MVA, con tensiones de 34,5 : 161 kV, con una reactancia de 10 %, se conecta a un sistema de potencia donde todos los otros valores de reactancias están en una base de 100 MVA y 34,5 kV o 161 kV. Determine el valor de la reactancia del transformador con los valores base del sistema. 324 ELECTROTECNIA III-325 SOLUCIÓN. El transformador de 50 MVA, 34,5:161 kV, con reactancia de 10 %, se conecta a un sistema de potencia donde todos los otros valores de impedancia están en una base de 100 MVA; 34,5 kV o 161 kV. Para cambiar la base del transformador, se usa la ecuación En virtud de que tenemos la misma tensión base en el sistema y el transformador, podemos utilizar una ecuación simplificada en la cual sólo se relacionan las potencias base. S 100 X n Bn X d 10 20% 0, 20p.u 50 S Bd en una base de 100 MVA y 34,5 kV del lado de 34,5 kV, o en una base de 100 MVA y 161 kV del lado de 161 kV. Ejercicio 7-2. Se tiene un transformador monofásico de dos devanados con una potencia nominal de 20,0 kVA, con tensiones de 480/120 V, de 60 Hz. La impedancia de dispersión equivalente del transformador referida al devanado de 120 V, designado como el devanado 2, es Z 2 0, 0525/ 78,10 . Usando las características nominales del transformador como valores base, determine el valor de la impedancia de dispersión referida al devanado 2 y al devanado 1. SOLUCIÓN. Los valores de base son, S B 20, 0kVA ; VB1 480 V ; VB 2 120, 0 V De donde, ZB2 VB22 120, 02 0, 720 S B 20, 0 103 La impedancia de dispersión, por unidad, referida al devanado 2 es, Z 2p.u Z 2 0, 0525 / 78,1 0, 0729 / 78,10 p.u Z B2 0, 720 Si Z 2 se refiere al devanado 1, 2 V 480 Z1 1 Z 2 0, 0525 / 78,1 0, 840 / 78,10 120, 0 V2 2 La impedancia base en el lado de 480 V del transformador es, 325 ELECTROTECNIA III-326 Z B1 VB21 4802 11, 52 S B 20, 0 103 Y la reactancia de dispersión referida al devanado 1, por unidad, es, Z 1 0, 840 / 78,1 0, 0729 / 78,10 Z B1 11, 52 Así, la impedancia de dispersión por unidad permanece sin cambio, cuando se refiere del devanado 2 al devanado 1. Z 1p.u Ejercicio 7-3. El generador y el transformador, mostrados en la figura Y Barra Barra G Sistema Transformador Fuente equivalente Sistema Ejemplo típico para combinar un generador y un transformador en una fuente equivalente tienen las características siguientes: Generador de 25 MVA; 4 kV; X”d = 25 %. Transformador de 30 MVA; 4,2:115 kV; en la derivación de 3,9 kV; donde XT = 10 %. Se combinan en una reactancia equivalente en una base de 100 MVA, 110 kV. Con el banco de transformadores operando en su derivación de 3,9 kV. La relación del transformador es, n 115 29, 5 3, 9 La tensión base del lado de baja tensión correspondiente a la base de 110 kV del lado de alta tensión es, 1 110 kVB BT kVB AT 3, 73kV n 29, 5 Puesto que esta base de 3,73 kV es diferente de la base especificada de la reactancia subtransitoria del generador, entonces, 2 X " Gn p.u X " Gd p.u kVBd kVA Bn kVBn kVA Bd 25 4, 00 100 1,150p.u 100 3, 73 25 2 en base de 100 MVA; 3,73 kV; o en base de 100 MVA; 110 kV. Similarmente, la reactancia del transformador en la nueva base es, 326 ELECTROTECNIA III-327 2 kV kVA Bn 10 3, 90 100 X Tnp.u X Td p.u Bd 0, 364p.u kVBn kVA Bd 100 3, 73 30 2 en base de 100 MVA; 3,73 kV ; o en base de 100 MVA; 110 kV Ahora las reactancias del generador y del transformador se pueden combinar en una reactancia equivalente, esto es " X eq X Gn p.u X Tn p.u 1,150 0, 364 1, 514p.u ambos en base de 100 MVA y 110 kV. Ejercicio 7-4. Tres zonas de un circuito monofásico se identifican en la figura (a). Las zonas están conectadas por medio de transformadores T1 y T2, cuyos valores nominales también se muestran. Usando los valores base de 30 kVA y 240 V de la zona 1, dibuje el circuito por unidad y determine las impedancias por unidad y la tensión de la fuente por unidad. Después calcule la corriente de carga tanto en amperes como en por unidad. La resistencia de los devanados y las admitancias paralelo de las ramas se desprecian. Zona 1 Zona 2 Zona 3 V f 220/0,0V T1 30 kVA 240/480 V Xe = 0,10 p.u X L = 2,00 Z car = 0,900 + j 0,200 T2 20 kVA 460/115 V Xe = 0,10 p.u (a) SOLUCIÓN. Primero los valores base en cada zona se determinaran. La potencia base S B 30, 0kVA es la misma para toda la red. También, la tensión base VB1 240 V se especifica para la zona 1. Cuando se desplaza la tensión a través de los transformadores, las tensiones base cambian en proporción a las relaciones de tensión de los transformadores, Así 480 VB 2 240 480 V 240 y 115 VB 3 480 120, 0 V 460 327 ELECTROTECNIA III-328 Las impedancias base en las zonas 2 y 3 son, VB22 4802 ZB2 7, 68 S B 30, 0 103 y ZB3 VB23 120, 02 0, 480 S B 30, 0 103 Y la corriente base en la zona 3 es, S B 30, 0 103 IB3 250 A VB 3 120, 0 Enseguida, las impedancias por unidad se calculan usando el sistema de los valores base. Puesto que S B 30, 0kVA es la misma que el valor nominal del transformador T1, y VB1 240 V es la misma que la tensión nominal de la zona 1 del lado del transformador T1, el valor por unidad de la reactancia de T1 es la misma que su valor de placa, X T 1 p .u 0,1p.u . Sin embargo, la reactancia de dispersión del transformador T2 se debe convertir de sus valores nominales de placa a los valores del sistema base. Usando 2 V S Z np.u Z d p.u Bd Bn VBn S Bd y VB 2 480 V 3 460 30, 0 10 X T 2p.u 0,10 0,1378p.u 3 480 20, 0 10 2 En forma alternativa, usando VB 3 120,0V , 115, 0 30, 0 10 3 X T 2p.u 0,10 0,1378p.u 3 120, 0 20, 0 10 2 Lo cual da el mismo resultado. La línea la cual está localizada en la zona 2, tiene una reactancia por unidad de, X Lp.u X L 2, 00 0, 260p.u Z B 2 7, 68 y la carga la cual está localizada en la zona 3, tiene una impedancia por unidad de, 328 ELECTROTECNIA III-329 Z car _ p.u Z car 0, 900 j0, 200 1, 875 j0, 417 p.u ZB3 0,480 El circuito por unidad se muestra en la figura (b). j X T 1p.u j X L p.u j X T 2 p.u j0,10p.u j0, 260p.u j0,1378p.u I f p.u + V f p.u Z car p.u 0,917 /0,00 p.u 1,875 + j0, 417 p.u Zona 1 VB1 = 240 V ZB1 = 1,920 SB = 30,0 kVA Zona 2 VB2 = 480 V ZB2 = 7,68 SB = 30,0 kVA Zona 3 VB3 = 120,0 V ZB3 = 0,480 SB = 30,0 kVA IB3 = 250 A (b) Donde se muestran los valores base de cada zona y la tensión de la fuente por unidad. La impedancia base de la zona y el valor de la fuente por unidad son, Z B1 V f p.u VB21 2402 1, 920 S B 30, 0 103 V f 220 / 0, 0 0, 917 / 0, 0p.u VB1 240 Ahora la corriente por unidad se calcula fácilmente de la figura (b) en la forma siguiente: I car p.u V f p.u j X T 1p.u X Lp.u X T 2 p.u Z car p . u 0, 917 / 0, 0 j 0,100 0, 260 0,1378 1, 875 j0, 417 0, 440 / 26, 0 0 p.u 329 ELECTROTECNIA III-330 La corriente real es, I car I car p .u I B 3 0,440 / 26,0 250 110,0 / 26,00 A Ejercicio 7-5. En la figura se ha representado el diagrama unifilar de un sistema eléctrico de potencia sin carga. Las características de los generadores, transformadores y las líneas de transmisión son las siguientes: Generador G1: 20 MVA; 6,9 kV; X” = 15 %. Generador G2: 10 MVA; 6,9 kV; X” = 15 %. Transformador T1: 25 MVA; 115 Y: 6,9 kV; X = 10 %. Transformador T2: 12 MVA; 115 Y : 6,9 kV; X = 10 %. Transformador T3: tres unidades monofásicas, cada una de 10 MVA; 75 : 7,5 kV; X = 10 %. Línea de transmisión L1: X = j 100 . Línea de transmisión L2: X = j 80 . T3 T1 L2 L1 G1 Y G3 Y Y Y Y Y T2 G2 Y Dibujar el diagrama de reactancias, poniendo todas ellas en por unidad. Elegir una base de 30 MVA y 6,9 kV. SOLUCIÓN. Las tensiones base en las diferentes partes del sistema son, Tensión base para el generador G1, kVBG1 6,9kV Tensión base para las líneas de transmisión L1 y L2, y las barras colectoras B1, kVBB1 kVB kVAT-T1 115 6, 9 115kV kVBT-T1 6, 9 Tensión base para el generador G2, kVBG2 kVBB1 kVBT-T2 6, 9 115 6, 9kV kVAT-T2 115 330 ELECTROTECNIA III-331 Tensión base para el generador G3, kVBG3 kVBB1 kVBT-T3 7, 5 115 11, 5kV kVAT-T3 75 La reactancia subtransitoria, por unidad, del generador G 1 es, X G" 1 X G" 1 % MVAn 100 MVAd 15 30 0, 225p.u. 100 20 La reactancia por unidad del transformador T1 es, XT 1 X T 1 % MVAn 10 30 0,120p.u. 100 MVAd 100 25 La reactancia, por unidad, de la línea L1 es, X L1 X L1 MVA B 30 100 0, 227 p.u. 2 kVBB1 115 2 La reactancia subtransitoria, por unidad, del generador G 2 es, X " G2 X G" 2 % MVAn 15 30 0, 450p.u. 100 MVAd 100 10 La reactancia, por unidad, del transformador T2 es, XT 2 X T 2 % MVAn 10 30 0, 250p.u. 100 MVAd 100 12 La reactancia, por unidad de la línea L2 es, X L2 X L2 MVA B 30 80 0,181p.u. 2 kVBB1 1152 La reactancia, por unidad, del transformador T 3 es, 2 X % kV MVA Bn X T 3 T 3 Bd 100 kVBn MVA Bd 2 10 3 7, 5 30 0,128p.u. 100 11, 5 3 10 La reactancia subtransitoria, por unidad, del generador G 3 es, 2 X " G3 X G" 3 % kVBd MVABn 15 13, 8 30 0, 216p.u 100 kVBn MVABd 100 11, 5 30 2 331 ELECTROTECNIA III-332 El diagrama de reactancias solicitado es, - + j 0,225 p.u. j 0,120 p.u. j 0,227 p.u. j 0,181 p.u. - j 0,128 p.u. j 0,216 p.u. + EG1 EG3 j 0,450 p.u. j 0,250 p.u. + EG2 Ejercicio 7-6. Los arrollamientos de un transformador de tres devanados tienen las características siguientes: Primario: Conectado en estrella; 6,6 kV; 15 MVA. Secundario: Conectado en estrella; 33 kV; 10 MVA. Terciario: conectado en delta; 2,2 kV; 7,5 MVA. Despreciando la resistencia, se obtienen a partir de las pruebas, las impedancia de pérdidas siguientes: Medidas desde el lado primario: Zps = j 0,232 , Zpt = j 0,290 . Medidas desde el lado secundario: Zst = j 8,70 . Determinar las impedancias del circuito equivalente en estrella, en por unidad, con una base en el circuito primario de 15 MVA y 6,6 kV. SOLUCIÓN. Con una base de 15 MVA y 6,6 kV; que corresponden a las características del circuito primario, las bases adecuadas para las impedancias por unidad del circuito equivalente son, 10 MVA y 33 kV para el circuito secundario y 7,5 MVA y 2,2 kV para el circuito terciario. Las impedancias por unidad son, Z ps Z ps MVABp Z pt Z pt MVABp Z st Z st 2 Bp kV 2 Bp kV 0, 232 15 0, 080p.u 6, 62 0, 290 15 0,10p.u 6, 62 MVA Bs 10 8, 70 2 0, 080p.u 2 kVBs 33 Zps y Zpt se han medido en el circuito primario y están ya, por consiguiente, expresadas en la base adecuada para el circuito equivalente. No es necesario hacer cambio de tensión para Zst. El cambio para la base en KVA solicitada se hace en la forma siguiente: 332 ELECTROTECNIA III-333 Z stn Z std MVA Bsn 15 0, 080 0,12p.u MVA Bsd 10 Las impedancias del circuito equivalente son, 1 Z P 1 1 0 Z PS Z 1 0 1 Z S PT ZT 0 1 1 Z STn 1 1 1 0 0, 08 0, 03 1 0 1 0,10 0, 05 0 1 1 0,12 0, 07 Z P 0,03p.u ; Z S 0,05p.u ; ZT 0,07p.u El diagrama de impedancias equivalente, por unidad, para las bases de 15 MVA y 6,6 kV; se muestran en la figura siguiente, j 0,05 p.u. S j 0,03 p.u. P j 0,07 p.u. T 333 ELECTROTECNIA III-334 UNIDAD 8. FUNDAMENTOS DEL ANÁLISIS DEL CORTO CIRCUITO. 1. INTRODUCCIÓN. El objetivo de un estudio de corto circuito es proporcionar información sobre corrientes y tensiones en un sistema eléctrico durante condiciones de falla. Esta información se requiere para determinar las características de capacidad interruptiva y momentánea de los interruptores y otros dispositivos de protección localizados en el sistema, calcular los esfuerzos electrodinámicos en barras colectoras de subestaciones y tableros, calcular redes de tierra, seleccionar conductores de alimentadores, así como para diseñar un sistema adecuado de relevadores de protección los cuales deberán reconocer la existencia de la falla e iniciar la operación de los dispositivos de protección asegurando así la mínima interrupción en el servicio y evitando daños a los equipos. 2. CORRIENTES DE CORTO CIRCUITO. Naturaleza de las corrientes de corto circuito. ¿Que es y como se origina una corriente de corto circuito? Una corriente de corto circuito es aquella que circula en un circuito eléctrico cuando existe el contacto entre dos o más conductores al perderse el aislamiento entre ellos o entre ellos y tierra. La magnitud de la corriente de corto circuito es mucho mayor que la corriente nominal o de carga que circula en un circuito. En condiciones normales de operación, la carga toma una intensidad de corriente proporcional a la tensión aplicada y a la impedancia de la propia carga. Si se presenta un corto circuito en las terminales de la carga, la tensión queda aplicada únicamente a la baja impedancia de los conductores de alimentación y a la impedancia de la fuente hasta el punto del corto circuito, ya no oponiéndose la impedancia normal de la carga y generándose una corriente mucho mayor. Corriente de corto circuito y sus efectos. Si se debe suministrar la protección adecuada a un sistema de energía eléctrica, el tamaño de dicho sistema también se debe considerar para determinar la magnitud de la corriente que será entregada. Esto hace que los interruptores o fusibles se seleccionen con la capacidad interruptiva adecuada. Esta capacidad de interrupción debe ser lo suficientemente alta para abrir con seguridad la corriente máxima de corto circuito la cual el sistema puede hacer que fluya a través de los interruptores si ocurre un corto circuito en el alimentador o circuito que proteje. La magnitud de la corriente de carga se determina por la cantidad de trabajo que se está haciendo y tiene poca relación con el tamaño del sistema que alimenta la carga. Sin embargo, la magnitud de la corriente de corto circuito es algo independiente de la carga y está directamente relacionada con el tamaño o capacidad de la fuente de potencia. Entre más grande sea el aparato que suministra la potencia eléctrica al sistema, mayor será la corriente de corto circuito. 334 ELECTROTECNIA III-335 Corriente de corto circuito = V/ZT = 100/0,1 = 1000 A Debe ser capaz de interrumpir 1000 A Barra infinita 1000 A 5A X A M F 100 V; 100 A Z = 0,1 Motor, corriente de carga 5 A, impedancia aparente 20 Corriente de corto circuito = V/ZT = 100/0,01 = 10 000 A Barra infinita 10000 A Debe ser capaz de interrumpir 10 000 A 5A X A 100 V; 1000 A Z = 0,01 M F Motor, corriente de carga 5 A, impedancia aparente 20 Figura número 1. Ilustración que muestra que la capacidad de la fuente de potencia tiene más efecto sobre la corriente de corto circuito que la magnitud de la carga Tomando como ejemplo un caso simple: un motor trifásico de 10 CF de 440 V toma alrededor de 13 A a plena carga y tomará solamente esa cantidad ya sea alimentado por una fuente de 25 kVA o de un banco de transformadores de 2 500 kVA. Así, si solamente se considera la corriente de carga cuando se selecciona el interruptor correspondiente a esa rama, se debe especificar un interruptor de potencia de 15 o 20 A. Sin embargo, el tamaño del sistema de potencia atrás del circuito tiene una fuerza real sobre la cantidad de corriente de corto circuito que puede fluir como el resultado de un corto circuito sobre el lado de carga del interruptor. De aquí que, se puede requerir un interruptor diferente para manejar la corriente de corto circuito que suministra el banco de 2 500 kVA que para la fuente de 25 kVA. Un ejemplo matemático simple se muestra en la figura número 1. Los números se han elegido por su fácilidad de cálculo más bien que para la representación de las condiciones reales del sistema. La impedancia que limita el flujo de corriente a la carga, consiste principalmente de los 20 de impedancia aparente del motor. Si ocurre un corto circuito en el punto F, la única impedancia que límita el flujo de la corriente de 335 ELECTROTECNIA III-336 corto circuito es la impedancia del transformador (0,1 comparados con los 20 del motor); por consiguiente, la corriente de corto circuito es de 1 000 A, o sea 200 veces más grande que la corriente de la carga. A menos que el interruptor de potencia A pueda abrir 1 000 A, la corriente de corto circuito deberá continuar fluyendo, haciendo un daño mayor. Supongase que la planta crece y requiere un transformador más grande, uno de 1000 A nominales, que sustituye a la unidad de 100 A. Un corto circuito en F, (parte inferior de la figura número 1) ahora será limitado por solamente 0,01 , la impedancia del transformador más grande. Aunque la corriente de carga permanece en 5 A, la corriente de corto circuito será ahora de 10 000 A, y el interruptor de potencia en A debe ser capaz de abrir tal cantidad. Consecuentemente es necesario considerar el tamaño del sistema de alimentación de la planta así como la corriente de carga, para asegurar que el interruptor de potencia o fusibles seleccionados tengan una capacidad de interrupción para poder manejar el flujo de corriente de corto circuito. Fuentes de corriente de corto circuito. Cuando se determinan las magnitudes de las corrientes de corto circuito, es extremadamente importante que se consideren todas las fuentes de corriente de corto circuito y que las reactancias características de estas fuentes sean conocidas. Existen cuatro fuentes básicas de corrientes de corto circuito, estas son, 1. Generadores. 2. Motores y condensadores síncronos. 3. Motores de inducción. 4. Sistema de la Compañía suministradora de energía. Todas ellas alimentan con corriente de corto circuito a la falla. TABLEROS DE LA INDUSTRIA 4 1 GENERADOR COMPAÑÍA SUMINISTRADORA X FALLA 3 MOTOR SÍNCRONO MOTOR DE INDUCCIÓN 2 FIGURA NÚMERO 2. FUENTES DE CORRIENTES DE CORTO CIRCUITO 336 ELECTROTECNIA III-337 Generadores. Los generadores son movidos por turbinas, motores diesel, u otro tipo de primomotores. Cuando ocurre un corto circuito en el circuito al cual está conectado el generador, éste continúa generando tensión debido a que la excitación del campo se mantiene y el primomotor sigue moviéndolo a velocidad normal. La tensión generada produce una corriente de corto circuito de gran magnitud, la cual fluye del generador (o generadores) al punto de falla. Este flujo de corriente se limita únicamente por la impedancia del generador y el punto a donde ocurre la falla. Si el corto circuito ocurre en las terminales del generador, la corriente queda limitada solamente por la impedancia de la máquina. Motores síncronos. Los motores síncronos están construidos substancialmente igual que los generadores; tienen un campo excitado por corriente directa y un devanado en el estator por el cual fluye la corriente alterna. Normalmente el motor toma la potencia de la línea y convierte la energía eléctrica en energía mecánica. No obstante, el diseño de un motor síncrono es tan semejante al de un generador de energía eléctrica, que puede producirla justo como un generador, moviendo el motor síncrono como un primomotor. Durante el corto circuito en el sistema el motor síncrono actúa como un generador y entrega corriente de corto circuito, en lugar de tomar corriente de carga de él como se muestra en la figura número 3. Tan pronto como el corto circuito se establece, la tensión en el sistema se reduce a un valor mucho más bajo. Consecuentemente el motor deja de entregar energía a la carga mecánica y empieza a detenerse. Sin embargo, la inercia de la carga y el motor impiden al motor que se detenga; en otras palabras, la energía rotatoria de la carga y el rotor mueven al motor síncrono como un primomotor mueve a un generador. 337 ELECTROTECNIA III-338 Corriente de carga del motor Sistema del suministrador MOTOR SÍNCRONO Corriente de corto circuito tomada del motor Sistema del suministrador MOTOR SÍNCRONO X Corto circuito FIGURA NÚMERO 3. Normalmente los motores toman corriente de la fuente o sistema suministrador, pero producen corrientes de corto circuito cuando ocurre un corto circuito en la planta. El motor síncrono viene a ser un generador y suministra corriente de corto circuito por varios ciclos después de que ocurre el corto circuito en el sistema. La figura número 4. muestra un oscilograma de la corriente desarrollada por el motor síncrono durante el corto circuito del sistema. 338 ELECTROTECNIA III-339 Corriente de corto circuito suministrada por el motor síncrono El corto circuito se inicia en este punto FIGURA NÚMERO 4. Trazo del oscilograma de la corriente de corto circuito producida por el motor síncrono. La magnitud de la corriente de corto circuito depende de la potencia, la tensión nominal y reactancia del motor síncrono y de la reactancia del sistema hasta el punto de falla. Motores de inducción.0 La inercia de la carga y el rotor de un motor de inducción tienen exactamente el mismo efecto sobre el motor de inducción como el motor síncrono; siguen moviendo al motor después de que ocurre un corto circuito en el sistema. Sólo existe una diferencia. El motor de inducción no tiene un campo excitado por corriente directa, pero existe un flujo en el motor durante la operación normal. Este flujo actúa en forma similar al flujo producido por el campo de corriente directa en el motor síncrono. El campo del motor de inducción se produce por la inducción desde el estator en lugar del devanado de corriente directa. El flujo del motor permanece normal mientras se aplica tensión al estator desde una fuente externa (el sistema eléctrico), sin embargo, si la fuente externa de tensión se elimina súbitamente, esto es, cuando ocurre el corto circuito en el sistema, el flujo en el rotor no puede cambiar instantáneamente. Debido a que el flujo del rotor puede decaer instantáneamente y la inercia sigue moviendo al motor, se genera una tensión en el devanado del estator cuando una corriente de corto circuito que fluye hasta el punto de falla hasta que el flujo del rotor decae a cero. Para ilustrar la corriente de corto circuito de un motor de inducción en un caso práctico, se tomaron oscilogramas de un motor de inducción de rotor devanado de 150 CF nominales, 440 V, 60 Hz, tres fases, 10 polos, 7 200 r.p.m. La resistencia exterior del rotor se puso en corto circuito en cada uno de los casos, con el objeto de que el efecto pudiera ser similar al que se obtiene con la resistencia baja de un motor de inducción de jaula de ardilla La figura número 5 muestra las corrientes primarias cuando la máquina inicialmente está corriendo con carga baja y se aplica un corto circuito trifásico en el punto correspondiente a sus terminales de entrada (estator), en el tiempo T1. Las corrientes mostradas se midieron en el lado del corto circuito del motor, así que la contribución a la corriente de corto circuito de la fuente de potencia no aparece, sino solamente la contribuida por el motor. 339 ELECTROTECNIA III-340 10 8 6 4 2 0 T1. El corto circuito se inicia en este punto FIGURA NÚMERO 5. Trazo del oscilograma de la corriente de corto circuito producida por un motor de inducción corriendo con carga baja Se hacen pruebas similares con la máquina corriendo inicialmente a plena carga en las cuales se observa que la corriente de corto circuito producida por el motor cuando ocurre el corto circuito substancialmente es la misma. Observe que la corriente máxima ocurre en la parte más baja del oscilograma y es alrededor de 10 veces la corriente nominal de plena carga. La corriente se desvanece casi completamente en cuatro ciclos, puesto que no hay corriente de campo sostenida en el rotor para suministrar el flujo, como en el caso de las máquinas síncronas. El flujo no es lo suficientemente grande para producir suficiente corriente de corto circuito para afectar la carga momentánea en el interruptor y la carga de interrupción en el dispositivo el cual se abre en uno o dos ciclos después del corto circuito. De aquí que, las corrientes de corto circuito producidas por los motores solo se deben considerar en ciertos cálculos. La magnitud de la corriente de corto circuito producida por el motor de inducción depende de su potencia, tensión nominal, reactancia del motor y la reactancia del sistema hasta el punto de falla. Consecuentemente, el valor inicial simétrico de la corriente de corto circuito es aproximadamente igual a la corriente de arranque a tensión plena del motor. Sistema de la compañía suministradora. Los sistema eléctricos modernos de las compañías suministradoras, representan una red compleja y grande de plantas generadoras interconectadas. En un sistema típico, los generadores no se ven afectados por las corrientes altas de corto circuito que se producen en una planta industrial, únicamente aparece en ellos un incremento en su corriente de carga que tiende a permanecer constante. Las líneas de transmisión y distribución, así como los transformadores, introducen impedancias entre las plantas generadoras y los consumidores industriales; de no ser así, las compañías suministradoras serían una fuente infinita de corriente de falla. La representación de la compañía suministradora para el estudio del corto circuito, será una impedancia equivalente referida al punto de conexión (punto de acometida). Reactancia de las máquinas rotatorias. 340 ELECTROTECNIA III-341 La reactancia de una máquina rotatoria no es un valor simple, como lo es la reactancia de un transformador o de un tramo de cable, sino que es compleja y variable con el tiempo. Por ejemplo, si se aplica un corto circuito a las terminales de un generador la corriente de corto circuito es como se muestra en la figura número 6. Corriente en estado estable determinada por la reactancia síncrona Corriente de corto circuito El corto circuito ocurre en este instante Debido a la gran magnitud del oscilograma total solamente se muestran aquí los dos extremos. Esta línea representa la interrupción entre las dos partes. FIGURA NÚMERO 6. Trazo del oscilograma de la corriente de corto circuito producida por el generador. Corto circuito en las terminales del generador. Las corrientes parten de un valor alto y decaen a un estado estable después de que ha pasado algún tiempo desde el inicio del corto circuito. Puesto que la tensión de excitación del campo y velocidad permanecen sustancialmente constantes dentro del pequeño intervalo de tiempo considerado, se puede considerar un cambio aparente en la reactancia de la máquina, para explicar el cambio en la magnitud de la corriente de corto circuito con el tiempo. La expresión de la corriente variable para cualquier instante después de que ha ocurrido el corto circuito es una fórmula complicada en función del tiempo así como de otras variables. Con el fin de la simplificación del procedimiento de los cálculos de corto circuito para la aplicación de interruptores y protecciones, se consideran tres valores de reactancia para los generadores y motores, estas son, reactancia subtransitoria, reactancia transitoria y reactancia síncrona. Las tres reactancia se pueden describir brevemente como sigue: 1. Reactancia subtransitoria. Es la reactancia aparente del estator en el instante en que se produce el corto circuito y determina la corriente que circula en el devanado del estator durante los primeros ciclos mientras dure el corto circuito. 2. Reactancia transitoria. 341 ELECTROTECNIA III-342 Se trata de la reactancia inicial aparente del devanado del estator si se desprecian los efectos de todos los devanados amortiguadores y sólo se consideran los efectos del devanado del campo inductor. Esta reactancia determina la intensidad de corriente que circula durante el intervalo posterior al que se indicó anteriormente y en el que la reactancia subtransitoria constituye el factor decisivo. La reactancia transitoria hace sentir sus efectos durante 0,5 segundos o más, según la construcción de la máquina. 3. Reactancia síncrona. Es la reactancia que determina la intensidad de corriente que circula cuando se ha llegado a un estado estable. Sólo hace sentir sus efectos después de transcurrir algunos segundos desde el instante en que se ha producido el corto circuito y por tanto carece de valor en los cálculos de corto circuito, para la aplicación en interruptores de potencia, fusibles, y contactores, pero es útil para el estudio de ajustes de relevadores. La figura número 7 muestra la variación de la corriente con el tiempo y asociada a las reactancias mencionadas anteriormente con el tiempo y la escala de corriente.. Antes de que la carga tenga efecto sobre la magnitud de la corriente de corto circuito suministrada por el ´ ´´ generador. Los valores de X d y X d que generalmente da el diseñador de la máquina son los más bajos que se pueden obtener. Las características de las corrientes de corto circuito se deben entender antes de que se haga el análisis del sistema. Corriente de corto circuito Corriente máxima determinada por la reactancia subtransitoria, Xd ´´ Corriente máxima determinada por la reactancia transitoria, Xd´ Corriente determinada por la reactancia síncrona, Xd Tiempo FIGURA NÚMERO 7. Variación de la corriente de corto circuito de una máquina rotatoria con el tiempo. Corrientes de corto circuito simétricas y asimétricas. Estos términos se usan para describir la simetría de las ondas de corriente alterna alrededor del eje cero. Si las evolventes de los picos de las ondas de corriente son simétricas alrededor del eje cero, la corriente se denomina como corriente simétrica, figuras números 8 y 9. Si las evolventes de los picos de las ondas de corriente no son simétricas alrededor del eje cero, la 342 ELECTROTECNIA III-343 corriente se denomina como corriente asimétrica, figura número 10. La evolvente es la línea que se dibuja a través de los picos de las ondas, como se muestra en las figuras 8 a 11. Las evolventes de los picos son simétricas alrededor del eje cero. FIGURA NÚMERO 8. Onda de corriente alterna simétrica Las evolventes de los picos son simétricas alrededor del eje cero. FIGURA NÚMERO 9. Corriente alterna simétrica de corto circuito de un generador FIGURA NÚMERO 10 Curvas de corriente alterna asimétricas. Las condiciones mostradas aquí son para propósitos ilustrativos solamente. Las componentes de corriente directa caerán rápidamente a cero. 343 ELECTROTECNIA III-344 Las evolventes de los picos no son simétricas alrededor del eje cero. FIGURA NÚMERO 11. Trazo del oscilograma de una corriente de corto circuito Con el objeto de explicación muchas de las ilustraciones, tales como las figuras 10, 14 a 18, muestran ondas de corriente senoidales uniformemente desplazadas algunos ciclos, Se debe hacer notar que en los circuitos prácticos la cantidad de asimetría disminuye rápidamente después de que ocurre un corto circuito en el sistema. Esta disminución de la asimetría se muestra cualitativamente en ilustraciones tales como las de las figuras 11, 19,22 y 24. Los oscilogramas muestran que las corrientes de corto circuito son casi siempre asimétricas durante los primeros pocos ciclos después de que ocurre el corto circuito. Ellas también muestran que la asimetría es máxima en el instante en que ocurre el corto circuito y que la corriente viene a ser gradualmente simétrica unos pocos ciclos después de que ocurre el corto circuito. El trazo de un oscilograma de una corriente de corto circuito típica se muestra en la figura número 11. Porque las corrientes de corto circuito son asimétricas. En los sistemas de potencia usuales las tensiones generadas o aplicadas son de forma de onda senoidal. Cuando ocurre un corto circuito, generalmente resultan corrientes de corto circuito de forma de onda senoidal. Por simplicidad en las discusiones siguientes se consideran tensiones y corrientes de forma de onda senoidal. En los circuitos de potencia ordinarios la resistencia del circuito es despreciable comparada con la reactancia del circuito. El factor de potencia de la corriente de corto circuito se determina por la relación de la resistencia a la reactancia de únicamente el circuito, no de la carga. Por consiguiente las corrientes de corto circuito en la mayoría de los circuitos de potencia se atrasa con relación a la tensión interna del generador en aproximadamente 90 grados (ver figura número 12). La tensión interna del generador es la tensión generada en las bobinas del estator por el flujo del campo. Si en un circuito que principalmente contiene reactancia ocurre un corto circuito en el pico de la onda de tensión, la corriente de corto circuito arrancara desde cero y describe una onda 344 ELECTROTECNIA III-345 senoidal la cual es simétrica alrededor del eje cero (figura número 13). Esta es conocida como una corriente de corto circuito simétrica. Si en el mismo circuito (por ejemplo uno que contenga una relación grande de reactancia a resistencia) ocurre un corto circuito en el punto cero de la onda de tensión, la corriente arrancará de cero pero no puede seguir simétricamente la onda de tensión alrededor del eje cero puesto que tal corriente debe estar en fase con la tensión. La forma de onda debe ser la misma que la de la tensión pero 90 grados atrasada. Esto puede ocurrir solamente si la corriente se desplaza desde el eje cero, como se muestra en la figura número 14. En esta ilustración la corriente es una onda senoidal y esta desplazada 90 grados de la onda de tensión y también desplazada del eje cero. Los dos casos mostrados en las figuras 13 y 14 son extremos. Si en un corto circuito que contiene solamente reactancia, el corto circuito ocurre en cualquier punto excepto en el pico de la onda de tensión, abra algo de desplazamiento de la corriente (figura número 15). La cantidad de desplazamiento depende del punto en la onda de tensión en el cual ocurre el corto circuito. Este puede variar desde cero (mostrado en la figura número 13) a un máximo (mostrado en la figura número 14). En un circuito que contenga tanto reactancia como resistencia, la cantidad de desplazamiento de la corriente de corto circuito pude variar entre los mismos límites que se tienen cuando solo se tiene reactancia. Sin embargo, el punto de la onda de tensión al cual debe ocurrir el corto circuito para producir máxima asimetría depende de la relación de la reactancia a la resistencia del circuito. La asimetría máxima se obtiene cuando el corto circuito ocurre a un ángulo de tiempo igual a 900 + (medido hacia adelante en grados desde el punto cero de la onda de tensión) donde la tangente de es igual a la relación de la reactancia a la resistencia del circuito. La corriente de corto circuito será simétrica cuando la falla ocurra a 900 de ese punto en la onda de tensión. Como ejemplo, considere un circuito que tiene igual reactancia y resistencia, la relación de reactancia a resistencia es igual a 1. La tangente de 450 es 1, de aquí que, el defasamiento máximo se obtiene cuando el corto circuito ocurre a 1350 desde el punto cero de la onda de tensión (figura número 16). 345 ELECTROTECNIA III-346 TRANSFORMADOR GENERADOR LÍNEA Corto circuito X Tensión interna del generador Impedancia del generador Tensión interna del generador aplicada aquí Impedancia del transformador Impedancia de la línea X R X R X R 10 % 2% 7% 0,7 % 2% 0,5 % Aproximadamente 90 0 Corriente de corto circuito Diagrama fasorial Reactancia X = 19 %, resistencia R = 1,4 % La resistencia es menor que 1/10 de la reactancia, de aquí que se pueda despreciar sin un error apreciable Aproximadamente 90 0 Tensión Corriente Tiempo 0 90° El diagrama muestra las ondas senoidales correspondientes al diagrama fasorial FIGURA NÚMERO 12. Diagrama que ilustra las relaciones de fase de la tensión y la corriente de corto circuito. Tensión generada Corriente de corto circuito t El corto circuito ocurre en este punto FIGURA NÚMERO 13. Corriente de corto circuito simétrica y tensión del generador para un corto circuito con factor de potencia cero. 346 ELECTROTECNIA III-347 Corriente de corto circuito t 0 Punto de corto circuito Tensión generada FIGURA NÚMERO 14. Corriente de corto circuito y tensión generada en un circuito con factor de potencia cero. La condición es teórica y se muestra solo con el propósito de ilustración. Corriente t Aquí ocurre el corto circuito Tensión FIGURA NÚMERO 15. Corriente de corto circuito y tensión generada con factor de potencia cero. El corto circuito ocurre en algún punto entre el punto cero y el pico de la onda de tensión generada. Esta condición es teórica y solamente se indica para propósitos de ilustración. La corriente de corto circuito viene a ser gradualmente simétrica en los circuitos prácticos. 347 ELECTROTECNIA III-348 Corriente de corto circuito 0 1350 1800 Tensión generda El corto circuito debe ocurrir aquí para producir el desplazamiento máximo FIGURA NÚMERO 16. Corriente de corto circuito y tensión generada en un circuito con reactancia igual a la resistencia. Esta condición es teórica y se muestra únicamente para propósitos de ilustración. La corriente de corto circuito viene a ser gradualmente simétrica en los circuitos prácticos. Componente de corriente directa de una corriente de corto circuito asimétrica. Las corrientes de alterna asimétricas cuando se trata como una sola onda de corriente son difíciles de interpretar para propósitos de aplicación en interruptores y ajuste de relevadores. También se requieren fórmulas complicadas para calcular su magnitud a menos que se resuelvan en componentes. Las corrientes de alterna asimétricas, para propósitos de aplicaciones prácticas en interruptores y ajustes de relevadores, arbitrariamente se dividen en componentes simples, las cuales hacen más fácil calcular la magnitud del corto circuito en ciertas cantidad de veces significativas después de que ocurre el corto circuito. Las corrientes alternas se comportan exactamente como si hubieran dos componentes de corriente fluyendo simultáneamente. Una es una componente de corriente alterna simétrica y la otra es una componente de corriente directa. La suma de esas dos componentes en cualquier instante es igual a la magnitud de la onda de corriente de alterna total asimétrica en ese instante. La componente de corriente directa referida aquí es generada dentro del sistema de corriente alterna sin considerar una fuente externa de corriente directa. En algunos casos, particularmente en las cercanías de trenes eléctricos de corriente directa, la corriente de corriente directa de los trenes fluye a través del circuito de corriente alterna vecino. Este tipo de corriente directa no se considera en estas discusiones o en los procedimientos de cálculo siguientes. Como un ejemplo de la solución de las corrientes alternas en sus componentes, refiriéndonos a la figura número 17 la cual muestra una corriente de corto circuito asimétrica la cual se resuelve en sus dos componentes, una simétrica de corriente alterna y una componente de 348 ELECTROTECNIA III-349 corriente directa como se muestra en la figura número 17. Si los valores instantáneos de las dos componentes (líneas punteadas) se suman en cualquier instante, el resultado será como el que se obtiene en la onda de corriente asimétrica. Corriente asimétrica total. Componente de corriente directa Eje cero Componente de corriente alterna FIGURA NÚMERO 17. Onda de corriente de corto circuito teórica para ilustrar las componentes de una corriente asimétrica. En circuitos prácticos, la componente de corriente directa debe decaer a cero en unos pocos ciclos. Como se menciono anteriormente, los ejemplos mostrados en las figuras números 14 y 17 son únicamente para propósitos de ilustración. En los circuitos prácticos la componente de corriente directa decae muy rápidamente como se muestra en la figura número 19. a = b, componente de directa Corriente asimétrica total. Componente de corriente directa a Eje cero b Componente de corriente alterna FIGURA NÚMERO 18. Componentes de una corriente de corto circuito asimétrica en la cual el corto circuito ocurre en algún punto entre el punto cero y el pico de la onda de tensión generada. Esta es una condición teórica, similar a la mostrada en la figura 17. Magnitud inicial de la componente de corriente directa. La magnitud de la componente de corriente directa depende del instante en que ocurre el corto circuito y puede variar desde cero, como en la figura número 13, hasta un valor inicial máximo igual al pico de la componente simétrica de corriente alterna, como en las figuras 349 ELECTROTECNIA III-350 números 14 a 17. Cuando el corto circuito ocurre en cualquier otro punto, tal como el mostrado en la figura número 18, la magnitud inicial de la componente de corriente directa es igual al valor de la componente simétrica de corriente alterna en el instante del corto circuito. Los límites anteriores se mantienen ciertos para la magnitud de la componente de corriente directa en sistemas haciendo caso omiso de la reactancia y la resistencia. Sin embargo, la componente de corriente directa no continua fluyendo con un valor constante, como se muestra en las figuras números 17 y 18, a menos que el circuito tuviera una resistencia igual con cero. Decremento. No hay en el sistema una tensión de corriente directa que mantenga constante el flujo de corriente directa; por consiguiente la energía representada por la componente de corriente directa se debe disipar como las pérdidas RI2 de la corriente de directa fluyendo a través de la resistencia del circuito. Si el circuito tuviera cero resistencia, la corriente de directa debería fluir con un valor constante (figuras números 17 y 18) hasta que el circuito se interrumpiera. Sin embargo, todos los circuitos prácticos tienen algo de resistencia, así que la componente de corriente directa decae como se muestra en la figura número 19. La combinación del decaimiento de la componente de corriente directa y la componente simétrica de corriente alterna da una onda asimétrica que cambia a onda simétrica cuando desaparece la componente de corriente directa. La proporción del decaimiento de la corriente se llama el decremento. Corriente total asimétrica Componente de corriente alterna Componente de corriente directa FIGURA NÚMERO 19. Trazo de un oscilograma que muestra como decae la componente de corriente directa y como la corriente de corto circuito asimétrica gradualmente viene a ser simétrica conforme desaparece la componente de corriente directa. Relación de reactancia a resistencia (X/R). La relación X/R es la relación de la reactancia a la resistencia del circuito. El decremento o relación de decaimiento de la componente de corriente directa es proporcional a la relación de la reactancia a la resistencia del circuito completo desde el generador al punto de corto circuito. La teoría es la misma que cuando se abre el circuito de una batería y una bobina inductiva. 350 ELECTROTECNIA III-351 Si la relación de la reactancia a la resistencia es infinita (por ejemplo, con cero resistencia) la componente de corriente directa nunca decae, como se muestra en las figuras números 17 y 18. De otra manera, si la relación es cero (todo es resistencia, sin reactancia), esta decae instantáneamente. Para cualquier relación de reactancia a resistencia entre estos límites, la componente de corriente directa toma un tiempo definido para disminuir substancialmente a cero, como se muestra en la figura número 19. En los generadores la relación de la reactancia subtransitoria a la resistencia puede ser del orden de 70:1; así que toma algunos ciclos en desaparecer la componente de directa. En circuitos lejanos a los generadores, la relación de reactancia a resistencia es más baja, y la componente de corriente directa decae más rápidamente. Conforme es mayor la proporción de resistencia a reactancia, hay más pérdidas RI2 de la componente de directa, y la energía de la corriente de directa se disipa más pronto. Consideremos que sucede cuando una tensión de corriente alterna se aplica a un circuito que tiene valores constantes de resistencia e inductancia. R i V L INT. FIGURA NÚMERO 20. La ecuación diferencial del circuito es, V sen t R i L di dt Y la corriente instantánea es, i V - Rt / L sen t e sen - Z Donde, Z R 2 L 2 y = tan -1 L / R El primer término de la ecuación de la corriente varía senoidalmente con el tiempo, el segundo término es aperiódico y decae exponencialmente con una constante de tiempo L/R. A este segundo término se le llama componente de corriente directa de la corriente. 351 ELECTROTECNIA III-352 Cuando = Cuando - = Tiempo Tiempo FIGURA NÚMERO 21. Constante de tiempo de corriente directa. Frecuentemente se dice que los generadores, motores, o circuitos tienen una cierta constante de tiempo de corriente directa. Esto se refiere nuevamente a la relación de decaimiento de la componente de corriente directa. La constante de tiempo es el tiempo, en segundos, requerido por la componente de corriente directa para reducir al 37 % de su valor original en el instante del corto circuito. Esta es la relación de la inductancia en henry a la resistencia en ohm de la máquina o circuito. Esta es solamente una guía de que tan rápido decae la componente de corriente directa. Establecida en otros términos, esto es el tiempo en segundos para que la componente de corriente directa alcance el cero si este continua decayendo con la misma relación que lo hizo inicialmente, como se muestra en la figura número 22. Componente de corriente directa b a Relación inicial de decaimiento de la componente de corriente directa a = 37 % de b (aproximadamente) Constante de tiempo en segundos FIGURA NÚMERO 22. Ilustración gráfica de la constante de tiempo Valor eficaz incluyendo la componente de corriente directa. El valor eficaz de las ondas de corriente alterna es significativo, puesto que los interruptores, fusibles, y arrancadores de motores se escogen en términos del valor eficaz de la corriente o kVA equivalentes. El valor eficaz máximo de la corriente de corto circuito ocurre en un tiempo de alrededor de un ciclo después del corto circuito, como se muestra en la figura número 19. Si no decayera la componente de directa como en la figura número 17, el valor eficaz 352 ELECTROTECNIA III-353 del primer ciclo sería 1,732 veces el valor eficaz de la componente de corriente alterna. En los circuitos prácticos siempre hay algo de decaimiento de la componente de corriente directa durante el primer ciclo. Un valor eficaz aproximado de un ciclo de una onda desplazada sea que este parcialmente o totalmente desplazada se expresa por la ecuación, c = a2 b2 Donde: c = valor eficaz de la onda de corriente desplazada o asimétrica en un ciclo. a = valor eficaz de la componente de corriente alterna. b = valor de la componente de corriente directa en el medio ciclo. Factor de multiplicación. El cálculo exacto del valor eficaz de una onda de corriente asimétrica en cualquier tiempo después del principio del corto circuito puede ser muy complicado. Factores de decremento considerados para componente de corriente directa en cualquier tiempo se requieren, así como factores exactos para la relación de cambio de la reactancia aparente de los generadores. El método exacto se puede usar si se desea, pero los métodos simplificados se han desarrollado por medio de los cuales la componente de corriente directa es estimada por factores de multiplicación simples. Los factores de multiplicación convierten los valores eficaces de las ondas de corriente simétricas en amperes eficaces de las ondas asimétricas que incluyen la componente de corriente directa. La magnitud de la componente de corriente directa depende del punto sobre la onda de tensión al cual ocurre el corto circuito. Para la aplicación de los dispositivos de protección solamente la componente máxima de corriente directa se considera, puesto que el interruptor se debe aplicar para manejar la corriente máxima de corto circuito que puede ocurrir en un sistema. En el caso general para un circuito arriba de 600 V nominales, los factores de multiplicación que se consideran para la componente de corriente directa es 1,6 veces el valor eficaz de la componente de corriente alterna simétrica en el primer medio ciclo. Para circuitos de 5000 V nominales o menos donde no hay generación local, esto es, donde la alimentación de las barras colectoras es a través de transformadores o líneas largas, el factor de multiplicación para calcular la corriente total en el primer medio ciclo se puede reducir a 1,5. Para circuitos de 600 V y menos, el factor de multiplicación para calcular la corriente total en el primer medio ciclo es de 1,25 cuando los interruptores se aplican sobre la corriente promedio en las tres fases. Donde se deben considerar condiciones monofásicas en circuitos de 600 V y 353 ELECTROTECNIA III-354 menos, entonces para estimar la componente de corriente directa en circuitos de una o tres fases un factor de 1,5 se usa para calcular la corriente total en el primer medio ciclo. Para algunos cálculos, la evaluación de la corriente eficaz en un intervalo de tiempo más largo que el primer medio ciclo, tal como tres u ocho ciclos correspondientes a los tiempos requeridos de interrupción de los interruptores, se determina por medio de curvas típicas publicadas en algunos manuales. Corriente total de corto circuito. La corriente total simétrica de corto circuito se forma de las corrientes de varias fuentes, ver figura número 24. En la parte superior de la figura se muestra la corriente de corto circuito proveniente de la compañía suministradora. Esta realmente viene de los generadores de una compañía, pero puesto que el sistema industrial es pequeño y remoto eléctricamente de los generadores de la compañía suministradora la corriente de corto circuito es simétrica substancialmente y constante. Si hay generadores en la planta industrial, entonces ellos contribuyen a la corriente de corto circuito simétrica la cual para todos los propósitos es constante durante los primeros pocos ciclos. Sin embargo hay un decremento ligero, como se indica en la figura número 24. Las otras fuentes son los motores síncronos los cuales actúan en forma similar a las plantas generadoras, excepto que ellos tienen una alta relación de decaimiento de componentes simétricas, y los motores de inducción los cuales tienen una relación de decaimiento muy rápida de la componente simétrica de corriente. Cuando todas las corrientes se suma, la corriente total de corto circuito es simétrica como se muestra en la curva típica de la figura número 24. La magnitud de los pocos primeros ciclos de la corriente de corto circuito simétrica además se aumenta por la presencia de la componente de corriente directa, figura número 25. La componente de corriente directa desplaza la onda de corriente alterna y, por consiguiente, la hace asimétrica. La componente de corriente directa decae a cero dentro de unos pocos ciclos en la mayoría de los sistemas de potencia industriales. Esta es la corriente eficaz de corto circuito total asimétrica, como se muestra en la figura número 25, esta se debe determinar para la aplicación de los dispositivos de protección. El problema de realizar esto se ha simplificado normalizando el procedimiento a un punto donde se determina el valor eficaz de la corriente asimétrica y solo se necesita dividir la tensión de línea a neutro por la reactancia apropiada o impedancia y posteriormente multiplicar por un factor apropiado. 354 ELECTROTECNIA III-355 1,5 1,0 0,5 0 -0,5 -1,0 -1,5 0 0,02 0,04 0,06 Compañía suministradora 0,08 0,10 1,5 1,0 0,5 0 4,0 3,5 3,0 2,5 2,0 1,5 1,0 0,5 0 -0,5 -1,0 -1,5 -2,0 -2,5 -3,0 -3,5 -4,0 0 -0,5 0,02 -1,0 0,02 0,04 0,06 Generador 0,08 0,08 0,10 FIGURA NÚMERO 24. -1,5 0 0,04 0,06 Total 0,10 4,0 1,5 1,0 3,5 0,5 3,0 0 -0,5 2.5 -1,0 -1,5 2,0 0 0,02 0,04 0,06 Motor síncrono 0,08 0,10 1,5 1,5 1,0 1,0 0,5 0,5 0 0 -0,5 -0.5 -1,0 -1,5 0 0,02 0,04 0,06 Motor de inducción 0,08 FIGURA NÚMERO 23. 0,10 -1,0 -1,5 0 0,02 0,04 0,06 0,08 0,10 Corriente de corto circuito con componente de directa FIGURA NÚMERO 25. 3. TIPOS DE FALLAS. 355 ELECTROTECNIA III-356 En un sistema eléctrico trifásico pueden ocurrir las fallas siguientes: a). Falla de una fase a tierra, llamada también falla monofásica. b). Falla entre dos fases, llamada también falla bifásica. c). Falla de dos fases a tierra, llamada también falla bifásica a tierra. d). Falla entre fases, llamada también falla trifásica. Para los tipos de fallas indicados se pueden considerar dos casos: Falla sólida o franca. Falla a través de una impedancia. Este último caso se presenta, por ejemplo, cuando la falla se establece a través de un arco eléctrico. Un corto circuito en un sistema trifásico simétrico produce una falla trifásica balanceada. Las fallas de una fase a tierra, entre dos fases y de dos fases a tierra producen fallas desequilibradas. 4. MÉTODOS DE SOLUCIÓN DEL CORTO CIRCUITO. 356 ELECTROTECNIA III-357 Corto circuito trifásico. Corto circuito simétrico. Equivalente de Thévenin : Método directo o método óhmico. Método de valores por unidad. Método de valores en por ciento. Método de los MVA. Corto circuito en general. Corto circuito simétrico o asimétrico. Método de las componentes simétricas. Método de la matriz de impedancias (Zbarra, Ybarra) Corto circuito trifásico simétrico. Falla trifásica. Falla simétrica. En este caso, la falla no introduce ningún desequilibrio en el sistema trifásico y por lo tanto no existirán corrientes ni tensiones de secuencia negativa ni de secuencia cero, independientemente de que la falla trifásica esté o no conectada a tierra. Falla Red de secuencia positiva P Ia a b c Va Vb Vc Ia Ib Ic FIGURA NÚMERO 26. Con el objeto de ejemplificar los métodos de solución de este tipo de falla, utilizaremos el ejemplo de la empresa productora siguiente: Determinar las corrientes y potencias de corto circuito en las barras colectoras de una empresa que cuenta para su proceso productivo con una instalación formada por, a).Una acometida de la Compañía suministradora de 13,2 kV, 3 fases, 3 hilos, 60 Hz, con una potencia de corto circuito de 250 MVA. b) Un transformador propio de 1 000 kVA, 13,2 kV-440/254 V, conexión delta en el primario y estrella con neutro sólidamente a tierra en el secundario, impedancia 5 %. c). Un motor de 5 CF, de 440 V, 60 Hz, con una reactancia de 25 %. d). Dos motores de 200 CF, de 440 V, 60 Hz, con una reactancia de 25 % cada uno. e). Dos motores de 100 CF, de 440 V, 60 Hz, con una reactancia de 25 % cada uno. f). Un transformador para servicios auxiliares, equipo de oficina y alumbrado, de 45 kVA, 440-220/127 V, conexión delta en el primario y estrella con neutro sólidamente a tierra en el secundario, impedancia 3 %. 357 ELECTROTECNIA III-358 Diagrama unifilar. 13,2 kV Compañía suministradora 13,2 kV, 250 MVA 1 1 000 kVA 13,2 kV-440/254 V Z= 5 % Y 440 V 2 M1 M2 M3 M4 M5 5 CF X = 25 % 200 CF X = 25 % 200 CF X = 25 % 100 CF X = 25 % 100 CF X = 25 % Y 220 V 45 kVA 440-220/127 V Z =3% 3 Servicios auxiliares, alumbrado y equipo de oficina FIGURA NÚMERO 27. Método directo o método óhmico. El método directo para el cálculo de las corrientes o potencias de corto circuito se utiliza cuando en el diagrama unifilar se tienen los datos del equipo y del sistema en volt, ampere y ohm directamente. En éste método hay que considerar las relaciones de transformación de los transformadores para determinar los valores de las impedancias conectadas en el lado de alta tensión en el sistema. Con los valores de impedancias en ohms, el sistema se puede reducir a una sola impedancia en el punto de falla por combinaciones sucesivas serie o paralelo o por transformaciones delta-estrella aplicando el teorema de Thévenin. 358 ELECTROTECNIA III-359 Z TH I TH V TH FIGURA NÚMERO 28. Entonces la corriente de corto circuito se puede calcular por medio de la relación siguiente: V I CC Z Donde V es la tensión de línea a neutro en el punto de falla en volt y Z es la impedancia equivalente en el punto de falla en ohm. La potencia de corto circuito por fase será, V2 PCC Z Procedimiento de cálculo. 1. Conversión de impedancias a ohm. 2. Dibujar el diagrama unifilar de impedancias en ohm. 3. Reducir la red en cada punto de falla y cálculo de corrientes y/o potencias de corto circuito. 1. Conversión de las impedancias a ohm. Compañía suministradora. 13, 2 10 3 V2 X PCC 250 106 2 0, 697 Transformador de 1 000 kVA. Por el lado de alta tensión: 2 3 X % kVAT 1000 5 13, 2 10 X 100 kVA 100 1000 2 8, 71 Por el lado de baja tensión: 359 ELECTROTECNIA III-360 X % kVBT 1000 5 0, 4402 1000 X 0, 00968 100 kVA 100 1000 2 Motor de 200 CF. (en forma aproximada 1 CF 1 kVA). X % kVm 1000 25 0, 440 2 1000 X 0, 242 100 kWm 100 200 2 Motor de 100 CF. X % kVm 1000 25 0, 440 2 1000 X 0, 484 100 kWm 100 100 2 Motor de 5 CF. X % kVm 1000 25 0, 4402 1000 X 9, 68 100 kWm 100 5 2 Transformador de 45 kVA, Por el lado de alta tensión. X % kVAT 1000 3 0, 4402 1000 X 0,1291 100 kVA 100 45 2 Por el lado de baja tensión: X % kVBT 1000 3 0, 2202 1000 X 0, 0323 100 kVA 100 45 2 2. Diagrama unifilar de impedancias en ohm. 360 ELECTROTECNIA III-361 0,697 1 8,71 (Lado de AT) 0,00968 (Lado de BT) 2 9,68 0,242 0,242 0,484 0,484 0,1291 (Lado de AT) 0,0323 (Lado de BT) 3 FIGURA NÚMERO 29. 3. Reducción de la red en cada punto de falla y cálculo de corrientes y potencias de corto circuito. Barras colectoras 1. 0,697 1 X Falla 8,71 2 0,0800 X eq 1 0,0800 1 1 1 1 1 9, 68 0, 242 0, 242 0, 484 0, 484 FIGURA NÚMERO 30. Impedancia del grupo de motores vista desde el lado de alta tensión del transformador de 1000 kVA. 2 kV 13, 2 X m X eq AT 0, 0800 72, 0 0, 440 kVBT 2 361 ELECTROTECNIA III-362 0,697 1 X Falla 0,697 8,71 1 X 0,691 Falla X 1 80,7 72,0 Falla 1 0,691 1 1 0,697 80, 7 FIGURA NÚMERO 31 Corriente de corto circuito, Tensión de fase a neutro en las barras colectoras 1 = 13200 3 7, 62 10 3 V VN 7, 62 103 ICC 11, 03 103 A =11,03kA Zeq 0, 691 Potencia de corto circuito. 13, 2 103 VL2 PCC Z eq 0, 691 2 252 106 VA = 252 MVA La potencia también se puede calcular en función de la tensión de fase a neutro. 7, 62 103 VN2 PCC 1 Z eq 0, 691 2 84, 0 106 VA = 84,0MVA PCC 3 PCC 1 3 84, 0 106 252 106 VA = 252 MVA Barras colectoras 2. 362 ELECTROTECNIA III-363 0,697 1 0,00968 X 2 Falla 0,0800 FIGURA NÚMERO 32. Impedancia de la compañía suministradora vista desde el lado de baja tensión del transformador de 1000 kVA. 2 kV 0, 440 X S X P BT 0, 697 0, 000744 13, 2 kVAT 2 0,000774 0,01045 0,00968 2 X 2 X Falla 0,0800 Falla 0,0800 0,00924 X 2 Falla 1 1 1 0, 01045 0, 0800 0, 00924 FIGURA NÚMERO 33. Corriente de corto circuito. Tensión de fase a neutro en las barras colectoras 2 = I CC 440 3 254 V VN 254 27, 5 103 A = 27,5kA Z eq 0, 00924 Potencia de corto circuito. 363 ELECTROTECNIA III-364 PCC VL2 4402 21, 0 106 VA = 21,0MVA Zeq 0, 00924 Barras colectoras 3. 1 0,01045 1 1 0, 0800 0, 01045 0,00924 2 2 0,0800 0,0323 0,0323 X Falla 3 X 3 Falla FIGURA NÚMERO 34. Impedancia del resto del sistema vista desde el lado de baja tensión del transformador de 45 kVA. 2 V 220 X S X P BT 0, 00924 0, 00231 440 VAT 2 Reducción de la red a las barras colectoras 3. 0,00231 0,0346 Falla X 0, 00231 0,0323 0, 0346 3 0,0323 3 X Falla FIGURA NÚMERO 35. Corriente de corto circuito. Tensión de fase a neutro en las barras colectoras 3 = I CC 220 3 127, 0 V VN 127, 0 3, 67 103 A = 3,67kA Z eq 0, 0346 364 ELECTROTECNIA III-365 VL2 2202 PCC 1, 399 106 VA =1,399MVA Zeq 0, 0346 Método de valores por unidad. Se empleará el método de valores por unidad, obteniendo con la aplicación del teorema Thévenin, una impedancia equivalente y una tensión en cada punto de falla. Procedimiento de cálculo. 1. Selección de las cantidades base. 2. Conversión de impedancias a una base común. 3. Dibujar el diagrama unifilar de impedancias en por unidad. 4. Reducir la red en cada punto de falla y cálculo de corrientes y/o potencias de corto circuito. 1.Selección de las unidades de base. Se elige, en este caso, los datos de las barras colectoras 1, esto es, potencia base 1000 kVA y tensión base 13,2 kV. 2. Conversión de impedancias a una base común. Compañía suministradora. X kVA B 1000 0, 004p.u. kVA CS 250000 Transformador de 1 000 kVA. X X % kVA B 5 1000 0, 05p.u. 100 kVA T 100 1000 Motor de 200 CF (en forma aproximada 1CF = 1 kVA). X X % kVA B 25 1000 1, 25p.u. 100 kVA m 100 200 Motor de 100 CF. 365 ELECTROTECNIA III-366 X X % kVA B 25 1000 2, 50p.u. 100 kVA m 100 100 X X % kVA B 25 1000 50, 0p.u. 100 kVA m 100 5 Motor de 5 CF. Transformador de 45 kVA. X X % kVA B 3 1000 0, 667 p.u. 100 kVA T 100 45 3. Diagrama unifilar de impedancias por unidad. 0,004 p.u. 1 0,05 p.u. 2 50,0 p.u. 1,25 p.u. 1,25 p.u. 2,50 p.u. 2,50 p.u. 0,667 p.u. 3 FIGURA NÚMERO 36. 4. Reducción de la red en cada punto de falla y cálculo de corrientes y/o potencias de corto circuito. Barras colectoras 1. 366 ELECTROTECNIA III-367 0,004 p.u. 1 X Falla 0,004 p.u. 0,05 p.u. X 1 0.00397 p.u. Falla 1 0,463 p.u. 2 X Falla 1 1 1 0, 004 0, 463 0,413 p.u. 1 1 1 1 1 1 50, 0 1, 25 1, 25 2, 50 2, 50 FIGURA NÚMERO 37. Corriente de corto circuito. I CC p . u . 1 252p.u. 0, 00397 Corriente base. IB kVA B 3 kVBarras 1 1000 3 13, 2 43, 7 A I CC I CCp .u . I B 252 43, 7 11, 01 103 A =11,01kA Potencia de corto circuito. PCC 3 VL I CC 3 13, 2 103 11, 01 10 3 252 106 VA = 252 MVA Barras colectoras 2. Corriente de corto circuito. I CC p . u . 1 20, 9p.u. 0, 0478 367 ELECTROTECNIA III-368 0,004 p.u. 0,054 p.u. Falla 1 0,05 p.u. 0,0478 p.u. X 2 X 2 Falla 1 2 Falla X 1 1 0, 054 0, 413 0,413 p.u. 0,413 p.u. FIGURA NÚMERO 38. Corriente base. IB kVA B 3 kVBarras 2 1000 3 0, 440 1312 A I CC I CCp .u . I B 20, 9 1312 27, 4 10 3 A = 27,4kA Potencia de corto circuito. PCC 3 VL I CC 3 440 27, 4 103 20, 9 106 VA = 20,9 MVA Barras colectoras 3. 0,054 p.u. 0,0478 p.u. 2 1 1 1 0, 054 0, 413 2 0,413 p.u. 3 0,667 p.u. Falla X 3 0,715 p.u. (0,0478 + 0,667) 3 0,667 p.u. Falla X X Falla FIGURA NÚMERO 39. 368 ELECTROTECNIA III-369 Corriente de corto circuito. I CC p . u . 1 1, 399p.u. 0, 715 Corriente base. IB kVA B 3 kVBarras 3 1000 3 0, 220 2, 62 103 A = 2,62kA I CC I CCp .u . I B 1, 399 2, 62 103 3, 67 10 3 A = 3,67 kA Potencia de corto circuito. PCC 3 VL I CC 3 220 3, 67 103 1, 398 106 VA =1,398 MVA Calcular las corrientes que circulan por cada uno de los elementos de protección. a). Circulación de corriente de falla por el fusible de alta tensión. 1 13,2 kV I B barra1 43,7 10, 93 103 A 10,93 kA X p.u 0,004 I 43, 7 B barras1 94, 2 A X p.u 0, 463 I CC X I CC Y 440 V 2 FIGURA NÚMERO 40. PCC barras1 250MVA ; PCC transformador 1 3 13, 2 103 94, 2 2,15MVA 369 ELECTROTECNIA III-370 b), Circulación de corriente de falla por el interruptor principal de baja tensión. 1 13,2 kV Y I CC I B barras 2 1312 24, 3 103 A 24, 3 kA X p.u 0,054 I CC 440 V 2 1312 525 A 2, 5 X M1 M2 M3 M4 M5 Y 220 V 3 FIGURA NÚMERO 41. c). Circulación de corrientes de falla por los interruptores de las derivaciones de las barras colectoras de 440 V. 440 V 2 I CC 24, 3 10 3 1050 1050 525 525 27, 5 10 3 A 27,5 kA I CC I B barras 2 1312 26, 2 A X p .u 50, 0 M1 5 CF FIGURA NÚMERO 42. 370 ELECTROTECNIA III-371 440 V 2 I CC 24, 3 10 3 26, 2 1050 525 525 26,4 10 3 A 26,4 kA I CC 1050 A M2 200 CF FIGURA NÚMERO 43. 440 V 2 I CC 24, 3 103 26, 2 1050 1050 525 26,9 103 A 26,9 kA I CC 525 A M4 100 CF FIGURA NÚMERO 44. 440 V 2 I CC 24, 3 103 26,2 1050 1050 525 525 27,5 103 A 27, 5 kA X Y 220 V 3 FIGURA NÚMERO 45. 371 ELECTROTECNIA III-372 Circulación de corriente de falla por el interruptor principal de servicios auxiliares, alumbrado y equipo de oficina. 440 V 2 Y I CC 3, 67 103 A 3, 67kA 220 V X 3 FIGURA NÚMERO 46. Método de los MVA. Donde no es necesario considerar la resistencia de los elementos que integran el sistema, se puede emplear un método sencillo para calcular la potencia de corto circuito simétrico en MVA y a partir de este valor calcular la corriente de corto circuito. Para este método únicamente hay que recordar las relaciones siguientes: 1. La impedancia del equipo deberá convertirse directamente a MVA de corto circuito por medio de la ecuación 1, si la reactancia del equipo está en % o por la ecuación 2 si la reactancia está en por unidad. MVACC MVACC MVAequipo 100 X %del equipo MVAequipo X p .u. del equipo (1) (2) 2. La impedancia de la línea y alimentadores (cables) deberá convertirse directamente a MVA de corto circuito por medio de la ecuación 3 si la reactancia está en ohm. MVA CC kVL2 X (3) Donde kVL es la tensión de línea en kilovolt del cable. 372 ELECTROTECNIA III-373 3. Dibuje dentro de rectángulos o círculos todos los MVA de corto circuito de equipos y alimentadores siguiendo el mismo arreglo que éstos tienen en el diagrama unifilar. 4. Sucesivamente combine los MVA de corto circuito del sistema hasta encontrar un valor equivalente en el punto de falla. a). Valores en paralelo se suman directamente. b). Valores en serie se combinan como si fueran impedancias en paralelo. 5. Con el valor encontrado en el punto anterior, calculamos la corriente de corto circuito trifásico, en amperes, para el punto de falla. I CC MVACC 1000 3 kVL Donde kVL es la tensión de línea en kilovolt, en el punto de falla. Procedimiento de cálculo. 1. Conversión de impedancias a MVA de corto circuito. 2. Dibujar el diagrama en MVA. 3. Reducción de la red en cada punto de falla y cálculo de potencias y corrientes de corto circuito. Utilizando el circuito del ejemplo. 1. Conversión de impedancias a MVA. Compañía suministradora. MVACC 250MVA Transformador de 1000 kVA (1 MVA). MVACC MVAequipo X p.u. 1 20, 0 0, 05 Motor de 200 CF (0,2 MVA). MVA CC 0, 2 0, 800 0, 25 373 ELECTROTECNIA III-374 Motor de 100 CF (0,1 MVA). 0,1 0, 400 0, 25 MVA CC Motor de 5 CF (0,005 MVA). MVACC 0, 005 0, 0200 0, 25 Transformador de 45 kVA (0,045 MVA). MVA CC 0, 045 1, 500 0, 03 2. Diagrama en MVA. 250 1 20,0 2 0,0200 0,800 0,800 0,400 0,400 1,500 3 FIGURA NÚMERO 47. 3. Reducción de la red en cada punto de falla y cálculo de las potencias y/o corrientes de corto circuito. Barras colectoras 1. 250 X 1 250 252 1 X 20,0 2 2,42 0, 020 0,800 0, 800 0,400 0, 400 1 X 250 2,16 2,16 1 1 1 20, 0 2, 42 FIGURA NÚMERO 48. 374 ELECTROTECNIA III-375 Potencia de corto circuito, PCC , MVACC 252 Corriente de corto circuito, I CC MVACC 1000 252 1000 11, 02 103 A =11,02kA 3 kVL 3 13, 2 Barras colectoras 2. 18,52 X 0,0200 0,800 X 2 2,42 0,800 0,400 2 0,400 18, 52 2, 42 20,9 18,52 1 1 1 250 20, 0 X 2 0, 020 0,800 0, 800 0,400 0, 400 FIGURA NÚMERO 49. Potencia de corto circuito. PCC , MVACC 20,9 Corriente de corto circuito, I CC MVACC 1000 20, 9 1000 27, 4 103 A = 27,4kA 3 kVL 3 0, 440 375 ELECTROTECNIA III-376 Barras colectoras 3. 18,52 18, 52 2, 42 20,9 2 X 2 2,42 1,500 1,500 X 3 X 3 1,400 1 1 1 20, 9 1, 500 FIGURA NÚMERO 50. Potencia de corto circuito. PCC , MVACC 1,400 Corriente de corto circuito, I CC MVACC 1000 1, 400 1000 3, 67 103 A = 3,67 kA 3 kVL 3 0, 220 CORTO CIRCUITO EN GENERAL. CORTO CIRCUITO SIMÉTRICO O ASIMÉTRICO. Método de las componentes simétricas. Con el objeto de ilustrar el método de componentes simétricas para la solución del corto circuito, utilizaremos un sistema de potencia, cuyo diagrama unifilar se muestra en la figura número 51, donde se indican las reactancias de secuencia positiva, secuencia negativa y secuencia cero, los neutros del generador y transformadores están sólidamente conectados a tierra; el neutro del motor está conectado a tierra a través de una reactancia XN = 0,05 por unidad en base a los datos de placa del motor. El generador está operando con sus MVA nominales, con un factor de potencia 0,95 atrasado y con una tensión 5 % arriba de su valor nominal. 376 ELECTROTECNIA III-377 1 2 T1 Línea Y G 100 MVA 13,8 kV X’’ = 0,15 p.u. X2 = 0,17 p.u X0 = 0,05 p.u T2 M Y X1 = X2 = 20,0 X 0 = 60,0 Y 100 MVA 13,8 kV : 138 kV Y X = 0,10 p.u. Y 100 MVA 138 kV Y: 13,8 kV X = 0,10 p.u. 100 MVA 13,8 kV X’’ = 0,20 p.u. X 2 = 0,21 p.u X 0 = 0,10 p.u FIGURA NÚMERO 51. a). Dibuje las redes de secuencia positiva, negativa y cero en valores por unidad tomando como bases 13,8 kV y 100 MVA, que son los datos del generador. b). Reduzca las redes de secuencia a su equivalente de Thévenin, vistas desde las barras colectoras 2. La tensión de prefalla es V F 1, 05p.u. La corriente de la carga en prefalla y el defasamiento de los transformadores no se tomarán en cuenta. c). Calcule las corrientes subtransitorias en las barras colectoras 2, para los tipos de falla siguientes: c1). Falla franca trifásica. c2). Falla franca de la fase A a tierra. c3). Falla franca entre las fases B y C. c4). Falla franca entre las fases B y C y tierra. SOLUCIÓN. a). La impedancia base de la línea de transmisión a su tensión es, Z B,línea kV B,línea 2 MVA B 1382 190, 4 100 La reactancia por unidad de la línea para las secuencias positiva y negativa es, X B,línea, p.u. X línea, X B,línea 20, 0 0,1050p.u. 190, 4 La reactancia por unidad de la línea para la secuencia cero es, X B,línea, p.u. X línea, X B,línea 60, 0 0, 315p.u. 190, 4 La reactancia por unidad de la línea para las secuencias positiva y negativa es, 377 ELECTROTECNIA III-378 X B,línea, p.u. X línea, X B,línea 20, 0 0,1050p.u. 190, 4 Las redes de secuencia, con las reactancias por unidad se muestran en las figuras 52, 53 y 54. I línea,1 1 2 T1 Línea T2 j 0,10 p.u j 0,1050 p.u j 0,10 p.u I motor,1 j 0,15 p.u j 0,20 p.u G V ''G 1, 05 / 0, 00 p.u '' M V M 1, 05 / 0, 00 p.u FIGURA NÚMERO 52. Red de secuencia positiva I línea,2 1 T1 Línea T2 j 0,10 p.u j 0,1050 p.u j 0,10 p.u j 0,17 p.u 2 I motor,2 j 0,21 p.u FIGURA NÚMERO 53. Red de secuencia negativa. En la figura número 54, puesto que el motor está a tierra a través de una reactancia XN, se incluye una reactancia igual a 3 XN en la rama del motor. 1 T1 Línea T2 j 0,10 p.u j 0,315 p.u j 0,10 p.u 2 j 0,10 p.u j 0,05 p.u j 0,15 p.u FIGURA NÚMERO 54. Red de secuencia cero. 378 ELECTROTECNIA III-379 b). De la figura número 52, la impedancia de secuencia positiva de Thévenin, vista desde las barras colectoras 2, es igual al paralelo de las impedancias a ambos extremos de las barras colectoras 2, esto es, Z 1 Z Th,1 j0,15 + j0,10 + j0,1050 + j0,10 j0, 20 j2 0, 0910 j0,1389p.u. j0,15 + j0,10 + j0,1050 + j0,10 j0, 20 j0, 655 La figura número 55 muestra la impedancia de secuencia positiva de Thévenin en las barras colectoras 2, con la fuente de Thévenin, la cual es la tensión de prefalla V F 1, 05 0, 0 p.u. 0 I1 Z 1 j0,1389p.u. + + V1 V F 1, 05 / 0, 0 p.u 0 - FIGURA NÚMERO 55. Red de secuencia positiva Similarmente la impedancia de secuencia negativa de Thévenin es, j0,17 + j0,10 + j0,1050 + j0,10 j0, 21 j2 0, 0998 Z 2 Z Th,2 j0,1456p.u. j0,17 + j0,10 + j0,1050 + j0,10 j0, 21 j0, 685 La figura número 56 muestra la impedancia de secuencia negativa de Thévenin. I2 Z 2 j0,1456p.u. + V2 FIGURA NÚMERO 56. Red de secuencia negativa. La red de secuencia cero, observando la figura número 54, la impedancia de Thévenin a las barras colectoras 2 consiste solamente de, 379 ELECTROTECNIA III-380 Z 0 Z Th,0 j0,10+ j0,15= j0,250p.u. debido a la conexión delta del transformador 2, ya que la red de secuencia cero vista desde la izquierda de las barras 2 está abierta. En la figura número 57 se muestra la impedancia de secuencia cero de Thévenin. I0 Z 0 j0,250p.u. + V0 FIGURA NÚMERO 57. Red de secuencia cero. c). Cálculo de las corrientes de falla subtransitorias en las barras colectoras 2. c1). Falla franca trifásica. Falla entre las fases A, B y C y tierra, en las barras colectoras 2. Recordando que para fallas trifásicas, las corrientes están balanceadas y solamente tienen componentes de secuencia positiva, entonces únicamente trabajaremos con la red de secuencia positiva. Las terminales de la red de secuencia positiva de la figura número 55 quedan cortocircuitadas como se muestra en la figura número 58. 380 ELECTROTECNIA III-381 I1 + Z 1 j0,1389p.u. + V1 0 V F 1, 05 / 0, 0 0 p.u FIGURA NÚMERO 58. De donde la corriente de secuencia positiva subtransitoria en por unidad es, V F 1,05 0,00 I1 7, 56 90,00 p.u. Z1 j0,1389 Por supuesto que las corrientes subtransitorias de secuencias negativa y cero son iguales a cero. Por consiguiente las corrientes de falla subtransitoria son, '' '' '' I A 7, 56 90, 00 p.u. ; I B 7, 56 210, 00 p.u. ; I C 7, 56 330, 00 p.u. La corriente base en las barras colectoras 2 es, I B,barra2 MVA 3 kVL2 100 3 13, 8 4,18kA Las corrientes de falla subtransitoria en amperes son, '' '' I A I B,barras2 I A,p.u. 4,18 7,56 90, 0 31, 6 90, 00 kA '' '' I B 31, 6 210, 00 kA ; I C 31, 6 330, 00 kA c2). Falla franca de fase a tierra. Falla de la línea A a tierra, en las barras colectoras 2. Las redes de secuencia positiva, negativa y cero de la figura número 55 se conectan en serie a las terminales de la falla, como se muestra en la figura número 59. 381 ELECTROTECNIA III-382 I0 Z 0 j0,250p.u. + V0 I1 + Z 1 j0,1389p.u. + V1 V F 1, 05 / 0, 0 0 p.u Z 2 j0,1456p.u. I2 + V2 FIGURA NÚMERO 59. Falla de fase a tierra. Puesto que el corto circuito es franco, ZF = 0. De conde las corrientes de las secuencias son, I1 I 2 I 0 VF 1, 05 0, 0 1, 965 90, 00 p.u. Z 1 Z 2 Z 0 j 0,1389 0,1456 0, 250 La corriente de falla subtransitoria es '' I A I 1 I 2 I 0 3 I 1 3 1, 965 90, 0 5, 89 90, 00 p.u. La corriente base en las barras 2 es, I B,barra2 MVA 3 kVL2 100 3 13, 8 4,18kA Por consiguiente, la corriente de falla subtransitoria en las barras 2 es, '' I A I B,barras2 I A,p.u 4,18 5, 89 90, 0 24, 6 90, 00 kA Las componentes de secuencia de la tensión en la falla son, 382 ELECTROTECNIA III-383 V 1 V F 0 V 2 0 0 0 Z V 0 0 Z1 0 0 0 I1 Z2 I 2 0 I 0 0 0,1389 90,0 0 1,05 0,0 1,965 90,0 0,777 0.0 0 0 0 0,1456 90,0 1,965 90,0 0, 286 180,0 p.u. 0, 250 90,0 1,965 90,0 0,491 180,0 0 0 0 De donde las tensiones de fase de línea a tierra en las barras colectoras 2 en el punto de falla son, V AT V 1 0 0, 777 0, 0 V BT A V 2 A 0, 286 180, 0 1,179 128, 7 p.u. 0, 491 180, 0 1,179 128, 7 V CT V 0 Tomando como tensión base a 110 kV, tenemos que las tensiones en volt son, V AT 0 ; V BT 110 1,179 128,7 129,7 128,7 0 kV ; V CT 129,7 128,7 0 kV c3). Falla franca entre dos fases. Falla franca entre la línea B y la línea C en las barras colectoras 2. Las redes de secuencia positiva y negativa de las figuras números 55 y 56 se conectan en paralelo en las terminales de falla, como se muestra en la figura número 60. I1 Z 1 j0,1389p.u. + V F 1, 05 / 0, 0 p.u 0 I2 + + V1 V2 - - Z 2 j0,1456p.u. - FIGURA NÚMERO 60. Con ZF = 0, las corrientes de secuencia de la falla son, I1 I 2 VF 1, 05 0, 0 3, 69 90, 00 p.u. Z 1 Z 2 0,1389 90, 0 0,1456 90, 0 I0 0 383 ELECTROTECNIA III-384 La corriente subtransitoria de falla en la fase B es, '' I B a2 I 1 a I 2 I 0 a2 - a I 1 3 90, 0 3, 69 90, 0 6, 39 180, 00 p.u. Usando la corriente base de 4,18 kA tenemos, '' I B I B ,barras2 I B ,p.u. 4,18 6, 39 180,0 26,7 180,00 kA Además, '' I A I1 I 2 I 0 0 '' I C a I 1 a2 I 2 I 0 a - a2 I 1 I B '' I A 0 ; I C 26, 7 0, 00 kA c4). Falla franca entre dos fases y tierra. Falla franca entre la línea B y la línea C y tierra en las barras colectoras 2. Las redes de secuencia positiva, negativa y cero de las figuras 55, 56 y 57, están conectadas en paralelo con la tensión de la falla, como se muestra en la figura número 61. I1 Z 1 j0,1389p.u. + V F 1, 05 / 0, 0 p.u 0 + + V1 V2 - - + I2 I0 V0 - FIGURA NÚMERO 61. Con ZF = 0, las corrientes de secuencia de la falla son, 384 ELECTROTECNIA III-385 I1 VF 1, 05 0, 0 4, 55 90, 00 p.u. Z2 Z0 0,1456 90, 0 0, 250 90, 0 Z1 0,1389 90, 0 Z2 Z0 0,1456 90, 0 0, 250 90, 0 Z0 0, 250 90, 0 0 I 2 I1 4, 55 90, 0 2, 88 90, 0 p.u. 0,1456 90, 0 0, 250 90, 0 Z2 Z0 Z2 0,1456 90, 0 0 I0 I1 4, 55 90, 0 1, 675 90, 0 p.u. Z Z 0,1456 90, 0 0, 250 90, 0 0 2 Transformando al dominio de fase, las corrientes subtransitorias de fase son, I ''A I 1'' 0 4, 55 90, 0 '' '' I B A I 2 A 2, 88 90, 0 6, 91 158, 7 p.u. 1, 675 90, 0 6, 91 21, 3 I ''C I ''0 Usando la corriente base de 4,18 kA tenemos, I ''A 0 0 I ''B 4,18 6, 91 158, 7 28, 9 158, 7 kA 6, 91 21, 3 28, 9 21, 3 I ''C De donde, '' '' '' I A 0 ; I B 28, 9 158, 70 kA ; I C 28, 9 21, 30 kA La corriente de falla a tierra es, I N 3 I 0 3 1, 675 90, 0 5, 02 90, 00 p.u. = 4,18 5,02 90,0 = 21,0 90,00 kA 385 ELECTROTECNIA III-386 Método de la matriz de impedancias de barra (Zbarra, Ybarra). Cuando se tienen sistemas de potencia trifásicos con n barras, es conveniente calcular las corrientes y tensiones de falla por medio del método de la matriz de impedancias de barra, el cual se basa en las ecuaciones de nodos. Las ecuaciones para n nodos son, Y 11 V 1 Y 12 V 2 Y 13 V 3 ... Y 1n V n ... Y 1 N V N I 1 Y 21 V 1 Y 22 V 2 Y 23 V 3 ... Y 2 n V n ... Y 2 N V N I 2 Y 31 V 1 Y 32 V 2 Y 33 V 3 ... Y 3 n V n ... Y 3 N V N I 3 . . . Y n1 V 1 Y n 2 V 2 Y n 3 V 3 ... Y nn V n ... Y nN V N I n . . . Y N 1 V 1 Y N 2 V 2 Y N 3 V 3 ... Y Nn V n ... Y NN V N I N En forma matricial, tenemos Y 11 Y 12 Y 13 Y 21 Y 22 Y 23 Y 31 Y 32 Y 33 . . . . . . . . . Y Y n2 Y n3 n1 . . . . . . . . . Y N 1 Y N 2 Y N 3 . . . Y 1n . . . Y 2n . . . Y 3n . . . . . . . . . . . . . . . Y nn . . . . . . . . . . . . . . . Y Nn . . . Y 1N V 1 I 1 . . . Y 2 N V 2 I 2 . . . Y 3N V 3 I 3 . . . . . . . . . . . . . . . . . . . . . Y nN V n I n . . . . . . . . . . . . . . . . . . . . . Y NN V N I N Y V I 386 ELECTROTECNIA III-387 Falla franca trifásica. El sistema se modela por medio de su red de secuencia positiva, donde las líneas y transformadores están representadas por reactancias en serie y las máquinas están representadas por fuentes de tensión constante; y todas las resistencias serie, admitancias en paralelo, e impedancias de carga no rotatorias se desprecian. Por simplificación, también despreciaremos las corrientes de carga que se tienen antes de la falla. Estas consideraciones se hacen por simplificación en estos apuntes, pero en la práctica no se deben hacer para todos los casos, por ejemplo, las resistencias de las líneas de transmisión, en algunos casos, pueden reducir significativamente las corrientes de falla. Para ilustrar el método utilizaremos el sistema mostrado en la figura número 51, el cual consiste de un generador síncrono que alimenta un motor síncrono a través de dos transformadores y una línea de transmisión. Consideraremos un corto circuito trifásico en las barras n (en nuestro caso las barras 1). Su circuito equivalente de secuencia positiva se muestra en la figura número 62(a), donde las ´´ ´´ tensiones V G y V M son las tensiones internas antes de la falla atrás de las reactancias subtransitorias de las máquinas, cerrando el interruptor INT se puede representar la falla. Para el ´´ ´´ propósito de calcular la corriente de falla subtransitoria, las tensiones V G y V M se consideran como fuentes de tensión constante. En la figura número 62(b) la falla se representa por dos fuentes de tensión opuestas con valores iguales al fasor de tensión V F . Usando el teorema de superposición se puede calcular la corriente de falla por medio de los dos circuitos mostrados en la figura número 62(c). Sin embargo, si V F es igual a la tensión antes de la falla, entonces el segundo circuito de la figura número 62(c) representa el sistema antes de que ocurra la falla, de tal manera que I F 0 y V F no tiene efecto, por lo que se puede eliminar del segundo circuito, como se muestra en la figura número 62(d). Analizaremos por separado los dos circuitos de la figura número 62(d). En el primer circuito, todas las fuentes de tensión de las máquinas se ponen en corto circuito y la única fuente se debe a la tensión antes de la falla. Escribiendo las ecuaciones de nodos para el primer circuito tenemos, Y barra V (1) I (1) (1) 387 ELECTROTECNIA III-388 Donde Y barra es la matriz de admitancias de barra de secuencia positiva, V de tensiones de barra, e I circuito. (1) (1) es el vector es el vector de las corrientes. El superíndice (1) se usa para el primer 1 2 T1 Línea 1 ´´ T2 IG 2 j0, 305 ´´ j 0,10 p.u j 0,1050 p.u I j 0,10 p.u j 0,15 p.u '' VM G I 1 ´´ M I ´´ F1 = I ´´ G2 1 j0, 505 ´´ I I M2 ´´ F2 + + + - + j0,150 VF ´´ VM (b) Corto circuito representado por dos fuentes de tensión opuestas. ´´ M1 - + VF VG j0, 505 I j0, 200 - + (a) Corto circuito trifásico. j0,150 + VF - ´´ G1 IM j0,150 j 0,20 p.u INT '' VG ´´ F VF + V - ´´ G + ´´ VM - - (c) Aplicación del teorema de superposición. j0,150 I 1 j0, 505 ´´ G1 I ´´ F1 I - = VF + ´´ F j0,150 I ´´ M1 1 j0, 505 IL + + + V ´´ G - ´´ VM - (d) V F Igual a la tensión antes de la falla. FIGURA NÚMERO 62. 388 ELECTROTECNIA III-389 Despejando el vector de tensión tenemos, V (1) 1 Y barra I (1) Z barra I (1) (2) 1 Donde Z barra Y barra . Z barra es la matriz inversa de Y barra , y se denomina como la matriz de impedancias de barra. Ambas matrices Z barra y Y barra son matrices simétricas. Puesto que el primer circuito solamente contiene una fuente, localizada en la barra n (barra 1) con falla, el vector de las fuentes de tensión contiene solamente una fuente de tensión (1) ´´ que no es cero, de donde I n I Fn . Además la tensión en la barra n durante la falla en el primer (1) circuito es V n V F . Ahora la ecuación número (2) se puede escribir como, Z 11 Z 21 . . Z n1 . . Z N 1 Z 12 . . Z 1n . . Z 22 . . Z 2n . . . . . . . . . . . . . . Z n2 . . Z nn . . . . . . . . . . . . . . Z N2 . . Z Nn . . (1) Z 1N 0 V 1 (1) Z 2 N 0 V 2 . . . . . . ´´ Z nN I Fn V F . . . . . . Z NN 0 (1) V N (3) El signo menos asociado con la fuente de corriente en la ecuación número (3) indica que ´´ ´´ la corriente suministrada a la barra n es la inversa de I Fn , puesto que I Fn fluye de la barra n al neutro. De la ecuación número (3), tenemos que la corriente de falla subtransitoria es, ´´ VF I Fn (4) Z nn También de las ecuaciones números (3) y (4), la tensión para cualquier barra k en el primer circuito es, (1) ´´ V k Z kn I Fn Z kn VF Z nn (5) 389 ELECTROTECNIA III-390 El segundo circuito representa las condiciones antes de la falla. Despreciando la corriente de carga antes de la falla, todas las tensiones en el segundo circuito son iguales a la tensión antes (2) de la falla, esto es, V k V F para cada barra k. Aplicando el teorema de superposición tenemos, (1) ( 2) V k V k V k Z kn V F V F Z nn Z V F 1 kn ; k 1, 2, ., N Z nn (6) Aplicaremos para nuestro ejemplo, el método descrito para determinar las fallas en las barras 1 y 2, considerando que la tensión antes de la falla tiene un valor de 1, 05 / 0, 00 p.u y que se desprecia la corriente de carga que se tiene antes de la falla. Determinaremos: a) la matriz 2 X 2 de impedancias de barra de secuencia positiva; b) para un corto circuito trifásico firme en las barras 1, calcular la corriente de falla subtransitoria y la contribución a la corriente de falla desde las barras 2 a través de la línea de transmisión; c) repita la parte b para un corto circuito trifásico franco en las barras 2. SOLUCIÓN. a) El circuito de la figura número 62(a) se vuelve a dibujar en la figura número 63, mostrando las admitancias de barra por unidad en lugar de los valores de las impedancias por unidad. 1 2 j3, 28 j6, 67 ´´ VG j5, 00 ´´ VM FIGURA NÚMERO 63. Circuito mostrando los valores de las admitancias por unidad. ´´ ´´ Despreciando la corriente de carga antes de la falla, V G V M V F 1,05 / 0,00 p.u . De la figura número 63, la matriz de admitancias de barra de secuencia positiva es, 390 ELECTROTECNIA III-391 9, 95 3, 28 Y barra j p.u 3, 28 8, 28 La matriz inversa de Y barra es, 0,1156 0, 0458 1 Y barra Z barra j p.u 0, 0458 0,1389 b) Usando la ecuación número (4) la corriente de falla subtransitoria en las barras 1 1 es, ´´ I F1 V F 1,050 / 0,0 j9,08 9,08 / 90,00 p.u Z 11 j0,1156 La corriente base en las barras 1 es, I B barras1 MVA B 3 kVB1 100 3 13, 8 4,18kA De donde la corriente de falla es, ´´ ´´ I F 1 I B barras1 I F p.u 4,18 103 9,08 / 90,0 38,0 10 3 / 90,0 0 A 38,0 / 90,0 0 kA En las barras 1 y 2 las tensiones durante la falla son, de la ecuación número 6, Z V 1 V F 1 11 0 Z 11 Z j0, 0458 0 V 2 V F 1 21 1, 050 / 0, 0 1 0, 634 / 0, 0 p.u Z 11 j0,1156 V 2 VB1 V 2 p.u 13,8 103 0,634 / 0,0 8,75 103 / 0,00 V = 8,75 /0,00 kV La contribución a la corriente de falla desde las barras 2 a través de la línea de transmisión se puede obtener por medio de la regla de la división de corriente, y de la figura número 62d, esto es, ´´ I 21 I F 1 j0,150 0,150 9, 08 / 90, 0 2, 08 / 90, 00 p.u j0,150 j0, 505 0, 655 391 ELECTROTECNIA III-392 I 21 I Bbarras1 I 21p.u 4,18 103 2,08 / 90,0 8,69 103 / 90,00 A 8,69 / 90,00 kA c) Usando la ecuación número 4, la corriente subtransitoria en las barras 2 es, ´´ IF2 V F 1, 050 / 0, 0 j7, 56 7, 56 / 90, 00 p.u Z 22 j0,1389 La corriente base en las barras 2 es, I B barras 2 MVA B 3 kVB1 100 3 13, 8 4,18kA De donde la corriente de falla es, ´´ ´´ I F I B barras 2 I F 2 p.u 4,18 103 7,56 / 90,0 31,6 103 / 90,00 A 31,6 / 90,00 kA En las barras 1 y 2 las tensiones durante la falla son, de la ecuación número 6, Z j0, 0458 0 V 1 V F 1 12 1, 05 / 0, 0 1 0, 704 / 0, 0 p.u Z 22 j0,1389 Z V 2 V F 1 22 0 Z 22 V 1 VB1 V 1p.u 13,8 103 0,704 / 0,0 9,72 103 / 0,00 V = 9,72 /0,00 kV j0, 455 2 j0, 200 I 12 VF FIGURA NÚMERO 64. 392 ELECTROTECNIA III-393 La contribución a la corriente de falla desde las barras 1 a través de la línea de transmisión se puede obtener por medio de la regla de la división de corriente, y de la figura número 64, esto es, ´´ I 12 I F 2 j0, 200 0, 200 7, 56 / 90, 0 2, 31 / 90, 00 p.u j0, 455 j0, 200 0, 655 I 21 I Bbarras 2 I 21p.u 4,18 103 2,08 / 90,0 8,69 103 / 90,00 A 8,69 / 90,00 kA La figura número 65 muestra un circuito equivalente de impedancias de barra que ilustra las corrientes de corto circuito en un sistema de N barras. A este circuito se le da el nombre de equivalente de rastrillo debido a su forma, la cual es similar a un rastrillo de jardín. 0 VF + Z 12 Z 2n Z nN Z 1n Z 22 Z 11 I1 I2 + 1 ... Z nn ... In + V1 V2 - - 2 Z NN IN + n Vn - + N VN - FIGURA NÚMERO 65. Circuito equivalente de impedancias de barra (equivalente de rastrillo). Los elementos de la diagonal Z11, Z22, ... , ZNN de la matriz de impedancias de barra, las cuales son las impedancias propias, se muestran en la figura número 65. Los elementos fuera de la diagonal, o impedancias mutuas, se indican por medio de una llave en la figura. Despreciando las corrientes de carga antes de la falla, las fuentes de tensión interna de todas las máquinas síncronas son iguales tanto en magnitud como en ángulo de fase. De tal manera que ellas se pueden conectar como se muestra en la figura número 66, y se pueden 393 ELECTROTECNIA III-394 reemplazar por una fuente equivalente V F desde la barra neutra 0 a una barra de referencia, denominada r. Esta fuente equivalente también se muestra en el rastrillo equivalente de la figura número 65. 0 ... ... VF + r ... ... Red de impedancias Red de impedancias incluyendo las impedancias de los generadores. FIGURA NÚMERO 66. Conexión en paralelo de las máquinas síncronas sin carga, fuentes de tensión interna. Usando la matriz de impedancias de barra, las corrientes de falla de la figura número 65, están dadas por, Z 11 Z 21 . . Z n1 . . Z N1 Z 12 . . Z 1n . . Z 22 . . Z 2n . . . . . . . . . . . . . . Z n2 . . Z nn . . . . . . . . . . . . . . Z N2 . . Z Nn . . Z1N I 1 V F V 1 Z 2 N I 2 V F V 2 . . . . . . (7) Z nN I n V F V n . . . . . . Z NN I N V F V N donde I 1 , I 2 , ..., I N son las corrientes de rama y V F V 1 , V F V 2 , ..., V F V N son las tensiones a través de las ramas. Si el interruptor INT de la figura número 65 se abre, todas las corrientes tienen un valor de cero y la tensión en cada una de las barras con respecto al neutro son iguales a V F . Esto corresponde a las condiciones antes de la falla, despreciando las corrientes de la carga. Si el 394 ELECTROTECNIA III-395 interruptor INT se cierra, correspondiendo a un corto circuito en las barras n, V n 0 y todas las corrientes excepto I n permanecen en un valor igual con cero. La corriente de falla es VF Z nn lo cual concuerda con la ecuación número 4. Esta corriente de falla también introduce una caída de tensión ´´ I Fn I n Z Z kn I n kn V F Z nn a través de cada rama k. La tensión en la barra k con respecto al neutro entonces es igual a V F menos esta caída de tensión lo cual concuerda con la ecuación número 6. Como se muestra en la figura número 65 así como en la ecuación número 4, las corrientes de falla subtransitorias a través del sistema de N barras se pueden determinar por medio de la matriz de impedancias de barra y la tensión antes de la falla. Zbarra se puede calcular construyendo primero Ybarra, por medio de las ecuaciones de nodos, y después invirtiendo Ybarra. Una vez que se ha obtenido Zbarra, se pueden calcular con facilidad las corrientes de falla. Las corrientes en las diferentes barras del circuito se pueden obtener con las tensiones y la matriz de impedancias por medio de la ecuación siguiente: I ij V i V j Z jk Z ik Z p ij Z p ij Z kk (8) Donde: V i Tensión en la barra i cuando ocurre la falla en la barra k. V j Tensión en la barra j cuando ocurre la falla en la barra k. Z p ij Impedancia primitiva entre las ramas i y j. Z jk Impedancia de barra entre las barras j y k. 395 ELECTROTECNIA III-396 Z ik Impedancia de barra entre las barras i y k. Z kk Impedancia de barra donde ocurre la falla. Ejemplo 8-1. Consideremos el circuito de la figura (a) y su representación equivalente de reactancias por unidad de la figura (b). 1 2 3 T1 T2 G1 G2 4 G3 1 J 0,3 (a) 2 J 0,3 J 0,1 3 J 0,05 J 0,1 4 J 0,3 J 0,2 J 0,3 J 0,1 J 0,15 + G1 + J 0,15 + G3 - G1 - - (b) 396 ELECTROTECNIA III-397 El circuito (b) es el equivalente monofásico del sistema, esto es su red de secuencia positiva, y elegimos para su ilustración una falla en las barras 2 y obtener la corriente de falla entre las barras 1 y 4, llamaremos V F a la tensión en las barras 2 antes de que ocurra la falla. Convirtiendo los valores de las impedancias por unidad de los elementos a valores de admitancia por unidad, obtenemos el circuito equivalente mostrado en la figura c. - j 3,33 - j 3,33 2 1 3 - j 10,00 - j 3,33 - j 3,33 4 - j 3,33 - j 4,00 - j 5,00 (c) Los elementos para construir la matriz de impedancias de barra Y barra son, Y11 = - j (3,33 + 3,33 + 3,33) = - j 10,00 pu Y12 = Y21 = - j 3,33 pu Y13 = Y31 = 0 Y14 = Y41 = - j 3,33 pu Y22 = - j (3,33 + 3,33 + 10,00) = - j 16,66 pu Y23 = Y32 = - j 3,33 pu Y24 = Y42 = - j 10,00 pu Y33 = - j (3,33 + 3,33 + 5,00) = - j 11,66 pu Y34 = Y43 = - j 3,33 pu Y44 = - j (3,33 + 3,33 + 10,00 + 4,00) = - j 20,7 pu 397 ELECTROTECNIA III-398 De donde la matriz de admitancias de barra es, 0 3, 33 10, 00 3, 33 3, 33 16, 66 3, 33 10, 00 Y barra j 0 3, 33 11, 66 3, 33 20, 7 3, 33 10, 00 3, 33 Determinando la matriz inversa de admitancias de barra obtenemos la matriz de impedancias de barra siguiente: 0,1502 0, 0807 1 Y barra Z barra j 0, 0431 0, 0701 0, 0807 0, 0431 0, 0701 0,1471 0, 0692 0, 0952 0, 0692 0,1227 0, 0601 0, 0952 0, 0601 0,1152 Considerando el valor de V F 1,000 / 0,00 pu, tenemos que la corriente de falla en la barra 2 es, ´´ IF2 V F 1,000 / 0,0 j6,80 6,80 / 90,00 pu Z 22 j0,1471 Y las tensiones durante la falla en las barras son, Z j0, 0807 0 V 1 V F 1 12 1, 000 / 0, 0 1 0, 451 / 0, 0 pu Z 22 j0,1471 V 2 0 Z j0, 0692 0 V 3 V F 1 23 1, 000 / 0, 0 1 0, 530 / 0, 0 pu Z 22 j0,1471 Z j0, 0952 0 V 4 V F 1 24 1, 000 / 0, 0 1 0, 353 / 0, 0 pu Z 22 j0,1471 La corriente de falla entre las barras 1 y 4 es, I 14 Z 42 Z 12 j0, 0952 j0, 0807 j0, 329 0, 329 / 90, 00 pu Z p14 Z 22 j0, 300 j0,1471 398 ELECTROTECNIA III-399 Fallas asimétricas. Para calcular las fallas asimétricas se puede representar cada una de las redes de secuencia como un circuito equivalente de barra (o como un equivalente de rastrillo), se puede obtener la matriz de impedancias de barra para cada una de las redes de secuencia, invirtiendo la correspondiente matriz de admitancias de barra. Con el objeto de simplificar los cálculos se desprecian las resistencias, las admitancias en paralelo, las impedancias de carga de las máquinas no rotatorias y se desprecian las corrientes de carga que se tienen antes de la falla. La figura número 67 muestra la conexión de los circuitos equivalentes de rastrillo de las impedancias de barra para las diferentes secuencias, para fallas asimétricas en las barras n de un sistema de potencia. Cada elemento de las impedancias de barra tiene un subíndice adicional , como 1, 2 y 0, que identifican el equivalente de rastrillo para la secuencia que se está representando. Las impedancias mutuas no se muestran en la figura número 67. La tensión antes de la falla V F se incluye en el equivalente de rastrillo de secuencia positiva. 399 ELECTROTECNIA III-400 - … … n N I n0 V 1 0 + 1 2 - - VF + + - … … n N I n1 … - 3 ZF + - + 2 … … … … n N I n2 V 1 2 1 2 n V 1 2 + - … V 11 V 1 1 1 VF N I n1 + 1 2 ZF (b) Falla de línea a línea. 1 2 n N I n2 (a) Falla de una línea a tierra - VF + - … … n N I n1 … … n N I n2 … … n N I n0 V 1 1 + 1 2 1 2 1 2 3ZF (c) Falla de línea a línea y a tierra FIGURA NÚMERO 67. Conexiones equivalentes de rastrillo de las redes de secuencia para fallas asimétricas en un sistema trifásico. (Las impedancias mutuas no se muestran.) De la figura número 67, las corrientes para cada tipo de falla asimétrica, en la barra n son, Falla de una línea a tierra (fase “a” a tierra). I n1 I n 2 I n0 VF Z nn1 Z nn 2 Z nn0 3 Z F (9) Falla de línea a línea (fases “b” y “c”). 400 ELECTROTECNIA III-401 I n1 I n 2 VF Z nn1 Z nn 2 Z F (10) I n0 0 Falla de línea a línea y a tierra (fases “b” y “c”). I n 1 VF Z Z 3ZF Z nn1 nn 2 nn 0 Z nn 2 Z nn 0 3 Z F (11) Z nn0 3 Z F I n 2 I n 1 Z nn 2 Z nn0 3 Z F (12) Z nn 2 I n 0 I n 1 Z nn 2 Z nn0 3 Z F (13) También de la figura número 67, las componentes de secuencia de las tensiones de línea a tierra en cualquier barra k durante una falla en la barra n son, V k 1 V F Z kn 1 V k 2 0 0 V k 0 0 0 0 Z kn 2 0 0 I n 1 0 I n 2 Z kn 0 I n 0 (14) Si la barra k está en el lado sin falla de un transformador -, entonces los ángulos de fase de V k 1 y V k 2 en la ecuación número 14 se modifican teniendo en cuenta el defasamiento para una -. También las corrientes de falla anteriores y las tensiones de secuencia se pueden transformar al dominio de fase por medio de las ecuaciones siguientes, IF A IS (15) V F AV S (16) Ejemplo 8-2. En el sistema de potencia de la figura número 51, se tiene en las barras 1 una falla franca de la fase “a” a tierra. La tensión antes de la falla es de 1,05 /0,00 por unidad. Las corrientes de carga antes de la falla se desprecian. Determinar: a) las matrices de impedancias de barra de las secuencias, b) la corriente de falla subtransitoria, en por unidad, c) repita el inciso b para una falla de la fase “a” a tierra en las barras 2, d) la tensión a tierra en por unidad en las barras 1 y 2 durante la falla de la fase “a” a tierra en las barras 1. SOLUCIÓN. 401 ELECTROTECNIA III-402 a) Las redes de secuencia con sus impedancias originales se muestran en las figuras números 52, 53 y 54, de donde sus correspondientes redes de admitancia son, 1 2 - j 3,28 p.u - j 6,67 p.u - j 5,00 p.u '' VM G V ''G M a) Red de admitancias de secuencia positiva 1 2 - j 3,28 p.u - j 5,88 p.u - j 4,76 p.u b) Red de admitancias de secuencia negativa. 1 2 - j 1,942 p.u - j 4,00 p.u - j 20,0 p.u c) Red de admitancias de secuencia cero. FIGURA NÚMERO 68 De la figura número 68a, la matriz de admitancias de barra de secuencia positiva es, Y 121 Y Y barra 1 111 Y 211 Y 221 j 6, 67 3, 28 9, 95 / 90, 0 3, 28 / 90, 0 j3,28 j3,28 - j 3,28 + 5,00 3, 28 / 90, 0 8, 28 / 90, 0 402 ELECTROTECNIA III-403 De donde la matriz de impedancias de barra de secuencia positiva es, Z 1 Z barra 1 Y barra 1 111 Z 211 Z 12 1 Z 22 1 1 9, 95 / 90, 0 3, 28 / 90, 0 0,1156 / 90, 0 0, 0458 / 90, 0 0, 0458 / 90, 0 0,1389 / 90, 0 3, 28 / 90, 0 8, 28 / 90, 0 De la figura número 68b, la matriz de admitancias de barra de secuencia negativa es, Y 12 2 Y Y barra 2 11 2 Y 21 2 Y 22 2 j 5, 88 3, 28 9,16 / 90, 0 3, 28 / 90, 0 j3,28 j3,28 - j 3,28 + 4,76 3, 28 / 90, 0 8, 04 / 90, 0 De donde la matriz de impedancias de barra de secuencia negativa es, Z 1 Z barra 2 Y barra 2 11 2 Z 21 2 Z 12 2 Z 22 2 1 9,16 / 90, 0 3, 28 / 90, 0 0,1278 / 90, 0 0, 0522 / 90, 0 3, 28 / 90, 0 8, 04 / 90, 0 0, 0522 / 90, 0 0,1457 / 90, 0 De la figura número 68c, la matriz de admitancias de barra de secuencia cero es, Y 11 0 Y 12 0 Y barra 0 Y 21 0 Y 22 0 0 0 20, 0 / 90, 0 j20, 0 0 4, 00 / 90, 0 - j4,00 0 De donde la matriz de impedancias de barra de secuencia cero es, Z 1 Z barra 0 Y barra 0 11 0 Z 21 0 Z 12 0 Z 22 0 1 0 0 20, 0 / 90, 0 0, 0500 / 90, 0 0 4, 00 / 90, 0 0 0, 250 / 90, 0 Observe que las reactancias de dispersión de los transformadores y las reactancias de las líneas de transmisión de secuencia cero, en la figura número 68c no tienen efecto sobre Z barra 0 . Las conexiones delta de los transformadores bloquean el flujo de las corrientes de secuencia cero de los transformadores a las barras 1 y 2. 403 ELECTROTECNIA III-404 b) De la ecuación número 9, con n = 1 y ZF = 0, las corrientes de falla de las secuencias son, I 11 I 1 2 I 1 0 1, 05 / 0, 0 VF Z 111 Z 11 2 Z 110 0,1156 / 90, 0 0,1278 / 90, 0 0, 0500 / 90, 0 3, 58 / 90, 00 pu Las corrientes subtransitorias de falla en las barras 1 son, I ´´1A I 1 1 3,58 /-90,0 10, 74 / 90, 0 ´´ I 1 B A I 1 2 A 3,58 /-90,0 0 3,58 /-90,0 0 I ´´1C I 1 0 ´´ ´´ ´´ I 1 A 10, 74 / 90, 00 pu ; I 1B 0 ; I 1C 0 c) Nuevamente de la ecuación número 9, con n =2 y ZF = 0, las corrientes de falla de las secuencia son, I 2 1 I 2 2 I 2 0 1, 05 / 0, 0 VF Z 221 Z 22 2 Z 22 0 0,1389 / 90, 0 0,1457 / 90, 0 0, 250 / 90, 0 1, 964 / 90, 00 pu Las corrientes subtransitorias de falla en las barras 2 son, I ´´2 A I 2 1 1,964 /-90,0 5, 89 / 90, 0 ´´ I 2 B A I 2 2 A 1,964 /-90,0 0 ´´ 1,964 /-90,0 0 I 2C I 2 0 ´´ ´´ ´´ I 2 A 5, 89 / 90, 00 pu ; I 2 B 0 ; I 2C 0 d) Las componentes de secuencia de las tensiones de línea a tierra, durante la falla en las barras 1, de la ecuación número 14 son, 404 ELECTROTECNIA III-405 V 11 V F Z 111 V 1 2 0 0 V 1 0 0 0 0 Z 11 2 0 0 I 1 1 0 I 1 2 Z 11 0 I 1 0 3, 58 / 90, 0 0 0 1, 05 / 0, 0 0,1156 / 90, 0 0 0 0,1278 / 90, 0 0 3, 58 / 90, 0 0 0 0 0, 0500 / 90, 0 3, 58 / 90, 0 0, 636 / 0, 0 0, 458 / 180, 0 0,1790 / 180, 0 Y las tensiones de línea a tierra en las barras 1 durante la falla en las barras 1 son, V 1 AN V 11 0, 636 / 0, 0 0 V 1 BN A V 1 2 A 0, 458 / 180 0, 985 / 105, 8 0,1790 / 180, 0 0, 985 / 105, 8 V 1 CN V 1 0 V 1 AN 0 ; V 1 BN 0,985 / 105,80 pu ; V 1CN 0,985 / 105,80 pu Las componentes de secuencia de las tensiones de línea a tierra, durante la falla en las barras 1, en las barras 2, de la ecuación número 14 con k = 2 y n = 1, son V 21 V F Z 211 V 2 2 0 0 V 2 0 0 0 0 Z 21 2 0 0 I 11 0 I 1 2 Z 21 0 I 1 0 0 0 3, 58 / 90, 0 1, 05 / 0, 0 0, 0, 0458 / 90, 0 0 0 0, 0522 / 90, 0 0 3, 58 / 90, 0 0 0 0 0 3, 58 / 90, 0 0, 886 / 0, 0 0,1869 / 180, 0 0 Observe que puesto que tanto las barras 1 como las barras 2 están en el lado de baja tensión de los transformadores en la figura número 51, no hay defasamiento en el ángulo de las tensiones de secuencia. De lo anterior las tensiones de línea a tierra en las barras 2, durante la falla en las barras 1 son, 405 ELECTROTECNIA III-406 V 2 AN 0,886 /0,0 0, 699 / 0, 0 V 2 BN A 0,1869 /180,0 0, 993 / 110, 6 0, 993 / 110, 6 0 V 2CN V 2 AN 0,699 / 0,00 pu ; V 2 BN 0,993 / 110,60 pu ; V 2CN 0,993 / 110,60 pu Ejemplo 8-3. En el sistema de potencia mostrado en la figura número 51, considere que se tiene una falla franca en las barras 2 entre las fases “b” y “c”. La tensión antes de la falla es de 1,05 /0,00 por unidad. Las corrientes de carga antes de la falla se desprecian Determine la corriente de falla subtransitoria, en por unidad. SOLUCIÓN. Considerando las redes de secuencia positiva y negativa del ejemplo 8-2 y la ecuación número 10, con n = 2 y ZF = 0, tenemos que las corrientes de secuencia para la falla son, I 2 1 I 2 2 1, 05 / 0, 0 VF 3, 69 / 90, 00 pu Z 221 Z 22 2 0,1389 / 90, 0 0,1457 / 90, 0 I 2 0 0 Las corrientes subtransitorias de falla en las barras 2 son, I ´´2 A I 2 1 0 3, 69 / 90, 0 ´´ I 2 B A I 2 2 A 3, 69 / 90, 0 6, 39 / 180, 0 0 6, 39 / 0, 0 I ´´2C I 2 0 ´´ ´´ ´´ I 2 A 0 ; I 2 B 6, 39 / 180, 00 pu ; I 2C 6, 39 / 0, 00 pu Ejemplo 8-4. En el circuito mostrado en la figura número 51, considere que se tiene una falla franca en las barras 2, entre las fases “b” y “c” y tierra, determine: a) las corrientes de falla subtransitoria, en por unidad, y b) la tensión a tierra, en por unidad, en las barras 1 y 2 durante la falla. SOLUCIÓN. a) Considerando las redes de secuencia del ejemplo 8-2 y las ecuaciones números 11, 12 y 13, tenemos que las corrientes de secuencia para la falla son, 406 ELECTROTECNIA III-407 I 2 1 1, 05 / 0, 0 VF 4, 55 / 90, 00 pu Z Z 0,1457 / 90, 0 0, 250 / 90, 0 Z 221 22 2 220 0,1389 / 90, 0 Z 22 2 Z 22 0 0,1457 / 90, 0 0, 250 / 90, 0 Z Z I 2 2 I 21 I 20 I 21 0, 250 / 90, 0 Z 220 4, 55 / 90, 0 2, 87 / 90, 00 pu Z 0,1457 / 90, 0 0, 250 / 90, 0 22 2 22 0 0,1457 / 90,0 Z 222 4,55 / 90,0 1,675 / 90,00 pu 0,1457 / 90,0 0, 250 / 90,0 22 2 Z 22 0 Transformado las corrientes subtransitorias al dominio de fase son, I ´´2 A I 2 1 4, 55 / 90, 0 0 ´´ I 2 B A I 2 2 A 2, 87 / 90, 0 6, 90 / 158, 6 ´´ I 2C I 2 0 1, 675 / 90, 0 6, 90 / 21, 4 ´´ ´´ ´´ I 2 A 0 ; I 2 B 6,90 / 158,60 pu ; I 2C 6,90 / 21,40 pu La corriente de falla a tierra es, I N 3 I 20 3 1,675 / 90,0 5,03 / 90,00 pu b) De la ecuación número 14, las componentes de secuencia de las tensiones de línea a tierra son, Para las barras 1, V 11 V F Z 12 1 V 1 2 0 0 0 0 V 1 0 0 Z 12 2 0 0 I 2 1 0 I 2 2 Z 12 0 I 2 0 0 0 4, 55 / 90, 0 0, 841 / 0, 0 1, 05 / 0, 0 0, 0458 / 90, 0 0 0 0, 0522 / 90, 0 0 2, 87 / 90, 0 0,1498 / 0, 0 0 0 0 0 1, 675 / 90, 0 0 En el dominio de fase las tensiones son, V 1 AN V 11 0, 841 / 0, 0 0, 991 / 0, 0 V 1 BN A V 1 2 A 0,1498 / 0, 0 0, 777 / 129, 6 0, 777 / 129, 6 0 V 1CN V 1 0 407 ELECTROTECNIA III-408 V 1 AN 0,991/ 0,00 pu ; V 1 BN 0,777 / 129,60 pu ; V 1CN 0,777 / 129,60 pu Para las barras 2, V 21 V F Z 221 V 2 2 0 0 V 2 0 0 0 0 Z 22 2 0 0 I 2 1 0 I 2 2 Z 22 0 I 2 0 4, 55 / 90, 0 0, 418 / 0, 0 0 0 1, 05 / 0, 0 0,1389 / 90, 0 0 0 0,1457 / 90, 0 0 2, 87 / 90, 0 0, 418 / 0, 0 0 0 0 0, 250 / 90, 0 1, 675 / 90, 0 0, 418 / 0, 0 En el dominio de fase las tensiones son, V 2 AN V 21 0, 418 / 0, 0 1, 254 / 0, 0 0 V 2 BN A V 2 2 A 0, 418 / 0, 0 0, 418 / 0, 0 0 V V 2 CN 2 0 V 2 AN 1, 254 / 0,00 pu ; V 2 BN 0 ; V 2CN 0 Ejercicio de cálculo de corto circuito, con componentes simétricas. Se tiene un sistema como se muestra en la figura número 1, el cual consiste de una estación de generación hidroeléctrica que tiene los generadores A y B, y una estación con generación por medio de vapor con generadores G e I. Las estaciones se conectan por medio de dos líneas de transmisión de 110 kV. Se calcularán los cuatro tipos de fallas. TC . GA Línea 1 110 kV TF . GH 33 kV 12 kV TD Línea 2 110 kV TE GG GB 12 kV GI 12 kV 12 kV ESTACIÓN 1 ESTACIÓN 2 FIGURA NÚMERO 1 408 ELECTROTECNIA III-409 Los aparatos considerados tienen las características siguientes: ESTACIÓN 1. Generador A, 50 MVA, 12 kV, reactancia subtransitoria 30 %, reactancia de secuencia negativa 50 %. Generador B, 20 MVA, 12 kV, reactancia subtransitoria 35 %, reactancia de secuencia negativa 60 %. Transformador C, 50 MVA, 12 kV delta a 110 kV estrella sólidamente a tierra, reactancia 8 %. Transformador D, 20 MVA, 12 kV delta a 110 kV estrella con el neutro flotante, reactancia 8 %. ESTACIÓN 2. Generador G, 25 MVA, 12 kV, reactancia subtransitoria 12 %, recatancia de secuencia negativa 12 %. Sistema H equivalente a 33 kV, reactancias a secuencia positiva y negativa 10 %, con una base de 50 MVA. Generador I, 50 MVA, 12 kV, reactancia subtransitoria 9 %, reactancia de secuencia negativa 9 %. Transformador E, 60 MVA, 12 kV estrella con neutro aislado a 110 kV estrella con neutro aislado, reactancia 8 %. Transformador F de tres devanados, 110 kV (P) estrella con neutro sólidamente a tierra, a 33 kV (S) delta, a 12 kV (T) delta. Las reactancias son: de P a S 10 % en una base de 25 MVA, de P a T 8 % en una base de 10 MVA, S a T 12 % en una base de 20 MVA. Línea 1. Longitud 80,5 km, con una reactancia total de J 40 . Línea 2. Igual que la línea 1. La reactancia de secuencia cero se considera que es 3,5 veces la reactancia de secuencia positiva para las líneas de transmisión. La exactitud deseada en los cálculos es tal que se pueden hacer las consideraciones siguientes: 1. Todas las tensiones generadas son iguales y están en fase. 2. Las resistencias componentes de las impedancias de los generadores y transformadores son despreciables, y las reactancias se usan como constantes concentradas. 3. Las fallas ocurren con el sistema sin carga, y las admitancias de magnetización de los transformadores y las capacitancias de las líneas de transmisión se desprecian. 4. Los circuitos de transmisión están separados por una distancia suficiente, de tal manera que las impedancias mutuas entre líneas para las corrientes de secuencia cero se pueden despreciar. Los valores de las impedancias se pueden usar fácilmente como reactancias. Todas las fallas se consideran que ocurren en la línea número 2 a un cuarto de distancia de la estación 1 a la estación 2. El primer paso es reducir todas las reactancias a valores por unidad, tomando como tensión base 110 kV, y como potencia base 50 MVA. Estación 1. 409 ELECTROTECNIA III-410 La tensión base del lado de los generadores, tomando en cuenta la tensión base de 110 kV y la relación de los transformadores C y D, es de 12 kV. Generador A. Puesto que el generador A tiene sus características iguales con las bases seleccionadas, entonces sus reactancias por unidad son, ´´ X GA 1 0, 300pu ´´ X GA 2 0, 500pu Generador B. Tiene tensión igual a la tensión base seleccionada, de donde sus reactancias por unidad son, S Bn ´´ ´´ X GB 1 X Bd 1 S Bd 50 0, 350 0, 875pu 20 S Bn 50 ´´ ´´ X GB 0, 600 1, 500pu 2 X Bd 2 20 S Bd Transformador C. Tiene sus características iguales que las bases seleccionadas, de donde XTC 0,800pu Transformador D. Tiene tensiones iguales a las tensiones base seleccionadas, de donde, S X TD X Bd Bn S Bd 50 0, 0800 0, 200pu 20 Estación 2. Las tensiones base del lado de los generadores, tomando en cuenta la tensión base de 110 kV y la relación de los transformadores E y F, son de 33 kV y 12 kV. Generador G. Tiene tensión igual a la tensión base seleccionada, de donde 410 ELECTROTECNIA III-411 S Bn 50 ´´ ´´ X GG 0,1200 0, 240pu 1 X Bd 1 25 S Bd ´´ ´´ X GG 2 X GG 1 0, 240pu Transformador E. Tiene tensiones iguales a las tensiones base seleccionadas, de donde, S 50 X TE X Bd Bn 0, 0800 0, 0667 pu 60 S Bd Sistema H. Tiene las mismas características que las bases seleccionadas, de donde X H 1 X H 2 0, 01000pu Generador I. Tiene tensión igual a la tensión base seleccionada, de donde S Bn ´´ ´´ X GI 1 X Bd 1 S Bd 50 0, 0900 0, 900pu 5 Transformador F. El transformador de tres devanados, tiene tensiones iguales a las tensiones base seleccionadas, de donde las impedancias equivalentes en estrella son, S X PS X PSd Bn S Bd 50 0,1000 0, 200pu 25 S 50 X PT X PTd Bn 0, 0800 0, 400pu 10 S Bd S X ST X STd Bn S Bd 1 50 0,1200 0, 300pu 20 X PTF 1 1 0 X PS 1 1 0 X 1 0 1 X 1 0 1 STF PT X TTF 0 1 1 X ST 0 1 1 X PTF 0,1500pu ; X STF 0,0500pu 1 0, 200 0,1500 0, 400 0, 0500 0, 300 0, 250 ; XTTF 0, 250pu Líneas de transmisión. 411 ELECTROTECNIA III-412 La impedancia base de las líneas de transmisión es, 2 k VL B 1102 ZB 242 MVA B 50 Línea de transmisión 1. X L11 X L11 ZB 40 0,1653pu 242 X L1 2 X L11 0,1653pu X L10 3,5 0,1653 0,579pu Línea de transmisión 2. X L 21 0,1653pu X L 2 2 X L 21 0,1653pu X L20 0,579pu Las reactancias de la línea 2 al punto de falla son, De las barras 1 a la falla, X L 21 F 1 0, 25 0,1653 0, 0413pu X L 21 F 2 0, 0413pu X L21F 0 0, 25 0,579 0,1448pu De las barras 2 a la falla, X L 22 F 1 0, 75 0,1653 0,1240pu X L 22 F 2 0,1240pu X L22F 0 0,75 0,579 0,434pu 412 ELECTROTECNIA III-413 2 1 0,300 0,875 0,0800 0,1653 0,200 0,0413 3 0,0500 0,1000 0,250 0,900 0,1500 0,1240 0,0667 0,240 X Falla (A). Red de secuencia positiva 2 1 0,500 1,500 0,0800 0,1653 0,200 0,0413 3 0,0500 0,1000 0,250 0,900 0,1500 0,1240 0,0667 0,240 X Falla (B). Red de secuencia negativa 0,0500 2 1 0,0800 0,579 0,1500 0,250 0,1448 3 0,434 X Falla (C). Red de secuencia cero FIGURA NÚMERO 2. Las redes de reactancia para las secuencias positiva, negativa y cero se pueden construir ahora con valores por unidad, como se muestra en la figura número 2. La red de secuencia positiva se dibuja sin la tensión generada. La red de secuencia negativa es la misma que la de secuencia positiva, excepto por los valores usados para los generadores. Los transformadores D y E no aparecen en la red de secuencia cero debido a que su neutro es flotante. 413 ELECTROTECNIA III-414 La reactancia de secuencia cero de los generadores B y G no aparece en la red de secuencia cero, debido a que la delta del devanado de baja tensión y la estrella con neutro flotante de los transformadores bloquean el flujo de las corrientes de secuencia cero. El paso siguiente es reducir las redes de secuencia positiva, negativa y cero, por separado, a una sola impedancia equivalente. Puesto que más de un tipo de falla se calcularán para la misma localización de la falla, es deseable trabajar en forma inversa en las redes para determinar los factores de distribución de las corrientes para cada una de las ramas de las redes. Considerando la red de secuencia positiva, de la figura número 2A, esta se puede volver a dibujar y se muestra en la figura número 3, donde además se muestran los pasos a seguir para obtener la reactancia equivalente de Thévenin. También es conveniente trabajar en forma inversa en las redes para determinar los factores de distribución de las corrientes, los cuales se indican entre paréntesis rectangulares [], en la misma figura. Los factores de distribución de la corriente, considerando que fluye una corriente unitaria de la red a la falla y realizando el trabajo en forma inversa, se obtienen en la forma siguiente: En las figuras números 3f y 3g el factor de distribución de corrientes es [1]. En la figura 3e los factores de distribución de corriente, aplicando la regla de la distribución de corriente son, 1 0, 209 0, 302 0, 409 ; 1 0, 591 0, 209 0, 302 0, 209 0, 302 Los factores de distribución en la delta de la figura número 3c se determinan de los factores de la estrella equivalente, haciendo uso del hecho de que las caídas de tensión entre terminales debe ser el mismo tanto para la estrella como para la delta, así tenemos 0, 0207 0, 409 0, 01549 1 0, 580 0, 0413 0, 0620 0, 591 0, 0207 0, 409 0,1705 0,1653 0, 0620 0, 591 0, 01549 1 0, 420 0,1240 414 ELECTROTECNIA III-415 (0,0500 + 0,1000) 1 [0,302] 0,380 [0,1705] 0,1653 2 [0,308] 0,1500 [0,272] 0,1500 1,150 (0,300 + 0,0800) [0,1068] 1,075 [0,580] 0,0413 [0,420] 0,1240 3 [0,283] [0,0355] (0,250 + 0,900) 0,307 X (0,875 + 0,200) (0,0667 + 0,240) Falla (a) 1 [0,302] 0,380 2 [0,308] [0,1705] 0,1653 [0,1068] 1,075 [0,580] 3 0,0413 0,1500 1,150 0,1500 0,1500 1,150 [0,283] 0,307 [0,420] 0,1240 1 [0,409] 0,281 0,283 2 [0,591] [0,1705] 0,1653 0, 380 1, 075 0, 380 1, 075 Za 0,1473 Zb 0, 283 0, 307 0, 283 0, 307 Zc 0,0413 [0,580] X 0,1240 [0,420] X 3 Falla Falla (b) (c) [0,409] 0,281 2 [0,591] 1 0,0207 0,0620 0,1473 [X] Factor de distribución de corriente 0,1653 0,1240 0,1653 0, 0413 0,1240 0,01549 0, 0413 0,1240 0,1653 0, 0413 0,1240 0,1653 0, 0413 0,1653 0, 0413 0,1240 [1] X 3 Falla [0,409] [0,591] 0,302 0,209 0, 281 0, 0207 0,1473 0, 0620 0,01549 [1] X 3 Falla (e) (d) 0, 302 0, 209 0, 302 0, 209 [1] 0,1235 0,1235 0, 01549 0,1390 [1] 0,01549 X 3 Falla X 3 Falla (g) (f) FIGURA NÚMERO 3. Pasos a seguir para la reducción de la red de secuencia positiva a una reactancia equivalente y los factores de distribución de corriente en todas las ramas. Los factores de distribución en la barra 1 de la figura 3b, del lado izquierdo son, 1, 075 0, 380 0, 409 0, 302 ; 0, 409 0,1068 0, 380 1, 075 0, 380 1, 075 415 ELECTROTECNIA III-416 Los factores de distribución en la barra 2 de la figura 3b, del lado derecho son, 0, 307 0, 283 0, 591 0, 308 ; 0, 591 0, 283 0, 283 0, 307 0, 283 0, 307 Los factores de distribución en la barra equivalente del transformador de tres devanados de la figura 3a son, 1,150 0,1500 0, 308 0, 272 ; 0, 308 0, 0355 0,1500 1,150 0,1500 1,150 En la figura número 4, tomando en cuenta la figura número 2B, se muestran los pasos a seguir para la reducción de la red de secuencia negativa, para obtener la reactancia equivalente de Thévenin, así como los factores de distribución de las corrientes. Los factores de distribución de la corriente, considerando que fluye una corriente unitaria de la red a la falla y realizando el trabajo en forma inversa, se obtienen en la forma siguiente: En las figuras números 4f y 4g el factor de distribución de corrientes es [1]. En la figura 4e los factores de distribución de corriente, aplicando la regla de la distribución de corriente son, 1 0, 209 0, 453 0, 316 ; 1 0, 684 0, 209 0, 453 0, 209 0, 453 Los factores de distribución en la delta de la figura número 4c se determinan de los factores de la estrella equivalente, haciendo uso del hecho de que las caídas de tensión entre terminales debe ser el mismo tanto para la estrella como para la delta, así tenemos 0, 0207 0, 316 0, 01549 1 0, 533 0, 0413 0, 0620 0, 684 0, 0207 0, 316 0, 217 0,1653 0, 0620 0, 684 0, 01549 1 0, 467 0,1240 416 ELECTROTECNIA III-417 (0,0500 + 0,1000) 1 [0,236] 0,580 [0,217] 2 [0,356] 0,1653 0,1500 0,1500 [0,315] 1,150 (0,500 + 0,0800) [0,0804] 1,700 [0,533] 0,0413 [0,467] 0,1240 3 [0,328] [0,0411] (0,250 + 0,900) 0,307 X (1,500 + 0,200) (0,0667 + 0,240) Falla (a) 1 [0,236] 0,580 2 [0,356] [0,217] 0,1653 [0,0804] 1,700 [0,533] 3 0,0413 0,1500 1,150 0,1500 0,1500 1,150 [0,328] 0,307 [0,467] 0,1240 1 [0,316] 0,432 0,283 0, 580 1, 700 0, 580 1, 700 [0,217] 2 [0,684] 0,1653 0,1473 Za Zb 0, 283 0, 307 0, 283 0, 307 Zc 0,0413 [0,533] X 0,1240 [0,467] X 3 Falla Falla (b) (c) [0,316] 0,432 2 [0,684] 1 0,0207 0,0620 0,1473 [X] Factor de distribución de corriente 0,1653 0,1240 0,1653 0, 0413 0,1240 0,1653 0, 0413 0,1653 0, 0413 0,1240 0,01549 0, 0413 0,1240 0,1653 0, 0413 0,1240 [1] X 3 Falla [0,316] [0,684] 0,453 0,209 0, 432 0, 0207 0,1473 0, 0620 0,01549 [1] X 3 Falla (e) (d) 0, 453 0, 209 0, 453 0, 209 [1] 0,1430 0,1430 0, 01549 0,1585 [1] 0,01549 X 3 Falla X 3 Falla (g) (f) FIGURA NÚMERO 4. Pasos a seguir para la reducción de la red de secuencia negativa a una reactancia equivalente y los factores de distribución de corriente en todas las ramas. Los factores de distribución en la barra 1 de la figura 4b, del lado izquierdo son, 417 ELECTROTECNIA III-418 1, 700 0, 580 0, 316 0, 236 ; 0, 316 0, 0804 0, 580 1, 700 0, 580 1, 700 Los factores de distribución en la barra 2 de la figura 4b, del lado derecho son, 0, 307 0, 283 0, 684 0, 356 ; 0, 684 0, 328 0, 283 0, 307 0, 283 0, 307 Los factores de distribución en la barra equivalente del transformador de tres devanados de la figura 4a son, 1,150 0,1500 0, 356 0, 315 ; 0, 356 0, 0411 0,1500 1,150 0,1500 1,150 En la figura número 5, tomando en cuenta la figura número 2C, se muestran los pasos a seguir para la reducción de la red de secuencia cero, para obtener la reactancia equivalente de Thévenin, así como los factores de distribución de las corrientes. Los factores de distribución de la corriente, considerando que fluye una corriente unitaria de la red a la falla y realizando el trabajo en forma inversa, se obtienen en la forma siguiente: En las figuras números 5f y 5g el factor de distribución de corrientes es [1]. En la figura 5e los factores de distribución de corriente, aplicando la regla de la distribución de corriente son, 1 0, 409 0,1524 0, 729 ; 1 0, 271 0,1524 0, 409 0,1524 0, 409 Los factores de distribución en la delta de la figura número 5c se determinan de los factores de la estrella equivalente, haciendo uso del hecho de que las caídas de tensión entre terminales debe ser el mismo tanto para la estrella como para la delta, así tenemos 0, 0724 0, 729 0, 0543 1 0, 740 0,1448 0, 217 0, 271 0, 0724 0, 729 0, 01041 0, 579 0, 217 0, 271 0, 0543 1 0, 261 0, 434 418 ELECTROTECNIA III-419 [0,729] 0,0800 1 [0,01041] 0,579 2 [0,271] 0,0500 [0,226] 0,1500 0,250 [0,0452] [0,740] 0,1448 [0,261] 0,434 3 X Falla (a) [0,729] 0,0800 1 2 [0,271] [0,01041] 0,579 [0,729] 0,0800 0,1917 1 0,579 0, 0500 0, 250 0,1500 0, 0500 0, 250 [0,740] Za [0,261] 0,434 3 0,1448 2 [0,271] [0,01041] 0,1917 Zb Zc 0,1448 [0,740] X 0,434 [0,261] X 3 Falla Falla (b) (c) [0,729] 0,0800 2 [0,271] 1 0,0724 0,217 0.1917 [X] Factor de distribución de corriente 0, 579 0, 434 0, 579 0,1448 0, 434 0, 579 0,1448 0, 579 0,1448 0, 434 0,0543 0,1448 0, 434 0, 579 0,1448 0, 434 [1] X 3 Falla [0,729] [0,271] 0,1524 0,409 0, 0800 0, 0724 0, 217 0,1917 0,0543 [1] X 3 Falla (e) (d) 0,1524 0, 409 0,1110 0,1524 0, 409 [1] 0,0543 X 3 Falla 0,1110 0, 0543 0,1653 [1] X 3 Falla (g) (f) FIGURA NÚMERO 5. Pasos a seguir para la reducción de la red de secuencia cero a una reactancia equivalente y los factores de distribución de corriente en todas las ramas. Los factores de distribución en la barra equivalente del transformador de tres devanados de la figura 5a son, 419 ELECTROTECNIA III-420 0, 0500 0, 250 0, 271 0, 0452 ; 0, 271 0, 226 0, 0500 0, 250 0, 0500 0, 250 Falla trifásica. Solamente la impedancia equivalente de secuencia positiva está involucrada en este caso. La corriente subtransitoria de secuencia positiva, por unidad es, I a1 V F 1, 000 / 0, 0 7,19 / 90, 00 pu Z1 j0,1390 Las corrientes subtransitorias de secuencia negativa y secuencia cero son, I a2 I a0 0 Las corrientes subtransitorias de falla son, I "A I a1 7,19 / 90, 0 7,19 / 90, 0 " 7,19 / 150, 0 I B A I a2 A 0 " 0 7,19 / 30 IC I a 0 " " " I A 7,19 / 90,00 pu ; I B 7,19 / 150,00 pu ; I C 7,19 / 30,00 pu La corriente base para la tensión de 110 kV es, kVAB 50, 0 103 I B 110 262 A kVB-110 3 110 Las corrientes subtransitorias de falla, en amperes, son, " " " " I A I B 110 I A (pu) 262 7,19 / 90,0 1884 / 90,00 A I B I B 110 I B (pu) 262 7,19 / 150, 0 1884 / 150, 00 A " " I C I B 110 I C (pu) 262 7,19 / 30,0 1884 / 30,00 A La distribución de las corrientes en la red, tomando en cuenta los factores de distribución es, 420 ELECTROTECNIA III-421 1 512 A 2 569 A 321 A 580 A 66,9 A 201 A 1093 A 791 A X 533 A 1884 A Las corrientes en el transformador C son, I A BT GA A I CA BT A TC I AB BT C I C AT I C BT C I BC BT I A AT I B AT B B I B BT 12 kV 110 kV I A AT 569 / 90,00 A ; I B AT 569 / 150,00 A ; I C AT 569 / 30,00 A I AB BT nTC I A AT 110 3 569 / 90, 0 3, 01 103 / 90, 00 A 12 I BC BT 3,01 103 / 150,00 A ; I CA BT 3,01 103 / 30,00 A I A BT 3 I AB / AB 30, 0 3 3, 01 103 / 90, 0 30, 0 5, 21 10 3 / 120, 0 0 A I B BT 5, 21103 / 240,00 A ; I C BT 5, 21103 / 0,00 A Las corrientes en el transformador D son, I A BT GB A I CA BT I AB BT C I C BT A TD I C AT C I BC BT I B BT 12 kV I A AT I B AT B B 110 kV I A AT 201/ 90,00 A ; I B AT 201/ 150,00 A ; I C AT 201/ 30,00 A 421 ELECTROTECNIA III-422 I AB BT nTD I A AT 110 3 201 / 90, 0 1064 / 90, 00 A 12 I BC BT 1064 / 150,00 A ; I CA BT 1064 / 30,00 A I A BT 3 I AB / AB 30, 0 3 1064 / 90, 0 30, 0 1843 / 120, 00 A I B BT 1843 / 240,00 A ; I C BT 1843 / 0,00 A Las corrientes en el transformador E son, GG A I C AT A TE I A BT I A AT I B AT C A I B BT B I C BT B C 110 kV C B 12 kV I A AT 533 / 90,00 A ; I B AT 533 / 150,00 A ; I C AT 533 / 30,00 A I A BT nTE I A AT 110 533 / 90, 0 4, 89 10 3 / 90, 00 A 12 I B BT 4,89 103 / 150,00 A ; I C BT 4,89 103 / 30,00 A Las corrientes en el transformador F, en el secundario son, TF A I A BT A I AB BT I C AT C I A AT I B AT B I CA BT I BC BT C 110 kV GH B I B BT I C BT 33 kV I A AT 512 / 90,00 A ; I B AT 512 / 150,00 A ; I C AT 512 / 30,00 A 422 ELECTROTECNIA III-423 110 I AB BTS nTFS I A ATS 3 512 / 90, 0 985 / 90, 00 A 33 I BC BTS 985 / 150,00 A ; I CA BTS 985 / 30,00 A I A BTS 3 I ABS / ABS 30, 0 3 985 / 90, 0 30, 0 1706 / 120, 00 A I B BTS 1706 / 240,00 A ; I C BTS 1706 / 0,00 A Las corrientes en el transformador F, en el terciario son, TF A I A BT A I AB BT I C AT C I A AT I B AT B I CA BT I BC BT C 110 kV GI B I B BT I C BT 12 kV I A AT 66,9 / 90,00 A ; I B AT 66,9 / 150,00 A ; I C AT 66,9 / 30,00 A I AB BTT nTFT I A ATT 110 3 66, 9 / 90, 0 354 / 90, 00 A 12 I BC BTT 354 / 150,00 A ; I CA BTT 354 / 30,00 A I A BTT 3 I ABT / ABT 30, 0 3 354 / 90, 0 30, 0 613 / 120, 00 A I B BTT 613 / 240,00 A ; I C BTT 613 / 0,00 A 423 ELECTROTECNIA III-424 Falla franca de línea a tierra de la fase A. Las reactancias equivalentes de las redes se conectan en serie para determinar de falla, como se muestra en la figura, Las corrientes de falla de las secuencias son, I1 I 2 I0 VF Z1 Z 2 Z0 1, 000 / 0, 0 j0,1390 j0,1585 j0,1653 2,16 / 90, 00 pu Las corrientes subtransitorias en el punto de falla son, I "A I1 2,16 / 90, 0 6, 48 / 90, 0 " I B A I 2 A 2,16 / 90, 0 0 2,16 / 90, 0 0 I "C I 0 " " " I A 6, 48 / 0, 00 pu ; I B 0 ; I C 0 424 ELECTROTECNIA III-425 I0 Z 0 j0,1653p.u. + V0 I1 + Z 1 j0,1390p.u. + V F 1, 000 / 0, 0 pu - V1 0 Z 2 j0,1585p.u. I2 + V2 La corriente base en el punto de falla (3) es, I B 110 kVAB 50, 0 103 262 A kVB-110 3 110 De donde las corrientes subtransitorias de falla, en amperes, son " " I A I B 110 I A (pu) 262 6, 48 / 90, 0 1698 / 90, 00 A " " IB 0 ; IC 0 425