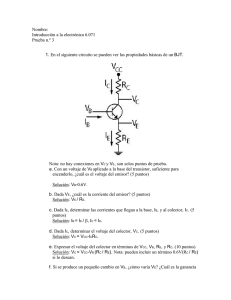
Diseño de la correa transportadora
A partir de: 2015-03-16
Se debe dimensionar un accionamiento para una cinta transportadora. Para este propósito,
se describen los principios de cálculo físico y eléctrico y se explican las tareas de muestra
asociadas.
×
BB altura de la cinta transportadora
ll longitud de la cinta transportadora
bb ancho de la cinta transportadora
αα pasoα
μμ coeficiente de fricción
rr el radio de los rodillos transportadores
FNFN fuerza normal (perpendicular aFH)
pesom⋅gFGFGm ⋅ gm⋅g
Fuerza de fricción:
Fr= μ ⋅ FN= μ ⋅ FG⋅ c o s α = micras ⋅ FG⋅ b / lFr=μ⋅FN=μ⋅FG⋅cosα=μ⋅FG⋅b/l
Fuerza de descenso:
FB= FG⋅ s i n α = FG⋅ h / lFB=FG⋅syonα=FG⋅B/l
Salida de transmisión de par de carga total:
M= ML a s tηL= F⋅ rηL= ( Fr+ FB) ⋅ rηLM=MLastηL=F⋅rηL=(Fr+FH)⋅rηL
P= M⋅ ω = PL a s tηL= F⋅ vηL= ( Fr+ FB) ⋅ vηLP=M⋅ω=PLunastηL=F⋅vηL=(Fr+FB)⋅vηL
n = vπ⋅ dn=vπ⋅d
P*= PηG e t r .P*=PηGetr,
yoG= n*nyoG=n*n
M*= MηG⋅ iGM*=MηG⋅yoG
×Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para ser
receptivo, de modo que se muestre sin problemas en todos los dispositivos.
Tarea 1
Se debe dimensionar una unidad para un transportador de cajas para una escalera a una
plataforma. Los transportadores son accionados por un motor, por lo que se debe alcanzar
una velocidad de la correa de 0.4 m / s. La carga máxima por cinta transportadora es de
200 kg por metro. Entre la cinta transportadora y la base, el coeficiente de fricción es μ =
0.4. La transmisión tiene una eficiencia de η G = 0.76 y se supone que la eficiencia de la
carga es 1.
a.
b.
c.
d.
e.
f.
Calcule el par de carga total de la cinta transportadora de la caja.
¿Cuál es la velocidad de los rodillos de la cinta transportadora?
¿Cuál es el requisito de potencia en el lado de salida (sin caja de cambios)?
¿Qué diseño de caja de cambios sería ventajoso para esta aplicación? Justifica tu decisión.
Calcule la potencia requerida del motor trifásico y seleccione un motor trifásico de jaula de
ardilla de 2 polos adecuado:
P fuera en kW
n B en min -1
4.3
2800
5.5
2854
6.1
2845
7.2
2860
8.4
2880
Calcule la relación de transmisión y el par del motor trifásico.
Solución »
a. M= 706 , 32 N m M=706.32 Nm
b. n
c. =
d. 38
e. ,
f. 2
g. m
h. i
i. n
j. - 1n=38.2 myon-1
k. P= 2825 W P=2825 W
l. Tipo de caja de cambios: engranaje helicoidal, autoblocante
m. P*= 3 , 715 k W P*=3.715 kW
4 , 3 k W 4.3 kW
n. yoG= 73 , 3yoG=73.3
M*= 12 , 68 N m
Polipasto de diseño de accionamiento
A partir de: 2015-03-17
Una unidad de grúa debe dimensionarse. Para este propósito, se describen los principios
de cálculo físico y eléctrico y se explican las tareas de muestra asociadas.
×
aceleración de la gravedad 9,81 m / s2gg
Diámetro del tambor de cuerdadTr o m .dTrom.
masa de la cargamm
velocidad de salida del variadornn
velocidadvv
frecuencia circular2πnωω2 πn2πn
eficiencia de cargaηLηL
ηGηG
M= ML a s tηL= F⋅ rηL= m ⋅ g⋅ dTr o m m e l/ 2ηLM=MLastηL=F⋅rηL=m⋅g⋅dTrommel/2ηL
P= M⋅ ω = PL a s tηL= F⋅ vηL= m ⋅ g⋅ vηLP=M⋅ω=PLastηL=F⋅vηL=m⋅g⋅vηL
n = vπ⋅ dn=vπ⋅d
P*= PηG e t r .P∗=PηGetr.
yoG= n*niG=n∗n
M*= MηG⋅ iGM∗=MηG⋅iG
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Diseño de impulsión de colección de fórmulas:
Tarea 1
El accionamiento de una grúa debe dimensionarse. La carga máxima es de 2 t. El diámetro
del tambor de cuerda es d tambor = 20 cm. El par del motor se transmite a través de un
engranaje fijo al tambor del cable. La velocidad máxima de elevación debe ser de 10 km /
h. La eficiencia de carga del tambor de cable es del 97%, la eficiencia de transmisión es
del 93%.
Calcular en el lado de salida de transmisión
a. el par,
b. el rendimiento
c. La velocidad.
d. Calcule la potencia requerida en el lado de entrada de la transmisión.
e. Los siguientes DASM están disponibles (ver tabla). Calcule el par nominal de los motores en
cada caso. ¿Cuál de estos motores es adecuado para el variador?
P fuera en kW
n B en min -1
37
1455
45
1465
52
1465
58
1475
64
1475
f. Calcule la relación de transmisión y
g. El par de entrada de la transmisión.
Solución »
a. M= FG⋅ rηLM=FG⋅rηL = m ⋅ g⋅ rηL= 2000 k g ⋅ 9 , 81 m / s 2⋅ 0 , 1 m 0 , 97=m⋅g⋅rηL=2000 kg⋅9,81 m/s2⋅0,
1 m0,97 = 2022 , 68 N m=2022,68 Nm
b. P= FG⋅ vηL= P=FG⋅vηL=2000kg ⋅ 9 , 81 m / s 2⋅ 2 , 78 m / s 0 , 97= 56 , 23 k W 2000 kg⋅9,81 m/s2⋅2,7
8 m/s0,97=56,23 kW
c. n = vπd= 2 , 78 m / s π⋅ 0 , 2 m = 4 , 42 s - 1n=vπd=2,78 m/sπ⋅0,2 m=4,42 s−1 = 265 , 2 m i n 1=265,2 min−1
d. P*= 28 , 25 k W P∗=28,25 kW
e. Par nominal del motor y selección del motor:
P fuera en kW
n B en min -1
37
1455
45
1465
52
1465
58
1475
64
1475
f. yoG= n*n= 1475265 , 2= 5 , 56iG=n∗n=1475265,2=5,56
g. M*= MηG⋅ iG= 2022 , 68 N m0 , 93 ⋅ 5 , 56M∗=MηG⋅iG=2022,68 Nm0,93⋅5,56 = 391 , 2 N m=391,2
Nm
Tarea 2
Una unidad para un ascensor debe dimensionarse. La carga máxima es de 1250 kg. El
diámetro del tambor de cable es d tambor = 400 mm. El par del motor se transmite a través de
un engranaje fijo al tambor del cable. La velocidad máxima de elevación debe ser de 2,1 m
/ s.
a. Dibuje la estructura de conducción del elevador e ingrese los valores característicos.
b.
c.
d.
e.
Se supone que la eficiencia de carga del tambor de cable es del 93%, la eficiencia de
transmisión del 98%. Calcular en el lado de salida de transmisión
el par,
el rendimiento
La velocidad.
Calcule la potencia requerida en el lado de entrada de la transmisión y seleccione un DASM de
4 pines adecuado de la tabla.
P fuera en kW
n B en min -1
M B en Nm
15
1460
98
18.5
1465
121
22
1465
143
30
1465
196
37
1475
240
f. Calcule la relación de transmisión y
g. El par de entrada de la transmisión.
Solución »
a. Construcción del ascensor
M= 2637 , 1 N m M=2637,1 Nm
p
= 27 , 69 k W P=27,69 kW
n = 100 , 27 m i n - 1n=100,27 min−1
P*= 28 , 25 k W P∗=28,25 kW
30 k W 30 kW
g. yoG= 14 , 61iG=14,61
h. M*= 184 , 18 N mM∗=184,18 Nm
b.
c.
d.
e.
f.
DC: máquina DC
A partir de: 2015-04-20
×
Los accionamientos eléctricos son cada vez más importantes en la industria y el comercio
gracias a su alta eficiencia. Por ejemplo, las cortadoras de césped con accionamiento
eléctrico se utilizan cada vez con más frecuencia en el sector de la jardinería y también
existe un cambio de tendencia en la industria automotriz.
El motor DC es el primer motor desarrollado en la historia. La variante estándar se llama
máquina con excitación extranjera. La parte giratoria se llama ancla porque el primer
diseño parecía apropiado. La armadura está diseñada como un electroimán, por lo que la
corriente se transmite a través de contactos de anillo deslizante en el eje. El estator está
en la salida de un electroimán o imán permanente. En el segundo caso, sin embargo, el
rendimiento es limitado.
Potencia:
Pzu= Ula⋅ yola+ UF⋅ yoFPzu=Tla⋅yola+TF⋅yoF
Eficiencia:
η= Pa bPzu= Pzu- PVPzuη=PunabPzu=Pzu-PVPzu
potencia suministradaPzuPzu
potencia entregadaPa bPunab
Pérdida de potencia:
PV= PVe l+ PVm e c hPV=PVel+PVmecB
Disipación de energía eléctrica:
PVe l= Rla⋅ yo2la+ RF⋅ yo2FPVel=Rla⋅yola2+RF⋅yoF2
mech. pérdida de potenciaPVm e c hPVmecB
resistencia de anclajeRlaRla
Tensión inducida:
Tyo= Ula- UR ATyo=Tla-TRla
Resistencia en serie:
RV= Ulax ⋅ Ila- RlaRV=Tlax⋅yola-Rla
resistencia de armadura de voltajeTR ATRla
factor limitante actualxx
Par de apriete:
M= Pa bω= Pa b⋅ 60 sm i n2 πnM=Pabω=Pab⋅60smin2πn
Par de fricción:
MR= PVm e c hω= PVm e c h⋅ 60 sm i n2 πnMR=PVmecBω=PVmecB⋅60smyon2πn
frecuencia angular2πfωω2 πF2πF
velocidad en min-1nn
Rango de anclaje: ( I F = const.)
yoA xyoA B= Mi xMyo B= MR+ MxMR+ MByolaxyolaB=MyoxMyoB=MR+MxMR+MB
nxnB= Ui xTyo BnxnB=TyoxTyoB
Mi xMyox
Myo BMyoB
yoA xyoA B= Mi xMyo B⋅ yoFByoFxyolaxyolaB=MyoxMyoB⋅yoFByoFx
nxnB= Ui xTyo B⋅ yoFByoFxnxnB=TyoxTyoB⋅yoFByoFx
nxnx
nBnB
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Máquina de recogida de fórmulas DC:
Tarea 1
Un motor de CC excitado por separado con los datos nominales U = 24 V, I = 2.5 A, n =
1000 min -1 tiene una resistencia de armadura de 1.4 Ω. Calcular
a. la tensión inversa inducida U i ,
b. la resistencia de arranque R V , de modo que la corriente de arranque sea como máximo 2 veces
mayor que I AB ,
c. La corriente de arranque sin resistencia R V (arrancador).
solución
a. Tyo= Ula- UR ATyo=Tla-TRla= 24 V - 1 , 4 Ω ⋅ 2 , 5 A = 20 , 5 V =24 V1.4 Ω⋅2.5 la=20.5 V
b. RV= Ulax ⋅ Ila- Rla= 24 V 2 ⋅ 2 , 5 A - 1 , 4 Ω RV=Tlax⋅yola-Rla=24 V2⋅2.5 la-1.4 Ω=3,4Ω =3.4 Ω
c. I
d. A n= Ula/ Rla= 24 V / 1,4Ω yolan=Tla/Rla=24 V/1.4 Ω=17,14A =17.14 la
Tarea 2
Se utiliza una máquina GM-EST DC en un dispositivo de elevación. La máquina tiene los
siguientes datos clasificados:
U A = 220 V, I A = 1.8 A, U F = 220 V, I F = 0.3 A,
P = 300 W, n = 2000 min -1 , R A = 12 Ω.
Para simplificar, se puede suponer que el par de fricción es constante en todo el rango de
velocidad y que las pérdidas del cepillo son insignificantemente pequeñas.
a.
b.
c.
d.
e.
Determine el par nominal de la máquina.
Determine la eficiencia nominal de la máquina de CC.
Determine las pérdidas eléctricas en el rotor y el estator.
Determine las pérdidas mecánicas y el par de fricción asociado.
Determine la corriente sin carga y la velocidad de ralentí de la máquina a la tensión nominal.
Hay un par de M x = 1 Nm. El voltaje de la armadura es U Ax = 150 V. ¿Qué velocidad se
establece?
g. La corriente de armadura es 0.5 A. ¿Cuál es el par en la máquina y cuál es la velocidad?
h. * La máquina DC funciona en modo generador para reducir la carga. La velocidad del motor
es n x = - 1400 min -1 , el par está en M x = 1.3 Nm. ¿Cuál es la corriente de armadura y qué
voltaje de armadura se aplica? Nota: El par de fricción del motor apoya el proceso de frenado.
i. ** El motor funciona en el rango de ajuste de campo. La corriente de campo se reduce a I Fx =
0.23 A. ¿Cuál es la corriente del inducido y qué velocidad se establece cuando el motor tiene un
par de 1 Nm? (Si el hierro del estator no está magnéticamente saturado, se considera una
buena aproximación I F ~ φ De ello se desprende. U i ~ n M ~ I A ⋅ I F .
solución
a. MB= 1 , 43 N mMB=1.43 Nm
b. η= 64 , 94 % η=64.94 %
c. P
d. Vla= 38 , 9 W PVla=38.9 WPVF= 66 W PVF=66 W
e. PVm e c h= 57 , 1 W PVmecB=57.1 W MR= 0 , 27 N m MR=0.27 Nm
f. I
g. Un 0= 0 , 286 A yola0=0.286 lan0= 2183 m i n - 1n0=2183 myon-1
h. nx= 1350 m i n - 1nx=1350 myon-1
i. Mx= 0 , 2 N mMx=0.2 Nmnx= 746 m i n - 1nx=746 myon-1
j. yoA x= 1 , 09 A yolax=1.09 laUA x= - 125 , 8 V Tlax=-125.8 V
k. yoA x= 1 , 75 A yolax=1.75 lanx= 2616 , 1 m i n - 1nx=2616.1 myon-1
f.
Tarea 3
Para la máquina anterior, configure la característica de carga n x = f ( M ix ) en el rango de
anclaje para tres voltajes de armadura diferentes ( U A1 = 80V, U A2 = 150V, U A3 = 220V)
con una aplicación de hoja de cálculo (por ejemplo, Excel).
nx= UA x⋅ nBTA B- yoA B⋅ Rlanx=Tlax⋅nBTlaB-yolaB⋅Rla- nB⋅ yoA B⋅ Rla( MR+ MB) ⋅ ( UA B- yoA B⋅ Rla)nB⋅yolaB⋅Rla(MR+MB)⋅(TlaB-yolaB⋅Rla)⋅ ( MR+ MB)⋅(MR+MB)
Compare las curvas con los valores calculados en la tarea correspondiente.
Tarea 4
Un destornillador inalámbrico Makitta con campo de excitación de campo permanente tiene
los siguientes datos:
U A = 18 V, I A = 2.8 A, U iB = 15.7 V, n = 400 min -1 ,
Las pérdidas mecánicas representan el 30% de las pérdidas eléctricas. En caso de
sobrecarga, la velocidad de rotación baja a 300 min -1 . Calcular
a.
b.
c.
d.
la caída de tensión en la resistencia de la armadura y R A ,
las pérdidas eléctricas y mecánicas,
el diseño impacto gard,
La corriente a la sobrecarga.
solución
a.
b.
c.
d.
e.
TR A= 2 , 3 V TRla=2.3 VRla= 0 , 82 Ω Rla=0.82 Ω
P
Ve l= PVla= 6 , 44 W PVel=PVla=6.44 W PVm e c h= 1 , 93 WPVmecB=1.93W
Pa b= 42 , 03 W Punab=42.03 Wη= 83 , 39 % η=83.39 %
yoA x= 7 , 59 A
DASM: máquina asíncrona trifásica
A partir de: 2015-03-22
Las máquinas asíncronas trifásicas se usan muy a menudo debido a su facilidad de
mantenimiento. Las bases de cálculo y las tareas de ejemplo se presentan aquí.
×
Las máquinas asíncronas trifásicas se fabrican con 1-4 pares de polos. En
consecuencia, se puede calcular la velocidad de campo giratorio n s . La velocidad del
motor n siempre es aproximadamente un 5 por ciento más pequeña que la velocidad
del campo giratorio. La velocidad se da en 1 / min, la frecuencia en 1 / sy, por lo tanto,
debe convertirse por un factor de 60.
Velocidad del campo giratorio slip:s=ns-n
ns= f/ pns=f/p
s = ns- nnss=ns−nns
Frecuencia de la tensión del rotor: Potencia y eficiencia:Pab=M⋅ω=M⋅2π⋅n/60,Pzu=√
FL= f⋅ sfL=f⋅s
Pa b= M⋅ ω = M⋅ 2 π⋅ n / 60 ,Pab=M⋅ω=M⋅2π⋅n/60,
Pzu= 3-√ Tyoc o s φ , η
Δ nxΔ nB= Δ MxΔ MB, U
= Pa b/ PzuPzu=3 UIcosφ, η=Pab/Pzu
xTB= fxFBΔnxΔnB=ΔMxΔMB.
TxTB=FxFB
Frecuencia nominal:
Fx= ( ns o l l+ Δ nx) ⋅ p60 s / m i n Fx=(nsoll+Δnx)⋅p60 s/myon
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Colección de fórmulas Drehstrom y DASM:
Tarea 1
Un motor asíncrono trifásico con los datos nominales P = 5 kW, U = 400/230 V, 50
Hz, η = 84%, cos φ = 0.90 yn = 1390 min -1 está conectado a un FC con U max = 400
V. Calcular
a. el deslizamiento
b. la frecuencia del voltaje del rotor,
c. La corriente en la operación nominal.
d. ¿En qué circuito debe conectarse el motor a la FI?
e. ¿Cuál es el momento nominal M B ?
f. Dibuje la característica de frecuencia-voltaje U = f ( f ) que el convertidor de frecuencia debe
conducir para tener el par nominal constante hasta la velocidad
nominal. La compensación IR debe ser del 27,5%.
g. Dibuje la curva correspondiente M = f ( n ).
h. ¿Por qué trabajar con una compensación IR ?
solución
a. s = ( ns- n ) / ns= s=(ns-n)/ns=(1500-1390)/1500=7,3% (1500-1390)/1500=7.3 %
b.
c.
d.
e.
f.
f
i.
Velocidad curva de par:
j.
Sin compensación IR , el par se rompe debido a la resistencia óhmica del devanado del
estator.
L=
f⋅ s = 3 , 7 H zFL=F⋅s=3.7 Bz
yo= Pa b/ (η⋅ 3-√⋅ U⋅ c o s φ ) =yo=Punab/(η⋅3⋅T⋅cosφ)=9 , 55 A 9.55 la
M
El motor debe estar conectado al variador en conexión en estrella ya que la tensión de fase
máxima permitida en el motor es de 230 V.
g. B= Pa b⋅ 60 / ( 2 πn ) = MB=Punab⋅60/(2πn)=34,35N m34.35 Nm
h. características de frecuencia-tensión:
Tarea 2
El motor asíncrono trifásico del laboratorio tiene los siguientes datos nominales:
U = 230/400 V, I = 0.97 / 0.56 A, 50 Hz,
P = 0.18 kW, cos φ = 0.73 yn = 1330 min -1 .
Está conectado a una unidad con U max = 230V. Calcule las siguientes variables de diseño:
a. el deslizamiento
b. la frecuencia del voltaje del rotor,
c. La eficiencia.
d. ¿En qué circuito debe conectarse el motor a la FI?
e. ¿Cuál es el momento nominal M B ?
f. Dibuje la característica de frecuencia-voltaje U = f ( f ) que el convertidor de frecuencia debe
conducir para tener el par nominal constante hasta la velocidad nominal. El Δ-boost debería ser
del 10%.
g. Dibuje la curva correspondiente M = f ( n ).
h. ¿Qué se entiende por área de debilitamiento del campo?
solución
a. s = 11 , 3 % s=11.3 %
b. f
c. L= 5 , 67 H zFL=5.67 Bz
d. Pzu= 282 , 1 W Pzu=282.1 W η= 63 , 8 % η=63.8 %
e. El motor debe estar conectado en conexión delta al variador para que se alcance un voltaje
de línea de 230 V en el motor.
f. MB= 1 , 29 N mMB=1.29 Nm
g. características de frecuencia-tensión:
h. Velocidad curva de par:
i.
Por encima de la velocidad nominal, el par se comporta inversamente proporcional a la
frecuencia. Esta área se llama área de debilitamiento de campo.
Tarea 3
Un motor síncrono trifásico con placa de identificación como se muestra se conecta en
conexión delta a un variador de 400 V.
Calcular
a. el deslizamiento
b.
c.
d.
e.
la frecuencia del voltaje del rotor,
la eficiencia,
El par nominal.
La velocidad está a 800 min -1 se llevan a cabo con la constante de par nominal. ¿Qué
frecuencia y voltaje tiene que configurar el variador?
f. La velocidad es a 600 min -1 se mantienen con 40% constante de par nominal. ¿Qué frecuencia
y voltaje tiene que configurar el variador?
g. La velocidad es a 600 min -1 se mantienen a 120% constante de par nominal. ¿Qué frecuencia y
voltaje tiene que configurar el variador?
solución
a. s = 4 , 7 % s=4.7 %
b. fL= 2 , 35 H zFL=2.35 Bz
c. η= 78 , 4 η=78.4
d. mB= 80 , 13 N m MB=80.13 Nm
e. f
f. = ( N + Δ nB) ⋅ p / 60 = 29 H zF=(n+ΔnB)⋅p/60=29 Bz
T= UB⋅ f/ fB= 232 V T=TB⋅F/FB=232 V
g. Δ nx= Δ nB⋅ Δ Mx/ ΔMBΔnx=ΔnB⋅ΔMx/ΔMB= 28 m i n - 1=28 myon-1
F= ( N + Δ nB) ⋅ p / 60 = 20 , 93 H zF=(n+ΔnB)⋅p/60=20.93 Bz
T= UB⋅ f/ fB= 167 , 44 v T=TB⋅F/FB=167.44 V
h. Δ nx= Δ nB⋅ Δ Mx/ ΔMBΔnx=ΔnB⋅ΔMx/ΔMB= 84 m i n - 1=84 myon-1
F= ( N + Δ nB) ⋅ p / 60 = 22 , 8 H zF=(n+ΔnB)⋅p/60=22.8 Bz
T= UB⋅ f/ fB= 182 , 4 V
Corriente alterna trifásica: conexión en estrella
A partir de: 2015-03-15
×
La corriente alterna trifásica consiste en tres voltajes alternos de igual frecuencia con
amplitud idéntica y un cambio de fase de 120 grados cada uno. Este llamado sistema
trifásico se caracteriza por un diseño económico de los generadores, la ruta de transmisión
y los circuitos de consumo. La conexión en estrella se utiliza para cargas simétricas y
asimétricas.
Voltajes:→U12=→U1N-→U2N,
T= 3-√⋅ USt rT=3⋅TStr
T12→= U1 N→- U2 N→.T12→=T1N→-T2N→.
T23→= U2 N→- U3 N→.T23→=T2N→-T3N→.
T31→= U3 N→- U1 N→T31→=T3N→-T1N→
Corrientes:→I1+→I2+→I3=→IN
yo= YoSt ryo=yoStr
yo1→+I2→+I3→=YoN→yo1→+yo2→+yo3→=yoN→
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Colección de fórmulas Drehstrom y DASM:
Tarea 1
Un calentador de sauna de 7,5 kW está conectado en conexión estrella a la red eléctrica
de 230/400 V. Cada espiral de calentamiento es del mismo tamaño, por lo que es una
carga simétrica.
a.
b.
c.
d.
e.
Calcule la potencia, corriente y resistencia de cada bobina de calentamiento.
Calcule gráficamente la suma de los voltajes trifásicos.
¿Cuál es el voltaje de la línea U 23 . Resuelve el dibujo.
Calcule gráficamente la corriente neutra.
Calcule gráficamente la corriente neutra si falla la bobina de calentamiento 3.
solución
a. PSt r= Pge s3= 2500 W PStr=Pges3=2500 W
yo= PSt r/ USt r= 2500 W / 230V = 10 , 9 A I=PStr/UStr=2500 W/230 V=10,9 la
R
=
U
St r/
I= 230 V / 10,9A=(230V )2/ 2500W = 21 , 1 Ω R=UStr/I=230 V/10,9 A=(230 V)2/250
0 W=21,1 Ω
b. U
c. ⃗ 1 N+ U⃗ 2 N+ U⃗ 3 N= 0 U→1N+U→2N+U→3N=0
d. U
e. ⃗ 23= U⃗ 2 N- U⃗ 3 N= 400 V T→23=T→2N-T→3N=400 V
f.
yo⃗ N= Yo⃗ 1+I⃗ 2+I⃗ 3= 0 I→N=I→1+I→2+I→3=0
g. l
h. ⃗ N= Yo⃗ 1+I⃗ 2= 10 , 9 A I→N=I→1+I→2=10,9 A
a. P
Tarea 2
Una estufa está desequilibrada. Al medir las corrientes trifásicas, se obtienen los
siguientes valores:
I 1 = 4 A,
yo 2 = 3 A,
I 3 = 2 A.
a. Calcule el consumo de energía en cada capítulo.
b. Determine gráficamente la corriente en el conductor neutro.
solución
Tarea 3
Un sistema trifásico se carga con una resistencia, una bobina y un condensador. Las
siguientes corrientes se miden en los conductores:
Yo 1 = 30 A
I w2 = 16 A, I bL2 = 36.7 A,
I w3 = 27A , I bC3 = 13.1A .
a. Determine gráficamente las corrientes de fase y la corriente en el conductor neutro.
Corriente alterna trifásica: conexión delta
A partir de: 2015-03-12
×
La conexión delta se usa para potencias superiores. Las cargas están conectadas
directamente a la tensión del conductor externo. No se necesita N conductor. Tenga en
cuenta que este tipo de circuito solo está permitido para la carga simétrica.
T= USt rU=UStr
yo= 3-√⋅ yoSt rI=3⋅IStr
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Tarea 1
Un calentador con tres bobinas de calentamiento, cada una de las cuales tiene 21.1 Ω, se
conecta inadvertidamente en una conexión delta a la red eléctrica de 230/400 V. Cada
espiral de calentamiento es del mismo tamaño, por lo que es una carga simétrica.
a. Calcule la corriente de fase de cada espiral de calentamiento.
b. Calcule la corriente del conductor externo.
c. ¿Con qué fusible tendrías que asegurar el horno y por qué esto no está permitido?
solución
a. yoSt r= USt r/ R=400V / 21,1Ω=18,96A IStr=UStr/R=400 V/21,1Ω=18,96 A
b. I
c. = 3-√⋅ yoSt r= 3-√⋅ 18 , 96 A = 32 , 84 A yo=3⋅yoStr=3⋅18.96 la=32.84 la
d. El horno debe estar protegido con más de 32.84 amperios, p. Ej. Fusible con 3 x 35
amperios. Sin embargo, esto no está permitido ya que las bobinas de calentamiento están
diseñadas para una corriente de solo 10.95 A.
Corriente alterna trifásica: potencia
A partir de: 2015-03-14
×
La potencia en los sistemas trifásicos puede verse influenciada por el tipo de conexión
(triángulo o estrella). El cálculo se basa en fórmulas idénticas. Sin embargo, tenga en
cuenta que el conductor externo o el tamaño del cable son diferentes en la conexión en
estrella y en triángulo. Como resultado, se logra un rendimiento 3 veces mayor en la
conexión delta.
Potencia aparente:
S= 3 ⋅ SSt r= 3 ⋅ USt r⋅ yoSt r= 3-√⋅ U⋅ yoS=3⋅SStr=3⋅UStr⋅IStr=3⋅U⋅I
Potencia activa:
P= 3-√⋅ U⋅ yo⋅ c o s φP=3⋅U⋅I⋅cosφ
Potencia reactiva:
Q = 3-√⋅ U⋅ yo⋅ s i n φQ=3⋅U⋅I⋅sinφ
×
Recuerde el entorno antes de imprimir estas páginas. El sitio está diseñado para estar libre
de barreras para que se muestre sin problemas en todos los dispositivos.
Tarea 1
Para una comparación de rendimiento, un calentador de sauna con tres serpentines de
calentamiento, cada uno de 21.1 Ω en estrella y conexión en triángulo a la red de 230/400
V que se conectará.
a.
b.
c.
d.
Calcule la corriente de fase para estrella y triángulo en cada espiral de calentamiento.
Calcule la corriente del conductor externo para la estrella y el triángulo.
Determine la potencia por filamento para estrella y triángulo.
Compara la potencia total de la estrella y el triángulo.
solución
a. yoSt r= USt r/ R=230V / 21,1Ω=10,90A IStr=UStr/R=230 V/21,1Ω=10,90 A
I
St r=
b. I
USt r/ R=400V / 21,1Ω=18,96A IStr=UStr/R=400 V/21,1Ω=18,96 A
c. = YoSt r= 10 , 90 A I=IStr=10,90 A
yo= 3-√⋅ yoSt r= 3-√⋅ 18 , 96 A = 32 , 84 A I=3⋅IStr=3⋅18,96 A=32,84 A
d. P
e. St r= USt r⋅ yoSt r= 2507 W PStr=UStr⋅IStr=2507 W
PSt r= USt r⋅ yoSt r= 7584 W PStr=UStr⋅IStr=7584 W
f. 3 ⋅ PSt r= 7521 W 3⋅PStr=7521 W
3 ⋅ PSt r= 22752 W 3⋅PStr=22752 W
El consumo de energía en la conexión delta es tres veces mayor que en la conexión en
estrella.
Tarea 2
Se proporciona la placa de identificación de un motor asíncrono trifásico. El motor funciona
en delta a 380V. El consumo de corriente es 0.64 A y el factor de potencia activo es 0.73.
a.
b.
c.
d.
Calcule la potencia activa del motor.
Calcule la potencia reactiva del motor.
Calcule la potencia aparente del motor.
Determinar la eficiencia de la máquina.
solución
a. P= 3-√⋅ U⋅ yo⋅ c o s φ = 307 , 50 W P=3⋅U⋅I⋅cosφ=307,50 W
b. Q = 3-√⋅ U⋅ yo⋅ s i n φ = 286 , 44 W Q=3⋅U⋅I⋅sinφ=286,44 W
c. S= 3-√⋅ U⋅ yo= 421 , 23 W S=3⋅U⋅I=421,23 W
d. η= Pa b/ Pzu= 58 , 5 %
LED de laboratorio
A partir de: 2015-10-01
info
LED, en resumen: LED, están disponibles en muchos colores diferentes. Examinamos
diferentes LED de colores en este laboratorio. Medimos su característica de IU ,
determinamos el punto de funcionamiento y la resistencia en serie necesaria. Por lo tanto,
el funcionamiento del LED se explica paso a paso y es fácil de entender. Además, se
examina la polaridad, la conexión en serie y en paralelo de los LED.
1 UI característica de un LED
Un diodo emisor de luz debe funcionar con una fuente de voltaje de
CC. Desafortunadamente, no tenemos una hoja de datos disponible de la cual podamos
tomar la corriente de funcionamiento permisible y el voltaje de funcionamiento. Para el
circuito, se utiliza una fuente de voltaje de CC con U 1 = 0 - 15 V y un LED. El límite de
corriente se establece en 50 mA.
a. ¿Cómo determinar la corriente I D mediante U Rv ?
b. ¿Qué resistencia eliges?
c. Mida la característica U D = f ( I D ) y muestre los datos en un diagrama.
U D en V
U Rv en V
I D en mA
Pon a prueba tu éxito de aprendizaje
a. ¿En qué dirección se opera el LED?
adelante
al revés
derecho
b. ¿Desde qué voltaje emite luz el LED?
debajo de U S
por encima de U S
derecho
falso
c. ¿A qué corriente es el LED suficientemente brillante?
por encima de 10 mA
por debajo de 10 mA
derecho
falso
d. ¿De qué corriente ya no es más brillante el LED?
10 mA
20mA
30 mA
≥ 40 mA
2 Determinación gráfica del punto de trabajo AP en la característica UI
a.
b.
c.
d.
El LED debe funcionar a una tensión de funcionamiento de U = 12 V. Determine
gráficamente el punto de operación AP y luego, matemáticamente, la resistencia en
serie R V para el LED utilizado en I D = 20 mA.
Ponga la característica del diodo (tarea 1) en un diagrama.
Coloque el punto de trabajo AP a 20 mA en el diagrama.
Dibuje una línea de trabajo a través del punto de trabajo AP y la intersección con el eje x en U =
12 V en el diagrama.
A partir de los datos, calcule la resistencia en serie necesaria R V en el punto de operación AP.
3 polaridad de LED
Indique cómo se debe polarizar el voltaje ( U 1 = 12 V) entre los terminales A y B para que
a. un signo menos
b. Se muestra un signo más.
c. Dimensione la resistencia en serie para que una corriente de 18 mA fluya a través de los LED.
indicio
El voltaje de tracción es U S = 1.6 V.
d. ¿Por qué están brillando? y eso no es igual a brillante?
B2U: puente rectificador
A partir de: 2015-10-27
×
Los rectificadores de puente se utilizan para rectificar el voltaje de CA. Tienen la propiedad
de rectificar tanto la media onda positiva como la negativa.
Voltaje de entrada $ U_1 $, voltaje de CC $ U_d $ y voltaje de resistencia $ U_S $: $$ \
has {U} _1 = U_ {dmax} +2 \ cdot U_S $$ , DC de tensiónUd y
SchleußenspannungUS :U1=Udmunx+2⋅UST1U1TdUdTSUS
T^1= Udm a x+ 2 ⋅ USU^1=Udmax+2⋅US
Dimensionar un condensador de suavizado: $$ C_G = \ frac {0.75 \ cdot I_L} {f_p \ cdot U_
{pss}} $$
CG= 0 , 75 ⋅ ILFp⋅ Up s sCG=0,75⋅ILfp⋅Upss
Tarea 1 B2U
La imagen muestra puentes rectificadores incompletos. Completa los circuitos.
a.
b.
c.
solución
a.
b.
c.
Tarea 2 B2U
La figura muestra un circuito de rectificación de puente con condensador de suavizado y
carga. El circuito debe dimensionarse para un voltaje de salida de 35V. El capacitor tiene
una capacidad de 1200 μF y la corriente de carga es de 0.8 A.
a. Calcule la tensión de entrada necesaria U 1 , si el componente de CC máximo del condensador
debe ser de 35 V.
b. Calcule el voltaje de ondulación (valor pico a pico) en el condensador. Nota: La frecuencia de la
red es de 50 Hz.
c. Dibuje la curva de la tensión de salida del puente rectificador cuando se opera con y sin carga.
solución
a. T1= ( Ud+ 2 ⋅ US) / 2-√= ( 35 V + 2 ⋅ 0 , 7 V ) / 2√= 25 , 74 v U1=(Ud+2⋅US)/2=(35 V+2⋅0,7 V)/2=25,74 V
b. Tp s s= 0 , 75 ⋅ ILFp⋅ CG= 5 V Upss=0,75⋅ILfp⋅CG=5 V
c.
FET: transistor de efecto de campo
A partir de: 2018-06-19
El transistor de efecto de campo es el transistor con la aplicación más común en todo el
mundo. Explica su estructura básica, su funcionamiento y varios tipos.
7 transistores como interruptor
Punto de funcionamiento AP AN : voltaje de la fuente de drenaje, corriente de drenaje
máxima
UDS=UAKRDSonRDSon+RLUDS=UAKRDSonRDSon+RL
ID=UAKRDSon+RLID=UAKRDSon+RL
Punto de funcionamiento AP APAGADO : voltaje de la fuente de drenaje, corriente de drenaje
máxima
UDS=UAKUDS=UAK
ID=0ID=0
Ciclo de trabajo, disipación de potencia:
g=ti/Tg=ti/T
PV=g⋅UDS⋅ID=g⋅RDSon⋅I2DPV=g⋅UDS⋅ID=g⋅RDSon⋅ID2
1 transistor de efecto de campo de información
El transistor de efecto de campo más comúnmente utilizado es el transistor de efecto de
campo de semiconductor de óxido metálico (MOSFET). El nombre de transistor se
compone de la palabra latina que significa "a través de la resistencia". Los transistores
permiten controlar la resistencia de un circuito El tipo de transistor es que el control de la
resistencia a través del campo eléctrico, es decir, un voltaje es posible, de modo que solo
las corrientes de carga y descarga de un flujo de condensador de corto tiempo.
Un transistor bipolar, que opera controlado por corriente, tiene mayores pérdidas. Debido a
esto, los FET han prevalecido en la mayoría de las áreas.
2 Estructura y función de un MOSFET de n canales
Der Transistor hat drei Anschlüsse: Gate G (Tor) - den Steueranschluss der durch Si-Oxid
vom Halbleiter isoliert ist, Drain D (Senke) und Source S (Quelle).
Legt man zwischen Drain D und Source S eine positive Spannung, können keine
Ladungsträger fließen, da, ohne freie Ladungsträger, der Widerstand der Drain-SourceStrecke zu hoch ist. Beim Anlegen einer positiven Spannung zwischen Gate und Source
werden jedoch freie Ladungsträger unter das Gate gezogen, so dass hier schon bei
geringen Spannungen ein leitfähgier Kanal mit sehr geringem Widerstand entsteht. Je
größer die Spannung UGS, desto leitfähiger der Kanal, bzw. desto kleiner der
Widerstand RDS.
3 Das Gate
Die Funktion des Gates kann man gut am Beispiel eines Tors in einer Weide verstehen.
Den Druck erzeugen die Hunde der Schafherde. Er entspricht der elektrischen Spannung
zwischen Drain und Source. Die Schafe entsprechen den einzelnen Ladungsträgern. Man
gut erkennen wann es am Tor zum erhöhten Widerstand kommt.
4 Schaltzeichen verschiedener FETs
Man unterscheidet verschiedene Arten von Feldeffekttransitoren, die entsprechend an den
Schaltzeichen erkennbar sind.
Das isolierte Gate erkennt man am fehlenden Kontakt zu Drain und Source.
Selbstleitende FETs, haben eine durchgehenden Kanal eingezeichnet, selbstsperrende
FETs eine gestrichelte Linie.
Und dann unterscheidet man noch zwischen n- und p-Kanal-Transitoren. Bei n-KanalTransistoren wird der Kanal durch freie Elektronen, bei p-Kanal-Transistoren durch freie
Löcher (fehlende Elektronen) erzeugt.
5 U-I-Kennlinien
Das sogenannte Ausganskennlinienfeld macht deutlich, dass mit steigender Gate-SourceSpannung immer höhere Ströme durch den Drain-Source-Kanal fließen können. Möchte
man den Kanal vollständig freischalten, so dass der Widerstand der Strecke RDS minimal
ist, ist darauf zu achten, dass die Spannung UGS je nach gefordertem Strom ID einen
Mindestwert hat. Begrenzt nämlich der Transitor den Strom, hat dieser hohe Verluste.
Unterhalb der sogenannten Abschnürrspannung UP (engl. pinch-off) hat der Kanal einen
nennenswerten Widerstand.
6 Transistor als Schalter
Feldeffekttransitoren werden in den meisten Fällen als elektronischer Schalter eingesetzt.
Um die Leistung an einem Verbraucher zu steuern, wird nicht etwa der Widerstand der
Drain-Source-Strecke um 50% erhöht, sondern eine pulsweiten modulierte Spannung auf
das Gate gegeben.
Diese PWM-Spannung sorgt dafür, dass der Transistor entweder zu (hochohmig) oder
ganz offen (niederohmig) ist. Nun entscheidet das Verhältnis von Impulszeit ti zu
Periodendauer T über die Leistung.
Der Vorteil: Die Verluste am Transistor sind minimal.
7 Transistor als Schalter
Punto de funcionamiento AP AN : voltaje de la fuente de drenaje, corriente de drenaje
máxima
UDS=UAKRDSonRDSon+RLUDS=UAKRDSonRDSon+RL
ID=UAKRDSon+RLID=UAKRDSon+RL
Punto de funcionamiento AP APAGADO : voltaje de la fuente de drenaje, corriente de drenaje
máxima
UDS=UAKUDS=UAK
ID=0ID=0
Ciclo de trabajo, disipación de potencia:
g=ti/Tg=ti/T
PV=g⋅UDS⋅ID=g⋅RDSon⋅I2DPV=g⋅UDS⋅ID=g⋅RDSon⋅ID2
1 transistor de efecto de campo de información
El transistor de efecto de campo más comúnmente utilizado es el transistor de efecto de
campo de semiconductor de óxido metálico (MOSFET). El nombre de transistor se
compone de la palabra latina que significa "a través de la resistencia". Los transistores
permiten controlar la resistencia de un circuito El tipo de transistor es que el control de la
resistencia a través del campo eléctrico, es decir, un voltaje es posible, de modo que solo
las corrientes de carga y descarga de un flujo de condensador de corto tiempo.
Un transistor bipolar, que opera controlado por corriente, tiene mayores pérdidas. Debido a
esto, los FET han prevalecido en la mayoría de las áreas.
Tarea 1 Característica de salida
a.
b.
c.
d.
La figura muestra la característica de salida del MOSFET IRL540N para diferentes voltajes
de puerta. Calcule para U GS = 2.5V y U GS = 4V
La resistencia de la ruta de la fuente de drenaje R DSon . Crea una tabla de valores para esto.
tabla de valores de complemento con la disipación de potencia en el drenaje-fuente
trayectoria P V .
Ponga todos los valores en un diagrama común dependiendo de U DS .
¿Desde qué valor de voltaje aumenta la resistencia R DSon sustancialmente y cómo se puede
reconocer esto en la característica de salida?
solución
Tabla de valores y diagramas para U GS = 2.5 V:
Tarea 2 Resistencia de la ruta de la fuente de drenaje
La figura muestra la dependencia de la resistencia de la fuente de drenaje con la
temperatura del MOSFET IRL540N.
a. Analiza el diagrama. Describa el comportamiento de R DSon en función de la temperatura.
b. Para un circuito, dos de estos MOSFET deben conectarse en paralelo para permitir un mayor
flujo de corriente en el grupo de trabajo. Se teme que los dos MOSFET tengan diferentes
niveles de pérdidas y, por lo tanto, uno de los MOSFET se destruya debido al
sobrecalentamiento.
Haga una declaración para una reunión. ¿Cómo se distribuirá la electricidad en los dos
componentes?
solución
a. La T más grande , la R DSOn más grande .
Con el aumento de la temperatura, la conductividad empeora y, por lo tanto, la disipación de
energía aumenta.
,
b. Cuanto más actual, mayor es la resistencia.
Menos corriente fluye a través del MOSFET con la mayor resistencia. Por lo tanto, se calienta
menos que el otro. Una temperatura más baja también significa una menor resistencia. Esto
iguala la resistencia de los dos MOSFET, lo que da como resultado una distribución de
corriente uniforme.
Sin embargo, si la característica tuviera una pendiente negativa típica de los
semiconductores, uno de los MOSFET se quemaría.
Tarea 3 Capacidad de óxido
La figura muestra la dependencia de la capacitancia del óxido con el voltaje de la fuente de
drenaje para el MOSFET IRL540N. Determinar para U DS = 1 V,
a. la capacidad de óxido C GS .
b. La puerta es accionada por un generador de frecuencia con R i = 50 Ω. ¿Cuánto tiempo lleva
cargar el condensador?
c. ¿Qué peligros surgen de qué frecuencias de conmutación durante la operación? Tasa.
solución
a. C= 1 , 75 n F C=1.75 nF
b. τ= Ryo⋅ CG S=τ=Ryo⋅CGS=50 Ω ⋅ 1 , 75 n F = 87 , 5 n s 50Ω⋅1.75 nF=87.5 ns
5 τ= 437 , 5 n s 5τ=437.5 ns
c. Durante la carga, la resistencia de la pista es alta, especialmente durante un τ y, por lo tanto,
también las pérdidas. Por esta razón, el tiempo de pulso más corto debe ser al menos el
doble del tiempo de carga, para que el transistor no se caliente de manera excesiva. Una
duración de pulso de 1 μs corresponde a una frecuencia máxima de 1 MHz.
Relájate primero ...
Aprender puede ser muy agradable. Aquí puede tener todo explicado nuevamente en
inglés. Pero no te preocupes, hay subtítulos en alemán.
Tarea 4 transistor como interruptor
a.
b.
c.
d.
e.
f.
g.
El transistor IRL540N debe dimensionarse como un interruptor a 2.5 kHz. La resistencia de
la ruta de la fuente de drenaje es R DSon = 44 mΩ, la tensión de alimentación en el circuito
de trabajo 10 V y la resistencia de carga R L = 2.5 Ω
¿Cuál es el voltaje de la fuente de drenaje U DS en el punto de trabajo encendido y apagado?
¿Cuál es la corriente de drenaje I D en el punto de trabajo de encendido y apagado?
Transfiera la característica de salida correspondiente y dibuje los dos puntos de operación
dentro y fuera de la curva característica.
¿Qué tan grande es el voltaje de fuente de puerta U GS necesario ?
Calcule la duración del pulso para un ciclo de trabajo del 25%.
Calcule la pérdida de potencia para un ciclo de trabajo del 25%.
¿Cuáles serían las pérdidas en U GS = 2.5 V?
solución
a. TD S= UUna KRD So nRD So n+ RL= 10 V 44 m Ω 2544 m Ω = 173 m V TDS=TlaKRDSonRDSon+RL=
10 V44 mΩ2544 mΩ=173 mV
TD S= UUna K= 10 V TDS=TlaK=10 V
b. yoD= UUna KRD So n+ RL= 10 V2 , 544 Ω = 3 , 93 A yoD=TlaKRDSon+RL=10V2.544 Ω=3.93 la
yoD= 0 A yoD=0 la
c. característica:
d. TG S= 6 V TGS=6 V
e. T= 1 / f= 1 / 2 , 5 k H zT=1/F=1/2.5 kBz
tyo= g⋅ T= 0 , 25 ⋅ 1 / 2 , 5 k H ztyo=g⋅T=0.25⋅1/2.5 kBz
f. PV= g⋅ UD S⋅ yoD= 0 , 25 ⋅ 173 m V ⋅ 3 , 93 A PV=g⋅TDS⋅yoD=0.25⋅173 mV⋅3.93 la
g. PV= g⋅ UD S⋅ yoD= 0 , 25 ⋅ 0 , 4 V ⋅ 3 A PV=g⋅TDS⋅yoD=0.25⋅0.4 V⋅3 la
Ideas de
S. Jensch - Escuela de electrónica Tettnang
Hoja de datos International Rectifier irf.com