Inferència
Anuncio
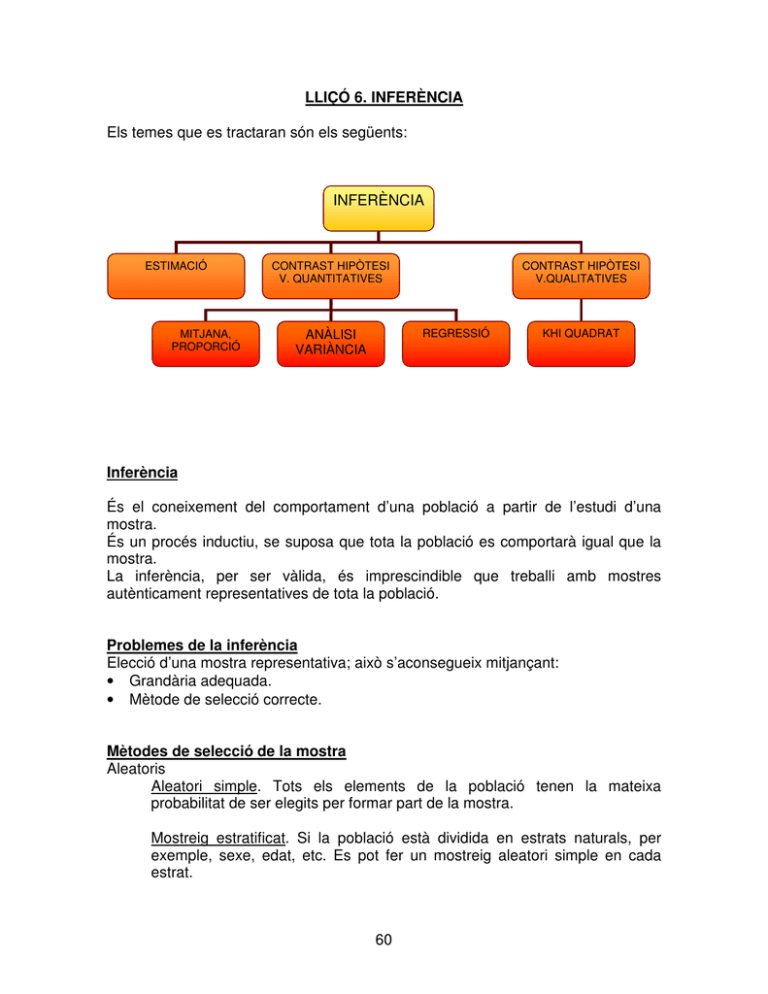
LLIÇÓ 6. INFERÈNCIA Els temes que es tractaran són els següents: INFERÈNCIA ESTIMACIÓ MITJANA, PROPORCIÓ CONTRAST HIPÒTESI V. QUANTITATIVES ANÀLISI VARIÀNCIA CONTRAST HIPÒTESI V.QUALITATIVES REGRESSIÓ KHI QUADRAT Inferència És el coneixement del comportament d’una població a partir de l’estudi d’una mostra. És un procés inductiu, se suposa que tota la població es comportarà igual que la mostra. La inferència, per ser vàlida, és imprescindible que treballi amb mostres autènticament representatives de tota la població. Problemes de la inferència Elecció d’una mostra representativa; això s’aconsegueix mitjançant: • Grandària adequada. • Mètode de selecció correcte. Mètodes de selecció de la mostra Aleatoris Aleatori simple. Tots els elements de la població tenen la mateixa probabilitat de ser elegits per formar part de la mostra. Mostreig estratificat. Si la població està dividida en estrats naturals, per exemple, sexe, edat, etc. Es pot fer un mostreig aleatori simple en cada estrat. 60 Mostreig per conglomerats. Com per estrats, però els estrats són zones geogràfiques. Sol fer-se per etapes. Mostreig sistemàtic. S’elegeix un element a l’atzar i a partir d’aquest, sistemàticament, cada n elements formaran part de la mostra. Per seleccionar una mostra representativa s’ha d’utilitzar un mètode aleatori. No aleatoris. Els elements de la mostra no són elegits per cap procediment a l’atzar. Errors La coincidència total entre l’estadístic mostral i la població no es produeix. Error és la diferència entre el valor desconegut de la població i el que s’obté de la mostra. • • Error de biaix. Es pot evitar utilitzant un bon mètode de selecció de la mostra. Error aleatori. No es pot evitar però es pot quantificar. Distribucions en el mostreig Paràmetres poblacionals. Són les mesures relatives a la població. Característiques mostrals. Són les mesures relatives a la mostra. Variables quantitatives Variables qualitatives Paràmetres poblacionals Mitjana poblacional µ Variància poblacional σ2 Desviació tipus poblac. σ Proporció poblacional Mida de la població π N Característiques mostrals Mitjana mostral x Variància mostral s2 Desviació tipus mostral s Proporció mostral Mida de la mostra p n Valors mostrals Cada un dels elements de la mostra els simbolitzem amb xi . D’una població determinada és possible seleccionar diverses mostres possibles d’una mateixa mida n. No totes les mostres proporcionen la mateixa informació, n’hi ha que s’aproximen més que altres a la població. Com que la inferència utilitza una única mostra, hi ha el problema de valorar la qualitat de la informació mostral. L’elecció d’aquesta única mostra, com que s’utilitza un mètode aleatori, depèn exclusivament de l’atzar. És una variable aleatòria. 61 Distribució de probabilitat d’un valor mostral Cada valor mostral és una variable aleatòria, per tant, podem fer-ne la distribució de probabilitat. Tot valor mostral xi seguirà la mateixa distribució de probabilitat que la població. L’esperança de la distribució de probabilitat de cada valor mostral és igual a la mitjana poblacional. E [xi ] = µ La variància de la distribució de probabilitat de cada valor mostral és igual a la variància de la població. 2 i V [x ] = σ Estadístic És qualsevol funció efectuada amb els valors mostrals. Estadístics més importants: les característiques mostrals (x, p, etc.). Tot estadístic serà també una variable aleatòria i tindrà una distribució de probabilitat. Distribució de probabilitat de la mitjana mostral La mitjana mostral és una variable aleatòria. x = x1 + x 2 + Λ + x n n L’esperança de la distribució de probabilitat de la mitjana mostral és igual a la mitjana poblacional. E[x] = µ La variància de la distribució de probabilitat de la mitjana mostral és igual a la variància poblacional dividida per la mida de la població. V [x La distribució de la mitjana ]= mostral σ N µ, n 62 σ n 2 segueix una distribució normal. Exemple Població. Distribució de probabilitat Edat 21 22 23 24 25 Prob. 1/5 1/5 1/5 1/5 1/5 µ = 23 σ2 = 2 Mostres possibles, amb reemplaçament i mitjana mostral 21 (21,21) 21 (22,21) 21,5 (23,21) 22 (24,21) 22,5 (25,21) 23 21 22 23 24 25 σ n 22 (21,22) 21,5 (22,22) 22 (23,22) 22,5 (24,22) 23 (25,22) 23,5 23 (21,23) 22 (22,23) 22,5 (23,23) 23 (24,23) 23,5 (25,23) 24 Mitjana mostral 21 21,5 22 22,5 Probabilitat 1/25 2/25 3/25 4/25 23 5/25 23,5 24 24,5 25 4/25 3/25 2/25 1/25 1 2 = 2 = 1 2 63 24 (21,24) 22,5 (22,24) 23 (23,24) 23,5 (24,24) 24 (25,24) 24,5 E [x ] = 23 V [x ] = 1 25 (21,25) 23 (22,25) 23,5 (23,25) 24 (24,25) 24,5 (25,25) 25 Mostres possibles, sense reemplaçament i mitjana mostral 21 21 22 23 24 25 σ n 2 (22,21) 21,5 (23,21) 22 (24,21) 22,5 (25,21) 23 22 (21,22) 21,5 23 (21,23) 22 (22,23) 22,5 (23,22) 22,5 (24,22) 23 (25,22) 23,5 (24,23) 23,5 (25,23) 24 Mitjana mostral 21,5 22 22,5 Probabilitat 2/25 2/25 4/25 23 4/25 23,5 24 24,5 Total 4/25 2/25 2/25 1 24 (21,24) 22,5 (22,24) 23 (23,24) 23,5 25 (21,25) 23 (22,25) 23,5 (23,25) 24 (24,25) 24,5 (25,24) 24,5 E [x ] = 23 V [x ] = 0 , 75 N − n 2 5 − 2 = = 0 , 75 N −1 2 5 −1 Distribució de probabilitat de la proporció mostral La proporció mostral és una variable aleatòria. L’esperança de la distribució de probabilitat de la proporció mostral és igual a la proporció poblacional. E [ pi ] = π La variància de la distribució de probabilitat de la proporció mostral és: V [p] = π (1 − π ) n Si la població és normal, la proporció mostral segueix una distribució normal: π (1 − π ) N π , n 64 ESTIMACIÓ Definició Estimar un paràmetre poblacional és assignar-li un valor aproximat a partir de la informació que ens dóna la mostra. Estimar 1. Per punt. Donar un número com a estimació del paràmetre poblacional. 2. Per interval. Donar un interval on s’estima que es troba el vertader valor del paràmetre poblacional amb una determinada probabilitat. Estimador Tota funció dels valors mostrals que ens serveix per estimar puntualment un paràmetre poblacional. Estimacions Els diferents valors que obtenim en aplicar l’estimador a les diferents mostres. Propietats dels estimadors Asimptòticament no esbiaixat No esbiaixat lim E[x ] = µ E[x] = µ n→∞ Eficient. El que té la variància més petita. Òptim = no esbiaixat + eficient Consistent. Ha de ser no esbiaixat o asimptòticament no esbiaixat i la variància ha de tendir a zero quan n tendeix a infinit. Estimadors puntuals Població Mostra µ x σ π ŝ p Estimació per interval Donar un interval on s’estima que es troba el vertader valor del paràmetre poblacional amb una determinada probabilitat. D’aquesta probabilitat que serà la probabilitat d’encertar se’n diu nivell de confiança (1- α ). α és el nivell de significació o probabilitat d’errar. 65 Per una mateixa mida de la mostra, en augmentar el nivell de confiança, augmenta la longitud de l’interval. El més habitual és treballar amb nivells de confiança del 95 % i del 99 %. Hi ha una relació inversa entre la mida de la mostra i la longitud de l’interval. Mitjana poblacional µ σ coneguda σ desconeguda x ± zα σ / 2 n s sˆ = x ± t (n −1 )α / 2 n −1 n x ± t (n −1 )α / 2 Proporció poblacional π π desconegut p ± zα / 2 p .q n Diferència de mitjanes µ1 - µ2 Variàncies desconegudes σ1 ≈ σ2 (n > 30) (x 1 Variàncies desconegudes σ1 ≈ σ2 (n ≤ 30) ( x1 − x 2 ) ± t ( n + n − x 2 ) ± t ( n 1 + n 2 − 2 )α 1 S 2 p 66 = ∑ (x 1 /2 Sp 2 − 2 )α / 2 − x1 )2 + n1 + n ∑ (x 2 − 2 sˆ12 sˆ 22 + n1 n2 1 1 + n1 n 2 2 − x 2 )2 Diferència de proporcions π1 - π2 ( p1 − Vàlid per a valors grans de n1 i n2 p 2 ) ± zα / 2 p1 q1 p 2 q 2 + n1 n2 Grandària de la mostra L’estadística proporciona les millors fórmules per trobar una mostra que sigui representativa de la població. Les fórmules es deriven de les de l’estimació per intervals. Abans de calcular la fórmula s’ha de decidir: 1. Nivell de confiança al qual volem treballar (95 %, 99 %, etc.). 2. Marge d’error sobre el paràmetre poblacional que estem disposats a assumir; se simbolitza amb d (±1, ±2, etc.). Les fórmules que utilitzarem són les següents: Una mostra Per µ σ coneguda Interval pobl. infinita pobl. finita pobl. infinita σ desconegud a Pobl. finita x ± z α/2 . σ n x ±z α /2 x ±t x ±t α /2 α /2 . σ n n= N-n N-1 . s n . s n n= n= N-n N-1 z α /2 2 . σ2 d2 z α /2 2 . σ2. N d2 . N - 1 + z α /2 2 . σ2 zα/2 2 . S Pobl. infinita Pobl. finita p ± zα/2 p ± z α /2 0,25 n 0,25 n 67 2 d2 2 z α /2 2 . S . N . n= d2 . N - 1 + z α /2 2 . S Interval Per π π desconegut Mida 2 Mida n≅ N-n n ≅ N-1 1 d2 es pren p = q = 0,5 N d . (N - 1) + 1 2

