Relaciones y funciones Lazaro

RELACIONES Y FUNCIONES DE IR EN IR RELACIONES BINARIAS RELACIONES DE R EN R FUNCIONES O APLICACIONES FUNCIONES REALES DE VARIABLE REAL FUNCIONES EXPONENCIALES Y LOGARÍTMICAS MISCELÁNEA MOISES LAZARO CARRION iÍiEoD OI T TO m n i R IA L l U V IJU ü M Sólo fines educativos - FreeLibros Autor : Moisés Lázaro Carrión Estudios : Lic. en Matemáticas Puras, Lic. en Educación, Maestría (Métodos Cuantitativos de la Economía U.N.M.S.M.), Maestría (Matemáticas Puras P.U.C.P.). Experiencia Docente: Pontificia Universidad Católica del Perú Universidad Ricardo Palmti Universidad Nacional Mayor de San Marcos Universidad Nacional de Ancash Santiago Antúnez de Mayolo Universidad Nacional del Callao Universidad Particular San Martín de Porres La presentación y disposición en conjunto de: RELACIONES ^Y FUNCIONES DE R EN R Autor: Moisés Lázaro Carrión Son propiedad del autor. Prohibida la reproducción total o parcial de esta obra, por cualquier medio, sin auto rización escrita del autor: ....... : 822 Decreto Legslativo... Hecho el Deposito Legal en la Biblioteca Nacional del Perú ... : 2009-13284 International Standard Book Number ISBN N°......................... : 978-9972-813-61-0 Derechos reservados O Primera edición: Octubre 2009 Obra editada, impresa y distribuida por: Distribuidora, Imprenta, Editorial, Librería MOSHERA S.R.L. RUC:20101220584 Jr. Tacna 2975 - San Martín de Porres Lima - Perú / Telefax: 567-9299 e-mail: editorialmoshera@hotmail.com PEDIDOS AL POR MAYOR Distribuidora - Imprenta - Editorial - Librería MOSHERA S.R.L. Jr. Tacna 2975 - San Martín de Porres T elefax: 5 6 7 -9 2 9 9 Impreso en el Perú - Printed in Perú Sólo fines educativos - FreeLibros Ú . m i q u a h id o h s ü u n a rw : J u liá n , p o A A u v a lio A a a y u d a , y c o la b o h a c ió n . Sólo fines educativos - FreeLibros ÍNDICE E RELACIONES BINARIAS Introducción ..... ............ ,..... Par Ordenado Igualdad de pares ordenados ............................................. Productos de Conjuntos............. .......y.......... .... Propiedades Producto Cartesiano.. .... El Plano Cartesiano ................... Relaciones Binarias. ...... ......................... Tipo de Relaciones: Reflexiva, Simétrica, Transitiva, de Equivalencia, Asimétrica, Antisimétnca, de prden parcial, Comparable, de Orden Total. .......... Problemas.. ......................................... Clase de Equivalencia y Conjuntó Cociente ....................... Propiedad del Dominio y rango de una relación .................... Relación Inversa, Dominio y rango ..... ....... :.¡........... Propiedades Composición de relaciones ..................................... Problemas................................................................ 1 2 2 4 5 6 7 9 17 19 20 2 RELACIONES DE R EN R .......... Plano Cartesiano Dominio y rango de unaxelación de R en R. .. ........ Gráfica de una relación de R en R ..... Problemas.! .... Relación de R en R con valor absoluto ....... Gráfica de relaciones lineales con dos Variables, rectas, semiplanos y planos en R2 ......................... Método práctico.. .............. Ecuaciones de l&s cónicas: Ecuación de la Circunferencia........ .......... .r........ Sólo fines educativos - FreeLibros 33 34 37 39 49 53 56 68 ,■........ 71 75 . La Parábola ................ La Elipse ........... ........................ La Hipérbola..,.......;....■....................................... 77 m FUNCIONES O APLICACIONES Introducción ........ .............,....... Función de A en B....... Definición Gráfico de una Función............ Dominio y rango de una Función ........ Igualdad de Funciones Función restringida .... .................... Composición de Funciones.. Propiedades de la Composición de funciones ............. Función Inyectiva Función Subyectiva..................... Función Biyectiva ...................................... Función Inversa ..................................... Imagen directa e inversa de un conjunto ..................... propiedades ................................................... Función característica........... ............................... Problemas....... ............................................ 81 83 84 89 90 95 97 105 s FUNCIONES REALES DE VARIABLE REAL Introducción ...... Función real de variable real -Forma intuitiva de percibir gráficamente una. función real de variable real ..... Gráfico de una función ...... Problemas resueltos ............... Forma de expresar la variable dependiente en función de la variable independiente ...... Sólo fines educativos - FreeLibros 117 118 123 125 ^ .......... 129 Definición geométrica de función ...... Tres formas de expresar una función cuando se conoce su regla de correspondencia y dominio ........................ Imagen directa e imagen inversa de un conjunto ........... Cálculo del dominio de funciones usuales ....... Función restringida.......... .... Cálculo del rango de una función ..... Funciones especiales ........... Algebra de funciones: suma, producto y cociente .... Composición de funciones............. Función Inyectiva, Subyectiva y biyectiva ..... Función Inversa ............ Propiedades ........... ......... Problemas....................... Funciones Monótonas: creciente y decreciente.... ..... Función periódica, par e impar ..... Funciones Trigonométricas ................. Funciones Trigonométricas I n v e r s a s ....... ............ Amplitud, período,Tase, frecuencia. 131 ............132 133 138 141 142 144 146 150 157 168 176 179 181 182 188 189 191 E FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Función Exponencial... ......... La Función Logaritmo .... Inecuaciones Logarítmicas.................. Inecuaciones Hiperbólicas ..... 197 198 201 203 E MISCELÁNEA Problemas relativos a composición de funciones e inversa de funciones ......... Gráfico de funciones con valor absoluto, Máximo entero y signo dé X ......... Sólo fines educativos - FreeLibros 205 225 ■0 RELACIONES - BINARIAS 0. INTRODUCCION En motemoti eos lo relocton entre dos elementos de un solo conjunto o de dos conjuntos diferentes , es muy importonte t de I cyol se deseen los conceptos* de * relaciones binarios tf unciones y operociones binorios. Estos, conceptos lo i remos definiendo poulotivomente. 1. PAR ORDENADO # E FíttICION — Dodo dos conjuntos A y i definimos el PAR ORDENADO DE COMPONEN TES o y b , o! conjunto. ( o , b ) « { { o } , {o,b}| tol que a 6 A i o} § f ( A y I ) L— 2ro 1*“ componente . {o.b}} EJEMPLO • Seon los conjuntos Se tiene e b6 i. a a {o,b} € ^(Au! ) (P(í?{Au8)) A ~ { o,b} , 8 22 {ej Au8 •* { o j b . c j Au B > = { 0 , { o} . { b J , {c} , {o.bj ,{a,c} , {to, c} , { A u § í ] ? (? (A u B | ) = { 0 , {0 },{M } •• 4 ( c } .lo .c }} , }{o } J o , c }} , {fe } , {Ü,cj| H tiene 28 » 256 elementos Sólo fines educativos - FreeLibros {{b } , { b , c } [ Moisés Lázaro C. E n el conjunto P (9 (A u B)) » ( o, c ) 6 not amos ){o } , {o,c)\ [{b } , {b ,c | J =* ( b , c ) 6 |{c j , {o ,c }} = { c ,o ) e 8 xA | {c } |b|c| j = ( c,b ) 6 B xA % A x B í p es to primero componente . {o} porque { o , el A xB . r , 2. IG U A LD A D DE P A R E S TEOREMA. (o ,b )= Demost rae ion .* Se (c,d ) ORDENADOS s í ,y solov si . o » c hoce a p l i c a n d o 3. PRODUCTO b = d. definición 1 • lo DE C O N JU N TO S DEFI NIC ION . As 9 = ^ El ^ ( o , b ) £ ( P f ¡P( A u B ) ) / o 6 A producto ordenados toles que de A por ( o, b*) o 6 A Por lo gene rol , ob vi om o s que Ax 8 = b 6 b } B , es el co nju nto de todos b 6 8. el | (o ,b ) / o € A » e)> conjunto. a b y sóto ofirmomos 6 |J Por lo tonto * s :i los pares al co nju nto P ( fo/b) ^ Ax© <=> o 6 A o ^ A a b 6 8. v b ¿ Sólo fines educativos - FreeLibros 8 Relaciones Binarias EJEMPLO 1 - Seon los conjuntos A = { o , b } , 8 = {e, d,e} Definimos .' A x B = { ( o , c ), ( o , d ), (o,e } , ( b , c ), ( b , d ) , ( b ,e ) } i [ { c,o ) , ( d , a ) , (e., o ) , ( c , b ) , ( d , b ) , (e ,b ) } x A * A x A * A* = | (a,o) , ( o, b) , ( b , o ) , ( b. dj j 8x8 =* 8** { ( c,c ), (c,d ) ,(c,e), (d,c), (d,d ), (d,e),(e,c) ,(e,d), (e,e ) } EJEMPLO 2 . Seo A=jo,b}. Se tiene 1) fP(A.) = { 0 , l o í , { bV , A\ 2) 9 ( A) xf>( A ) = { ( 0 > ) . {0 ,{o l ) , ( 0 ,{b V ) , (0 .A ), í lo| .0 ), ( ( • ' » , . « • * > ( i b) , 0 ) , a b } , / o M , í i ) , . t bf ) , ( Jbf . A ) , ( A , 0 ) , (A,|o| ) , ( A ,{b> ) , ( A , A ) } • EJEMPLO 3* Seo A = |o,1 ,2} tenemos (Ax A ) x A = A*x A = | ( (o,o),O ) , ( (0,01,1 ) , ( (0,01,* ) ,( (0,i) ,o) , ( (o,*) ,i ¡ A3 = ( ( *,*i , * ) y | ( 0 , 0 , 0 ) , ( 0 , 0 , 1 )• ,.......... . . , ( 2 , 2 , 2 ) } t—tiene 18 elementos . Sólo fines educativos - FreeLibros - Moisés -Lázaro C. 4. P R O P IE D A D E S p1 A • X i A x 6 pr P3 • == f P( í P{ A u B }) * 8x A = 0 x*/3i' 'A x 0 A x 8 = 0 P4 , } si A ^ A = "0 V ¿ =*> 0 (Ax 8 ) u { A x C ) / A x ( B n C ) -■ ( A x8 ) n ( A x C ) . A x ( ( A x8 ) - ( A * C) ' pe P 7 si V - 8- C ) ss 8 A «* A x 8 P9 . ( A x E ) u P si . NOTA: A «a ( i x F A 8 Se dem u e stra n 4 .1 8 ; Propiedades x8 x A )« C «= A x 8 ( A 11 8 . «a D »> a p lic a n d o l as ) x A d e f i ni c i o n e s dadas en f » * 0 8 L É lÍ Á S D e m o s tra r cada uno de tas siguientes pro p o sicjones 1. [ ( A * 8 ) - 2. ^ Á x 3. ( =jgA u g ’ B ) * € c 4. ( A x f B Si A « ^ B ( A x C ) J C CZ ( A x B ) - ( Ax C y d (C x g O D n 5 g ( ( A n B ) xC ) € = a x ( 0 - B ) ] u [ Ax o j u ) ( A u C } x £ f .( B n 0 ) 0 De mo s t r ar usando p r o piedades [ ) C < g (A x B ) ) U Distribu tiv os =*> ' A . 5. 8 a A x ( BuC ) a P3 10 8 que { ( A-G ) x d Sólo fines educativos - FreeLibros ] = C x B 3.1 Relaciones Binarias ■ © — 6. Seon los conjuntos A, 8y C. Si A« C y 8«S |SC , demostró r aplicando definiciones que! [ i x ( Aü ) J n [ ( - ) x ] *■ x C 8 C A 7. Demostrar que : «P { A x ( B n C | J » 8 A íP ( A x i ) n f P ( A n C ) 8.Demostror £ ( M -A ) x n J y [Mx (N- 8) j C [ (MxN)-{AxÉ) J 9 Demostrar : 0 ( C xD ) CT (jgCxD) u Í C x g D ) y C*C x<g 0 ) 10. { A ? x 8 1 ) n ( Agx §2) « ( A1n A ? ) x ( 8f n ®? ) sabiendo que Ai y A* son subconjuntos de X y 8i , B? subconjuntos de Y. D e m o s t r a r que 5. PRODUCTO C A R TE S IA N O Si ' A S (í C A R TE S IA N O * J 8 , entonces *A x 8 de A por 8 . y 8 tomo el nomfe re de PRODUCTO P o r tanto Ax 8 = | ( o , b )6 fft x IR / o e A A be-ej EJEMPLO T EJEMPLO 2. Seon A = { 1,2, 3} B ={ 2, 3} Luego Seon A = |x e .R /- 3<x ¿2} 8 = { y 6 I R /1 * y < 3 } Graficar A x i A x B = { ( f , 2 ) ,( 1 , 3 ) , < Í , Í ) , < 1 , 3 ) , { 3 1U{3, 3> REPRESENTACION GRAFICA I JR x j r . Sólo fines educativos - FreeLibros Moisés Lázaro C. OBSERVACION En el ejemplo 1 , los conjuntos A y B ^ón fin itos, por tanto Ax 8 también es f i n i t o . En e I e j e m p l o 2 . t los consecuencia AxB 5.1 o ) il PLANO conjunte» estom bíe n 8 Ay son in fin ito infinitos no numerables, e n no n u m e r a b l e . C ARTE SI A NO \2 R X JR = m * - a | ( x , y ) / x 6IR A y i JR ) es el PLANO C A R TESIA N O en e I que .* X .* es el efe de los obscisos Y : e s el ej e de los ordenodps Los ejes X e Y se perpendicularmente (0,0) es el o r i g e n b ) f? x ft x IR ~ intercepton en ( 0 , 0 ) que de c o o r d e n a d a s . I R * * | ( x #y , z ) / x 6 R , * y e j R , z € i J e s el ESPACIO T R I - 01 M E N S I O N A L . c ) Hx 1 x IR x . . . . . x IR » fRn ~ | '(X|,x2l x 3 l.... , xftJ / x j 6 IR | es el espacio n - dimensional n veces 9.2 PROBL EMAS 1. D e t e r m i n a r dad los valores d e x é y a) (x+6y , 7x-3y> = (27,9) R: b) x- 3 Hr-4 , Vs-5 (3x+Sy, 2x-y) = (7-4) R *. x s - j d) (7x+ 9 y, »2x+iOy) = («,-4 ) R: f y- 4 U x - l y . , 5 x * 8 y ) = (-*,- 60 ) R c) } d e m odo q u e s e c u m p l a kt tqaal e n cqdtx c a s o : x=- 1Z ; y = i4 *) (tx -I8 y , 14 x - sy ) s (-85, - 5) ft- x r | , y =5 H ( x - s y ,-7 x + 8 y > s ( 8 , 2S) " y *=2 Sólo fines educativos - FreeLibros R; x = - 7 , y = - 3 Relaciones Binarias & R e l a c io n e s G.1 DEFINICION b in a r ia s Dados dos conjuntos A y 8 } llam am os d e la c ió n B in a r ía de A en B a todo suboon ju n to R de A xB * e s t o e s : R e s una relación de A en 8 s il R c: A xB Según kx definición 6.1 dados dos conjuntos A y B ce un " vínculo'" entre los elem entos de A y Q EJEMPLOS • En cada uno d e la s s ie te s preposición e s lo e n tre los e le m e n to s d e dos ju n to s P R O P O S IC IO N N0T4CKW es h ijo d e a b se estable s e e s ta b l e c e u n vm a j RELACION A SOBRE LOS«4A C O N JU N T O S LESSEDBstNfiA ser hijo & €A = conjunto de hijos xR. y Ser ca pita l a ítb ser m e n o r x € X - conj. de ciudades y c y r conj. de países a e A =conj. 4e números x íy d iv id e a aR b ser m ú ltip lo a R b 8 x conjunto 3e pad^s X es c a p ita l de y a es menor gue b X d iv id e a a es A e s tá in c lu id o en 8 V m ú ltip lo d e b b e 8 = conJ - Je mímeros « e X = oeyij. éenúm.taiwB y e y = conj. d e tom» tniwos estar in c lu id o A A 8 cl€ A c 2Z b e B c l e íP(u) 8 e 5*W> A E JE M P LO S n u m é r i c o s : 1. Dado los conjuntos ? A =t °> ■ 8 = {2,4} se tiene : A x 8 = j (o,z,, <o,A), ( t,« , (1^), (2i2); (^41, (3,*), U,4) } • a t ie n e 2 subcon juntos . Todos los subconjuntos de AxB son re la cio n e s de A en 8 filguflGSréloicionesde A en Q son : El con jun to A xB Jfcf ={(0^2j} R3 = j(a,fe)€AxS/aabJ ={(2,2)} Rz - \ «>,*>,(1,2), l ',4 ) j ft4 = | u , Y ) € A * 8 / y - x i 3 } nota : \j y AxB son relaciones d e A en 8 <£ e s la relación vacCq de A x B AxB es la relación totaí de A x g 0 Sólo fines educativos - FreeLibros Moisés Lázaro G. 6. 2 DEFINICION Sea A un conjunto *. Decimos que R es uncí, relación en A Sí ; y sólo si } R es uno relación de A en A . £s decir R Dado EJEM PLO : Son 6 .3 es una relación en A fN^= 10 , 1, 2 , * , . . .... J re la c io n e s e n IN • lo s R : cl R b 4=> a -b S : a. S b ¿o b-n 2 K - 1 3" *. a T b a R d A xA Su s i g u i e n t e s s u b co n juntos '• es m ú ltip lo de 3 es p rim o r e l a t i v o con b . NOTACION (a,b)€ R a ft b Son equivalentes las notaciones : t r, 6 .4 c o n ju n to oe p a rtid a v c o n ju n to f * Q. e s t á e n te fe ctóh c o n b ^ m f d ia n te .R oe Se lee : Cl par ordenado ( a ,b ) p e r t e n e c e a la reía cáoñ R . l l e g a d a m u n a n M \M m Si R es una relación de A en B. ;} es decir R c A x g ■ <%_ cintos que : A es «I conjunto de partida y Q es ei conjunto de llegada . 6.5* y d o m in io S ed R |EL Do m i n i o de Ra n g o o e u n a r e l a c ió n uno relación R| de A en 8 y es el conûn (A c Ax B) - definimos : E L Ra n g o de R| , e s el conjun to de t o s p r i m e r a s c o m p o n e n t e s d e lo s p a r e s l * > y ) p e rt e to JormadLo por tas segundas componentes ( ^ y ) pertenecien n e c ie n t e s te s a a A * dom(Jí.) = |x 6 A / Jy 68^ (*,¥>€*} R rang(R) ={ ye B / 5 x e A , C*,y)€R J x e dom (R) 3 y e B / Oc,y>€ R y<= ra n g lR ) «¿> x *+ y € 8 y^ mngCR)^ 4 dom , (%,?>£ J2 t A /< x ,y)6 £ ; M nanglRlci B domlR)czA Sólo fines educativos - FreeLibros Relaciones Binarias 7. T IP O S OE R E L A C IO N E S Los siguientes de f i n i c i o n e s sedan de soto en " r e l a c i o n e s un conjunto sobre sí mismo. D EFIN IC IO N R es uno relació n D e c i r ". R en A sii R d AxA es uno r e l ac i ó n en A es equi val e nt e a d e c i r R es uno relocio'n de O) Diremos o (2) que es uno relación R /V\ x € A implica ( x, x ) € R t x C im plica x Rx A Se dice que R es u no r e t ac i o ' n (x,y )€ R implico REFLEXIVA <=> S IM E TR IC A ( y ,x ) € R , A en A . en A s í f y solo s í D ( A ) *= R * «-•* 81conjunto diácono 1 é§ A si',y solo si (x,y) 6 R que es e qu i va le n te a x R y (3) Se d ic e im p lica que R y Rx es una f ( x , y ) € R ■a a [ x Ry (4 ) D i r e mo s q u e R , ( x, y ) € relación ( y , z ) €R j y Rz J R TRANSITIVA implica implico es uno reioeion de ( s í , y s o lo x, Z ) ^ si R xR 2 EQ U IVA LEN CIA Sólo fines educativos - FreeLibros sí , y solo Moisés Lázaro C. <5)Se di c e que R es un© relocicín I m M L f j e m p l o 1 seo impltco A » sol© si íxt y } R j •hombres j Ñ m J ( x ,y ) € y si',y ASIMETRICA Ax A /x es hijo de y} ^ es ©sime'trico (i> R es A N T I S I M E T R I C A [ ( x, y ) C R * si, solo si ( y . x J C R ] . «>■ x= y , -r ( x,y ) E jem plos : 1. Lo relocidn H & en l o s numer o s p orque. 2. Lo rel oci dn de in c lu s ió n / '«e " trico (7 ) A &'£.© J porque: Diremos Ejem plo* Lo Diremos que solo s i [y~ x y © « a qu e a J de b . es uno re loe ion im p lico A= antis i me 8. P A R C I A L , si es reflexivo ORDEN tra n s itiv o . R e$ uno r e l a c i ó n # A a a R tsm m A = IR , V y € IrJ relacio'n ontisim etnca , transitivo y **<= M en c o n j u n t o s . COM PARABLE [ *¥•y € A conjunto p o r q u e [ *V* x € IR Di r e mo s i o= en conjuntos r e l o c i d n de in c lu s ió n Ej e mpl o : E n e l (f) A * es uña relocio'n antistmétrtca implico que R e s una r e l o c i o ' n ontísimefrico ( &) [ reoles ( x, y ) €R v ( y, x ) i lo re la c ió n " & im p lico de ( © conexo ) s i, [ x¿ ORDEN c o m p a ra ble . Sólo fines educativos - FreeLibros y 8 y ] es c o m p a r a b l e , v TOTAL, y - x ] si es re f le x i v o , Retaciones Binarias En el conjunto Ej e mpl o: oréen 00} R es uno de el R « ^ ( x , y ) / uno o) R R * A « { x d iv id e o y } a de P R E -O R O E N o, b , C j d j de relación equivolencio en A , pu e s' es re f le x iv a , por Que es \ { o , o ), ( b , b }, { c , e ), ( d, t í ) } «= R s im é tric o , porque ( X, y ) 6 R im p lico (o ,o )6 R => ( o, o ) e R (b,b) € R »> ( b, b ) € R ( c,c ) 6 R => ( c,c ) 6 R (d,d )6 R => ( d, d ) 6 R ( y , x ) 6 R , -V- ( x,y ) 6 R ( c, a ) r R r => ( b,d ) € R s> { d, b ) 6 R (d,b)£ R =t> ( b,d ) € R ( c ,o ) e R O T I O RI C O S (o,c )6 R c) x t ronsitivo.-. R * j ( o , o M M T , (c, e ) , ( d Éd > ,í ó tc ) , ( c fa ) , ( b, d }, ( d , b ) | P ( A ) b) € 22 x2 cumple I R es uno relocion c o n ju n t o Lo r e l a c i ó n es y , d e fin im os lo r e l a c i ó n *>*00 L I M A S Seo P R E - OROEN, sí es r ef l exi v o Si en el conjunto & se 7.1 M es uno re l o c i ó n de TOTAL. relación E je m p lo .' A ~ IR , lo relocion ■ { o, c ) i R és ' t r a n s i t i v o porque { o ,o ) € R a { o ,c ) i R »> ( o ,c ) € Sólo fines educativos - FreeLibros R Moisés Lázaro C. ( b , b ) e R a => ( b , d ) € R ) € R a ( c,o ) 6 R - > { c, o ) 6 R ( d,d ) € R a ( d, b R => ( d , b ) 6 R ( c,c ( o, c ) € R , a ) € ( c, o )6 R => ( o ,o) 6 R ( c , o )€ R a ( o ,c ) 6 R => ( c , c ) 6 R ( b, d )€ R a ( d ,b )6 R ®> ( b , b ) 6 R ( d, b )€ R a ( b,d) € R »> ( d , d ) £ R N O T A .* t ) Po ro p r o b l e m a s t e ó r i c o s no se So lo se o p l i c o olvidar 2 ) No son (2 ) ( b , d ) 6 R Seo los ¿ Es R uno INx JN , de los r e l a c i o n e s b in o rio s definido por o + d =s b + c relación S o lu c ió n m añero ORDENADOS. R una re loe ion en ( o ,b 1 R { c , d ) <*> de "esto definiciones correctam ente, que los ele mentos PARES procede de equi v o le a cio f A A Tenemos * Los elementos de R o ) ¿ Es R son de lo f o rm o re fle xivo ? Se cumpl e que : ^ ( a, b ) , ( a , b ) ^ x porque ^ (o ,b ) , ( c , d ) J • 0 + b ~ b +o € ü if* ( o , b ) i x es x verdadero Sólo fines educativos - FreeLibros -V* o tb € H x ^ A IN . Relaciones Binarias b ) d E s R simétrico ? Si pruebo que o f i r m a ra' Veamos ( ( 0,b) , ( c ,d ) ) € R que R es s i m é t r i c a . ! L o h ip ó t e s i s Pero implico ( t c , d ) , { c , b) ) 6 R es .* ( ,4))-f ( (o ,b ) , < c , d ) ) € R <» > R o fd » b+c f operamos c * La s u m a es Gonrnutatîva . . . Por c) ¿Es tonto í R ...c o + d , la igualdad es stméfnca. b m d■+ © indico ( ( ,ct d ) , ( 0 , b | )S R es r e f l e x i v o . R s i mé t r i c o ? Si pruebo Que [ ( ( o , b ), ( c, d)) 6 R í ( o , b ) , ( m , n ) } € R , afirmaré a que ( ( c ^ d) , ( 01,0 ) ) € R ] implico R es s i m é t r i c o . Veamos Por hipo'fesis, tenemos : [ ( < o , b ) , ( c , d ) k R * ( ( c , d ) , ( m, n) ) o -f d s b + c 6 r J c +n = d + m 4 4 I• J s u m a r m Lmmbro a mi embr o L. ( o t d ) + { c 4 n } es' ( o*n } + ( d X ¿ ) o 4 o ( ( o , b) .( r n .o ) ) Lo cuoi prueba que R es * (b +c } * { d+m ) ( b + m ) 4- ( c \ d ) * * b4 m i R . transitiva. Sólo fines educativos - FreeLibros Moisés Lazara"€ . Porque es re f l e x i v a , s i m é t r i c a R y t r a n s i t i v a , afirmamos que R es una relación de equivalencia . De igual monero t pro c eda Se o R uno r e l a c e n ( a ,b a) ) Anotizor d) en las s i g u i e n t e s R ( c ,d ) si R NoWor definido los <«> pores 2 + x 2 * , por en o d « es uno r e l a c i ó n ( c #dP) problemas : be e q u i v a l e n c i a ... de que cumplen ( 2,3) R ( c td ) So lu cion 4) o ) R es b) ( e . d ) * K ( 2,3 ) Seo R uno rel aci ón cion de e q u i v a le n c i a ( b tc ) € Dado el conjunto sigu ie nte X R Y Mollar t ^ K € M , uno retare ¡--oh. re f le x i v o entonces de l de equivalencia R sí , y K # 0 ' en A. Demostrar que R solo si (a,b) € R y es una r e í a - ( o,c ) € R R . A a , b - , c j • D e fina m os la r e l a c i ó n R en modo <~> X u Y = A a X n Y = 0 por e x t e n s i ó n . Respuesta ’ R » | Í 0 . A ) , f A , 0 > , ( { o } , í b, c } ), ( { M } .1*»!) M R N <=> f ( N ) «* f (M ) Sólo fines educativos - FreeLibros { o . c } ) , ( { o , c } , { bj } Relaciones Binarias Analizar si "fl " es uno relocio'n a) reflexiva, h ) arrti simétrico. c ) tronsitivo . d ) de orden par c i a l . © S e a A = { p / p es una proposición \ 3 s e a d ada por : ( p , q j € J l S L f y so lam ente s i A n a liz a r s i SL e s una re la ció n . (a) reflexiva u n a re la c ió n en A ( p =^q) e s ve rd a d e ra . ? ib) simétrica } (c) transitiva ^ y (d) ant¿simétrica . ( f ) S e a A s j P / p e s una proposición j y se a J l ; una re la c ió n e n A d efinida por *. (P,q) * ^ St, y Analizar s i «R e s una re la c ic ít : (a) reflexiva (b) sim é tric o ^ le) ® Sea £ una rela ció n en J í. =| (a ; b )€ Z so lam ente S¿ e s v e rd a d e ro . t r a n s it iv a , ¿e e q u iv a le n c ia .. d e fin id a , p o r : (a -b ) e s m últip lo de 7 } / ¿ £s .R una relación d e e q u iv a le n c ia ? ® Pag P ro b a rlo . Sea T el conjunto de trián g u lo s en e l plano IR* «íj 'sea. S una relación en T definida, del sigte modo ‘ (x ; y) € S x e s se m e ja n te a. y . •Demostrar qu e S e s u n a relación d e e q u iv a le n c ia . © Sea i e l conjunto de rectas en el plano íR x ÍR una rdacton en «£ d e fin id a por *. (Lf, U ) * 5 ¿ Es S ® Sea íP(A) (X ,Y) e) conjunto © €5* ¿ Es ¿ E s JL S- sea es paralelo a Lz una relación d e equivalencia en f Definimos U* y ? Rfobarlo . p o te n c ia d el co njunto A . relación & en íP(A) del siguiente modo *. <=* X C una relQ cion Y e q u iv a le n c ia \ una relaacñ antisim étrica ? P ro b a r . Ju stifiq u e . Sea # una relocio'n en IR deftntdo por *. Ó. R b A n alizar s i .R es una relació n *, ta) re fle x iv a } Ib) s im é t r ic a y c<c)t r a n s it iv a . Sólo fines educativos - FreeLibros a a £ b Analizar si S es una relación : (a) reflexivo y Cb)sim etó ca , (c> t ra n s it iv o , Cd) antis i métrica ^ l«> comparable , (*> de orden total . (§) La igualdad de conjuntos ¿ es una relación d e equivalencia J Probarlo . * d§) La igualdad de números reates é es una relación de e q ui valencia 7 Probarlo . © S ea una función f : IR —» SM®} cualquiera . De finamos en IR la siguiente relación S : <x 5 b i) Demostrar que ti) -% i f(o ) < O numero O * (§) Sea S 7 ^ flb) >O e s de equivalencia» }c a ra cte riza r Icl c la s e una relación (a,b) € f ( <=❖ de equivalen cia del en TL por : definida s í y sólo s í e ü . a) Analizar si 51 es relación de equivalencta b) Si iR. es de equivalencia } caracterizar las quivalencia. ^ por comprensión . (§) Sccx. A » | 3 k / K£ 2 L } Se define en A la relación ¿R siguiente : l*,v) £ ¿R y sí **) Demostrar que : b) Analizar c) (jj) solo sí i ílíl? € A 2 (x , y) £3 1 a (v,x)ejR D e m o s tra r q u e la rela ció n (S ) S e a ^ ^ te relación : f; A-vA ^ ^ Re f l e x iv a . una función . S<z define en íP(A) la stguten , M 51 N ta> f (N) d f(M) Si ** t r a n s i t iv a - e $ u n a relación d) d e o rd e n S e a 6 ^ =-| S u cesion es <2) Sean clases de e - (& n )€ fí$ - = { ■ bn a) r e f le x iv a - ó) a n tis im é tric a ^ p a rc ia l • reates que son acdtaalas y (bn) € 6 ^ . Se define la suce sió n (c n) m ediarle; ? n tnipar Probar que (Cn) c e # Para fan) £ y (t>n)€e# ^ s e define la relacton en de la si^tre manera. *. (bn)) e-R. <=» (a.n-bn) e s convergenteDemostrar que es relacton de eqtnvalencia. % b) Nota : (ctn) y I b * ) no son n e c e s a r i a m e n t e « r o n v e r s ^ r it e s » Sólo fines educativos - FreeLibros Relaciones Binarias « C L A S E DE EQUIVALENCIA Y CONJUNTO COCIENTE a ) si R es uno definimos de relación equivolencio en A , p o r o codo x 6 A # el conjunto : [ x ] = i y 0 A V ( y , x ) € R] Lnio llomodo b) CLASE E l conjunto OE dé todos los ' closes dé CON JUNTO denoto E Q U IV A L E N C IA A C O C IE N TE de x . de equivolencio de A.tomo el nombre con respecto- o lorelocioV R A /R . C < lC M P L Ü I • seo A S | o , b , c , dJ R “ | ( o, o) , { b , b ) , ( c , c ) , ( d.d ) , { o , c ) , ( c,o ) , ( b,d ) , (d , b ) J En este coso se tiene que R es uno relación de e q u i v o l e n c i o en A Se tiene•; 1) [o] = j o , c) = j y eA / ( y ,o ) 6 R } = j z 6 A / ( z . b ) e fí} [b } ={b,d| [ c ] = í c» ° } = { me A / (m.c ) € R } [d ] = { d , ’b} = jn6A / ( n, c ) 6 R ) Donde i [ o ] es lo clase de equivolencio de a £b ] ii ii ir ii » ii b , [c ] II II II l II n c . [d ] ii ii II H í 2 ) El con junto cociente A con respecto n d. o R es Sólo fines educativos - FreeLibros ! y se Moisés Lázaro C. EJEMPLO 2 - Se o Z* = Z -|0} y «o Definomos en S lo re la c ió n ( (o,b), (c,d ) ) o) Dem ostra r que b) Hallar 6 S R <=> R = Z » 2#' por od «b e R* es una re la ció n dee q u i v o le n c i o [ (0,2) ] y en S. [ (3,1) ] S O L U C IO N : o ) E s similar al problemo b ) i) [(0,2)]* Pero : (7 ) { (o,b ) C 5 / ( í o , b ), ( 0 , 2 ) ) £ R ¡ ( ( o , b ) , ( 0 , 2 ) ) 6 R <=> { o ) ( 2 ) =( b ) ( Ó) 2o = O 0 «S O e r } Luego : [ ( 0 , 2 ) ] * { (O.b ) e £ /.b S Z * } «) [ í 3. 1) ] * : I ( x , y ) e S / ( ( *,y ) , ( Pero : ( ( * , y ), (3,1) ) 6 R <=> 3,1 )) ( x ) (1 ) = ( y ) ( 3 ) x Luego: [(3,1)]* | (3y,y)€S = 3y / y £ Z * } = | y (3,1) e s / y € Z * j Sólo fines educativos - FreeLibros Relaciones Binarias 9. PROPIEDADES DEL DOMINIO Y RANGO DE UNA RELACION. Seon R y $ OEL dos relociones de A en 8 , se cumplen los siguientes propiedades 1 DOMINIO DEL RANGO Df ) D o m ( R u S ) = Dom { R )u Dom( S ) Rt ) R o n g ( R u S ) = Rong( R ) u Rong( S ) 0? ) Dom ( R n S R?) Rong ( R n S ) <£ R ong( R ) n Ron g { S ) Oom( R) n Dom { S ) R3) R o n g ( R - S >31 Rong { R ) - Rong ( S ) D j ) Dom (RHS ) s> D o m ( R ) - O o m ( S } S U G E R E N C IA .* Poro hocer demos tro ció n es Ud. los conjuntos y sus elementos representor en un diogromo de Venn debe poro aplicar correctamente los definiciones respectivos . Por ejemplo Los definiciones gue debe opiicor son ‘ a ) x 6 Dom (R)<=>ly 6 8 / { x , y ) € R o ) y £ Rong (R ) <*> 3 x 6 A / { x , y ) £ IR b ) x ^ 0 o m (R )< »> -V y £ 8 , ( x , y ) f R b) y j^R ong (R )< a > -^x £ A, { x , y ) ^ R Ademos tener en cuenta la siguiente implicación Lo proposición verdodero " y £ 8 , ( x , y ) j í R " implico ** 3 y € 8 " f(x,y Iguolmente . " *V* x 6 A , f x, y ) f. R "implico “ 3 x £ A , ( x , y ) j , R " 10. RELACION INVERSA DEFINICION Si R es uno relocidn de A en 8 entonces R E LAC IO N (es decir R c R-1 es uno relocion de 8 en A (es decir INVERSA Ax8 R 1c DE R . Sólo fines educativos - FreeLibros ) 8 x A ) llomodo R Moisés Lázaro C. Oe m o d o que ‘ eq u iv a len tem en te : E J E M P L O . Sean Seon ñ « ( re la c io n e s ( y , x ) € R ~ '« * > ( x , y ) { y , x ) 6 ( x , y ) 6 R * 1 <=> Jo s ^ o n j u n t o s 6 R R A - |o , b , c , d | , 8 » { ( a , f n ) , (g ,ft )•,( b » p ) } y q, r } S = { { b ,m ) #( c * n ), ( d , p ) | de A e n 8 . Lo reíocio'n inverso de R e s cz 8 xA L o re la c ió n inverso de S es $**« | ( m , * ) , ( n tc ) , ( p Id ) y € - 8 xA R es uno rela ción Oom ( R ) R~* = ^ { m,o ) , ( n , d ) , ( p , d ) } de A e n 8 = { a ,b | Rong( R ) * { m, n , p j Oom (R-1) » R o n g l R ) = { m, n , p } Rong ( dos R* 1 ) = Oom ( R ) * { o,b} S es uno r e l a c i ó n d e A en @ 06m { S ) = | b ,c , d J R o n g í S ) ss \ m . n , ? } - O om ( S "*) Rong( S )* { m ^ p j R on g { S"f > « Oom ( S ) » f b , c , d j Sólo fines educativos - FreeLibros Relaciones Binarías DOMINIO Y RAN60 DE UNA RELACION INVERSA KM - Si R es uno deR , se re ío c io V » d e A en ( R"*1 ) ast Rong { R " 1) » 10.2 PROPIEOAOES R y S p, pí ' P3 • d o s re k ic io n e s Dom {R ) S"1 (R -S T S"1 1 “ - = fi "1 ¿ re lo e i¿ n de estos C u m p le n propiedodes se hoce con los de finic io nes R “ 1 <=> { x , y ) 6 R ) / R'\<=> { x , y) ^ R OE RELACIONES uno re loción de A en 8 S uno reloción de 8 lo re loción “ y en C S o R * (R compuesto con S ) del sigoiente * modo : S o R v_y 35 i in v e rs o s” R Definimos lo IN V E RS A A e n 8 t Se de ( R n S I*1 * R ‘ r n 10.3 COMPdSIClON Seon ( R ) s - • ( y, x ) 6 ,x R ong ( R U S i *’ * R 1 u Lo demostrocion •{ y * R 1 es DE LA RELACION ( Rá S ) ■’ P4 , ‘ y c u m p le n ‘ D om Seon 8 (x , z ) € A x G / 1 i y 6 8, ( x , y ) € R a ' ( y t z • R c o m p ue st o con S o " R e loe ion ) S $ } j c o m p ue s to Sólo fines educativos - FreeLibros de R y S Moisés Lázaro C. Lo S = S 0 retocion ” R compuesto c o n NOTA' Lo r el ac i ón EJEMPLO 1. S©R Seon los de 8 R = { S Hollar a) perm ite hocer ef siguiente existe si', y soto si R o ng(R ) ft O o m { S ) ^ ^ f conju ntos C= | b , c,g , h j S nos |o,b,c,d j A- definí mos en C del las r e l a c i o n e s ^ fJ , de A en 8 y siguiente m o d o ' ( b , c ) , ( c , d ) , ( d, e ) , { d , d ) , ( d , f ) ) = [ ( c , c í , ( t , c ) , ( d, b ) , í f , g j Se c, d , e, , 8 R b ) I ' R o S Solución a) Hollemos R c o mp u e s t o E n l o n o t ac i ón § © R- con S , es decir tener en cuento que ' el de r e l a c i ó n de PARTI DA retmio'n Con di ogro mos S© R . de f lechos SoR dé lo derecho es lo y el de lo izquierdo llegada . es ! A Sólo fines educativos - FreeLibros R —— -♦ 8 S — —♦ C . es la Relaciones Binarias Este dio gromo de f le chos nos indico .* de A d i r i g i m o s o 8 y de 8 gimos. Con esto nooiod es muy sencillo R0 S . obtener Veomos R » I ( b t c ) f { c , d ) , { d,e ) , ( d # d ) f Cd , f ) i l ( S / ^ a | { t, e ) , ( < c Los flechos ) , C * 0 ) , ( f¡ g ) | nos indicon que SoR = { b ) Hollé m os S 0R , is ! { b, c ) , ( c , b ) , ( d, b ) , ( d , c ) , ( á , g ) } Ro S 8 • Róog { S ) n S * { ( c , e ) , ( e ,9 ) R = ( ( b*7c ( R o S — | EJEM P LO 2 nos Dom ( R ) — - — -*■ 8 , ( d j b ) , ( f, g ) V \ Las flechas • ' T, ht, d } indican , ( d, e ) , í d, d ) , ( d , f ) } R© S que ( c , d ) , ( e, d ) , ( d,c ) j Dado los conjuntos h allar 1 A UoT es A (?© >c ; D ? VoU , VoU oT y la s . t Observando e í diagrama, obtenemos directamente * i)VJoT = ^ a , b ) > Ib,*»), (C,S>,<CA>} « ) V o U . = $ < «,«),.(d ,n ^ e ,p ), tti) V o U o T = ^ (a ,n T ) tcVP>, j - Sólo fines educativos - FreeLibros relactjones diri Moisés lázaro C. PROBLEMAS I. Seo. y sea una relación de A2 en A dada, por R = { feV),*) € A2 X A : 2 = x-t-y-1 a x*yf Determinar por 'extensión el domirno d e & *. ■' Z. Sea la siguiente^ relación en 2 * Jt r {(x,y) e 2 x 2 ¡ 3 K e 2 * x —*•y J Analizar *s í B. 5. S tra n sitiv a 9 y m ediarte ■C*,Y)€ Jt <=» ^ C t?A € A 2 / * tY = 4 } Determ inar todos los elem entos del conjunto S Dado o! conjunto A = | a 7fc>,cj . Definamos la relación íR en íPca) d€i l u i e n t e modo : X $ y ** X u 7 ■= A a 7 LO T = 0 Hallar J?. por extensión « Sea tra r Si una relación binaria cualquiera de A en B . íR R ’1 6. o-) ref lexiva - b) sim étrica ^ d) aniisim étrica . Sea @l oonjunto . u n iv e rsa l‘U = un Subconjunto de U . Definimos en A una relación í t y A. 5 ?. e s *. e s la re la ció n de B que es s im é tric a A -$-z,-);o,t,2} 8 = Í - i, o e n A 0 in v e r s a d e S t y seto s i J?. - R ^ dem os . ^2, 3 } Se definen los siguientes relacióneos S de A en B y T de BenA mediante c x ; y )€ S C*, y ) € T 7. (x+y) e A <=* ( 2 x - y - l ) € JB 3) Hallar ( Dom S - Oom T ) b) H a lla r (S A T ) c) d) HaUar gg ( RanT) n ^ (Ron S ) D e fin a una relación K s im é tric a Dom ( R ) (AnB) . en AHB tal. que S e d e fin e en IN la siguiente relación R ? m e d ia n te <x-,v> e R ( x*f y ) e s par . Averiguar SÍ R e § . reflexiva ; s im é 'tric o ? tran sitivex . ¿ E s de e q u iv a le n c ia ? 8. S i ^ JR. y S dos relaciones tra n s it iv a s en A a) D em ostrar que ( R O S ) e s tra n sitiv a . . b) ¿ E s R u S ? una relación t r a n s it iv a 7 ^ Fbr q u é ? S. Sean R a) Bi b> S i y R R 3 relaciones A . Dem ostrar > ta m b ié n *. y S son re fle x iv a s yS son s im é tric a s ? también lo son R n S Sólo fines educativos - FreeLibros lo s a n f t O S ’ g y R ü S * RuS . Relaciones Binarias Si R e s s im é tric o ^ ta m b ié n t e es R ‘ l y 7 § R R e s sim étrica. Si y solo s i R~' = R. . O) d) 10. S e d e fin e e n 1N *La s ig u ie n te (:>c, y) £ R 4=^ X-y~5K ^ a) D e m o s tra r que- R es relación b) D e s c rib ir ; por co m p re n s ió n ^ r e la c i ó n R V para algún K € Z • d e e q u iv a le n c ia . tas c la s e s d e e q u iva le n cia Sean ios conjuntos I A = j 2 , 3 , 8 ,.9-J binaria d e A en B , d e fin id a por H a lla r la relacia’h inversa de R . 11- 12. Sean R y S relactones y B =| 4 ,7,c ] y R una relación : R = | (x,y) g A x B / *<v } * definidas en A ^ • /Diga cuáles de las siguientes proposiciones son v e r d a d e r a s o- j a l so s : P : S i R e s reflexiva yS e s s im é t r ic a R u S és simétrico., g. : S i R- es transitiva y S* és tra n s itiva => R u S es tr a n s itiv a , r : 3 i lx,v) e R a- (y ,z )£ R */y>2 G A d ife re n te s R e s tá n 13. s it iv a . Sea A = { - 3 , - 1 ¿ Cuales P : ,3/6 , 5 } de las s ig u ie n te s proposiciones son -v e r d a d e r a s ? R , r | u ; y) e A x A '/ xy fle x iv a ,} s im é t r ic a y divisible por 2 } e s u n a tm n s itiv e x , ; S r j ÍX/V) e A* A / x+.y. divisible por B J equivalencia en A . . r : T = f Oqy)£ A * A / x -y divisible por B \ flexiva y transitiva en A . 14. D e finim o s en el c o n ju n to re la ció n no re e s una relación de e s una relación re A =| 1 , 2 , 3 j la s ig u ie n te re ía cion R =1 ( ' / ) ((3,2); C2,2),(S,S),(4>?),14<4 ) ; ( 3 ,X ) ^ 3 ^ )^ (y,X) , l *,*)_, Bi R es relación de equivalencia en A | h allar 2 x + 3 y - 2 Solución ; 8 15. A c | 1, 2 , 3 ^ Sea , vof s e 'd é f t n e n .la s s ig u ie n t e s r e la c io n e s én A *■ R , . c | CX,y? e A 2 / 2 x * Y 2 } R 2 = { i X, y ) £ a V X - 1 - 2y j R v = j ( x , y ) e A 2/ V «s }‘ R4 - { (x ,y )€ A2/ 5 x < 3 y -Q } ¿Cuales p : Ri v r : R2 R4 de las’ siguientes afirm aciones son verdaderas ? es reflexiva y R/* « s s im é t r i c a y r 3 Son f u n c io n e s d e t r a n s it iv a . A en A . Sólo fines educativos - FreeLibros Moisés Lázaro C. ^ * Pora relaciones binarias definidas afirmaciones *. 0) (2) A ^ ^ } de las siguientes S i R es s im é tric a , y tr a n s ítiv a . en to n ce s R es re flexiva. P a ra E ^ ^ .S e a A = fP(E)'- . D a d o B c E , la re la c ió n : ( X , Y ) € R <=^ X O B r Y O B es de e q u iv a le n c ia en A ». 13) S t A ttfd., ^ ? la rela ció n V ^ (a , b ) , (c ,d ) 5(d ,d ) , Ccsô ^ (d ,c) ^ es t r a n s it iv a pero n o e s S im é tric a . ¿C u á les son v e r d a d e r a s ? "W* S e d el conjunto A = ^ 1,2,3.,4f y c o n s id e re m o s la S ig u ie n te re lación tran sitiv a en A : J t = ^ (1 ,» i(1 ,3 ),(3 ,l) , ( 3 , 3 1 , U , 2 ) , <2 ,4) , (4,2) ( 4 ,4 ) } d) Probar que es reflexiva, y sunétricoi . ¿ E.s ít de equiva le n c ia ? b) c.) Para tó e lo * €. A ^ definimos : C*3- = { Ve A / (y >x> € vR } Según e s ta d e f i n i c i ó n ; h alla r L i 1 5 C.21 ; L B 3 yLA} . Decir s i e s v erd a d ero», cr f a l s a , cqdex u n o d e la s s i g u ie n te s a fir m a c io n e s ^ ju s t i f i c a n d o c o d a r e s p u e s ta * , ít) tfc. Sea C l ] n C A l = S ¿ >7 ( ii) L 3 1 = C 4 1 la * j tot) I i l u U l = A s e g u ie n te r e la c ió n : e n . í l é \ lx,y) e 2 x 2 1L / ^ k.€ 2 \ : x-*y } A nalizar s i IR e s ; a) R eflexiva 9 b) Simétrica c) Transitiva y d) Antí simétrica. Sea A •={ xe 2 / x e s múltiplo d e 3 ]• . S e define- en A la relación siguiente I *R y <=» <x'- y) es m ú ltip lo de A .. a.)Demostrar que íR es u n a re la c ió n de e q u i v a l e n c i a . b) D e t e r m i n a r e l c o n ju n t o cociente A / f t ; esto e s , el con # J u n t o de t o d a s l a s c l a s e s d e e q u i v a l e n c i a . *0. Sea R la celactoln d e f in id a p o r . R= j ( x , Y) €- 2 x 2 / 2 divide a (x-y.) f , e q u iv a le n t e m e n te : * R y < = » x = y(m ód2.) . h Analizar s i la v a le n cta . l«e x. es congruente con y md dato 2 ” congruencia, m odulo 2 e s una relación, de equi Sólo fines educativos - FreeLibros Relaciones Binarias — 21 Se on A - c = [ - 1, 0 , 1 ; 2 } lo s conjuntos lación d e A e n B y S R = f lx,y) / Cx+y) e A J y 8 una re la ció n d e y — — © — - H , un a r e B en C 7 daofcxs p o r ; 5 = \ U , y ) / Y 2= x } Belcrminar por exten sión ; a> S O R ^ b) - (rang ( S o R ) ' 1) ñ ( d o m R ) . . • ' 22. Seqn A =| X€ ÍN / * [unción tal que no e s mayor que 12 } y .í : A —*_IN. > uno. J(x) = m á xim o del conjunto {1,X} (asi por ejem p lo : f(z > = m á x im o del conjunto { i ,2 }ê s 2 ^ Se de|Lne en A la r e la c ió n R m e o l i a n t e (*,y) G R <í=£ *f(Y) = 3 fC x ). : D e t e r m i n a r t o d o s lo s p a r e s d e R . 23. Sea t r ic o Si A = [i,2 ,3 J . R , S y T son re la c io n e s t ra n s it iv a 5 r e s p e c t iv a m e n t e • y . e n A , r e f le x iv a } s im e - R - [ ( 1 , 1 ) ,(2,3) , (ol,2) } ( S , b ) V S = \ (1,3), ( c , d ) } T = [ ( 3 , e ) , (2 ,3 )} Hallar : ( b- cxj 4- ( c - d h + e Sólo fines educativos - FreeLibros Moisés Lázaro € , 1. Problemas Resueltos © Se a n los conjuntos Donde: Áx B A = {1 ^ 3 } 8 = { A,s ; G¿7 \ = { ( I A ) ) (1<5))(l,(,) ) C 1 ,7 );(2 ,4 ),U ,'5 ),(2 ,« ,U m Ahora } ve a m o s D IA G R A M A D e ,l ,z ,b ) ,<.-*,!)} ^ 3 ,* .) los siguientes conjuntos : O.) S ls ={<1,4), (1,5) ,0 , 4 ) } v A g u í b) y fii d AxB =>es una relación d e A en B . VENN R z = { ( 4 , i ) >(4 *2),(5j)/(5,2)}.'-/A qui Bx A es una relación de Ben A. ! •' / * * OomCRj) = {4 ,5 } cz B R a n g (R 2y = \i,2\ o D IA G R A M A d e •4 .5 (m 7 A d ia g r a m a VEN N Considerando el universo U A } > tabular y cas de caolo uno de Las Siguientes retactones *. © r e c t a n g u l a r construir las 9r á ^ J f,-{lV ltU * Ú /y = x j S O L U C IO N ■ 1o Tabulando 2o * el c o n j u n t o . - , obtenemos íti - \0^),O,2),(t3,3); l14,4)^ El gráfico : ver Jig j ^ a de m a s : Dom (#i) = { l , 2>3,4} Rang(R*i) r { 1,2,3,4} Sólo fines educativos - FreeLibros ______________________________ Relaciones Binarias ( 5 ) A z ~ {(* ,* )« U * l/ / x t -y r 3) So l u c i O m t*) Tabulando el conjunto M i obtenemos : J l z - { U ,4 ) ' (<•,!), ( 2,3 ), (3,2 ) J Oom( * , ) : \ i ,A ,2 ,1 S } Banjo (X i) = J * , 1 . 3 , l j 2?) £1 jfo/zco de J l z .£3 @ v* ' fty -2 . r | (* ,3 ) « U x U / * = 2 } s o l u c ió n j*) Ta bu lan do <zl conjunto D w n& tf r i 2J } 2?) El gráfico de JZ 3 ® obtenemos : - j ( 1 , - j ) , ( i ti ) ? ( 1 , 3 ) , ( 2 , 4 ) } ;£»*9DC#3) ¿s I 1,2,3,¿} \ ver f 'S - 3 . ftt, z { (*, *) € U x U / y =3 J SOLUCION J*) Tabulando el conjunto O om ) *•) £/ gráfico obtenemos : JZi, r j (1,3) f (2 ,3 ) t (3 , 3 ) , (A ,3^ j = j J, 2 , 3, A } ■j R a n g o £ £ 4 ) r J 3 } ^2 4 ate ver fig./t . = { ( * , y ) « ü*U / y < x .j (o ) SOLUCION 1») Tabulando Cl conjunto Domí. 8 5 ) = { 2 , 3 , A ) ?*) £/ gra fito (7 ) ^6 ver o b te n em os:fís - {(* , 1) , Í3,l>, < 4 ,1 ),( 3, 21, ( 4.,2) , ( A , » } ) Ftan<j0 ( $ s ) - { i,2 ,3 ) . //^. 5 . = {(* ,y ) € U x tf / y ¿ x j S O LU C IO N i») Antes de ta b u la r , tener en cuenta <fue y ( x O y x Zueyo : -»6 = | ( * , y ) € U x t / / y ^ x J = { ( i , j y , ( i , 2 ) , ( i , 3 ) , ( l , Z ) , ( 2 , 2 ) , ( í , 3 ) 1( 2 , Z ) , ( j >s ) )(3 ^ ) j ( A ) M | DomC*c) = R o n jo ( jl G) = { 1 , 2 , 3 , A} 2*) £7 g rá fic o de vér f ig 6 . Sólo fines educativos - FreeLibros Moisés Lázaro C. u : ; t ....4 - I - — 1 i Í ¡ .....^ 5 ' j : • i V i ! t . : i - -r « i : : 1 i 3 * t ~ : ■ 4 i 3 4 i J ? ! 4 ¿ ( 2 .. J . - - L • • : ► i 3 , V w 1 2 U ; .....f - r - f - r — » ’• J i 4**1...... . • ' ¿ » ¿ H- *u 4 -J -4 4 ' i -é_L. 1 2 } i i 2 3 A -►U /*>.5 figJ, _L 2 2 /*?.6 £ n cacfo uno de ¿os fijara dos del' 8 al U } asió dardo una re lerdón <¿n al coa'juaô ^ 1 , Z 3 4 S 6 7 .^ ^ Cuá/as de astas retardones son reflexivos ? © |C 3 ,7 1 , ( 7 , 2 1 , ( 6 , n , n , ( 7 , 7 y ¡ © j ( * , y ) / x 2 ■fy2 ^ ( £ ) | ( * , y ) / y es un factor de oc J @ 25} j ( * , v ) / y - x es múltiplo de 3 J A/OTA : " & **25 cofís/dtfcréo como, un multrp o de cualquier número • SOLUCION © >vo #s r e fle x iv a 7 porque poro serlo as na cosario que estén ¿os pares .* (1,1), r Z 2 ;,(3 ¡3 ),C ¿ ,6 ),(5 ,5 l,(6 ,6 ) © 1 a , i ) , á , 2 ) , ( i , }),(/ ,6 ), (2,1.) ,(2 ,2 ),(i, 3 )', (2,Z), (3,1) , 0,2) , (3 ,3 ), (3,2.) ,(4 ,l) ,(4 ,2 l, (4,1) j NO ES R E FLEX IV A @ } U fÓ lto n ¿OS Í4 ,4 ), (5,5) ; (G,6) f (7,7) . | u , j 1 ,(2, J ) ,U ,21 , ( 3 , í ) , ( í , i ) , ( 4 , J 1, (4 ,2 ) , (4,6 1 ,(5 ,l1 ,(S ,5 l,(6 ,ll,(6 ,l),(6 ,3 ),fc ,6 ),(T ,l),(7 ,7 ) £5 Reflexiva .© y (7 , 7 ) . j . I (3,J l.f i ,21,a ,6 ) , tí,71 ,(2,71,(2,3),(7,s i,(3 ,31,(3,61,(3,61,(4,61,16,51,(4,71,(5,51,(5,61,(6,61,(6,71,(7,71} ES aeFLEKtVA. Sólo fines educativos - FreeLibros Relaciones Binarías En codo uno de los e/erac/ós del 2? ot 25 esto dado uncrre/aaon en ei conjunto lo i i 3 . 4,s} . ' * d Cuates ote ¿wtm relaciones son simétrica* © { ( I . r t , ( í > n , { 3 ,« I(5l*><( l,f l,( * 1J ) ,n l3 ^ (b ) { ( * , » ) / 7 a. 2 * + 5 } @ |(*,y) / * > + y í = © j < *> *)/ 23 } *7 > O J S o l u c ió n : @ £ S smárncA @ no ss smérmcA @ s s smmmtcá £rt codo uno de tos ejereJobs det ig al 19 @ &s simétrica . esto dado uno relación en t i conjunto de los e n te ro s ¿ Cuates de estas relaciones son transitivas ? {(* ,y )/ y r x 2 | ® @ ¡(x ,y) / x > y j @ \ <*,vV/ x < * } (j* ) SI E S @ { <*,?) / x + y : 6 @ > 0 FS SOLUCION ® @ S/F5 H0 £ S . Cí/oies de los siguientes relaciones en ei conjunto j 1,2,3,4] son : feo £¿*¿£x/vas ■ (te) simeTQtcAg t (q) transitivas ? i Cuates son relaciones de equivalencia ? M x 2 { (x,Y) / X +y = 5 | 2?3 = j (x,y) / y ¿ x j .£5 = { <x,y) / | y - x I CS múltiplo d e 2 } M i z | <x,y) / y < X } £4 r | (x/y) / x : 2 j Me - |(x,V>/ |x-y | ± J j SOLUCION J lk Z |0 ,0 ; U , 3 > ,1^,2') } £S x 2 = | u , n /(3; n , ( 4 , n >(3,2Y) (A J2 ^ ( C , 3 ' ) } SIMETRICA É S TR & N S /T/V A # 3 = | 0 , 11, 0 ,2^ , íi í 3 ) /0 , 4 ) } '<2,2^(2>3 ) ; { 2^ ^ 13;3 ); (3>A 3 , (A , 0 1 .£S mcLExtvA Y £3 transitiva . Lo notación : y d t x Jtl, ~ { (2,1) ,(*,?) ,(2,3) , (2,A) J se lee *f y no es menor oue x NO £S nePLÍtlYA , NI $fM . ; además y f x y V* /V/ TR&NS . J ?5 ; j ( i . l l / ' . l ) , ( 2, 1) , ( 2 ,I I , (Z,31, (3 , 2 > , U , i , •),('.,!>, (1,31, (3,1), (3,M , (<,,3) , (¿.,¿.1 ¡ £ 5 R E F L E X IV A } £ 5 S IM E T R IC A Me Y N O E S T R A N S IT IV A = { (1,2) ,(2;!) , ( 3 , 2 ) , ( 2,3) , ( 4 , 3 ) , t t , 4 ) j £S SIMETRICA . (5 ^ Dem ostrar Que lo rela ción M z j ( a , a ) } íb tb \ t (c ,c ) , ( ¿ , 4 ) , (o , c ) , { c , g ) el conjunto ) a ; b , C , d } es uno relación de equivalencia . DEMOSTRACION Sólo fines educativos - FreeLibros (tu Moisés Lázaro C. i) es a e rie x iv A , porqué: (a,a) < R ifl e s StmtTOKA) porqut: í • (b,bl tR. ■ (c ,o s X ( a ,O E J 2 ¡ (<*,«)£ X (c,a) f £ =* (.4 ,b )tR (b,eDí X til) es t r a n s it iv a ¡ porquz: <«,») « X A «x,c) e X . =» (a,c) s X (c,c)«R A (c,Oi) £ A => (c.a )ÍJl¿ fa ,c ) e A A (e ,a )s í =» (a ,a )e R (câiíB A (a.aleR =0 (c,a|(S {c,ayeJ? A (a,ey eR => ( c , c ) í J? A (cr,b)É tf <&,b) Í R A =* (b,d ) £ X t b, d) <J l A (<*,<í)e.R => (b ,c n € R <b,d)C« (b,d)*A A ( í , 6) í j e =4 (b ,b > c £ (d.byíR‘ A ( b ^ s R = * (d .b u R (d ,b )íR =* ( S ) Deinosiror t/ut lo relación J i - j (*,y) / y* = x* j A (b ,d )€ R (d ,b líR en el conjunto dé los enteros ¡ es uno rilación de zgutv ofenda . D e m o s t /z a c / o a j i) jQ. e s fíE^LE x/va J porque 5i (x.#x ) c l x l n) es stM¿TwcA t porqua Si /Y/o y2 A X2 r x* (x,y) € z^> y2 r x 2 x2 x2 - y2 w ) JQ. es TQAfi/smva ; po^fue St (*,y) € £ A y 2 r X2 A r $ (*,<*)€ ^ . ; antonez* ( y , x ) € ^ (v ^ ií, Z2 r V (*¿£)€.R 1 ' t 2 = X2 ( 23) Considerando' <?/ universo U - j o i , 2,3,4 r -.,9j , 5e p/bfc : ía) Tabular y construir los gráficos de codo uno de las relaciones de V nn U } ib) Hattoi el dominio y rango de codo relación; fe) t C úál dé las relaciones es reflexiva i simé trio o transitiva l 5 i= | < * , « / r - x - oj 5tó =l(*,v)/s’ + y ^ s í S j n. St9 =|w,A / x - y =5 | S2 = ¡ ( « Á > / X 4 y = 4.} S„ =1«M0/ *2+y2s<25} 520 = ¡<*,y)/ lx-y| = 5 } 5 } = ( (* ,v l/ xy ; I ) 5b = |<* , « / **♦>* > »}■' Su = ) i W l* - y | í5¡ 5¿, = j (*,v) / x = 3 } 5,3 - | <*,vV A - y 3 = 4 } SM y1 = x 1 -9 | S5 : | ( V ) / y = 5 j 514 = Su SG = }(*,y>/x =o| 515 = ¡ »*>») / y > x j S2A 57 Sií : 1t*iY)/ y1 r 4xj Sas x |lx,Yí/ 1*1 +y = 1 ] 517 = |( x , y '/ *J ; 4 y | sl t = i'*<v'/ |y-* l = 3| 518 = l u *v ) / x + * =10} 5 jy :) t* ,Y )/ 58 r | Ujy’) / y - oj _ { ( * , y) / *y í 4 j 5 9 = j<x,y)/ yJ -* 2 :flj y<x} Sólo fines educativos - FreeLibros :| (* ,Y 1 / |X| 4 3 } yV lv | < 3 } xl +yz Z ¿ } — — @ — «^.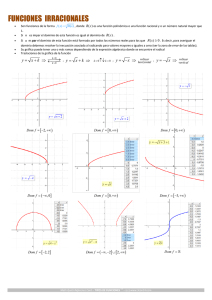elaciones de IR en IR 1. a rr/ M c io iv E l p ro d u c to c a r te s ia n o ml rMxfR do. se cfe fin e íR x /R s| ( * , y ) / x € / R como s ig u e : A y £/£ J 1.2 PLANO CARTESI ANO Él píono Cartesiano S€ /oz/jto por la intersección de dos recias perpendiculares llamados ejes. Donde : El eje H om m N ThL f se lla m a El e je v e r t i c a l } e je p e la s o r de /v a da 5 : y se lla m a E l punto de in te rs e c c ió n e je d e la s a b s c is a s : X se lla m a Ca d a .punto d e l p la n o «s un Pa r Gráficamente at p la n o c a r t e s ia n o fkxfU o r ig e n ; (o,oy ordenado : (*,y) «s como sôe •/ «¿a >&y efe AOTTesfaondenua. biumívoca. M : -A cacto puntó del plano Iz correspondí un par ordenado: y fctcijarc>cetrneint& ** - | ^ ^ AF/CA ° g p a r e s O Q O fM A D Q S p <*>y ) Gro/icor los siguientes puntos:/© ( 1 , 2 ) ; P2(-fer .O ; P j K r 5/2) . Sólo fines educativos - FreeLibros (~5; 3 ) } Moisés Lázaro C. 2. m i & c /O N g s d e M en M ® § r Í N Í c i®N~s* E l conjunto J l es sí uño reloaon efe fR c & Se tu :* 0$ t í <//> 5«/óccwyt//ô n ». en Í& f k x ik producto Cortesano de 0 por Tombién " jk esto conierudo ó es yt/el a Mxffl 2.1 D O M IN IO Y PANGO D E U N A Q£L AC IO N D E fñ £ N ífí. £s el conjunto de valores reales JDOMiNtoy que toma (a variable, independíente x RAA/<aO> £ s e¿ conjun to de v a lo r e s re oXos que to m o ¿o v a r ia b le d e p e n d ie n t e y ( j - componente). Dt'cfios valores por ¿o yenerd (2 - pertenecía, in te r v a lo s que son subconjvntos g e mrai perten ecen a in t e r v a lo s que son: del Sobconjuntos del £/£ PEAL X . e je por b REAL V. N O T A C IO N '. NOTACION: D o m (M ) c o m p o n e n te ). D ic h o s valores - Jx . € $ / 3 y€/£ a (x , y )€ . f t j E J E M P L O : S e o Jo re la c ió n Do/n (S) - Ronqo(n) = { y c ^ / 3 x/k A( x, y) e £ j S r(í*/yi€¿Sx¿R/ xa>4y1-4 =o) X € [-2,2] Sólo fines educativos - FreeLibros «a /? g o ( S ) - y€ [-1 ,1 ] Relaciones de IR en IR 2 .2 ID E A í n un Plano Cartesiano se pueden %tof/car: rectos IN T U IT IV A F U N D A M E N T A L 7 corvos ; planos y samipíanos . Por lo tonto *} (a s rectas } ¿as curvas } ¿os píanos y l&S mi pía nos son relaciones d e /& en fl¿. c ff l^ e h r a ic a m e n t e /af recta y las curvas v a r i a b l e s Mx ,* e M>/“ rfa Lo fo rm o E JE M P LO G P Á T IC O d e son e c u a c io n e s a lg e b r a ic a s con % F C ^ y l ^ O - LAPEC TA y C U Ñ V A S C O N O C I D A S ( cQ N Í C A S ) LA PEC TA f tiene como e cuación oí : A x f 8 y + C z O LA PAO AMÓLA } p u e ¿/étfe como ecuación D o n d e • 0 = *n?vto Ot/ncü'oocióq ) m r- ^ o : p e n o ib n t e d o s • fo fm o s ; ( x -h )2 = 4 p ( y - K ) ÍP ; LAÓK.UNTE¡UNCÍA;tízn<¿ como ect/oc/on <?; (x-hUíy-Kl1 z r* ( y -K ) 1 = A p ( x - h ) ce/tfro : ÍN*) Donde V (h,K ) es et v é r t ic e y p e s la cfrM_ 3a O/O : T tanda. ¿írigicíá c/cí vftr^'cc al foco p. LA ELIPSE, i teñe Como ecuación Q . <x-/»? a* jy-K )1 _ i b1 “ XJdndcM,*) €S «/ centroây b longitud de ¿ossemiejes LAHlPERmoLA^tem como Ccuauon <*0 ™ ' Cx-h^ o1 (y -k )2 _ » ”b* ~ Do/>de {*,k) es el emim^ a y b Longitud de ios Semiejes. Sólo fines educativos - FreeLibros Moisés Lázaro C. - ® — — Jfh jG b rtx tC o tm € n tZ ¿os planos y szrniplonos son c/QS/yuatdadescon Z *o n'a b/cs} pt/e paeáv) s e r de ¿as jormas : í ^ V * < ^ l F (*, y ) > O E JEM P LO G P E F/C Ó V DE PLEN O S y S E M /P ¿ A A FO $ <>4 x * +• y Z F (*,Y ) £ O F (x,y) ^ O 2 x - 3y - G £ O PLANO: circulo de radio rs 2 S£A^/p¿>a/vo y2 t C x - A <0 y2 ^ 4 x - 4 Sem 4 x + 5 y -2 0 í o <o r 'L A N O iplen o rínter secc ión de cin-y V co s e m ip lo n o s . ) 3 X “ 4y * J2 3x _2y _ 6 <-0 X >„0 Y >,0 £S/<? ¿¿PO ote l#£CUACtQAl£S LIN EELES mos var/ob/cs d e dos Ó pertenecen al estudio de la Pqogaa MACION LINSAL O CUrSOS C0/700/0^05 CO/7 €/ OOftlbrC de IN V ES T IG A C IO N O PEHúTlVA OBC/3 ION £ S . Sólo fines educativos - FreeLibros O T£OQ/& O T LdS ________ 3. ._________ Relaciones de ÍR en JR ¿ jrá f ic a de a n a | Q g f / M i c i O N |Sz Llama f \ < i ! o t c i o n d<¿ ¡R g r Áe ic a oe c/a/a /^¿ a c/O/y d e m IR /p en IR al conjunto de pun lo s cuyos coordenadas sa tis /a ja n dicha retoc/oh. Donde no olyidemos quz una re ia u d n puede ser de la form a : F l ^ , y ) : 0 i n e s d e io s J o r / n a s : F (*¿Y) < O } F ( x ^ ) £ 0 3.1 ■• " d is c u s ió n V P (x ,v ) > 0 in zc u a u a ¡ F (x ,y )> ,0 . . d e la g r á f ic a de i una (C O N S TR U C C /O N 0 £ CURVA s } r e l a c ió n fZoclemod sdefA xir Q JP/xrv- Jra z o r ¿ t /om/iccr xte Jpnxx Jt<Á40.uUñ%. F ( X; V ) “ O pa sos : ‘ ‘ * ( j f ) DETEQMlNáCfÓN P E ÍAS INTERSECCIONES CON LOS EJES COOR D&NAOQS Intersección con el eje X ! Sz hdez ; 5 in te rs e c c ió n con et eje y @ ) D ^ e hacz Se rzs u e lv t la ecuación x -o A a lo s x • " 2)éte aumpjir/ii Je yoropoáiUcm. <*/ e/e Y S-tSe ¿ju.mp&r¿t Jo. yorryocrúcum. Simetría con respecté Simetría con respecto ai origen: 2)eóe /xtmplirAz Ja . ^moyooixciem. d l t e p m in a c iq n d e la e x t e n s i ó n d e la c u P va F ( x ; o.) se resuelve la ecuación R -M IN & c í Ó n . d e l a s i m e r n í a o e l a c u r v a c o n r e s p e c t o Simetría con respecto o i rtjz @ ) y ro A e je s y - O F (o , y ) z Q al o r ig e n F ( X f~V ) - F (* y y) F (-x ;y) - FCX, Y) F ( - x , - y ) “ F ( x ; y) y Consto de dos pasos: C a lc u lo del D o m i n i o . C a n u to del R o n y o . © ACION DE LAS P C u a q / q n c S Ü E ¿AS A S IN T O T A S : ye/tf/co/és, horizonta les y ñfdtrtnc q u e ¿a curve* p u e d e te n e r. ^5) TABULA c/Ó/v ‘ Sg c a lc u lo /ico. (g ) tr a z a d o áPara Los d e la un num ero s u fic ie n te de pun tos p a ra ob tener u n a g/q adecuado. curva : M o p e o d e p a r e s o rd e n a d o s . zfe c io s de ¿os/ eyevc/c/'as p ráctico s tos m a s ¿mp>or ¿ a n te s s o n ; Cal cu/o de/ dominio C álcu lo del r a n q o T a b u la c / o h Sólo fines educativos - FreeLibros Moisés Lázaro C. — ® - ¿Por ro z o m s CQ/cu/or e l Q ) t d & i t i z o s J Sugiero D o m /n io y zl seguir <¿t criterio de l siguiente Q o n g o de u ñ ó r e la c ió n F ( x ; vl : 0 cuadro p á n x a lg e b r a ic a . : CÁLCUJjO DEL D O M INIO 'D E UNA RELACIÓN DE ¡R EN ¡R 5c despeja uy * en términos d *"x». CASOS DOMINIO FÓPMA y 0POI//VOM/O = a 0f O j* bo.2%1*-■4aftx71 08S£GVAC/0#£S X € <-oo,oo> Q/C/3Q , 77CZ* ® PA/Z CUADRA&A A ¿ x € / R / P f x j 0. Los valores reales de ' y -'2 2 “ <?<*) g>PAC/0/VAL X f íR - {*€ W /q m =o J j*(x) A Q(x) $on polinomios primos entra s í . Se obtienen efe M3c** Q{x) - O Son /os ASin TÓ TOTAS VEPT/CALES. CÁLCULO D E L RANGO DE UN A RELACION DE IR EN1R 5 c u X d esp eja n o s c te i'y ” *' e n /e > /n i' . FORMA CASOS D O M IN IO o a s f P v A c /o /v fs - X z b o + b / y + h j y 1 + ■■ + b n y * ® Y € < -0 0 , 00) P O LINO M IO b t € /0 , ® « 4 / Z C i/OOPAO . x x /> € '2 f z s/p(y) f ^ N Y € m / P ( Y )> ,0 X. ■* Z ííl - ¿os v ó b n s **y u 9 ^ « j a x Q (y > 0 P ac io n a y € f R “ |y€«/Q m roj i P /y ) Caso 6CNÉQAL : A Q (y ) E n general Dominio y z pm C |(y )= o As í n t o t a s son polinomM .sF de + GW * P(x) $cx) ^ zntonczs : r Dom ( p ) f) Dom ( Q ) 0 D o m ( R ) fj D o m ( s ) Sólo fines educativos - FreeLibros rea fes d e o b tie ne n son la s horizontales . Relaciones de IR en R 3.2 PROBLEMAS RESUELTOS Discutir ¿o groj/co efe ÍO relación J l z f (x}y) £ fRxfU / 3? f x y2 - / 2 r o j Q • S OL UC ION ( I ) EXTENSION ( g ) fN 7 £& S E C C tO N £ S a ) c á lc u lo d e l Dom inio y ¿ j z despeja, " y De X 3 + xy2 i y 2 - Q cC)Intersección con ai EJEX ; Se hoce x- x3 y2 ( x - i) CON ¿OS E JE S *n lo ecuacrpn u<*/$jrr :. x x1 f 0 -0 entonces y2 = * ¿ x y 2- y 2 yro -o '■ zO x :0 Cste despeje Sirve paró obtener el y =íx\ DOnnñtQ y porO- b) in t e r s e c c ió n con e í e /e y : h o c z x -o tabular. en la Por ser ai caso B : e c u a c ió n : x 3 f x y 2 - y2 z 0 } entonces : o f o y x e Dom(&) o (H ) - a) ^ X £ [ 0 ; l) Por Se/ C¿ CASO n nociendo S/iHrrg/AS ; Simetría con re spe cto o / e j e X : De be ser : ♦ P(*,-y) ! 7) ene como denominador x- 1 , x - j z 0 obtenemos í'o ecuación d e lo z O . Z x 3 *-x{-y}2 _ (-y)2 - x 3 f x y 2 - y 2 Por lo tonto ; * F ( X; Y) . es simétrica con raspé cío ai 2/eX. manto v e r t ic a l . fbr lo tanto b ) Simetría con respecto-al ejé Y ; D o m (ñ ) z j *€/»/_ x c [o;l J cumplirs* gue\ con una ASINTOTA V£ñT/CóL: X -l -O . . ti i) b ) C a lc u lo det Pongo r* 5c despeja .x D z : x 3 + xy2 -y2 Co/77o vemos to m o "y >} itS c u e n ta , q u e ; r -x3-xy2_ y 2 r PU;V*' P f -x ,-y ) (jv )' TEButAcroru p ( x ;y) . . y g p o f íz o . =+\jE Z **-1 es ve/ qué valores asignam os a " x ” valo 9 ue pertenecen al intervalo ad rem o s te} pues no podemos despejar “ x ” Cuando /£ (-x)3 + [-x )y 2 - y 2 /Vo fe simétrico con y e Y. P (x ,y ) - c) S//77ef^á co/7 /-especio Qtf Q r i ^ e n ; N o exj§ z O csifo/Jces ¿o 9 ue hocemos P i” * ,* ) : Debe • y nos £a/?qó ( £ ) z ‘ y e Sólo fines educativos - FreeLibros Q.3 í o.S í 0.5 0.7 Í2.G 0.9 í 2.7 Moisés Lázaro C. ¿o ^2^ D is c u t ir g r á f ic a de la S 2 j (x,y) r e l a c ió n € foX/R / yx-x2 -l 20 } SOLUCIOM el eje y . (I) E X T E N S IO N a) Calculo del dominio £ Se despejo 'y * yx - x z - J Da ~o Por set el caso ÉL: * a ) Simetría con respecto al eje X : <=* yx z x* + 1 cDam( x x€ 5 ^ ti) De Cálculo d e l rango yx - x 2 -1 =o W xz - y'x - o - -b t\/b2-QQC 2á v (V ) y é- 2 5 z hace o - x 2- i y z o e/> ro x* + J : o & x-tJ-T $ imaginario que no h o y intersección con X . ti) In te rs e c c ió n con el eje Y en (a e c u a c ió n entonces : S e /? a c e x :0 y x - x 2— J - 0 0- 0 -í X ' - * 2*1 V x -x 2 - l ro , e /e m -l zo b :0 $$ m - 1 -1 qs y z lx :o & -1 2 O .Lo cual in d ic a Que no hoty intersección con Sólo fines educativos - FreeLibros -hO yr x : TA S O LA C/O/v X a ) In te rs e c c ió n con el e/e X e/ D£ y2>, V IN T E R S E C C IO N E S Lo c u a l in d ic a mx2 +bx - x 2 -i= 0 .<**► c=$ ye. [ 2^ 0 0 ) 0 < - o o ; - z ] €/7&>/?ces: z m x + b yes yx - x 2 - i = o , E n to n c e s ¿a' a s ín to ta y >/ 2 ¿ó e cu a ció n y <=> {m -J )x 2 +bx - I z o <=£ O (H ) de la curva Sí//7jxy*¿)x - x 2- j ro don y 6 #0/790 (S) ol e/e y : F .(x; y) . //O e x i s t e asíntota : La recta asíntota <=} £ ofespey'o‘*x *’ r' $e Usa/ /o {ármi/lo : Simetría con respecto P ( - x ; y) /R - { ° ) C Q n ASIN TOTA V£fZTtCaL XzO tr} P { xt y ) . Nú ix is r c £ - -* 1 t L y 7 & (m ) SthñTñtAS -2 -3‘/3 -J -2 -y? -yj -3* -*/4 Yi n Vi A% Vb 2 ^ Relaciones de IR en IR (3 ) D/scut/r /o gráfica de La relación S = J (x,v) € /fe2/ yx2 - x - 4 y ro j . SOLUCION! ( l ) ¿XT£/>/S/OA/ a) cálculo de/ dom inio ~ /3e despe/a y D e fot licuación y *2 - x - <4 y r O - <=> y (x 2- 4 ) - * * **-4 D o m (<5 ) <=> x € /R - \ x2- 4 = 0 } Enionces, * € . ÍR c o n cfos a s im to t& s v e n r tc & L e s J• r^c = -2. (xs2 6) Cal cu/o de/ rango •*' /&e /de^peyo. “ x 3> D e /a e c u a c ió n yx2 - * - A y Luego: y € £q/?ô(S) <=> <z> <=* « O O i - 4(yK -4y) >, 0 A 2y a i -/■ 16 y 2 y € /$ . 1 í >/l- 4 ( y ) M y ) x 2y p o £s¿a proposición es Verdadera y £ o con t//?o asíntota horizontal y - O <=> ( H ) ///ífg S gC C /O A /fS a') C 0/7 £ 7 e X h/accr e/ y r o e /7/o e c u a c ió n : yx2 -x - A y r O O £>) C 0/7 e/ e je Con <zi atiben La curva poecl por (op) . ( m ) $ i m e t p ./a s : 7^0 c d s t c s is e ó n o s con r e s p e c t o 'Pacto ol oripn. Pues F ( x ; - y ) t / í x ; y) CS) ta b u l &c io n : . O x r O. ^ y :0 . y - o e n ¿a e c u a c ió n :y x 2 - x - A y - O Y :P la c e r . c) - x - O - Ó - 4 |-3 */.5 O - o - Ay = 0 * • * o l eje X , 0 / e/e Y /?/’ con- /es. • R -x /y ) ¿ J.5 Sólo fines educativos - FreeLibros £ { - x ,- y ) :£ P (x ,y ). Moisés Lázaro C. — - ^ 4 2 ) — ------- — --- ----------------------------- ( 4) D¡SCutif I q La ecuación ; ^ : ¡ (x;y) € /R2 y^yx2 - 4 y - x 2 =0 j gráfico de S O LU C IO N (I) E X TE N S IO N / a ) Co/cu/o : £)e La ecuación Entonces'. <í d e / dominio y íe d e s p y a y yx2 - 4 y - x2 : o 3c € D o m (R i) >•> y= <=> y(x*- 4 ) z: x 2 4=£ x £ ÍR - | *?-4 - ° } a-\ JC£ J R - { - 2 , 2 1 con dos a s í n t o t a s yx 2 - 4 y - x 2x o Entonces'. y € R a n g o ) V- J £: °) >;o *=> , con A S IN T O T A v- 1 = 0 . * Con et E J E X : hacemos y r 0 e/7 /a ect/oc/’on e je Y : h acem os x : 0 e/7 ¿á-ecuación (f f l) C0/7 el orig e n : 4 a 5iM£m/As : ccrK a -x 2 :0 <=> x : 0 . O - 4 y -0 =O soasa. &or ( 0, 0) F ( * ,y ) z y x 2 - sói HORIZONTAL yx2 - 4 y - x 2 : o => c) 4 y -x 2 . entonces., P ( x , - y ) r - y x 2 ¿ ¿ y - x 2 . £ f-x ,y ) z yí-x )2 - 4 y á) (U ) í-x )2 - y x 2- 4 y - x 2 . ^ ( - ^ y ) ~ £“(Xj Y) ? e n to n ce s s/m etrico co n /e s p e c io a / x< “ 2 T A B U L A C/O/v ; X -2 4 x < 2 -A , -3 -25 -1-5 - J 0 '•3 . /-8 2.7 -1:2 - 0.3 O Sólo fines educativos - FreeLibros e je x>2 1.5 2.5 3 - 0.3 -/.z 2.7 /-8 /.A I _ __ * =±^/S -0 y x 2- 4 y o -O ¿>) Co/? e/ 2= _ 4y x2 y -j -4=> x2 (Y- i ) x 4 y ^ y e <-00 ,► ®] ‘u < l , + oo)> í n ) Av r f ^s f c c / O / v e s v e r t ic a l e s = -2 2 h ) Co/cu/o o/e/ s o n g o .** jd e d & ip y O L '* x ** D e /q ecwc/cv? x 2-4 d=> 3.5 y . y - 0. Relaciones de IR en (5 ) o istu t/f la g rá fica efe ¿o re la c ió n S = j C*,y) € ffi2/ y2x - 3y2 - i r o j S O LU C IO N (I) E x t e n s í Óh • o ) Cálculo del o lp m tn / o /b e . ¿¿edpyiaf* y * Z)€ fa eci MuÓn: y2x - 3 y 2 - l ' = 0 <=> y3 ( x- 3 ) z i <=> y2 r Entonces: x € Z ) o m ( s ) <=> ^ o O . <5 <=> Y - í " ^ ¿ 5 © X € < 3 ,+ o o > Con «/no A$tf<tTOTA vean c a l : x - 3 z o 6) Calculo del rango /° X Íe De Inecuación: “ x >> y 2x - 3 y z - i Entonces: y € Rango ( S ) :0 y2x = 3y 2 + l <=> y € / R - \ y 2r-o}' ^ ye R -| o j- x' - c o n (//vü as/a/tota wo«/20/wtaíl: . y =0 Ca) //yrgA sgcc'/o/vg s: o ) Con ai ñjs x : -Se toce y r o en /o e c u a c ió n . y2x - 3 y 2 - i “ o o -o 6) Con e l- e j e Y : 5c Aace x : o F ( * ty) r . /Vo ex/s¿e. en to ecuación y 2 x - 3y2- 1 zo =V BU) stMETÑ/A: / í ¿ - 1r o O - O - I ro . Ato «x/sfe'. y2 x - 3 y 2 - i P(Xj-y) r f*y)2x -3f-yJ2- i = y2x - 3 y 2 - i E n to n c e s :• Pí - x , y) z: y 2(-x) - 3 y 2- j r - y 2x - 3 y 2- l . S e c u m p le qutt ^ (x ^ -y ) — e n to n c e s e s s / ' n e t o ’c o con r e s p e c t o o i c j f X . J D T&eULACtOM x>3 X >=«\S . 3.2 í 2.1 3.5 4.5 £1 5 + a8 £0.7 Sólo fines educativos - FreeLibros Moisés Lázaro C. (g) D'Sut/r ¿a gráfica de ¿a relación S : | <*,v) € /fc2 / x2y2 - Ax2 - A y2 r O J SOLUCfQlM ( I ) gxrf/vS/O/V : a) Cafe uto ote/ dominio r~ ¿ U /de4/oyioJr y *’ -D* la ecuación # 2 y 2 - 4 x 2 - 4 y 1 — o C=^ y2(x2- 4 ) n 4 x 2 <=0 .y2 ¿í/e<ô: x € Dom (S) <=¿ c=* 2 ,A* / x2 - 4 > O x1> A <=> X >2 V 2* <r¿> y .= + * v*cr x <- 2 <=> x €<^2 ; +.apy U ^-*oo >- 2 ^ , con as/* tota $ v£ñ Tícal£% " , j V..<" X í - 2 I x r 2 ¿>) Cd/ca/o ate¿ ranô r* /dz Jc¿e¿f>y'a. ** x 5> I X Zae c u a c ió n x 2 y 2- 4 x 2 - 4 y 2 — O ^ X2 ( y 2 - 4 ) . 3 L y 2 ‘ E n t o n c e s '. Y € R .a h g o ( S ) <=> Y 2 - 4 v—y > O v2 _ X — -a s ín to ta s < = > ( Y - 2 ) ( y +■ 2 1) > ^ n r1 ^ •v—y s X, y^-i. H O f f iz o n r A tE S : y 2 - 4 = o y = te O -2 —O— <=> y € < < - o o , - W ) S^£JA/A : Si 2> U C _— _4- -_2X_ /—■" •* VYz- t 2 ,+ o o> .. 2 -O - © F (* ,v } - F (x ,-y) = x1 ( - y ) I - A x 2- A ( - y ) 2 z © x2 y 2 - 4 x 2 - 4 y 2 x2y2 _ 4 x 2 _ A y 2 . F ( - x , y ) iz ( - x ) 2 y 2 - 4 ( - x ) 2 - A y 2 z x2 y 2 - 4 x 2 - A y,2 . a; F f x ^ y ) = p fx ,y) £>) F ( - x , y ) c) F tX jY ) • e/tfooces e s s im é t r ic a con / - e s p e c io o í e/e X - e n to n c e s es s i m é t r i c a con r e s p e c t o a l eje Y F f x r y \ r F Íx ;y ) (in ) IN T E R SgCC/Q/V^S : e n to n c e s es 5f xro s im é tr ic a } e n to n c e s Sólo fines educativos - FreeLibros y r con r e s p e c t o t'mofînorr/b ai . a ríg e n . Relaciones de IR en ÍR -0 ( J ) Discutir la yrófico d é la siguiente relación ; 5 = j (*>?)€ ffíx/ñ / - -x 2 - 4xy-h4 y=o| X2/ SOlucioM ( I ) E XT E M S ÍÓ n d ) Cate uto del dom inio A /Ój¿ dcópeja.u y ** x * y - x 2 - ¿txy + U y De ÍCf ecuación - O <=* y (x2- 4 x * 4 ) = x2 y: <=> entonces : b) * e D o m (S ) C=$ x c /R - ¡ x-2 z o } £9 x €/£ ~ j 2'J Cálculo del ñ anga /* j con una Asiruroro ye P - t /c a l : * - 2\ xíe dedpe/xx ír x ** D e l a e c u a c ió n x2 y - x 2 - 4xy * 4 y : Q ^ (Y - i)x 2 AsH Br - 4V c - 4^ - 4 yx * 4 y = o - B±s/a2‘-ÂC 2A A y + V 1 c y 2 - 4 ( y- i ) ( M x : ------ — ------------ ---- — 2 (y-j) x- ¿*y t ¿ 4 ^ ^ 2(7-0 Entonces : (jO y c^ o/ ?ô Í S ) IN T £ & S E C C /O f V E S \ ( n i ) S/M £TX2/4S : (15) Ta £=¿> / >, O A [o, +cd^ ^ y f S« x có j con u n a a s í n t o t a } en ton ce* y =o . x >2 -2 0 J/z 1 0.36 0.25 0.1 0 0.1 2 -3 -i /■5 2.5 9 25 3 4 9 4 5 G 2.7 2.2 y=i C *5 *4 -J -Z i Y1- i h o q ./ z o n t a i : ¿ o c í/z 'v q /yo e x is te n . X 27 t 2>^ ~ Y - i :£ o : b u l a c ió n x - i Sólo fines educativos - FreeLibros pa sa , p o r y -i -o . ( 0, 0 ) Moisés Lázaro C. E C U A C IO N E S E n coa*» uno efe/os sgtes ajarc/cios, F A C T O Q IZ A B L B S foclonzor lazcuac/on Correspondiente y trotar Id %r áj /’c a . (ñ ) /R2/ x } -x ? y S O L U C IO N Zxy1 z o j . '* *3 _ x2 y _ l x y 2 = ó factor icemos la e cuación. X ( x * - x y - 2 y 2) r O x (x - J y ) ( n f v ) : o » V x - 2y =o * =° í v **Y*O ! ’ © ¿or (¿cucró¿n 0 e c u a c ió n 0 es uña re c ta q u e p a s a p o r e / o rig e n , la e c u a c ió n 0 C$ i/n o re c to que p o r e l o rig e n S © as e/ ¿y£ y La (? ) \ = j x 3 + x 2 4 pasa 2xy 2 4 2y2 -M x - U . r o } S O LU C IO N p a c to r/c e m c s ¿a e c u a c ió n : x* + x 2 4 *2 (x + iy 4 2x y 2 f 2y2 - 4 x - A 2y 2 ( x 4 l ) - (x + l ) ( x 2 4 2y2 - A ) A (x +i ) - O ± O' - o x +• 1 - O v x 2+ Z y 2- ^ ^ 0 * ^ © 'L a e c u & c / o n . 0 La © (I ) e c u a c ió n es. r e c t a debem os v e rtic a l : d is c u tir la x f i : o ^ x : - l . l ' £xr¿r//s/av a .) C a l c u l o c / e l d o m i n i o y / $ £ d e s p e j o " y " De la e c u a c ió n x 2 4 2 .y2 - 4 =0 <=£ ¿ y 2 z: 4 - x ? £=> x 2 é£ £$ y 2 r i (4 -* * ) VF ¿í/epo / ace Don) í=* 4 - x 2 )>,o » x € [-2 , 2 ] <=> Sólo fines educativos - FreeLibros -2íx£2 ® Relaciones Jde (R en R 1.47. £>) Cálculo del Rancp y J e despejo, *' x n De /o ecuación x2 4- 2y2 - 4 r o Luegot y e P ango & x 2 z A -Zy2 A - 2 y 2 >, «. 0 ^ x = i\/4-2y2 ty 2 ¿4 ->fé¿x¿váP x 6 H *\, / f ) ( j i ) INTERSECCtONE s OL) Con aleje X * Se hace y - o a n ia ecuación x2 * 2y2 - 4 ~o ' =$ 6) Con el y e y ( m ) S í m é t q /a hocé x z o : A l P { * , v) z ^ (x ,-y) r Entonces : - 4= 0 <=£ x2 £4 <zn laituaci&n x * + 2 y 2- 4 ro => 0 -4-2y2 - 4 :0 x2 + 2 y2 - 4 . P t/ts¿ a x2 4-2 ( - y ) 2 - 4 P C-xr y) - (-x)1 + 2 (-y )2 - 4 r x 2 4-2 y 2— 4 ; entonces 2 $ simétrico -f í *,»). con respecto al E/E X . entonces es simétrico con respecto al EJE y . Como P - x •- y ■= r x,y ^ ■entonces es s>me trica con respecto a i OMiGEn c m El Gr á f ic o de Las ecuaciones x + 1 :o ,V x2 + 2 y ^ - 4 - 0 , s e ra : SOLUCION POc toncamos ta ecuación 9x ( 3 X 4*2y -2 y ( 2x - 6x2> xy - 2y2 + 7x 4- 7y - 3 ~ O $um*n¿o : 7x 4 3) (Jy -3x y 4xy -O y *»- * 3x+2y-]rO v2*-y.*5=0 S«rtH»/KÍÓ : fy xy Sólo fines educativos - FreeLibros ^ xstt & ystvf* x 2 f 2 y 2- 4 = x2 f 2 y 2 - 4 z x 1 4-2y2 - 4 ti) Como F.(-*,y)= c (x; y) y2 z2 e<«/ac/or> e i F Í-*,Y* - (-* )1 4-- l y 2 ■— A á ) Cb/no F (*,-/> z P (x ;y) c) x2 4- o -o MoisésLázamC .,( Donde: Lo ecuación (¿> 3 x + 2 y - l - O La ecuación © «s uno recto .•.rot^tamábS z Q, es í x - y +3 otro recta . Toóistom cta Ó/ EJERCICIOS: Grupol D h c u lir lo pondiente. *ca de todo uno de las sigtes relmuoaet ^ ’ .z ^ Sj = ) íx,yi<¿ /J?2/ x y - 3y - 5 r o j (Q curva co/tes •■■ . — **«U»roJ S2 =¡<x,y>€/R2/ yx2 - 2Sy - x r o | £ 2) 4j*+4u -o j \ r ) (x,y)c/£2 / yxv - 2 5 y - x 2 s o ) S5 = l < *,*> € /R2/ * y - z x - y -2 rO | -o } S6 “ | (*ly 3 € ^ 2 / x y - 2 x - 2 y y - 2 = Sl t r oj 0} roj 3 7 - J { x ;YH / a 2 / x A ; - 9 x * - y :o J S e % í s | i ^ y W f c ^ / x - 3 = o }4 58 =•j•(*,*!€/£*/ x1 - xy + 3 y = 0 } 5 9 = | U ,y V € # 2/ x y * > x y - 6 xT~3 =°} ;o | ’ S 30 = V ( x ^ t C l í ^ / y ^ A y f Ax Syo =| tx,y )€ ^ 2-/ x 2 + y 2 -2 5 = 0 } 5j_, = •Su = j (x ,Y > € / ® 2 / > 2 * y 2 - 2y-3 : o ) $& = j t*,yK tfi2 /’ y S 3 3 - ^ Ix,y>€/*2/ Srt r | c*,y) €.-**/ 4 x 2 * 9y2 - 36 - o j S27 r \ (x (yyfe/i? 2/ A x 2 - 9 y 2 -3G - o ) 5n 3. | c'*,Y)'€dl1/ x 2- y 2 z 4 ] =J } x * 5x”3-2 :ó). } !*,*)€ /fc2/ Y-«*-J zOj \ fc^ U lR 1/ * 1 -**-** * ¿ y - 3 ~o{ S j r - J ^ m ^ / x y ^ A x 2 - 3y2 + » x =o } 5 mr J (x,y ) e m 2l X2 + 4xy +y2 * 2 x - 2 y - J r o j S ^ p | <*,»>e # 1/ -o) S*¿» ^£ftgv§*&*/ A*2-y2 - q ] St4 - j «x,Yí € /K2/ x2 - Ay 2 - 2x .* J6y *1 r oj ;r i t * ? / y1 Vixx* - x z r o | - 3X+Z-1 R7¡ y-< t* V -ó } Sis- } ( * , m M2/ x 2 + Ay2 - 2 x +2Gy ¿ i zo f S)9j |í * , y ) € ^ 2/ y2x - y 2 - x =oJ r© } ^ U,Y)E /B2 / y- 2X :o| S« - | (x ,y )€ ^ 2/ xz +y2 -zx ■f-cy - 6 - q | S* r -8 t»,vU * * / 6xt l-2y2 f x - í y s © | * A*2 + fOy*~á* + I! - € r <*f $»=)*•»>** A 1 / *1 #y, - 2 y y - í ro j SM z | « » » » « * V ^ l >yl - 4 * y - < =o| Sólo fines educativos - FreeLibros . - Relaciones de IR en IR & la la cione s ote ÍR e n ÍR. con '¡fctlor C r i s o l uto 3 .3 yr)troc(uccion C uondo <zí estudiante se encuentre* con problemas donde aparece el ya lo r a eso lu to generalmente J no Sobe q u e h a c e r* . £s¿o / ocurre t porgue sen 0 “* cilhmente Se olvidó déla definición o que nunca antes lo aprendió correctamente. Por esta, razón , m e he permitido en escribir nuevamente ¿a definición y hacer muchos eJtfD p h s a l re sp zcio . S e a 0 . c u a lq u ie r e x p re s ió n a lgebrotrcoLj e n to n c e s e l v a l o p a q D 6 P //V /C /O N Q de socoro a } se d e f in e = a , sí -o l í o ■a , si a <o { 5e o La mismo ex- ; £ l valor absoluto es cómo sigue ; presión que está en barras ; 5¿’ d/c/ja ex- ; ¿ l valor absoluto es igual al inver ,U ; 'iQwxúivópi ¡a expresión e/? be*iras es presión es pos/Y/Vo o cero V n e g a t iv o * EJBQCÍCi o s ^ t r a f ic a r cada uno de ¿as siguientes relaciones . H a lla r sudominib y rango i (5 ) * r j (x,n c /e x /s? / y =:lx 2- ¿ | } SOLUC tOM En primer•/¿/$?or , definimos el valor absoluto ! í y = |x*-4¡ : | x 2- 4 , Si x2-AVO Donde : x2-4> o v x2> , U x>,z v x*-2' <,»> ] _ (k 2- A ) , St x2- 4 < o Donde ; x2_ ¿ » x o ^ x2 ¿ 4 si x£ <-oo,-2]u [ 2,+co> x2-4 , -* 2+4 , si x Z <-2,2> Sólo fines educativos - FreeLibros x . e < -a o 4- i } - 2 < x <.2 u L2,oo> <=* *c <-*,2> Moisés Lázaro C. Como vemos io relación' ~ |xz-41 H cf/Y/de c/j la unión d t dos &£iác/o*£s cométete m ffédiferm trnSj q u e son] z I t ^ W ^ / y i x ' . A ^ x í í - o o r ^ u í 1, ^ » ) ] ^ j l*,Y)( « ’/ y r - x ’ + i* £1 gró/fco de & =#<#j u /? 2 es : ' O W » W S <~€JQ,GQ> /&»!fOP3) 3 [0,00^ © S = { ‘v i e ® 2/ y : | ( x + | x | ) j doluckdn : De/motmos e/ vo/or ob soJuto Ix I | ( x + k) } sí x >,0 y = ( (* + 1* 1) =| i(x -x ) , sí xeo x € fO;Q0 > y = O , >€ <-oo;o> (í?) ^ =j (¿¿y)**2 / y4 |2x*l | =o} SOiucion ; Qzfinir «/valor absoluto y + |ax-i{ : o «=» Í \lx- ] | . y f 2X-1 r o } sí 2x- j >,0 y -2x4-1 = o , SÍ 2x-l <Ó - y + 2X-J =Q , SÍ ■ *>, */2 Y - 2 x 4-1 ro } Sí X 4 VZ BQfíóe: X va 1 00 Yr-tx-f 1 O -J -00 Di y +2x -I : O 0e y-2x4J : o y =-2x 41 ; x >,V2 y - 2x-J , x < ^ X y = ix -i x»V i y» 0 -«6 0 -1 -O0 Sólo fines educativos - FreeLibros Borní*) = x€/& *«090 (*) = ye <-oo; o ] Relaciones de M en (2 ) S : ¡ (* | Y v e «* / so lu c ió n ix i + ly l = 2 } jytfiñpff*0$ coda valor absoluto . A s í obtemos 4 ecuaciones dijere ¿es Vzamos: x*y = 2, -XVY I* 11 [y( s 't si *>,© a y>/© r 2f' s» x<0 A YVO = 2, a «4 x -y s v<o -x-y 2X#»(S) = * £ 1:2,21 « ( 5 ) ^ 2 = (*,*>€ IR1/ , p - * 2, I ** 1*1*1 vzJ W 17? > * Ron 90 a y € [“2,2] , 2 **>* \ £ n c s f e c o s o , atetem os d e s a rro lla r (OS restricciones Aj/^ tendremos que : jx I ¿ i lx i > j Entonces t lo relación & <£> x > i « v x <-1 xc [-j y lx |> ] . ] xf m <-oo,-i > j j se puede expresar def siguiente modo: ( £ ) S r j t x . m f R 1/ lx ‘ y l En zstc -i < x o. Entonces: j x-v| z4 €* x-y : 4 V V x -y - -A (t> -4 -A Sólo fines educativos - FreeLibros Moisés Lázaro G. — 0 - Como poetemos apreciar t ¿o grajtca efe lo ecua don |x-y { ~¿4 t i lo unión efe los gmf/cás efe ¿os ecuaciones: ® y © *-ys-4 . X- / k ‘X+yrA y| (n ) ^ ~ \ c*>»« /s/ Y 4 (y - 1 1 + x* - 3 3 0 I SOLUCION ; y -i + x2 - 3 = o , Si y -u o - (y -i) + x2-3 = o > Si H < 0 |y-i|+x2-3 =o n < , \ x*r 4-v \/ i........I -2 j 0 x1 +y-4 i | (f) x2 - y - 2 P o n g o cte ¿a e c o a rc /o n (¿ ) ; -ó if l -1 L *t V i y * ' YM = O V si 3 ** *2 ,Dom(M)~ *« [-^,V3 ) y ,o A Y>, 1 Y + 2 > .0 A y CX rí4 A Y U V ^ -2 a y - 2ÍY í l E J E R C IC IO S - 6 0 UPO 2 ■Grojfcor codo uno Pe ¿as siguientes ecuodones . //o/Zor $u correspondiente c/ommto y rango . 0 y~x* -}x | : 0 © v = t¿T ® y = x fx| © y - Zft~3! Z li © ® © y2 -A jx| r o x2 - 4 |y| : 0 © y = ixi fx t 3 ® y r y r l*- 2 | ® y2 - © 1x2- y J =4 © |x2- y 2 | r 4 0 |y-2 I - X 1 4*2 © x |y1 - y - 2 =0 © |2x - y I l A © Y 1*1 -Y -2 : O © |xy | = 1 ® IY-3 l - 4 x 2 + 5x x-3 =ó Sólo fines educativos - FreeLibros |x 2- 9 J t * -4 I r o : o < V Relaciones de IR en ÍR < § > - Srájica de$.ÚQcionesoti'maks con dos Variables Atelos t ¡éemipLanosy (Planosen IR1 3 .4 © gq &eica o e nECTAs En fc2 Tofo éeuacm ■tmeot- con dos variables efe la forma Ax+ay+CsO; tiene comp^ró/ica una recta en IR2. Pgra graftear una recta H necesitan sólo dos puntos pertenecientes a la recta. \ejem plos (g ) Gráficar la relación !R z j txfY) e f%2 j 2x - 3 y - & z O } 501UUON X y r 0t -2 Busquemos fos puntos 3 0 * ya*i 2x - 3 Í O ) - 6 r O ^ * r 3 ¿DOtf?{^ = X€fc P a n g o (M ) - ye m = j <xfy) e /á 2 ¡ 2 x - 3 y - 6 G r a f ic a r z O ^ x | J s o lu c ió n ; Co/7?pore/5705 ¿os ¿o re la c ió n J k . jeetaciones y 3¿ y T ¿ i ‘. t ie n e n ( a m is m a e c u a c ió n . La diferencia radica en sus dominios. Jîentras que el dominio de 71 es iodo IR de jZj es un su6 conjunto del dominro de E s d e c ir : f ¿ , + co> . C Z í R .... oomtnp E s to s o n ¿os casos de D o m (£ ) lo s ¿ la m a fo s : Q E S T Q i c c /Q n Por lo tantoj e¿ gráfico d e ¿a ecuación 2x - 3 y - 6 -O Q£L d o m in io paro x>, i X € C l,-K )D > «V i X y 1 -V j 2(fl-3y-6 =0 t* 2 -V j 2ftW y-0r© +00 ♦co y 'fs.-a/á oom (£ ; ) r x €'[i#+Qb)T « 0/790 (*?,) z y e [ - M > Sólo fines educativos - FreeLibros señó * Moisés Lázaro C. (S S ) G rafica r ¿a re¿oc/on z |<x,n€/ 8 2/ 2x - l y - G : 0 , 1 < * kC j SOLUCION Como v « mes ¡ f e «cu©*/©/? c/i- 2 *s /o /»*/»o gue en M y J t2 efe ios eyerttetos @ 9 </e e/ dominio cíe la £/ g ra f/c o d e M % esém ^**sr*//*G/oo a"'intervalo *€ 0 , 6 ] * empeca en x r i y termine* es u/> SM8MEHT0 D E & £ c t a ** n s 6 . y@ } ■ 4t rA0 Ul*CtON x j y -4<* 2 &om (-*2) - *c < i,c ] Gongo (G2) z y€ <~*/¡ , 2 ] ( 2^ Gmf/cor te mímiéñ solución Z j ( * , Y ) € 2 x - 3 y - 6 r 2>U [4,?> } : Por se/* J?3 ono ecuación con dom inio restringido / hagamos ¿o sgtz tcrMoc/on ; r a B ula cíó h X -2 O tí y 2 -V3 4 */3 7 8/3 2 DemlA%\ = * € f- 2, 2> U C^,7> . 2 .2 .] yjj » v5 #o/?ôí^) - y € [-Ky3r 2/3> y [ ^ 3, % > © 0* QnÁnc a semíplanos Todo th&cuocian u n e a l con 005 v a ñ / a Qi e s efe fers formas Ax * # y f c < O Ax + 8 y +C ^ o Ax + B y + C > 0 A x f S y fC Son szm tpícm os e n í# }. Donde (o ecuación Á ic + B y + C z Q vmm a ser /o COTA Oe /o te/ación ( m f a ) y ios m ecuec/cm s Áx + § y t c > 0 v A x + b ^ c < o 50/7 /Cr5 R B 5 /O N E 5 (s e m ip ío n o ) Sólo fines educativos - FreeLibros Relaciones de ÍR en IR fíUST RACION CfAAr/CA {e je m p l o l \ £ i g r á f ic o d é lo J l = j (x,y)€yt2/ r e la c e n 2x - 3 y +<>¿o) es : D onde: - ¿O ecuación 2 x - 3 y + G = o La es la tnecvorcto'fi 2 X - J y f 6 < 0 d rt io ty v n t o A . cota *3 /o Q £G i¿N SOMBREADA. '.***• v *< C07A } u n a £ /r nuoóJro 4 rutees f p e r t e n e c e *jjw m plcr J l a . a l c& njM jn to y co rA - o tra * n rtc e a f n o 9</e e s ¿a r e c t a . f ° e r f t n e c c o í * e a * y jm á . P x ~ 3 y f6 ro — pe rttt* \± cc a l c .o y * t n ¿ o fl £ n c o n s e c u e n c ia j l*,vV«/»2/2*-Sy *6<-0 | - j<*,y)€/»l / 2*-3y+'6-=óJ-U J l*/Y)€/SV,lx-3y+ 6 <oJ t COTA EJEMPLO 2 Seo la relación b e g /o n 5 zjuync/E^/ x^+y2 <2, j # .. f inetuactáfit £¡ gráfico efe S n O u n EAL En c¡<xr dos e s to Lo 1- nec.e «i S- ilu s t r a c ió n 2S n o c o n o c id o cota d e l co n ju n to x2 + y2 s k } p e ro co n el n o m b re S no e s la p e r te . * Lo re^/bfl es <//? pía de cía cul o . fkmos pod do observar que una LfNÉÁ (recta ó curva) divide ai plano en dos regiones . y *, dos p o d e m o s o p te co so s; c. i r e . u n f e r e n c i a CONCLUS/Orj so m 8 upada neófones cvATfío nmtoNés tü£s me*&ves Sólo fines educativos - FreeLibros * j ~~® ~ _________________ Moisés tizare C. 3.4.1 J^é to d o práctico f & m Si “ JR * JO rm p s as F : uno relación da ffc en fQ a p re s a d o ( x ,Y ) fm -ficó r COTA ^SQMBñfAR ** teftexca a F ( *, y) £ O f F ¿ a c i ó n 7? 0 se û /V Pora ®s%> se & ( * ,v ) > 0 gsgion , F (x |y ) £ mtonces o , p o ro F (*,Y) - q . que satisfaga a ¿o relación M . — y Se reemplazo en lo 6 de los dos p a s o s : } es decir J a ecuación /o como uña inecuocion busca un punto (x O}y0) cualesquiera del plano IR2— pero CO TA Si (* o ,y 0) punto } < O 1*) G ra fic a r ¿a 22) ¿traficar ¿una Cfntcu&ú&rv { plano y sem /p ia n o ) relación ^ entonces Se sombrea 90c no P * . la q e q iq n donde se encuentra el lo Q E G IO n donde no e s te ' e l p u n to (x o ,y * ) . Si Cxo; y0 ) ft Ó Q ¡ e n to n c e s se so m b re o tx-o,y& ). de fácil sustitución* son ^ O J O : Los puntos del plano IR* (5?) Graficor lo relación (o,o) |(oti> y ( i p ) . 3 =•|(«,y) € /£* j 2x - 3y - 6 <0 } . SQ Lt/C /Q /v: /-br ser S una inecuación f seguir dos posos T 7o) G ra fe a r ¿o corA 4 « s abe/r /o licuación 2x -3y - G : O . X Y 0 -2 0 3 2í©V-3y-6~o £M =-2 2* -3ío^-G =0 «%*=3 A V , ¿memos que ¿o recta 2*-3y ~Q> c o j a a v d do al plano fk* en dos regiones:A>yB Paro e/lo pro vemos siel punto ( 0, 0) satisfa- 2$) Busquemos qué región ‘sombrear CQ a /Q imcumjón 2x-3y-G<0. Veamos 2ioi-3(oi -G 'co ;* ' E s ta propo tc/an <*s Como : (oto ) € A A ío,o) € S , entonce: vepoadeqA. £s Cfec/r (0,0}€ 3 se sombreo lo á&s/Ón A Sólo fines educativos - FreeLibros Relaciones de IR en IR oj El gráfico dz v S L es c/ £J£ Y . Dom(Sj) - j o} £0/790 cs^- ye#. G raficar S i z J <x,yV€ ÍRl j *^0 j SOLUCION Por s«/ S i ] ?) una d<Lsigtraídad; SCgu/r dos posos : Grafícar la c o ta decir la ecuación x - o . f es - A s í tenemos Que ¿a recta x r o , h a dividido 0 / plano 2*) (S ) « n dos regiones : Busquem os, es e/ se mi p ía no o io d e re c h a d e l x>o eje Y («£<3/0/v J52) . El S 3 - j <*,y) € ÍR2/ g rá fic o de S3 Graftcar Z>om(Sj) - * € [O j +GD> #0/790 (S2) - Y€ [R . y r O J >=0 J.__ es e/ eye X . DomCs3) = x€ Ik (te) x=o-í que regió n s o m b r e a r .’* L a i n e c u a ció n G ra ftc a r y &2 • iz * i: . # 0 /790(S 3) .jo} z = j <*,*) € /R2/ V ^ O } y Seguir dos posos: SOkucfÓM J í) Grap'car (q ecuación yzO 2?) ¿q inecuación y > o es el szmiplono hacia " arriba del d/e % #2 (pzgion Dom( \ ) = * € <-00 ,o o )} pango (S¿) = Y € [o; +od> . (n ) G ra ftca r S 5 r | (V > * Como pod em o s x >0 A y ^ o ) observar el gráfico de S 5 és /o intersección de S¿ y $4 de /05 e/erdeios 25 y 26 D onde respectivamente . S3 0 = S5 z l - r cu a d ra n te . 1 xyofT)( s§) = x € [o;voo> -j £0/790 cs5) - y € ro, +oo>. Sólo fines educativos - FreeLibros Moisés Lázaro C. ( S ) d*roftC&r T j r J (x,y> f ir2 / j < x 4 4 A 2 4 y < SOLUCtOKI ¿cr q r é f t k o Dom de (Tt ) = x# 7¿ € » «/ /’C c t a n y u l o AQ CD . < J ,4 r ] /?a/ôC5> = y € f 2 , 5 } 1 T j - { <x#yy € 0I2 / 3 , -i < X ^ 5 { it ^ -r* ($*) Grcrf/cor ».v. -J*■;■ 3D¿w».C7i) '= * * < - i , 5 ) /2a/?ô(Tj) = r € <-<¡o, 3] x:-i S ) G ro f/ c o r T j ~ j (X,Y) € /£2/ y = 3 00/77 ( T j ) 3 ♦ ^*= 5 * ^5j = .x c < -J,5 ] S Q o n g o a ¡) = [3 ] ( 3l )G ráficof X f’ r 7^ j lx ,y * € /£ * / x x (S?) Grctftcctr T5 r j (x,y>£ fH2/ x < 4J r/.j ñ •1 3 * 1 i** * x X Dom{%) z |Aj zm(r5) zx€<-ó»;a) &>fl$o<r5)zy€m S y ^ G ra ftca f = { (x,y)€/52 / x ^ y , £ 2x } So l u c i ó n ; ¿a relac/ón * ^ y ^ 2x es 'e q u iv a l e n t e a x^ y A V £5 cfccjr, la relación S gs /o intersección e/e /as Sólo fines educativos - FreeLibros y^2x sl /e¿ac/b/?es Sj y S¿ Relaciones de (R en IR S «4 f f / O U £ M O s LA M £LáC¡0*t S E G u /D A M S N T E f G O A P fC A Q LA G ELACtOH : X, 4 y $€füir dos posos : Sty jir dos pasos: P ) 6 rapcor ¿a acc/ocioh \ i-) Graficar Lo ec uocion : y r 2x x - y ÂaytAc/oW TASULACfOfx 22) Sombrear: X 0 y 0 1 i ¿ ( l, o ) € ( u y ) ftaspuesta: 22) ? 1 < 0 «*65 as £sto fthr% decirf quz hq s« sombrea ¿a región ‘ Pi ; 5X +*Ay 4 4 % : 5x^y > « g : X ^ o : ^ ^&ROA&£0.0 en el punto CV,G}. réloc/ones siguientes ; 200 Ri : 3x + 5y : 8x - 4 y ¿ a,o ) € /30 - 80 ^ S o l ye/o a/ ; Grafiquemos codo reíouon gpÁc/c a p£ /2j : siguiendo dos po sos ; 5 x + 4 y 4 200 J-) Graficar ia ecuación : 5 x f 4 y - 200 p ) pora hombrear f probemos si c/ punto (ofo) satis - m&uLáció# X 0 40 y 50 O /ace /a Y 4 2* 0<2ín f o< 1 Lusyo t$z sombreo ¿o rzyión doñdt esto' donde esto a¿ punto (1,0). ( 34) Grof/cor Lo intersecaron de ¿05 seis Sombreo/*: «espc/esta*. inecuación 5a +¿*y < 200 Sólo fines educativos - FreeLibros — Moisés Lázaro C ( S > 5 (o) * 4 fo> < 2oo Vbom m : O < 700 ***£$ V Como esYerdadeno ¿a proposiciónf entonces se sombréa la rty/on donde está dpunto (0,0). Goafko DE fíz ; 3x + 5 y 4 ¿50 l8) 6ra/icor ¿a zcuaciáfi : é (o,o) € 79) S om bre ar; TABULACION 3x f 5 y - 150 50 X 0 Y 30 O 3x * 5 y < *50 ? Pospuesta 3(o)+5(o> <150 0 OSO► £s V, entonces sombreomos /a donde esto e/ pt/nfo fo,o). G ráfica de Ñ y . P) Graf/car ¿O 5 x f 4 y V JO O ecuación : 5x * 4y -/0 0 2^) Sombrear ; TAat/¿¿c/cw X 0 20 y 25 0 ¿ (0,0) € 5x > 4 y > ioof R e sp u e sta ; 5f©M4foj > 100 Falso } entonces} do sombrear ¿a región 0 > loo donde esto et punto (o,o) ^ $//?o ¿o fo g ió n op<¿esta.\ G ró /rc o d z Ñ¿, : 8'X - 4 y - $0 ’ ] - ) Graficar ¿o e cu a ción ; 8 x ~ 4 y r¿&c/¿.Ac/o*/ X 0 -10 r - 80 y 20 0 29) S o ^ /^ e o r ; c' (o,o) £ pospuesta : S x - 4 y > '- 8 o ? 8 (o) - 4 (o) > - 80 o > - 80 ^■£sV, entonces sombrear la región don de es/óf e/ p<//7¿o (o,o ). . x >, o GR¿riCk pe ? 2 s e/ semiplano o ¿o derecho de/ e/e Y incluyendo af eje. y. GQáF/cn DE R q : -*aa=!=B5s=* a==a^ y >/ O y es Qj sem¡plano hacía arriba de! e/e x incluyendo al e/e >c. Sólo fines educativos - FreeLibros Relaciones de IR en IR D ado /K Ó * {Z ) ~ .2 * ¡ **3*2 la fu n d ó n Sujeto a los siguientes newtricc/oné$ : *»: . f - x j * *2 4 1 ^ 2: *1 t i * i 411 **< I X j + X* ^ Ü m : *i ’ » O *s t ' *2 D ^ o £/d. ¿ po/ü Qué va/ores de xi / x2 /a fmcmn /%m ¡ i) se hoce máximo |SOLUCtÓftf] fV e e je rc x b es cw « o s 2£A*| Poro resolver GQ&ztc&MMwr* l 5)G ra fica r é a te a s í e/ «4en<$3. la s ¿toco P lh N O Peo 6£¿M&c/ON ate 2 variables . é s t e problema f seguir ios Siguientes p a s o s : restriccion es ( ce**» m&tncóon et un $*mipf&no en m ^ o b íe m é n C o rv v S X Q ASCD £ j Qu<¿ es ¿o intersección d e la s cinco resfrie ~ 2?) Sustituir } ano por uno ; ftx*os /os ve///ce$ efe/ p&y/7o convexo Á8c¿>£ ©7 /o /t*? a'oír P tó x (Z ) - 2xj + 3 x 2 la fanc/oó /x>ra comprobar cual d e dichos vértices hace m áxim o a /Tox (£ } . Sólo fines educativos - FreeLibros Moisés Lázaro C. Vk&mos: (i) Sustitvyendo el vértice Á (oto) en h función: ffóxil) r 2x¿f3x2 ; obtenemos JfoxCZ)= 2fO) +3(oj 00 Sustituyendo t í vértice 8 (0,1) en lo Junción: /Tox (Z} -2*,+3x2 ) obtenemos JKáx(Z) z 2»» f 3(r> : 3 C (3/) an lo june ton: JKáxtZ) z 2x¿ f 3x2; obtenemos Méx(t)zl(y\î(A) - jg (fv) Sustituyendo di vértice D i3,3) c/? /o Junción; y^fox(2) r 2x; 1 sx2) obtenemos Máx(Z) ~ 2(5) 1 30) n 9 (v? Sustituyendo di vertice E(6,o) <¿n lo Junción: />Tox (Z) = 2x/ +3x2 ; obtenemos ffáx&) z 2(o) +3(oi r ¿2 rComo acabamos ate probar ¡a Junción M.óx (Z) Se /x>ce máximo cuando dom* s?á* (Z) = 19 . £1 problema que acotamos 5 y xi de resolver por el método qrofteo 3 Solo una iUi$ toc/o'f) Som era de UN MODELO MATEMATICO OE PROGRAMACION UNEAL CON DOS VARIA. &LBS cuya ^ solución no requiere de mucho trabajo . Pero} en el mundo moderno que vivimos Se plantean problemas de 100} 4oo} . ..} o 4o,ooo variables ñ a s ^ de. amplio } cuya solución requiere del uso de ¿as Com putadoras Moder conocimiento m atem ático . los problemas de Programación timzal plantean y resuelven &a>t~¿o minimizar costos ifo maximizar pononc/as. Sólo fines educativos - FreeLibros tópicos en los croles «£. Relaciones de IR en IR — — ® — /Qe otver ¿os Siguientes problemas de Programación ¿meal por el método p rp /tco. (36) STáx (Z ) = 3x, + x 2 0 5 .0 . /n á * (Z ) r 2 x ,-6 x 2 s . a. 2x, + x 2 ^ 26 *|-*2 * -i *i - 3*2 4 9 X |- 2X2 * 1 *j> ,o 2X| + 2 X 2 < G * 2 > ,0 *. >/0 X2>,0 g ) - *2 />?á* ( z ) = 4 @ S.a. * |- * 2 2,000 x , + 4 ,0 0 0 X 2 50X, ^ 1 *1 * 0 * i >.0 *2 ^ 0 *2 M o * (Z ) Z 2X, + 5 * 2 ¡42) s .a . ' *0 /I) ~ x, t %2 -2 x , + X 2 4 1 4200 9X , f 7x? 4 300 Xí 4 2 x, + x 2 43 Xt } 2 0 Xi>„o x, * 0 O x2*o M á x i j ú .-z $ xt + Z%t . ;/ S .a.. 0 ■ -2Xj * x 2 x, * * 2 /*ÍOx f£) - 3 xJ + 2 x2 s.a. 41 2x, 4- x 2 43 *t> 0 ’ X| * 0 x2* 0 > 2*0 5 .Q.. <2 1 X¿ * 4 x 2 ^ 12 *1 4 2 NOTA ; + 200 X 2 s.a. 3x, ■*•4 x , S) 6 *, f 2i x ; s.a. 3x, + 4 x 2 ^ 5 g ) jy [ in ( Z ) = « sujeto ct ¿os restricciones ** Sólo fines educativos - FreeLibros 6,000 >, 2 0 0 — 0 0 ) Moisp" Lazaro C. - G ra ftc a r í a rei&eten M * | f c ,m * -y < o a (x -y )(x * 2 y ) < C J * * iy>o v X -y > O A *+2 y< © #/i primer tugar 9 m. grafrca (a intersección de fots re/aciones x -y < o A x +2y >0 . g n wgttndo tugar, s* gmf/ca ¿a intersección ate fas ttf&t/ones x -y >0 A x f 2 y < 0 , g n tercer fegm ¿ f e f//>e /os resudados obtenidos en ¿os. dos p meros per sos . £7 matada pue Aemos seguido as : /£?) #A*//C€*f /o Qct/otc/OP ( * -y ) (* * 2y) z O £/ grd/i co efe tas «te sacrones © y © x -y -O © V x + 2y = o © ton dbs rectas yue sé co/tan . <1 2S) So/n¿reo/- ; Ar/cr <?/£>; probemos si el punto (o, i ) satisface o t o x -y -d inecuación «**y=o (* - y ) ( * * 2 y ) < o W Veo/7?os (o - J ) ( 0 * 2 M ) < 0 A e*#« #í - % a^ ~ ; -2 < 0 ^ ésta propos 1 crén «3 vQrefodt ’O. £ n consecuencia sobreamos h m smo m odo probarem os rayón Q . con tas regiones ' £) C y Á. Veam os: *0 sg#s«ía* la££¡e/o/v C H,o) € c A f-ifi)-m satisface o to inecuación (x-y)(xf 2y) e 0 .. •. 1< (or l)€ D A (0,-í) satisface a la inecuación ♦*- es p m s o (x-y)( x* 2y) <0 -2 (1,0) € A A 0 ( 1,0 ) PÓ satisface o /a mcûaciún <O =£ D. c$ VseOAoefio (x-yXx *2y) < O i <0 Sólo fines educativos - FreeLibros S0M8ncA& la rb&iqn /vosomaa£4Q ¿Aa¿r«/<w «S MASO Relaciones de IR en IR { § > (£ 5) la re loctpn G ra /fc o r = S 3/ | íx ,y )£ M * * ^ - O j S o m e to w ¿ O in e c u a c ió n x2 - 6 x y +5 y * í e s fo c to r/z a b M : O <=» ( x - 5 y ) ( x - V ) :>■O A h o ra , d is c u t ir e m o s G r a n je a r l s) la é sto e c u a c ió n <=> g r á f i c o an d o s p o s o s : (x -5 y )(x -y ) x -5 y - o V 2 q x -y s o * - 5=0 Ar3 f/ grafito efe ¿a ecuación (¡j es í//7Qt rector y a/ grá fic o efe lo ecuación (2) es otro r e c ta . Ambos rectos se cor to n en e l origen . 2*0 Som bree*r: ¿as dos r e c ta s g $0, c o rta n en e l orige n h a n d/vrdido a f p ia d o fR2 en cuatro regiones : Ñ 2 } Q2 ¡ ^3 y ^ 4. . En consecuencia si el punto P¿€ Sombrear ¿o r e g ió n R{ , , . A satisface /o inecuación <x-5yX*-y) > O ' %. V eam os: i* &i) (o ,i ) 6 A satisface a la //^cc/oao/i ( x - s / X x - y ) > O => Se sombrea la región . -*"*■*■*. ' 5 > O ♦w es Ve/cforctero (V )^ 2 A (2,i ) M> Satisface a ¿a inecuación (x-5y)(x-y) >0 ato s« so/j?¿veo /a /tararí . . . . ^ * ’• ;■■ ••*••••*--, ' .. - 3 > O _«*- es «eso £* ^j¡) (2,0) €#3 A (2,0) satisface a la inecuación (x-5yXx-yl > 0 *• * se sombrea la regio* ■ % 4 > 0 r 1- es vcrcroctero *« fíi) A H / 0 /vo satisface a la.inecuación (x-5yXx-y)>0 a?0 se sombrea la región '...................~‘y ^4 -3 > O ♦x es r*¿$o ^¿ jG ro f/c o r to relación s o lu ció n r* T z \ (*,*) £ M 2/ ( v ~ * ) ( r + *V ( 2 y - x ) < O } . .Sepcfir'r otos p o s o s : Graficar La ecuación: (y -x )(y + x )(2 y -x ) ~ o *$4 H : 0 ® Sólo fines educativos - FreeLibros v y+x : 0 ® v 2y~* ® - O Moisés Lázaro C i os ecuaciones ® ; © y © son fots rectas que se corten en el origen y dividen el plano fll* en seis regiones. 2S) S om brear ¿a i/re c u a c b 'n : (Y-xXy+x){2y-x) < o . . ./•O Po/’o elfo y se pruebo con un ponte efe v t* ccrOo /¡ey/on X?»' ; i*J,2t 3,4, 5,6 . Veamos: ín tfj) (-2,0 )r pj A (-2,0 ) SQÍi$farce a . lo irm c u & c ió n : (y-x)(y+x ) U y - x ) < O ___ - 8 < 0 «n/tsV. entonces sombrear ¿a región P¡ . £/> ^ 2) (Q,2) € P j. A (0,2) no satisface la.;inecuación (*-*)(y+xy(iy-x) co ^ no sombmar /ó región j g < o <*v. es F. $ # % )) {!,% })€ R3 A (i,?A) s atisface la inetuoúón fy-x){Y+x)( 2y -x ) < 0 Sombrear Lo región M j , - ¿ < 0 -u es,V. n E n Q A a p y e fí4 A (2,o) m s a tis fa c e te inecuación: (y-x)(y*xK 2y-x) < 0 =$ no sombrear la región : ' •.....'*.......- ................... *4 8 < O «SP? En Q $f(of-2 ) e % A ( 0;- 2) satisface la inecuauon (y -x )('t+ x )(iy-t) < Q -26 < O => Sombrear lo región P 5 es V. (-i,“%)€/% A (-2,-Vj) no so^/s/oce l& inecuación {Y-xXy+xfzj-x.) < O => no sombrear la región ' - /? 6 — .' < o *•*- «s ^ 27 Qroficar te relación 5 = ( (xA )€ 7t 2/ xy 4 2 ] ■ solución y Seguir dos pasos : 1®^ (7raficar te ecuación: xy■-1 g ) calculo oel dominio r Se despeja Y . 2>e 2a e c u a c ió n *yz 1 - y r Sólo fines educativos - FreeLibros .. Relaciones de R e n -R - x eDomimo b) caic uto «=* x c ÍP. “ { *=oJ ye am igo c) €§ donde k z o una - os/ntoto v e r í / c a í . $% despeja x. oet r a m ®o De í& ecuación f 0 xy r i x r y€lR-{y=oJ > úfosrwtfe y - 0 m uno a& 'nioia hor&ontmi ta &ulam &o -i S om brear í q inecuación xy < \ Como vamos, la curvo xy - 1 qu<¿ tizne, tíos romas } ha dividido a l piano en iré s regi unes : \&i,. &z y #3 . (o,0V € Ñ 2 A (0 ;o) s a tis fa c e ia inecuación x y <1 => Sombrear lo mytón Rz O €•■#*/4 y 2 - x ^ o j . S e g u ir dos p « » 5 b 5 ; |t )G rq //c o ^ ía e cu a ció n 4 y2 - x z o ♦ Discutir ía e cu ació n : ■0 d o m in i o .** D e s p e ja r Y de la ecuación 4 y2 - x r o x c Dominio i*> *AA*eo* D e s p e ta r *x* ote iot ecuación 4 y z - x = 0 Y= í ~ O x > ,o . c* $=> x : ¿ y 2 ye bango Sombrear ¿aineación 4 y 2- x > 0 . Como vamos t ía curva 4y2~ x r O al plomolk2 en dos regiones: * z r R, ha dividid o y Rg. (i,o) c &2 A ( 1,0 ) /vo satisface ¿o inecuación 4y2- * > 0 entonces rvo sombrear # 2 s /00 # 2 * > -l>0~^z$F. Sólo fines educativos - FreeLibros x c [ o f *ao> Moisés Lázaro C. *— — (^ 6 ^ 3 .5 E c u a c io n e s PE u s 3.5.1 .c ir c u n f e r e f K i^ p o r d b o k ^ lip ^ é h v p c r b o la c ó n ic a s fo c ucrcion efe / o i ?c u n f e r e n c / a iyipntc/ón y ó¿ct circunferencia.} es e/ conjunto de puntos P(*,y) 91/ese mueven en un pfa, efe Tal manera que >/o distancia ote P (x,y) ó otro punióJijo llamado . es una cantidad constante ¿lomado radio.. \é e u & C fO /V £ 3 © x ‘ *• D E LA C '/ t Z C U H F E ñ E N C l A Ec. de 7o circunfa rancio efe centro en (0 ;o) y rad/o r rJ (x-ft)2> Cy-k)1 - r* Ec. de la circunferencia de centro en ( hfK) y radío f > O. x 2 + y 2 + p x > E y 4- f z o E c u a c ió n G e n e ra l d e la P a r o q ra ftc a t' u n a circunferencia Pdr ¿o ta n to } ¿as ecuaciones (f) y ® O tón. , @ 770 s í puedc.graficor r >O . ' C ir c u n f e r e n c ia . ba sto conocer el centro ( h ,K ) y el radio T>Q . $e grof/can d ire c ta m e n te . £/?' c a m b io } lo e tu o . ./ - \ - d ire c ta m e n te . Sin embargo’ la ecuación . e @ se - ' convierte en la . Q.CIACX c/on @ E JE completando cuadrados-pe r/ectos con respecto a #*x *' octetos G E S u E l ros S O L U C IO N SOI l/C/O/v Sólo fines educativos - FreeLibros i/o con respecto i Relaciones de R en IR (51J Groficar J i z { Cx,y>€ IR2/ 2xx 4-2y2 - l O x 4-Gy -2 5 = 0 } SOLUCION Se t e ; 2x2 + 2yx - 10x f 6y - 15 z o DfVtdir por Z 1 Computar x2 * Y 2 - 5 x 4- 3y - =O cuadrados con respecto ( x * - 5 x - t - ....) (x* - 5x + t (jl o 'r i )> *}>+••■) e “ y*1: = y f ( y * ♦ 3 y+ -y -V ' r -3-+ -2. + -| - ( x - l )1 -+ (Y + f f = J6 Donde: ctntro = ( % , . - y ) Radio zv/lG = 4 (52) Groficar ¿a relación S = [■(*,*)€ JP2/ 4 ¿ x* + y So l u c ió n ; 5e í¿e/*2 que : ¿ « x 2* y 2 ^: 25 Z 4 x2 + y2 A x 2 + y 2 4 25 0) Discutir la inecuación © 1^) Groficar la ecuación 4 z x 2+ y 2 | estor ecuación 2®) es una circunferencia, Discutir ¿o inecuación (?) 1®) G roficar la ecuación x2 4- y 2.-zs £ 5 ¿or ecuación es a n o circunferencia, de centro en el origen y radio T z 2 . centro en el origen y radio Sombrear La inecuación: 4 < x24-y2 2*5 Sombrearía inecuación: x2 + y 2 <25. ¿(0,0) satisface o /o inecuación 4 < xHy1? ¿ {o ,o ) satisface o ¿o inecuación Veamos: o2 + o2 <25 Veamos: 4 < o 2 * o 2 4co r .:5 . O < 25 •es¿c* proposición es F? ‘-e s f o p ro p o s ic i ón es V. entonces debo sombrear h región que entonces debo sombrear ¿a región pue éstó fuera de ¿a circunferencia 4=x2f y2 f e r e .n c ic L Se encuentra d e ntro d e ¿a circun x2 y2 r 25 . Sólo fines educativos - FreeLibros ” Moisés Lázaro C. SjOroficor los intersecciones de los re lo d o n e s S y T ¡ donde: 5 ~ |t*,yn fe 2/ x 2 + y 2 ^ 9 j = j u,v)€ m }/ *2-y 2 ^ o j . 54^Grofi cGr S f t T ; si : 5 - j cx,y ) € IR2/ +-y* £ l<á} , T - j<*/0€ fR2/ x 2¿ y A S s ) G r o f * c o r S f i T ; Si • S r|<x,Y>€ /S2 / x 2 > y A x2 ^ - y ] @ j(x ,y)€ fc2 / x 2+-y2 < 3 G } Groficor S D T ; Sí : S - }(*,*>€ IR*/ x 1 + y* x< 1&J , T - j (*,y) 6 IR2/ Grof.icor S = l ('x.yjeff?*/lx+yi 1 i ■ *\ -y ] ** Xa ¿ 1 } ( 0 ) Q rafic ar S ={(*,v)e IR ^ / l * - y | > i } # v . Graficor I (59) $ r j(x,y)c fR 2/ P | x 2- y } ¿ i ( 0 ) Groficar $ r {c*,YV€ S*Y x 2y2 ^ i i Sólo fines educativos - FreeLibros Relaciones de IR en (R 2. L A PARABOLA I N T R O D U C C I O N . Lo porobolo , visto en el plono cortesiono IR2 ,es uno curvo que tiene lo siguiente formo ! vi/ |Ú i2 Parábola q u e Reabre Parábolo. que abre, hacta. ab a jo hacia a rriba , y síu y/iu. e j b es p a r a e/e es paralelo a l le la elj£ y . al e je Y P a r ó b o lo , q u e s e Parábolo que a b r a h a c ia , la. de s a a b re h a c í a l a i z q u ie r d a , y s u r e c h n . y se/ B J £ & s p a r a l e l o a l© e* P a r á b o la , d e E M OBLICUO . aje. z paralelo el yo x . Antes de dor lo definición de lo PoróboíOjes necesorio conocer los elementos de lo porobo lo : Los elementos de lo porobolo son.' V i vértice F .* Foco ( punto. fijo ) EJE de lo Porobolo ( recto que poso por V y F }■ .*DIRECTRIZ ( recto per pendí color ol EJE) • donde IFVI = I VL ILo porobolo, como lugor geométrico se define del siguiente modo ! D E F I N I C I O N . ^ = [ P C IR / I F P 1= d ( P , f ) j 1- £ó. para.bo*CL es e l conjunta c¿e p o n to * d el piano , t&l que. la. d ista n c ia d el fo c o a un ¡¿unto de. la parcCbola&s LcjUctl cc ,&(x. dlstck.nc.zcC de.1 prento dk. lo. parábolo a la., directriz . TEOREMA 1 . Lo ecuocioo de lo porobolo de veVtice en el origen y EJE eje X , es y2 ~ 4 px. el PRUEBA Teniendo en cuento que ; P = (x,v) es un punto d e l a F = ( p,c> es el J-ooo 7 p a r á b o la p> o v-íoô) es «ti vértice ^ Aa ecuación de la. ^¿ re ctriz £ os> x-~p Aplicamos la. definición de ^cucúbolG. : I FP| = |PA| donde f 1^ 1 = \A*-P>*+y2' |PA| = j 3 C - ( -p ) J - Sólo fines educativos - FreeLibros ¡ X + P| Moisés Lázaro C u o fK fe tic e x- P f + y 2* =• lx + o í => Y2 = 4 p x - ( j ) lo i p « s ia POCO y a l d ir e c triz ío n g a u a . del a e iv e i v é r t ic e R- . LADO RECTO (a Córelo Focol) es lo cuerdo perpendicular al EJE de lo parabala que posa por el FOCO* Lo longitud del lodo recto es: | 4 P |NOTA.' Nuestro proposito en este copítulo del libro es solo aprender a groficar los pordbolos de ejes poro lelos o coincidentes con los ejes coordenados. £1 estudio completo corresponde o lo Geometría Anolífico PLANA. Poro groficor uno parábolo bosto conocer tres cosos! el vértice , eI volor de p y su EJE. RESUMEN jJ Poróboio de vértice en el origen y EJE el ¡ ] Po o el verfice en el origen y EJE el eje Y eje X. x*= 4py y*8 4 p * ~ © Donde! o) b) íi - 0 Donde p > O * > lo poro bolo se abre p o r derecha . a ) si p>0 -> la parábolo se abre hacia a rrib o . p < O * ) lo pora bolo se obre por izquierda. b ) s i p <O -> ia parábolo se abre hacia a b a jo . £ ■s p >o . __ E / p i M ,y ky 1» ,e . Jt r\r p <0 p >o p <o LAOO RECTO : jMM|=|4 P| LADO 1.1 Parábolo de vértice { h,k) y EjE paralelo ol EJE X .' R EC TO i (WH| * |4PÍ 2.1 Porobolo de vértice ( h,k ) y EJE porotelo ol eje Y ! ( x- h )2= 4p (y-k) & x^mx+ny* 4.2:0 ( y-k )?5=4 p (x-h ) ep y2+pyv*c|)i+rso ’) E J £ ^pamleÍQQl O -i ( Y - 2)7 - 0 ( x - M ) 2)VERT1CE :V r ( -1 ,2 ) . ) 8 f »>£JE *. paro-ldo ®i eje Y £J-1 ( x + 2 ) 2 - - 4 ( Y + íj F o c o *. F = ( - I4p| - 8 U D O 2,-l-l) < 1) eje . pardolo al «y* Y 1 flVEWIct : V=( - 1 ,2 ) *> V¿rtice 3) -2 = A p * c (-2 ,-2 ) R E C T O ’. Í 4 P I - 4 O'BJÜ l'pafcikfeai cje X El-2 Vértice V - ( 2, 1 ) U )- 4 = 4 p + p = -1 4 p -> P = 2 POCO ’. F=(- 1+2^2) =. ( 1,2) LAOO R E C TO f- i) p r -* /2 5 -= 4 p FO CO : F = ( % - l >-»/2> = t1/-V 2 ) POC£> l P = ( - § , = : ( - § , B ) LAOfc RECTO : |4pj = 2 LADO Sólo fines educativos - FreeLibros R EC TO l 4 p l-5 ■ Relaciones de IR en IR (problemas r a g r a f t c a r se com pletan cu a d ra d o s; ( i ) Graficar la relación : K = {(vo efR 1/ Y*í 41xt , * W é 4 \ y2 - 4 SO LU C IQ N - - 2 X .-G + 4 y + 4 2 ÍY -z V . , (OEJEz/ejeX. -2 (X + 1 ) I . Pasos a s e g u ir pa ra g r a f t c a r : >2¿ 4 fxj 1° G r a f ic a f l a f r o n te r a > V 2 r 4 lxj (3 ) -2 = 4 P LM>0 RECTO \ U*pV=2. P = -V 2 2° S o m b re a r: Paro . v * = 4 .| x l* * | ^ =4K ' S U > ° (o,o) s a t i s f a c e : y 2- 4 y - f 2 * + & > o ^ I V = _¿,x , S i x<0 *por ta n to Se Som brea la donde: <*) Y2= 4 x e s u n a p a r a b a la de eje para lelo al eje X ; v é r t ic e V e(o,o) * 4 í 4 p -* p =1 , s e a b re porderech<j. b) V2= - 4 x f con - 4 « 4 . p - > P =-1 seob*e por iz q u ie r d a . nagion e x t e rio r. D is c u tir S : Y2- 4 y - 2 * + 6 en dos p a s o s . Io Graficar l a frontera : Y 2- 4 y - 2 x + G = O -y\-4y + .... y .. 4_ - (e s u n a p a rá b o la ) = 2 x -6 r 2 X -C + 4 (OElE//ejeX 2 (Y -2 ) i: 2 ( x - t ) <zj V - ( | ^ ) l3) La d o r e c t o *. I4 p l= 2 2 .-4 p P = 2o S o m b r e a r (o,o) s a t i s f a c e 2 o £} s o m b re o : ü ,o ) s a tis fa c e l a in e c u a c ió n ^ 2 < 4 U I ? s e sombra? la región II . p a r a g r á f ic a r l a » 'x z + y 2 ¿ 4 . inecuacic¿\ 1o Gráficar la fro n te ra : x 2 + yz = 4 que e s una c irc u n f e re n c ia d e 2o £| sombreo ‘ cóm o (o,o) s a tis f a c e La d e sig u a ld a d b re a (¿ ) cen el o rig e n ( 0 ,0 ) y radio r - 2 en la tr a fic a r La r e g ió n e x te rio r . D is c u tir T IXI ■ H y - 2 Í . é 2 *. Es e q u iv a le n t e SL X^q> A Y ex 4 >,2 Y<2 Sí *> O A Si x<o! A y^2 SC Xco A y <2 x*+y2 ¿ 4 } s>e s o m p a r te i n t e r i o r , R nS O T J l = | ex,y) e IR2/ y 2-4 y +2x -hé ¿ o } S = { ( x , Y ) € R V v 2- 4 y - 2 x + 6 £ o } T = {(* ;* ) e & 7 |x'|-H y-?|éZ } SOLUCION D is c u t t r B : Y S 4 y * 2 x + G Io y2- 4 y - 2 x -h G > o ^ S (n a d e inte rior) Pasos a s e g u ir tr o : por t a n t o ; se s o m b re a G r a f i c a r *. v - 4 y t 2 x + G r O que e s u n a . p a r á b o l a /que. p a Sólo fines educativos - FreeLibros ^ ^ in e c u a c io n e s ; X -f-y -2 ^ 2 x - (V - 2) G 2 =» -x + y -2 ^ 2 =* -K -(y -2 )é :2 Moisés lázaro C. ( j ) Qrajicaf lo. relación ^ = jlx,Y)GíR2/ Y2 £ lx-2| > x2- 4 x - 4 y - i 2£0 f Y ^ ° } 4- Solución Discutir R, t V2£ l * - 2 | Vz t (x- 2) f si x ^2 Y2 < -(x - 2) , si x<2 d Ís *0 • 4 c u t i r r z : x2- 4 x - 4 y - l 2 £ Q X z - 4 x 4x •- 2- 4 x + 4 (X - £ 4y+12 £ 4 y 4 l2 + 4 2) ^ 4 R2 Discutir R3 : yÔ .es el semiplano -enci ma del . X £ 4y +8 X x -z )2 £ 4(y+2) tproblemas Graficat los siguientes relaciones : © ,R= {cx,v>6 i r V xl - 2*-4y*-M>.o J ® (2 ) 5 = {(x,y) € í r V x2+2X -4 y Graftcar ftO$ . ^ 0} ® T=j(x,y)€íR2/ x2$-4(v-'Z) , 4 (y+2) J (S) R = {u,y)€R2/y>^|xV4| ^ (D s y ¿ 12} - flx>v)€ IR2/ y2-4 x -i€ < o >2x-y-4 £oj- © S i ={(x,ykkV x-y +1 ô/y2~4x>.0 , y>o } ® S z ^ W ^ IR 2/ yz +4x + 2y + 925. 0 } © S3=|(x,y)€ |RV X+2y < 0 } © S 4 = {U ,y )€ ÍR 2/ @ Graficar V^-1 } S 20 S3 n S 4 ^ 1*1 s |(*,yí€íR2/ 4y 2- 4 8 x - zoy <71 } R2 = \ l*>y) efR*/4y2- 4 8 x - 20 y > 7 1} ® R3 =‘{cx>y>€lR2/9x2 +24X+-72 y +1& £ O} ® R4 r.{u ,y)€ fc2/ 9X2424X+72y*Mé< O} © R 5 - {(x,y)€fR2/ 4x2+48y 4-12X < 159} (g) R4 = {lx,y) e ÍR2/ Y2+ 4 x + 2 y -1 9 > o J @ s 9 = |tx,V)€ ffí}/ * 2- CX- 4 y 4 1 £ O, iv-z| £ 1 J © Rr = { <x,yl e fRV ^ -f e X -.ív + IV i.o } © S ,0s {<x'y)€lR7 ® Rg = ^(x,y)€R’/**-V-8£o A 3x+y-2i0} (S) Gfaricar ® @ 55={<VYI€R7x2 6x+5y-í 1>0, yÍ8y+4x-81Q> 2x-y 43 } © S e = }(*/*)€ IR2/ y2- x 4- 4 Y 4- G £0 ^ © Si = \ < v ) € iR2/ x < |yi4| } @ = ^(x,YKfR2/y £ £ + X -X 2 ; ® Su = ^(x>y)€g?y |x1.x|->,y n Rg Sólo fines educativos - FreeLibros IY-HS2} ? x2+ y 2 £ !4 } ? xs2j Relaciones de (R en 3 La Elipse, . Lq to s e lip s e fijo s ta n c ia s ta n te = | una c u rv a c e r r a d a d e de cada fo c o s fo c o y c u m p le a. u n fo rm ó A v a l a d a ” g u e tie n e la p u n to p r o p ie d a d d é la e lip se d o s pun la S u m a d e l o s d t s e s i^ u a l a la cons - 2 a ** Com o £ ^ lla m a d o s lu g a r g e o m é t r ic o se d e f in e d e f s ig t e P € (R 2 / i P - F , ! + I p - F j I = 2 a L m odo: } t. d istan cia d e P a F? d is t a n c ia d e P a Ff Los e le m e n to s d e ia e l i p e s o n *. C - { h }K) x‘ : centro de lo e l i p s e : e je focal F1 1 Focos v i ,V 2 4 v é rtic e s [Y !,V 2 ] = 2 ci'*. e je m a y o r r \ l 8i ,v 2] - 2 b ' « j e m e n o r ^ a > b CFr > F2] = 2 c ; d is t a n c ia f o c a l . a : lo n g itu d del s e m í -e j e m a y o r b : Longitud del S em i e j e m e n o r e j e focal , c o in c id e o e s p a r a l e l o a u n o E c u a c io n e s 0E l a ELIPSE cuyo OE LOS EJES COORDENADOS La ecuación de una elipse de c e n tro 2 [ Lgl ccuoicijcm d e u n a e lip s e . d e cen n r «n el o rig e n 5e i e Focal el e j e O L , d t s ^ t r o en el origen^ e j e -focal el e j e IT , d is tancia focal igual a 2c y cantidad ta n c ia -focal iQ u aí 2 c y c a n t i d a d cons con stante igual a 2a e s : , t a n t e igual a 2 a, e s : y2 + -2? - 1 a * + tí* z' Vz(o,a) í 82 IbjOl * J i-M l / Víio^-a) Lo ecüQeioñ de la elipse decentroen d punto (b,K) y eje focai parólela al ejeX^ es ; (x-M 2 iy-K)2_ t a1 La e c u a c i ó n de la elip s e de c e n t r o en el pun to (h,K) y eje focal p a ralelo al eje “Y e s : b* ” k ( y - k )2 Relaciónentre a.byc : o1 s V t d (x-h)2 , 1 b* j ct>b Sólo fines educativos - FreeLibros Moisés Lázaro C. Nuestro único proposito es aprender cl tr a fic a r una elipse conociendo solo cuatro elem en tos * SU eje ^ centro de La elipse, longitud del Semt-eje mayor y del se m i-eje menor • Para e s te o b je tiv o ^ b a s t a r a e x p re s a r Or d i n a r i a ; ver cuadro a n te rio r . l a e lip s e en su fo rm a Eje m p lo s : © @ Q r a j t c a r : 4 x 2+ 9 y x - 3 4 = o G r á f i c a r : x2+4y2- c x + I6y +21 = o S o m c to n Bastara dividir entre 36*. A Xa ■ 9y2 36 36 36 3t =0 JLl + J l ~ 1 9 4 “ 0 ( x2-6 x +-•--•) t 4 ( y2 + 4 y + •*?.+ 2 ? 4- dz3 centro Bastara co m pleta r cuadrados con respecta a^ x' y con respecto a Y . As i : ( x 2 - 6 x + - -...) + (4-y2 + 16y+* ••) = -2t - 4 1 (X2-6x + 9) + 4 ( y24-4 y+ 4) r - 21 + 9 +16 b -1 (X-3)2 + 4 ( Y+2)2 c = ( 0, 0) EJE coincide con el ejeX. 5^(0, 2> 4 b=1 T e n e r n o s -. 1) B|(0,- 2) Como Q. =2 e s t á debQ jo d e La v a n o s i n d ic a que el EJE • r ia b te Y * de l a elipse es Qraficxxr Y7 + 4 x 2- 4 = 0 SOLUCION Dividú entre 4 y ordenar : y* vi T + t 4 4 a r2 c e n tro E JE DIVIDIR ENTRE 4 1 >1 a=2 - ------ ? — © ¿"4 ^ 0 +2)* : 1 (x -3 )2 4 <-v>V •) i Z) c e n tro 3) 4) Serni - eje Serni - eje = 1 b -I c- = l o , o ) o o in c id e con e je Y . Sólo fines educativos - FreeLibros p a r a le lo al E JE X c = ( 3,- 2 ) mayor *a = 2 menor : h -1 Relaciones de IR en IR 4, Lq H ip é r b o l a DEFINICION ; Dados dos puntos fijo s *Pi. y toles qu e I R , 1 = 2c y d a d o u n á .c o n s t a n t e ’^ c l ^ Se. d efin e La h ip é r b o la Üf> c omo * <fc- - S o , m i / lio d istin tos (-focas) t a l que o < a ( C 5 'p .p 2| | - 2a I di-fe ren cía de Las distancias de P a F1 y de P a F? ) es igual a La constante Za . Elementos *. C V, >V2 Fv ; F2 x' [v 1;v2] ; centro : vértices : -focos v foaaL = Za : eje tr a n s v e r s o [ b 1#b 2] = Z b ; e je c o n ju g a d o 1^ - C |= I Fz- c | = c : asíntotas ECUACIONES DE LA HIPERBOLA CUYO EJE FOCAL COINCIDE O ES PARALELO A UNO DE LOS EJES COORDENADOS JJ Leí e c u a c ió n ole l a h ip é r b o la d e a e n . j*j L a e c u a c ió n d e la h ip é r b o la d e c e n t r o e n el o rig e n , e je -focal a o in c L tro en e l orig e n } e j e -focal co inciden te d e ñ t e c o n d e j e 11^ y -fo c o s L o s p u n con el e je X , v focos Los Puntos (qo) to s (o ,c ) y ( o r c ) , e s ; y C -c ,0) , e S ; _x2 j} a* R g la c io 'n e n t r e a ;b yc La ecuación : cz gq 2+ b 2 Puede s e r La d e u n a h ip é r b o la d e el pu n to (h,K) y eje focal para lelo al e j e X ? £S d e la forma * ce n tro (x-h )2 CV-K)2 *. a b o a=b e c u a c ió n d e la h i p é r b o l a centro en (h ,K ) y al d e la f o r m a *. e je Y . y e s \jy e je fo c a l / l v-K)2 az " Sólo fines educativos - FreeLibros de p a r a le lo 1 b* ~ Moisés Lázaro C. jV~uzstro objetivo es sólo aprender a gra fica r u n a hipérbola.; co nociendo : su centro ■' s u E J E y ¡os valores de Ci y b . Eje m |. plos : : 4 x2 - 9 y2-36 = 0 Q r a f ic a r Veamos: Dividir entre 3G *. 4 X 2 Qv2 9 y2* 3c 3G - 1-0 L L - 2- = 1 •9 - 4 i 4 a=3 b =2 Tenemos centro = (o>o) : coincide con et eje X a = 3 .6 = 2 3. Gro.ficar : 4 x 2- 9 y 2 -f-32X -*-36y + 64 - O Mojamos : £■:/? es¿e caso j fo primero gue s e ¿ace es : c o m p l e t a r c u a d r a d o s con respecto a " x * y am respecto cl y • 4 s f : 4 x2 v-32x f •••• -9 y 7 +3éy + - - =-C4 4 (x 2+ 8 x 4 *•' ) ~ 9 ( y - 4 y + * - ) = -C4 4 ( x2+ 8 x + 14) ~9 (y 2-4 y-f 4 ) = -64tC4-36 4 ( x + 4 )2 - 3 ( V - 2 >2 = -3G -4 (x + 4 ) 2 +• 9 (y-2)2 = 3G Dividir entre 3€> y ordenar *. 9 (V- 2)2 = 1 - 4 (*+4)2 34 (y-2)2 4 3e (M r 9 4 Q ra fic a r : Veamos ; 2. Vlvidir entre 4 ; b=3 y2- x2 - 4 =o y2- x 2 v2 *2 4 4 4 i ar 2 =4 = í Tenemos centro E JE E n este caso tenem os : Centro : (o,o) HTE : coicide con el eje Y a = z } k > -2 . ’ ¿3" preciso y a f i c a r Las diagon aler d el rectángulo} g Ue son las Asíntotas. Sólo fines educativos - FreeLibros (6, Ai) = (-4 ,2 ) paralelo al «7e / > porque Ol —Z e sta debajó deT. Relaciones de IR en < s > - 4 . G raftcar : 3x2-y 2 +30 x +78 —o Veamos'* Debemos cojnp te ta r solo con respecto V «* CX X . fro n te ra e s : La a.) x2+ y 2- que es u n a c i r c u n f e r e n c i a d e e e n tro e n ( 0 , 0 ) y radio r= 3 . ; Ordenando te n e m o s 3x2 +30x + ••- - y 2 3(x2 + iox + •••• ) - y 2 3 (x2+ iox + 25 ) - y 2 ( 0 ,0 ) b) s a tis f a c e --7 8 cu a l in d ic o = -7 8 ía re g ió n que : *z +y z < 9 se d e b e > lo s o m b re a r in te rio r . --7 8 + 7 5 3 ( x + 5)z - 7 2 - _ 3 ^ _ , - (x+5)2 + -^- te) Discutir ; x2 + y 2 < 9 t3<25’ ^-dividir entre-3 1 _y_* _ ( x+5)2 3 — ^ 1 '4 4 a-TJ b- 1 Tenemos : E\ centro*. (h,K) = (-*5,0). EJE : e s paralelo al e je "Y . G. Grofícor íq rdlacion : T A S o R T (x,y)6IRZ/ |xl-|Y|<l| S = { ( X , m i R 2/ V - 4 x 2 i 4 ^ R s J (XjY) t i r 2/ Ix V+ lvl ~ 4 ) Solución G ra ftq u e m o s la. f r o n t e r a d e cada relación : ( 1) F r o n t e r a d e 5. Groficar ¿a relación : S ^ c ^ v i e n ? 2/ * » 1- * 2* ^ * x2+y2 í 9 } Si Si Si S¿ T t x l -1 y j = 1 x >0 a y >0 => x - y =1 x>o a y < 0 ^ v +y =1 * < o a y>,o - x - y -1 x<o a y<o *-x + y = i Solución (?) D is c u tir : 4 y 2 - x2 12) F r o n t e r a d e 4 <*) La f r o n t e r a e s : 4 y 2- x 2 = 4 y 2_ 4, a -1 b) 4 -- t ^ ^ ip é r b . + fc>- 2 ( 0, 0 ) hace v 4(o )T4 O >4 t- PALSO Lo cual indica que S ! H ip é r b o la - 2-*> Y2 - 4 x 2 = 4 - x2 = 1 (3) F ro n te ra de R : lx| + |y|= 4 Si X>oav>o 4 x + Y =4 x - y - 4 Si x >0 a y <0 **> Si X<o A y » o * » — x + y = 4 St x<o a V<04 se debe^som - br^Q r * la región interior d e la h ip é r bola . Sólo fines educativos - FreeLibros -x -y =4 Uraj- ic a r Problemas tas siguientes relacionesAiguientes ; JL.S, =|üi,v)€/R2/ y z £ 8 X a <x-3)z+y2£9} 16. SMn S12 O S í3 2 . S 2 = J ( x ; y)€fR2/ x z- y zi 1 x xZ4-yZé 1¿ } |7. T, 3 -5 3 = j (x,y)€ IR2/ Xz- y Z£. 1 A 18 . r z =-{<X/yje IRZ/ IVI ^2 = {(x,y)e1R2/ JXl £lYÍ£2 | ' y#y lx ~'|l l X-1 ‘ . 19 . Tj rzjcXjyielR2/ lx |> Ixléyj. 4 .S 4 = f (x,Y)en?2/ Xz_ 4 v z- 2 X + ) > 0 } 5 . Ss = | (XjVJfc tRz/ 9 x i- y J_ 3 cx - 2 y>««| 20. T4 ={(x,y) € IR2/ lx l> y 2 , I x I l l Y l } 21. Ts = {(X jY )e (R2/ lx y l£ 4 } 6 . St = j ( x, y) e íRz / x y <4 } 7 . 5 7 = | (x.,v)€ ( r 7 - £ + - £ S i } * 8 14 10 . S 9 \ 2 3 . T7 .s 6 n s 7 9 . 58 22. ' = { (x ,y )€ R 2/ 4 x 2- y 2-i4 | (x,y)elR2/ (y-2)X*.1j- = |(x Jv)e iR 7/ 4 x 2- 9 y 2 s 144} 24 . Tg = ^(x,y)6 (R2/ Ú -i)2- (y-2)2é 4 } = { <x,y) 6 IR2/ V2- x2 £ 4 } 25. T<y ^{(x,y)e1Rz / H -.S j0 = j ( x ; y)tn ? z / ixi< 4 } 2 C. 9 lü±i>2< 1 1 4 1 Tío = \ CXjylelR2/ (y-2)z + (x+0 ¿ 4 } 27. T9 n T )0 i 2 . S j - n s l0 18. 5 it = j l M i e IR2 / x2-9 y 2¿ 9 } 28. 'T,, = j lx;y)6iR2 / (x-2)2-(y -3 )2>4} 14. *3|2 = { lX,y)€ (R*/ y-3 ¿ Ix| J 2 9 . T i2 - | . ( V ) € I R 2 / ^ 15. S ) 3 = ■{ (X ,y )e í1 ? y I x l i S , y Í - 3 | Sólo fines educativos - FreeLibros + ^ 1} FUNCIONES o APLICACIONES O. IN T R O D U C C IO N Tomarvdo dos .conjuntos A y B hemos c o n s t r u i d o el conjunto R,tol que , R c z A x 8 . Al conjunto Eje m p lo : R le llom om os Dado los conjuntos relocion de A A ~ ^ o ,b '¿ c ,d j construimos los siguientes relociones R = { ( o , 1} , ( o , 2 ) , ( b , 3 ) , ( b , 4 ) 5 = | ( o ~'í) , ( b , 3 ) , ( b , 4 ) , ( d , 5 ) } F = | ( o . l ), ( b , 2 ) , ( c ,2 ) , < d , 3 ) J 6 = { (o,5), í en 8 y de ; 8 = jV ,2 ,3 , 4 , 5 j A en B ) b . S ) , ( c , 5 ) , ( d, 5 } J % que ol r e p r e s e n t a r , codo uno , en un diogrómo de Venn Dom { R ) Sólo fines educativos - FreeLibros tendremos! Moisés Lázaro C Fensemos, por un i ) ti J momento , en dos cosos En el dominio de codo uno deios rela cio nes , y en lo dominio correspondencia con un elemento En ¡a re la c ió n i) E l dom inio del R de de un elemento de! conjunto de de cada relación llegada. tenem os R es un subconjunto propio del co n ju n to de p o rf id o . Pues D om ( R) <= A | o, b | c= it) L o correspondencia es elementos 1 y 2 ol e le m e n t o E n lo re la c ió n S éi i b€ A -En lo . r e N m ó n . F y en ' al elemento o B A lo oigo ponde d a s ele m en to s 3 y 4 t ) lo re la c ión G de 8 . ocurren de» porticuiortdades¿ten re locio'n F , tenemos ! D om ( F ) s dos sim ilo r. di t e r e n c í o dos £ n correspo n de ; c o rre ocurre a A t. todo el co nju nto de p a rtid o . Sólo fines educativos - FreeLibros Funciones o Aplicaciones ii) o codo elemento elemento E n lo t ) Ü ) del conjunto re la ción Dom de l conjunto port¡'do corresponde un único de lle gado. G , tenemos : (G ) » A o codo elemento de A Pues b i e n , e s t o s F y G de van a dos elemento de 8 . un único p a rtic u la rid a d e s que gozon las de fin ir N O TA .* A p l i c a c i ó n co n ju n to corresponde uno s ig n ifico A P L IC A C IO N o FU N C IO N cu yo r e lo c ío n e s de A en 8 . FU N C IO N dominio es todo el de P A R T I D A . E n e i presente l i b r o , usaremos corno sinónimos f uncio'n o api i cocí oo. 1. FUN CIO N OI DEFINICION EN 8 1 conjuntos A y 8 , llamamos función Dado dos correspondencia mento A f que asocio o codo elemento y € 8 . Tam bién de A x 6 A con en 8 un único e le % podemos decir f es uno e le m e nto f u n c ió n definido en A x € Acorresponde y con valores un único elemento y en 8 ,si o codo 6 8. N O TA C IO N La notación f .*■ A ■— x Se lee o o toda F — *♦ 8 y se f c x ) A en 8 “ " f es uno función de “ f es una función definida en A y con valoresen Sólo fines educativos - FreeLibros 8 Moisés Lázaro C. — Lo N O TA C IO N - y = f (X ) H y y A d e la s ! 1.1 y - es lo imagen de x me diente f es el f en x fix) valor de la función • es equivalente GRAFICO DE D EFINICION - UNA : A G R A F IC O O I f al ( % # f ( x ) } , "V* x t A . sea Sun bal ico mente : ir (f } « A* DEFINICION conjunto de todo (* i f ( x ) ) / x€ Según esta definición el los pares de la A G r ( f ) es una relación de A e n , i , es decir 8 . 2. Si el Gr ( f ) es una relación de A en 8 que goza de las siguientes p r o - , piedades ! , 1) Dom ( G r ( f ) ) s 2) St una Gr(f) 8 | Gr ( f ) ( x , f (x ) } € a FUN CIO N f Se Mama form a se iee : { x, y ) € A Gr ( f ) función de a A ( x , z } € G r { f ) »> y = z ¡ diremos que f en 8 , Sólo fines educativos - FreeLibros es Funciones o Aplicaciones * EJEMPLO 11 ) D efin im o s Seon lo s lo fu n c ió n 8 =j m ^s^r J y 2 ) Definimos lo f uncio'n g.‘ A -+ Q modo.' de I s i g u i e n t e f \ A~+B A = | p,b,.c,d j co n ju n to s deí siguiente modo f ( o) = m g{a ) » t f { b ) n ■g I b ) » t f (c ) n g f { d ) s g ( d ). = ( C ) ass t t A Podemos observar , cloromente , que en ambos todo el conjunto de partida , esto e l lo En combio el rango es un el rango de una función o uno f u n c ió n El que defin e es todo e i conjunto o uno el mas es a p lica ción de llegada. A de llegadat esfo que estudiaremos dominio vo a veces definir adelante. B A S IC A : co nju nto .d e 'p a rt id a todo funciones ubconjunfo del c o n ju n to su rye ctiva ACLARACION B y de llegada pueden ser de cualquier naturaleza; lo que .'debemos hacer . es'■definir bien a uno'función. EJEMPLO 2. Sean los conjuntos A a B - { D e f in im o s lo función p /p es uno O .l } (p .: A —* 8 del siguiente modo Sólo fines educativos - FreeLibros proposición j y Moisés Lázaro C. \O 0f~ f EJEM PLO 1 , si p es verdadero O , si p es folso . (p ) * 3 . Seo f e l conjunto A = \ - 1, 0, 1^ A x A — |( - 1 , - 1 ) f ( x, y ) = x f definimos , 0 ,1) | — * A lafunción delsiguiente modo y o ) Hollar e J 6 r ( f ) b ) H a lia r ei Ranfo de f. Sofücio'n o) Como ef conjunto A tiene solo sentar en un diagrama Así 3 elementos , podemos intuir y repre d.e Venn lo función f. : ElSrOfico de f son PARES del conjunto de partido ordenados que se forma tomando un elemento ( x , y ) y un elemento del conjunto de llegada { x+ y ) 6 A A si obtenemos ! Gr { f ) — | ( ( -i .o ) f - i ) , í ( 0 , - 0 , ~ i ) , ( { - i , i ),0 ) , ( ( i ~ i ) ,0 ) , ( ( 0 ,1 ), 1 ), ( ( i , 0 ) , i ) , ( ( o to } , 0 ) I • Sólo fines educativos - FreeLibros Funciones o Aplicaciones - 0 b ) Rong { f ) * A . €í d o m in io de f , f es uno Dom (f ) » Se d e f in e sie m p r e sero todo e I conjunto de o p lí c o c io n . A IJ6 H P L 0 XA 4 . ( ( - 1 , - 1 ) , ( 1,1 ) ] A — { 0 , 1,2 Seo lo f u n c i o 'n f : A -* A así i X+- 1 , si (X + 1 ) € A f XX) = , o ) H o llo r b ) H o llo r él Sr si y (x + i) a . (.() el ra ng o de f . S o lu c ió n o ) Bosto dor vo tares o x paro h ollor f ( x) . Asi 7 ! f { O í— 0 + 1 * 1 , 'pues (0 + 1) £ A f ( ! ) = T+ 1 s 2 , pues ( 1 + 1) 6 A f ( 2 ) * 2+ 1 — 3 , pues ( 2 +1) 6 A f ( 3 ) = 0 , porgue (3+1)= 4 / A Donde ! f { O ) a 1 indico f ( 1) = 2 indico que lo que ( 0 ,1 ) 6 (1,2) f ( 2 } 1= 3 indica que f ( 3 ) » 0 indica que ( 3 , 0 ) y Po r — tonta : Gr ( f ) € { 2, 3 ) € € Gr ( f ) Gr ( f ) Gr ( f ) < G r { f ) = | ( 0,1 ) , ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 0 ) } Sólo fines educativos - FreeLibros porf ido, porque ■ Moisés Lázaro C, b ) fteng ( f ) * { 1,2,3,o} * A . RECOMENDACION* To d o vez que se tener en cuento siguiente 1. lo Id e n t i f i c a r lo formo L L E G A D A codo p u la r 2. lo No del conjunto y= ol de P A R T I D A dominio olvidar que el D O M IN IO » Seo f ff? fN porahollar f ( x ) . C O N JU N TO f <n}=* 2. Seo f dt Seo g .* [ - 3 , 3 ] Seo F .* F IR2 | ~ ,— | definido por 2X‘+1 2 ~~~* [ 0 , 3 ] g(X)~ 4. por . 2n -1 4n - 1 | O,I | — * f {X)=s 3. , d e fin id o , definido por x2' — * IR ( x, y ) » x - , definido por y n 5. Seo H IR IR , definido por x.,+ x 2+ — del conjunto de sedeun valor Ejemplos ; 1. y en mani x€ A . vez que de Jo fu nción uno f u n c i ó n , y tener cuidado f (xl , codo e stu d ia r ! que decimos f * A ~-*8 vez y tener cu ida do .'.perteneciente de recomendocion corres pondencia A n a liz a r froto + Xr Sólo fines educativos - FreeLibros P a r tid a . a 11 x “ Funciones o 'Aplicaciones. 1.2 DOMINIO Y RANGO . Sí f .* A —* 8 DE se lee UNA FUNCION o APLICACION f e v uno función de A en 8 . definimos ! o ) Dom ( f ) = A b ) Rong ( f ) = 2. IGUALDAD Seon f ( A ) = | f { x) / x € A j DE FUNCIONES f y g dos funcio nes D ecim o s E JE M P L O - de A en 8 que f y gson ig u a le s . s í Seo n f ( x ) ~ y solo si f (x ) = g (x ) , V x 6 A , x ^ O y g (x ) - j x Se cum ple 3. FUN CIO N x >0 x <o g {x ) , *V* x € IR- j O j y A , si'd e fin im o s RESTRINGIDA Sea lo fu n c ió n g * £ f (x ) ~ ’ l -1 , f \ A —* B 8 , de t o l modo que £ « lo fu n c iV n % (x } =/ ( x } , “V* x 6 Edecimos que g \ es lo R E S T R IC C IO N de f o í c o n ju n to E que deno tomos p o r f |^ ♦ E je m p lo s ; 1. Seo f ! IR —♦JR definido por Lo función, g : . [ 0 ,oo y * — > IR es lo r e s t r i c c ió n f ( x ) ~ - 2 x 4*5 d efinid o por g (x ) = - 2 x + 5 de f oi conj unto [ 0,oo )■ Sólo fines educativos - FreeLibros Moisés Lázaro C. (m )- — 2. Seo h •[ - 4 , 4 ] — ♦*[ 0 , 4 J definido p o r Lo f unción j .* [ 0 , 4 ] — ♦ [ 0 , 4 ] r e s tr ic c i ó n de ■ h oí c o n ju n to -■\ 4. C O U P O 91 C I O N Seon los funciones codo •D E gff(x>) € C", • , ' A sí quedo es lo [0,4]* ♦8 — A 8 " y "o o codo x€A ► C ¿ toí codo f ( x ) € B corresponde que , si o corresponde g { f ( x l ) 6 C “. ■' ' lo nuevo función. ge f ' A -» C Hornodo FU N C IO N j(x)= 7 4 - 7 F U N C I OH ES f Jx ) € entonces ; i. definido definido por f y g , donde x € A corresponde h ( x) ~ v/4~ x2> . definido por COM PLETA/ de { g 0f ) <*) == g ( f i x } ) f yg. 9o i 1) g N O T A C IO N E S 0 f se lee “ f compuesto con g “ o “ función compuesto de f y g " En lo composíckm Q0 f t o lo función délo derecha llamaremos FUNCION de PARTIDA y o ¡a función de la izq uierda llamaremos FUNCION 2) La notación (g o f . ) ( x ) & g l f ( x ) } **f com puesta 3 } Poro f a c ilita r f u n c í on por con g se lee o piteado en x , es iguol a el aprendizaje es con veniente uno de L L E G A D A . f lecha . Sólo fines educativos - FreeLibros g aplicado en f de x ** re p r e s e n t a r c o do Funciones o Aplicaciones • COM POSICION DE D IA G R A M A FU N C IO N ES FLEC H A S f g A ---- ♦B — go f Donde DE S compuesta con g ( 9 0 f)(*> = 9&<*>)■: go f jo h $ h com p ue sta con j j oh M -X * N Donde : ( j o h ) t * ) = j ( h f r ) ) C X í hafoQ h0 f 0 g í M compuesta, con i campu&da can h D onde’, (ho foj)(x \c(h o f)(3 (x i) A— f fír — > C ---- ♦ D f0g * Tombien se puede ~ h [í(3 W )] A - ± ¡ X»®*''." _________ . £i x T * n P R O P O S IC IO N ; Lo composición g Q f existe sí, y sóío si Rong ( f ) n Dom ( g ) # 0 Sólo fines educativos - FreeLibros hocer 9 Moisés Lázaro C. EJEMPLO 1. Seon los conjuntos A = j o, b , c , d j , 8 = | f M ,s -, p Seon~los fundones f siguiente 8 A y g ' B —* C , , qj , C =j a .n ^ b .c cuyos gráf icos¿s.def inen ^ del modo ! G r ( g ) = | { o,m)^ ©r { f ) = I { b,n ) , { c ,s ) , ¡ d ,s ) | (m,o ) , (n ,a ) , ( s,n ) , ( p,s ) , ( H ollor : o ) Gr ( g 0 f ) b ) Gr ( f0 g ) ^ ,b ) j SO LUCIO N o ) Poro Gr ( g 0 f ) h o llo r vez que el a 10 2 - co mponente componente en un par Obtenemos ' Gr { g 0 f ) s b } Gr ( g ) = hocer un transito de de un por del Gr ( g ) Gr ( f f a g codo o ) a p a re c e com Gríj-) G rl3 )~ \V n p .),in p L )A ¿ $ Ó >(fiJA)Jl'f¡b)} * | ( o , o ) , ( b , o ) , ( c , n ) , í d, n ) j | ( m ,p ) , ( n , o j , ( s , n ) , ( p , s ), ( q_,b ) l Gr(f del bosta )= -^ " j («í'TnV) , { b r n T ”, ( c , s ) , ( d. s ) Así obtenemos ! Gr ( f o P e ro Ud. , a )= I ( m ,m ) , ( n,m ) , ( q , n ) j si est e recurrir pro".ce'di m ie n to --;ie est o d a v ía a los d i a g r a m a s . de Venn. Así : Sólo fines educativos - FreeLibros n d i f íc il ", puede Funciones o Aplicaciones Pora hol lar gQ f Para hollor f Q g Com o ! Rong (g ) s | 0 ,0 , s , b | D oír) ( f ) = | A | S e t iene : Rong { 9 ) n D o m ( f ) ~ j o , b j # Luego f 0 g- exi st e El dio gromo de f lechos es 8 — -*■ Rg n A 9 o f existe sii Rong ( f ) n Rong (g)?¿ 0 0 i 8 £1 dia gra m o de Venn es 8 Com o ! 9 C A f B Rong { f ) = j" ¡n,n,s j Dom se tiene (g ) = | B j R o n g íf ) n Dom{ g 0 Luego Luego G r ( g 0 f ) - | ( a tú ) t { b ta ) t ( c tñ) , { átc\) Gr ( f 0 g ) a I ( m , m ) , ( n/n ) , ( EJEMPLO Dado 2 los conjuntos A = | 0 , 1 , 2 ] , 8 = | 0, 1, 3 , 5 ] , C = {1 ,2 ,3 , 6 } seo lo función f ‘ A —♦8 y g X B -* C lo función defin i do definido por por f í 0 ) = 1 , f { 1 ) = 3 , f ( 2) = 5 g ( 0 )= l , g(t) = 2 , g{3)~ 3 , g í 5 } ■= 6 ■ Hollor q,n ) j o ) g o f y b ) f o 9. Sólo fines educativos - FreeLibros Moisés Lázaro C S O LU C IO N o) P o ro o bte ne r g 0 f , lo primero que debemos hdllor es R o ng ( f ) n Oom ( g ) • Se tiene-! Rong { f ) = | t, 3 ,5 j Oom (g ) f A firm am os Y B | Rong ( f ) n Dom ( g ) = ( 1,3,5 } ^ 1 j ^ que existe 0 g© f . H o lle m o s g o f- a p l i c a n d o ( g 0 f )(*! = g ( f ( x) lo definición } x € A V e a m o s: ( 9 o f ) C i ) s g(f ( g o f ) l o ) 35 g ( f ( o ) ) S / "-' f d e f in id o )5 ( go f ) (2) = g í f ( 2 ) ) « g ( i ) = g (3 ) = g (5 ) » 2 « 3 « L u e g o , lo f unción 9o (1 : go f { o , T, 2 j 6 es ! ------► { 2 , 3 , 6 } ( g 0 f ) (O) = 2 , ( go f ) <1 > = 3 , ( g0 f ) U )•= 6 . por \ i) P o ro obtener Rong ( g ) n Se f 0 g , lo primero que debemos h a llo r es Oom { f ) . tiene .* Ron g ( g ) =r | 1 , 2 , 3 r§ j Oom ( f ) = [ A J Afirm am os Hollemos que ex i s t e m> Roag(g) n Dom (f) ~ { 1, 2} ¿ 0 f o g f © g , apíicoaóo lo definición í f o g ) ( x ) « f ( g c x } ) , *¥• x 6 8. Veamos ( f o 9 ) í o l ~ f (g ( O) ) * ffí) (f ogld f ( 9. o ) 'V '" ’ ~ f ( 2) = 3 Sólo fines educativos - FreeLibros ) (fog)w ~ f (g (3) ) = f (3 ) ' ~ 3 _________ Funciones o Aplicaciones { f d 9 |(3 ) - f í 0( 3) ) = f (6 ) = / Luego , l o f u n c i ó n f©g sero i f O0 . { o . l j — {3,5 } definido por ( f o g ) ( d ) - 4. 3 PROPIEDADESDE P1 } Seon los funciones Qo f # ( f <>8 ) < i ) s 5 . , LA f : A COM POSICIO N 0 y g .' DE FUNCIONES B - » C , en genero! f o g ( L o composición de funciones no es c o n m u t a tiv o ) ) Seon los funciones se cumple si f , g , h f .* A — * 8 , g .* 8 -rt C , h ( hoQ ) o f = ho l Qp f ) C — *D propiedod asociativa . son funciones reales de va ria b le r eo! , se cumplen : P ) ( f + g ) o h- » 3 i f oh + gob Ley distríbu tiv o de lo c omposicíon respecto de. lo sumo. ^4 ) í f g ) © b » {f © h ) •( g© b ) Ley d i s t r i b u t i v a respecto P8 ) f o í * t é f 38 f , T f , de lo composición de lo m u lt i p lic a c i ó n . donde I es es lo función I< X) * x , ^ i d e n t id a d . x € IR J z ír /f 5. F U NC IO N INV E CT IV A , SÜRYECTIVA Y ■ B IY E C T IV A 5.1 FUNCION INVECTIVA DEFINICION D odo lo función, f A - t .B , diremos que f es I N Y E C T I V A Sólo fines educativos - FreeLibros t í, y Moisés Lázaro C. que es e q u i v© lente a lo si g u i ente f es IN Y E C T I V A t si y solo si o# d e f in ic ió n b implico f ( ó ) # f { b) , ¥ a , b i A ** 0 FO R M A PR A C TIC A DE y euondo no. (T ] fu ncion e s ' Foro ID E N TIF IC A R con cuando ÍS» P uno f u n c i ó n es inyectiVo pocos, elemen tos .’ Unofaocion NO cuando lo segundo" co mponente / ., . ■' / se re p ite dos o mos veces. EJE M P L O S .S e a n los funciones Gr l f ) = | ( a , m ) , (b , p ) , { c , p } ,*{ d , q ) A , f,g, de -a lg ú n p o r { x / y ) ■ *■■■ t hcuyos gmficos NO del G r á f i c o t son 7 ES I N Y E C T IV A , porque en ( b, p) * es IN Y E C T I V A y' { c , p ) se re p ite ” p " dos veces , G r ( g ) 53 ( [ ( o fm ) t ( b , m ) , ( c , p ) , ( d , p )>-*-x.NO ES IN Y E C f l VA , porque en t f f f J * (o,m ) y (b, m ) se repite m ; adema's en { c, p ) y { d, p ) se repite p , 6 :r ( h ) « ( o . m ) f{ b, p ), ( c, q ) t ( d > r } j *-*es INYECTIVA , porque ninguno de los segundos componentes se repite. UQ Én funciones r eol es de variable real cuyos r*ecto-s o c u r v a s , un o función in y e c tív o Cüolquter recto boVizonío! . S i de 10 función en un sol o re cto h©rizantal la r ect o gráficos son se identifico frozondo hor i zont al c o r t a aJ gr áf i c o punto , entonces es i n y e c t iy a . Si c u a l q u i e r co rto ol gráfico dé la función en dos o e n to n c e s id fum io'n I ¡neos' NO es I N Y E C T I V A . Sólo fines educativos - FreeLibros mos puntos Funciones ó Aplicaciones Ejemplos qrafleos Respuesto ■ Cuondo v i do d ■ * r 3.2 FUNCION se froto ‘de probor teo'ri Gómente lo in y e c t i- de un o f u nc ion. ■/ SUNYSCTIVA — DEFINICION 1— — — — — r— Dodo lo fiíncion D ecimos que f e s f i ------— ------ — — A — »■ 8 S U R V E C T IV A s í , y so'íó si V y € B ^ * € A Esto definición nos "y" dice que . Todo elemento, del conjunto de llegada menos olquno /y=í¿x) preimoqen*'x" tiene por Jo perteneciente ól conjunto de portido , tol* que ^ y= f (X ) * t. y es imagen de x p or f v -DEFINICION t Lo función f 1 A-+8 es SURYEC l IVA sí , y solo sí f (A ) — B L conjun fo día Bwie ( f } fl agota • Sólo fines educativos - FreeLibros Moisés Lázaro C. L 0 segundo definición de f coincide e je m p lo s nos dice que f es S u r y e c t i ^ o cuondo el Rango con el conjugo de He godo. : f , J ►m ►n *P í ) 1) g e f es inyecfivo 1 } h no es i nyec t i vo inyecto vo f¡Wesn¿€V r doip suryecti va , 2 } g no es suryectiva, f } f es s u r y e c f i v o ) porque f ( A ) = 8 2)h porque f( A ) # C rango áe } porque f(M}~N Pues : f 3 , 6 , 9} Pues f ( A ) s : { 2, 4 ,6 , 8 } Ranso ee 9 NOTA Probablem ente el e stu d ia n te *e planteare lo interrogante ¿ C uénóo usor lo definición 1 y cuando la 2 ? Sugiero usor lo d e f in ic ió n ' de funciones pocp$ .. se trota de probar lo j teóricamente- planteados. Perom&trata elementos reglo de 1 cuando © de f u ncione s correspondencia cuyo suryecti vidod de funciones con dominio es un intervalo y tiene algebro icg > a p lic a r lo definición 2 . Sólo fines educativos - FreeLibros ^, Funciones o Aplicaciones EJEMPLO 1— Seo lo ' Probor que f f • ( A x 8 ) x C —♦ función defin ido por f { ( x ty ) , z ) = Ax ( 8x C ) { x , (y , z ) ) es s u r y e c f i v a . Demos tro c ion d e fin ic ión 1 Lo Dodo f : M— * N f es s u r y e c t i v o i NOT A dice .‘ todo y 6 N , 3 x € M / y » <»> Poro E n lugOr de decir P ord todo' y E N f |x| diré dodo y € N. Veomos .* Se tiene f A x ( 8 xC) ( A x B )x C — ♦ definido por ' f (■ ( x, y ) t z ) =? ( x , ( y , z ) ) t se empiezo por aquí Así ( x, ( y, z) ), x 6 A , y G 8 , z 6 C Dodo tol que f {(o,b),c ) = Se froto Es Io ) de d e c ir Holl em os encontrar { x , ( y, z ) ) probar ( i ) lo existencia de ( ( x t y ) t 2 ) € A sólo debo p robar que a ~ x t b = y , c - f se tiene ! • f ( ío .b ), c ) = ( a t ( b , c ) ) ( 1 } se tiene Por 3o ) Ig uo lo r (2 ) ( 1 ) Est o igualdad se cumple , cuondo Esto ptueba l o, - exi st enci a p ru e b a epae / e s ) • • . . * • . . ( 1 ) ( x , ( y, z ) ) o= x , b = y , c = z , x ,yy, 2 ) € A de (< f ( í x , y >t2 ) = ( x t ( y , z ) } , cual (x^cy.z) : ( o, { b, c ) } = Lo -------------- ---------* ••• ( 2 ) f((o,b),c ) = con z C( o, b ) , c ) 6 ( a * b ) x C la imagen de Según la definición de 2o ) í ( o, b) ( c ) 6 ( A x B )x C s u ry ^ a t¿va ( x #{ y , z) ) € , tol que A x ( 8 xC) . Sólo fines educativos - FreeLibros Moisés Lázaro C. * - c j c m p l o Seo la f unción f ! £ - 2 , 3 ] - — **[“* 3 , 7 ] f (X ) * - 2 x ¿Es f definido por + 3 S u ry t e fiv Q ? Probar. , • En tsfe c # 6 , bastara hollar el rango de f y compararlo con e l conjunto [- 3 , ? ] de llegada a s . » : S i tiern x € por [ - 2 ,3 J <=> - 2 - x ~ 3 -2 ®> 4 ^ - 2x & - 6 Sumar 3 »> 7 - f »> f (x j ~3 ~2x + 3 e ( x ) [-3,7 ] f {[-2,3] ) =[-3 ,7 ] Se cumple : P o r tonto , of i r momos que f es Sur y ec ti va , 8*1 FUNCION B IY EC TI V A OEFINICION Lo f u n c ió n f • f ti i A infectiva y EJEM P LO Seo a 6 A Oéf m o m o s y lo t . iió n 8 es ÍIYECTIVA s í} ) S u ry e ctivo . A # 0 , y lo functon f ! A —•A fijo. : 8 = | { x to ) / x € A j función F : A —♦ i D e m ostrar que F es solo si toi que F (x ) « biyecr-tv-o . Sólo fines educativos - FreeLibros ( f (X }, a biyecfivo . Funciones o Aplicaciones D€M OST R A C IO N . L a s h ip ó te s is so n *. i) . — {101 u = ¿ ^ j « A - * A e só /y e c tiV c . .e s d e cir <, %.. j *0 ff¡) F ; A^ 8 V o ^ 0 ) La i ny e e H vidod. ^ f l = |fx ,a ) / x ^ A Aplicar lo definición de inyecfivo . b ={<x^ / k€A} ‘“FIJO Supongamos que F.’( X't ) ® deba probar q u e X j 35 x¿ , x t € A F {x ' ) , ( f ( x 2),a) ífC xf) , o } » => f ( xt} ^ £ A -.í» f { x* } a según o= a definición de F según la igualdad de pares ordenados. f es I N Y I C T I V A «> x?» Por tanto , a firm a m os b) La x¿ que según hLPÓtests F es inyectivo> S u ry e c t iv id o d . Lo de fin ic ión de F es F ! A— ► 8 x i— ► ( f ( x) , a ) 1 ■ . partir de aquí % Según lo definición de suryectividod , d e b o probar ■-V- (f (* ),o ) € i , 3 * € A / { f( x), o) = F t se prueba lo existencia de x El estila de Dado ff U ) demostración es como sigue! ,a ) 6 S, x€ A encontrar m 6A / ( f { x) , a i - F { m ) Debo ............ {# ) probar que " m ,‘ es " x " Veamos ! ( 1) Pero (2 ) Remplazar F (m ) = { f { m } , o ) . { 1 ) en ( * ) ..... .................... segúnla definición de F ! ( f ( x } ,o ) 4 { f ( m ) , a ) Sólo fines educativos - FreeLibros {# * ) Moisés 1x1/aro C. {3} Pero f es s y y e c t i v © (según hipótesis f es biyectivo ) entonces sé cumple * t yi A ,3 x € A / y = f (x ) f ( 4 ) Según ( 3 ) existe e liJe m e n t o ' V , x € A y según ( # - * J se tendrá f (x ) » f í m ) Como f es i n y t c f i v o , entonces m= x. ( 5 } A s / , se ho probado que ! O odo ( f (x ) , o ) , 3 x 6 A EJEM PLO 2. Seo / ( f m ,o F ( x) . lo fu nción f : ] ~ ® , 2 ] definido por Probor f { x ) = ~3 que f es — •. ] ~oo - 3 ]' ( x - 2 )2 bi yecf i v a. Pe m os tro c ion o ) Lo ¡n yecti vidod ... Suponer que Pero : ... fío) -3 -~ (o -2 )* 4 í —f { b ) = - 3- — 4 ' * | 0 - 2 ( 3» => Debo, probor que o = b ( b - 2 }* (b-2)* fb-2j Pero - 0^ 2 =»> . >> => -(o-2 } - (b-2) Pe r o b * 2 => >> Lo cuol pruebo que OjbCj-oOjO) f es inyecfiva. Sólo fines educativos - FreeLibros o- 2 ~ O |o-2'|»-'(o-8 ) b - 2 & 0 | b - 2 1 * - ( b - 2) ___________________ b) Funciones o Aplicaciones__________ . La S u r y e c t i v i d a d . H r l l o r el R A N G O P artir de f deí dominio .* x £ ] — oo, 2 ] <~> x - 2 ==>*{ x - 2) ~ O Por - 4 - 4 Sumor - 3 : ( x - 2) 2 - 3- f (x ) => fix) £ => ( x -2 )* '* O => - 4 - ( x- 2 ) ? - 0 4 & -3 6 -3 ] ~co , - . 3 ] E l rango de f es ] - o o 3 J Como vemos rango de f pruebo que f es c) 6. Como f con el conjunto de llegado , lo cual Suryectivo. es inyecfivo FUNCION coincide y suryectivo , entonces es bi yectí va. INVERSA DEFINICION Si f l A — ►© f * 1; g _ > £ la condición es uno FUNCION 8 i Y E G T I V A , entonces existe Mamado inversa de f , y« f (x ) <=> defin id a x~ por y }. í- inversa d i f EJEMPLO 1 • Do do Definimos lo función los c on juntos f i A B f { o ) =s m , íí b ) = n , f ( c ) ~ p Hollar inverso la A = | o t b , c ,d delsiguiente j .modo* , f ( d) = q. de f , si exi ste. Sólo fines educativos - FreeLibros y 6 = j m.n, p, q | Moisés Lázaro C Sotuc ion L o función f A —*8 Lo in v e rs o r es biy e cfivo, entonces 8 -f A f ( o )= m <=> def inido ) = n <=*> b a f ' 1 ( n ) f ( c ) = p <=> c ~ f - 1 ( p ) f í d ) = q <*> d = f “ r C q ) o p i romos ir ( f ) » condición por con el g r á f i c o de f , tendremos { ( o , m ) , ( b, n ) , ( c , p ) , { d , q i } i r { f " 1) m y | ( m .o ) , ( n , b ) , ( p , c ) , ( q ,d ) } • EJEMPLO 2. Seo lo función defin ido Se cumple que f es d e fin id o por Hollemos f f :]~co,2] — * ]-00,-3 ] f ( x ) = - 3 - - 24 por b iy e c t iv o .e n t o n c e s ( x- 2 ) * f tie ne f *1 : ] - 0 0 , - 3 ] — » L o inverso" de f es i s ) Hocer . f- 1 f y ) =s 2 — 2 / - y - 3 f (x i = y : y * - 3 - - i - ( x - 2 )* : 4y = — 12 - ( x - 2 )* ( x - 2 )2 = - 12 — 4 y =»> inve rso. ] --©,2] 1 -t s ( y ): 2 S ) Despejor x *> f * ’1 o - f "*1 ( m )- f ( b Si existe |x—2 | = - ( x -2 ) x -2 = / - I 2 - 4y 2 / - y-3* = - 2 ' / - ' i - 31 x = 2-2 V V ? ......^... ..../ f - r(y) Sólo fines educativos - FreeLibros Como x 6 ] -o o , 2 J => x 4 2 *> x - 2 4.0 => |x -2 | = - (x -2 ) ■■Funciones, o .-Aplicaciones* 7. IMAGEN 7-M DIRECTA IM A GE N 01 R E CTA E INVERSA OE ÚN C O N JUN TO 'A ;M E D IA N TE , ______ DE UN CONJUNTO 7 2 1 IM A G E N f. IN VER SA DE 8 , M EDIANTE f . Seo f T E r* F uno .opíicocion y 8 « F. Seo f E — * F. uno oplicacion y A«= E. E 1 conjunto .* r ’íBjajxee / fu ie f ( A ) = | f ( x )6 F / x 6 A j <= F recibe el nombre de I MAGEN’ DIRECTA . de A, mediante E I con junto .* e] > e recibe el nombre de IMAGEN INVERSA de B med ionfe f . f f. ax pftoyecaoN de 8 sobre E es í" í®) l a PfcOyEecjow de A sobre F es í (A) EJEMPLO Seo la función f : E —* F EJEMPLO Sea lo fundón f ; E ~~~*F dado en el sigíe. diagrama. c dado en el sig fe. dio g r ama , / . F f / Y {f i }(M) =ÍP ,<0 f(N) - )<*,,*} j(Maw) - {<$} JVMN =:{ct/e} ¡(MVN) = Mun ■z\blcJd)e l S\ j(E ) í'^/ S e tiene se tiene *. f ( A ) = b ___-V c ■—--\ ' el - \—T S ^ r J \ e jz> = } P,<* , a } t rango de í NOTA ; La imagen D ire cta ,e ubconjunfo de) ■conjuntp..-de llegado í" ({P}) = K bí i-'(B) €) {•' (D ) i'1ÍBnD) = { c , d ,e) ,BaO-z{$,r} 5'<.bud)= £ ; BUD={p,<*,r,,d J-'.co-b) * ; p-B ={/4j Lo imagen inverso,es su b co n ju n to del conjunto de Pa r t i d a. Sólo fines educativos - FreeLibros Moisés Lázaro C. IJE M PLO t ** Seo Sé def i na Poro- IN; ÍR IN | 2n /n6 /N | A H .Ollar fA A « lo l q ue , fA ( x ) = 3n/n£ (N | y 8 C = (-1,0,1 | :v i») f A •{ f ^ i c ) ) S O L U C ION Sugerencia ’ Cuándo e l problema no e encilia de résolver , acuda al diagrama de V ena con algunos volares de A y 8 . Veamos Algu nos elementos de A y S son O Z ,4 , 6 t B , 10, 1 2 , ....... A= •B = [ o , 3 , 6 , 9 , 1 2 ,1 5 ,........ .. £ I d i o g ama de • Vean es i ) En primer lugar ¡ haífdr ÍN Mirando el diagrama fA ( B) = {liO A hora hallemos obtenemos } la imagen inversa de { 1 , 0 } f ; T( ■> * N - £*s decir ; f 1-1 í f í B ) ) = IN A A L i ) E n primer lugar M ira ndo haliemos f ~ 7 í C } , donde el diagrama , o b t e n e mo s ! Sólo fines educativos - FreeLibros C ~ j -7,0 , 1 } ) = fA ( 8 ) A u 8 Funciones o Aplicaciones A horo, hallemos lo imogen directa de A u S ! ft '(A«8 ) * ( l , 0 | Por tonto! ) = {. 1,0 }. PROPIEDAOES DE L A IMAGEN OE LA DIRECTA seo la función f : IM AGEN INVERSA sea la función f ! E — ►F £ — ►F Elegir dos subconjuntos de E .digamos! Elegir dos subconjuntos de F,diga m os! M «* £ 8 « F N « 0 « F £ Se cumplen los siguientes propiedades Se cumplen los --siguientes, propiedades! f> } f ( £ ) = Pongo de f , E = Oom ( f ) r,) y f(M)-Rong ) , f(M ) « f ( E ) ( r ’(0)«-0 I ? ) si B *= D P ,) f í 0 ) ^ 0 Ij)YA<= £ P3 ) si M «s N implica f ( M )«= "f ( N ) I 4) P^} f ( M u N ) s I f { M ) u f (N) P ) f { M n N } €B f { M ) n f ( N ) s P6 ) M « # implica f ( N - M ) « f Í N ' H f M ) 5 f unci ón A«*f_,(f(A)) ) r ’ ÍB u D ) = f - ' ( B ) u r ' ( D I I 6) f -1( 8 nD ) = r ’ ( B ) n f ’ í D ) I ?) 8 * 0 implico f ' l O - e j s f tD)-f**( 8 ) B TEOREMA 2 TEOREMA 1 la implico V 8 « F implico f t r U 8 ) ) •= 8 1e ) r ' (^ Seo implico f ’ í-Bjc f ’ ( 0 ) f ! £ S e o la f unción fes f ! E—F S U R Y E C TIV A <=> f ( f ' 1(B)) = B | T B = Sólo fines educativos - FreeLibros F Moisés Lázaro C. H O T A • Estos propiedades se demuestren opticondo corree tómente é e f i niciones 1) de ímogen De imagen dire cto. j é t a • 2) De imcgen inverso directo e inverso. f ' E DE R j. fe x ) 6 f { A ) <=> x 6 A tíe o f : E si l * m Ñ »> Se pidedemostrar Se empieso T ) seo t <*> fex) 6 B f cx i 6 Pero si Sí Por f ( N) teniendo f (M) como hipótesis M « x€N M e N. ouxi i i ar d e f i n i c i ó n de N , ^ x€M »> 4) : P R U E B A de P 8 im agen d irecta hipótesis i m p lic o x S N f <x ) 6 1} y P a r t i r de h ip ó te sis M . Cotonees 4) f (M} « { M } «= f ( N ) E B « por f ( M ) % ) * * > % € 3) f » A *= E F c f*m PRUEBA f( N ) f (M ) « f (MnN ) « , f x 6 M ...........U hítem nJ* l»¿U*su& i y. defin ición de imagen directo f(N) . f ( M ) n f { N ) . f ( fetoN } r Ho&ra d p i cosos : c u on do Mn N = 0 y f ( M n N ) ** 0 .m cu o n d o MnN # 0 CASO 1 Cuondo MisN * 0 *? f ( M ) n f ( N ) ^ CASO 2 Cu ondo 1} V lo s MnN # y € f( 0 M nN ) implico fue existe oigan x© Sólo fines educativos - FreeLibros tal que y~ f ( x© ) Funciones- o Aplicaciones 2 ) C o mo . y = f ( x e ) 6 f (M nN ) -> x0 6 ( MnN } "3) ■=> Xo 6 M 4) => *o6 N a f{xo)6 f { Mí a 5) => y 6 f {Mí a 6) => 7 )P o / 6) 1) y S U G E R E N C IA : igu oldo d de S .- '- y' € f (N) y 6 [ f(M) n f í N ) ] concluimos ‘ f(MnN) Cuondo se t ro t o conj unt os 6 f (N ) fíxo) '-y..... - « f (M ) n f { N } , de de mostrar uno i n c lu s ió n o uno siempre ¿dr ¡a/2out£RDA ée.1 sím bolo cz c r - é z patAir ¿a rsests... EJEMPLOS. f) V A c z E implica s) Probar: f ( t n n N ) e : fCm) a J(N) A ó / 'V m )) partir de a ^ u t . t. partir ¿ e o fm ' t) Y B < z r ¿m ptica ^cN ¿=-B tmptica. c ; £(w) 1 paré trefe Pruebo de 1 2 ) Se t r o t o de 8 «= 0 si demos trar t i p a rtir d e implico (NI) ouû l { 8 ) «= f*° ( 0 ) f f 1 ( 8 ) *= f~ * ( 0 ) , ten ien do como h ip ó te sis 8 c 0 Porfir de f w|( B ) 1) sed 2 } => f ~T( 8 ) x € f (X ) G i 3} Pero ! i 4) L u e go f ( x ) 5 ) C om o definición de imagen * 0 P R U E B A ' de Po rtir de f sea x . { € ~> f ’f i n D ) f~ -( 8 n i « x € f**1^ 0 i se cumple 5 ) a in v e rsa . según hipótesis. 8 implica f (x) 6 0 ,. *V* f {x } € f fx ) 6 0 6 ) Por 1 ) Asi hipótesis auxiliar •• * 6 8 ... (&ef im ánete írKhstm). definición de imagen inversa « f 1( 0 } r T ( 8 )n r Tí D ) f> ) ~ , 0 .) * > P RU E § A de 1 7 8 <= 0 Partir de f ^ i D - S ) f (x im plica ) i ( ® n Ú ) *> . f ~ 1{ D ~ É } * f ~ U D ) ~ f ~ l l B > y usar la hipófisis i « 0 . Sólo fines educativos - FreeLibros /-j -|q\ 8 Moisés Lázaro C FUN C IO N C A R ACTER ISTICA Se.o A «s W Definimos, ,U ’f conjunto universal i i f — * | 0 , l } , lo FUNCION C A R A C T E R I S T I C A de A , según lo reglo de correspondencio siguiente 1 , f si x 6 A (X ) ■ ' { Q , si x C ( i r - A ) Probór tos siguientes propiedodes .!► . S i A « A* B % BJ , B« = ttf s.s.s fA «B ( X ) “ ígl*) fA « * Í V X| . "V- x 6 W- . * A <* > + fB.«*> “ fA ( x ) V * > f*. ^ < s ) * t - f A(x) *5’ ft - » l x í * V * * [ * “ V %' f A6B t t ) M p. * A « e <=> ■ . V V X) w , -v x e x1 ] ' + f 8 t x> “ 2 V n C I * * 6 117 X) f e I X ) ' ' V x € U - f .o u a f ( x ) . i f x e i j A ' “ * fA <* > f B <y > > . y> e i j x u Pruebo de 1 ) Si x 6 •( A ü*S )<»> U x 6 A I v x f li Sólo fines educativos - FreeLibros Funciones o Aplicaciones 2 ) Si x/ (AuB) <=> x ¿ A » V i V r V lx)S° fA 3) 8 a Como lo función corocteristico tienesoio dos volores volé 1 , si el elemento esto' en el conjunto volé 0 , si el elemento no esto' en el conjunto ; entonces tendremos .* si x I (A í I ) => f. _ t x ) * X tí (a V i ) t d x r A«S *> * o (%) AHÍ o } Cuondo x € { Au f í } ocurren 3 cosos L u e go: fA>B( x ) = 1 fA <x>+ * ' fg- (x T + = 1 1 = O 'x b J Cuondo x ^ + a x 6 8 x € A A XX B xX A a x6 8 > - fA( x ) ¿ f (x ) i — (1 í C 1J o 1 , si x€A a x S i - 1 1 x i A - { U (O ) , si- x£ A - ( O) (1 , si x X * A ) ( A u 8 ) ocurre sólo un coso x Jtí A Lueqo f. J X ) = A tf 0 0 * 0e mortero, simi l or f A (X) +-f _ { X ) B . 0 4- se pruebon O - A _(x) 8 (O ) ( O ) los otros propiedodes: Sólo fines educativos - FreeLibros A a x X s X e8 x X ® Moisés Lázaro C. Problemas ( j ) Sea/? lo s a p lic a c io n e s J : A b y 3 ' b ->.c Probar yoe : v a; Si f y g so?7 i*y ecf¿yas ^ entonces J o f e$ ,una funcióíi iiiy e c tiv a . 3 ^ j es infectiva y entonces / «s in f e c t i v a . c) Si f y g son Suryactivas ^ enton 6) S i C<zs St ces Jcf es Sa/yecfzya. : y ©y «s- S£//yecz*tVa ^ enton jf es © S e a í : TL—+IL una función b i yectiva, . Analizar la verdad cr false d a d de ccudcL una de tq s siguéen les a f ir m a c io n es ¿ ju s tific a n d o cada re s p u e s ta \ <x) Ó?? xe W ^ y e % / j< x ) -z y { t x ,t < x )) f x e 2 j es v / ( x )= o £//?a r e f a c í a n a nti s im é tric a en T¿ \ ■ c) Si A c 2 v entonces se cumple que f ( < $ A ) ~ <¡g: ( f t A ) ) ' si/ryect iv a . Sea í A - > 8 u ñ a f unción cual quiera , . ■ S e a n M y N sub conjuntos f (A x B )x c — > A x C B x c ) de A . £ y ^ sub conjuntos de 8. d a f in id a par f ( ú /v),%)'z pa a)* Probas q u e : f (Afrw) C l í(M)nf(N) ra to d o (U,vf;Z) €• (A x s )x C es • b) Anoíczar Sí se cum ple •: en a b iy e c o io T L . © ® Probar q u e La explicación (x,(y,Z)) f í/ w)nf (/vj.cr f(M n N ) . ‘ ® Sean ¿as funciones cr a p l i c a c) Probar que E C F im p lic a . j ' r (F -E ) - í ' ^ ) - f'é H ) . c io n e s f : A -*b y g: B->c . Dem ostrar q u e s i f y § son b i y e c t i v a s ^ en to n c e s g o f es © S e a £>e/R fyo .y s e a b iy e o tiv a @ fun ció n ^ * x e t R ; Sea A = \ 0 )? , 2 } un conjunto que representa Las notas m ín im a y iji te rm e d ia y m á x im a s de un tur so*. - ■■■ ' ■ xfea A 3 -VfR t/â función definida por f(xflx2/x3>r **±3+*3* ¿¿amada, fu n cion prom edio . a) H a lla r e t Gr(j) Hadar el rango de f . (s) Se denotamos con P a l conjun to de toda s tas funciones d e fi n id a s en un conjunto B y con valores en { °} l } 0 °v sea £n Cx) = n x + b ne fN + } % pa ra c ie r to 9 2 A) P b) í © S e a n e H a l l a r f ^ f f ^ il) . 13 , q x d) f : /W**^ íft y e n - a h a lla r A ) . a *6 (j o ) S e a 10 u n a j-uncron f(2)-b y f ( n) _ f < n - 3 ) , <¥ n > . 4 f 1) son • ( 1 ?st xéA donde ^ A(x) - {• , «¿a [6 .,s i x fA que $ 3) . ? cj¿?y-c ^ d ) a + h t e d e La s V ^ y g 'C l s ig u ie n t e s v e r d a d e r a s fíKx) r f< x -y ) k f(x) es b iy e c t iv e u . Sólo fines educativos - FreeLibros = . una Junción A a ¿ que ® ? proposición ? k: £ ¡ H - { ó } 2) . . f (O) - O > ÍA ) - a y. ’ f í 310) -h f (loo) fl) Q-y-c C u a les n e s £q / 9 ^ 7-f(3)-c ¿ (x fv y ^ fU í + ^ y ) d P ro b a r con S i s e so b e que f n (fn2Í0)) = n+b b) Sea i a aplica ción $ : íPce) -* F d e fin id a m e d ia nte l a igua lda d , ffx j> ffy) . ' Funciones o Aplicaciones Sea ® : . j x/x A Se 4a d e f i n e J es u n a p r o p o s i c i ó n } f u n c ió n f : J ' S e i i ene e n to n c e s : í ( • -f ( S e ja n e s t o p A - y IR. • p ) lo /si x es falsa. es ; . e)/íp) + H $ ) (§) S e a >s \ * e s v e rd a d e ra f ( x ) - \ ' - f ( P) -f(y ) = 7 - f CP) P) , fC p A q y A) o r c) f c p K f -f c g j), o) f (p y -f (< f Y y g dos funciones de A en A } ta le s que A = j i , 2 , 3 , 4 ^5 J ^ sean f sr{* > = |.(i,2) <u-,x) ,(2,3),(3,5) ,(y,n>(5,2)] er(g) = { ( 1 , 5 ) j ( 1 , 1) , ( 3 , 2 ) , ( 4 , 4 ) ., H Q lla r ‘ f « i í l t l í i n 1 (5,3) s (3) f m +-ÍM) J A) 1/5 , 8) V2 ^ c) 5 yo) 2 ^ £) ©Sea } f : IN Ninguna de Los a n te rio re s IR definida inductivamente por : ÍIO) =2 f O) =.3 feh) = 3 fín- 1)— 3 fín - 2 ) y * n>>2 Si g : b\i ir %<n> - £ «s fa lq u e : fÓ O entonces * es : f(n) A) 1 > 8) © S eo A diez q u e 2 , c) , O) 4 3 un c o n ju n to dé e s sim é trico si 4 y , B) 5 e le m e n to s . solo s i f .. Una fu n c ib h e s b iye ctivcc y A -> A si se fíx)-y e n to n ce s f i y ) - x £/ numero de fu n c io n e s s im é tric a s de A en A es l Á)' 5 : 8) * ^ ,ic).10/- o) lo , £ ) A/in$uft* de las a n te rio re s • . (g) Sea f ; JN—*\tN ^ tal que f<*> - Zx ÍA 2 íd 2 <í Cuales I) «í ,JI) de. las Siguientes afirm aciones 7 s>i x es Im p a r son falsas ? (§of>Í X) r X (f«8 )W =* ífo § )(X ) é x - 1 v * X=2K ^ v x in yectiva . . A) sólo H y XII , B) Solo IV iv) Si x es par ^ =2X41 ) K€ W • ^ K € lM es } c) sólo J1I y IV , D) sólo XXI f E) solo X y IZ . Sólo fines educativos - FreeLibros Moisés Lázaro C. Problemas i. Sea j uncx fu n c ió n d e fin id a en H p u e c u m p le J i x + z ) ~ f(x> +- f o y f a z d cuáles de tas s ig u ie n te s prop osicio ne s son v e rd a d e ro s ? : f (O) zr O I ) Sean } 11) : ÍR -* ÍR f , % y h , f - ( - 3 ) - H 3 ) si f(7 2 )= 4 íi3 > t i l ) g (x )-2 x 4 i ; * §(h(x>+i(x)) = x2 % (h (x )+ 2 f(x )) = 3 - X2’- 3X e n to n c e s , AV o 3. % (h ( - £ ( * ( i>))} e s : 8) 1 Sean f , cy 2 y § A ) -5 . , 4. Sean ■ A ?B ta le s que : • s a b ie n d o que ( , D) 4 sub e p n ju n to s f u? 3 ¿ i hallar x * -3 > -c)-I 5 q u ie ra ^ ta l q u e 31 •, de R £ ) - 2- . V se a í : f > (C ) * c a / f o o e C ' V c = \ * 6 IR / § )lt> = \ B una función cual- \, w C c B . <1 } f 1( c ) . A) 3 - 4 , | ] _ { l } 5. , ' 11 ( S“\> f ) ( t - — ) B) inyec.ttvas . g -'íx jx ü X+3 Hallar e ) 4- funciones reales f U> - -*±i_ . D) 3 / , 8) ,2 C > =) D - | , A L - M , O) 3 f ,t l , E U |,|.L Hallar la sum a ale va ld re s e n te ro s de K para que la -función -f(x) = 4 x 2 - k ( 4 x - i ) + 6 ño te n g a in te rc e p te s con el eje X A) Ó , 8) 1 - c ) -z ; D) 3 . , E) 4 . ,9 Qf. o - * Sean las funciones reales de variable real ( X+2 f(x) = 1 §(*) = - x2 +1 ó .Cuáles dé la s I) (S°í) íx) = - x 2 _4 x II) I II) ' x>,0 siguientes proposiciones , x í l - 21 1 ] 3 D o m ( g aj ) - o o m f ( § o j)U l e -X .2 4-2 X , xt t - 2 /c o [ . ■ son v e r d a d e r a s 7 A)sólo X 7. , B) solo I y X I I Sean las funciones } c) soló I I y I I I j D) T©das reales de vqrtable real f(x) , - ) x+2 r ká 1 (*-1 S<*)~ *2 Sólo fines educativos - FreeLibros E) Ninguna . , x >1 , ‘x<o Funciones o Aplicaciones d CuQÍes l) de las siguientes a firm a cton e s ( § ° í ) (X) II) §o* ÍIJ ) = -1-4 (§ ° í) < x ) = xz - z x + i son v e rd a d e ra s ? A) sólo I I 8. X2 + 4 X , X 6 IR es función inyectivai } x e ]-o o ,-2 [ B) soto n i } j e) sólo X y I I ; o) Todas ^ E) Ninguna,. ¿ Cuates d é la s siguientes afirm aciones : f(x) = |x1 - zx| inyectiva en [l,+<»k I I ) Los únicos valores d e C para los cuates f (x )= x2- z x + c c o rto al eje "X p e rte n e c e ol -intervalo t P , l [ ' I) I I I ) El ra n g o d e f (x ) = x2 - 2 X + C e s subconjunto de t°j+°c>[ s i c e [ I ^ oóC son v e rd a d e ra s ? A) Solo I I I ^ 8 ) soló I y I i , c) sólo TI. y I I I - °) Todas yE) Ninguna . 9-. Sean tas funciones reales de variable real entonces Dom f HDomg n Ranf n Ran§ es iûal a *. A)I-<x>, 1] } 8) C1,2] } c) 3-00^2] 10. Se definen §(x> = * 2 %(x) =. } t>) ^ f<x) = V o 7 s i y 1-1 > si 1 U-zM**-c| } e) Ninguna de las anteriores . tas siguientes funciones (1 , s i X>1 s e a firm a n ; fon - _V2-x’ +3 ^ x -1 de U en IR *. >h ( x ) - f (x -i) x <1 I) Ran (H) = Ran (f) I I ) R a n (fe g ^ - { 0 , 1 } III) °om (fo% ) - ¡R Son ve rdaderas A) Sólo I 11. La y fu n c io 'n : I I ; 8) Soto I I y I I I ; c) Sólo I y I I I } t>) solo I I I ^ ) Todas. o le i IR en IR d e f in id a por f(x )- — t i Ixi+Z tiene A) -3 12. rango C ^ V M ] ^Sea 3 B) -l ; c) y í *. IR . H a lla r 2 M - I m ; D) 5 , e )7 definida por f (1) = 4 ; f-(z )- 4 p f (n+2) = 4 + f (n) 5 e a firm a *. 1) f{8) = IG II) III) V -h e • í (n) es m últiplo d e 4 . f (35) ~ son verdaderas : A) sólo I } B) sólo 1 y I I . c) sólo I I D) sólo I y -I I I Sólo fines educativos - FreeLibros E> Todas . Moisés Lazaro C, 13. Sea f ; C®, i) a.) probar q u e b) *4. |R una f unción de fin id a por : f(x> = | * >$¿ ■* *s racional fof - I d e n Co,í} h - x ? six es irracional probar e ^ = £0,13 Ram gf Dada la función de variable real : f <x> - — 1_____ tx-ti-ix -21 a fir momos: (f> Oomf es astntcrtQ ve rtical } (SJI&ngf =1- ^ - 1] u [J,too C / «!* = § ¿ Cualesafim actones son verdaderas. 13. S «a definido Se a fu m a : U ) f (2X) + f ( 3 y ) z O U) j ^ f par a y es impar ] , } * X JI-C H <3) son por f t x j - . j ' 1 > st '* *****'. 1-1 , s i x es impar ct€ *H ta l q u e : § «**) = c¿ -fcx) ; ^X€BM verdaderas : A) s<ka O) > B) sólo W y (2) ,'C)' Salo z ? t>) sób cz) y (3) > e) sob (3) 16. Dadas la s f u n c io n e s r e a le s : f(x>= ( z - 3 x| (x + i) gOC) « v/S-SX -2X? Saan A = Oom(g) y 8 = Rang ( f > . Hallar : A V C -3 ,-i] 17. , AOQ B )fc -3 ,f| } , c) ,> )3 -C o ,-8 ] , E) C Í > f | ] Sea fíxy = 2x2 - 4 x - f 3 u n a función con d o m i n i o A o IR Se a f ir m a n :. O) Si A = £-2,21 }- entonces R a n (f ) = I1;13] U> Pora A = 3 - 0 0 , 1] y f e s in vectivo. £ ) Si A = IR. y fc x )¿ 9 } e n to n c e s xe L ° ; 33 son verdaderas : A) sólo O ) ; B) só lo m ■ c ) só lo (Si y-O ) só lo <2) y (3) J el) s o b ti) y (2). 18* Hallar la sum a d é lo s v a lo re s e n te ro s d e K p a ra q u e la función c u a d r á tic a -f(x) z 4 x 2 + K ( i - 4 x ) + 2 no t e n ^ a in te rc e p to s con e| e je X . A) o , 8)1 , c) 2 , 0 ( 3 ) , e ) A • 1 19. D a d a s ta s f u n c io n e s reales *f(x.) = VJ-x ^ §u> = — - Si A = Dom (fo §) ; hollar A )3 -V T ; \/2 C - W 20. />B )l-\f2 ,r l [ u 3 i >y2,[ ; c ) 1 - ^ ñ í j D) 3-oo,^]ur^£x>r Sean las funciones * S r ( f ) r { ( 2^ 0 , 5), (4, 2), ,(8 ,4 )f Br(%)=í(2fV ), (S,*),^,*), (5,1), <&,*♦) , a,C)A(S,é)} S e a h la función con dom inio Í ^ A ^ / S f t al que § = hof Hallar h (n +-h(Z) + h (4 )+ h (5 ) + h( 8) A) 17 ; 8 ) 16 , c) 19 , 0)20 , e/ 21 .. Sólo fines educativos - FreeLibros < § )- FUNCIONES REALES DE VARIABLE REAL 4 0. INTR ODUCCIO N. E n aste capítulo sólo Es decir t de funchones de llegada paro dé v a ria b le real. y el conjunto de IR a coincide n co n IR . las d e fin ic io n e s , da da s en el los funciones F UNCION R Í A L reales en el que el conju nto de p a rtid a son subconjuntos N O TA : Todos 1. trataremos d* funciones DE ca p ítu lo 3 son va lida s reoles de v a ria b le r e a l . VAR IABLE RE AL . D EFIN ICIO N -I. Sean A y i - dos subconjuntos de' IR . Diremos que f es uno función existe un único número reol Lo notación y = f ( x ) se lee * y es Jo im agen de x de 'A en © , si pora íodó y € 8 * y es igual o f E ntre o tro s íx). de x f en x " "y depende de x ” & y ~ f(x ) ■"x " e es que que . “ y esfunción de cosos ! Lo notación ein d ic a por f o que "y es el valor de la. función Tam bién «ndico que , tal que y « f numero real x € Á , nos in d ic o que .* lo y M es lo vonaole^ independiente variable dependiente . Sólo fines educativos - FreeLibros x “ Moisés Lázaro C. Lo f : A —♦ 8 notación ,donde A ~ IR , i - R * x 4 -«y «f{x ) nos indico que 1. 2 1 ) f es uno función de 2 ) A * ©om ( f ) 3) -V- * « A , 3? y e 8 / y * f { x ) 4) f ( A ) » Rongo* de f, FORMA UNA IN TU ITIV A FttliCiOÜ 0C ACAL A en I . donde f ( A ) « e § ; PCRSIVIR OE En el proceso de lo enseFonzo suges t i yo e int uit i v © o gráfico poro qtié recurrir VARIA8LE ACAL. aprendizaje no hoy noaa a lo aprender el s i g n if i c a d o rep re $ e ntoc ¡o n y función. * 6 róficomente , si f ^ A - » Í es uno f u n c i ó n co n ju n to d e p a r t i d a Migodo 8 está PLA N O XY esto g e om e t r ¡ c o luego la d e f i n i c i ó n Los puntos conj un tos in f in i t o s numerables o Ademas , el dominio ir(f } sobre el $r ( f ) sobre el x € A corresponde un 6 íx ,y ) eje 6r rango de f tínico A , puntos del y € 8 . ( f )c o n f o r m a n conjuntos infin itos de f , que es eje X y el de real contenid o en el e je Y ; además ek G r ( f ) , s o n en el que o codo más de vorioble real ; el ' contenido en el eje X y el conjunto de t A GR AFICAM ENTE c o n ju n to s f initos discret no numerobles es loP R O Y E C C I O N es lo P R O Y E C C IO N Y. Sólo fines educativos - FreeLibros . del del Funciones Reates de Variable Real Eje m p lo s ■ ^ u y— Gro fíeos EJEM PLO 1 EJEM PLO 2 Seo g i IN *—* IR , definido - * { 2 , 4 , 6 ,8 } Seo f : 1 1 ,2 ,3 , 4 } por g < n J = (- r , " i i z i . definid o p or * Si tobulomos f { i") = 3 por y luego poro n impar obtenemos*. f ( 2) «4 o ) P o ro n par } tenemos .* Z 4 6 f í 3} = 6 f (4 )= 8 Su g r á fic o e s por se porado poro n g ( n ) = { 7 / 3 ,1 5 / 7 ,2 3 / 1 1 , i— : 2} - «J «a con junto inf inito n om orob lo Cuondo n es muy g ra n de , la función se aproximo o 2 bj Poro n impar , i i m m ó s i 3 5 g t n ) = | - 3 , - 1 1 / 5 , - 1 9 / 9 ........ -* - 2 } Cuando n es muy.gronde lo función se 6 aproximo ol número - 2 . 6 4 i i i » -tr— I------- 1~ I Z 3 4 6r ( f ) S f M, 2 ),( 2 ,4 ),( 3,6 ), (4,8 l} En este coso d is c r e t a fin ito. f es uno f u n c ió n Oom ( f ) * ¡ 1, 2 , 3 , 4 } =A Rong í f ) * | 2 , 4 , 6 , 8 } = B En este coso decimos que g es uno función de variable d i s c r e t a junto in f in ito y forman un con n u m e ra b le . Discreta, indico puntos separados que no se pueden unir trozando una re c t a o curvo. Sólo fines educativos - FreeLibros Moisés Lázaro C. EJEMPLO 3 EJEMPLO 4 f (x ) * 3X5- 20 x3 +16 cuyo dominio es Esto cur vo ,es uno funcion^rooiónol cuyo reglo de corresponde itfio es ! todo IR y cuyo rongo es todo R . En este eoso f es uno fu n ció n de yorioble c o n tin u a infinito NO X- i y form ar un conjunto Su dominio es x G IR - { i } * NUM ERABLE. , que es lo proyección dé lo curvo so bre el eje X. CO N TIN U A , significo que los* puntos del 3r ( f ) se pueden unir., obteniéndose un TRAZO decir de c u r v o CON T I N U A O A , es podemos t r o z o r lo curvo uniendo los puntos ( x , y ) sin levontor Su rongo es ] - ® u [ 2, + » [ , que , es lo proyección de lo curvo sobre el eje. Y;. En este coso, tombie'n, f ( x } es u no función de variable continua. *1 t o p u . Pero hay un detalle, la curvo se hc,,roto,, En este co so , el Anolisis Motemotico en x~1 . nos dice que f es uno funeio o Pero estos cosos,el Anolisis Motemotíco nos dirá' que f ( x ) es D I S C O N T I N U A continuo en todo IR. en x = 1 . Pero N O T A .* E l nombre de función independiente x f ( x) es continuo e n 3 -i»,iC u 1 i t® C- reol de vorioble reol es porque lo voriob le tomo valores reales yiavorioble que es" y " tombie'n tomo vofores reoles . Esto f u n c io n e s vectoriole s que es yno fu n ció n de de variable IR en reol IR* . Sólo fines educativos - FreeLibros tal dependiente f ( x ) difie re de los como f (t ) ~ { Funciones Reales de Variable Real f.y EJEM PLO NUMERICO PARA CONJUNTOS FINITOS Seon los conjuntos: A ={ ' i , * , S i 7 } dónale. : y B =j o , 2 / j . AxB :\ü,o) ,(1,2) ,(i,4)((3,o),(3l« , ( 3 ^ \ { s , o) 1C 5 , i 5 j | - ix A : |(o,tv(o,sv1(o,s),(o> T)i(2ii),«,v),(i,s)j2,l),(i,n,(¿,3Uí',5),(4IT) j . De ios siguientes conjuntos que s* don a continuación ¿ diya tM. cuál de ellos es uno. función de A en 8 , cuál de B en A C O N JU N TO D£ P A R E S O & ÜEHA& O S Gfíífc ^(1.2) ,(S il),(S ,l'> ,(T ,I) y cuál i» es uto función? D / a $ «a m á s os veñn J va % y q f i ^(1,0), (3 ,2 ), (5 ,e )p A K (2,2) } b r (h )- ^ ( 2 * ),(* .,s ),(o ,?> | 6r(j)= (j r W r j c o . i y í j y . ? ) } Sólo fines educativos - FreeLibros V :'# ;V: Moisés Lázaro C. SO l ü c i o n : a) f / es u na fu n c ió n ote A an 3 y se dzn ota a s t donde ; D o m (f) s : A -+ B }■ =A fíonfof/) r j i j C i 6) O no oí funa'on d a A en B } p o r y un a l com ponentes ote ¿os p o rte s o r tiz n a d o s efe f p¿¿a dos ve ce s . ¿© fue genes gue dé pon d a r ía y e¿ " 4 * &t a firm a r s ó lo Ade/nés : c) son e¿ " 2 ” fu n c ió n g u ia ré d e c i r qué a "3 ' se re - ¿e corresponde do* /roa ; /o cu©/ contradice a la d e f im e t ó n deb a corres- rancho . del = { 1, 11, 5,7 ] = A D o m (§) A es c/no función e n c o n tra m o s g u a * 3 " Qi codo éC em en to de/ dom inio puz un e le m e n t o } ¿ o d a s ¿os prim eras observar da B en Á y s e denoto cxsí h : B -* A Donde ; . Dom(h)' z ¡ 2,4,0 ! = B A o n 9 0 (/ > ) z ¡ 3t5; 7 ) c d) ^ et Donde f/na función D om (j) da A«l?j en 3 F es í/nar función Donde y se denota a s i z \ 3, 1,5 } C A £© ngo ( j ) *) A = \o,2 } C da 8 B en A y se Don? ( F ) r { 0 , 2 , 4 } - denota a s i F *. B A 1 £a/?9o(F) r { 3 ,7 } C A NíCfTA «k Ac O5Í14C/0/V Ûrm . form am uAjA&n&ilto.<Jk reconocer p a rte , crraLznouícr) jVLirnc/taA £4 jumsx fMmcicm. , ¿ 4 A zrm p c m tv t& i cázb&i Sólo fines educativos - FreeLibros JUmCoiy*vri6xate mofo- 9me /áxfo /Svt /djft/t&nfoá, . Fu n d o n e s Reales de Variable Real Í.A 0QAFICO DE UNA FUNCION a b t f i T i i c i Ó T L •'¿ d e a - J a . Ju m c io n . f : A — * B *• ' . ción efe A en B ** jáe Jtixmxx. GAAF/ca emf mt AuJb&>7LjM¿n£ct y^rcxúcüSr ¿méGdikno' de AxB quecumple <&s condiciones ; t) Eemf&rw) xA U ) S i (X ,y )€ § r (f ) A (* ,2 J 6 (jr ff) yToíia e t c * n ; g ró f ( f ) = r~ 2 [ ( x , fe * )) / x € A } EJEMPLO 1 | . S « t a funció n: : i ¡* 4 }(* )- i x -5 * t[í,3 ]s A •"?v/V.: *'3 J- r|*^ i » * » - * m m *« M = b . . i m m A í 1 ;>b 1¡ 4 i £am© v t A*B >u * -j .* f i g A -2 EJEMPLO 2 1 Sea la función l* § ( x ) = Z \ñ e x € [0 ,5 > 1 fOústvC =M y€ [ o , 2 v ¥ > = N ia : i Com e w m e $ C f ( ^ ) C M x N ’ * l 1 * i 4 S 4 » M EJEMPLO 3 1 §t©i l á f u n c ió n , h Cx) ~ xC < O , + 0 0 > = * ! . hí«r - l4 !1 y* < 0 ,+ a D > -$ ji 1 1 .j R Sólo fines educativos - FreeLibros « Moisés Lázaro C. 19 ¡yyôiactori pam las <ffync¿Qnti$ *<£<*% funuon&i AeaJt* (fa va. - AtaJb&e /tmo¿ /han v<M «aW f* r Ja* /tita* . / , § , h } i , j , m. U J , « fm* Í o a JtsJfe&A 7ruxy¿4&uf&d •' F j®, H, I , J , U . V , w . jExvmbíén, sée <m&an yíué^noUced , mwmtíkr A& Atf&fm t M “ frvLLt/uxó M fAtmevcmm . * p r n f d o ;. f , J t , }s , ........, 1 n ,S » % > % ,% > \ U ví^cjíoi de to m o , h^ efe. fu n c ió n uno c a lc u la r * j la ai j de g s e rá será 1 ) , (*, lyfe), C3,, Si cia de h será es F ü lg é B Q M c á ; *. } ( * ) que p o ro f . te n d re m o s que lo reglo d e { ( t ) z }-x cq - , x£2* j , tendremos que lo mgk* ck corres gcx>= 2x - i , xe J ) tendremos fuela mqla ét corresponden h(x> - ¿ [EJEMPLO 4 1 3 t W P )r {(x t 2ae?- i ) J *. c fR | de F E x p re s ió n dominio d e Si & § )= | (l>l ) ( 2 l3 ) l (3 ,5 )l ( A , t ) |pandando EJEMPLOS] a, ( 2/r> #f 3,Q , ^ S > , : ....... Si /responda n eta efe EJEMPLO 2 1 >5 e le m e n tó de l p o r o rden o do(x,f<x>) e l se g u n d o v a lo r d e H x rt q u e p e r t e n e c e EJEMPLOí T j dt ummfímtion > Homoreglade corresponde nciá c o r r e s p o n d e n c ia de nos p e rm ite , hl , • tendremos 9ê la reófa de cor/esponcfenetQi i x > = 2 x ? -1 z j I EJEMPLO 5 1 S tfríG ) = {(.* , ^ e' ’ /!) / I f <- oOj + c o ^ j. tendremos - ponderre/m ofe G es G <*> r vTT í? (? ■1 . Sólo fines educativos - FreeLibros 90c ía re^/ad* co/res-i Funciones Reales de Variable Real 1.7 ¡D e te r m in ó le io n oto. una. f u n c i ó n * U n a J u n c ió n “f * q u zcü x b ie n te r m in a d o ( también se oít’ce : bren d e fin id a )} St St conocen : a) y 3 u regía cíe co/re spondene tcx / ( x ) (a ^«ot ¿a ecuación, ofe ¿a función) b) Su dom i r u ó : PROBLEMAS © Determine <¿t dom inio y rango d e /a fu n c ió n J (x ) r R ESUELTO S con una asinto ta horizonta l : y r o . 5u gráfico es : * Solución: a ) -x s t ) o m ( f ) « x € fR - j x*®/**i=o| C=> x € ÍR - f - 1 } Con una asíntota ver. ftcaí ; * r-i , b) Paro d e te rm in a r el ranô de uno fun ción } procedamos üeí sgte modo : $ Hacemos } (*) a y 2®) Des peja r n o s x en t é r m in o s de y l ñ D isc u tim o s ¿os d if e r e n t e s cos09; i orno en el c a p itu lo re fe r e n te a © t ^ t e m i n e e l d o m v m y m ngo<k & /</naon §<x) - ^ m ia c io n e s P a r a al presante Y= '3 3 T e je r c ic io te n d re m o s a) x 6 Domfg) <=» ,xe ° y<x * o = i <=Oyx+y : | «=> yx S o iU C tQ N <=* x € |R - 0 = i- y * * x€ IR «a* X y Luego : y £ Rongo(f) Csp ye (R * {**/>«©■} *=* y e ÍR- {o } b ) D e t e r m in a c ió n i 9) H a g a m o s Sólo fines educativos - FreeLibros del ra n g o : § (x ) = y Moisés Lázaro C. Despejar x ; y = -fx $ 0 Como ^ 7(x\l) ~ I <=» X1 + y C l y • ^ T '^ 0 O i <=* Z S < 0 , 1 ] y x V = i-y Hollar el dominio da / (x )r Ln/l ___ _ SOLUCION : v/5? f (x )r Ln\Á~ T Pero r i U ( l - £ ) 3e Ánaliaorf: v e Rongo ( g ) L-r <-> - ¿ - L >ô V - --f Por lo tomto : x € Dom(f) y- í o l T <=4 q l-~ p >0 €=> 4 - 3 Í > 0 * y€ < 0 , 1 ] «=4 4 >x2 . <a* Con os*nío¿a hartionfarl y =o . . x*<4 ^ 4 -2 < x < 2 «> xc<- 2, 2> (5 ) peterminor el dominio de £(x) = / x Lna SOLUCION : St }{x ) ~^J x {n x x e D o m {f ) <=^ t entonces ; x lnxÔ x>0 @ I n x }y Q A V - % L m i^ rm in e «¿ dom inio y ro/jô de x N <o A *>,o A f v [ x^0 A i Ln x 4 o ¿n / t / n c iV n h ( x ) = ^=r¡7¡SOLUctQfsJ ; á) x 4 D o m (h ) <=£ c=* x ^ o x e [o , 4*co> Cs*i#eftb d a l fango, hocemos h ( x ) = Y y ~ / 1— vGt *1 » c=> <=> . *=> X £ [ l , + OD> Donde: y (V x + 1) •I ' *=$ O < x 4 1 =♦ i i) LnxÔ «=»■ V v^x t y = 1 . yV>T vT = i- y xê° <=* ti) Lnx 4: Cl i x x<<?* a a >O N<1 A x >O = -íf ** <3^ Sólo fines educativos - FreeLibros > O <x ¿ i Funciones Reales de Variable Real e l d o m in io d e c/ajl de &*S s i t i e n fa lla r ízs /tinciones: (g )/< x f (x ) r 2 x2 - Y * -1 Sea *€ <-oo,-2>u<J,2> @ ) Sea | (x ) : *€ C l,4 ] *€<-co,Z>u <3,£»> ¿x+C @ © Solución ; 0 ^ 0 , S v K *) “ 2x / * € {£ -¡-2 ,2 } © fe*) = ■ *€ <- l,o>u <o;oo> © H x > = U>g(’c © Sx) © f ( x ) r \ / x 2- X - V + ^ U X - X J' y del producto O . ^ (x ) z x2 + 4 . J (l)c p (3 ). Solución : -g* " » 39.. i»3(i + x> <X< */2 + 2 XJJ Para %*. cfe. lasfunciones de los eêr Cicios cteí © 2 3] *€¡ , *« [2,3> V 3+2 a }(*> = - = = = ; V x 2-X + 2 al @ ?hallar F(*)z ü » l ^ T .f S con h / 0 . © í( x ) z '5 0 j ( x ) z - 2 x 4- FW s o 0 {(* > = 2X 1 - ! 3 F < * )= -2 FO O z4 x + 2 h *€ <-CD,-í>ü<2,CO> © { ( * > = . 3x2 - 2x +2 F(x) = Gx + 3 H -2 - x ¿ ^ + 2K7I «2 0 © $<x>- \ / s e n x - i 0 fjo c )-a rt S e n . i i _ l o ^ ( 4 - x ) xc[i,¿> $<*> = - ± C(>0 : 3-2X ( ® t(* )= 7 -~ ------- -f V x + 2 ^ * 105(1- X) X€Í2,0>U<0,Ji > ® f(x) Z xeíR -1 . v t ^ a x +i ' F(x ): - - 0 f(x )r 4 - X F lx ) r - 1 . ® H x )z X F (* )rl / Vi Í**M-U*h)-»5 f ( x ) : lo§ s c n ( x - 3 ) -i- v/ i g - © }<*) z n/'3 - x ' 4- ore eos x2 x.€<3/] ix 1+x2 f(x )r l - x - 2 x 2 (*) z -1 -4x - 2h f G r a jic a r la s Siguientes funciones : X € [-l,3 l ' © ÍP 0 = . " © © , x íl [— 5W= j * - ‘ i 3. *€ P , XZ1 I X * -¿ xe P - (-1, i ) © * * > = £ ? © l(T )r ± Ü L x€|R-\oJ @ *<*>= 2x-3 *€ IR - \ 3á } »<«>= ^ X€ !P -{-2 ,2 } j<*) r'/zx+A x >, - 2 @ i<*)= * x= 2 ■x1 - @ j(* ) = x>C x t2 -2 , x ~ -2 S X -1 3 X + & © ) - Y * 2 -4 + *€ <-cn,-2juT3,«>> ^ © ; x t Já y X Z 3/^ , X ± 2x - 3 $(*>= 4 © (3-2(**.hl)( 3-2*) (37) f (x ) = \/2X1- X 4- 5 i © . gO) . H a lla r el valor num érico d e lo fra cció n £ 3 f(x) z log U - X2 | © f(2} , . ^ - G x V f n x -G H a lla r : § ( i ) , g (2 ) , x ^ S x +C . Hallar Sóiixtdn. : 4 , -1 ^ X€ <-3,3> ) = Lti ( 9 - x * ) ( ? ) f (x ) = L-n ( © | 8 x 2 +18x {(»> = <■’ — z í ^ r [ -3 Sólo fines educativos - FreeLibros >5 lA . y *x r'Vt Moisés Lázaro C. a En cacto u a o cié los ejercicios del © a l © 44 X 2-C } 3t€ < - < » , - l > “5 > X € [-1 ,K )> I @ N * )- ac-15 > xc <KJ,oo> * -l ,1 A I , {(x/OctR2/ y = - S x > 3 ] -1 í * < 3 © |l*#y )s m V © J{* , v)HRV x>, 3 , !<*>=<Í 2 X - 1 W *)r. @ V (x )r . í 1 , 1-1 , ili X x V4 © h(W).= j (*,yK jp2/ v* - x1 = 9 1 {<x ,y)€ írV y r - v í ' - x ' } © |(x , yK ÍP2/ y2 z 4 x , una fórm ula p a ra la función otesertta : © La junción 6 bajo la cual X ^ 1 Xr un c í r c u l o d e r a d i o 3 l xi - 4 | , ¡xi - 5 , }x|s<5 © La f unción F b a ja la cuál P (x) es el volumen de una esfera de radio x . © La función V bajo Va cual V ( x ) es el volumen de una caja ete base un c u a d ra d o de lodo x y altura que es el doble creí lado qfe la b a s e . ^ IxJ>5 Hollar e l » Ixj 4 }xl 4-4 |X1 >2 f n/®- > - i . \ / * 7-2 s" , 1x1 > 5 1*1 4:5 XX(x)r 5 @ f (x > :: |Xl 4- l x - l l © g (x )- 2 |x i- 3 |* + i{ © h (*)- x* - ix i © j ( ac) r A * 2 - l*-ll © K (x )- l * a- 4 | © 5¿ 6 (x ) = — @ 5t ¿ E xiste G Í 2 )? ¿ G (- 2) 2 rango cíe las Siguientes funciones: © f(x) r - i / T T , xN <j @ § {x ) z 2 x 2- 5 , xeR (§) h (x )z 2 x 2-5 x€ <-2#2] © xc [-5,3] P (x )r n/25-x 1 © G M --m -x ? , x< [-5 , 5 ] © H (*)= -33C + 5 , xc < -2,3} © f(x) r , < 0 ,4 > , ^ € £ 4 ,4 5 |x - }¡ © S (x ) = | * * - 2 5 | © h(x) r - 10x 4-20 , x c <-0 0 , 3] © P (x ) c \ / x - x 2 x c [o.-, l ] © puesta. ~ ¿ E * ste §( i) 7 Exphquc °°r {*i* * 'too r i Existe h(-3)? i t p itz c s t su«w vSr ' x*3 Puesta? ^ c_ x1 -3x~Sólo IB ¿ £xlSte (-3)7 £xpli fines 5educativos , G (^ l) Z “ 2 5 ^ 4- 5 0 2 Existe bo) ? Explicar su res g (x ) - x + es el area de |x|>2 | \J *’ -2S (S) 6 (t) T . ( © La fu nevón H bajo la cual H ( ! ) es el volumen de un cubo de arista X. 1 > 1X1 4 2 x y*2 r J C - X ?) * * 0 Ixi f(x) = 4 ] E n cada uno de los ejercicios del X a l 79 dar X -J $<*}= ■; @ © x<0 0 © Y=4 | ll ^ v ) € lR 2/ x * 4 -y 2 = : 9 } <§) ¡ <^y)€fR V Ix-H f(* ) = y r *H z J *>o , X ^0 0 ® © -xf í< -}* <¿ ’ x J - )6 > © © [ (*,*)€IR2/ y2=: - 1Cx J * < -L S* ' 4 * © razón pona SU respuesta . En cada ejercicio obte ner la g ráfica y dar su dominto y contradom io . @ , d*c‘f si las relacionas dadas son o no funciones y dar una 5l - FreeLibros , Funciones Reales de Variable Real 1.8 FORMA EN OE EXPRESAR FUN CIO N Do do uno ecu ocio n despejar " y " Si se puede DE en d,os en términos T) De : de **x ” y otros direm os DEPENDIENTE IN D EPEN DIEN TE F {x ,y )~ O , íeVminos contrario VARIABLE V A R IA B LE v ó ri.a b le s d e s p c j o r “ y ,, en e x p l í c i t o s ,en coso E je m p lo s LA LA unos veces es posible veces es im posible . de " x " se ob tie n e n funciones q u e y ~ f(x) es dado implícitamente. .* Ax + By + C = O 3) sí 8 jé O • -> _ JL 8 y : y = Despejar O e : x* + y* = 9 8 X 9 _ x* y* a y * í y/9 - x*'1, donde 9 - x2 - O s> A s í o b te n e m o s .* - 3 fe x fe 3 n *f ,( x )* = - —A x - ■—C 8 , B*0 x .e f-3 ,3 ] 8 Donde' f|x ) ■.€.« <~> A s í , hemos d e f in id o x 6 IR l no la f u n c i ó n es codo f u n c io n x , porque p o ro 6[~3,3] corres m=-| ponde dos X € IR v o lo r e s un p o s i t i v o y lla m a d o un n e q o t i v o . F u n c ió n 4 } De: 2) de y , De : { x - o ) ( y - b ) = y ( x 2- 9 ) - 2 - 5 L n ( x Z- 4 ) = o K , 'kWÓ 2 4- 5 L n ( x 2- 4 ’ } K =>N y — w b = ----------- ' y ~x2 - 9 -x ~0 Dónde v K => . y e m <=> . X* - 4 r = -b + <=*> Donde y 6 IR <^> x 6 IR - J o } A s í , hemos d e f i n i d o fix )> b f x- o lo f u n c ió n .x 6 IR - { a } > O a X2 - 9 ?4 o x2 > 4 <=> [ x > 2 v x < -2 ]a x# Í3 Así quedo bien definido lo fu n cio n Z«-5 L n ( X * - 4 ) f ( x ) « ------ ----- y -----------. X - 9 reola oc co» we« p»«- oeiMcn/iL. Sólo fines educativos - FreeLibros x £ <-°°r2>u<2xc»>-{'3tx3} DOMINIO Moisés Lázaro C. 5) S i.* © * es ío voriobfe in d e p e n d ie n te siguientes ecuociones q ) r a» 3 sen# b ) r'* 3 {1-eos © j c ) que r es f u n c i ó n de que r es f u n c i ó n de 0 • r ss - sen 5 © Lo n o íocion r«f{© ) ecuoc ion r1* grá fico es : Lo cuyo in d ic o 2c os0 “Ó © no expreso urro función tsóto es uno relocion 1.8.1 v PROBLEM AS Coól de lo * s¡guientes conjuntos A •* | { x, y ) / x y ?- x * definen funciones 2} H - | íx, y ) / C = { ( x, y ) / l y l - x } I 0 = { ( x , y ) / y * íxl ) J = E > { = ( x ,y )/ ( y-T I- { { x , y ) / I y. I - I x-1 I = £>} L> 1x1 = 0 , 6 , M, I ..J*, L . no son funciones , A , B , C y 3 ■= x } ( x , y ) / ' 2 y - x3 - 2 x2 = x, y }/ y x2 ~ 4 y - x o j = O| K = { íx , y ) / y4 * x * ~ 4 } S O L U C IO N Son funciones y = f(x ) G = { ( x, y ) / y = 3 - j x - 2 | } 8={{x,y J / - U - I } F 6 r =s 2 eos 3 0 -d } §} expresan y*r* lo vúriobte dependiente, Jos , E ,F , K Sólo fines educativos - FreeLibros j C * ,y) / y * 2 J x - 2 | , Funciones Reales de Variable Real 2. DEFINICION GEOM ETRICA V A R IA 8 L E DEFINICION 2. 1 del REAL 0£ f. de A rn de f es rectos . d i r e m o s ción FUNCION RE AL Seo f uno r e í a c i m S i el Gr á t i c o DE u no 8 , A & IR , ü r e c to , curvo F . o u n ió n de curvo s y /o que f es uno función de A en 8 sí , y sólo si lo intersec G r {f > con c u a lq u ie r re cto porolelo ol eje Y es só lo un punto. P R O B L E M A S Oiga cuol de las siguientes G r á f i c o s r e p r e s e n t a n una u u ■ll ■ i “" S i IV y /■R . X / ( / u ±1 y ,y \ función / il ly NX ¿ y /H L- ' y ^ x . ay V - c^ (J - x dodos en * / iA \y/ 1 Y / X / " ....■ » V * SOLUCION . Son funciones tos g r á f i c o s No son f u n c i o n e s 3. TRES S i : FORMAS CONOCEN 2, 3 y 8 1 ,4 ,5 , 6 ,7 . 0£ S tf EXPRESAR RSSL A DE UNA FUNCION C O R R E S P O N O E N C IA D OM IN IO . Los CUANDO tres siguientes t o r m o s , e x p r e s a n a la mismo f u n c ió n . Sólo fines educativos - FreeLibros Y Moisés Lázaro C. FORMA 1 FO RMA 2 f .*] ~ 2 » 2 [ IR por f (x ) « , d e f in id o f (X ) » x2- 4 FORMA 4. 3 Gr { f ) ■ I M A 0 CN UN o) ( x, J _ - ) / -2 C M A S E N D IR E C T A <x < 2 ] INVERSA OE CON J U N T O . I MASEN Seo de j DIRECTA ro función A al f : conjunto OE X — ►Y y A « f ( A ) , en el UN CONJUNTO X se que A. H om o I M A C E N f { A ) s j f ( x ) / x€ A 01 R E C T A «= y ] L.ei s subeonjunto del rango de f IL U S T R A C IO N f(A ) f iR A F IC A . es lo proy e c c¡on del T R A Z O OSCURO OE L A C U R V A f sobre el eje Y , L -IM A ÍIN de A . Sólo fines educativos - FreeLibros Funciones Reales de Variable Real b) IMAGEN IN VER SA Sea lo f u n c i ó n IN V E R S A de f : X -*•*Y 8 j | « i j * 61 y meéionfe CONJUNTO § m y ^ se Hamo I M A G IN f , al c o n j u n t o f~ ?(S ) d e fin id # p o r : / f u i x € X UN i i| CZ x ) í- es subconjunto del dominio de f. ILUS TR AC IO N ÍR A FICA f“ ( í ) = I T u u 2 3 son fel'proyecciones de los tres romas oscuros de lo curvo sobre el eje X. L I MA6EN INV6RSA d « B EJEM PLO 1 - Seo lo función f : < - 8 , t ] tí { » 0 } — * definido por i , -8 < x ■± x . ± 2 * f( x ) = ■ 4“ 2 , -5 * < - S x < -1 í x " 3 , l + ® , -1 * * < v -4 , x » 9. -6 x * 10 Sólo fines educativos - FreeLibros )R Moisés Lázaro C. c u y o g r á f i c o es; Se pide h o l l o r : O f C -6 )+ 2 f ( 9 ) 2) 5) f - ’ l { 7 } ) 9 ) í ( {9 ,7 0 } ) 6) f ' 1 ( { - 4 , - 6 } ) 10) f ( { 3 , - 3 } ) I I ) r 1( { 6 , 4 } ) . 3 f ( 3 } - 5f ( - 1 ) 3f(tO)-2f (-3) 3) f(<-8,-5>) 7 ) f ' ’( < - 3 , - l ] ) 4) f([-3 .3 ) ) 8 ) f ' X í 2 ,5 ] ) S O LU C IO N 1) f ( - 6 )= 7 ,f ( 9 ) - - 4 ; luego f ( - 6 ) + 2 f ( 9 ) = Sólo fines educativos - FreeLibros 7 + 2 (-4 )* -l Funciones Reales de Variable Real 2) í (3 ) — 6 , f ! - 1 ) = 2 , f (1 0 ) = - 6 , Luego; f ( - 3 ) = - - § - (-3 )--£ • = = 3f í 3 ) - 5 f í - 1 ) _ 3 (6 ) - 5 (2 ) 3 f (10 ) - 2f ( - 3 ) “ 3 ( - 6 ) - 2 (4 ) = 3) f { < - 8 , - 5 > ) — | f (x ) / x € < - 8 , - 5 > } 4) f ( C- 3 , 3 > ) * _ 4 8 ¿ 7 » | f tx } / x 6 C - 3 , 3 >} Leste , ínter velo toco porte de los inte r v a l o s C- 5 , - i > y d e t ~ T , 9 > . Cuando esto ocurre debemoeporficionorlo ( p a r t i r l o } en l a unían de dos intervolos. Así : [-3 ,3 > = [ “ 3 ,-1 > Luego: x 6 [ - 3 , 3 ) <=> U [-1 ,3 x 6 [ -3 ,-l) <=> - 3 6 x < -1 2 * 4 ^ -j x x < 3 somor - 3 -4 - 2 1 sum ar- — x 6 L -> ,3 > -1 i por - 3 / 2 2 V > t >1 x- 3 < 0 4* - { x-3 ) > 0 a l cuadrado 16 ¿ f (x ) 6 { x - 3 )* > O <1,4 ] por - 4 A -'4 4 - ' ( x - 3 )* < 0 sumar 6 2 & - 4 - { x - 3 }*+& < 6 _4 ^ f íxJ f(x>e[2,6> Por tonto; f ( t - 3 ,1 > ) * ■< 1 , 4 J U [ 2 ,6 > * < 1 ,6 > Sólo fines educativos - FreeLibros Moisés Lázaro C. 5) f _1 ( 1 7} ) » |x € < - 8 , 9 3 u { i o J / f < x ) 6 { 7 } j , f < x ) C | 7 } < s > f ( x ) = 7 « 6) x € <-8,-5 > f ”’ ( | .X 6 , <- a ,9 3 u jio} | 9|10} <- 3 , - i 3 toco al j -4 , <*> f ( x ) « - 4 v f(x )a ~ 6 <»> v x = 10 x «f / f { X) 6 < - 3 , - 1 3 Rango de f ( x ) ** - -y- ( x - 3 f entonce*: f ( x ) € ^ - 3 , - i ] s»> - 3 e ftrs f t x ) € { - 4 , - « J 7 ) f " ’ ( < - » , - » I ) » j x É <-* ,9 3 U { « J Come / f<X ) + 6. < f ( x ) fe - 1 - 3 < - - r ( x - 3 ) *+ 6 fe-1 4 -9 < -y 9 ( x-3)* & 4 > ~ 36 > ( *-3)* * 4 ( x - 3 )* * -7 7 28 % ( x - 3 )* * 2 0 x-3* 2yT ( x* 3 + 2 % ^ v a x - 3 fe - 2 V P * x* 3 - 2 v * F ■ bm —3 le ) i 0 * ( x - 3 ) * < 36 -6 < x -3 < 6 -3 < <9 4 = -— ^ 3+ f / F 9 Lutô : #"T( < - 3 , - 0 ) * [ 3 + 2 / f , 9 > Sólo fines educativos - FreeLibros x Funciones Reales de Variable Real 8) U \ 10} / í 2,§ I ) = | X € < - 8 , 9 ] Como [ 2 , 5 ] toco el rongo de f{x) fíx J i [2 ,5 ]| = - A x .-l. y f(x) * - ^ ~ { x -3 ) * 4 6 , Entonces e [2 ,5 ] 2 Á- - ¿ x - A 2 2 * V ( - ^ - <x - 3 J2 + 6 ) 2& 5 6 ( x-3 )* 4 + _ 4 ¿ . i _ ( x- 3 ' ) * 24 4 1 * .A * 2 -5 * -A * 16 ü é 2 2 3x * á (X- 3 ( x - 3 }* - 4 -11 x-3* 2 » x- 3 L 3 x é 5 y 6 4 5 4 - 1 )* * 4 a( x - 3 ) * £ l 6 * -2 x - [2 ,5 ] a 1 - 4 - %- 3 4 4 a -1 - x £ -1 iL 3 L u e g o : f ^ í í z ,5 ] ) = §) f ({9,1 0} Pero ) a | f (X) / X€ { x € {f,T O | <*? L u e g o .' 10) f ({9 ,1 0 }) f ({3 ,-3 } ')■ { Pero A 3 U [-1 ,1 ] U [ 5 ,7 ] 9 ,J 0 }} x = 9 v x = 10 f{9 H = ~ 4 v f (10) » - 6 = {-4 ,-6 } f (x ) /x £ { 3 , - 3 ) } x € { 3 ,-3 } <»> x= 3 V f V f ( 3 ) » - -1- ( 3 - 3 >* + « 4 - f c -3 )* - A ( . 31- A 2 2 - Luego .* f ( { 3 ,-3 } ) » { 6, 4 ] Sólo fines educativos - FreeLibros 7 Moisés Lázaro C. 11) f ’ { i 6 ,4 }') a j x e < - 8 . 9 ] U V 'O } / f ( X ) 6 {6 ,4 }} Oonde I Í C x i e f6 ,4 V '*>■ f{xj = 6 3 1 - y X - y m 6 V V f(x ) = * ,, -y(X-3)+6-6 X»~y- X --Í--4 i X-3 V Z ■ 4 - ~ ( X -J)* + 6 = »4 « X =* — 3 X* 3 Í4 / ? Lu e g o I f -1 ( j 6 , 4 } ) — I - — J , 3 , - 3 , 3 + 2 y / 2 1 , 3 - 2 \/~? 9. DOMINIO Y NANEO OE UNA FU NCI ON DEFINICION OoOo to fuAcion o o p lico c io n f A —• 8 , AS ÍR , B S IR d e fin im o s ; o) D o m { f ) =s A = | b) Ronflí f ) s* | f ( x ) 6 8 9.1 x € A / 3 | y 6 8 , / x £ A } ■«= CALCULO OEL DOMINIO 1. De SÍ => 2. un f(X ! j 8 OE FUNCIONES USUALES P o lin om io a 0# X*+0H XH * f - ..........+ 0 , 1 , Oj € , n € iN D om ( f ) = H . De uno R A I Z Si y = f(x ) CUADRADA f (x ) * / u <x ? => Dom ( f ) = I x S IR / u (x ) - Oj En g e n e r a l , si f <x } = \/u ( X ? => Dom(f) = | x € 0 ? / u { x ) ^ o j Sólo fines educativos - FreeLibros Funciones Reales de Variable Real 3. DE UNA FU N C IO N P( x) 5 i f ( X) = R A C IO N A L => Dom ( f ) = IR— -/ x € IR / Q (x ) - O } l i Q (( xx )) 4. DE U N A F U N C IO N L O G A R I T M O Si f (x) » u (x ) log 0 5. D E Si , 2. UN A Si f ( x ) = 0 U<X) EXPONENCIAL *> Oom { f ) = _ 3x + 5 2x V x - X3 ' f (x ) ~ Dom(f) = x € > O J ASINTOTAS ;M ( x ) = 0 F U N C IO N E J SUPLO 9 : |x 6 R / u |x) =>Dom { f )= => Oom (f)= * ~> Dom ( f ) : x - x3 - O x3 ~ x 1 ] u [o , i ] <-co Ulx) Dom - O x (x-lHx + t ) = — © 0 i - © 1 3. Sí f ( x) = - x ■x -o — => O o m ( f ) : - 5 — = !()«= > 1- X o- x*~T <=> x e [ o , i > 4. X* Si f (x ) = — j => O o m (f )= R -| 2 ,-2 ] , x -4 pues x2- 4 = 0 l V x = ±2 Sólo fines educativos - FreeLibros Moisés Lázaro C. 5. S i f*|x) * *>■ 2x - Dom ( f ). L n ('1 -.2 x } : 1 - 2x A síntota. : S. • s> X <1/2 <=» ! -2 x = O - JL 0 Si f U ) * >0 <=£ x -y 2 Oom , pm s X-1«Ü A sín to ta ; x -t = o 7. Si S. Si *> f(x)s -30 fíx js «> 2 1^9 (f ) úom —X ( 4— X 2 ) - : x2 4 - ~ 2 < X *> 0©m ( f ) € A sín to ta s : 0©m ( f ) = Sea >(*) w X *—O. D om a) : x -z a 5e X2— 1 # 0 < 2 < -2 ,2 4 - x2- o X # i 1 > - ( ? >o ( x - a ) ( x2 f a x - i - a 2) X -2 Q . a _ > fcx>= J S Í Í 2 Í Ix i-M B* x IR - 12. ÍÜO = I x , % = •*' 1°} >o 13 0 ) x :- i t ti. > -1,1 =o ^ a>o V X -2Ql íft o > x ~±2 9. X = 1 J W = |x J + \/x - | x l 7 Dj = <-oo; oo> 0 X€ <r®®>, a ] U < 2 a ifo6> Asíntota vertical : x - z a - O . D í = t - x , 1 > U < 1 ) 2> • Hallar él é c m iñ io de 15. fx > = J ü i í i r i h í 10. Un) X -f\4[ X * -S x 4 -x 24? ~ V X*-S | X -2 | -1 D5. * <-eo, 1] u < 3 , oo> X€ 4.-00 ^tlK-Vs^-|]ü[I,n/5’>UE3/oo,> A s e n t ó la s v e r t i c a l e s : * - í Sólo fines educativos - FreeLibros __________ 3.1.1 Funciones Reales de Variable Real FUNCION RESTRINGIDA Godo lo fimcio'n Si defi ni mos f .* A 8 g.* E — ♦ 8 , ' t ol que decimos que lo función, y E « Á. g t x ) = f < x ) , ■¥ x € g es lo R E S T R IC C IO N de f E . ol co nju nto £ . EJEMPLOS nr IT ir Seo g : [ - j . , 3 ] - * [ o , 3 ] Seo f : i r - * [ o , m > definido p o r f t x ) =»x* definido po r _ Seo f : ñ — • IR definido por f t X) *- ' 2x + 3 g (X ) « V e - x * * Lo f unción g [©,*> definido por g ( x ) » x 2 , es Io r E s t r i c c i o n de f ol conjunto [ o ,« > * Lo fu n ció n h:[0,3]-+ > [0¿] Lo funcio'n j.’i o . s j - ^ i í definido por definido por fi <x)=s / 4 - x 1 » es lo restricción #1 h ol es lo restricción d e jo l j ( x ) = - 2x 1*3 conjunto [ o , 3 ] • conjunto [ o , 3 ] Sólo fines educativos - FreeLibros •j42)'-- 5.2 Moisés Lázaro C. CALCULO DEL RANGO OE UNA FUNCION. Hóllor el rongo es muy importante , sobre todo pora hollor lo inverso de lo función , si existe. Trotaremos tres cosos i #cuondo lo función esta definido en todo su dominio , cuando la función es CASO restringido y cuando la función es inyectiva. l Cuando lo función esto x en terminas ■de y , poro seo que Ejemplo definido en TODO luego o nal i zar su dominio , bastoro despejar que" valores reales tomo V \ p o r a real. seo x2 f ( x } = — -------x - 4 , Oom ( f ) = IR - Hollor su rango * (1 } Hocer f (x ) ~ y => y — x2 ■T * - 4 (2 ) Despejar x * x2y - 4 y ® X* x 2 <<«> -> <*>. (3 ) Anolizor : «6 R W -— Xx2 { y — 1} = 4 y x ¿.0 y-1 <=£ y €<-«6,o ] u<i,oo) Cuondo el dom»nto esto © - © R E S T R INGI D O . Ê J E M P L 0 : , Seo lo función f ! [ Q-, S J — ^ IR Hollar el Rango I 2 definido p o r f ( x ) = ^ - { x - z ) - 2 de f . Solución Por definición el rango de f es Donde x € [0,6] Sumor - 2 : <=> O* f ( [ o , e ] ) 2 | f ( x ) / x € [0 ,6 ] j x ‘6 6 -2 * x -2 ¿ 4 Sólo fines educativos - FreeLibros Funciones Reales de Variable Real No podemos e le vor ol c u o d ro d o porque el extremo i z q u i e rdo es N E G A T I V O y el derecho es p o s it i v o . E n este coso hoy dos Subintervolos ; tomando lo p o r t e Asi' -2 <=> -2 »> p° r - r : 4 & w n o r- 2 : P A R T I R el i n te r v a lo en N E G A T I V A y la parte p o s i t i v a . x - 2 fe 4 fe x - 2 fe O 2 * - => fe que v O < x -2 fe 4 ( x - 2 ) feO 4 fe ( x - 2 ) * feO v 0 < ( x - 2 ) * fe 16 Ife - j * ( x - 2 ) * f e O 4 v O < 4 - ( x - 2 )* fe 4 4 -1 fe J - ( x - 2 ) * - 2 f e -2 4 v -2 < - j - ( x - 2 )* - 2 fe 3 4 y y y fe-1 .V -• _ v ____________________ -2 < ~-___________ y ¿ 3 ;___________ UNION ye [-2,3] CASO 3 Cuondo lo función es I N Y E C T I VA Seo lo función f : [ - 2 , 3 > — ►IR , definido por f ( x ) = - 3 x f 4. Hollor el rongo de f. Solución Como f es in y e e t i v o , bosto i n te r v o l o de los e x t r e m o s [ - 2, 3 ) =* D o m ( f ) . - Así: hollor los imogenes Oe £ - 2 , 3 > | J ^ f { ~ 2 ) = - 3 ( - 2 ) + 4 = lt) f ( 3 ) --3 (3 )4 - 4 = - 5 f<~2) f ( 3 ) « N K> P o r tonto . -5 R ong ( f ) = ( - 5 , 1 0 ] Sólo fines educativos - FreeLibros del Moisés Lázaro C • * F U N C IO N E S ESPECIALES Codo función especio i se define con su respectivo reglo de c oríes pondencio y su dominio: F 1 F UNCIO N LINEAL AFIN FUNCION f {si FU N C IO N IO C N T IO A O « x ♦ b t x « ft . f ( x )» K , i ( x ) * % , *« m o#0 C O N S TA N TE íe s , m «. S e gráfico #« ese reefe Se gref leo **e*e reefegee NO pese per el ertgeft. horítonfel v'* Rong íf) = |K} Rongff) » R 3 FUNCION .5] ÑOLA FUNCION RAIZ CUADRADA fu>*.é, t t » . **Q ¥ FUNCION CUADR ATICA « ¡ t í - o ^ + bx + e sy gmfico coincide con el ,*«#». = < ^K + & f+ J|h ¿ ,a * e eje x. . t x _ aac-b7 "íót » K- - « c r ,» vemic£=(h/J. y V> y*e Ov i X RMft (f)« joj >** * [ 0 , ® > S ta > o ,la > 4 ia < o ,la parábo la se parcdoola. se abw hacia amba *a» « o : abajo • R&n&o : y^K H FUNCION C A N A C TEN IS TIC A ü # f: A definido ri , *e a p#f fu>a J O FUNCION ESCALON UNITARIO DE PASO o f (X ) (o , x < e abahotío. y.&n sr FUNCION VALOR A 8SOLUTO « * , * i * i * 1 * >x *° (t , xe e •x , X < o ,i/a /1 « óo Pang íf)» 10,i) V*-X*A x P a o g í f l'* V s ,i} Sólo fines educativos - FreeLibros Rofiq(f) s y e £ o ,© ) Funciones Reales de Variable Real F U N C IO N M AYO R E N T E R O f (x ) s ( xJ , FU N C IO N S IG N O x € IR -1 , x < 0 f ( X) * donde 0 , xs O 1 , x >0 f * | * K <*> K i* x < K + l •V K 6 Z . o 1 -1 Q- Rong (f ) = { Rong ( f } = 2Z F U N C IO N j P O L IN O M f C A P ( x ) a o n xf t 4 0 ^ ' + • - + 0^ + o fl , x 6 IR t n I R , @f i Q . E je m p lo s : P(x)* 2 P íx)> - 5 x + 2 P U ) * 2 x * - * x 41 P (x) « x3 - x S o n funciones polinomicos d e g r a d o .* 0 , 1 , 2 y 3 re sp e ctiv a m e n te . Sólo fines educativos - FreeLibros Moisés Lázaro C. ?. A L G E B R A D£ FUNCIONES SUMA, D I F E R E N C I A REALES , PRODUCTO DE V A R I A B L E Y CO C IE N TE DE F U N C I O N E S REAL. P R O P O S I C I O N 1. Seon f y g dos funciones ó ) L o sumo f + g , con lo d i f e r e n c io Dom { f ) n Dom ( g ) £ 0 b) El dominios cociente f-g Dom ( f ) y D o m ( g ) t re s pe c t i vame nt e . y el producto fg exi st en, sr y sólo si • existo sr y solo si Dom ( f ) n Dom ( g } # 0 y g # O * PROPOSICION f . o) Lo FUNCION S U M A fV g quedo bien definido f f * g í ( x i m f ( x ) + g' ( x) donde b) B r ( f -f.g ) x € Dom { f ) n O o m ( g ) (x , f ( x ) + g | x ) ) / x € Dom(f )n Dom ( g ) j Lo FUNCION D IF E R E N C I A * f - g , quedo bien definido (f donde c) -g )(x ) f ex j - g Br ( f - g ) » ( x) x Lo FU N C IO N P R O D U C T O donde Lo fg Dom ( f ) n Do m ( g) | quedo bien definido C L IE N T E s.s.s x € Dom ( f ) n Dom ( g ) © r (f .g )s s | ( x, f ( x ) g ( x ) FUNCION 6 s.s.s | ( x, f ( x ) - g ( x ) ) / x € D o m (f )n D o m ( g ) | ( f f t ( x ) * f ( x) . g ( x ) d) s.s.s. ) / x € Dom(f )n Domfg ) j quedo bien definido s. s . s x € D o m { f ) n Dom(g) co n §<x) £ o . Sólo fines educativos - FreeLibros Funciones Reates de Variable Real donde 6 1 ( - 5- ) = | ( x , ~ A d o r e m o s estos t é t m p i o ) 6r 6 D o m ( f ) n Dom ( g ) | definiciones con tres ejemplos diferentes. 1 . Cuondose t r o t o de f unc i ones Seon f / x y g dos funciones Discretos F i n i tos cuyos giró'ficos son ( - 1 , - 2 ) , ( 0 , 0 1 , ( 1 , 2 ) , ( 2 , 4 ) , ( 4 , 6 ), (f ) = { ( 6, 8 ) } S r ( g ) = { ( - 1 , - 3 ) , ( 1, 3) , ( 4, 12) , ( 6,18) } Hollor e) e I GRAFI CO 2f-3g - de o) f+g 1 f) - — g + 2g 5 g -2 f 2 , b ) f-g , c ) f.g , d) y 3f - g S O LU C IO N PASO T HeMor I PASO 2 Como Dom ( f ) n O o m ( g ) = { - 1 , 1 , 4 , 6 } Oomf f ) n O o m ( g ) procedemos o ef ect uor es lo s difire íê del v o c io , e ntonces o p e r o c io n e s i ndi codos T o d o lo que se hoce es o p e ro r con los imo'genes de - 1 , 1 / 4 y 6 . A si tendremos o) 6r < f+ g ) = { ( - 1 , - 2 - 3 ) , ( 1, 2 + 3 ) , ( 4 , 6 + 1 2 ) , ( 6 , 8 + 1 8 ) } = { ( - 1 , - 5 ) , (. 1, 5) b) 6r ( f - g , (4,18), (6,26 ) } ) = { (-1 , - 2 + 3 ) , { 1, 2 - 3 ) , { 4 , 6 - E ) , ( 6 , 8 - 18 ) } = { (-1,1), (1,-D ,(4,-6), (6,-10) Sólo fines educativos - FreeLibros } ¡Moisés Lázaro C. -< g > c) Gr ( f g ) = í - 1 , (-2) í-3 ) ), (V, ( 2 )(3)) , { 4 , Í6KI2) ), í 6, (8){I8)) = (~1 ,6) , (1,6) , (4,72 } , (6,144) = ■('■{■) l i C l Y * f ~* 9 ) - f-J J t l t 2 t 2 ! \ A ■ \ quedo f } 15(12 ) - 2 (6 ) / ’ \ e je rcic i o . $umd de j-unciones la s s i g u ie n t e s 7—x } ( * , de variable cóntinuct -f u n c to n e s *. x<2 í y ZéxcS - 3 H a lla r : 2(2 ) - 3 ( 3 >\ / . Z [61-3(12 ) \ / 2( 81-3 (IB ) > ’ 5( - 3) -2t -2 ) /' \ ’ 9( 3 H? '( 2 ) / ' \ como EJEMPLO 2 Dadas ■ l 4' 81' ( 6> f ) g (x )iÍ3 X -2 X>;5 * a) í+ % A s e g u ir 9 x<3 j 3 ¿x < C » 1“ 2 ^ to * -§ , c) ^ ^ X>,fc d) 1 Solución M E TO D O ; 1° * Representar g rá fica m en te ■ ' e n una recta horizontal } cada función con sus domintos y su s im ágenes ? respectivamen 2° 3o te . Buscar a p re cia r St la i n i & r s e c c io n de los dom inios que s e pueden en el dtgfarna. hech o e n el primer p a so . existen f u n c ió n € s ; p li c a r o o p e r a c ió n las in fte rs e c c io n e s e n tre ios dom inios e n to n c e s O PERA M O S o. de la s s u m a r ( re s ta r } m ulti d iv id ir ) la s i m á g e n e s d e la s fu n cto n e s . E s t a l a re a liz a m o s h a s ta te rm in a r con t o d a s la s irrter s e c c io n e s , Sólo fines educativos - FreeLibros Funciones Reales de Variable Real veamos : , ¿■■■>■7 y ■„ -f OO *SS ' s S SsSy ' 4-co X -1 Las interseco tones de los dom inios d e ^ y g s o n '.O -o b ^L -O t^L^^S ] y Céâ>c. En estos in te rv a lo s se o peran con la s im á g e n e s de f v ^ t e niéndose : [ í t - x y 4-(x-1> X 4- I X -i ) * +C3X -2) <í+S>00 = f -3 + - 3 4- ( - 2 ) (3x-2) 0 -x } “ (x -i) X - (x -l) X - (3 X -2 ) ( í - § ) t x ) =< -3 - - 3 - (3 X -2 ) ( - 2) O , x € ]-o o ,2 [ * « ] - < » ,2C 2X-1 , x í t s A C ' > x«C2,3[ » xfe [3 ,5 t ’ x t C s .tC > *£ r6 ,+ oot _S , X€ [6 , +<»[ , Xír]-0O, 2 [ , x« I " 00 ,2 [ ,X £ 1 « [2 ,3 ’ x« 13, 5 1 [2,3 [ > XÉ [ 3 , 5 [ ($-§K*)= » x« , xe > x é [ 5) 6 C ’ x 6 [ &^+00C -( X- I )2 X € ] - O o , 2*[ X e [2 , 3 [ (f% )(X ): (ÍS )W = [2 ,3 [ 3x -2 x ( x€ ^ ^ 6 _X _ 3x-2 -3 3X-2 -3 w -2 x« [ 2 , 3 [ , X€[3,5 C / xt [ 5 , 6 [ -i X > ■ x-l ( f ) M= 1 X X€ > x€ [2,3 [ , X€ [3, 5 [ 3x-2 , X€ [ G , + 0 0 [ l ri (l) w = << ^ >*€ [Gj+oo); st (— 1 X 1---l 1 .8 f\3 1--- 1 l^ + O O t X X-1 , xe]-<»,2[ ,* í - 9x2 +& , x6 j-5)& j- X6 [ 5 , c [ 1-X x-í C5,G [ [ 6 , +oo [ x2- x 2 **[3,5[ [ -3 3X-2 V ** [S,G[ 3 2 , Ké [<=>,+oo[ Sólo fines educativos - FreeLibros — Moisés Lázaro C, ^50)- S 4- C O M P O S IC IO N Si sedan OE P U N C IO N E S dos fu n c io n e s reaies d e v a ria b le re a l } cada uno con su re s p e c tiva re gla d e cor re s p o n d e n cccx y d o m in io : f : Dom Cf ) — ► Wl 7 y ■= jcx v % : Dom (§)■ — ► R 0 y =§<>g Junció n e x is te La €c s í D o m (f ) flR a n (g ) £ <f> t— u La composición de f yg 5> Or cc f com puesta con g 4i Donde I ó*) E J b) .d o m in io d e D o m (g o J ) = [ x / La regla d e * X€ D o m ( f } A c o rre s p o n d e n c ia f(x ) € D o m (§ )^ de go-J ^ e s ! (g o f U x ) = % (jc x )) EJEM PLO 1. Sean las fu n c io n e s : f(x) - 2 -3 x gu) = 5 - x - z x 2 HdilQr i) SOLucio'n a) goj de ? ti) Jo g . 9 xe E -t>5C 5 x ^ H ; i oL s i e xiste n . i) 6n p rim e r lu g a r D om ( § o f ) } h a lle m o s e l d o m in io ;r j x / x e D om (*) x € C-1 ,S C de § o J A J(x) € D o m (§ ) A ,tt**3XK 3 1,10 c ; 1< 2 - 3 X < 10 ■' -1 < -3 x < 8 1 > 3 x > -8 xe t ',% 1 a j_ . 4 — ^ i y x >_ £ ------------------------------ = = -1 °v 3 = b) En segundo lu g a r . C -i/ / 3 [ hallemos la- fegia d e Sólo fines educativos - FreeLibros ¿ ----------------- 5' * Funciones Reales de Variable* Real CONCLUSION *. S o l u c ió n a) -<151)— ? (§ o f )(X ) = -18X? +27* - 5 *'e C" ^ V3 I d e ii) Dominio de $03 : Dom (fo g ) = \ */ x€ Dom (3 ) a gtx> c Dom( 4) ■XGlijlo.i- * - i é- 5 - X . - 2 X . } 1 ( 5 - X - 2 X 2) € 1 L < 5 A [-1¿5-X _ixz \ [ 2X2 + X ¿ 5+1 x’ + i x l - .4 3 > * + H É í3 + ií -2 < * » 5 -2 x ¿ ]i, 4= 10C D om ( f o g ) b) - X ¿ 1 -0 0 J-Vz [ u 1 o , + 0 0 L O 3/z \ ( * e É v f e 'lú ló / s / j}) = i-C 2 /v £ 1/2 0 1 a. 3'? 1 10 = x e ] i , 3 / 2] Regla d e (}° § )w c o rre s p o n d é ñ c c o c d e : = '= - 2 - 3 ( S - x -2X*) 2 - le ¥3X HhGX2 z: GX2 + 3X -13 . CONCLUSION *. Xf °§)CX) =* GX2+ 3X- V3 / X€ ] 1 , 3/¿] .. EJEMPLO 2 Dadas tas funciones : ílx) ssi/x+4 * ? x€ |*-3>5-[ . x íB r l l - ^ { H a lla r -s i e x i s t e , f o g . 1 ^ 1 sl x = -4 v sí x £ > 4 , o [ 5 sí *e[?,3 [ Sólo fines educativos - FreeLibros Moisés Lázaro C. * sbtocCón. Lo primero que se d ebe Hq c e r ; es e x p re s a r. %(x) e n su fo rm a .m a s S im p lific a d a . . ;— r . r__. N ecesitam os $¿m p?ificar : [“ 2 I en el intevalo ] - 4 , o [ • Veamos: 0) ^ «-n 'ei in te rva lo 0 , 3 [ ; ' StmpUficar * £-|.| , en el intervalo 3-4^0 L Se Sabe que Drrl es un ENTERO*6*4 que se def ine así: f-f-J=K El 0 — ; problema* es bailar K= ? <*41 2K¿~X<2ÍK41) -2*55, *>-2(k«i) // \' • Una Se form a d e hallar el parte d e l in te rva lo J - 4 , o [ Asi *. \ por - -b 2 como sigue : porque ( H f ! esta d e fin id o e n l - 4 p [ a Partir de este intervalo " construir * La <zxpresión • 7* 'v 2iL . „ v * \ _ Observamos que -A . e s ta a c ó k ta d o en el intervalo J O ,2 [ L _ .— - — — Le a p l i c a m o s j j >que es la funcidh A 9 mayor entero. 0 — ...— < m v -.J .............. V 0 < - f S i 1x - < 2 < 2 2 < - x < 4 > x > - 2. | = { ’ ’ i ° * | -2 > SÍ 1 - e ^ l l - f l = 1 -4 1 < x < -2 - 2 C X < 0 S i retornam os a © obtendremos el m is m o resultado p a ra Kc1* ^ t : 0 con X ^ 2 ,X ^ 0 Sim plificar | — Z2<°1 e n el intervalo l Z j 3 í . Conviene dividir : 7x -26 -7x +28 «7 Luego I , *2L< X <3 5 6 , X -.2 . Sólo fines educativos - FreeLibros • Funciones Reales de Variable Real < § > — Donde e l entero f J } P°r defintcton es ; = « K i <=$ E L p ro b íem Q es 2 *-* < K+1 ■K¿ — + 4 > . x > A +K 2+i hcxllar Partir del íntervolo [2 #3 [ y -formar la expresión 2 ¿i x < 3 Asi 2.-4 Sumar - 4 invertir < x -4 < 3 - 4 -2 £ 1 por 2. X -4 < -1 1 V > - 2 t -a p li c a r ! J -2 Ov Gradear -1 — O* ^ T Si Sí Luego x - - 2 < - 1 . <-1 3 2 > X >2 • t e l = f t “"2 ’ 51 *"x<3 1 ^ Si X=2 V 4 O) E n consecuencia?la junción queda strnpii-Jicado o- lo. forma. I -1 .'-2 G -4x -1 Si -4 < x £ -2 > Si -2 j» si X r 2 > SÍ 2< X < 3 7 -4 > - > 7 ~¿i Y*—... ¿L > > 2 x -4 x -2 % H * < x <0 1 6 x2(i)-4 x x2(o)-4x x*í - t X II %lx> = 2 — = -1 x~4 < x ¿ -2 2 < x <■ O v ^2 2 < x <- 3 Sólo fines educativos - FreeLibros I t =t 1 Moisés Lázaro C. (4) Ahora y a podemos h o lla r 6 , x*-4x ■ §<*)=< - 4 x , x =-4 - 4 < x ¿ -2 -\ X ’=. 2 2 CX<3 i-* • 5<x) n/x+4* ^ x€ ^ te n ie n d o : 1 2 __ 3^ -2 < x < 0 > ,, í° § 4 r [-3^[ ei dom in io d e s d e 1 h asta 5 . Para ello y e m p e c e m o s a d e f i n i r Veamos : 1. a) x e p o rn (% ) O om (fog) xe {-4} A got) e D a m U ) A 6 € [-3,5 [ - v ........ pALSO -v— * Entonces 2. a) ! ^ í° § • Dom x cD o m t^V *4<X6.2 A gcxre D om (í) A ( x J- 4 x ) € [ - 3 , 5 [ - 3 . < %7- 4 x < 5 resolver esta ' -3+4 ¿ xz-4x+4<5+* Inecuación . 1 * (X -2 )Z < 9 1¿ tx-2>2 a <9 v x-2*-i) A -3 <■ x-¿<3 (x ^ 3 V X6 1) -1 ~ 4 Entonces 3. <. X S - 2 A » 3 3 - ',» lu L 3 > C f°S x G Dom ( g> a») Dom (f o g ) - 2 < x < O A §<*)€ D om ( ^ ) A - 4 x 6 &3.,3C -3 6 -4 .x < 5 -= > x > - 4 4 B o m (fo g } - “2 -V4 ] - 5/4 0C -1 < x<5 0 Va x g Sólo fines educativos - FreeLibros '■ A 5 Funciones Reales de Variable Real b) 4. (J o g H x ) = H s o o ) = V -4 X + 4 q p o m( '.= Z Í - x + l Do m( < 3 ' ) '**{*} a> %<x> e A -le D om (f ) [-3 ) 5 [ es verdadero D o m íí.,,,1 2 ) U ! < ![-« ( Lq regla de corre sp o n d e n cia e s ’. t>) =(2( (f° g )te ) = = f(-i) = '/ ? 5. a.) pom (f o g V í x e D o m (§ \ a 2.< x <3 A g(x)fe D o m (í) -2 s x< 3 A C-3/51 es Verdadero, *-3 Dom b) (fo % ) - 2 3 5 X€ ]2 ,3 [ (5 ° 3 ) I x) = 4 (% U l) = í(-2 ) = V^T2T ^yfz 2 \ T x+J CONCLUSION 1 (f O Cx) = j •l EJEMPLO 3‘ * ? X€ ] - V ^ ó [ < 'fS 7 'f? , x e ]2 ,s c Sean las Junciones : X= 2 fcx) = H i i ü i i í l l . -i< x<4 ' I X-Hi * 3 L a ( * -£ ) ,« 2 %M= i Hallar gef SOLUCION. En p r im e r l u g a r , Se d ^ e ±d ^ e xp re sa r ** A ' la fun ció n fu v Vemos : = lx + 11 como : -4<x¿4 =$ o <•x + 1< 3 = - 2 (2x - n Luego = -a * + ¿ > 1*4-11 = x+i sumar 1 Sólo fines educativos - FreeLibros x <4 a fo rm a sencC lia . E s t o se logra d e f in ie n d o el vator a b s o lu to y fo c to rie a n d o e l trin o m io 1- X - 2 X2 , íoc, = * ^ m ás jx+il pom -i<.x¿4 Moisés Lázaro C. Ahora. tenemos f<x) =-4x4*2 ,-1< x 4A i< L ' A continuación y term inando (n desunamos «t dominio dé §<>f } empezando por U) por ( 2 ) . a )D p m (^ J ):x c D O * n < 4 V -U X i4 $<*> € a Oom(s) A (*4X41)^ i*)a) Dom(fH) *x€Dom(4) a $<xk Dom(%) - ux <4 A (-4 x 4 2 )€ £ 2,4 C • Z ¿ - 4 x +2»*4 -4X4-2 < 2 x >o • O i - 4 X < 2 -i < ,x c 4 a o V x > ~ j O O B tfK go f)* X t J o ^ C *fc Dom(? .íV = x€]-VZ;o£ *5 {%®í)(*) = § ( f w ) *4 = 3 U (* -= $ & ) . = 3 in x 3Lnx c o n c l u s ió n ; EJEM PLO 4 » * 6 ] o,l L , X € .]-'^ 0 [ _ 1 # " 4 A ^ (§ o í)t x ) = Sea L a funcuciñ f(x i = a x - t - b a) Si hU) =J(x) + f W = | x + | b) Si ge») = lx*sV-lx+il •' f x € t -3 ,3 ] gtx) - D« t<x> = a x+b , sí too=y =4 Y=*x+i> y ai «xiste . ■ r-2 , 12X4*4 > 2 x _ JLV _ u - * ■****■ (a + ¿ )x + (b -|) = | x + f a+¿ J--r 5. = ~S z = =?* “a=2 ■=' ) -S L , > **-* (3)^ , Ahora, hademos (1) i) Dom(*og) = d (2) i) Dorn ($■*§) = K€ [~ V 11 tí) - l = ! <*L x<-3 -3 ¿ X < -1 f(* )= 2 X 4 3 b hex) s OX4-b+¿X-~ Q. =| X4*1 ^ a > l/2 , halla* a y b hallar j-°g SO U JC IO N ; *) 4 (í*S>O0= f(§ O O y = 2 (2 X 44 )4 3 = 4 x4 11 * (3) i) Domüog) s x c [1,33 § IX) - |X43 l - | x 4 i | { -< X +3 }-(-x -t) ^ x<-3 X+3-C -xH ) t i) Ct * 8 )0 0 = í (%<*>) s W > 3 C O N C L U S I O N : >.f X43-(.*40 r x H Sólo fines educativos - FreeLibros . (4 X + I1 . , (í° 5 W = t 7 =7 X.€ .tr3,-tC X€ti¿3l Funciones Reales.de Variable Real 9. INYECTfVA FUNCION — t SUNYECTIVA Y — <§ 81 Y E C T I V A . 0.1 FUNC ION INYECTIVA DEFINICION 1. Seo lo funcion f ,f es I N V E C T I V A A <=> 8 , A S iR [ f ( x , ) - f ( X2) , 8 — JR ? A = D o m (f ) => x " x 2 , "V x1 , x2 6 a ] E s t o d e f i n i c i ó n nos indico q u e ; o codo yo lo r “ y " del r o n g o le corres ponde un so lo valor "x' d e l d o m in i o . DEFINICION 2 . f e« IN Y E C TIV A DEFINICION O odo lo D ir emos M <=> [ x , ¿ %z => f ( x , ) # f ( x., >,'V- x,, x 2 6 A J 3 f uncida f (x ) = . f i (x ) » x € Dom ( f 1 ) f2 ( x ) , x € Do m ( f 2 ) f 3 (x ) , x 6 Dom ( f3 ) que ? es I N V E C T I V A - s i , y- solo st cumple dos co ndic iones; t ) Coda función f ¿ ( x ) ti) Rong f t 7 ) n Rong C f ^ ) f= 0 Rang ( f 1 ) n Rong ( f 3 ) = 0 Rong ( f 2 ) n Rong{ f 3 ) =0 FUN CIO N es inyectivo . SU N YECTIV A D E F I N I C I O N 1. Seo lo función f * A —►8 , A ~ ÍR , 8 - f es S UR Y E C T I VA V IR y€ 8 , 3 x CA / y= f(x) DEFINICION 2. f es S U R Y E C T I V A • <-> f (A } = 8 i , ,r-ango de f es igu a l di co nju nto de llegado. Sólo fines educativos - FreeLibros JVtoisés-Lázaro'C.. 9.3 F U N C I O N función f Seo lo f es BlYECTtVA EJEMPLO Dado BIYECTIVA 1. <=> Digo Ud. , AS , B ^ IF jr f es inyectivo y suryectivo. Fo ro f unc io oes di s c re tos f *n it o s . conjunte el A -* 8 A * j — 1, O, 1 , 2 , 3 j ctidles de io y 8 = fF . funciones de A en IF; cuyos gráficos se don, son ¡nyectivos. Justif i que o ) ©r { 1 } » / 1 ( - i , 2 * , (O, 2 I 1, 2 ) , ( 2,5 ) , Í 3,5 ) f f t »)ér(f).« [ ( - 1 , 2 ) , ( O , '3) ,1.1,4), (2,5), ( 3 , * ) } . c)6 r I (h )* i 1 t ( - t *OÍ , { 0 , 2 ) , ( 1 , 4 ) , ( 2 , 2 ) , ( 3/S ) } 1 f f é ) 6 r ( j ) * | ( -1 , 1 ) , ( 0 , 3 ) , ( 1 , 5 ) , ¡ 2 , 7 ) , ( 3 , 9 ) 1 J S O LUC IO N Foro est e tip o de f un cio n e s , o codo ,volor,ly M bastará aplicar la def inición .1 que dice;. de i rango corresponde un único “ x"deldominio. Bichó de otra manera : Ninguna dé los segundos componentes debe repetirse. Aplicando este criterio , tenemos ! o) f no es inyectivo porque í 2 se repite tres veces. Es decir 2tiene tres •preimogenes>]>O y 1. 5 se repite p) f es dos veces. Es decir 5 INVECTIVA , porque todo tiene dos preimogenes ; 2 y 3. los segundos .componentes diferentes . Sólo fines educativos - FreeLibros son Funciones Reales de Variable Real c) ’ h N® es tnyectiv o , p o r q u e en ios p orejos f 0 , 2 ) y ( 2 , 2 } , lo segundo d) se re p ite dos veces. ¡ es I N Y E C T I V A , porque ninguno de los se g u ndos co mponentes de lo s CJ com ponente purés IM P L O (x,y ) I 2 - ®r ( ) ) Poro Oo#e j o funcio'n se f u n c io n e s re p ite n . de vo rio b le f (x ) * 4 ( x -1 }* - 5 ¿ E s f in y e e t iv o ? t C O N TIN U A . x € [ - 3 , 5 j .P ruebe SoluctQn Por f d e f in ic ió n : es I N Y E C T I V A Debo <■> [ f ( . * ) * f . ( b ) *> demos t ro r donde que - 3* o * 5 , o=b -3 o = b , V- Oj b 6 [ - 3 , 5 ] o p o r t i r de lo b igu o ld o d J f ( o ) = f (b ) . Veomos Sed «> 2 4 ( o -l ) - I ® *> ( o - 1) « o -1 ' * i «> * o -i En este coso - 3 * Sumor Como Esto 2 vemos niego - 5 y 4. , ixtretr re ¡z cuod rodo. ( b -T ) b - 1 v ss b o - > = - v dos volores que son b y 4 $ H - b; * - 5 *> S * - b + b € [ - 3 , S ] in y e e t i v o de ( b - i ) o » - b + 2 »> lo d e fin ic ió n L u e g o f no es b *■ 5 2 Mo H a d m i t e b ^ 5 - 3* 5 , sim p íif ic o r (b - 1} * o 5 , i 4 ( b-1) i si . - 3 £ .0 f { o ) * f ( b ) , donde y 2 > - 3 ( - b +2 ) € [ ~ 3 #S J i nyeet i vo. sobre [ - 3 , 5 ] Sólo fines educativos - FreeLibros t i, porque 160) - _______- ______ EJEM PLO Seo Moisés Lázaro C. 3. f<x)s 4(x~Tf~5 # x € [ 1,5 ] d £$ f ( x ) t n y e c U m ? Pruebe . PRUE 8 A S úpeme r q u e »> {#) f {o )* f { b ) , 1& o - 4(o-1 ) * - 5 = 4 { b-1 )*-5 ••••• { o - 1 )* = ( b - 1 )* , como 5 , 1- b - 5 o - 5 => 0 - o -l 1 á b é 5 => *> . ss b - 1 o - l »> . o NO TA. l o £#) * b , • se puede porque Luego o p iic o o -? Ó - b -1 ^ 4 y b -7 son positivos f es I N YE C T I V A lo pro p ie da d Io - 4 so bre { 1,5] * T 1 1= y o A tt ; De (o - l / * ( b - l )*■ => | o -1 [ » I b -1 j Pe ro 1 -o ~ 5 , 7 - e »>. V O * o -7 * # V - o —T ■'* b “ 1 ■ O =3 b J b - u 4 %V O * b -1 * 4 H V ¡ O - l ] = 0 - 7 ¡ b - l l =5 5 -7 L o c u o l p ru e b o E J EMPLO quef ( x ) Lo f u ncial en todo lin e a l Lo sobre fu n ció n f (x)= su [ 1,5 dominio , los siguientes ofin f {x ) = oxt b , o 2) i nyecfi va ]• 4. Son IN Y E C T I V A S 1) es O , x § ft. Logaritm o t ef g- x , x > O . Sólo fines educativos - FreeLibros funciones* 5 Funciones Reales do Variable Real 3} Lo f u n c ió n f (X ) * o * 4 ) Lo exponencioi , x € JR . función hiperbólico. x--« R r | • J 5) Los funciones hiperbólicos f x c m f <x) « — --------- ,x€ Lo* fonctonos que NO son m EJEMPLO 3. v e rt ir en in y e e f i v o s II coso típico I N Y E C T I V A S , en su restringiendo dominio, se pueden con~ su dominio. se presento en lo porübofalo e l i ps e, lo hipeVbolo y lo circunferencio. E je m p lo s: o) L o función f ( x ) » o ( x - h }* + k , n o es in yectiv o en su dom in io. Pero .* g.* + $ , tol que Tbmbien ^ : ^ e o , h ] - * £t , fot que. x 6 IR = Dom ( f ) * g (x ) - o ( x ~ h f + k es inyectivo. ) ~ o (x - h )* *f k Sólo fines educativos - FreeLibros es in y e c fiv e . b) LQ fmción f (x ) s v/o* ~ x2 * , x 6 [ - 0 , 0 J Pero y g por g ( x ) = x¿\ es inyecfivo. h ’ [ - & , O ] -♦ IR ^ d e f ini do por h { x } ~ s/a*~ j ? Igualmente Pero [ O ,a ] —* íR , definido NO es inyecfivo . ft ( x ) » - g^ : [ 0 , d j ~ * f x £ [-0 1 ,6 1 } , definido por g^í x ) = - , definido p o r H O es o*- x*1 , fombiénes inyeetivo. inyeotivo y ( x) ~~ y/o2 - **' son Sólo fines educativos - FreeLibros in y ac t i v os . Funciones Reales de Variable Real EJEM PLOS En los el sobre siguientes funciones ejemplos bo stora de lo función rango O odo tos siguientes cuáles 1. poro comparo r el c o n j u n t o de líe godo con o f i r m o r si lo función fu ncio nes , di ga Ud. c u á le s son es su ry e c tiv o ó no. s u ry e c t i v o s y NO. Seo lo función 2. Sea SU R Y€CTIYA S - f 3. Seo lo función lo función 5. Seo lo IR , d e f in id o p o r g : ( - 00 , O ) u lo función 4. Seo IR h * ( 0 , o o ) — * IR IR j ‘ [— 2 ,3 ^ — ♦ f (x ) = ox* b , o # 12,t3 j definido por j ( x ) » - 5x + 3 por f ( x ) = 2 f .* f - 3t 0 J u ^ 0 ,4 j — * [ ~ 5 , ~ 2 ] x -2 definido p o r d e f in id o por g ( x ) = - ^ - definido por h (x ) ~ - 5x 4* 3 función f.*fá — * ( - 0 0 , 0 ] , de fin ido 6. Seo lo función , O . - 3 - I x~2 J u (2 ,3 ] x * 0 f (x 5 = 2 + - Í - U - 2 )*, 0 < x 6 4 SO LU C IO N 1. M ETODO 1 A p lic a n d o lo definí cio'n si f { IR ) =* IR => f es Survcctiva. v— —y V H o l l a r el rango de f ( x ) » Veamos r Seo. ,a y* O a p a r t i r dfei d o m i n i o xcfR>:Dc>mC$> X€ /£ a ( a x ) € lR aá o x •+b Rc«god<*5 a a € IR ^ (axOe IR b e IR. (a x +- b ) € ÍR v P o r tonto .* R o ng { f )-= Co mo Rong ( f ) coincide f es Suryectivo. ~ con el co nju nto de ílegodo , 0f írmom os que ^ M E T O D O 2 . Aplicando lo definición’ f es inyectivo <=*> t x 6 IR . , i . y 6 Í / y= f {x) Sólo fines educativos - FreeLibros Moisés Lázaro C. D ebem os probar dos cosas existencia, de Y , ti)ademas que y=f(x) ÍÜOTA * Si pru e bo q . u e / Y ' e s un numero reai a pro bando i) let C o m o o cy a . y b '» ¿*¿ En la ecuació n Despejor x : A p l i cor f Cama p a rtir de xeíR e sto / e xiste n cia r e a l e s , e n t o n c e s (aac/¿) = y so n • f(x)*s ox + b y = x = -5 - y - , hacer f(.x)* t a m b i é n e s te a l. y (ix f b , co m o x6 « => ( t Y~J~) e ** f ( x) = f { -y y - - J - ) f(x>» ox + b , entonces *•> ss f(x) y — o ------b h •b" a. — o « y * y o - b + b A s r , hemos probado que y€ ff*, t a l que x ■» y = f(x) 2. H a IIe mos Ha c e r e i r ong o g íx ) = y " y es Jo imagen de x de x =s — y g (x) — *1 • : : . x * T & jl y < 0 , 00 ) = < ~ a o ,0 > U < 0 v — > o y u ^ y » V y € < - c o tO > 1 O y Es decir h e mo s S U R y e c T IY A . Despejar x Analizar j € fR * t - s e lee Por t a n t o * f es T o, + a> y = > 0 Rango ( g ) Sólo fines educativos - FreeLibros D om ( f ) h o lla d o Funciones Reales de Variable Real Al comporor el rong (g ) con el conjunto de llegado, que es que Rong { g ) # £7 . to n to , a f i r m a m o s que g no es s u r y e c t i v o . Po r 3. tenemos h no es suryecti vo. Porqué j h ([-2 ,3 » = h tx) /x 6 [ - 2 , 3 ) -2 Por -5 : - 10 i Sumor 3 : <3 x -5x > -15 13 — - 5 x + 3 > - 12 f (X) Í ( X ) e < -1 2 ,1 3 ] Luego, el rango de h es'. h (í-2 .5))= < -1 2 ,1 3 ] # IR c o n ju n to de 4. j es Ve r 5. f el 6. f s u r y e c t í v a , porque' j ( [ - 2 , 3 X ) = problema es < - t 2 , 13 ] 3. s u r y e c t i v o , porque Rong { f } = < ~ aa, O ] , I© c uoJ c o incide c o n conju nto es llego do . de llego do. suryectivo, f ( [-3 ,0 ] porque U < 0 ,4 ]) = [ - 5 , - 2 ] Sólo fines educativos - FreeLibros U <2,3] Moisés Lázaro C. C J fM -F L O S Di go S 'O 'M C FUN CIO N ES codies de tei sigwientes 1. Seo f f* — * f 2 } funciones son , de fin ido 2. Se© g ' [ - 2 , 4 ^ & IYECTIV A $. ^0, 3 ] por bi y e c f i v os . f { x) ~ 2 . definid© por g ( x ) 535— x 4- 2. - x. , - *f e x < o 1. Se© h : [ - 2 , 2 ] -♦ £0.f4 í] d e fin id a p o r h (x ) * x 2, o fe x 4r z x , - * -A X < © 4. Seo f . [ - 2 , 2 ] - * [ - 2 , 4 ] definido por f <x ) « 312 5. Se© g .*| 0 , 1 , 2 , 3 } 6 . Seo hv [ ~ 2 , 2 ] - ♦ [ 0 , 2 j , defin ido 7. Seo f .*[ 0 , 2 ]-*♦ [ 0 , 2 ] , d e f in id o i. l-tjtjS jS j* Seo g.*[ 0 , 3 ^ [ 0 , definido p o r g(x)« O é % & 2 3 x -1 . por h ( x ) - v^4 - x * * por 3 ^ , defin ido f ( x ) 38 ^ 4 — x1 * por f <xj ^ I x j t \/x - f x J 1 x - 2 , - 4 fe x < ~ 2 % f. Seo h : [ - 4 , 4 ] -* [ - § , 2], definido pmr h <x ) « - x* , - 2 * x < O \ / T , 0 fe x fe 4 10. Seo f I H-eW , de finido Tf. Seo g : <*- 00 , o ) o po r f ( x ) » < o , co > Ln ( x + < -o o , o ) ) u <o,oo>, d e f in id o por g (x j a L n 12. Seo h.‘ < - 1 , i ) -* J f * , definido por h ( x ) » ^* Ln 13. Seo f .*^ - 00 , - 1 ) ^ -o © ,0 ) u (0,o©\ Sólo fines educativos - FreeLibros ^ d e fin id o __________ Funciones Reales de Variable Real por 1 / x -m \ f |x ) * y L e í — ) • 14. Seo g . [ 1 , 0 © ) — » [ 0 , 0 3 ) y . — ", «i , definid© p or g e * ) 28 L n ¡ x + / x 2- 1 } S O L U C IO N 1. f « o e s i n y e d i v o , f es N O T A .* L os s u ry e c tiv o -t f no e$ b i y e c t i v o . funciones no son ¡n y e c tiv o s . 2. g es in y e ctiv o 3. h no es in y e c t iv o , ñ e r o es s o r y e c t i v o ; 4. f es 3. g es i n y e c t i v o 6. b io.y e cf»v© y s u r y e c t i v o , g es b i y e c t i v o . su rye ctivo , f y s u r y e c t i v o , g es es f no es b i y e c t i v o . biyectivo. bi yect i vo. no es i n y e c t i v o , pero es su r y e c t i v o ¡ h 7. f es 8. g es in y e ctiv o inyectivo L o s funciones J u s ti f i que de y constantes in y e c tiv o y su rye ctivo ?; f y suryectivo del 10 ; g es hósto el 15 no es biyectivo. es b i y e c t i v o . bi yect i vo. son b i y e c t i v o s . codo uno de es to/s respuestú s o pli cando la def in ic i on y suryectivo. Sólo fines educativos - FreeLibros Moisés Lázaro C. 10. FU N C IO N _ _ ¡N V tftS A DEFINICION $ ton A y 8 dos Si lo función s u b c o n ju n to s f A— ►8 de J R es biyecti vo ,enrtonces t iene Lo inverso f es f ' 1.' 8 — * A .definido por lo 'ysfUI W Lo notocio’n 10.1 f - 1( y ) inversa . condición. x = f“ ’ ( y ) indico lo inverso de f. PROPOSICION Siel GRAFICO de lo función f es Gr( f )= j fac ,f ( x) ) /x G Dom(f ) j y f es BIYECTIVA , entonces Gr ( f'’)= j { f( x) , x ) /xeOom( f ) j Ejemplos por simple inspección © Sea ■ G ríf) entonces 0 Sea = [ t i , 2 ) , U , 4 l , ( 3 ^ 1 4 , 8 ) } el GRAFICO d « í Gr (f*V =. \ ( V ) , ( 4 , 2 ) , (G,3),C8,4)} «S el Gráfico de f*' j : IR-► Co}+oo> definido por fW- entonces } '* : Co,t®> -» p. © S e a . § : ir definido ( 5 , fco> «n to n c e s g " 1 :< S + o o > — * (R por f -,(y )= V 2 « » d e fin id o p o r la¡nvefsa d e f g (x > = 5 + 2 X d e f in id o p o r JL + JL log ( Y - 5 ) 3 3 2 es fa inversa d e g . ® Sea h I í - oo- i y— entonces lí1: -2> definido por h(x>- - 2 - ^ ; Í*H)2 <-oo,-t> definido por h~1(v) - -1 - 2 /-y -T es la inversa de h X -X ® Sea tffcnces f • R — - < -V > fin id o por f w s — —* ffl definido por f ’Vy) - 1 inversa de f . Sólo fines educativos - FreeLibros e ... ^-Xlí J ia . Funciones Reales de Variable Real E J E M P L O I - Pora Seo 10 funciono Como g es Lo inverso funciones discretos finitos . g í j G, 1 ,2 , 3 } £ - 1 , 2 , 5 , 8 } definido por g ( x ) = 3 x — 1 biyec ti va ( Probar lo ) , tiene inverso: de g es g**1 : | - 1 , 2 , 5 , 8 } —* | 0 ,1 ,2 ,3 } d e f in id o p o r g-* { y ) S . 1 y + J_ Donde g^fy) se obtiene haciendo g(x>»y .* y » 3 x ~ 1 des pe jondo " x " y y+1 ®3x X ss y 4- -ij~ g~M y) En este próbleme , el gráfico de g es : W ( g ) s | ( 0 , - t ) , (1^2 ) , ( 2 ,5 ) , { 3 ,8 ) } ,^z— «s »n Goniunf© discreto finito. Lutfo S r í g ' 1) = EJEMPLO 1. Seo Como 2. ( 2 , 1 ) , ( 5 ,2 ), { 8 , 3 ) Poro funciones de vorioble lo función g.es biyec tiv o Lo inverso de g es : NOTA. g * [ -2 , 4 ^ —* { 0 , 3 ] ( P r o b a r Jo ) , g- 1 : ( o , 3 Lo reglo di , d e f in id o por g t x ) - -^ de definido por g*”1 ( y)®5- 2y * 4 , g-* se obtiene modo .’ f0 ) Hocer g (x) » y en g ( x } = - j x y * - i 2°) Despejor x : x +2 tiene inverso . £-2,4) corrésôn dencio continuo. + 2 % 4*2 2y * ~ x + 4 Sólo fines educativos - FreeLibros del siguiente 170)_____________ 2. Seo lo f (X) = - ¿Moisés Lázaro C. función f i < -o o ,-2 ) - v - i - (x + 2 f -Z f es b i y e c t i v o Como reglo de (P r o b a r lo } , tiene c o rre s p o n d e n c ia { x + 2 )* - 3 => y = - 4 y = - { x+2)2 = - 4 y - 12 2 )2« 4 { - y -3 , hocer C-x 4 2 )* - 3 ,luego I x +2 1 = 2 / - y - 3* f (x> = y de spejor , , = 2 n/ - y - 3 * ^ lo l $ X < ~ 2 Calculo . ~ En => | x +2 J = - ( x+2) / lo inversa de h. h~7 . IR — * IR , d e f i n i d o por h ^ í y != correspondencia —— i — ------- -■ . : . ,n h <xJ f* L n ( x 4 y x 2+t y = h ( x ) = Ln { x 4 v ^ + T } ( p ro b a r lo ) , exi st e d é lo reglo de . x 4 2 < 0 h ; IR — ► JR , defin id o por L o in v e rs o de h es f poro definir el votor l x4zl ■■ Asi.* x € < - 0 0 , - 2 / = D o m ( f ) jT—————!*| b iy e c tiv o , oplicor lo propíedod .absoluto 1 íy ) es é a i z cu a d r a d a . usar el dominio de x a - 2 / - y -3 - 2 „----------— * h x ) ’**- ol extroer x + 2 = - 2 y^-y-31 Como del siguiente modo ( x + 2 ) 2 - 12 P - 3, Seo lo función inverso. de f ~ 7 se o b tie n e f (x ) = - ( x 4 2) por 3 ^ - * < - o o , - 2 X definido por f~7{ y )= - 2 y ^ y - 3 -2. En {x4 defin id o ■ Lo inverso de f es f~\‘ <~eo Lo < -0 0 ,-3 } ) , Ln ( x 4 v ^ 4 ? ).**- de h~r ! —-- —■-- hocer h <x) = y despejor x Sólo fines educativos - FreeLibros e T- e “y — ----------- Funciones Reales de Variable Real < 3> — ey = x + y/x*+1 ' Pues y = Ln u ❖=> Q1 = u e*y- 2 xe»+x 2 = x*+1 e*y- i = 2 xe g*y - i = X 2ey 2 h"1 (y) E J E M P L O 3 ■ Poro funciones F U N C IO N E S DOS [T] CON que. tienen 2 o más imágenes. X M A S E N E S . E s decir f = f, u f? Seo lo función f : ] - c o , 2 [ — » ] - 8 , o o [ x , x < 2- 4 definido p or - 2 f ( X) -? x -4 H o llo r , ~2* x < 2 ío inverso de f , si existe. SO LUC IO N PASO T ¿ Como sa b e r q u e R e s p u e sta .-f (1) Codo f tiene inverso P tiene inverso si', y solo si cumple dos co ndicio ne s! fu nción f. ( x ) ~ x2 - 4 , y ^(x) = - 2 x -4 , x < --2 -2 - x < 2 SON I N Y E C T I VAS . (2 ) R o n g ( fr ) n Rong ( f2 ) = 0 Sólo fines educativos - FreeLibros Moisés Lázaro C. Ve o m os 1 H) o) P robem os si es inyeetivo f , í o ) ~ f2 ( b ) Seo -> o*-4 = P e ro - o * - b Entonces b) — Gomo b < - 2 o => l b i ~ - b b P r o b e m o s ,si ' f 2 { o) = -2 o - 4 O Lo cuot es in y e e tiv o o no. f ? (b ) , - 2 & Pongo f (]- ■b pruebo que de od. o < 2 , - 2- b<2 = - 2 b -4 f2 es inyeetivo. ( 2 ) - A hora , hollemos los rangos de f t y si o <**2 ~> io f., es i n y e e t i v o . Seo o) , b <-2 i* b J o | « íbl o o <-2 b * -4 O* » => , e no. f2> res pe c ti vamen te., ( ] - oo , ~ 2 [ ) - 2 [ ) = { f I X » / x e J - ® I- 2 Í x € j - 0 0 ,-2 [ -> x <- 2 - x > 2 A y a i cu o d rd o => Su mor - 4 => | x2 > 4 x 2— 4 >O f í x) => Luego Rong ( f ) ~ y >0 y E ] 0, + Sólo fines educativos - FreeLibros od [ • Funciones Reales de Variable Real b) Rango de ^ * ^ ( [ - 2 , 2 0 f _ í C - 2 .2 [ ) » j f ( X ) / x e [ - 2 , 2 [ } -2 - x <2 por - 2 => 4 ^ - 2x sumor - 4 *> O & -2x-4 Luego .’ Rong(f2 )= A h o r o , hollemos de los rongos Rong ( f 2 ) n R o n g ( fj ) sr 3 - 8 , 0 ] y >-8 <=> y € } - 8 , 0 ] y 6 ]-8 ^ 0 ] lo intersección G om o los f u n c io n e s > -4 ft ’ y de f 2 y f t n í O f oo [ « 0 #2 son i n y e c t i v o s en su r e s p e c f i vodom inio R o n g { f , ) n R o n g { f2 ) = 0 , o f i r momos q u e f es IN Y E C TIV A . PASO 2 Ahoro o) hollemos los regios de c o rre sp o nde ncios de f j 1 y f2 1 L o reglo de correspondencia de f ~ , l se h o llo ó porfir de fT(x ) = x2- 4. Mocer f (x ) = y D es pe jo r x => y ss x2- 4 »>■ x* s y+4 => IxI a - x / y + 4 1, c om o x < - 2 -> I x l = - x . = / y i 4* x = - \/y 44* f^Cy) A s i , obtenemo f y ) sr,<— y/y * 4* ^ y C } 0 ,00 [ Sólo fines educativos - FreeLibros Moisés Lázaro C. <174} b) La r e g l a de c o r r e s p o n d e n c i a de f z , se obtiene o p a r t i r de í fx )'* - 2x - 4* y « Hoeer f z ( x ) --y . De pejor x -2x-4 2x = - y - x 4 -2 f2 ( y ) Así obte ne m os C O N C L U S IO N -- ; f “l ( y ) = - ^ y - 2 , y G ] ~ 8 ,0 ] Lo inve rso f ^ 1 : ] - 8 , 0D[ de f es — ♦ ] ~ 00 ,2 [ -iy-2 , .* , d e fin ido y 6 ]-8 ,0 ] y 6 ] O , 00 [ por f ’( y ) V' y + 4' , [ 2] F U N C I O N E S CON Seo lo f un c i ó n TRES IMA6ENES . E s decir f= ^ u u f 5 t ‘S >*r2Vut2#2>u&/l í y — ^<r'Pft/*^>u0^4)u[4, 10) definido p o r' Sólo fines educativos - FreeLibros r Funciones Reales de Variable Real {175} f O L U C IO N (1) f( x- ) tiene in v e rsa , porque H ) Las (ii) funciones .* f Ro ng ( f, ) cumple , f2 y n Rong ( f* son inyectivos en su dominio ) .« 0 Rong ( f , ) n Rong ( f 3 ). s 0 Rong ( f2 ) n Rong { f 3 ) ® 0 Quedo como e j e r c i c i o , p roba rlo. (2) Hollemos los inversos de í 1\ y -8 ~ x C-2 x < 2 -2 - De £,(*) z: _ * _ v Y = De f2( x j = x + 2 )* 2 6 x < 11 De f 3( x ) = 4 + 2 V x - 2 1 , x2- 4 YX2- 4 Y - X .*• r espec ti vom&nt t y = - ~ ( x + 2)* 4 4y = ( x+ 2) y = 4 + 2\Zxr 2 1 y - 4 = 2 / x -2 ’ yx2 - x - 4 y = 0 x2- 1 x - 4 y ( x + 2 )* = 4y -O f x + 2 | = 2v T x2- l x + ~ - 4 4 y 4y* 4y* x +2 i \2 _ % y 24*i (x-¿) = x- 2 íVy ( y — 4 )* x = 2 ^ 7 -2 . ¿ (v ) x _ - L = + -L 2y *” 2y t .e s c g @ E R 4 - 2y =í> Como x e ¡j-6 , "2 [ "V «'* 2 + - 4 “ “ = X • .-v r ' Donde: ÍX4-2| - x +2 ^porche SÍ =*> X = Como: (y ~ 4 )2 — fjMy) -2 £ :X < 2 O Sí x+2 < 4 l X+21 — x + 2 X e [-2 2 [ , * * Kl-2),*2) 4 4» Rong^zye[o ,4 [ Como : =» x e [z,ll [ $00 £ [fy * ',í3(ii>[ 4 i i R ong ( f j ) = y € [ 4,1.0 [ Rango ÍM-ye]-<x>,-^] Sólo fines educativos - FreeLibros Moisés Lázaro C. — CONCLUSIOJM : Si Pf ) f .* A - * 0 es uno fu n c ió n 8 I Y E C T I V A ( f • f ” *) ( y ) = y Trmbten (f of , » .’ -V y e 8 , donde (/o/” ' ) ( y ) = f (f*l¡y ) ) podemos )W se c u m p l e expresar como : , x 61 x «esto f o r m o x i i f{ f l x ) ) = x e s conveniente poro api i c o r e n di v e r s o s problemas Tombiense P2) cumple.* INVERSA Si los (■ f“ © f ) (x-) » x DE U N A a p lica c ione s COMPOSICION. ( o funciones ) so n b i y e c t iv o s , e n to n c e s Por lo t ant o , g ©f , •¥* x € A . g cf tiene * A f .* A -» 8 C es inversa. Sólo fines educativos - FreeLibros y g .* B-+ C b iy tc f iv o . Funciones Reales de Variable Real Lo inverso de g © f , es y cumpIe lo propie dad ‘ P j ) ■€1 g r á fic o de f o lo f u n c ió n (g0f ) y l C -* A (g o f ) " 1ss f ' 1 o ' . r 1 e l g r á f i c o de f* son identidad S IM E T R IC O S con respecto y* x . EJEMPLOS j J | u y =: - L ( : 2 \ Z x + z , s | l C x + ,)2 ^ : _ Z , . . . . . . o s « 4 y , ‘ ; - v J YrX v A ■ / i * - Y = X ---------------------------------- / / /i / f / 3 - / r _y ^ 5 t , 2* // ' ! 1 * -4 A -3 -2 ¡ ' .i — ^ ! / * 1 t / 1 I V 2 3 x / i / , M k ' í - 3 ,*4 > € 6 r ( f J 4 H - I ) € & r ( f ' 1) < - l o ) s G r ( i ) ^ (o ,-y )€ S r í f 1} -2 •• $ ¿ ( - 2, 0 ) 6 ^ i f C5 > = £ ( 0 , - 2) e (3 r ( f ~0 / ✓ S i I0 l 2 t t , 4 ) € ( ai r ( í > =$> ( 4 , 2 ) Se aplico LA ( 1,1 )6 6 r « ) ° 4 / € A P L IC A C IO N D i 1/ c . _ ______ __ PHOPUDAD ( f 0 f T) ( x ) = pora hollar la i n v e r s a de funciones . Ejemplo 1 Seo la f un c i ó n f ( k ) - ~ 2x + 4 , * (3, < ♦ ) € & ( « * - 2 - x < 3 Hollar la inverso de f . SO LUCIO N H olla re m os el Dominio de f 1y su r e g l o de correspondencia . Sólo fines educativos - FreeLibros x. 0 , t ) e ( f ( f ) ( 4 ,3 ) € & r ( f - ' ) Moisés Lázaro €. 178) ú) Dominio de f Dom ( f " 1) = R o n g (f ) Hoí temos é I mng o de f Como -2 * x < 3 ¿ sr p*'- - 2 4 4 - 2 x > - 6 « j r - s umor 4 8 i -2 x + 4 > - 2 f (x ) *> b) Regio f ( X> e 3 -2 ,8 ] de A portir d corres pondenc i o e f de f. f o f " 1) ( x ) = x f { rN x ) ) á x ^ 2f~7+ 4 f"1* Conciusicm f ~T( x ) = 2 - i introducir f en f ( x j ~ ~ 2 x 4 4 sr x x 2 --S - X . , - 2 <x ¿ 8 . _<T+€ [EJEMPLO a] xíea la funciob í • O orn(f) — > R a n g lf) cfej-tm do p o r f íx ): e x- c o.) h a l l a r el d o m i n i o <y rango d e £ ^ b) p ro b a r q u e S e s in v e c ijé va v- x e D o m U ) y c ) h a lla r f s i e x is te . * a) x€ t> o m ($ ) & £— £ >e2x- y - c 2x+-i qô ex - - L eax ( Y - i > = y+1 Va e íx- i *o 2X £ = y+r L n ( € 2% l n ( W ) 2 X qt O x = L n t~ ) X£ 0 J-Uy) / . Dom C*) =: xe<'-doô>u<o>+oo> Pqra hallar el desjarse Nacer rango de J ^ debe x ' en términos de 'y". f(x > -y f así tendrem os .* .£ * ± £ T ezx-n Y € Rango (£) 4=> ~ b) S e a > o 4=4 y€<~<x>/»>uO/*> $ Ca) - j a ; b € Dom(J) e%e~a _ eb +e“b ea-e'a ~ eto_e'b a -b ex - e 'J e C) f fc< : Voo,-1>U<LOO> -4-(-00^0)y <0^00) S-'cx>= l . L o ( ^ ) Sólo fines educativos - FreeLibros Funciones Reaíes de Variable Real mmL 1 h k iU o r l a i n v e r s a o'e ccxdo. u n o c/e t a s s ifu i'm r ^ é s ■ fu n cio n e s : t. fíK) - 2X-3 7 2. Htxj = 2 x 3 - 3 Í x€ C1,C> , gOO= x24 2 Hx¿? , 2£X<4 X€R 12. 3. x<l -V-x-M X - ttxl 3 x -s ^ , - 3 é: X < O gix) 3x <1,ao> ^ o <. x < 4 x-b hoc)*!* /* 13. , *>.1 ■fíx) = I _ Vx-2 x>G [ - 2X4 10 ícx) _ A 2£ _ 1 1+2V~* *5. -4 x2 . ? _ |?x* - 9 X-h M 8. hcx) =-i ' * * I 2Vx 9. ±*V, tO . , t. cl) Rallar % ( x > - 5 - 2 l n ( 2 X - \ ) ? x >1/2 goj x<o 8. M 9. f ‘« ) = i'cx) = i x + | í4 ** ?; ? .^ r x* + 2 7. . , Vx Tr r is í, f ’í v i r J ”! ^ osx<4 ? x >4 y<o e 5j? -t-KJ x+1 Ib 3 fiT(x) ~ b + Ln ( x -a ) H*. f- Lnl-^) ^ 11. x<2 ^ xeR V x<o > © * x <1 y 14 rX <f 13. x€<-2,ó> - Í x+5> ? x e <- 00,-23 f. * i x í -3 t i ’ x-4 11. x € Lh ° ° > xe <o,oq> 5. f W Í ' ‘íx)s, 7 X €<- ooô> ©< x s4 ' L n íV ) lo. £'<«> = -t. + T x x>o b) S t % of : Dom(ôjí) — * B ^cketcr minar B para que g&f ten g a inversa y hallar la fu n ción im e rs a correspondiente. x eiR SOLUcton X<C _1_ X x <o -5 X ’ %Cx) O £.X¿-4 fu ) = 2-ae x>4 1-2X t o< x ¿2 ■) X€0 S®cin los Junciones f y § x-co 7 x>o ;> ta le s qu é ; 7 H4-1 > -H)*SO X vo , 2X-Í fu> = | U. 2¿x<6 I 4x2 ►x + 4 X€ IR -x X<-2 *2- 4 7. h(x> s a + € é 12 ? « " ‘ ) *>a -kx<1 , x >1 <*) l§*j)(x>= ~ I*-*)2 “ 1 * #*,4 b} í%*4)’lX) s 4 4*2\/x41 *>±742 Sólo fines educativos - FreeLibros ; X>.-1 — Moisés Lázaro C (l8 0 )- Problemas: Nivel II I. Sea f : IR — * Rar» (* ) la . fu n c ió n d e f i n i d a . p o r fe*) = .5 - e x + e '* O.) D e m o s tra r q u e ------f (x ) = 1 -------- - — <Z?* + \ b) c> d) D e m o s tra r D e m o s tra r que que f> H a lla r ; R a n (£ ,| C 1 -1 , t£ * f «^S in y e .c ± iv c L . R a n (f ) _ ^ i R r _ V~X } - 4 í:X < 0 Rdníf) definida por í cx>-srr*-cH i 51. Sea f • D©m[J) | 1 T ! X -|2 x I.,0 * X ¿ 2 H a lla r 3. f *. S<?Qt la funcion f : Co,+ooL — { oo . H a lla r la in v e r s a 4 . Sean yôoC) ; deftntdCL por e 2x - e ' 2x 2 de f . tas funciones *. f (x) ■= log^x' ^ x>o f lx> ss 2 x-1 , xefR a) H a lla r ( f ^ y 1 ^ s i e x i s t e ^ b) G r a f ic a r (f o g V ' y n o ia m o 5. D ad o S is te m a c o o rd e n a d a s te c ta n ^ u L o re s . las funciones : Í ± v 2_a 4 * 3 2X-1 CL) Malta»* b) d e en e t Hallar , ~7 < x < o , J o< xÂ f -+ % lo- In v e r s a de H*> s f+ g o<x<£ ■-/ a l intervalo X - r e s tr in g id o x2 7. SÍ S U d o m in io S e r e s t r i n g e D a d o la fu n c ió n f lx ) - lop x <*) H a llo r x7« b> G r a f t c a r , . Dado la función e) R e s o lv e r ..-A^x-co l-^X^x+l e x iste . 6. S e p id e f ~ x -f 3 *#±3 /3 . hallar la inversa d e 4 in te rv a lo I= J o ,3 l~ x>o ' J y 5~* e n e l rru s m o p la n o : loo 12*-?) - f ( l ) -2 5 Vs <**) R e s o l v e r : lop ( 2 x - i ) - l o o , Cx-d <1 s,/3 V3 f lo g ^ x -9 ) 8. Sea f : C<V03-♦ Ran(f) cjue fcx) =< Hallar ta In versa d e f ; Si e x is te ,■ _ ■ Sean la s funciones : r fcx> r x 2 .> o < x < y [ ( 2) 2xZ-Í2x4*2 - ¿ ■gao =< T x +jP V x -3 H a lla r í a g , 12 < X<10 ,, 2x-i 3 24.x ^3 x >3 i n d ic a n d o Su d o m in io y su resgla d e correspondencia. Sólo fines educativos - FreeLibros _____________________ Funciones Reales de Variable Real TI. FUNCIONES MONOTONAS : C R EC IEN TE , A S IR , Y DECRECIENTE DEFINICIONES Seo lo función f ! A -» 8 R , A = Dóm ( f ) (1 ) f es NO D E C R E C I E N T E <=> x , < x ? implico f ( x , ) * f (x2 ) , - V x „ x ?e D o m (f) (2 ) f es C R E C I E N T E <a> x ,< x 2 implico (3) f e s N O C R E C I E N T E <=> (4) f es D E C R E C I E N T E <=>x,< x2 implico (5) f ( x , ) < f (x2 ) , •V x ,j X 2 € D o m ( f ) x,< x? im p lico f { xt ) — f ( x2) ,V- x, , x 2 6 D o m f f ) f ( x f) > f Í X j ) , x (> %z 6 O o m (f ) f es M O N OTONA <=> f cumple olguno de las 4 definiciones a nteriores . E J E M P L O 1. F u n c i o n e s que son monótonos en todo Su d o m in i o . 1. Lo función lineo! o fin f(x)~ox+b es C R E C I E N T E cuondo o > 0 Por y es decreciente cuondo , es Creciente 2 fex) =s-Ln x, Dom { f ) : es creciente g(x) = 5 x en todo IR = D o m ( f ) , p o rq u e a = 2 > o <o x>O x >O . es creciente *V* x 6 IR ~ Dom (g ) 4. h{x)~ 85 A c re c ie n t e f 5. f ( x ) = e**x , x € ñ es d e c re c ie n te 0>. o < O • , es decreciente en todo IR 9 porque a - - | g(X) =s - — x + 5 3. cuyo dominio es t odo ejemplo ! f (x ) = 2x ~ 3 2. , a#0 x 6 ÍR . x € IR . f u ) r= n/2x7i ^ x^,V 2 7 . J( x) = 1+ ~ (x-2)7 ; x €í R es creciente no es m on oto na porque crece en <‘x,oo> crece en <“ Oo,2> . Sólo fines educativos - FreeLibros ^ de Moisés Lázaro C. EJEMPLO 2. Fu nciones »que son crecientes in t e r v o lo s contenidos y decrecí entes en cie rtos en el d o m in i o . Por ejemplo f f (*>« cumple x*- 4 es creciente s o b re <-<&,-*> f es creciente sobre <-?, o > f es de c r e c i e n t e sobre f es decreciente < 0 ,2 > sobre MOTA : C R E C IE N T E INDICA subir lo curvo,cuan do x avanza de tzouierda a de recha. D ECR EC IEN TE INDICA bojor lo curvo, cuando x avanza de fequíer da ck derecha». I t . FUNCI ON P E R I OD I C A DEFINICIONES Seo 1. lo función PUNCION t PAR E I MP AR : f : A -* 8 , Dom(f) PERIODICA f es PERIO DIC A <*> 3 un numero reo! T ^ O (x + T ) 6 Dom( f ) y E l mínimo número p o s i t i v o T , tol que Homo PERIO DO tol que x € O o m ( f ) , implico f { x + T ) « f { x ) ¡ 'V’ x € Dom(f ) f ( x + T ).■* f ex) tV* x € Dom ( f ) ; se de f . Por ejemplo o) II b } II e) período de seno , c o s e n o , secante y cosecante período de tangente £1 período de f U ) ^ , | x | es y cotangen es IT. 1. Sólo fines educativos - FreeLibros es 2TT. _____________ Funciones Reales de Variable Real 2. F U N C I O N fes PAR . PA R <-> x 6 D o m (f ) implico-x € Dom ( f ) Por e je m p lo . o) f(x) = x 2 , es p or, porque x2 — x * -4 9( X ) ~ — b) •V- X - f ( ~ x ) = ( ~ x }2= x2 = f ( x ) , *V- x6 IR. e (R - { - v T , v/T1j h(x) s eosx , es por porque d) f(x)ss ixl , es por 3. F U N C I ON V x 6 0^ (“ X )2 x2 es por,- porq ue g < ~ x ) = - -------------------------------------------- == g (x ) (~ x r - 4 x — 4 c) fes y f (-x )= f (x)f Y porque hfr-x ) = eos ( - x ) - cosx = h ( x ) , *V* x 6 IR . f x I ~ x r » Ix I = í ( x ) , “V* x € IR . IM PAR IM P A R <=> x € Dom ( f ) implica - x 6 Dom ( f ) y f ( - x ) = - f ( x ) , x € Dom( f ) . Por ejemplo * o jf íx )b) x3 es impor , porq ue f { - x j - f ( x ) = sen x es i m p o r , p o rq u e (~x )3 « - x 3 == ~ f ( x ) , - V - x € I R. f ( - x ) = sen ( - x ) = - sen x = -f(x),tx6 R 12.1 PROBLEMAS N O T A I No olvido/ que el pert'odo fol que @ es el m enor NUM£RQ P O S I T I V O f ( x + T ) ~ f ( x } , -V- x € D o m { f ) H o lla r, el período de ,( x + T ) 6 Dom(f). f { x ) ™ sen x , x € Í R . So lu cion Supongamos que existe f { x -f T ) =s f ( x ) sen ( x + T ) ^ -T T>0 , x e IR toí , que ( x + T | 6 IR . senx<<*~“\ esta iguoldod se cumple poro todo Sólo fines educativos - FreeLibros T x £ IR . Moisés Lázaro C. En p a r t i c u l a r sen T - sen 0 sen T « 0 se c u m p l i r á pora x- 0 , obteniéndose .* y / € : x*+y?~ i L 0 ,0) T es un arco positivo de lo e írcu nfe re nc ía y sen T ^ ------ ^ es lo segunda componente de los pares ( x , y ) pertenecientes a lo Razonemos 4 T I . 671 . positivo y sen T ~ 0 , entonces T e s 2Tt* «te. El menor T Luego, si T es un or c o así í c irc u n fe r e n c ia positivo el período Hollar es 2TÜ , de sen x el período de es Ts 21T . eos x Solucio'n E I razonamiento es i d é n t i c o a í l ) , so lo es lo 2 a Componente de { c e n t r a e n e ! o rig e n Í3 J Maltor el (x,y ) y radio período ‘de f(x)~ del aplicar Hacer Bx-ZTT => Luego el p e río d o de f { x ) es Tambie'n , podemos hacer del A p a r t i r de Asen ( 8 x ) f(x)= período => Asen perteneciente o lo cir eunferencio uni tari o ) * Bosforo' Si T es el el p e r í o d o tener en cuento que el coseno Asen seno T = i 8 x ). que es 2IÍ 2TT B siguiente modo ' ( 8. (x + T ) ) ~ A sen ( 8 x + 8 T ) Asen 8 x 25 A sen 8 x Sólo fines educativos - FreeLibros , 8 >0 del siguiente modo Funciones Reaíes de Variable Real doode , necesaria mente (4) Dado B T = 2TT , pues 2 lí es el período lo fu nción fCx)=*fx| , x € IR • ¿ Es de seno . f ( x ) p e rió d ica ? Pro b a rlo . Solució'n (1) Supongamos qué existe f ( x + T ) - f ex) , ( 2) £ x + t ] (3 ) En = £ xI pa r t i c u la r do > O , "V- x e tal que m . x e ir . / , -r pora T x~ O Id i g u a ld a d en (2) se se güi ra cumplien , o b ten i t n d ose !_ cn-fo] T 1 = [ L En e.l Seo lo funcio'n b ) G rá fic o r (1) 0 ~ T < 1 fíx) = | x | a } Ha lia r Solución lo solución de esto ecuación in te rva lo Luego ( 5) 0 el /no es no e xi s t e es O - m ínim o T < 1. pos i t i v o. p e rió d ic a / f e x ) '==. x - [ x J , x 6 ff? pe río do de f { x } f {x) • de o ) Supongamos f (x +T que exi st e T > O , tal que ' f e x >, -V- x G fñ (2) x +T - £ x + T 1 = { 3} La i g u a ld a d en t { x + T ) 6 IR. x - | x ] (2 ) se cumple poro todo x 6 ÍR , en p a r t i c u l a r Sólo fines educativos - FreeLibros se Moisés Lazaro C. <186} c u mp l i r á ' par o x = 0 t o+-T-£o+rJ= T - Í T J o-[o] = 0 •' . ' ir r= L t es un e nteró . Com o T > 0 , entonces entero Entonces el conjunto solu ción T = { 1,2,3........ sero pos v H vo * b) El gro'fico (6 ) HdIJor el debe ser } L e s el menor entero L u e g o , el p e r í o d o T positivo. que cumple 5{*+t ) = $(*) v-xeíR + Cx4-T)eíR T = 1 es de f ( x ) == x - £x J , x € IR \ es ! p e río d o de f ( x ) = 5 x — [ 5 x | , x € IR . S o lu c ió n Como es semejante aJ p r o b l e m a cuyo p e r i o d o es 1, b a s í a r á Sólo fines educativos - FreeLibros hacer , • ______ de r e s o l v e r Ot ro forma Suponer Funciones Realesde Variable Real * que.3 T > 0 ,to lq ue f(x + T ) ~ 5{ x + T ) - [ 5 ( x + l T ) 1 5x + 5 T f ( x ) l'V'x€JR , ( x + T ) 6 = 5 x -f5 * J -| 5 x + 5 T j= 5x -[5 x J -,•••(] ) Lo iguoldod í 1 ) se cumple poro todo x 6 tf?, en porticuiorse cumplirá poro y x = 0. ’ m - 5T-f5 T| = 0 | 5 T l = 5T es un entero. Gomo T > 0^ entonces el entero 5T= 1 5T=2 T ~ 1/5 , , 5T = 5 T. debe ser 3 , .. .... T ~ 2 / 5 > T =. 3 / 5 es et mínimo reol positivo. Luego T = 1 /5 es el peno do NOTA' G ráficam ente el período T de una función periódica es la LONGITUD de un intervalo, sobre el cual eJ gráfico de la función sa repite id é n tic a formo. - Sólo fines educativos - FreeLibros Moisés Lázaro. C 13. O T R A S F U N C I O N E S 13.1 FUNCIONES TRi 60 W M ETNICAS Cuondo los funciones t r i g o n o m é t r i c a s se estudion funciones ‘r eoles , entonce* bostoro’ expresor el coniunto ( dom in io ) , él conjunto como simple de portido de He godo (rango) y su respectivo re gla de • funciones trigonométricos bien definidos , correspondencio. As/ obtenemos que los si se co n o ce n su dominio , su se expresan en el siguiente rango quedaron y su reglo de correspondencia • , como cuadro. Sólo fines educativos - FreeLibros Funciones Reales de Variable Real Poro graficor los funciones trigonométricos — se don v alo res o x en rod iones Por ejemplo siguientes tes poro va valores FUN CIO N ES 1 1 ” i Ü S L 6 ’ 4 * 3 12 * 3 1 6 TRIGONOM ETRICAS R e s t r in g i e n d o los tobularse el dominio debemos de f i ni r de codo funcio'n lo función ir 37T •7 r * 2 IN V ER S A S trigonomeVrica obtenemos inversos de seno , coseno , tongente , co ta ngente , Antes con Jos conocidos IT I - i n 3 1 4 ’ 6 1 -21T,. 13.2 graficor el seno y coseno , deberá secante y cosecante . L O N G I T U D de A R C O . < Seo | ( x , y ) / x2+ y2 » con centro en (.0 ,0 ) • un ARCO Sea u a " 1 j de una circunferencio medido en radianes en sen tido on tih o ro rio basto el punto Entonces , lo L O N G I T U D de A R C O de r a d i o desde 1 el punto (1 ,0 ) P(x,y) es lo función L * t ? — ► IR L (a ) definido por Algunos eos ex ^sena ) <xrco -X corresponde *1 furrio (casd^send) a v a lo r e s de lo funcion Longi tud de A R C O , son : ir si or= — 4 v ( , ir , , => ir ir . L ( — ) = (eos — , sen 4 4 4 ) A <x * r/4 Jíl.O) si <x= Y => L ( y ) = ( eos Y = .flota, i S i eí cltco &yai¿YO * , se n ^ -) ^ \< x-ir/2 (0,1 ) s e m u eve en s e n tid o horaria es ^ senC(-«O C sen -*) n-send -- XÍe cumpla I c o s ^ . cosol Sólo fines educativos - FreeLibros Moisés Lázaro C. si »> m&W L í ít ) - ( c o s í , sen! ) " a ( “ 1, 0} v » I « W s* « s ~ ~ p S> L { Íf- * / / W\ / W\ \ ) * { c o s í - j ) t sen( - j ) ) « Hociendo de el combio codo f u n c i ó n tricos inversos (0,-D convencional "ot*' por ' x " y trigonom étrico , obtenemos ios expr esodos en ei siguiente x ] * y « sen x : funciones trigonom é cuadro . SU INVERSA FUNCIÓN TRIGONOMÉTRICA i restringiendo e i dominio A rc s e n :[-l,l]-— [ - f , f ] yH*x=Arcseny \* fv J K >>2 eos: [ o ,ir] - . [ - i . i J x * y=senx Are eos: [ - 1 , 1 ] — [O . f f l y - * x = A rcco y V [y ° A rcfg : R — » ] - f , j [ x i— > y= tg x y h-* x s Are tg y ^ S- V V&1 Sólo fines educativos - FreeLibros Funciones Reales de Variable Real cofg : J 0 , IT[ Are cofg .*IR-*]0 , 3 [ x l— ►y=cotgx y H-x=Arccotgy sec [o,ir] Arese c.']- « . - t f u j t . o o f — £ o , itJ x I— ►y s s ec x — y > — — ►x = A r c $ e c y > Are esc .*■]- M C . ' F f . f j - H - ' J ' - . - ’l u W x I--------» y=csc x E 13.2.1 AMPLITUD .P E R IO D O , Seo f { x ) = Asen {8 x + C ) 3t "2 FASE, FR EC U EN CIA . , A > 0 , 8 >O , C > 0 uno curvo sinosoido!. Definimos ampiilud de f es o) Lo b) E l período de f t se hallo hociendo 8x = 2 TT 2ir El c) — período es Lo frecuencia ZTT es U ) = i T 8 2 IT ci cl os/s eg Sólo fines educativos - FreeLibros Moisés lázaro C, Lo ó) FASE Hoftar s e ' h oHo haciendo Bx 4 C = la ó m p l i t u d , p e r í o d o , f a s e y 0 frecuencia. Solución a) Lo a m plitud b j £1 período Luego e s j 2 1 25 2 l se halla el período c) La f ftcuenero es d) L o fose , se hofla es haciendo x ~ 2TT. T = 2TT . : u) = ^ haci endo ~ ciclos/seg x + j - 0 4 a) Amplitud ! | b) Período : 2x * | ~ -|* 2F ; ~> * * IT Sólo fines educativos - FreeLibros Miscelánea - Problemas E J E M P L O 3 . Demostrar que, para cualesquiera^, B , y C, y = A s e n c x + Bcosex representa una onda sinusoidal y determinar su amplitud, período y fase. SUGERENCIA: Tómese cos0 - — J a2 + J b2 2 + B2 eos (9 A B sen# a2 + b2 = y [ Á 2 + B2sen0. ( 1) Solución: Se trata de convertir y - A sen ex + B eos ex a la forma y - M sen( N x + P ) 2 , r>2r y = \T A 2 + B 2 c o s 6 s e n c x: + + y¡ y jA A z + B^senOcoscx Sustituir (1): yt:— + B2sen ex eos 9 + eos ex sen 9 y = \ l A 2 + B 2 sen (e x + 6 amplitud = 4 A2 +B2 Tenemos: hacer P E R ÍO D O : c x -2 n 2n FASE: , donde 9 - árceos f hacer ex 4- 9 - 0 [ J E JE M P LO 4 . Para un período completo dibujar^ a) y = 2sen*-eos* b) y = sen 4* 4- 2 eos 4x Veamos a) Aplicando el problema 3 tenemos A = l A = 2 < C=1 b) Tenemos 1 •B = 2 C =4 Sólo fines educativos - FreeLibros ^ a2 +b2 Moisés Lázaro C. 1) * v^ 4 + T 1) « / A*+ 8*' = V 5 = >/5 ib — - ore cosf eos 0= ib -} — - ' V*1 / € 3) y = sen 4x + 2 eos 4 x s V ? eos ( 4 x + 0 ) ,0 3) y= Zsenx - eos x = y's'sen ( x + 0 ) , 0 = 2 6 - 5 6 ° = 0 - 4 6 rod. = 2.23 sen (x + 0.40) EJEMPLO 4.2 G ro f ic o r y = sen(Bx+C) y y = senx, B ) 0 , C ) 0 y 3 sen ( B x + C ) y »' senx PROBLEMA S. Demostrar que Jo ecuócion de Momplifud modulódo w y - A» f 1 + m ten 2Wwf ) ütt 2 ¥ Se puede escribir en lo f o r mo ! y ~ A 0 s e n 2 T w Bf + - — 5 - eos 2TT ( v * - w e ) t , - ^ ? p - cos2W ( w f w>>' Sólo fines educativos - FreeLibros Funciones Reates de Variable Real Demosfroeidh y « A 0 ( 1 4 m sen 2 f wt ) sen21Tv*>t 5 s A 0s e n 2 ¥ w « t « 4 A^rnsm 2 ? wt sen21T w0t A 0s e n 2 f v*>t 4 Á©m *-• êos(2 1Twt~2ffwbt ) - c o s ( 2 W w t 4 2TT w®! ) J T = A 0 sen2TTw0f + y A*m eos 2 1 { w - w 0) t — AajMpfi y - eos 2 IT ( w + w 0 ) t PROBLEMAS Resolver los siguientes e cu a c io n e s trigonom é tricos D 1 senx = T „■ í IT 51 1 R “ ( t - T J o, 2} 1 cosx - - y „ f R = J 3) fg x = 1 R = | X (^ 4) se n 2 x = y TT 5f 12 1 ’ 12 1 5) tg 2 x = 1 ir 8 -» 1 8 * 65)\ sen —* = y^ Resolver los 1) Resolver 4) 4TT l 3f i } | J IB ir I7W lZ * 12 §T I 3¥ » 8 '{ ^ 1 siguientes ecuaciones c6$ ~1 ( 2 x ) ~ t r i g o n o m é t r ic o s cos~1{ x ) > — 2) R e s o l v e r ! . t o n ^ í x / í ) 4 cosec- 1 3 ) R e s o lv e r : 2TT f o n " 1— ! R a|~V 2j 1^- 4 tan*1 x =» Resolv er ! á r c e o s ^x 4 y ^ inversos 4 are cosx 4 ore c o s ^ Sólo fines educativos - FreeLibros R = ÍV 2 / 3 l R s í/ Ü T = 3TT 2 Moisés Lázaro C. — (¡96)- Id e n tid a d e s c o n fu n c io n e s tr ig o n o m é tr ic a s in v e r s a s : 1) P r o b a r q u e : are s e n x = a r e c o s e c - 2) Probar qu e: are c o s x = j r c s e c - , x ^ 0 , x * 0 y 3) Probar qu e: - y 4) P robar q u e: , si x > 0 , si x < 0 a rctg x + a rc tg y = a re c o tg y , si x > 0 are c o t g - - ; r , si x < 0 - 2 sen 1x. a rctg x = l( 2 x ¿ - 1 ) = - y 5) P robar qu e: sen 6) P robar q u e: s e n '1( 2 x 2 - 1 ) = - y + 2 se n _1x Sólo fines educativos - FreeLibros , V x g [ -1 ,0 [ , V x € ] 0 ,1 ] Funciones Reales de Variable Real FU N C IO N E S EX P O N EN C IA LES y En es fe capítulo estudiaremos rítmicos , "como funciones FUNCION Uno es f ( x ) = ó* a tos funciones exponenciales y loga reates de vorioble reoI que eston bien defin idos ¡ codo uno con su respectivo regla 1. LOGARITMICAS de correspondencia .y dominio. EXPONENCIAL función exponencial , es: aquella coni o > o a o ffe.1 y dominio cuyo reglo de correspondencia todo F Es decir! f Cx) = a* M II base a a >o a 0 7*1 Lo función exponencial y e IR* x€ F y = a* R A H 0O DOMINIO y » o e s A .H . puede ser creciente Á.H * ASINTOTA HORIZONTAL o decreciente , dependiendo de la base " a " . CASOS CASO 2. si o < o t 1,1a funcidn exponen^ C A S 0 1. si o > l , la función exponencial f(x )= ox , x € F es estrictamente creciente. * ■■ X X Es d e c i r ! xr < x2 implica a l < a EJEM P LO ! f (x )= 2 X , x 6 í R. xf€ F Xj£ F * ciol f( x) = a? , x £ F es estric tamente decreciente. Es decir : x,< x2 implica aX l> a X2i x 1€ F . x 2€ EJEMPLO g(x)= ( £ ) = Z %, x E I R . Sólo fines educativos - FreeLibros F Moisés Lázaro C Propiedades: Propiedades: P\. ax = 1 x- 0 W aX P2 . 0<ax-<\ <=> x <0 P2. 0<ax <1 P3. a*>l P3. ax > 1 c=> x>0 P4 . La función exponencial es biyectiva (inyectiva y suryectiva) P4 ! La función exponencial es biyectiva P5 . *Cuando x -»+oo, P5. Cuando x -» -oo^ entonces ax —>0 entonces Qx -±Q P6 . Cuando x -» P6 . Cuando x -> + 00 , - 00, entonces ax —» + 0 0 entonces ax -» +00 2. LA FUNCIÓN LOGARITMO 2.1 DEFINICIÓN Si a > 0 a a* 1, definimos: log^ x = y x = ¿r Vx >0 La notación \ogax = y se lee “logaritmos de x en base “a”*es igual a y. 2.2 LA FUNCIÓN LOGARITMO COMO INVERSA DE LA FUNCIÓN EXPONENCIAL Dado la función / : R -> JR+ definida por f(x)-, ax, con a > 0 a a ^ 1, existe x*-> y — a La función / —i :R . -> i? definida por condición y = a <=> x = \ogay y l->. * = loga y De esta manera, hemos obtenido la función logaritmo de base “a” con a > 0 a a * 1 , que se puede expresar como; g(x) = loga .V con a>0 a 1 Regla de correspondencia x>0 Dominio La función loga x puede ser creciente o decreciente, dependiendo de la base “¿z” . Sólo fines educativos - FreeLibros Miscelánea - Problemas CASOS CASO 1 Si a > 1 . La función g(x) = log¿7x, x>0es es trictamente creciente. Es decir: xj < x2 implica ¡ogaXj < lógax2 . Ejemplo: Sea g(x) = log2 x , x > 0 CASO 2 Si O< a <1 La función g(x) = \ogax , x > O es es trictamente decreciente. Es decir: Xj < x2 implica logfl xj > \ogax2 Ejemplo: Sea h(x) = log1/2 x , x > O PROPIEDADES: PROPIEDADES: 1. logflx = 0 » x=l .loga.x<0 <=> 0 <x <l 3. loga x > 0 <=> x > l '1. \ógax = O 2. 2. \ogax < 0 4. Si x -» 0+ entonces logfl x -* -oo 5. Si x —>+qo entonces loga x -» +oo 4. Si x -> 0+ entonces log^ x -» +oo 3. logflx > 0 5. Si x —» + oo entonces log^x-»-oo Sólo fines educativos - FreeLibros Moisés Lázaro C, -H200> 2.3 PROPIEDADES FUNDAME NTALES DE LOS LOGARITMOS i>) •V x > O ,y > O , o> O , o # l se verifico ! •og0 ( x y ) — fog0 x + log0y 3. ECUACIO NES CASO 1. cuondo los boses son iguoles .* si o > O a o # 1 i enfonces ‘ Q f(x) _ Q 9tx) <=> f(xJ = g {x) • P2) Y x > 0 , Q > O l tn 6 ñ se verifico ! CASO 2. cuando los boses son diferentes, ajé O log x" « n.log x o o EXPONENCIALES Tienen lo incógnito en el exponento . b> 0 , b ^ l Of(x)= Q 9(x) <d> f { x ) .lo g o =g(x).togfe 9 " f>) v- X > 0 , y >0 , o >0 , a # 1 se 4. EC UA CIO N ES v erific a togo( y ) - logax - logoy L O G A R IT M IC A S Lo incógnita esto' bajo el signo del logaritmo. * log u { x ) = K e 2.4 OTRAS PROPIEDADES t. *og*(o*)s x 2. tog X a ® = x 3. x x.Lria o =e . 7° ) UNIVERSO:[ o>0 A O j í l ] A [ g ( x ) > o ] 2°)Hocer togau(x)=xK <*> .u ( x ) = aK 5. I N E C U A C I O N E S E X P O N E N C IA LE S CASO 1. cuondo lo exponenciot es decreci ente. 2.5 CAM8ia 0 £ BASE PROPIEDADES 1) afíx* < o9txV-> f{x)>g(x) 2) o, W > a,txW si O < a < 1 *> P,- »ó9b.X “ -l-lo g ^X Pr log / ' ^ - f - l o g X O O P„. l o g a , bg 3 • O ff f(x)< g (xj CASO 2. .cuondo lo exponencial es b =1 c re cie n te . •°9„x p4- 10V b * = T 1} ofU) < o°<X,<=> f í x ) < g (x ) log-b t í a > 1 ?> _. 2} a P5 ‘ { log C ) (log b) b o tog»c = •°ok° cambio de lo base V a Jo base” b'r P. s Jog X « - lóg X *i/b & Sólo fines educativos - FreeLibros g(x), v . >o <=> f{x) > g (x) Funcioftes Reales de Variable Real 6. CASO 1. INECUACIONES {201} LOGARITMICAS Cuondo el logoritmo es D E C R E C IE N T E !0 < o <1 eny = logQu (x) UNIVERSO (1)‘ s¡ [ 0<o< 1 ( 2) [0<o< sí CASO 2. u(x) > O ] entonces [ log flu{ x) > K <=> u (x ) < o K J a 1 a u(x) > o ] entonces [ logQu ( x j < K > oK ] cuondo el logoritmo es C R EC IEN TE ! o >1 en y = log s i [ o >1 a u (x) / u n iv e r s o (3) u(x) <=0 u (x ) > 0 J (4 ) si [ o > V X u ( x ) > o ] entonces [ log- u (x ) > K entonces [ logfl u i x ) < K <»> <» > u (x} > o* ] u ( x ) < o K. ] Resolver! l o g ^ ( 2 x - 3 ) > - 2 (v) x Solución. Es el coso T - ** X > 7 ■f* universo . 2 x - 3 > O <=> x > 3/2 2° lo g ^ l 2 x - 3 )> - 2<=>-2x-3 < ( i ) - * S 2/3 C8* 2X-3 < * •X < 7/2 :7n log 5/2 { 2x - 5 ) > 2 7 C $ = x c j 7, + m [ • (?) Resol v e r ’ log j f 2 x - l I > 2 Solución : coso 2 - ( 3 ) 1e x - x € j ¡ 2 / 3 ,7 /2 ( ? ) Resolver 2X- 5 >9 > 5/2 ( T •) 2 i f > 0 X #1/2 A I 2X- 7 I > 3 Á | 2X-1 | > 9 2X-1 >9 V 2 X - 1 < - 9 Solución : coso 2 - ( 3 ) 2x- 5 > O a 2x~ 5 * X * 1/2 > 32 C s = x g J - « f- 4 A X >5 [ U J 5, + o o [ Sólo fines educativos - FreeLibros V X < ~4 202' — -_______ Resolv er! Soluci ón. Moisés Lázaro C. log { í s x ~ * l - 3 j < O E n est e coso lo báse a = 1 2X~ii es funcio^n de x, por tonto, h obra ' que o n o l i z a r s e t o á o s l o s c o s o s . CASO I cuando e l logorit mo es cre c i e nt e 1 _______ ^ u m iv er so j* I 2X-1 I > 1 A I 5X-2 I - 3 > 0 ] . »> ( I 5X-2 1 - 3 ( I5X.- 2 | - 3 < 1 ) t [(2X -T M y 2 X - 1 . < - l ) A ( f 5 X- 2 l > 3 )] A ( 5 X- 2 > 3 f ( X >1 V X'< O ) A V ( X >1 5X-2 < - 3 ) ] *=> I 5X- 2. I VX< -.«i- ) 1 *> <4 **4 < 5 X - 2 < 4 *_______________________________________________ - ‘ - 4 ^ 3»— -1/5 -2 < 2/5 < -^ k = = = = = = = = = = = ^ \ X < 6/5 O y : <-C30l-y> U < l,+ 00 > 5> ^ j [ ( x < A in te r s e c t o r; 4 wmd> -2/5 ------------ -V5 1 6/5 Luego, el conjunto solución poro el coso 1 , es S - y ) ^ ^ ) CA SO 2 . cuando el lo g a rit m o e i decreciente .‘ { O C I 2X- 1 l< 1 A i SX- 2 1-3 > Q \ «> ( I2X-1 I > O. A I 2 X- l l < 1 ) a ( ) ( X ?k ! /I A -1 < 2X-1 4 *»> ( X > 6/5 2, es S? = o- -1 /5 O t/2 1 I L u e g o , el c o n j u n t o solución C O N CLUSION : C9 — S , e,.* x e poro el coso U s2 r ) u C Sólo fines educativos - FreeLibros . t ) > I 2X-1I0) > 1 > 4 V 5X ~ 2 <’- 4 ) . V X <~2/5) *x<e Funciones Reales de Variable Reai 8. FUNCIONES HIPERBOLICAS Introducción » Sumondo los funciones exponenciales se obtienen nuevos f unciones t liomodos funciones c* f(x) = — y g {x } = e-x hiperbólicos . DEFINICIONES 8.1 IT EL SENO HIPERBOLICO di x j j EL COSENO HIPERBOLICO LA TANGENTE HIPERBOLICO di x . d i x. sen h .]-® ,® [ — *•] - ® f® [ tgh! cosh : ] - « , « [ - - * [ i , ® [ e*-e~* sen h (x ) « — - — , e*+e~* tgh(x) i cosh { x ) * — ------ IT E L COSECANTE HIPERBOLICO de x . c o ü c h :]-® ,o[ u j o , ® ^ - ® , © ^ ! ^ cosec h(x) « l/senh{x) j y LA SECANTE HIPERBOLICA d i x. 1 -i,i [ siithfx) CO» htX) LA COTANGENTE HIPERBOLICA d i x. sseh . : ] - * , « [ - * ] o , l ] cotg h,:]-®,o[u3o»®H-®,-1 [u] l,® [ s e c h ( x ) » l/ cosh(x) coig h ( x) * 1/ fg h( x) Sólo fines educativos - FreeLibros Moisés Lázaro C 8. 2 FUNCIONES HIPERBOLICAS I T 1" s eVn h — se n ffx i. ] - « l iJ — INVERSAS c o s hh - '.- [r i 2L ^ t g h ~ L ] - V ’ [• e o s h‘ x s L b ( x * V * * - ? J i - u *** V • -» -2 1 i a 2 - t 1 ■ ! * n a 3 1 - 1 : v -V*' / -1 V I '1 -i ,*a i -« ! 5 4 j cotac h * :]-© ,f [ « 3 * 4 - 4 » . « í 4 4 cosach x » U n ( - . l i Z l i x V 1*1 ) — 1 ü € j f , : ] o l i ] 1— p L , cofgh x = * y Ln 3> L 2. 1. -a , cotoh’ 1:]-<»,> »[u] if< ' 3 -s iJ 3 o co[ , ^ teeh x = Ln { -i i 2 3 1 2 -1 ! <1 S-) ■3 i 1 ! . 3 1 .2 .1 i-1 L 1 Z -1 . -2 -2 i -3 _____ 1 _________L ___ 8.3 IDENTIDADES H I P E R B OL I CAS f ■. Se cumpíein tos siguientes identidades hiperbólicas cqshV - seph2 x - 1 * sech*x sen h (x~y )~senhx coshy— coshx senhy cotg h2 x - cosec h*x = 1 . .2 — 14 sen h x « — ■ — » cosh 2 x -— — 14 =CO$h2X eos I r x = — i sen b ( x 4*y ) = senhxcoshy 4 cóshxsenhy ....... eosh ( x 4 y )== coshx.coshy 4 sen hx.senhy c os h ( x - y ) == eos hx coshy - senhx sen hy senh2 x - 2 sen h x eos hx cosh2x = cosh2 x 4senf?x Sólo fines educativos - FreeLibros . 3 M I S C E L A N E A PROBLEMAS RELATIVOS A COMPOSICION DE FUNCIONES E INVERSA DE FUNCIONES P R O B L E M A 1 Seon la s fu n cion es re a le s de va ria b le ■ÍZ) g ( x ) =\ x 2 , x < o f ( X ) Á * 1- XZ ■ , X ^ h a lla r. ( f o g h x ) <-/ ■ S O L U C IO N : o M ET O D O x < o a X2 e ' X > !• [X -1 y d a r s u d o m in io. Dom ( f o g ) = x 6 O) / s í + 2 <-co,n P R Á C T IC O Dg a g ( x ) € Df J(J q Is i x < o X2* l a x‘ e > . X2 > 1 ■ -I á£Y* 1 X >1 3 — -I real "i^1 (3) X. afi.l' O V X<-1 x r .. 1 x e t - i , o > í f o g } ( x ) = f ( g l x ) } = f ( x l ) = x z +2^ ( f 0 g ) ( x j = f l g ( x ) } = f ( x 2) = x * - i : Sólo fines educativos - FreeLibros Moisés Lázaro C. t (gíx) j= t - x 2 + 2 f (gix))=* 3 - x 2 C O N C L U S IO N : 2 x 2+ P R O B L E M A Z sea , x e [ - 1,0 > X 2- i , x £ ( - o o > 3— X2 , xe [ o,+co) , X < -2 f(x ) 2+X 2 aX / ‘2 - 1 2 X + 2 g ( x ) == X- f 2 1 X v; X - 3 H a lla r f~o g S O L U C IO N (1 ) in d ica n d o L a do m inio > 3 y re g la de : H a lle m o s p rim e ro Com o su < X sí 3 -2 f ( x ) es in v e rsa la i n v e r s a in y e ctiva V x de f se de / f. x <-2 h a lla a l r e s o lv e r : f ( f \x)) = x i -i — ---------— = x ' 2 D e s p e ja r f."1 .*■ + f "! = 2 x + x f ~ l t-r f (i - x) =? 2 x = Rong ( f } l-X 8 •*T V II 2X Sólo fines educativos - FreeLibros co rre sp o n d e n c ia . Misc€ 1 nea Donde 2X <=> x G D f J i Problemas 1- X 2X > 2 X — 1 2X -2 X -f 2X-2X +2 X - 2 (2) P oro Dom h o lla r , f~o g ( f og ) = x 6 > 0 I >0 X — 1 X >0 >1 h a lle m o s en Dg g (x ) G a p r im e r lu g a r su d o m inio D o m f*1 f o g X € ( 1, + r n ) g = ( 1)■ D o m lf'o g )= x £ Dg = -2 = -2 < X * § W € < X ¿ 3 3 A t t o m í r 1) ( 2 X - 1 2 X + 2 ) 6 ( 1 , + a> ) 2 X 2- 1 2 X + 2 > 1 2 X 2 - 12 X +1 > 0 X 2- 6 X ¡f\ x. i i OÓ W 2 l 2 X 2- l 2 X + 2 ) = ----------- x----- — -------1 - ( 2 X 2- 1 2 X + 2 ) 4 ( X * - 6 X + 1) - ( 2 X * - I 2 X + 1) + j- > 0 X Z- 6 X J L 9 - 9 - h j ( X - 3 )* ( X - 3 )*> - f -j- =>X-3 - 2 < * i. 3 Sólo fines educativos - FreeLibros > 0 > 0 v x ~ 3 < ~Ít Moisés Lázaro C m a) V >3 X X f 2 X - 3 < ? , *c d > € 71 X 4 -2 1 X —3 X+ 2 X - 3 tm m ü--------- © -* - — 0 > A i X+2 >2 X - 3 X*2 ( f f lr n m - X -3 3 © í >0 x+2 - x + 3 <-ooi -2>U<3/09> x -3 Á : X -3 x >3 A < -0 P ,-2 > U < 3 ,O O > /\ x>3 X + 2 b) f o g =» 2 / X + 2* X -3 X+2 ' C O N C L U S IO N / X - 3 * - / x +• 2' : r 4 ( X , -2 < X < - 6 X +1 ) - l 2X*-I2X + 1 ) f o g = 2 / x T F /X -3 ' - /X +2 X >3 1 Sólo fines educativos - FreeLibros 3 - > o X > 3 -> o Miscelánea - Problemas ¡P R O B L E M A X 3 / - 2 X Sean la s p o s i b l e , h a lla r a) se ( f de 2X-5 f( X ) S O L U C IO N ( L ) fu n cio n e s X < 1 g U )= - si e s ■<209)— o g )(x) iy X —2 su va ria b le re a l , X < 2 —^ , X ±2 d o m in io . ^ e m p ie za por Dom ( f o g ) = e l d o m in io x 6 Dg x <1 a g ( x ) 6 Df a ( X * - 2 X ) e <-oo,2> : X i X 2 - 2 X +1 < 3 • I - 2X < 2 ( X -V * .< 3 i -/?<.x-i <VT X<1 A 1 - V3 < x < 1 + V T éHVr Dom(fog) = x€ < 7 - / 3 1, T> Sólo fines educativos - FreeLibros ( 1) 13) <20 Mi Moisés Lázaro C. X (3 ) a ) 7 <Z A l. £ < -o o , 2 > e* X9.1 V. < Ln 2 < 0.6 -= 3 - T Cn2 0.6 7 t») (4) X X A ._______ < 2 a) y x » t © C 2 ,+ ® > e e* >, a X >. L n 2 . m m mmm X 6 [ 1 , oo> ( b) fo g ) (x ) = - e * - 2 C O N C L U S IO N (f0 g ) (x, ; 4 ¡ P R O B L E M A Ln2 ] sean t x3 (0S x < o g ix ) x 2- 1 H o jia r fog y 2X - 4 X - 5 f X e < 1-vT, 1 > -X* + 2 X - 2 ,X € <-a>, t-\/PJ - e * -%■ ,X € Cl , + D> 0 fu n d o n es — p ffx) = \Z Tf T , - í * x < 2 , x * o i (2) . g ra fica rla S O L U C IO N : j s P a ra h a lla r fo g , debem os } su dom inio h a lla r 2 ° ) su regla de corres p on dencia. Dom (fo g) — x V eam os ; (D { x <o a € Dg ffxj e a g ( x ) € Df { x — o a ( x * - o e c - J . 2 >} Sólo fines educativos - FreeLibros 0 Miscelánea - Problemas - I Í ffxj < ? | | x <0 A { XÔ A. - f é x 2- t < 2 j u CxJ * - 1 A £ x j < 2 r X<0 A O - A X X < 2 X<0 A A x 2< 3 A -V3'<X <V3 (R -/3?< ■x<'ÍT X ÍO A -I < 3 0 *x2 í X3S-1 - 2 o t x < VJ -1 & x < 2 - i í x <o [ -1 ,0 > [ o ,\/T > U T ~ f ( g exj } = f ( E x V ) - / í + Cx j ‘ ~ r ~ f ( g i x ) ) — f ( x * - i ) * \Zt+x*-i* = * ^ / i + Éx J CONCLUSION: ( f o g ) ( X) = * , x e c - 1,o > j X € C O, / f X 5 / P R O B L E M A E n c o n t r a r s i e x i s t e la f u n c i ó n X +. 2 v v f(x) 2 - Si J f "7 g r a fic a r f S O L U C IO N (1 ) / P ara que y f~ 1en el +1 , in v e rsa d e : - Í ^ X é l/2 7 2 < X+7 m ism o > X < 4 p la n o : f .te n g a in v e rsa , d eb e d o s im á g e n e s, e s in v e c tiv a s e r in y e ctiv a . Com o f tie n e <4 R a n g o ( f , ) D R a n g o ( f ¡ ) = 0 fc>) Caxlct es cnyectivcL . - 1 ^ X £ 1/2 i f(~U 1/ 0*M fl I y e fd/i) 11 3/2 +1 n 5/2 Cl , 5 / 2 3-Rango Sólo fines educativos - FreeLibros (-fj) Moisés Lázaro C. n2> b) dt E l rango fz<x>* 2 ~ tx*né& : t) ^(ct) = f 4(4>) poro i < X < 4 1 1 fti) II {2 ) vem os u) fl 2-JL a «b *^ct,fo€ < Z ,4 > . & a 3/5 y e <-</3,3/5> * Como C~i,V2l fí4) “ 3 // -*/3 a. = b : Ronpo(f2) < - t/ 3 ,3 / s > fi [1 ,5 / 2 ]= 0 s i f, ix> = v /x - x * + 2 ' + i y ol resolver f , ( f * x > } = * obtenemos y / í f - f F + í '+ t í * «mversade ‘X y/qf-lf+ 2' » X - f * lf-lf-+ 2 = IX-1)Z ■ 2 - ( X - 1 )z - f* 2 -1 X -1 )* + -? = f ? - f * + ~ i - ( x - v * = d o n d e -| í* -l-h -(^ i) t* » | - 1 / 9 - 4 ( X - f ; 2 ‘ -1 * 4?*V2 (3 ) si f* ix i = 2 - ) = 2 y x + i x al r e s o lv e r : conclusión: i - 1 obtenem os: & ,= 7 - f* + l 2fg + 2 ~7 ■X f* + X fi l 2 - X ) ~ X + 5 f* Y X4g 2-X X e < 4 > f> Sólo fines educativos - FreeLibros 4ÍX-0* , X € D ,SÁ 1 M iscelánea - Problem as 2X-1 , X < - f aj s e o f una fu nción h a lla r b) sea d e f i n i d a e n IR la fu n ció n una fu n ció n f~ ', s i d efin id a p o r: f(x) 4X2 , - f *• X * 0 X + 4 , X >O e x iste . en IR por la r e g l a : 3 x - 4 o f ( X) t¡ f* (3 )«2 e -3 b hollar et'valor de y f *( 3 ) » 3 o f * ( Ó - 3 b I > donde b í-* es la i nversa. d« $ . Solución de a ) (1) f>V >V * Para saber q u e f ( x ) es inyectivo,debo probar que:) ^ S íü o s : ^ lio a ^ í, t i ) Cauda. f u / ic i¿ n ms t.ny êstiva, mn mu rmmpG.c'éivo d b m in io . . i ) Añora, y h a lla r e¿ rango dm cetc/a. función. - e s ínyecrtiva íf < fjí-D < f2 i o i * o * . J > y 6 C 0 ,4 J = R, 4 ,* '-'^ f^ -D = 2 s 3 Se fien#; , % , n R f,= ¿ , Rj, n » $ -,= # (2) a) INVERSA DE f( <x f » 2X-1 b) INVERSA DE f¡ (4o f*3(X )= X f} ( f * x j 3 = X 4f* 2 ff - J = x em \ U x < -3 * X ~ 4 >'■ ~T" con # <* ~ *“ *2 o 2 pues*. *í=¿ VF , porqoe-I ¿ 5* <O Sólo fines educativos - FreeLibros c; INVERSA D£ fe f3 o f 3 = X f* + 4 f* * X -4 Moisés Lázaro C. 2 Por tonto : a f*( x ) 2 ' -J- V P , x € C 0,43 X - 4 , X € <4 ,+m ■ Solución 4o b ) ’ (1 ) f (x ) = De 3 Xg ~ ~ f h o lla r l f o t * } ( XI = / 3 f*- 4a ■ = x 3 f* - SS8> (2) De 4o = 5X f/V,3® ** 3 f * ( 3 ) = 2 a - 3b. ~ X C 1 De f*í5 ) . -------= 2 o - 3 b = 3o+b 1 5 + 4o 2 5 + 4o „ ' — =3 o + b 15 + 4 a = 6 o — 9b 25+ 4a = 9o + 3b 15 — 2 a - 9b ----------------------j _ ---------------- 2 5 = 5o+3b f 2 a - 9 b — 15 por 3 | 5 o + 3b — 25 f 2a-9b |j5 o + 9 b n a =15 = 75 = 9 0 90 17 _ , D onde : L u e g o : a -3 b 90 = — ;— 17 ,+ v jf s ^ _ ( 17 ‘ _ , 3 ' 17 . _ ’ 25 “ 51 25 , 90 25 115 51 ' 17 (7 117 ir ) _ 5 Sólo fines educativos - FreeLibros 575 + 3 6 0 _ 935 17(5 1 “ 85 Miscelánea - Problemas ¡PROBLEMA l \ y si f g son la s fu n c io n e s Sgn ( X - 3 I + X 2 , X + 36 g (x f h a lla r (ü) <-9 , - 9 ¿ X <0 ) , (i) X sig u ie n te s i sm | ( X , / 7 - X ' ) / x 2- f* + g d o m in io , ÓExiste , in d ica n d o § ° § f su a» o x 4 9 a» o j (f* ¿s u inversa <*» s y ju s t if iq u e . SOLUCION: ( i) T ra tem o s de sim p lifica r , sí -i (a) sg n lx -3 1 s g n l x - 3 ) x - i < o 0 , si X-1 = o 1 , si X -1 >Ó -1 , X <1 0 ,X = 1 1 según la f u n c i ó n , g(x) : X >1 e l d o m i n i o , la r e s t r i c c i ó n es para x < - 9 fe n t o n c e s x x -9 tom a m os : s g n i x - 3 ) = - l 3 x ) = - i , = K4 y x < -9 4 +- 1 < K .fí . donde l Tamban Se puede hacer a&C: <=> 9 K A X < 9 ( K+U 9 K » - 9=» K = í P o r ta n to 4 + í ' f - J — 4 - 1 - 3 , Si - 9 *»X < 0 Sólo fines educativos - FreeLibros Si - 9 s x <o iN rl: 9 -t * — <o 9 =* I f l H Moisés Lázaro C. <216} \A -í (C) +«',9Í 1 < ;+*,*/ O í x<1 x <+ oo )/lX-ll+8 ' * ✓x+T? U -1|= -tM l*-i|s jc- i , X <-9 VX * J / 9 - X1 , O^X < f Por ta n to , g t x ) se re d u c e X <- 9 v i i ( - u + x 2' , 44 a: , -9 * X <0 < -f J V s -x 7 Vx +7 > Xv 1 = / ? - * ' Tenemos : f (x I ,-9¿X<0 3 <-> m * )= (2 ) v/x -# f g(xi = < , 0 ¿xM ' V x+7 , si 7 - x a* o O é :X < 1 X¿1 J x x 2- 4 9 a * 0 7 *X XSÉ7 (X-7>{X+7jasO f ( X i - v / 7 - X 1, X ¿ - 7 t = -7 (3 ) La se in v e rsa de h a llo p o r : f ( x f f ? r - x ^ 7 7 -X 14 x H T e Cvf4%,+<»> A h o ra , h a lle m o s f * + g . V e r la s in t e r s e c c io n e s d e lo s d o m in io s 'X * -! ' 3 soto se puede sumor en Luego f*+ g /9 -x ' el in te r v a lo Sumar 7 iAí- xl % VE - f*1 = x 7 - f* = X2 xa» y / r r Í4 ) L X í-7 ) * /7 -x * ( ñ x > ) - 3 de f * y v/Xf / ' x ^ /h Í1 se 7 - x > / x + V \ xas ✓ W Sólo fines educativos - FreeLibros g — Miscelánea - Problemas ;— ;— .— .— Solución de ii ) (5 ) P ara ( g0 p o d e r d eterm in a r R a n g ( g ) D g rango de g, ~ i / x E l rango de g2 g o g deberá 2- ® * * ** 3 x »- 9á X < < - 9 és o = » /9 -X * , E l ron go d e g4 = / x + 7 ', x ^ j es y to d os * x <7 o lo s ra n g o s — — —i - (6 ) ( 7) E l d o m in io d e Luego g e s : es . ii) > 3 <\/P, y 3 j € < o t +a>> - - - - -— ► D o m ( g ) ~ < 0 J+ m ) fog Dada < 0 ,* a > C v C ,+ ® > £ e s y 6 D IR < 0 }+co> = 0 . la fu n ció n : m « { X' _ 1----------- — -------------- ' i)-H a lla r que: IR Í1 e zciste . d i y — - dmmimii R a n g (g ) Po/- ia n to j M ¡P R O B L E M A cu m p lirse y€ es g3 de ----------- ) —P E l rango d e u n ió n ;— D o m ( g ) ¥= 0 El La _— * f ’X >0 J -/-X -1 » lX^ - i f * , si e x iste G ra fica r f y f * en mismo un p la n o . Solución de i ) " ■ (/) P ara co n firm a r que f tie n e in v e rsa debe # p robarse qué f sea in y e ctiv a . Una p ro p o sició n in d ica quef si fixi tie n e d o s im á g e n e s ( i ) . Rg*n{&})n R a n (Í2 ) =: <j> ento n ces tie n e in v e rsa .. a .(z) cada $ { ; { - i ,2 E n el p ro b le m a ten em os l) Hallemos el rango,de §•) : Si O) f (x>= - X*+2X (x + i )2 +1 x . <zs in y é c tiv a . , X >•o =£ x t l >1 ^ + 2 , x > o < Ron (*,) ■ : v > 2 ] “ ti)> é «.c u m jp te : J , { * y 0 V* X , , X 2 6: Sólo fines educativos - FreeLibros *1 > 2 ’ =$> Xj = x 2 (pjCOy - Moisés Lázaro C. 't) Hallemos Sí : **~1 ti) c) Al d) L a ft ( x ) — -x -1 ^ Í 5 o - i- x - A £Q =£ Rgr?(^2): yeQ A e c u m & e : L (x ,} e f ,tk ¿ > => x , = x* Ran$i)flRan(Í2)= 4> .Pártante $ <z.s inyectiva. in te rs e c ta rlo s r a n g o s in v e rsa d e rango de f 2 : =$> - X ^ l x 2+ 2X + 2 = (X + i )2 + f se h a lla com o sig u e i como Por P r o p i e d a d : f,( f *<X) ) = X =* =x ( f * r t f + i =í> : x>o . x+i > 1 ix -t-H -.x + l ig u a lm e n t e : D e s p e ja r i" : Cf * + 1 ; 2 = =*> X -J Í4*+ ,I ~ f * = - e) La se in v e rsa h a lla d e de - f+V x r ? x e < 2 , + a> > - - /- x - i' fz ( x ) f 2* x ) ; = , x ^ - t x / - f * - J 1— x / ^ r ? = - x ( 2 ) Luego - i + V x f*(x)— (3 ) EL (í? + l)= / x M : f2( • líSilaf'+l / x ~ 1 ‘ <=* - x 2- * G R A F IC O : - f 2* - r = 1 1 , x e < 2 ,+co , x e < - > 00, o 1 l*. Sólo fines educativos - FreeLibros X2 ■ 0 Miscelánea - Problemas P R O B L E M A 9~ ¡ [ Hallar 25 — X T f(x) = fog TI T — , si e x i s t e , p a r a : X+2 ] ’ 7 T 7 <0 // 1 - X * P , X , X€ [ 3 , 4 ) , X€[4,8> 4 ¿ X < 6 g( x) = I 4 — X* I SOLUCION (1) s i m p l i f i c a r l a s i m á g e n e s y r e s o l v e r l a in e c u a c ió n : X—— ¿t En f a>E" f = r ^ r ] = [ T í r H 1 - x ^ - J = 1+1- 18 X~? X+2 J 1+f - T r r - ] > K H a lle m o s el e ntero Asi • 1 por -18 L lie g o , para 4 mm- e f " 2 -4 > l a j.uncto’h a p a rtir d e t . -2 < x <4 Sumar - 7 tnv e ft ir x -2 <0 es un entero a co ta n d o * € (-2 intervalo 7 X - 4 _ L > -L . > .i_ 9 x -7 3 ' 3' V~ ^ ~ iL X 7lM s??ÍM St 4 2. < 2<-£-<3 'l - 9 < x -T < -3 < & x-7 t . ApUCQfíO el O K =2^ 3 ,4- , 5 ^ -,5 v Si 4- x-? i x ^ l“4 Si 4 -il< 5 x-> b h b s Si 4 S$-i?L x x c C4,6) g(x) , donde I4-X2 |=1x2- 4 | = K2- 4 V - x e LdyB> . Sólo fines educativos - FreeLibros x<4 Moisés Lázaro C. — (220)(2) P ara h a lla r x f o g , s e g u ir e l sig u ie n te , x e [ 3 ,4 > XZ- 4 x £ x 6 /\ Dg ■[ 3 , 4 > x '. X 6 < - 2 , 4 >* — g(x) A I , p rá ctico i/x - 1 ' , 4 í X < 6 , X€[4,8> D e fin ir : D o m f f o g ) = A ) 1+ K f(x) = g (x) = m étodo £ ♦?- Df £ <-2,4 > ¿mwim wníL - -í x£ [3,4 > (fog )(x>—f( g<x)) = ftx) = i +K B) x £ [3,4 > X £ [ 4 , 6 ) 0 f 0g C ) x e [ 4 }8 > A ( -2 X2— 4 ) £ <—2 , 4 > < X - 4 2 < < 4 X2 < 8 X 2> 2 ( x > V? v x < - / F ) A -x? *•€ C«,8> -v/T> 0 Sólo fines educativos - FreeLibros X2 < 8 A vT1 -v / o 1 < X ( V 5"1 v f Miscelánea - Problemas D) X 6 ( X - 4; A C 4 ,8 > e C4,6> 4 á X - 4 8 * X 2 < JO X*^ < 6 8 A X ‘ < 10 (x iV S 'y x í-»S )A (-y/RP < X < VW ) /\ -✓ ¡0' [ C 4,8> -v T 1 vf»' vio’ n([->fig,.xfg>u[>re^>X e n to n c e s 0 no existe f og . CONCLUSION 3<x<*1fc ( fog J(XJ = t + K , x € [ 3 . 4 > , donde 3 , X e , X € 11 ¿ x <4 o— -------- 2 - o * — 2---------------- ,— o f =3A *=* [ 3 ,3.4) (fog)<x) = ¡PROBLEMA 9 I £>#terminar f *o g X s g n (-^ j-) f (x)~ C 3 .4 , 4 ) , s¡ existe^ paro ’ , - 3 <X <2 I X + 4 I * - ? - /zx-\ gt xh , X&2 , I i-x j X *—X -12 X <1 , 1 , X - SOLUCION : ( 1) Antes de hallar Veamos : f*y f*o g , conviene sim plificar J ~ 2 - 3 <x< 3 f(x): X 10) , si X 4 -3 = 0 A -3 < X < 2 t— t & 1Áx = -3 X ll ) x - Í - — ¡ 2 X43 — > o yA fe — A ~ 3 < X <2 5 <-1vx> 2 , X * 2 Sólo fines educativos - FreeLibros f y g. < X <2 2 4 Moisés-lázaro C. A) f r |- D e < * O x f c '< -3 ,2 > + B) De C) De - |± |- * o -3 0 2 X=- 3 / „ > o Luego ® -3 -X A ) gt (x ) ~ 4 l pa ra ' x +4 / z X - 11 D/ Í X > * 2* ' pues' - = ---------- P o r -1 sum ar *X , si x f f - 4, i > , si xe < - © , - 4 > -1 a < : £ i punto crítico efe IX+4Í l**4|=X+4 t i i •> l ■ ' x • 4 E n g(x) ----—o------ re d u ce o . , f (x) s e f (x ;= (2 ) o x >-X ( í/¿X~/‘ . -a g »- (x )~ 2 2 >- 2 O >t-x>-? »> -f < f - x < o P o r fonfo.- g(x) = <=> £ t - x j as- i V -X - 4 X+ 4 -/2X-í' i , x e <-oo,-4 , x eí-4,i > , x e < 1,2 > X2— X - 12 , > x e £ 2 , + co > Sólo fines educativos - FreeLibros Miscelánea - Problemas (3 ) , A h o ra No h a lle m o s o lv id a r que la in v e r s a f(xl tie n e de l) Rianíf,) n R x x n ^ r ^ f(x)- in v e rsa s!y sobsi <4¿) Gckdck. £ u n otc*l '• .ii y 5“z «s<s iny«c Veam os ■^ív c l e.n s u dora i nio. í) Com o ffíx) ,x e , su rongo e$ r Camo ,* £ £ 2 ^ 0 0 )i ye <-2,3> : porgue.•. ~ 3 < x < 2 acctando: ^ xe[z,oo> * y f< -* 0 , - 2 j ^>,2 Xx £ 4 por-r • D o n d e ti) Rango ft itt») = -x Rango f2 = <-oo,- 2 j n <-*, 3> ^ J2Í n es =^SuraQr4'. -1 ™ i n y e c t i vo . pana todo '*€ <~3,Z> Pues: J - i ( a ) = 5,(1») -a. a - «4 a ^b v a ^ b € < -3 ,2 > -fe b 5*U ) = - 1 - ~ “ e s ínyecttva para todo x e [ 2 ,00) P|¿*s ; 5*<a> = f 2(b) =¿> a= k ^ ^ c io ) ■ rrr=^f 0? = b* " (al = |b| * = “ En Jai. 512 ^ - l¿l=a ¿ „ , » lbl=b c o n s e c u e n c ia . §- in y e s tiv a . - x La inversa de = -i-*?- 4 es < x <. 2 X>;2 5 loo=J zV~x^? Com o: 3 , ■- y por ta n to tie n e , ' X « -2 £ « * -x-4 x +4 9 x<-4 , -’4 ¿ x < 1 - VÜm 7 § (x ) = -< X2- x - 12 ^ U x <2 x ^2 . Hallemos el dom inio de $*©g Sólo fines educativos - FreeLibros in v e rs a .. Moisés.Lázaro C. D o ro C j^ g ) : A x€ B o m (g ) X <-4 0) sgcx> € D o m ( 4 * ) - 2 <- X- 4 < 3 •7< x <-1 A -7 < x < - 4 x < -4 te) - x - 4 ¿ -2 x > -2 A .... ..—v ----■<p, (3) — 4 <x <1 - Z < *-f-4 < 3 < x <-1 A - A i x <- 1 (4) - 4 A XA1 x + 4 < -2 *<-& A Y ,J. 0 1* X < 2 (5) A . -2 < - V ix^r < 3 2 > Jíx -í > -3 X <5/2 ^ ... < X <2 1< x <2 (« y V -NÍ2X-Í <-2 A ' 0 (7) x V2 X^.^2 ..... a ~1 < x2- x - ? 2 < 3 3 i< ( x - i f < £ !- UV3T* , ^ y n >C£r z 2 (0 ) x> ,2 a xz- x -l 2 < -2 C x - i ) 2 é 41 4 2 < * < 2 ^ Por tanto: x*4 , -7<x<-4 Sólo fines educativos - FreeLibros Miscelánea - Problemas 8.32 GRAFICO DE FUNCIONES ENTERO Y S I6 N 0 CON VALOR A B SO LUTO , MAXIMO OE X . Para groficor funciones con valor absoluto, con máximo entero y signo de X,se debe recurrir o lo definición de dichas funciones. [7| VALOR ABSOLUTO lilxv , St ULtx) £ 0 En lo áefinicio'n de vaíor absoluto ’ |u ix )| : J -U ü ) , UUx) < o se observé dos cosos bien definidos,que son:las restricciones y ios ima'genes.' Si ; u ( X ) * Oj *> uc x i l = + u (XI si i u ( X } < O ; => U(X)| = - U (X) IMASEMES R E 5 T R ICCIOtsiES Ejemplos 0 y= 12x— 1 1 y* S, I X - 1, SÍ I X- 1 * 0 IXI-2 , X 3k 2 X* r2 X * 2 X-2 - ( 2 X - U , s» ex—t < o V -(IX l-2 ) , - 2 < X < 2 X -X-2 , s í e x - i , x ai i/e 1/2 2 -2(X SO 1 - ( e x - i ) , x < 1/2 -(X-2), O < X <2 Su gráfico: X -2 y= X* 2 -X-2 X«-2 X+ 2 -2 < X S O -X + 2 O < X <2 $ 0 VÉRtm & M & l 2 X - 1 « 0 * > X * f/2 Punto crítico 0 : 2x - t * o *> x * 1/2 y * I lx l -2 I fX I - 2 , si Ix I —2 ^0 - ( IX I - 2 ) , SI Í X l - 2 < O Sus Los puntoscríticos; ¡IxI- 2|*o *> x* 2, x *-2 vartícds : (-2,0) } (0,2) ; (a,©) Sólo fines educativos - FreeLibros Moisés Lázaro C. X"~ 4 ^ , SI ^ t -X*4*4 X -4 * mi -2 < X < 2 # X ^4 SO 4# X * 2 , X a* ~ 2 A C L A R A C I ON E S f Cuondo se define ei volor absoluto , se obtienen dos imogenes diferentes,codo imagen con su dominio restringido. 2. Todo io que se debe tener cuidodo es el signo del vofor obsoí uto , dicho signo dependero' de Jo restricción de i dominio. 3. si $e esta' analizando uno función con dos o mo's valores absolutos, es mejor recurrir al método practico de los PUNTOS CRITICOS. Los PUNTOS C R I T I C O S se obtienen igualando a cero codo valorobsoluto. Los puntos críticos par ti ció non a la recta real en la unión de intervalos4. Algunas veces la presencia del valor absoluto en las funciones están por demos, porgue son positivos poro todo x 6 I R . 2+ x , si x - O E jemplos ’ ( J ) y = I 2 + I x I f== 2+1 x I .= < 2 —x , si x < O ( J ) £n y =2 2 I x2 + 4 I - 2 x I x - 1 1 * 2 ( x 2+ 4 ) - 2x I x-1 I = 2 ( x2+4) - 2x ( x - I ) , s i x-1 ^ O 2 (x2 + 4) - 2 x ( - x f l) ,si x-1 < 0 2x + i , x *1 4x*-2x + f , x < 1 Sólo fines educativos - FreeLibros Miscelánea - Problemas ( £ ) En {2 27 } y = | 3 + lx l2 f - 3 j x2 4 1 j m 3 4 1x I * — 3 (x*+l ) donde Ixl2 - x2 3+ x2 - 3x2- 3 « - 2 x2 / © En y& 3 f 2 4 lx l| - 2 Ixl Ix* + 4 1 - I x 1* - 3 (2 + Ixl ) - 2 Ixl I x 1+6 X4 6 4 !+ 4 - x* 8} 6r«rfi cor lo funcio'n -x+ 6 , si x i 0 , si x < O f(x )= lx * -4 x + 3l - 2 |x -2 | + x|x| Solución se puede e s c r i b i r a s í : í. f(X) 2. Puntos críticos 3. f ( X ) = | { x - 3 ) ( x—t } | - De | ( x - 3 ) { x - i ) | « G ~> x* 3 , x * i De | x —2 | —O »> x * 2 De =a> X » o Ix l» O 2 fx-2 ¡ + x [x| Gr& fimr los punios críticos en fo recto reaf . Así : o I 2 3 Los puntos críticos' 0 ,f ,2 ,3 han particionódo o la recta real en la unían de cinco intervalos = < - € 0, O> ü [ 0 , ) > U [ f,2> U [ 2,3) U [ 3 , + oo> Codo intervalo es cerrado par izquierda y abierto por derecho. 4. Ahora , hallemos las imágenes de f ( x ) • Coda imagen esta restringido aun intervalo y el signo de codo valor absol uto der endera de los valores de x en codo intervalo. Sólo fines educativos - FreeLibros Moisés Lázaro C. f(x) = a) |(X-3)(X-1) i - 2| x - a I + xj xj si x £ < - « , 0 > => f ( x ) s + (x2-*4x43 )— 2 ( ~x42) 4 x (-x ) cm x~«i £ <-», 0 > 6} sixe-Xo,i> conX— 0.8 = -2x-1 => f(V= {X2- 4x + 3)-2(-x + 2) + x( x) 6 Co,i> = 2xz- 2 x - i c) si x6 Ci.2 > => f(X) s-( x1-4x+3) - 2 (-x+2 ) + x (x ) conX»i . $€Ci , 2 > d) ti x £ t 2, 3 > = 6x-7 => f ( X ) = - ( x - 4 X + 3 ) - 2 ( x—2 ) 4 x f x ) COOX»2.3 £ t 2,3 > e) - sí x £ £3, + eo> *> f {X)~ (x2- 4x43 ) - 2 { x - 2 ) + x ( x ) con x»5 € C3,+00> 5. 2X 41 = 2x2- 6x 4 Como sé observora ,en cada intervalo hemos lomado un valor arbitrario de x que pertenece al intervalo y con dicho valor $e prueba qué signo tiene coda valor obsofuto. Por ejemplOjOn a ) con x»- t€<~«, o> êí signo de íx 2-4x***3 I e$ + {x2-4X43) porgue 114 4+3 í »f+e I ; el signo de I x - 2! = - { x- 2 )=v-x + 2 porque l - i - 2 l = 1-3.1»- (-3) - el signo de I xl = - x porque l- lI s - (-i ) • £1 mismo resultado : f(Xt=-2X - 1, se obtiene si escogemosX=-3l-4,~8# etc* que son valores pertenecientes al intervalo <-oo,o> . De moñero similor se opera en ; 6. En conclusión f<X) f (X ) b),c) ,d ),e ) • es .* 2 X —1 , X£ <-00» 0> 2X2~ 2X - I , X£ I O, t > 6X — 7 , X 6 C f,2 > 2X +1 2X^- 6 X + *7 v X € C 2 ,3 > , X £ £3,00 > Sólo fines educativos - FreeLibros , En lo definición de máximo entero .* ^ u txt f K+1 2 se observan dos cosas bien definidas g>ue>son la imapn ,,K:,tqoe es un número entero y la restricción de la; fene ion ujxt si k i u í x X k + l que está dentro del CORCHETE, |u t x il= K,Vk6 2 . ACLARACIONES f. [ u i x i ] es un entero y Ja función utxtque seencuentra dentro del corchete, esto entre dos enteros consecutivosfujy ffü]!-M,cerradopor izquierdo y abierto por derecha : 2. uixi < í u j + I . [Tul ^ u(X) < f f u j + l es uno desigualdad que nos permitiréhaítar el dominio (recorrido de x) poro cada entero ffu j . 3. Es conveniente conocer affunos propiedades usuales de máximo entero, que son: Pt) f u (XI ♦ x | * f u(x>3+ * , si k€ 2. P2) C I u IX j I ! * I u ( X ) l Sólo fines educativos - FreeLibros — Moisés Lázaro C. (230)- x-CxJîxiOA Cxl*o,il o, x€ f|) Ixí-fxJ -‘X-ffx2íSÍ X<0 AIx ls ■-,-2,-1 -i , x 6 -Cx j rsf x es entero P4) tn x js X hx < K4-1 y r l x l - l ,en otro caso. P8) I x + y l = f x l + íy J v C xlf fyH-1 Ke2 . CASOS C-x I 3 P) E*x J = Ex j + £ x + t /2 3 9. o) si n€ 22* , «l intervul© I K tiene b) siñ€¿~ } qL Qí0 : Clc&rckete I 1 «s unentero:.»..-*,-s cambia de int erval o ..... ^ Dentro det corche.le Aay-funciones llix) que están acotados por tosenteros "O * y* |j-M** sentido ■ Ejemplos : vltl-"" ** — — SC £ ~ B - 2 y entonces 2 é ~ < 3 « * *<G *n & x < n ÍX+D **•.....-*>-...............’ S i H Vx-1 ][ - -I k entonces K 6 Vx-f < k+1 S iK í.o =^ x-1 < ( k + i )z o) SI n e 7L+ *> I K se alargo. b) K *+l <. X < 1 K K + 1 )2 K = lo, 1,1,3,...,} si n6 22 ~ »> I K se otorga y cambio de 5 t fljx - il ]|= K * * i í s I x - i | < k + i sentido. 4. K»o« K = {0 ^ ,2 ,...} En consecuencia-, cada vez que vemos una funcio'n con máximo entero,se procede a dar un valor entero a resol viendo la inecuación : entero que s e le a s t g r e 5. . fj0)[[5X3 = [x|+C x+i/3l+ f x + 2/3 I lonfí t»d CASOS < . re >» luí X)J y luego hollar los inte»votes para x [ u J-& uw teniendo andado que el valor a. {[uix)]| d e p e n d e , del RANGO de ta funcion ILO) , El gráfico de f <x ) = E u (X) J son segmentos a semirectas horizontales que a su vez, son proyecciones verticales dé la funcio'n y = u(x) en cada uitervato (queresulta. de resolver la inecuación : C al £ UOQ < £uj + i E JE M P LO S (7 ) Graficor la función f ( x ) ~ I V 3 P j So loe idn y Sé tie n e : mw - í i . 1. Dom (f ) = Dom (a) : x^,o Z . Q m H m r * t m á x im o m i m o : & ** ^ ■ > Fân^{/u.) ; y>0 =[Vx 1 = K *-> Si K¡to *9 K ± f x k7 i Sólo fines educativos - FreeLibros <k+i x dc+i)z } k es entero M iscelánea - Problemas ¿ ó i n t e t i 2 m .n d Q : 7 K2 ¿X<^K+1)2 *=to,1 ■ 0, 0 - x < 1 í ,M x < 4 fíK)SS 2,4-x < 9 D o m ( f ) = x 6 C o, + # > Rcmg.(f ) * ÍN s jo , 1,2,3 ,— | (2 ) .G r a f ic a r to función f ( X J Soluc ion f. El g r á f i c o d e f ( X) so n r e c t o s >ucws - X+3 2. D o m (f ) - x 6 IR - 3. horizontales,proyecciones v e rtic a le sd e 3 l = D o m ía } • , Rong ( f ) ~ 2 . t -2 < -f X+ 3 -1 X+ 3 O a— f(X )=< 1 :— <O < 1 X+3 J & _ —— . < 3 X+3 < 4 X+ 3 0 , X€ [-5/2,2 > , X€ [ - 2 , + ©> , x e { - ® , - 4> 1 , x€ C - 4 , -7/2 > 2 , x6 c - 7 / 2 , -10/3 > O , X€ < - » , - 4 > -2 - 1 f(X) = f CXJ as -1 K -4 J-3 -l , X6 [ - 2, + 1» > v P r -( 3K+l) ,-( 3 K+ 4? \ _ r ■XfcL K ’ K+1 / K K O , K * - 1 , K€ Z Sólo fines educativos - FreeLibros Moisés Lázaro C. ( J ) Graftcar f {x ) ix M ] Sol uci ón 1. £1 gráfico de f ( x ) = £ X2- 4J son los p r o y e c c i o n e s v e r t i c a l e s v ol o def i ni do en Dom (f ) » Bonr><u) *=. ÍR 3. D efinir el máximo entero £ X2- 4 j * K + + > K+4 i K ¿ X2- 4 < K + t , K € Z A X2 < K f 5 k +?< x <Vk+T*) SI X + 3 > O K — -4 K >-5 Los intervalos para * ve>-4 tienen K62 m r n m ii -vlt+ 4 1 / k+T / k+ ? laforrnQ ■ esto in te r se c ció n se cumple só lo p o ro k * - 4 KSZ Poro oigunos enteros K - - 4 ) fafuncio,n f { x ) es f (X ) = { en codo i n t e r - OU*) es un polinomio K + 4 — -O - / x T iP X 2- 4 ... ; porgue m ( x í n/km1 v x ^ - v / í f í T ) a ( - V Sr h o r i z o n t a l e s , que K4 4 ¿ X 2 < K + 5 4+ X2- d e l g r á f i c o 4c <zl p a s o 3 . 2. ♦* son segmentos de rec t os -4 ,x é < -),o ]u C o ,i> = < -i,i> -3 , x6 X -v^.-iJu -2 , x 6 < - V T , - ' / 5 1J ut/J.v/S1 ) -i , x £ < - 2 , - v ' T , 3 u [ \Z3\ 2> o. , x6 <-vSV* 3 i' ; * 6 < - v í ’ , - ^ 1] u l v ? 1 , # ) z , x € < -v ? V v?1 > u [ i . v T 1) - u [* .vT> > Sólo fines educativos - FreeLibros . Miscelánea - Problemas @ - 0 — G r a í ic c i r : f Cx) = DL<=osx| Solución jt i) En -fex) = [ c o s x j , s e t i e n e D o m (a ) : x€ IR ¿ux> = c o s x RanoíAx) : Y € E l ^ 11 \ V^f /- 5 J -i» -ij[\ íw i ~1T 5^-. «4— 0 3T1 O fW o 4 OomT^)= Dorn(u) : x€l& 1) Ahoroi definimos el ma.yor entero E co s* 1 = -1 ^ - l^ c o s x - ([COSX J V ~ < X Como <O < -|*1T V - H c o s x ^ l êntonces t c°Sx]J={-1>oi} . ¿T T < X ,!(» « ) „ « « W f < 2JI V . . . . . r U J Kspar T~~ * — 2— L ssO . >► O - COSX < 1 .....v -a ¿ X íf v ft is x s 5. í t v ..... - ^ x*o [ 2 * ^ 2 , E í E 1] K=impw (|í+im n ca £cosx J =5.1 *-*, f = COSX , no puede s e r : 4 X - 2 K.TT , X € 2 1< cosx<2 En consecuencia , lo regla de correspondencia de f ( X) = ¡ [ e o s x j e s ' ’-l f (X) = ' 0 1 O TR O S ( 5) G ro fic a r , Si * € ] & £ ? * , « ™ [ . , « _ par , sí * £ [S ™ ? , £í¿2L"]-{<K4i>rr} ^ K= Cmpar , Si X •r.zn'H E JE M P L O S DE FUNCIONES CON MAXIMO EN TER O f (x )= 2 [ - 2 X - 3 J + £ - 2 X 4 - 6 B - 2 X Solución f. Aplicando la propiedad f (X) - 2 (1-2X1 ? = 2 l-2 x l-'6 -3 ) P, , la función f { X ) se reduce a lo siguiente ! + I- 2 X J + 6 - 2 X ’ +¡[-2Xl + 6 - 2 X = 3 't - 2X J - 2 X Sólo fines educativos - FreeLibros Moisés lázaro C. 2. Definir t[~ 2X Upará todos los enteros — , - 1, o. i,••• y y lo función f(x) se reduce o lo siguiente De f ( X ) = “ H-5 --*4 3 Í - 2 X ] I - 2X «SNTFRO f (X ) » 3 (-1 ) - 2 X , £i - I Í - 2 X 3 (O) —2X , SÍ O - - 2 X 3 (i ) — 2X , <.0 <1 I — - 2X < 2 — f— — — - , O < X * - 3 - 2X - 2X ¡s: 1/2 1/2 1/2 , -1/2 < X ^ O f<X) - < 3 \ -1< X — — 1/ 2 ^ D o m f#) @ s R ■ ' ~ f* a n g (* ) = ? J r * r * í u í ° j [ u [*> 5 [u Grafícor f tx » = f x f f j ] SOLUCION Tener en cuento Q u e f-j-J y | * f ^ | | son enteros . 1. Dom ( f ) == x € - { 0 } == <~po,o > u <ó, + ©> 2. Analicemos paro x>o y poro x < o A) x >o Para Definomos|~-j==n B) pora n= o , 1,2 ,3 ,.... frl =n Defina mos W - " Bf) ;j.j= 0 por x xJ y I í* [ =* t ~ 0 aíi - ' 1 -L a -L<1 ^ x >o a 5lS o J = 0 «-► x > t P o ra si x<o J == n , si n = <-> n - ,-3,~ 2',- <n+-i n =-1 B-I=- « -V-T <O | <-> x -1 miiftiplicor por x = - m , m € Z + ■ * > ’ É =0 f(X)=0,SÍX>1 Sólo fines educativos - FreeLibros Miscelánea - Problemas A J si n >o :• 2 n *+ w Aplicar.máximo entero n - — < n +1 x ,£ xÍ t J .<m + i x > — x n+i n m - f(x) -m por x : x £ - * -] =nx £ «-» * x > - (m+ t ) a nx > f (x) = m [ f j =nx x ( - i ) <m + i < nx ¿ n+1 -(m + 1 ) < x <-m ,m € Z * 1 B 2 ) si n < - i , e s d e c ir 4,- n= 3, - 2 definimos! <-* o < nx < 1 v n x *i-í n - - y- < n + 1 x » x é ix|t J n+1 £ XI T i l i = 0 iP o rn .s' x = jr x í{ 7 ] 1 < nx í — n = 1,s¡ x = y O < nx - 1 s> I f( X) » 1, SÍ XJS*— Resumiendo.^ O , x >i f (X) = i o í • “rTiT< x ( } ' " e z + , x =*— , n é H + J -J x a° V [ijx-'.sixzfi f ( X) f<x) = 0> si < X < -y- Hs-2,-3,-4 f(X) « 11SÍ X = 7P n --2,-3,-4,... Resumiendo! m ,-( m+i) < x <-m , m 6 Z * f (x)= 0 • n Í r <x < Í T > " » - * c > . Sólo fines educativos - FreeLibros (? ^ Graficar f ix í = [ xJ 4* £ - x J n o ta : T<znar cotejado enophear <zl mayor. ísajtS&o a funciones. Solución 1. Úominio .* x € IR. 2. Vamos a definir [ x j y I~xJ A) si x * n # ( x l *B ff n V \-*¡[xl+ E-x 1® =- n/ * Por ejemplo *. De 1< 2 sed ed u ce; l 1 Aplicar EL1 Por -1 4 4 W s» i ApUcar C H "n + " _ T = o C.-X-J--2 D e. t < * < 7 í ñ+1) - ( n f i n -*x < - n » V .(£-* J * - ( n+r) , se deduce: ? 2 3 4 «l c^ ? St HX <2 =1 3t 5$*<A-»|xl]r5 si ^éx<34 0XB =2 5¿ Si 3á,x<-4=M£xf::3 Si 4i x< *5^ Cxlc4 Sólo fines educativos - FreeLibros M iscelánea - Problemas Sumar: f ' x J + C -x 'J * n - ( n + i ) »'-1 t si n < x < n + i 0 r si 0 3. Luego donde f (X ) * | x j + f - x J = si n < x < n+1 , n 6 Z Rang ( f ) = { 0 , 1 } -3 -2 •- 8) -1 x * n *n € Z t1 • • I x - H x U I , si 1 x 3 es por | x - C x +12 [, si C x I es impar. Graftcar f (X ) = < Solución 1. A nal i ce mos f,tx)= | x - ttxfll , [[xB es'par si £ x J es par, definimos; lx j = ' 2n ~ x 2n >» X < 2n + f ,nez e [ 2 n , 2 n +1 > = A Luego .* x - 2n , si x —2n - O A xBA ..... *r\ 2fHI Jtn ■ i — w*n *€[>n»2n-H> 1x -2n I = tyx) = I x - 2 n I = x - 2 n f,{X ) = x ~2n , x 6 [ , s i 2 n -c x < zrM-1 zn , 2 n +i > Sólo fines educativos - FreeLibros Moisés Lázaro C. x +2 , x € [-2 ;-i> ,si n = -i , x 6 [ 0 ,1 > , si n = o x X— Z. 2 , Xe [ 2 , 3> Ahora analicem os : sifxj [ es 1 =: l x - B > + 1 ] } | = t x ~ f t x j - i j i m p a r , def i mmos x 1 = 2n*M Luego ! , si n - <~t 2 n + 'l ~ x < 2n ++ x 6 [ 2 n + i ,2 n + 2 + 2 >= B | x - ( 2 n + i ) ~ t | = | x - 2n - - 2 | Donde x —2n*■2 , si x-2n~2 - o a x 6 8 *¿.20+2.* X$B . 2ívm zn$2 1 • 20+1 ¿U ^ 2H-+2 |x-2n-2|=s •*(x **2,n — 2) , si |x-2n-2l= - ( x - 2n -2) Luogo : f2í x ) ~ El gráfico de J 2Í141 ¿ X < 2n+2 -(x-2n~2) *-x , x -2n - 2 < 0 a x € B X <. 20+2 A», x € B ,X £ [ 2 0 + í , 20 + 2> ne2T , x 6 [ -i ,0) ,s i n = - t -X + 2 , X€ -X 4 4 , x l [3,4> [ 1,2 ) , si 0 = 0 , si 0 = 1 x " 2n > * € | -(x ~ 2 n -2 ) , * € [zn+i,2rt+2> Donde Rong = [o , 1J Sólo fines educativos - FreeLibros Miscelánéa - Problemas m) SIGNO DE X -i , sí x < o o , si x = o Lo definición de función signo de x es .* sgn( x ) = D o n d e : Dorr>(sgn)= fR R o n g (s g «) = {-1 ,o ,1 J [ f , Si X > O Pero, sí en lugor de "x " se escribe otro 'función u(x), entonces definimos* , si U (X ) < 0 Bon(sgou<x)) = Dom(u.y r- i sgn{u(xj) » < 0 , si U Cx i » 0* 1 , si U( X) >0 ' A A Limdgenes Lr esfricciones Donde observamos que las imágenes son-¡-1, 0 , i} y los re stricc io n e s Son los inecuaciones: u(x) < o ? u(xl > o y la ecuación u(x) =o que deberán resolverse paro hallar los valores de x. Ejemplos @ G ro fic a r f ( x ) = sgn ( x2- 4 ) $ a lu cia n f. signo de ( x 2- 4 ) , se obtiene ; Al definir la función y - 1 ,SI h fíx)ssgn (x2-* 4) = X - 4 < 0 0 , Si X2 - 4 = 0 * 1 , -I f(X) ss Luego : SI X , SÍ - 2 < X < O ,S Í X = í 2 t ,S i X >2 V - 4 >0 2 2 -2 X <- 2 2 . ' . Dom ( f ) = É Rong ( f ) = | - i , o , i j Sólo fines educativos - FreeLibros y=-i X Moisés Lázaro C. (? ) f c x) G ra fica r ‘jQLüctQN : •1. 2 = sgn v^x-i1 . tiene u.(xi - / xh T D o m ( f ) z D o m (u ) : x -1 > o => x > i Al d e f i n i r si gno / x - i \ obtendremos'. 2. 2 ( - 1 ) j si < o * * e s absurdo,. f(-X)sfi|2(0) , SÍ VrX;- l ‘ *Íp X t i ) , SÍ y ^ n >0 I 'fíxr= 8,32.1 o , X = I 2 , X 3 a >1 GRAFICO OE FUNCIONES COMBINANDO E L V A LO R A B S O L U T O , CON M A X I M O E N T E R O (T ) 2 Y SIGNO DE X Hottor el dominio , rango y bosque ja r el gráfico de la funcio'n f definida en JR por * 3- x f (X ) * - 1*1 - t x J Solución t. Como fe XI es una función raciono^ entonces e I denom inador debe ser diferente de cero. Es decir * ; Txi- Ix l * 0 o | xf # f x | , donde [ x ] € 1 Resglver: J-x.I s f * ] ** Cx 1 ~ O x>o A j x = ff x J A V x=-£xj j V x =0 | ¡hT~ Luego: el conjunto solución de Ig ecuacidh IxI — C x 1 =s o es fcs-rN 3. Por tanto : Dom (f) = x e(/R -IN ) Sólo fines educativos - FreeLibros Miscelánea - Problemas 4. Definamos el valor absoluto Ixl del denomnodor de f(x) y asi obtendremos dos fom i tíos de funcione s Veomos ! Oe fu ) *- 3 - x Dom(f) = IR/* IN ix r - ix 3 si x ai o , entonces 3 — x f un x -E x J 3 - X X f i x )« 0 < X < 1 • 3 X X - I si x < o , e n t o n c e s ; 1 <; X < 2 2 <X < 3 . 3 - X X-3 -X> I X-í 3 —X X-3 -X + 2 f (xl*. 3 - X %;-* x* -x - E x 3 3 1 • i * x <o X —2 x , - 3 & X <- 2 r4C4*3 X - 2 I z J L r-i - 3 < x < 4 X —3 ,4 3- X X -3 -X4-4 X- 4 < X <5 Sólo fines educativos - FreeLibros -4 - X <-3 .6. Rong ( f } ~ y € > ü f - 1 } iJ <o, + »> Sólo fines educativos - FreeLibros M iscelánea - Problemas (T ) sean t) f = j ( x ,-|- v /» - x * * ) / l x l - 3 < © } g <x> » sgn — [^ r K ( ^ “^ p ) , Hallar el dominio de H i x ) » f ( x ) .g ( x ) + ft(x) ü ) Bosquejar el gráfico de H<x). SOLUCION i ) DOMINIO PC H (x ) 1) Dom* ( H ) == Dom ( f ) n O o m ( g ) n Oom ( h ) 2) Debemos bollar el ddmmto de f , g y h. Veamos : 3 ) Hollemos el dominio Como de f fex)38 *1“*i / t - x ] , si ix I - 3<o ; entonces el domiiiio de f es : x € Dom { f ) *-> 9— <-* H «->. — o X2 £ - -3¿ X i a 9 3 A A X 6 <-3,~ 3 > Dom (f ) a* x € < - 3 , -3 > Luego ; f <x) » y v4 - x2 lxl-3 < o X < - 3 ,3> Sólo fines educativos - FreeLibros IX I -3 < < 3 X < 3 Moi e Lazaro C 4. Hollemos el dominio de g ; Como g{x i = sen ^ a si ^ 9definamos la f u n c i ó n . g <x> x + ?- s o , VJLiLza o * i X- 2 X = ~ 2 , ^ J L íjL > o x € <2 ,+ © > X—2 Resolver signo de u(x — -■> O X- 2 X >- 2 -2 Bes0(v#r: v ^ A X-2 < O A X < 2 2 = X -2 Resol ver ; J Ó í £ ¿ x -2 >o VT+T > o A X- 2 > 0 x >-2 A X > 2 4* -2 2 x € < 2, + oo > 5. Ha f i e m o s Como el h ( X ) '=* éo m in ió de h. 2X+6 X+ 4 2+ 2X + 6 ] - 2 X+ 4 f —2 x -e - I- -2 Sólo fines educativos - FreeLibros 2 Miscelánea - Problemas llf x ) X 4*4 A n a liz a n d o el denominador, obtenemos 6. Ahora , hollemos la fundón H íx ) Dom(h } = f (x ) g (x r IR —1 - 4 } + h .ex-) Lo formo mos sencillo de hollár el producto f.g y lo sumo f.g+h es diagromondo en lo recto reol codo función r poro observar y hallor lo intersección de los dominios y luego operar el producto y la sumo de funciones: 7. ^ ,— — t i3. / 9 -x 2 Por. tanto ~ \Z9- X*' ( - 1) + 1 + £ - - ^ - J ffx >gc xr *h(x) a 4 V 9 - x*'( O ) 4- 1 f £ - ,-2 j < X < 2 , x*-2 2 <x< 3 3. A h o ra d e b e m o s coi cu la r valo < - 2, 2 >^ en el p u n to Para ello p ro c e d a m o s En Sum ar 4 : v a lo r d e l e n te ro t **4! en ínter x = -2 y en intervalo < 2 , 3 ;>. Qt a c lo ta p i : -2 < x < 2 2 < x+ 4 < 6 Sólo fines educativos - FreeLibros Moisés Lázaro C. Aplicar I B ' . b) ~ 1 = ~1 3i x =-Z =» c) En 2 <•* < 3 £ < *+4 < 7 Sumar 4 ; in v e rtir : ± > ± > ± - . 1 < -_ 2 _ c '- i - p or - Z 3 x+4 -V3 -V7 Aplicar t í 7 O > En consecuencia* lo funeidn H ex) se reduce a lo sígte : , - i < X < 2 Htx) X = - 2 — 2 < X < 3 — x?i 10. El gráfico de Hfx) ; Sólo fines educativos - FreeLibros Miscelánea - Problemas © Sea la función y = f ( x ) . definida por f (.x) VZX^~161 = | [x * -i ó } Ñafiar eI dominio de f . b } Gr af i oor f ( x ) Solución a) Hallemos el dominio de f analizando la rai 2 y e f denominador i x e Dom ( f ) 44 x* - 1 6 - 44 x* a 16 O A [ x * - t ; A R - f 44 ( x 3*4 V X flft-4 ) A 44 ( X — 4 A V X 4 ) ■ -y y r *4 ■-ÍR - 6 ]¿ 0 x6 I R / £ x * - « I - o f < -v1 tl-4 3 ü C 4 ,|# l > < - ® , V ? 7 j U < - 4 , 4 > U [ v / f ’. - f ® ) -4 4 v^1 x € < - » , -y ír1 l u C v ^ . + é > - Dome*) Luego ! Oom ( f x€ )= y/ñi <-oo J U Cy/íP.+oo > , V i - p * 4-12 Al resolver f XZ- t 6 Í = 0 44 xf — 44 O * X - 16 < 1 44 ® á 16 XJ A ( X - 4 V XSÉ-4 I 17 x* < 1 7 • ! 44 < : A - v'F1 ' < X ■ < VTP -------:---- -— —<|HüiltlIilÉA -X w m m m ► - —4 y/W1 x € < - # , -43 ü C4 .-VW > Sólo fines educativos - FreeLibros Moisés Lázaro C, — V x 2- ^ se obtiene f oVifmente dondo valores b j £ I gráfico de f ( x ) «s f x ’- . J enteros a £ x 2- 4 J , tal que no seo cero y teniendo en cuento el domi„ nio de f . El problemo en esje coso , consiste en precisar <fcon que enteros empezar o operar ? Veamos Definimos : f x 2~ 4 j » x k ** x* - 4 < k-m K+ 4 e x2 >, K+4 ( * ^ / k +4 X2 ( ; xe? K 4*5 x2<K+5 a V X S - f iS h l) A ^ ^ K Í i -v¡s? -v E íí « < X < / /ES M k +S ) -V W " ) Para Inter Secta r con e) dcvrumn de í , debe ser k+4 =17 =$> * - 13.9 K>13 R e su m ien d o. x € ]-V * + 5 r v /íS ]u [V k S ^ ^ s C H * t = ¿ ¡E ± K ' K€2. x e ] - /i- v ^ J u C v 'ñ , vlg^ tí ’ , IÍM ; k> .13 X6 ]-V?5, 0 Í J u [vfíe v i ? £ , ^ ].v S i. v ^ } u [ v ^ iN^ ,[ Sólo fines educativos - FreeLibros Miscelánea - Problemas (7 ) seo lo fimcidh real o ) Sra fie o r f (x i = | 2x - 1 1 - 1 g <x )* .f )- b ) si g (x) esto definido enCi/4,3/4> y h (x ía inversa de u (x ) graficar )Va g (x ) , 1/4 * x < 3/4 hCX 1, X * ; 3 / 4 , c) Hallar la inversa de u (x) Solución < 2. f(X)ss )= | 2 ( 2 X -I ) - 1 M * | 4X - 3 I - f f ( 2X- I )= f fl-2X)J I « |— 4X4 11 — I » Í 4X- 1Í - 1 Luego .* | 4 X- 3 1 - 1 — 14X— 114- i - Ahora analtcam ós las valores a b s o lu to s : |4x-3l y |4x-l| . ( - ( 4 X - 3 ) - ( - 4 X + 1))^,SÍ _ X < 1/4 | 4 X — 3| — ( 4 X - 1 [ [ - { 4 X - 3 ) - ( 4 _ X - 1 >]£,S¡ 1/4 — X < 3 /4 2 U X - 3 - ( 4X- . I ?SÍ X*3/4 . Los puntos crítico s x - ’/4 H ^ - ^ 4 disiden (párticiónan) a la re cta recxl en tres intervalos • E n acida, interva lo s e a n a lie a el sioiio d e c a d a v a la r ab soluto . • ■ xo/V L o fu n d a n §o<) x ^.3^4 >/+¿x<^4 «/4 3/4 re d u c id a ( e-s v ✓ 1 gtx): , X < 1/4 -4 X + 2 , 1/4* X < 3 /4 -1 , X * 3/4 Sólo fines educativos - FreeLibros Como uí x) y su inverso son simétricos con respecto o lo recto ys x, entonces el g rá f i c o de lo inversa de u ( x r se obtiene por .simetría. Veamos c) Como u íx) es I-* hallemos lo inyeetivo r entonces existe ta in versa de uexv. inversa de g tíoser § í x t » y «I tx) = -4 x + 2 ; x 6 í 1/ 4 , 3/4 > y =s-4x + 2 4xss_ y + £ X 3S -J- y 4 t ye <gt3/4)t9(1/4jjt*'<~1,il f*«y) => . g~?{x ) « - ¿ x t *5- , x € <-í,i 3 2^® Hallemos la inversa de h(X) == -j- ( x Hocer h (x) = y => y =~-(x-*|-) Sólo fines educativos - FreeLibros + 2 +2 x * 3/4 M iscelánea - Problemas < §> - / =S> 3 A* t ; ' ( x “ => l > - í i H a K II V í x = — + \/y-2 , y 6 [ h1 3 /4 ) , h<x-k»>) = [2,+®> . h-'(y)___ => ■(,-» ( X ) s a i + 2 Por tanto y / X - 2* , X . i x + i , 6 [ > , + » )' X U*'(Xj i + 2 , X[*,+•) Solución 1. Ho Mimos en I - * logar el domio de f. Poro ello ano Meemos el denomino dor y la ra i2 cuadrado, asi': x 6 Dom(f) *-£*1«-* 2 -íx J > o W £x I < 2 X 0 a 2- f x j # o <2 DOMIN 10 2. Definir el valor óbsoluto I x I «n x < 2/ Ixfft-x 3. Al definir txl ¥ x a ki función í m se desdobla: V2 - f si xxo ttx i f <*> = < x -S >l , si o * x < 2 \/z t 3 Sólo fines educativos - FreeLibros X <0 1x1=3, °00x<2 punto crítico de 1* 1; es x=o Moisés Lázaro C ; 4 , Ahora J definam os m ayor entero ÍL*I ^xeiR/x<¡>.. Una m anera muy se n cilla efe definir el MAyoR e n te ro [x]] pana x<2 e s o b s e r v a n d o e n la re cta r e a l . Ix B r -2 -OS A sí tx != -i ---------- -o©— -2 -2*x<-1 "1 “í+ x co # 1x11=0 O ix i- i —: O*-------- — ■ — —O 0*x<l I 1¿x<2 Z fcx> e s : X- I , si 1* X < 2 X vT» , si 0*X < 1 f(X) = -X + 1 , f» - í « X < 0 V T ~X+ 2 2 ~x+3 , -2 * X < - 1 * -3 ir x < -2 sea la f une ion f ex > • x I x —I xl I Hollar el dominio y rango de f. lxl-|x 3 Solución 1. EL Dominio de f ; x € Dom ( f ) A noli zomas safo eí denominador ' <=?> I x l - f x J ^ 0 si x& o •> [x ]»x * > x € fN <»> l f - { x € IR /tx i-1x1=0}, donde ‘f x f - fxf*^ V ^ si X <0 <3s> tu s s*x|x|*-x m 0 - | o , i , 2 , 3 , ............ } => Dom (f ) = x € { IR - IH) Én lo recto real, el dominio de f es 2. Rango de f Pora lid llar - 2 - 1 0 1 2 3 4 5 —h — <— - o— o—-o— o— o-— o- el rango , definir el valor absoluto y el máximo entero en cada intervalo de lo forma < K , x+f > para k* o ,i;z,...y en cada intervalo de lo forma [ k , k + i > pora k = - i . - 2 . - 3 , ...... Sólo fines educativos - FreeLibros M iscelánea - Problemas X I X -x i x- 2 X IX - X I - ^ 2 < X <3 o , 2 < x <3 , donde y = o o , i < x <2 , donde y =o , o < x 1 -X X 1X4X1 -X +1 , -i e» x < o X I X+ XI -X-+ 2 ^ -2 * x <-i X -1 - f u>* s> X 1X4X1 -X + 3 ; - 2X 2- X - 2X 3- X , -26 x <- t , donde y 6 C-2,-2/3 > , -3 6 x < -2 , donde *C-3 ,-e/5> -3 6 X < - 2 Rong (f )®fo} ü r - i , o > u [ - e . - e / s ) u [ - 3 , - e / 5 > u 3. G rá fico de f(X) Sólo fines educativos - FreeLibros (0 ) Moisés Lázaro C. --- ^7^ Hollar el dominio* y rango de los funciones a) f ( X ) = /ix l* - I ( x l ¿I ’ x | x - Ix I I b ) g ix ) = SOLUCION dt o) t . CALCU LO D EL Anúlizor P O M IN IO lo S & b ra é ic Q l DÉ f ' .2 Ix I - I Ix I *#>2 1 £ o f tf I X I* 85 x2 - ( IxI + 2 } ^ o , ptüs s i. . * X2 . ' , .. . . i frx>+?fa fxL+2 , porque*/1x1+2¿*o V x € IR ft X - Ixl - 2 £ 0 ■■ ■•*»»-* At ) SÍ X ^ O Ix I =8X => X2 — X— 2 ^ O At« x e [2,+»> -I O 2 ( X - 2 ) { X + t . ) áf 0 Af ) si X <o *> x 4* x - 2 ^ O ( X + 2 ) { X- l ) ^ 0 .m mó -2 l y - d O 1 A2 = X e <~GD , - 2 ] Sólo fines educativos - FreeLibros Miscelánea - Problemas Bf ) En lo 1~ imogen f t( X ) s y 02 ) En la Segundo imagen , ( X ) = y = / x‘ + x - i ss y / X 2- X - 2 1 x2 - x ^ - J L - ? y = s -/ x * + X + -5 --y --2 l y * y/( x + ^ - f - • J ^ 1 sí x € C 2,00) ~> => X - - í - ái — 2 como Xe <-00,-2 3 => X ^ -2 Xi 2 2 • => X+ — -2 + y t => { X --1 v a, / i x - ± f . ± ' é > / w ¿ 1 %* { X + j / - • — y — ~ O t o qc/e l o s e x tr e m o s son po s it tv o s D o r a ” to d o x íz—Z . y * => 04 e le v a r c u a d r a d o , puss 0 O r => / ( x + 4 - ) * - 4 ./ - 0 y- o Luego .* Rong ( ff ) = y 6 C o, +00 > Luego Rong ( f2 )= y 6 C o , +00 > Por tonto el rengo de f será : Rong (f )= Rong ( ) U Rong (f¿) = y 6 [ o , + oo > S o l u c ió n de b ) §(* ) = x | x- ixj| )(l+ \/C x fl-x') 1. Para funciones que tienen Raíz c u a d r a d a ^ lo primero que de be reí h a cerse es } ánaltsar Iq subradtcal . £n ®ete problema haremos 1 x -IM ^ O a E x l-X . - x + í j x i so a>i ^* Ex. B < x a La solución d e a s t a in e c u a ción e s todo flR ¿) x ^ E *3 t a soiucioh d e es t a in e c u a c io h es : S . La inecuación : (T x Il< x < E x | l+ 1 s e cum ple -para v x £ |R Pues : 1 x 3 = K «=* K 6 x < K + 1 ^ |xl<: x < E x l + 1 Sólo fines educativos - FreeLibros Moisés Lázaro C. íi) x * í* l <£=> x = |£xj X < Ix-J '------* 2. Como %(k > - '2 H*> Hoq. u(y) siendo < {< * ) s x | x - I x l j Danr»(4) = ÍR Ôt) z 1 - \ / x - |[ x ¿ ^ ÉNarn(hl * ÍF? ttcx> = 1+ V l M - x , D o m (U )ís Z S e iendm t : Dom (%> =. Dom ( i ) n D o m (h i n Q om Ou) ? h o o ^ o , ucx>£0 2: 3. ¥ x6 I s e cumple Lyega : 1 \/* - f x D sgtx) ss x| x - t x i | , l x -( - x ) | = í1-2X2 ° st x ^ o » -2-1 * 3 4 5 y s í x<o X 4 - - -2 ? xs l ~ *e 2f+w{o) « r - ,’ é - ...... - 8 4 R a n g (§ ) = { o >-2 J - 8 ^ - t S - - , -*** . . . . } K e a r-. . PROBLEMA : Docks Iq Luncion Se =0 V ? x €']£*« {o } ■i.x |2.xt S<x> = \/|xJ - X , x€ % x|x- x | O A =0 &s/- X t<>0 = -9X-2Q - I x t 8 | -t-x |x+3| + |x+G| + |x-1{ 4 -x + 4 p id e : a) Hallar «d dominio de f b) SfCLficcir c) Hallar el f (x). Ba¿N©e de {• . SOLUCION 1- En Primer tugar La re s tric c ió n ( O a n a liza r t£x Ra í z cuadrada universo) 2 S - x 2- 9 x - 2 0 > 0 ' • 4=4 x24*9x>20 ¿ O 44 (* +S)(x + 4 ) < 0 2. En Seoundo logar anáLizor el s i^ n a de cada va/or a b s o lu to } a p a rtir d e - 5 £ :X é r - 4 -5 -« X € C -5 ,-4 ] i « um ar 8 : 3 .< x+8 <. 4 i |x+8l=x+8 sumctr 3 - 2 ± x+3 ¿--1 IX+ 3|=:-x-3 sum ar q i< :x + g f2 * Ix+6|s * * £ Sólo fines educativos - FreeLibros sumar -1 - g < x- i ^ - 5 i |x,t|s-.x+1 Miscelánea - Problemas 3. . Sustituir en f t x ): $(x) - — 8 y^-x2-9 x 20 -(*+S)+x - x-3 +* +G- x- M + *44 8y-X -9X-20 - 8 , ■f«) = \/-x2_9 x-2 0 -1 x e e -s -o ¡y -* -4 r H : ......... ...... -Vt -i c) calculo dei rango a p a r tird é S u m o r l. * -4 “ 5 ~ “t 4 *+§ * .< * ♦ *> * 4 <CÍ V )l<o O£ V * + §• < ± o J- y V 0 Í 4 ' V -1 < ^ - 1 sumar - í 0$ v J >, ( * + f f > 0 í _ (*+f , fo rn rre rn o s - 5* | t x + | < - 4 + | 4 4 * ^ »• 'i V 'iO -4- > ,-i -j— ’ y y PROBLEMA 8 Do dos los funciones .* l + X f ( x>- -1 < > /ixíTr X* S I x I £ s g n CJt' lf , - 31 # - 3 < x < 1 X | < 4 § (X ) ■ / x 4 * x'‘ * f g o ) Hoffor lo función producto b ) Hollar la función compuesto r y gr&fimrto. Sólo fines educativos - FreeLibros 4luí*tr: Moisés Lázatip C- Solución de o) I. En f(X ), Ii b r o m o s debemos i nt er v al o -i si U (X) K — < x < t , par a < K*-f 1 del máximo e l l o t d e b e mo s recordar i mpl i co £ U (X ) J - K a p ar t i r entero la del definición! siendo k € 22 Veomos si -1 < x < 1 => ex t r ae r 1 < X+ 2 < 3 sumor 2 RAIZ invertir 1 i < \/T7777 < s/T => I 1 > > VÎX + 21* Com o: ‘ o f jé I /P v'TxTi? < 1 1 /P f implica vT x+ir Luego f ex> se convierte en ; X , - t < X s , X 25 1 <1 f ( X> • 2. in g (X) , debemos cuento libremos de tx I y de £sgn(X)J teniendo en le resfriecio'n - 3 < X < 4- Veomos: X \ i) X\ I x ls —x_______ lxl= x i. .. ■— ........ — i. , O- X < 4 , , - f < X < ' O — — -3 i i ) Oe lodefiniciónde signo de x ‘ - 1 sgn(x) =s { , si . x < o O , si x *o t , si x > o Sólo fines educativos - FreeLibros Miscelánea - Problemas Deducimos si x < o entonces sgn ( x) =- t y por tonto f sgn ( x ) J =-1 si x entonces sgn ( X ) s*o si x > o = 0 entonces sgn ( X ) = y por tonto £ sgn (x) J y por tonto [ sgn (x ) | = 1 = 0 1 ti i) Poro multipficor ios funciones fx| y [ sgn (x)J,se intersecton los dominios Así : (tsgntx)J = 1 ts^ncx)D=0 Es§n<x)]|=-1 ?v) De esto monero , io función g( x) se reduce o lo siguiente .* ( - X ) ( - 1 ) , si - 3 < X < 0 g<x> = , si ( X ) { 0) X* 0 x , si - 3 < x o , si x , si o < x x mo = > g ( x )= í X) (1) , si 0 <X < 4 v/x- 3» , si 46 X é 7 v / x - 7 , si 4 * X ^ _ 3 < x <4 X g(x) = < /x-3‘ , 4 £ X£? 1 3. Como fas funciones f y g se han reducido a Jo sigte f(x) = < o x , -i < x 5 , x - t < i x , x € 1 -3 ,4 C /x-3 ' ,*X 6 C 4 , 7 3 g (x) = Ahora, hallemos el producto f g : Xntuttivonnenfe. es sencillo si observam os ern e l s ig u ie n te dicL^rcxmcL ' Sólo fines educativos - FreeLibros <4 * 7 Moisés Lázaro C. En coda interseca ton que observemos en el diagrama > Se ho u Ce la multipltcactort . abien-ien dose : ' 5X 5 n/x- 3 • s o l u c ió n b) de ^cx) = -1 <x < 1 u x <4 x £7 , * Se pide bailar * , V*Z? í ó§ *£ > 3 , 4 [ — — ,■x c ' C ^ T ] ¡ i | [ x Ib -f ( x ) : > , , LJ© xe [T ,+ o o [ Com o g tie n e dos im á g e n e s § “* ^ f tiene dos im a g e n ® 3 í =^ == la composición f© g la. h a lla re m o s X 5 en 4 p a rte s . V eam os ' © i, Dom ( ^ ■ «) j x / x€ DomC^ a %,C'x) € D om (£ ,) J X € 3-3,¿MI a x € 3 -M C x € j - 3 , 4 c n ] - i ; ic - x e ]-i,i[ -3 (í»o 8 ,)(x j ¿ - Í 1 (x ) = X , pues g, Cx) 1 -i n X Luego :■ © t) Dorri (f z ° § t ) = | x € / * e D o m (§ ,) X €1-3,4 [ a A Sp<> € D o m C íz l} x € [1,+ oot x e ] -3 , a l O [1 ,0 0 Q X € C1,-4E- = D ,4 L üy © ° §,)<*> .= f íf s ,(x ó -^ ( y ) pues g, (x> - x ^ Sólo fines educativos - FreeLibros Miscelánea - Problemas lu e go: (D i) (^2°§l)<X> =; 5 -y * € [1 ,4 [ D o m ( i 1D g 2 ) Z { X/ X € D o m ( § 2) a | 2(x y e D o m ($*> =<€ 0 » ,T] A \^ 3* € 3 - 1^1 [ A < 4t-% -1 <1 t >/x-3’ >-1 V A JR <1 ©S^X-3 AX~3<| A x¿4 [V * [ - -Wy- — @ i) — C3/*[ = 14,7] nC3,4C; = 0 Luego ; ^ } f i° § 2 D o m ^ o g j ) = | x / x e D o m íS z V XtGVU' a g 2cx) e O o r n ( í z ) } a vT¡r? e [ 4 , 7 ] 4 ir s T x ^ ^ l 1 6 ^ x -3 ^ 4 9 13 £ x £=*52 A X C 0 9 ,5 2 ] E »,7 ] - it) (f20g2)<X) = í 2 (f*C*>) r f 2 (W X-3*) =s U<2 § 0 *. ( f 2 0 g 2)(x ) s: 5 , X € [ 4 , 7 ] J * , X € E-1, it "1 V 3U greifteo: Sólo fines educativos - FreeLibros x € t f;,7) . Moisés Lázaro C. (0 } PROBLEMA ai <3ra{¿car y hallar el ranô de í<x) = | lx-i|-2 | Soiuctoo P ara D e b e m o s d e s h a c e rn o s d e los va lo re s a b s o lu to s . ello pro c e d e m o s d e l stgtfe-rnodo • ^°) O b t e n e r t od b s fos puntos crí ii m s *-\ ^ I * * 1~ ° ja* x ~1 \ne. | lx - t f-2 1 = O |y - l|- 2 = 0 f*) U b i c a r los puntos c r í t i c o s X -í = 2 en Ja retóte resal. • * -i 3°) E n cada a) b* t C) d) in te rv a lo . r4 ¿anOffescif !d e lo s va lo re s a b s o l u t o s * I X - 1 - 2 | = lx- 3l « # £ « * 4 m - | X-1 - 2 | $4 j-f r r í Í X4-1 fttf. ^ x = 3 Jfeó r | e t - x - 1 1 _ Ix+i | = - x - í = ( - * > # - * 1 = I-X-1| = |X + 1| = í ti ■ t. -x+3 X-3 > X<-1 , < - ,í*x* < isx<. *^3 , , R o n ^ ( t ) =. y e. to ^ Ix -1 ! = 2 V x - 1 = -2 V x --1 X+ 1 = -x+3 1 3 ód ) Do do lo función PROBLEMA 9 f ÍX> = * * | - T J a ) Hoflor el rrngo b ) Graficar f , $ i x e < 0, « ] - 4X J y | de f . (X) . Solución de o) f. Como í * J >M son enteros , debemos hallar los intervalos en el que estos mox irnos enteros es fon definidos -V X € <o,G], Veamos i) -f- < K 4, «> [ f | = k 2K — X < 2 ( K4*M » > U b = o : o ^ x <2 m> |* j |= 0 , K «1 : 2 * X < 4 =*> f - f - J 32 1 kK = 2 4~ X <6 => IT-r I s 2 ‘ K * 1 6 o x < 8 ' *> Sólo fines educativos - FreeLibros | -A . J ss 3 Miscelánea - ..Problemas, U ) Si K * - i < K4 1 «> f “v | s K • 3 K *. X < 3 ( K f t í => f *3^1 s K*0 :0 * X <3 *> K al ; 3 * X < 6 s> | ¿ J a K -2 : 2. £n el intervalo < o ; G ] f [4 1 * 2 tra fiq u e m o s v r e s f s e c t i v a m e n t e ; tosin intervalos en ope esta h d e fin id o s [ 4 J V 1"% 1 Luego , hadam os las o p e ra c io n e s d « p r o d u c t o m s u m a en ca d a intersección Pa/tx e x p re sa r fcx) d e m ane/a re n c illa , e exD llclta - |4 i= o W b=i tt)=o Luego! f c x ) * x 2 [ 4 3 “ 4 x [ 4 1 f(x) = X2 ( 0 ) - 4 X { 0 > , SÍ 0 < X < 2 , Si 2 * X < 3 X2C1 ) - 4 X (1) , Si 3 * X < 4 J?{2)-4X (1 ) * Si 4 * X < 6 , Si 0 f(X)s X» < < 2 X 2 ~ X < 3 X2 - 4 x 3 ■* X < 4 2X2— 4 X 4 4 X < 6 60 X « [fl=1 6 X I¿ l= j ^ V - x C < 0, 6 3 es lo unión ée ! X*(1 ) - 4 X ( Ó ) X*( 3 I - 4 X { 2 ) H | =2 6 Rong ( f ) = y 6 [ - 3 , o ] u [ 4 ,6 [ u [ i $, 4| . [ ü { $ oJ ^ Sólo fines educativos - FreeLibros Moisés Lázaro C. PROBLEMA 10 Dodo o) fa función f{X)=- |2X- l|-f z| X+!| - 7 ‘ ,-2 < x < f Hallar el rango de f . fe) G r a f i c a r . SOLUCION 1. Poro hollar el rango y poro gr&fkar f , debo definir el máximo antera J £- p -2 < x y los valores absolutos | 2 x - t | ,lx > ’l[ restringido al dominio <1/2 • Veamos ! tt) donde si x - - < 2K # - X C k+i 2{ K-M ) => k »-2 :2< x £ 4 => £ --f - 1 = ~2 -2CX4f ) < X ^ - 2 K => [ - - § - ] - K ^ K ^ - i : 0 < X S 2 = ) | - - | - | = - l = 0 K « O :-2< X ¿ 0 = ) iti) En los volores absolutos , necesitamos^los puntos críticos x = t/2 , % x ®- 1 que dividen a la recto reo! en tres intervalos. A h o ra o o e íe m o s en cada» in te rs e c c ió n ou e e x iste é n tre lo s in te rv a los d e f in id o s en tt * y ios intervalos d e fin id o s por ios puntos críticos cié los v a lo r e s a b s o lu t o s : 1*+11 x-x-i |ax~ij=-2x+i 2. Existen 3 intersecciones y en codo intersección definimos lo función ■+ 3 X +> 2 f(X) = - | 2X - 1 1 2 | X +1 | - 7 Sólo fines educativos - FreeLibros N O TA | Uno f o rm a m u y s e n c i f l o d e d e f in ir el M a y o r e n t e r o a - :p m f t i r d e l in t e r v a lo - 2 < x < e s com o sigue : Por - 1 AP*toar | | 1 1 H aciendo un d ia g ra m a en la recta re a l M isu a ltza re m os y d e du cire m os la. ima gen del m ayor e n t e r o y su re s p e c t iv o DOIVMNJO . & ) Rang ( f ) = y i ] - r/e , i / 4 [ Sólo fines educativos - FreeLibros ~ j 2cg Moisés Lázaro C. PROBLEMA k t al es II 2 f ( X - 2)== x 2+ 2 , si gue el r a n g o de g(X) sea la s v a l o r e s hallar <- 2, 2> , donde 9(X) = r e a l e s de *— -2 •~ ~ f <3X -2 ) + x Solucio'n■ 1. • 2 Oe 2 f i x - 2 ) = x + 2 2. Hacer x-2« y X2 f(x-2)=-— + 1 2 2 £ *443^ V x = y> 2 , luego f (y) = -----— - 4r 1 obtenemos =*> * fv - . 3. Oonde . * % f(3X-a) 2 ( ( 3X —2 ) +■2 )* , V --------- ; *f 1 2 _ ex2 v . 2 + )-KX g (X ) - - V - ---------- - 2 * i-2 * * ± L »X + , + x 9*-»+?x+2 2 5. Como el rango de 9 ( X) es <— 2 , 2 > , en ronces : - 2 < g <x ) < 2 9 x2 — 2 K X 4» 2 <»>.-*< —— IX /como el denominador es positivo t -x 6 IR , se puede m u l t i p l i c a r entonces ex2 + n <2 +IX4 2 42 s por -2 9 ^ x 2 + -|- x + •••• y por 2 ; pues - 4- 2 x2 9 f( * ‘ + ± -= x -x + - iL- )J V ■m 9 et / + í - e 2 I X 4- -¿~ ) 4- 1 1 ^ es P O * it w o ** x e íR (**+)■ < a > - t e x 2~ 4 X - 4 <s>-.iex <»> 2 2 - 4X— 4 O < 27 X2+ *> ( 4 - 2K ) 2 - < < 9X « 2 K X + 2 4(27) (£ ) < < 0 , * x €JR - 9^2* < 2 - K * I S X ^ 4X+4 9 X - 2K X + 2 A O< 9 X ? + ( 4 + 2 K ) X + 2 A ( 4 + 2 X )2 - 4 (9)(2) A ( 4 + 2 K )2 < A ~ 2 ( 3) / ? < 9 VÍ* A - 3V F * < -2 + 9 V 2 A -2-3 Sólo fines educativos - FreeLibros < 2 I8X + 4 X 4 4 A 4 <27)(6) < 4 - 2 K < )$ V F 2 -9 V F < ( 2 (4 -2 K )X + 6 (4 - 2X ) 2 - OX2- 2 X X > 2 < O ,*xe(R 4(9 )(2 ) C 4 +2 K < 2 ( 3 ) * / ? <2 + K /F < K < 3 a/ ? < - 2 + 3 v/1P Miscelánea - Problemas - 10.7 < k < 14.7 -10.? 6. - 4.24 -4.2 ,2.2 Luego .' « I - < - 2 - 3 / P , - 2 + i t / T < * < 2.24 14? } ti PROBLEMA 12 . Dodo to función ixi-tv^nj f (x» a ✓* -f * i ‘ o ) HoWbr et dominio b) Sroficor rango de y f (x) f (X) Sofuéion !xI 1 . En f ( X ) , tenemos tres funciones que debemos definir, que son< iv ^r ffxl 2. El dominio de Ixl es IR. El dominio d e C v P J es x - Q , porque El denominodor 3. y/z- Ex I v/P 6 IR x ^ O no puede ser cero , pero s í:e -C x 2>og»>Íxixe «*> r< t E l dominio de f f x ) es lo interseco i oh de los' dominios : m n J® ,+eé > n 2) >. -Hollemos .tas imágenes de fcx; ^ definiendo M* i IlVx 1 y M partir del intervalo CP,2> •* a PUNIO 06 B&RTIOA r Ixlsx 06 X < 2 1 l o í Vx <VF O < í^xB <Vz ■ q i |[^J*0-" •v • o¿vx 0 > o<x<l = rr ui) S. > * x € O j 2> . lx| = x i. ,4x « ITxlrj í O , 1. » Ahora ; operem os 'en' c a d a 0< X<1 iax<2. in t e r s e c c ió n 0 --- que hollemos ’ lxl = x Ixl [tfn l CxJJ»0 5 .* Viendo, ios intersecciones, de los intervalos en que han sido definidos Ix l . , I v 5P j , C * l , obtenemos x ~ 0 v^rgr» f {X) ~ x- r /T rp x Y T f (X) I si X i Co , t > x€ [ 1 » 2 > , si x e [o 11 ) sí x-e [ i , 2 ) =r X -r 1 6. , si Su gráfico .* Dom ( f ) = x € [o tS> Rang(f) = y 6 [o ,t> Sólo fines educativos - FreeLibros Miscelánea - Problem as P R O B L E M A 13 Hallar el dominio , el rango y g ra fica r la función..' [ i - x. ] -i f x - i ] : , f (X) s gn Solución: O - X < 2 2 - )/ I X I - C x l ' Ix t —1 f - n u a .) \ C x 1l V <»#x£o s e c o m p íe ix j= x . 1. El numerador se puede reducir á jo sigte. .* 1 í* - x | * i ♦ I - x | v £ x - i 1 =* £ x J - i y [ t - x j + [ x - i j *; i + .| - x| + £x| - 1 / f o ,*¡ x 6 2 1 2 r - — r -— r 2 . Teniendo en cuenta lo restricción o ^ x < 2 , lo imagen í, se reduce: o 2 -V ^ O ’ f ( X ) 55 1 [ i - X J + fx - i ] I - x| + £ x j .......... ..........— -—- 2S ....... „ 2- / i x l - E x .1 * 2 - v / lx l - C x l ‘ -s < -1 2 -v 'X ^ » ’ , 0 2- / T T T 1 ? _L .2 -v T rn Sólo fines educativos - FreeLibros ’ X = O O < X < t X as i . 1 < X < 2 Moisés ‘Lázaro C o - L uego ft (Xf » Ahora, definam os r lo p f o n t o : ¥ x ^ 2 Al d e f i n i r I 0 < X < 1 I 1 < X <2 v ^ n -2 I x € { 0 , 1} /5 P -2 1 3. , f2(x )= ^ ,^ L J . ^ ^ si sgn x - 2 =* |xl = x . la f u n d ó n s i g n o , o b t e n e m o s .* 1 T T * * . 1 , sí x € o , si <-*», o > u <i,+oo> x -1 0 4 #0r 4. lo re stricció n , U n ien d o , si > »f solo r x i * - 0 “ < , x = o CxH tom am os f, y f 2 , obtenem os f2i x ) - 1 f Sólo fines educativos - FreeLibros , x - 2 1 Miscelánea - Problemas PROBLEMA 14 (271) Se o I o función f ( x } = • V i-txl* X C 2X-1 3 - 2X Hollar el dominio de f ( x ). x € Dom Cf ) <=»> * * L * x ~ ■*!'- 2x #o <=r> £x j * I A IR - | x 6 I R / x f a x - t J -2X=so} <=> X < 1+ 1 A x ( [ex - 1 1 - 2 ) * O <=> X < 2 <=> X < 2 A Dom (f i » X 6 <-CD,0> PROBLEMA V X a O V fax - 1J » 3/2 2 2 * 2X — 1 < 3 J R - { x € IR / X » 0 I ¿WMWm/MWM h O X as. O V 3/2 * x < 2 } -ó 2 U <0,3/2) Dado las .funciones 15 f (X) = |x+3| - | x +1 ]• x 2 sgn f x r Q( X) = { / s - x .* I Ix + i l - 5 I i ) Hallar H ( X) i i ) G ra ficé r H = (X) f (x j -+•g ,x 6 [ - 1 , 1] ,x 6 <1,3] ,x e < 3 , r ] (x ) y hallar su rango . Solución t . Definir los valores absolutos en f ( xi , teniendo en cuento los puntos crítico s | * ~ j3 Sólo fines educativos - FreeLibros Moisés Lázaro C. 2. Teniendo en cuento los i ntersecciones de l os ínter votos , obtenemos f (X) — | x + 3 1‘ — I ‘ - X - 3 - ( - X - I J . , SI r f (X) « X 4 3 - (-X -1 ) , SÍ - 3a x + 3 - ( x + 1j , si xe - , X < - 3 2X44 , -3 * 3. Afloro, definamos, fa función X M - 2 X < -1 1 ' • W f (X » =* X < - g (x ) Tenemos * o) g -U) - x r tgn ( x ) , x € [ - 1,1 ] sn%cx| x Luego , I) (x ) « (-ij . ti - 1 4 x <0 x2 toi , si x » o ,2, X (1í , Si -X X* , 0 < X s< 1 7 X€ <3 , 7 ] ) A v e r i g u a r d q u e signo tiene (x-4 1 1,-V-x 6 <3,5 T se <o o , x **o =>• g t ( X ) •** OXKÍrl I 3 (X|S? | IX+11 - 5 | , -1 |X tiene .* I x + 1 1 =* x + l - X 4*4 , ix + t|r l— - -1 3 3 <X <4 Luego ! g (X.) = I x + f - 5 l = l x - 4 I = X - 4 , 4 * X * 7' tfr^fs-Wf«-4|aX-4 *m M **W M P s 4. Por tanto.* 4 '-x 2 v 0 x2 , g<x)= < /3-x’ , -X 4 4 , , X ~ 4 , - I * X < 0 Xa 0 0 <X 4 1 X 6 <1, 3 3 * 3 r -X £ . . ,r 1<: * éo X2 J O < x < 1 4 *cx>s-, v C 7 .j 1 < x 6 3 -X + < X < 4 4 e x a 7 Sólo fines educativos - FreeLibros * 4 , 3 < XC4 . 2- X , - 1 S< X v< O » o < x ¿1 Ht X) * 2 + y/z - X ' , 1< X £ 3 - x -h e , 3< X < 4 X— 2 . 4¿X 7 Sólo fines educativos - FreeLibros Moisés Lázaro C. PR OQ L E M A 16 G ro fica r f ( X ) = x 2sg n ( x 2- i ) § Ix-flsgn ( x + 'i ) , X 6 [ * 3 , 3 >'• Sol uc i ón f. Codo uno de los funciones#: sgn ( x 2- i ) , de-finiéndo d e n t r o , 1 x —11 y sgnt x + i) sevan d e la. re s tric c ió n - 3< x<3 .y se representan en lineas rectas , para poder observar las intersecciones de los intervalos y a s í o o d e r hallar fcx) . V e a m o s .* 1 1 1> || J v j i- 1 t 1 j> : - K1<> X<3 2. Observando las intersecciones , obtenemos f (X) x 2 sgn C X * . l | - [ ^ L | | x - . - f . | - sgnC x +1) X2 ( t ) - ■ < - * ) . { - X + 1 ) ¡ M ) , si -3 * X <- 1 x 2 co ) - ( - t ) C - X -M) CO) , Si x 2>t ) - C- f t C - X - M ) ( 1 ) , si - 1 < X < 1 x2 - CO) C x - U M ) tm X*1 - C O ) íX —I ) c 1-0 , si 1< X < * coj x2 c 1 ) X2 + 2 X — 2 , 0 so f cxn X -4- 1 - X2 o X , 2 - 3 * X* a* X — 1 , -V < X , X * 1 , 1 < x X » - i < 1 < 3 Sólo fines educativos - FreeLibros < -1 NOTA : D educción d e Jas i m á g e n e s d e o kPUNTO DEL RüüRTlDA. partir del intervalo E3/3> ~ ■y*— ---------- ——" - 3< x < 3 - 4 ^ x -i < 2 -2 < *£Í < 1 -2 i -2 ^ [¥ 1 -2 |^r J -2 V¥l*0: S 5 = -i $ * -2 í -^ < í - 4 < *-t <-2 -3 < X4-1 - 3 < x < -1 XC1 ■ A.......--.9 It 1=i “1O ■,* - 1<1 <x<3 -t< ^ « ->2.á x-l<0 O í: X - 1 ¿ 2 - 1 < X<1 1 < X<3 l - X + f x J - | l - x l , si P R O B L E M A 17 i) Dodo lo función f ( X) = SfflíX*-.#).,!! K X í 4 | 1X- 4| ♦ x j - X , Si 4 < X < 9/2 6/ofícar f (X) ti ) Hallar el rango de f. Solución 1 Simplificar ft (X) = 1 - x + - £ x j - | i - x J , si . = o í x í i 1- x ♦ f x l - ( 1 o * x * i +f-x j ) Sólo fines educativos - FreeLibros Moisés Lázaro C. ( 0 )- 'PARTIDA, 0£Xé1 Jl 1 f,(XJ = = f -X - X a p u c a r |[ B t l x|- i - t - * J + [ x ] - [ [ - x j , 8i0<*x*t -1^£-x1<0 ^ :... -4 -------- O 4 .....- <4-— o o S'h... ~2 t x io - X 4- O - ■ •{ - i í , Si 0 < X <1 3 4 -X * 0 - (0) "0 £ -X £ -1 oíW<v , si X- t il,, W 5*’ M»o t t 0£X<J X “ 1 * ... * -tZ O 1 >X>0 XsO k-X +• 1 - (-1 ) # si x* ' -X +f í*X)a< 0 f 1 Cxb4 ° . 0- xu •11, *=■> , 0 < X <í 1 X« 0 , X» 1 ü-xl=. ■t ¿0<X£J !*|aO flxj o4— 11*1 ^ceQpX]jr O 2. Simplificor f? ( * >= (-jp -x - 2 j sgn ( x^4) Í-X l= -1 , Si 1 < X — 4 (-t) ,si 1<X< 2 ^“ - x - 2 ^ <o),si x**2' -I , X -4<044-2<X< 2 s$ n (x-4 )» 0 ,X2-4a0f>Xat¿ 1 ,X%4 >044 X>2 V t i ) Lutgo : lX-41. = X-4 f$í#J » f x - 4 *+► x | -*x ss-4 4 [l X j-X , 4 < X < 9/2 Sólo fines educativos - FreeLibros x<-1 Miscelánea - Problemas Definamos I 2X1 a partir del intervalo 4 < x < y f3 (X ) = - 4 + 8 - X , 4 < X < 9/2 ' Por2 : f ( X ) 2= ; - X + 4 ,SÍ 4 < X < 9/2 y . 8 <2X4 9 aplicar O * $ 12x1 = 8 f l ^x31 J v x € <- i , t > f ( X ) ,=* < | lx -3 i j + X , X€ [ i ,4 > 1x^ 4! X +2 , X 6 <-2,1 > Q(X) - Hollar .* 2 f - 3 g. Sólo fines educativos - FreeLibros Moisés Lázaro C í D cíin if a) y s í m p h f i c a r * f w /) <X) - Í I X3 |J , X 6 C -,J> o -1 =f x | x í | o- -o e - -o txh?-x f-X ^j ^ ' - 1 < X <-0 flt*> = X3 1 Punto crítico d « jxi=ro # xso fxi=-x exonde t) S i I 1 * -1 < x < o 0 ¿ X c1 1 > - x > o 1> x2 >o =$ =* .- 1 * -1 < x<o í|W = ^ O 6 X <1 ít) S t 06x<1 O i X2 < 1 =4 =* b) - x z < 0 l-x23 --i =0 £x2j , x€ C1,4 > f*«<) = | | x - 3 | j t x 3 £-x+3l+ X , 1Sx<3 i* ~ n +x 9 3 4 x <4 I ~x| + 3 + x 7 1Sx<3 ‘ ■ 3 < x <4* Ixj- n x ' -1 +3 +1 - - 3 + 3 +x , , rexé? 2< x < 3 w 3 - 3 +X , 3< x < 4 x+f x l * y x =i y y > 1.< x < 2 2 < x< 3 3 < x <4 f 3 fz w = } > x+1 3 u ? Luego -1 X rl 1 <•x < 2 "2 < x ¿ 4 , 0 f ( x) r t l* -3 | = -X + 3 Dond e : i) Sí ~ ~3 < flrXjH-1 -3 r - :— -2 — l - x ] j = -2 t - 3 <- x<-2 - 2 £ x <-1 3 \ X = 1 ■' 1< x ! 2 X ? 2 t 2 >, x > 1 3 > x >2 U) -I -O# — frXl=:-3 5i - 1<x < O 0 « X <1 x+j lx -3 j -y -3 1£ x < 3 = » - 1 > . - X > - 3 X rl < -2 +3 + x ’ 3 -o * - _y < X<4 Sólo fines educativos - FreeLibros -1 Xsl -2 - 3 Z < 3 < X <4 1*1 = 3 1<x <2 X<3 Sr*]M -1r-X 1=X _ 2* _ _______ Miscelánea - Problemas D e ítn i’r y s im p lif ic a r |xV4| a) g .w ) x e < - 2,1 > X+2 |x- 2l|X+2l S X+2 iX -2 l = - x + ? IX -2 l — - X + 2 |x -2 fs X -2 U + 2 |= '- x - 2 |- X + 2 |s X + 2 iX+21 r X+2 (* X + 2 ) ( X+ 2 ) X+2 - X+ 2 b) > X € <-2, 1> 2X -1 §2'«> = [ | i xe[i,io> *X+5 x x-1 = íil h ■oiov. Donde: t) s i ü ) Si 14X 00 lx| rX 1^ X > 1 K = 1 I < x < 1 0 ° O ciu ccicyi d e lós m a y o re s e n te ro s P AR T I DA de § 2 a p a r t i r d e l intérvcô D ,» 0 > . " * 1 < X < 10 — li tIO t; — p©i 3: l i'. 4X - > 10 — +s : <— X \í 1 invertir • isrlít 4r >, 3X+S r-f r» > *s fc 35 :!l - - f V 3 I 3* 3X< 30 . 8 < ÍX+5 < 35 J3 24 1 . -13/3 13 2 . 3 |* ~ 3X+5 3 35 < 2.4. -J& ? < X _13_ ' . 3 30*) o < 3x+5. M- 3 < * -3*> t' 1¿- l u í =o 10 > X> 1 2X-1 3x +5 r e s t a r ib-i-bu X- } Sólo fines educativos - FreeLibros ] = 0 , X€[l,10> Moisés Lázaro C — ^280^ 3. HóH'emos 2 f - 3 § ' 2C-1) - 3 < - x + 2 ) -1 < X < . 0 2 ( €>) •- 3 ( - X + 2 ) CK< X < 1 2 í3 ) — 3 (! ) X* 1 2 (X+.1) 1< X * 2 2 f - 3 g » - 3(0) 2< X <4 2 ( X ) - 3 (0 ) , -1 < x <o 3X- % 3X - €» ¿ o ^ x < 1 6 , X=1 H CXI-í ax-i-z , 1 <X 4 2 2X , 2<X < 4 Ix P R O B L E M A 19 O&éo , X 6 <-3 , 2 3 f (x ) = x [ l x -2 IJ - 2 s n g <2, 4> Groficer f(X). f . Antes de grafrco r 7definamos : i x I , £ I x-e 0} En ftcx) = x2- f x f y sng (-X ) , - 3 <X < 0 X* - (X ) , IX í=~ En ft ( X ) a x* + x , - 3 < x <o x2 - x , - o * x | lx - 2 11 - 2 - í sng ^ —il vi 0 » X .4 2 *j5f ) 2 (1 ) , X 6 *■ X | x - 2 j - Ixf* X 0 4 X 4 2 n n t w m t* i b) ^ x€< 2 ;4 > x 6 <- 3, 2 3 X2 - sr < ij <2, 4 > X ( O) - 2 / 2 <X < 3 X (1 i - 2 , 3 4 X <4 - 2 , 2 <X <3 X~ 2 , 3 4 X <4 * X 6 <2 , 4 > Donde : bi) Si 3tf«rktr.z Sólo fines educativos - FreeLibros *2 < X < 4 o < * -2 < 2 | X -2 | = X -2 M iscelánea - Problemas -! X— 2 bi) (281) X— 2 <0 X- 1 X-4 X -2 > 0 X-1 ( t t ) 1 1 f 2< X <4 m x* 2 -OTRA FORMA. OE D6P»NJA Cx*2l t* Aplica* ^ propi-edaol |x ^2l¿IÎ~E 2* Defi n ir ffxB sng 1 ( « i’ > <*, 4 > I b3) A hora definam os él | x - 2 1 a partir dei «itervoío Veamos: a p a r tir d e < 2 ,4 > 2 < x <4 2< | x | < 4 Á CxJs62 2 < K.< 3 . v h r iío a — r- ?o ’4 W = 3 3^ x <4 ■ turnar -2* A p lic a r H 1 : o * £*~2§<2 't :-' l í o o < *-«<1 * 2 «*^3 J4*Sl<2 2. Luego: X > X . I -3CX<0 f(X )á x2- x , oe x e 2 -2 , t <X <3 X - 2 , Í * X <4 Sólo fines educativos - FreeLibros 2<X<3 l 1 /3 < x <4 •Moisés Lázaro; C. PROBLEMA 20 si f está u -*■ C - 2 , 2 ] J <3,9 definido por J- X*+- I , X e [ - 4 , - 2 ) f(X) = 4s/x + 2 1 - f D em o strar X € [ -2 , * , X e ,23 < 2 , 6 3 que f es b i y e c t i v a . PRUEBA 1) f a# BIYECTIVA <-> f es inyectivo y suryectivo 2) En este coso, fes inyectivo <=> códa , 1 = i ,2 ,3 es inyectivo y la intersec ción 4e tos rangos tómatelos de dos en dos ,r e s <j> • ■ ♦ Veamos : o ) ^ 8 *ff ( X r = j X 2+ I , X e f - 4 , - 2 > Pirro o firm o r que f, es inyectivo , debo probar ff <xf i = Veam os. ft ( x2 i implica x, = x 2 , . que C- 4 , - 2 > f,(x,l = j x [ + i >■ f ( X , ) = f ( X 2) f 2 ( x2 ) = ^ x f > i x2+ 1 2 2 x f = X2 ^ > lxt|a|X2| b) seo f2 ( X ) ss Poro si f 2( X l ) xi - *2 v /x + T , x a fir m a r que f2 ( X ) « f 2t x 2) 6 [- 2, 23 c) seo xt = x2 f (X)= 1- y X implica xf , f3 ( x f ) = .•f 3 cx2 ) 4 ix¿l =-X2 xt ,X2 e C - 2 . 2 ] -2* **£2 -2 6 X2 *2 =*. Oí x24-2*4^0<VxíiTíl , , luego* f 2 es inyectivo , X 6 <2,6 ] Poro ofirmor que f 3 es inyectivo , debo probar que si t4<X2<-2 es inyectivo debe cumplirse : veamos: i/x^+z ~ y / x ^ P ^ , -4 OCi <-2 - X1 r -X 2 Luego ft es inyectivo. ' implica x1 = x2 , -V- x, , x 2 € < 2 , p ] Sólo fines educativos - FreeLibros Miscelánea - Problemas * 1 - ~ *1 = 1 - T X2 => x,= Xj 2<X,<£ 2 <• X 2 Luego f3 es d) inyectiva. Para a fir m a r cumpl i r s e : que f , que es lo unión de f 1 , f2 y f 3 ¡ es i n y e c t i v a debe R an$(íiM R o u g e t =<£ , Rang($i) n RangC^) =0, Rcm$íf2)nttaog03M. Veamos . * / f (~ 4 ) » j (t6)+1 =*9 En fl ( x , - i x * + .. . x e [ - 4 , - 2 > < \ye<>.»]-r«fl(U . > f { - 2 ) * y (4)+1 = 3^ < f 2 (-2 ) = v /- 2 + 2 = 0 \ y 6 [ o . z j -ro n g (f2) fJ ( 2) = / ? + ? = 2 • / En f, <x> = i~ 4-x , x e <2,6 ] < 3 2 e) La i n1er sección délos rangos Por tanto . f es inyectiva. f (2) = 1-4- (2)=»0 ■ \ f (6) =t - l . ( e ) = - 2 ' ^ i ( 3t 9 ] n [O , 2] s 0 } > ye[-2 ,o)=»nong{f3) t-ô) ro,2i n tr2yo>=:^ 2 ) La unión de los rangos .* ( 3 ,9 ] u [o , 2} u [ - 2 , o > = [-2 , 2] u < 3 , 9 ] Cómala unron de los rangos coincidecon " elconjunto de llegada t entonces afirmamos que f es SURYECTIVA. 3) CONCLUSION ! Por ser f inyectiva y suryectiva/decimos que es biyectivo. PROBLEMA f (X) = ----------- -------- ----- . x C A ^ C - a . o l x-2 1 Hollar analíticamente f ( A ) Dado lafunción Solución t.En lugar, determinar elentero Veamos! quecorresponde a — J ^ x { - 2,o ]- A Ahora, se reduce a determinar el entero que corresponde á Como : x 6 <-2,o ] => por - = Por tanto -2 < x é-0 > « t > - 2L * o o* - « < 1 - . >[-«.].j 1 +O = 1 , -V-x 6 < - 2 ,o ] Sólo fines educativos - FreeLibros y*J .* Moisés Lázaro C. 2. L u e g o , to f unci ón x2 f(X) f ( X ) se ha reducido a ’ ( t 40) + 3 x —i =*- X- 2 X*4 3X - 1 f ( X ) -s» 3. X -2 • T eni endo en cuenta que x . 6 Í - 2 t o ] * Á debemos hollar l a i m a g e n d e ) c o n ©3) . Para; «este p ro b le m a y no e s -fácil- hallar flA ) a c o t a n d o a p a rtir d e - 2cx<o. Resolveremos , d e sp e ja n d o x en té rm in o s d e y para re rsa /v e r *. - 2 <<3 lv> < 0 Y eam os• * as junto t°) decir h a ll a r e m o s H a c ie n d o f ( x ) = y s e o t d ie n e Y ~ X' + 3X-1 X-2 A h o ra } d e s p e ja r x ; yx - 2 y 33 x2 4 3 x - 1 => 0= x* + 3 x - x y + 2 y - t *> 0 a x* + ( 3 - y ) x + 2 y - 1 «> x »•* - ( 3 - f ) ± V ( J -y )* -4 ti Míy-i) 20) ty -3 s> x s ) 14 y 4 1 3 , donde I 4. como x € <-2, o3 => - 2 < => - 2 < « > - 4 S X - y- 1 < / y ?- 14y 4 Í 3 * 6 < —y —I x * y G Rang(f )&$ y 2- 14 y>13 ^ ó j . ......» « - 13 4 ( y . - i 3 ;) { y - t ) i o y G <-® r l J.-U C 13,4<30> => ^ o y - 3 — V ^ 2- 1 4 y - t 13 ú0 y- 3 < - - / y * - 14 y 4 13* 6 y ^ r ¿ - 1 4 y 4 13 ^ V 3 - y V fy2-i4YH3 >.-cy+o a i/yí#y+i3 ¿ 3 - y) ^ 3 — y - y - t < -Vy2-14y 4 13* 6 3 - y y4 1 > V/ X€U \Z?L¡4y7r? t 3-Y y-> V z yctr y r n é y— 3 y - 3 < Vy2-í4 y+i3 < Y + r ,4¿ y-3>o => (y-3)7£; yL»4Y4l3<(y4J)2>y€U y^ 3 ^ y-CY-t-9^yz-i4y+i3<vV2y4í y> 3 4 Y-Gyt9^V-l4y4l3Ar-4y4í3<y+2y+1 y2-f4y+13 ¿ 4 - ¿ y f y 2} si y-wy-Nj> o a 3-y¿& 4 <: 8y 0 a y<-3 y>^3 ^ 8>f4 a f2 < íéy ys 1/2 a y > 4 1 0 [ v2,'3 CONCLUSION ' u 0 Í(A) = [V2^1] Sólo fines educativos - FreeLibros

Relaciones y funciones Lazaro

Documentos relacionados

Productos

Apoyo

Relaciones y funciones Lazaro

Documentos relacionados

Añadir este documento a la recogida (s)

Añadir a este documento guardado

Sugiéranos cómo mejorar StudyLib