Introducción a la economía. Teoría de la producción
Anuncio

UNIVERSIDAD DIEGO PORTALES
FACULTAD DE CIENCIAS DE LA INGENIERÍA
DEPARTAMENTO DE INGENIERÍA INDUSTRIAL
CURSO DE INTRODUCCIÓN A LA ECONOMÍA / 2DO. SEMESTRE 2002
PROFESOR J. SCAVIA
3RA SERIE DE EJERCICIOS: Teoría de la Producción
SECCIÓN 02
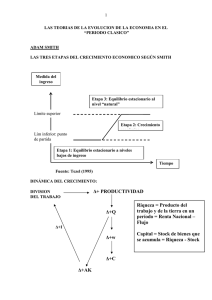
1. Considere la siguiente función de producción: q = f(K,L) = KL – 0,2L2 – 0,8K2.
(a)
Construir las funciones de producto medio y producto marginal para el factor trabajo.
(b)
Considere K = 10. ¿Para qué valores de L el PMe y PM del trabajo son iguales a cero?
(c)
¿Satisface esta función de producción la ley de los rendimientos decrecientes en ambos factores?
2. Considere una función de producción de la forma: q = f(K,L) = K 1/2 L1/2.
(a)
Calcule la productividad media del trabajo y el capital.
(b)
Represente gráficamente el producto medio del trabajo correspondiente a K = 100.
(c)
Demuestre que ene esta función PML = (1/2)PMeL y que PMK = (1/2)PMeK . Utilice este hecho y añada al
gráfico anterior la curva del PML (suponiendo de nuevo que K = 100). ¿Qué tiene de particular esta curva?
(d)
Represente la isocuanta correspondiente al nivel de producción q = 10.
(e)
Calcule la TST de la isocuanta referida en la pregunta anterior para los puntos L = 10, L = 4, y L = 25. ¿Es la
TST decreciente?
3. Considere una función de producción de la forma: q = f(K,L) = βo + β1(KL)1/2 + β2K + β3L, con βi entre 0 y 1
(i=0,...,3).
(a)
¿Qué condición deben satisfacer los βi para que esta función presente rendimientos constantes de escala?
(b)
Demuestre que en el caso de que la función presente rendimientos constantes de escala, los factores tienen
productividades marginales decrecientes y que estas productividades son homogéneas de grado 0.
(c)
Calcule la elasticidad de sustitución para este caso. ¿Es constante?
4. Suponga que la función de producción de cierto proceso está dada por f(x1, x2, x3) = λx1ax2bx3c.
(a) Demuestre que si a + b + c > 1, entonces la función posee rendimientos crecientes de escala.
(b) Suponga que es posible definir un insumo “compuesto” yB = x2bx3c y que por comodidad escribimos
ahora x1a = xA. Luego, la función de producción se puede escribir como: f(x, y) = λ xA yB. Determine
para qué valores (positivos) de λ, A y B esta función presenta rendimientos de escala de tipo (i)
crecientes; (ii) decrecientes y (iii) constantes.
1
(c) Determine para qué valores (positivos) de λ, A y B el producto marginal del factor x es decreciente.
(d) Determine para qué valores (positivos) de λ, A y B la relación técnica de sustitución es decreciente.
5. Fábrica de bustos de bronce. Bruñidos S.A. produce bustos de bronce. Como se sabe, el bronce es una
aleación de Cu y Zn utilizados en proporciones fijas. La función de producción está dada por
f(x1, x2) = min{ x1, 2x2}, donde x1 es la cantidad de Cu utilizada y x2 es la cantidad de Zn utilizada en el proceso
de producción.
(a) La función de producción, ¿presente rendimientos crecientes, decrecientes o constantes de
escala?
(b) Si la empresa quiere producir 10 bustos, ¿qué cantidad de cada elemento necesitará?
(c) Si la empresa se enfrenta a los precios de factores (1,1) (el precio del factor 1 y 2
respectivamente), ¿cuál es la combinación de factores más económica para producir los 10
bustos?
(d) Generalice el resultado anterior, es decir, encuentre la combinación más económica de factores, si
sus precios son (w1, w2), para producir y bustos.
2