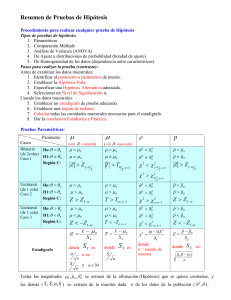
Resumen de Pruebas de Hipótesis Procedimiento para realizar cualquier prueba de Hipótesis Tipos de pruebas de hipótesis: 1. Párametricas 2. Comparación Múltiple 3. Análisis de Varianza (ANOVA) 4. De Ajuste a distribuciones de probabilidad (bondad de ajuste) 5. De Homogeneidad de los datos (dependencia entre características) Pasos para realizar la prueba (contraste): Antes de examinar los datos muestrales: 1. Identificar el parámetro o parámetros de interés. 2. Establecer la Hipótesis Nula. 3. Especificar una Hipótesis Alternativa adecuada. 4. Seleccionar un Nivel de Significación α. Usando los datos muestrales: 5. Establecer un estadígrafo de prueba adecuado. 6. Establecer una región de rechazo. 7. Calcular todas las cantidades muestrales necesarias para el estadígrafo. 8. Dar la conclusión Estadística y Práctica. Pruebas Paramétricas: Parámetro Casos conocida) 0 0 (con Bilateral (de 2colas) Caso 1 Ho: 0 H1: 0 Región C: Z Z1 2 conocida) 0 0 2 p 2 02 pˆ pˆ 0 pˆ pˆ 0 T T 2 12 ( sin ; n1 2 2 02 2 Unilateral (de 1 cola) Caso 2 Unilateral (de 1 cola) Caso 3 Ho: 0 H1: 0 Región C: Ho: 0 H1: 0 Región C: ; n1 Z Z1 2 ; n 1 0 0 2 02 Z Z1 T T ; n1 2 2; n1 Z Z1 0 0 0 0 T T ; n1 2 02 pˆ pˆ 0 pˆ pˆ 0 Z Z1 x 0 Sx donde S x es: ó es: n S n T 2 pˆ pˆ 0 pˆ pˆ 0 2 0 2 02 2 12 ; n1 x 0 Sx 2 Sx donde donde S n es: 2 2 0 0 Z Estadígrafo 2 (n 1) S 2 0 2 n = tamaño de muestra Z Z1 Z pˆ pˆ 0 S pˆ donde S pˆ es: pˆ 0 (1 pˆ 0 ) n y n 30 Todas las magnitudes 0 , pˆ 0 ,02 se extraen de la afirmación (Hipótesis) que se quiere contrastar, y las demás ( x , S , n, k ) se extraen de la muestra dada o de los datos de la población ( 2 , ) . Pruebas de Comparaciónes Múltiples (con conocida) 1 , 2 ( sin conocida) 1 2 ,2 2 H1: 1 2 Región C: 1 2 1 2 Z Z1 1 2 1 2 1 Ho: 1 2 1 2 1 2 Parámetros Casos Bilateral (de 2colas) Caso 1 Unilateral (de 1 cola) Caso 2 Unilateral (de 1 cola) Caso 3 Ho: 1 2 1 , 2 T T 2 1 1 2 Z Z1 T T ; n1 Ho: 1 2 1 2 1 2 donde S x es: ó es: Estadígrafo n S n y n 30 T x1 x2 Sx donde Sx 1 2 22 F F ;V 1,V 2 1 2 22 n = tamaño x x2 Z 1 Sx 2 2 1 2 22 1 2 T T ; n1 Z Z1 F F ;VM ,Vm 2 1 2 1 2 2 2 12 22 H1: 1 2 Región C: H1: 1 2 Región C: (n>29) 2 ; n1 2 es: (n1 1) S12 (n2 1) S 22 n1n2 (n1 n2 2) n1 n2 p1 , p 2 F F ;V 2,V 1 S M2 S m2 donde M es: F la muestra de mayor varianza p1 p2 p1 p2 Z Z1 p1 p2 p1 p2 Z Z1 p1 p2 p1 p2 Z Z1 Z pˆ 1 pˆ 2 S pˆ donde S pˆ es: 1 1 p(1 p) n1 n2 y p x1 x2 n1 n2 ANOVA Modelo general de ANOVA: medias Muestra 1 y11 , y12 ,..., y1n y1 Muestra 2 y 21 , y 22 ,..., y 2n y2 Muestra k y k1 , y k2 ,..., y kn yk y Hipótesis: H 0 : 1 2 ... k H1 : i j , para i j Las medias son iguales o difieren Ó H 0 : 1 2 ... k 0 H1 : i 0, 2 para un i El factor afecta o no afecta por igual las muestras F F ;k 1; N k Región crítica: F Estadígrafo: SCR /( k 1) SCE /( N k ) Donde k cantidad de muestras Tamaño de la muestra i ni k N ni Total de datos observados i 1 n Ti yij Suma de los datos de la muestra i j 1 k T Ti Suma de todos los datos de las muestras i 1 C T2 N Constante k n SCT yij2 C Suma de cuadrados totales k T 2 SCR i C i 1 ni Suma de cuadrados de los residuos SCE SCT SCR Sumas de los cuadrados de los errores i 1 j 1 Tabla ANOVA: Fuente de variación G.L S.C. C.M. Residuos k-1 SCR MSCR =SCR/(k-1) Error N-k SCE MSCE =SCE/(N-k) Totales N-1 SCT F MSCR / MSCE Pruebas No paramétricas Ho: Oi Ei Ha: Oi Ei Región C: Estadígrafo Contraste de Bondad de ajuste Oi Ei Oi Ei Prueba de homogeneidad Oij Eij ( A y B son Independientes) 2 2; k r 1 2 2; ( m1)( n1) Donde: k = número de clases r=0 Donde: m = número de filas n = número de columnas k 2 Oij Eij ( A y B son Dependientes) Oi Ei 2 i 1 k 2 Ei i 1 j 1 ij Eij 2 Eij 2 Clases Oi Pi Ei=n*Pi Oi-Ei Intervalo 1 O1 P1 E1 Intervalo 2 O2 P2 E2 Intervalo 3 . . . Intervalo k O3 . . . Ok P3 . . . Pk E3 . . . Ek (Oi-Ei)2 (Oi-Ei)2/Ei (chi-cuadrado) 2 2 Segunda porción de Primera porción de . . . . . . n es la suma de las Oi, o total de datos observados. P1 = p(Intervalo 1) = pasos lógicos = valor de probabilidad 1 P2 = p(Intervalo 2) = pasos lógicos = valor de probabilidad 2 … Pk = p(Intervalo k) = pasos lógicos = valor de probabilidad k 2 O se usa tabla de contingencia para calcular 2 se usa tabla de frecuencias para calcular 2 Tabla de frecuencias para cálculo de n (O1 E1)2 (O2 E 2)2 (Ok Ek )2 ... E1 E2 Ek k-ésima porción de 2 Tabla de Contingencia para cálculo de a1 a2 . . . am totales 2 b1 b2 b3 … bn totales O11 (E11) O21 (E21) . . . Om1 (Em1) Tb1 O12 (E12) O22 (E22) . . . Om2 (Em2) Tb2 O13 (E13) O23 (E23) . . . Om3 (Em3) Tb3 … O1n (E1n) O2n (E2n) . . . Omn (Emn) Tn Ta1 … . . . … Ta2 Tm T (O11 E11) 2 (O12 E12) 2 (O1n E1n) 2 ... E11 E12 E1n (O 21 E 21) 2 (O 22 E 22) 2 (O 2n E 2n) 2 ... E 21 E 22 E 2n (Om1 Em1) 2 (Om 2 Em2) 2 (Omn Emn) 2 ... ... Em1 Em2 Emn 2 En estos casos, se puede calcular los valores esperados como Ei = Tm*Tn/T, por ejemplo: E13 = Ta1*Tb3/T