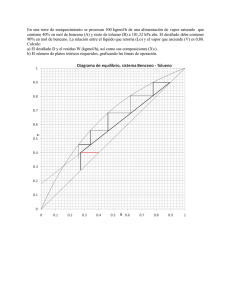
ABSORCIÓN Ejercicio 1 En una torre se extrae acido clorhídrico difundido en aire mediante una solución acuosa que tiene 0.350 [kmol de acido clorhídrico/kmol de solución], esta concentración se eleva después del paso por la columna, mientras que la concentración en el aire en el mismo tiempo desciende des 0.3 hasta 0.165 [kmol de acido clorhídrico/kmol de gas] en el tope de la columna. La operación se lleva de tal manera que se garantiza que las fuerzas impulsoras en el tope y en el fondo de la torre sean iguales. Experimentalmente se encontró: Equilibrio X 0.238 0.2593 0.2857 0.3333 0.3548 0.371 0.3865 0.4048 Y 0.0889 0.0887 0.0979 0.1413 0.1731 0.2021 0.2334 0.2745 a) Determine el porcentaje de aumento en la concentración de agua una vez abandone la columna. b) La pendiente de la línea de operación. c) Flujos de gas y liquido si se desean extraer 2000 kg de acido clorhídrico en 4 horas. d) Los flujos instantáneos en el tope y en el fondo de la columna. e) Las composiciones en la interface. Ejercicio 2 Una torre de paredes mojadas se alimenta con soda caustica como liquido en la pared y una mezcla de CO2-AIRE como gas en la parte central. A cierto nivel de la torre las concentraciones son: 215 ppm de CO2 en el aire y 61ppm en el líquido. T=26.7°C; P=1atm. Se conoce también que m’’=3.6111 Equilibrio X(ppm) 15 25 36 45 53 68 79 88 a) Hallar: b) Para Y(ppm) 185 325 390 415 444 462 534 615 y el porcentaje de resistencia a la fase gaseosa y la fase liquida. encontrar y Ejercicio 3. El soluto A se absorbe de una mezcla gaseosa de A y B en una torre de paredes mojadas por el líquido que fluye hacia abajo por la pared como película. En un punto de la torre la concentración general del gas es yAG = 0.380 fracción mol y la concentración general de líquido es xAL = 0.100. La torre opera a 298 K y 1.013 x 105 Pa y los datos de equilibrio son: x y 0 0 0.05 0.022 0.10 0.052 0.15 0.087 0.20 0.231 0.25 0.187 0.30 0.265 0.35 0.385 Mediante correlaciones para soluciones diluidas en torres de paredes mojadas, se predice que el coeficiente de película de transferencia de masa para A en la fase gaseosa es kY = 1.465x10-3 kg mol A / s m2 fracción mol y para la fase líquida es kX = 1.967 x 10-3 kg mol A/ s m2 fracción mol. Las concentraciones en la interfaz son yAi = 0.197 y xAi = 0.257 y el flujo específico es NA = 3.78 x 10-4 kg mol / s m2. Considere que: a) Existe una difusión equimolar de A y B en sentidos opuestos. b) El soluto A se difunde a través de B en reposo en la fase gaseosa y después, a través de un líquido que no se difunde. Calcule los coeficientes globales de transferencia de masa KX y KX, el flujo específico y el porcentaje de resistencia en la película gaseosa. Ejercicio 4 Se absorberá NH3 de aire a 68ºF a presión atmosférica en una torre rellena en contracorriente utilizando agua como absorbente. Se usará un flujo de gas a la entrada de 1540 ft3/h y un caudal de agua, libre de amoníaco, de 75 lb/h. a) Si la concentración de NH3 debe reducirse de 3.52 a 1.29% en volumen, determinar la relación (Ls/Gs) real/(Ls/Gs)mínimo. Los datos de equilibrio para el sistema a 68ºF y 1 atm son los siguientes: X, lbmol NH3/lbmol H2O 0.0164 0.0252 0.0349 0.0455 0.0722 Y, lbmol NH3/lbmol aire 0.021 0.032 0.042 0.053 0.08 Ahora se pretende realizar la misma absorción pero en cocorriente y utilizando una corriente de agua equivalente a 1.37 veces el caudal mínimo. Determinar: b) (Ls/Gs)mínimo c) El caudal de agua de operación. d) La concentración de NH3 en el agua de salida de la torre. Ejercicio 5 Ejemplo 5.2 Treibal. Pág 147 Cuando cierta muestra de jabón húmedo se expone al aire a 75 °C, 1 atm de presión, la distribución en el equilibrio de la humedad entre el aire y el jabón es la siguiente: % en peso de humedad en el jabón 0 2.40 3 .76 4.76 6.10 7.83 9.90 12.63 15 .40 19. 02 Presión parcial de agua en el aire, mm Hg 0 9.66 19.20 28.4 37.2 46.4 55.0 63.2 71.9 79.5 a) Se colocaron 10 kg de jabón húmedo que contenía un 16.7% en peso de humedad, en un tanque que contenía 10 m3 de aire húmedo, cuyo contenido inicial de humedad correspondía a la presión parcial agua-vapor de 12 mm Hg. Después de que el jabón alcanzo un contenido de humedad de 13.0%, el aire en el tanque se reemplazó completamente por aire fresco con el contenido original de humedad y se le permitió al sistema alcanzar el equilibrio. La presión total y la temperatura se mantuvieron a 1 atm y 75 °C, respectivamente. ¿cuál será el contenido final de humedad del jabón? . b) Se desea secar el jabón de 16.7 a 4% de humedad continuamente en una corriente de aire a contracorriente cuya presión parcial agua-vapor inicial es 12 mm Hg. La presión y la temperatura se mantuvieron a 1 atm y 75 °C. Para 1 kg inicial de jabón húmedo, ¿cuál es la cantidad mínima de aire que se requiere? c) Si se utiliza 30% más de aire que el determinado en (b), ¿cuál será el contenido en humedad del aire que abandona el secador? ¿A cuántas etapas ideales será equivalente el proceso?. Ejercicio 6 Para recuperar el benceno contenido en una mezcla de benceno aire de composición 6% en volumen de benceno se trata en contracorriente en una torre de absorción, empleando como líquido absorbente un hidrocarburo no volátil de peso molecular 250. La mezcla gaseosa entra en el absorbedor a razón de 500 m3/h a 20°C y 1 atm; la absorción se efectúa isotérmicamente e isobáricamente a 20°C y 1 atm y puede suponerse que la solubilidad del benceno en el hidrocarburo se ajusta a la Ley de Raoult. Calcúlese: a) La cantidad mínima de hidrocarburo a emplear si ha de recuperarse el 95% de benceno. b) El número de etapas teóricas de la torre de absorción, si la cantidad de hidrocarburo empleado es 60% superior a la mínima. Presión de vapor del benceno a 20°C es de 76 mmHg. SOLUCIÓN a) De acuerdo a la ley de Raoult además la absorción se efectúa isotérmicamente e isobáricamente. PT*y=pA*x Para expresar la línea de operación como una línea recta: ; Entonces: Hallamos entonces los datos para el equilibrio: Y X 0 0 0.005 0.01 0.05235 0.1098 0.02 0.2438 0.03 0.4110 Benceno la entrada: 20.81*0.06=1.249 Kmol/h Benceno adsorbido 1.249*0.95=1.186 Kmol/h Benceno sin adsorberse 1.248-1.186=0.062 En el tope ( ( ) ( ) ) 0.04 0.6234 0.05 0.9087 0.06 0.07 1.3041 1.891 0,08 0,06 0,04 0,02 0 0 0,5 1 1,5 2 De la gráfica ( ) ( ) La cantidad de hidrocarburo sera: ( ) b) La relación ( ) sera: ( ) ( ) ( ) El número de etapas es aproximadamente 6. Ejercicio 7 Una solución acuosa que contiene un soluto valioso esta colorada con pequeñas cantidades de una impureza, antes de la cristalización se va a eliminar la impureza por adsorción sobre un carbón decolorante que solo adsorbe cantidades insignificantes de soluto principal, mediante una serie de pruebas se estableció el siguiente equilibrio. X(unidad de 1080 1000 825 663 395 223 color adsorbido/kg de carbón) Y(unidades 9.6 8.6 6.3 4.3 1.7 0.7 de color adsorbido/kg de solución) Se desea reducir el color al 10% del valor original (9.6). Calcular la cantidad de carbón fresco que se requiere por 1000g de solución para una operación a una etapa, para un proceso de dos etapas a corriente cruzada que utiliza la misma cantidad total de carbón y para una operación en dos etapas a contracorriente. DESTILACIÓN Ejercicio 1 Los datos vapor – líquido a 1 atm, los calores de solución, las capacidades caloríficas y los calores latentes de evaporación para el sistema acetona – agua son: Una mezcla líquida que contiene 60% mol de acetona y 40% mol de agua a 26.7ºC, se va a evaporar instantánea y continuamente a 1 atm de presión, para evaporar el 30% mol de la alimentación. a) Cuál será la composición de los productos y la temperatura en el separador, si se establece el equilibrio? b) Cuánto calor, en kJ/kmol de alimentación, se requiere? Ejercicio 2 Se destila diferencialmente la solución líquida del problema anterior a 1 atm de presión para evaporar el 30% en mol de la alimentación. Calcule la composición del destilado, y del residuo compuesto. Compare con los resultados del problema anterior. Ejercicio 3 Una columna de destilación continua que posee 5 platos teóricos se utiliza para separar 1000 kg/h de mezcla de A y B de composición 20% molar en A en un producto de cabeza con 90% molar en A y otro de fondo con 10% molar en A. Esta separación se logra con una temperatura de alimentación de 50°C. La temperatura de ebullición de la mezcla de alimentación es de 200°C y la de condensación del destilado a xD = 0.9 es de 180°C. Otros datos son: CpA = 4.061 kJ/kg K λA = 628 kJ/kg MA = 105 CpB = 3.852 kJ/kg K λB = 502.4 kJ/kg MA = 90 Datos de equilibrio del sistema (fracciones molares) a) Calcular la masa de destilado y residuo, las relaciones de reflujo externa (R) e internas (L/G) en ambas zonas de enriquecimiento y agotamiento, los caudales de vapor en las secciones de enriquecimiento y agotamiento, e indicar el plato en el que entra la alimentación. b) Si ahora incrementamos la temperatura de alimentación hasta 190°C y mantenemos constante su caudal y su composición y las relaciones de reflujo en ambas zonas, calcular las composiciones y caudales del destilado y residuo a obtener. c) Alimentando a 190°C y deseando un destilado de composición x D = 0.1 y un residuo con xW = 0.9, calcular las relaciones de reflujo externa e internas que cumplan con lo solicitado. Ejercicio 4 Debe proyectarse una columna de destilación continua para separar 2000 kg/h de una mezcla de metanol/agua, de composición 30% en peso de metanol en un producto de cabeza y otro de cola de composiciones 95% y menor del 4% en peso de metanol respectivamente. Determinar: a) La cantidad de destilado y residuo obtenidos por hora. b) La relación de reflujo mínima si la alimentación entra en un plato intermedio de la columna como mezcla de líquido y vapor saturado en la proporción 3 a 1 (en peso). c) El número de platos necesarios si la relación de reflujo empleada es un 42% superior a la mínima y la eficiencia media de los platos es de un 69%. d) El plato real de alimentación. e) La relación de reflujo a emplear en la columna ya construida si la alimentación entra como vapor saturado. Datos de equilibrio del sistema (en fracciones másicas) Ejercicio 5 Una columna de rectificación de 3 platos ideales se alimenta de 0.4% mol de NH3 y 99.6% mol de agua. La alimentación es vapor saturado y entra entre los platos 2 y 3. Ln = 1,35. La vaporización en el intercambiador de calor es 0.7 mol/molF. El equilibrio viene dado por y=12.6x. Calcular fracción mol de amoniaco en: a) Producto residual que sale del hervidor. b) El destilado. c) El líquido de reflujo que sale del plato de alimentación. Ejercicio 6 Una corriente de alimentación liquida en su punto de ebullición contiene 3.3% mol de etanol y 96.7% mol de agua y entra por el plato superior de una torre de empobrecimiento. Se inyecta el vapor saturado directamente al líquido en el fondo de la torre. El vapor superior que se extrae contiene 99% del alcohol de la alimentación. Suponga derrame equimolar. a) Para un número infinito de etapas teóricas, calcule el mínimo de moles de vapor necesarias por mol de alimentación. b) Empleando el doble del mínimo de moles de vapor, calcule el número de etapas, composiciones del vapor superior y del residuo. Ejercicio 7 Se desea destilar una alimentación de etanol-agua que contiene 50% en peso de etanol a 101.3 kpa, para obtener un destilado con 85% de etanol, un residuo en el que no se pierde más del 2% de etanol alimentado y su entalpia es de 100.16 Kj/kg. La relación de reflujo interna en la zona de enriquecimiento (L/G), que es el doble de la relación de reflujo interna mínima, en dicha zona se estima que estas consideraciones, la eficiencia global de la torre será de 57%. Calcular: a) Numero de platos ideales y reales. b) Caudales de residuo y destilado en Kg/h y la capacidad de producción de vapor del rehervidor. c) Carga térmica del rehervidor y del destilado. Cp etanol liquido=2.64 Kj/kg*°C Cp agua líquida= 4.189 Kj/kg*°C Fracción másica etanol 0 0.1 0.3 0.5 0.7 0.9 1 Entalpia líquida (Kj/kg) 418.9 371.7 314 285.9 258.4 224.7 207.0 Entalpia vapor (Kj/kg) 2675 2517 2193 1870 1544 1223 1064 Todas las entalpias están referidas a 0°C Equilibrio liquido vapor a 101.3 kpa (en fracción másica de etanol) x y 0 0 0.1 0.2 0.525 0.65 0.3 0.7 0.4 0.74 0.5 0.76 0.6 0.8 0.7 0.82 0.8 0.85 0.9 0.91 1 1 Ejercicio 8 Una columna de rectificación en continuo se usa para separar 20000 kg/h de una mezcla de cloroformo-benceno cuya composición es 0.35 molar de cloroformo, para suministrar un producto de cabeza de composición 0.97 en fracción molar de cloroformo y producto de fondo de composición 0.97 molar de benceno. La columna ha de trabajar a la presión atmosférica, y la alimentación entrara a 16°C. La cabeza de la columna va provista de un condensador total, y tanto el reflujo como el producto destilado salen del condensador a la temperatura de condensación. Calcular: 1) 2) 3) 4) 5) Caudales de alimentación, producto de cabeza y producto de fondo. La ecuación de la recta q. La relación de reflujo mínimo. El número mínimo de platos teóricos. Ecuación de la recta, sección de enriquecimiento y empobrecimiento si la relación de reflujo es de 20% superior a la mínima. 6) El número de platos teóricos y la posición del plato de alimentación. 7) Calor retirado en el condensador. Los datos de equilibrio cloroformo benceno a presión atmosférica. (Composiciones en fracción molar) Dentro del intervalo de temperaturas de operación pueden tomarse los siguientes valores medios para los calores específicos y para los calores latentes. Cloroformo: Cp=0.23 Kca/Kg°C λ=6800 Kcal/Kmol Benceno: λ=7420 Kcal/Kmol Cp=0.44 Kca/Kg°C El valor medio de la volatilidad relativa es α=1.70 El peso molecular promedio será: El flujo de alimentación: 1. Haciendo un balance de masa total y de soluto: Resolviendo el anterior sistema, 2. Para determinar la recta q, hay que calcular la fracción liquida, por lo que debemos tener las entalpias del líquido y vapor saturados, así como la de la alimentación. El calor específico promedio será: De los datos de equilibrio, la temperatura de ebullición de la mezcla correspondiente a la composición de la alimentación es T=76.8°C ( ) ( ) Suponiendo que la temperatura de referencia es de 0°C, y tomando el Sabiendo que promedio. es igual al calor latente de vaporización de la alimentación. Ahora sí: Entonces La pendiente de la recta será La ecuación de la recta q es entonces: . El corte será 3. La relación de reflujo mínimo la obtenemos gráficamente En el punto Pinch y Obteniendo: 86 4. Se pude determinar gráficamente o analíticamente. Analíticamente obtenemos: (( = (( ) ( ) ( )) )) 5. La relación de reflujo a emplear será: La ecuación de la recta superior: 6. El número de platos teóricos se hace partir de la gráfica. El número de platos aproximado es de 24, es decir 23 + el reervidor. El plato de alimentación es el número 7. 7. Para calcular el calor retirado del condensador se realiza los balances de energía correspondientes: Sí: y además de un balance en el condensador V=L+D Entonces ( ) De un balance de la sección superior: Entonces: ( ) DISEÑO DE TORRES EMPACADAS Y DE PLATOS 1. Se debe llevar a cabo una desorción con vapor de agua de una solución acuosa de metanol. Las condiciones elegidas para el proyecto son: Vapor: 0.2 kmol/s, 18% molar de metanol Líquido: 0.6 kmol/s, 2.9% molar de metanol T=368K P=101.3 kPa. Se proyectó una torre de bandejas perforadas dando un diámetro de 1.57 m. Se desea saber qué diámetro de torre obtendríamos para los siguientes proyectos: a) Torre de bandejas con casquetes de burbujeo b) Torre rellena con: anillos Raschig cerámicos de 25 mm Monturas Berl de 25 mm Anillos Pall de 25 mm (de plástico) Adoptar una caída de presión de 327 Pa de agua/m de relleno en todos los casos. 2. Se desea calcular el diámetro de la torre, necesario para una absorción isotérmica, en la cual se absorberá el 95% de amoníaco contenido en una mezcla amoníaco-aire, que posee a la entrada del equipo 2% en volumen de NH3. El gas se tratará en contracorriente con agua, a un caudal de 1.8 veces el mínimo. La torre operará isotérmicamente a 28ºC y 1 atm, con un caudal de gas de 3000 kg/h. El relleno será de anillos Raschig cerámicos de 25 mm y la torre operará al 60% de su velocidad de inundación. A 28ºC, las soluciones de NH3-agua siguen la ley de Henry hasta el 5% molar de NH3 en el líquido, siendo m = 1.41. Datos: Viscosidad del líquido: 9.5 10-5 N/s m2, densidad del gas a la entrada: 1.17 kg/m3. ABSORCIÓN DE GASES EN TORRES EMPACADAS Y DE PLATOS 3. Se absorbe SO2 del aire en agua a 20°C, en una columna de planta piloto empacada con anillos Rasching metálicos. La sección empacada mide 10m de altura. La presión total es 2 741mmHg. El agua que entra es pura con un flux de 100lb/ft h. El agua que sale contiene una fracción molar de 0,001 de SO2 y la concentración del gas de entrada .es de 0,03082 fracción molar. Ls/Gs=15. La constante de la ley de Henry es H=22,5mmHg/fracción mol de SO2 líquido. a) (5ptos) Determine si la resistencia de la fase gaseosa o la fase líquida controlan el proceso de absorción b) (15ptos) Calcular HtL Información adicional 1 1 1 = + K X k x Hky N tL = xA xAsalida xAsalida xAentrada ln xA xAsalida xA xAentrada xA xAentrada 4. Se está absorbiendo sulfuro de hidrógeno en agua a 15ºC. El agua que entra es pura. El gas alimentado contiene 0.0012 fracción molar de sulfuro de hidrógeno y se desea eliminar 97% del mismo con el agua. La tasa total de flujo de gas es 10 kgmol/h. La tasa total de flujo de líquido es 2000 kgmol/h. La presión total es 2.5 atm. Puede suponer soluciones diluidas. Los datos de equilibrio vienen representados por la siguiente ecuación: Presión parcial de sulfuro de hidrógeno (atm) = 423 x Siendo x la fracción molar de sulfuro de hidrógeno en agua. a) Calcule las fracciones molares de sulfuro de hidrógeno en el gas y en el líquido de salida. b) Calcule la cantidad de etapas de equilibrio necesarias, usando un Diagrama de Mc CabeThiele. Corroborarlo utilizando la ecuación analítica correspondiente. c) Si L/V = M * (L/V)min calcule el multiplicador M (M>1) d) ¿Por qué no es práctica esta operación? ¿Qué haría un ingeniero para hacerlo práctico? d. No es recomendable esta operación ya que prácticamente se esta trabajando con el caudal mínimo, por esto no esta dando tantos platos, lo cual no resulta viable económicamente. 5. Determinar el diámetro de la torre y la altura de relleno necesaria para un proceso de absorción isotérmica en el cual se desorberá acetona de una mezcla acetona-aire (1.5% de acetona en volumen) con agua en contracorriente en forma continua. El caudal de agua será de 1.5 veces el mínimo y se desea absorber el 98% de la acetona del gas de entrada. El caudal gaseoso a tratar será de 450 kg/h. Considerar la solución gaseosa con comportamiento ideal. El relleno estará compuesto por anillos Raschig de 2” y se operará la torre al 50% de su velocidad de inundación. La relación de equilibrio es y = 2.47 x. La temperatura de operación es de 75ºC y la presión de 1 atm. Considerar, para simplificar los cálculos, que las propiedades del líquido a la salida de la torre son iguales a las del agua, y las del gas a la salida iguales a las del gas de entrada. 2 DAB = 341.88 cm /h (acetona-aire) 2 DAB = 0.0447 cm /h (acetona-agua)