Ingeniería de Calidad: Problemas de Aplicación ANOVA
Anuncio
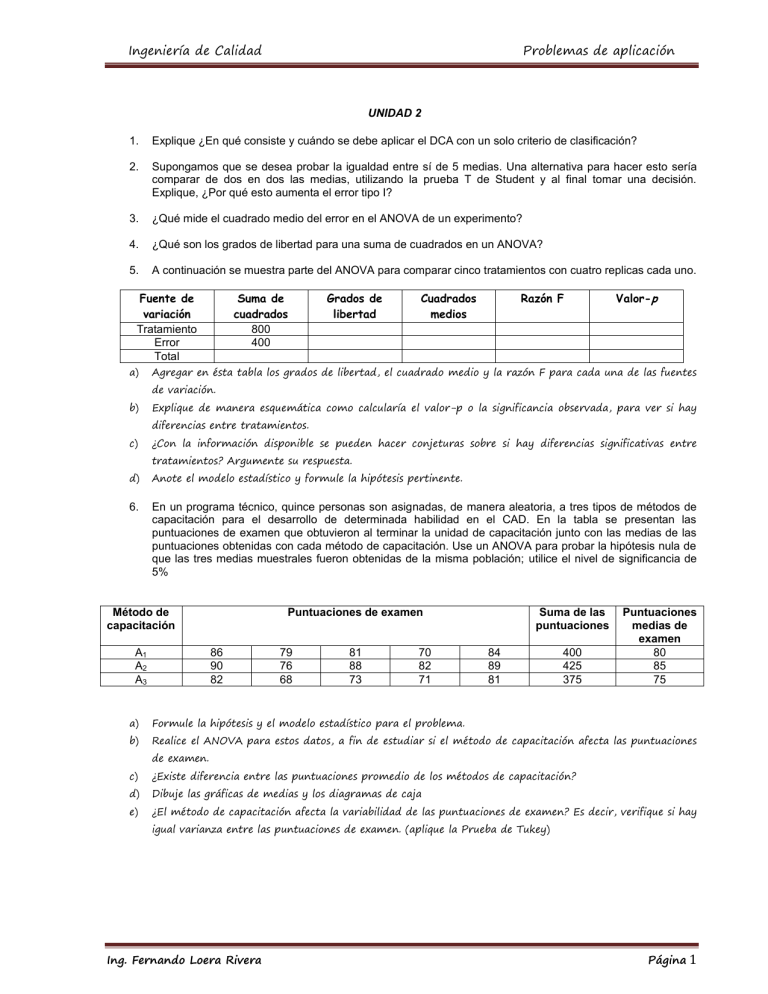
Ingeniería de Calidad Problemas de aplicación UNIDAD 2 1. Explique ¿En qué consiste y cuándo se debe aplicar el DCA con un solo criterio de clasificación? 2. Supongamos que se desea probar la igualdad entre sí de 5 medias. Una alternativa para hacer esto sería comparar de dos en dos las medias, utilizando la prueba T de Student y al final tomar una decisión. Explique, ¿Por qué esto aumenta el error tipo I? 3. ¿Qué mide el cuadrado medio del error en el ANOVA de un experimento? 4. ¿Qué son los grados de libertad para una suma de cuadrados en un ANOVA? 5. A continuación se muestra parte del ANOVA para comparar cinco tratamientos con cuatro replicas cada uno. Fuente de variación Tratamiento Error Total a) Suma de cuadrados 800 400 Grados de libertad Cuadrados medios Razón F Valor-p Agregar en ésta tabla los grados de libertad, el cuadrado medio y la razón F para cada una de las fuentes de variación. b) Explique de manera esquemática como calcularía el valor-p o la significancia observada, para ver si hay diferencias entre tratamientos. c) ¿Con la información disponible se pueden hacer conjeturas sobre si hay diferencias significativas entre tratamientos? Argumente su respuesta. d) Anote el modelo estadístico y formule la hipótesis pertinente. 6. En un programa técnico, quince personas son asignadas, de manera aleatoria, a tres tipos de métodos de capacitación para el desarrollo de determinada habilidad en el CAD. En la tabla se presentan las puntuaciones de examen que obtuvieron al terminar la unidad de capacitación junto con las medias de las puntuaciones obtenidas con cada método de capacitación. Use un ANOVA para probar la hipótesis nula de que las tres medias muestrales fueron obtenidas de la misma población; utilice el nivel de significancia de 5% Método de capacitación A1 A2 A3 Puntuaciones de examen 86 90 82 79 76 68 81 88 73 70 82 71 Suma de las puntuaciones 84 89 81 400 425 375 Puntuaciones medias de examen 80 85 75 a) Formule la hipótesis y el modelo estadístico para el problema. b) Realice el ANOVA para estos datos, a fin de estudiar si el método de capacitación afecta las puntuaciones de examen. c) ¿Existe diferencia entre las puntuaciones promedio de los métodos de capacitación? d) Dibuje las gráficas de medias y los diagramas de caja e) ¿El método de capacitación afecta la variabilidad de las puntuaciones de examen? Es decir, verifique si hay igual varianza entre las puntuaciones de examen. (aplique la Prueba de Tukey) Ing. Fernando Loera Rivera Página 1 Ingeniería de Calidad 7. Problemas de aplicación Se cultivaron cuatro diferentes clonas de agave tequilana bajo un mismo esquema de manejo. Se quiere saber qué clona es la que responde mejor a dicho manejo, evaluando el nivel de repuesta con el porcentaje de azucares reductores totales en base húmeda. Los datos se muestran a continuación: 1 8.69 6.68 6.83 6.43 10.30 Clona 2 3 8.00 17.39 16.41 13.73 12.43 15.62 10.99 17.05 15.53 15.42 4 10.37 9.16 8.13 4.40 10.38 a) Mediante ANOVA compare las medias de las clonas y verifique residuales. b) ¿Hay una clona que haya respondido mejor al esquema de manejo? Argumente su respuesta. c) En caso de que exista un empate estadístico entre dos o más clonas, ¿Qué propondría para desempatar? 8. Uno de los defectos que causan mayor desperdicio en la manufactura de discos ópticos compactos son los llamados “cometas”. Típicamente, se trata de una partícula que opone resistencia al fluido en la etapa de entintado. Se quiere comprobar de manera experimental la efectividad de un tratamiento de limpieza de partículas que está basado en fuerza centrípeta y aire ionizado. A 12 lotes de 50 CD se les aplica el tratamiento y a otros 12 lotes no se les aplica; en cada caso se mide el porcentaje de discos que presentan “cometas”. Los resultados son los siguientes: Con tratamiento 5.30 4.03 4.03 4.00 2.56 2.05 5.06 4.06 2.08 4.03 2.04 1.18 Sin tratamiento 8.02 13.18 7.15 8.23 9.11 6.66 12.15 16.3 9.20 6.35 7.15 8.66 a) Con el ANOVA vea si es efectivo el tratamiento de limpieza. ¿Debería implementarse? b) ¿Es razonable suponer en el inciso a) que las varianzas son iguales? c) En qué porcentaje se reducen los discos con “cometas” 9. En un artículo de ACI Materials Journal se describen varios experimentos para investigar el varillado del concreto para eliminar el aire atrapado. Se usó un cilindro de 3 x 6 pulgadas; y el número de veces que esta barra se utilizó es la variable del diseño. La resistencia a la compresión resultante de la muestra de concreto es la respuesta. Los datos se muestran en la tabla siguiente: Nivel de varillado 10 15 20 25 Resistencia a la compresión 1530 1530 1440 1610 1650 1500 1560 1730 1530 1500 1490 1510 i) ¿Hay alguna diferencia en la resistencia a la compresión debida al nivel de varillado? Utilizar ii) ¿Existe diferencia entre la resistencia promedio de los niveles de varillado? Ing. Fernando Loera Rivera 0.05 Página 2 Ingeniería de Calidad Problemas de aplicación iii) Dibuje las gráficas de medias y los diagramas de caja iv) ¿El nivel de varillado afecta la variabilidad de la resistencia a la compresión? Es decir, verifique si hay igual varianza entre las resistencias a la compresión. (aplique la Prueba de Tukey) 10. A continuación se muestran los resultados de un diseño factorial. Conteste los siguientes incisos haciendo las operaciones de manera manual. Réplica A + + B + + I 82 78 71 89 II 80 82 70 88 III 84 79 66 93 Total (1) = 246 (a) = 239 (b) = 207 (ab) = 270 a) ¿Qué nombre recibe este diseño y por qué? b) ¿Cuántos tratamientos tiene este diseño, cuántas réplicas? c) En total son 12 corridas experimentales. Señale en qué orden debieron correrse y explique por qué. d) Explique los efectos que se pueden estudiar a través de este diseño. e) Obtenga los contrastes para los efectos principales de A y B, e interprételos. f) Calcule los efectos principales y el efecto de interacción. g) Haga las gráficas de los efectos principales de A y B, e interprételas. h) Realice le grafica de la interacción entre los factores A y B, e interprétela con detalle. i) ¿Desde su punto de vista el factor B parece tener influencia sobre Y? argumente su respuesta 11. En una fábrica de dientes se tiene problemas con la calidad: porosidad (burbujas de aire dentro de los dientes), manchas blancas, dientes sucios, dientes quebrados. En los intentos por resolver los problemas han hecho cambios en algunos factores o variables del proceso. Se decide correr un diseño de 3 experimentos 2 . Los factores y niveles son: temperatura de prensado (90° y 130°), tiempo de prensado (8 y 15 minutos) y tamaño de partícula (sin tamizar y con tamizado), la variable de respuesta fue porcentaje de diente bueno en cada corrida (un lote de producción). Los datos son los siguientes: Temperatura Tiempo Tamizado de partícula 90 130 90 130 90 130 90 130 8 8 15 15 8 8 15 15 Sin tamizar Sin tamizar Sin tamizar Sin tamizar Con tamizado Con tamizado Con tamizado Con tamizado a) Estime todos los posibles efectos y diga cuales son significativos. b) Realice un ANOVA de estos datos y obtenga conclusiones generales. c) Verifique residuos, ¿Qué observa que sea notorio? d) ¿Hay un tratamiento ganador? Ing. Fernando Loera Rivera Porcentaje de diente bueno 76.4 y 76.9 76.3 y 76.9 80.4 y 81.0 77.9 y 79.6 84.4 y 84.6 84.7 y 84.5 82.7 y 83.2 85.0 y 84.7 Página 3 Ingeniería de Calidad e) Problemas de aplicación ¿Qué condición de proceso sugiere emplear a futuro? Tome en cuenta, además, que a mayor tiempo y mayor temperatura, mas costos. f) Las condiciones que se utilizaban antes del experimento eran: temperatura de 130°C y tiempo de 15 minutos. ¿Por qué cree que se eligieron niveles inferiores de prueba para estos factores? g) Estos resultados, aunque positivos, no son suficientes; por lo tanto, qué sugiere usted, (¿explorar más niveles de los factores ya estudiados?, ¿considerar otras causas? O ¿Qué? Argumente. Ing. Fernando Loera Rivera Página 4