Análisis de Curvas de Declinación: Exponencial, Hiperbólica y Armónica
Anuncio

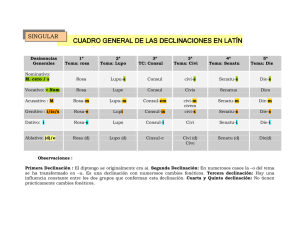
Análisis de curvas de declinación Exponencial, Hiperbólica y Armónica En general la declinación exponencial es el método más comúnmente utilizado al inicio de la historia de producción de un pozo o campo, como una forma conveniente. Las gráficas muestran las ecuaciones de las tres curvas de declinación y concuerdan al principio, los dos primeros años y después marcan notables diferencias en sus pronósticos. La curva de declinación Hiperbólica requiere calcular “Di” y el exponente “b”, estas curvas han sido utilizadas en muchos casos, particularmente con historias de presión que apoyan la producción. Si el objetivo del pronóstico es una proyección con un diseño de instalación, entonces los métodos Armónico e Hiperbólico pueden ser empleados. También el gasto de aceite en BPD, puede ser MSCF de gas. • En campos con bombeo artificial y altos volúmenes de agua producida, existe una relación lineal entre el log del % de agua y la producción acumulativa de aceite, lo que nos refleja una declinación Armónica. • Una relación lineal entre el % de agua y la producción acumulativa de aceite, sugiere una declinación Exponencial. Nomenclatura. qi = Gasto inicial q(t) = Gasto a un tiempo t Q(t) = Producción acumulativa Di= Gasto de declinación b = Utilizada en declinación Hiperbólica b = 1 para Armónica. Curva de declinación exponencial • El lado izquierdo de las gráficas están basadas en un gasto de 15 años para los tres modelos • La declinación de la curva Armónica es aplicable cuando la gráfica del loggasto vs tiempo tiene una pendiente constante, la declinación inicial de la gráfica del gasto vs producción acumulativa, también presenta una línea recta. • El modelo Exponencial es: Cuando es obtenida a partir de una gráfica semilog, se divide entre 2.3 para convertirse a una escala log natural. q(t) = qi x exp (-Dit) Curva de declinación Armónica • La declinación Armónica es un caso especial de la curva Hiperbólica para b = 1. La pendiente de la gráfica ln(q) vs producción acumulativa es igual a Di/qió log10, entonces la pendiente es: Curva de declinación hiperbólica • La declinación Hiperbólica utiliza dos parámetros, Di y b. donde α = 1- b • Toda la teoría de curvas de declinación se inicia desde la definición de la tasa de descenso instantáneo o real (D) de la siguiente manera: • D es "la variación relativa de la tasa por unidad de tiempo", frecuentemente se expresa en "% por año". En el siguiente diagrama, D = Pendiente / Tasa. • • • • Esta es la forma más general de la ecuación de declinación. Cuando b es igual a 1, la curva se dice que es armónica. Cuando 0 <b <1, la curva se dice que es hiperbólica, Cuando b = 0, esta forma de la ecuación se convierte en indefinido, sin embargo, se puede demostrar que es equivalente a la declinación exponencial. Una comparación de la declinación exponencial, hiperbólica, y armónica se muestra en el siguiente diagrama. Gasto de declinación nominal • Cuando la producción sigue un descenso exponencial (también conocido como porcentaje de disminución constante), hay dos maneras diferentes de calcular el pronóstico del gasto. Ambos dan la misma respuesta. Uno de ellos es más adecuado para la manipulación de datos tabulares, y utiliza un "gasto de declinación nominal", y el otro es el enfoque clásico gráfico basado en la ecuación de caída exponencial tradicional. Se trata de mostrar las interrelaciones que existen en la declinación del gasto nominal y exponencial. • Por lo general, el gasto de declinación nominal, d, se utiliza cuando se trata de yacimientos con datos en formato tabular en lugar de gráfico. • La equivalencia del gasto en la declinación (real) exponencial, D (como se usa en la ecuación de declinación exponencial) y el "nominal" gasto de declinación, d (tal como se utiliza en muchos cálculos gráficos) como se muestra a continuación: