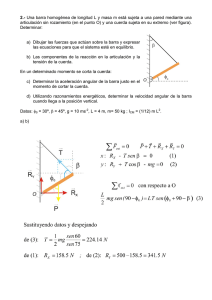
lOMoARcPSD|4855906 Ejercicios - Momento Angular FISICA (Universidad Nacional Mayor de San Marcos) StuDocu no está patrocinado ni avalado por ningún colegio o universidad. Descargado por Valeria Jimenez Gallardo (ocioval@hotmail.com) lOMoARcPSD|4855906 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS FISICAS Estudios Generales FÍSICA I MOMENTO ANGULAR 2018-II 1.-¿Cuál es la cantidad de movimiento angular de una bola de 0.210 kg que gira sobre el extremo de una delgada cuerda en un círculo de 1.10 m de radio y una rapidez angular de 10.4 rad/s? 2.- a) ¿Cuál es la cantidad de movimiento angular de una rueda de alfarero cilíndrica uniforme de 2.8 kg y 18 cm de radio cuando gira a 1500 rpm? b) ¿Cuánta torca se requiere para detenerla en 6.0 s? 3.- Una persona está de pie, con las manos a sus costados, sobre una plataforma que gira a una tasa de 1.30 rev/s. Si la persona eleva sus brazos a una posición horizontal, figura -01, la rapidez de rotación disminuye a 0.80 rev/s. a) ¿Por qué? b) ¿En qué factor cambió su momento de inercia? 4.- Una rueda de alfarero gira alrededor de un eje vertical que pasa por su centro con una frecuencia de 1.5 rev/s. Se puede considerar que la rueda es un disco uniforme de 5.0 kg de masa y 0.40 m de diámetro. Entonces el alfarero lanza un trozo de arcilla de 3.1 kg, aproximadamente con la forma de un disco plano de 8.0 cm de radio, sobre el centro de la rueda en rotación. ¿Cuál es la frecuencia de la rueda después de que la arcilla se adhiere a ella? 5.- Un disco uniforme da vueltas a 2.4 rev/s alrededor de un perno sin fricción. Una barra no rotatoria, de la misma masa que el disco y longitud igual al diámetro del disco, se suelta sobre el disco que gira libremente Figura – 02, Entonces ambos dan vueltas alrededor del perno con sus centros superpuestos. ¿Cuál es la frecuencia angular en rev/s de la combinación? 6.- Una persona de 55 kg está de pie en el borde de una plataforma giratoria de 6.5 m de diámetro que está montada sobre unos cojinetes sin fricción y que tiene un momento de inercia de 1700 kg.m2. La plataforma giratoria inicialmente esta en reposo, pero cuando la persona comienza a correr con una rapidez de 3.8 m/s (con respecto a la plataforma) alrededor de su borde, la plataforma comienza a girar en la dirección opuesta Calcule la velocidad angular de la plataforma. 7.- Una persona participa en el diseño de un ensamble de embrague que consta de dos placas cilíndricas, de masas 6.0 y 9.0 , con radios iguales R = 0.60 m. Inicialmente están separadas, figura – 03, se acelera desde el reposo hasta una velocidad angular 7.2 / en el tiempo ∆ 2.0 . La placa y b) la torca que se requirió para acelerar a desde el Calcule a) la cantidad de movimiento angular de c) A la placa , que en principio esta en reposo pero es libre de girar sin fricción, se le deja reposo hasta caer verticalmente (o se le empuja mediante un resorte), de modo que esté en firme contacto con la placa (sus giraba a constante. Después del contacto, superficies de contacto son de alta fricción). Antes del contacto, ¿a qué velocidad angular constante girarán las dos placas? Descargado por Valeria Jimenez Gallardo (ocioval@hotmail.com) lOMoARcPSD|4855906 8.- En el instante de la figura - 04, un 2.0 kg. La partícula P tiene un vector de posición de magnitud. 3.0 m y ángulo 45° y una velocidad vector de magnitud 4.0 m /s y ángulo. 30°. Fuerza de magnitud 2.0 N y ángulo = 30° , actúa sobre P. Los tres vectores se encuentran en el plano xy. Sobre el origen, que son(a) magnitud y (b) dirección del momento angular de P y la (c) magnitud y (d) dirección del par Actuando sobre p? 9.- En un instante, la fuerza = 4.0 ̂" actúa sobre un objeto de 0,25 kg. Que tiene vector de posición = % % 2.0#̂ − 2.0 m y vector de velocidad & = −5.0#̂ + 5.0 sobre el origen y en notación unidad-vector, cuales son (a) el momento angular del objeto y (b) el momento Torsión actuando sobre el objeto? 10.- Un objeto similar a una partícula de 2.0 kg se mueve en un plano con velocidad componentes &( = 30)/ y&* = 60 )/ a medida que pasa por el punto con coordenadas (x, y) de (3.0, 4.0) .determine el vector momento angular con respecto al (a) la origen y (b) el punto ubicado en (2.0 , 2.0 )m ? 11.- En el instante de la figura -05, Dos partículas se mueven en un plano xy. La partícula + tiene una masa de 6,5 kg y velocidad & = 2.2 )/ , y es a distancia = 1.5 ) desde el punto O. La partícula + tiene masa 3,1 kg y velocidad. & = 3.6 )/ , y está a una distancia1 = 2.8 ) desde el punto O.¿ Cuáles son? La (a) la magnitud y (b) dirección del momento angular neto de las dos partículas sobre O? 12.- En la figura-06,, tres partículas. De masa m = 23 g se sujetan a tres varillas de longitud d =12 cm y masa despreciable. El montaje rígido gira alrededor del punto O en la velocidad angular w= 0.85 rad / s. sobre O, ¿cuáles son (a) las Inercia rotacional del ensamble, (b) la magnitud del momento angular de la partícula media, y (c) la magnitud del momento angular del ensamble? 13.- Una varilla delgada y uniforme de longitud 0.500 m y masa 4.00 kg. Girar en un plano horizontal alrededor de un eje vertical a través de su centro. La barra está en reposo cuando una bala de 3,00 g viajando en el plano de rotación se dispara en un extremo de la varilla. Según lo visto desde arriba, la trayectoria de la bala hace un ángulo de = 60° con la barra (Figura – 07). Si la bala se aloja en la barra y la velocidad angular de la barra es de 10 rad / s inmediatamente después de la colisión, ¿cuál es el valor de la bala? Velocidad justo antes del impacto? 14.- En la figura- 08, una bala de 1.0 g es disparado en un bloque de 0,50 kg unido a el final de una varilla no uniforme de 0,60 m y 0.50 kg de masa El sistema bloque-barra-bala luego gira en el plano de la figura, alrededor de un eje fijo en A. La inercia de rotación de la barra solo alrededor deleje en A es de 0.060 kg.m2 .Tratar el bloque como partícula. (a) cual es la inercia rotacional del sistema bloque-barra-bala sobre el punto. (b) Si la velocidad angular del sistema es aproximadamente A justo después del impacto es 4.5 rad / s, ¿cuál es la velocidad de la bala justo antes del impacto? 15.- Dos balas de 2.00 kg están unidas a los extremos de una varilla delgada de longitud 50.0 cm y despreciable. la barra es libre para girar en un plano vertical sin fricción. Sobre un eje horizontal a través de su Centro. Con la varilla inicialmente horizontal, figura- 09, una masilla de 50.0 g. cae sobre una de las bolas y la golpea a una velocidad de 3.00 m / s apegándose a ella. (a) ¿Cuál es la velocidad angular del sistema? ¿justo después de que la masilla golpea? (b) ¿Cuál es la relación de la energía cinética del sistema después de la colisión del taco de masilla antes y después (c) ¿En qué ángulo girará el sistema antes de que se detenga momentáneamente? Descargado por Valeria Jimenez Gallardo (ocioval@hotmail.com) lOMoARcPSD|4855906 16.- En la figura - 10, un pequeño bloque de 50 g. se desliza por una superficie sin fricción a través de la altura h = 20 cm y luego se adhiere a una barra uniforme de masa 100 g y longitud 40 cm. La varilla pivotea sobre el punto O , deteniéndose momentáneamente a un ángulo . Encuéntrate . 17.- Un ave de 500.0 g vuela horizontal y distraídamente a 2.25 m/s, cuando de repente viaja directo hacia una barra vertical estacionaria, golpeándola a 25.0 cm debajo de la parte superior ,figura – 11, La barra es uniforme con longitud de 0.750 m y masa de 1.50 kg, y tiene una bisagra en la base. El choque aturde al ave, de modo que después simplemente cae hacia el suelo (aunque pronto se recupera para continuar volando felizmente). ¿Cuál es la velocidad angular de la barra, a) justo después de que es golpeada por el ave, y b) cuando esta llega al suelo? 18.- Un bloque de madera de masa M, que descansa sobre una superficie horizontal sin fricción, está unido a una barra rígida de longitud l y masa despreciable (figura- 12 ). La barra se articula en el otro extremo. Una bala de masa m, que viaja paralela a la superficie horizontal y perpendicular a la barra con rapidez v, golpea al bloque y queda incrustada en él. a) ¿Cuál es la cantidad de movimiento angular del sistema bala–bloque? b)¿Qué fracción de la energía cinética original se convierte en energía interna en la colisión? 19.- Una barra rígida sin masa tiene tres partículas con masas iguales unidas a ella, como se muestra en la figura 13, La barra es libre de dar vuelta en un plano vertical en torno a un eje sin fricción perpendicular a la barra a través del punto P y se libera del reposo en la posición horizontal en t = 0. Si supone que se conocen m y d, encuentre: a) el momento de inercia del sistema (barra más partículas) en torno al eje, b) el momento de torsión que actúa sobre el sistema en t = 0, c) la aceleración angular del sistema en t = 0, d) la aceleración lineal de la partícula 3 en t = 0, e) la máxima energía cinética del sistema, f) la máxima rapidez angular alcanzada por la barra, g) la máxima cantidad de movimiento angular del sistema y h) la máxima rapidez alcanzada por la partícula 2. 20.- Un cilindro con momento de inercia . da vueltas en torno a un eje vertical sin fricción con rapidez angular / .Un segundo cilindro, con momento de inercia . y que inicialmente no gira, cae sobre el primer cilindro (figura – 14 ). Debido a la fricción entre las superficies, con el tiempo los dos llegan a la misma rapidez angular. 0 . a) Calcule 0 b) Demuestre que la energía cinética del sistema disminuye en esta interacción y calcule la proporción de la energía rotacional final a la inicial. Descargado por Valeria Jimenez Gallardo (ocioval@hotmail.com)