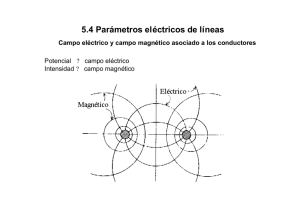
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUEPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA UNIDAD ZACATENCO Análisis de sistemas eléctricos de potencia I Cuestionario Segundo parcial Carlos Manuel Cortés Gaona conductores y tierra. Generalmente no se considera la conductancia entre conductores de una línea aérea, porque la fuga en los aisladores llega a ser despreciable. Sin embargo, las pérdidas de fuga varían fuertemente con las fluctuaciones atmosféricas y con las propiedades conductoras de la contaminación que se deposita en los aisladores. En altos voltajes existen adicionalmente las pérdidas por efecto corona, originadas por la ionización del aire que rodea el conductor que produce descargas debidas al alto campo eléctrico. 1 𝑅= 𝑅 Inductancia. Con base en la teoría y la formulación corrientemente conocidas para análisis de sistemas de potencia y particularmente para cálculos de líneas de transmisión, la inductancia total de una línea aérea monofásica por unidad de longitud, conocida como inductancia por milla de malla, se puede calcular como sigue: 𝐷 𝐿 = 4 × 10−7 𝑙𝑛 1 𝑟𝑒 −4 Donde r es el radio externo del conductor y D es la distancia de separación entre centros de los conductores. La inductancia se mide en Henry (H). Capacitancia. La capacitancia para una línea de transmisión aérea por unidad de longitud se puede calcular como: 2𝜋𝑘 𝐶= 𝐷 𝑙𝑛 ( ) 𝑟 Donde k es la permitividad del material que rodea el conductor y k = 8,85 × 10^−12 F/m es la permitividad para el espacio libre2. La separación entre conductores es D, y r es el radio exterior del conductor. La capacitancia se mide en Farad (F) ABSTRACT – Investigation of parameters of an electrical energy system, also the system [pu] for energy flow parameters. RESUMEN – Investigación de parámetros de un sistema eléctrico de potencia, así como el sistema [pu] para cálculos de flujo de potencia. I. INTRODUCCIÓN Como parte del estudio de los sistemas eléctricos de potencia, se deben conocer con mayor amplitud algunos conceptos más especializados a los flujos de potencia, como son los parámetros usados en estos sistemas, y un sistema en por unidad muy comúnmente utilizado en el análisis de sistemas eléctricos de potencia. II. DESARROLLO Cuestionario. 1.- Describir los parámetros de un sistema de potencia, incluyendo su unidad de medida. Una línea de energía eléctrica tiene cuatro parámetros que afectan su capacidad para cumplir su función como parte de un sistema de potencia: resistencia, inductancia, capacitancia y conductancia. Resistencia. La resistencia de los conductores es la causa más importante de la pérdida de potencia en las líneas de transmisión. Cuando se habla de resistencia se hace referencia a la resistencia efectiva. La resistencia efectiva de un conductor es: 𝑃 𝑅= 2 𝐼 donde P es la pérdida de potencia en el conductor en watts e I es la corriente efectiva o rms en ampers. La resistencia efectiva es igual a la resistencia de corriente directa del conductor, solo si la distribución de corriente a través del conductor es uniforme, se da en ohms (Ω). Conductancia. Las pérdidas de fuga o por conductancia dependen de la calidad y diseño de los aisladores y se producen por pequeñas corrientes que circulan entre conductores o entre 2.- Describir las diferencias relevantes entre un sistema de potencia regulado y un sistema de potencia desregulado. Existen 4 principales diferencias: 1) En el sistema regulado se encuentran los clientes residenciales y pequeña industria, y en el sistema no regulado se encuentra el comercio y la industria. 1 2) Con el cliente regulado se aplica la tarifa estandarizada mientras que el cliente no regulado, tiene la posibilidad de negociar su comercialización. 3) Al cliente regulado, se le aplica un contrato en condiciones uniformes, mientras que al cliente no regulado tiene la posibilidad de pactar condiciones en un contrato establecido. 4) El cliente regulado tiene un medidor de energía electrónico normal, y el cliente no regulado debe tener un medidor horario y telemedido. 3.- Describa la importancia del uso de sistemas en por Unidad (P.U.). El valor numérico de los parámetros eléctricos (tensiones, potencias, impedancias, corrientes) para un análisis de un Sistema Eléctrico de Potencia, está generalmente expresado en un valor relativo, ya sea en por ciento [%] o en por unidad [pu]. Esto resulta como consecuencia de referenciar los valores absolutos de dichos parámetros (dados en kV, MW, Ω, kA) a sus correspondientes valores bases. Esta forma relativa de expresar los valores numéricos presenta las siguientes ventajas: a) Brinda información de magnitud relativa, comparando mejor las máquinas, los elementos de diferentes valores nominales y los parámetros eléctricos. b) El circuito equivalente de un transformador puede ser simplificado, desapareciendo la relación de transformación en la representación de este. Las impedancias, tensiones, corrientes, expresadas en [pu] no cambian cuando se refieren a un lado del transformador o al otro. c) Las impedancias en [pu] de equipos eléctricos similares se encuentran en una estrecha faja de valores cuando los valores nominales de estos equipos son usados como valores Bases. Los Datos de placa de los elementos del SEP son los siguientes: Pasos en la Construcción del Diagrama de Impedancia a) Se identifican las diferentes zonas del circuito (Figura 1), dadas por los diferentes lados de los transformadores (lado de alta y lado de baja). Zona 1: El generador G1 y el arrollamiento de baja del T12. Zona 2: El arrollamiento de alta del transformador T12, T34 y T56, la línea de transmisión LT23 y LT35. Zona 3: El Motor M o demanda D4 y el arrollamiento de baja del T34. Zona 4: El generador G6, la demanda D6 y el arrollamiento de baja del T56. b) Se eligen los dos valores bases trifásicos independientes (se podría haber elegido también valores bases por fase). Si bien los valores bases pueden ser cualquiera, es recomendable que el valor base de la potencia sea del orden de la potencia que maneja el sistema, y que la tensión base de la región sea la del lado del transformador correspondiente. 𝑆𝐵 3𝛷 = 15 [𝑀𝑉𝐴] (es el mismo para todo el SEP) 𝑈𝐵(𝑧𝑜𝑛𝑎1) = 8 [𝐾𝑉] c) Se encuentran las tensiones bases para el resto de las zonas: 𝑈𝑇𝑟 (𝑧𝑜𝑛𝑎 𝑚) 𝑈𝐵 (𝑧𝑜𝑛𝑎 𝑚) = 𝑈𝐵 (𝑧𝑜𝑛𝑎 𝑘) 𝑈𝑇𝑟 (𝑧𝑜𝑛𝑎 𝑘) 4.- Describa la ecuación general para el calculo de una cantidad en P.U., así como las relaciones básicas de la potencia aparente, activa, reactiva, impedancia, reactancia, corriente y tensión. Para encontrar los valores relativos en [pu] se calcula como: 𝑉𝑎𝑙𝑜𝑟 𝑒𝑛 [𝑝𝑢]𝛼 = 𝑉𝑎𝑙𝑜𝑟 𝑀𝑒𝑑𝑖𝑑𝑜 [𝑢. 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑒𝑛𝑡𝑒]𝛼 0 𝑉𝑎𝑙𝑜𝑟 𝑏𝑎𝑠𝑒 𝑒𝑙𝑒𝑔𝑖𝑑𝑜 [𝑢. 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑖𝑒𝑛𝑡𝑒]0 El Valor Base Elegido es siempre un valor real (ángulo de 0º), por lo que el ángulo resultante α del Valor en [pu] es el mismo que el del Valor Medido. 5.- Mostrar el cálculo de las cantidades en por Unidad de un sistema de potencia de prueba (seleccionar dicho sistema de potencia). cálculo de las cantidades en por Unidad de un sistema de potencia de prueba: 2 𝑈𝐵(𝑧𝑜𝑛𝑎 2) = 𝑈𝐵(𝑧𝑜𝑛𝑎 1) 𝑈𝐵(𝑧𝑜𝑛𝑎 3) = 𝑈𝐵(𝑧𝑜𝑛𝑎 3) 𝑈𝐵(𝑧𝑜𝑛𝑎 4) 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 2) 132 =8 = 132 [𝐾𝑉] 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 1) 8 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 3) 7 = 132 = 7 [𝐾𝑉] 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 3) 132 Transformador 34: 7 2 15 𝑍𝑇34 = 0,12 ( ) = 0,12 [𝑝𝑢] 7 15 Transformador 56: 7 2 15 𝑍𝑇56 = 0,11 ( ) = 0,090 [𝑝𝑢] 6,69 20 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 4) 7 = 𝑈𝐵(𝑧𝑜𝑛𝑎 2) = 132 = 6,696 [𝐾𝑉] 𝑈𝑇𝑟12 (𝑧𝑜𝑛𝑎 2) 138 Línea de Transmisión 23: 𝑋𝐿𝑇 [Ω] = 𝑋𝐿𝑇 [Ω/𝑘𝑚] × 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑[𝑘𝑚] d) Se encuentran las corrientes bases en todas las zonas: 𝑆𝐵3𝛷 [𝑀𝑉𝐴] 𝐼𝐵(𝑧𝑜𝑛𝑎 𝑘) [𝐾𝐴] = √3𝑈𝐵(𝑧𝑜𝑛𝑎 𝑘) [𝐾𝑉] 𝑆𝐵3𝛷 15 𝐼𝐵(𝑧𝑜𝑛𝑎 1) = = = 1,083 [𝐾𝐴] √3𝑈𝐵(𝑧𝑜𝑛𝑎 1) √3 8 𝑆𝐵3𝛷 15 𝐼𝐵(𝑧𝑜𝑛𝑎 2) = = = 0,066 [𝐾𝐴] √3𝑈𝐵(𝑧𝑜𝑛𝑎 2) √3 132 𝑆𝐵3𝛷 15 𝐼𝐵(𝑧𝑜𝑛𝑎 3) = = = 1,237 [𝐾𝐴] √3𝑈𝐵(𝑧𝑜𝑛𝑎 3) √3 7 𝑆𝐵3𝛷 15 𝐼𝐵(𝑧𝑜𝑛𝑎 4) = = = 1,294 [𝐾𝐴] √3𝑈𝐵(𝑧𝑜𝑛𝑎 4) √3 6,696 e) Se encuentran las impedancias bases en todas las zonas: 𝑈 2 𝐵(𝑧𝑜𝑛𝑎 𝑘) 𝑍𝐵(𝑧𝑜𝑛𝑎 𝑘) [Ω] = 𝑆𝐵3𝛷 𝑈 2 𝐵(𝑧𝑜𝑛𝑎 1) 82 𝑍𝐵(𝑧𝑜𝑛𝑎 1) = = = 4,266 [Ω] 𝑆𝐵3𝛷 15 𝑈 2 𝐵(𝑧𝑜𝑛𝑎 2) 1322 𝑍𝐵(𝑧𝑜𝑛𝑎 2) = = = 1161,6 [Ω] 𝑆𝐵3𝛷 15 2 𝑈 𝐵(𝑧𝑜𝑛𝑎 3) 72 𝑍𝐵(𝑧𝑜𝑛𝑎 3) = = = 3,266 [Ω] 𝑆𝐵3𝛷 15 𝑈 2 𝐵(𝑧𝑜𝑛𝑎 4) 6,692 𝑍𝐵(𝑧𝑜𝑛𝑎 4) = = = 2,989 [Ω] 𝑆𝐵3𝛷 15 f) Se construye una Tabla con todos los valores Bases obtenidos de las diferentes Zonas: 𝑋𝐿𝑇 [𝑝𝑢] = 𝑋𝐿𝑇 [Ω] 𝑍𝐵 (𝑧𝑜𝑛𝑎 𝑘) 𝑋𝐿𝑇23 = 0,46218 × 150 = 69,3[Ω] 69,3 = 0,0597 [𝑝𝑢] 1161,6 Línea de Transmisión 35: 𝑋𝐿𝑇35 = 0,46218 × 100 = 46,218[Ω] 𝑋𝐿𝑇23 = 𝑋𝐿𝑇35 = 46,218 = 0,0398 [𝑝𝑢] 1161,6 Demanda 6: 𝑍𝐷6 [𝑝𝑢] = 𝑍𝐷6 [Ω] 𝑍𝐵(𝑧𝑜𝑛𝑎 4) [Ω] 10 + 𝑗2 = 3,346 + 𝑗0,669 [𝑝𝑢] 2,989 h) Se calculan las Tensiones de los Generadores en [pu]: Se supone que la tensión del generador 1 detrás de su reactancia directa es un 10 % superior a su tensión nominal y posee un ángulo de 0º : 1,1𝑥𝑈𝐺1 [𝐾𝑉] 8,8 𝐸𝐺1 = = = 1,10° [𝑝𝑢] 𝑈𝐵(𝑧𝑜𝑛𝑎 1) [𝐾𝑉] 8 Se supone que la tensión del generador 6 detrás de su reactancia directa es un 5 % superior a su tensión nominal y posee un ángulo de -4º : 1,05𝑥𝑈𝐺6 [𝐾𝑉] 7,35 𝐸𝐺6 = = = 1,098−4° [𝑝𝑢] 𝑈𝐵(𝑧𝑜𝑛𝑎 4) [𝐾𝑉] 6,696 h) Con los valores encontrados en [pu] se construye el diagrama de impedancias de secuencia directa mostrado en la Figura 2: 𝑍𝐷6 = g) Se calculan las impedancias de todos los elementos en [pu], realizando los cambios de base correspondientes: Generador G1: 𝑈𝐵−𝐺1 [𝐾𝑉] 2 𝑆𝐵 [𝑀𝑉𝐴] 8 2 15 𝑍𝐺1 = 𝑍𝐺1 ( ) = 0,11 ( ) = 0,1375[𝑝𝑢] 𝑈𝐵 𝑍𝑂𝑁𝐴1 [𝐾𝑉] 𝑆𝐵−𝐺1 [𝑀𝑉𝐴] 8 12 Generador G6: 𝑈𝐵−𝐺6 [𝐾𝑉] 2 𝑆𝐵 [𝑀𝑉𝐴] 7 2 15 𝑍𝐺6 = 𝑍𝐺6 ( ) = 0,13 ( ) = 0,1421[𝑝𝑢] 𝑈𝐵 𝑍𝑂𝑁𝐴4 [𝐾𝑉] 𝑆𝐵−𝐺6 [𝑀𝑉𝐴] 6,69 15 Motor M4: 𝑈𝐵−𝑀4 [𝐾𝑉] 2 𝑆𝐵 [𝑀𝑉𝐴] 7 2 15 𝑍𝑀4 = 𝑍𝑀4 ( ) = 0,13 ( ) = 0,12[𝑝𝑢] 𝑈𝐵 𝑍𝑂𝑁𝐴3 [𝐾𝑉] 𝑆𝐵−𝑀4 [𝑀𝑉𝐴] 7 15 no cambia de valor, ya que las bases del elemento son las mismas que las del sistema. Transformador 12: Se observa que el diagrama obtenido es un circuito eléctrico sin transformadores, donde se pueden aplicar los teoremas convencionales de resolución de circuitos para encontrar todas 𝑈𝐵−𝑇12 [𝐾𝑉] 2 𝑆𝐵 [𝑀𝑉𝐴] 8 2 15 𝑍𝑇12 = 𝑍𝑇12 ( ) = 0,10 ( ) = 0,10[𝑝𝑢] 𝑈𝐵 𝑍𝑂𝑁𝐴1 [𝐾𝑉] 𝑆𝐵−𝑇12 [𝑀𝑉𝐴] 8 15 3 las corrientes, tensiones y potencias presentes en [pu]. Para saber cuánto valen en [KA], [KV] y [MW] se multiplican estos valores encontrados en [pu] por la base de la zona correspondiente. III CONCLUSIÓN El sistema por unidas [pu] con facilita la simplificación de lo que podrían llegar a ser sistemas eléctricos de potencia muy extensos, en diagramas unifilares en los cuales utilizar los valores seria de una forma más sencilla y posteriormente también sus unidades correspondientes. REFERENCIAS [1] Henry Bastidas Mora., “Fundamentos teóricos para el cálculo de los parámetros técnicos de las líneas eléctricas aéreas de baja tensión para su uso en telecomunicaciones”, Revista Ingeniería e investigación Vol. 20, No. 2, agosto 2009, pp. 107-111. [2] Grupo http://www.scielo.org.co/pdf/iei/v29n2/v29n2a17.pdf Celsia “Informacion regulatoria para clientes” https://www.celsia.com/es/nuestra-empresa/marcoregulatorio [3] Jorge A. González “SISTEMAS POR UNIDAD”, Universidad Nacional de Tucuman, 2015, Argentina. https://catedras.facet.unt.edu.ar/sep/wpcontent/uploads/sites/20/2015/03/SEP-Sistemas-porUnidad.pdf 4