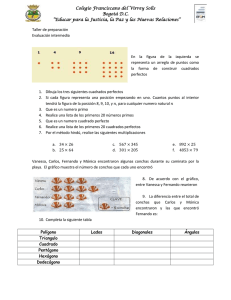
Ubicar raíces cuadradas en la recta numérica Objetivo: Estimar y representar raíces cuadradas. Las raíces cuadradas definen números que pueden ser naturales o no, y que aparecerán de forma recurrente en muchos problemas geométricos. Por lo tanto, es importante conocer su orden a partir de su ubicación en la recta numérica. ¿Qué pasa si una raíz cuadrada no es número entero? Podemos aproximar la raíz cuadrada usando cuadrados perfectos. Para hacer esto, miramos los cuadrados perfectos que generan un número cerca de la raíz cuadrada que estamos buscando. Si buscas la raíz cuadrada de 30 (√30), primero tenemos que encontrar dos cuadrados perfectos cercanos a 30. Uno debería ser menor que 30 y uno mayor que 30. 5∗5=25 6∗6=36 25 es el cuadrado perfecto menor que 30. 36 es el cuadrado perfecto mayor que 30. Debido a que 30 está entre el 25 y 30, podemos decir que la raíz cuadrada aproximada de 30 está entre 5 y 6. Es probablemente cercano a 5,5. Así es como podemos aproximar una raíz cuadrada usando cuadrados perfectos. ¿Cómo podemos estimar la parte decimal? Cuando estimamos una raíz cuadra inexacta, debemos buscar entre que cuadrados perfectos se encuentra, para ello elegimos el menor más cercano. Entonces para encontrar su parte decimal podemos realizar la siguiente operación: √30 1° El cuadrado perfecto más cercano a 30 es 25, como lo vimos en el caso anterior. 2° teniendo este valor, procederemos con la siguiente operación. √30 = 30 + 25 55 = = 5,5 10 10 El cuadrado perfecto más cercano a la cantidad sub-radical Corresponde a la cantidad sub-radical Es el doble del número que multiplicamos para obtener la raíz cuadrada más cercana, en este caso es: 5 x 5 =25 El doble de 5 es 10 Este método es bastante útil, pero en algunos casos este método no será efectivo ya que nos dará un valor muy alejado del valor real. Ejemplo: √15 = 15+9 6 = 24 6 = 4, en este caso no nos sirve, ya que sabemos que 4 es la raíz de 16. En estos casos podemos aplicar le siguiente método. Buscamos los cuadrados perfectos más cercanos a 15. √9 < √15 < √16 Sabemos que la raíz de 9 es 3 y la raíz de 16 es 4. Como el 15 es más cercano a 16 comenzaremos a probar con decimales más cercanos a 4, por ejemplo: 3,9 x 3,9 = 15,21 es un valor cercano a 15 así que lo podemos considerar como estimación, pero podemos ser un poco más exactos y podemos probar con un número un poco menor. 3,8 x 3,8 = 14,44 nos alejamos un poco, entonces podemos considerar un decimal más. 3,87 x 3,87 = 14,97 este valor es mucho más cercano a 15, lo podemos considerar como una estimación más cercana. Entonces, √15 ≈ 3,87 Otro método de estimación es el siguiente: 1° se identifican los cuadrados perfectos más cercanos a la raíz que queremos estimar. 2° Se calcula el promedio entre estos números, y luego se divide la cantidad sub-radical de la raíz que queremos estimar por el promedio obtenido. 3° Para una buena aproximación de la raíz, realizaremos una división entre los cocientes obtenidos anteriormente. Ejemplo: Paso 1: √15, los cuadrados perfectos cercanos son √9 𝑦 √16 Paso 2: calculamos el promedio entre las raíces de los cuadrados perfectos cercanos. 3+4 2 = 3,5 Ahora dividimos la cantidad sub-radical por el promedio 15 = 4,28 3,5 Paso 3: aproximación más cercana. 3,5 + 4,28 = 3,89 2 Ejemplo de ubicar raíces en la recta numérica: Actividades para desarrollar: Libro de matemática, páginas 66 y 67. Cuadernillo, páginas 32 y 33. PAUTA LIBRO PAUTA CUADERNILLO