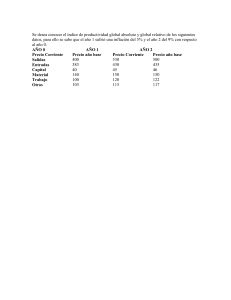
Facultad de Ingeniería EAP INGENIERÍA CIVIL UNIDAD TEMÁTICA N° 1: NOCIONES BÁSICAS DE LOS ERRORES 1) Se tiene un rectángulo cuyos lados han sido medidos aproximadamente en: l=3 metros y h=2 metros. Se desea obtener el área del rectángulo con un error no mayor al 5%. ¿Qué errores en la medida de l y h son permisibles? 2) Una barra de acero en voladizo sufre una deformación máxima en su extremo llamado flecha (f), la cual se puede calcular con la siguiente fórmula: f 4FL3 3 calcular con la fórmula: 1 1 I r 4 sen 2 Si r=2 m y Ѳ=π/5. 4 2 ¿Cuál debe ser el error relativo permisible en la medición de r y Ѳ Si el error máximo permitido para el cálculo de I es del 2 %, aplicando el principio de igual efecto? 6) La tensión T en una cuerda de yoyo en la figura es: , F=10000 N ±2%, Ea b L=1m±1%, E=210x109Pa, a=0.2m y b=0.04m. Determine el error absoluto de la flecha en mm, considerando que E, a y b son constantes. 3) Sea la pirámide truncada mostrada en la figura: T mgR 2r 2 R 2 Donde m es la masa del yoyo, g es la aceleración de la gravedad, R es el radio mayor y r es el radio menor. Considerando R=0.03 0.001 (en m), r= 0.007 0.001 (en m). Donde m=0.2 kg, g=9.8 m/s2 Cuyo volumen es: V abh 3H 2 3Hh h 2 a) Calcule el valor estimado de la Tensión b) Estime el error debido a la propagación en la función. 7) Una partícula se mueve según la siguiente a ecuación: . eb b 2 1 . 3H 2 Si a=5 cm, b=8 cm, H=18.5 cm, h=9.111 cm. ¿Cuál es el error absoluto permisible en las variables, tal que V tenga un error inferior al 0.5%? Nota: usar el principio de igual efecto. Si Ѳ=0.235, b=0.15 y a =12.25. ¿Cuál debe ser el error permisible en las variables a fin de que ω tenga un error no mayor al 5 %? 4) Se tiene un trapecio de base menor a, base mayor b y altura h, si d es la distancia de la base mayor a un eje centroidal paralelo a dicha 1 2a b base. d h . Si a=4 ± 0.1 m, b=2 m ± 1 3 ab %, h=2.25 medido con una precisión de 2 cifras decimales exactas. Estime d (m), indique su error absoluto y relativo esperado e indique en que rango se encontrará su valor exacto. 8) Un disco giratorio obedece a la siguiente ecuación: k 2 2 M . I Si Ѳ=0.235 ±0.001 rad, I=104 ± 1 % m4, 490≤M≤491 N-m y k=25.13 con una precisión de 2 cifras decimales exactas. Estime la velocidad angular ω (rad/s), indique su error absoluto esperado e indique en que rango se encontrará su valor exacto. 5) Un sector circular de radio R y ángulo 2Ѳ, cuyo momento de inercia con respecto a un eje que divide al sector en dos partes iguales se puede Prof. Carlos Deudor Gomez 1 INGENIERÍA MATEMÁTICA II 9) Sea la siguiente expresión para calcular el torque (N-m) en un anillo circular que gira alrededor de un eje en contacto con una capa de fluido: T 1.57 Re 4 Ri 4 a) Calcule el valor aproximado de la velocidad angular (ω) en rad/s b) Calcule el error absoluto y relativo del resultado anterior c) Cuantos decimales exactos tendría, considerando que el valor exacto de la velocidad angular fuera 10.5 rad/seg. 14) El coeficiente de descarga Cq de un orificio puede determinarse colectando el agua que pasa por él durante un tiempo determinado cuando está bajo carga constante h. La fórmula w es Cq , donde: t A 2 gh Si 0.05Pa-s, 100rad/s, 0.001m, Re=0.2 m y Ri=0.1 m ¿Cuál es el error absoluto permisible en las variables tal que T tenga un error inferior al 5%? 10) Mediante ensayos se ha determinado la siguiente fórmula para estimar la ubicación de una partícula que se desplaza sobre una línea Asen B cos t x t 17 w 900Lb-m , A 62.36 , Lb-m constante , d 0.5pulg , pie3 Si Cq debe medirse dentro de 5% (de Cq), para los valores numéricos dados, ¿qué errores son admisibles en los datos medidos? 17 . a) Calcule el valor estimado de la posición b) Estime el error debido a la propagación en la función. 11) Sea la siguiente expresión: 1 r r0 1 15) Dada la fórmula H Ae T 4 Con = 5.67 ×10−8, A = 0.1 ± 1%, e = 1.0, T = 600°± 20° Utilizando propagación de errores de funciones de varias variables: a) Aproxime H b) Estime el error absoluto de la aproximación de H. c) Estime el rango para el valor exacto de H. 16) Se desea calcular el valor de la expresión Si r0= 42.375 fue medido con una precisión de 0.001 y 0.2450.255. a) Estime la magnitud r y determine error absoluto esperado en el cálculo de r. b) ¿En qué rango se encuentra el valor exacto de r? 12) Sea la siguiente expresión: 1 r r0 1 7 4 3 4 utilizando el valor aproximado 3 1.73205 (con todas sus cifras decimales exactas) a) Demostrar que las siguientes formulas son numéricamente equivalentes 4 1 1 74 3 4 2 74 3 97 56 3 Si r0= 42.75 y 0.235, ¿cuál es el error absoluto permisible en las variables r0 y tal que r tenga un error inferior al 5%? 13) Cuando un objeto gira alrededor de un punto, se cumple que: Fc 2 mR . Se tomaron las siguientes mediciones: Fuerza centrípeta (Fc) = 4 kN con 1% de precisión Masa(m) = 20 kg con una aproximación de ±0.5 kg Distancia hacia el centro R =2 m con 2% de precisión Prof. Carlos Deudor Gomez 4 3.1416 constante , h 12pies , pie g 32.17 constante , t 600seg , seg 2 Considerando A=35 0.1%, B=18 con precisión de 0.5, t = 15 0.1% (ángulos en radianes) y truncando a 2 decimales para d2 2 97 56 3 18817 10864 3 1 18817 10864 3 2 INGENIERÍA MATEMÁTICA II b) Aplicando la teoría de propagación de errores determine ¿Cuál de las anteriores es la forma más precisa de calcular? x0 v Si v ms 1 g.8ms2 con una precisión de 0.05 y h m. ¿Cuáles son los límites de variación de x0? 17) El ensayo de dureza Brinell involucra la compresión de una bola de acero de carburo de tungsteno, de un diámetro D exactamente de 10 mm, contra una superficie, con una carga P en Newtons de 500± 1%, si d es 5.75 mm. medido con una precisión de 0.001 mm, d es el diámetro de la huella impresa en la superficie del material a ensayar entonces, el número de dureza de Brinell HB será: HB 2P D D D2 d 2 2h g 20) El periodo (T (seg) ) de un péndulo simple, para /12 rad., se puede calcular mediante la siguiente relación: L 2 T 2 1 g 16 Si L 0.30 0.001m., g 9.8 m/ seg 2 con una precisión de 0.01 y 3.1416 el cual tiene las 4 cifras decimales exactas, si 0.2 rad. cuyo valor fue medido con una precisión de 1%. a) Estime el valor de T. b) ¿Que precisión (%) se espera tener para el valor de T? Considere que =3.14 tiene sus 2 cifras decimales exactas a) Aproximé HB b) Estime el valor absoluto de la aproximación HB c) Estime el rango para el valor exacto de la dureza HB 21) Un cono truncado de radio mayor R, radio menor r y altura h cuya área lateral se puede calcular con la fórmula A g R r , si r = 2 m, R = 4 m y h = 6.65 m Con que precisión debe medirse h, si el área obtenida tiene un precisión de 10% los radios fueron medidos con una exactitud de 3 % y 3.142 con sus 3 cifras decimales exactas. . 18) Se pretende calcular el área de un círculo de radio aproximadamente de 25 cm., con error absoluto, que en módulo, no exceda a 0.05 cm2. Con qué precisión absoluta se debe medir el radio del círculo y cuántas cifras decimales en el valor aproximado de ? 19) El punto de impacto de un proyectil que es lanzado desde un avión puede ser calculado por la siguiente expresión: Referencia Bibliográfica N° [1] [2] [3] [4] [5] [6] Autores Titulo Páginas Métodos numéricos para ingenieros Steven C. Chapra 965 Análisis Numérico Richard L. Burden y J Douglas Faires 831 Análisis Numérico Gutierrez, Olmos, Casillas 421 Análisis Numérico Axel Osses A. 163 http://www.robcas64.com/Numerico/Numerico1.html http://ocw.upm.es/matematica-aplicada/programacion-y-metodos-numericos Prof. Carlos Deudor Gomez 3 INGENIERÍA MATEMÁTICA II