caida libre diapositivas
Anuncio
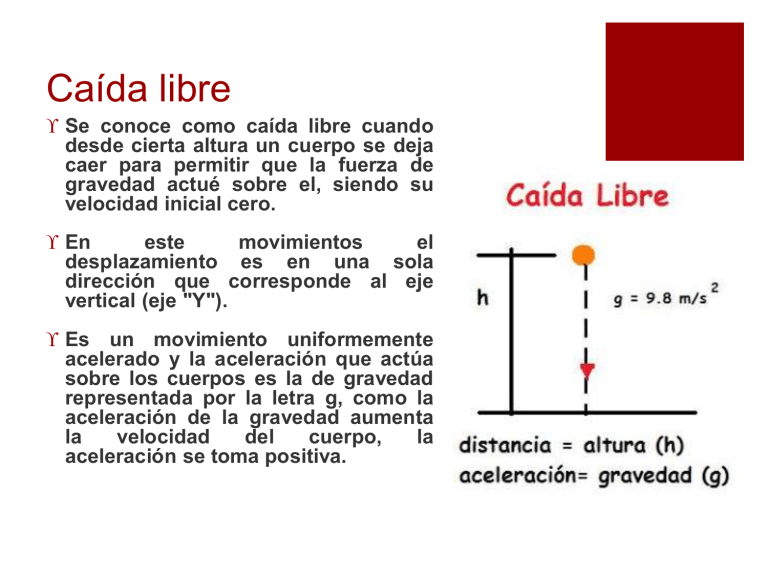
Caída libre Se conoce como caída libre cuando desde cierta altura un cuerpo se deja caer para permitir que la fuerza de gravedad actué sobre el, siendo su velocidad inicial cero. En este movimientos el desplazamiento es en una sola dirección que corresponde al eje vertical (eje "Y"). Es un movimiento uniformemente acelerado y la aceleración que actúa sobre los cuerpos es la de gravedad representada por la letra g, como la aceleración de la gravedad aumenta la velocidad del cuerpo, la aceleración se toma positiva. Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas: NOTA: Cuando se informa que “Un objeto se deja caer” la velocidad inicial será siempre igual a cero (v0 = 0). En cambio, cuando se informa que “un objeto se lanza” la velocidad inicial será siempre diferente a cero (vo ≠ 0). Conclusiones -La caída libre cuando desde cierta altura un cuerpo se deja caer para permitir que la fuerza de gravedad actué sobre el. -La velocidad inicial es siempre cero. -Todo cuerpo que cae libremente tiene una trayectoria vertical -La Gravedad es una fuerza que trata de jalar los objetos hacia abajo. -En la caída libre no se toma en cuenta la resistencia al aire Tiro vertical Es un movimiento hacia arriba y en línea recta. La velocidad disminuye conforme asciende; la aceleración de la gravedad retarda el movimiento del cuerpo hasta que éste se detiene y empieza a caer de vuelta a la superficie de la tierra, entonces aumenta su velocidad y alcanza la máxima que tenía del punto donde se lanzó. El movimiento comprende solo la subida y bajada · La velocidad inicial Vo nunca es cero · La gravedad g es negativa (-9.8 m/s2) · Cuando el objeto alcanza su altura máxima, su velocidad V en este punto es 0 m/s. · Mientras que el objeto se encuentra se subida el signo de la velocidad V es positiva. · La V es 0 a su altura máxima. · Cuando comienza a descender su velocidad V será negativa. · El objeto tarda el mismo tiempo t en alcanzar su altura máxima y en regresar a la posición original. · Si el objeto tarda por ejemplo 2 s en alcanzar su altura máxima tardará 2 s en regresar a la posición original 1.- Un cuerpo es lanzado verticalmente hacia arriba con una velocidad inicial v0 = 30 m / s. Considerar que g = 10 m / s2 y se desprecia la resistencia del aire. a) ¿Cuál será la velocidad del cuerpo 2 segundos después del lanzamiento? Datos: v0 = 30 m / s g = 10 m / s2 Fórmulas v = v0 + g * t g = -10 m / s2 Substitución y resultado v = 30 m / s – 10 m / s2 * 2.0 s v= 10 m / s b) ¿Cuánto tarda el cuerpo en llegar al punto más alto de su trayectoria? Datos: En el punto más elevado tenemos que la velocidad es igual a 0 v=0 Fórmula: v = v0 + g * t t = v0 g Sustitución y resultado 30 m / s 10 m / s2 t=3s Tiro parabólico horizontal Se caracteriza por la trayectoria o camino curvo que sigue un cuerpo al ser lanzado al vacío, resultado de dos movimientos independientes: un movimiento horizontal con velocidad constante y otro vertical, el cual se inicia con una velocidad cero y va aumentando en la misma proporción de otro cuerpo que se dejara caer del mismo punto en el mismo instante. La forma de la curva descrita es abierta, simétrica respecto a un eje y con solo foco, es decir, es una parábola. Si se desea calcular la distancia recorrida en forma horizontal puede hacerse con la expresión: d = vt, pues la pelota lanzada con una velocidad horizontal tendrá una rapidez constante durante su recorrido horizontal e independiente de su movimiento vertical originado por la aceleración de la gravedad durante su caída libre. Tiro parabólico oblicuo Se caracteriza por la trayectoria que sigue un cuerpo cuando que es lanzado con una velocidad inicial que forma un ángulo determinado con eje horizontal. El tiro oblicuo es un caso de composición de dos movimientos perpendiculares, uno rectilíneo y uniforme(MRU) sobre el eje X y otro rectilíneo uniformemente variado(MRUV) sobre el eje Y. A partir de las ecuaciones de posición, velocidad y de la ecuación de la trayectoria(parábola) se resuelven todas las situaciones posibles(prescindiendo del rozamiento con el aire).