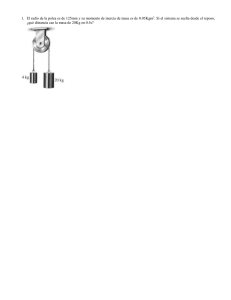
Curso/ Clase Docente Unidad Dinámica Facultad Ingeniería Asunto Practica Idrogo Córdova, Julio César IV Carrera Ingeniería Minas y Civil N° “7” Tema CINETICA PLANA DE UN CUERPO RÍGIDO Tipo Ejercicios Ciclo: 2020-4 1. La doble polea se compone de dos partes conectadas entre sí. Pesa 50 lb y tiene un radio de giro con respecto a su centro de masa de k0 = 0.6 pie. Si gira con una velocidad angular de 20 rad/s en el sentido de las manecillas del reloj, determine la energía cinética del sistema. Suponga que ninguno de los cables se desliza sobre la polea. 2. Cada uno de los dos remolcadores ejerce una fuerza constante F en el buque. Estas fuerzas siempre actúan perpendiculares a la línea de centro del buque. Si la masa de éste es m y su radio de giro con respecto a su centro de masa G es kG, determine su velocidad angular después de que gire 90°. El buque originalmente está en reposo. 3. El carrete pesa 150 lb y su radio de giro es k0 =2.25 pies. Si se enrolla una cuerda alrededor de su núcleo interno y el extremo se jala con una fuerza horizontal de P = 40 lb, determine su velocidad angular después de que el centro O ha recorrido 10 pies a la derecha. El carrete comienza a moverse del reposo y no se desliza en A cuando rueda. Ignore la masa de la cuerda. 4. Si el sistema comienza a moverse a partir del punto de reposo, determine la velocidad de los cilindros de 20 kg A y B después de que A ha descendido una distancia de 2 m. La polea diferencial tiene una masa de 15 kg con un radio de giro con respecto a su centro de masa de k0 = 100 mm. 5. El carrete tiene una masa de 100 kg y un radio de giro de 400 mm con respecto a su centro de masa O. Si se suelta desde el punto de reposo, determine su velocidad angular después de que su centro O desciende por el plano una distancia de 2 m. El coeficiente de fricción cinética entre el carrete y el plano inclinado es μk = 0.15. 6. En el instante que se muestra, la barra de 50 lb gira en el sentido de las manecillas del reloj a 2 rad/s. El resorte conectado a su extremo siempre permanece vertical debido a la guía de rodillo C. Si la longitud no alargada del resorte es de 2 pies y su rigidez es k = 12 lb/pie, determine el ángulo θ, medido con respecto a la horizontal, hacia la cual la barra gira antes de que se detenga momentáneamente. 7. Una cadena cuya masa se ignora está colgada sobre la rueda dentada que tiene una masa de 2 kg y un radio de giro de k0 = 50 mm. Si el bloque A de 4 kg se suelta del punto de reposo desde la posición s = 1 m, determine la velocidad angular de la rueda dentada cuando s = 2 m. . 8. La barra AB de 25 lb está conectada a un resorte BC cuya longitud no alargada es de 4 pies. Si la barra se suelta desde el punto de reposo cuando θ = 30°, determine su velocidad angular cuando θ = 90°. 9. La barra AB de 25 lb está conectada a un resorte BC cuya longitud no alargada es de 4 pies. Si la barra se suelta desde el punto de reposo cuando θ = 30°, determine su velocidad angular cuando el resorte vuelva a su longitud no alargada. 10. El sistema se compone de un disco A de 20 lb, una barra delgada BC de 4 lb y un collarín C de 1 lb. Si el disco rueda sin deslizarse, determine la velocidad del collarín cuando la barra está horizontal, es decir, θ = 0°. El sistema se suelta desde el punto de reposo cuando θ = 45°. 2