DS60: Aplicación Práctica en Edificios Reales - Análisis Estructural
Anuncio

Taller Aplicación práctica del DS60
Ejemplos Edificios Reales
ICH – 01/2012
Jorge F. Carvallo Walbaum
Ingeniero Civil en Estructuras, Magister MIEG, Pontificia Universidad Católica de Chile.
1
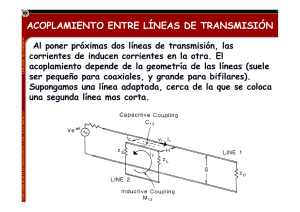
Acoplamiento
Ejemplo 1
Ejemplo 2
PCA R&D Serial No. SN2961
Ejemplo 3
Response Verification of a Reinforced
Concrete Bearing Wall Building Located in
An Area of High Seismic Hazard
by Marios Panagiotou, Geonwoo Kim, Andre Barbosa,
and José I. Restrepo
Lw
5420 Old Orchard Road
Skokie, Illinois 60077-1083
847.966.6200 Fax 847.966.8389
www.cement.org
Ls
Lw
©Portland Cement Association 2009
All rights reserved
2
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
1
1
2
2
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DV
hi
SDV
5
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
6
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 1. Edificio de 10 pisos + 1 sub.
7
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo.
8
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Muro A.5.
9
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Muro A.5.
Alma
comp.
10
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Análisis Muro 5, Sección T
20
Zona
Suelo
H-22.5
0.66
875
2158
93
5.4
26
0.002
4f32
M.V.f8a25
540
Hormigón
Período bruto (s)
Pu (tonf)
Mu (tonf m)
Vu (tonf)
Lw (m)
H (m)
ey
3
D
M.V.f8a25
20
4f22
M.V.f8a25
4f25
680
4f22
11
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Muro A.5.
26m
Ala
comp.
Alma
comp.
ELÁSTICO
ELÁSTICO
Sección con
demanda cíclica
inelástica
12
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Muro A.5.
min 25%*H=6.5m
S-1
Cc
Lw , Mu/(4Vu)
P1
Lw , Mu/(4Vu)
P2
13
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Muro A.5.
Para estimar la deformación
elástica, ¿qué “Lw” uso?
?
Lw=7.3m
?
Lw=5.4
?
?
✓
14
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Espectro Pseudo Desplazamiento Zona 3 Suelo D
15
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Demanda según DS 60
21-7 (a)
21-7 (b)
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
Donde:
16
Acoplamiento
Ejemplo 1
Definición SAP2000 Material Hormigón
Hormigon H-22.5
Ejemplo 2
Ejemplo 3
Definición SAP2000 Sección Designer
Muro T
17
Ejemplo 1
Acoplamiento
Orientación de la sección
Section Designer
Ejemplo 2
Ejemplo 3
Curva M- Ф
C
T
εs
90
εc
180
T
εs
C
o
o
εc
0o
εs
εc
C
T
εs
T
C
270
o
εc
18
Acoplamiento
Section Designer
Ejemplo 1
Ejemplo 2
Ejemplo 3
Sección Original H-22.5 e = 20 (cm)
e = 0.2 m
4 Ф 32
DM Ф 8 a 25
C
Coordenada
(0,0)
C.G. sección
bruta
5.4 m
DM Ф 8 a 25
4 Ф 25
4 Ф 22
e = 0.2 m
6.8 m
4 Ф 22
19
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Definición de Hormigón No Confinado según SAP2000 H-22.5
Botón derecho
en la sección
f'c = 1800
f2 = 1561
20
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M- Ф SAP2000
Número de puntos en
el gráfico
Carga axial Pu
(negativo = compresión)
Máximo en eje X
Ángulo según
dirección de análisis
21
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Definición de Hormigón Confinado H-22.5 según SAP2000
Botón derecho
en la sección
f'cc = 2311
f'cu = 2073
0.0055
0.015
22
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo de Curva M- Ф Hormigón No Confinado H-22.5 e = 20 (cm)
εc = 0.003
Фe=0.00042
∆y=0.078
εc = 0.003
εs = 0.0017
Фu=0.0009
∆u=0.092
c = 3.4 (m)
Pu = 875 (tonf)
μ= 1.4
εs = 0.0017 < εy
23
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo de Curva M - Ф Hormigón confinado según SAP2000
H-22.5 e =20 (cm)
εc = 0.008
εc = 0.003
c = 3.3 (m)
c = 2.7 (m)
Pu = 875 (tonf)
μ= 2.8
εc = 0.003
εs = 0.0019
Ф= 0.00091
Фy=0.0005
∆y=0.093
εc = 0.008
εs = 0.0081
Фu=0.003
∆u=0.259
εs = 0.0019 < εy
εs = 0.0081 > εy
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
Cumple (b) pero no cumple (a).
24
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejercicio propuesto:
Modificar sección de manera de
cumplir con la demanda de giro
unitario fu ,sin incluir la deformación
elástica, según DS60.
25
Acoplamiento
Ejemplo 1
H-22.5
0.66
875
2158
93
5.4
26
0.002
Zona
Suelo
Ejemplo 3
3
D
26m
Hormigón
Período bruto (s)
Pu (tonf)
Mu (tonf m)
Vu (tonf)
Lw (m)
H (m)
ey
Ejemplo 2
7.3m
5.4m
26
Acoplamiento
Section Designer
Ejemplo 1
Ejemplo 2
Ejemplo 3
Verificación de la sección con espesor e=30 (cm) H-22.5
e = 0.3 m
24 Ф 18
DM Ф 10 a 20
Coordenada
(0,0)
C.G. sección
bruta
5.4 m
DM Ф 10 a 20
4 Ф 25
4 Ф 22
6.8 m
e = 0.3 m
4 Ф 22
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo de Curva M - Ф Hormigón H-22.5 No confinado e = 30 (cm)
c = 2.54 (m)
εc = 0.003
Pu = 875 (tonf)
Фy=0.00048
∆y=0.089
εc = 0.003
εs = 0.0034
Фu=0.0012
∆u=0.137
μ= 1.5
εs = 0.0034 > εy
Necesita
confinamiento
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M - Ф Hormigón confinado según SAP2000 H-22.5 e = 30 (cm)
εc = 0.008
εc = 0.003
c = 2.3 (m)
c = 1.88 (m)
Pu = 875 (tonf)
εc = 0.003
εs = 0.0038
Ф = 0.0013
Фy=0.0005
∆y=0.093
μ= 3.6
εc = 0.008
εs = 0.0149
Фu=0.00426
∆u=0.343
qu=1.3%
εs = 0.0038 > εy
εs = 0.0149 > εy
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
Cumple con ambos casos
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
La curva de hormigón confinado con Ф8 a 10 (cm) del SAP2000 considera aumento
en la resistencia por confinamiento y deformación unitaria última de 1.5%.
¿ f'cc = 2311 ?
f'cu = 2073
0.0055
0.015
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Se puede hacer una curva constitutiva del hormigón sin aumento de
resistencia por confinamiento.
Acoplamiento
Ejemplo 1
Ejemplo 2
Hormigón H-22.5 e = 30 cm confinado según Usuario
f'c = 1800
cero acero
Ejemplo 3
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M - Ф Hormigón confinado según Usuario H-22.5 e = 30 (cm)
εc = 0.003
εc = 0.003
εs = 0.0032
Ф = 0.0011
Фy=0.00051
∆y=0.0948
εc = 0.008
εs = 0.0105
Фu=0.0034
∆u=0.287
εc = 0.008
c = 2.31 (m)
c = 2.72 (m)
Pu = 875 (tonf)
μ= 3
εs = 0.0032 > εy
εs = 0.0105 > εy
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
A diferencia del caso con aumento de
resistencia por confinamiento, sólo cumple
con el caso b.
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Para cumplir con 27-7 (a) y 17-7 (b) se cambió de H-22.5 a H-30
Curva M - Ф Hormigón confinado según Usuario H-30 e = 30 (cm)
εc = 0.003
c = 1.68 (m)
c = 1.85 (m)
Pu = 875 (tonf)
εc = 0.003
εs = 0.0052
Ф = 0.0015
Фy=0.00049
∆y=0.091
εc = 0.008
εs = 0.0161
Фu=0.00448
∆u=0.356
εc = 0.008
μ= 3.9
εs = 0.0052 > εy
εs = 0.0161 > εy
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
Cumple ambos casos
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
¿ Cuánto se debe confinar?
Curva M - Ф Hormigón confinado según Usuario H-30 e = 30 (cm)
εc = 0.003
εc = 0.003
εs = 0.0052
Ф = 0.0015
Фy=0.00049
∆y=0.091
c = 1.85 (m)
Pu = 875 (tonf)
εc = 0.008
εs = 0.0161
Фu=0.00448
∆u=0.356
μ= 3.9
εs = 0.00576 > εy
Acoplamiento
Ejemplo 1
Ejemplo 2
Configuración del refuerzo
0.025 (m)
0.025 (m)
Ef8a10
Tf8a10
Según D.S. 60
Cc = 1.1 (m)
S≤
Ejemplo 3
Acoplamiento
Ejemplo 1
Cálculo del refuerzo de confinamiento
según D.S. 60
Ф 18
Ф 8
Ф 10
Ф 18
Ejemplo 2
Ejemplo 3
Acoplamiento
Diagrama de interacción
Ejemplo 1
Ejemplo 2
Ejemplo 3
Altura de confinamiento
H = 5.8 (m)
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Comparación curvas M-Ф sección original y sección re-diseñada
Pu = 875 (tonf)
Фy=0.0005
∆y=0.093
μ= 1.4
Фy=0.00042
∆y=0.078
εc = 0.003
εs = 0.0017
Фu=0.0009
∆u=0.092
μ= 3.7
εc = 0.003
εs = 0.00467
Ф = 0.0014
εc = 0.008
εs = 0.0148
Фu=0.00425
∆u=0.342
Curva M-Ф considerando hormigón no confinado H-22.5 e =20(cm)
Curva M-Ф considerando hormigón confinado por usuario H- 30 e =30(cm)
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
c = 0.1 (m)
Dirección que comprime el ALA, Hormigón No Confinado H-30 e = 30 (cm)
εc = 0.0019
εc = 0.0019
εs = 0.09
Фu=0.017
εs = 0.09 > εy
εs
T
180o
C
εc
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0041
Фu 27-7 (b) (1/m)
0.0030
Se cumple Фu.
Falla primero el acero por
tracción que el hormigón por
compresión
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Análisis Muro Sección T
90
o
εc
C
T
Condición de proyecto
Hormigón
Período bruto (s)
Pu (tonf)
Mu (tonf m)
Vu (tonf)
Lw (m)
H (m)
ey
H-22.5
0.394
875
2158
93
6.8
26
0.002
Zona
Suelo
εs
3
D
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Espectro Pseudo Desplazamiento Zona 3 Suelo D
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Demanda según DS 60
21-7 (a)
21-7 (b)
Donde:
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0016
Фu 27-7 (b) (1/m)
0.0009
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M- Ф SAP2000
Ángulo según
dirección de análisis
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo Curva M - Ф Hormigón No confinado H-30 e = 30 (cm)
εc = 0.003
c = 2.04 (m) Фu
Pu = 875 (tonf)
μ= 1.9
Фy=0.00048
∆y=0.0892
εc = 0.003
εs = 0.0069
Фu=0.00147
∆u=0.171
εs = 0.0069 > εy
D.S. 60
Suelo D
Фu 27-7 (a) (1/m)
0.0016
Фu 27-7 (b) (1/m)
0.0009
Acoplamiento
Ejemplo 1
Ejemplo 2
Cuando no se requiere confinamiento
2 Ф 22
2 Ф 22
S≤
Cuantía vertical:
Ejemplo 3
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Comparación curvas M-Ф sección original y sección re-diseñada
Pu = 875 (tonf)
Фy=0.00048
∆y=0.0892
μ= 1.9
μ= 1.5
Фy=0.00043
∆y=0.079
εc = 0.003
εs = 0.0069
Фu=0.00147
∆u=0.171
εc = 0.003
εs = 0.0034
Фu=0.00095
∆u=0.12
Curva M-Ф considerando hormigón no confinado H-22.5 e =20(cm)
Curva M-Ф considerando hormigón no confinado H- 30 e =30(cm)
24Ф18
E+TФ8 + 9TФ10 S = 10 cm
DMФ10@20
S≤
4Ф22
DMФ10@20
4Ф25
EФ8@10
4Ф22
EФ8@10
S≤
EФ10@15
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 2, EDIFICIO EN REÑACA
18 PISOS + 2 SUBTERRANEOS
HORMIGON
ACERO
: H-35
: A63-42H
ZONA SISMICA
SUELO TIPO
: 3
: C
Ejemplo 1
Ejemplo 2
Ejemplo 3
Acoplamiento
PLANTA ESTRUTURA CIELO PISO TIPO SECCIÓN A ANALIZAR
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
PLANTA ESTRUTURA CIELO PISO TIPO SECCIÓN A ANALIZAR
GEOMETRÍA DE LA
SECCIÓN
HEDIF = 52 m
L14 = 8.09 m
LD
= 5.76 m
Diseño “Muro L” en ejes 14 y
D – Zona Crítica.
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
ESTRUCTURA - ANALISIS MODAL
Peso total:
9,730
ton
MODO X =
Dirección
3
MODO Y =
2
Período est:
UX
0.91
UY
0.93
R*:
8.41
8.47
Q R=1
37.4%
3,635
41.3%
4,023
Qmax:
1,430
14.7%
Qmin:
681
7.0%
Qbasal:
432.2
4.4%
DESPLAZAMIENTOS DE DISEÑO.
475.0
fu_14 = 0.001281/m
fu_D = 0.001871/m
4.9%
Sde(Tn)
Sa
14,0
du_14 = 27 cm qu_14 = 0.0052
du_D = 28 cm qu_D = 0.0054
0,40
12,0
0,35
10,0
0,30
8,0
0,25
6,0
0,20
0,15
4,0
0,10
2,0
0,05
0,0
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
0,00
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE 14
La carga de compresión que determina el diseño es la que se
produce cuando se comprime la cabeza libre del alma,
Pu=1747 [T] (Pu/(Aw*f’c)=0.29)
Diagrama de Interacción – Dirección Eje 14
10000
Carga Axial {T]
8000
6000
4000
2000
0
-20000 -15000 -10000
-5000
0
5000
10000
15000
20000
-2000
Momento[T-m]
La cabeza de compresión en la dirección analizada
es de 30x150 cm.
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE 14
VALORES DISEÑO
s=0.00515 para c=0.003. La
profundidad de lafibra neutra
es mayor al límite, por lo que se
debe confinar cconf=0.36 m.
f14
= 0.0010 1/m
c14
=
2.96 m
s14
=
0.52 %
clim14 =
cconf1
=
4
2.60 m
0.36 m
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE 14
Se verifica que para el hormigón confinado, sin aumento de
resistencia, se tenga una deformación unitaria de compresión
menor que 0.8%, dada la curvatura de diseño fu14 = 0.00128[1/m].
VALORES DISEÑO
Lasección cumple con el DS 60 en la
dirección analizada.
f14
= 0.00128 1/m
c14
=
0.37 %
s14
=
0.66 %
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE 14
Notar que como el confinamiento es necesario en los primeros 36 cm, se debe cumplir
con la cuantía de confinamiento y con hx solamente en ese tramo. En el resto de la zona
crítica, donde se espere que la armadura fluya, se debe disponer de estribos o trabas a
una separación máxima de 6fb.
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
DISEÑO EJE D
La carga de compresión que determina el diseño es la que se
produce cuando se comprime la cabeza libre del alma,
Pu=1206 [T] (Pu/(Aw*f’c=0.23)
Diagrama de Interacción – Eje D
10000
8000
Carga Axial [T]
6000
4000
2000
0
-8000
-6000
-4000
-2000
0
2000
-2000
Momento[T-m]
4000
6000
8000
10000
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE D
VALORES DISEÑO
Se tiene una deformación del acero en
tracción s=0.0035 para c=0.003. El
valor de la fibra neutra es mayor al
límite, por lo que se debe confinar
cconf=0.87 m.
fD
= 0.00113 1/m
cD
=
2.65 m
s D
=
0.35 %
clim14 =
1.78 m
cconf14 =
0.87 m
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE D
Se verifica que para el hormigón confinado, sin aumento de
resistencia, se tenga una deformación unitaria de compresión
menor que 0.8% para la curvatura de diseño fu14 = 0.00187[1/m].
VALORES DISEÑO
La sección cumple con el DS60 en la
dirección analizada.
f14
= 0.00187 1/m
c14
=
0.47 %
s14
=
0.61 %
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
DISEÑO EJE D
A diferencia de la cabeza de compresión del eje 14, en ésta se necesita confinar 87
cm, casi todo el largo del elemento de borde.
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 3
•
•
•
•
•
•
•
N° de Pisos: 21
Zona Sísmica 3
Suelo Tipo D
Hormigón H-35 y Acero A420H
Altura de primer piso:4.5[m]
Altura de entrepiso de los demás pisos: 2.48 [m]
Definiendo nuestra zona crítica en el piso uno se
tiene un Hw=54.1 [m]
• Y un largo de muro de Lw=7.15 [m]
• Pu=2100 [tonf]
62
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Caso a analizar
Θux(DS 117)=0.82%
Θuy(DS 117)=1.2%
Planta primer piso
63
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
• Se modeló el edificio no agrietado se obtuvo:
– Período Fundamental en dirección X: 1.28 [s]
– Período Fundamental en dirección Y: 0.93 [s]
• Se puede obtener el desplazamiento de techo
como:
δu= 1.3 Sd(Tag)
Se asume Tag como 1.5Tf
64
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Espectro de pseudo desplazamiento elástico de la
NCh 433 of. 96 modificada 2010
• Por lo tanto, Tagx=1.91 [s] y Tagy=1.39[s]
60
50
50
Sd [cm]
40
36
30
20
10
0
0
0,5
• δux=65 [cm]
• θux= 1.2%
1
1,5
2
2,5
Periodo [s]
δuy=47[cm].
θuy= 0.82%
65
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
• Se define:
0.00056 [m-1]
45 [cm]
66
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
Según DS 60, la demanda de curvatura última es:
0.00242 [m-1]
a)
ó
b)
0.00061 [m-1]
67
Caso a analizar
Planta primer piso
69
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Plantas
1° Piso
Dilatación = 10 mm
2° Piso
70
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Elevación del Muro a analizar
Θux(DS 117)=0.82%
54.1 m
71
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Diseño original
5φ22
5φ22
5φ22
5φ22
50cm
Lat. 33+33 φ22
410 cm
Lat. 16+16φ22
110 cm
195 cm
Pu=2100 [tonf]
72
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
Diagrama de Interacción
10000
8000
6000
4000
2000
0
-15000
-10000
-5000
0
5000
10000
15000
-2000
-4000
Mu,Pu
φMn,φPn
φMn,φPn
Pn,Mn (fy=1.25 fy)
Pn,Mn (fy=1.25 fy)
73
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Diseño original
• Del análisis Pumáx=2100 [Tonf] y Pu/(Ag*Fc’)= 0.23
• Para este nivel de carga axial, cuando el hormigón
alcanza un εc=3‰, la deformación unitaria del acero
εs=8‰
es εs≈4‰
εc=8‰
εc=3‰
φy=0.65‰
Δy=52.5cm
εs=εy
εc=3‰
φu=2.248‰
Δu=83cm
εs=4‰
75
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Verificación de capacidad de deformación para la
sección diseñado
• Capacidad última de la sección:
76
Acoplamiento
Ejemplo 1
Ejemplo 2
εs=10.8‰
c=cte
εcmáx=8‰
Ejemplo 3
εs=4‰
εc=3‰
• C=3/7 Lw=3.06 [m]
• Para una demanda
→εc=7.4‰<8‰
y
εs=9.8‰
77
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Comparación curvas M-φ para hormigón confinado
para diseño original
εc=4.73‰
εc=5.78‰
Considerando aumento de la resisten
No considerando aumento
de la resistencia
φu=0.0024[m-1] (DS60a)
78
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
Re-diseño para cumplir DS60, sin considerar
deformación elástica.
Section Designer
Sección H-35 e = 40 (cm)
5 Ф 22
5 Ф 22
5 Ф 22
e = 40 cm
5 Ф 22
Lat. 33+33 Ф 22
Lat. 16+16 Ф 22
410 cm
110 cm
C
εs
T
195 cm
270
o
εc
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M - Ф Hormigón confinado por usuario H-35 e =40 (cm)
εc = 0.008
εc = 0.003
c = 3.5(m)
c = 3.6 (m)
Pu = 2100 (tonf)
εc = 0.003
εs = 0.0032
Ф= 0.00086
Фy=0.00048
∆y=0.39
μ= 2.6
εc = 0.008
εs = 0.0079
Фu=0.0022
∆u=0.71
εs = 0.0032 < εy
Фu (1/m)
εs = 0.0079 > εy
0.00024
No cumple con la demanda.
Se debe cambiar espesor a 45 (cm)
Acoplamiento
Section Designer
Ejemplo 1
Ejemplo 2
Ejemplo 3
Sección H-35 e = 45 (cm)
5 Ф 22
5 Ф 22
5 Ф 22
e = 45 cm
5 Ф 22
Lat. 33+33 Ф 22
Lat. 16+16 Ф 22
410 cm
110 cm
C
εs
T
195 cm
270
o
εc
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M - Ф Hormigón confinado por usuario H-35 e =40 (cm)
c = 3.3 (m)
c = 3.1(m)
εc = 0.003
εs = 0.0039
Ф= 0.00097
Фy=0.00048
∆y=0.39
εc = 0.008
εc = 0.003
Pu = 2100 (tonf)
μ= 2.7
εc = 0.008
εs = 0.0091
Фu=0.00241
∆u=0.75
εs = 0.0039 < εy
Фu (1/m)
εs = 0.0091 > εy
0.00024
Cumple con la demanda
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Diseño según DS 60 considerando deformación elástica.
Pu/(Ag*Fc’)= 0.33
5φ22
5φ22
5φ22
5φ22
35 cm
Lat. 33+33 φ22
410 cm
Lat. 16+16φ22
110 cm
195 cm
La sección debe alcanzar el nivel de curvatura dado por:
b)
0.00061 [m-1]
83
Ejemplo 1
Acoplamiento
Ejemplo 2
Ejemplo 3
Diagrama de Interacción
7000
6000
5000
4000
3000
2000
1000
0
-10000
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
10000
-1000
-2000
-3000
Mu,Pu
φMn,φPn
φMn,φPn
Pn,Mn (fy=1.25 fy)
Pn,Mn (fy=1.25 fy)
84
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Curva M - Ф Hormigón confinado por usuario H-35 e =35 (cm)
Фy=0.0005
∆y=0.38
c = 3.8 (m)
c = 3.7 (m)
Pu = 2100 (tonf)
εc = 0.003
εs = 0.0027
Ф= 0.00081
εc = 0.008
εc = 0.003
μ= 2.5
εc = 0.008
εs = 0.0069
Фu=0.00211
∆u=0.64
εs = 0.0027 > εy
εs = 0.0069 > εy
Cumple con:
0.00061 [m-1]
Comparación entre el diseño original y DS 60
considerando deformación elástica
Diseño sin considerar
deformación elástica
δu=47cm
εc=1.9‰
εs=2.0‰
εc=3.0‰
εs=2.4‰
εc=2.6‰
εs=2.0‰
εc=3.0‰
εs=4.6‰
εc=8‰
Δu=87cm
εc=8‰ φu=0.00243[m-1]
Δu=80cm
φu=0.00192[m-1]
Diseño considerando la
deformación elástica
86
Acoplamiento
Ejemplo 1
Ejemplo 2
Ejemplo 3
Confinamiento
T φ10 a 10
2E+T φ12 a 10
Cuantía mínima:
Cuantía suministrada:
87
Confinamiento
88
Confinamiento
89
90
91