Potencia CA y Factor de Potencia: Guía Completa
Anuncio

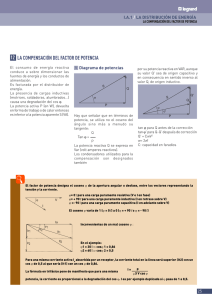
1.-POTENCIA EN CA Y FACTOR DE POTENCIA Solo para recordar, en un circuito resistivo puro en CC la Potencia es P=VI En corriente alterna la potencia consumida por una carga, depende de su naturaleza y más concretamente del desfase que provoque dicha carga entre la tensión y la corriente que circula por el circuito. Si la carga es resistiva pura, la tensión y la corriente están en fase, en este caso la potencia es siempre de signo positivo (ya que tensión y corriente tienen el mismo signo en cada instante) y su valor es el producto de los valores eficaces de la tensión por la corriente. Si la tensión y la corriente no están en fase (debido a que la carga no es resistiva pura), habrá momentos en los que tengan distinto signo, por ello la potencia será menor que en el caso anterior. La potencia en este caso es igual al producto de la tensión por la corriente eficaces multiplicados por un factor reductor llamado factor de potencia o cos Ø (coseno del ángulo que forman la tensión y la corriente en un circuito ). Éste, que siempre es menor o igual a la unidad, representa la relación entre la potencia entregada a la carga y la potencia consumida (y por tanto aprovechada) por la misma. Cuanto más pequeño sea el factor de potencia menor será la potencia aprovechada. 1.1.-La potencia efectiva o activa P (es la que se aprovecha como trabajo) se mide en Watt (W), y se obtiene: P=VICos Ø (W) 1.2.-La potencia aparente (S) es la que circula por los conductores y se mide en volt-amperes [VA]. Se obtiene S= VI (VA) 1.3.-La potencia reactiva (Q) es una potencia que no es consumida por la carga sino que está continuamente circulando entre la carga y el generador. Provoca pérdidas al hacer circular más corriente de la necesaria por los conductores y hace que deban Sobredimensiona se. Se mide en voltamper reactivos [Var]. Q=VISen Ø (Var) 2.-MEDICIÓN DE POTENCIAS MONOFASICAS Cuando se debe medir potencia una de las consideraciones es el tipo de circuito, Monofásico o 3F y de ahí los instrumentos necesarios para realizar dicho procedimiento, por esto las analizaremos por separado. Para medir potencia activa (efectiva) en circuitos monofásicos se utilizan: -Wattmetros -Pinzas amperimetricas que miden potencia -Analizadores de redes electricas. Básicamente se deben medir el Vac y la Iac, como se muestra en la siguiente imagen. Son ejemplos de tenazas que miden Potencia. Fp: a) Tenaza TES 3060 (Power Clamp Meter) http://www.itm.com/pdfs/cache/www.itm.com/tes/power_quality_analyzer/tes_3600/manual/tes_tes_3600_power_quality_analyzer_manu al.pdf b) Tenaza Metrel 9240 (Power Clamp Meter) https://www.metrel.si/en/shop/DMM/clamp-meters/md-9240.html 3.-MEDICIÓN DE POTENCIA TRIFÁSICA. Como se observa en la imagen, para medir la potencia que consume un Sistema 3F desequilibrado (también se puede aplicar este método en un sist. 3F equilibrado), en c/u de las fases se puede: a) Medir la Iac (en serie) de una fase, medir el Vac (en paralelo) y el cos Φ de la misma fase, con las lecturas se debe clacular la P, recordar que P=VICos Ø (W) b) Medir directamente la P usando Wattmetro (se debe medir en las 3 fases), este instrumento entrega la P, sin necesidad de hacer cálculos. Como se observa, en la imagen superior el Wattmetro mide Iac y Vac. c) Usar un Analizador de Potencia, el cuál se conecta como se muestra en la figura siguiente, las tres tenazas miden la Iac de c/u de las fases y las pinzas se mide el Vac (entre Linea y Neutro (Vln)). Este instrumento entrega P, Q, S, Fp, Thd, gráficos, entre otros. Además se puede registrar mediciones en memoria o enviarlas al PC. 2.-FACTOR DE POTENCIA (Fp) • El factor de potencia se define como el cociente de la relación de la potencia activa entre la potencia aparente; esto es: Fp = P / S o Fp = Cos Ø • Comúnmente, el factor de potencia es un término utilizado para describir la cantidad de energía eléctrica que se ha convertido en trabajo. Y es adimencional. El valor ideal del factor de potencia es 1, esto indica que toda la energía consumida por los aparatos ha sido transformada en trabajo. • Por el contrario, un factor de potencia menor a la unidad significa un mayor consumo de energía necesaria para producir un trabajo útil. 4.-TRIÁNGULO DE POTENCIA Es un triángulo rectágulo que relaciona las 3 potencias de un circuito, entregando información como el Fp, el ángulo de desface Φ (entre el V e I) y la carácteristica del circuito (inductivo o capacitivo). Del triángulo se observa: a)Cos Φ = P / S b) Como sabemos FP= P / S Por lo tanto: FP= Cos Φ c) S2 = P2 + Q2 d)Si de: Cos Φ = P / S despejamos Φ, tenemos Φ = Cos-1 (P / S) El ángulo Φ, indica si el Vca y la Ica se encuentran en face o desfazadas Dependiendo del tipo de carga, el Fp puede ser: Carga Resistiva pura en CA Vca e Ica están en face Ø = 0° Fp = Cos 0 = 1 Carga Inductiva en CA La Ica atrasa en Ø° al Vca 0 < Ø < -90° 0 < Fp < 1 en atraso Carga Capacitiva en CA La Ica adelanta en Ø° al Vca 0 < Ø < +90° 0 < Fp < 1 en adelanto Cosenofímetro análogo de panel: notar que oscila entre 0 y 1, indicando si el F pes Capacitivo o Inductivo. Si estamos en un circuito en el que la tensión y la intensidad van desfasadas un determinado ángulo el diagrama quedará de otra forma. Por ejemplo, supongamos un circuito inductivo en el que la intensidad va retrasada un cierto ángulo j respecto de la tensión. Vemos que no se aprovecha toda la potencia que se absorbe de la red (potencia aparente). Parte de la potencia se aprovecha y es positiva (potencia activa) y parte no se aprovecha y es negativa (potencia reactiva). COMO CONCLUSIÓN: a) Mientras más inductivo es un circuito, mayor es el desface (φ), mayor en la Q y la S, pero menor es el FP (cos φ) b) Si un circuito es exclusivamente Resistivo, la P=S y Q=0, por lo tanto, φ=0 y el Fp es 1. a)EN LAS CARGAS RESISTIVAS: • En las cargas • Por lo tanto, Fp = Cos 0 • En este caso, se tiene un factor de potencia unitario resistivas como las lámparas incandescentes, el voltaje y la corriente están en fase. b)EN LAS CARGAS INDUCTIVAS: • En las cargas inductivas como los motores y transformadores, respecto al voltaje. • Por lo tanto, 0 < Fp < 1 en atraso • En este caso se tiene un factor de potencia en atraso. la corriente se encuentra retrasada c)EN LAS CARGAS CAPACITIVAS: • En las cargas capacitivas como los condensadores, la corriente se encuentra adelantada respecto al voltaje. • Por lo tanto, 0 < Fp < 1 • En este caso se tiene un factor de potencia adelanto . d)DIAGRAMA FASORIALES DEL VOLTAJE Y LA CORRIENTE SEGÚN EL TIPO DE CARGA: Carga Resistiva pura en CA Vca e Ica están en face Ø = 0° Carga Inductiva pura en CA La Ica atrasa en Ø° al Vca Ø = -90° Carga Capacitiva pura en CA La Ica adelanta en Ø° al Vca Ø = +90° e)EL BAJO FACTOR DE POTENCIA: Causas: • • Para producir un trabajo, las cargas eléctricas requieren de un cierto consumo de energía. Cuando este consumo es en su mayoría energía reactiva, el valor del ángulo disminuye el factor de potencia Factor de potencia VS ángulo de desface Ø Ø 0 FP=Cos Ø 1 30 0.866 60 80 0.5 90 0,173 0 se incrementa y 5.-GUIA DE EJERCICIOS 6.-PROBLEMAS POR EL Fp a)Problemas técnicos por el Fp: • Mayor consumo de corriente. • Aumento de las pérdidas en conductores. • Sobrecarga de transformadores, generadores y líneas de distribución. • Incremento de las caídas de voltaje. Pérdidas en un conductor VS factor de potencia kW 9 6 3 0 FP 1 0.9 0.8 0.7 0.6 0.5 0.4 b)Problemas económicos: • Incremento de la facturación eléctrica por mayor consumo de corriente. • Penalización de hasta un 120 % del costo de la facturación. 7.-BENEFICIOS AL CORREGIR EL Fp a)Beneficios en los equipos: • Disminución de las pérdidas en conductores. • Reducción de las caídas de tensión. • Aumento de la disponibilidad de potencia de transformadores, líneas y generadores. • Incremento de la vida útil de las instalaciones. b)Beneficios económicos: • Reducción de los • Eliminación del cargo por bajo factor de potencia. costos por facturación Eléctrica. • Bonificación de hasta un 2.5 % de la facturación cuando se tenga factor de potencia mayor a 0.9 8.-COMPENSANCIÓN DEL Fp • Las cargas inductivas requieren potencia reactiva para su funcionamiento. • Esta demanda de reactivos se puede reducir e incluso anular si se colocan capacitores en paralelo con la carga. • Cuando se reduce la potencia reactiva, se mejora el factor de potencia. P 2 Q 1 S2 S1 QL QC En la figura anterior se tiene: QL es la potencia reactiva producto de las cargas inductivas y S1 es la potencia aparente que se demanda product de QL Qc es la potencia reactiva producto de las cargas Capacitivas y que se resta a QL, compensa La compensación de Qc no afecta el consume de potencia efectiva, es decir, P permanence constante. Como efecto del empleo de los capacitores, el valor del ángulo 1, se reduce al ángulo 2 Producto de la compensación, la potencia aparente S1 también se reduce a S2 Como lo analizamos, al reducir el ángulo de desface, esto aumenta (mejora) el Fp TAREA: RECUERDE DESCARGAR EL SOFTWARE DE SIMULACIÓN GRATUITO “CADESIMU” PREGUNTAS DE AMPLIACIÓN: 1.- De acuerdo, a la norma Eléctrica en Chile ¿Cuál es el Factor de Potencia a partir del cual se multa a las empresas? 2.- ¿Por Qué se usa un banco de condensadores para mejorar el factor de Potencia? 1. 2. 3. Corriente total Corriente activa Motor de inducción sin compensación Corriente reactiva Corriente activa Motor de inducción con capacitores de compensación Corriente total Corriente reactiva Capacitores MÉTODOS DE COMPENSACIÓN Son tres los tipos de compensación en paralelo más empleados: a) Compensación individual b) Compensación en grupo c) Compensación central A) COMPENSACIÓN INDIVIDUAL Aplicaciones y ventajas • Los capacitores son instalados por cada carga inductiva. • El arrancador para el motor sirve como un interruptor para el capacitor. • El uso de un arrancador proporciona control semiautomático para los capacitores. • Los capacitores son puestos en servicio sólo cuando el motor está trabajando. Desventajas • El costo de varios capacitores por separado es mayor que el de un capacitor individual de valor equivalente. • Existe subutilización para aquellos capacitores que no son usados con frecuencia. DIAGRAMA DE CONEXIÓN arrancador M C B) COMPENSACIÓN EN GRUPO Aplicaciones y ventajas • Se utiliza cuando se tiene un grupo de cargas inductivas de igual potencia y que operan simultáneamente. • La compensación se hace por medio de un banco de capacitores en común. • Los bancos de capacitores pueden ser instalados en el centro de control de motores. Desventajas • La sobrecarga no se reduce en las líneas de alimentación principales Diagrama de conexión arrancador M arrancador M C C) COMPENSACIÓN CENTRAL Características y ventajas • • • Es la solución más general para corregir el factor de potencia. El banco de capacitores se conecta en la acometida de la instalación. Es de fácil supervisión. Desventajas • Se requiere de un regulador automático del banco para compensar según las necesidades de cada momento. • La sobrecarga no se reduce en la fuente principal ni en las líneas de distribución. Diagrama de conexión C Cálculo de los kVARs del capacitor (1/2) • De la figura siguiente se tiene: Qc P QL Q • Como: Q Qc 1 P *Tan P(Tan • Por facilidad, Qc Q 2 P*K S2 S1 1 Tan 2 ) QL QC Cálculo de los kVARs del capacitor (2/2): Coeficiente K FP actual 0.3 0.4 0.5 0.6 0.7 0.8 0.9 FP d e s e a d o 0.8 0.85 2.43 2.56 1.541 1.672 0.982 1.112 0.583 0.714 0.27 0.4 0.13 0.9 2.695 1.807 1.248 0.849 0.536 0.266 0.95 2.851 1.963 1.403 1.005 0.692 0.421 0.156 1 3.18 2.291 1.732 1.333 1.02 0.75 0.484 Ejemplo • Se tiene un motor trifásico de 20 kW operando a 440 V, con un factor de potencia de 0.7, si la energía se entrega a través de un alimentador con una resistencia total de 0.166 Ohms calcular: • a) La potencia aparente y el consumo de corriente • b) Las pérdidas en el cable alimentador • c) La potencia en kVAR del capacitor que es necesario para corregir el F.P. a 0.9 • d) Repetir los incisos a) y b) para el nuevo factor de potencia • e) La energía anual ahorrada en el alimentador si el motor opera 600 h/mes Solución (1/3) a) La corriente y la potencia aparente I P 3 *V * Cos S S1 3 *V * I 3 * 440V * 37.49 A P 3 *V * FP I1 28.571 _ kVA b) Las pérdidas en el alimentador Perd 3* R * I 2 Perd1 3* 0.166 * 37.49 2 700 _ W 20,000W 3 * 440V * 0.7 37.49 _ A Solución (2/3) c) Los kVAR del capacitor Nos referimos a la tabla del coeficiente “K” y se escoge el valor que está dado por el valor actual del FP y el valor deseado: QC P*K QC 20kW * 0.536 10.72 _ kVAR d.1) La corriente y la potencia aparente I2 S2 20,000W 3 * 440V * 0.9 3 * 440V * 29.16 A 29.16 _ A 22.22 _ kVA Solución (3/3) d.2) Las pérdidas en el alimentador Perd 2 3 * 0.166 * 29.16 2 423.45 _ W e) Energía anual ahorrada • La reducción de las pérdidas: P • Perd2 P 700 423.45 276.55 _ W La energía ahorrada al año: E • Perd1 P * hrs / mes *12 _ meses 1000 E 276.55W * 600h / mes *12meses 1000 1990.8 _ kWh Considerando a $ 0.122 por kWh, se tienen $ 242.88 de ahorro tan sólo en el alimentador Ejemplo corrección factor de potencia Mes Enero Febrero Marzo Abril Mayo Junio Julio Agosto septiembre Octubre Noviembre Diciembre Demanda Factor de (kW) potencia FP 315 294 293 298 326 328 322 329 326 333 321 321 0.8888 0.7894 0.8583 0.9249 0.9321 0.9218 0.8898 0.9021 0.8237 0.8893 0.8930 0.9044 0.90 Potencia Reactiva (kVAR) requeridos para elevar el FP a: 0.92 0.94 0.96 0.98 12 103 40 -26 -37 -25 11 -2 79 12 8 -5 34 123 60 -5 -15 -2 33 21 102 35 30 17 57 145 82 17 10 22 57 45 126 60 54 42 84 170 107 42 38 50 85 73 154 88 81 69 117 201 138 74 72 85 119 108 188 123 115 103 FP promedio = 0.8848 Calcular porcentaje de bonificación con un FP deseado de 0.98 1.00 193 272 208 146 151 164 197 187 267 204 193 180 Potencia reactiva (kVAR) Potencia aparente (kVA) Potencia reactiva (kVAR) Potencia activa (kW) tg 1 kVAR kW tg FP Cos kVAR kW Cos 1 FP Potencia reactiva: kVAR kW * tg kVAR kW * tg Cos 1 FP Compensación del FP Potencia reactiva requerida Potencia reactiva requerida para elevar el FP1 a un FP2 kVAR kW tg cos 1 FP1 tg cos 1 FP2 Corrección de potencia reactiva debida al voltaje kVAR totales V kVAR 2 V1 2 V1 = Voltaje de línea V2 = Voltaje de diseño banco de capacitores Ejemplo: Compensación del FP Datos: Dem anda (k W ) 315 F a c t o r d e p o t e n c ia A c tu a l (F P 1) D e s e a d o (F P 2) 0 .8 8 8 8 0 .9 6 0 0 V1 = 440 Volts (voltaje de línea) V2 = 480 Volts (voltaje de diseño banco de capacitores) Potencia reactiva requerida kVAR 315 tg cos 1 0.8888 tg cos 1 0.9600 Corrección de potencia reactiva debida al voltaje kVAR 71 totales 440 2 84 71 Ejemplo: Compensación del FP 480 Ejemplo: Compensación del FP Calculo del porcentaje de penalización con un factor de potencia promedio anual de 0.8848 3 Penalización (%) 0.9 5 100 1.1 1 0.8848 Calculo del porcentaje de bonificación por mejorar el FP a 0.98 Bonificación (%) 1 4 1 0.9 0.9800 100 2.1% Nota: Los cargos o bonificaciones económicas se determinan al multiplicar la suma de los cargos por demanda y consumo de energía, multiplicados por los porcentajes de penalización o bonificación, según sea el caso Consideraciones del FP (1) • Cargos y bonificaciones máximas FP = 0.30 Penalización máxima 120% FP = 1.00 Bonificación máxima 2.5% • Compensación individual de transformadores – De acuerdo con las normas técnicas para instalaciones eléctricas, la potencia reactiva (kVAR) de los capacitores, no debe exceder al 10% de la potencia nominal del transformador Consideraciones del FP (2) • Compensación individual de motores – Generalmente no se aplica para motores menores a 10 KW – Rango del capacitor • En base a tablas con valores normalizados, o bien, • multiplicar los hp del motor por 1/3 • el 40% de la potencia en kW Bancos automáticos de capacitores (1) • Cuenta con un regulador de VARS que mantiene el FP prefijado, ya sea mediante la conexión o desconexión de capacitores conforme sea necesario • Pueden suministrar potencia reactiva de acuerdo a los siguientes requerimientos: – constantes – variables – instantáneos • Se evitan sobrevoltajes en el sistema Bancos automáticos de capacitores (2) • Elementos de los bancos automáticos: – Capacitores fijos en diferentes cantidades y potencias reactivas (kVAR) – Relevador de factor de potencia – Contactores – Fusibles limitadores de corriente – Interruptor ternomagnético general • Los bancos de capacitores pueden ser fabricados en cualquier No. De pasos hasta 27 (pasos estandar 5,7,11 y 15) Bancos automáticos de capacitores (3) • El valor de los capacitores fijos depende del No. De pasos previamente seleccionado, así como, de la cantidad necesaria en kVAR’s para compensar el FP a 1.0 • A mayor No. de pasos, el ajuste es más fino, dado que cada paso del capacitor es más pequeño, permitiendo lograr un valor más cercano a 1.0, no obstante ocasiona un mayor costo • La conmutación de los contactores y sus capacitores individuales es controlada por un regulador (vármetro) Esquema de un banco automático de capacitores