Mecánica teórica
Anuncio
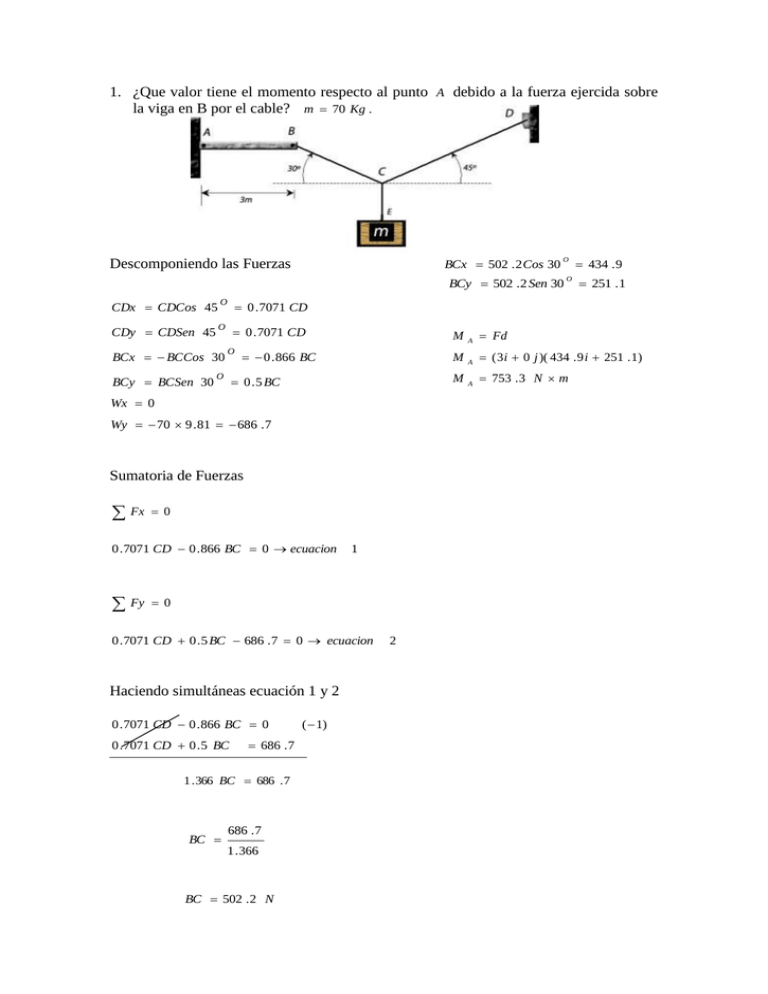
1. ¿Que valor tiene el momento respecto al punto A debido a la fuerza ejercida sobre la viga en B por el cable? m 70 Kg . BCx 502 . 2 Cos 30 Descomponiendo las Fuerzas O BCy 502 . 2 Sen 30 CDx CDCos 45 O 0 . 7071 CD CDy CDSen 45 O 0 . 7071 CD BCx BCCos 30 BCy BCSen 30 O O 0 . 866 BC 0 . 5 BC Wx 0 Wy 70 9 . 81 686 . 7 Sumatoria de Fuerzas Fx 0 0 . 7071 CD 0 . 866 BC 0 ecuacion Fy 1 0 0 . 7071 CD 0 . 5 BC 686 . 7 0 ecuacion Haciendo simultáneas ecuación 1 y 2 0 . 7071 CD 0 . 866 BC 0 0 . 7071 CD 0 . 5 BC 686 . 7 1 . 366 BC 686 . 7 BC 686 . 7 1 . 366 BC 502 . 2 N ( 1) 2 O 434 . 9 251 . 1 M A Fd M A ( 3 i 0 j )( 434 . 9 i 251 . 1) M A 753 . 3 N m 2. En la figura los cables AB y AC se extienden del punto A sobre el piso a los puntos B y C en la s paredes, la tensión en el cable AB es de 10 KN y la tensión en el cable AC es de 20 KN ¿Que valor tiene el momento con respecto al punto 0 debido a las fuerzas ejercidas sobre A por los cables? 1) r 4 i 0 j 6k 4i 6 j 2 k 2 ) FAB 10 7 . 48 FAB 5 . 3475 i 8 . 0213 j 2 . 6737 k 2i 3 j 6 k FAC 20 7 FAC 5 . 71 i 8 . 5714 j 17 . 14 k 3 ) Mo ( r FAB ) ( r FAC ) Mo i j k 4 0 6 5 . 35 8 . 02 2 . 67 i j k 4 0 6 5 . 71 8 . 57 17 . 14 Mo ( 99 . 54 i 60 . 04 j 66 . 36 k ) KN m 99 . 54 i 60 . 04 j 66 . 36 k 3. La tensión en el cable AB mostrada es de 2 KN . ¿Cual es la magnitud del momento respecto al árbol CD debido a la fuerza ejercida por el cable en A ? 1) CD 0i 2 j 0 k 0i 1 j 0 k 2 2) 3) r 3i 0 j 0 k 0 i 2 j 1k F 2 2 . 236 F 0 i 1 . 79 j . 8944 k 4) 0i MCD 3 0 1j 0k 0 0 1 . 79 . 8949 MCD 2 . 6847 j KN m 2 . 6847 j 4. La tensión en el cable mostrado es de 1 KN . Determínese el momento con respecto al eje X debido a la fuerza ejercida sobre la compuerta por el cable en el punto B . ` 1) r 0 i 0 j 0 .6 k 0 .6 i 0 .3 j 0 .6 k 666 . 66 i 333 . 33 j 666 . 66 k 0 .9 2) F 1000 3) Mx i j k 0 0 0 .6 666 . 66 333 . 33 666 . 66 Mx ( 200 i 333 . 33 j ) N m 200 i 333 . 33 j 5. Se aplica una fuerza de 20 lbs . A la barra de control AB inclinada. Si se sabe que la longitud de la barra es de 9 ft y que 25 O , determínese el momento de la fuerza con respecto al punto B . 1) r BA 9 Cos 60 O 9 Sen 60 O r 9 . 80 i 8 . 15 j 2 ) F 20 Cos 25 i 20 Sen 25 O O j F 18 . 126 i 8 . 45 j 3 ) MB r F MB 3 . 8 i 8 . 15 j 18 . 126 i 8 . 45 j MB 115 . 6 lb ft 6.-Se aplica una fuerza de 300 N en punto A como se muestra. Determinar: a) El momento de la fuerza de 300 N con respecto al punto D . b) La fuerza mínima aplicada en B que producirá el mismo momento con respecto al punto D . b) 2 r ( 0 .2 ) ( 0 .2 ) F ? 1) r ( 0 . 1m ) i ( 0 . 2 m ) j MD r F F MD r 41 . 70 . 2828 F 147 . 4 N 2 ) F 300 Cos 25 i 300 Sen 25 O O j F 271 . 9 i 126 . 8 j 3) MD r F MD 0 . 1i 0 . 2 j 271 . 9 i 126 . 8 j MD 41 . 7 N m (a (b 2 7. Sobre la ménsula ABC se aplica una fuerza de 200 N como se indica. Determinar el momento de la fuerza con respecto al punto A . 1) r C A ( 0 . 06 m ) i ( 0 . 075 ) j 0 k 2) F 0 i 200 Cos 30 Ni 200 Cos 60 Nk O O F 0 i 173 . 2 Nj 100 Nk 3) i MA 0 . 06 0 j k 0 . 075 0 173 . 2 100 7 . 5 i 6 j 10 . 38 k MA 7 . 5 N mi 6 N mj 10 . 39 N mk 8. Se emplean 3 cables par sostener un recipiente en la forma indicada. Determínese el ángulo formado por los cables y AD . 1) AB 56 i 90 j 0 k AD 52 i 90 j 18 k 2) AB AB ( AB )( AD ) Cos BAD Cos BAD Cos BAD Cos BAD ( AB ) ( AD ) ( AB ) ( AD ) ( 56 i 90 j 0 k ) ( 52 i 90 j 36 k ) 56 ) 2 ( 90 2 52 56 90 90 106 110 BAD arcCos 5188 11660 =63.58º 52 ) 2 ( 90 ) ( 36 2 2 9. Una sola fuerza P actúa en C en dirección perpendicular al asa BC de la manivela mostrada. Determínese el momento Mx de P con respecto al eje X cuando θ = 65º, si se sabe que My = -15 NM y Mz = -36 NM. 1) rc 0 . 25 m i 0 . 2 m Sen j 0 . 2 m Cos k 2) P P cos j PCos k 3) i j k 0 . 2 Sen 0 . 2 Cos . PSen PCos Mo rc P 0 . 25 0 Mx 0 . 2 m PSen ( ) ecuacion 1 My 0 . 25 m PCos ecuacion 2 Mz 0 . 25 m PSen ecuacion 3 Tag Tratando simultaneas 2 y 3; se obtiene que Mz ecuacion My Sumando el cuadrado de 2 y 3 My 2 Mz P 4 m 2 0 . 25 P Cos 0 . 25 P Sen 1 My 2 2 2 Mz 2 2 2 ecuacion Sustituyendo My 15 N m Tag 36 15 67 . 38 P 4 2 2 5 Mz 36 N m y 2 . 40 O 15 2 . 36 2 156 N Sustituyendo en 1 los valores obtenidos Mx 0 . 2 m 156 N Sen 65 O 67 . 68 O 23 N m en 4 y 5 4 10. El armazón ACD esta articulado en A y en D y sostenido por un cable que pasa por un arco en B fijo a unos ganchos en G y H. Sabiendo que la tensión en el cable es de 1125 N. Determínese el momento con respecto a la diagonal AD de la fuerza ejercida sobre la armazón por la porción BH del cable. 1) AD AD 0 .8i 0 j 0 .6 k AD 0 .8i 0 j 0 .6 k 1 2) rB A 0 .4 i 0 j 0 k 3) FB BH FB BH BH 1125 N 0 .3i 0 .6 j 0 .6 k 0 .9 F BH 375 N i 750 N j 750 N k 4) 0 .8i M AD 0 .4 375 M AD 0j 0 .6 k 0 0 750 750 180 N m 180 N m 1125 N 11.-Una fuerza F 100 i 40 j 20 k N actúa en la parte media del mango BC de la manivela. Determínese los momentos: Mo , M B y M manivela esta en la posición mostrada. Con Respecto en el punto 0 1) r 0 i 0 .4 j 0 .4 k 2) F 100 i 40 j 20 k N 3) MO i j 0 .4 100 40 k 0 . 4 24 i 40 j 40 k 20 Con Respecto en el punto A 1) r 0 i 0 . 4 j 0 . 1k 2) F 100 i 40 j 20 k N 3) MO i j 0 .4 100 40 k 0 . 1 12 i 10 j 40 k 20 Con Respecto en el punto B 1) r 0 i 0 j 0 . 1k 2) F 100 i 40 j 20 k N 3) MO i j 0 .0 100 40 k 0 . 1 4 i 10 j 0 k 20 A de la fuerza cuando la 12. ¿Que valor tiene el momento de la fuerza F mostrada en la figura, con respecto a la barra BC? 1) 0i 4 j 3k 0 i 0 .8 j 0 .6 k 5 BC 2) r 4 i 2 j 5k 3) F 2 i 6 j 3k 4) M BC 0i 0 .8 j 0 .6 4 2 5 2 6 3 14 . 4 k 8 j 2 . 4 k 9 . 6 j M BC 1 . 6 j 16 . 8 k KN m