Método Simplex: Resolución de problema de programación lineal
Anuncio
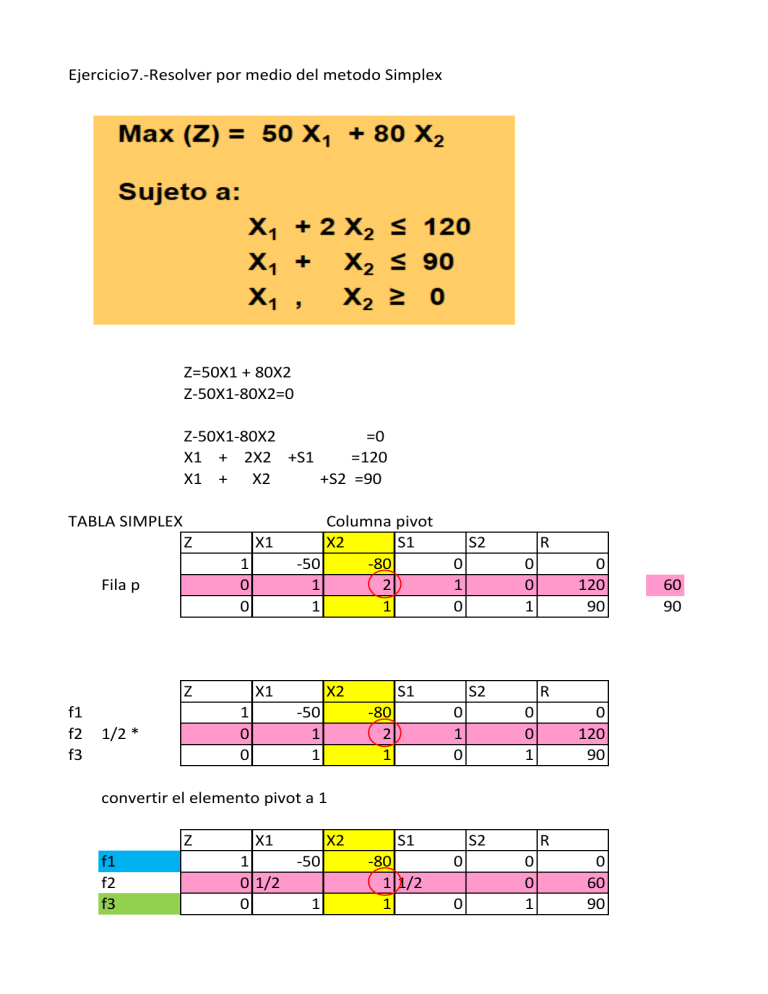
Ejercicio7.-Resolver por medio del metodo Simplex Z=50X1 + 80X2 Z-50X1-80X2=0 Z-50X1-80X2 =0 X1 + 2X2 +S1 =120 X1 + X2 +S2 =90 TABLA SIMPLEX Z X1 1 0 0 Fila p Z f1 f2 f3 X1 1 0 0 1/2 * Columna pivot X2 S1 -50 -80 1 2 1 1 X2 -50 1 1 S2 0 1 0 S1 -80 2 1 R 0 0 1 S2 0 1 0 0 120 90 R 0 0 1 0 120 90 convertir el elemento pivot a 1 Z f1 f2 f3 X1 1 -50 0 1/2 0 1 X2 S1 -80 1 1/2 1 S2 0 0 R 0 0 1 0 60 90 60 90 f1 f3 80*f2= f1= suma 0 1 1 80*f2+f1 = origen a la f1 40 80 40 0 -50 -80 0 0 -10 0 40 0 4800 0 4800 -1f2+f3=origen a la fila f3 -1 -1/2 0 1 1 0 1 0 -1/2 1 -60 90 30 -1*f2= f3= suma 0 -1/2 0 0 1/2 Nueva matriz Z f1 f2 f3 columna pivot X1 X2 1 -10 0 1/2 0 1/2 S1 S2 0 40 1 1/2 0 -1/2 R 0 0 1 4800 60 30 f1 f2 f3 fila vipot Z X1 X2 1 -10 0 1/2 0 1/2 f1 f2 f3 Convertir el elemento pivot en 1, multiplivando a f3 por 2 Z X1 X2 S1 S2 R 1 -10 0 40 0 4800 0 1/2 1 1/2 0 60 0 1 0 -1 2 60 S1 0 40 1 1/2 0 -1/2 S2 R 0 0 1 4800 60 30 Convertimos los elementos de f1 y f2 de la columna pivot en ceros 10*f3+f1= da origen f1 f1 10*f3= f1= Suma= f2 -1/2*f3 f2 Suma= 0 1 1 10 0 -10 -10 0 40 0 0 30 -1/2*f3+f2= da origen a la f2 0 -1/2 0 1/2 0 1/2 1 1/2 0 0 1 1 20 0 20 600 4800 5400 -1 0 -1 -30 60 30 120 60 Nueva tabla simplex Z X1 f1 1 f2 0 f3 0 Deducir mi solucion: Z= 5400 X1= 60 X2= 30 X2 0 0 1 S1 0 1 0 S2 30 1 -1 R 20 -1 2 5400 30 60