Sistemas electricos lineales 2 Funcion de transferencia 3D

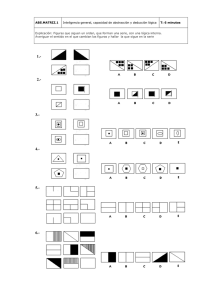
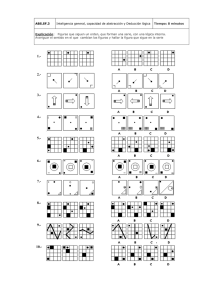
Primera actividad evaluada
GRAFICO DE FUNCION DE TRANSFERENCIA (H(S)-JW-SIGMA)
Rodrigo Salvador Martinez Ortiz | SEL2 | 25 de agosto 2020
1. Función de transferencia
En la tarea previa se pidió encontrar la función de transferencia de un circuito, la cual la
definimos como:
𝐻(𝑆) =
𝑉(𝑠) 10 ∗ 𝑠 2 + 50 ∗ 𝑠 + 60
=
𝐼𝑖(𝑠)
𝑠 2 + 8 ∗ 𝑠 + 10
Ecuación 1. función de transferencia a analizar
La cual consta de:
Polos: 𝑆 = −3 , 𝑠 = −2, Ceros: 𝑆 = −(√6 + 4) , 𝑠 = (√6 − 4)
A partir de la función de transferencia encontrada se puede determinar un gráfico para el
análisis de los polos y ceros, el cual se representa en dos dimensiones. Entonces tomaríamos
nuestro plano Z = 𝜎 + 𝜔𝑗, donde sigma representa la parte real y omega representa la parte
imaginaria del plano, este comúnmente se le conoce como diagrama de Argand.
Figura 1. Diagrama de Argand
Con base a esto podemos hacer un análisis análogo incluyendo la magnitud de la función
de transferencia. Gracias a la tarea anterior se determinó la magnitud previamente:
𝑎𝑏𝑠(𝐻(𝑆)) =
10 ∗ √𝑤 4 + 13 ∗ 𝑤 2 + 36
√𝑤 4 + 44 ∗ 𝑤 2 + 100
Ecuación 2. Magnitud de la función de transferencia.
Si replicamos este proceso en Matlab, bastaría con añadir las siguientes líneas de código
para encontrar la magnitud.
b= [10 50 60]; %Numerador de la FT
a= [1 8 10]; %Denominador de la FT
[r,im]=meshgrid(-4:1/10:4);
z=r+(im)*j;
modT=abs(polyval(b,z)./polyval(a,z)); %Magnitud de la TF
PAGE 1
2. Gráfico abs[H(S)]-JW-SIGMA.
A partir de la malla creada con la función meshgrid podemos añadir unas cuantas líneas
extras que nos permitirán ver la figura.
2.1. Push button [Mostrar FT]
%Al pulsar ‘Mostrar FT se ejecuta lo siguiente
b= str2num(get(handles.edit3,'String')); % Extrae de edit 3 (Num)
a= str2num(get(handles.edit4,'String'));% Extrae de edit 4 (Den)
syms s
TFnum= b(1,1)*s^2+ b(1,2)*s+ b(1,3);
TFden= a(1,1)*s^2+ a(1,2)*s+ a(1,3);
TF= TFnum/TFden ;
set(handles.edit1,'String',char(TF)); % Muestra la FT en edit1
2.2. Push button [Desplegar grafica]
%Al pulsar ‘Desplegar graficas se ejecuta lo siguiente’
b= str2num(get(handles.edit3,'String')); %Numerador de la FT
a= str2num(get(handles.edit4,'String')); %Denominador de la FT
[r,im]=meshgrid(-4:1/10:4);
z=r+(im)*j;
modT=abs(polyval(b,z)./polyval(a,z));
meshc(handles.axes1,r,im,modT);
title(handles.axes1,'Grafico de la funcion de transferencia')
grid on
grid minor
zlabel(handles.axes1,'Magnitud\bf')
ylabel(handles.axes1,'\fontsize{15}\bf\omega\fontsize{10}(Parte
imaginaria)')
xlabel(handles.axes1,'\fontsize{15}\bf\sigma \fontsize{10}(Parte
real)')
2.3. Zoom y rotación 3D [Group button]
Zoom button
Rotación 3D button
valor0=get(hObject,'Value');
if valor0==1
zoom on
else
zoom off
end
valor=get(hObject,'Value');
if valor==1
rotate3d on
else
rotate3d off
end
PAGE 2
2.4. Resultados
En principio la interfaz grafica nos muestra una vista general de la funcion de transferencia,
donde al ejecutar los botones despliega la siguiente pantalla.
Figura 2. Vista general del grafico abs[H(S)]-JW-SIGMA.
Si en la interfaz seleccionamos rotación 3D podemos apreciar desde una vista inferior cómo
se comporta los polos y ceros de la función de transferencia:
Figura 3. Vista lateral del grafico abs[H(S)]-JW-SIGMA.
PAGE 3
Además, si colocamos con rotación 3d una vista superior y luego colocamos zoom podremos
aprecias los puntos de interés de nuestros polos y ceros, los cuales son los sectores huecos
del plano, tanto desde una vista superior como una vista desde inferior
Figura 4. Vista superior del grafico abs[H(S)]-JW-SIGMA.
Figura 4. Vista inferior del grafico abs[H(S)]-JW-SIGMA.
PAGE 4