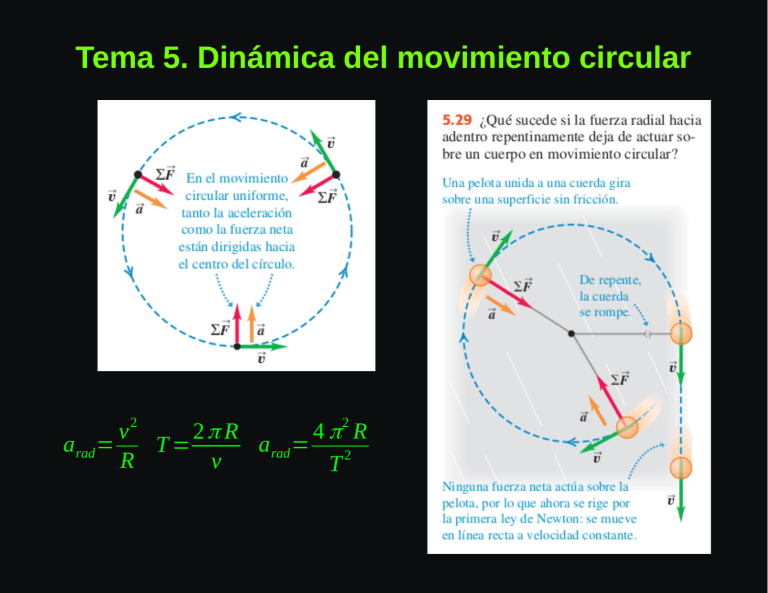
Tema 5. Dinámica del movimiento circular 2 2 2π R 4π R v a rad = a rad = 2 T= R v T Fuerza en el movimiento circular uniforme v2 F neta =marad =m R Ejemplo 1. Un trineo con masa de 25 kg descansa en una plataforma horizontal de hielo prácticamente sin fricción. Está unido a un poste clavado en el hielo con una cuerda de 5 m. Una vez que se le da un empujón, el trineo da vueltas uniformemente alrededor del poste. Si el trineo efectúa cinco revoluciones completas cada minuto, calcule la fuerza F que la cuerda ejerce sobre él. Ejemplo 2. Péndulo cónico. Un inventor propone fabricar un reloj de péndulo usando una lenteja de masa m en el extremo de un alambre delgado de longitud L. En vez de oscilar, la lenteja se mueve en un círculo horizontal con rapidez constante v, con el alambre formando un ángulo constante β con la vertical. Este sistema se conoce como péndulo cónico porque el alambre suspendido forma un cono. Calcule la fuerza de tensión F en el alambre y el periodo T en términos de β. Ejemplo 3. Recorrido en una curva plana. Un automóvil deportivo va por una curva sin peralte de radio R. Si el coeficiente de fricción estática entre los neumáticos y la carretera es µs, ¿cuál es la rapidez máxima vmáx con la que el conductor puede tomarse la curva sin derrapar? Ejemplo 4. Recorrido en una curva peraltada Para un automóvil que viaja a cierta rapidez, es posible peraltar una curva con un ángulo tal que los autos que viajan con cierta rapidez no necesiten fricción para mantener el radio con que dan vuelta. El auto podría tomar la curva aun sobre hielo húmedo. Un ingeniero propone reconstruir la curva del ejemplo anterior de modo que un auto con rapidez v pueda dar la vuelta sin peligro aunque no haya fricción ¿Qué ángulo de peralte β debería tener la curva? Ejemplo 5. Un Un pasajero en una rueda de la fortuna se mueve en un círculo vertical de radio R con rapidez constante v. El asiento permanece vertical durante su movimiento. Deduzca expresiones para la fuerza que el asiento ejerce sobre el pasajero en la parte superior e inferior del círculo.