3. Movimiento Armónico

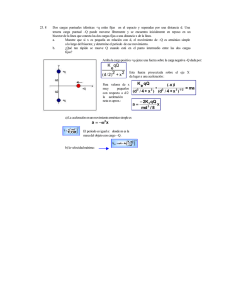
ASIMOV
-1-
MOVIMIENTO
ARMÓNICO.
Mov Armónico
ASIMOV
-2-
Mov Armónico
MOVIMIENTO ARMÓNICO - RESUMEN
El movimiento Armónico es la proyección de un movimiento circular sobre un eje. Uno
mira lo que hace la sombra del movimiento circular al proyectarla en una pantalla :
Lo que uno hace es usar trigonometría para calcular cuanto valen la posición, la velocidad y la aceleración al proyectarlas sobre el eje vertical
El resultado es que la posición, la velocidad y la aceleración varían sinusoidalmente con
el tiempo. Las ecuaciones están dadas por:
La característica fundamental de este movimiento es que la aceleración es proporcional
a la separación de la separación de equilibrio pero de sentido contrario. ( a = - ω2. x ).
Esto es lo mismo que decir que la fuerza que genera el movimiento tira siempre hacia el
centro. ( Fuerza restitutiva ). Toda cosa que vibra tiene movimiento armónico. Los péndulos y los resortes con cosas colgadas tienen movimiento armónico. El período de oscilación para un péndulo y para un resorte están dados por :
ASIMOV
-3-
Mov Armónico
MOVIMIENTO ARMÓNICO
TEORÍA
Para entender movimiento armónico hay que saber movimiento circular, hay que saber
trigonometría y y hay que saber resortes. (Ley de Hooke y todo eso). Va acá un repaso,
(podés pasarlo rápido).
MOVIMIENTO CIRCULAR
Cuando uno cosa da vueltas se dice que tiene movimiento circular. ( Una calesita, la Tierra alrededor del Sol, las agujas de un reloj, un compact disc, etc.).
La velocidad de giro se llama velocidad angular omega (ω o Ω). Se mide en radianes por
segundo en la física y en revoluciones por minuto en la industria. ( RPM ). El pasaje de
unidades es así: como 1 vuelta son 2 π rad, si me dan una velocidad angular de 20 RPM
tengo:
El tiempo que tarda en dar una vuelta se llama período T. Se mide en segundos. El Nro
de vueltas que da en un segundo se llama frecuencia F y se mide en Hertz ( 1 Hz =
1/seg ). Si pensás un poco te vas a dar cuenta de que:
También está esta otra expresión:
Si la velocidad angular es constante se dice que el movimiento es circular UNIFORME.
En este apunte, siempre que yo diga: "tal cosa se mueve con movimiento circular", voy a
estar refiriéndome a movimiento circular uniforme.
ASIMOV
-4-
Mov Armónico
Si un auto va a velocidad constante, el movimiento de las ruedas es circular uniforme.
Si el auto acelera, el movimiento de las ruedas es circular variado.
Puede haber movimiento circular variado cuando ω aumenta o disminuye. (Como en el
caso del auto que va cada vez más rápido, como un trompo que se frena y todo eso).
TRIGONOMETRÍA
Si uno tiene un triángulo rectángulo así
Ellos definen las funciones trigonométricas sen αlfa y cos αlfa como:
La cuestión es que al representar el valor de estas funciones para ángulos que van de 0°
a 360° se obtiene una cosa así:
Lo que hay que saber acá es que sen αlfa y cos alfa son la misma función, sólo que una
es la otra corrida 90° para la derecha. Sen a y cos a son funciones PERIÓDICAS, quiere decir que pasado un determinado lugar, empiezan a repetirse siempre igual. El movimiento armónico también se repite siempre igual. Hay una relación muy importante entre el movimiento armónico y las funciones seno y coseno. Esto no es casualidad. La explicación la pongo después.
Vamos a otro tema que vos ya creías olvidado:
ASIMOV
-5-
Mov Armónico
LEY DE HOOKE (RESORTES)
Si uno tiene un resorte y lo quiere estirar, tiene que hacer una fuerza. Más fuerza uno
hace, más se estira.
Este asunto de que a mayor fuerza, mayor estiramiento se conoce como Ley de Hooke y
se escribe en forma física cómo F = K x X . El valor K es una constante, y sin hilar fino
digamos que no depende del estiramiento. K es una medida de la "estirabilidad" del resorte, es decir, que tan fácil o tan difícil es de estirar ( a mayor K, el resorte es más
duro). X es lo que se suele llamar estiramiento o elongación. (Elongar = estirar). Ahora
vamos a las siguientes aclaraciones:
* Atención, la elongación es el estiramiento medido desde la posición de equilibrio
(Momento en que el resorte no está ni comprimido ni estirado).
* La ley de Hooke vale tanto para el estiramiento como para la compresión.
* La ley de Hooke no sólo dice que a mayor fuerza, mayor estiramiento, sino que
indica que el aumento de la fuerza es LINEAL con el estiramiento. ( Lineal = directamente proporcional ).
Bueno, vamos ahora a la cuestión del signo Θ que es importante
EL SIGNO Θ EN LA LEY DE HOOKE. (LEER)
La pregunta es esta: cuando uno dice que la fuerza ejercida es K.X… ¿ se refiere a la
fuerza que uno hace sobre el resorte o a la que el resorte ejerce sobre uno ?
Posible respuesta: Bueno, eso no importa. Las dos fuerzas son iguales. Son par acción–
reacción. Cualquiera de las dos en módulo vale Ka por equis. Bueno, justamente, EN
MÓDULO son iguales. Pero vos sabes que en física el signo de un vector indica el sentido, es decir, para qué lado apunta. Cuando viste Ley de Hooke en dinámica, al signo de
F = Θ K.X no se le daba importancia. Ahora va a haber que tenerlo en cuenta. Así que
hay qué decidir bien de qué fuerza estamos hablando, si la del resorte sobre el cuerpo
o la del cuerpo sobre el resorte. Bueno hagamos un dibujito: Tengo un resorte estirado
que tiene agarrado un cuerpo de masa m. Acá está el dibujo:
ASIMOV
-6-
Mov Armónico
En los problemas de movimiento armónico lo que importa es la fuerza que actúa sobre lo
que oscila. Y lo que oscila es la masa m. De manera que la fuerza que voy a considerar es
la que actúa sobre el cuerpo. O sea, esta:
Ahora fijate, según el dibujo, la fuerza que actúa va para
allá. Pero el estiramiento
x va para
allá. Por lo tanto, al tener sentidos contrarios los vectores fuerza y
elongación, la ley de Hooke queda así:
No hay que buscarle un significado extraño al signo menos. El signo Θ solo reemplaza a
la frase "en sentido contrario al desplazamiento". ( O sea, F es lo que va contrario al
desplazamiento ).
Ahora quiero que veas lo siguiente: las fuerzas que ejercen los resortes no son constantes. Varían con la posición. Entonces al ser variable la fuerza que actúa sobre el
cuerpo… también lo será su aceleración. (Atento ! ). Es decir que tengo esto:
Según la ley de Newton la fuerza es m.a. Entonces:
K es una constante. La masa m es una constante. De manera que el choclazo Θ Ka sobre
eme es constante. Quedaría:
De esta ecuación podemos sacar una conclusión importante :
LA ACELERACIÓN QUE TIENE UN CUERPO QUE ESTÁ ATADO A UN RESORTE
ES VARIABLE CON EL ESTIRAMIENTO DEL RESORTE. MÁS CONCRETAMENTE,
ES PROPORCIONAL A LA ELONGACIÓN Y DE SENTIDO CONTRARIO.
ASIMOV
-7-
Mov Armónico
A ver si nos entendemos. Supongamos que tengo un cuerpo atado a un resorte. Por
ejemplo, este
El cuerpo sube y baja en un extraño movimiento al que ellos llaman oscilatorio.
¿ Es este movimiento un MRU ? Rta: No. En un MRU la aceleración es cero.
¿ Es este movimiento un MRUV ? Rta: No. En un MRUV la aceleración es constante.
Entonces, ¿ qué tenemos acá ?
Rta: Tenemos un nuevo movimiento que no es ni MRU ni MRUV. Este movimiento tiene
aceleración variable. La característica principal de este movimiento es que su aceleración es Θ constante por x. Es decir, su aceleración es proporcional a la elongación pero
de sentido contrario.
¿ Y por qué hago tanto hincapié en esto de
?
Rta: porque justamente el movimiento de una masa colgada de un resorte es armónico
y la cuestión de que
es la característica fundamental del movimiento armónico. ( Esto tenés que saberlo).
NOTA: La fuerza de un resorte es la primera de las fuerzas variables que se ven en
física. La segunda es la gravitatoria, que varía con la altura. Después vas a ver millones
de fuerzas variables ( Por ejemplo, las eléctricas, las magnéticas y demás )
Fin Repaso
ASIMOV
-8-
Mov Armónico
MOVIMIENTO ARMÓNICO (Acá empieza la teoría)
El movimiento armónico es un movimiento que va y viene en donde la posición, velocidad
y aceleración de lo que se mueve varían sinusoidalmente con el tiempo. Como a las funciones seno y coseno se las llama armónicas (no sé por qué), al movimiento se lo llama
armónico.
¿ De dónde viene esto de que la posición, velocidad y aceleración dependen del tiempo
en forma senoidal ? Fijate: Supongamos un disco que gira que tiene un clavo clavado.
Pongo un proyector de diapositivas y miro lo que hace la sombra del clavo en la pared :
¿ Qué veo ? Rta: Veo que la sombra del clavo sube y baja en un movimiento alternativo.
(Alternativo = que va y viene). Pues bien, este movimiento de vaivén, alternativo, de ida
y vuelta, oscilante, vibratorio, o como lo quieras llamar, es lo que queremos estudiar. En
física estudiar un movimiento significa hallar las ecuaciones de posición, velocidad y
aceleración en función del tiempo.
POSICIÓN EN FUNCIÓN DEL TIEMPO EN EL MOVIMIENTO ARMÓNICO
Hagamos un dibujito que represente lo que está pasando:
La sombra va subiendo y bajando y su posición oscila alrededor del medio ( punto 0 ). Si
el disco giró un ángulo αlfa, la separación de la sombra de la posición de equilibrio vale
r.sen alfa. Fijate:
ASIMOV
-9-
Mov Armónico
Lo que estoy haciendo es PROYECTAR el Movimiento Circular sobre un eje vertical.
No analizo lo que hace el movimiento circular. Analizo lo que hace LA SOMBRA del
movimiento circular. Por eso ellos dicen que el movimiento armónico es la proyección
de un movimiento circular sobre un eje. Ahora analicemos esto: ¿ Cuál es la máxima
separación que puede tener la sombra de la posición de equilibrio ?
Bueno, esa separación vale r y se produce cuando la sombra está arriba de todo, es
decir, cuando el ángulo vale 90°. Pero en un movimiento que sube y baja no hay radio.
Hay una distancia que es la máxima separación de la posición de equilibrio, así que a
esa distancia la vamos a llamar A, de amplitud. Por otro lado, el ángulo girado vale la
velocidad angular por el tiempo. Entonces la fórmula que me da la separación de la
posición de equilibrio ( x ) queda como x = A.sen ωt
En definitiva, la posición en un movimiento armónico varía sinusoidalmente con el tiempo. ( A esto es a lo que quería llegar). La ecuación de la posición está dada por:
Esta ecuación me va dando las distintas posiciones que tiene la partícula en función del
tiempo. Grafiquemos:
Ahora, puede pasar que al empezar el movimiento el ángulo inicial no sea cero sino que
sea una cosa así:
ASIMOV
- 10 -
Mov Armónico
A este ángulo inicial de desfasaje se lo llama FASE INICIAL. Se lo suele poner como Fi
cero. También se lo llama delta cero tita cero o alfa cero. Entonces, suponiendo que hay
un desfasaje inicial, la ecuación híper-completa para la posición en el movimiento armónico quedaría :
Esto es todo con respecto a la posición en el movimiento armónico. Vamos ahora a deducir la velocidad.
VELOCIDAD EN EL MOVIMIENTO ARMÓNICO
El punto original se mueve dando vueltas por la circunferencia. Buscamos la velocidad
con la que sube y baja su sombra por el eje vertical. Hago este dibujo:
Al ser un movimiento circular, la velocidad del punto es la tangencial que vale omega por
erre. Bien, ahora para hallar la velocidad vertical de la sombra del punto sobre el eje
tengo que hacer una proyección. La velocidad tangencial se puede descomponer en una
vertical y otra horizontal. Ampliemos un poco el dibujo:
Lo que hice en el dibujo fue tomar las componentes de la velocidad. Si te fijás bien vas
a ver que todos los ángulos que marqué como ωt valen efectivamente ωt. En ese caso la
componente vertical de la velocidad vale VT por coseno de ωt. Pero VT es ω.r que es lo
mismo que ω.A. Entonces:
ASIMOV
- 11 -
Mov Armónico
Analicemos un poco esta velocidad que obtuvimos. La velocidad es A.ω cos ωt. Será
máxima cuando cos ωt sea 1, es decir, ωt = 0º. Eso pasa cuando el punto pasa justo por
el origen de coordenadas. De la misma manera V será mínima (cero) cuando cos ωt sea
cero, es decir, ωt = 90º. Esto pasa cuando el punto está arriba de todo.
Es decir, el punto pasa rápido por el medio y se va frenando a medida que va llegando a
las puntas. ( arriba o abajo ). Podés comprobar esto poniendo a oscilar un resorte. Vas a
ver que al pasar por la posición de equilibrio la velocidad es máxima y al llegar a las puntas la velocidad es cero.
Podés intentar poner a la velocidad v en función de x. ( Ayuda: sen2 a + cos2 a = 1 )
Una cosa: La velocidad también se podría haber obtenido derivando la posición. Fijate :
A veces ellos deducen la ecuación de velocidad así. ( Derivando ). Es una manera más
rápida de llegar a la ecuación de velocidad, pero para mi gusto se pierde el concepto.
ACELERACIÓN EN EL MOVIMIENTO ARMÓNICO
Vamos a ver ahora que pasa con la aceleración. Cuando una cosa se mueve con movimiento circular tiene una aceleración centrípeta que vale ω2 r. Otra vez, lo que busco es la
proyección de esa aceleración sobre el eje vertical. Hagamos un dibujito :
ASIMOV
- 12 -
Mov Armónico
Ahora dibujamos el triángulo con mayor detalle y fijémonos que ángulo es que ángulo:
La aceleración del punto que oscila será a = acp sen ωt . La aceleración centrípeta es
ω2r . Entonces me queda: a = ω2.r sen ωt. Ahora, el radio r es la amplitud A. Entonces la
aceleración me queda: a = A ω2 sen ωt. Pero en esta deducción falta tomar en cuenta el
signo. La cuestión es que el eje X apunta para allá ( ) y el vector aceleración va justo al
revés ( ). Quiero decir que el vector aceleración siempre va a tener sentido contrario
al vector posición. Entonces la fórmula no será A.ω2.sen ωt sino MENOS A.ω2.sen ωt.
Queda:
Lo que el signo menos indica acá es que el vector aceleración va siempre al revés que
vector posición. Cuando el cuerpo está arriba ( posición así x ), la aceleración va para
abajo (es decir, así a ). Y viceversa.
Al igual que antes, la aceleración se podría haber obtenido como la derivada de la velocidad con respecto al tiempo.
Otra vez. Al derivar uno gana rapidez y elegancia pero pierde comprensión de lo que
está pasando. Esto lo vas a ver muchas veces en la facultad ( y no sólo en física ).
ASIMOV
- 13 -
Mov Armónico
Me refiero a que muchas veces ellos hacen las cosas de la manera más elegante posible
aunque eso haga que el tema resulte incomprensible para el alumno. ( Bienvenido a la
Universidad de Buenos Aires ).
Vamos que ya terminamos con la teoría. Veamos ahora como varía la aceleración en función del tiempo. Hagamos un grafiquito. Tenemos que la aceleración va a ser máxima
cuando sen ωt sea 1, es decir, para ωt = 90º o para ωt = 270º. ( sen ωt =-1 ). La aceleración será mínima (cero) cuando sen ωt sea cero, es decir, ωt = 0 u ωt = 180º. Resumiendo, el valor de la aceleración en módulo será máximo arriba de todo o abajo de todo. Y será cero al pasar por la posición de equilibrio. Represento y me queda así:
Falta ahora que veas sólo una cosa. Tenemos como varía la aceleración con el tiempo.
Tratemos de buscar como varía la aceleración con la posición. Quiero que veas este
truco. Las ecuaciones del movimiento armónico resultaron ser:
Ahora, si te fijás en la 3era ecuación verás que tengo esto :
La velocidad angular es constante, quiere decir que el término – ω2 también es constante. Entonces la ecuación a = ω2X me está indicando que la aceleración en el movimiento
armónico varía LINEALMENTE con la distancia a la posición de equilibrio. Es más, la aceleración es proporcional a la distancia a la posición de equilibrio y de sentido contrario.
¿ Me seguiste ? Esto es importante porque es justo la base del asunto. Fijate. Voy a
hacer otro dibujito:
ASIMOV
- 14 -
Mov Armónico
La idea es que partiendo de proyectar un movimiento circular sobre un eje se obtiene
un movimiento en donde la posición, la velocidad y la aceleración varían armónicamente
con el tiempo. ( Armónicamente = sinusoidalmente ). La característica fundamental de
este nuevo movimiento es que la aceleración es proporcional a la separación de posición
de equilibrio y de sentido contrario. Ahí está. Aceleración proporcional a estiramiento.
Ese es el concepto que tenés que saber.
FUERZA EN EL MOVIMIENTO ARMÓNICO
Ya tenemos la aceleración en el Movimiento Armónico. Calculemos ahora la fuerza que
causa esa aceleración. Ley de Newton: F = m.a. Quiere decir que si la aceleración es
proporcional a la separación de la posición de equilibrio, la fuerza también lo será. Entonces otra manera de definir movimiento armónico es decir que es un movimiento en
donde la fuerza que actúa apunta siempre hacia el centro y su valor es proporcional a la
distancia a la posición de equilibrio.
Entonces tenemos un cuerpo que tiene este movimiento: si uno lo deja en la posición de
equilibrio se queda quieto y no se mueve. Si uno lo separa del equilibrio, aparece una
fuerza que lo trata de llevar de nuevo al medio. A esta fuerza que tira para el centro
se la suele llamar RESTITUTIVA porque trata de restituir al cuerpo a su posición original. Y ahora vamos a probar un poco tu sabiduría....
¿ Qué fuerza conocés que tire siempre hacia el centro con un valor proporcional a la
separación ? ¿ Qué fuerza sigue la ecuación Θ constante por equis ? ¿ Qué fuerza es la
fuerza restitutiva por excelencia ?
Rta: Es… ¡ La fuerza de un resorte !
Yes sir. Las fuerzas que ejercen los resortes están dadas por la ley de Hooke que dice
F = - k.x. Cualquier cosa que oscile atada a un resorte tendrá un movimiento armónico.
ASIMOV
- 15 -
Mov Armónico
Podés comprobar esto colgando un cuerpo de un resorte y poniéndolo a oscilar. Si vas
siguiendo el movimiento del cuerpo trazando círculos con la mano, vas a ver que tu dedo
sigue aproximadamente un movimiento circular uniforme.
No hace falta que me creas. Podés agarrar un resorte y verificarlo. Un último comentario. Hooke demostró este asunto de F = Kk.x en 1660. ( Hooke era contemporáneo de
Newton. Se peleaban bastante, por cierto ). El tipo se puso muy contento cuando descubrió que en un resorte el alargamiento era proporcional a la fuerza aplicada. El master lo puso en forma de anagrama. (Anagrama = cambiar las letras de lugar). Lo que él
escribió fue CEIIINOSSSTTUV. Esto es lo que se conoce como el anagrama de Hooke
y corresponde a la frase en latín: ut tensio sic vis. ( A tal alargamiento, tal fuerza ).
Fin de la teoría de Movimiento Armónico
ASIMOV
- 16 -
Mov Armónico
EJEMPLOS DE MOVIMIENTO ARMÓNICO
Todo este asunto del movimiento armónico salió de proyectar un movimiento circular
sobre un eje. Pero… ¿ Por qué esta ocurrencia de proyectar un movimiento circular ?
¿ Por qué no proyectar un movimiento elíptico, parabólico o helicoidal ? ( o lo que sea )
La respuesta es que el movimiento armónico aparece muy seguido en la naturaleza. Aparece en la física y aparece en la ingeniería. Muchísimas cosas se mueven siguiendo un
movimiento armónico. Nunca le prestaste atención. Fijate. Vamos a ver unos ejemplos
¿ Notaste que cuando un avión vuela las alas se mueven todo el tiempo para arriba y
para abajo ?
La gente cree que los edificios son estáticos. Falso. Los edificios se mueven. Se mueven
cuando les pega el viento. Se mueven cuando abajo pasa un subte. Se mueven con los
temblores de tierra
La Tierra misma vibra armónicamente con los temblores. La vibración en el suelo que
uno siente cuando pasa el subte es un movimiento armónico. ( El subte, un tren, un camión, lo que sea ). Los autos son máquinas que tienen todo tipo de movimientos armónicos. Por ejemplo, el movimiento de la suspensión es armónico
Dentro del auto tenés los pistones que suben y que bajan con movimiento armónico.
ASIMOV
- 17 -
Mov Armónico
En el caso de la suspensión el movimiento es en realidad armónico amortiguado. Amortiguado significa que se va frenando. Se va frenando justamente por la acción de los
amortiguadores.
Hay más ejemplos. ¿ Alguna vez viste el movimiento de los pedales de una bicicleta ?
Los pedales se mueven con movimiento circular, pero si los mirás de atrás, lo que estás
viendo es un movimiento armónico
En electrónica hay una cosa que se llama "circuitos oscilantes". En principio no hay nada
que vibre físicamente. Pero la tensión y la corriente se comportan como si estuvieran
vibrando.
La transmisión de la electricidad suele hacerse con corriente alterna. Alterna significa
que la tensión y la corriente varían en forma sinusoidal con el tiempo. Y si bien no hay
algo "concreto" que se mueva con mov. armónico, la tensión y la corriente varían en
forma armónica. ( = sinusoidal ).
La tabla de un trampolín vibra. Las cuerdas de la guitarra vibran. Los parlantes vibran.
La cuerda de una guitarra deja de vibrar después de un rato. Su movimiento es amortiguado. Lo mismo pasa con la tabla de un trampolín.
.
Hay muchos más cosas que vibran con movimiento armónico: Los bordes de un diapasón,
los instrumentos musicales cuando suenan. Los conos de los parlantes de un equipo, los
vidrios cuando hay un ruido fuerte. Los puentes cuando pasan los camiones… En general
toda cosa que vibra lo hace con movimiento armónico. Prendé el auto y poné la mano sobre el capot. Verás que vibra. Levantá el capot y mirá el motor. Vibra. Estos son movimientos armónicos.
Muchas máquinas tienen piezas que suben y bajan o que van para adelante y para atrás.
Esto es lo que suele llamarse movimiento alternativo. Generalmente estos movimientos
ASIMOV
- 18 -
Mov Armónico
son armónicos. Y si no son armónicos, son muy parecidos. Acá tenés algunos ejemplos
sacados de la ingeniería mecánica :
Y si querés ver un movimiento armónico ya mismo podés apoyar una regla contra la mesa. La tenés apretada con una mano mientras que con la otra le hace tingui-tingui.
Así como ves, muchos movimientos de la vida real son armónicos. Sin embargo la gente
dice: Muy bien, ya lo entendí. Muchas cosas se mueven con movimiento armónico. Pero
¿ qué sentido tiene estudiar el movimiento armónico ? ¿ Qué gano yo con saber que la
amplitud de las oscilaciones varia como A por seno de omega te ?
Rta: Bueno, en realidad saber la amplitud de las oscilaciones en un movimiento armónico
no es muy importante. Tampoco es importante saber que la velocidad varía como A por
ω por coseno de ωt… Entonces ¿ Qué es lo importante ?
Rta: Lo importante es la ACELERACIÓN
Claro, fijate. La aceleración de algo que se mueve con movimiento armónico NO es
constante sino que aumenta y disminuye variando sinusoidalmente con el tiempo.
¿ Y eso que significa ?
Bueno, F = m.a, quiere decir que la FUERZA que actúa también varía con el tiempo de la
misma manera. Entonces necesitamos conocer las aceleraciones que actúan para poder
calcular las fuerzas que ejercen. Y lo importante acá es entender que esas fuerzas…
¡ Pueden ser ENORMES ! Busquemos algo que se mueva con movimiento armónico. No
pienses en un osito de juguete colgado de un resorte… Imaginate hélices…, motores de
máquinas, rotores de centrales eléctricas, paletas de turbinas, o más simplemente, de
los pistones de un motor de un auto. Un motor puede girar a unas 3.000 vueltas por minuto, de manera que los pistones están sometidos a aceleraciones que son del orden de
1.000 veces la gravedad. Las fuerzas que aparecen son GIGANTESCAS. Y lo que es
ASIMOV
- 19 -
Mov Armónico
peor, cambian todo el tiempo de signo. ( Es decir, en un momento son de tracción y después son de comprensión ).
Este asunto de someter a las piezas a tensiones alternativas de tracción y compresión
es terrible para la ingeniería. Es lo que se llama "fatiga". Las tensiones alternas causan
fatiga y DESPEDAZAN a las piezas de las máquinas. ( A las piezas de las máquinas, a
las alas de los aviones, a lo que sea ). La fatiga es el mismo efecto que permite romper
un alambre doblándolo para un lado y para el otro. ( Lo vas a ver en estabilidad II ).
Para la ingeniería es muy importante conocer la magnitud de estas fuerzas para poder
diseñar las piezas. Esa es la cuestión. ¿ Ves cómo es la cosa ?
Y si me permitís ahora, dejame que te de otros ejemplos de movimientos armónicos.
El ejemplo híper-clásico de movimiento armónico es el de un cuerpo atado a un resorte
que sube y baja. El otro ejemplo que ellos suelen dar es el de un péndulo. Un péndulo
que oscila tiene un movimiento armónico.
La demostración de porqué un péndulo tiene un movimiento armónico está en uno de los
problemas que resuelvo al final. En realidad el movimiento es casi armónico. Es casi armónico porque no está sobre una línea recta sino sobre un arco de circunferencia. Cuanto más chicas son las oscilaciones, más se aproxima el movimiento de un péndulo a uno
armónico simple.
También es armónico el movimiento de algo que flota en el agua. Puede ser un corcho,
un telgopor o una botella de Coca. Vos tenés algo flotando. Lo hundís y lo soltás. El movimiento que sigue es armónico.
ASIMOV
- 20 -
Mov Armónico
En 1969 los norteamericanos llegaron a la Luna. Uno de los instrumentos que colocaron
fue una especie de sismógrafo para medir vibraciones. Cuando se fueron, dejaron caer
el módulo lunar sobre la luna para probar si el aparato funcionaba.
¿ Qué si el aparato funcionaba ?!
¡ Funcionaba ! ¡ La Luna quedó vibrando varios días como si fuera una campana ! (El movimiento de la Luna fue armónico, por supuesto).
Pegale a la baranda del balcón. Fijate que queda vibrando. Dale una patada a una parada
de colectivo. Vibra. Mirá los árboles. Fijate como se balancean cuando les llega una ráfaga de viento. Y las ramas. Mirá las ramas como se mueven.
¿ Tenés lavarropas en tu casa ? Fijate lo que pasa cuando centrifuga. Va para acá y para allá. Vibra. ¿ Escuchaste alguna vez una explosión ? ¿ Observaste cómo tembló toda
la casa ? ¿ Y los vidrios ? ¿ Viste lo que pasó con los vidrios ?
Andá a una catedral. Mirá las lámparas que cuelgan del techo. Vas a ver que tienen un
ligero balanceo. En realidad son inmensos péndulos. Midiendo el período se puede saber
la longitud del hilo. (O sea, la altura del techo). Galileo descubrió las leyes del péndulo
mirando una de estas lámparas. ( La lámpara todavía está. Podés verla en la Catedral de
Pisa, cerca de la torre inclinada ).
Y siguiendo con las lámparas, te propongo lo siguiente: Mirá para arriba. ¿ Vés la lámpara que cuelga del techo en la habitación donde estás ? Bueno. Subite a un banquito y
hacela girar unos 30º. Ahora soltala. ¿ Ves lo que pasa ? La cosa empieza a girar para un
lado y para otro. Esto es lo que se llama péndulo de torsión. ( Hay varios en el laboratorio de física I ). Cavendish usó un péndulo de torsión para medir la constante de gravitación universal.
ASIMOV
- 21 -
Mov Armónico
Si pensás un poco te vas a dar cuenta que este movimiento alternativo de torsión también es armónico simple. (Atención, ahora acá lo que varía sinusoidalmente es la posición
angular, es decir el ángulo de giro).
…Y todavía hay más ejemplos de movimientos armónicos …También es armónico el cabeceo de la proa de los barcos…
También es armónico el movimiento de subida y de bajada que tiene algo que está flotando cuando pasa una ola:
Siguiendo con el agua, también es armónico el movimiento de un líquido que oscila en un
tubo en U.
Andá a una fábrica y mirá los motores que mueven las máquinas. Vibran. O más fácil:
andá a la cocina y prendé la batidora. ¿ Vibra o no vibra ?
Las vibraciones en los motores aparecen porque la masa que gira no está uniformemen-
ASIMOV
Mov Armónico
- 22 -
te distribuida alrededor del eje de rotación. Lo mismo pasa con las ruedas de los autos.
Fijate que a veces el volante de los autos vibra. Eso pasa porque la rueda está desbalanceada. La goma o el disco de freno se gastaron en forma despareja. La rueda está
girando alrededor de su centro geométrico y no de su centro de masa. Eso provoca las
vibraciones. ( Hay que balancear ). Se puede demostrar que estas vibraciones son armónicas. Ellos suelen simbolizar un motor desbalanceado así:
Si las vibraciones son muy grandes, las fuerzas pueden ser muy grandes. Pueden romperse los tornillos de la base. Puede romperse el eje. ( accidente, heridos, la fábrica
se para, etc. ¿ quién tiene la culpa ? ¡ el ingeniero ! ).
En mecánica vas a ver como se calcula el valor de estas fuerzas. ( complicado ). En estabilidad III y en elementos de máquinas vas a ver como se hace para diseñar las piezas para que aguanten estas tensiones. ( Agarrate ). Acá en física lo que ellos quieren
es que tengas una idea de lo que es el movimiento armónico. Y que sepas manejar las
ecuaciones, claro. O sea, que sepas que la posición, la velocidad y la aceleración varían
así
con el tiempo. Y que la aceleración ( y la fuerza ) apuntan todo el tiempo hacia
el centro y que son proporcionales al estiramiento y de sentido contrario. Ahí está. Con
que sepas esto, alcanza.
Con respecto al parcial, te digo que probablemente no te van a movimiento armónico.
(¡¿ Y ahora me lo dice ?!). La cosa es así: Vos tenés que saber movimiento armónico por
la simple razón de que este tema es la puerta de entrada a otro tema bien peludo que
es… ¿ Cuál es ?! Por supuesto, ondas.
Una onda es un movimiento armónico que avanza. Es decir, es la composición de un movimiento vibratorio así
con un MRU así
.
Ellos no te van a tomar problemas de movimiento armónico. Te van a tomar ondas. Por
eso necesitan que manejes los conceptos y las ecuaciones del movimiento armónico.
Yo puse muchos ejemplos de situaciones donde aparecen movimientos oscilatorios. La
idea era que vieras la cantidad de veces que aparecían estos movimientos en la vida diaria. Y también puse tantos ejemplos para que te dieras cuenta de 2 cosas:
1 - La Ingeniería es fantástica.
2 – Se necesita saber física para resolver problemas de Ingeniería .
Si lograste captar estas ideas, ponete las pilas y enfrentá los problemas que siguen.
Y prepararte para entrar en el verdadero tema gordo que es ondas. ( Y que es lo que
te van a tomar)
Fin teoría de Movimiento armónico
ASIMOV
- 23 -
Mov Armónico
a)- Recordemos las ecuaciones que definen la posición, velocidad y aceleración para una
cosa que se mueve con movimiento armónico.
Por favor acordate que en estas ecuaciones A es la amplitud, ω es la velocidad angular
asociada al movimiento armónico, t es el tiempo y fi cero es la fase inicial. Me dicen que
a 6 cm de la posición de equilibrio está en reposo. Quiere decir que A = 6 cm
Si el período es 2 cm, planteo:
Fijate que según el dibujo en t = 0 el punto está en X = A.
Las ecuaciones van a quedar:
Dando valores a t podes sacar la posición, velocidad y aceleración en ese instante.
b) - Piden los valores máximos de x, v y a. Bueno, el valor máximo de x tendría que ser 6
cm, que es la amplitud. ( 6 o - 6, digamos ). Veamos si da. Para que la ecuación x = 6 sen
( πt + π/2 ) tome su valor máximo, seno del choclazo tendría que ser 1. En ese caso me
queda efectivamente Xmax = 6 ( 1 ) = 6 cm. ( dió ).
El otro valor máximo que puede tomar el seno es - 1 y en ese caso tendría la otra respuesta, Xmax = - 6 cm.
ASIMOV
- 24 -
Mov Armónico
¿ Cuándo ocurre esto ?
Rta: Cuando seno ( choclo ) = 1, o sea, escribámoslo:
t = 0 es justo cuando el coso pasa por la posición superior. Después de este instante, la
posición volverá a ser máxima cuando sen ( choclo ) = - 1. O sea:
Vamos ahora a la velocidad. Busquemos el máximo. La expresión que teníamos era
El máximo va a estar cuando el coseno del paréntesis sea 1 ( o -1 ). Por lo tanto, el máximo valor de velocidad será de 6π cm/seg. Con respecto al instante donde pasa esto…
bueno, veamos. Si el coseno vale 1 ( o -1 ) el ángulo será de 0 grados o 180 grados ( π ).
O sea:
Esta solución equivale a decir "medio segundo antes que se comenzara a medir el tiempo". Por lo tanto no se considera. Probemos con la otra. El paréntesis tiene que ser
180º…
Con respecto a la aceleración, es la misma historia. La ecuación es:
Mirándola un poco veo que el valor máximo de la aceleración será de 6π2 en módulo.
Esto se producirá cuando sen ( paréntesis ) = 1 o ( -1 ) o sea: ( ) = 90º ( o 270º ).
O sea:
Aclaración: A veces en los problemas de movimiento armónico uno usa fórmulas de movimiento circular. Por ejemplo, T = 2πf o T = 1 / f o ω = 2π/T o acp = ω2.r. Incluso se
ASIMOV
- 25 -
Mov Armónico
habla de velocidad angular ω. Y uno dice ¿ Por qué usan cosas de movimiento circular
si tengo un movimiento armónico que sube y baja ? ¿ De qué velocidad angular están
hablando ?
Rta: Bueno, lo que pasa es que el movimiento armónico es en realidad la proyección de
un movimiento circular sobre un eje. Es decir yo tengo un punto que se mueve con movimiento circular. La SOMBRA de ese punto es lo que me va dando el movimiento armónico. Las magnitudes circulares a las que uno hace referencia son las de ese movimiento
circular base.
Hagamos un dibujito:
a)- Para un cuerpo de masa m atado a un resorte de constante K, el período de oscilación está dado por:
Período de un resorte
con una masa colgada
La deducción de esta fórmula está en uno de los problemas que vienen después. Despejo la constante K :
Reemplazando por los datos m = 3 Kg y F = 2 1/seg:
ASIMOV
- 26 -
Mov Armónico
Multiplicando arriba y abajo por metro me queda en Newton/m:
b)- ¿ Cuál es la energía total del movimiento ?
Bueno, me deben estar pidiendo que calcule la energía mecánica, es decir la suma de
la cinemática, la potencial y la elástica. El valor de esta energía debería ser constante
porque sino hay rozamiento el resorte debería oscilar forever. Cuando el resorte está
arriba de todo ( o abajo de todo ) NO hay energía cinética. Toda la energía mecánica
está en forma de energía elástica.
¿ Hay energía potencial ? Daría la impresión de que sí, pero en realidad NO. Fijate.
Cuando uno cuelga el cuerpo del resorte antes de ponerlo a oscilar, el peso del cuerpo
obliga al resorte a estirarse un poco. De esa manera el peso del cuerpo se compensa
con la fuerza del resorte.
Una vez que uno pone el sistema a oscilar, el cuerpo sube y baja, pero como el resorte
tenía un estiramiento inicial, es como si P y Fres se estuvieran compensando todo el
tiempo. De esa manera uno puede no tomar en cuenta la energía potencial. ( Es como si
el cuerpo no pesara ). Si esto te resulta complicado de entender, podés suponer que el
resorte está acostado y el sistema oscila en forma horizontal. ( O sea, así:
)
De esta manera la fuerza peso no molesta.
Hecha esta aclaración, cuando el cuerpo está arriba ( o abajo ), toda la energía estará
en forma de energía elástica. Como la elongación es de 10 cm, esta energía valdrá:
c)- Piden que escriba la ecuación de la posición en función del tiempo. Bueno, en un movimiento armónico la posición X viene dada por:
La amplitud A ya la tenemos, vale 0,1 m. Calculemos la velocidad angular ω del movimiento circular asociado al movimiento armónico.
ASIMOV
- 27 -
Mov Armónico
La ecuación de la posición en función del tiempo queda:
Una aclaración: con respecto al ítem b), yo podría haber calculado la energía total de
oscilación de la siguiente manera: cuando el cuerpo pasa por el medio sólo tiene energía
cinética que vale ½ m V2 ( es decir, en la posición de equilibrio ). Calculemos con que
velocidad pasa por ahí. La expresión de la velocidad del movimiento armónico es:
Al pasar por el punto medio, la velocidad es máxima, por lo tanto cos ωt = 1. Entonces:
Es así que la energía cinética ( = a la Etotal ), valdrá:
Este valor coincide con el que calculé antes. La idea es que veas que mientras el sistema
masa-resorte se mantenga oscilando, en todo momento la energía mecánica que posee
va a ser de 0,24 π2 Joule. ( Constante ).
Dicen que tengo una masa unida a un resorte y que el sistema oscila. Bueno, hagamos un
dibujito aclaratorio:
ASIMOV
- 28 -
Mov Armónico
a) - El sistema oscilando tiene una energía mecánica que es igual a la suma de la cinética
más la elástica. Al igual que en el problema anterior no hace falta tener en cuenta la
energía potencial. ( El sistema podría estar puesto acostado
).
Tonces:
La energía total que tiene el sistema es igual a la elástica que tiene el resorte cuando
está todo comprimido o la cinética que tiene el cuerpo cuando pasa por el punto medio
( x = 0 ). En x = 0 el ángulo ωt vale cero y cos ωt = 1. Entonces la Ecin en ese punto será:
De la misma manera puedo calcular la energía total a partir de la energía Elástica.
Cuando la compresión es máxima o el estiramiento es máximo, x = A. Por lo tanto:
Tengo 2 expresiones para la energía total. ¿ Cuál de las dos me conviene usar ?
Rta: Cualquiera de las dos. Es un poco más simple con la energía elástica, así que agarro
por ahí. Me piden que diga cuánto vale la relación Ecin/Etot para X = A/2. La energía
total ya la conozco. Vale ½ K A2 . Calculo entonces el valor de la Ecin para X = A/2.
Para una elongación X igual a la mitad de la amplitud la Energía elástica vale:
Como me pedían que calcule Ecin/Etot para X = A/2 hago:
ASIMOV
- 29 -
Mov Armónico
b)- Preguntan cuál será la elongación para que se cumpla que la energía cinética sea
igual a la potencial. Supongo que habrá querido decir " Potencial elástica ". Potencial
gravitatoria ya sabemos que no hay ( O que no hay que tomarla en cuenta, digamos ).
Hecha la aclaración, calculemos el valor de x tal que Ec = EEl . En cualquier punto del recorrido, la energía total es la suma de la cinética más la elástica. Bueno, planteemos
esto: Etot = Ecin + Eel .
La energía mecánica total ya la teníamos de antes, valía ½ K A2. La energía elástica
cuando la elongación es equis vale ½ K x2. Bien. ¿ Cuánto vale ahora la energía cinética
para esa elongación equis ? Muy fácil. El problema pide que valga lo mismo que la energía elástica. Por lo tanto la energía cinética para la elongación X vale ½ K x2.
Reemplazando:
Tenemos un movimiento armónico de T = 0,25 s y A = 0,15 m. Supongamos que lo que
está vibrando sea algo como esto:
Las expresiones de la posición, velocidad y aceleración, son:
ASIMOV
- 30 -
Mov Armónico
La velocidad angular ω del movimiento circular asociado al movimiento armónico vale:
Las ecuaciones quedan:
Las energías valdrán:
La energía de la masa será ½ de la masa por la velocidad al2.
Para calcular la Energía elástica podría calcular la constante del resorte y hacer ½ K x2
Como en realidad no me dicen que el sistema está formado por una masa y un resorte,
voy a calcularla como Etot – Ecin :
Para calcular los valores máximos que toman x, v, a, Ecin y EE considero que el coseno del
(choclo) y el seno del (choclo) tienen que valer 1. Para calcular los valores mínimos considero que tienen que valer cero. Empecemos con la posición:
ASIMOV
- 31 -
Mov Armónico
Esto va a ocurrir cuando sen ( choclo ) sea 1. O sea :
De la misma manera, el valor mínimo de la posición será X = 0 y eso ocurrirá en t = 0.
Vamos a la velocidad:
Esto ocurrirá cuando:
En este momento la elongación valdrá X (t=0) = 0. La velocidad será mínima cuando cos
( 8πt ) sea = 0, o sea 8πt = π/2
En ese momento la elongación valdrá:
Así habría que seguir haciéndolo para las magnitudes que faltan. Creo que no vale la pena porque es más que nada hacer millones de cuentas. Aparte en realidad habría que
dar los valores en forma general lo que es más pesado todavía. ( Ej: la velocidad máxima
en módulo es de 3,77 m/s y esto ocurriría en t = 0, t = 1/8, t = 2/8, etc ). Sí creo que vale
la pena indicar DONDE ocurrirán estos valores máximos y mínimos marcándolos a ojo
sobre la trayectoria. Fijate:
Convendría darle una mirada a los gráficos que indican como varían estas magnitudes en
el tiempo. Fijate :
ASIMOV
- 32 -
Mov Armónico
Fijate que tanto la posición como la velocidad y la aceleración, varían armónicamente
( = sinusoidalmente ) con el tiempo. Vamos a lo gráficos de las energías que es algo que
también conviene ver :
Para graficar estas funciones tuve en cuenta que la energía elástica es ½ K x2 =
½ K ( A sen ωt )2 = ½ K A2 sen2 ωt.
De la misma manera la Ecin = ½ m V2 = ½ m ( A ω cos ωt )2 = ½ m A2 ω2 cos2 ωt. Por lo
tanto la curva de la energía elástica tiene forma de seno cuadrado y la energía cinética
tiene forma de coseno2.
¿ Qué eso de "superponer movimientos armónicos" ?
Rta: Básicamente es obligar a una cosa a que se mueva con dos movimientos armónicos
a la vez. A ver si nos entendemos. Supongamos que tengo dos resortes. Cada uno tiene
una masa colgada. Cada resorte vibra con su propio movimiento armónico:
ASIMOV
- 33 -
Mov Armónico
Ahora hago lo siguiente: pongo los dos resortes uno a continuación del otro… Entonces
la pregunta es: ¿ Cuál será el movimiento resultante de la masa del resorte de abajo ?
Para resolver este asunto uno puede suponer que la vibración de cada resorte NO influye sobre el otro. Cada resorte vibra como si el otro no existiera.
Lo que uno hace para resolver esto es decir: bueno, si el resorte 1 vibra con la ecuación
x1 = A1 sen ω1t y el resorte 2 vibra con la ecuación x2 = A2 sen ω2t, la vibración resultante será la suma de las 2. O sea :
x = A1 sen ω1t + A2 sen ω2t.
¿ Es correcto esto ? Rta: Sí, es correcto. Vamos a hacerlo para que veas como da.
Los movimientos son:
Notá lo siguiente:
1) A la elongación no la llaman equis sino y (Es lo mismo. Se la puede llamar x o y porque
es una posición).
2) Los 2 movimientos que dan tienen la misma pulsación ω. Esto quiere decir que "giran"
con la misma velocidad angular. O sea, tienen el mismo período y la misma frecuencia.
( Tardan los mismo en dar una vuelta, digamos ).
3) Los 2 movimientos tienen la misma amplitud. ( A = 5 )
Aclarado esto, hagamos la suma. Recordá que sen ( α + β ) = sen α . cos β + sen β . cos α.
ASIMOV
- 34 -
Mov Armónico
Entonces:
Bueno pero… ¿ Cómo hago ahora para resolver este choclazo ? Habría que ver a que
es igual la expresión sen α + cos α. ( Alguna fórmula debe haber ). Bueno, hay un truco.
Multiplico y divido por √2/2. ( Que es igual al seno de 45º ) .
Ahora el choclo que está en el paréntesis es sen ( ωt + π/4 ). Entonces :
Racionalizando :
Esto que hice fue hallar analíticamente la ecuación del movimiento resultante. Voy a
representar esto en un grafiquito para que veas cómo es cada una de las funciones y
como da la función suma. Fijate :
Acá se ve un poco mejor por qué la función resultante tiene amplitud √50 ( ≈ 7, 07 ).
Y también por qué está corrida en pi sobre 4. Para obtenerla fui sumando punto a punto
los valores de las otras dos funciones.
ASIMOV
- 35 -
Mov Armónico
Todo esto es muy lindo pero muy engorroso. Hay que andar haciendo gráficos complicados y sumando senos y cosenos usando trucos matemáticos. Por eso se buscó otra manera de hacer esto y se encontró. Se llama representación Fasorial de Fresnell.
( Atento ).
METODO FASORIAL (REPRESENTACIÓN DE FRESNELL)
Fresnell dice lo siguiente: habíamos quedado en que podíamos representar a la función
Y = 5 sen ωt tomando la sombra de un punto que gira en una circunferencia de radio 5
y velocidad angular omega. Bien. Lo mismo podemos hacer con la función y = 5 sen ( ωt
+ π/2 ). Fijate:
Ahora Fresnell dice: Asociemos a cada punto que gira un vector rotatorio. Llamémoslo
Fasor . Ahora vamos a decir que el movimiento armónico está dado por la proyección de
este Fasor sobre el eje vertical. Fijate:
¿ De qué sirve todo esto ? Ahora vas a ver. La trampa es esta. Si yo digo que cada uno
de los movimientos está dada por un vector, el movimiento resultante ( suma ) estará
dado por la suma de los 2 vectores. ( Hablo de suma vectorial ). O sea, esto:
¿ Qué hemos obtenido ?, dice Fresnell. Hemos obtenido otro vector rotatorio ( Fasor)
tal que su sombra sobre el eje vertical nos da el movimiento resultante. Atención. Los 2
fasores que me daban inicialmente giraban con velocidad angular ω. El nuevo fasor que
ASIMOV
Mov Armónico
- 36 -
estoy hallando también gira con velocidad angular ω. O sea, los tres vectores giran con
la misma omega. Lo que dibujé es una foto de los 3 en el instante t = 0. Hallemos la amplitud y la fase inicial del fasor resultante:
Por lo tanto el movimiento armónico resultante tiene por ecuación:
Este choclín coincide con la que habíamos calculado antes. Obtuvimos la misma expresión por un procedimiento más corto. Si nos hubieran dado 3 movimientos armónicos, la
solución analítica hubiera sido INFERNALMENTE complicada.
Notá la diferencia entre vector y fasor. Un vector es un vector. Un fasor es un vector
que gira. ( Vector rotatorio ). Ahí está. Eso es lo que tenés que saber.
El método fasorial hay que saberlo. No tanto porque te lo vayan a tomar ahora. No te lo
van a tomar. ( Y si te lo toman te matás de risa porque es sumar vectores ). Tenés que
saberlo porque lo vas necesitar más adelante para entender temas más peludos como
interferencia y difracción. También vas a usar fasores en electricidad cuando haya que
representar tensiones y corrientes alternas. ( Física II ). Conclusión, aprendete lo de
los fasores. ( Creo que fui claro, no? ).
Y unas últimas cositas: 1) Repito, el movimiento resultante está dado por la proyección
del fasor resultante sobre el eje vertical. Este fasor gira todo el tiempo con velocidad
angular ω al igual que los otros dos. Cuando uno los dibuja, lo hace para un instante dado de tiempo. Yo podría haberlos dibujado también así:
2) Para poder aplicar el método de suma fasorial todos los fasores tiene que tener la
misma velocidad angular. Si no, no se pueden sumar. ( Ej: y1 = 5 sen 5 t e y2 = 5 sen 4 t
no se pueden sumar porque los vectores giran con diferente velocidad ).
3) Los movimientos armónicos componentes pueden ser uno
dos resortes puestos así:
al otro, como si tuviera
Esto da lugar a unos dibujitos raros que se llaman curvas de Lissajous. Tienen forma
ASIMOV
- 37 -
Mov Armónico
algo parecida a un ocho ( 8 ). Son las curvas que los electrónicos andan mirando todo el
tiempo en los osciloscopios. Acá tenés unas curvas de Lissajous :
CURVAS DE
LISSAJOUS
También podés ver las curvas de Lissajous en las viejas series de la tele cuando los tipos querían mostrar la super tecnología que tenían. ( Ejemplo: Rumbo a lo desconocido,
El Tunel del tiempo, etc )
Voy a hacer el diagrama fasorial para poder hacer la suma. Pi sobre 3 equivale a 60º,
pi sobre 6 equivale a 30º y 2π/3 equivale a 120º. Entonces lo que tengo es esto :
Para hallar el fasor resultante descompongo en X y en Y. ( Se podría hacer gráficamente también pero no da exacto ). Veamos:
Por lo tanto el módulo resultante será:
ASIMOV
- 38 -
Mov Armónico
El ángulo que se forma con el eje horizontal es
Por lo tanto el fasor resultante es:
Piden verificar analíticamente el valor obtenido. Bueno, para hacer eso tendría que sumar matemáticamente las 3 funciones seno que me dan… Como poder hacer, se puede,
pero es un choclazo. Lo siento, que lo hago otro.
El enunciado no se entiende bien. Por el dibujo que me dan interpreto lo siguiente:
Parece ser que hay una cosa que se mueve alternativamente para la derecha y para la
izquierda con movimiento armónico. Sobre esa cosa se quiere poner otra cosa sin que
la cosa de arriba resbale sobre la de abajo. Bueno, calculemos lo parámetros del movimiento armónico. Dicen que la frecuencia es de 15 oscilaciones por minuto. Por lo tanto:
La amplitud es de 1,5 m y ω vale 1,57 1/s. Las ecuaciones de este movimiento van a ser:
ASIMOV
- 39 -
Mov Armónico
Ahora vamos a esto: ¿ Qué significa la frase "que no resbale" ? Bueno, acá hay que pensar un poquito. Tengo una plancha que está oscilando. Yo le pongo un cuerpo arriba. Si la
plancha acelera o frena bruscamente, el cuerpo de arriba puede llegar a patinar. O sea
que tengo que ver qué pasa con la aceleración. Ahora bien, en un movimiento armónico la
aceleración no es constante. Varía con la posición. De manera que la mayor posibilidad
de deslizamiento ocurrirá donde sea mayor la aceleración.
Pregunta: ¿ En qué lugar de la trayectoria pasará esto ?
Rta: En las puntas. Ahí la aceleración es máxima.
¿ Puedo calcular esa aceleración máxima ? Bueno, mirá las ecuaciones. El valor de a está
dado por a = Θ 1,5 . 1,572 sen 1,57 t. Su valor máximo ocurrirá cuando sen 1,57 t valga 1.
Entonces:
Tengo la aceleración máxima. Hagamos el diagrama de cuerpo libre del cuerpo de arriba
para ver qué fuerzas actúan. Veamos:
Uno pensaba encontrarse con un diagrama de cuerpo libre complicado, pero fijate que
en dirección horizontal hay una sola fuerza que actúa sobre el cuerpo. ( Interesante ).
Estoy en el caso de aceleración máxima, entonces la fuerza de rozamiento también tiene que ser la máxima. Es estática porque el cuerpo no patina. Planteo :
ASIMOV
- 40 -
Mov Armónico
Este coeficiente de rozamiento que calculé es estático, porque partimos de la base de
suponer que el cuerpo no deslizaba. Este mu es el MÍNIMO posible. Con cualquier coeficiente de rozamiento mayor tampoco habría resbalamiento.
Vamos a ver como es esto. Tenemos un cuerpo que oscila hacia arriba y hacia abajo con
Amplitud A = 0,5 m. ( Una plataforma ). Ahora pongo arriba de la plataforma otro objeto. Quiero que el objeto no se despegue de la plataforma de abajo. Pero… ¿ De qué están hablando ? ¿ Por qué habría de despegarse ?
Rta: Bueno, como siempre, hagamos un dibujito y pensemos. Para eso somos ingenieros.
Tenemos la capacidad de analizar situaciones que los demás mortales no pueden ver.
Vamos. El asunto quedaría así :
LA PLATAFORMA VA PARA
ARRIBA Y PARA ABAJO SOSTENIENDO SIEMPRE UN CUERPO ARRIBA DE ELLA
Lo que pasa es lo siguiente: cuando la plataforma sube y está llegando arriba, va frenando. La frenada podría ser tan brusca que el objeto podría llegar a seguir para arriba
por inercia. Podés imaginarte lo que sentirías vos si estuvieras en un ascensor que está
subiendo y de pronto se pone a frenar de golpe.
Lo mismo podría pasar cuando la plataforma arranca hacia abajo después de haber llegado arriba. ( Ahora la "acelerada" debería ser muy violenta para que el cuerpo se despegue ). Hagamos el diagrama del cuerpo libre para aclarar las cosas. Supongamos que
el tipo está llegando arriba con la plataforma frenando :
Tomé el momento en que la plataforma está llegando arriba de todo porque ese es el
momento en donde la aceleración es máxima. Atención, esta aceleración apunta hacia
abajo porque la plataforma está frenando.
ASIMOV
- 41 -
Mov Armónico
( Pregunta: ¿ Hacia dónde apuntaría la aceleración si considero el momento cuando la
plataforma está arriba arrancando hacia abajo ? ). Planteemos la ecuación de Newton
según el diagrama de cuerpo libre:
P–N=ma
Esta ecuación vale mientras la plataforma y el objeto están en contacto… pero…
¿ Qué pasa en el momento exacto en que el objeto se separa de la plataforma ?
Rta: Deja de haber contacto entre ellos, es decir, desaparece la fuerza normal.
Dicho de otra manera, en el momento crítico ene vale cero. Bueno, planteemos esto:
Esta es la conclusión a la que había que llegar: para que el objeto se separe, la aceleración de la plataforma debe ser la de la gravedad. ( Es decir, la de la gravedad o mayor).
La aceleración de la plataforma vale a = Θ A ω2 sen ωt, así que la máxima aceleración
posible es A ω2 ( O sea, sen ωt = 1 ). Lo planteo:
Pongamos la pulsación ω en función del período por medio de ω = 2π / T:
Reemplazando por los datos ( A = 0,5 m , g = 10 m/s2 )…
Este es el período de oscilación que tiene que tener la plataforma para estar en el caso
límite. ( O sea, a punto de despegarse de la plataforma ). Al disminuir el período aumenta la velocidad angular porque omega es dos pi sobre Te. Creo que se entiende que
con cualquier período menor a este se producirá la separación. ( Ej T = 1,3 s )
ASIMOV
- 42 -
Mov Armónico
Pongamos una masa colgada de un resorte y analicemos un poco:
Cuando cuelgo el peso del resorte este se estira una distancia X0. Ahí queda el cuerpo
colgado en equilibrio. En ese momento el peso P es equilibrado por la fuerza inicial que
hace el resorte. ( Fres0 ). El diagrama de cuerpo libre sería este :
EQUILIBRIO
Ahora tiro del cuerpo hacia abajo y lo suelto. Estoy sacando al sistema del equilibrio
y el cuerpo empieza a oscilar. Cuando el cuerpo oscila… ¿ Qué fuerzas actúan ?
Rta: Fijate el truco: Daría la impresión de que están la fuerza del resorte y el peso.
Pero no. O sea, si pero no. Uno puede considerar que la única fuerza que tira del cuer
po es la del resorte por que el peso se encuentra permanentemente compensado por la
fuerza que surgió del estiramiento inicial. ( Fres0 ). Entonces cuando el cuerpo está oscilando lo que tenemos es esto:
Es decir, tenemos un cuerpo que está movido por una fuerza que es proporcional a la
separación de la posición de equilibrio pero de sentido contrario. Esta es la característica fundamental del movimiento armónico. Por lo tanto, en principio, el movimiento de
una masa que oscila colgada de un resorte tendría que ser armónico simple. ( Por definición de movimiento armónico ). Pero vamos a demostrarlo como ellos quieren.
Si el movimiento es armónico las ecuaciones de posición, velocidad y aceleración van a
ser:
ASIMOV
- 43 -
Mov Armónico
Mirá la 3era ecuación. Fijate que el valor A sen ωt es la elongación x. Entonces la ecuación de la aceleración se puede poner como a = Θ ω2.x. Entonces planteando la ley de
Newton ∑ F = m.a me queda :
Puedo poner a la velocidad angular omega como 2π sobre T.
Analicemos un poco lo que obtuvimos. ¿ De qué depende el período de oscilación ?
Rta: de la constante del resorte y de la masa del cuerpo que cuelga. Fijate que el peso
no aparece en la expresión del período. Esto me está diciendo que el período de oscilación de un sistema masa-resorte depende de la masa del cuerpo que cuelga pero no
de su peso. Esto es importante porque significa que el período T es el mismo en cualquier lugar del universo donde uno ponga el sistema oscilante. Es decir, si acá en La
Tierra el período de oscilación es de 1,27 segundos, en La Luna también será de 1,27
segundos. ( En La Luna, en Marte, donde fuera ). El resorte no se ve influido por el valor de la gravedad del lugar donde uno haga el experimento.
FUNCIONA !
Pregunta: ¿ Qué pasa en un lugar donde no hay gravedad ? ¿ Oscila un sistema masaresorte en una nave espacial que flota en el espacio ? ( cuidado )
ASIMOV
- 44 -
Mov Armónico
Para responder esta pregunta hagamos un pequeño razonamiento. Pregunto :
¿ Vos ves que en la fórmula del período aparezca el peso del cuerpo ?
( Rta: No ).
¿ Ves que aparezca g ?
( Rta: no ).
Entonces quiere decir que el período de oscilación de un sistema masa-resorte no depende ni de P ni de g. Por lo tanto, en un lugar donde no hay gravedad el sistema debería oscilar exactamente igual que en un lugar donde hay gravedad.
Conclusión: Si acá en La Tierra el período de cierto sistema masa-resorte es de 1,27
segundos, en un lugar donde no hay gravedad también será de 1,27 segundos.
Esta deducción es correcta. Es más, este es uno de los métodos que se usa para "pesar"
un cuerpo en una nave espacial. Lo que se hace es atar el cuerpo a un resorte de constante conocida y se lo hace oscilar. Se mide el período y se despeja la masa.
Uno podría decir: Bueno, para comprobar el resultado teórico predicho por la ecuación
T = 2 Pi x Raíz m/K habría que ir a un lugar donde no haya gravedad.
Respuesta: No hace falta. Podés poner el cuerpo a oscilar en forma horizontal:
Ahora el peso no influye. Y el período de oscilación será el mismo.
Fijate también que el período tampoco depende de la Amplitud las oscilaciones. ( El
valor de A no figura en la fórmula ). Lo estires más o lo estires menos, el resorte siempre tarda lo mismo en ir y volver. ( Hay que pensar un poquito para darse cuenta de por
qué esto es así ). Lo mismo pasa con un péndulo común, valga la casualidad. El período de
oscilación de un péndulo no depende de la amplitud de las oscilaciones. ( ¿ Casualidad ? )
ACLARACIÓN: Para hacer esta deducción consideré que el resorte no tenía masa. No lo
dije, pero en realidad supuse que toda la masa que oscilaba estaba concentrada en el
peso que colgaba. En la realidad real esto no es así. Los resortes tienen masa y eso tiene una ligera influencia en el período de oscilación. Pero como pasa siempre, si la masa
del resorte es muy chica comparada con la del cuerpo que se cuelga, bueno, el efecto
de la masa oscilante del resorte es muy chico y se puede despreciar.
NOTA: El sistema masa-resorte es un concepto muy importante para la física. Suele
llamárselo "oscilador armónico". Vas a volver a ver esto muchas a lo largo de la carrera.
Por ejemplo en electricidad, cuando tengas circuitos con inductancias y capacitores.
Ahí va a volver a aparecer la frase "fijensé que el sistema se comporta como un sistema oscilante masa-resorte". ( Ahí lo que va a oscilar en forma alterna va a ser la tensión y la intensidad )
ASIMOV
- 45 -
Mov Armónico
Pongamos el péndulo a oscilar y analicemos un poco el asunto:
Mirá el diagrama de cuerpo libre. La tensión y el peso en Y no molestan. Ninguna de las
2 tiene influencia sobre el movimiento del péndulo. La fuerza que obliga al cuerpo a moverse es el peso en X. Voy a plantear ahora la 2da Ley de Newton ∑ F = m.a, pero antes
fijate esto:
1er truco:
La trayectoria que sigue la bolita del péndulo es un arco de circunferencia. Esto sería
una especie de movimiento armónico curvilíneo. Pero yo quiero un movimiento armónico
sobre un eje. Así que lo que hago es "enderezar" la trayectoria, o si lo preferís de otra
manera, miro la sombra de la bolita sobre el suelo.
Pregunta: ¿ Es válido hacer esto ? Bueno, en realidad no. Pero uno puede suponer que
las oscilaciones son muy chicas. ( Es decir, de pequeña amplitud ). En ese caso, a medida
que el ángulo α disminuye, la diferencia entre la recta y el arco de curva se achica.
( Alfa es el ángulo de separación de la posición de equilibrio ). Aclarando esto planteamos la segunda ley de Newton en x:
El porqué del signo Θ de Px es el siguiente: yo tomo el eje x con su origen en la posición
de equilibrio. Pe equis apunta al revés, por lo tanto es negativa. Me queda:
ASIMOV
- 46 -
Mov Armónico
2do truco: Tenemos un movimiento tal que su aceleración es proporcional al seno del ángulo de la separación de equilibrio y de sentido contrario. ( a = - g sen α ). Pero yo no
quiero un movimiento proporcional al seno del ángulo. Para tener un movimiento armónico yo necesito que la aceleración sea proporcional a alfa, no a seno de alfa. ¿ Qué hago ?
Y bueno, en vez de tomar sen αlfa, tomemos αlfa en radianes, que es parecido
Pregunta: ¿ Se puede hacer esto ? Bueno, más o menos. Uno puede suponer que las oscilaciones son muy chicas, es decir de pequeña amplitud. En ese caso, a medida que el ángulo de separación disminuye, la diferencia entre alfa en radianes y seno de alfa se
achica. Por ejemplo, sen 10° = 0,1736. Y 10° puestos en radianes son 0,1745
Entonces, suponiendo ángulos chicos, puedo poner a = - g sen α como:
Ahora puedo decir que tengo un movimiento armónico. ( Suponiendo que la amplitud de
las oscilaciones es chica y alfa es chico y toda la película ). Entonces como para los movimientos armónicos se cumple que la aceleración es Θω2X, reemplazo:
( Equis es la separación de la posición de equilibrio, es decir, la elongación ) . Por otra
parte el ángulo α en radianes se puede poner como arco sobre radio.
ASIMOV
- 47 -
Mov Armónico
Vamos a analizar ahora la frase "pequeña amplitud". ¿ Qué es "pequeña amplitud" ?
¿ Pequeña amplitud es αlfa = 5º ? ¿ αlfa = 1º ? ¿ Para qué valores de αlfa es válida la
fórmula del período de un péndulo ?
Bueno, la suposición básica que hicimos fue remplazar sen αlfa por αlfa. Hagamos una
tabla de valores y comparemos αlfa con sen αlfa:
La conclusión es que para α = 15º la diferencia entre α y sen α es de 0,003. ( 1 % ).
Para 10º es de 0,0009 ( 0,5 % ). Para 6º es de 0,0002 ( 0,2 % ). Una medición con un
error relativo de 1 porciento es una buena medición. Por lo tanto, para amplitudes de
hasta 15º podríamos decir que la fórmula anda bastante bien. Y su uno quiere ser exigente, puede tomar amplitudes de hasta 5 o 6 grados. Ahí el error relativo es del 0,2
porciento. ( Una medición excelente ).
Ahora contestemos la otra parte de la pregunta: ¿ De qué depende el período de un
péndulo ?
Bueno, el período de un péndulo es
,
Las únicas magnitudes que aparecen en esta fórmula son la aceleración de la gravedad
y la longitud del hilo. A medida que aumento la longitud del hilo aumenta el período.
A medida que aumenta la gravedad del lugar, disminuye el período. ( El péndulo oscila
más rápidamente ). Ahora... pregunta, ¿ Puede oscilar un péndulo en la luna ?
Rta: Si, pero va a oscilar más lentamente. Es decir, su período será mayor porque gLUNA
‹ gTIERRA
PREGUNTA: ¿ Oscila un péndulo en un lugar donde no hay gravedad ?
( Lo siento, esta pregunta tendrás que contestarla vos ).
EPÍLOGO:
Movimiento Armónico es un tema poco tomado. Por un lado es como que a los profesores no les gusta. Por otro lado, ellos prefieren tomar ondas ( En donde hay que saber
los conceptos de Movimiento Armónico ).
ASIMOV
- 48 -
Mov Armónico
Esto a veces lleva a la gente a decir: bueno, entonces Movimiento Armónico no lo estudio y chau. Pero no master ! Tenés que saber Movimiento Armónico porque esto es la
puerta de entrada a ONDAS. A su vez, ondas te va a preparar para entrar en interferencia y difracción. Y más adelante en electricidad y magnetismo. ( Agarrate ! )
Lee el resumen que puse al principio. Si te resulta más o menos comprensible, podés
seguir adelante.
FIN MOVIMIENTO ARMÓNICO
ASIMOV
- 49 -
Mov Armónico
MOVIMIENTO ARMÓNICO - EPILOGO
Van acá unos temas que tendrías que saber. Tal vez no los tomen, pero son conceptos
que vas a necesitar más adelante en la carrera ( o incluso en la vida ).
MOVIMIENTO ARMÓNICO AMORTIGUADO
El Movimiento Armónico que vimos acá nunca ocurre en la práctica. Una cuerda de guitarra vibra un rato y después se para. En la realidad real los movimientos se frenan.
Los péndulos se paran. ( o sea, hablando en forma teórica, no, pero en la práctica siempre hay algo de rozamiento). El movimiento real de un sistema masa-resorte es amortiguado. Un sistema masa-resorte sin rozamiento con el aire y sin rozamiento en el soporte también se va a frenar. Esto pasa porque al comprimirse y estirarse el resorte,
las moléculas rozan entre sí. Esto le va quitando energía a las oscilaciones y al final el
sistema se para.
¿ Cómo ? ¿ Y dónde va la energía ?
Rta: Se convierte en calor. Al final el resorte está quieto pero calentito. ( Debería, digamos ). Si vos graficas la Energía mecánica en función del tiempo para un Movimiento
Armónico Amortiguado te va a dar esto:
Fijate lo que pasa con las oscilaciones. Las oscilaciones van disminuyendo su amplitud:
A medida que pasa el tiempo la amplitud de las oscilaciones va disminuyendo. Esta disminución es exponencial. Esto es lo que pasa con un péndulo, con un sistema masaresorte o con una cuerda de guitarra. Esto es lo que pasa después de pegarle una patada a un caño. Esto pasa con cualquier cosa que esté oscilando.
ASIMOV
Mov Armónico
- 50 -
En realidad vos ya conocés muy bien el movimiento amortiguado desde que eras chico :
Es el movimiento de una hamaca. ( Te habías olvidado, ya ! ). Las hamacas al rato se paran. Hay que empujarlas para que se sigan moviendo. ( Una hamaca es un péndulo, por
cierto )
LOS AMORTIGUADORES DE LOS AUTOS
Los autos están sostenidos por resortes ( los elásticos ). Estos resortes se ponen para
que el auto se adapte a los pozos del camino. Pero a los autos se le ponen también amortiguadores. La función de los amortiguadores es evitar que el auto quede oscilando después de pasar por un pozo. Su función es disminuir esta vibración hasta cero. Los amortiguadores adentro tienen aceite. Amortiguan la vibración, de ahí viene el nombre.
Esta es la idea de movimiento armónico amortiguado. Las ecuaciones son un poco feas.
No hace falta que las sepas. Las vas a ver dentro de un par de años cuando curses Mecánica Racional. ( La materia Mecánica racional vendría a ser física I pero vista con un
grado gigantesco de complejidad. Agarrate ).
RESONANCIA
Este es un concepto que tenés que conocer. Aparece mucho en la física y aparece mucho en la ingeniería. La resonancia es causa de muchos problemas y de muchos accidentes. El asunto es así: Imaginate que tenés una hamaca. Vos la empujás para que se mueva. La hamaca oscila entre 2 puntos A y B. Supongamos que vos querés aumentar la amplitud de las oscilaciones. Para que eso pase tenés que empujar exactamente en el
momento en que la hamaca pasa por A y está volviendo hacia B .
HAY QUE EMPUJAR JUSTO ACÁ
B
A
Si vos empujás en otro momento, la hamaca se va a mover en forma medio rara. Por
momentos la vas a acelerar, por momentos la vas a frenar. Incluso se puede llegar a
ASIMOV
- 51 -
Mov Armónico
parar. Los empujones tienen que ser rítmicos y siempre "ayudando" a la hamaca. Es decir, dando el empujón en el momento exacto cuando la hamaca está yendo de A hacia
B ( y no al revés ). La gente sabe esto. Las madres que hamacan a sus hijos lo saben.
Saben que es así pero no saben por qué.
Analicemos lo que pasa: La hamaca tiene cierto período de oscilación. Supongamos que
sea de 4 segundos. Tarda 2 segundos en ir y otros 2 segundos en volver. La frecuencia
sería f = 1/T = 1 / 4 seg = 0,25 Hz. A esto se llama "frecuencia propia de oscilación".
Esta frecuencia no se puede cambiar. Está impuesta por la geometría del cuerpo. Uno
no puede hacer que la hamaca "vaya más rápido". Lo que sí se puede hacer es aumentar
la amplitud de las oscilaciones. Para lograr esto hay que dar los empujones con una frecuencia exacta. Concretamente, hay que dar un empujón cada 4 segundos. O sea, los
empujones tienen que ir en fase con la frecuencia propia de oscilación. Este es el
concepto de resonancia. Resonancia es empujar a un ritmo dado de manera tal que ese
ritmo coincida exactamente con la frecuencia natural de oscilación del objeto.
RESONANCIA: CONSISTE EN PEGARLE A UN OBJETO A INTERVALOS
RÍTMICOS DE MANERA QUE LA FRECUENCIA DE LOS GOLPES COIN
CIDA CON LA FRECUENCIA NATURAL DE OSCILACIÓN DEL OBJETO
RESONANCIA
Si entendiste esto, entendiste el concepto de resonancia.
¿ QUÉ PASA CUANDO HAY RESONANCIA ?
A esto quería llegar. Este es el concepto que tenés que entender. La pregunta es esta:
Supongamos que vos le pegás a algo a intervalos regulares de manera de hacerlo entrar
en resonancia. Yo le sigo pegando, y le sigo pegando y le sigo pegando.
¿ Qué pasa ?
Rta: Bueno, hay que pensarlo un poco. Con cada golpe que vos das entregás energía al
objeto que vibra. Esto hace que aumente la amplitud de las oscilaciones. A medida que
vos le vas pegando, la amplitud va aumentando. Mientras vos le sigas pegando, la amplitud va a seguir aumentando. En la práctica los movimientos son siempre es amortiguados. Entonces pueden pasar 3 cosas :
1 – Si la energía que entregás con cada golpe es MENOR que la que se come el rozamiento en cada oscilación, la amplitud va a ir disminuyendo. El cuerpo va a oscilar un rato y
después se va a parar.
2 – Si la energía que entregás con cada golpe es LA MISMA que la que se come el rozamiento en cada oscilación, el cuerpo oscila con amplitud constante. Se crea una especie
de equilibrio. Uno se limita a entregar la energía que se pierde por el rozamiento. Esto
es lo que pasa cuando hamacás a alguien. Vos empujás, pero la amplitud de las oscilaciones no aumenta. Se mantiene siempre en el mismo valor.
ASIMOV
- 52 -
Mov Armónico
3 – Si la energía que entregás con cada golpe ES MAYOR que la que se come el rozamiento en cada oscilación, entonces la amplitud va a ir aumentando. ( Aunque haya rozamiento ). Hablando en forma teórica, la amplitud tendería a infinito. Hablando en forma
práctica, el objeto no aguanta y se rompe antes. Esto es lo que pasa en la realidad real.
Cuando vos obligás a una cosa a entrar en resonancia, el objeto termina rompiéndose.
La resonancia es importante para la ingeniería. Si una máquina entra en resonancia puede romperse. ( Una máquina, un edificio, un avión, un puente, lo que sea ). Y cuando algo
se rompe… bueno, vos sabés lo que pasa. La fábrica se para, líos, se pierde plata, puede
haber heridos, juicios, etc. Y finalmente, la frase: ¡ Llamen al ingeniero ! ( Esto es algo
que vas a aprender con el tiempo: Cuando en algún lado algo se rompe… ¿ quién tiene la
culpa ? Rta: el ingeniero ).
Vamos a unos ejemplos concretos de resonancia:
EL CAPUCHÓN DE LA BIROME
Uno puede soplar en el capuchón de una birome para sacar un silvido. Lo que está pasando es que la columna de aire dentro del capuchón está entrando en resonancia. Los
instrumentos de viento como una flauta funcionan por resonancia. ( Lo vas a ver en ondas ).
LA GUITARRA
Las guitarras tienen una caja de madera que sirve como caja de resonancia. Si vos sacás esa caja, el sonido de las cuerdas se escucha menos.
LOS TEATROS
Un teatro no puede tener cualquier forma. La acústica de los teatros tiene que ver con
la resonancia de las ondas del sonido. Si la sala está mal construida, la acústica es mala.
EL RUIDO DE LOS MICRÓFONOS
A veces uno deja la guitarra eléctrica cerca del parlante y se empieza a escuchar un
ruido cada vez más fuerte. Es resonancia. El sonido de las cuerdas es guitarra es captado por el micrófono de la guitarra. El micrófono manda la señal al amplificador que lo
amplifica. El sonido sale por el parlante y vuelve a ser captado por el micrófono de la
guitarra. Y así sucesivamente.
También es resonancia el "piiiiiiii" agudo que a veces se escucha en los micrófonos.
LOS SERRUCHOS DE LA RUTA
A veces en las rutas ponen unas bandas en el piso. ( Se las suele llamar serruchos o
despertadores ). Generalmente están antes de las vías del tren o de los cruces peligrosos. El serrucho de la ruta tiene como objetivo hacer que te despiertes y disminuyas la
velocidad. Hay que pasarlos a 20 o 30 por hora. Si los pasás a 100 por hora, el auto pega tantos saltos que parece que se rompe todo. Los autos tienen una frecuencia propia
ASIMOV
- 53 -
Mov Armónico
de vibración. El serrucho está calculado para que el auto entre en resonancia al pasar a
unos 100 km por hora. Al pasar por el serrucho hay que bajar la velocidad o vas a sentir
que el auto explota.
Atención, para disminuir la vibración hay que alejarse de la frecuencia de resonancia.
Instintivamente uno tiende a bajar la velocidad. Pero si uno quisiera, también podría
SUBIR la velocidad. Tal vez pasando a 200 por hora se sienta la misma vibración que
pasando a 20 por hora. Habría que ver. ( No lo hagas ).
LOS SOLDADOS Y LOS PUENTES
La gente cree que los puentes y los edificios son cosas estáticas. No es así ( ¡ justamente no es así ! ). Los puentes y los edificios se mueven todo el tiempo. Vibran todo el
tiempo. ( Los ingenieros civiles suelen decir: Lo que no se mueve, se rompe ). Podés probar pararte en un puente cuando pasan los camiones. Vas a ver como todo el puente se
sacude. Puentes y edificios tienen una frecuencia propia de vibración. Entonces la historia es esta: A veces los soldados van marchando. Esto significa que todos golpean el
piso con el mismo pie en el mismo momento. Se dice que cuando los soldados llegan a un
puente se les ordena romper formación. Supuestamente esto es porque la frecuencia
de los pasos podría entrar en resonancia con la frecuencia propia de oscilación del
puente. En realidad esto es un mito. Nadie sabe si es verdad. Los de Mithbusters trataron de comprobar este asunto e hicieron el experimento. La conclusión a la que llegaron no importa porque el experimento que hicieron fue medio así nomás y con poco rigor científico.
¿ UN GRITO PUEDE ROMPER UN VASO ?
Dicen que un cantante con voz muy aguda y muy potente puede llegar a romper una copa
de cristal. Supuestamente para lograrlo tiene que mantener una nota aguda durante un
rato. ( Esto también es un mito ).
Ahora, un sonido fuerte puede romper un vidrio. Esto sí es verdad. A veces las explosiones rompen vidrios a una cuadra de distancia. Al vidrio no lo rompe la explosión. Lo
rompe la onda sonora.
SIETE VUELTAS DARÁS ALREDEDOR DE LA MURALLA
Se dice que la caída de las murallas de Jericó fue producida por el estridente sonar de
muchos cuernos de carneros. Probablemente esta historia esté escrita en La Biblia en
sentido figurado. Ni mil cuernos, ni 10 mil cuernos sonando a la vez pueden tirar abajo
una muralla. Pero en teoría la idea es correcta. Se puede tirar abajo una casa o una muralla con un sonido muy fuerte. Pero para tirarla abajo no creo que alcancen mil cuernos, ni 10 mil cuernos. Supongo que se deben necesitar 10 millones de cuernos. Pero en
ese caso, la gente que estuviera soplando los cuernos moriría antes de que se cayeran
las murallas.
Fijate que en las canchas de fútbol tenés como 50 mil personas gritando gol al mismo
tiempo y la cancha no se cae. ( La vibración se siente, eso sí )
ASIMOV
- 54 -
Mov Armónico
LA VIBRACIÓN EN EL VENTILADOR
Cuando uno prende un ventilador la paleta acelera desde cero hasta llegar a su velocidad angular final. Esto dura 2 o 3 segundos. En el medio de ese proceso puede haber un
momento donde todo el ventilador vibre más fuerte. Eso quiere decir que en ese momento estás pasando por la frecuencia de resonancia. Después la paleta sigue acelerando y la vibración se calma. Lo mismo pasa cuando uno apaga el ventilador. Este mismo
efecto lo podés ver en cualquier aparato que gire. Por ejemplo, una amoladora. ( Piedra
de afilar ).
LAS CANILLAS
A veces abrís una canilla y hace un ruido tipo piiiiiiii. Si la abrís más, el ruido para.
Eso es resonancia. Por algún motivo, para cierta velocidad de salida del agua, alguna
parte de la válvula se pone a vibrar. Y el agua la hace vibrar justo a la frecuencia de
resonancia. Por eso vibra mucho y hace ruido. Abriendo más la canilla ( o cerrándola ),
el ruido tendría que desaparecer.
LA AMISTAD
A veces uno conoce una persona, charlás un rato y decís: che, que tipo macanudo tu
primo. Es resonancia. Las cosas que te dijo tuvieron eco en vos. Por eso crees que te
cae simpático. Sus ideas resuenan con las tuyas. Cuando una persona le cae bien a alguien se dice que "tiene buena onda". ( Oh, casualidad ! )
Es probable que el amor sea un caso de resonancia. Dicen que existe el amor a primera
vista. Si existe, ponele la firma que es resonancia.
BOLITA EN UNA PALANGANA
Resolvamos este problema ( supuestamente ) infernal
SE COLOCA UNA BOLITA EN UNA PALANGANA SEMICIRCULAR DE RADIO R COMO
INDICA LA FIGURA. CALCULAR EL PERÍODO DE LAS OSCILACIONES DE LA BOLITA
En principio este problema no parece tener manera de resolverse. Pero hay un truco.
El truco es este: Fijate qué pasa si tengo un péndulo de longitud eLe:
ASIMOV
Mov Armónico
- 55 -
A
Quiero que te fijes en el diagrama de cuerpo libre de la bolita del péndulo. Lo hago para el punto A. El diagrama es este :
DIAGRAMA DE CUERPO
LIBRE PARA UN PÉNDULO
Ahora fijate cómo es el diagrama de cuerpo libre para la pelotita en la palangana :
DIAGRAMA DE CUERPO
LIBRE PARA LA BOLITA
EN LA PALANGANA
Fijate que los 2 diagramas de cuerpo libre son iguales. O sea, la diferencia es que en
uno está la tensión y en el otro está la Normal. En uno está la longitud del péndulo y en
el otro está el radio de la pista. Pero bueno, es lo mismo. La fuerza normal cumple la
misma función que la tensión. ( = Anula a PY ). La longitud del hilo cumple la misma función que el radio R. En los 2 casos las fuerzas que actúan son las mismas. La trayectoria
va a ser la misma. El movimiento va a ser el mismo. Entonces, para un péndulo el período
es :
Y para la bolita en la palangana el período será :
NOTA 1:
Para esta deducción van las mismas aclaraciones que para el péndulo. Concretamente, la
fórmula deducida no es totalmente exacta. Se hace más exacta a medida que disminuye
la amplitud de las oscilaciones. Podemos tener una fórmula bastante buena para ángulos
de oscilación menores a 5 º.
NOTA 2: Fijate que el período de oscilación no depende de la masa de la bolita. Quiere
ASIMOV
- 56 -
Mov Armónico
decir que el mismo período tendría un autito que se dejara caer por la palangana o un
chico que estuviera haciendo skate con una patineta.
EL PERÍODO NO CAMBIA.
SOLO DEPENDE DE R Y DE g
LOS SALTOS EN LOS RECITALES
Habrás notado que la gente salta en las canchas y en los recitales. Y no son 100 personas las que saltan. Son MILES. Esos saltos de miles de personas a la vez son complicados. Por un lado, cuando una persona está parada, la fuerza que ejerce sobre el piso es
su peso. Cuando una persona salta, la fuerza que ejerce es de varias veces su peso.
Por otro lado, el problema es que la gente que salta, CANTA mientras va saltando. Es
decir que las miles de personas que saltan, lo hacen a un mismo ritmo. O sea, golpean el
piso en el mismo momento todos a la vez. Si ese salto coincide con la frecuencia de resonancia del lugar donde la gente está parada.... Desastre.
Por eso es relativamente común que se caigan balcones en los casamientos o en las despedidas en los boliches. Vos podés poner 10 personas en el balcón de tu casa. Podés poner 20 también. No pasa nada. El balcón no se va a caer. Está calculado para eso. Lo que
no podés hacer es poner 10 personas en un balcón que estén todas saltando a la vez.
PUEDE SER MULTIPLO TAMBIEN
Una aclaración: Para hacer que una cosa entre en resonancia, no hace falta golpear
exactamente con la frecuencia de resonancia. La frecuencia de los golpes puede ser un
múltiplo de la frecuencia de resonancia. O sea, supongamos que la frecuencia de resonancia de una cosa es de 100 vibraciones por segundo. Vos para hacer que el objeto entre en resonancia también podés golpear con una frecuencia de 10 golpes por segundo.
LA ROTURA NO ES INMEDIATA
Si hay resonancia, el objeto no se rompe inmediatamente. O sea, no es que cuando se
llega a la frecuencia de resonancia el objeto explota. Depende como esté construido.
Una máquina o un puente puede vibrar mucho tiempo estando en resonancia.
ASIMOV
- 57 -
Mov Armónico
MOVIMIENTO ARMÓNICO FORZADO
Suponé que tenés un motor que vibra. Lo ponés sobre una mesa y el motor obliga a la
mesa a vibrar. Se dice que la mesa tiene una vibración forzada. No vibra porque quiere.
La obligan a vibrar.
Esta situación de vibración forzada aparece mucho en la ingeniería. Por ejemplo, un auto que tenga una rueda desbalanceada, obliga a toda la carrocería a vibrar. Por un lado,
esta vibración es molesta para la gente que va en el auto. Por otro lado, si la rueda está
MUY desbalanceada y vos vas a 200 por hora... y bueno, podés romper el eje de la ruda.
( accidente ).
Algo parecido podés ver en el lavarropas de tu casa. A veces la vibración es tan grande
que el lavarropas literalmente hablando, camina.
Las turbinas de los aviones tienen unas paletas que giran a gigantesca velocidad ( Los
alabes ). Estos alabes tiene que estar muy bien balanceados. A la menor desviación, toda la turbina empieza a vibrar.
Ni te cuento si se llega a romper un alabe ! Ahí sí, toda la turbina podría llegar a desarmarse por la terrible vibración. ( Ha pasado ).
Las ecuaciones de movimiento armónico forzado son feas. Las vas a ver en Mecánica.
ECUACIÓN DIFERENCIAL DEL MOVIMIENTO ARMÓNICO
En el movimiento armónico la aceleración está dada por a = - ω2. x . Esto lo puedo poner
así :
Hablando matemáticamente, la velocidad de un movimiento es la derivada de la posición.
Y a su vez, la aceleración es la derivada de la velocidad. Quiere decir que uno puede
poner que la aceleración es la derivada segunda de la posición. O sea :
ASIMOV
- 58 -
Mov Armónico
Entonces puedo poner a = - ω2. x en forma de ecuación como :
A este choclín se lo llama "Ecuación diferencial del movimiento armónico". Una ecuación
diferencial es una ecuación que no tiene números. Tiene funciones y sus derivadas. En
una ecuación común la incógnita es un número. En una ecuación diferencial la incógnita
es una función. Todo esto lo vas a ver en análisis II. ( Agarrate )
¿ qué sentido tiene poner esto así ?
Rta: Bueno, nada. Es una manera matemática de ver las cosas. A los matemáticos les
gustan las ecuaciones. A los matemáticos les fascinan las ecuaciones. Un matemático se
emociona al ver una expresión de este tipo. Para un matemático esta ecuación tiene una
belleza inimaginable que no cualquier persona puede ver. Es una ecuación que me dice
que yo tengo una función x(t) que no conozco. No conozco la función x(t) , pero sé que es
una función tal que si la derivo 2 veces, eso me da lo mismo que una constante ω2 multiplicada por la función.
Además, dicen ellos, sé que si mañana descubro otra ecuación que tenga la forma
DERIVADA SEGUNDA + K FUNCIÓN = 0
Esa ecuación me está diciendo que lo que tengo es un movimiento armónico. Por ahora
alcanza con que sepas que en movimiento armónico se puede poner como una ecuación
diferencial. En análisis II ya vas a ver con lujo de detalles todo esto de las ecuaciones
diferenciales.
EL PUENTE DE TACOMA
En el año 1940 los yanquis construyeron un puente colgante gigantesco. En ese momento
era uno de los más grandes del mundo. Tenía casi 2 km de largo. Cruzaba el río de Tacoma. Acá tenés un dibujo:
Pues bien, resulta que un día empezó a haber mucho viento y el puente se empezó a balancear. La estructura estaba entrando en resonancia con las ráfagas de viento. La vibración no era hacia arriba y hacia abajo sino que era torsional. ( O sea, el puente se
ASIMOV
- 59 -
Mov Armónico
retorcía como cuando uno retuerce un hilo ). Tanta fue la vibración que finalmente el
puente se cayó. Esto le mostró a los ingenieros lo terrible que puede llegar a ser la resonancia.
TACOMA
FELIZ CUMPLEAÑOS
Amigo, quiero hacerte un regalo por haber aguantado y haber llegado hasta acá. Resulta que el puente de Tacoma estuvo oscilando largo rato. De manera que a uno se le ocurrió filmarlo. Conclusión: La caída del puente de Tacoma está filmada. Te pido un favor.
Dejá todo lo que estás haciendo y buscá una computadora. Poné "Puente de Tacoma" en
el Google y mirá la filmación. Haceme caso. Yo sé lo que te digo.
ASIMOV
- 60 -
Mov Armónico