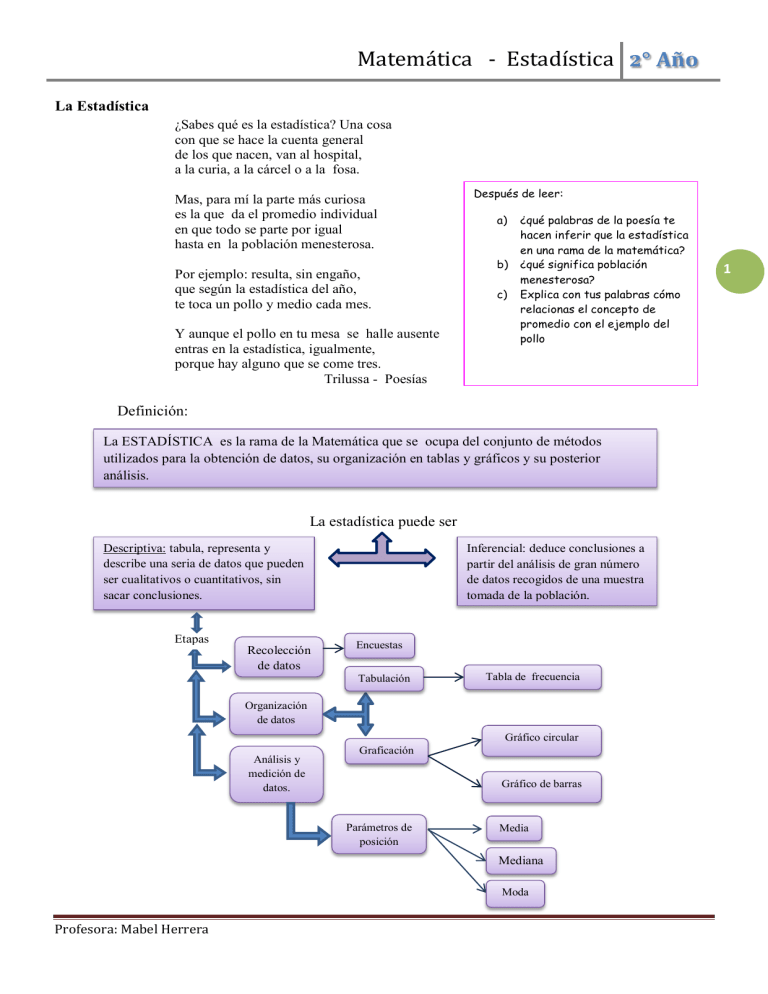
Matemática - Estadística 2° Año La Estadística ¿Sabes qué es la estadística? Una cosa con que se hace la cuenta general de los que nacen, van al hospital, a la curia, a la cárcel o a la fosa. Mas, para mí la parte más curiosa es la que da el promedio individual en que todo se parte por igual hasta en la población menesterosa. Por ejemplo: resulta, sin engaño, que según la estadística del año, te toca un pollo y medio cada mes. Y aunque el pollo en tu mesa se halle ausente entras en la estadística, igualmente, porque hay alguno que se come tres. Trilussa - Poesías Después de leer: a) b) c) ¿qué palabras de la poesía te hacen inferir que la estadística en una rama de la matemática? ¿qué significa población menesterosa? Explica con tus palabras cómo relacionas el concepto de promedio con el ejemplo del pollo Definición: La ESTADÍSTICA es la rama de la Matemática que se ocupa del conjunto de métodos utilizados para la obtención de datos, su organización en tablas y gráficos y su posterior análisis. La estadística puede ser Descriptiva: tabula, representa y describe una seria de datos que pueden ser cualitativos o cuantitativos, sin sacar conclusiones. Etapas Recolección de datos Inferencial: deduce conclusiones a partir del análisis de gran número de datos recogidos de una muestra tomada de la población. Encuestas Tabulación Tabla de frecuencia Organización de datos Gráfico circular Análisis y medición de datos. Graficación Gráfico de barras Parámetros de posición Media Mediana Moda Profesora: Mabel Herrera 1 Matemática - Estadística 2° Año En la recolección de datos debemos tener en cuenta algunos conceptos importantes: Población: conjunto de individuos o elementos que se analizan en un estudio estadístico. Si es muy numeroso, se toma una muestra representativa y se extienden los resultados a toda la población. Variable: Característica que se analiza. La variable puede ser: a) Cualitativa: relativa a alguna cualidad, se expresan a través de una palabra. Por ejemplo color preferido, tipo de transporte, religión, etc. b) Cuantitativa: relativa a la cantidad, se expresan a través de un número. Por ejemplo la cantidad de hermanos, edad, estatura, etc. Dentro de las cuantitativas pueden ser: Continuas: se miden con números reales, tales como estatura, peso, etc. Discretas: Se miden con números enteros, tales como número de hijos, número de goles, etc. Actividad: 1.- Determina si estas variables son cualitativas o cuantitativas y en ese caso si es continua o discreta: a) b) c) d) e) f) Color de ojos Cantidad de menús comprado en un local de comidas rápidas. Número de libros que se leen en vacaciones. Altura de los jugadores de básquet de la liga juvenil. Cantidad de horas por semana que una persona realiza actividad física Género de películas que prefieren. 2.- Una consultora preparó dos encuestas. La primera se realizará a 1.200 alumnos de nivel secundario de la ciudad de Córdoba y, la segunda, a 1.500 alumnos universitarios de la misma ciudad. Indica en cada caso cuál sería la población y cuál es la muestra. Luego rodea con color azul las variables cuantitativas y con rojo las cualitativas. NIVEL UNIVERSITARIO NIVEL SECUNDARIO Horas de lectura semanales Deportes que practica. Horas diarias que juega a la Play. Población: Muestra: Redes sociales que utiliza Horas semanales que concurre a la universidad. Música preferida. Población: Muestra: Las respuestas obtenidas se denominan datos. Una vez que contamos con los datos, debemos organizarlos y presentarlos. La frecuencia o frecuencia absoluta (f) de un dato es la cantidad de veces que ese dato se repite. La frecuencia relativa (fr) indica la relación entre la frecuencia de un dato y la cantidad total de datos (n) La frecuencia porcentual f% es otra forma de expresar la relación anterior y facilita el gráfico circular. Profesora: Mabel Herrera 2 Matemática - Estadística 2° Año Ejemplo: Se consultó a 75 personas sobre la estación del año que prefieren: Estación Frecuencia absoluta Invierno 6 Verano 30 Otoño 18 Primavera 21 Totales 75 Frecuencia relativa Porcentaje 3 1 100% Actividades: 3.- Completa la tabla de frecuencias que muestra las edades de los 40 alumnos que van a representar al colegio en una competencia deportiva. La cantidad de chicos de 16 años es el doble de los que tienen 14. Edad 14 15 16 17 Total f fr f% a) ¿Cuánto suman las ? ¿y las f%? b) ¿Cuántos son menores de 16? ¿Qué porcentaje representan? 8 12 c) ¿Qué fracción del grupo representan los de 15 y 16 años juntos? d) ¿Qué porcentaje representan los menores de 17 años? 4.- Hacé de profe: Juli completó con color la tabla de frecuencias, pero cometió algunos errores. Encontralos y escribe los números correctos. Tipo de novela f fr f% De aventuras 12 0.2 2 Romántica 22 0,44 44 Histórica 16 0,36 36 Total 50 1 82 Los resultados de una encuesta se pueden presentar con gráficos estadísticos. Los gráficos de barras se utilizan para representar la frecuencia absoluta de variables cualitativas o cuantitativas discretas. Son rectángulos de igual base y cada uno corresponda a un valor de la variable. La altura de cada rectángulo indica un valor (f) sobre sobre un eje vertical con una escala determinada. Profesora: Mabel Herrera Matemática - Estadística 2° Año Ejemplo: En la tabla se registra la cantidad de botellas de gaseosas de cada sabor que se compran para una reunión. Sabor Cola Naranja Pomelo Lima- Limón Agua Tónica 8 6 4 2 0 Frecuencia 6 3 5 4 3 Cola Naranja Pomelo Lima limón Agua tónica Los gráficos circulares o de torta se utilizan para mostrar el porcentaje de cada valor de la variable, y es un círculo dividido en sectores circulares. El ángulo central de cada sector circular es proporcional a la frecuencia y se halla multiplicando la frecuencia relativa de cada valor de la variable y 360°. Ejemplo: Medio litro de jugo contiene 200 cm3 de agua, 125 cm3 de jugo de frutas naturales y 175 cm3 de colorantes y conservantes. Frecuencia relativa Ángulo central Jugo de frutas 0,25 0,25.360°=90° Agua 0,4 0,4.360°=144° Colorantes y conservantes 0,35 0,35.360°=126° Jugo de frutas Agua colorantes y conservantes Actividades: 5.- Realiza los gráficos de barra y circular del ejercicio 3. 6.- Se realizó una encuesta acerca de la red social preferida (se podía elegir una sola). Completa el gráfico y la tabla usando las pistas. La opción menos elegida fue Twitter que, junto con wathsapp, la más votada, llegan la mitad de los votos. El ángulo central correspondiente a Instagram es de 72° 48 personas votaron por Facebook. Redes sociales Twitter Waathsapp Instagram Facebook Total f 10% f% Instagram 7.- El gráfico muestra los resultados de una encuesta que se les realizó a 200 personas sobre su comida preferida (se podía elegir solo una) Profesora: Mabel Herrera 4 Matemática - Estadística 2° Año a) ¿Cuántas personas prefieren comer piza? b) ¿Es cierto que más de la mitad de los encuestados prefiere comer milanesas o ravioles? ¿Cómo te das cuenta sin hacer ningún cálculo? Pizza 18% Milanesas Empanadas 36% c) Los que prefieren ravioles, ¿son más de la cuarta parte de los encuestados o son menos? ¿Qué porcentaje más o cuánto menos? 28% Asado Ravioles 8% 5 Análisis y medición de datos – Medidas de tendencia central Cuando las variables son numéricas, es útil buscar valores que representen la muestra, como la media, la moda y la mediana que dan idea de “alrededor de qué número” están los datos. Promedio o moda (̅): se obtiene como el cociente entre la suma de todos los datos y la cantidad de datos. Moda ( ): Valor que tiene mayor frecuencia. Puede ser que no haya moda (si los datos no se repiten o si todos tienen la misma frecuencia) o que exista más de una moda. Mediana ( ): Valor que ocupa el lugar central al ordenar los datos de menor a mayor. Si la cantidad de datos es par, se promedian los datos centrales. Ejemplo: Estas son las notas que obtuvieron ocho alumnos en la evaluación de Historia: 10 5 6 7 8 6 8 8 El promedio es ̅ La moda es Mo = 8 La nota que aparece más veces. Para obtener la mediana primero se ordenan los datos de menor a mayor: 5 6 6 7 8 8 8 10 significa que la mitad de los alumnos obtuvo notas por debajo de 7,5 y la otra mitad, por encima de ese valor. Actividades: 8.- Los alumnos de un curso armaron un blog. La tabla muestra la cantidad de visitas que tuvo el blog en los primeros días de la semana pasada Lunes Martes 137 Miércoles 143 141 Jueves 137 Viernes 139 Sábado 137 a) ¿Cuál fue el promedio diario de visitas durante esos días? ¿Cuáles fueron la moda y la mediana? b) El domingo de esa semana hubo un problema de conexión y solo pudieron entrar 6 personas en el blog. Calcula nuevamente el promedio, la moda y la mediana. 9.- Los datos siguientes corresponden a las horas por semana que destina un grupo de estudiantes a hacer la tarea. 12 – 5 – 10 – 4 – 14 – 12 – 10 – 12 – 15 - 10 12 – 5 – 15 – 8 – 6 – 12 – 10 – 4 – 6 - 8 Profesora: Mabel Herrera a) ¿Cuál es la mediana? ¿Qué representa ese valor? b) ¿Cuál es el valor más frecuente? ¿Qué medida representa ese valor? c) ¿Cuántas horas semanales destinan estos estudiantes, en promedio, a hacer la tarea?









