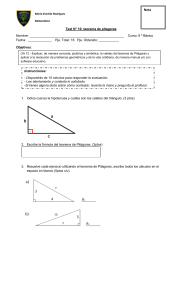
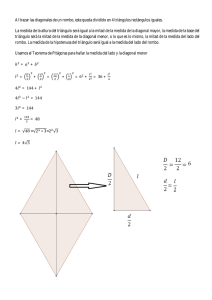
Matemáticas en TODO y para TODOS… Ciclo 2019 - 2020. ´ ´ ENTRENAMIENTO OLÍMPICO NIVEL INTERMEDIO. Del teorema anterior se tienen las siguientes ecuaciones: 𝑐 = √𝑎2 + 𝑏 2 Raíz cuadrada y teorema de Pitágoras 𝑎 = √𝑐 2 − 𝑏 2 Problema 1.- Utilizando las sugerencias del video 1 calcula las raíces cuadradas positivas de los siguientes números: a) √64 b) √900 c) √225 d) √441 e) √72 f) √300 g) √1500 h) √77 Problema 2.- Utilizando las sugerencias del video 2 para lados enteros y usando el teorema del pañal, encuentra las medidas del lado que falta en los siguientes triángulos rectángulos: 𝑏 = √𝑐 2 − 𝑎2 Problema 4.- Utilizando las sugerencias del video 3 y usando el Teorema de Pitágoras, encuentra las medidas del lado que falta en los siguientes triángulos rectángulos: 8 cm 18 cm 4 cm 24 cm 65 cm 12 cm 9 cm 5 cm 63 cm 12 cm 17 cm PASOS A SEGUIR PARA VER LOS VIDEOS. 1. 2. 15 cm Problema 3.- Utilizando las sugerencias del video 2 y usando el teorema del pañal, para lados no enteros encuentra las medidas del lado que falta en los siguientes triángulos rectángulos: 3. 4. 5. Entrar a Facebook. Escribir en el buscador (Kuviká Consultoría de matemáticas) Dar click en la opción de grupos. Entrar al grupo Prenacional Básico. Mandar solicitud de aceptación al grupo. 12 cm 10 cm 6 cm CEL: 247 104 5313. CORREO: roger_rr1@hotmail.com 10 cm 16 cm 12 cm TEOREMA DE PITÁGORAS En todo triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. 𝑐 2 = 𝑎2 + 𝑏 2 C a Diseño del problemario: Prof. Roger Ramos Ramos. b Síguenos en nuestra página de facebook: Kuviká Consultoría de Matemáticas Prof. Roger Ramos Ramos Cel: 247 104 5313 Matemáticas en TODO y para TODOS… Ciclo 2019 - 2020. ´ ´ ENTRENAMIENTO OLÍMPICO NIVEL INTERMEDIO. Problema 7.- (ONMAPS 2018) Se tiene tres hexagonos regulares como se muestran en la figura. Encuentra el área sombreada, si el lado del hexágono más pequeño mide 2. Aplicación del teorema de Pitágoras Problema 1.- Un cuadrado se encuentra inscrito en una circunferencia de radio 3 cm como se muestra en la figura. Calcular el área sombreada. Problema 2.- Calcular la medida de la diagonal del cuadrado si el perímetro de la circunferencia es de 8π. Problema 8.- (ONMAPS 2018) En el pentágono 𝐴𝐵𝐶𝐷𝐸 se tiene que 𝐴𝐵 = 𝐵𝐶 = 8, 𝐶𝐷 = 4√3 y 𝐷𝐸 = 6. Además, 𝐴𝐵𝐶 = 60𝑜 , 𝐵𝐶𝐷 = 𝐶𝐷𝐸 = 150𝑜 . Determina el área de ABCDE. Problema 3.- Calcular el área de un hexágono si la medida de su lado es de 2 cm. Problema 4.- En la siguiente figura se tienen dos triángulos equiláteros de lado 4 cm y 8 cm respectivamente. Calcular el área del triángulo BCD. D C Problema 9.- (ONMAPS 2017) Sea 𝐴𝐵𝐶 un triángulo cuyo ángulo en 𝐴 vale 135𝑜 . Sea 𝑀 el punto medio de BC, si A 4 cm B E 8 cm 𝑀𝐴𝐵 = 90𝑜 y 𝑀𝐵 = 5. ¿cuánto vale el área de 𝐴𝐵𝐶? Problema 5.- Calcular la medida de la altura trazada desde el vértice C del triángulo BCD. B D Problema 6.- En la siguiente figura se tiene un triángulo equilátero y un cuadrado. Si el lado del triángulo equilátero mide 8 cm. Calcular el valor del área sombreada. Diseño del problemario: Prof. Roger Ramos Ramos. Síguenos en nuestra página de facebook: Kuviká Consultoría de Matemáticas Prof. Roger Ramos Ramos Cel: 247 104 5313
