j.renene.2015.01.068

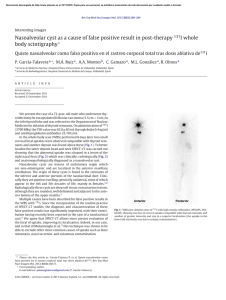
Renewable Energy 80 (2015) 275e285
Contents lists available at ScienceDirect
Renewable Energy
journal homepage: www.elsevier.com/locate/renene
Effect of hydrofoil flexibility on the power extraction of a flapping tidal
generator via two- and three-dimensional flow simulations
Tuyen Quang Le b, Jin Hwan Ko a, *
a
b
Korea Institute of Ocean Science & Technology, Ansan 426-444, Republic of Korea
Institute of High Performance Computing, Singapore 138632, Singapore
a r t i c l e i n f o
a b s t r a c t
Article history:
Received 10 February 2014
Accepted 30 January 2015
Available online
In this study, we investigate the effect of hydrofoil flexibility on the power extraction of a flapping tidal
stream generator with hydrofoils down-scaled for a water channel in an experiment with a typical
Strouhal number and frequency. The described deformations in the chord and spanwise directions are
imposed onto the surfaces of the hydrofoil to analyze the flexibility effect. In a two-dimensional (2D)
simulation, parameter studies of the chordwise flexure are conducted and a 30% improvement in the rate
of the power-extraction efficiency is then achieved when the chordwise flexure is 20% of the chord
length. In a three-dimensional (3D) simulation, the chordwise flexure of 20% achieves a 15% improvement in the rate of the power-extraction efficiency for the hydrofoil with an aspect ratio (AR) of 5, which
is less than that in the 2D simulation due to 3D effects such as tip loss and a spanwise vortex. Meanwhile,
the effect of the spanwise flexure on the power extraction is minor as compared to that of the chordwise
flexure. It was also found throughout the parametric study of the AR variation that the 3D effect of the
chordwise flexible hydrofoil is slightly stronger than that of the rigid hydrofoil.
© 2015 Elsevier Ltd. All rights reserved.
Keywords:
Flapping tidal generator
Chordwise flexure
Spanwise flexure
Power-extraction efficiency
Three-dimensional effect
1. Introduction
Tidal stream energy has been considered as one of renewable
energy sources in order to reduce our dependency on fossil fuels.
So far, most tidal stream generators have been developed in three
types: horizontal axis, vertical axis, and flapping type generators
[1]. Among them, the flapping type devices are still in a nascent
status as compared to the rotary-type turbines with horizontal
and vertical rotational axes [2e5]. In 21 century, the several
flapping systems as commercial products have been designed,
developed or installed. Meanwhile, the flapping systems still
need improvement in power-generating capability, controllability and structural safety in order to be considered as a viable
alternative of the rotary-type generators despite the fact that
they are known to be eco-friendly systems due to relatively low
tip speed [6].
* Corresponding author.
E-mail address: jhko@kiost.ac (J.H. Ko).
http://dx.doi.org/10.1016/j.renene.2015.01.068
0960-1481/© 2015 Elsevier Ltd. All rights reserved.
The flapping generators have been investigated in both experimental and numerical studies in recent years. As a first attempt, in
the 1980s, an experimental study showed that wind energy could
be extracted from a flapping foil while coupling the pitch and
plunge motions in the proper conditions [7]. Later, the optimal efficiency of a flapping generator was determined through parameter
studies. An experimental study with an aluminum NACA0012 hydrofoil explored power-extraction efficiency as the function of the
Strouhal number, the phase angle between the pitch and plunge
motion, and the angle of attack. A maximum efficiency of 43% was
achieved under an optimal condition in which Strouhal number
was 0.4 and the maximum angle of attack was 34.4 with a phase
angle difference of 90 between the pitch and plunge motions [8].
The pitching axis location within chord lengths of 0.2e0.5 from the
leading edge was recommended based on a study considering
constrained sinusoidal pitching motion [9]. When the pitching axis
was close to the downstream area of the mid-chord point, selfinduced oscillation was presented in experimental studies, particularly those of Semler [10]. For a dual-foil configuration, the results
from a two-dimensional simulation showed good agreement with
the experimental results of a 2 kW prototype, and the three-
276
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
dimensional effect on a flapping tidal generator was also investigated by Kinsey and Dumas [11,12]. In that study, the drop in the
hydrodynamic performance due to the finite span length was
determined as compared to a two-dimensional case. According to
the results, the endplate at the foil tip and the high aspect ratio foil
were proposed to minimize the tip loss; with them, the reduction in
the performance of the three-dimensional foil could be limited to
around 10% as compared to the two-dimensional foil.
Thus far, wing flexibility mimicked from flapping flying or
swimming creatures is well known as a key factor to improve the
level of propulsive efficiency. Experimental studies on the propulsive systems were intensively conducted, hence optimal efficiency,
correlation between leading edge vortex (LEV) and spanwise flow
were figured out [13e15]. When the Strouhal number is larger than
0.2, moderate spanwise flexibility can induce a slight increase in the
thrust and a slight decrease in the required power, yielding high
propulsive efficiency in a water channel experiment [16]. A stronger LEV in a flexible wing was observed in these experiments as
compared to that in a rigid wing. A two-dimensional numerical
simulation with a fluidestructure interaction model showed that a
flexible ray with leading edge strengthening could improve the
thrust and propulsive efficiency [15]. In contrast to propulsive
systems in which thrust is required, the flapping tidal generator
creates a high drag while its power is mainly extracted from lift.
Therefore, chordwise and spanwise flexibility can be utilized to
improve the power-extraction efficiency of a flapping tidal generator by alternating the size of the LEV and by synchronizing the
phase of the instantaneous lift force and plunge velocity. Recently, a
two-dimensional numerical simulation of a flapping hydrofoil with
local described deformation was carried out to investigate the
benefits of flexibility on the extraction of power [17]. The results
showed that a flexible hydrofoil is beneficial to enhance the powerextraction efficiency by increasing the peak of the lift and shifting
the phase between the instantaneous lift force and plunge velocity
in a favorable pattern.
In this study, the effects of chordwise as well as spanwise flexure
on the power-extraction efficiency of a flapping hydrofoil are
investigated through two-dimensional and three-dimensional numerical simulations with an in-house code. The dimensions of the
flapping hydrofoil and the operating condition were determined by
considering the water channel in lab-scale experiments. The
amounts of chordwise and spanwise deformations were directly
determined by quadratic functions in the simulations. In addition,
the effects of the aspect ratio of the hydrofoil on the powerextraction efficiency were explored.
2. Numerical method
2.1. Flow solver
The power extraction performance of a flapping hydrofoil is
estimated by an in-house parallelized multi-block structured
NavieseStokes solver, which is named as KFLOW [18,19]. The timedependent viscous flow around the flapping foil is simulated by
solving the preconditioned Reynold-Averaged NavieseStokes
equation as below
G1
vWT vW vðFi þ Fvi Þ
þ
þ
¼0
vt
vxi
vt
ði ¼ 1; 2; 3Þ;
(1)
where G1 is the time-derivative preconditioning matrix, t is the
pseudo time, t is the real time, WT is the primitive flow variable, and
W is the conservative flow variable; Fi and Fvi are the inviscid and
viscous fluxes in each direction, respectively. WT, W, Fi and Fvi are
defined as follows:
2
2
3
3
3
r
p
rui
6
6 7
6
7
7
WT ¼ 4 ui 5; W ¼ 4 rui 5; Fi ¼ 4 rui uj þ pdij 5;
T
rE
rui H
3
2
0
7
6
7
6 t þ t*
7
6 ij
ij
Fvi ¼ 6
7:
7
6 5
4
vk
ui tij þ t*ij qj þ ðml þ sk mt Þ
vxi
2
(2)
Here, the pressure p and the temperature T are expressed in perturbed forms to decrease the round-off and the cancellation errors
in very low Mach number flows. r is the density and ui is the velocity component. E is the total energy and H is the total enthalpy.
The quantity tij and t*ij are the laminar and turbulent stresses,
respectively, and qi is the heat flux in each direction. G1 is used to
contain the compressible effect and to reduce the stiffness problem
in low Mach number flows by scaling the acoustic wave speeds
with a preconditioned velocity scale [20]. The governing equation
was used in the numerical simulations for flexible flapping wing
propulsion as well [21].
The accuracy of KFLOW in studying a flapping foil was validated
in previous works [22e25]. Inviscid, laminar and several turbulent
models are available in KFLOW. In the following simulations of the
flapping tidal generators, a turbulent scheme, k-u is used; it has
been selected to simulate turbulent flow in energy extraction from
flapping foils [12,17,26]. For the spatial discretization, the Roe flux
difference slitting scheme and the third-order MUSCL are used with
Van Albada limiter to obtain the secondary accuracy of inviscid flux.
The central difference is used to calculate the variable gradient of
viscous flux. The dual-time stepping with the diagonalized alternate directional implicit (DADI) method is used to advance the
solution in time. This allows not only the use of a large time
increment but also the maintenance of temporal accuracy. Moreover, the dual-time stepping also eliminates factorization and
linearization errors by iterating the solutions along a pseudo-time,
and the detail description is provided in Ref. [27].
The Chimera mesh option is used due to its advantage in
handling the relative motion between meshes [28]. In this Chimera
overset method, a cut-paste algorithm is applied to compose a
cross section that exchanges information between grids, which
enables the generation of overlapping grids with moderate mesh
interface regions. The overlapped grid method combines two major steps: hole cutting and donor identification [29]. Specially for
flapping tidal power extraction, a large pitch angle is mandatory;
hence, the Chimera mesh is essential. Fig. 1 shows the body-fitted
and domain meshes used in the simulations. The Chimera mesh is
composed of a C-type mesh around a hydrofoil as the body-fitted
mesh and an H-type mesh for the rest of the computational
domain as the domain mesh in two-dimensional (2D) and threedimensional (3D) simulations. In the 2D simulation, the distance
from the foil (the body) to the far-field and inlet boundaries is set
to 20 times of the chord length (20c), while the distance from the
foil to the outlet boundary is elongated to 25c; thus, domain size
becomes 40c 45c. Specially, in order to resolve vorticity shedding
well, a fine mesh is created in the downstream zone, as shown in
Fig. 1A. In this study, the power extraction of the flapping foil
directly depends on force and moment on the foil, therefore high
quality grid that obeys the criterion of orthogonality and stretching
near the foil is used as shown in Fig. 1B. Similarly, the domain sizes
of the 3D simulation are 25, 20 and 20 times of the chord length in
length, height and width directions, as shown in Fig. 1C. The closed
view of the mesh in vicinity of the 3D foil is depicted in Fig. 1D. The
numerical convergence by the grid density variation will be presented in Section 3.1.
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
277
Fig. 1. Chimera meshes for the simulations of a flapping tidal turbine of two-dimensional (A and B) and three-dimensional (C and D) foils: A. Domain size, boundary condition and
mesh in the 2D foil, B. Closed view of the mesh in vicinity of the 2D foil, C. Domain size of the 3D foil (LeHeW are 25e20e20 chord length), D. Closed view of the mesh in vicinity of
the 3D foil.
2.2. Kinematics of a flapping hydrofoil
2.2.1. Flapping kinematics
The hydrofoil is subjected to plunge and pitch motion as a
function of time as follows:
hðtÞ ¼ h0 sinðut þ 4Þ
qðtÞ ¼ q0 sinðutÞ;
(3)
where h is the instantaneous plunge position (m), h0 is the amplitude, u (u ¼ 2pf) is the angular frequency (radian/s), q is the
instantaneous pitch angle (radian), q0 is the pitch amplitude, 4 is
the phase angle and t is the time. The forced harmonic plunge and
pitch motions yield the following angle of attack (AOA):
aðtÞ ¼ arctan
_
hðtÞ
U∞
2.2.2. Quadratic functions for flexibility
Following equation presents the described chordwise and
spanwise flexure functions:
y ¼ Aðx=cÞ2 sinðutÞ
y1 ¼ Bð2z=bÞ2 sinðutÞ:
(5)
Here, y is the described chordwise flexure function, for which A is
the coefficient of the chordwise flexure amplitude and c is the
chord length. In addition, y1 is the described spanwise flexure
function, for which B is the coefficient of the spanwise flexure
amplitude and b is the span length. The flexible flapping hydrofoil is
!
qðtÞ;
(4)
where U∞ denotes the free-stream velocity.
Considering the water channel of the subsequent lab-scale experiments, the operating conditions and the dimension of the hydrofoil are determined as follows: the chord length c is 0.15 m, the
free-stream velocity, U∞ is 0.6 m/s, and the amplitude of the plunge
motion h0 is 0.1125 m. Therefore, h0/c is 0.75, the frequency f is
0.5 Hz, and the maximum pitch angle q0 is 60 . The center of
rotation is located at 30% of the chord length from the leading edge.
The total swept distance of the hydrofoil at the trailing edge d is
1.98c for a rigid hydrofoil. The phase between the plunge and pitch
motion (4) is 90 . Hence, non-dimensional values are derived as
follows: the Strouhal number (St ¼ 2fh0/U0) is 0.1875, the reduced
frequency (f* ¼ fc/U0) is 0.125, and the maximum angle of attack
(amax) is 29.5 . The Reynolds number (Re) is 90000; therefore, a
k u turbulence model is appropriate for all simulations.
Fig. 2. Kinematics of a flexible flapping hydrofoil with the pitching axis located at a
chord length of 30%, where the arrow shows the direction of instantaneous
motion (left) and the definition of angle of attack (right).
278
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
driven by the plunge and pitch motion function expressed by Eq.
(3), and the location of each node of the surface then changes according to the value of y or y1 of the chord or the span flexure. Fig. 2
shows the typical kinematics of the chordwise flexible hydrofoil
used in this study.
2.2.3. Definition of power extraction
The power extracted from the flapping hydrofoil is composed of
the components of the plunge and pitch motion; thus, the powerextraction efficiency (h) is defined as the total extracted power
from the foil over the ideal potential power of the flow using the
following definition:
P ¼ Lh_ þ M q_
3
Pideal ¼ 0:5rU∞
bd
h ¼ P=P
ideal
Fig. 3. Benchmarking test of the in-house code in the current study with a highefficiency flapping tidal turbine.
(6)
;
where L is the lift, M is the moment, d is the total swept distance of
the hydrofoil at the trailing edge, b is the span length of the flapping
foil and r is the free-stream density.
Fig. 4. Hydrodynamic performance of a 2D rigid hydrofoil: (A) CL, CM, CD and (B) power extracted from plunge and pitch motions with the mesh convergence checked.
Fig. 5. Effect of chordwise flexure on the hydrodynamic force coefficients in 2D hydrofoils: (A) lift coefficient and (B) moment coefficient.
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
Table 1
Effect of the chordwise flexure on the hydrodynamic performance of a 2D flapping
hydrofoil.
Amplitude of
chordwise
flexure (A)
Drag
(N/m)
Power_Plunge
(W/m)
Power_Pitch
(W/m)
Efficiency
(%)
A ¼ 0.0 (rigid)
A ¼ 0.10
A ¼ 0.15
A ¼ 0.20
A ¼ 0.25
A ¼ 0.30
31.33
42.52
48.82
55.05
61.37
67.63
8.576
10.520
11.402
12.104
12.650
13.056
1.368
1.795
1.969
2.114
2.276
2.338
30.5
36.1
38.0
39.2
39.8
39.6
The case of the bold entries is chosen for investigating the effect of the chordwise
flexure.
2.3. Numerical validation
279
plunge motion, and a reduced frequency of 0.14. The pitching center
is located at x ¼ 1/3 chord. The solution is converged after three
cycles with 500 time steps per cycle. Fig. 3 shows the good agreement of our results, which are extracted in 5th cycle, with the
reference data.
As a counter-effect, the high pitch angle causes greater drag than
lift in the given condition, as shown in Fig. 3. Thus, we chose 60
instead of 75 in this study. The NACA0012 hydrofoil is also
frequently used in flapping generators [8,26] due to its high efficiency. Therefore, we selected the NACA0012 hydrofoil instead of
the NACA0015 hydrofoil as the hydrofoil section. The numerical
convergence will be checked in terms of the independence of the
solution on the number of time steps and the grid density before
exploring the flow characteristics of the flapping tidal generator.
3. Results and discussion
A benchmarking simulation of a high-efficiency (h) flapping
tidal generator [12] was conducted in order to validate our numerical method. A single NACA0015 hydrofoil undergoes flapping
motion with a pitch angle of 75 , one chord length of amplitude
3.1. Two-dimensional (2D) numerical simulation
First, a 2D numerical simulation is conducted under the operating conditions described in Section 2.2 for a rigid hydrofoil. The
Fig. 6. Pressure and vorticity contours around rigid and flexible hydrofoils at typical time steps (A ¼ 0.2).
280
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
results of CL, CD, and CM of the rigid hydrofoil are depicted in Fig. 4A.
The maximum value of CD is still large, but its value (CDmax ¼ 2.5) is
reduced considerably compared to CDmax with a pitch angle of 75
(CDmax ¼ 4.2), while the maximum of CL (CLmax ¼ 2.3) is slightly
reduced as compared to that with a pitch angle of 75 (CLmax ¼ 2.7).
The components of the generated power in the downstroke and the
upstroke are similar to each other after L and M are multiplied to
the translational and rotational velocities, respectively, as shown in
Fig. 4B. The power is mainly extracted from the plunge motion
during the middle stroke periods, i.e., 0.15 < t/T < 0.35 or 0.65 < t/
T < 0.85, due to the synchronization between the maximum value
of the translational velocity and the instantaneous lift. Here T denotes the time of one cycle of the flapping motion; hence, t/T becomes non-dimensional time. Meanwhile, the pitch motion merely
contributes to the power extraction at beginning stages of each
stroke, i.e., t/T ¼ 0.05 or 0.55. The average extracted power in a
single stroke is 30.5% in the 2D simulation. Fig. 4B also presents the
numerical convergence when the grid density is varied. Four grid
levels were checked for mesh independence: first-layer thicknesses
from the wall of 1E4 m to 1E5 m are used in this study. Three
time step numbers, 200, 300 and 500 in a single cycle, are used
with 200 iterations in one time step to check the convergence of the
number of time steps. The tolerance of 1E4 is used for each time
step. The difference in the power-extraction efficiencies of all cases
is less than 2%; thus, the simulation is considered to be converged
with the mesh of 1E5 m as the first-layer thickness from the wall
and 300 time steps. In case of 1E5 m as the first-layer thickness,
the Chimera mesh consists of 44,325 cells in the body-fitted mesh
and 122,535 cells in the domain mesh in the 2D simulation. It took
almost 78 h to finish 5 cycles in the 2D simulation by running the
single core of AMD Opteron 2.1 GHz CPU. Similarly, the Chimera
mesh consists of 1,807,344 cells in the body-fitted mesh and
5,551,643 cells in the domain mesh, and it took around 102 h to
complete 5 cycles in the 3D simulation by using the 64 cores of
AMD Opteron 2.1 GHz CPU.
Next, the effect of chordwise flexure on the power extraction is
investigated with various chordwise flexure amplitudes in 2D
simulations. The A coefficients in Eq. (5) are 0.1, 0.15, 0.2, 0.25 and
0.3, which mean that the maximum chordwise flexures are 10%,
15%, 20%, 25% and 30% with respect to the chord length. Fig. 5
shows the effect of the chordwise flexure amplitude on the
magnitude and phase shift of the hydrodynamic force coefficients.
The chordwise flexure is set in the same phase with the pitch
motion, as expressed in Eqs. (3) and (5); therefore, the phase shift of
the lift coefficient between rigid and chordwise flexible foils is not
significant. As the chordwise flexure is enlarged, high lift is
observed in a wider translational period. For example, the lift coefficient, CL is 2.7 at t/T ¼ 0.1, after which it is reduced slightly
to 2.1 at t/T ¼ 0.45 when A ¼ 0.2, while it is 2.6 at t/T ¼ 0.1
and 1.8 at t/T ¼ 0.45 when A ¼ 0.1. Meanwhile, the reduction of
the lift coefficient is serious in the rigid foil; specifically, CL ¼ 1.1 at
t/T ¼ 0.45. Hence, it is expected that more power could be extracted
from the plunge motion in flexible hydrofoils as compared to their
rigid counterparts. Fig. 5 also shows the variation of the moment
during the rotational period, that is, when t/T ¼ 0.4e0.6, due to the
chordwise flexure. As the chordwise flexure becomes greater, the
peak value of the moment increases and is shifted ahead in time,
and the peak then becomes synchronized with that of the pitch
velocity in terms of their phases.
Table 1 lists the average extracted power during a single stroke
from the flapping hydrofoil when various chordwise flexure amplitudes are considered. The results of the drag are included in
order to explain the trade-off between the power and drag generated from the flapping hydrofoil. The results of the rigid hydrofoil
are also included in the table as reference values. According to
Table 1, the efficiency increases from 30.5% in the rigid hydrofoil to
39.8% at a chordwise flexure amplitude of 0.25. However, the drag
is also enlarged significantly as the chordwise amplitude increases.
Therefore, A ¼ 0.2 is chosen as a typical value for investigating the
effect of the chordwise flexure on the power-extraction.
Fig. 6 presents the contours of the pressure and vorticity around
the hydrofoil at typical time steps t/T of 0.0, 0.2, 0.4 and 0.7 for the
rigid hydrofoil with a chord flexure A of 0.2. Generally, the vortices
activity in a flexible hydrofoil is stronger than that in a rigid one. For
example, clockwise vortices (blue color, in the web version) above
the section of the hydrofoil at t/T ¼ 0.0 and counter-clockwise
vortices (red color, in the web version) at the leading edge at t/
T ¼ 0.2 and 0.4 in the flexible hydrofoil are larger in size than those in
a rigid hydrofoil. Subsequently, the blue color (in the web version) of
the pressure contour in the flexible hydrofoil is enlarged in size,
corresponding to the location of the vorticity contours. It is recognized from the results that the instantaneous pressure distribution
Fig. 7. Iso-surfaces of the Q-criterion around a 3D chordwise flexible hydrofoil at
typical time steps (A ¼ 0.2, AR ¼ 5).
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
281
Fig. 8. Comparison of the hydrodynamic performances of two- and three-dimensional flapping hydrofoils: A. Lift coefficient, B. Moment coefficient.
depends on the vortices activity. The effect of the flexible hydrofoil is
also amplified by its cambered shape, which generates high positive
pressure (red color, in the web version) from the flow at t/T ¼ 0.2 and
0.7. As a result, the instantaneous hydrodynamic forces of the flexible foil are increased in amplitude, as shown in Fig. 5.
3.2. Three-dimensional (3D) numerical simulation
All of the fluid and kinematic parameters in the 2D simulation are
utilized to explore the effects of the chordwise and spanwise flexure
of 3D hydrofoils with their aspect ratio (AR) fixed by 5, which means
that the span length is five times the chord length. The 3D effects of
the AR variation also are investigated at the last subsection.
3.2.1. Effect of chordwise flexure
Throughout the 2D simulations, the chordwise flexure of 20%
(A ¼ 0.2) showed the optimal performance in terms of the power
extraction in the operation conditions of our experiment. This value
is also adopted in the 3D simulations. Fig. 7 shows the iso-surfaces
of the Q-criterion, which is colored by the pressure magnitude,
around the 3D chordwise flexible hydrofoil at typical time steps t/T
of 0.0, 0.2 and 0.7. The vortices describe rotational flow structures,
and a considerable pressure drop is normally observed near their
core region. Here, Q-criterion is chosen among local vortexidentification criteria. The Q-criterion is defined by the second
invariant of a velocity gradient tensor by Hun et al. [30]. At t/T ¼ 0.0,
when the hydrofoil is horizontal and at the top position, the
Fig. 9. Iso-surfaces of the Q-criterion around 3D flapping hydrofoils at t/T ¼ 0.0 and t/T ¼ 0.7 in rigid (left) and flexible (right) cases. The arrows indicate the sections of which
quantitative pressures are presented in Figs. 10 and 11.
282
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
spanwise vortices that were not captured in the 2D simulation are
clearly observed on the top surface, and the tip vortices are shed
toward the downstream direction. When the positions of the hydrofoil are close to the middle of the stroke, i.e., at t/T ¼ 0.2 and 0.7,
the generations of a leading-edge vortex (LEV) and tip vortices are
well visualized as well. The differences in the magnitude and phase
shift of the instantaneous lifts and moments from the 2D and the
3D simulations for the rigid and flexible hydrofoils can be clearly
recognized in Fig. 8. The time series of the lift coefficients from the
3D simulation are smoother with less fluctuation as compared to
those from the 2D simulation. Moreover, the lift coefficients of the
3D hydrofoils reach their maximum values upon each stroke and
then decrease gradually, while they sharply drop from the peak
point to the valley point of the 2D hydrofoil. Regarding the moment,
a distinguishable difference in the trend of the moment from 2D
and 3D simulations is captured. Sharp changes and fluctuations are
also shown in the 2D hydrofoils, but not in the 3D hydrofoil, as in
the time series of the lift coefficients. This difference is apparently
caused by the vorticity activity of the 3D hydrofoil, specifically by
the tip vortices and the leading-edge vortex along the spanwise
direction. In the 3D hydrofoils, an improvement of the lift coefficient by the chordwise flexibility is clearly shown in terms of its
amplitude, which mainly causes the difference in the power
extraction, as in the 2D hydrofoils.
In order to explore the 3D and flexible effects in detail, the isosurfaces of the Q-criterion at t/T ¼ 0.0 and 0.7 are presented in
Fig. 9. In addition, the instantaneous pressure coefficients of the 3D
foil are depicted in the sections with z ¼ 0, 50 and 90%,
corresponding to z ¼ 0*Lz/2, 0.5*Lz/2 and 0.9*Lz/2, where Lz is the
spanwise length. The pressure coefficients of the 3D hydrofoils can
be compared to those of the 2D hydrofoils in the rigid and flexible
cases, as presented in Figs. 10 and 11 at t/T ¼ 0.0 and 0.7,
respectively.
First, with regard to the 3D effect, at t/T ¼ 0 the pressure coefficient on the upper surface of the 2D hydrofoil is deeply negative
due to the existence of a strong clockwise vortices (blue color, in the
web version), while the pressure coefficient on the upper surface of
the 3D hydrofoil is wholly different in terms of its trend: negative at
z ¼ 50%, slightly negative at z ¼ 0% and positive at z ¼ 90%. The
difference in the absolute values of the pressure coefficients on the
upper and lower surfaces yields the large difference in the lift coefficient between the 2D and 3D hydrofoils shown in Fig. 8. In
addition, at t/T ¼ 0.0, the integration of the pressure coefficients on
the upper and lower surfaces with respect to the location of the
pitching axis, i.e., x ¼ 0.333c, also induces a large difference in the
moment in the 2D and 3D hydrofoils, Fig. 8. At t/T ¼ 0.7, when the
hydrofoil is close to the middle of the upstroke, a new and strong
leading-edge vortex (LEV) is generated on the upper surface, while
tip vortices are created near the wing tip, as shown in Fig. 9. The
differences in the pressure coefficients in the 2D hydrofoil and the
sections of the 3D hydrofoil are minor except for the section near
the wing tip in the rigid case, as shown in Fig. 11. In the flexible case,
the aspects of the pressure coefficient curves are also similar among
the 2D hydrofoil and the sections of the 3D hydrofoil, except for the
section near the wing tip. However, the pressure coefficient curves
of the 2D flexible hydrofoil show considerable differences in the
Fig. 10. Quantitative pressure comparison at different sections of 3D rigid (top) and 3D flexible (bottom) foils at t/T ¼ 0.0. 2D result is added for the comparison. Vorticity contours at
the sections are presented in the right column.
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
amplitude near the leading edge due to the stronger LEV of the 2D
hydrofoil compared to that of the section of the 3D hydrofoil as
shown in the cut-out images of Fig. 11. The tip loss is clearly
recognized by the significant reduction of the pressure coefficient
of the lower surface at the section near the wing tip, z ¼ 90%, in the
rigid and flexible foils.
Next, with regard to the chordwise flexibility effect, at t/T ¼ 0.0
the aspects of the pressure distributions and corresponding pressure coefficient curves of the 3D flexible hydrofoil are similar to
those of the 3D rigid hydrofoil, with a small difference in magnitude
shown in Fig. 10, which yields the small differences in the hydrodynamics coefficients shown in Fig. 8. However, at t/T ¼ 0.7, the
effect of the chordwise flexibility on the lift coefficient becomes
obvious in the enlargement of the difference in the pressure coefficients between the upper and lower surfaces when the left and
right figures in Fig. 11 are compared. This difference yields a significant increment of the power extraction in the plunge motion
due to the chordwise flexibility, as shown in Fig. 12. Meanwhile, the
chordwise flexibility also causes more power to be required during
the pitch motion. In the summation of both components of the
power extraction, the power-extraction efficiencies from the 3D
rigid and flexible hydrofoils with AR 5 are 23.2% and 26.7%,
respectively.
In Table 2, the 3D effect is quantitatively presented when the
power-extraction efficiency is dramatically reduced from 30.5% to
23.2% in the rigid hydrofoil and 39.2% to 26.7% in the flexible hydrofoil. The improved rate of the power-extraction efficiency, 30%
283
caused by the chordwise flexibility for the 2D hydrofoil is larger
than that of the 3D hydrofoil, 15%. This difference is discussed in
Section 3.2.3.
3.2.2. Effect of spanwise flexure
The effect of a spanwise flexure is also investigated for various
amplitudes of the 3D hydrofoil with AR 5. Similar to the chordwise
flexure, the spanwise flexure is described by the assumed function
in Eq. (5), in which B varies by 0.05, 0.1 and 0.2. Fig. 13 shows a
comparison of the power components extracted from the rigid and
spanwise flexible hydrofoils. The effect of the spanwise flexure on
the power extraction is mostly negligible because the small increment of the power extraction from the plunge motion is canceled
out by the power required during the pitch motion. The maximum
improved rate arises with the flexible hydrofoils when B ¼ 0.2
(20%), and this value is only around 2.5%, which actually shows a
degradation as compared to the rigid hydrofoil.
3.2.3. Three-dimensional effect of the aspect ratio on rigid and
flexible hydrofoils
The effect of the aspect ratio (AR) of the 3D hydrofoil is also
investigated in this study. The AR is varied here by 2, 5, and 10. The
results of the rigid and chordwise flexible cases are depicted in
Fig. 14. In the rigid case, the 3D effect when AR ¼ 2 is much more
serious than other ARs because the power-extraction efficiency of
the 3D hydrofoil is 15.7% which is almost half that of the 2D hydrofoil. When the AR increases from 2 to 5 and to 10, the power-
Fig. 11. Quantitative pressure comparison at different sections of 3D rigid (top) and 3D flexible (bottom) foils at t/T ¼ 0.7. 2D result is added for the comparison. Vorticity contours at
the sections are presented in right column.
284
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
Fig. 12. Effect of chordwise flexure on the power extraction of a 3D flapping tidal
turbine (A ¼ 0.2, AR ¼ 5).
Fig. 13. Effect of spanwise flexure on the power extraction of a 3D flapping tidal turbine (AR ¼ 5).
extraction efficiency of the 3D hydrofoil correspondently increases
from 15.7% to 23.2% and to 29.1%, which is close to 30.5% of the
efficiency of the 2D hydrofoil. Similar characteristics for the rigid
foil were also reported in previous work [11], which reported that
the 3D tip loss is limited to approximately 10% when the hydrofoil
has somewhat of a longer span length with respect to the chord
length, such as when the AR is equal to or larger than 10. In the
chordwise flexible case, as the AR changes from 2 to 5 and then to
10, the power-extraction efficiency increases from 19.9% to 26.7%
and then to 33.0%, still showing a considerable difference from the
value of 39.2% of the 2D hydrofoil, because the activities of the
spanwise and tip vortices in the flexible hydrofoil are stronger than
those of the rigid hydrofoil, as shown in Figs. 10 and 11. The strong
3D effect in the flexible hydrofoil is a reason why the improved rate
of the power-extraction efficiency by the chordwise flexure of the
3D hydrofoil is smaller than that of the 2D hydrofoil in Table 2,
where the AR is fixed at 5. Meanwhile, the spanwise flexure is in
proportion to the span length; thus, the effect is predicted to be
similar even if the AR changes.
plays an important role in the improvement of the power extraction in a flapping tidal generator, showing 30% and 15% improvements in the rate of the power-extraction efficiency are achieved
with 20% chordwise flexure under 2D and 3D simulations,
respectively. The lower improvement rate associated with the 3D
hydrofoil as compared to the 2D hydrofoil is due to the 3D effects,
specifically the spanwise and tip vortices activities. Meanwhile, the
effect of the spanwise flexure on the power extraction is minor as
compared to that of the chordwise flexure. With regard to the 3D
effect, the tip loss is serious for a short hydrofoil, with an aspect
ratio (AR) of 2, of which the power-extraction efficiency is reduced
to almost half as compared to that of the 2D hydrofoil, but the effect
is significantly reduced as the AR increases. The 3D effect of the
chordwise flexible hydrofoil is stronger than that of a rigid foil;
thus, a longer span length is required to obtain performance close
to that of a 2D flexible hydrofoil. Further experimental studies to
4. Conclusion
The effect of the flexibility of the hydrofoil on the power
extraction of a flapping tidal generator is investigated through both
two-dimensional (2D) and three-dimensional (3D) numerical
simulations at a typical Strouhal number and frequency, and the
dimensions of the hydrofoils are determined by considering the
water channel in subsequent lab-scale experiments. In a numerical
set-up, the described deformations in the chordwise and spanwise
directions are directly determined in an effort to analyze the effect
of flexibility. The numerical results show that chordwise flexibility
Table 2
Hydrodynamic performance of 3D rigid and flexible flapping hydrofoils (A ¼ 0.2).
2D hydrofoil
3D hydrofoil,
AR ¼ 5
Rigid case
Chord-flexure
Rigid case
Chord-flexure
Power_Plunge
(W)
Power_Pitch
(W)
Efficiency
(%)
8.576
12.104
6.314
8.325
1.368
2.114
0.713
1.067
30.5
39.2
23.2
26.7
Fig. 14. Effect of the aspect ratio on the power extraction of 3D and 2D flapping tidal
turbines.
T.Q. Le, J.H. Ko / Renewable Energy 80 (2015) 275e285
validate our results in a water channel and numerical studies using
full-scale models will be conducted in our next study.
Acknowledgments
This work was supported by the New & Renewable Energy R&D
program of the Korea Institute of Energy Technology Evaluation
and Planning (KETEP) via a grant funded by the Korean government's Ministry of Knowledge Economy (No. 20113020070010) and
was supported by the project titled “Core Technology Development
for Hybrid Power Generation Based on Tidal Current Energy” funded by the Korea Institute of Ocean Science and Technology
(PE99323). This work was also supported by the PLSI supercomputing resources of the Korea Institute of Science and Technology Information.
References
[1] Khan MJ, Bhuyan G, Iqbal MT, Quaicoe JE. Hydrokinetic energy conversion
systems and assessment of horizontal and vertical axis turbines for river and
tidal applications: a technology status review. Appl Energy 2009;86:1823e35.
[2] Bahaj AS, Batten WMJ, McCann G. Experimental verifications of numerical
predictions for the hydrodynamic performance of horizontal axis marine
current turbines. Renew Energy 2007;32:2479e90.
[3] Kirke BK. Tests on ducted and bare helical and straight blade Darrieus hydrokinetic turbines. Renew Energy 2011;36(11):3013e22.
[4] Han S-H, Park J-S, Lee K-S, Park W-S, Yi J-H. Evaluation of vertical axis turbine
characteristics for tidal current power plant based on in situ experiment.
Ocean Eng 2013;65(0):83e9.
[5] Khan MJ, Bhuyan G, Iqbal MT, Quaicoe JE. Hydrokinetic energy conversion
systems and assessment of horizontal and vertical axis turbines for river and
tidal applications: a technology status review. Appl Energy 2009;86(10):
1823e35.
[6] Xiao Q, Zhu Q. A review on flow energy harvesters based on flapping foils.
J Fluids Struct 2014;46:174e91.
[7] McKinney, DeLaurier. The wingmill: an oscillating-wing windmill. J Energy
1981;5(2):109e15.
[8] Simpson BJ, Hover FS, Triantafyllou MS. Experiments in direct energy
extraction through flapping foils. In: Proceedings of the eighteenth international offshore and polar engineering conference. Vancouver, BC, Canada;
2008.
[9] Zhu Q, Peng Z. Mode coupling and flow energy harvesting by a flapping foil.
Phys Fluids 2009:21.
285
[10] Semler CS. Experimental investigation of an oscillating flow generator. In:
Naval postgraduate school; 2010.
[11] Kinsey T, Dumas G. Three-dimensional effects on an oscillating-foil hydrokinetic turbine. J Fluids Eng 2012;134(7):071105.
[12] Kinsey T, Dumas G. Computational fluid dynamics analysis of a hydrokinetic
turbine based on oscillating hydrofoils. J Fluids Eng 2012:134.
[13] Anderson JM, Streitlien K, Barrett DS, Triantafyllou MS. Oscillating foils of high
propulsive efficiency. J Fluid Mech 1998;360:41e72.
[14] Read DA, Hover FS, Triantafyllou MS. Forces on oscillating foils for propulsion
and maneuvering. J Fluids Struct 2003;17:163e83.
[15] Beem HR, Rival DE, Triantafyllou MS. On the stabilization of leading-edge
vortices with spanwise flow. Exp Fluids 2012;52:511e7.
[16] Heathcote S, Wang Z, Gursul I. Effect of spanwise flexibility on flapping wing
propulsion. J Fluids Struct 2008;24:183e99.
[17] Liu W, Xiao Q, Cheng F. A bio-inspired study on tidal energy extraction with
flexible flapping wings. Bioinspir Biomim 2013;8(3):036011.
[18] Park SH, Kwon JH. Implementation of keu turbulence models in an implicit
multigrid method. AIAA J 2004;42:1348e57.
[19] Park SH. Prediction methods of dynamic stability derivatives using the
NaviereStokes equations [PhD thesis]. Korea Advanced Institute of Science
and Technology; 2003.
[20] Park SH, Lee JE, Kwon JH. Preconditioned HLLE method for flows at all Mach
numbers. AIAA J 2006;44:2645e53.
[21] Yang W, Song B, Song W, Wang L. The effects of span-wise and chord-wise
flexibility on the aerodynamic performance of micro flapping-wing. Chin Sci
Bull 2012;57(22):2887e97.
[22] Le TQ, Ko JH, Byun D, Park SH, Park HC. Effect of chord flexure on aerodynamic
performance of a flapping wing. J Bionic Eng 2010;7:87e94.
[23] Le TQ, Han IS, Park SH, Ko JH. High power extracted from flexible flapping
tidal generator. In: Asian wave and tidal energy conference. Hyatt Hotel, Jeju
Island, Korea; 2012.
[24] Le TQ, Ko JH, Byun D. Morphological effect of a scallop shell on a flapping-type
tidal stream generator. Bioinspir Biomim 2013;8(3):036009.
[25] Le TQ, Truong TV, Park SH, Truong TQ, Ko JH, Park HC, et al. Improvement of
the aerodynamic performance by wing flexibility and elytraehind wing
interaction of a beetle during forward flight. J R Soc Interface 2013;10(85).
[26] Xiao Q, Liao W, Yang S, Peng Y. How motion trajectory affects energy
extraction performance of a biomimic energy generator with an oscillating
foil? Renew Energy 2012;37:61e75.
[27] Park SH, Kwon JH. NaviereStokes computation of pitchedamping coefficients
using steady coning motions. J Spacecr Rockets 2004;41(5):754e61.
[28] Sa JH, Kim JW, Park SH, Park JS, Jung SN, Yu YH. KFLOW results of airloads on
HART-II rotor blades with prescribed blade deformation. Int J Aeronaut Space
Sci 2009;10(2):52e62.
[29] Cho KW, Kwon JH, Lee S. Development of a fully systemized chimera methodology for steady/unsteady problems. J Aircr 1998;36(6):973e80.
[30] Hunt JCR, Wray AA, Moin P. Eddies, streams, and convergence zones in turbulent flows. Center for turbulence research report CTR-S88. 1988.
p. 193e208.