Fisica Apunte

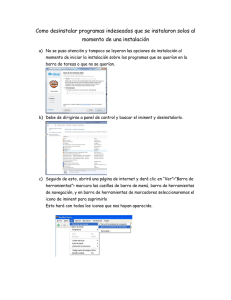
Apunte: Leyes de Newton
1.
Leyes de Newton
Definición de fuerza
Antes de comenzar con las leyes de Newton, es bueno definir el objeto de estudio.
¿Qué es fuerza?
Fuerza es cualquier interacción entre dos o más objetos; esta definición nos permite identificar las situaciones en donde aparece una fuerza, a su vez, nos permite reconocer aquello
que NO es fuerza.
Por ejemplo: fuerza no es velocidad. Un objeto que se mueve a mucha velocidad no posee
fuerza; del mismo modo, un fisicoculturista no “tiene” fuerza. La fuerza no es algo que se
posea, aparece sólo cuando hay interacción entre dos objetos; y desde el punto de vista de la
física, la fuerza de voluntad queda fuera de este marco de estudio ¿Te queda claro? Espero
que sí.
Pues bien, ahora que redujimos el objeto de estudio a un concepto claro y específico,
debemos estudiar las características de la fuerza. Las leyes de Newton se refieren a las características de las fuerzas, los efectos que producen.
1.1.
Primera Ley de Newton
También conocida en el mundo del hampa como ley de Inercia. De manera formal se
expresa así:
Todo cuerpo permanecerá en estado de reposo o de movimiento rectilíneo uniforme a
menos que una fuerza lo extraiga de dicho estado.
Esto significa que, en ausencia de fuerzas, existen dos estados posibles para los objetos:
1º reposo o, 2º movimiento rectilíneo uniforme.
Te lo voy a explicar en palabras un poco más coloquiales, en lenguaje de calle. La primera
ley de Newton responde la siguiente pregunta:
¿Qué efectos producen las fuerzas?
Esta pregunta tiene varias respuestas (música de suspenso).
Las fuerzas:
Producen movimiento: Los objetos en reposo se moverán sólo si alguna fuerza actúa
sobre ellos. NO existe el movimiento espotáneo. En este curso tampoco estudiamos
fantasmas ni telekinesis.
Detienen el movimiento: Cualquier objeto esté en movimiento y se desee detener, o
sólo disminuir su velocidad, necesita de la acción de una fuerza que frene el movimiento,
¿me entendés querido?
1
Impiden el movimiento: Esta es interesante. Usualmente, cuando vemos un objeto
reposando sobre la mesa, pensamos que sobre él no hay fuerzas: CRAAANK! Error.
Sobre el objeto hay un conjunto de fuerzas que se anulan entre sí y que impiden el
movimiento.
Cambian la dirección del movimiento: Basta con observar nuestro sistema solar.
Los planetas se mueven en órbitas elípticas gracias a la fuerza de atracción gravitacional
del sol. De otro modo, vagarían por el universo en movimiento rectilíneo y con velocidad
constante.
Producen rotación: ¿Quieres que una rueda rote? Aplícale una fuerza.
Deforman objetos: Ejercicio: vaciar una lata de cerveza. Una vez vacía, sujetarla con
los lados de la mano (derecha o izquierda), aplicar fuerza y observar lo que ocurre.
[Obs: en el experimento se sugiere vaciar la lata, lo que se haga con el contenido no es
responsabilidad de este autor]
¿te aclara todo esto la primera ley de Newton?, ¿te quedan dudas, comentarios, quejas? Toma
nota y lleva esas dudas a clases, por favor.
1.2.
Tercera Ley de Newton
¿Y la segunda?
La dejo para el final.
La tercera ley de Newton es conocida como la ley de “Acción y reacción”.
A ver, recordemos la definición de fuerza: Fuerza es la interacción entre dos o más objetos.
Consideremos dos objetos que interactúan; esa interacción se produce porque ambos objetos ejercen fuerza uno sobre el otro; por lo tanto, lo que tenemos son dos fuerzas: una
para cada objeto. Llamamos a una de esas fuerzas “Acción”, y a la otra fuerza (adivina)
“Reacción”. De este modo, cada vez que aplicamos una fuerza sobre un cuerpo, éste ejerce
una fuerza sobre nosotros, de igual magnitud (misma intensidad) en sentido opuesto y en el
mismo punto donde se produce la interacción.
A partir de la tercera ley de Newton se pueden explicar varios fenómenos.
Saltar: Ejercicio: ponte de pie y salta. Demasiado simple. Ahora, explícame ¿cómo es
que puedes vencer la gravedad por unas décimas de segundos y elevarte por el aire cual
Ícaro, aunque sin sus alas de cera? Respuesta: para saltar debes empujar el suelo hacia
abajo(acción); como respuesta, el suelo te empuja a tí hacia arriba (reacción)
Nadar: Ejercicio: introducirse en la laguna tres pascualas y nadar. Explicar el fenómeno
utilizando la 3º LdN. [Ayuda: necesitas empujar el agua para que el agua te empuje a
vos]
Remar: Muy parecido a nadar.
Paren la prensa: tengo un mensaje importante. NO debes confundir acción y reacción con
causa y efecto. Te doy un ejemplo para que caches la diferencia.
Lanzas una piedra contra el vidrio. La piedra viaja a cierta velocidad y el vidrio espera
en reposo (aunque muerto de miedo). Mientras la piedra no entre en contacto con el vidrio
no hay fuerza. La piedra alcanza al vidrio, interactúa con él (ahí hay fuerzas), ejerce una
fuerza sobre el vidrio (acción) y el vidrio reacciona ejerciendo de igual intensidad, pero en
sentido contrario sobre la piedra (reacción). Hasta aquí te he descrito el par acción/reacción.
El resultado, el efecto de ese atrevimiento es que quizás el vidrio termine roto. Ésto último
2
es el efecto de lanzar la piedra contra el vidrio, aunque eventualmente podría no romperse
(si se trata de un vidrio grueso)
Otro ejemplo: Das un puñetazo a la pared. Cuando tu puño interactúa con la pared
aparece el par acción/reacción ¿cuál es cuál y sobre quién? Sin embargo, la consecuencia, el
efecto es que posiblemente quedes con un par de huesos rotos.
¿me entendés? NO es lo mismo acción/reacción que causa y efecto.
Es importante saber reconocer los pares acción/reacción en distintas situaciones para
poder trabajar en ortodoncia, porque aunque no lo creas, tu ortodoncista sabe usar el par
A/R para realizar su tratamiento.
1.3.
Segunda ley de Newton
En el colegio debieron hablarte de esta ley. De seguro te dijeron que la fuerza es la masa
por la aceleración
F=m·a
No está mal, pero es una definición incompleta.
Cuando un objeto está sometido a un conjunto de fuerzas, éstas se suman y dan como
resultado una fuerza resultante
Σ→
− →
−
(0, 0) equilibrio
F =F
−
m·→
a dinámica
=R
{
→
−
Cuando la suma de las fuerzas es 0 = (0, 0) significa que todas las fuerzas que actúan
en un cuerpo se anulan entre sí, dando como resultado el equilibrio de fuerzas. Ese es el caso
de equilibrio, o caso estático.
−
Cuando la suma de las fuerzas es m · →
a el objeto acelera en la dirección de la fuerza
resultante, se produce movimiento acelerado. Este es el caso dinámico.
Así, tenemos dos situaciones: caso estático donde las fuerzas se anulan, y caso dinámico,
donde la fuerza resultante produce aceleración.
2.
Aplicaciones
Voy a ocupar un poco de espacio para mostrarte algunas aplicaciones.
2.1.
Diagrama de Cuerpo Libre: DCL
Para desarrollar una metodología de trabajo es necesario tener algunas herramientas
útiles.
El diagrama de cuerpo libre permite hacer la transición desde la teoría a la práctica. No
siempre es una tarea sencilla pasar de la teoría a la práctica.
¿En qué consiste el DLC?
Es un esquema que representa de manera geométrica un objeto sobre el cual están actuando un conjunto de fuerzas. Así de simple; y dibujarlo es también bastante sencillo.
Acá te dejo un ejemplo:
3
(a)
(b)
Figura 1: (a) objeto sometido a fuerzas, (b) Diagrama de cuerpo libre
El DLC nos sirve para poder llevar las fuerzas a vectores de manera más simple, porque
una vez montadas en el sistema coordenado XY, escribir las componentes de las fuerzas
resulta fácil, o no?
Te dejo unos ejercicios. Debes dibujar el diagrama de cuerpo libre en las siguientes situaciones
Un tipo de masa M que está sentado (ver figura 2.a)
Una bola de masa m , que está atrapada en el ángulo de una pared (ver figura 2.b y
entrégate a tu dios)
(a)
(b)
Figura 2: Dibuja el DLC considerando el peso de cada objeto señalado
2.2.
Ejemplo fácil 1: Objeto sometido a tres fuerzas
Este ejemplo pretende ilustrar de manera sencilla lo que hemos visto hasta ahora. Se
trata de un objeto de masa m=5kg sometido a tres fuerzas. De momento, vamos a ignorar
la fuerza peso (fuerza de gravedad); más tarde la voy a incluir en otros ejemplos. El objetivo
pedagógico es que entiendas la metodología para trabajar con las leyes de Newton, te parece?
(a)
(b)
Figura 3: Ejemplo fácil
4
En la figura aparece el objeto de 5kg y al lado hice el DCL. Fíjate que sólo hay que
escribir las fuerzas en coordenadas rectangulares. Está re fácil, no crees? A estas alturas eso
es pan comido. Aquí las pongo a cada una
→
−
F 1 = 32, 45^i + 13, 11^
jN
→
−
F 2 = −49, 74^i + 33, 55^
jN
→
−
^ − 44, 55j
^N
F 3 = 22, 69i
Ahora, aplicamos 2º Ley de Newton. ¿Qué dice la segunda ley de Newton? Dice que la
suma de todas las fuerzas es... bah, mejor lo escribo como ecuación
Σ→
−
→
−
→
−
→
−
F = F1+ F2+ F3
recuerda que en los vectores se suman sólo las componentes homólogas entre sí. Entonces,
esto da
Σ
^
^
→
−
F = 5, 4i + 2, 11j
Antes te dije que si la suma de las fuerzas daba (0,0) estábamos en presencia de un caso
estático o de equilibrio estático. Bueno, en otro caso estamos en el caso dinámico. El resultado
de la acción de esas tres fuerzas sobre el objeto, produce una fuerza resultante que está en el
primer cuadrante (¿por qué?). Así que el cuerpo debería moverse en la misma dirección de
la fuerza resultante.
Esta fuerza resultante se encuentra en el primer cuadrante (+,+) y forma un ángulo
.
Σ
2, 11
α = arctan
= 21, 34o
5, 4
con respecto al eje X. Esa es la dirección en la que se debería mover el objeto
2.3.
Ejemplo fácil 2.
En este ejemplo un objeto sometido a tres fuerzas. Me voy directo al DCL para ahorrar
tiempo
Figura 4: Ejemplo 2
Escribo las fuerzas en coordenada rectangulares
→
−
F
= 76, 60 ^i + 64, 28 ^
j N
→
−1
F 2 = −93, 96 ^i + 34, 20 ^
j N
→
−
F 3 = 17, 36 ^i − 98, 48 ^
j N
5
Si sumamos todas las fuerzas (recuerda: entre componente homólogas)
Σ→
−
→
−
→
−
→
−
F = F 1 + F 2 + F 3 = (0, 0)
la suma de las fuerzas da cero, por tanto, el objeto se encuentra en equilibrio estático. ¿Fácil,
no?
2.4.
Ejercicios
1. En una pieza dentaria, dada una fuerza F1 = 40g, y una fuerza F2 = 100g, ambas
actuando desde un mismo punto. Trabaje las fuerzas en gramos
a) descomponga ambas fuerzas en sus coordenadas rectangulaes
b) Calcule la fuerza resultante .
Figura 5: problema 1
2. Ahora vas a resolver unos problemas que tienen un grado de dificultad mayor.
a) En la figura 6.a el bloque está suspendido tal como lo puedes observar. La tensión
T1 = 100 N ; la magnitud de la tensión T2 = 120 N , Determine la magnitud y
dirección de la fuerza resultante. (Ignore el peso del bloque)
b) La figura 6.b muestra el bloque en otra configuración. La tensión T1 = 100 N , el
peso del bloque es p = 40, 53 N . Determine la magnitud de la tensión T2.
(a)
(b)
Figura 6: Problema 2
6
3. La figura 7 muestra la forma del tendón del cuádriceps al pasar por la rótula. La
tensión del cuádriceps presiona a la rótula contra el fémur. Como la rótula está en
equilibrio, el fémur realiza una fuerza sobre la rótula que anula a la fuerza proveniente
de la tensión del cuádriceps ¿entiendes la idea? Lo que debes hacer es encontrar la
magnitud y dirección de la fuerza que ejerce el fémur sobre la rótula. Los datos son los
siguientes: la tensión del cuádriceps tiene magnitud T = 140 kg . No tengo una figura
mejor, pero si no los ves, los ángulos son 37º y 80º, respectivamente.
Figura 7: Ejercicio 3
7
Apunte 2: Torque
1.
Preliminar
Antes de comenzar te quiero comentar que para entender bien este capítulo debes tener
claras las leyes de Newton y peinarte con ellas, es decir, deber comprenderlas, debes saber
resolver un par de ejercicios, reconocer lo que es fuerza y, por supuesto, deberías poder
reconocer aquello que no es fuerza... no sé si me explico.
Así que un pequeño cuestionario para vos; trata de responder lo más que puedas
¿Qué es fuerza?
Es correcto decir ¿El vehículo venía con fuerza?, ¿por qué?
¿Qué es más correcto decir: a) muerde con más fuerza, b) aplica más fuerza al morder?
¿puedes decir de memoria la tercera ley de Newton? ¿Y la primera?
Un auto está detenido. Otro auto idéntico viaja hacia el primero a 100km/h y lo impacta
de frente. ¿cuál de los dos debería quedar más dañado? ¿Por qué?
De acuerdo con la primera ley de Newton, ¿Un objeto puede cambiar su estado de
movimiento por sí mismo?
¿Qué significa que la fuerza resultante sobre un cuerpo sea cero?
¿Qué es el peso?
Ok, creo que con eso basta. No tienes que escribir las respuestas, sólo discutirlas con tus
compañeros, con tu pareja, o con tu familia el domingo durante la sobremesa (overtable)...
en fin, vamos con torque
2.
Torque
La primera ley de Newton dice que las fuerzas pueden producir rotación (¿lo recordás?)
Es cierto, las fuerzas pueden “eventualmente” producir rotación (subraya la palabra eventualmente). Todo esto depende del punto de aplicación de la fuerza. Si la fuerza es aplicada en
el centro de rotación de un objeto no se producirá rotación. Tú sabes ésto, lo has experimentado más de una vez; ntuitivamente sabes que si quieres hacer rotar una rueda debes aplicar
la fuerza en cierto lugar y no otro. Y cuando abres una puerta no la empujas en las bisagras,
ni cerca de ellas, sino donde está el pomo (manilla). Entonces, todos estos conocimientos ya
los tienes tú, yo sólo los voy a sistematizar un poco.
1
Échale un vistazo a estas figuras
Figura 1:
Un par de rectángulos que no demoré nada en dibujar. Con un poco de imaginación
puedes pensar que se trata de un teléfono móvil, o de un diente. El punto negro representa el
Centro de Rotación (CR). El CR es el punto o lugar geométrico alrededor del cual se produce
la rotación; pero ya hablaremos de eso.
Me interesa que observes la flecha roja y la línea punteada. La flecha representa una
fuerza y la línea punteada es la línea de dirección de la fuerza; esta línea pasa por el CR,
por lo tanto, en esas circunstancias, el objeto no va a rotar, ¿por qué? Pues porque la línea
de dirección pasa por el centro de rotación, ¿no me crees? Intenta mover tu móvil aplicando
una fuerza que vaya dirigida aproximadamente al centro del teléfono. Esa fuerza sólo podría
desplazar al objeto, moverlo de un lado a otro, sin hacerlo rotar.
Ahora, fíjate en estas figuras
Figura 2:
Estos objetos sí van a rotar. La razón es que la línea de dirección de la fuerza no pasa
por el CR.
2.1.
Definición de torque
Voy formalizar un poco.
Hasta ahora sólo te he mostrado situaciones a través de ejemplos; espero que tu intuición
te guíe un poco.
Tres hechos importantes que debes tener en consideración:
Las fuerzas pueden producir rotación
Cuando la línea de dirección de la fuerza pasa por el CR, no hay rotación
Cuando la línea de dirección de la fuerza pasa a cierta distancia del CR, sí hay rotación.
2
Te lo voy a definir:
Torque (o momento) es una medida de la capacidad de una fuerza de producir rotación.
Esta capacidad depende, naturalmente, del punto de aplicación.
¿Qué crees que ocurre si la línea de dirección de la fuerza pasa por el centro de rotación?
No hay torque.
EXACTO!
¿Hay alguna fórmula para esto?
La hay; es re simple. Aquí va
M=F·b
M: es el torque (o momento)
F: es la fuerza aplicada, y
b: se llama brazo-palanca.
La clave de todo esto es el brazo-palanca. De aquí en adelante, tu problema será identificar
y calcular el brazo palanca. Sin brazo palanca no hay Momento; la fuerza es inversamente
proporcional al brazo-palanca1 y cosas así.
Pero estudiemos esto paso a paso. ¿Qué es el brazo-palanca?
Respuesta: Mira estas figuras...
Figura 3:
Es la distancia entre el CR y la línea de dirección de la fuerza. De manera más formal:
El brazo-palanca es la distancia perpendicular entre el eje de rotación (o punto de
apoyo) y la línea de acción de la fuerza.
Destaqué distancia perpendicular porque, de hecho, es así de preciso, se trata de la distancia más corta entre el punto y la línea. Si la distancia entre la línea y el punto es cero el
torque vale cero. Por tanto, es necesario que el brazo-palanca sea distinto de cero para que
se produzca torque.
¿En qué caso el brazo-palanca puede ser cero?
Respuesta: cuando la línea de acción de la fuerza (o línea de dirección de la fuerza) pasa
por el CR.
Lo sé, lo sé: estas son cuestiones puramente teóricas.
¿dónde están las aplicaciones?, ¿para qué sirve esto?
Vamos a ver un par de ejemplos que quizás te iluminen un poco, ¿te parece?
1¿Qué significa
tu respuesta:
inversamente proporcional? Escribe aquí
3
2.2.
Ejemplos
Un ejemplo fácil
Figura 4:
Se trata de una barra que está apoyada en O; la barra puede rotar alrededor de O, por
lo tanto ese es su centro de rotación. Sobre la barra actúan dos fuerzas de 2N y 1N, a las
distancias señaladas en la figura. Por ahora, voy a ignorar el peso de la barra.
Pues bien, vamos a calcular el momento de cada fuerza. Primero la de 2N. Recuerda que
la fórmula de Momento (torque) es M=Fb. La distancia entre el eje de rotación y la fuerza
es de 1m, por lo tanto
M = F · b = 2N · 1m = 2N.m
¿difícil? Lo dudo.
Calculemos el otro momento. La distancia entre O y la línea de aplicación de la fuerza es
2m, por lo tanto
M = 1N · 2m = 2N.m
¿Viste? Dos fuerzas de distinta magnitud, producen el mismo momento cuando son aplicadas en lugares distintos.
¿significa algo eso? Claro que sí.
No sé si lo notaste, pero la fuerza de 2N va dirigida hacia abajo; esa fuerza haría a la
barra rotar en sentido horario m. Diremos entonces que se trata de un momento de magnitud
2N.m en sentido horario2.
Por su parte, la fuerza de 1N va dirigida hacia arriba; esa fuerza haría a la barra rotar en
sentido antihorario m. Diremos por tanto que la fuerza produce un momento de magnitud
2N.m en sentido antihorario.
Así que tenemos dos fuerzas que producen torque de la misma magnitud, pero en sentidos
opuestos, ¿hacia dónde crees que rota la barra?
Un ejemplo fácil e interesante
Fíjate en la figura
Figura 5:
2Horario:
en el mismo sentido del movimiento de las manecillas del reloj. Antihorario: en el
sentido opuesto al movimiento de las manecillas del reloj.
4
¿Cuál es el valor del momento producido por la fuerza de 100N? ¿400 N.m?, ¿25 N.m?,
¿0 N.m?
Si proyectas la línea de acción de la fuerza verás que pasa por el apoyo, por tanto, el brazopalanca vale 0 m; en consecuencia el momento producido por esa fuerza vale cero también.
M = 100N · 0m = 0N.m
Ahora bien, te quiero comentar algo importante que no debes confundir. El resultado
anterior dice simplemente que el momento de esa fuerza es cero y, por tanto, esa fuerza no
induce rotación. Esa fuerza no hace rotar la barra, sin embargo, la empuja hacia la izquierda,
y presiona al apoyo.
Esta parte de la trama es un poco delicada, así que la analizaremos con calma. Echemos
un vistazo a esta figura:
Figura 6:
Es el diagrama de cuerpo libre de la barra. Hacia la izquierda va la fuerza de 100N; hacia
la derecha, la reacción del apoyo, R. Como la barra está en equilibrio, la suma de las fuerzas
debe dar cero. HaciendoΣFx = 0, resulta esta ecuación
R − 100 = 0 =⇒ R = 100N
Este resultado dice que para que la barra permanezca en equilibrio el apoyo debe ejercer una
fuerza hacia la derecha de igual magnitud a la fuerza aplicada.
De esto vamos a sacar una conclusión. Un objeto está en equilibrio si se cumplen
dos condiciones.
1º Condición de equilibrio: La suma de todas las fuerzas que actúan sobre él es
igual a cero
Σ→
−
→
−
Fi = 0
2º Condición de equilibrio: la suma de todos los momentos es igual a cero
Σ
Mi = 0
Estas son las condiciones de equilibrio traslacional y rotacional.
Un objeto va a estar completamente en equilibrio si se cumplen ambas condiciones a la
vez, que las fuerzas se anulen entre sí, al igual que los momentos.
En la siguiente página voy a desarrollar un caso más complicado que los anteriores.
En el ejemplo voy a utilizar las dos condiciones de equilibrio para determinar las variables
desconocidas. Trataré de resolverlo con todo el detalle posible, pero quizás se me escape algo,
en tal caso, te agradecería completaras tú lo que falte y lo discutamos en clases.
5
Se trata de una barra apoyada en O en cuyo extremo superior se suspende un bloque de
2000N de peso, y sujeta a la pared a través de una cuerda de tensión T (figura 7.a). El
objetivo es encontrar la magnitud de la tensión T y la fuerza de reacción del apoyo sobre la
barra. El apoyo está en O; las distancias son OA=15m y OB=22m. Ignoramos el peso de la
barra.
(a)
(b)
Figura 7:
¿Se entiende la idea? Resolvámoslo??
El objeto de estudio es la barra. Las fuerzas que actúan sobre la barra son: - peso del
bloque 2000N, -tensión de la cuerda, -reacción del apoyo. El diagrama del sólido libre está
en la figura 7.b.
Voy a calcular el momento de cada fuerza, comenzando con el peso del bloque. Este
esquema (figura 8.a) representa el lugar donde se encuentra el brazo palanca del peso del
bloque. Recuerda: es la distancia perpendicular entre el punto de apoyo y la línea de la fuerza
(a)
(b)
Figura 8:
Según la figura 8.a el brazo-palanca es
b = 22 · cos 57
Por tanto, el momento del peso es
M = 2000 · 22 · cos 57 m
esta fuerza induce una rotación en sentido horario, por tanto es negativa.
La figura 8.b contiene el esquema para determinar en brazo-palanca de la tensión. De
acuerdo con ella, el brazo palanca es
b = 15 · sin 18
y en consecuencia, el momento de la tensión es
M = T · 15 · sin 18 m
6
esta fuerza induce una rotación en sentido antihoraria, por tanto es positiva.
Como la reacción no induce rotación, su momento vale cero.
Para que la barra permanezca en equilibrio, los momentos en sentido horario deben igualarse a los momentos en sentido antihorario.
2000 · 22 · cos 57 = T · 15 · sin 18
y de aquí se despeja la tensión
T=
2000 · 22 · cos 57
= 5169, 96 N
15 · sin 18
¿Cómo calcular la fuerza que ejerce la reacción sobre la barra?
Respuesta: Diagrama de cuerpo libre y primera condición de equilibrio. Te lo dejo de
tarea.
3.
Ejercicios
1. Dada la figura 9a, calcular el momento resultante y la magnitud y dirección de la
reacción del apoyo en O. (R: M=0 Nm , Ry = 1 N )
(a)
(c)
(b)
(d)
Figura 9: (a) Problema 1, (b) Problema 2, (c) problema 3, (d) problema 4
2. Considere la figura 9b. Calcular el momento resultante con respecto al apoyo en O
[R: MT = 300 Nm Ç].
3. Dada la figura 9c, calcular el momento de la fuerza y la reacción del apoyo, sabiendo
que la barra está en equilibrio.
4. Calcular el momento de la fuerza en la figura 9d y calcule la reacción del apoyo.
5. Considere la figura 10a. Calcule la magnitud de la fuerza F para que la barra se encuentre en equilibrio rotacional. Calcule además, la magnitud y dirección de la reacción
en el apoyo.[R: F = 22, 5 N , Ry = 37, 5 N hacia abajo]
7
(a)
(b)
Figura 10: (a) problema 5, (b) problema 6
6. La persona en la figura 10b puede ejercer una fuerza máxima de 50 N en el extremo
de la barra que sostiene un bloque cuyo peso es de 200 N. Calcule la distancia a la que
debe ubicarse el bloque para que la barra permanezca en equilibrio rotacional. Calcule
además la magnitud de la reacción del apoyo. [R: d=0,25 m. Ry = 150 N ]
7. Considera la barra sin masa de la figura 11.
Figura 11: Problema 7
a) Calcula el momento de cada fuerza con respecto al apoyo en O.
b) Calcula la magnitud de la fuerza F de manera que la barra se encuentre en equilibrio [R: F=16,42 kg].
c) Calcula la magnitud y dirección de la reacción del apoyo. [R: Ry = 291, 42 N ]
8. El peso de la barra homogénea de la figura 12 es de 100 N y su longitud OA=2,5 m.
La barra está apoyada en O y en su extremo superior se aplican 3 fuerzas, F1 = 50 N
paralela a la barra, F2 = 70 N perpendicular a la barra, y F3 = 115 N vertical hacia
abajo.
Figura 12: Problema 8
a) Calcula el momento que produce cada fuerza (incluso el peso de la barra) y el
momento total.
8
b) Si la barra está en equilibrio traslacional, calcula las componentes de la reacción
del apoyo. [R: MT = −254, 25 Nm, Rx = −1, 81 N , Ry = 126, 21 N ]
9. La figura 13.a muestra el esquema de un pie en posición de puntillas. La fuerza T
representa la tensión ejercida hacia arriba por los músculos de la pierna. La fuerza F
representa la fuerza de contacto por la articulación del tobillo. La figura 13.b es el
diagrama de fuerzas de la situación. El apoyo está en 0 y las distancias son OA=22cm
y OB=18cm ; además, la fuerza T forma un ángulo α = 12º con la vertical, y F un
ángulo β = 15º con la vertical. Por su parte, el ángulo θ = 55º. Si una persona de 60kg
se pone en puntillas sobre un solo pie y R es la reacción del apoyo
a) Dibuje un diagrama de cuerpo libre de la situación indicando los ángulos
b) Escriba las ecuaciones de equilibrio de fuerzas en el eje X e Y
c) Escriba la ecuación del momento de cada fuerza y la ecuación de equilibrio rotacional
d) ) Calcule la magnitud de T, F y de R
e) La tensión del cuádriceps
(a)
(b)
Figura 13: Problema 9
Buena Suerte y...
Bendiciones
9
Apunte Calor: Resumen Ejecutivo
Definición de Calor: El calor es un mecanismo de transporte de energía. Calor no
es lo mismo que temperatura. La temperatura es algo que podemos percibir con nuestros
sentidos. Es super fácil detectar cuando algo tiene mucha temperatura (está caliente) o tiene
poca temperatura (está re-frio); SIN EMBARGO, es imposible medir el calor que posee un
cuerpo sencillamente porque el calor no se posee, es calor es el mecanismo de transferencia de
la energía. Si tú transfieres energía en forma de calor a un objeto entonces ese objeto absorbe
esa energía y el resultado más probable será que el objeto aumente su temperatura. El objeto
queda con mayor temperatura porque absorbió energía en forma de calor. Al revés, si extraes
energía en forma de calor de un objeto, entonces, lo más probable es que el objeto disminuya
su temperatura. O sea, la temperatura del objeto disminuye porque perdió calor.
Figura 1: Transmisión de calor del cuerpo cálido al frío
Así que, calor y temperatura no son la misma cosa, pero están relacionadas. El calor se
transmite desde los objetos más cálidos a los menos cálidos, es decir, desde los cuerpos con
mayor temperatura hacia los cuerpos con menos temperatura.
Transmisión de Calor: Como acabo de contarles, el calor fluye desde los cuerpos calientes
a los frios. Pero podemos hilar más fino en esta definción y mencionar tres mecanismos en
los que se transfiere calor: Convección, conducción y radiación.
Brévemente, porque se nos acaba la clase
Convección: El calor se transmite a través de un fluido. Por ejemplo: el calefactor de
la sala. El calefactor calienta el aire que está cerca a su alrededor y luego, este aire tiende
a moverse hacia lugares más fríos, de este modo, el calor se transmite desde el calefactor, a
través de la sala, utilizando como medio de transporte el aire.
Conducción: Ocurre conducción cuando pones en contacto dos medios materiales a
diferente temperatura. Por ejemplo, si sientes frío, abrazas con las manos tu taza de café que
está “calientita”; entonces, se transfiere calor de la taza a tus manos, a través del contacto
directo, sin utilizar un medio de transporte como en el caso de la convección.
Radiación: Esta forma de radiación ocurre sin la utilización de un medio material. O
sea, el calor viaja a través del vacío. Es así como el calor del Sol no llega todas las mañanas,
pues se transporta a través del espacio vacío.
Listo, eso es todo. Espero que la unidad “Calor” haya sido de tu agrado. Suerte!!
1
Francamente, pienso que una página es poco para contarte todo este rollo. Si quieres
quédate con eso, pero yo voy a continuar acá con un poco más. No te obligo a leerte todo el
resto de la historia, pero esto entra en el certamen, perdón, en el Solemnus, Solemnis.
Lo que pasa es que tengo que incluir un par de ecuaciones porque en el fondo de mi
corazón siento que un apunte de física queda incompleto si no incluyo unas cuantas fórmulas,
flechas, cuchillos con los cuales herirte a la hora de la evaluación... je je je. Pero mira, te voy
a contar la historia fácil, a prueba de diputados ¿te parece? y te voy a contar la historia en
un lenguaje y entorno que te resulte familiar ¿está claro?
Como les dije en clases, y ya lo comenté al comienzo de este resumen para ejecutivos: cuando una substancia absorbe calor lo más probable es que aumente su temperatura; podemos
cuantificar eso, es decir, escribirlo como una fórmula. ¿Cuánto calor absorbe una sustancia
que tiene temperatura inicial Ti y se calienta hasta alcanzar una tempertatura final Tf ? Acá
va la respuesta
H = m · c · (Tf − Ti)
(1)
donde... ¿tengo que explicar lo que significan cada uno de esos valores?
m: es la masa del objeto o sustancia que absorbe o cede calor, medida en kg
c: es el calor específico, medido en J : te recuerdo que el calor específico es una
kg°C
medida de cuán fácil o difícil es cambiarle la temperatura a algo con calor.
Puedes verificar tú mismo que la unidad de medida resultante de la ecuación (1) es el
Joule (Julio, J).
Para que te entretengas este fin de semana te dejo esta tabla con calores específicos. Debes
memorizar todos los valores porque entran en la siguiente prueba.
Agua Líquida
Hielo
Cobre
Acero
Hierro
Oro
Plata
Mercurio
Calores
Específicos
(J/kg°C)
4186
2090
385
447
443
130
235
138
Cuadro 1: Tabla de Calores específicos
Fíjate que metales como el oro o la plata tienen poco calor específico, esto significa que
esos metales aumentan mucho su temperatura con un poco de calor. ¿Cómo se comportan
mecánicamente estos metales cuando se calientan? ¿Se dilatan con falicidad?, ¿se deforman?
IMPORTANTE: todo lo anterior no es válido en los cambios de fase.
¿Cuántos estados tiene la materia?
Sólido, líquido, gas y plasma. Puedes buscar en cualquier libro de química o física o
googlear el tema en internet y vas a encontrar las característica de cada uno de los estado.
Lo que me importa a mí es aclararte un par de cosas, relativas al calor, en el momento preciso
en que una sustancia pasa del estado sólido al líquido, del líquido al gaseoso, o viceversa.
Llamamos cambio de fase o cambio de estado al momento en que el hielo se derrite o el
agua se evapora. ¿qué ocurre con la sustancia en esas circunstancias?
2
Calor y cambio de estado
Durante un cambio de estado la temperatura se mantiene constante. Por ejemplo, mientras
el hielo se derrite, la temperatura se mantiene estable a cero grado centígrado. Y mientras el
agua se evapora,o sea, mientras está hirviendo, se mantiene a 100 grados.
Para derretir más hielo, necesitas más calor. Esas magnitudes son directamente proporcionales. Pero con la misma cantidad de calor con que derrites un kilo de hielo puedes derretir
15 kilos de plomo (claro que debes tener esos materiales a su temperatura de fusión: cero
para el hielo, 327°C para el plomo).
Resumiendo: el cambio de estado no sólo depende de la cantidad de materia que cambia,
sino también de una propiedad intrínseca de la materia llamada calor latente que se simboliza
con la letra L mayúscula:
LF , calor latente de fusión (cuando algo pasa de sólido a líquido), y LV , calor latente de
vaporización (cuando algo pasa de líquido a gaseoso).
Entonces, cuando quieres calcular la cantidad de calor que se necesita para derretir una
cantidad m de alguna sustancia usas la siguiente fórmula
H = m · Lf
y cuando quieres calcular la cantidad de calor que se necesita para evaporar algo usas
H = m · LV
Ahora bien, los valores de los calores latentes están en tablar; no tienes que deducirlos ni
calcularlos. Así que para complementar te dejo una tablita con algunos calores latentes
conocidos...
Sustancia
Agua
Cobre
Oro
Plata
Mercurio
T fusión °C
0
1083
1064
961,9
-38,87
Lf ×103(J/kg)
334
214
66.9
103
11.5
T Ebullición °C
100
2360
2856
2212
357
LV ×103(J/kg)
2260
5410
1738
2390
300
Cuadro 2: Calores Latentes de Fusión y Vaporización
3
Ejemplo:
Veamos un ejemplito para visualizar de manera un poco más concreta toda esta historia.
Lo que haremos es calcular cuánto calor necesitan 100 g de hielo a -20°C para transformarse
en vapor a 100°C.
Anotemos los datos:
m= 100 g= 0.1 kg (hay que pasar la masa a kilogramos !!!)
chielo = 2090 J/kg°C este es el calor específico del hielo... ver tabla 1
Lf = 334 · 103 J/kg este es el calor latente de fusión del hielo... vea la tabla 2
LV = 2260 · 103J/kg esto es el calor latente de vaporización del agua ....... tabla 2
cagua = 4186 J/kg°C es el calor específico del agua. .... tabla 1
Ti = −20°C .... es la temperatura inicial del hielo
Tf = 100°C es la temperatura final del vapor de agua.
Bien. Esto se hace ordenadamente; por pasos. El hielo no se transforma inmediatamente en
vapor. Primero el hielo se calienta hasta alcanzar los 0°C; luego, el hielo se derrite formándose
agua a 0°C. Después, el agua se calienta hasta hervir a 100°C y, finalmente, el agua se evapora
para formar vapor de agua a 100°C.
Paso 1: calentar el hielo. Calentar el hielo de -20°C a 0°C
H1 = m · chielo · (Tf − Ti) = 0, 1 · 2090 · (0 − (−20)) = 4180 J
se necesitan 4180 J de calor para calentar el hielo.
Paso 2: Derretir el hielo. Esto ocurre a T° constante
H2 = m · Lf = 0, 1 · 334 · 103 = 33.400 J
Paso 3: Calentar el agua. Tenemos agua a 0°C y debemos calentarla hasta los 100°C.
OJO: la masa sigue siendo la misma. 100 g de hielo se transformaron en 100 g de agua...
H3 = m · cagua · (Tf − Ti) = 0, 1 · 4186 · (100 − 0) = 41.860 J
Paso 4: Evaporar el agua. Esto ocurre a T° constante
H4 = m · LV = 0, 1 · 2260 · 103 = 226.000 J
Finalmente, la respuesta a la pregunta resulta de sumar todo, el calor total es la suma
del calor en cada proceso
H = H1 + H2 + H3 + H4 = 305.440 J
Listo!!! Fácil, no?? ¿¿quién dijo que la física era difícil??
Te dejo una tarea:
1. ¿Cuánto calor se requiere para derretir 1 g de plata que está inicialmente a 20°C?
2. ¿Cuánto calor se requiere para derretir 10g de oro que está inicialmente a 24°C?
4
Transmisión de Calor
El calor es energía fluyendo de un cuerpo a otro. En forma espontánea ocurre en una
única dirección posible: desde el cuerpo más caliente hacia el cuerpo más frío. De manera más
delicada: desde un cuerpo de mayor temperatura hacia un cuerpo de menor temperatura.
Se llama trasmisión del calor a los procesos por los que el calor pasa de un cuerpo a
otro. Básicamente se distinguen 3 procesos: Conducción, convección y radiación....
y adivina... en esta sección estudiaremos cada uno de esos procesos. ¿Qué te parece?
Interesante ¿verdad?
Conducción
Su nombre lo dice. La conducción consiste en conducir el calor a través de un médio
sólido. Ocurre cuando dos objetos, a distinta temperatura, están en contacto; entonces, el
calor viaja por el interior del medio material, ¿desde donde? Desde el cuerpo más caliente al
más frio.
Para estudiar esta historia vamos a contar con dos cuerpos fuente. Llamamos fuente a
aquellos cuerpos que reciben o ceden calor. Acá la figura te aclara un poco de qué estoy
hablando
Figura 2: Conducción de fuente caliente a fuente fría
Si te fijas bien (y fíjate, por favor) las fuentes están unidas por una especie de tubo
cilíndrico de área transversar A; naturalmente, ambas fuentes podrían estar en contacto
directo e inmediato (hombro con hombro). El área que te menciono juega un rol importante
en este cuento, porque, si lo piensas un poco, mientras mayor sea el área de contacto más
energía fluye de un lado a otro. ¿Tiene sentido, verdad?
Otra cosa importante es la distancia entre las fuentes, ∆x. ¿Qué dice tu sexto sentido
respecto de la distancia? Si la distancia es mayor, ¿fluye más o menos calor? Pues bien, el
flujo de calor disminuye cuando aumenta la distancia.
La temperatura de las fuentes también tiene algo que decir en esto. Claramente, si las
temperaturas de las fuentes son iguales, entonces no se produce flujo de calor; siempre tiene
que haber una diferencia de temperaturas, y mientras mayor sea esa diferencia, mayor será
el flujo de calor.
Bueno, con todo esto en mente, vamos a escribir una ecuación de la “velocidad” con la
que fluye el calor de aquí pa’llá.
Uuhh!! Si digo velocidad del flujo de calor es porque en realidad quiero decir la velocidad
con la que se transmite la energía, es decir, cuántos Julios por segundos se transportan desde
la fuente caliente a la fría, y tú ya sabes que cuando hablamos de Julios por segundo (J/s)
estamos hablando de potencia y de watts. llamemos R a esa velocidad
R=
Calor
tiempo
=
H
∆t
5
Entonces, si A es el área de contacto entre las fuentes, ∆x es la distancia que debe recorrer
el flujo de calor desde la fuente caliente a la fría, T1 es la temperatura de la fuente caliente
y T2 es la temperatura de la fuente fría, entonces, la velocidad del flujo de calor (redoble de
tambores trrrrr) es....
H
k · A · (T2−
R=
=−
(2)
T 1)
∆t
∆x
Sí, sí, sí... puse una letra k que nadie sabe qué significa, pero acá te la explico. Esa k es la
conductividad térmica que depende del material (vidrio, madera, metal, plástico, piel, sangre,
tripas). Por supuesto que hay tablas de conductividad térmica y, obviamente, en un ejercicio
te voy a indicar de qué materiales estamos 7hablando, de modo que tú consultas la tabla y
haces el cálculo. La ecuación (2) tiene nombre y autor. El autor es J. Fourier (1768-1830) y
la ecuación se denomina “ley de Fourier”.
¿Dije tabla? Así es, acá va la tabla con algunas conductividades. si de pronto necesitamos la conductividad de otro material, te lo doy o te señalo dónde buscarlo...
Sustancia
Agua
Aire
Vidrio
Plata
Oro
Mercurio
Hierro
Conductividad Térmica k
W/(m · °C)
0,59
0,024
1
418
308,2
8,34
72
Cuadro 3: Conductividades Térmicas
¿Ejemplo?
Bueno, resolvamos un ejercicio ejemplo para ver cómo opera este rollo ¿te parece?...
Calculemos la velocidad de transmisión del calor de una lámina de oro de 1, 2 m × 2, 4 m
y 0, 8 cm de espesor si una de sus caras está a 22°C y la otra a 4°C...
Datos:
Ancho: 1, 2 m
Alto: 2, 4 m
A=2,4×1,2=2,88 m2
Espesor: 0,8 cm=8·10−3 m = ∆x es la distancia que debe recorrer el flujo de calor entre
una cara y la otra.
k=308, 2 W/(m°C) es la constante de conductividad del oro (vea la tabla 3)
T1 = 22°C
T2 = 4°C
Directamente en la fórmula (2) reemplazamos los datos...
k · A · (T2 − T1)
308, 3 · 2, 88 · (4 − 22)
R=−
=−
≈ 2 · 106W
∆x
8 · 10−3
Como puedes ver, este ejemplo demuestra que la física es super sencilla... pero ya estudiaremos casos un poco más interesantes...
6
Radiación
El calor puede viajar en forma de radiación. Cuando viaja de este modo puede hacerlo
dentro de un medio material o en el más absoluto vacío. La radiación que transporta el calor
no necesita materia para desplazarse.
Te estoy hablando del tipo más común de radiación, la que llena todo el universo y
se llama radiación electromagnética. Esta imagen representa el espectro continuo de la
radiación electromagnética desde los rayos más energéticos y penetrantes (arriba) hasta los
más blandos e inofensivos (abajo). La columna de la izquierda representa la longitud de la
onda, es decir, el tamaño de la onda
Te explico un poco la figura: (puedes echarle un vistazo mientras parloteo)
La máxima energía se corresponde con la longitud de onda más pequeña; en ese extremo
se encuentran los Rayos Gamma. Por suerte hay muy pocos en el universo.
Le siguen los Rayos X. Son tan penetrantes que atraviesan nuestros cuerpos y sirven para
hacer fotografías de transparencia (radiografías). No son inocuos, no hay que exponerse a los
rayos X sin una necesidad expresa.
La luz ultravioleta sigue siendo penetrante. No atraviesa todo nuestro cuerpo pero es
capaz de producir lesiones en nuestra piel y ojos.
Continúa un estrecho rango de longitudes de onda que para nosotros es el más bonito: la
luz visible. Va desde el violeta hasta el rojo.
Con menor energía siguen las ondas infrarrojas y comienza la porción "térmica" o infrarrojo lejano que es la longitud de onda a la cual se transmite el calor.
Sigue el rango de las microondas y más allá tenemos las ondas de TV, FM y radio AM.
Todo lo que existe en la naturaleza irradia energía, en todas las direcciones: irradian
energía las personas, las nubes, los gases atmosféricos, los vegetales, los objetos metálicos,
etc.
La intensidad de la energía que un objeto irradia depende básicamente de su temperatura
(absoluta, en Kelvin). En especial, la radiación de energía en forma de calor está descripta
por la Ley de Stephan-Boltzmann
H
=σ· ε· A· T4
∆t
esta ecuación-fórmula expresa (aunque no lo oigas) la velocidad a la que pierde calor un objeto
que se encuentra a la temperatura T.
De esta ecuación te puedo decir que A es el área del objeto, medido en m2. σes la constante
de Stephan-Boltzmann, cuyo valor es
σ = 5, 67 × 10−8 W/(m2 K 4 )
y ε es la emisividad del cuerpo, un número sin unidad de medida que adquiere valor entre 0
y 1, representa la propiedad superficial del cuerpo, que lo hace más opaco o más reflectante
a la radiación. La emisividad de un espejo vale 0 y la del cuerpo negro vale 1. Las pieles
humanas de cualquier tonalidad valen más o menos lo mismo, con un valor muy cercano a 1
(la diferencia de color sólo afecta en el rango visible, pero no en el rango térmico).
Uuufff... denso. ¿escuchemos algo de música? Te propongo una canción ideal para relajarse
un rato... puedes ir a prepararte un tecito o un cafecito (amargo como la vida) mientras se
conecta la canción... sólo haz click en el siguiente vínculo: April come she will. Esta canción
es de la banda sonora de la película “El Graduado (1967)” que trata de un tipo joven de 21
años que ya terminó su carrera y que tiene la vida resuelta y, sin embargo, no tiene deseos de
hacer nada (¿te ha pasado alguna vez?). Se involucra con una mujer mayor hasta que conoce
a Elaine y todo adquiere sentido en su vida... tienes que verla, el final es genial!!!
7
Convección
Los transportadores de calor más comunes y eficientes son los fluídos, debido a la facilidad
que tienen para moverse de un lado a otro. Y el "motor" más frecuente es la diferencia de
flotabilidad de los fluídos menos densos dentro de los fluídos más densos.
¿Recuerdas el principio de Arquímedes? Deberías. Pues bien, dentro del principio de
Arquímedes subyace la idea de que los cuerpos menos densos flotan dentro de los cuerpos
más densos, es decir, sin empujados por los cuerpos más densos. Entonces, el aire caliente es
menos denso que el aire frío, de modo que si tenemos una masa de aire caliente dentro de
una masa de aire frío mucho más grande y que envuelve a la caliente, la masa de aire frío se
elevará, como se eleva un corcho depositado en el fondo de la bañera.
Las corrientes ascendentes toman calor en los niveles inferiores y lo transportan a los
niveles superiores.
Para la convección no hay leyes simples ni generalizadoras, de modo que nos contentamos
con entender el proceso y en general (al menos en los cursos de Física iniciales) no nos interesa
medirlo.
Sin embargo, te menciono algunos ejemplos de convección:
1) El humo del cigarrillo. El humo del cigarrillo es menos denso que el aire, por eso flota
dentro de éste. Como al abandonar el cigarro, el humo tiene mayor temperatura, asciende,
formando espirales hacia la atmósfera, pasando a ser parte de los gases que contaminan
nuestro mundo... (qué lindo!!)
2) ¿Has viajado por las carreteras en verano? Entonces a lo lejos y sobre el asfalto las
imágenes se ven temblorosas. La explicación es simple. El sol caliente el asfalto y éste caliente
el aire que está sobre él; cuando el aire se caliente disminuye su densidad y comienza a
ascender, es en ese movimiento e intercambio en el que los objetos se ven medios deformados
sobre la superficie.
3) Basta por hoy. Yo también quiero descansar.
Dilatación Térmica
Una cosa más. Rápidamente, necesito que echemos un vistazo a los cambios que sufren los
objetos cuando absorben o ceden calor. Es bien sabido que si calientas un metal éste aumenta
su temperatura y se dilata. La dilatación térmica es el aumento de longitud, volumen o alguna
otra dimensión métrica que sufre un cuerpo físico debido al aumento de temperatura que se
provoca en él por cualquier medio.
La expansión o contracción de un objeto, cuya longitud inicial es L0 y cuya temperatura
cambia de Ti a Tf está dada por
L(Tf ) = L0 · (1 + α · (Tf − Ti))
donde α es el coeficiente de dilatación térmica propio de cada material. Este coeficiente es una
medida de la facilidad con la que se expande o contrae un material, mientras más pequeño
sea α menos se expande (o contrae) con los cambios de temperatura. La tabla al margen
consiga algunos coeficientes de dilatación térmica.
8