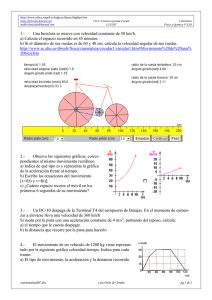
Fuerzas y Movimiento: Cinemática y Dinámica (Bachillerato)
Anuncio

BLOQUE 9 COMPLETO LAS FUERZAS Y EL MOVIMIENTO 1º.- INTRODUCCIÓN En este tema vamos a estudiar el movimiento, que es un fenómeno que sucede a nuestro alrededor constantemente. Antes de iniciarlo vamos a aclarar y/o definir algunos conceptos previos necesarios. A) Se llama MECÁNICA a la parte de la Física que estudia el movimiento. ➢ La mecánica a su vez se divide en dos partes: ➢ CINEMÁTICA: Es la parte de la mecánica que estudia el movimiento para “describirlo”. Conocer cómo sucede, y qué conceptos y magnitudes son necesarias para su descripción, en concreto: o la trayectoria de un movimiento. o la posición del móvil o la velocidad o la aceleración ➢ DINÁMICA: Es la parte de la mecánica que estudia el movimiento, relacionando las variables que lo describen (en concreto la aceleración) con las causas que lo provocan, que son las fuerzas. La Cinemática estudia y describe cualquier el movimiento, desde el que realiza una hormiga que se mueve por una mesa, hasta el que sigue La Tierra alrededor del Sol. La Dinámica se encarga de analizar las causas de esos movimientos, es decir de las fuerzas. Entender las fuerzas significa saber por qué y cómo se mueven las cosas, y predecir los efectos que se producirán a lo largo del tiempo. B) CONCEPTO DE MAGNITUD Y TIPOS DE MAGNITUDES B.1 Concepto de magnitud En la ciencia se llama magnitud física a cualquier propiedad que puede ser medida, ejemplos son: el tiempo, la longitud, la masa, el volumen, la velocidad, la densidad, etc. Algunas propiedades de la materia o de los objetos no son magnitudes, porque no se pueden medir, por ejemplo: el color, el olor, la belleza, la soledad, tristeza… se puede estar muy triste o poco triste pero no es posible asignar un número para medir la tristeza, y si se intenta, ese número será subjetivo, es decir cada persona puede asignar números diferentes a la misma situación. La Física sólo maneja propiedades que se pueden medir, es decir magnitudes. B.2 Unidades En Física cada magnitud o propiedad tiene asignada una “unidad de medida”, que hay que indicarla siempre al lado del valor de la magnitud, por ejemplo: ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 1 de 29 − − − el tiempo se puede medir en segundos, minutos, horas,… la longitud se mide en metros, centímetros… la velocidad en m/s o Km/h. B.3 Tipos de magnitudes: magnitudes escalares y magnitudes vectoriales (vectores) ➢ Se llaman magnitudes escalares a aquellas propiedades que para conocerlas basta con conocer un dato numérico, es decir un número que indique su valor. Por ejemplo para conocer la masa de un cuerpo sólo hay que decir su valor ej. 20kg, para conocer la longitud de una mesa basta con dar un número por ej. 1,5m. La mayoría de las propiedades o magnitudes que manejamos diariamente son de este tipo: longitud, tiempo, masa, volumen, densidad, presión etc. ➢ Se llaman magnitudes vectoriales aquellas que para conocerlas no basta con dar un dato o valor hay que dar más, en concreto tres datos. la fuerza aplicada a un objeto o la velocidad que lleva son ejemplos de magnitudes vectoriales. Por ejemplo: para conocer completamente la velocidad con la que se mueve un coche no basta con decir que su velocidad es de 100km/h, para conocer de verdad cómo se mueve hay que indicar además en qué dirección lo hace y en qué sentido se produce esa velocidad, es decir tres datos: o módulo o intensidad de la velocidad: 100km/h o dirección es la recta donde se produce el movimiento o sentido (hacia la derecha o hacia la izquierda) Este tipo de magnitudes se representan con unos “entes” matemáticos llamados vectores. B.3 Características de los vectores ➢ De forma intuitiva se puede definir y representar un vector como un segmento orientado, es decir una flecha. 𝑣⃗ Notación: al vector le pone nombre utilizando una letra, por ejemplo v, y para indicar que es un vector se escribe 𝑣⃗ ➢ Información que aporta un vector: Al dibujar un vector nos transmite mucha información, por ejemplo supongamos que el vector representado es la velocidad de un vehículo: ➢ el tamaño de la flecha (llamado módulo del vector) no indica el valor de la velocidad, si el módulo es grande significa que la velocidad es grande, y si el módulo es pequeño no indica que la velocidad es pequeña. ➢ La dirección de la flecha (dirección del vector) nos indica en qué dirección se está moviendo el vehículo, es decir la dirección de la velocidad ➢ la punta de la flecha no indica el sentido del movimiento, puede haber dos sentidos (derecha/ izquierda) (arriba/abajo) Evidentemente, dependiendo de la magnitud que represente el vector y la situación concreta la dirección del vector puede ser cualquiera: ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 2 de 29 ➢ Operaciones con vectores: Los vectores pueden sumarse, restarse y multiplicarse, pero no siempre siguen las reglas de la suma resta y multiplicación de los números, por ejemplo dos vectores de módulo 4 y 5 no siempre dan como resultado un vector de módulo 4+5=9, el resultado depende de la dirección relativa que tengan ambos vectores y de sus sentidos respectivos. NOTA: En la segunda parte del tema, la dinámica, aprenderemos a sumar vectores. 2º.- DESCRIPCIÓN DEL MOVIMIENTO (CINEMÁTICA) 2.1 DEFINICIÓN DE MOVIMIENTO Decimos que un cuerpo se mueve si cambia su posición respecto al sistema de referencia, en caso contrario decimos que está en reposo. Por comodidad, a un objeto que se mueve, le vamos a llamar "móvil". 2.2 EL MOVIMIENTO ES RELATIVO De la propia definición de movimiento se deduce que un objeto puede estar o no moviéndose dependiendo del “punto” o “sistema de referencia” desde el que lo observemos. Por ejemplo si una persona está sentada viajando en un tren, un observador situado en la vía observará que esa persona está moviéndose (porque se mueve el tren), en cambio si quien observa es otro pasajero del tren la distancia entre ambas personas no cambio por lo que para ese observador la persona está en reposo. Esto se resume diciendo que el estado de movimiento o reposo de un cuerpo no es absoluto sino que es “relativo”, es decir que depende del sistema de referencia desde el que se observe al cuerpo. 2.3 DEFINICIÓN DE SISTEMA DE REFERENCIA Llamamos sistema de referencia a un punto fijo desde el que observamos la evolución o movimiento de un cuerpo. Desde el sistema de referencia observamos y medimos la posición inicial y la posición en cada momento distinto, según va pasando el tiempo, de éste modo podemos conocer las características del movimiento del cuerpo. El sistema de referencia es el marco con respecto al cual vamos a indicar la posición de un cuerpo. En Física, un sistema de referencia es un punto y un sistema de ejes (ejes de coordenadas que se cortan en el origen), y que se toman como referencia para medir observar la posición y medir la distancia a la que se encuentra el objeto. Dependiendo de las dimensiones necesarias para describir el movimiento se utilizan tres sistemas de referencia posibles: sistema referencia de dos dimensiones • Una dimensión - Movimientos Lineales eje y P • Dos dimensiones - Movimientos en el Plano • Tres dimensiones - Movimientos en el Espacio O eje x La mayoría de los movimientos que ocurren a nuestro alrededor ocurren en tres dimensiones (por ejemplo el vuelo de un pájaro, una mosca etc.) en este caso el sistema de referencia debe tener tres dimensiones para marcar la posición del móvil en cada momento. Otros movimientos, como los que realiza un patinador o un futbolista en un partido ocurren en un plano (la superficie de la Tierra) en este caso se necesita un sistema de referencia de dos dimensiones. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 3 de 29 En ambos casos para indicar la posición del cuerpo en cada instante necesitamos utilizar vectores. Sin embargo si conocemos la línea o trayectoria que sigue el cuerpo en su movimiento podemos utilizar un sistema de referencia de una sola dimensión. En un sistema de una dimensión, para conocer la posición del cuerpo en cada instante bastará con medir la distancia al origen u observador (distancia medida sobre la línea de la trayectoria). Es decir no necesitaremos usar vectores pues con un solo dato (la distancia) sabremos la posición del cuerpo. Este es el caso por ejemplo de un coche sobre una carretera. Sabiendo la distancia al origen conocemos la posición del cuerpo. En los movimientos que estudiemos en detalle más adelante utilizaremos sólo una dimensión. 2.4 DEFINICIÓN DE TRAYECTORIA Se llama trayectoria a la línea imaginaria que dibuja el cuerpo al moverse. De otro modo, trayectoria es la sucesión de puntos por donde pasa un móvil. Hay dos tipos de movimientos según sea su trayectoria: • Rectilíneo: cuando su trayectoria es una recta. • Curvilíneo: cuando su trayectoria una curva. El más conocido es el movimiento circular. trayectoria curva trayectoria recta 2.5 MAGNITUDES QUE INTERVIENEN EN EL ESTUDIO DEL MOVIMIENTO, Y SUS UNIDADES. Cuando un cuerpo se mueve respecto a un observador, ocurre que su posición cambia con el tiempo, esto provoca que recorra una cantidad de espacio en un cierto tiempo, además el ritmo al que se desplaza puede cambiar también durante el movimiento. De esta realidad se deduce que para describir el movimiento, además de conocer la posición del móvil en cada momento, la cinemática necesita las siguientes magnitudes: el espacio (e), el tiempo (t), la velocidad (v), y la aceleración (a). ➢ Posición: en un movimiento unidimensional la posición se conoce sabiendo la distancia al observador. ➢ El espacio recorrido (e) por un móvil en un determinado tiempo es la longitud de la trayectoria descrita por el móvil en ese tiempo. ➢ La Velocidad (v): es una magnitud que mide y nos informa de lo rápido que se desplaza el objeto, es decir el “ritmo con el que cambia de posición” si la velocidad es grande su posición cambia ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 4 de 29 muy rápido y recorre mucho espacio en poco tiempo. 𝑣= La velocidad se calcula con la fórmula 𝑒 𝑡 donde “e” es el espacio recorrido en una determinada cantidad de tiempo y “t” es el tiempo. Ejemplo si un cuerpo recorre 20 metros en 5 segundos su velocidad será 𝑒 20 𝑡 5 𝑣= = ➢ =4 𝑚𝑒𝑡𝑟𝑜𝑠 𝑠𝑒𝑔𝑢𝑛𝑑𝑜𝑠 =4 𝑚 𝑠 Aceleración (a): En muchos movimientos la velocidad no se mantiene constante, sino que cambia continuamente, esto quiere decir que la velocidad crece o decrece. Para medir esta situación se define la aceleración. Se llama aceleración (a) a la magnitud que mide el “ritmo con el que cambia la velocidad”. Si la aceleración es grande la velocidad cambia rápidamente, si la aceleración es pequeña la velocidad cambia lentamente y si la aceleración es cero la velocidad no cambia es decir es constante. La aceleración se calcula con la fórmula: 𝒂= 𝒗𝟐 − 𝒗𝟏 𝒕 Donde “v2” es la velocidad final, “v1” es la velocidad inicial y “t” es el tiempo que tarda en que el cuerpo pase de la velocidad inicial a la velocidad final UNIDADES Las magnitudes físicas está asociadas a la “unidad” en la que se miden, por ejemplo la longitud se mide en metros, o en centímetros o en kilómetros… esta unidad hay que indicarla siempre al lado del valor de la magnitud. No basta con decir que una mesa mide 2 hay que decir que mide 2metros, 2m. Todas las magnitudes físicas tienen muchas unidades con las cuales se pueden expresar. Por ejemplo, una distancia se puede medir en metros (m), en centímetros (cm) o en kilómetros (km), y hay que saber cómo se pasa de una unidad a otra. Pero siempre (salvo excepciones) se usarán las unidades del Sistema Internacional de Unidades (S.I). En la siguiente tabla se indican las magnitudes que se utilizan en la cinemática, junto con sus unidades en el S.I. magnitud Unidad (S.I) símbolo Espacio recorrido (e) metro m Tiempo (t) segundo s Velocidad (v) metro/segundo m/s Aceleración (a) Metro/segundo2 m/s2 Para medir la velocidad, además del m/s (S.I), es muy utilizado el km/h. Hay que saber pasar de una a otra. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 5 de 29 Cuando los datos de un problema no estén expresados en las unidades del S.I. y se necesite, se deberá hacer el cambio correspondiente a las unidades del S.I: 3.- CLASIFICACIÓN DE LOS MOVIMIENTOS SEGÚN SU TRAYECTORIA. Según sea la trayectoria hay dos tipos de movimientos: • Rectilíneos: cuando su trayectoria es una recta. • Curvilíneos: cuando su trayectoria es una curva. El más conocido y sencillo de estudiar es el movimiento circular en el que la trayectoria es una circunferencia. 4.- DIFERENCIA ENTRE LOS CONCEPTOS DE “ESPACIO RECORRIDO SOBRE LA TRAYECTORIA” Y “DESPLAZAMIENTO” − El Espacio recorrido es la longitud de la trayectoria descrita por un cuerpo entre la posición inicial y la final (distancia medida sobre la trayectoria). − El Desplazamiento es la diferencia entre la posición inicial y final de un cuerpo, es decir la distancia en línea recta entre la posición final y al posición inicial. Ambas magnitudes son longitudes y su unidad en el S.l. es el metro (m), sin embargo sus valores no son coincidentes. Espacio recorrido Desplazamiento Sólo coincidirá espacio recorrido y desplazamiento en el caso de que la trayectoria sea rectilínea y el móvil no cambie de sentido. Ejemplo Me doy un paseo por el pueblo siguiendo el camino dibujado en el mapa de la derecha: Salgo de mi casa (punto A), tomo la avda. Juan Carlos I, giro a la derecha por la calle San Marcos, a la derecha por la calle García Lorca, conecto con la calle Ramón y Cajal hasta la gasolinera, y de allí regreso a mi casa (punto B). a)¿Cuál ha sido la trayectoria de este movimiento? Respuesta: la marcada en el mapa b) ¿cuál es el valor del desplazamiento realizado. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 6 de 29 Respuesta: el desplazamiento es cero porque sale de un punto y llega al mismo punto. La distancia entre ambos en línea recta es cero c) Coincide con el espacio recorrido en el paseo?, ¿por qué? Respuesta: no, el espacio recorrido sobre la trayectoria es grande es toda la longitud del camino seguido, mientras que el desplazamiento ha sido cero. 5.- INTERPRETACIÓN GRÁFICA DEL MOVIMIENTO. REPRESENTACIONES GRÁFICAS En el estudio de los movimientos es útil hacer representaciones gráficas que relacionan dos variables, del análisis de estas gráficas se puede conocer mucho del movimiento. Vamos a analizar dos graficas: A) Gráfica posición-tiempo (espacio-tiempo) (e - t): En esta gráfica se representa la posición del móvil en el eje vertical y el tiempo en el eje horizontal. Hay que dar valores al tiempo, y mediante la ecuación se calcula la posición /el espacio recorrido en cada tiempo, completándose así, la tabla de valores. Nota; Del aspecto de esta gráfica se puede obtener mucha información de cómo es el movimiento, pero ninguna sobre la forma de la trayectoria. Es decir la forma de la gráfica no es la forma de la trayectoria. Ejemplo1 Supongamos que la gráfica (posición – tiempo) de un móvil se la que se ve en la figura, Tiempo (s) Obsérvala y contesta a las preguntas: a) b) c) d) e) f) g) ¿En qué posición se encuetar el móvil cuando el tiempo es cero?,¿y cuando es 40s . ¿Qué le ocurre al móvil durante los primeros 15 segundos? ¿Qué le ocurre al móvil desde el instante t=15s hasta t=25s? ¿Cuál es el tramo de tiempo donde el móvil va más rápido? ¿Qué velocidad máxima alcanza?, ¿en qué instante ocurre esto? ¿Qué ocurre desde los 50 s hasta los 70s? , ¿qué significa esto? ¿qué velocidad tiene en ese momento? Nota, observa; o En los tramos donde la grafica es una recta inclinada la posición varia uniformemente. Por lo tanto la velocidad es constante. Se tratará de un movimiento “uniforme” (v=cte) o En los tramos donde la gráfica es una línea recta horizontal el móvil está parado (no cambia la posición) ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 7 de 29 o En los tramos donde la recta es inclinada, pero invertida, el móvil se ha dado la vuelta y regresa la origen Ejemplo2 Supongamos que la gráfica (posición – tiempo) de un móvil es la que se ve en la figura, Responde a las preguntas: a) ¿Cuál es la posición inicial (t = 0 s.) del móvil? b) ¿En qué instante la posición del móvil coincide con la del observador de sistema de referencia? c) ¿Con qué velocidad se mueve el móvil? d) Hay un instante en que el móvil da la vuelta y regresa sobre sus propios pasos, ¿de qué instante se trata? e) ¿En qué posición se encuentra en el instante t = 7 s? ¿y en t = 13 s? B) Gráfica velocidad tiempo (v - t): En esta gráfica se representa la velocidad en el eje vertical (eje de ordenadas) y el tiempo en el eje horizontal (de abscisas). Al igual que la grafica (posición–tiempo) puede obtenerse mucha información, pero la forma de la gráfica no coincide con la forma de la trayectoria Ejemplo3 Supongamos que la gráfica (velocidad – tiempo) de un móvil es la que se ve en la figura, velocidad tiempo ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 8 de 29 Obsérvala y contesta a las siguientes preguntas: a) ¿con qué velocidad inicial parte el móvil? b) ¿En qué periodo de tiempo está detenido? c) ¿Qué velocidad alcanza a los 30 segundos? d) ¿En qué instante de tiempo alcanza su velocidad punta? e) ¿Cuántos segundos tarda en pararse por completo? 6.- ESTUDIO DETALLADO DE LOS MOVIMIENTOS RECTILÍNEOS MÁS SENCILLOS. Vamos a estudiar con detalle (y con las fórmulas necesarias para poder hacer cálculos), los dos movimientos más sencillos que existen que son: el movimiento rectilíneo y uniforme MRU, y el movimiento rectilíneo uniformemente acelerado MRUA. 6.1 MOVIMIENTO RECTILÍNEO Y UNIFORME MRU El movimiento rectilíneo y uniforme (MRU) es aquel cuya trayectoria es la línea recta y su velocidad (módulo, dirección y sentido) permanece constante, no varía, durante todo el recorrido. Es decir se mueve en línea recta con un ritmo constante de un punto A otro B. A B FÓRMULAS La ecuación que usaremos para resolver los problemas de este tipo de movimiento es: 𝒗= 𝒆 𝒕 y las que se obtienen despejando el espacio y el tiempo: e= v.t y 𝑒 𝑡=𝑣 Ejemplo 1: Un ciclista recorre 500 m empleando para ello un tiempo de 25 s. ¿Cuál ha sido su velocidad? Aplicando la fórmula tendremos el resultado 𝒗= 𝒆 𝒕 = 𝟓𝟎𝟎 𝒎 𝟐𝟓 𝒔 = 𝟒 𝒎/𝒔 Ejemplo 2: Un coche viaja a una velocidad de 20 km/h. ¿Qué espacio recorrerá en 6 minutos? - primero pasamos los datos al SI. 20k/h = 20𝑘𝑚 ℎ = 20𝑥1000 𝑚 3600𝑠 =5,56m/s - 6minutos = 6x60 segundos = 360 s Aplicando la fórmula tendremos el resultado e =v.t = 5,56 ACT II Bloque 9. El movimiento. Cinemática y Dinámica 𝑚 . 360𝑠 𝑠 = 2001,6 𝑚 Página 9 de 29 Ejemplo 3: Un vehículo se mueve con MRU con una velocidad de 10m/s, ¿qué tiempo tardará en recorrer 400m? 𝑒 𝑣 Aplicando la fórmula tendremos el resultado e =v.t => t= = 400𝑚 10 𝑚/𝑠 = 40 𝑠 MÉTODO DE RESOLUCIÓN DE PROBLEMAS Para resolver un problema se recomienda seguir los siguientes pasos: 1°) Se ponen los datos conocidos, con sus correspondientes unidades. 22) Se revisan las unidades y en caso necesario se cambian, para que todas estén en el S.I. 32) Se elige la fórmula a utilizar. 4°) Se calcula la incógnita pedida. 52) Se analiza el resultado obtenido. Veámoslo con un ejemplo más: Si un coche va a una velocidad de 25 m/s, calcular que espacio recorrerá en 2 h. 1°) Datos: v = 25 m/s, t = 2 h 2°) Unidades: hay que pasar las horas a segundos, 2 h x 3600 s/h = 7200 s 3°) Fórmula: e = v . t , 4°) Cálculos: e = 25 . 7200 = 180000m. 5°) Análisis: Es correcto, ya que si recorre 25 m en un segundo, en 7200 s, recorrerá 180000 m. 6.2 MOVIMIENTO RECTILÍNEO Y UNIFORMEMENTE ACELERADO (MRUA) Es aquel cuya trayectoria es una línea recta y su aceleración es constante. Es decir la velocidad no permanece constante, varía con el tiempo, pero esta variación se produce siempre al mismo ritmo, es decir, es aquel que tiene aceleración y que además es constante. − Si el movimiento del cuerpo se produce de forma que aumenta su velocidad (acelera) se asigna a la aceleración signo positivo (+). Por ej. a=+3m/s2 (a= 3m/s2) − Si el cuerpo disminuye su velocidad (va frenado) se asigna a la aceleración sino negativo (-). Por ejemplo a= -3m/s2 FÓRMULAS Las ecuaciones que verifican este tipo de movimiento son dos: − la ecuación del espacio: − la ecuación de la velocidad: e = v0.t+1/2.a.t2 v= v0+a.t --→ equivale a la ecuación a = 𝒗𝒇 −𝒗𝟎 𝒕 Donde: e → es el espacio recorrido en metros v0→ es la velocidad inicial en m/s t → es el tiempo en segundos a → es la aceleración en m/s2 v → es la velocidad en un determinado momento del recorrido, es decir, es la velocidad instantánea. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 10 de 29 Ejemplo1 Un coche pasa de 0 a 100 km/h en 8 segundos. ¿Cuál ha sido su aceleración? − Lo primero es poner las velocidades en m/s. Tendremos entonces que: V1 = 0 m/s − v2 = 27,8 m/s Ahora aplicamos la fórmula: m 27,8 s − 0 m/s v2 − v1 a= = = 3,5 m/s t 100s Explicación del resultado: − Que la aceleración sea de 3,5 m/s2 quiere decir que la velocidad del coche aumenta 3,5 m/s cada segundo que transcurre. Ejercicios 1º.- Un fórmula 1 pasa de 0 a 100 km/h en tan solo 2,5 segundos, ¿con qué aceleración lo hace? (las velocidades están en km/h, hay que pasarlas a m/s) Sol.: 11,11 m/s2 2º.-El fórmula 1 anterior va a 320 km/h en la recta de meta, pero se acerca una curva y debe reducir su velocidad hasta los 80 km/h en 3 segundos ¿Cuál es ahora su aceleración?. En este caso debe salirte negativa, ya que va frenando. Sol.: - 22,22 m/s2 3ª¿Qué aceleración ha llevado un cohete espacial si ha pasado del reposo a 27875 km/h en 4 minutos y 20 segundos? Sol.: 29,78 m/s2 4ªLanzamos verticalmente hacia arriba una pelota con una velocidad de 29,4 m/s. Tarda en detenerse 3 segundos. Calcula su aceleración. ¿Qué signo tiene la aceleración?, ¿por qué? Sol.: - 9,8m/s2 5º.La gráfica de la imagen representa el movimiento de un fórmula 1 durante su entrada y salida a boxes para repostar. Obsérvala con atención y contesta a las preguntas que se te plantean v (km/h) 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10 11 t (s) a) ¿Cuál es la velocidad con la que el vehículo empieza su entrada en boxes? b) ¿Y la velocidad aproximada con la que sale? c) ¿Cuánto tiempo tarda en detenerse? d) ¿Cuánto tiempo está detenido? ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 11 de 29 e) ¿Cuánto tiempo transcurre desde que termina de repostar hasta que sale de boxes? f) Razona el tipo de movimiento (acelerado, uniforme o reposo) que lleva el coche en cada intervalo de tiempo: INTERVALO DE TIEMPO TIPO DE MOVIMIENTO g) Marca la respuesta correcta en cada caso: 1)¿En qué intervalo de tiempo su aceleración de frenada es mayor? o Entre los 0 y los 2 segundos o Entre los 4 y los 5,25 segundos o Entre los 10,25 y los 11,25 segundos 2) ¿Qué aceleración lleva entre los 0 y 2 segundos? 3) 4) o 12 m/s o 12 m/s2 o -12 m/s2 ¿A qué velocidad constante recorre parte del trayecto antes de detenerse? O A 0 m/ s O A 28 m/s O A 28 km/h ¿Con qué aceleración sale de boxes? o o o 5) 12 m/s2 42m/s2 22,4 m/s2 Observando la gráfica, ¿qué podemos decir respecto a la trayectoria que sigue el fórmula 1? O Nada O Que es rectilínea O Que es rectilínea, pero a trozos MÉTODO DE RESOLUCIÓN DE PROBLEMAS Vamos a seguir los mismos pasos recomendados en apartados anteriores, con el siguiente ejemplo: Ejemplo1 Un ciclista se está moviendo a 12 m/s cuando tiene que frenar al cruzársele un gato a 2,5 m delante de él. Consigue detenerse transcurridos 0,4 segundos. Se pide: a) ¿Qué aceleración tuvo el ciclista? b) ¿Qué distancia recorrió antes de detenerse? c) ¿Atropelló al gato? ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 12 de 29 Resolución: 1°) Datos: vo = 12 m/s; v = 0 (puesto que se detiene); t = 0,4 s; distancia del gato = 2,5 m 2°) Unidades: En este caso no hay que hacer cambios. 3e) Fórmulas: "v = v0+a-t” y "e = v0-t+l/2-a- t2 “ 4°) Cálculos: a) v = vo+ a t , utilizando esta fórmula y sustituyendo los datos que tenemos podemos calcular la aceleración del ciclista: 0 = 12 + a- 0,4 despejando: a = -12/0,4 → a = -30 m/s2. b) De forma análoga pero con esta fórmula: e = vo-t+l/2-a.t2 e= 12 . 0,4 + ½- (-30) . 0,42 = 4,8 - 2,4 → e = 2,4 m 5°) Análisis: Es lógico que nos salga una aceleración negativa ya que el ciclista va frenando. El espacio que nos sale hasta que se para nos permita contestar a la tercera cuestión: Según el resultado obtenido en el apartado anterior vemos que el ciclista recorre 2,4 m antes de detenerse. Como el gato estaba a 2,5m del ciclista cuando éste comienza a frenar, podemos concluir que el gato se salva por los pelos. Ejemplo2 : Un automóvil parte del reposo (v0=0) con una acelerción constante de 2m/s2. calcula: a) La velocidad del móvil a los 8 segundos de iniciado el movimiento b) La distancia (espacio) recorrída en ese tiempo. Resolución: a) usamos al ecuación de la velocidad: v= v0 +a.t => v =0+2.8 =0+16 =16 m/s b) Usamos la ecuación del espacio: e = v0.t+1/2.a.t2 ---> e = 0.8 + 2.82 2 = 2.64 2 =64 m Ejercicios: 1.-Una moto pasa por un punto a una velocidad de 60 km/h; en ese instante, acelera uniformemente durante 5 segundos hasta alcanzar la velocidad de 80 km/h. Calcula: a) Aceleración de la moto en ese intervalo b) Distancia que recorre la moto en esos 5 segundos 2.-Un tren de alta velocidad (AVE) viaja durante media hora con una velocidad constante de 252 km/h. A continuación reduce su velocidad hasta pararse en 14 segundos. a) ¿Qué tipo de movimiento lleva durante la primera media hora? b) ¿Qué tipo de movimiento lleva durante los 14 segundos restantes? c) Calcula la aceleración desde que empieza a frenar hasta que se detiene. d) ¿Qué distancia de frenado recorre hasta que se para? ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 13 de 29 7.-LISTAS DE REPASO DE CINÉMÁTICA 1ª LISTA DE EJERCICIOS DE REPASO (CINEMÁTICA) 1.- Un representante de jamones hace el siguiente recorrido: • Córdoba-Fernán Núñez (25 km) • Fernán Núñez-Montilla (15 km) • Montilla-Montemayor (11 km) • Montemayor-Fernán Núñez (4 km) En Fernán Núñez finaliza su jornada de trabajo, fin de trayecto. a) ¿Qué distancia ha recorrido el representante durante su jornada de trabajo? Sol.: 55km b) ¿Cuál ha sido su desplazamiento? Sol.: 0 Km 2.- Un ciclista recorre 15km en 30 minutos. a) ¿Cuál ha sido su velocidad? Exprésala en Km/h Sol.: 30Km/h b) Transforma la velocidad de Km/h a m/s Sol.: 8.33 m/s 3.- a) Expresa la velocidad de 54 km/h en m/s b) Expresa la velocidad de 20m /s a Km/h c) Expresa 45m/s a Km/h d) Expresa 120 km/h en m/s Sol.: 15 m/s Sol.: 72 km/h Sol.: 162 km/h Sol.: 33.3 m/s 4.- ¿Qué velocidad lleva una moto que completa una vuelta a un circuito de 4268 m en 1 minuto y 12 segundos? Sol.: 59,28 m/s MRU 5.- Un tren lleva una velocidad constante de 45m/s. ¿Qué distancia recorre en 120 segundos? Solución: 5400 m. 6.- ¿Cuánto tiempo debe pasar para que el tren anterior recorra 6780 m? Sol.: 150,67 s 7.- ¿Qué distancia recorre en 5 minutos un coche que lleva una velocidad constante de 20m/s? Sol.: 6000m 8.- Una moto lleva una velocidad constante de 150 Km/h a) Expresa dicha velocidad en m/s Sol.: 41,67 m/s b) Calcula la distancia, en Km que recorrerá en 2 horas y media Sol.: 375 Km c) Calcula el tiempo que tardará en recorrer una distancia de 450 Km Sol.: 3 h 9.- Un ciclista se mueva a una velocidad de 13,8 m/s durante una hora. ¿qué distancia recorrió en ese tiempo? Sol.: 49680 m = 49,68 Km 10.- Un ladrón huye en su coche a una velocidad de 117 Km/H. 10 segundos más tarde sale en su persecución un coche de policía a 144 Km/h a) b) c) Expresa ambas velocidades en m/s Sol.: 32,5 m/s ; 40 m/s ¿Qué ventaja le lleva el ladrón al policía? Sol.: 325 m (mayor dificultad) Teniendo en cuenta que en el preciso instante en que la distancia recorrida por ambos coches sea la misma, significa que atrapa al ladrón. ¿Cuánto tiempo tarda en ser atrapado el ladrón, contado desde que comenzó a huir en coche? Sol.: 53,33 s ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 14 de 29 INTERPRETACIÓN DE GRÁFICAS 11.- velocidad en m/s La siguiente gráfica describe las velocidades de un objeto durante 14 segundos. Calcula: a) b) c) d) e) f) Su aceleración en el periodo de 10 a 12 segundos. Sol.: -7,5 m/s2 ¿En qué periodos de tiempo la aceleración es cero? Sol.: de (2 a 4 s); (8 a 10 s); (12 a 14 s) Su aceleración en el periodo de 4 a 6 segundos Sol.: 5m/s2 Qué tipo de movimiento tiene en el tramo de 0 a 2 segundos. Sol.: m.r.u.a. Qué tipo de movimiento tiene en el tramo de 2 a 4 segundos. Sol.: m.r.u. Qué tipo de movimiento tiene en el tramo de 10 a 12 segundos. Sol.: m.r.u.a. (frenando) 12.- Considerando la siguiente tabla de valores de un movimiento, haz la gráfica posición-tiempo y contesta a las preguntas: Tiempo (s) 0 5 10 15 20 25 30 Posición (m) 0 100 300 300 400 500 ° a) Dibuja la gráfica de este movimiento b) ¿Cuál ha sido el desplazamiento? c) ¿Cuál ha sido la distancia total recorrida? d) ¿Qué velocidad llevaba el cuerpo entre el inicio y los 10 segundos? MRUA 13.- Un auto con una velocidad de 2m/s acelera a razón de 4 m/s2 durante 2,5 s. ¿Cuál es su velocidad después de 2,5 segundos? Sol.: 27 m/s 14.- Un avión al aterrizar toca la pista con una velocidad de 100m/s y frena a un ritmo de -5 m/s2 hasta detenerse. a) ¿Cuánto tiempo tarda en detenerse? Sol.: 20 s b) ¿Qué espacio recorre en ese timpo? Sol.: 1000 m ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 15 de 29 2ª LISTA DE EJERCICIOS DE REPASO (CINEMÁTICA) 1.- Cambiar de unidades según se indica: a) b) De 36 km/h a m/s De 20m/s a Km/h Sol: 10 m/s Sol.: 72 km/h 2.- Un móvil recorre 98 km en dos horas. Calcula: a) Su velocidad expresada en km/h Sol.: 49 Km/h b) Su velocidad expresada en m/s Sol.: 13,61 m/s c) Distancia que recorrerá en 3 horas con esa misma velocidad 3.- Un móvil que viaja a una velocidad de 80 km/h recorre una distancia de 640 km. ¿Cuánto tiempo tardará? Sol.: 8 h 4.- ¿Qué espacio recorrerá un móvil que se desplaza a 75 km/h en 8 minutos? Sol.: 10000 m 5.- Un móvil se mueve con una velocidad de 120 km/h y otro móvil lo hace con una velocidad de 45 m/s ¿Cuál de ellos va más rápido? Sol.: el segundo va más rápido 6.- Se produce un disparo a 2 km de donde se encuentra un policía. La velocidad del sonido es de 340 m/s aproximadamente. ¿Cuánto tiempo tarda el policía en oír el disparo? Sol.: 5,88 s ------- 7.- Un conductor circula a 12 m/s. Acelera y pasa a circular a 20 m/s al cabo de 10 segundos. ¿Qué tipo de movimiento lleva?. Calcula la aceleración del coche. Sol.: m.r.u.a. ; 0,8 m/s2 8.- Una pelota que rueda por el suelo con una velocidad de 2 m/s tarda en detenerse 10 segundos. ¿Cuánto vale la aceleración de frenado?. ¿Qué tipo de movimiento lleva? Sol.: - 0,2 m/s2; m.r.u.a. 9.- La aceleración a la que se ve sometido un avión es de 2 m/s 2. Si el avión, partiendo del reposo, tarda en despegar 25 segundos, a) ¿Cuál es la velocidad que lleva el avión cuando despega? Sol.: 50m/s b) ¿Qué espacio ha recorrido sobre la pista de despegue? Sol.: 625 m 10.- Un conductor circula en coche 72 km/h. Frena y se para en 20 segundos. ¿Cuál ha sido la aceleración durante la frenada?. ¿Qué tipo de movimiento ha tenido? Sol.: - 1m/s2 11.- Un tren sale de la estación con una aceleración de 1,2 m/s 2. a) ¿Cuál será su velocidad al cabo de los 10 segundos? Sol.: 12m/s b) b) ¿Qué espacio habrá recorrido en esos 10 s? 12.- Sol.: 60 m Un coche circula con una velocidad inicial de 25 m/s. Acelera a razón de 3 m/s2 durante 5 segundos. Calcula la velocidad final alcanzada en Km/h. Sol.:144km/h 13.- Un automóvil se desplaza a 180 km/h por una autopista. Al llegar al peaje frena y para en 20 segundos. ¿Cuál ha sido la aceleración durante la frenada? Sol.: - 2,5 m/s2 ----------- 14.- El siguiente gráfico muestra el movimiento de un fórmula 1 que circula con velocidad constante por una recta del circuito: a) Cuántos metros ha recorrido en 1 segundo? Sol.: 35 m ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 16 de 29 b) ¿Cuál es su velocidad? Sol.: 35 m/s c) ¿En qué punto de la recta se encuentra en t =1s? Sol.: a 22,5 m del observador 15.- El siguiente gráfico muestra el movimiento rectilíneo 16.- de un móvil: a) ¿Qué distancia recorre en los 4 primeros segundos? Sol: 2 m b) ¿Cuánto tiempo está detenido y en qué posición? Sol.: a los 4 metros se detiene 2 segundos c) ¿Qué velocidad lleva entre los 8 y los 12 segundos? Sol.: 2m/s d) ¿Se trata de un movimiento rectilíneo uniforme?, ¿por qué? Sol.:Sí. Gráfica es recta inclinada e) Razona el tipo de movimiento que lleva en los siguientes tramos: 1) de 0 a 2 segundos. Sol.: m.r.u. 2) de 2 a 4 segundos. Sol.: m.r.u. 3) de 4 a 6 segundos. Sol.: reposo 4) de 6 a 8 segundos. Sol.: m.r.u. 5) de 8 a 12 segundos. Sol.: m.r.u. 6) de 12 a 16 segundos. Sol.: m.r.u. (se ha dado la vuelta) 8.- DINÁMICA ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 17 de 29 Como se dijo en la introducción, la Dinámica estudia el movimiento relacionándolo con las causas que lo producen o alteran que son las fuerzas. 8.1 CONCEPTO DE FUERZA Las fuerzas pueden definirse como “la causa capaz de modificar el estado de movimiento o de reposo de un cuerpo o producir su deformación". En este tema nos vamos a centrar en el efecto sobre el estado de movimiento de un cuerpo. La fuerza es una magnitud vectorial y se representan mediante un vector. Para definir un vector, y por lo tanto una fuerza, debemos conocer las siguientes características: • Módulo: o “intensidad” es el valor numérico de la fuerza, la cuantía de la fuerza. La unidad en que se miden las fuerzas es el Newton (N) • Dirección: es la recta que incluye a la fuerza. • Sentido: es la orientación que toma el vector (fuerza) dentro de su dirección. Todas las direcciones tienen dos sentidos. Punto de aplicación: es el punto donde se ejerce la fuerza. Salvo que se diga lo contrario, coincidirá con el centro de gravedad del cuerpo, que es su centro geométrico. Módulo -----------------------------------------------------------------------------------------------Dirección Punto de aplicación Sentido No es lo mismo aplicar una fuerza con un módulo determinado en una dirección que en otra, ni en un sentido que en otro. Las magnitudes vectoriales se representan con un símbolo y encima una flechita indicando que son vectores. Por ejemplo 𝐹⃗ , si sólo escribimos el símbolo sin la flechita “F” nos referimos sólo al módulo. La unidad de fuerza en el S.I. es el newton (N), aunque también se utiliza el kilopondio (kp), 1kp =9,8N. Las fuerzas se miden con un aparato llamado dinamómetro que consiste en un muelle que se estira cada vez más al aplicarle una fuerza mayor. Para conocer el efecto de varias fuerzas aplicadas sobre un mismo cuerpo hay que sumarlas, pero debido a su naturaleza vectorial la suma de fuerzas no sigue las reglas de la suma de números. Hay que aprender a sumar vectores. 8.2 SUMA DE FUERZAS, FUERZA RESULTANTE (COMPOSICIÓN DE FUERZAS) ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 18 de 29 Sumar o componer varias fuerzas consiste en calcular una fuerza única, llamada “fuerza resultante” que haga el mismo efecto que todas ellas juntas. ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗ 𝑅 = 𝐹⃗ + ⃗⃗⃗⃗⃗ 𝐹 1 2 Los principales casos que pueden darse son: 1) SUMA DE DOS FUERZAS DE LA MISMA DIRECCIÓN Y SENTIDO: La resultante es otra fuerza de la misma dirección y sentido, y de módulo, la suma de los módulos. 𝐹⃗1 𝐹⃗2 𝑅⃗⃗ Ejemplo: F1 = 3 N, F2 = 4 N => R= 3 + 4 = 7 N 2) SUMA DE FUERZAS DE LA MISMA DIRECCIÓN Y SENTIDO CONTRARIO: La resultante es otra fuerza de la misma dirección, sentido el de la mayor, y de módulo, la diferencia de los módulos. ⃗⃗⃗⃗ 𝐹1 ⃗⃗⃗⃗⃗ 𝐹2 𝑅⃗⃗ Ejemplo: F1 = 3 N, F2 = 4 N => R = 4 - 3 = 1 N 3) SUMA DE FUERZAS PERPENDICULARES: Para calcular gráficamente la resultante se emplea la regla del paralelogramo: Ejemplo: F1 = 3 N, F2 = 4 N → aplicando el teorema de Pitágoras R2 = 32 +42 =9+16=25 => R= 5 N Para realizar el cálculo numérico se emplea el Teorema de Pitágoras: “En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 19 de 29 catetos”. “h” es la hipotenusa, “a” y “b” son los catetos h b h2 = a2 + b2 a Ejemplo: si en un triángulo rectángulo los catetos valen 5 y 10 ¿Cuánto valdrá la hipotenusa? aplicando el teorema de Pitágoras: h2 = a2 + b2 = 52 + 102 = 25+100 = 125 => h =√125 =11,18 Ejercicios: 1. Calcula la hipotenusa de un triangulo rectángulo cuyos catetos valen 3 y 4 unidades Sol.: 5,83 2. Calcula la hipotenusa de un triangulo rectángulo cuyos catetos valen 6 y 8 unidades Sol.:10 3. si en un triángulo rectángulo ha hipotenusa vale 10 y uno de los catetos vales 6 ¿cuál será el valor del segundo cateto Sol.: 8 4) SUMA DE DOS FUERZAS EN CUALQUIER DIRECCIÓN: Se aplica la regla del paralelogramo, geométricamente se R F1 (Para el cálculo numérico tendríamos que utilizar el “teorema de F2 coseno” que no es objeto de este curso) Ejercicios: 1. Si sobre un cuerpo actúan dos fuerzas de igual dirección y sentido, y de módulos F1=50N y F2= 50N. Dibuja la situación y calcula cuál será el valor de la resultante R. Sol.: R =100N 2. Si un alumno empuja una mesa hacia la derecha con una fuerza F1 de 100N y otro alumno empuja hacia la izquierda con una fuerza F2 de 80 N. a) Dibuja la situación y calcula cuál será el valor de la resultante R. Sol.: R = 20N b) ¿En qué sentido se moverá la mesa? Sol.: hacia la derecha 3. Sobre una caja actúan dos fuerzas: F1 actúa en la dirección horizontal y está dirigida hacia la derecha, la otra F2 actúa en la dirección vertical y está dirigida hacia arriba. Haz un dibujo de la situación. ¿En qué dirección se moverá la caja? ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 20 de 29 RELACIÓN DE LAS FUERZAS CON EL MOVIMIENTO. Las fuerzas aplicadas sobre un cuerpo están íntimamente relacionadas con el movimiento del cuerpo, o más exactamente con los cambios que se producen en el movimiento de éste. Esta relación fue descrita en 1687 por el mayor científico de todos los tiempos, el científico inglés Isaac Newton, en el famoso libro “Principios matemáticos de filosofía natural” donde exponía todos los estudios y descubrimientos que había realizado hasta la fecha. En relación al movimiento general de los cuerpos, sus conocimientos se sintetizan en tres leyes llamadas LEYES DE NEWTON de la dinámica. Son tres leyes, en las que se fundamenta toda la Física clásica, que siguen siendo aplicables a la mayoría de los casos. Tan sólo a nivel microscópico o cuando nos acercamos a la velocidad de la luz, es necesario acudir a la Física moderna que inició Einstein. 9.- LEYES DE NEWTON DE LA DINÁMICA 1ª LEY DE NEWTON O “LEY DE INERCIA” Dice lo siguiente: “Sí sobre un cuerpo no actúa ninguna fuerza, o la resultante de todas las fuerzas que actúan sobre él es cero, el cuerpo mantendrá su estado de movimiento (mantendrá su velocidad). En consecuencia permanecerá en reposo (si estaba así) o en un movimiento rectilíneo y uniforme MRU”. La “tendencia” de los cuerpos a conservar su estado de reposo o de movimiento se llama inercia. La inercia es la propiedad de un cuerpo que mide la resistencia del mismo a variar su estado de reposo o de movimiento. Veremos que cuanto mayor sea la masa de un cuerpo, mayor será su inercia. Ejemplos: − Si un balón de futbol está parado en el campo, permanecerá parado indefinidamente, salvo que se le aplique una fuerza. − Si un tren frena bruscamente o choca, todo lo que no esté bien sujeto tenderá a seguir el movimiento que tenía hacia adelante, es decir a mantener la velocidad. Nota, paradoja: En los lugares donde hay gravedad, como en la superficie de la Tierra, esta ley parece que en ocasiones no se cumple. Por ejemplo, si un automóvil adquiere una velocidad en una carretera rectilínea, según esta ley, debería continuar con esa velocidad aunque se apagase el motor. Del mismo modo una pelota que rueda con una cierta velocidad no debería detenerse nunca. En ambos casos parece que no actúan fuerzas sobre el cuerpo y en consecuencia según la 1ª Ley de Newton deberían continuar con MRU. En realidad hay un error en el razonamiento, porque sí actúan fuerzas sobre el coche o la pelota, es la fuerza de rozamiento que actúa siempre, y que se opone al movimiento para frenarlo. En el espacio esta fuerza de rozamiento no existe, y sí se mantendrá en movimiento perpetuo. Si recordamos las películas del espacio, vemos que, si por ejemplo una llave se lanza o sale despedida con una velocidad, no se detiene nunca. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 21 de 29 2ª LEY DE NEWTON O “LEY FUNDAMENTAL DE LA DINÁMICA” Esta es la ley más importante, porque es la que nos permite hacer cálculos sobre el movimiento de los cuerpos. Dice que: La suma o resultante de todas las fuerzas que actúan sobre un cuerpo es igual al producto de la masa del cuerpo por la aceleración que provocan las fuerzas. Se resume en la fórmula: ⃗𝑭⃗ = 𝒎. 𝒂 ⃗⃗ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗ = 𝒎. 𝒂 ∑𝑭 ⃗⃗ o más exactamente Donde ∑ 𝐹⃗ representa la suma de todas las fuerzas que actúen sobre el cuerpo. Es decir esta ley dice que si la suma o resultante de todas las fuerzas que actúan es distinta de cero, entonces sí se altera el estado de movimiento del cuerpo (la velocidad), y se provoca una aceleración (cambio en la velocidad). Este cambio del estado de movimiento será más o menos grande dependiendo de la masa del cuerpo. Con la misma fuerza, si la masa del cuerpo es grande la aceleración producida será pequeña (el cambio en la velocidad será pequeño), y si la masa es pequeña la acelración será grande (cambiará mucho la velocidad) Unidades de fuerza: La unidad de fuerza en el S. I. es el Newton (N) 1 Newton = 1N = 1 kg . 1 m/s2 => 1N =kg.m/s2 Se define el Newton como la fuerza que aplicada a 1 kg de masa le produce una aceleración de 1 m/s2. • Otra unidad de fuerza es el kilopondio (kp) (o kilogramo fuerza) , que es la fuerza con que la Tierra atrae a 1 kg de masa: 1 kp = 9,8 N Ejemplo: Si sobre un cuerpo de 50 kg de masa actúa una fuerza de 10 N, ¿cuál es su aceleración? Basta aplicar la fórmula: F = m.a I0 N = 50 kg. a Despejamos como ya sabemos: 10 𝑁 a= 50 𝑘𝑔 = 0,2 𝑚/𝑠 Ejercicios: 1. Si aplicamos una fuerza de 200 N y provocamos una aceleración de 0,5 m/s2, ¿qué masa tiene el cuerpo? Sol.: 400kg 2. ¿Qué ocurre cuando un autobús que está parado comienza a andar?, marca lo correcto. O Que nos vamos hacia adelante por la inercia O Que nuestro cuerpo se va hacia atrás por la inercia O No pasa nada ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 22 de 29 3. De un cuerpo de 500 gramos de masa se tira hacia la derecha con una fuerza de 2 N. calcula la aceleración que le produce. Sol.: 4m/s2 4. Si a una caja de 5 kg se la aplica una fuerza de 80 N hacia adelante y el rozamiento con el suelo que se opone al movimientos es de 30N a) Calcula la fuerza neta que actúa sobe la caja. Sol.: 50N b) calcula la aceleración con la que se moverá. Sol.: 10m/s2 3ª LEY DE NEWTON O “LEY DE ACCIÓN Y REACCIÓN” “Si un cuerpo ejerce una fuerza sobre otro (acción), simultáneamente el segundo cuerpo ejerce una fuerza igual y de sentido contrario sobre el primero (reacción)”. Hay que tener en cuenta que: − Las dos fuerzas son simultáneas a una se le llama acción y a la otra reacción, pero es una forma de hablar para poder distinguirlas, pero las dos fuerzas se producen a la vez. − A pesar de tratarse de fuerzas iguales y de sentido contrario, estas fuerzas nunca pueden anularse entre sí, porque actúan sobre cuerpos distintos. Esta ley tiene una profunda implicación con la naturaleza de las fuerzas que se producen en el universo. El hecho de que la acción y la reacción sean simultáneas implica que el origen de las fuerzas es la interacción entre dos trozos de materia. Interaccionar significa acción mutua. La materia interactúa entre sí, y la forma de hacerlo es ejercer fuerzas unos cuerpos sobre otros. Esto también significa que en el universo las fuerzas aparecen y actúan por parejas, porque son el producto de la interacción entre fragmentos de materia. Siempre que sobre un cuerpo actúa una fuerza, habrá otra fuerza igual y de sentido contrario actuando sobre el otro cuerpo con el que está interactuando el primero. Sin embargo normalmente en los problemas que analizamos sólo nos interés lo que le pasa uno de los cuerpos, por lo que sólo usamos una de las fuerzas de la pareja acción- reacción. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 23 de 29 Nota: Existen situaciones en que las que esta ley se ve claramente − − − − Por ejemplo cuando se dispara un arma (cañón, escopeta, etc.) la bala sale impulsada hacia adelante, pero el arma sale impulsada hacia atrás, es lo que se llama “retroceso” del arma. La acción actúa sobre la bala y la reacción sobre el arma. Cuando una persona intenta saltar a tierra desde una barca, la persona empuja la barca hacia atrás (acción) para que la barca le empuje hacia adelante (reacción). Acciones tan cotidianas como andar o nadar se explican por este principio, al andar empujamos al suelo hacia atrás y el suelo no empuja hacia adelante. Al nadar empujamos al agua hacia atrás y el agua nos empuja hacia adelante. Si no hubiese suelo o agua con la que interactuar no podríamos andar o nadar. El vuelo de los aviones y cohetes también se basa en este principio, el cohete impulsa a los gases hacia atrás y los gases impulsan al cohete hacia adelante. En otras ocasiones el efecto de esta ley parece no producirse o estar oculto. − Por ejemplo, la Tierra nos atrae con una fuerza que llamamos Peso. Cuando saltamos de un precipicio caemos porque las Tierra nos atrae, sin embargo nosotros ejercemos la misma fuerza sobre la Tierra y también la atraemos, ¿por qué nosotros nos movemos y la Tierra no?, la razón está en la 2ª ley de Newton F = m.a, con la misma fuerza ,como la masa de la Tierra es enorme la aceleración que se le produce es despreciable. − Otro ejemplo: Esta ley viene a decir que “si yo empujo a una persona, esta persona, aunque esté desprevenida también me empuja. Deberían moverse las dos personas. Sin embargo sabemos ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 24 de 29 que si la persona empujada está desprevenida se moverá, pero la que empuja, que sí es consciente de lo que hace no se mueve. La razón es que al “estar prevenida” la persona que empuja maximiza el rozamiento con el suelo, y este rozamiento compensa la fuerza que la otra persona ejerce sobre ella. En el espacio, donde no hay rozamiento se vería muy claro que el hecho de empujar algo hace retroceder al que empuja. Ejercicio: Una pelota de golf tiene una masa de 45gramos y es golpeada con una fuerza de 200N. Contesta: a) Calcula la aceleración que adquiere la pelota. Sol.: 4444,44 m/s2 b) Calcula la fuerza que ejerce la pelota sobre el palo de golf. Sol.: 200N 10.- FUERZAS QUE ACTÚAN DE FORMA COTIDIANA A NUESTRO ALREDEDOR Vamos a ver con detalle tres fuerzas que actúan en nuestra vida cotidiana: el peso, la fuerza “normal” y la fuerza de rozamiento. PESO El peso es la “fuerza de la gravedad” con la que la Tierra (u otro planeta) atrae a un cuerpo. Está originado por la acción del campo gravitatorio que crea un planeta, en nuestro caso La Tierra, sobre todos los objetos que están en sus inmediaciones. Por ser una fuerza, el peso se representa como un vector, definido por su módulo, dirección y sentido, aplicado en el centro de gravedad del cuerpo y dirigido hacia el centro de la Tierra (por eso siempre se dibuja vertical y hacia abajo). Su módulo se calcula con la fórmula: P =m.g Donde “P” es el peso, “m” es la masa del cuerpo y “g” es el valor del “campo gravitatorio terrestre” o “aceleración de la gravedad”, su valor en la superficie de la Tierra es g= 9,8 m/s2 Cada objeto celeste, estrella, planeta, o satélite, tiene un valor de la “gravedad” distinto. Pr ejemplo en la Luna vale 1,7 m/s2, por lo que los objetos allí pesan bastante menos, unas cinco veces menos. El Peso, como es una fuerza Se mide en el S.I. en newton (N) y a veces en Kilopondios Kp. DIFERENCIA ENTRE PESO Y MASA Peso y masa son dos magnitudes físicas muy diferentes, aunque en el habla cotidiana, el término “peso” se utiliza a menudo erróneamente como sinónimo de masa. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 25 de 29 La masa de un cuerpo es una propiedad que mide la cantidad de materia que posee, y es una magnitud escalar, es decir no necesita de vectores como el peso. Además, la masa de un objeto no varía con su posición, ni de un planeta a otro, mientras que el peso depende de la gravedad del planeta en el que se encuentre, pudiendo incluso ser cero, cuando se aleja de ellos, lo que se conoce como ingravidez. Una persona de masa 80 kg tendrá siempre la misma masa, pero su “peso” será diferente si está en la Tierra, en Marte, la Luna, etc. FUERZA “NORMAL” N (a una superficie) La normal (N) es la fuerza que impide que un cuerpo se meta dentro de otro. Siempre es perpendicular a la superficie que soporta al objeto, y dirigida hacia arriba. Esta fuerza la ejercen las superficies sobre los cuerpos colocados sobre ellas, ya que si no estuviera esa superficie, el objeto se caería debido a la acción del peso. La dirección de la normal siempre es perpendicular a la superficie y su sentido hacia arriba. N P Cuando un cuerpo está apoyado en una superficie horizontal, la normal tiene que compensar al peso, ya que el objeto ni sube ni baja, por lo tanto, se calculará de la siguiente forma: N = P = m.g FUERZA DE ROZAMIENTO La fuerza de rozamiento Fr es una fuerza opuesta al movimiento que aparece en la superficie de contacto de dos cuerpos cuando se intenta deslizar uno sobre otro. Como se opone al movimiento la dibujaremos en sentido contrario al movimiento. El valor de la fuerza de rozamiento depende de la fuerza que aprieta una superficie sobre otra y del estado de pulimento de las superficies en contacto. Cuanto mayor sea la rugosidad mayor será el rozamiento. Por eso cuando queremos disminuir el rozamiento se pulen las superficies. Fr F Si tenemos un objeto situado en una superficie, y tiramos de él con una fuerza horizontal hacia la derecha (F), se moverá con esa misma dirección y sentido, y automáticamente aparecerá en sentido contrario la fuerza de rozamiento (Fr), que intenta oponerse al movimiento. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 26 de 29 11- LISTA DE CUESTIONES Y EJERCICIOS DE DINÁMICA A) CUESTIONES Teniendo en cuenta las leyes de Newton de la dinámica razona la respuesta a las siguientes cuestiones 1.- Si la primera ley de Newton dice que “si sobre un cuerpo no actúan fuerzas, éste permanecerá en movimiento rectilíneo y uniforme, es decir con velocidad constante”, ¿por qué cuando viajamos en coche en una recta horizontal, y apagamos el motor del vehículo, su velocidad no permanece constante sino que disminuye y se para? 2.- En el espacio, sin gravedad, si una nave apaga los motores ¿qué ocurrirá?. Razona la respuesta. o Se frenará o su velocidad permanecerá constante o acelerará 3.- Si aplicamos la misma fuerza a una pelota de tenis y a una de billar ¿cuál se moverá con mayor aceleración?. Cita la ley que aplicas para la respuesta. 4.- La razón de que la Tierra gire alrededor del Sol es la fuerza gravitatoria de atracción que el Sol ejerce sobre la Tierra, según la ley de acción y reacción la Tierra ejerce la misma fuerza atractiva sobre el Sol, ¿por qué el Sol no gira alrededor de la Tierra? 5.- Teniendo en cuenta que la tercera ley de Newton podría resumirse en “si yo te empujo, automáticamente tu me empujas”, ¿cómo podríamos salir del centro de un lago helado donde no hay rozamiento y no podemos caminar? 6.- ¿Qué ocurriría si estando en el espacio sin gravedad un astronauta lanza hacia adelante un objeto? B) EJERCICIOS 1.- Calcula gráfica y analíticamente la fuerza resultante de las siguientes fuerzas: F1 = 7N F2 =5N F3=3N Sol.: R = 15 N 2.- Calcula gráfica y analíticamente la fuerza resultante de las siguientes fuerzas: F1 = 7N F2 =5N F3=3N Sol.: R = 5 N 3.- Imagina que tienes que arrastrar horizontalmente una caja de 10 kg de masa. a) Calcula el peso de la caja en Newton. Sol.: 98N b) Aplicando la segunda ley de Newton, calcula la fuerza horizontal necesaria para que la caja se mueva con una aceleración de 5 m/s2. Se supone que no hay rozamiento. Sol.: 50 N 4.- Determina el valor de la fuerza resultante que actúa sobre el objeto de la figura: ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 27 de 29 F1=3N F2= 2N F3 =4 N Sol.:3N 5.-La masa del siguiente bloque es de 20 kg. La fuerza con que la mano tira de él es de 40 N y la fuerza de rozamiento es de 15 N. Calcula: a) La fuerza resultante Sol.: 25N b) La aceleración que le produce sol.: 1,25 m/s2 6.- Un cuerpo de 20kg de masa inicialmente en reposo sufre una fuerza constante de 200N. Calcula su aceleración. Sol.: 10 m/s2 7.-Un vehículo tiene una aceleración de 3,5 m/s2. Si su masa es de 1200 kg. ¿Qué fuerza ejerce el motor? Sol.: 4200 N 8.- Un automóvil frena con una deceleración de 6 m/s2. Calcula la fuerza que ejerce el cinturón de seguridad sobre el conductor si este tiene una masa de 75 kg. Sol.: 450 N 9.-Calcula la masa de un cuerpo cuyo peso es de 600 N. Sol.: 61,22 kg 10.-En una superficie con rozamiento, se tira de un cajón de 100kg con una fuerza de 300N paralela al suelo. El cajón se mueve con MRUA con una aceleración de 2m/s2. Calcula la fuerza de rozamiento. Sol.: 100N 11.-El motor de un vehículo de 1500 kg lo impulsa con una fuera de 3500N. Haz un dibujo de la situación y de las fuerzas que interviene y calcula la aceleración en los siguientes casos: a) No existe rozamiento. Sol.: 2,33m/s2 ACT II Bloque 9. El movimiento. Cinemática y Dinámica b) La fuerza de rozamiento es 2000 N Sol.: 1m/s2 Página 28 de 29 12- EL EFECTO DEFORMADOR DE LAS FUERZAS; ESFUERZOS A LOS QUE SE ENCUENTRAN SOMETIDOS LOS MATERIALES Al definir las fuerzas se dijo que pueden causar dos efectos: − − Cambios en el estado de movimiento de los cuerpos. La deformación de los cuerpos y los materiales. ➢ El efecto sobre el movimiento viene descrito por las tres leyes del movimiento de Newton y ya se ha estudiado. ➢ Ahora vamos a hablar brevemente del efecto deformador de las fuerzas aplicadas sobre los materiales Cuando a un cuerpo o material se le aplican fuerzas su comportamiento respecto a la deformación puede ser muy distinto de unos materiales a otros, pudiendo distinguirse las siguientes situaciones: o Materiales “elásticos”: Al aplicarles fuerzas se deforman pero cuando cesa la fuerza recuperan su forma original. Ejemplos un muelle. o Materiales “plásticos”: Al aplicarles fuerzas se deforman pero cuando cesa la fuerza la deformación permanece. Ejemplo la plastilina o Materiales “rígidos”: Al aplicarles fuerzas no se deforman o la deformación es imperceptible. Si la fuerza es demasiado intensa el material se rompe. Ejemplo las rocas. o Materiales “frágiles”: Al aplicarles fuerzas no se deforman pero se rompen aunque la fuerza sea muy débil. ejemplo la mayoría de los vidrios. En general esta clasificación o división de los materiales por el comportamiento es relativa, y válida sólo para un determinado rango de fuerzas. Por ejemplo si la fuerza es excesiva, un material elástico como un muelle, deja de serlo y la deformación causada es permanente. ACT II Bloque 9. El movimiento. Cinemática y Dinámica Página 29 de 29