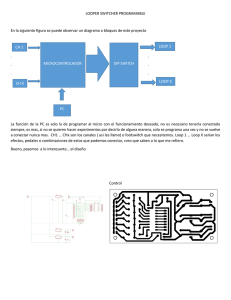
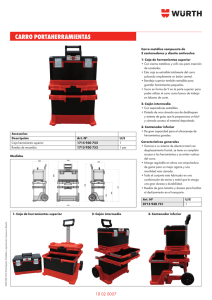
Montaje y Procedimiento Para la realización de este experimento necesitaremos. -un sistema de reticulado pasco montaña rusa -un carro con masa y obturador -una fotocelda -un computador con programa capstone El montaje de la estructura consta de X pasos: 1- Mediante un soporte universal anclamos firmemente la estructura del riel, utilizando una pinza de nuez dejándola bien firme para reducir el movimiento del riel. 2- A partir del cálculo teórico de la altura mínima en el que el carro de prueba debería pasar el loop, soltamos nuestro carro desde el punto encontrado teóricamente en un estado de reposo. 3- Luego se prueba con alturas cercanas hasta encontrar la menor altura experimental sobre el riel desde la cual el carro logra dar una vuelta al loop y se registra este valor correspondiente. 4- A posterior instalamos en el loop una fotocelda que medirá la velocidad del carro en la parte superior del loop, 5- Abrimos el programa capstone y conectamos la fotocelda a un adaptador que permite conectarse vía usb al computador, para luego configurar el computador seleccionando el sensor fotocelda y la lámina obturadora a seleccionando la regleta con una constante de 0,01 metros. 6- Después de haber calibrado el sensor se seleccionan ocho alturas en el riel sobre la altura mínima. 7- Para cada altura medida se registra el valor de esta y se suelta el carro desde el reposo en esa posición y se anota la velocidad del carro en la parte superior del loop medida por el programa. Y se repite como mínimo cinco veces la medición para cada una de las ocho alturas. 8- Finalmente registramos el radio del loop, para esto consideramos que el carro posee un disco en la parte inferior, por lo que la distribución de la masa dificulta la determinación de su centro de gravedad Análisis Teórico 1- Para el cálculo de la velocidad del carro en el punto más alto del loop, debemos suponer que no existe una fuerza de rose por lo cual hay conservación de energía en el sistema asumiendo que la energía el inicio es igual que la del final, además de tener claro que existen 2 tipos de velocidades la 𝑣𝑡𝑒𝑜𝑟𝑖𝑐𝑎 y 𝑣𝑟𝑒𝑎𝑙 ,siendo la teórica la que es medida mediante la fotocelda con su respectivo radio y la real aquella que se asume como radio el del loop . Para encontrar una similitud aplicaremos la igualdad de las velocidades angulares real y teórica para relacionar estas velocidades tangenciales, esta igualación se hace con la base de que esta velocidad angular solo depende del ángulo y el tiempo transcurridos. 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 𝑣𝑟𝑒𝑎𝑙 𝜔= 𝑟𝑙𝑜𝑜𝑝 𝜔= 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 𝑣𝑟𝑒𝑎𝑙 = 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 𝑟𝑙𝑜𝑜𝑝 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 = 𝑣𝑟𝑒𝑎𝑙 ∗ 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 𝑟𝑙𝑜𝑜𝑝 Obtenida ya la relación entre las velocidades tangenciales, vemos que existen una diferencia entre la velocidad teórica y real la cual, nos muestra que esta si depende del radio, por lo cual si ambos radios son diferentes esta sería diferente. Para el calculo del radio de la fotocelda tenemos que calcular que tan alejado esta del centro del loop, para esto hacemos la suposición de que el centro se encuentra en la mitad de su altura del loop, por lo que debemos hacer la resta: 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 = ℎ𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 − ℎ𝑙𝑜𝑜𝑝 ∗ 1/2 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 = 0,19 − 0,25 ∗ 1 2 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 = 0,065 𝑚 Mientras que para calcular el radio del loop debemos restarle la distancia que posee el centro de masa a la mitad de la altura del loop: 𝑟𝑙𝑜𝑜𝑝 = ℎ𝑙𝑜𝑜𝑝 ∗ 1 − ℎ𝐶𝑒𝑛𝑡𝑟𝑜 𝑑𝑒 𝑚𝑎𝑠𝑎 2 1 𝑟𝑙𝑜𝑜𝑝 = 0,25 ∗ − 0,01 2 𝑟𝑙𝑜𝑜𝑝 = 0,125 − 0,01 𝑟𝑙𝑜𝑜𝑝 = 0,115 𝑚 Ahora ya calculados los datos del radio del loop y de la fotocelda remplazamos en la ecuación de la velocidad teórica: 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 = 𝑣𝑟𝑒𝑎𝑙 ∗ 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 𝑟𝑙𝑜𝑜𝑝 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 = 𝑣𝑟𝑒𝑎𝑙∗ ∗ 0,065 0,115 El único dato faltante que nos queda es la velocidad real la cual podemos calcularla mediante conservación de energía asumiendo que no existe un rose con el riel o el viento, con esto asimismo que la energía en el comienzo es igual en cualquier punto, por lo que vamos calculando la velocidad igualando la energía en el punto de lanzamiento con el punto más alto del loop: 1 𝑚 ∗ 𝑔 ∗ ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 = 𝑚 ∗ 𝑔 ∗ (ℎ𝑓𝑖𝑛𝑎𝑙 − ℎ𝐶𝑒𝑛𝑡𝑟𝑜 𝑑𝑒 𝑚𝑎𝑠𝑎 ) + 𝑚 ∗ 𝑣 2 2 1 𝑔 ∗ ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 = 𝑔 ∗ (ℎ𝑓𝑖𝑛𝑎𝑙 − ℎ𝐶𝑒𝑛𝑡𝑟𝑜 𝑑𝑒 𝑚𝑎𝑠𝑎 ) + ∗ 𝑣 2 𝑆𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑚𝑜𝑠 𝑙𝑎𝑠 𝑚𝑎𝑠𝑎𝑠 2 𝑔 ∗ ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 − 𝑔 ∗ (0,25 − 0,01) = 1 ∗ 𝑣2 2 2(𝑔 ∗ ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 − 0,24) = 𝑣 2 2𝑔(ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 − 0,24) = 𝑣 2 √2 ∗ 𝑔(ℎ𝑖𝑛𝑖𝑐𝑖𝑎𝑙 − 0,24) = 𝑣𝑟𝑒𝑎𝑙 Como la altura 2R es lo mismo que la altura de la base del loop, es de 0,25 m y para calcular la velocidad de cada punto de lanzamiento diferente, vamos remplazando las 8 alturas correspondientes, que fueron calculadas y se encuentran en el siguiente gráfico: Altura de lanzamiento (m) 1,03 m 1,11 m 1,2 m 1,26 m 1,27 m 1,62 m 1,7 m 1,25 m Velocidad Real del carro en lo más alto del loop (m/s) 1,82537667 m/s 1,95499361 m/s 2,04323273 m/s 2,16887067 m/s 2,29189878 m/s 2,80699127 m/s 2,96984848 m/s 2,1552726 m/s Ahora ya teniendo todas los datos de velocidades reales y los radios somos capaces de calcular la velocidad teórica en cada punto de lanzamiento, multiplicando las velocidades reales anteriores por 0,065 y dividiendo por 0,115. Altura de lanzamiento (m) Velocidad Teórica del carro en lo más alto del loop (m/s) 0,41 m 1,03173464 m/s 0,435 m 1,10499639 m/s 0,463 m 1,15487068 m/s 0,49 m 1,22588342 m/s 0,518 m 1,29542105 m/s 0,652 m 1,58656028 m/s 0,7 m 1,67861001 m/s 0,487 m 1,21819756 m/s 22.1 Las fuerzas que actúan en el carro en el punto más alto del loop serian la fuerza normal y la fuerza peso. 2.2 El valor de la aceleración centrípeta se sacó en cada punto de la altura, remplazando cada velocidad en lo alto del loop en la fórmula 𝑎𝑐𝑒𝑙𝑒𝑟𝑎𝑐𝑖ó𝑛 𝑐𝑒𝑛𝑡𝑟í𝑝𝑒𝑡𝑎 = 𝑣2 𝑟 obtenido así los resultados de la tabla. Por un lado, tenemos la aceleración marcada por la fotocelda que seria la teórica que su 𝑣𝑡𝑒ó𝑟𝑖𝑐𝑎 2 fórmula se expresaría como , que aplicándola obtenemos: 𝑟𝑓𝑜𝑡𝑜𝑐𝑒𝑙𝑑𝑎 Altura de lanzamiento (m) Aceleración Teórica (m/s^2) 0,41 m 0,435 m 0,463 m 0,49 m 0,518 m 0,652 m 0,7 m 0,487 m 16,3765595 (m/s^2) 18,7848771 (m/s^2) 20,5188658 (m/s^2) 23,1198488 (m/s^2) 25,8171645 (m/s^2) 38,7257467 (m/s^2) 43,3497164 (m/s^2) 22,8308507 (m/s^2) Mientras que por el otro lado tenemos a la aceleración real en donde ocupamos las 2 𝑣 velocidades reales y el radio del loop, ocupando 𝑟𝑒𝑎𝑙 dándonos como resultado la 𝑟𝑙𝑜𝑜𝑝 siguiente tabla de datos. Altura de lanzamiento (m) Aceleración Teórica (m/s^2) 0,41 m 28,973913 (m/s^2) 0,435 m 33,2347826 (m/s^2) 0,463 m 36,3026087 (m/s^2) 0,49 m 40,9043478 (m/s^2) 0,518 m 45,6765217 (m/s^2) 0,652 m 68,5147826 (m/s^2) 0,7 m 76,6956522 (m/s^2) 0,487 40,3930435 (m/s^2) 2.3 Cuando el carro posee una velocidad mínima para poder dar la vuelta este posee una normal mayor a 0, que permite que el carro no se despegue del riel donde va dando la vuelta y así no perder el contacto con la pista en ningún momento, en caso contrario de ser igual a 0 el carro no podría dar la vuelta porque significaría que ya no estaría en contacto con algunas superficies. La no En caso de estar apoyado en una superficie, la base responde con una fuerza igual y contraria a la manifestada por el efecto centrífugo, de tal forma que el objeto permanece 'pegado' a la superficie por efecto del equilibrio de fuerzas Hay que notar que la fuerza centrífuga tiene relación con la resistencia al cambia de la dirección impuesta por una fuerza centrípeta, debido a esto el efecto no se genera cambios en la trayectoria. Velo así, la fuerza centrífuga está relacionado a una resistencia al cambio de dirección impuesta por una fuerza centrípeta. Es por eso que el efecto centrífugo se genera debido al cambio de trayectoria impuesto por la fuerza centrípeta. Hola profesor, esperando que se encuentre bien quisiera preguntar respecto al sentido de la normal, pues en las diapositivas informativas no queda claro si N>0 se refiere a la fuerza normal o exclusivamente a su módulo, pues en caso de ser lo primero entra en conflicto con lo dicho en la diapositiva anterior en el punto 3: "En caso de estar apoyado en una superficie, la base responde con una fuerza igual y contraria a la manifestada por el efecto centrífugo, de tal forma que el objeto permanece 'pegado' a la superficie por efecto del equilibrio de fuerzas." Agradeceríamos que respondiera si la normal tiene dirección vectorial hacia arriba o hacia abajo en el momento que este se encuentra en el punto más alto del loop. se refiere al módulo. El sentido depende de la posición del carro en el loop y apuntará al centro del loop. Modificaré la diapositiva con esto 2.4 El calcular el caso mínimo en donde el carro pueda dar la vuelta al loop, asumimos que la normal tiende a 0 −𝑁 − 𝑚 ∗ 𝑔 = −𝑚 ∗ 𝑎𝑐 𝐴𝑠𝑢𝑚𝑖𝑒𝑛𝑑𝑜 𝑙𝑎 𝑛𝑜𝑟𝑚𝑎𝑙 𝑡𝑒𝑛𝑑𝑖𝑒𝑛𝑑𝑜 0 −𝑚 ∗ 𝑔 = −𝑚 ∗ 𝑎𝑐 −𝑚 ∗ 𝑔 = −𝑚 ∗ 𝑔= 𝑣2 𝑟 𝑣 = √𝑔 ∗ 𝑟 𝑣2 𝑟 𝑎𝑐 = 𝑣2 𝑟 𝑆𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑚𝑜𝑠 𝑙𝑎𝑠 𝑚 𝑦 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑝𝑜𝑟 − 1 𝐴𝑝𝑙𝑖𝑐𝑎𝑚𝑜𝑠 𝑟𝑎𝑖𝑧 𝑐𝑜𝑛 𝑢𝑛 𝑟𝑎𝑑𝑖𝑜 𝑑𝑒 0,25 𝑣 = √9,8 ∗ 0,25 𝑣 = √2,45 𝑣 = 1,565 m/s 3- Predecir de forma teórica la mínima altura desde la que se debe soltar el carro para que este de la vuelta completa al "loop" sin perder contacto con el riel Experimento montaña rusa Para la realización de este experimento necesitaremos. Este experimento tiene como objetivo determinar teóricamente y medir experimentalmente los parámetros necesarios para que el carro de prueba realice una vuelta completa loop sin perder el contacto con el riel. Para realizar el experimento requieres lo siguiente: -un sistema de reticulado pasco montaña rusa -un carro con masa y obturador -una fotocelda -un computador con programa capstone Considere que los datos mostrados en este vídeo son sólo un ejemplo de cómo fueron obtenidos los datos del set y no representan los datos puntuales con los cuales los estudiantes deben trabajar cuando veas este vídeo usa todos tus sentidos para percibir las diferencias cualitativas entre los distintos lanzamientos ¿te has subido a una montaña rusa en un parque de diversiones cuando pensamos en ellas recordamos la adrenalina que nos produce pero probablemente no nos ponemos a pensar en los desafíos técnicos e ingenieriles que requiere su diseño e implementación a través de este experimento descubriremos la física detrás de las montañas rusas, trabajaremos con un riel inclinado que termina en un loop y un carro de pruebas Iniciemos el montaje del experimento: 1-Con un soporte universal anclamos firmemente la estructura del riel para ello se utiliza una pinza de nuez es muy importante que quede bien firme para reducir el movimiento del riel, nuestro riel es plástico y flexible. ¿cómo se comportará ante la pasada del carro? Por su composición se deforma cuando el carro pasa sobre él y genera mucho ruido para este experimento es necesario encontrar la altura mínima sobre el real desde la cual el carro logra dar una vuelta completa al loop para ello 2-a partir del cálculo teórico de esta altura mínima en el que el carro de prueba debería pasar el loop iniciamos el trabajo experimental soltando nuestro carro desde el punto encontrado teóricamente en un estado de reposo 3-posteriormente se prueba con alturas cercanas hasta encontrar la menor altura experimental sobre el riel desde la cual el carro logra dar una vuelta al loop se registra este valor 4-en el loop ha instalado una fotocelda que medirá la velocidad del carro en la parte superior del loop abrimos el programa capstone y conectamos la foto celda a una adaptador que permite conectarse vía usb al computador luego debemos configurarla en el computador seleccionando el sensor fotocelda y la lámina obturadora a seleccionando la regleta con una constante de 0,01 metros 5- una vez que ha librado el sensor se seleccionan ocho alturas en el riel sobre la altura mínima 6-para cada altura se registra el valor de esta se suelta el carro desde el reposo en esa posición y se anota la velocidad del carro en la parte superior del loop medida por el programa es recomendable repetir al menos cinco veces la medición para cada una de las ocho alturas y el último dato que se registra es el radio del loop 7- finalmente en este experimento se debe considerar que el carro posee un disco en su parte inferior por ende posee una distribución de masa que dificulta la exacta determinación del centro de gravedad El informe: - Nombre y Fecha - Título - Resumen (Muy corto: Principales resultados obtenidos y conclusiones más relevantes.) 0.5 pts - Introducción - Objetivo (Breve: Planteamiento, ¿Qué se quiere comprobar?, Motivación.) 0.25 pts - Hipótesis (Breve: ¿Qué se espera obtener?) 0.25 pts - Marco teórico 0.5 pts - Montaje y Procedimiento (Esta información será extraída del video.) 0.5 pts - Análisis - Análisis de errores 1 pto - Análisis de los resultados 1 pto - Interpretación y discusión de resultados 0.5 pts - Conclusiones (Los resultados obtenidos en relación con los objetivos propuestos.) 1 pto Calidad del informe Tablas y gráficos deben incluir un título corto y deben ser numeradas secuencialmente. 0.25 pts Las unidades usadas deben especificarse claramente en las tablas y ejes de los gráficos. 0.25 pts