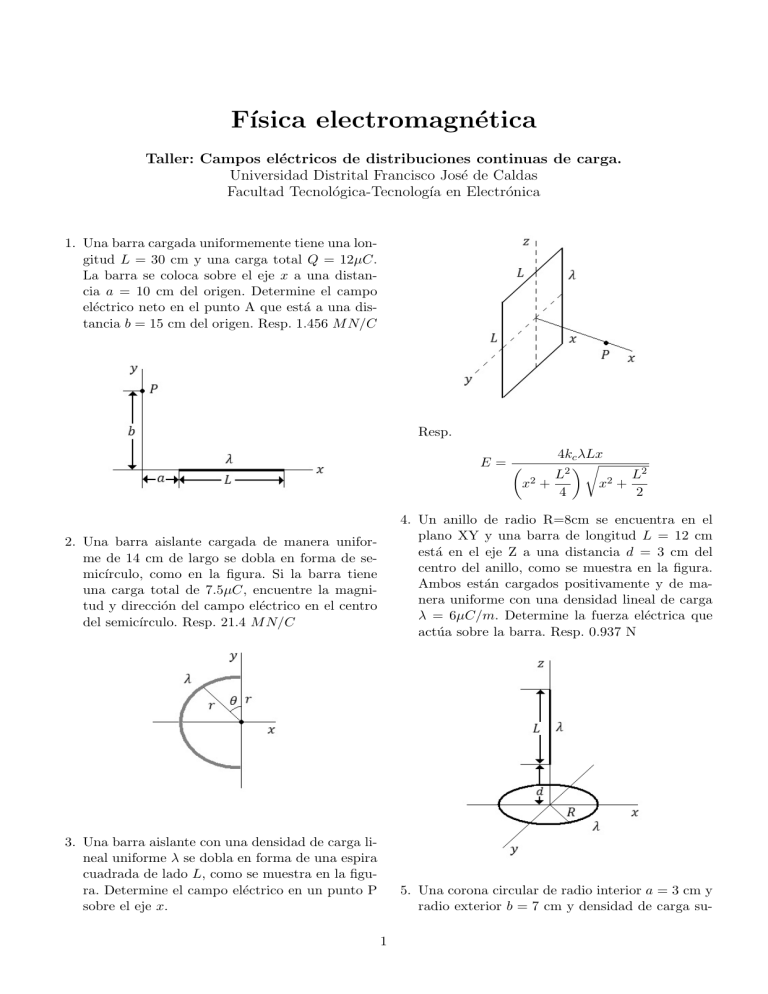
Fı́sica electromagnética Taller: Campos eléctricos de distribuciones continuas de carga. Universidad Distrital Francisco José de Caldas Facultad Tecnológica-Tecnologı́a en Electrónica 1. Una barra cargada uniformemente tiene una longitud L = 30 cm y una carga total Q = 12µC. La barra se coloca sobre el eje x a una distancia a = 10 cm del origen. Determine el campo eléctrico neto en el punto A que está a una distancia b = 15 cm del origen. Resp. 1.456 M N/C Resp. E= 4kc λLx r 2 L L2 x2 + x2 + 4 2 4. Un anillo de radio R=8cm se encuentra en el plano XY y una barra de longitud L = 12 cm está en el eje Z a una distancia d = 3 cm del centro del anillo, como se muestra en la figura. Ambos están cargados positivamente y de manera uniforme con una densidad lineal de carga λ = 6µC/m. Determine la fuerza eléctrica que actúa sobre la barra. Resp. 0.937 N 2. Una barra aislante cargada de manera uniforme de 14 cm de largo se dobla en forma de semicı́rculo, como en la figura. Si la barra tiene una carga total de 7.5µC, encuentre la magnitud y dirección del campo eléctrico en el centro del semicı́rculo. Resp. 21.4 M N/C 3. Una barra aislante con una densidad de carga lineal uniforme λ se dobla en forma de una espira cuadrada de lado L, como se muestra en la figura. Determine el campo eléctrico en un punto P sobre el eje x. 5. Una corona circular de radio interior a = 3 cm y radio exterior b = 7 cm y densidad de carga su1 perficial σ = 25µC/m2 se encuentra en el plano XY y una barra de longitud L = 12 cm y densidad de carga lineal λ = 9µC/m está en el eje Z a una distancia d = 5 cm del centro del disco, como se muestra en la figura. Determine la fuerza eléctrica que actúa sobre la barra. Resp. 0.208 N distancia d del lado derecho del cilindro, como se muestra en la figura. (El elemento diferencial de área de un cascarón cilı́ndrico de radio R y ancho dx es: dA = 2πRdx) (2) Resuelva el mismo problema pero esta vez suponga que el cilindro es sólido. (El elemento diferencial de volumen de un cilindro sólido es: dV = 2πrdrdx) Resp. ! 1 1 √ −p R2 + d2 R2 + (d + h)2 p p 2kc Q Ex = 2 h + R2 + d2 − R2 + (d + h)2 R h kc Q Ex = h 6. Dos barras delgadas de longitud L yacen a lo largo del eje de las x, una entre x = a/2 y x = a/2 + L y la otra entre x = −a/2 y x = −a/2 − L. Cada barra tiene una carga positiva Q distribuida uniformemente en toda su longitud, como se indica en la figura. 8. Una barra de longitud L se encuentra a lo largo del eje x con su extremo izquierdo en el origen y tiene una densidad de carga lineal no uniforme λ(x) = λo x, donde λ0 es una constante. Calcule el campo eléctrico en los puntos A y B. (1) Calcular el campo eléctrico producido por la segunda barra en puntos situados a lo largo del eje positivo de las x (2) Muestre que la magnitud de la fuerza eléctrica que ejerce una barra sobre la otra es F = Resp. λ2 (a + L)2 ln | | 2 4πo L a(a + 2L) 2q L2 L L−a − ln EA = kc λo L−a a b EB = 2kc λo 1 − √ b2 + L2 λo = (3) muestre que si a L, la magnitud de esta fuerza se reduce a F = λ2 /4π0 a2 (Use el desarrollo en serie de potencias: ln(1 + z) = z − z 2 /2 + z 3/3 − ... válida con |z| 1. Lleve todos los desarrollos al menos hasta el orden L3 /a3 ). Interprete el resultado. 9. Una barra aislante se dobla en forma de un semicı́rculo de 60 cm de radio. La barra está cargada con una densidad lineal de carga no uniforme λ(θ) = λo sin θ. La carga total en el semicı́rculo 7. Considere un cascarón cilı́ndrico circular recto con una carga total Q, radio R y altura h (1) Determine el campo eléctrico en un punto A, a una 2 es 12µC. Determine (1) la constante λo (2) el campo eléctrico en el centro del semicı́rculo (3) la fuerza total sobre una carga de 2µC colocada en el centro del semicı́rculo. Resp. (1) 10µC/m , (2) 0.233 M N/C, (3) 0.466 N 3









