docdownloader.com-pdf-1538029223714-s-3-practica-domiciliaria-resuelto-dd 5bc13e6d13b6292ad629afd3c148de67
Anuncio

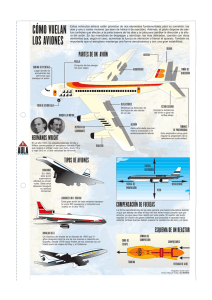
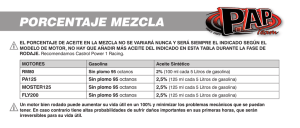
PRÁCTICA N°3 ESCUELA : INGENIERÍA INDUSTRIAL DOCENTE : ING. HUGO DE LA CRUZ DE LA CRUZ ASIGNATURA : INVESTIGACION DE OPERACIONES TEMÁTICA : PROGRAMACIÓN DE MODELOS LINEALES CICLO : 2018 - l PROBLEMA N° 01 Una pequeña refinería mezcla 5 crudos para producir 2 grados de gasolina “A” y “B”. El número de barriles diarios disponibles, número de octanos y el costo por barril, aparecen en la tabla siguiente. CRUDO #OCTANOS BARRILES/DIA 1 2 3 4 5 70 80 85 90 99 2,000 4,000 4,000 5,000 3,000 COSTO x BARRIL 80 90 95 115 200 El número de octanos de gasolina “A” no puede ser menor de 95 y de la “B” menor de 85. Asumir que una disposición gubernamental obliga a producir por lo menos 8,000 barriles de gasolina tipo “B”. La gasolina de tipo A se vende a los distribuidores a 375 por barril y la B a 285 por barril. Los crudos no utilizados para producir gasolina “A” y “B” siempre y cuando tengan al menos 90 octanos se vende como gasolina de aviación a 257 por barril y aquellos con 85 octanos, como máximo se vende como “extra” a 125 por barril. Si deseamos maximizar las utilidades diarias. ¿Cuál debe ser la producción de gasolina “A” y “B”? ¿Cómo debemos mezclar los crudos? 1 SOLUCIÓN Sea X ij = Números de barriles del i-ésimo crudo dedicados al j- és im o gr ad o de ga so lina y al cr ud o que no se ut iliza (C) i = 1; 2; 3; 4; 5 Sabemos que: j = A, B, C UTILIDAD = VENTAS - COSTOS DETERMINACIÓN DE LAS VENTAS: Ventas=375(X 1A +X 2 A +X 3A +X 4A +X 5A )+285(X 1B +X 2B +X 3 B +X 4B +X 5B )+275(X 1 C +X 2 C + X 3 C +X 4 C +X 5C ) DETERMINACIÓN DE LOS COSTOS: Costos=80(X 1 A +X 1B +X 1 C )+90(X 2A +X 2B +X 2 C )+95(X 3A +X 3B +X 3 C )+115(X 4A +X 4 B +X 4C ) + 200(X 5A +X 5B +X 5 C ) EL PROGRAMA LINEAL ES: Max:Z=295X 1 A +285X 2A +280X 3A +260X 4A +175X 5 A +205X 1B +195X 2B +190X 3B +45X 1C +35X 2 C +30X 3C +160X 4C +174X 5 C Sujeto a: Restricciones debido al octanaje de Gasolina “A” (70X + 80X + 85X + 90X + 99X ) (X + X + X + X + X ) ≥ 95 70X + 80X + 85X + 90X + 99X ≥ 95X + 95X + 95X + 95X + 95X −25X − 15X − 10X − 5X + 4X ≥ 0 Restricciones debido al octanaje de Gasolina “B” (70X + 80X + 85X + 90X + 99X ) (X + X + X + X + X ) ≥ 85 70X + 80X + 85X + 90X + 99X ≥ 85X + 85X + 85X + 85X + 85X 2 −15X − 5X + 5X + 14X ≥ 0 Se debe producir al menos 8 000 barriles diarios de gasolina tipo “B” (X + X + X + X + X ) ≥ 8 000 Restricciones debido a la disponibilidad de los crudos X 1 A +X 1B +X 1 C = 2 000 X 2 A +X 2B +X 2 C = 4 000 X 3 A +X 3B +X 3 C = 4 000 X 4 A +X 4B +X 4 C = 5 000 X 5 A +X 5B +X 5 C = 3 000 X ij ≥ 0, i = 1; 2; 3; 4; 5 ; j = A, B, C PROBLEMA N° 02 Aero Perú está considerando la probabilidad de adquirir aviones de pasajeros en el mercado mundial: U.S.A., Inglaterra o Rusia. El costo del avión (USA) A es de $6.7 millones, el avión (Inglés) B en $5 millones y el avión (Ruso) C de $3.5 millones. El directorio de dicha empresa ha autorizado la compra de aviones por valor de 150 millones. Los economistas de Aero-Perú han calculado que cualquier que sea el tipo A de mayor capacidad proporcionará una utilidad neta de $ 420.000 anuales, el avión B proporcionará una utilidad neta de $ 300,000 y el avión C una utilidad de $ 230,000 anuales. Por otro lado se conoce que la fuerza Aérea Peruana sólo le podría proporcionar 30 pilotos debidamente entrenados. Si sólo se adquieren los aviones más pequeños, los servicios de reparación y servicio con que cuenta Aero-Perú solamente podrán mantener en operación un máximo de 40 unidades. Además se sabe que mantener un avión B requiere 1 1/3 más que el avión C y que el avión A requiere 1 2/3 más que el C Determine el número de cada tipo de avión que se debe comprar para maximizar las utilidades. 3 SOLUCION Definiendo las variables: X1: Cantidad a comprar de aviones A X2: Cantidad a comprar de aviones B X3: Cantidad a comprar de aviones C FUNCION OBJETIVO: MAXIMIZAR UTILIDADES Max: Z = 420 X 1+ 300 X2 + 230 X3 Restricciones: Por el costo de cada avión: 6,7 X1 +5 X2 + 3,5 X3≤ 150 Por la cantidad de pilotos disponibles: X1 + X2 + X3≤ 30 Capacidad de mantenimiento de los aviones: X1≥ 0 ; X 2≥ 0 ; 1 + 1 + ≤ 40 X 3≥ 0 4 SOLUCIÓN Definiendo las variables: X1: Número de aviones a comprar en el mercado europeo X2: Número de aviones a comprar en el mercado asiático X3: Número de aviones a comprar en el mercado latino Función Objetivo Max Z=450X1 + 350X2 + 250X3 (en miles $) Sujeto a: Presupuesto: 7.2X1 + 6X2 + 4.2X3 ≤ 200 (millones $) Pilotos: X1 + X2 + X3 ≤ 35 Mantenimiento: (7/4) X1+ (6/5) X2+ X3 ≤ 45 No negatividad: X1≥0 ; X2≥0 ; X3≥0 10