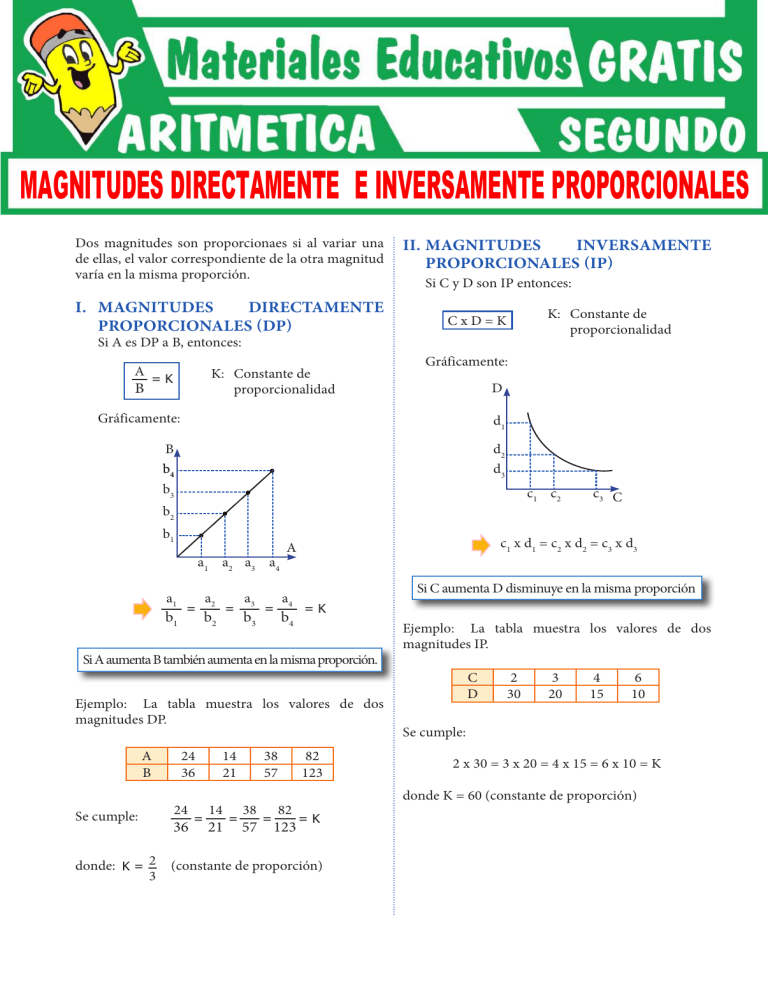
MAGNITUDES DIRECTAMENTE E INVERSAMENTE PROPORCIONALES Dos magnitudes son proporcionaes si al variar una de ellas, el valor correspondiente de la otra magnitud varía en la misma proporción. I. MAGNITUDES DIRECTAMENTE PROPORCIONALES (DP) II. MAGNITUDES INVERSAMENTE PROPORCIONALES (IP) Si C y D son IP entonces: K: Constante de proporcionalidad CxD=K Si A es DP a B, entonces: A B K: Constante de proporcionalidad =K Gráficamente: D Gráficamente: d1 d2 d3 B b4 b3 c1 c2 b2 b1 a1 a2 a3 a4 a1 b1 = a2 = b2 a3 b3 = c1 x d1 = c2 x d2 = c3 x d3 A a4 b4 Si C aumenta D disminuye en la misma proporción =K Si A aumenta B también aumenta en la misma proporción. Ejemplo: La tabla muestra los valores de dos magnitudes DP. A B Se cumple: donde: K = 2 3 24 36 24 36 = 14 21 14 21 = 38 57 38 57 = 82 123 c3 C 82 123 Ejemplo: La tabla muestra los valores de dos magnitudes IP. C D 2 30 3 20 4 15 6 10 Se cumple: 2 x 30 = 3 x 20 = 4 x 15 = 6 x 10 = K donde K = 60 (constante de proporción) =K (constante de proporción) Trabajando en clase 9. Del gráfico, calcula a + b. Integral 1. Si A es DP a B2 cuando A es 16 y B = 2, calcula A cuando B = 8. y 24 2. Si A es IP a B cuando A = 24 y B = 8, ¿cuál será el valor de A cuando B = 16? a 4 3. Si A es D.P. a B3, cuando A = 48 y B = 2, calcular A cuando B = 3. Católica 4. Si A es DP a B cuando A = 6 y B = 4, calcula A cuando B = 9. Resolución: Como A DP B , entonces: A = K 5 10. Dos ruedas de 48 y 32 dientes engranan y están girando, si la primera rueda da 200 vueltas. ¿Cuántas vueltas dará la segunda? 11. Calcula (a + b)2. y B A 9 6 = 4 b x 15 ∴A=9 20 Rpta.: 9 5 2 5. Si A es DP a B , cuando A = 15 y B = 36, ¿cuánto valdrá B cuando A = 5? 6. Si A es IP a C2 cuando A = 18 y C = 5, calcula A cuando C = 3. 7. Si A es DP a B , calcula m + n. 2 A B 4 m n m+5 m+6 2m UNMSM a 12. El precio de un diamante es proporcional al cuadrado de su peso. Si un diamante de 4 gramos vale S/. 1280. ¿Cuál es el peso de un diamante que vale S/. 3920? Resolución: (Precio) DP (peso)2, entonces: Precio = K Peso2 12 a Rpta.: 7 2 12 Resolución: Según el gráfico x DP y: 3 12 c = = 2 Rpta.: 26 a 12 20 x UNI 8. Del gráfico, calcula a + c. y 3 b c x ∴ a = 8 y c = 18 entonces a + c = 26 1280 3920 = 42 x2 x = 7 gramos 13. El precio de un diamante es directamente proporcional al cuadrado de su peso. Si un diamante que pesa 20 gramos cuesta $ 4000, ¿cuánto costará otro diamante que pesa 25 gramos? 14. Si A es IP a B y DP a C. Si cuando A = 5, B = 10 y C = 4. ¿Cuánto vale A si B = 15 y C = 10?