8º GUIA ENETEROS (ADICIÓN - SUSTRACCIÓN - MULTIPLICACIÓN - DIVISIÓN)
Anuncio

GUIA DE NÚMEROS ENTEROS
(CONJUNTO Z)
NOMBRE:
CURSO:
FECHA:
En la vida se nos presentan muchas veces situaciones que no
pueden expresarse mediante los números naturales. En este
caso se necesitan otro tipo de números, que son los números
enteros.
Los números enteros son:
→ Positivos: +1, +2, +3, +4, +5, ....
→ Negativos: -1, -2, -3, -4, -5, ....
→ El cero: 0. (El cero es el único número que
no es ni positivo ni negativo).
Los números positivos expresan situaciones relacionadas con Los números enteros positivos (+2, +6…) se
‘sumar’, ‘tener’, ‘estar por encima de’, etc. En cambio, los pueden escribir sin usar el signo (2, 6…).
negativos se relacionan con situaciones de ‘restar’, ‘deber’,
‘estar por debajo de’, ‘gastar’, etc.
Los Números negativos. es cualquier número cuyo valor es - 1 se lee menos uno.
menor que cero.
- 2 se lee menos dos
Se representan añadiendo un signo menos delante de ellos (-1). - 3 se lee menos tres.
Los números enteros negativos se utilizan para representar
pérdidas, deudas, disminuciones o decrecimientos, años
pasados, entre otras cosas.
El cero es un elemento neutro y va al centro de la recta sin signo
SU UTILIDAD:
Valores de temperaturas
Plantas de edificios
Los años en las líneas del tiempo
-7º, siete grados por debajo de cero; +3º, tres grados por encima de cero.
-1, planta por debajo de la calle; +5, cinco plantas por encima
-1.500 = 1.500 años a.C. / 1.500 d.C. = *1.500
REPRESENTACIÓN GRÁFICA Y ORDENACIÓN DE NÚMEROS ENTEROS
Los números enteros se representan, de forma ordenada, sobre una recta llamada la recta numérica:
En el dibujo anterior vemos que el cero
se sitúa en la mitad de la recta. Los
positivos se representan a la derecha del
cero y los negativos a su izquierda. Esta
representación en la recta numérica nos
sirve para poder comparar números
enteros.
Es mayor el número colocado más a la
derecha de la recta numérica. Por
ejemplo+2 es mayor que -1; -2 es mayor
que -3
VALOR ABSOLUTO
Se llama valor absoluto de un número a la
distancia desde un número al punto de origen o
cero.
Para representar el valor absoluto se utilizan
dos barritas verticales.
EJEMPLO:
- El valor absoluto de | -7 | es 7
- El valor absoluto de |+4 | es 4
Como puedes ver, el valor absoluto de -5 y 5 son equivalentes,
es decir, están a igual distancia del cero.
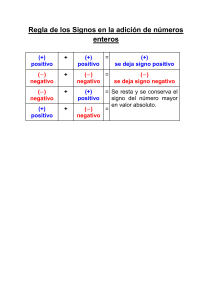
ADICIÓN DE NÚMEROS ENTEROS
Vamos a distinguir tres casos:
a) Si todos los números son positivos se suman y el
resultado es positivo:
3 + 4 + 8 = 15
b) Si todos los números son negativos se suman y el
resultado es negativo:
(-3) + (-4) + (-8) = -15
c) Si se suman números positivos y negativos, los
positivos suman y los negativos restan:
3 + (-4) + 5 + (-7)
Por un lado sumamos los números positivos:
3+5=8
Por otro lado sumamos los números negativos:
(-4) + (-7) = -11
Ahora el resultado positivo suma y el negativo resta:
8 - 11 = -3
SUSTRACCION DE ENTERORS
Si tenemos una sustracción, la cambiamos por EJEMPLO:
adición del inverso aditivo del entero que ocupa el +8 – +3 —-> cambiamos el – de la operación por + y
lugar del sustraendo.
en lugar de +3 ponemos su inverso -3.
Nos queda: +8 + -3 =
A continuación, resolvemos la adición obteniendo
como resultado +5.
Realizaremos el siguiente ejercicio:
-5 – -6 – +7
Aplicamos adición de inversos aditivos y nos queda:
-5 + +6 + -7 = -6
En el caso del conjunto Z, ya no decimos que solo se
pueden restar 2 números.
ADICION Y SUSTRACCION CON PARÉNTESIS
Los paréntesis indican prioridad de ejercicios.
Primero se resuelve lo que está en los paréntesis
redondos, luego lo que va en los paréntesis
cuadrados o de corchete, y finalmente lo que está
en los de llave.
En los paréntesis, las sustracciones también deben
cambiarse por adiciones del inverso aditivo.
-8 + ( -3 – -9 + +5)
Bajamos el número que está fuera del paréntesis y
dentro de él aplicamos adición del inverso en lugar de
sustracción
-8 + ( -3 – -9 + +5)
-8 + (-3 + +9 + +5)
Sumamos dentro del ( ).
-8 + (-3 + +9 + +5) = - 8 + +11
Al tener un solo número de resultado, el ( )
desaparece
Resultado de la operación es +3
– { 3 – [ -2 – ( -6) ] }
Sacamos el ( ) – { 3 – [ -2 – -6 ] }
– { 3 – [ -2 + +6] }
Aplicamos dentro del [ ] adición del inverso en lugar
de
sustracción.
Resolvemos
[
]
– { 3 – +4 }
Aplicamos inverso aditivo – { 3 + -4 }
– -1
Aplicamos inverso aditivo.
Este es el resultado final +1
MULTIPLICACION Y DIVISION DE ENTROS
A) Si multiplicas o divides dos
números enteros positivos, el signo
del producto o cuociente será
siempre positivo.
EJEMPLOS:
+16 x +3 = +48
+48 : +3 = +16
B) Al multiplicar o dividir dos
números enteros negativos, el signo
del producto o cuociente será
siempre positivo.
C) Por último, si multiplicamos o
dividimos dos números enteros de
distinto signo, es decir, uno positivo
y otro negativo, el producto o
cuociente será siempre negativo.
EJEMPLOS:
-12 x -4 = +48
-12 : -4 = +3
EJEMPLOS:
+50 x -2 = -100
+60 : -6 = -10
-50 x +2 = -100
-60 : +6 = -10
De esa forma, se tiene que:
El papomudas es procedimiento estándar que 1) Pa: paréntesis, corchetes o llaves.
establece cuál es el orden que debe ser seguido
cuando se debe dar solución a una expresión, que 2) Po: potencias y raíces.
está compuesta por una combinación de
PAPOMUDAS:
operaciones como suma resta, multiplicación y
división.
Con este procedimiento se establece el orden de
prioridad de una operación con relación a las otras
en el momento en que serán resultas; es decir,
cada operación tiene un turno o nivel jerárquico
para ser resuelta.
El orden en que deben resolverse las diferentes
operaciones de una expresión es dado por cada
sigla de la palabra papomudas.
3) Mu: multiplicaciones.
4) D: divisiones.
5) A: adiciones o sumas.
6) S: sustracciones o restas.
¡¡¡¡¡AHORA PONGAMOS EN PRACTICA LO APRENDIDO!!!!!
RESUELVE
ADICIÓN DE ENTEROS
SUSTRACCIÓN DE ENTEROS
MULTIPLICACIÓN DE ENTEROS
DIVISIÓN DE ENTEROS
CALCULA EL VALOR DE LAS SIGUIENTES OPERACIONES
RESUELVE LOS EJERCCIOS SEGÚN LA PRIORIDAD DE LAS OPERACIÓN (PAPOMUDAS)