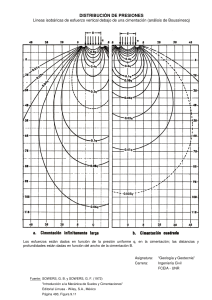
DISTRIBUCIÓN DE PRESIONES EN LA MASA DE SUELOS 1. PRINCIPIO DE ESFUERZO EFECTIVO El esfuerzo efectivo es la diferencia entre el esfuerzo total y la presión de poros, quedando expresado de la siguiente forma: σ = σ – μ. El concepto fue descubierto por Terzagui, dando pie al nacimiento de la Mecánica de Suelos. Éste comprendió que el suelo es un compuesto de tres fases: sólida, líquida y gaseosa, en el que las partículas sólidas en contacto forman un sistema intersticial entre los vacíos o poros que pueden estar parcial o totalmente llenos de agua. De manera que en la naturaleza podemos encontrar suelos saturados con agua y nada de aire en los vacíos, suelos secos sin nada de agua en los vacíos y suelos parcialmente saturados, con agua y aire en los vacíos. De lo anterior se concluye que la respuesta de un suelo ante la aplicación de cualquier carga o la transmisión de los esfuerzos de esa carga al interior del conjunto sólido, agua y aire, es una acumulación del comportamiento de los tres componentes, haciendo que los fenómenos de transmisión de esfuerzos sean complejos. Debido a la naturaleza incompresible del agua, la presencia de ésta en el suelo, juega un papel importante en el comportamiento del mismo, puesto que si por efecto de presiones exteriores el agua adquiere presiones elevadas, ésta tenderá a fluir hacia zonas de menor presión, dando lugar a la compresibilidad (relación esfuerzo – deformación) de la masa sólida del suelo y en consecuencia a el asentamiento del mismo, tomando en cuenta que el tiempo tendrá gran influencia en estos efectos. El esfuerzo total (σ) representa la relación entre la carga total actuante sobre el área transversal cubierta por dicha carga. σ = P / A El esfuerzo efectivo (σ) representa la parte del esfuerzo total que es tomada por la fase sólida del suelo, transmitiéndose entre los granos de la misma. La presión de poro (μ) representa la presión a la que está sometida el agua en los vacíos del suelo. También es conocida como presión neutral por la incapacidad del agua para tomar esfuerzos cortantes. 2. ESFUERZOS DEBIDOS A CARGAS EXTERNAS Las cargas que se aplican en las superficies de los suelos generan dos tipos de esfuerzos, esfuerzos superficiales (presiones de contacto) y esfuerzos subsuperficiales. 2.1. Esfuerzos Superficiales (Presiones de Contacto): se generan en la superficie de contacto suelo-cimentación, es la reacción que ofrece el suelo sobre la estructura de cimentación. Estas presiones nos permiten conocer todos los elementos mecánicos mediante los cuales es posible diseñar estructuralmente a la cimentación. 2.2. Esfuerzos Sub-Superficiales: son inducidos por las cargas superficiales en el interior del suelo, su conocimiento resulta básico en el cálculo de desplazamientos. Existen diferentes métodos aproximados para la determinación de los esfuerzos normales verticales en la masa del suelo, debidos a la acción de las cargas uniformemente distribuidas actuando en los estratos superficiales del terreno. Todos ellos suponen que los esfuerzos dentro de la masa se transmiten como una pirámide truncada cuyas aristas tienen pendientes entre 1:1 y 2:1. La magnitud de los esfuerzos se va reduciendo con la profundidad, y además, fuera de los límites de la pirámide, estos métodos suponen que las presiones debidas a las sobrecargas pueden despreciarse. 3. INCREMENTO DEL ESFUERZO BAJO UNA CARGA APLICADA 3.1. Carga Puntual, según Boussinesq: para el desarrollo del modelo matemático, Boussinesq planteó como hipótesis que el suelo es un material homogéneo, isótropo, elástico-lineal, semi-infinito y continuo, y estableció la validez de los principios de objetividad e indiferencia y el principio de superposición. Es importante resaltar que en la realidad las hipótesis anteriores no se cumplen, debido a que el suelo no es homogéneo pues sus propiedades mecánicas no son las mismas en todos los puntos de su masa, ni isótropo pues en un punto dado esas propiedades varían, en general, en las diferentes direcciones del espacio, ni linealmente elástico, pues las relaciones esfuerzodeformación que se producen no tienen ese comportamiento y por último, tampoco es semi-infinita ninguna masa de suelo. Cuando una carga puntual actúa sobre el suelo, el esfuerzo σz a una profundidad z queda definido por la siguiente expresión: σz = (P/z2) * Po Donde Po es el coeficiente de influencia y ya está estipulado en tablas. Po = (3/2π) * (1/(1 + (r/z)2)5/2) Al hacer un análisis de este caso, la distribución de los esfuerzos da como resultado un bulbo de presiones que no es más que la zona del suelo donde se producen incrementos de carga vertical considerables por efecto de una carga puntual. Esta zona está conformada por isobaras que son curvas que unen puntos de igual esfuerzo y están representadas desde la del 10% hasta la del 90% en intervalos de 10%. Este método se puede aplicar para calcular en una primera aproximación la distribución de tensiones producida en el terreno por una o varias zapatas. Ejemplo: Obtener el valor de σz aplicando la ecuación de Boussinesq para el caso de una carga concentrada de 100 T. Se requiere el esfuerzo a 3 metros de profundidad y a una distancia radial de metro y medio. σz = (P/z2) * Po r/z = 1.5/3 = 0.5 De la Tabla “Valores de Po” Po = 0.2733 σz = (100/9) * 0.2733 = 3.036 T/m2. Además de Boussinesq, otros autores dedujeron ecuaciones para una fuerza concentrada vertical: Westergaard. 3.2. Cargas rectangulares, según Fadum: Fadum realizó la integración de la solución de Boussinesq para el caso de la carga puntual, extendiéndola para el caso de una superficie rectangular, estableciendo que para un punto cualquiera (a) debajo de la esquina de una cimentación rectangular, de ancho B y largo L, cargada con un valor de esfuerzo de contacto (q) uniformemente distribuido, en una profundidad dada (z), el esfuerzo será: σz = I * q (m,n) I = valor de influencia que depende de m y n m = relación entre el ancho del rectángulo y la profundidad z. n = relación entre el largo del rectángulo y la profundidad z. Este método se puede aplicar para calcular en una primera aproximación la distribución de presiones en la masa del suelo producida por una losa rectangular de fundación. Ejemplo: Calcular la presión en un punto a 5.0 m por debajo de la esquina de una zapata de 1.0 m de ancho por 1.2 m de largo que soporta una carga uniforme q de 2 Kg/cm2. m = B/z = 1.0 / 5.0 = 0.20 n = L/z = 1.2 / 5.0 = 0.24 De la Tabla “Valores de I para los esfuerzos verticales debajo de una esquina según Fadum” I = 0.023 σz = I * q = 0.023 * 2.0 = 0.046 Kg/cm2. Fadum también obtuvo la ecuación para una carga lineal, estableciendo que ésta siempre estará sobre el eje y alojada a una distancia x ≥ 0, ésta deberá empezar tocando el eje x, el punto de cálculo debe estar sobre el eje z. 3.3. Cargas circulares, según Fadum: es la integración de la ecuación de Boussinesq para carga puntual, aplicada a una superficie circular en la que el área se divide en diferenciales de área. Para un punto cualquiera (a) debajo del centro de una cimentación circular, de radio R, cargada con un valor de esfuerzo de contacto q uniformemente distribuido, en una profundidad z cualquiera, el valor del esfuerzo será: σz = ϝ * q () 3.4. Esfuerzo bajo un terraplén, según Osterberg σz = ϝ * q (B1 y B2) Donde ϝ es el valor de influencia que depende de B1/z y B2/z. B1 = ancho donde se desarrolla la pendiente del terraplén y donde varía la carga hasta cero. B2 = ancho donde se considera que actúa la carga rectangular de longitud infinita uniformemente distribuída (q). q = sobrecarga de forma rectangular uniformemente distribuida de longitud infinita, actuando en el ancho B2 que en el caso de un terraplén uniforme de altura H y peso específica ϒ, será q = ϒ*H. 3.5. Carta de Newmark: es un método gráfico que permite encontrar de manera aproximada el incremento de esfuerzo vertical debajo de cualquier punto de una fundación, con cualquier tipo y forma de carga, basado en la solución para un punto bajo el centro de una fundación con carga uniformemente repartida con forma circular. La forma de encontrar el incremento del esfuerzo vertical σ z bajo cualquier punto de la fundación o fuera de ella a una profundidad z, es: caracterizar la carta de Newmark con la que se va a trabajar, que consiste en identificar el valor de influencia y en identificar la referencia de la escala que es la línea que representa la profundidad z a la cual se va a encontrar el incremento del esfuerzo, adoptar la profundidad z y la línea de la escala se volverá igual a la profundidad z tomada, se deberá dibujar la fundación en planta de acuerdo a la escala definida, para luego colocar este esquema en la carta de Newmark, haciendo coincidir el punto bajo el cual se desea conocer el incremento de esfuerzo con el centro de la carta, finalmente se contarán cuantos cuadros quedan dentro del esquema de la fundación, sumándose cuantos cuadros completos y las fracciones de recuadros con el cuidado de una buena apreciación. σz = V i * q * N Vi = Valor de influencia de la carta de Newmark de referencia. q = sobrecarga uniformemente distribuida producida por la cimentación. N = número de divisiones de la carta de Newmark de referencia, que estén dentro de la planta de la cimentación. 3.6. DISTRIBUCIÓN DEL ESFUERZO EN SISTEMAS NO HOMOGÉNEOS, SEGÚN BURMISTER Burmister estudió la distribución de esfuerzos y desplazamientos en un sistema no homogéneo formado por dos capas, cada una de ellas homogénea, isótropa y linealmente elástica. La primera capa es infinita horizontalmente, pero tiene espesor finito h. La segunda capa, subyacente a la anterior, es semi-infinita. Se supone que entre las dos capas existe un contacto continuo, siendo la frontera plana entre ellas perfectamente rugosa. E1 y E2 son los módulos de elasticidad de las dos capas; se estudió el caso de interés práctico, con la aplicación al diseño de pavimentos, en el cual E 1 >> E2. Las curvas de influencia de Burmister muestran los esfuerzos en cualquier punto de la masa del medio y no sólo en la vertical, bajo el centro del área cargada y además determinó que el desplazamiento vertical elástico del sistema depende de un factor adimensional que a su vez depende de la relación E1/E2 y h/r, de la presión uniforme del área circular, del radio del circulo y del módulo de elasticidad de la capa semi-infinita. Δ = 1.5 F ( p r/ E2) Recientemente se están haciendo estudios en medios semiinfinitos no lineales y no homogéneos, es decir, con materiales que al ser sometidos a compresión simple muestran una relación esfuerzo-deformación del tipo indicado en la figura. Las conclusiones dan como resultado que los esfuerzos verticales bajo la carga concentrada son menores que los determinados por Boussinesq y que los desplazamientos verticales de los puntos bajo la carga ocurren en forma mucho más concentrada en la cercanía de la superficie, justificando que para el cálculo de asentamientos se debe considerar una profundidad entre una y media y dos veces el ancho del cimiento. 4. ASENTAMIENTOS ELÁSTICOS Es un movimiento vertical debido a la deformación (vertical) elástica del medio poroso, en este tipo de asentamiento la compresión ocurre de inmediato después la aplicación de la carga y la deformación elástica vertical es preeminente a otra deformación (ej. Horizontal).