PROYECTO FORMATIVO

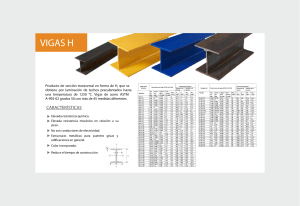
PROYECTO FORMATIVO
APLICAMOS TEOREMAS, LEYES, PRINCIPIOS Y CONCEPTOS FÍSICOS-MECÁNICOS EN
ESTRUCTURAS ESTÁTICAS REALES PARA SU REPRESENTACIÓN ANALÍTICA Y GRÁFICA
Nombre completo integrantes:
Nombre completo docente:
Asignatura:
Turno:
Unidad de contenido:
Grupo
Univ. Rafael Choque Flores
Univ. Quiroz Mamani Humberto
Univ.
Ing. María Eugenia Rollano Quintana
Isostática I
Noche
Proyecto formativo
6
PRIMERA PRESENTACIÓN
Realizar la investigación y síntesis de los siguientes conceptos, se debe incluir la bibliografía
empleada.
1. Marco teórico referencial (extensión máxima 10 hojas)
a.
Estática y ecuaciones de equilibrio
b.
Sistema estructural
c.
Vigas
d.
Tipos de vigas
e.
Tipos de apoyos en vigas
f.
Fuerzas internas en vigas (Axial, Cortante y Momento flector)
g.
Relación entre carga, cortante y momento flector
INDICE
Contenido
ESTÁTICA Y ECUACIÓN DE EQUILIBRIO ...............................................................................................4
1.1 La Estática.................................................................................................................................4
1.2. Ecuaciones de equilibrio ..........................................................................................................4
2. SISTEMA ESTRUCTURAL .................................................................................................................6
2.1. Definición y Características .....................................................................................................6
2.2. Tipos de Sistemas Estructurales ..............................................................................................6
2.2.1 Muros Portantes ................................................................................................................6
2.2.2. Sistema Aporticado ..........................................................................................................7
2.2.3. Sistemas abovedados, Arco y cúpula ................................................................................7
2.2.4. Perfiles Metálicos .............................................................................................................7
2.2.5. Perfiles carpintería metálica .............................................................................................7
2.2.6 Perfiles Metálicos Estructurales ........................................................................................7
2.2.7. Cerchas metálicas .............................................................................................................7
2.2.8. Concreto Armado .............................................................................................................8
2.2.9. Muros Portantes ...............................................................................................................8
2.2.10. La Madera como elemento estructural ..........................................................................8
3. VIGAS..............................................................................................................................................8
3.1. Definición de vigas ................................................................................................................8
4. tipos de vigas y su uso ....................................................................................................................9
4.1. Vigas Flitch ..............................................................................................................................9
4.2. Viga de soporte .......................................................................................................................9
4.3 Viguetas ..................................................................................................................................10
4.4. Dinteles .................................................................................................................................10
4.5 VIGAS DE ACERO L ..................................................................................................................10
4.5.1 Vigas IPE ..........................................................................................................................10
4.5.2. Vigas IPN .........................................................................................................................11
4.5.3. Vigas UPN .......................................................................................................................11
4.5.4. Vigas HEB ........................................................................................................................11
4.2. CLASIFICACIÓN DE VIGAS ......................................................................................................11
.................................................................................................................................................12
4.2.1. HIPERESTATICAS .............................................................................................................12
.................................................................................................................................................12
4.2.2. ISOSTATICAS ...................................................................................................................12
.................................................................................................................................................12
4.3. DEFLEXION DE VIGAS.............................................................................................................13
5. TIPOS DE APOYOS EN VIGAS .........................................................................................................13
5.1. APOYO DE ARTICULACION .....................................................................................................13
5.2. APOYO DE RODILLOS .............................................................................................................14
5.3. APOYO EMPOTRADO .............................................................................................................14
5.4. APOYO MOVIL .......................................................................................................................14
6. FUERZAS INTERNAS EN VIGAS (axial, cortante y momento flector) .............................................15
6.1. DEFINICIÓN DE FUERZA CORTANTE Y MOMENTO FLECTOR. ................................................16
6.1.1. Fuerza Cortante: ...........................................................................................................16
6.1.2. Momento Flector: ..........................................................................................................17
7. RELACIÓN ENTRE CARGA, CORTE Y MOMENTO FLECTOR ............................................................19
7.1. Relación Carga – Corte: .........................................................................................................20
V
2
X
1
.....................................................................................................................................20
7.2. Relación Corte – Momento: ..................................................................................................21
ESTÁTICA Y ECUACIÓN DE EQUILIBRIO
1.1 La Estática
Estática es un vocablo de origen griego, de “statikos” que significa estacionado o
quieto o en equilibrio. Algo decimos que está estático, cuando se halla inmóvil,
carente de movimiento. Lo opuesto a la estática, es la dinámica, que implica
movimiento.
La estática es una rama de la ciencia Física que estudia cómo actúan las fuerzas
sobre los cuerpos quietos.Para que un cuerpo se halle en equilibrio se necesita
que la suma vectorial de todas las fuerzas que sobre él actúan, sea nula, debiendo
también ser nula la suma del momento de la fuerza, que es una magnitud vectorial
que produce rotaciones, cuya dirección está dada por el sentido de la fuerza. El
momento de una fuerza se mide en relación a un punto, y es el producto de la
fuerza, por la distancia que separa el punto de la recta de aplicación de la fuerza.
Como las fuerzas producen aceleraciones, la ausencia de fuerzas sobre cuerpos
en reposo hace que ellos se conserven en el mismo estado de quietud. La
ausencia de momentos asegura que los cuerpos no roten.
Si un cuerpo ejerce sobre otro una fuerza, y éste a su vez genera una reacción
sobre el primero del mismo valor, ambas fuerzas son iguales y opuestas (tercera
ley de Newton).
1.2. Ecuaciones de equilibrio
ya se dijo, un cuerpo está en equilibrio cuando el sistema de fuerzas se
puede reducir a un sistema equivalente nulo Cualquier sistema de fuerzas
se puede reducir a una fuerza resultante única y a un par resultante
referidos a un punto arbitrariamente seleccionado.
la fuerza resultante es cero, el cuerpo, debido a las restricciones impuestas, no se
podrá trasladar, perdiendo así tres grados de libertad; de otra parte, si el par
resultante es cero, el cuerpo no rotará alrededor de cualquiera de los ejes
coordenados. En forma vectorial, lo anterior se puede expresar así:
Descomponiendo los vectores en sus componentes rectangulares se obtiene:
Estas ecuaciones independientes son las disponibles para resolver problemas de
equilibrio de cuerpos en tres dimensiones. En problemas bidimensionales las
ecuaciones se reducen a tres, número que corresponde a los grados de libertad
de un Si por ejemplo el plano en que actúan las fuerzas es el plano xy, las
ecuaciones de equilibrio son: movimiento plano; dos de translación y uno de
rotación.
De acuerdo a lo anterior, el máximo numero de incógnitas que puede
tener un problema para poder solucionarlo completamente, es de seis
para situaciones en tres dimensiones y de tres para dos dimensiones.
Cuando en un problema hay tantas incógnitas como ecuaciones
disponibles y se pueden hallar todas, se dice que el problema es
estáticamente determinado. Si existen mas incógnitas que ecuaciones, el
problema es insoluble en su totalidad por los métodos de la estática y el
problema es estáticamente indeterminado.
Equilibrio
No Equilibrio
2. SISTEMA ESTRUCTURAL
2.1. Definición y Características
Una estructura es un ensamblaje de elementos que mantienen una forma y su
unidad, teniendo como objetivo resistir las cargas resultantes de su uso y su
propio peso dándole forma a un cuerpo, obra civil o maquina. Ejemplos de
estructuras son: puentes, torres, edificios, estadios, techos, barcos, aviones,
maquinarias, presas y hasta el cuerpo humano
2.2. Tipos de Sistemas Estructurales
2.2.1 Muros Portantes
También llamado como sistema tipo túnel se conoce a los arreglos entre placas
verticales (muros), las cuales funcionan como paredes de carga, y las placas
horizontales (losas). Este sistema genera gran resistencia y rigidez lateral, pero si
la disposición de los muros se hace en una sola dirección o se utiliza una
configuración asimétrica en la distribución de los muros, se generan
comportamientos inadecuados que propician la posibilidad del colapso.
2.2.2. Sistema Aporticado
Está formado por vigas y columnas, conectados entre sí por medio de nodos
rígidos, lo cual permite la transferencia de los momentos flectores y las cargas
axiales hacia las columnas. La resistencia a las cargas laterales de los pórticos se
logra principalmente por la acción de flexión de sus elementos. Para los edificios
con sistemas de pórticos rígidos se estima que en zonas poco expuestas a sismos
el límite puede estar alrededor de 20 pisos, Y para zonas de alto riesgo sísmico
alrededor de 10 pisos.
2.2.3. Sistemas abovedados, Arco y cúpula
El concepto básico del arco es tener una estructura para cubrir claros, mediante el
uso de compresión interna solamente. El perfil del arco puede ser derivado
geométricamente de las condiciones de carga y soporte. Para utilizarlo se
necesitan materiales que aguanten bien los esfuerzos de compresión, por lo que
tradicionalmente se han construido en ladrillo cerámico o piedra.
2.2.4. Perfiles Metálicos
Los perfiles estructurales son productos fabricados para la construcción de
estructuras, son perfiles de sección cerrada, conformado en frio y soldado
eléctricamente por alta frecuencia, formando elementos tubulares de sección
cuadrada, circular, rectangular, T, TT, vienen en longitudes de 12 metros.
2.2.5. Perfiles carpintería metálica
La carpintería metálica es un campo ocupacional mediante el cual se diseñan
muebles y estructuras metálicas de cerramiento, también conocida como
cerrajería, hace uso de perfiles de acero y aluminio para la producción de bienes
para la construcción.
2.2.6 Perfiles Metálicos Estructurales
Son productos de acero estructural de alta resistencia mecánica conformado en
frío y soldado eléctricamente por alta frecuencia, formando tubos de sección
cuadrada, distribuidos en longitud de 6,00 m.
2.2.7. Cerchas metálicas
La cercha es una composición de barras rectas unidas entre sí en sus extremos
para constituir una armazón rígida de forma triangular, capaz de soportar cargas
en su plano, particularmente aplicadas sobre las uniones denominada nodos. Las
cerchas (armaduras) son uno de los elementos estructurales que forman parte del
conjunto de las estructuras de forma activa.
2.2.8. Concreto Armado
La técnica constructiva del concreto u hormigón armado consiste en la utilización
de concreto reforzado con barras o mallas de acero, para mejorar su resistencia.
También se puede armar con fibras, tales como fibras plásticas, fibras de vidrio,
fibras de acero o combinaciones. El hormigón armado se utiliza en todo tipo de
edificaciones edificios, puentes, presas, túneles, y obras variadas. El acero a
utilizar debe ser corrugado para formar una pieza mas sólida mejorando la
resistencia a la tracción y la compresión.
2.2.9. Muros Portantes
Se denomina muro portante o de carga a las paredes de una edificación que
poseen función estructural; es decir, aquellas que soportan otros elementos
estructurales del edificio, como techos, arcos, bóvedas, vigas. Cuando los muros
soportan cargas horizontales
2.2.10. La Madera como elemento estructural
La madera por su carácter orgánico- vegetal tiene características propias que la
diferencian de otros materiales de construcción por ejemplo el acero y el
hormigón, en consecuencia, el diseño, cálculo y construcción con madera, debe
tener en cuenta sus particularidades. Las características de la madera, la facilidad
y rapidez para trabajarla, su poco peso, la disponibilidad de diversos elementos de
unión: ensambles, tornillos, grapas, etc
3. VIGAS
Una viga es un instrumento estructural que normalmente se coloca en una
posición horizontal que se apoyan sobre los pilares, destinados a soportar cargas.
3.1. Definición de vigas
El concepto de viga desciende del latín biga, un término que se empleaba para
hacer referencia al carro de una pareja de caballos. La viga, con ‘v’, permite
identificar a la pieza curva (que puede ser tanto de hierro como de madera),
presente en los coches antiguos con el propósito de permitir el enlace entre el
juego delantero y el de la parte posterior.
Según los expertos en construcción, la viga es un elemento que funciona a
flexión, cuya resistencia provoca tensiones de tracción y compresión. Cuando las
vigas se ubican en el perímetro exterior de un forjado, es posible que también se
adviertan tensiones por torsión.
4. tipos de vigas y su uso
Las vigas, son una pieza fundamental en la mayoría de proyectos de construcción,
ya sean residenciales, comerciales o públicos. Son el soporte que toda estructura
necesita. Elementos diseñados para sostener cargas lineales, concentradas o
uniformes, en una sola dirección.
En la actualidad existe una variedad de vigas, las cuales se clasifican por su
forma, tamaño y usos. Algunos tipos de vigas y sus principales usos son:
4.1. Vigas Flitch
Las vigas Flitch son híbridas de
madera y metal, generalmente acero,
hecha con capas una encima de otra.
4.2. Viga de soporte
Este tipo de viga es aquel que se lo
utiliza principalmente en ventanales,
balcones y puentes, ya que se
encargan de redistribuir el peso de
cualquier estructura que esté unida a
las principales vigas estructurales de
la casa o edificio.
4.5 VIGAS DE ACERO L
Estas son las vigas que puedes
encontrar en los centros de DIPAC.
Denominada de esta manera debido
4.3 Viguetas
Son aquellas que se caracterizan por
a su singular forma que se asemeja a
la letra “L
ser elaboradas a base de acero,
madera o concreto. Su función
4.5.1 Vigas IPE
principal es ser el soporte o cimiento
de pisos superiores.
Este tipo de vigas son los principales
elementos estructurales utilizados en:
grandes edificios metálicos, sistemas
4.4. Dinteles
Su función es soportar el vacío de
ventanas puertas, por lo que
regularmente están a la vista de
todos, pues se colocan en las
aberturas de las paredes.
estructurales de gran envergadura,
puentes, túneles.
4.5.2. Vigas IPN
Las vigas UPN se caracterizan por
ser un producto laminado, cuya
sección tiene forma de “U”.
4.5.4. Vigas HEB
La IPN es una viga de alta resistencia
a la fricción, al peso y a los golpes.
Es ideal para el soporte de polipasto
en plantas industriales.
4.5.3. Vigas UPN
Las vigas HEB son un tipo de perfil laminado cuya sección transversal tiene forma
de doble T, con alas más anchas que un perfil doble T de tipo IPN o IPE. Este tipo
de viga es ideal para formar los elementos estructurales como: pilotes, columnas,
4.2. CLASIFICACIÓN DE VIGAS
Las vigas se clasifican de acuerdo con la maneras en la que se encuentran apoyadas.
Se presentan varios tipos de vigas utilizadas con frecuencia.
4.2.1. HIPERESTATICAS
Estructura hiperestática o indeterminada presenta un mayor numero de incógnitas,
no basta con las ecuaciones estáticas sino se incorporan nuevas expresiones.
(Beer y Johnston, 1979; Das, Kassimali y Sami, 1999).
4.2.2. ISOSTATICAS
Una viga Isostatica o simple es aquella en el que el número de reacciones en todos
el apoyo es igual al número de ecuaciones de equilibrio disponibles. ∑Fy, ∑Fx, ∑M;
esto implica que el número de reacciones en la viga sea igual a tres-
4.3. DEFLEXION DE VIGAS
La deformación es, en sentido generalizado, el cambio geométrico que experimenta
un cuerpo no rígido bajo la acción de las fuerzas externas y de volumen o de inercia
que a él se aplican.
5. TIPOS DE APOYOS EN VIGAS
Es el sistema de unión entre la estructura y tierra firme; impiden el desplazamiento lineal y/o
desplazamiento angular de la estructura.
5.1. APOYO DE ARTICULACION
Punto que sirve de unión y en el que se apoya el arranque de un arco o bóveda.
5.2. APOYO DE RODILLOS
Apoyo estructural que impide la traslación en cualquier dirección excepto la del propio
plano. También llamado rodillo.
5.3. APOYO EMPOTRADO
Es capaz de evitar movimientos debido al paso de fuerzas por el apoyo como también
a los giros producidos por otras fuerzas. Ejemplo: palo empotrado en un hoyo de hormigón.
5.4. APOYO MOVIL
Solo es capaz de generar una reacción en una dirección determinada.
6. FUERZAS INTERNAS EN VIGAS (axial, cortante y momento flector)

Fuerza Cortante: se produce con dirección perpendicular al eje de la
viga y su efecto es similar al generado por una tijera al cortar un papel, es
decir una fuerza cortante paralela a la cara de la sección de la viga.

Fuerza Axial: se produce cuando la disposición de las fuerzas
externas no es totalmente perpendicular al eje de la viga, existiendo
componentes de ellas a lo largo del eje. Cuando aparece esta fuerza junto
con la flexión, se genera un esfuerzo combinado de flexión con esfuerzo
axial. Este estudio está fuera del alcance del presente trabajo.

Momento Flector: es una fuerza del tipo “par”, que contribuye a
equilibrar la rotación del sólido en un eje perpendicular a su eje y fuera de
su plano, y que produce sobre la viga un efecto de curvatura a largo de su
eje.

Momento Torsor: es una fuerza del tipo “par”, que contribuye a
equilibrar la rotación del sólido según un eje paralelo al eje longitudinal de
la viga, y que produce sobre la misma un efecto de giro alrededor de su
propio eje. La aparición de esta fuerza interna depende de la aplicación de
las fuerzas externas, de tal manera que generen alguna componente de
momento alrededor del eje de la viga. Esta fuerza no se considera en este
estudio.
6.1. DEFINICIÓN DE FUERZA CORTANTE Y MOMENTO FLECTOR.
En la figura se muestra una viga horizontal elemental, isostática de un
solo tramo, con una carga puntual “P”, en la sección a-a se hace un
corte imaginario para observar las fuerzas internas que aparecen para
satisfacer las condiciones de equilibro, tal
como se muestra en el diagrama de cuerpo
libre de abajo.
6.1.1. Fuerza Cortante:
del equilibrio de fuerzas verticales practicado
a cualquiera de los dos segmentos de viga
separados, aparece una fuerza interna “Vaa”, llamada resistente, debido a que se
opone al efecto de las fuerzas activas
externas, cuya dirección es perpendicular al
eje longitudinal de la viga AB, el cual coincide
a su vez con el eje “X” del sistema de
referencia particular “XY” de la viga . Para el caso de vigas
inclinadas la fuerza cortante Va-a, tiene la misma inclinación,
puesto que se orienta según el eje particular de la viga y no
según el sistema global vertical-horizontal.
En este sentido se define la fuerza cortante como la sumatoria de
la componente perpendicular al eje, de las
fuerzas externas
situadas a la izquierda o a la derecha de la sección de viga
estudiada:
Va-a = ΣFyizqa-a= ΣFydera-a.
La convención de signos más común, es aquella que considera positiva la fuerza
cortante que hace deslizar hacia arriba, la porción de viga situada a la izquierda de
la sección estudiada, en caso contrario se considera negativa. En otras palabras
cuando la sumatoria de fuerzas a la izquierda de la sección es positiva la fuerza
cortante tiene el mismo signo, igual para el caso contrario, tal como se muestra en
el siguiente diagrama fig 1.3.a. En la Fig. 1.3.b. se muestra la convención de signos
desde el punto de vista de la deformación de un elemento diferencial situado justo
en la sección a-a.
6.1.2. Momento Flector:
el equilibrio rotacional de los segmentos de viga estudiados se logra con la
aparición del Momento Flector Ma-a, señalado en el diagrama de cuerpo libre
anterior. De esta manera este se puede definir como la sumatoria de los
momentos de las fuerzas externas situadas a la izquierda o a la derecha
de la sección estudiada, considerando que el plano de aplicación de las
fuerzas es XY (hoja de papel), y la dirección del momento flector es
perpendicular a este, es decir el eje particular Z:
Ma-a = ΣMiizqa-a= ΣMidera-a
En cuanto al signo del momento flector, es importante resaltar que este no
depende de su sentido de rotación, tal como sucede con el momento de
equilibrio, sino más bien de la curvatura que sufre la viga por la aplicación del
mismo. De tal manera que una curvatura cóncava hacia arriba se considera
positiva, lo contrario es negativo.
En la siguiente figura se ilustra esta convención.
Los momentos flectores positivos generan tracción o alargamiento en las fibras
inferiores de la viga y compresión o acortamiento en las superiores, los negativos
producen lo contrario, como se muestra en la parte superior de la figura anterior.
En los gráficos inferiores, de la figura anterior, se muestra el efecto de fuerzas
individuales y el sentido de curvatura de la viga, considerando un empotramiento
imaginario en la sección a-a.
7. RELACIÓN ENTRE CARGA, CORTE Y MOMENTO FLECTOR.
Resulta particularmente importante, conocer no solo el valor del corte y del
momento flexionante en un punto de la viga, sino más bien a lo largo de todo el
elemento, debido a que, en su diseño, se debe considerar la condición más
desfavorable de esfuerzo resistente en el interior del sólido, por lograr esto se
construyen los llamados diagramas de fuerza cortante y momento flector. La
realización de estos diagramas requiere conocer la relación existente entre las
cargas externas y las fuerzas internas de corte y momento flector.
En el siguiente gráfico, se ha considerado una viga simplemente apoyada, con un
sistema de cargas distribuida general “q”, de signo positivo, por tener sentido
vertical hacia arriba. 1 y 2 representan dos secciones de la viga separadas una
distancia dx. A la derecha se ha graficado en forma ampliada, el diagrama de
cuerpo libre del elemento diferencial de viga contenido entre las secciones 01 y 02,
que incluye tanto las fuerzas externas “q”, como las fuerzas internas V y M, las
cuales se supusieron con signo positivo. Para la cara de la sección 01, los valores
de fuerzas cortantes y momentos flexionantes son respectivamente V y M, mientras
que para la sección 02, son los valores de la sección 01 más un cierto diferencial
dV y dM respectivamente.
Equilibrando el elemento diferencial tenemos :
7.1. Relación Carga – Corte:
por sumatoria de fuerzas verticales,
∑ Fy = 0
dV = q ∙ dx
V
2
X
1
Integrando ∫V dV = ∫X q∙dx
1
1
1-2
V2 – V1 = ∆V =
(Área)Carga
De esta manera se encuentran las siguientes relaciones:
1corte
q = dV q: intensidad de carga; dv: Pendiente diagrama de
dx
dx
1.a - El signo de la carga, define la inclinación de la pendiente
del diagrama de corte.
1.b - La intensidad de la carga “q” define la variación de la
pendiente del diagrama de corte.
2-
Se puede calcular el corte en la sección 02, con el corte
anterior en la sección 01, más el área del diagrama de carga existente
entre las secciones 01 y 02:
1-2
V2 = V1 + (Área)
carga
7.2. Relación Corte – Momento:
por sumatoria de momentos en el punto “0”:
∑MB = 0
dM = V∙ dx
x2
Integrando: ∫ dM = ∫ V∙ dx
M1
x1
M2
1-2
M2 – M1 = ∆M = (Área)corte
Las relaciones entre corte y momento son:
3V
= dM
V: intensidad del diag. de Corte; dM: Pendiente diag. de Momentos
dx
dx
3.a El signo del diagrama de corte, define la inclinación de la
pendiente del diagrama de Momentos:
3.b La Intensidad del diagrama de corte, define la variación
de la pendiente del diagrama de
muestra a continuación:
Momentos, como se
4-
Se puede calcular el momento en la sección 02, con el
momento anterior en la sección 01, más el área del diagrama de corte
existente entre las secciones 01 y 02:
1-2
M2 = M1 + (Área)
Corte
BIBLIOGRAFIAS
https://deconceptos.com/wp-content/uploads/2010/01/concepto-de-estatica300x116.png
Bibliografía http://www.arqhys.com/articulos/estructuras-membrana.html
http://www.materialeslosandes.com/tproductos.php?pagina=losacer http://
www.construdata.com/BancoConocimiento/R/r120membranas/r120membranas.as
p http://es.wikipedia.org/wiki/Celos%C3%ADa_(ingenier%C3%ADa)
http://es.wikipedia.org/wiki/Malla_espacial
http://www.civil.cicloides.com/cestructurales/2.3.3/
http://www.sencamer.gob.ve/sencamer/normas/2897-95.pdf
© AQSO arquitectos office