PROYECTO
Anuncio

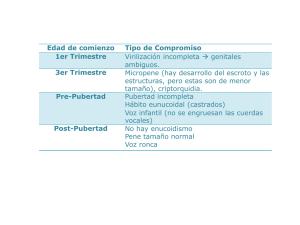
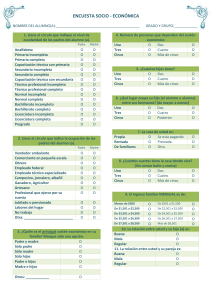
TABLA DE CONTENIDO CAPÍTULO I. GENERALIDADES DE LA INVESTIGACIÓN............................................................................... 3 Introducción.................................................................................................................................................................... 4 Objetivo General ....................................................................................................................................................... 5 Objetivos Específicos .............................................................................................................................................. 5 CAPÍTULO 2. ASPECTOS METODOLÓGICOS ...................................................................................................... 6 Fuentes de información ......................................................................................................................................... 7 Población ..................................................................................................................................................................... 7 Tipo de muestra y muestreo ............................................................................................................................... 8 CAPÍTULO 3. ANÁLISIS E INTERPRETACIÓN DE LOS RESULTADOS................................................... 10 Prueba de proporciones de dos muestras ..................................................................................................... 1 Prueba ANOVA .......................................................................................................................................................... 3 Coeficiente de correlación de Spearman ........................................................................................................ 6 Aplicación de la Distribución Binomial a los datos observados en las encuestas ......................... 8 CAPÍTULO 4. CONCLUSIONES............................................................................................................................... 11 Conclusiones ........................................................................................................................................................... 12 Bibliografía .............................................................................................................................................................. 13 ANEXOS ..................................................................................................................................................................... 14 CAPÍTULO I. GENERALIDADES DE LA INVESTIGACIÓN Introducción El estudio estadístico es una rama de la matemática que ayuda a tomar decisiones según los datos que se presenten en el estudio realizado. No podemos hablar de la toma de decisiones a nivel social, económico y empresarial sin el estudio previo, y para ello es que necesitamos la estadística. El presente trabajo de investigación tiene como finalidad brindar un acercamiento en presentar los análisis estadísticos de diferentes tipos, a razón de mencionar algunos temas (Prueba ANOVA y Prueba de proporciones de dos muestras) entre otros, vistos en la clase de estadística 2, del segundo cuatrimestre del año 2020, cada uno con el fin no solo de demostrar los pasos a seguir en cada estudio, sino para detallar la importancia de la implementación de estos, para así lograr evidenciar los resultados que arroja, en cuanto a la hora de determinar el impacto que genera tal situación del estudio, que a su vez nos va permitir evaluar distintas situaciones de proceder desde una óptica de mejora, realizar un cambio o transformación, como lo es en este caso la educación del sector privado y público, o sea la estadística es de suma importancia por ejemplo para detallar un caso a nivel nacional y ver qué tipo de decisiones se podrían o se deberían de tomar y ejecutar, con base en los resultados obtenidos. Se presente reconocer como la desigualdad territorial en el acceso a la tecnología afecta negativamente la calidad y equidad de la educación en Costa Rica. Cada caso contendrá no solo un enunciado que presente los datos, sino la acción que se pretende impactar según el resultado que se propone ante los mismos. Asimismo, el presente trabajo poseerá paso por paso y el nombre de cada método utilizado para su estudio. Objetivo General Describir e interpretar inferencias mediante cálculos estadísticos sobre la influencia que tiene la brecha digital en el nivel de escolaridad alcanzado en las zonas urbanas y rurales Objetivos Específicos 1. Determinar cálculos estadísticos inferenciales mediante muestras aleatorias. 2. Hallar la incidencia en el acceso a internet en la educación de las zonas de planificación de Costa Rica. 3. Evidenciar la inequidad en acceso a internet y otras las coberturas en Costa Rica. CAPÍTULO 2. ASPECTOS METODOLÓGICOS Fuentes de información El Instituto Nacional de Estadística y Censos (INEC) es una institución autónoma del gobierno de Costa Rica, encargada de la producción y divulgación estadística en el país. El INEC como entidad coordinadora del quehacer estadístico nacional, mediante la Encuesta Nacional de Hogares (ENAHO) indaga las condiciones de las viviendas y servicios, con el fin de averiguar cuáles son las principales características sociodemográficas, nivel educativo, la situación del empleo y aseguramiento, así como los ingresos en los hogares, lo cual permitirá dar cuenta de los niveles de la pobreza y desigualdad en los que se encuentra el país. La producción estadística del INEC y sus servicios se sustenta en metodología estadística sólida, procesos estadísticos adecuados, es oportuna, confiable y accesible. Por lo anterior, en aras de obtener datos oportunos y confiables, como fuente primaria de información se utilizan los resultados obtenidos con la Encuesta Nacional de Hogares (ENAHO) realizada en el mes de julio del 2019 por el Instituto Nacional de Estadística y Censos (INEC). La encuesta se realiza mediante entrevistas personales a una muestra probabilística de viviendas distribuida en todo el país, e investiga características de esas viviendas, de los hogares y de las personas, para obtener información sobre las condiciones de vida de la población y que son la base para determinar los resultados del presente proyecto de investigación. Población El término “población” se refiere al conjunto de elementos que se quiere investigar, estos elementos pueden ser objetos, acontecimientos, situaciones o grupo de personas. En este sentido, la población seleccionada para realizar la Encuesta Nacional de Hogares (ENAHO) está definida como el conjunto de todas las viviendas individuales ocupadas y sus ocupantes residentes habituales, tanto del área urbana como del área rural de Costa Rica. Tipo de muestra y muestreo Los marcos muestrales de viviendas son los instrumentos utilizados para la selección de muestras de encuestas a viviendas. El INEC utiliza el llamado Marco de Áreas, que se caracteriza porque sus unidades son superficies geográficas con límites claramente definidos, y donde los hogares se encuentran asociados a las respectivas viviendas individuales ubicadas dentro de estas unidades; esto hace posible tener una medida muy aproximada de las probabilidades de selección de los hogares. El diseño muestral de la Encuesta Nacional de Hogares (ENAHO) considera como dominios de estudio el total país, zona urbana y rural, y las seis regiones de planificación. Para realizar la selección de la muestra inicialmente se realiza un muestreo estratificado, de tal manera que se divide la población por características geográficas en común y se conforman con el objetivo de que estén representadas en la muestra y así incrementar la precisión general de las estimaciones de la encuesta, y en una segunda etapa dentro de cada unidad se seleccionaron viviendas con probabilidades iguales de selección, mediante un muestreo sistemático con arranque aleatorio. Según se indica en el informe de Resultados Generales de la ENAHO 2019, se debe aclarar que la muestra inicialmente seleccionada no es igual a la muestra efectiva básicamente por dos razones: las viviendas cambian de actividad o desaparecen, o no se obtiene información de algunas viviendas de la muestra, es decir, los residentes de las viviendas se niegan a dar información o no pueden ser localizados durante el período de recolección de la encuesta. Instrumentos y técnicas utilizadas en la recopilación de datos La Encuesta Nacional de Hogares (ENAHO) utiliza tres cuestionarios, estos están asociados con la secuencia lógica de las preguntas y sus temas. Para efectos de esta investigación el documento que se utilizará corresponde al “Cuestionario Hogar”, el cual estudia la vivienda, el número de hogares dentro de ella y las personas que conforman cada hogar. Dentro de este se identifican seis grandes secciones, de los cuales tres serán los principales ejes de estudio y se indican a continuación: Vivienda y Servicios: El objetivo de esta sección es conocer las condiciones de la estructura física y el acceso a los servicios que tienen las personas residentes habituales de las viviendas seleccionadas. Por eso se estudian diferentes características de la vivienda, por ejemplo, los materiales de construcción y su estado actual, el abastecimiento y procedencia del agua, la tenencia y disponibilidad de servicios sanitarios, el equipamiento con electrodomésticos, el acceso a internet, entre otros. Sección A. Características Sociodemográficas: El estudio de las características sociodemográficas de una población permite conocer aspectos relacionados con la tipología de los hogares, la estructura etaria para hombres y mujeres, el estado conyugal y los patrones migratorios. Además, esta sección mide el nivel de escolaridad y las transferencias que reciben los hogares por medio de los programas sociales. La investigación de estas características facilita la identificación de grupos específicos para el diseño de política pública. Sección N. Módulo de Tecnologías de Información y Comunicación Este módulo propuesto tiene como objetivo principal, medir aspectos relacionados al acceso y uso de las tecnologías de información y comunicación (TIC) en la población de 5 años y más. De manera que se ofrezca el cumplimiento al grupo base de indicadores requeridos internacionalmente por la Unión Internacional de Telecomunicaciones (UIT) a nivel de vivienda y personas para el territorio nacional. CAPÍTULO 3. ANÁLISIS E INTERPRETACIÓN DE LOS RESULTADOS La Encuesta Nacional de Hogares (ENAHO) investiga diversos temas sociales que son fundamentales para el diseño y seguimiento de la política pública, entre los que destaca el nivel y características del ingreso de la población, la condición de pobreza y además se indaga sobre las características de la vivienda. En este apartado se realiza una breve descripción de los resultados generales que arroja la ENAHO 2019 relacionados con el acceso artefactos de tecnologías de información y comunicación en la vivienda y la asistencia a educación formal y nivel educativo de la población según zona y región de planificación. Cuadro 1. Costa Rica: Cantidad y porcentaje de viviendas que poseen diferentes TIC por zona según tendencia de TIC, julio 2019 Tenencia de TIC Zona Total Viviendas Urbana % Viviendas Rural % Viviendas % 1 578 161 100.0 1 142 766 100.0 435 395 100.0 1 573 230 99.7 1 141 772 99.9 431 458 99.1 480 204 30.4 392 830 34.4 87 374 20.1 1 517 994 96.2 1 104 277 96.6 413 717 95.0 35 509 2.3 26 151 2.3 9 358 2.1 1 073 299 68.0 737 598 64.5 335 701 77.1 444 695 28.2 366 679 32.1 78 016 17.9 13 925 0.9 12 466 1.1 1 459 0.3 741 165 47.0 604 714 52.9 136 451 31.3 262 783 16.7 229 913 20.1 32 870 7.5 1 362 554 86.3 1 020 305 89.3 342 249 78.6 Con televisor 1 532 023 97.1 1 121 867 98.2 410 156 94.2 Con televisión pagada 1 118 109 70.8 853 280 74.7 264 829 60.8 893 060 56.6 677 777 59.3 215 283 49.4 Total de viviendas en Costa Rica Con electricidad Con teléfono residencial Con teléfono celular Con teléfono residencial y sin teléfono celular Con teléfono celular y sin teléfono residencial Con teléfono residencial y con teléfono celular Con fax Con computadora Con tableta Con servicio de internet en la vivienda Con radio Fuente: INEC-Costa Rica. Encuesta Nacional de Hogares, 2019. Gráfico 1. Cantidad de viviendas que poseen diferentes TIC, por zona. 2019 1 020 305 604 714 342 249 229 913 136 451 32 870 Con servicio de internet en la vivienda Con computadora Urbana Con tableta Rural Fuente: Elaboración propia con datos de la ENAHO 2019, del INEC. A partir de los resultados, según la Encuesta Nacional de Hogares del 2019, un total de 1 362 554 familias cuentan con servicio de internet en la vivienda, de lo cual un 75% corresponde a la zona urbana y tan solo un 25% a la zona rural. Estas diferencias en el acceso a los recursos tecnológicos reflejan las desigualdades territoriales históricas del país, que se asocian al bajo desarrollo socioeconómico que históricamente ha caracterizado las zonas y en el contexto actual, profundizan las diferencias en el de acceso a la educación. Cuadro 2. Costa Rica: Población de 5 años o más por nivel de instrucción según región de planificación y sexo, julio 2019 Zona, región de planificación y sexo Total Nivel de instrucción Secundaria académica Primaria Secundaria técnica Educación superior Pregrado Posgrado y grado Sin instrucción Incompleta Completa Incompleta Completa Incompleta Completa 2 976 762 1 423 131 1 553 631 154 961 77 378 77 583 438 157 203 902 234 255 610 701 290 488 320 213 586 202 291 153 295 049 405 489 196 841 208 648 41 982 21 738 20 244 63 820 31 758 32 062 599 269 271 434 327 835 76 181 38 439 37 742 Chorotega Hombres Mujeres 361 906 180 045 181 861 24 846 13 164 11 682 68 118 33 675 34 443 75 607 40 116 35 491 74 602 40 990 33 612 53 772 25 919 27 853 6 732 3 395 3 337 4 895 2 399 2 496 49 672 18 744 30 928 3 564 1 545 2 019 Pacífico Central Hombres Mujeres 278 799 139 833 138 966 22 568 12 640 9 928 60 270 33 349 26 921 58 756 27 766 30 990 62 803 30 816 31 987 31 543 14 401 17 142 6 612 3 391 3 221 5 105 2 628 2 477 28 772 14 193 14 579 2 370 649 1 721 Brunca Hombres Mujeres 346 444 164 164 182 280 31 141 14 504 16 637 78 915 39 367 39 548 82 206 41 489 40 717 66 390 32 285 34 105 37 445 16 892 20 553 7 316 4 080 3 236 4 368 1 845 2 523 34 651 12 348 22 303 4 012 1 354 2 658 Huetar Caribe Hombres Mujeres 418 358 203 768 214 590 38 779 21 162 17 617 94 875 45 036 49 839 97 518 50 319 47 199 87 664 43 876 43 788 53 710 23 791 29 919 6 314 3 812 2 502 4 540 1 904 2 636 32 592 13 321 19 271 2 366 547 1 819 Huetar Norte Hombres Mujeres 384 251 191 484 192 767 42 342 22 501 19 841 97 810 48 492 49 318 88 019 46 820 41 199 75 495 37 285 38 210 39 642 17 814 21 828 6 378 3 343 3 035 4 598 2 008 2 590 27 008 11 471 15 537 2 959 1 750 1 209 Región de planificación Central Hombres Mujeres Fuente: INEC-Costa Rica. Encuesta Nacional de Hogares, 2019. Prueba de proporciones de dos muestras El analfabetismo se ha empezado a combatir en el país desde el momento en que la educación se declaró gratuita para todas las personas en Costa Rica, sin embargo, es de conocer que no todas las personas son no analfabetas, o no han tenido una educación académica como tal. Se quiere saber si en las mujeres costarricenses, existe alguna diferencia entre las que viven en zona rural o en zona urbana, para saber sí el no tener educación depende de donde viven, para empezar a mejorar la calidad educativa o las oportunidades a las mujeres en zonas rurales, si no es así es un problema a nivel nacional. Con esto y según los datos de la INEC se obtuvo que, de 1 569 200 mujeres de más de 15 años de zona urbana, 37 034 no han tenido instrucción académica en su vida, y de 534426 mujeres de más de 15 años de zona rural, 26447 no han tenido instrucción académica alguna. Con un nivel de significancia de 0,05, ¿se puede decir que existe una diferencia significativa entre la proporción de mujeres de más de 15 años que viven en zona rural y que no han tenido instrucción académica y las mujeres de 15 años que viven en zona urbana y que no han tenido instrucción académica? Paso 1: Planteo de la hipótesis nula. Para este caso la hipótesis nula es que las proporciones propuestas son iguales, la hipótesis alternativa es que estas sean diferentes H0: �1=�2 H1: �1≠�2 Paso 2: Nivel de significancia. Para este caso se toma un nivel de significancia de 0,05. Paso 3: Estadístico de la prueba. El estadístico sigue la distribución normal estándar y se siguen los pasos para pruebas de proporciones de dos muestras que provienen de poblaciones iguales. Paso 4: Regla de decisión. Con el nivel de significancia del paso 2, el valor crítico toma un valor de 1,96. Con este valor y el valor del paso 5 se determinará la decisión sobre la hipótesis nula. Como es de dos colas el valor debe de estar entre -1,96 y 1,96. Paso 5: Toma de decisión. 𝑋1 p1 = 𝑛1 = pc = z= 37 034 1 569 200 𝑋2 = 0,0236 p2 = 𝑛2 = 𝑋1 + 𝑋2 37 034 + 26 447 = 𝑛1 + 𝑛2 1 569 200 + 534 426 𝑝1 − 𝑝2 𝑝𝑐(1−𝑝𝑐) 𝑝𝑐(1−𝑝𝑐) √ + 𝑛1 𝑛2 = 26 447 534 426 = 0,0495 = 0,0302 0,0236− 0,0485 0,0302×(1−0,0302) 0,0302×(1−0,0302) + √ 534 426 1 569 200 = -91,87 Con estos valores obtenidos tenemos que z < -1,96. Con esto se determina que las proporciones son diferentes y se rechaza la hipótesis nula. Conclusión: Podemos determinar que las condiciones de las mujeres que viven en zona rural y urbana son diferentes. Prueba ANOVA Con el tema de educación igualmente, se estudiará las personas que no han terminado diferentes niveles de educación (Primaria, Secundaria Académica, Secundaria Técnica), con los datos de la Tabla 1 se hará el siguiente estudio. ¿Con los datos de la Tabla 1 se puede decir que existe un nivel de diferencia entre la cantidad de personas mayores de 15 años que no han terminado o están incompletos sus estudios? Con un nivel de significancia de 0,01. Cuadro 3. Datos de personas en Costa Rica que no han terminado grados académicos. Primaria Secundaria Académica Secundaria Incompleta Incompleta Incompleta 15 a 17 años 4 596 174 509 36 419 18 a 24 años 11 044 166 176 19 762 25 a 39 años 78 336 244 163 6 138 40 años y más 344 834 296 627 4 303 Edades Técnica Fuente: INEC-Costa Rica. Encuesta Nacional de Hogares, 2019. Paso 1: Planteo de la hipótesis. Para este caso la hipótesis nula es la igualdad de todas las medias de las personas que no han terminado sus estudios. La hipótesis alternativa determina que no todas las medias son iguales. H0: �1=�2=�3 H1: No todas las medias son iguales Paso 2: Nivel de significancia. El nivel de significancia para este caso de 0,01 Paso 3: Estadístico de la prueba. El estadístico de la prueba sigue la distribución F. Se seguirán los pasos para hacer una tabla Anova. Paso 4: Regla de decisión. Para determinar la veracidad de la hipótesis nula necesitamos el valor crítico que se determina por los grados de libertad. Los grados de libertad son: gl del numerador = k – 1 = 3 – 1 = 2 gl del denominador = 12 – 3 = 9 Con estos valores, obteneos el valor crítico de 8.02 obtenido de la tabla. Con el valor del paso 5 se tomará la decisión. Paso 5: Toma de decisión Variación total ẊG = ∑𝑥 𝑛 = 1 386 907 = 12 115 575,58 Diferencia entre dato – media global Primaria Incompleta Secundaria Académica Incompleta Secundaria Técnica Incompleta -110 979,58 58 933,42 -79 156,58 -104 531,58 50 600,42 -95 813,58 -37 239,58 128 587,42 -109 437,58 229 258,42 181 051,42 -111 272,58 Primaria Incompleta Secundaria Académica Incompleta Secundaria Técnica Incompleta 1,23 x 1010 3,47 x 109 6,27 x 109 1,09 x 1010 2,56 x 109 9,18 x 109 1,39 x 109 1,65 x 1010 1,20 x 1010 5,26 x 1010 3,28 x 1010 1,24 x 1010 Se elevan al cuadrado y se suman. SS = 17,237 x 1010 Variación aleatoria Ẋ(Primaria Completa) = 109 702,5 Ẋ(Secundaria Académica Incompleta) = 220 368,75 Ẋ(Secundaria Técnica Incompleta) = 16 655,5 Primaria Incompleta Secundaria Académica Incompleta Secundaria Técnica Incompleta -105 106,5 -45 859,75 19763,5 -98 658,5 -54 194,75 3106,5 -31 366,5 23 794,25 -10 517,5 235 131,5 76 258,25 -12 352,5 Primaria Incompleta Secundaria Académica Incompleta Secundaria Técnica Incompleta 1,10 x 1010 2,10 x 109 0,39 x 109 9,73 x 109 2,94 x 109 0,01 x 109 0,98 x 109 0,56 x 109 0,11 x 109 5,53 x 1010 5,82 x 109 0,15 x 109 Se elevan al cuadrado y se suman. SSE = 89.09 x 109 Tabla Anova Variación Suma de Grados de Media Cuadrados Libertad Cuadrática Tratamientos 8,32 x 1010 2 4,16 x 1010 Error 8,91 x 1010 9 0,99 x 1010 Total 17,237 x 1010 F 4,20 Con el valor F obtenido la hipótesis nula se acepta ya que F < Valor crítico. Por lo tanto, las tres medias de tratamiento son iguales. Coeficiente de correlación de Spearman Cuadro 3. Cálculo de coeficiente de correlación por rangos de Spearman Rango Diferencia Con servicio de Secundaria Con servicio de Secundaria internet en la académica internet en la académica vivienda completa vivienda completa Central 741 642 405 489 6 Chorotega 76 009 53 772 Pacífico Central 64 316 Brunca Región de Rango d d2 6 0 0 3 5 -2 4 31 543 1 1 0 0 81 138 37 445 4 2 2 4 Huetar Caribe 95 661 53 710 5 4 1 1 Huetar Norte 66 691 39 642 2 3 -1 1 planificación 10 Fuente: Elaboración propia con datos de la ENAHO 2019, del INEC. 6∑𝑑2 𝑟𝑠 = 1 − 𝑛(𝑛2 − 1) Donde: d2= 10 n= 6 𝑟𝑠 = 1 − 6(10) 6(62 − 1) 𝑟𝑠 = 0,714 Según los resultados de la Prueba de correlación de Spearman entre: el acceso al servicio de internet y el nivel académico completado en las regiones de planificación de Costa Rica, se tiene un coeficiente de correlación de 0,714, según la escala de Correlación, indica que se tiene una correlación positiva considerable. Hipótesis estadísticas H0: No existe una relación significativa entre el acceso al servicio de internet con el nivel académico completado. H1: Existe una relación significativa entre el acceso al servicio de internet con el nivel académico completado. Determinación de la zona de rechazo de la hipótesis nula Valor de significancia: α=0,05 Datos: n=6 Grados de libertad: 6-2=4 Valor crítico: Tabla=2,132 Regla de decisión: Si el valor estadístico es mayor que el valor crítico, se rechaza la H0. 𝑛−2 𝑡 = 𝑟𝑠 √ 1 − 𝑟22 𝑛−2 𝑡 = 𝑟𝑠 √ 1 − 𝑟22 6−2 𝑡 = 0,714√ 1 − 0,7142 6−2 𝑡 = 0,714√ 1 − 0,7142 𝑡 = 2,03 Siendo el valor estadístico mayor al valor crítico, existen razones suficientes para rechazar la hipótesis nula, por lo que podemos inferir que existe una relación significativa entre el acceso al servicio de internet con el nivel académico completado. Aplicación de la Distribución Binomial a los datos observados en las encuestas De acuerdo a la encuesta realizada a las mujeres y varones de 15 a 17 años en el cuadro 9 con problemas de acceso a la educación se buscará evaluar y ver cómo influye el acceso al sistema escolar en la educación de estos mismos aplicando la distribución binomial. Aplicación 1. En el caso de las encuestadas con problemas de acceso al sistema escolar son en un total 1596, de estos 1236 dejaron secundaria incompleta, 360 solamente completaron primaria. Ninguna llego a acabar la educación secundaria, y también se indica que ninguna llego a optar por secundaria técnica. De acuerdo a esto entonces 77.5% Educación Secundaria incompleta 22.5% Educación primeria completa 0% Secundaria completa, primaria incompleta y educación técnica. -Calcule la probabilidad tomando una muestra aleatoria de 10 mujeres, de que al menos solamente 1 tenga primaria completa. 1) 10C1 * (0.225)*(1-0.225)^(9) = 0.02269 R/ La probabilidad de que 1 de cada 10 mujeres solo haya acabado primaria es de 22.69% -Calcule la probabilidad tomando una muestra aleatoria de 10mujeres, de que al menos 8 tengan secundaria incompleta. 2) 10C8 * (0.775)^8 * (1-0.775)^2 = 0.29 R/ la probabilidad de que 8 de cada 10 mujeres tenga al menos secundaria incompleta es de 29% Se puede observar que a pesar de que el número de ensayos es mucho mayor en un caso de otro la probabilidad es bastante cercana, por lo que puede deducirse que el porcentaje de mujeres con secundaria incompleta es muy alto, y las mujeres con solamente primaria es un dato atípico. Aplicación 2. En el caso de los hombres encuestados con problemas de acceso al sistema escolar son un total de 804, de estos 244 tienen educación primaria incompleta, 275 primaria completa, y 285 con secundaria incompleta. 30,35% Educación primaria incompleta 34,2 % Educación primaria completa. 35,45% Educación secundaria incompleta. -Calcule la probabilidad tomando 10 hombres al azar, de que solamente 1 tenga primaria incompleta, de que 2 tengan primaria completa, y de que 3 tengan secundaria incompleta. Interprete los datos para ambas poblaciones como un conjunto encuestadas en base a las observaciones por separado. 1) 10C1 * (0,3035)*(1-0,303)^9 =0,117 R/ la probabilidad de que uno tenga incompleta es de 11,7% 2) 10C2 * (0,342)^2 * (1-0,342)^8 =0,185 R/ la probabilidad de que 2 tengan solo primaria completa es de 18,5% 3) 10C3 * (0,3545)^3 * (1-0,3545)^7 = 0.25 R/ la probabilidad de que 3 tengan secundaria incompleta es de 25% Por lo que puede observarse en los casos con dificultad de acceso a la educación tanto hombres como mujeres en su mayoría terminan la primaria, por lo que puede deducirse que hay una buena repartición de escuelas incluso alrededor de zonas con difícil acceso. Sin embargo, hay un porcentaje mucho mayor de hombres que no termina la primaria, este dato coincide con la gran diferencia de hombres que en el cuadro especifican que tiene que trabajar, o prefieren trabajar. Puede notarse una cantidad bastante grande, aproximadamente un tercio de estos dejaron la educación primaria y secundaria para trabajar. En el caso de la educación secundaria puede observarse que la mayoría cursaron tanto hombres como mujeres, pero ninguno la llego a finalizar, esto podría deberse a que estas zonas reclutan personal con niveles de educación que no requieren más allá de secundaria. También es notable que a pesar de que todas las mujeres llegaron a secundaria ninguna la concluyo y ninguna especifico que era por trabajo, de estas aproximadamente un 40% específico que era por matrimonio o embarazo o desinterés en avanzar la educación. Además de que el mayor porcentaje que indicaba que no podía pagar más educación en comparación con los hombres coincide exactamente con la diferencia de que ninguna indico dejar secundaria para trabajar. Véase cuadro 9. Estas observaciones indican que en los casos con dificultad de acceso a la educación la parte social o falta de planificación influyen grandemente y que la mayoría opta por abandonar la educación después de secundaria para formar familias rápidamente con un modelo tradicional. En el caso de la educación técnica resalta bastante el hecho que nadie ni siquiera llego a cursar la secundaria técnica por lo que podría deducirse aún más concretamente que hay un claro problema en por el cual personas con dificultad de acceso ni siquiera están teniendo la oportunidad de la educación secundaria técnica CAPÍTULO 4. CONCLUSIONES Conclusiones El factor educación es clave, pues las desigualdades en el acceso a la educación y particularmente en el acceso a la educación de calidad tienen un especial vínculo con la equidad o inequidad territorial. La investigación determina que una proporción importante de estudiantes tiene poca o nula conectividad y que afecta no solo a aquellos que viven en hogares de menor nivel socioeconómico, sino también en territorios fuera de la Región Central. Estas brechas en el acceso a los recursos tecnológicos reflejan las desigualdades territoriales históricas del país, asociadas al bajo desarrollo relativo y socioeconómico que ha caracterizado a las regiones de la periferia y en el contexto actual, profundizan las diferencias en el acceso a la educación. En efecto, los centros educacionales de zonas céntricas suelen tener mejores rendimientos en niveles escolares que aquellos de zonas alejadas del centro. El mismo ejemplo se repite cuando comparamos las unidades educativas urbanas con las rurales, siendo éstas últimas más desfavorecidas. Bibliografía 1. INEC. (2020). Instituto Nacional de Estadística y Censos. Recuperado el 04 de agosto de 2020: https://www.inec.cr/ 2. INEC. (2019). Encuesta Nacional de Hogares Julio 2019. Recuperado el 04 de agosto de 2020, de INEC, https://www.inec.go.cr/sites/default/files/documetos-biblioteca- virtual/reenaho2019.pdf 3. INEC. (2019). Artefactos de tecnologías de información y comunicación en la vivienda según zona y región de planificación, julio 2018 y julio 2019. Recuperado el 04 de agosto de 2020, de INEC, https://www.inec.cr/encuestas/encuesta-nacional-de-hogares 4. INEC. (2019). Asistencia a educación formal y nivel educativo de la población según zona y región de planificación, julio 2019. Recuperado el 04 de agosto de 2020, de INEC, https://www.inec.cr/encuestas/encuesta-nacional-de-hogares ANEXOS